Model of Vascular Desmoplastic Multispecies Tumor Growth

Abstract

We present a three-dimensional nonlinear tumor growth model composed of heterogeneous cell types in a multicomponent-multispecies system, including viable, dead, healthy host, and extracellular matrix (ECM) tissue species. The model includes the capability for abnormal ECM dynamics noted in tumor development, as exemplified by pancreatic ductal adenocarcinoma, including dense desmoplasia typically characterized by a significant increase of interstitial connective tissue. An elastic energy is implemented to provide elasticity to the connective tissue. Cancer-associated fibroblasts (myofibroblasts) are modeled as key contributors to this ECM remodeling. The tumor growth is driven by growth factors released by these stromal cells as well as by oxygen and glucose provided by blood vasculature which along with lymphatics are stimulated to proliferate in and around the tumor based on pro-angiogenic factors released by hypoxic tissue regions. Cellular metabolic processes are simulated, including respiration and glycolysis with lactate fermentation. The bicarbonate buffering system is included for cellular pH regulation. This model system may be of use to simulate the complex interactions between tumor and stromal cells as well as the associated ECM and vascular remodeling that typically characterize malignant cancers notorious for poor therapeutic response.

Graphical abstract

1. Introduction

Following the six hallmarks of cancer (Hanahan and Weinberg, 2000), carcinogenesis occurs when genetically defected cells acquire the ability to be self-sufficient in growth signals, insensitive to growth-inhibitory signals, have the ability to evade apoptosis, replicate with limitless potential, sustain angiogenesis, and ultimately invade surrounding tissue and metastasize. These acquired capabilities are supported by enabling characteristics (Hanahan and Weinberg, 2011) including the genomic instability in cancer cells (Hanahan and Weinberg, 2000; Lengauer et al., 1997; Luo et al., 2009; Negrini et al., 2010; Nowell, 1976) and tumor-promoting inflammation (Colotta et al., 2009), as well as reprograming of cellular energy metabolism and active evasion of immunosurveillance (Kroemer and Pouyssegur, 2008). The state of cancer cells is also characterized by the presence of DNA replication stress (Halazonetis et al., 2008), oxidative stress, mitotic stress, proteotoxic stress, and metabolic stress (Luo et al., 2009).

Genomic defects in a tumor cell alter its intrinsic cellular programs. Loss of cell cycle check control and programmed cell death mechanisms, along with modified differentiation and transformed metabolism, propel tumor cells to a hyper proliferating state. In the initial avascular growth phase, relying on diffusion of oxygen and nutrients from nearby existing blood vessels, tumor cells quickly outgrow the supply and reach a quiescent state with a hypoxic or necrotic core (Chaplain, 1996). In order to survive, hypoxic tumor cells upregulate an array of cytokines, growth factors, and proteases. The loss of appropriate balance in these molecules leads to the stimulation of new vessel growth, degradation of the extracellular matrix (ECM), and recruitment of immune cells. The resulting neovasculature provides additional oxygen and nutrients for the neoplastic growth. The destruction of normal ECM facilitates tumor angiogenesis and directed migration of invading tumor cells during metastasis. The infiltrating immune cells are subsequently coopted to promote tumorigenesis. Thus, advancing through the stages of normal, benign, malignant, and metastatic, cancer cells depend not only on changes inside the cell itself but also on what their environment is able to provide.

Since Paget’s seed-and-soil hypothesis (Paget, 1889) over a century ago, much has been understood about the importance of the tumor milieu on cancer growth and metastasis. A typical dynamic microenvironment in which tumors reside consists of cancer stem cells, highly proliferating neoplastic cells of different phenotypes, necrotic tumor cells, infiltrating innate and adaptive immune inflammatory cells, cancer-associated fibroblasts (CAF), ECM, blood vessels, endothelial cells (ECs), pericytes, host cells, and a variety of soluble molecules (de Visser and Coussens, 2006; Hanahan and Weinberg, 2000; Perez-Moreno, 2009; Tlsty and Coussens, 2006; Whiteside, 2008). The process of tumor progression is driven by the communication between the tumor cells and their surroundings. It is this tumor microenvironment that dictates the tumor progress from its unregulated neoplastic growth to eventual metastasis. An adequately and appropriately posed tumor model could be useful in predicting cancer behavior. Striving to mimic true biological aspects, we present here an attempt to model solid tumor growth with tumor-induced interactions in its heterogeneous milieu. The ultimate goal would be to predict tumor dynamics and treatment response so that good correspondence is achieved with in vivo or in situ tumor growth data.

Mathematical models of tumor growth have concentrated on simulating tumor behavior in response to certain stimuli in each of the stages of growth, including avascular and vascular conditions. These models generally fall into three categories: (i) continuum models (including single phase and multiphase/mixture mechanochemical approaches), (ii) discrete models, and (iii) hybrid models representing a combination of continuum and discrete approaches. In continuum models (see recent reviews (Andasari et al., 2011; Bachmann et al., 2012; Byrne, 2010; Chaplain, 2011; Cristini and Lowengrub, 2010; Deisboeck et al., 2011; Edelman et al., 2010; Frieboes et al., 2011; Kreeger and Lauffenburger, 2010; Lowengrub et al., 2010; Michor et al., 2011; Oden et al., 2015; Osborne et al., 2010; Preziosi and Tosin, 2009a; Rejniak and McCawley, 2010; Rejniak and Anderson, 2011; Roose et al., 2007; Tracqui, 2009; Vineis et al., 2010) and references therein), cell populations and molecular species that influence the cell cycle events are treated as continuous variables. These models typically make use of ODE or PDE approaches to describe an advection-diffusion-reaction system. For models which involve several cell types, tracking of the interfaces is necessary and may be accomplished using the level set method. Continuum multiphase/mixture mechanochemical models incorporate mechanical and chemical interactions between phases (cell types or species) (see (Araujo and McElwain, 2004; Astanin and Preziosi, 2008; Byrne et al., 2006; Graziano and Preziosi, 2007; Hatzikirou et al., 2005; Lowengrub et al., 2010; Preziosi and Tosin, 2009a; Quaranta et al., 2005; Roose et al., 2007; Tracqui, 2009) and associated references). Typical models of this approach introduce a stress tensor, pressure, and velocity for each phase by enforcing the mass, momentum, and energy balances (Ambrosi et al., 2002; Araujo and McElwain, 2005a; Araujo and McElwain, 2005b; Astanin and Preziosi, 2008; Bresch et al., 2010; Breward et al., 2002; Breward et al., 2003; Byrne and Preziosi, 2003; Byrne et al., 2003; Galle et al., 2009; Graziano and Preziosi, 2007; Klika, 2014; Preziosi and Tosin, 2009b; Preziosi and Vitale, 2011; Preziosi et al., 2010; Sciume et al., 2013). Related to the continuum multicomponent mixture models is the diffuse interface approach (Chen et al., 2014; Hawkins-Daarud et al., 2012; Oden et al., 2010). The square gradient theory can be used in this approach to describe the smooth transition within a thin interfacial region. The gradient contributes to the Helmholtz free energy, from which the component velocities, pressures, and diffusive terms are derived (Chen and Lowengrub, 2014; Wise et al., 2008). Continuum single- or multi-phase models that consider the effects of cell-cell and/or cell-ECM adhesion include among others (Ambrosi and Preziosi, 2009; Bearer et al., 2009; Chatelain Clément et al., 2011; Escher and Matioc, 2013; Frieboes et al., 2007; Frieboes et al., 2013; Kuusela and Alt, 2009), while in (Arduino and Preziosi, 2015; Gerisch and Chaplain, 2008; Preziosi and Tosin, 2009b; Psiuk-Maksymowicz, 2013; Sciume et al., 2014a; Sciume et al., 2014b; Wu et al., 2013), the ECM is represented as one of the key components of the tumoral tissue.

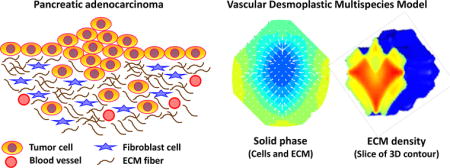
In this paper, we present a tumor growth model consisting of heterogeneous cell types in a multicomponent-multispecies system. Taken into consideration are the effects of metabolic molecules, tumorigenic factors, and desmoplastic reaction, coupled with tumor-induced angiogenesis. Since tumors may contain as many as 10⁵ to 10⁷ cells per mm³ (Fang et al., 2000; Fidler and Hart, 1982; Holmgren et al., 1995; Zheng et al., 2005), a continuum scale is thus appropriate to model tumor growth. Starting from a mixture system similar to Frieboes et al. (2010), we implement the diffuse interface approach, as derived in Wise et al. (2008), where thermodynamically consistent Darcy velocities and Fickian diffusive terms are determined from the energy variation. The square gradient model is used in the Helmholtz free energy equation (Cahn and Hilliard, 1958; Rowlinson, 1979; Yang et al., 1976) to describe interfaces arising from the adhesive properties of different cell components. Unlike Frieboes et al. (2010), continuous blood and lymphatic vessel densities here are modified from cell fluxes employed in Anderson and Chaplain (1998), Chaplain (1996), and Mantzaris et al. (2004), with different sprout initiation conditions included (Levine et al., 2000; Levine et al., 2001a; Levine et al., 2001b). We model the ECM as its own species to interact with the tumor cell species, and include an elastic energy that provides elasticity to the connective tissue. Stromal cells representing cancer-associated fibroblasts are modeled as principal contributors to the ECM remodeling. The stromal cells further support the tumor growth through the release of growth factors. For the tumor cells, we include the cellular metabolic processes of respiration and glycolysis with lactate fermentation, and a bicarbonate buffering system to simulate the cellular regulation of pH. Interactions between angiogenic factors, proteolytic enzymes, and ECM components described by Levine et al. (2001b) are also incorporated. Nutrients and waste products from cell metabolism are governed by fluxes and consumption/production rates modified from Casciari et al. (1992). We note that previous work has evaluated the important roles of glucose metabolism and microenvironmental acidity in tumor progression, including (Smallbone et al., 2008; Smallbone et al., 2005; Smallbone et al., 2007).

This paper develops as follows. An overview of relevant biology is outlined in Section 2 where the scope of the model biological hypotheses is described in detail. All components considered as well as interactions between each component are discussed. In Section 3, the model formulation is described, including the derivation of velocities, fluxes, and source terms. Governing equations are presented and the system of nonlinear partial differential equations is nondimensionalized. Numerical schemes for the solution are discussed in Section 4. In Section 5, simulation results of three-dimensional tumor cases are delivered and discussed. Finally, conclusions and the direction of future work are described in Section 6.

2. Biological Background and Hypotheses

The tumor system is a complex domain that includes heterogeneous cell types and stroma maintained by a vast interplay of signaling pathways. Enumerated in this section are key components on which we focused in modeling the neoplastic growth in the tumor microenvironment.

2.1. Tumor and Host Cells

Whether tumors originate from a single or multiple transformed cells, the resulting cancer cells from neoplastic progression within tumors display diverse phenotypes that may have varying proliferation and metastatic potentials (Fidler and Hart, 1982; Gupta et al., 2011; Heppner, 1984; Lobo et al., 2007). Although tumor heterogeneity is generally believed to be an outcome of genomic instability and selectivity (Grady and Markowitz, 2000; Heng et al., 2006), cancer stem-like cells (CSC) have been shown to play a role as well (Campbell and Polyak, 2007; Dontu et al., 2003; Marotta and Polyak, 2009). Multiple types of CSCs (Marotta and Polyak, 2009) may potentially arise from normal stem cells or transit-amplifying progenitor cells with oncogenic mutations (Clarke and Fuller, 2006; Lobo et al., 2007). Supported and protected by the CSC niche (Borovski et al., 2011), these stem-cell-like phenotypes retain their abilities to self-renew and differentiate (Clarke et al., 2006; Lobo et al., 2007), subsequently driving the tumor growth and metastasis (Borovski et al., 2011; Clarke and Fuller, 2006; Lobo et al., 2007; Marotta and Polyak, 2009). Cancer is also genetically related to autophagy malfunctions, a normally regulated cellular catabolic response to stress and nutrients deficiency in order to maintain homeostasis and facilitate cell survival (see refs (Kimmelman, 2011; Mathew et al., 2007; Mizushima et al., 2008; White, 2012; White et al., 2010)), which is cytoprotective and contributes to the survival of cancer cells in low nutrient environment and their resistance to anticancer treatments.

In this study, we make the simplifying assumption that there is only one viable tumor cell component, one dead tumor cell component, and a healthy host cell component: original viable phenotype (V), dead/necrotic tumor cell (D), and healthy host cell (H). Viable tumor species may undergo mitosis, apoptosis, and necrosis, whereas host cells are assumed to be homeostatic. Viable tumor species can also derive molecules like growth factors (refer to Section 2.5), angiogenic factors (Section 2.6), and matrix degrading enzymes (Section 2.7).

2.2. Stroma

In addition to the tumor cells, host cells, and infiltrating immune cells, a neoplastic tissue environment also consists of other resident cells such as fibroblasts and vascular cells that constitute the local blood and lymphatic vessels, ECM, interstitial fluid, as well as molecules secreted by cells. Among these secretions are ECM components, growth factors, cytokines, chemokines, proteases, and various metabolites. Note that stroma defined here encompasses all components stated above, excluding the tumor, host, and immune cells (which are accounted for in previous sections).

The ECM is a vital framework that plays a monumental role in tumor progression. In addition to providing cells with a mechanical scaffold for adhesion and migration, ECM also interacts with cells to directly or indirectly regulate developmental processes and control cellular activities such as cell differentiation, proliferation, and apoptosis (Aumailley and Gayraud, 1998).

Under homeostatic conditions, fibroblasts and vascular cells synthesize the appropriate amounts of ECM components (Bosman and Stamenkovic, 2003; Kalluri, 2003). Composition of ECM may vary considerably depending on the type of tissue and the location within the tissue. Furthermore, it may fluctuate to adapt to varying signals during normal developmental processes as well as pathological processes (Tlsty and Coussens, 2006). In general, the constitutive ECM components of most tissues include both fibrillar and nonfibrillar collagens, noncollagenous glycoproteins, and proteoglycans, which share common domains but have different physical and biochemical properties (Aumailley and Gayraud, 1998; Bosman and Stamenkovic, 2003; Oezbek et al., 2010; Whittaker et al., 2006). These components constitute the basement membrane and the interstitial matrix. Basement membrane is more compact and less porous than the interstitial matrix. It also consists of epithelial, endothelial, and stromal cells, keeping epithelium and endothelium separated from the stroma, and providing a scaffold for cell adhesion (Kalluri, 2003; Lu et al., 2012). Interstitial matrix is highly charged and hydrated. Rich in fibrillar collagens, proteoglycans, and various glycoproteins, it is also a main factor in the tensile strength of tissues (Egeblad et al., 2010).

The most abundant structural components of ECM are collagens, which have a propensity to form highly organized polymers (Aumailley and Gayraud, 1998). While the major component of basement membranes is collagen IV (Aumailley and Gayraud, 1998), roughly 80–90% of all collagenous proteins in soft tissues are type I collagen (Tlsty and Coussens, 2006). Type I collagen can release diffusible signaling molecules upon breakdown (Aumailley and Gayraud, 1998). It belongs to an ECM protein family that is crucial in maintaining the structural integrity of organs and tissues, and contributes to regulations of cell phenotype, polarity, survival, and migration (Vuorio and Decrombrugghe, 1990). Several classes of proteoglycans having various sizes and protein cores also constitute to the ECM. Proteoglycans function as a joint between various collagenous and glycoprotein networks by binding to other ECM molecules, thus regulating the structural arrangement and stabilizing the ECM architecture (Aumailley and Gayraud, 1998). Other than collagens and proteoglycans, noncollagenous glycoproteins also make up a prominent meshwork of the ECM. One of the most studied glycoproteins in the interstitial connective tissue is fibronectin. Fibronectins are known to initiate matrix assembly and form fibrils, but the polymerization is cell dependent and direct interactions with cell surface integrin receptors are required (Kadler et al., 2008; Singh et al., 2010). Embedded between endothelial and perivascular cells perivascular cells (Astrof and Hynes, 2009), it has also been shown to promote cell adhesion (Pierschbacher and Ruoslahti, 1984; Pierschbacher et al., 1984) and blood vessel development.

The diverse structural, biochemical, and biomechanical functions of the ECM components contribute to the regulation of essential cell behavior (Lu et al., 2012). The ECM provides cells with contextual biological information and a mechanical scaffold to respond appropriately following the onset of certain stimuli (Bissell et al., 2002; Howe et al., 1998; Weaver et al., 2002). Its physical features, such as rigidity, porosity, spatial arrangement, and orientation, allow it to support tissue architecture and integrity (Lu et al., 2012). The ECM is also a highly charged protein network that can directly initiate signaling events (Hynes, 2009; Lu et al., 2011), bind to a wide range of growth factors (Hynes, 2009), and transmit biochemical signals via cell-surface adhesion receptors (Hynes, 2002), thus controlling the accessibility, limiting the diffusive range, and dictating the signaling direction of ligands to their cognate receptors (Norton et al., 2005). Biomechanically, the elasticity of ECM governs how external forces are perceived by a cell (Gehler et al., 2009; Lopez et al., 2008; Paszek et al., 2005), guiding cellular behavior in response to environmental changes (DuFort et al., 2011; Fernandez-Gonzalez et al., 2009; Koelsch et al., 2007; Montell, 2008; Pouille et al., 2009; Solon et al., 2009), leading to the determination of cell differentiation and tissue function (Engler et al., 2006; Gilbert et al., 2010; Lutolf et al., 2009).

While ECM remodeling with a tightly regulated balance may be essential for maintaining tissue integrity (Bosman and Stamenkovic, 2003; Kalluri, 2003; Ruiter et al., 2002), abnormal ECM dynamics have been seen in tumor development (Bergers and Coussens, 2000; Cox and Erler, 2011; Egeblad and Werb, 2002; van Kempen et al., 2003). For instance, pancreatic cancer, especially pancreatic ductal adenocarcinoma (Pandol et al., 2009), exhibits dense desmoplastic reaction which is identified by a significant increase of interstitial connective tissue (Gress et al., 1995). Cancer-associated fibroblasts (CAFs, or myofibroblasts) are the main contributors of the ECM remodeling enzymes (Bhowmick et al., 2004; Orimo et al., 2005) in tumor tissues and are responsible for the synthesis, deposition, and remodeling of the ECM (Aboussekhra, 2011; Liu et al., 2011; Nakagawa et al., 2004; Östman and Augsten, 2009; Rasanen and Vaheri, 2010; Sirica et al., 2011) (refer to Section 2.4). To sustain neoplastic growth, it is essential for solid tumors to coopt fibroblasts, inflammatory, and vascular cells to upset the balance between ECM synthesis and degradation (Ruiter et al., 2002). Perturbation to the control mechanisms disorganizes the ECM and changes its architecture (Clarijs et al., 2003), facilitating oncogenic transformations (Levental et al., 2009) and upregulating signals that can promote cell survival and proliferation (Paszek et al., 2005; Wozniak et al., 2003). Deregulation of ECM modeling may also lead to apoptotic evasion due to the antiapoptotic effects exerted by fragments of various ECM components (Mott and Werb, 2004).

Another main component of the stroma is interstitial fluid. Increased peritumor interstitial fluid convection (Dafni et al., 2002) and higher lymphatic drainage to the sentinel lymph node (Harrell et al., 2007; Proulx et al., 2010) have been reported, suggesting an increased in interstitial flow within the tumor microenvironment. The hypoxia resulting from rapidly growing tumor fuses atypical angiogenesis, generating leaky tumor vessels that cause the accumulation of macromolecules in the neoplastic tissue. This condition, coupled with the mechanical stress from ECM remodeling (DuFort et al., 2011; Xu et al., 2009), leads to increased interstitial fluid pressure (IFP) within the tumor, ranging from 10–40 mmHg (Fukumura and Jain, 2007; Heldin et al., 2004). Tumor IFP may reach the levels of capillary pressure (Boucher et al., 1996) while normal tissue exhibits pressures ranging from −2 to 0 mmHg (Wiig, 1990).

In our model, stroma is assumed to be made up mainly by interstitial fluid (W) and the interstitial matrix (E). Here, we do not differentiate between various ECM components. Their secretions by viable cancer cells (V), ECs (B), LECs (L), and especially by myofibroblastic cells (F) are modeled. The decay of ECM involves proteolytic reactions with matrix degrading enzymes (refer to Section 2.7). Since ECM macromolecules diffuse very slowly (Levine et al., 2001b), we assume that the individual diffusive flux of various macromolecules within ECM are negligible. In our model, within the ECM component, we track the blood and lymphatic vessel densities (refer to Section 2.3), myofibroblastic cell density (Section 2.4). Concentrations of growth factors (Section 2.5), cytokines (Section 2.6), proteases (Section 2.7), and metabolites (Section 2.8) are also monitored within the interstitial fluid phase.

2.3. Blood and Lymphatic Vessels

According to Kerbel (2000), the term “tumor angiogenesis” was coined by Shubik in 1968 (Greenblatt and Shubi, 1968). From studies done by other investigators (Algire and Legallais, 1947; Algire et al., 1945; Greenblatt and Shubi, 1968; Ide et al., 1939; Warren and Shubik, 1966) and his own (Folkman, 1970; Folkman, 1972; Folkman, 1974; Folkman, 1976; Folkman and Gimbrone, 1971; Folkman et al., 1963; Folkman et al., 1966; Folkman et al., 1971), Folkman first hypothesized in 1971 that tumor growth is angiogenesis dependent and that angiogenesis could be a relevant target for tumor therapy. He suggested that tumor cells may produce a diffusible chemical signal to switch ECs from a resting state to a rapid growth phase, which in turns aids the otherwise diffusion-limited dormant tumor mass to expand relentlessly. These theories are now widely accepted with the discoveries of pro-angiogenic molecules, generally known as Tumor Angiogenic Factors (TAFs) (see Section 2.6).

Avascular tumor outgrowth is limited to 1–3 mm in diameter (Folkman et al., 1966; Macklin et al., 2009; Marmé and Fusenig, 2007). To sustain anabolic growth, tumor cells must recruit new blood vessels from the nearby pre-existing vasculature network. The first step of angiogenesis involves rearrangements and recruitments of ECs from the parental vessel to form new sprouts (Cliff, 1963; Paweletz and Knierim, 1989; Schoefl, 1963; Schoefl and Majno, 1964; Warren, 1970). The ECs also begin to secrete matrix degrading enzymes (see Section 2.7) to break down the surrounding ECM, making chemotactic migration up signal gradient possible (Mantzaris et al., 2004; Patel and Nagl, 2010). Proliferation of ECs occurs later, about 36 – 48 hours after the initial response (Sholley et al., 1977; Sholley et al., 1984; Warren et al., 1972), near the base of the sprout (Cliff, 1963; Schoefl, 1963; Schoefl and Majno, 1964). Following the development of lumina within solid strands of ECs formed in the ECM, neighboring sprouts join to form loops and enable circulation (Paweletz and Knierim, 1989).

Vascular tissue is composed of two cell types that interact with each other. While ECs line the inner wall of a vessel, pericytes (also known as Rouget cells, mural cells, or referred to as vascular smooth muscle cells VSMCs) embrace the abluminal endothelium wall and are embedded within the basement membrane. Microvessels are mainly consisted of ECs surrounded by a basal lamina loosely wrapped by single pericytes. Larger vessels are coated abluminally with multiple layers of smooth muscle cells and surrounded by collagenous fibers (Cleaver and Melton, 2003). On top of functioning as a scaffold, pericytes also communicate with ECs via gap junctions and adhesion plaques (Rucker et al., 2000). The cell-cell contact mechanisms may also be crucial in vessel maintenance and modulation of EC growth by pericytes (Orlidge and Damore, 1987).

In addition to angiogenesis, tumors also drive lymphangiogenesis in their microenvironment (Swartz and Lund, 2012). In many human tumors, increased lymphatic vessel density, along with high expressions of lymphangiogenic growth factors (refer to Section 2.8), are correlated with poor prognosis, invasion, and metastasis (Mumprecht and Detmar, 2009; Skobe et al., 2001; Tammela and Alitalo, 2010). Cancer cells are thought to first spread to a sentinel tumor-draining lymph node by recruiting lymphatic vessels and entering local lymphatic circulation (Swartz and Lund, 2012). From the lymphatic system, the malignant cells are transported to the blood circulation and subsequently spread via blood vessels to distal organs (Fujisawa et al., 1995; Taubert et al., 2004; Weiss and Ward, 1987).

Lymphatic flow plays an important role in circulation. Extravasated plasma leaking from blood capillaries, together with macromolecules and leukocytes, make their way through the interstitium and drains into local lymphatic vessels. The physiological function of lymphatic networks is to collect the lymph fluid at regional lymph nodes for immune surveillance and transfer them to the blood circulation (Pepper and Skobe, 2003; Stacker et al., 2002; Witte and Witte, 1987). Lymph flow from tumors has also been shown to be elevated (Dafni et al., 2002; Harrell et al., 2007) and increased lymph drainage has been correlated positively with metastasis (Pathak et al., 2006).

Tumors may go through a phase of lymphangiogenic switch. Similar to the angiogenic switch, it is likely to involve the over production of lymphangiogenic growth factors and downregulation of relevant inhibitors (Cao, 2005). A range of lymphangiogenic factors can be produced by tumor, inflammatory, and stromal cells (Cao et al., 2004; Chang et al., 2004; Veikkola and Alitalo, 2002), reflecting the presence of complex processes comparable to those involved in angiogenesis. Lymphatic Microvessels consist of an irregular wider lumen, contained by a single thin layer of overlapping non-fenestrated lymphatic endothelial cells (LECs), and either lack or have an incomplete basement membrane (Leak, 1971; Saharinen et al., 2004). The lymphatic capillaries are tethered to the ECM to ensure the patency of the vessels, and the capillary wall also exhibits valve-like structures that facilitate the uptake of fluid (Saharinen et al., 2004). Microvasculature found within a tumor environment is usually disorganized and leaky. Not surprisingly, studies found that peritumoral and intratumoral lymphatic microvessels are also disorganized and lack drainage function (Isaka et al., 2004; Padera et al., 2002). This structural irregularity might contribute to their susceptibility to invading malignant cells (Kim et al., 1988).

In our model, densities of blood (B_n) and lymphatic (L_n) vessels are tracked, represented by their respective endothelial cells, ECs and LECs. They secrete factors (refer to Section 2.5) that promote the growth of tumor cells and produce ECM macromolecules (Section 2.2). They also generate and uptake tumor angiogenic and lymphangiogenic factors (Section 2.6) as well as produce proteolytic enzymes (Section 2.7). The densities of these vessels also affect the supply of nutrients and the clearing of waste products (Section 2.8) within the tumor tissue.

2.4. Myofibroblastic Cells

It is well established that myofibroblasts play a vital role in wound healing and pathological ECM remodeling. In addition, the protagonistic involvement of myofibroblasts in the stroma reaction of epithelial tumors may stimulate cancer cell invasion (De Wever and Mareel, 2003).

Depending of the type of tissue and organ, myofibroblastic cells found responsible for the desmoplastic reaction in tumor stroma may come from a heterogeneous origin including residential fibroblasts or mesenchymal stem cells, vascular smooth muscle cells, pericytes, ECs, epithelial tumor cells via epithelial-mesenchymal transition, circulating fibrocytes or bone marrow–derived mesenchymal stem cells, adipocytes, hepatic stellate cells, and pancreatic stellate cells (PSCs) (De Wever et al., 2008; Hinz et al., 2007; Hinz et al., 2012; Östman and Augsten, 2009).

Under normal conditions in intact tissue, crosslinked ECM stress-shields fibroblastic cells, which produce little ECM and show few to no actin-associated cell-cell and cell-matrix contacts (Tomasek et al., 2002). After an event of tissue injury where the continuous remodeling of ECM disrupts the protective mechanical environment (Tomasek et al., 2002), or via coercion by malignant tumor cells, these fibroblastic cells undergo some phenotype changes and become myofibroblastic, the activated state. Myofibroblasts regulate connective tissue remodeling by synthesizing ECM components (Hinz, 2007), mediated by cytokines produced by inflammatory, resident (Werner and Grose, 2003), or malignant epithelial cells (De Wever and Mareel, 2003), and by exerting traction forces through their stress fibers (Tomasek et al., 2002) reminiscent of the contractile filaments on smooth muscle cells. In fact, the expression of α–smooth muscle actin (α–SMA) has been commonly used as a molecular marker for myofibroblast differentiation.

There are two stages to the formation of myofibroblasts. When fibroblasts experience mechanical tension, they acquire the proto-myofibroblast phenotype capable of generating contractile force, forming cytoplasmic actin-containing stress fibers that meet at fibronexus adhesion complexes, as well as expressing and organizing cellular fibronectin with ED-A splice variant at cell surface (Tomasek et al., 2002). In addition to extracellular stress, platelet-derived growth factor (PDGF, refer to Section 2.5) appears to be important in proto-myofibroblast formation (Lindahl and Betsholtz, 1998; Martin, 1997), where the absence of PDGF-A results in the lack of proto-myofibroblasts (Boström et al., 1996). Under persistent mechanical stress and the presence of both transforming growth factor–β1 (TGF–β1, refer to Section 2.5) and ED-A fibronectin (Desmouliere et al., 1993; Hinz et al., 2001; Serini et al., 1998), proto-myofibroblasts can further develop into differentiated myofibroblasts, distinguishable by their elevated ED-A fibronectin expression, amplified stress fibers–fibronexus assembly and complexity (Dugina et al., 2001; Vaughan et al., 2000), and most identifiably, their expression of α–SMA. In a tumor environment, myofibroblast differentiation is also induced by oxidative stress caused by reactive oxygen species (Toullec et al., 2010). After the extracellular tension has been resolved, as occurs after an event of tissue repair, the stress release leads to myofibroblast apoptosis (Grinnell et al., 1999).

CAFs also produce various soluble paracrine growth factors (refer to Section 2.5), such as epithelial growth factor, hepatocyte growth factor, or transforming growth factor-β (Kalluri and Zeisberg, 2006). These tumor-promoting growth factors are known to regulate cell proliferation, morphology, survival, and death (Tlsty and Coussens, 2006). Persistent DNA damage found in human precancerous lesions (Gorgoulis et al., 2005) and during the early stages of human tumorigenesis (Bartkova et al., 2005) has been reported to result in enhanced secretion of IL-6 and IL-8 by fibroblasts (Rodier et al., 2009). CAFs are also found to increase their secretion of cytokines and chemokines, including COX-2, CXCL1, CXCL2, IL–1β, IL-6, and CXCL14 (Augsten et al., 2009; Erez et al., 2010). Vascular endothelial growth factor (Dong et al., 2004) and fibroblast growth factor (Pietras et al., 2008) derived from CAFs are found to be crucial for tumor angiogenesis. A study with breast CAFs showed that their secretion of CXCL12 led to the recruitment of bone marrow-derived endothelial precursor cells into the tumor site (Orimo et al., 2005). In addition, CAFs are also able to buffer the acidity generated by tumor cells (Koukourakis et al., 2006), and most importantly, have a direct effect in promoting metastasis (Karnoub et al., 2007). The proliferation rate and taxis potential of activated PSCs, which are found in area of fibrosis and dispersed throughout the pancreatic tumor (Vonlaufen et al., 2008), have been shown to be upregulated by PDGF. Activated PSCs upregulate their production of ECM degrading enzymes (MMPs, refer to Section 2.7) and their inhibitors during pancreatic tissue remodeling (Phillips et al., 2003). Fibrosis by myofibroblastic cells is also induced by a hypoxic environment (Masamune et al., 2008). The behavior active PSCs exhibit and effects these cells exert in a tumor environment are similar to those of CAFs (see reviews (Apte and Wilson, 2012; Omary et al., 2007)).

Here, we neither distinguish between proto-myofibroblast and differentiated myofibroblast, nor the origins and types of myofibroblastic cells. All myofibroblastic cells are grouped under one species (F). Proliferation and migration of the myofibroblastic species are induced by tumor growth factors (Section 2.5). Myofibroblastic species in our model produces ECM (Section 2.2), tumor growth factors (Section 2.5), tumor angiogenic factors (Section 2.6), and upregulate their secretion of MDEs (Section 2.7). The species F is assumed to migrate towards sites of tumor, indicated by the presence of tumor growth factors. Their secretion of ECM macromolecules in the model is also set to be hypoxia induced.

2.5. Tumor Growth Factors and Growth Hormones

As one of the hallmarks, cancer can acquire the capability to sustain proliferation signaling which may be achieved in several ways (Hynes and MacDonald, 2009; Lemmon and Schlessinger, 2010; Perona, 2006; Witsch et al., 2010). Cancer cells can produce growth factors, and in an autocrine manner, respond by expressing their cognate receptors themselves. They may also signal stromal cells to secrete various paracrine mitogenic factors (Bhowmick et al., 2004; Cheng et al., 2008). High levels of receptor proteins as well as receptor molecules with altered structures may be expressed at the cancer cell surface, raising their responsiveness to growth factors (Hanahan and Weinberg, 2011).

In addition, cancer cells can avoid negative regulation of cell proliferation and evade apoptosis. Several families of growth factors can stimulate tumor cell proliferation and survival, including the epithelial growth factor (EGF) family, platelet-derived growth factor (PDGF), the insulin-like growth factor (IGF) family, hepatocyte growth factor (HGF), the fibroblast growth factor (FGF) family, and the transforming growth factor-β (TGF-β) family (Bhowmick et al., 2004; Lewis and Pollard, 2006; Siveen and Kuttan, 2009). Among these factors, HGF, EGF, TGF-α, FGF-2, FGF-7 (or keratinocyte growth factor, KGF), and FGF-10 are known to increase proliferation of tumor cells, while IGF-1, IGF-2, TGF-β1, TGF-β2, and TGF-β3 act as tumor cell mitogens and apoptosis inhibitors (Bhowmick et al., 2004). While CAFs are capable of secreting most of these growth factors, a number of them, such as EGF, PDGF, TGF-β1, and FGF-2, are also expressed by TAMs and are upregulated under hypoxic conditions (Goswami et al., 2005; Lewis and Murdoch, 2005; Osullivan et al., 1993; White et al., 2004).

EGF receptor (EGFR) belongs to the polypeptide growth factor receptor tyrosine kinase superfamily and its ligands belong to the EGF family, including EGF and TGF-α (Hynes and MacDonald, 2009; Tang et al., 1997). Elevated levels of EGFR and TGF-α have been implicated in malignant glioma and in the development of other solid tumors (Gullick, 1991; Holbro and Hynes, 2004; Nister et al., 1988; Schlegel et al., 1990; Yung et al., 1990), reflecting their growth-stimulatory functions involved in the carcinogenic process. In fact, studies have indicated that they are involved in a key autocrine loop in sustaining proliferation of human tumors (Sporn and Todaro, 1980; Tang et al., 1997), leading to unregulated neoplastic growth. In addition to production by fibroblasts, TGF-α is also expressed constitutively by cancer cells (Tang et al., 1997) and EGF is synthesized by TAMs in response to tumor-derived colony stimulating factor-1 (CSF-1) (Lewis and Pollard, 2006).

First isolated from platelets, PDGF was later found to also come from other cell types. Having mitogenic activity in connective tissue and glial cells, it is essential in wound healing and directs the chemotactic movements of fibroblasts, muscle cells, neutrophils, and monocytes (Perona, 2006). PDGF expressed by malignant skin cells may induce fibroblasts to express FGF-7 (Brauchle et al., 1994), which stimulates the proliferation of epithelial cells, leading to enhanced carcinogenesis (Yan et al., 1992).

The IGF family includes the polypeptides IGF-1 and IGF-2. Synthesized in the liver and are abundant in human infants, both IGFs and their receptors hold a key role in the regulation of malignant cell proliferation, inhibition of apoptosis, and tumor transformation (Perona, 2006). HGF is a stroma-derived paracrine growth factor (Bhowmick et al., 2004) predominantly produced by fibroblasts. However, its cognate receptor, c-Met, is mainly expressed by epithelia (Nakamura et al., 1997). Commonly observed in many cancers, the overexpression of c-Met may be caused by ligand-independent activation (Michieli et al., 2004) or increased sensitivity to physiological HGF levels (Pennacchietti et al., 2003).

Members of the TGF-β cytokine family exist as TGF-β1, TGF-β2, and TGF-β3. Elevated levels of plasma TGF-β1 are detected in cancer patients and linked to early metastasis (Shariat et al., 2001a; Shariat et al., 2001b; Tsushima et al., 2001). Nearly all human cell types are responsive to TGF-β (Massague, 2008), while most cell types are capable of both expressing and responding to the chemokine. Cellular sources of TGF-β in tumors vary and may include cancer cells, stromal fibroblasts, and inflammatory cells (Gold, 1999; Lewis and Pollard, 2006; Massague, 2008; Tlsty and Coussens, 2006). The presence of leukocytes, macrophages, bone marrow-derived endothelial, mesenchymal, and myeloid precursor cells in tumor milieu correlates to TGF-β secretion, suggesting that these cells are potential sources of tumor progressive TGF-β1 accumulating at the invasion front of tumors (Dalal et al., 1993; Yang et al., 2008).

The TGF-β family can impose both tumor suppressive and tumor promoting functions. This growth factor may act as a growth inhibitor in tumor suppression (Amendt et al., 1998; Bottinger et al., 1997; Gorska et al., 2003; Pierce et al., 1995; Tucker et al., 1984), its presence in the tumor microenvironment may also enhance pro-tumorigenic stroma, promote angiogenesis, and impair immunosurveillance (Bhowmick et al., 2004). Under normal conditions, tissue homeostasis is maintained by TGF-β via the regulation of cellular proliferation, differentiation, survival, adhesion, and environment (Massague, 2008). Malignant cells, however, can circumvent these suppressive effects either through inactivation of the TGF-β receptors or alter the signaling pathway downstream. In fact, increased expression of TGF-β in carcinoma cells is often detected along with loss of TGF-β sensitivity by the cells (Bhowmick et al., 2004). Pathological forms of TGF-β signaling permit loss of cell adherens junctions and activate a cellular program termed the epithelial-to-mesenchyme transition (EMT), awarding malignant cells with changes that favor invasion and metastasis (Akhurst and Derynck, 2001; Hanahan and Weinberg, 2011; Ikushima and Miyazono, 2010). Furthermore, TGF-β1 can inhibit cytotoxicity of TAMs (Ben-Baruch, 2006; Elgert et al., 1998) and may recruit other stromal cell types to generate a pro-tumorigenic microenvironment (Massague, 2008).

Tumor necrosis factor-α (TNF-α), a pivotal cytokine in inflammatory reactions, may be produced by epithelial tumor cells or stromal cells, including mononuclear phagocytes, neutrophils, activated lymphocytes, natural killer (NK) cells, ECs, mast cells, and TAMs (Balkwill, 2002; Borish and Steinke, 2003; Lewis and Pollard, 2006). TNF-α affects neoplastic growth directly by regulating the proliferation and survival tumor cells (de Visser et al., 2006). It controls the activation state and cellular localization of nuclear factor of kB (NF-kB) (Pikarsky et al., 2004), which is found to be constitutively activated in some types of cancer cell (Karin et al., 2002). The activated NF-kB is translocated into the cell nucleus (Senftleben et al., 2001), where it ignites a series of alterations involving immunoregulatory and inflammatory genes, antiapoptotic genes, positive cell proliferation regulating genes, and encoding genes for negative regulators of NF-kB (Karin et al., 2002), leading to changes in cell functions that promote proliferation and inhibit apoptosis (Beg and Baltimore, 1996; Liu et al., 1996; VanAntwerp et al., 1996; Wang et al., 1996). Activation of NF-kB is also linked to ECM destruction by cancer cells (Bond et al., 1998; Takeshita et al., 1999; Wang et al., 1999b) and anticancer drug or radiation treatment resistance (Wang et al., 1999a).

In our model, only one group of growth factors is currently included. Tumor growth factors (tgf) represent all the aforementioned factors and molecules which engage in autocrine or paracrine signaling. They are produced by the viable tumor cells (V), vascular cells (B, L), and myofibroblastic species (F). Another group of endocrine factors, termed tumor hormonal growth factors (h), which are carried by blood circulation and disseminated via microvessels in the tumor milieu, is not currently modelled and will be included in future studies. Both species diffuse through the tumor tissue with a certain rate of decay and are consumed by binding to tumor cell surface.

2.6. Tumor Angiogenic Factors

Avascular tumor can undergo angiogenic switch to attain vascular tumor development. The angiogenic switch induces the growth of neovasculature, subsequently increases the blood vessel density in tumor mass, enabling tumors to overcome growth restrictions imposed by insufficient oxygen and nutrients supplies. Potent inducers of angiogenic growth include fibroblast growth factors, vascular endothelial growth factors, and angiopoietins (Folkman and Kalluri, 2003).

The first angiogenic proteins to be isolated, basic fibroblast growth factor (bFGF or FGF-2) and acidic fibroblast growth factor (aFGF or FGF-1), are among the most potent angiogenic proteins in vivo (Folkman and Shing, 1992; Shing et al., 1984). The involvement of bFGF in tumorigenesis is evidenced by elevated levels of bFGF found in the serum, urine, and cerebrospinal fluid of cancer patients with different types of tumors (Li et al., 1994; Nguyen et al., 1994). Stored in ECM and synthesized by tumor cells and ECs in the tumor vasculature, these FGFs have high affinity for heparin and can stimulate EC mitosis and migration in vitro (Folkman and Kalluri, 2003). Some tumors are also known to recruit and activate macrophages to secrete bFGF, while others may attract mast cells to sequester bFGF due to their high heparin content (Schulzeosthoff et al., 1990). Under hypoxic condition, bFGF is upregulated by TAMs and tumor cells (Lewis and Murdoch, 2005). Tumors with elaborated bFGF levels may have heightened immune-tolerance attributable to the ability of bFGF to interfere with leukocyte adhesion to the endothelium (Melder et al., 1996).

Vascular endothelial growth factors (VEGFs) are a family of cytokines secreted by the majority of tumor cells and a wide variety of normal cells, including ECs and TAMs (Folkman and Kalluri, 2003; Lee et al., 2007; Lewis and Pollard, 2006; Maharaj et al., 2006). The VEGF gene family consists of VEGF-A, VEGF-B, VEGF-C, VEGF-D, VEGF-E, and placental growth factor (PIGF) (Ferrara et al., 2003; Kim et al., 2002; Shibuya, 2006). Among them, VEGF-A (initially vascular permeability factor VPF) is the most important molecule that dictates blood vessel morphogenesis with known correlation between its expression and angiogenesis in tumors (Adams and Alitalo, 2007; Saharinen et al., 2011). It exists as five isoforms and two of its receptors are found predominantly on ECs (Devries et al., 1992; Terman et al., 1992). Shown to be an EC mitogen and motogen in vivo (Connolly, 1991; Dvorak et al., 1991), VEGF-A is also essential in the differentiation of endothelial precursor cells, assembly of ECs into vasculature, and vessel remodeling (Adams and Alitalo, 2007). In addition, it can bind to a receptor expressed on tumor cells. The autocrine secretion of VEGF-A by tumor cells facilitates the generation of a surface-bound VEGF-A gradient, leading to the chemotaxis of ECs to the tumor cells (Folkman and Kalluri, 2003). In several experimental systems, it was also shown to stimulate lymphatic growth (Hirakawa et al., 2005; Hong et al., 2004; Nagy et al., 2002). However, the mechanisms might be indirect and involve the recruitment of inflammatory cells and increased VEGF-C expression (Baluk et al., 2005; Cursiefen et al., 2004). In contrast to VEGF-A, VEGF-C binds to a receptor that is expressed predominantly on lymphatic endothelium (Chang et al., 2002). As a key regulator of lymphangiogenesis (Adams and Alitalo, 2007), it induces the proliferation and survival of LECs, hence, promoting the sprouting of lymphatic vessels (Karkkainen et al., 2004). Also showing lymphangiogenic activity is VEGF-D, though might not be crucial for lymphatic development (Baldwin et al., 2005), it has been linked with poor prognosis, invasion, and metastasis (Mumprecht and Detmar, 2009; Skobe et al., 2001; Tammela and Alitalo, 2010). Moreover, VEGF-C and VEGF-D participations have been indicated in angiogenesis under pathological conditions (Laakkonen et al., 2007). While VEGF-A expression by tumor cells is known to be upregulated by hypoxia and elevated near necrotic tumor areas (Bando et al., 2003; Folkman and Kalluri, 2003; Koong et al., 2000; Lal et al., 2001; Lewis and Pollard, 2006), hypoxic regulations of VEGF-C and VEGF-D remain unclear. While some studies showed that VEGF-C and VEGF-D are upregulated by hypoxia or correlates positively with hypoxia-inducible factor-1α (HIF-1α) (Currie et al., 2004; Daluvoy et al., 2009; Nilsson et al., 2004; Okada et al., 2005; Schoppmann et al., 2006; Simiantonaki et al., 2008; Tzao et al., 2008), others have reported contrarily (Enholm et al., 1997; Okada et al., 2005; Simiantonaki et al., 2008).

Another group of important angiogenic signaling molecules is the angiopoietins. Angiopoietin-1 (Ang1), Ang2, and Ang3/4 bind to the Tie1 and Tie2 receptors on ECs (Davis et al., 1996; Maisonpierre et al., 1997; Saharinen et al., 2010; Suri et al., 1996), hence are EC specific growth factors (Folkman and Kalluri, 2003). While VEGFs are involved in the initial assembly of the vasculature, the Ang-Tie system plays an essential role in the later stages of vascular development when the vessels remodel and recruit pericytes for coating (Saharinen et al., 2010). Ang1 is secreted and incorporated into the tumor-associated ECM, but Ang2 is not found to be ECM bound (Xu and Yu, 2001). While Ang1 can readily activate Tie2, Ang2 only induces Tie2 phosphorylation under certain conditions, such as in stressed ECs or at high levels of Ang2 (Daly et al., 2006; Kim et al., 2000). Ang1 is not an endothelial mitogen but induces ECs to recruit mural cells for the vessel wall (Folkman and Kalluri, 2003). Hence, overexpressing Ang1 leads to non-leaky vessels (Suri et al., 1998). Whereas Ang2 in the presence of VEGF-A may increase angiogenesis, Ang2 alone acts as an antagonist of Ang1, causing EC apoptosis, destabilizing vessels, and eventually regression of new microvasculature (Holash et al., 1999; Maisonpierre et al., 1997; Thurston et al., 1999). In the normal vasculature, Ang1 is produced mainly by periendothelial mural cells while Ang2 and Tie2 are expressed by ECs (Helotera and Alitalo, 2007; Saharinen et al., 2010). In activated endothelium found within a tumor microenvironment, Ang2 secretion exceeds that of Ang1, causing pericytes detachment and vessel regression, leading to hypoxia which drives the release of VEGFs and initiation of angiogenesis (Ahmad et al., 2001; Holash et al., 1999; Maisonpierre et al., 1997; Reiss et al., 2009; Yancopoulos et al., 2000).

In our model, the total effects of all TAFs are combined and modeled under one species (taf). We do not differentiate between angiogenic and lymphangiogenic growth factors, assuming that the growth factors affect ECs and LECs in a similar manner. Upregulated by hypoxia, production of the species is taken to come from viable tumor cells (V), host cells (H), ECs (B), LECs (L), and myofibroblastic cell species (F). The species, decaying at a certain rate, diffuses through the tumor tissue and is used by growing ECs and LECs. It is also involved in directing the chemotactic migrations of ECs and LECs.

2.7. Matrix Degrading Enzymes

Matrix metalloproteinases (MMPs) are matrix degrading enzymes (MDEs) involved in promoting the inflammatory response, tissue remodeling, wound healing, and angiogenesis. In a tumor environment, these proteinases are upregulated, leading to destruction of normal ECM (Bissell and Radisky, 2001). Degradation of ECM may indirectly enable the selection of apoptosis-resistant carcinoma cells and enhanced invasive potential (Mitsiades et al., 2001; Sethi et al., 1999). The ability of MMPs to bind to specific receptors on tumor cell surface, coupled with MMP retention on cell surface by ECM adhesion receptors, provide spatial control of its proteolytic activity and directional signals to invading tumor cells (Yu and Stamenkovic, 2000).

The MMP family of at 25 or more highly homologous, either secreted or plasma membrane-associated zinc-binding proteinases can be produced by nearly all cell types (Egeblad and Werb, 2002; Sternlicht and Werb, 2001). They are matrix degrading enzymes (MDEs) consisting of collagenase (MMP-1), gelatinase A (MMP-2), stromelysin (MMP-3), matrilysin (MMP-7), gelatinase B (MMP-9), and others (Siveen and Kuttan, 2009). Various studies have reported a correlation between elevated expression of MMPs in human malignant tissue and poor prognosis (Egeblad and Werb, 2002).

While some MMPs are secreted by ECs, the major source of the enzymes in both human and mouse cancer models is activated stromal cells, mainly innate immune cells and others, such as fibroblasts and vascular cells (Egeblad and Werb, 2002). MMPs can lead to the formation of distant metastases by remodeling cell-cell and cell-matrix adhesion molecules, as well as both soluble and insoluble ECM components. These restructurings relax the connective tissue supporting a tumor and alter intracellular signaling pathways, enabling malignant cells to detach from tumor mass and disseminate (Egeblad and Werb, 2002; Lamagna et al., 2006). Released by the proteolytic cleavage are bioactive cryptic protein fragments embedded within some ECM molecules (Egeblad and Werb, 2002; Kalluri, 2003). These protein fragments antagonize angiogenesis and could be used as potential drugs for tumor retardation.

Another involvement of MMPs in tumor growth is in angiogenesis. Highly expressed proangiogenic growth factors such as VEGFs, bFGF, and TNF have limited bioavailability because they are either bound to ECM molecules or tethered to cells (Bergers and Coussens, 2000). MMPs regulate the release of these growth factors, exposing them to their associated receptors on ECs, and promoting the development of neovasculature (Bergers and Coussens, 2000; Egeblad and Werb, 2002).

Hypoxia is known to upregulate TAM production of MMP-7 (Burke et al., 2003), while MMP-9 secretion by monocytic cell lines, blood monocytes, and brain macrophages can be elevated by macrophage chemoattractants CCL2 and CCL5 (Azenshtein et al., 2002; Cross and Woodroofe, 1999; Locati et al., 2002; Robinson et al., 2002). MMP-9 can mobilize ECM-sequestered VEGF (Bergers et al., 2000) and both MMP-2 and MMP-9 can activate latent TGF-β residing in the matrix (Yu et al., 2002), which lead to the proliferation of perivascular and ECs and stabilization of nascent microvessels (Jain, 2003; Jain, 2005). Being a major source of MMP-2 and MMP-9 (Lewis and Pollard, 2006; Siveen and Kuttan, 2009), TAMs also induce their productions by tumor cells in the presence of ET-1 and ET-2, stimulating the invasiveness of tumor cells (Grimshaw et al., 2002).

Here, we model the MMP family as a single MDE species (m). It is produced by viable tumor cells (V), ECs (B), LECs (L), and myofibroblastic cell species (F). The species diffuses through the tumor tissue with a certain rate of decay. It is involved in the degradation of ECM (E) and its expression can be upregulated by hypoxia. We acknowledge that diffusion-type MMP models can be problematic, as explored by (Mumenthaler et al., 2013) and (D’Antonio et al., 2013), since in reality MMPs are often membrane-bound or have very short diffusion distances. For simplicity, here we assume that diffusion is the main physical mechanism, even if over a short distance.

2.8. Nutrients and Waste Products

Specific to tumor cells is their altered metabolism first postulated by Nobel Laureate Otto H. Warburg. In papers published by Warburg and coworkers in the 1920s (Warburg, 1924; Warburg et al., 1924; Warburg et al., 1927), tumor tissues were shown to metabolize approximately tenfold more glucose to produce two orders of magnitude higher of lactic acid compared to normal tissues even under aerobic conditions (Koppenol et al., 2011). The use of tracer 2-[¹⁸F]fluoro-2-deoxy-D-glucose (FDG) with positron emission tomography (PET) (Gambhir, 2002) has been successfully used to identify many human cancers (Czernin and Phelps, 2002) and to show that primary and metastatic lesions display increased glucose uptake (Gatenby and Gillies, 2004).

The increase in glucose consumption as a carbon source for anabolic reactions and glycolytic ATP production facilitates tumor growth in several ways (Kroemer and Pouyssegur, 2008). By shifting towards glycolysis, tumor cells evade uncertainties in oxygen supply and mitigate their dependence on oxygen under hypoxic conditions. Lactic acid, a product of glycolysis, has been shown to suppress human T lymphocyte proliferation and its cytokine production up to 95%, leading to the reduction of its cytotoxicity by half (Fischer et al., 2007). Carbon dioxide released by cellular respiration is wetted in the interstitium to generate carbonic acid. Together with lactic acid, they contribute towards low extracellular pH levels that promote tumor growth and invasion (Swietach et al., 2007). The avoidance of acidic death is achieved by synchronized buffering between cancer and stromal cells. Lactate is pumped from cancer cell cytoplasm to the ECM and absorbed by stromal fibroblasts to use as fuel in pyruvate production. The excess pyruvate within fibroblasts is then exported to the ECM and taken up by cancer cells as fuel in lactate fermentation, ending in lactic acid production (Koukourakis et al., 2006). Furthermore, intermediates from the glycolytic pathways may also be deviated by cancer cells to participate in anabolic reactions that linked to cell growth and proliferation (Kroemer and Pouyssegur, 2008).

Another essential nutrient for most cancer cells is glutamine (Eagle, 1955). Cancer cell proliferation is also found to depend on glutamine, in which oxidative glutamine metabolism contributes to lipogenesis (Anastasiou and Cantley, 2012). Under hypoxia where HIF is stabilized and mitochondrial functions are impaired, malignant cells rely predominantly on glutamine to provide carbons for lipid production via reductive glutamine metabolism (Metallo et al., 2012; Mullen et al., 2012).

In our model, cellular metabolic processes considered are respiration and glycolysis with lactate fermentation. The bicarbonate buffering system is included for cellular pH regulation. Sodium and chloride ions are pumped across cell membranes. Oxidative and reductive glutamine pathways will be included in our future work. Nutrients and waste products involved in these reactions are glucose, oxygen, lactic acid, carbon dioxide, water, and carbonic acid. Water is assumed to exist in abundance and therefore is not a limiting factor. Both lactic and carbonic acids are also assumed to dissociate completely and exist only in ionic forms. We model the concentrations of glucose (g), oxygen (n), lactate ion (ℓ), carbon dioxide (w), bicarbonate ion (b), hydrogen ion (a), sodium (s), and chloride (r) ions.

3. Mathematical Model

The soft tissue in our model consists of a viable tumor cell species, a necrotic tumor cell species, and a healthy host cell species living within the stromal component (as defined in Sections 2.1). The stroma consists of mainly ECM and interstitial physiological fluid, with myofibroblastic cells (Section 2.4), vascular and lymphatic vessels (Section 2.2 and 2.3).

Variables of different cell components of the mixture are identified by the subscripts W, V, D, E, and H, representing interstitial fluid, viable tumor cells, necrotic tumor cells, ECM, and healthy host cells respectively. Whenever appropriate and necessary, we interchangeably denote the components in the order listed with the numeric subscripts 0 to 4:

• 0– Interstitial physiological fluid (W)
• 1− Viable tumor cells (V)
• 2− Dead/necrotic tumor cells (D)
• 3– Extracellular matrix (E)
• 4– Healthy host cells (H)

The cell and ECM components are collectively considered as a solid phase and the interstitial component is taken to be an aqueous fluid phase, denoted by subscripts α and β respectively. Note that subscripts W, 0, and β are used interchangeably for the aqueous interstitial component.

Dependent variables in the continuum mixture model include the cell-ECM α phase pressure p, volume fraction ϕ_α, density ρ_α, and velocity vector u_α; interstitial fluid β phase pressure q, volume fraction ϕ_β, density ρ_β, and velocity vector u_β. Within the solid cell-ECM α phase, component volume fractions are denoted as ϕ_α,1,⋯,ϕ_α,4, cell component densities as ρ₁,⋯,ρ₄, and velocities relative to stationary coordinates u₁,⋯,u₄.

Figure 1 presents a graphical overview of the main model components and their interactions. The exchange of key diffusible elements between these components, including tumor and angiogenic growth factors as well as nutrients and oxygen, drives the evolution of these components, and ultimately determines the net amount of viable tumor tissue and stroma at any given moment in time.

Figure 1.

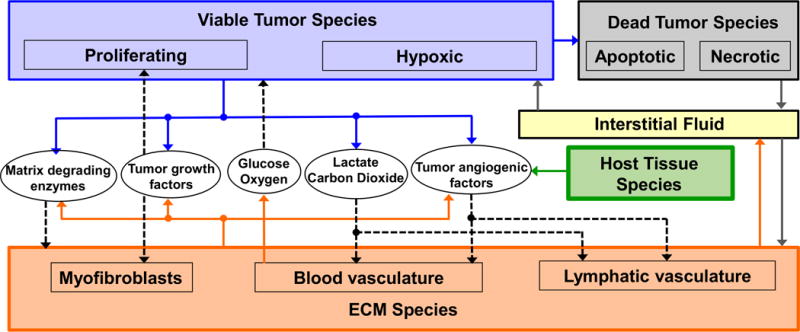
Graphical overview of the main model components and their interactions. Solid arrows indicate outputs from a component, while dashed arrows indicate particular inputs. Arrows penetrating into the boxes highlight specific recipients associated with particular input. For example, tumor growth factors are output by the viable tumor species and the stromal elements, and the growth factors in turn influence the behavior of proliferating tumor cells and myofibroblasts.

3.1. Basic Equations

The tumoral tissue is taken to be a mixture of solid cell-ECM phase α and interstitial fluid phase β. Assuming that there are no voids in the tissue, the saturation constraint implies that volume fractions

$${\varphi }_{\alpha }+{\varphi }_{\beta }=1.$$ (3.1.1)

Assuming that the volume fractions are continuous in a tissue domain Ω, a mass balance equation is written for each phase:

$$\frac{\partial ({\rho }_i{\varphi }_i)}{\partial t}+\nabla \cdot ({\rho }_i{\varphi }_i{\mathit{u}}_i)=S_i$$ (3.1.2)

where i = α,β. S_α and S_β are the rates of production of phase α and β, respectively. These rates include mass exchange between the cell-ECM components and the interstitial fluid, mass gain or loss by biological processes, as well as external source/sink.

Following mixture theory, the mixture density is defined as

$$\rho ={\rho }_{\alpha }{\varphi }_{\alpha }+{\rho }_{\beta }{\varphi }_{\beta }$$ (3.1.3)

and the composite velocity of the mixture is defined as the weighted average of the phase velocities:

$$\mathit{u}=\frac{1}{\rho }({\rho }_{\alpha }{\varphi }_{\alpha }{\mathit{u}}_{\alpha }+{\rho }_{\beta }{\varphi }_{\beta }{\mathit{u}}_{\beta }).$$ (3.1.4)

Summing Eq. (3.1.2) for α and β, and taking Eqs. (3.1.1), (3.1.3), and (3.1.4) into account, we get the mass conservation equation for the total mixture:

$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \mathit{u})=S_{\alpha }+S_{\beta }.$$ (3.1.5)

Assuming there are no external mass source and sink, the law of conservation of mass may be enforced by letting

$$S_{\alpha }+S_{\beta }=0.$$ (3.1.6)

and Eq. (3.1.5) is reduced to the equation of continuity for the mixture. Note that the circulatory systems are assumed to be co-located and the formation of edemas is excluded; these simplifications may not hold for some types of tumors, and deviations will be explored in future studies. The total mass flux, N, of each of the cell-ECM and interstitial phase is the resultant of the bulk tissue motion and the total nonadvective flux J:

$${\mathit{N}}_i={\rho }_i{\varphi }_i{\mathit{u}}_i={\rho }_i{\varphi }_i\mathit{u}+{\mathit{J}}_i$$ (3.1.7)

where i = α,β. The nonadvective fluxes arise from movements associated with mechanical interactions between solid and fluid phase. Summing Eq. (3.1.7) over α and β yields

$${\mathit{J}}_{\alpha }+{\mathit{J}}_{\beta }=0.$$ (3.1.8)

Now, assume that the solid phase is closely packed with all cells and ECM components, leaving no voids in the solid mixture. The saturation constraint implies that

$${\displaystyle \sum _{i=1}^4{\varphi }_{\alpha ,i}=1,1\le i\le 4}$$ (3.1.9)

where ϕ_α,i is the volume fraction of component i in phase α. The volume fractions are assumed to be continuous in the tissue domain Ω. Similarly, a mass balance equation of the following form can be written for each component in the solid phase:

$$\frac{\partial ({\varphi }_{\alpha }{\rho }_i{\varphi }_{\alpha ,i})}{\partial t}+\nabla \cdot ({\varphi }_{\alpha }{\rho }_i{\varphi }_{\alpha ,i}{\mathit{u}}_{\alpha ,i})=S_{\alpha ,i},1\le i\le 4$$ (3.1.10)

and S_α,i are the source/sink terms that include interphase and external mass exchange, as well as mass gain/loss due to cellular progression.

Again, following mixture theory, the solid cell-ECM mixture density is defined as

$${\rho }_{\alpha }={\displaystyle \sum _{i=1}^4{\rho }_i{\varphi }_{\alpha ,i}}$$ (3.1.11)

and the composite velocity of the solid mixture is defined as the weighted average of the cell component velocities:

$${\mathit{u}}_{\alpha }=\frac{1}{{\rho }_{\alpha }}{\displaystyle \sum _{i=1}^4{\rho }_i{\varphi }_{\alpha ,i}{\mathit{u}}_{\alpha ,i}.}$$ (3.1.12)

Summing Eq. (3.1.10) over all constituents and taking Eqs. (3.1.11), and (3.1.12) into account, we get the mass conservation equation for the solid (α) phase, appeared in Eq. (3.1.2), where

$${\displaystyle \sum _{i=1}^4{S}_{\alpha ,i}}=S_{\alpha }.$$ (3.1.13)

Also, the mass flux, N_α,i, of each cell component is the resultant of the bulk tissue motion and the total diffusive flux of the component:

$${\mathit{N}}_{\alpha ,i}={\varphi }_{\alpha }{\rho }_i{\varphi }_{\alpha ,i}{\mathit{u}}_{\alpha ,i}={\varphi }_{\alpha }{\rho }_i{\varphi }_{\alpha ,i}{\mathit{u}}_{\alpha }+{\mathit{J}}_{\alpha ,i},1\le i\le 4$$ (3.1.14)

where J_α,i are diffusive fluxes that arise from movements associated with mechanical interactions among cell-cell and cell-ECM components and biological driving forces such as chemotaxis and haptotaxis:

$${\mathit{J}}_{\alpha ,i}={\mathit{J}}_{\alpha ,i}^{\mathit{mechano}}+{\mathit{J}}_{\alpha ,i}^{\mathit{chemo}}+{\mathit{J}}_{\alpha ,i}^{\mathit{hapto}},1\le i\le 4$$ (3.1.15)

Summing Eq. (3.1.14) over all cells and ECM components and using Eqs. (3.1.11) and (3.1.12), we get

$${\displaystyle \sum _{i=1}^4{\mathit{J}}_{\alpha ,i}}=0.$$ (3.1.16)

Therefore, Eqs. (3.1.6) and (3.1.16), together with Eq. (3.1.13), are enforced as consistency constraints for sources and diffusive fluxes. Letting ϕ_i = ϕ_αϕ_α,i and assuming constant ρ_i, Eq. (3.1.10) can be rewritten as

$$\frac{\partial {\varphi }_i}{\partial t}+\nabla \cdot \left({\varphi }_i{\mathit{u}}_{\alpha }+\frac{1}{{\rho }_i}{\mathit{J}}_{\alpha ,i}\right)=\frac{1}{{\rho }_i}{S}_{\alpha ,i},1\le i\le 4$$ (3.1.17)

Expressions for velocities, diffusive fluxes, and source/sink terms for the cells and ECM components will be derived and discussed in Sections 3.2 and 3.3. The governing equations for dissolved species and vessels will be discussed separately in Sections 3.4 to 3.6.

3.2. Diffuse Interface Method

In diffuse interface theories, the sharp interface between phases is replaced by a diffuse interface of non-zero interface thickness, which arises from the finite range of molecular interactions. Cell-cell and cell-ECM interactions, combined with elastic effects and taxis potential, are considered and accounted for by a non-local contribution to the Helmholtz free energy (Cahn and Hilliard, 1958; Rowlinson, 1979; Yang et al., 1976), where the local free energy density depends on the both the local composition and the composition of the nearest surroundings.

We follow the energetic variational approach presented by Wise et al. (2008). The total Helmholtz free energy of the system is

$$E={\displaystyle \sum _{i=0}^4{E}_i={\displaystyle \sum _{i=0}^4{\displaystyle \int {\overline{E}}_{i}d\mathit{x}={\displaystyle \int \overline{E}d\mathit{x}}}}}.$$ (3.2.1)

Here, the tumoral tissue is considered an isothermal system. To construct the constitutive relations for velocities and fluxes that are consistent with the second law of thermodynamics, we begin with a generalized Helmholtz free energy equation of component interactions, with the added taxis potential term posed by Cristini et al. (2009). One way to model the elasticity is by evolving natural configurations and introducing the time derivative of the stress (Giverso and Preziosi, 2012; Giverso et al., 2015; Preziosi et al., 2010). Here, we opted to add the effects of elasticity to the free energy equation via an elastic energy term. Therefore, the generalized Helmholtz free energy equation can be expressed in the following form:

$$\overline{E}(\mathit{\varphi },\nabla \mathit{\varphi },𝛆)=F_b(\mathit{\varphi })+{\displaystyle \sum _{i,j=0}^4\frac{{\kappa }_{ij}}{2}(\nabla {\varphi }_i\cdot \nabla {\varphi }_j)}+{\displaystyle \sum _{i=0}^4\left({\varphi }_i{\displaystyle \sum _{l=1}^L{\chi }_{il}{\sigma }_l}\right)+w(\mathit{\varphi },𝛆)}$$ (3.2.2)

where E̅ is the Helmholtz free energy density of the system F_b and is the bulk free energy of components due to local interactions; the second term on the right hand side represents gradient energy due to interactions with nearest surroundings, κ_ij > 0 are the strength of component interactions; the third term is the energy contribution due to the taxis of cell components, χ_il is the taxis coefficient of cell component i with respect to the chemical species l, and σ_l are the concentrations of taxis inducing species; the last term is the elastic free energy density contributed by component where $𝛆$ is the infinitesimal strain tensor.

The time derivative of the total free energy is

$$\frac{dE}{dt}={\displaystyle \int \left(\frac{\partial \overline{E}}{\partial {\varphi }_{\beta }}\frac{\partial {\varphi }_{\beta }}{\partial t}+{\displaystyle \sum _{i=1}^4\frac{\partial \overline{E}}{\partial {\varphi }_i}\frac{\partial {\varphi }_i}{\partial t}}\right)}d\mathit{x},$$ (3.2.3)

where the boundary terms are dropped and omitted hereinafter. At equilibrium, the total Helmholtz free energy of the system has a minimum. By assuming that the volume fraction of the aqueous interstitial phase is constant ${\varphi }_{\beta }={\stackrel{\sim }{\varphi }}_{\beta }$, the volume fraction of the solid cell-ECM phase is reduced to ${\varphi }_{\alpha }={\displaystyle {\sum }_{i=1}^4{\varphi }_i=1-{\stackrel{\sim }{\varphi }}_{\beta }=}{\stackrel{\sim }{\varphi }}_{\alpha }$. To impose the two constraints on the volume fractions, Lagrange multipliers p* and q, solid and aqueous pressure respectively, may be introduced. Using Eqs. (3.1.2) and (3.1.17), the time derivative in Eq. (3.2.3) is rewritten as

$$\frac{dE}{dt}={\displaystyle \int \left\{\left(\frac{\delta E}{\delta {\varphi }_{\beta }}+q\right)[-\nabla \cdot ({\stackrel{\sim }{\varphi }}_{\beta }{\mathit{u}}_{\beta })]+{\displaystyle \sum _{i=1}^4\left(\frac{\delta E}{\delta {\varphi }_i}+p^{\ast }\right)[-\nabla \cdot ({\varphi }_i{\mathit{u}}_{\alpha }+\frac{1}{{\rho }_i}{\mathit{J}}_{\alpha ,i})]}\right\}}d\mathit{x}.$$ (3.2.4)

Using Gauss divergence theorem, it can be rewritten as

$$\frac{dE}{dt}={\displaystyle \int \left[{\stackrel{\sim }{\varphi }}_{\beta }\nabla \left(\frac{\delta E}{\delta {\varphi }_{\beta }}+q\right)\cdot {\mathit{u}}_{\beta }+{\displaystyle \sum _{i=1}^4{\varphi }_i\nabla \left(\frac{\delta E}{\delta {\varphi }_i}+p^{\ast }\right)}\cdot {\mathit{u}}_{\alpha }+{\displaystyle \sum _{i=1}^4\frac{1}{{\rho }_i}\nabla \left(\frac{\delta E}{\delta {\varphi }_i}+p^{\ast }\right)}\cdot {\mathit{J}}_{\alpha ,i}\right]}d\mathit{x},$$ (3.2.5)

where new boundary terms are dropped and omitted hereinafter. Using Eq. (3.1.16), let ${\mathit{J}}_{\alpha ,4}=-{\displaystyle {\sum }_{i=1}^3{\mathit{J}}_{\alpha ,i}}$ and rewrite the solid pressure term as presented by Wise et al. (2008):

$$p={\stackrel{\sim }{\varphi }}_{\alpha }{p}^{\ast }+{\displaystyle \sum _{i=1}^4{\varphi }_i}\frac{\delta E}{\delta {\varphi }_i},$$ (3.2.6)

the time derivative of energy in Eq. (3.2.5) can be manipulated and rewritten as

$$\frac{dE}{dt}={\displaystyle \int \left\{{\stackrel{\sim }{\varphi }}_{\beta }\nabla \left(\frac{\delta E}{\delta {\varphi }_{\beta }}+q\right)\cdot {\mathit{u}}_{\beta }+\left(\nabla p-{\displaystyle \sum _{i=1}^4\frac{\delta E}{\delta {\varphi }_i}\nabla {\varphi }_i}\right)\cdot {\mathit{u}}_{\alpha }+{\displaystyle \sum _{i=1}^3\nabla }\left[\frac{1}{{\rho }_i}\frac{\delta E}{\delta {\varphi }_i}-\frac{1}{{\rho }_4}\frac{\delta E}{\delta {\varphi }_4}+\frac{1}{{\stackrel{\sim }{\varphi }}_{\alpha }}\left(\frac{1}{{\rho }_i}-\frac{1}{{\rho }_4}\right)\left(p-{\displaystyle \sum _{j=1}^4{\varphi }_j\frac{\delta E}{\delta {\varphi }_j}}\right)\right]\cdot {\mathit{J}}_{\alpha ,i}\right\}}d\mathit{x}.$$ (3.2.7)

Taking each term to be separately dissipative, constitutive relations that are thermodynamically consistent can be written for velocities and fluxes:

$${\mathit{u}}_{\beta }=-k_{\beta }\nabla \left(\frac{\delta E}{\delta {\varphi }_{\beta }}+q\right),$$ (3.2.8)

$${\mathit{u}}_{\alpha }=-k_{\alpha }\left(\nabla p-{\displaystyle \sum _{i=1}^4\frac{\delta E}{\delta {\varphi }_i}\nabla {\varphi }_i}\right),$$ (3.2.9)

$${\mathit{J}}_{\alpha ,i}=-M_i\nabla \left[\frac{1}{{\rho }_i}\frac{\delta E}{\delta {\varphi }_i}-\frac{1}{{\rho }_4}\frac{\delta E}{\delta {\varphi }_4}+\frac{1}{{\stackrel{\sim }{\varphi }}_{\alpha }}\left(\frac{1}{{\rho }_i}-\frac{1}{{\rho }_4}\right)\left(p-{\displaystyle \sum _{j=1}^4{\varphi }_j}\frac{\delta E}{\delta {\varphi }_j}\right)\right],1\le i\le 3,$$ (3.2.10)

where k_α and k_β are motilities of the solid and liquid phase respectively, and M_i is the mobility of the component. The constant volume fraction ${\stackrel{\sim }{\varphi }}_{\beta }$ is absorbed into k_β.

Let the bulk energy of local interactions be the summation of potentials over the liquid and solid phases (Cogswell and Carter, 2011):

$$F_b({\varphi }_0,\cdots ,{\varphi }_4)={\stackrel{\sim }{\varphi }}_{\beta }{F}_{\beta }({\stackrel{\sim }{\varphi }}_{\beta })+{\stackrel{\sim }{\varphi }}_{\alpha }{F}_{\alpha }({\varphi }_1,\cdots ,{\varphi }_4),$$ (3.2.11)

where ${\stackrel{\sim }{f}}_{\beta }={\stackrel{\sim }{\varphi }}_{\beta }{F}_{\beta }({\stackrel{\sim }{\varphi }}_{\beta })$ is a constant and $F_{\alpha }({\varphi }_1,\cdots ,{\varphi }_4)=E_a^{\ast }{f}_{\alpha }({\varphi }_1,\cdots ,{\varphi }_4)$ with positive $E_a^{\ast }$ as an energy scale for adhesion. Therefore the bulk energy of local interactions does not depend on the liquid component, ∂F_b/∂ϕ_β = 0. Similar to the approach by Wise et al. (2008), we do not distinguish between the adhesive properties of various tumor cells (V and D):

$${\varphi }_T={\varphi }_V+{\varphi }_D={\varphi }_1+{\varphi }_2.$$ (3.2.12)

As a start, we assumed the free energy term of a ternary system can be described by the following form, adapted from the one constructed by Kim and Lowengrub (2005):

$$f_{\alpha }({\varphi }_T,{\varphi }_E,{\varphi }_H)=A_1{\left(\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)}^2{\left(\frac{{\varphi }_H}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)}^2+\left(\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}+A_2\right){\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}-A_3\right)}^2+\left(\frac{{\varphi }_H}{{\stackrel{\sim }{\varphi }}_{\alpha }}+A_4\right){\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}-A_5\right)}^2$$ (3.2.13)

where A₁ to A₅ are a set of constants. The collective tumor species T and healthy cell species H are immiscible, and the ECM species is more miscible with species H. For example, with A₁ = 1000, A₂ = 0.2, A₃ = 0.4, A₄ = 0.2, and A₅ = 0.2, the free energy as stated in Eq. (3.2.13) has two minima, at (ϕ_T, ϕ_E, ϕ_H) = (−0.00002, 0.23485, 0.76517) and (0.63788, 0.36216, −0.00003), that fall slightly out of the Gibbs triangle. We note that the slight negative composition is not a concern here, since volume fractions of small negative values are taken to be zero, the combined tumor and ECM volume fraction (ϕ_T + ϕ_E) is generally maintained below 1, and the volume fraction of the healthy cell species is calculated post smoothing by ϕ_H = 1 − ϕ_T − ϕ_E.

Again using ϕ_T in Eq. (3.2.12) and the relation in Eq. (3.1.9) to eliminate ϕ_H, the gradient energy term in Eq. (3.2.2) can be rewritten as

$${\displaystyle \sum _{i,j\in \{V,D,E,H\}}\frac{{\kappa }_{ij}}{2}(\nabla {\varphi }_i\cdot \nabla {\varphi }_j)}=\frac{{{\epsilon }_T}^2}{2}{\left|\nabla {\varphi }_T\right|}^2+\frac{{{\epsilon }_E}^2}{2}{\left|\nabla {\varphi }_E\right|}^2+{{\epsilon }_{TE}}^2(\nabla {\varphi }_T\cdot \nabla {\varphi }_E)$$ (3.2.14)

where the adhesive flux of the liquid component is assumed negligible, κ_0j = κ_i0 ≈ 0. The interface energy terms ε_i and ε_ij are

$${{\epsilon }_i}^2={\kappa }_{ii}-2{\kappa }_{iH}+{\kappa }_{HH}$$ (3.2.15)

$${{\epsilon }_{TE}}^2={\kappa }_{TE}-{\kappa }_{TH}-{\kappa }_{EH}+{\kappa }_{HH}$$

where κ_ij = κ_ji, κ_iV = κ_iD = κ_iT, and κ_VD = κ_DV = κ_VV = κ_DD = κ_TT.

While the elastic energy contribution may take various forms, we currently adopt the generalized elastic energy density of the system following Leo et al. (1998) and Garcke (2005) given by

$$\mathcal{W}(\mathit{\varphi },𝛆)={\epsilon }_e\frac{E_e^{\ast }}{2}[𝛆-{𝛆}^{\ast }(\mathit{\varphi })]:\mathcal{C}(\mathit{\varphi })[\mathbf{𝛆}-{𝛆}^{\ast }(\mathit{\varphi })]$$ (3.2.16)

where $E_e^{\ast }$ is an energy scale for elastic effects ε_e, is an interfacial strain energy coefficient. The infinitesimal strain 𝛆, the elastic stiffness (a fourth order tensor) $\mathcal{C}(\mathit{\varphi })$, and the stress-free strain (eigenstrain) 𝛆*(ϕ) are all symmetric tensors defined as the following:

$$𝛆=\frac{1}{2}[\nabla {\mathit{u}}_d+{(\nabla {\mathit{u}}_d)}^T]\Rightarrow {\epsilon }_{ij}=\frac{1}{2}\left(\frac{\partial u_i^d}{\partial x_j}+\frac{\partial u_j^d}{\partial x_i}\right)$$ (3.2.17)

$${\mathcal{C}}_{ijkl}(\mathbf{\varphi })=L_1(\mathbf{\varphi }){\delta }_{ij}{\delta }_{kl}+L_2(\mathbf{\varphi })({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})$$ (3.2.18)

$${𝛆}^{\ast }(\mathbf{\varphi })=Q_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right){𝛆}_E^{\ast }+\left[1-Q_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\right]{𝛆}_C^{\ast }$$ (3.2.19)

where u_d is the displacement vector with components $u_i^d$, δ_ij = 1 for i = j and δ_ij = 0 for i ≠ j; 𝛆E* is the constant misfit tensor for the ECM component; we do not differentiate between cell types, and thus assume all cell components to have the same constant misfit tensor 𝛆C*. The cubic interpolation function for 0 ≤ γ ≤ 1 is given by Q₃(γ) = 3γ² − 2γ³. Assuming that all cell components have the same elastic properties, the two volume fraction dependent terms L₁(ϕ) and L₂(ϕ) used are given by

$$L_i({\varphi }_E)=Q_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)L_i^E+\left[1-Q_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\right]L_i^C,i=1,2$$ (3.2.20)

where $L_1^E$, $L_2^E$, and $L_1^C$, $L_2^C$ are Lamé constants in regions of pure ECM and cells respectively. Hence 𝛆*(ϕ) is reduced to ${𝛆}^{\ast }({\varphi }_E)$. Similarly, $\mathcal{C}(\mathbf{\varphi })$ and ${\mathcal{C}}_{ijkl}(\mathbf{\varphi })$ are reduced to $\mathcal{C}({\varphi }_{{\rm E}})$ and ${\mathcal{C}}_{ijkl}({\varphi }_{{\rm E}})$ respectively. The cell types are also not differentiated here. Furthermore, from Eq. (3.2.18), we define

$${\mathcal{C}}_{ijkl}^{\theta }=L_1^{\theta }{\delta }_{ij}{\delta }_{kl}+L_2^{\theta }({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}),\theta =E,C$$ (3.2.21)

therefore ${\mathcal{C}}^E$ and ${\mathcal{C}}^C$ are constants.

From Eqs. (3.2.1), (3.2.2), (3.2.11), (3.2.14), and (3.2.16), together with the Euler-Lagrange equation δE/δϕ_j = ∂E/∂ϕ_j −∇  ·  ∂E/∂∇  ϕ_j, the variational derivative of the energy with respect to each component is

$$\frac{\delta E}{\delta {\varphi }_j}=\frac{\partial F_b}{\partial {\varphi }_j}+\frac{\partial \mathcal{W}}{\partial {\varphi }_j}+{\displaystyle \sum _{l=1}^L{\chi }_{jl}{\sigma }_l}-{\displaystyle \sum _{i\in \{T,E\}}{{\epsilon }_i}^2{\nabla }^2{\varphi }_i\frac{\partial \nabla {\varphi }_i}{\partial \nabla {\varphi }_j}}-{{\epsilon }_{TE}}^2\left({\nabla }^2{\varphi }_T\frac{\partial \nabla {\varphi }_E}{\partial \nabla {\varphi }_j}+{\nabla }^2{\varphi }_E\frac{\partial \nabla {\varphi }_T}{\partial \nabla {\varphi }_j}\right)$$ (3.2.22)

From Eqs. (3.2.16) – (3.2.21), it is concluded that

$$\frac{\partial \mathcal{W}}{\partial {\varphi }_E}={\epsilon }_e{E}_e^{\ast }\left\{\frac{1}{2}[𝛆-{𝛆}^{\ast }({\varphi }_E)]:\frac{\partial \mathcal{C}({\varphi }_E)}{\partial {\varphi }_E}[𝛆-{𝛆}^{\ast }({\varphi }_E)]-\frac{\partial {𝛆}^{\ast }({\varphi }_E)}{\partial {\varphi }_E}:\mathcal{C}({\varphi }_E)[𝛆-{\mathbf{𝛆}}^{\ast }({\varphi }_E)]\right\}={\epsilon }_e{E}_e^{\ast }\frac{\partial }{\partial {\varphi }_E}\left[Q_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\right]\{\frac{1}{2}[𝛆-{𝛆}^{\ast }({\varphi }_E)]:[{\mathcal{C}}^E-{\mathcal{C}}^C][𝛆-{\mathbf{𝛆}}^{\ast }({\varphi }_E)]-[{𝛆}_E^{\ast }-{𝛆}_C^{\ast }]:\mathcal{C}({\varphi }_E)[𝛆-{𝛆}^{\ast }({\varphi }_E)]\}$$ (3.2.23)

where $\partial \mathcal{W}/\partial {\varphi }_j=0$ for j ≠ E. Assuming that the mechanical equilibrium is reached on a much faster time scale than mass diffusion and growth, a quasi-equilibrium is used for the displacement u_d:

$$\nabla \cdot \mathcal{S}=\mathbf{0},$$ (3.2.24)

where $\mathcal{S}$ is the symmetric stress tensor defined by

$$\mathcal{S}=\frac{\partial \mathcal{W}}{\partial 𝛆}={\epsilon }_e{E}_e^{\ast }\mathcal{C}(\mathit{\varphi })[𝛆-{\mathbf{𝛆}}^{\ast }(\mathit{\varphi })],$$ (3.2.25)

and Eq. (3.2.24) can be rewritten as a vector with the i component expressed below:

$$[L_1({\varphi }_E)+L_2({\varphi }_E)]{\displaystyle \sum _{k=1}^3\frac{{\partial }^2{u}_k^d}{\partial x_k\partial x_i}}+L_2({\varphi }_E){\displaystyle \sum _{k=1}^3\frac{{\partial }^2{u}_i^d}{\partial x_k^2}}+\frac{\partial L_1({\varphi }_E)}{\partial x_i}{\displaystyle \sum _{k=1}^3\frac{\partial u_k^d}{\partial x_k}}+{\displaystyle \sum _{k=1}^3\left(\frac{\partial u_k^d}{\partial x_i}+\frac{\partial u_i^d}{\partial x_k}\right)}\frac{\partial L_2({\varphi }_E)}{\partial x_k}=\frac{\partial L_1({\varphi }_E)}{\partial x_i}{\displaystyle \sum _{k=1}^3{\epsilon }_{kk}^{\ast }}+L_1({\varphi }_E){\displaystyle \sum _{k=1}^3\frac{\partial {\epsilon }_{kk}^{\ast }}{\partial x_i}}+2{\displaystyle \sum _{k=1}^3{\epsilon }_{ki}^{\ast }}\frac{\partial L_2({\varphi }_E)}{\partial x_k}+2L_2({\varphi }_E){\displaystyle \sum _{k=1}^3\frac{\partial {\epsilon }_{ki}^{\ast }}{\partial x_k}}.$$ (3.2.26)

The displacement components $u_i^d$, $u_j^d$, and $u_k^d$, determined from Eq. (3.2.26) and satisfying Eq. (3.2.24) above, are used to compute the elastic contribution via Eq. (3.2.23) to the potential of the ECM phase, given in Eq. (3.2.29) below.

Because there is no taxis χ_0l = 0 and ∂∇  ϕ_{T,E}/∂∇  ϕ_β = 0, we get δE/δϕ₀ = δE/δϕ_β = 0. Eq. (3.2.8) is therefore reduced to

$${\mathit{u}}_{\beta }=-k_{\beta }\nabla q.$$ (3.2.27)

Since tumor cells are assumed to be not migratory, χ_Vl = χ_Dl = 0, we rewrite Eq. (3.2.22) for tumor cells as

$$\frac{\delta E}{\delta {\varphi }_V}=\frac{\delta E}{\delta {\varphi }_D}=\frac{\delta E}{\delta {\varphi }_T}=\frac{\delta F_b}{\delta {\varphi }_T}-{{\epsilon }_T}^2{\nabla }^2{\varphi }_T-{{\epsilon }_{TE}}^2{\nabla }^2{\varphi }_E.$$ (3.2.28)

There is no taxis of ECM macromolecules and healthy host cells, therefore χ_6l = χ_7l = 0. Eq. (3.2.22) can be written for ECM and host cells as

$$\frac{\delta E}{\delta {\varphi }_E}=\frac{\partial F_b}{\partial {\varphi }_E}+\frac{\partial \mathcal{W}}{\partial {\varphi }_E}-{{\epsilon }_E}^2{\nabla }^2{\varphi }_E-{{\epsilon }_{TE}}^2{\nabla }^2{\varphi }_T,$$ (3.2.29)

$$\frac{\delta E}{\delta {\varphi }_H}=\frac{\delta F_b}{\delta {\varphi }_H}.$$ (3.2.30)

Substitute ${\varphi }_H={\stackrel{\sim }{\varphi }}_{\alpha }-{\varphi }_T-{\varphi }_E$ into Eq. (3.2.13) and subsequently into Eq. (3.2.11), we get

$$\frac{\partial F_b}{\partial {\varphi }_V}=\frac{\partial F_b}{\partial {\varphi }_D}=\frac{\partial F_b}{\partial {\varphi }_T}=E_a^{\ast }\left[2A_1\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}\left(1-\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}-\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\left(1-2\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}-\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)+\left(2\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}-A_5-A_3\right)(A_5-A_3)\right]$$ (3.2.31)

$$\frac{\partial F_b}{\partial {\varphi }_E}=E_a^{\ast }\left\{2\left(\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}+A_2\right)\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}-A_3\right)-2A_1{\left(\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)}^2\left(1-\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}-\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)+\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}-A_5\right)\left[2\left(1-\frac{{\varphi }_T}{{\stackrel{\sim }{\varphi }}_{\alpha }}+A_4\right)-3\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}+A_5\right]\right\}$$ (3.2.32)

$$\frac{\partial F_b}{\partial {\varphi }_H}=0$$ (3.2.33)

Let μ_T = δE/δϕ_T and μ_E = δE/δϕ_E. Eqs. (3.2.30) and (3.2.33) implies that δE/δϕ_H = 0. Substitute Eqs. (3.2.28), (3.2.29), (3.2.30), and (3.2.33) in Eq. (3.2.9), we get an expression for the solid phase velocity:

$${\mathit{u}}_{\alpha }=-k_{\alpha }[\nabla p-{\mu }_T\nabla {\varphi }_T-{\mu }_E\nabla {\varphi }_E].$$ (3.2.34)

Assuming that the cell species densities are matched, ρ_i = ρ, and let M_i = Mϕ_iρ², the diffusive fluxes of cell-ECM components given by Eqs. (3.2.10) and (3.1.16) become

$${\mathit{J}}_{\alpha ,1}=-M{\varphi }_V\rho \nabla {\mu }_T$$

$${\mathit{J}}_{\alpha ,2}=-M{\varphi }_D\rho \nabla {\mu }_T$$ (3.2.35)

$${\mathit{J}}_{\alpha ,3}=-M{\varphi }_E\rho \nabla {\mu }_E$$

$${\mathit{J}}_{\alpha ,4}=M\rho ({\varphi }_T\nabla {\mu }_T+{\varphi }_E\nabla {\mu }_E)$$

where the mobility M is a positive constant.

3.3. Solid Tumor Cell Volume Fractions

Using fluxes given in Eq. (3.2.35) and by letting S_α,i/ρ = S_i, the continuum multicomponent equations of change in Eq. (3.1.17) can be rewritten as

$$\frac{\partial {\varphi }_V}{\partial t}+\nabla \cdot ({\varphi }_V{\mathit{u}}_{\alpha })=M\nabla \cdot ({\varphi }_V\nabla {\mu }_T)+S_V$$

$$\frac{\partial {\varphi }_D}{\partial t}+\nabla \cdot ({\varphi }_D{\mathit{u}}_{\alpha })=M\nabla \cdot ({\varphi }_D\nabla {\mu }_T)+S_D$$ (3.3.1)

$$\frac{\partial {\varphi }_E}{\partial t}+\nabla \cdot ({\varphi }_E{\mathit{u}}_{\alpha })=M\nabla \cdot ({\varphi }_E\nabla {\mu }_E)+S_E$$

$$\frac{\partial {\varphi }_H}{\partial t}+\nabla \cdot ({\varphi }_H{\mathit{u}}_{\alpha })=-M\nabla \cdot ({\varphi }_T\nabla {\mu }_T+{\varphi }_E\nabla {\mu }_E)+S_H$$

where chemical potentials μ_T and μ_E are given in Equations (3.2.28) and (3.2.29), respectively.

The source terms for solid species may be written as a combination of rates (r) related to biological processes. The viable tumor cell species (V) is subjected to mitotic gain (r_M,V), apoptotic (r_A,V) and necrosis loss (r_N,V), as well as metastatic disseminations via the blood (r_B,V) and lymphatic (r_L,V) vessels. The viable tumor cell species is also assumed to potentially undergo autophagic degradation (r_de,V). The dead tumor cell species, which accounts for both apoptotic and necrotic loss of viable tumor cells, undergoes lysis (r_L,D) and is eventually released into the interstitium. Fibronectin may be secreted by viable tumor cells (r_V,E), endothelial cells (r_B,E, r_L,E), and myofibroblastic cells (r_F,E). The source term also includes its degradation (r_de,E) by matrix degrading enzymes. The healthy host cell species is assumed to maintain homeostasis with negligible changes compared to the tumor and immune cell species, therefore S_H = 0. We obtain the following expressions for species source terms:

$$S_V=r_{M,V}-r_{A,V}-r_{N,V}-r_{B,V}-r_{L,V}-r_{de,V}$$

$$S_D=r_{A,V}+r_{N,V}-r_{L,D}$$ (3.3.2)

$$S_E=r_{V,E}+r_{B,E}+r_{L,E}+r_{F,E}-r_{de,E}$$

Summing all the source terms in Eq. (3.3.2), and using the relations in Eqs. (3.1.6) and (3.1.13), we get the mass exchange terms between the solid cell and aqueous interstitial components:

$$S_{\beta }=-S_{\alpha }=\rho (-r_{M,V}-r_{V,E}-r_{B,E}-r_{L,E}-r_{F,E}+r_{L,D}+r_{B,V}+r_{L,V}+r_{de,V}+r_{de,E})$$ (3.3.3)

As indicated in the expression above, ECM produced and mitotic gain of cells are assumed to come from aqueous interstitial components. Metastatic loss of tumor cells, degraded ECM, catabolized tumor cells due to autophagy, and lysed dead tumor cells are assumed to contribute to the interstitial component. We also assume that the phagocytosed tumor cells and degraded tumor cells by autophagy are processed and released to the interstitial space instantaneously.

The rate expressions used in source terms in Eq. (3.3.2) are given in Table 1. In the table of rate expressions, λ_M,V, λ_A,V, and λ_N,V are the mitosis, apoptosis, and necrosis rate constants, respectively, for viable tumor cell species V; λ_L,D is the lysis rate constant of the dead tumor cell species; λ_B,V and λ_L,V are the rate constants for metastatic dissemination via the blood and lymphatic vessels, respectively, for viable tumor cell species V; r_de,V is the autophagic degradation of viable tumor species V whereas r_de,E is the degradation of ECM by MDEs; r_i,E is the rate of fibrosis contributed by cell species i; given by B_n and L_n, respectively, are the total EC and LEC concentrations in number of cells per volume tissue.

Table 1.

Rate expressions from Eq. (3.3.2).

$r_{M,V}={\mathrm{\lambda }}_{M,V}{\mathcal{A}}_{M,V}{\varphi }_V$	$r_{L,V}={\mathrm{\lambda }}_{L,V}{\mathcal{A}}_{L,V}{\varphi }_V$	$r_{B,E}={\mathrm{\lambda }}_{B,E}{\mathcal{A}}_{B,E}{B}_n$
$r_{A,V}={\mathrm{\lambda }}_{A,V}{\mathcal{A}}_{A,V}{\varphi }_V$	$r_{de,V}={\mathrm{\lambda }}_{de,V}{\mathcal{A}}_{de,V}{\varphi }_V$	$r_{L,E}={\mathrm{\lambda }}_{L,E}{\mathcal{A}}_{L,E}{L}_n$
$r_{N,V}={\mathrm{\lambda }}_{N,V}{\mathcal{A}}_{N,V}{\varphi }_V$	$r_{L,D}={\mathrm{\lambda }}_{L,D}{\mathcal{A}}_{L,D}{\varphi }_D$	$r_{F,E}={\mathrm{\lambda }}_{F,E}{\mathcal{A}}_{F,E}F$
$r_{B,V}={\mathrm{\lambda }}_{B,V}{\mathcal{A}}_{B,V}{\varphi }_V$	$r_{V,E}={\mathrm{\lambda }}_{V,E}{\mathcal{A}}_{V,E}{\varphi }_V$	$r_{de,E}={\mathrm{\lambda }}_{de,E}{\mathcal{A}}_{de,E}{\varphi }_E$

Tumor cells proliferate aggressively until a threshold level of hypoxia is reached. In areas where oxygen concentrations fall below the threshold level, tumor cells may stop proliferating and switch to anaerobic glycolysis for continuous energy production (Brown, 2000). Including the effects of mitogens and hypoxia, the adjustment factor for the mitosis rate constant of viable tumor cell species can be written as

$${\mathcal{A}}_{M,V}=\left(\frac{n}{n_{\infty }}\right)\left(1+{ℱ}_{\mathit{tgf},V}^M\frac{\mathit{tgf}}{tg{f}_{\mathit{sat}}}\right)\mathscr{H}(n-n_h),$$ (3.3.4)

where n_h is the hypoxic threshold of oxygen level, g_v,V is the glucose viability limit for viable tumor species V, ${ℱ}_{\mathit{tgf},V}^M$ is the effective factor of tumor growth factors on the mitosis rate of viable tumor species V, tgf_sat is the saturation level of tgf species.

Taking into account the inhibition of apoptosis by tumor growth factors and desmoplasia, the adjustment factors for viable tumor species apoptosis rate may be given as

$${\mathcal{A}}_{A,V}=\left(1-{ℱ}_{\mathit{tgf},V}^A\frac{\mathit{tgf}}{tg{f}_{\mathit{sat}}}\right)\left(1-{ℱ}_{E,V}^A\frac{{\varphi }_E}{{\varphi }_{\alpha }}\right),$$ (3.3.5)

where ${ℱ}_{\mathit{tgf},V}^A$ and ${ℱ}_{E,V}^A$ are the effective factors of tumor growth factors and ECM macromolecules, respectively, on the apoptosis rate of viable tumor species V.

Factors potentially affect the lysis rate constant of dead tumor cells are not considered here, hence, we let ${\mathcal{A}}_{L,D}=1$. We assume that necrosis in the viable tumor species can be triggered when one of the nutrients drops below their viable thresholds. Therefore, the adjustment factors for necrosis rates are taken to be

$${\mathcal{A}}_{N,V}=1-\mathscr{H}(n-n_{v,V})\mathscr{H}(g-g_{v,V}),$$ (3.3.6)

where n_v,V is the oxygen viability limit and g_v,V is the glucose viability limit for the viable tumor species V. Note that the effect of pH is not included here.

In experimental animals, tumor cells may appear in the circulation continuously after neovascularization of the primary tumor; the number of tumor cells shed has been shown to correlate positively with the density of blood vessels in the primary tumor and the number of metastases observed (Liotta et al., 1976; Liotta et al., 1980). The leaky fragmented basement membranes of proliferating capillaries facilitate the metastatic emigration of tumor cells (Dvorak et al., 1988; Liotta et al., 1976). High lactate levels in the primary tumor also correlate positively to the metastatic spread of carcinomas (Walenta et al., 2000). Therefore, we let the adjustment factors for the rates of metastatic dissemination via blood and lymphatic vessels be

$${\mathcal{A}}_{B,V}={ℱ}_{B,V}^{\mathit{met}}{Q}_3\left(1-\frac{p}{p_{t,B}}\right)\mathscr{H}(p_{t,B}-p),$$ (3.3.7)

$${\mathcal{A}}_{L,V}={ℱ}_{L,V}^{\mathit{met}}{Q}_3\left(1-\frac{p}{p_{t,L}}\right)\mathscr{H}(p_{t,L}-p),$$ (3.3.8)

where the threshold pressures p_t,B and p_t,L represent upper limits, above which blood and lymphatic vessels are considered crushed. The factors ${ℱ}_{B,V}^{\mathit{met}}$ and ${ℱ}_{L,V}^{\mathit{met}}$, termed Metastatic Index here, act as indications of the likelihood of viable tumor cell dissemination via the blood and lymphatic vasculatures respectively. We let

$${ℱ}_{B,V}^{\mathit{met}}=Q_3\left(\frac{\ell }{{\ell }_{\mathit{sat}}}\right)Q_3\left(\frac{B_n}{B_{\mathit{max}}}\right),$$ (3.3.9)

$${ℱ}_{L,V}^{\mathit{met}}=Q_3\left(\frac{\ell }{{\ell }_{\mathit{sat}}}\right)Q_3\left(\frac{L_n}{L_{\mathit{max}}}\right),$$ (3.3.10)

where ℓ_sat is the maximum level of lactate, B_max is the maximum density of blood vessels, and L_max is the maximum level of lymphatic vessels.

Although pancreatic ductal adenocarcinoma is found to have elevated levels of autophagy even when nutrients are abundant (Yang et al., 2011), we let the onset of autophagy in our model be related to metabolic stress, hypoxia, and, potentially, growth factors:

$${\mathcal{A}}_{de,V}=Q_3\left(\frac{n-n_{v,V}}{n_h-n_{v,V}}\right)Q_3\left(\frac{g-g_{v,V}}{g_{de,V}-g_{v,V}}\right)\left(1+{ℱ}_{\mathit{tgf},V}^{de}\frac{\mathit{tgf}}{tg{f}_{\mathit{sat}}}\right)\mathscr{H}(n_h-n)\mathscr{H}(n-n_{v,V})\mathscr{H}(g_{de,V}-g)\mathscr{H}(g-gv,V),$$ (3.3.11)

where we assumed that the process occurs only when both oxygen and glucose levels fall between a certain range and the rate is decreasing as nutrient levels approach their viability limits; g_de,v is the glucose upper limit for viable tumor species, below which autophagy may occur; ${ℱ}_{\mathit{tgf},V}^{de}$ is the effective factor of tumor growth factors on the autophagic degradation rate of viable tumor species.

The adjustment factors of ECM production and degradation are

$${\mathcal{A}}_{i,E}=\left(1-\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\left[1+{ℱ}_{n,E}^i\frac{n_h-n}{n_h-n_{v,i}}\mathscr{H}(n_h-n)\right]\mathscr{H}(n-n_{v,i}),$$ (3.3.12)

$${\mathcal{A}}_{de,E}=\frac{m}{m_{\mathit{sat}}},$$ (3.3.13)

where i = V, B, L, F, m_sat is the saturation level of MDEs in tissues, and ${ℱ}_{n,E}^i$ are the effective factors of hypoxia in upregulating the production of ECM molecules by species i. Note that another expression for ECM degradation rate r_de,E is discussed in Section 3.5.

3.4. Nutrients and Waste Products Concentrations

Molar concentrations of glucose (g), oxygen (n), lactate ion (ℓ), carbon dioxide (w), bicarbonate ion (b), hydrogen ion (a), as well as sodium (s) and chloride (r) ions in tissues follow the mass conservation equation given in Eq. (3.1.17). Nutrients and waste products diffuse through interstitial fluid space and may be permeable to the cellular membrane. Since the transport of these species in tissues is dominated by diffusion and takes place at time scales that are orders of magnitude shorter than cellular proliferation (seconds versus day or longer) (Wise et al., 2008), we use the following quasi-steady state governing equations for nutrients and waste transport in the interstitial space:

$$\frac{\partial \sigma }{\partial t}+\nabla \cdot ({\mathit{u}}_{\beta }\sigma )=-\nabla \cdot {\mathit{J}}_{\sigma }+S_{\sigma }\Rightarrow 0=-\nabla \cdot {\mathit{N}}_{\sigma }+S_{\sigma },$$ (3.4.1)

where σ = g, n, ℓ, w, b, a, s, and r. The molar flux and source term of species σ are given by N_σ and S_σ respectively. The molar flux term of uncharged species follow Fick’s law of diffusion:

$${\mathit{N}}_{\sigma }=-D_{\sigma }\nabla \sigma ,\sigma =n,g,w,$$ (3.4.2)

where the diffusivity of specie σ in the tissue is D_σ. Following Casciari et al. (Casciari et al., 1992) for charged species, the flux is given by charged migration and diffusion:

$${\mathit{N}}_{\sigma }=-(z_{\sigma }{u}_{\sigma }\mathrm{F}\sigma \nabla \psi +D_{\sigma }\nabla \sigma ),\sigma =\ell ,b,a,s,r$$ (3.4.3)

where z_σ and u_σ are the charge and mobility of species σ, F is Faraday’s constant, and ψ is the electrical potential. Assuming dilute solution, the Nerst-Einstein equation links the mobility of species σ to its diffusivity by

$$u_{\sigma }=\frac{D_{\sigma }}{RT}$$ (3.4.4)

where R and T are the gas constant and temperature respectively. Since there is no net current, electroneutrality gives

$${\displaystyle \sum _{\sigma }{z}_{\sigma }\sigma =0,\sigma =\ell ,b,a,s,r.}$$ (3.4.5)

Hence, the sum of the charge fluxes due to the ionic species z_ℓJ_ℓ + z_bJ_b + z_aJ_a + z_sJ_s + z_rJ_r = 0. Using this fact and Eq. (3.4.4), the molar flux of the charged species given by Eq. (3.4.3) can be rewritten as

$${\mathit{N}}_{\sigma }=D_{\sigma }\left[z_{\sigma }\sigma \left(\frac{z_{\ell }{D}_{\ell }\nabla \ell +z_b{D}_b\nabla b+z_a{D}_a\nabla a+z_s{D}_s\nabla s+z_r{D}_r\nabla r}{z_{\ell }^2{D}_{\ell }\ell +z_b^2{D}_{b}b+z_a^2{D}_{a}a+z_s^2{D}_{s}s++z_r^2{D}_{r}r}\right)-\nabla \sigma \right],$$ (3.4.6)

where σ = ℓ, b, a, s, r. Assuming that all species diffusivities in the ECM D_σ,E and cell D_σ,C domains may be different, let

$$D_{\sigma }=D_{\sigma ,E}{Q}_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)+D_{\sigma ,C}\left[1-Q_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\right]$$ (3.4.7)

and the species diffusivity in the cell domain is given by

$$D_{\sigma ,C}=D_{\sigma ,T}{Q}_3\left(\frac{{\varphi }_T}{{\varphi }_C}\right)+D_{\sigma ,H}\left[1-Q_3\left(\frac{{\varphi }_T}{{\varphi }_C}\right)\right],$$ (3.4.8)

where D_σ,T and D_σ,H are species diffusivities in the tumor and host regions, respectively. The concentration of chloride ion is not modeled through the mass balance equation in Eq. (3.4.1), but via electroneutrality in Eq. (3.4.5).

While nutrients like oxygen and glucose are supplied via the vasculature network (r_B,n, r_B,q) and consumed by the cell species (r_U,n, r_U,g), waste products are produced (r_W,w, r_W,ℓ, r_W,b, r_W,_a) and may leave through blood vessels (r_B,w, r_B,ℓ, r_B,a). We let S_r = S_s = 0, and the remaining source terms of nutrients and waste products are

$$S_n=r_{B,n}+r_{U,n},S_g=r_{B,g}+r_{U,g},S_w=r_{W,w}+r_{B,w},$$ (3.4.9)

$$S_{\ell }=r_{W,\ell }+r_{B,\ell },S_a=r_{W,a}+r_{B,a},S_b=r_{W,b}.$$

Although healthy host cells are assume to be at homeostasis with negligible nutrient consumption and waste production compared to tumor cells, their nutrient consumption terms are included in the model. Thus, the rates of supply and consumption of oxygen and glucose are

$$r_{B,\sigma }={\mathrm{\lambda }}_{B,\sigma }{\mathcal{A}}_{B,\sigma }({\sigma }_C-\sigma )$$ (3.4.10)

$$r_{U,\sigma }=-\left({\mathrm{\lambda }}_{U,V,\sigma }{\mathcal{A}}_{U,V,\sigma }+{\mathrm{\lambda }}_{U,H,\sigma }{\mathcal{A}}_{U,H,\sigma }\right)\sigma$$

where σ = n, g. λ_B,σ is the transfer rate coefficient of species σ from capillaries, λ_U,i,σ is the uptake rate constant of σ by cell species i, σ_C is the concentration of σ in the capillaries, and $\mathcal{A}$ are adjustment factors. Assuming that oxygen consumption is reduced during hypoxia and glucose glycolysis is increased, the adjustment factors are given as

$${\mathcal{A}}_{B,\sigma }=\left(\frac{B}{B_{\mathit{max}}}\right)Q_3\left(1-\frac{p}{p_{t,B}}\right)\mathscr{H}(p_{t,B}-p)$$ (3.4.11)

$${\mathcal{A}}_{U,i,n}={\mathcal{A}}_{U,i,g}=\left(\frac{{\varphi }_i}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)$$ (3.4.12)

where σ = n, g and i = V, H. Assuming that the nutrient transfer coefficients in the ECM λ_B,σ,E and cell λ_B,σ,C domains may be different, let

$${\mathrm{\lambda }}_{B,\sigma }={\mathrm{\lambda }}_{B,\sigma ,E}{Q}_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)+{\mathrm{\lambda }}_{B,\sigma ,C}\left[1-Q_3\left(\frac{{\varphi }_E}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\right]$$ (3.4.13)

and

$${\mathrm{\lambda }}_{B,\sigma ,C}={\mathrm{\lambda }}_{B,\sigma ,T}{Q}_3\left(\frac{{\varphi }_T}{{\varphi }_C}\right)+{\mathrm{\lambda }}_{B,\sigma ,H}\left[1-Q_3\left(\frac{{\varphi }_T}{{\varphi }_C}\right)\right]$$ (3.4.14)

where λ_B,σ,T and λ_B,σ,H are the nutrient transfer coefficients in tumor and host regions, respectively.

Metabolic waste products such as CO₂ and lactic acid may enter blood circulation, we let r_B,a = r_B,ℓ and

$$r_{B,\sigma }=-{\mathrm{\lambda }}_{B,\sigma }{\mathcal{A}}_{B,\sigma }(\sigma -{\sigma }_C)$$ (3.4.15)

where σ = w,ℓ. λ_B,σ is the transfer rate coefficient of species σ to the capillaries and takes the form of Eqs. (3.4.13) & (3.4.14), and adjustment factors share the same expression as ${\mathcal{A}}_{B,\sigma }$ given in Eq. (3.4.11).

We consider the anaerobic and aerobic glycolysis, as well as the bicarbonate buffering system as presented by Casciari et al (Casciari et al., 1992):

$${\mathrm{C}}_6{\mathrm{H}}_{12}{\mathrm{O}}_6\to 2{\mathrm{C}}_3{\mathrm{H}}_5{\mathrm{O}}_3^{-}+2{\mathrm{H}}^{+}$$ (3.4.16)

$${\mathrm{C}}_6{\mathrm{H}}_{12}{\mathrm{O}}_6+6{\mathrm{O}}_2\to 6{\text{CO}}_2+6{\mathrm{H}}_2\mathrm{O}$$ (3.4.17)

$${\text{CO}}_2{+\mathrm{H}}_2\mathrm{O}\leftrightarrow {\text{HCO}}_3^{-}+{\mathrm{H}}^{+}$$ (3.4.18)

Following the stoichiometry of the metabolic pathways given above, the production rate of lactate ion based on oxygen and glucose consumptions is

$$r_{W,\ell }=-\left(2r_{U,g}-\frac{1}{3}{r}_{U,n}\right).$$ (3.4.19)

Similarly, the production rate of CO₂, bicarbonate and hydrogen ions may be written as

$$r_{W,w}=-r_{U,n}-k_{f}w+k_{r}ba,$$

$$r_{W,b}=k_{f}w-k_{r}ba=-r_{W,w}-r_{U,n},$$ (3.4.20)

$$r_{W,a}=r_{W,\ell }+r_{W,b},$$

where k_f and k_r are the forward and reverse reaction rate constants in Eq. (3.4.18).

3.5. Tumorigenic Species Concentrations

Essential in the neoplastic expansion of tumoral tissues are factors that facilitate cell growth and induce favorable environmental conditions. Tumorigenic factors considered in this model (refer to Sections 2.4 – 2.7) are the tumor growth factor, tumor angiogenic factor, matrix degrading enzyme, and myofibroblastic cell species. Molar concentrations of these molecules are represented by tgf, taf, m, and F respectively.

Similar to nutrients, tumor growth factors and angiogenic factors diffuses through tissues. Since their diffusions take place at much shorter time scales compared to cell proliferation, molar concentrations of these species follow Eqs. (3.4.1) and (3.4.2):

$$0=\nabla \cdot (D_{\sigma }\nabla \sigma )+S_{\sigma },\sigma =\mathit{tgf},\mathit{taf}.$$ (3.5.1)

Since the diffusivity of matrix degrading enzymes is much smaller than that of oxygen (Macklin et al., 2009), the transient species concentrations obey:

$$\frac{\partial m}{\partial t}=\nabla \cdot (D_m\nabla m)+S_m.$$ (3.5.2)

The myofibroblastic cell species is assumed to reside only within the ECM component. The reduced weighted myofibroblastic cell concentration, F, per unit volume of tissue is defined as F = ϕ_EF_E, where F_E is the concentration of myofibroblastic cells within the ECM component, defined per unit volume of ECM. The governing equation for the ECM residing myofibroblastic cell species which taxis to tumor sites is

$$\frac{\partial (F_E)}{\partial t}+\nabla \cdot (F_E{\mathit{u}}_E)=-\nabla \cdot (D_F{F}_E\nabla \mathit{tgf})+S_{FE}$$ (3.5.3)

where S_FE is the specific source term defined per unit volume of ECM and we also let ϕ_eS_FE.

All species diffusivities D_σ are assumed to vary in the tumor D_σ,_T, ECM D_σ,_E, and host D_σ,_H domains, therefore following the averaged diffusivity function given in Eqs. (3.4.7) & (3.4.8). Although myofibroblastic cells only reside in the ECM component, its diffusivity D_F is also assumed to be affected by the surroundings.

The tumor growth factor species is produced by the viable tumor species (r_V,tgf), as well as endothelial (r_B,tgf, r_L,tgf) and myofibroblastic (r_F,tgf) cells. The source term also includes its degradation (r_de,tgf) and uptake (r_U,tgf) by tumor cells:

$$S_{\mathit{tgf}}=r_{V,\mathit{tgf}}+r_{B,\mathit{tgf}}+r_{L,\mathit{tgf}}+r_{F,\mathit{tgf}}+r_{de,\mathit{tgf}}+r_{U,\mathit{tgf}},$$ (3.5.4)

and

$$r_{i,t,gf}={\mathrm{\lambda }}_{i,\mathit{tgf}}{\mathcal{A}}_{i,\mathit{tgf}}(tg{f}_{\mathit{sat}}-\mathit{tgf}),i=V,B,L,F$$

$$r_{de,\mathit{tgf}}=-{\mathrm{\lambda }}_{de,\mathit{tgf}}\mathit{tgf},$$ (3.5.5)

$$r_{U,\mathit{tgf}}=-{\mathrm{\lambda }}_{U,V,\mathit{tgf}}{\mathcal{A}}_{U,V,\mathit{tgf}}\mathit{tgf},$$

where λ_i,tgf is the production rate constant of tgf by species i, λ_de,tgf is the degradation rate constant of tgf, and λ_U,V,tgf is the tgf uptake rate constant of the viable tumor species. Adjustment factors are given as

$${\mathcal{A}}_{V,\mathit{tgf}}=\left(\frac{{\varphi }_V}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)$$

$${\mathcal{A}}_{\sigma ,\mathit{tgf}}=\left(\frac{\sigma }{{\sigma }_{\mathit{max}}}\right)\left[1+{ℱ}_{n,\mathit{tgf}}^{\sigma }\frac{n_h-n}{n_h-n_{v,\sigma }}\mathscr{H}(n_h-n)\right]\mathscr{H}(n-n_{v,\sigma })\left[1+{ℱ}_{\ell ,\mathit{tgf}}^{\sigma }\frac{\ell -{\ell }_{\mathit{tgf}}}{{\ell }_{\mathit{sat}}-{\ell }_{\mathit{tgf}}}\mathscr{H}(\ell -{\ell }_{\mathit{tgf}})\right],$$

$${\mathcal{A}}_{U,V,\mathit{tgf}}=\left(\frac{{\varphi }_V}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right),$$ (3.5.6)

where σ = B, L, F. F_max is the maximum concentration of myofibroblastic cells in ECM. ${ℱ}_{n,\mathit{tgf}}^{\sigma }$ and ${ℱ}_{\ell ,\mathit{tgf}}^{\sigma }$ are the effective factors of hypoxia and lactate level in upregulating the production of tgf by endothelial and myofibroblastic cells. ℓ_sat is the saturation level of lactate in tissues, and ℓ_tgf is a threshold lactate level that triggers tgf upregulation.

The tumor angiogenic factor species is produced by viable tumor (r_V,_taf), endothelial (r_B,_taf, r_L,_taf), and myofibroblastic (r_F,_taf) cells. The source term also includes its degradation (r_de,taf) and uptake (r_U,B,taf, r_U,L,taf) by endothelial cells:

$$S_{\mathit{taf}}=r_{V,\mathit{taf}}+r_{B,\mathit{taf}}+r_{L,\mathit{taf}}+r_{F,\mathit{taf}}+r_{de,\mathit{taf}}+r_{U,B,\mathit{taf}}+r_{U,L,\mathit{taf}}$$ (3.5.7)

and

$$r_{i,\mathit{taf}}={\mathrm{\lambda }}_{i,\mathit{taf}}{\mathcal{A}}_{i,\mathit{taf}}(ta{f}_{\mathit{sat}}-\mathit{taf}),i=V,B,L,F$$ (3.5.8)

$$r_{de,\mathit{taf}}=-{\mathrm{\lambda }}_{de,\mathit{taf}}\mathit{taf},$$

where λ_i,taf is the production rate constant of taf by species i, λ_de,taf is the degradation rate constant of taf. The uptake rates of taf will be discussed later in this section. To include VEGF upregulation by lactate accumulation (Kumar et al., 2007; Philp et al., 2005), adjustment factors are given as

$${\mathcal{A}}_{V,\mathit{taf}}=\left(\frac{{\varphi }_V}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)\left[1+{ℱ}_{n,\mathit{taf}}^V\frac{n_h-n}{n_h-n_{\nu ,V}}\mathscr{H}\left(n_h-n\right)\right]\mathscr{H}(n-n_{\nu ,V})\left[1+{ℱ}_{\ell ,\mathit{taf}}^V\frac{\ell -{\ell }_{\mathit{taf}}}{{\ell }_{\mathit{sat}}-{\ell }_{\mathit{taf}}}\mathscr{H}\left(\ell -{\ell }_{\mathit{taf}}\right)\right],$$

$${\mathcal{A}}_{\sigma ,\mathit{taf}}=\left(\frac{\sigma }{{\sigma }_{\mathit{max}}}\right)\left[1+{ℱ}_{n,\mathit{taf}}^{\sigma }\frac{n_h-n}{n_h-n_{\nu ,\sigma }}\mathscr{H}\left(n_h-n\right)\right]\mathscr{H}(n-n_{\nu ,\sigma })\left[1+{ℱ}_{\ell ,\mathit{taf}}^{\sigma }\frac{\ell -{\ell }_{\mathit{taf}}}{{\ell }_{\mathit{sat}}-{\ell }_{\mathit{taf}}}\mathscr{H}\left(\ell -{\ell }_{\mathit{taf}}\right)\right]$$ (3.5.9)

where σ = B, L, F. ${ℱ}_{n,\mathit{taf}}^V$ and ${ℱ}_{\ell ,\mathit{taf}}^V$ are the effective factors of hypoxia and lactate level in upregulating the production of taf by the viable tumor species. Similarly, ${ℱ}_{n,\mathit{taf}}^{\sigma }$ and ${ℱ}_{\ell ,\mathit{taf}}^{\sigma }$ are effective factors of hypoxia and lactate level in upregulating the production of taf by endothelial and myofibroblastic cells. ℓ_sat is the saturation level of lactate in tissues, and ℓ_taf is a threshold lactate level that triggers taf upregulation.

The matrix degrading enzyme species is produced by viable tumor (r_V,m), endothelial (r_B,m, r_L,m), and myofibroblastic (r_F,m) cells. The source term also includes a first order decay (r_de,m):

$$S_m=r_{V,m}+r_{B,m}+r_{L,m}+r_{F,m}+r_{de,m}$$ (3.5.10)

and

$$r_{i,m}={\mathrm{\lambda }}_{i,m}{\mathcal{A}}_{i,m}(m_{\mathit{sat}}-m),i=V,F$$ (3.5.11)

$$r_{de,m}=-{\mathrm{\lambda }}_{de,m}m,$$

where λ_i,m is the production rate constant of m by species i, λ_de,m is the decay rate constant of m, and m_sat is the saturation level of m in tissues. We defer the discussion of enzyme production rates by endothelial cells until later in this section. Adjustment factors are given by

$${\mathcal{A}}_{V,m}=\left(\frac{{\varphi }_V}{{\stackrel{\sim }{\varphi }}_{\alpha }}\right)$$ (3.5.12)

$${\mathcal{A}}_{F,m}=\left(\frac{F}{F_{\mathit{max}}}\right)\left[1+{ℱ}_{n,m}^F\frac{n_h-n}{n_h-n_{\nu ,F}}\mathscr{H}(n_h-n)\right]\mathscr{H}(n-n_{\nu ,F})$$

where ${ℱ}_{n,m}^F$ is the effective factor of hypoxia in upregulating the production of matrix degrading enzymes by the species F.

Source term of myofibroblastic cells includes the rates of mitosis (r_M,_F), apoptosis (r_A,_F), and necrosis (r_N,_F). Similar to tumor and immune cells, the source term and rate expressions with corresponding adjustment factors are shown below:

$$S_{FE}=r_{M,FE}-r_{A,FE}-r_{N,FE}$$ (3.5.13)

and

$$r_{i,FE}={\mathrm{\lambda }}_{i,FE}{\mathcal{A}}_{i,FE}{F}_E,$$ (3.5.14)

where the subscript i represents processes M, A, N. λ_M,FE, λ_A,FE, and λ_N,FE are rate constants of mitosis, apoptosis, and necrosis respectively. The adjustment factors are given as

$${\mathcal{A}}_{M,FE}=(1-F_E)Q_3\left(\frac{n-n_h}{n_{\infty }-n_h}\right)\left(1+{ℱ}_{\mathit{tgf},F}^M\frac{\mathit{tgf}}{tg{f}_{\mathit{sat}}}\mathscr{H}(\mathit{tgf}-tg{f}_{FE})\right)\mathscr{H}(n-n_h),$$ (3.5.15)

$${\mathcal{A}}_{N,FE}=1-\mathscr{H}(n-n_{\nu ,F})\mathscr{H}(g-g_{\nu ,F})$$

$${\mathcal{A}}_{A,FE}=1$$

where, ${ℱ}_{\mathit{tgf},F}^M$ is the effective factor of tgf on the mitosis rate of myofibroblastic cells. tgf_FE is the trigger threshold of tgf, above which the mitosis rate of myofibroblastic cells is upregulated by tgf. n_v,F and g_v,F are the viability limits of oxygen and glucose, respectively. The effects of pH on the mitosis and necrosis rates of myofibroblastic cells are not considered here.

Tumor angiogenic factors bind to receptors on the endothelial cell wall, activating the secretion of proteolytic enzymes. We follow the mechanisms for the formation of matrix degrading enzymes and the degradation of ECM used in (Levine et al., 2001b):

$$\mathit{taf}+R_{\sigma }\leftrightarrow [\mathit{taf}-R_{\sigma }]\to m+R_{\sigma }$$ (3.5.16)

$$m+C\leftrightarrow [m-C]\to m+C^{\prime }$$

where σ is B_n and L_n. R_σ denotes receptors on ECs and LECs. We let C and C′ be the concentrations of ECM macromolecules and degraded ECM macromolecules per volume of tissue. Assuming the number of moles of ECM macromolecules per unit volume of ECM is constant and represented by C_E, therefore C = C_Eϕ_E and r_de,E = −r_de,C/C_E.

Tumor angiogenic factors are assumed to bind to LEC in the same mechanism. The rate of production of the matrix degrading enzyme species may be expressed in relation to taf as

$$r_{B,m}=-r_{U,B,\mathit{taf}},r_{L,m}=-r_{U,L,\mathit{taf}}.$$ (3.5.17)

The rate of ECM degradation and angiogenic factor uptake can be expressed following mass action or Michaelis-Menten kinetics:

$$r_{de,C}=-{\mathrm{\lambda }}_{de,C}mC\text{or}{r}_{de,C}=-\frac{k_{\mathit{cat},C}mC}{K_{m,C}+C}$$ (3.5.18)

$$r_{U,\sigma ,\mathit{taf}}=-{\mathrm{\lambda }}_{U,\sigma ,\mathit{taf}}\mathit{taf}{\sigma }_n\text{or}{r}_{U,\sigma ,\mathit{taf}}=-\frac{k_{\mathit{cat},\sigma }\mathit{taf}{\sigma }_n}{K_{m,\sigma }+\mathit{taf}}$$ (3.5.19)

where σ = B,L, λ_U,σ,taf is the taf uptake rate constant by species σ, k_cat,C and k_cat,σ are rate constants of the reaction steps in Eq. (3.5.16), and K_m,C and K_m,σ are Michaelis constants. We also make the assumption that the number of receptors per endothelial cell remains constant and the cell receptor density is absorbed in the reaction rate k_cat,σ.

3.6. Angiogenic and Lymphangiogenic Vessel Densities

Included in the model are new blood (B_n) and lymphatic (L_n) vessels densities defined per tissue volume. These vessels are assumed to reside within the ECM component in the model. The concentrations of new vessels within the ECM component, defined per unit volume of ECM, are $B_n^E$ and $L_n^E$. The reduced weighted and specific vessel concentrations are related via $B_n={\varphi }_E{B}_n^E$ and $L_n={\varphi }_E{L}_n^E$.

When an initial tumor mass outgrows the capacity of preexisting vasculature, angiogenic stimuli are secreted by hypoxic tumor cells to initiate angiogenesis. Endothelial cell rearrangement and migration are the first induced by angiogenesis (Paweletz and Knierim, 1989). Cell division is a secondary response and occurs a short distance behind newly formed sprout tips. A general mass conservation equation can be written for EC and LEC densities:

$$\frac{\partial ({\sigma }_n^E)}{\partial t}+\nabla ·({\sigma }_n^E{\mathit{u}}_E)=-\nabla \cdot {\mathit{J}}_{\sigma nE}+S_{\sigma nE}$$ (3.6.1)

where σ is used for B (EC) and L (LEC) throughout this section. J_σnE and S_σnE are the fluxes and source terms, respectively, defined per ECM volume for neovessels. To account for the chemotactic response of ECs and LECs to angiogenic factors, as well as haptotaxis upgradient of ECM macromolecules, we let the flux terms be

$${\mathit{J}}_{\sigma nE}={\mathrm{\chi }}_{\mathit{che},\sigma nE}{\mathcal{A}}_{\mathit{che},\sigma nE}{\sigma }_n^E\nabla \mathit{taf}+{\chi }_{\mathit{hap},\sigma nE}{\mathcal{A}}_{\mathit{hap},\sigma nE}{\sigma }_n^E\nabla {\varphi }_E-D_{\sigma nE}{\varphi }_E\nabla {\sigma }_n^E,$$ (3.6.2)

where χ_che,σnE and χ_hap,σnE are the chemotactic and maximum haptotactic coefficients respectively. The last term represents the motility of vessels with diffusivity D_σnE. Assuming that the EC and LEC diffusivities in the tumor D_σnE,T, ECM D_σnE,E, and host D_σnE domains are different, D_σnE is computed using Eqs. (3.4.7) & (3.4.8).

Adjustment factors for chemotactic rates are assumed to depend on the concentration of angiogenic factors following the receptor kinetic law (Anderson and Chaplain, 1998):

$${\mathcal{A}}_{\mathit{che},\sigma nE}=\frac{k_{\mathit{che},\sigma nE}}{k_{\mathit{che},\sigma nE}+\mathit{taf}}{ℱ}_{\sigma n},$$ (3.6.3)

where k_che,σnE are positive constants and ${ℱ}_{\sigma n}$ is the fraction of σ vessel species that are sprouting. Assuming that the numbers of receptors on ECs and LECs stay constant and let the ratio of minimum to maximum taxis strength of σ vessel cells be ω_σn, the adjustment factor for haptotaxis strength follows the functions given below:

$${\mathcal{A}}_{\mathit{hap},\sigma nE}=\{\begin{array}{cc}\hfill {\mathrm{\omega }}_{\sigma n}{ℱ}_{\sigma n},\hfill & \begin{array}{l}{\varphi }_E<{({\varphi }_E)}_{\mathit{min},\sigma n}\\ {\varphi }_E>{({\varphi }_E)}_{\mathit{max},\sigma n}\end{array}\hfill \\ {ℱ}_{\sigma n}\left\{(1-{\mathrm{\omega }}_{\sigma n})Q_4\left[\frac{{({\varphi }_E)}_{\mathit{max},\sigma n}-{\varphi }_E}{{({\varphi }_E)}_{\mathit{max},\sigma n}-{\varphi }_{\mathit{min},\sigma n}}\right]+{\mathrm{\omega }}_{\sigma n}\right\},\hfill & {({\varphi }_E)}_{\mathit{min},\sigma n}\le {\varphi }_E\le {({\varphi }_E)}_{\mathit{max}},\hfill \end{array}$$ (3.6.4)

where (ϕ_E)_min,σn and (ϕ_E)_max,σn are ECM volume fractions that correspond to the minimum and maximum haptotaxis strengths, respectively. The interpolation function is a quartic polynomial given by Q₄(γ) = 16γ² (1 − γ)² for 0 ≤ γ ≤ 1.

Neovessels are remodeled (r_de,σnE) by fibronectin and may be destroyed (r_crush,σnE) due to high pressure of the tumor tissue. Additionally, there are proliferative vessel (r_m,σnE) sections located near growing sprout tips. Let the source terms be

$$S_{\sigma nE}=r_{m,\sigma nE}+r_{de,\sigma nE}+r_{\mathit{crush},\sigma nE}.$$ (3.6.5)

The destruction rate of σ cells follow the functions given below:

$$r_{\mathit{crush},\sigma nE}=-{\mathrm{\lambda }}_{\mathit{crush},\sigma nE}{\mathcal{A}}_{\mathit{crush},\sigma nE}{\sigma }_n^E,$$ (3.6.6)

$${\mathcal{A}}_{\mathit{crush},\sigma nE}=\mathscr{H}(p-p_{c,\sigma n}).$$ (3.6.7)

The mitosis rate for σ species is given by

$$r_{m,\sigma nE}={\mathrm{\lambda }}_{m,\sigma nE}{\mathcal{A}}_{m,\sigma nE}{\sigma }_n^E,$$ (3.6.8)

where λ_m,σnE is the maximum mitosis rate constant. To account for endothelial cell mitosis as a secondary response to angiogenesis, proliferation is assumed to occur only when a threshold concentration of angiogenic factors (taf_σ) has been reached (Chaplain, 1996). Therefore, the adjustment factor is set to be

$${\mathcal{A}}_{m,\sigma nE}={ℱ}_{\sigma n}\left(1-{ℱ}_{lg,\sigma n}\frac{{\sigma }_n^E}{{\sigma }_{n,\mathit{max}}^E}\right)Q_3\left(\frac{\mathit{taf}-ta{f}_{\sigma n}}{ta{f}_{\mathit{sat}}-ta{f}_{\sigma n}}\right)\mathscr{H}(\mathit{taf}-ta{f}_{\sigma n}),$$ (3.6.9)

where ${\sigma }_{n,\mathit{max}}^E$ is the maximum attainable density for the σ vessel species. If logistic growth is considered (Chaplain and Stuart, 1993; Sholley et al., 1984), the effective factor ${ℱ}_{lg,\sigma n}$ is set to 1. Otherwise, ${ℱ}_{lg,\sigma n}=0$.

Note that the processes of anastomosis and secondary sprouting can be modeled via a periodic function in the vessel remodeling rate term (Chaplain, 1996). In which case, an additional term accounting for these two processes would be included in the remodeling rate:

$$r_{de,\sigma nE}=-{\mathrm{\lambda }}_{de,\sigma nE}{\mathcal{A}}_{de,\sigma nE}m{\sigma }_n^E-{\mathrm{\lambda }}_{as,\sigma nE}{\mathcal{A}}_{as,\sigma nE}{\sigma }_n^E,$$ (3.6.10)

$${\mathcal{A}}_{de,\sigma nE}={\mathcal{A}}_{as,\sigma nE}={ℱ}_{\sigma n}{Q}_3\left(\frac{\mathit{taf}-ta{f}_{\sigma n}}{ta{f}_{\mathit{sat}}-ta{f}_{\sigma n}}\right)\mathscr{H}(\mathit{taf}-ta{f}_{\sigma n})$$ (3.6.11)

where λ_de,σnE is the degradation rate constant of the vasculature due to remodeling by MDEs (Macklin et al., 2009) and λ_as,σnE is the periodic rate constant that accounts for the anastomosis and secondary sprouting of the σ neovessels. The periodic rate constant should be a function with zero average over a period. Therefore, the net gain due to anastomosis and the net loss due to secondary sprouting can be accounted equally.

3.7. Nondimensionalization of Governing Equations

Following the set of governing equations derived above, dependent variables (Table 2) and parameters (Table 3 – Table 6) are nondimensionalized accordingly. The resulting dimensionless independent variables, space ${\stackrel{\sim }{x}}_i$ and time $\stackrel{\sim }{t}$, are obtained by scaling with the reaction-diffusion length of oxygen and the mitosis rate constant of viable tumor cell species:

$${\stackrel{\sim }{x}}_i=\frac{x_i}{ℒ}\text{where}ℒ=\sqrt{\frac{D_{n,T}}{{\mathrm{\lambda }}_{U,V,n}}}$$ (3.7.1)

$$\stackrel{\sim }{t}=\frac{t}{\mathcal{T}}\text{where}\mathcal{T}=\frac{1}{{\mathrm{\lambda }}_{M,V}}$$ (3.7.2)

Table 2.

Dimensionless Dependent Variables.

Dimensionless Dependent Variable	Biological Representation	Scaling Factor (e.g. ${\varphi }_V=\frac{{\stackrel{\sim }{\varphi }}_V}{{\stackrel{\sim }{\varphi }}_{\alpha }}$)
${\stackrel{\sim }{\varphi }}_{\mathit{V}}$	Viable tumor cells	${\stackrel{\sim }{\varphi }}_{\alpha }$ (fixed solid volume fraction)
${\stackrel{\sim }{\varphi }}_{\mathit{D}}$	Dead tumor cells	${\stackrel{\sim }{\varphi }}_{\alpha }$
${\stackrel{\sim }{\varphi }}_{\mathit{E}}$	Extracellular Matrix	${\stackrel{\sim }{\varphi }}_{\alpha }$
${\stackrel{\sim }{\varphi }}_{\mathit{H}}$	Healthy host cells	${\stackrel{\sim }{\varphi }}_{\alpha }$
$\stackrel{\mathbf{\sim }}{\mathit{n}}$	Oxygen	${\stackrel{\sim }{n}}_{\infty }$
$\stackrel{\mathbf{\sim }}{\mathit{g}}$	Glucose	${\stackrel{\sim }{g}}_{\infty }$
$\stackrel{\mathbf{\sim }}{\mathit{w}}$	Carbon dioxide	${\stackrel{\sim }{n}}_{\infty }$
$\stackrel{\sim }{\ell }$	Lactate	${\stackrel{\sim }{n}}_{\infty }$
$\stackrel{\mathbf{\sim }}{\mathit{b}}$	Bicarbonate	${\stackrel{\sim }{n}}_{\infty }$
$\stackrel{\mathbf{\sim }}{\mathit{a}}$	Hydrogen ion	${\stackrel{\sim }{n}}_{\infty }$
$\stackrel{\mathbf{\sim }}{\mathit{s}}$	Sodium ion	${\stackrel{\sim }{n}}_{\infty }$
$\stackrel{\sim }{r}$	Chloride ion	${\stackrel{\sim }{n}}_{\infty }$
$\stackrel{\sim }{\mathit{t}\mathit{g}\mathit{f}}$	Tumor growth factors	$tg{f}_{\mathit{sat}}$
$\stackrel{\sim }{\mathit{t}\mathit{a}\mathit{f}}$	Tumor angiogenic factors	$ta{f}_{\mathit{sat}}$
$\stackrel{\mathbf{\sim }}{\mathit{m}}$	MDEs	$m_{\mathit{sat}}$
$\stackrel{\mathbf{\sim }}{\mathit{F}}$	Myofibroblastic cells	$F_{\mathit{max}}$
${\stackrel{\mathbf{\sim }}{\mathit{B}}}_{\mathit{N}}^{\mathit{E}}$	New blood vessels	$B_{\mathit{max}}$
${\stackrel{\mathbf{\sim }}{\mathit{L}}}_{\mathit{n}}^{\mathit{E}}$	New lymphatic vessels	$L_{\mathit{max}}$
${\stackrel{\mathbf{\sim }}{\mathit{\mu }}}_{\mathit{T}}$	Tumor cell potential	$E_a^{\ast }$
${\stackrel{\mathbf{\sim }}{\mathit{\mu }}}_{\mathit{E}}$	Extracellular matrix potential	$E_a^{\ast }$
${\stackrel{\mathbf{\sim }}{\mathit{\mu }}}_{\mathit{H}}$	Healthy host cell potential	$E_a^{\ast }$
$\stackrel{\mathbf{\sim }}{\mathit{p}}$	Solid phase tumor cell pressure	$\mathcal{P}$
$\stackrel{\mathbf{\sim }}{\mathit{q}}$	Interstitial fluid phase pressure	$\mathcal{Q}$
${\stackrel{\mathbf{\sim }}{\mathit{u}}}_{\mathit{\beta }}$	Interstitial fluid velocity	$ℒ/\mathcal{T}$
${\stackrel{\mathbf{\sim }}{\mathit{u}}}_{\mathit{\alpha }}$	Solid cell velocity	$ℒ/\mathcal{T}$

Table 3.

Dimensionless Diffusivities.

Dimensionless Parameter	Biological Representation	Scaling Factor*	Value Assigned
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{n}}$	Effective diffusivity of O2	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{n}\mathbf{,}\mathit{E}}$	Diffusivity of O2 through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{n}\mathbf{,}\mathit{T}}$	Diffusivity of O2 through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{n}\mathbf{,}\mathit{H}}$	Diffusivity of O2 through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{g}}$	Effective diffusivity of glucose	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{g}\mathbf{,}\mathit{E}}$	Diffusivity of glucose through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{g}\mathbf{,}\mathit{T}}$	Diffusivity of glucose through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{g}\mathbf{,}\mathit{H}}$	Diffusivity of glucose through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{w}}$	Effective diffusivity of CO2	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{w}\mathbf{,}\mathit{E}}$	Diffusivity of CO2 through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{w}\mathbf{,}\mathit{T}}$	Diffusivity of CO2 through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{w}\mathbf{,}\mathit{H}}$	Diffusivity of CO2 through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\ell }$	Effective diffusivity of lactate	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\ell \mathbf{,}\mathit{E}}$	Diffusivity of lactate through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\ell \mathbf{,}\mathit{T}}$	Diffusivity of lactate through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\ell \mathbf{,}\mathit{H}}$	Diffusivity of lactate through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{b}}$	Effective diffusivity of bicarbonate	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{b}\mathbf{,}\mathit{E}}$	Diffusivity of bicarbonate through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{b}\mathbf{,}\mathit{{\rm T}}}$	Diffusivity of bicarbonate through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{b}\mathbf{,}\mathit{H}}$	Diffusivity of bicarbonate through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{a}}$	Effective diffusivity of H+ ions	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{a}\mathbf{,}\mathit{E}}$	Diffusivity of H+ through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{a}\mathbf{,}\mathit{T}}$	Diffusivity of H+ ions through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{a}\mathbf{,}\mathit{H}}$	Diffusivity of H+ ions through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{s}}$	Effective diffusivity of Na+ ions	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{s}\mathbf{,}\mathit{E}}$	Diffusivity of Na+ through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{s}\mathbf{,}\mathit{T}}$	Diffusivity of Na+ ions through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{s}\mathbf{,}\mathit{H}}$	Diffusivity of Na+ ions through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{r}}$	Effective diffusivity of Cl− ions	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{r}\mathbf{,}\mathit{E}}$	Diffusivity of Cl− through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{r}\mathbf{,}\mathit{T}}$	Diffusivity of Cl− ions through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{r}\mathbf{,}\mathit{H}}$	Diffusivity of CE ions through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{g}\mathit{f}}$	Effective diffusivity of TGFs	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{g}\mathit{f}\mathbf{,}\mathit{E}}$	Diffusivity of TGFs through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{g}\mathit{f}\mathbf{,}\mathit{T}}$	Diffusivity of TGFs through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{g}\mathit{f}\mathbf{,}\mathit{H}}$	Diffusivity of TGFs through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{a}\mathit{f}}$	Effective diffusivity of TAFs	Dn,T	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{a}\mathit{f}\mathbf{,}\mathit{E}}$	Diffusivity of TAFs through ECM regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{a}\mathit{f}\mathbf{,}\mathit{T}}$	Diffusivity of TAFs through tumor regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{t}\mathit{a}\mathit{f}\mathbf{,}\mathit{H}}$	Diffusivity of TAFs through host regions	Dn,T	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{m}}$	Effective diffusivity of MDEs	${ℒ}^2/\mathcal{T}$	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{m}\mathbf{,}\mathit{E}}$	Diffusivity of MDEs through ECM regions	${ℒ}^2/\mathcal{T}$	0.05
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{m}\mathbf{,}\mathit{T}}$	Diffusivity of MDEs through tumor regions	${ℒ}^2/\mathcal{T}$	0.01
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{m}\mathbf{,}\mathit{H}}$	Diffusivity of MDEs through host regions	${ℒ}^2/\mathcal{T}$	0.01
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{F}}$	Effective diffusivity of Myofibroblastic cells (MFC)	${\overline{\overline{D}}}_F$	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{F}\mathbf{,}\mathit{E}}$	Diffusivity of MFCs through ECM regions	${\overline{\overline{D}}}_F$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{F}\mathbf{,}\mathit{T}}$	Diffusivity of MFCs through tumor regions	${\overline{\overline{D}}}_F$	0.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{F}\mathbf{,}\mathit{H}}$	Diffusivity of MFCs through host regions	${\overline{\overline{D}}}_F$	0.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{B}\mathit{n}\mathit{E}}$	Effective diffusivity of ECS	${ℒ}^2/\mathcal{T}$	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{B}\mathit{n}\mathit{E}\mathbf{,}\mathit{E}}$	Diffusivity of ECs through ECM regions	${ℒ}^2/\mathcal{T}$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{B}\mathit{n}\mathit{E}\mathbf{,}\mathit{T}}$	Diffusivity of ECs through tumor regions	${ℒ}^2/\mathcal{T}$	0.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{B}\mathit{n}\mathit{E}\mathbf{,}\mathit{H}}$	Diffusivity of ECs through host regions	${ℒ}^2/\mathcal{T}$	0.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{L}\mathit{n}\mathit{E}}$	Effective diffusivity of LECs	${ℒ}^2/\mathcal{T}$	computed
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{L}\mathit{n}\mathit{E}\mathbf{,}\mathit{E}}$	Diffusivity of LECs through ECM regions	${ℒ}^2/\mathcal{T}$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{L}\mathit{n}\mathit{E}\mathbf{,}\mathit{T}}$	Diffusivity of LECs through tumor regions	${ℒ}^2/\mathcal{T}$	0.0
${\stackrel{\mathbf{\sim }}{\mathit{D}}}_{\mathit{L}\mathit{n}\mathit{E}\mathbf{,}\mathit{H}}$	Diffusivity of LECs through host regions	${ℒ}^2/\mathcal{T}$	0.0

^*For example, ${\stackrel{\sim }{D}}_n=D_n/D_{n,T}$

Most diffusivities are assumed to be on the same order of magnitude as D_n,T, hence the nondimensionalized values are set to 1. A wider range of values will be tested and analyzed in future work.

Table 6.

Dimensionless Constants.

Dimensionless Constant	Biological Representation	Scaling Factors*	Value Assigned
${\stackrel{\mathbf{\sim }}{\mathit{\epsilon }}}_{\mathit{T}}$	Interaction strength for tumor cells	$\overline{\overline{\epsilon }}$	0.05
${\stackrel{\mathbf{\sim }}{\mathit{\epsilon }}}_{\mathit{E}}$	Interaction strength for ECM	$\overline{\overline{\epsilon }}$	0.05
${\stackrel{\mathbf{\sim }}{\mathit{\epsilon }}}_{\mathit{T}\mathit{E}}$	Interaction strength between tumor cells and ECM	$\overline{\overline{\epsilon }}$	0.02
${\stackrel{\mathbf{\sim }}{\mathit{\epsilon }}}_{\mathit{e}}$	Strain energy coefficient	${\overline{\overline{\epsilon }}}_e$	0.001
${\stackrel{\mathbf{\sim }}{\mathit{n}}}_{\mathit{h}}$	Hypoxic level of O2	n∞	0.3
${\stackrel{\mathbf{\sim }}{\mathit{n}}}_{\mathit{C}}$	O2 level in capillaries	n∞	1.0
${\stackrel{\mathbf{\sim }}{\mathit{g}}}_{\mathit{C}}$	Glucose level in capillaries	g∞	1.0
${\stackrel{\mathbf{\sim }}{\mathit{w}}}_{\mathit{C}}$	CO2 level in capillaries	n∞	0.0
${\stackrel{\sim }{\ell }}_{\mathit{C}}$	Lactate level in capillaries	n∞	0.0
${\stackrel{\mathbf{\sim }}{\mathit{n}}}_{\mathit{v}\mathbf{,}\mathit{V}}$	O2 viability limit of viable tumor cells	n∞	0.21
${\stackrel{\mathbf{\sim }}{\mathit{n}}}_{\mathit{v}\mathbf{,}\mathit{B}}$	O2 viability limit of ECs	n∞	0.1
${\stackrel{\mathbf{\sim }}{\mathit{n}}}_{\mathit{v}\mathbf{,}\mathit{L}}$	O2 viability limit of LECs	n∞	0.1
${\stackrel{\mathbf{\sim }}{\mathit{n}}}_{\mathit{v}\mathbf{,}\mathit{F}}$	O2 viability limit of MFCs	n∞	0.21
${\stackrel{\mathbf{\sim }}{\mathit{a}}}_{\mathit{v}\mathbf{,}\mathit{V}}$	H+ viability limit of viable tumor cells	n∞	0.7
${\stackrel{\mathbf{\sim }}{\mathit{a}}}_{\mathit{v}\mathbf{,}\mathit{F}}$	H+ viability limit of MFCs	n∞	0.7
${\stackrel{\mathbf{\sim }}{\mathit{g}}}_{\mathit{v}\mathbf{,}\mathit{V}}$	Glucose viability limit of viable tumor cells	g∞	0.1
${\stackrel{\mathbf{\sim }}{\mathit{g}}}_{\mathit{v}\mathbf{,}\mathit{F}}$	Glucose viability limit of myofibroblast-like cells	g∞	0.1
${\stackrel{\mathbf{\sim }}{\mathit{g}}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{V}}$	Threshold level of glucose leading to the onset of autophagy for viable tumor cells	g∞	0.3
${\stackrel{\sim }{\ell }}_{\mathit{s}\mathit{a}\mathit{t}}$	Saturation level of lactate in tissues	n∞	1.0
${\stackrel{\sim }{\ell }}_{\mathit{t}\mathit{g}\mathit{f}}$	Threshold lactate level for tgf upregulation	n∞	0.8
${\stackrel{\sim }{\ell }}_{\mathit{t}\mathit{a}\mathit{f}}$	Threshold lactate level for taf upregulation	n∞	0.8
${\stackrel{\mathbf{\sim }}{\mathit{z}}}_{\ell }$	Charge of a lactate ion	za	−1.0
${\stackrel{\mathbf{\sim }}{\mathit{z}}}_{\mathit{b}}$	Charge of a bicarbonate ion	za	−1.0
${\stackrel{\mathbf{\sim }}{\mathit{z}}}_{\mathit{s}}$	Charge of Na+	za	1.0
${\stackrel{\mathbf{\sim }}{\mathit{z}}}_{\mathit{r}}$	Charge of Cl−	za	−1.0
${\stackrel{\sim }{\mathit{t}\mathit{g}\mathit{f}}}_{\mathit{F}\mathit{E}}$	Threshold level of corresponding to the onset of the upregulation of myofibroblastic cell proliferation	tgfsat	0.1
${\stackrel{\sim }{\mathit{t}\mathit{a}\mathit{f}}}_{\mathit{B}\mathit{n}}$	Threshold level of taf corresponding to the onset of EC proliferation	tafsat	0.2
${\stackrel{\sim }{\mathit{t}\mathit{a}\mathit{f}}}_{\mathit{L}\mathit{n}}$	Threshold level of corresponding to the onset of LEC proliferation	tafsat	0.2
${({\stackrel{\mathbf{\sim }}{\mathit{\epsilon }}}_{\mathit{E}}^{\ast })}_{\mathit{i}\mathit{j}}$	Eigenstrain for the ECM component	$\overline{\overline{\epsilon }}$	1.0
${({\stackrel{\mathbf{\sim }}{\mathit{\epsilon }}}_{\mathit{C}}^{\ast })}_{\mathit{i}\mathit{j}}$	Eigenstrain for the cell components	$\overline{\overline{\epsilon }}$	0.0
${\stackrel{\mathbf{\sim }}{\mathit{L}}}_1^{\mathit{E}}$	Lamé constants for ECM component	$L_2^E$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{L}}}_1^{\mathit{C}}$	Lamé constants for cell components	$L_2^E$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{L}}}_2^{\mathit{C}}$	Lamé constants for cell components	$L_2^E$	1.0
${({\stackrel{\sim }{\varphi }}_{\mathit{E}})}_{\mathit{m}\mathit{i}\mathit{n}\mathbf{,}\mathit{B}\mathit{n}}$	Concentration of ECM macromolecules corresponding to the minimum EC haptotaxis strength	${\stackrel{\sim }{\varphi }}_{\alpha }$	0.2
${({\stackrel{\sim }{\varphi }}_{\mathit{E}})}_{\mathit{m}\mathit{a}\mathit{x}\mathbf{,}\mathit{B}\mathit{n}}$	Concentration of ECM macromolecules corresponding to the maximum EC haptotaxis strength	${\stackrel{\sim }{\varphi }}_{\alpha }$	0.8
${({\stackrel{\sim }{\varphi }}_{\mathit{E}})}_{\mathit{m}\mathit{i}\mathit{n}\mathbf{,}\mathit{L}\mathit{n}}$	Concentration of ECM macromolecules corresponding to the minimum LEC haptotaxis strength	${\stackrel{\sim }{\varphi }}_{\alpha }$	0.2
${({\stackrel{\sim }{\varphi }}_{\mathit{E}})}_{\mathit{m}\mathit{a}\mathit{x}\mathbf{,}\mathit{L}\mathit{n}}$	Concentration of ECM macromolecules corresponding to the maximum LEC haptotaxis strength	${\stackrel{\sim }{\varphi }}_{\alpha }$	0.8
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{c}\mathit{h}\mathit{e}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}$	Positive chemotaxis constant for ECs	tafsat	1.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{c}\mathit{h}\mathit{e}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}$	Positive chemotaxis constant for LECs	tafsat	1.0
${\stackrel{\mathbf{\sim }}{\mathit{p}}}_{\mathit{t}\mathbf{,}\mathit{B}}$	Threshold pressure corresponding to the onset of blood vessel loss	$\mathcal{P}$	0.6
${\stackrel{\mathbf{\sim }}{\mathit{p}}}_{\mathit{t}\mathbf{,}\mathit{L}}$	Threshold pressure corresponding to the onset of lymphatic vessel loss	$\mathcal{P}$	0.6
${\stackrel{\mathbf{\sim }}{\mathit{p}}}_{\mathit{c}\mathbf{,}\mathit{B}\mathit{n}}$	Threshold pressure corresponding to the maximum rate of neo-blood vessel loss	$\mathcal{P}$	0.8
${\stackrel{\mathbf{\sim }}{\mathit{p}}}_{\mathit{c}\mathbf{,}\mathit{L}\mathit{n}}$	Threshold pressure corresponding to the maximum rate of neo-lymphatic vessel loss	$\mathcal{P}$	0.8

^*For example, ${\stackrel{\sim }{n}}_h=n_h/n_{\infty }$.

Nondimensionalized Eigenstrain ${({\stackrel{\sim }{\epsilon }}_E^{\ast })}_{ij}$ and all Lamé constants are set to 1 as an initial value in this study. A wider range of values will be tested and analyzed in future work.

Other scaling factors are listed in Table 7. The dimensionless set of cell-ECM species equations is summarized below:

$$\frac{\partial {\stackrel{\sim }{\varphi }}_V}{\partial \stackrel{\sim }{t}}+\nabla \cdot ({\stackrel{\sim }{\varphi }}_V{\stackrel{\sim }{\mathit{u}}}_{\alpha })=\stackrel{\sim }{M}\nabla \cdot ({\stackrel{\sim }{\varphi }}_V\nabla {\stackrel{\sim }{\mu }}_T)+{\stackrel{\sim }{S}}_V,$$ (3.7.3)

$$\frac{\partial {\stackrel{\sim }{\varphi }}_D}{\partial \stackrel{\sim }{t}}+\nabla \cdot ({\stackrel{\sim }{\varphi }}_D{\stackrel{\sim }{\mathit{u}}}_{\alpha })=\stackrel{\sim }{M}\nabla \cdot ({\stackrel{\sim }{\varphi }}_D\nabla {\stackrel{\sim }{\mu }}_T)+{\stackrel{\sim }{S}}_D,$$ (3.7.4)

$$\frac{\partial {\stackrel{\sim }{\varphi }}_E}{\partial \stackrel{\sim }{t}}+\nabla \cdot ({\stackrel{\sim }{\varphi }}_E{\stackrel{\sim }{\mathit{u}}}_{\alpha })=\stackrel{\sim }{M}\nabla \cdot ({\stackrel{\sim }{\varphi }}_E\nabla {\stackrel{\sim }{\mu }}_E)+{\stackrel{\sim }{S}}_E.$$ (3.7.5)

Table 7.

Scaling Factors

Dimensional Scaling Factor	Biological Representation	Expression
ℒ	Characteristic length	$\sqrt{\frac{D_{T,n}}{{\lambda }_{U,V,n}}}$
$\mathcal{T}$	Characteristic time	$\frac{1}{{\lambda }_{M,V}}$
$\mathcal{P}$	Characteristic cell pressure	$\frac{{ℒ}^2}{{\overline{\overline{k}}}_{\alpha }\mathcal{T}}$
$\mathcal{Q}$	Characteristic fluid pressure	$\frac{{ℒ}^2}{{\overline{\overline{k}}}_{\beta }\mathcal{T}}$
ℳ	Characteristic mobility	$\frac{{ℒ}^2}{\mathcal{T}{E}_a^{\ast }}$
$\overline{\overline{\epsilon }}$	Characteristic interaction strength	$ℒ\sqrt{\frac{E_a^{\ast }}{{\stackrel{\sim }{\varphi }}_{\alpha }}}$
$\overline{\overline{\epsilon }}$	Characteristic Strain	$\sqrt{\frac{E_a^{\ast }{\stackrel{\sim }{\varphi }}_{\alpha }}{E_e^{\ast }\overline{\overline{\epsilon }}{L}_2^E}}$
${\overline{\overline{\mathit{D}}}}_{\mathit{F}}$	Characteristic Myofibroblastic diffusivity	$\frac{{ℒ}^2}{\mathcal{T}tg{f}_{\mathit{sat}}}$

The volume fraction of healthy cell species can be solved using the relation ${\stackrel{\sim }{\varphi }}_H=1-({\stackrel{\sim }{\varphi }}_V+{\stackrel{\sim }{\varphi }}_D+{\stackrel{\sim }{\varphi }}_E)$. The dimensionless chemical potentials are

$${\stackrel{\sim }{\mu }}_T=\frac{\partial {\stackrel{\sim }{F}}_b}{\partial {\stackrel{\sim }{\varphi }}_T}-{{\stackrel{\sim }{\epsilon }}_T}^2{\nabla }^2{\stackrel{\sim }{\varphi }}_T-{{\stackrel{\sim }{\epsilon }}_{TE}}^2{\nabla }^2{\stackrel{\sim }{\varphi }}_E,$$ (3.7.6)

$${\stackrel{\sim }{\mu }}_E=\frac{\partial {\stackrel{\sim }{F}}_b}{\partial {\stackrel{\sim }{\varphi }}_E}+\frac{\partial \stackrel{\sim }{\mathcal{W}}}{\partial {\stackrel{\sim }{\varphi }}_E}-{{\stackrel{\sim }{\epsilon }}_E}^2{\nabla }^2{\stackrel{\sim }{\varphi }}_E-{{\stackrel{\sim }{\epsilon }}_{TE}}^2{\nabla }^2{\stackrel{\sim }{\varphi }}_T,$$ (3.7.7)

$${\stackrel{\sim }{\mu }}_H=\frac{\partial {\stackrel{\sim }{F}}_b}{\partial {\stackrel{\sim }{\varphi }}_H}=0$$ (3.7.8)

where ${\stackrel{\sim }{F}}_b=F_b/({\stackrel{\sim }{\varphi }}_{\alpha }{E}_a^{\ast })$ is the dimensionless bulk free energy given below:

$$\frac{\partial {\stackrel{\sim }{F}}_b}{\partial {\stackrel{\sim }{\varphi }}_T}=2A_1{\stackrel{\sim }{\varphi }}_T(1-{\stackrel{\sim }{\varphi }}_T-{\stackrel{\sim }{\varphi }}_E)(1-2{\stackrel{\sim }{\varphi }}_T-{\stackrel{\sim }{\varphi }}_E)+(2{\stackrel{\sim }{\varphi }}_E-A_5-A_3)(A_5-A_3)$$ (3.7.9)

$$\frac{\partial {\stackrel{\sim }{F}}_b}{\partial {\stackrel{\sim }{\varphi }}_E}=2({\stackrel{\sim }{\varphi }}_T+A_2)({\stackrel{\sim }{\varphi }}_E-A_3)-2A_1{({\stackrel{\sim }{\varphi }}_T)}^2(1-{\stackrel{\sim }{\varphi }}_T-{\stackrel{\sim }{\varphi }}_E)+({\stackrel{\sim }{\varphi }}_E-A_5)[2(1-{\stackrel{\sim }{\varphi }}_T+A_4)-3{\stackrel{\sim }{\varphi }}_E+A_5]$$ (3.7.10)

Dimensionless elastic energy term $\stackrel{\sim }{\mathcal{W}}=\mathcal{W}/({\stackrel{\sim }{\varphi }}_{\alpha }{E}_a^{\ast })$ involved in Eq. (3.7.7) can be written as

$$\frac{\partial \stackrel{\sim }{\mathcal{W}}}{\partial {\stackrel{\sim }{\varphi }}_E}={\stackrel{\sim }{\epsilon }}_e\frac{\partial Q_3({\stackrel{\sim }{\varphi }}_E)}{\partial {\stackrel{\sim }{\varphi }}_E}{\displaystyle \sum _{i,j=1}^3[\frac{1}{2}{({\stackrel{\sim }{\epsilon }}_T)}_{ij}:{\stackrel{\sim }{𝕋}}_{ij}^{\prime }-{({\stackrel{\sim }{\epsilon }}_T^{\prime })}_{ij}:{\stackrel{\sim }{𝕋}}_{ij}]},$$ (3.7.11)

where

$${({\stackrel{\sim }{\epsilon }}_T)}_{ij}={\stackrel{\sim }{\epsilon }}_{ij}-{\stackrel{\sim }{\epsilon }}_{ij}^{\ast },$$ (3.7.12)

$${({\stackrel{\sim }{\epsilon }}_T^{\prime })}_{ij}={({\stackrel{\sim }{\epsilon }}_E^{\ast })}_{ij}-{({\stackrel{\sim }{\epsilon }}_C^{\ast })}_{ij},$$

$${\stackrel{\sim }{\mathbb{T}}}_{ij}=2{\stackrel{\sim }{L}}_2{({\stackrel{\sim }{\epsilon }}_T)}_{ij}+{\stackrel{\sim }{L}}_1{\delta }_{ij}{\displaystyle \sum _{k=1}^3{({\stackrel{\sim }{\epsilon }}_T)}_{kk}},$$ (3.7.13)

$${\stackrel{\sim }{𝕋}}_{ij}^{\prime }=2(1-{\stackrel{\sim }{L}}_2^C){({\stackrel{\sim }{\epsilon }}_T)}_{ij}+({\stackrel{\sim }{L}}_1^E-{\stackrel{\sim }{L}}_1^C){\delta }_{ij}{\displaystyle \sum _{k=1}^3{({\stackrel{\sim }{\epsilon }}_T)}_{kk}},$$

$${\stackrel{\sim }{L}}_1=Q_3({\stackrel{\sim }{\varphi }}_E)({\stackrel{\sim }{L}}_1^E-{\stackrel{\sim }{L}}_1^C)+{\stackrel{\sim }{L}}_1^C,$$ (3.7.14)

$${\stackrel{\sim }{L}}_2=Q_3({\stackrel{\sim }{\varphi }}_E)(1-{\stackrel{\sim }{L}}_2^C)+{\stackrel{\sim }{L}}_2^C,$$

$${\stackrel{\sim }{\epsilon }}_{ij}^{\ast }=Q_3({\stackrel{\sim }{\varphi }}_E)\left[{({\stackrel{\sim }{\epsilon }}_E^{\ast })}_{ij}-{({\stackrel{\sim }{\epsilon }}_C^{\ast })}_{ij}\right]+{({\stackrel{\sim }{\epsilon }}_C^{\ast })}_{ij}.$$ (3.7.15)

The dimensionless Lamé constants are ${\stackrel{\sim }{L}}_1=L_1/L_2^E$, ${\stackrel{\sim }{L}}_2=L_2/L_2^E$, ${({\stackrel{\sim }{\epsilon }}_T)}_{ij}={({\epsilon }_T)}_{ij}/\overline{\overline{\epsilon }},$ ${({\stackrel{\sim }{\epsilon }}_T^{\prime })}_{ij}={({\epsilon }_T^{\prime })}_{ij}/\overline{\overline{\epsilon }}$, ${\stackrel{\sim }{\epsilon }}_{ij}={\epsilon }_{ij}/\overline{\overline{\epsilon }}$, ${\stackrel{\sim }{\epsilon }}_{ij}^{\ast }={\epsilon }_{ij}^{\ast }/\overline{\overline{\epsilon }}$, ${\stackrel{\sim }{\mathbb{T}}}_{ij}={\mathbb{T}}_{ij}/\overline{\overline{\epsilon }}{L}_2^E$, and ${\stackrel{\sim }{𝕋}}_{ij}^{\prime }={𝕋}_{ij}^{\prime }/\overline{\overline{\epsilon }}{L}_2^E$. Adjustment factors ${\stackrel{\sim }{\mathcal{A}}}_i$ are given in Table 8. The nondimensional solid and interstitial fluid velocities are given by

$${\stackrel{\mathbf{\sim }}{\mathit{u}}}_{\alpha }=-{\stackrel{\sim }{k}}_{\alpha }\left[\nabla \stackrel{\sim }{p}-\frac{{\stackrel{\sim }{\gamma }}_T}{{\stackrel{\sim }{\epsilon }}_T}{\stackrel{\sim }{\mu }}_T\nabla {\stackrel{\sim }{\varphi }}_T-\frac{{\stackrel{\sim }{\gamma }}_E}{{\stackrel{\sim }{\epsilon }}_E}{\stackrel{\sim }{\mu }}_E\nabla {\stackrel{\sim }{\varphi }}_E\right],$$ (3.7.16)

$${\stackrel{\mathbf{\sim }}{\mathit{u}}}_{\beta }=-{\stackrel{\sim }{k}}_{\beta }\nabla \stackrel{\sim }{q},$$ (3.7.17)

where ${\stackrel{\sim }{\gamma }}_i={\epsilon }_i{\stackrel{\sim }{\varphi }}_{\alpha }\sqrt{{\stackrel{\sim }{\varphi }}_{\alpha }{E}_a^{\ast }}/(\mathcal{L}\mathcal{P})$ is a dimensionless cell adhesion parameter, for i = T,E. With fixed volume fractions ${\stackrel{\sim }{\varphi }}_{\alpha }$ and ${\stackrel{\sim }{\varphi }}_{\beta }$, Eq. (3.1.2), together with the mass conservation law given in Eq. (3.1.6), yield the continuity equations for the solid and fluid species:

$$\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{u}}}_{\alpha }={\displaystyle \sum _{i=1}^4{\stackrel{\sim }{S}}_i},$$ (3.7.18)

$$\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{u}}}_{\beta }=-{\mathrm{R}}_{\alpha ,\beta }{\displaystyle \sum _{i=1}^4{\stackrel{\sim }{S}}_i},$$ (3.7.19)

where ${\mathrm{R}}_{\alpha ,\beta }={\stackrel{\sim }{\varphi }}_{\alpha }/{\stackrel{\sim }{\varphi }}_{\beta }$. Combining Eqs. (3.7.16), (3.7.17), (3.7.18), and (3.7.19), we obtain the Poisson equations for both pressure terms:

$$\nabla \cdot \left\{{\stackrel{\sim }{k}}_{\alpha }\left[\nabla \stackrel{\sim }{p}-\frac{{\stackrel{\sim }{\gamma }}_T}{{\stackrel{\sim }{\epsilon }}_T}{\stackrel{\sim }{\mu }}_T\nabla {\stackrel{\sim }{\varphi }}_T-\frac{{\stackrel{\sim }{\gamma }}_E}{{\stackrel{\sim }{\epsilon }}_E}{\stackrel{\sim }{\mu }}_E\nabla {\stackrel{\sim }{\varphi }}_E\right]\right\}=-{\displaystyle \sum _{i=1}^4{\stackrel{\sim }{S}}_i},$$ (3.7.20)

$$\nabla \cdot ({\stackrel{\sim }{k}}_{\beta }\nabla \stackrel{\sim }{q})=R_{\alpha ,\beta }{\displaystyle \sum _{i=1}^4{\stackrel{\sim }{S}}_i}.$$ (3.7.21)

Table 8.

Adjustment Factors.

From Eq. (3.7.22)

${\mathcal{A}}_{M,V}=\stackrel{\sim }{n}\left(1+{ℱ}_{\mathit{tgf},V}^M\stackrel{\sim }{\mathit{tgf}}\right)\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_h\right)$

${\mathcal{A}}_{A,V}=\left(1-{ℱ}_{\mathit{tgf},V}^A\stackrel{\sim }{\mathit{tgf}}\right)\left(1-{ℱ}_{E,V}^A{\stackrel{\sim }{\varphi }}_E\right)$

${\mathcal{A}}_{N,V}=1-\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,V}\right)\mathscr{H}\left(\stackrel{\sim }{g}-{\stackrel{\sim }{g}}_{v,V}\right)$

${\mathcal{A}}_{B,V}={ℱ}_{B,V}^{\mathit{met}}{Q}_3\left(1-\frac{\stackrel{\sim }{p}}{{\stackrel{\sim }{p}}_{t,B}}\right)\mathscr{H}\left({\stackrel{\sim }{p}}_{t,B}-\stackrel{\sim }{p}\right)$

where ${ℱ}_{B,V}^{\mathit{met}}=Q_3\left(\frac{\stackrel{\sim }{\ell }}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}}\right)Q_3\left(\stackrel{\sim }{B}\right)$

${\mathcal{A}}_{L,V}={ℱ}_{L,V}^{\mathit{met}}{Q}_3\left(1-\frac{\stackrel{\sim }{p}}{{\stackrel{\sim }{p}}_{t,L}}\right)\mathscr{H}\left({\stackrel{\sim }{p}}_{t,L}-\stackrel{\sim }{p}\right)$

where ${ℱ}_{L,V}^{\mathit{met}}=Q_3\left(\frac{\stackrel{\sim }{\ell }}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}}\right)Q_3\left(\stackrel{\sim }{L}\right)$

${\mathcal{A}}_{de,V}=Q_3\left(\frac{\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,V}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,V}}\right)Q_3\left(\frac{\stackrel{\sim }{g}-{\stackrel{\sim }{g}}_{v,V}}{{\stackrel{\sim }{g}}_{de,v}-{\stackrel{\sim }{g}}_{v,V}}\right)\left(1+{ℱ}_{\mathit{tgf},V}^{de}\stackrel{\sim }{\mathit{tgf}}\right)\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,V}\right)\mathscr{H}\left({\stackrel{\sim }{g}}_{de,V}-\stackrel{\sim }{g}\right)\mathscr{H}\left(\stackrel{\sim }{g}-{\stackrel{\sim }{g}}_{v,V}\right)$

From Eq. (3.7.22)

${\mathcal{A}}_{L,D}=1$

From Eq. (3.7.22)

${\mathcal{A}}_{V,E}=\left(1-{\stackrel{\sim }{\varphi }}_E\right)\left[1+{ℱ}_{n,E}^V\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,V}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,V}\right)$

${\mathcal{A}}_{B,E}=\left(1-{\stackrel{\sim }{\varphi }}_E\right)\left[1+{ℱ}_{n,E}^B\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,B}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,B}\right)$

${\mathcal{A}}_{L,E}=\left(1-{\stackrel{\sim }{\varphi }}_E\right)\left[1+{ℱ}_{n,E}^L\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,L}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,L}\right)$

${\mathcal{A}}_{F,E}=\left(1-{\stackrel{\sim }{\varphi }}_E\right)\left[1+{ℱ}_{n,E}^F\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,F}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,F}\right)$

${\mathcal{A}}_{de,E}=\stackrel{\sim }{m}$

From Eqs. (3.7.26)

${\mathcal{A}}_{B,n}=\left(\stackrel{\sim }{B}\right)Q_3\left(1-\frac{\stackrel{\sim }{p}}{{\stackrel{\sim }{p}}_{t,B}}\right)\mathscr{H}\left({\stackrel{\sim }{p}}_{t,B}-\stackrel{\sim }{p}\right)={\mathcal{A}}_B$

${\mathcal{A}}_{U,V,n}={\stackrel{\sim }{\varphi }}_V$

${\mathcal{A}}_{U,H,n}={\stackrel{\sim }{\varphi }}_H$

${\mathcal{A}}_{B,g}={\mathcal{A}}_B$

${\mathcal{A}}_{U,V,g}={\stackrel{\sim }{\varphi }}_V$

${\mathcal{A}}_{U,H,g}={\stackrel{\sim }{\varphi }}_H$

${\mathcal{A}}_{B,w}={\mathcal{A}}_B$

${\mathcal{A}}_{B,\ell }={\mathcal{A}}_B$

From Eq. (3.7.33)

${\mathcal{A}}_{V,\mathit{tgf}}={\stackrel{\sim }{\varphi }}_V$

${\mathcal{A}}_{B,\mathit{tgf}}=\stackrel{\sim }{B}\left[1+{ℱ}_{n,\mathit{tgf}}^B\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,B}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\left[1+{ℱ}_{\ell ,\mathit{tgf}}^B\frac{\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}}\mathscr{H}\left(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,B}\right)$

${\mathcal{A}}_{L,\mathit{tgf}}=\stackrel{\sim }{L}\left[1+{ℱ}_{n,\mathit{tgf}}^L\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,L}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\left[1+{ℱ}_{\ell ,\mathit{tgf}}^L\frac{\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}}\mathscr{H}\left(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,L}\right)$

${\mathcal{A}}_{F,\mathit{tgf}}=\stackrel{\sim }{F}\left[1+{ℱ}_{n,\mathit{tgf}}^F\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,F}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\left[1+{ℱ}_{\ell ,\mathit{tgf}}^F\frac{\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}}\mathscr{H}\left(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{tgf}}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,F}\right)$

${\mathcal{A}}_{U,V,\mathit{tgf}}={\stackrel{\sim }{\varphi }}_V$

From Eq. (3.7.33)

${\mathcal{A}}_{V,\mathit{taf}}={\stackrel{\sim }{\varphi }}_V\left[1+{ℱ}_{n,\mathit{taf}}^V\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,V}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,V}\right)\mathit{where}{ℱ}_{\ell ,\mathit{taf}}^V=0$

${\mathcal{A}}_{B,\mathit{taf}}=\stackrel{\sim }{B}\left[1+{ℱ}_{n,\mathit{taf}}^B\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,B}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\left[1+{ℱ}_{\ell ,\mathit{taf}}^B\frac{\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{taf}}}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}-{\stackrel{\sim }{\ell }}_{\mathit{taf}}}\mathscr{H}\left(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{taf}}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,B}\right)$

${\mathcal{A}}_{L,\mathit{taf}}=\stackrel{\sim }{L}\left[1+{ℱ}_{n,\mathit{taf}}^L\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,L}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\left[1+{ℱ}_{\ell ,\mathit{taf}}^L\frac{\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{taf}}}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}-{\stackrel{\sim }{\ell }}_{\mathit{taf}}}\mathscr{H}\left(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{taf}}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,L}\right)$

${\mathcal{A}}_{F,\mathit{taf}}=\stackrel{\sim }{F}\left[1+{ℱ}_{n,\mathit{taf}}^F\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,F}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\left[1+{ℱ}_{\ell ,\mathit{taf}}^F\frac{\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{taf}}}{{\stackrel{\sim }{\ell }}_{\mathit{sat}}-{\stackrel{\sim }{\ell }}_{\mathit{taf}}}\mathscr{H}\left(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_{\mathit{taf}}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,F}\right)$

From Eq. (3.7.33)

${\mathcal{A}}_{V,m}={\stackrel{\sim }{\varphi }}_V$

${\mathcal{A}}_{F,m}=\stackrel{\sim }{F}\left[1+{ℱ}_{n,m}^F\frac{{\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}}{{\stackrel{\sim }{n}}_h-{\stackrel{\sim }{n}}_{v,F}}\mathscr{H}\left({\stackrel{\sim }{n}}_h-\stackrel{\sim }{n}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,F}\right)$

From Eq. (3.7.33)

${\mathcal{A}}_{M,FE}=\left(1-F_E\right)Q_3\left(\frac{\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_h}{1-{\stackrel{\sim }{n}}_h}\right)\left[1+{ℱ}_{\mathit{tgf},F}^M\stackrel{\sim }{\mathit{tgf}}\mathscr{H}\left(\stackrel{\sim }{\mathit{tgf}}-{\stackrel{\sim }{\mathit{tgf}}}_{FE}\right)\right]\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_h\right)$

${\mathcal{A}}_{N,FE}=1-\mathscr{H}\left(\stackrel{\sim }{n}-{\stackrel{\sim }{n}}_{v,F}\right)\mathscr{H}\left(\stackrel{\sim }{g}-{\stackrel{\sim }{g}}_{v,F}\right)$

${\mathcal{A}}_{A,F,E}=1$

From Eqs. (3.7.37)

${\mathcal{A}}_{\mathit{che},\mathit{BnE}}={ℱ}_{Bn}$ where the effect of TAF is not considered.

${\mathcal{A}}_{\mathit{hap},\mathit{BnE}}=\{\begin{array}{cc}{\stackrel{\sim }{\mathrm{\omega }}}_{Bn}{ℱ}_{Bn}& {\stackrel{\sim }{\varphi }}_E<{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{min},Bn}\mathit{and}{\stackrel{\sim }{\varphi }}_E>{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Bn}\\ \left[\left(1-{\stackrel{\sim }{\mathrm{\omega }}}_{Bn}\right){\mathit{Q}}_4\left(\frac{{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Bn}-{\stackrel{\sim }{\varphi }}_E}{{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Bn}-{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{min},Bn}}\right)+{\stackrel{\sim }{\mathrm{\omega }}}_{Bn}\right]{ℱ}_{Bn}& {\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{min},Bn}\le {\stackrel{\sim }{\varphi }}_E\le {\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Bn}\end{array}$

where ${\stackrel{\sim }{\mathrm{\omega }}}_{Bn}=\frac{{\stackrel{\sim }{\chi }}_{\mathit{hap},Bn}^{\mathit{min}}}{{\stackrel{\sim }{\chi }}_{\mathit{hap},Bn}}$

${\mathcal{A}}_{\mathit{che},\mathit{LnE}}={ℱ}_{Ln}$ where the effect of TAF is not considered.

${\mathcal{A}}_{\mathit{hap},\mathit{LnE}}=\{\begin{array}{cc}{\stackrel{\sim }{\mathrm{\omega }}}_{Ln}{ℱ}_{Ln}& {\stackrel{\sim }{\varphi }}_E<{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{min},Ln}\mathit{and}{\stackrel{\sim }{\varphi }}_E>{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Ln}\\ \left[\left(1-{\stackrel{\sim }{\mathrm{\omega }}}_{Ln}\right){\mathit{Q}}_4\left(\frac{{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Ln}-{\stackrel{\sim }{\varphi }}_E}{{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Ln}-{\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{min},Ln}}\right)+{\stackrel{\sim }{\mathrm{\omega }}}_{Ln}\right]{ℱ}_{Ln}& {\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{min},Ln}\le {\stackrel{\sim }{\varphi }}_E\le {\left({\stackrel{\sim }{\varphi }}_E\right)}_{\mathit{max},Ln}\end{array}$

where ${\stackrel{\sim }{\mathrm{\omega }}}_{Ln}=\frac{{\stackrel{\sim }{\chi }}_{\mathit{hap},Ln}^{\mathit{min}}}{{\stackrel{\sim }{\chi }}_{\mathit{hap},Ln}}$

From Eqs. (3.7.38)

${\mathcal{A}}_{m,\mathit{BnE}}={ℱ}_{Bn}\left(1-{ℱ}_{lg,Bn}{\stackrel{\sim }{B}}_n^E\right)Q_3\left(\frac{\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Bn}}{1-{\stackrel{\sim }{\mathit{taf}}}_{Bn}}\right)\mathscr{H}\left(\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Bn}\right)$

${\mathcal{A}}_{de,\mathit{BnE}}={ℱ}_{Bn}{Q}_3\left(\frac{\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Bn}}{1-{\stackrel{\sim }{\mathit{taf}}}_{Bn}}\right)\mathscr{H}\left(\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Bn}\right)$

${\mathcal{A}}_{as,\mathit{BnE}}={ℱ}_{Bn}{Q}_3\left(\frac{\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Bn}}{1-{\stackrel{\sim }{\mathit{taf}}}_{Bn}}\right)\mathscr{H}\left(\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Bn}\right)$

${\mathcal{A}}_{\mathit{crush},\mathit{BnE}}=\mathscr{H}\left(\stackrel{\sim }{p}-{\stackrel{\sim }{p}}_{c,Bn}\right)$

${\mathcal{A}}_{m,\mathit{LnE}}={ℱ}_{Ln}\left(1-{ℱ}_{lg,Ln}{\stackrel{\sim }{L}}_n^E\right)Q_3\left(\frac{\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Ln}}{1-{\stackrel{\sim }{\mathit{taf}}}_{Ln}}\right)\mathscr{H}\left(\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Ln}\right)$

${\mathcal{A}}_{de,\mathit{LnE}}={ℱ}_{Ln}{Q}_3\left(\frac{\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Ln}}{1-{\stackrel{\sim }{\mathit{taf}}}_{Ln}}\right)\mathscr{H}\left(\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Ln}\right)$

${\mathcal{A}}_{as,\mathit{LnE}}={ℱ}_{Ln}{Q}_3\left(\frac{\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Ln}}{1-{\stackrel{\sim }{\mathit{taf}}}_{Ln}}\right)\mathscr{H}\left(\stackrel{\sim }{\mathit{taf}}-{\stackrel{\sim }{\mathit{taf}}}_{Ln}\right)$

${\mathcal{A}}_{\mathit{crush},\mathit{LnE}}=\mathscr{H}\left(\stackrel{\sim }{p}-{\stackrel{\sim }{p}}_{c,Ln}\right)$

The two velocities are calculated a posteriori in each iteration after the pressures have been computed. The nondimensional source terms are given below:

$$\begin{gathered} {\stackrel{\sim }{S}}_V={\stackrel{\sim }{r}}_{M,V}-{\stackrel{\sim }{r}}_{A,V}-{\stackrel{\sim }{r}}_{N,V}-{\stackrel{\sim }{r}}_{B,V}-{\stackrel{\sim }{r}}_{L,V}-{\stackrel{\sim }{r}}_{de,V}= \\ {\mathcal{A}}_{M,V}{\stackrel{\sim }{\varphi }}_V-{\stackrel{\sim }{\mathrm{\lambda }}}_{A,V}{\mathcal{A}}_{A,V}{\stackrel{\sim }{\varphi }}_V-{\stackrel{\sim }{\mathrm{\lambda }}}_{N,V}{\mathcal{A}}_{N,V}{\stackrel{\sim }{\varphi }}_V-{\stackrel{\sim }{\mathrm{\lambda }}}_{B,V}{\mathcal{A}}_{B,V}{\stackrel{\sim }{\varphi }}_V-{\stackrel{\sim }{\mathrm{\lambda }}}_{L,V}{\mathcal{A}}_{L,V}{\stackrel{\sim }{\varphi }}_V-{\stackrel{\sim }{\mathrm{\lambda }}}_{de,V}{\mathcal{A}}_{de,V}{\stackrel{\sim }{\varphi }}_V, \end{gathered}$$

$${\stackrel{\sim }{S}}_D={\stackrel{\sim }{r}}_{A,V}+{\stackrel{\sim }{r}}_{N,V}-{\stackrel{\sim }{r}}_{L,D}={\stackrel{\sim }{\mathrm{\lambda }}}_{A,V}{\mathcal{A}}_{A,V}{\stackrel{\sim }{\varphi }}_V+{\stackrel{\sim }{\mathrm{\lambda }}}_{N,V}{\mathcal{A}}_{N,V}{\stackrel{\sim }{\varphi }}_V-{\stackrel{\sim }{\mathrm{\lambda }}}_{L,D}{\mathcal{A}}_{L,D}{\stackrel{\sim }{\varphi }}_D,$$ (3.7.22)

$${\stackrel{\sim }{S}}_E={\stackrel{\sim }{r}}_{V,E}+{\stackrel{\sim }{r}}_{B,E}+{\stackrel{\sim }{r}}_{L,E}+{\stackrel{\sim }{r}}_{F,E}+{\stackrel{\sim }{r}}_{de,E}={\stackrel{\sim }{\mathrm{\lambda }}}_{V,E}{\mathcal{A}}_{V,E}{\stackrel{\sim }{\varphi }}_V+{\stackrel{\sim }{\mathrm{\lambda }}}_{B,E}{\mathcal{A}}_{B,E}\stackrel{\sim }{B}+{\stackrel{\sim }{\mathrm{\lambda }}}_{L,E}{\mathcal{A}}_{L,E}\stackrel{\sim }{L}+{\stackrel{\sim }{\mathrm{\lambda }}}_{F,E}{\mathcal{A}}_{F,E}\stackrel{\sim }{F}-{\stackrel{\sim }{\mathrm{\lambda }}}_{de,E}{\mathcal{A}}_{de,V}{\stackrel{\sim }{\varphi }}_E,$$

where adjustment factors are listed in Table 8.

The dimensionless governing equations for nutrients and waste products are

$$0=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{N}}}_n+{\stackrel{\sim }{S}}_n,$$

$$0=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{N}}}_g+{\stackrel{\sim }{S}}_g,$$

$$0=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{N}}}_w+{\stackrel{\sim }{S}}_w,$$ (3.7.23)

$$0=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{N}}}_{\ell }+{\stackrel{\sim }{S}}_{\ell },$$

$$0=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{N}}}_b+{\stackrel{\sim }{S}}_b,$$

$$0=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{N}}}_a+{\stackrel{\sim }{S}}_a,$$

$$0=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{N}}}_s\cdot$$

The chloride ion concentration is not modeled directly. It is calculated at the end of each iteration step by the relation given by electroneutrality, $\stackrel{\sim }{r}=-({\stackrel{\sim }{z}}_{\ell }\stackrel{\sim }{\ell }+{\stackrel{\sim }{z}}_b\stackrel{\sim }{b}+{\stackrel{\sim }{z}}_a\stackrel{\sim }{a}+{\stackrel{\sim }{z}}_s\stackrel{\sim }{s})/{\stackrel{\sim }{z}}_r$. The nondimensional flux terms for uncharged and ionic species are given below:

$${\stackrel{\mathbf{\sim }}{\mathit{N}}}_n=-{\stackrel{\sim }{D}}_n\nabla \stackrel{\sim }{n},{\stackrel{\mathbf{\sim }}{\mathit{N}}}_g=-{\stackrel{\sim }{D}}_g\nabla \stackrel{\sim }{g},{\stackrel{\mathbf{\sim }}{\mathit{N}}}_w=-{\stackrel{\sim }{D}}_w\nabla \stackrel{\sim }{w},$$

$${\stackrel{\mathbf{\sim }}{\mathit{N}}}_{\sigma }={\stackrel{\sim }{D}}_{\sigma }\left[{\stackrel{\sim }{z}}_{\sigma }\stackrel{\sim }{\sigma }\left(\frac{{\stackrel{\sim }{z}}_{\ell }{\stackrel{\sim }{D}}_{\ell }\nabla \stackrel{\sim }{\ell }+{\stackrel{\sim }{z}}_b{\stackrel{\sim }{D}}_b\nabla \stackrel{\sim }{b}+{\stackrel{\sim }{D}}_a\nabla \stackrel{\sim }{a}+{\stackrel{\sim }{z}}_s{\stackrel{\sim }{D}}_s\nabla \stackrel{\sim }{s}+{\stackrel{\sim }{z}}_r{\stackrel{\sim }{D}}_r\nabla \stackrel{\sim }{r}}{{\stackrel{\sim }{z}}_{\ell }^2{\stackrel{\sim }{D}}_{\ell }\stackrel{\sim }{\ell }+{\stackrel{\sim }{z}}_b^2{\stackrel{\sim }{D}}_b\stackrel{\sim }{b}+{\stackrel{\sim }{D}}_a\stackrel{\sim }{a}+{\stackrel{\sim }{z}}_s^2{\stackrel{\sim }{D}}_s\stackrel{\sim }{s}+{\stackrel{\sim }{z}}_r^2{\stackrel{\sim }{D}}_r\stackrel{\sim }{r}}\right)-\nabla \stackrel{\sim }{\sigma }\right]$$ (3.7.24)

where σ = ℓ, b, a, and s. Diffusivities in the two equations above can be written in dimensionless form as

$${\stackrel{\sim }{D}}_{\sigma }={\stackrel{\sim }{D}}_{\sigma ,E}{Q}_3({\stackrel{\sim }{\varphi }}_E)+{\stackrel{\sim }{D}}_{\sigma ,C}\left[1-Q_3({\stackrel{\sim }{\varphi }}_E)\right]$$

$${\stackrel{\sim }{D}}_{\sigma ,C}={\stackrel{\sim }{D}}_{\sigma ,T}{Q}_3\left(\frac{{\stackrel{\sim }{\varphi }}_T}{{\stackrel{\sim }{\varphi }}_C}\right)+{\stackrel{\sim }{D}}_{\sigma ,H}\left[1-Q_3\left(\frac{{\stackrel{\sim }{\varphi }}_T}{{\stackrel{\sim }{\varphi }}_C}\right)\right]$$ (3.7.25)

where ${\stackrel{\sim }{\varphi }}_C={\stackrel{\sim }{\varphi }}_T+{\stackrel{\sim }{\varphi }}_H$. The nondimensional source terms of nutrients and waste products listed below:

$${\stackrel{\sim }{S}}_n={\stackrel{\sim }{r}}_{B,n}+{\stackrel{\sim }{r}}_{U,n}={\stackrel{\sim }{\mathrm{\lambda }}}_{B,n}{\mathcal{A}}_{B,n}({\stackrel{\sim }{n}}_C-\stackrel{\sim }{n})-({\mathcal{A}}_{U,V,n}+{\stackrel{\sim }{\mathrm{\lambda }}}_{U,H,n}{\mathcal{A}}_{U,H,n})\stackrel{\sim }{n},$$

$${\stackrel{\sim }{S}}_g={\stackrel{\sim }{r}}_{B,g}+{\stackrel{\sim }{r}}_{U,g}={\stackrel{\sim }{\mathrm{\lambda }}}_{B,g}{\mathcal{A}}_{B,g}({\stackrel{\sim }{g}}_C-\stackrel{\sim }{g})-({\stackrel{\sim }{\mathrm{\lambda }}}_{U,V,g}{\mathcal{A}}_{U,V,g}+{\stackrel{\sim }{\mathrm{\lambda }}}_{U,H,g}{\mathcal{A}}_{U,H,g})\stackrel{\sim }{g},$$ (3.7.26)

$${\stackrel{\sim }{S}}_w={\stackrel{\sim }{r}}_{W,w}+{\stackrel{\sim }{r}}_{B,w}=-{\stackrel{\sim }{r}}_{U,n}-{\stackrel{\sim }{k}}_f\stackrel{\sim }{w}+{\stackrel{\sim }{k}}_r\stackrel{\sim }{b}\stackrel{\sim }{a}-{\stackrel{\sim }{\mathrm{\lambda }}}_{B,w}{\mathcal{A}}_{B,w}(\stackrel{\sim }{w}-{\stackrel{\sim }{w}}_C),$$

$${\stackrel{\sim }{S}}_{\ell }={\stackrel{\sim }{r}}_{W,\ell }+{\stackrel{\sim }{r}}_{B,\ell }=-\left(2R_{g,n}{\stackrel{\sim }{r}}_{U,g}-\frac{1}{3}{\stackrel{\sim }{r}}_{U,n}\right)-{\stackrel{\sim }{\mathrm{\lambda }}}_{B,\ell }{\mathcal{A}}_{B,\ell }(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_C),$$

$${\stackrel{\sim }{S}}_b={\stackrel{\sim }{r}}_{W,b}=-{\stackrel{\sim }{r}}_{U,n}-{\stackrel{\sim }{r}}_{W,w}={\stackrel{\sim }{k}}_f\stackrel{\sim }{w}-{\stackrel{\sim }{k}}_r\stackrel{\sim }{b}\stackrel{\sim }{a},$$

$${\stackrel{\sim }{S}}_a={\stackrel{\sim }{r}}_{W,a}+{\stackrel{\sim }{r}}_{B,a}={\stackrel{\sim }{r}}_{W,\ell }+{\stackrel{\sim }{r}}_{W,b}+{\stackrel{\sim }{r}}_{B,\ell }=-\left(2R_{g,n}{\stackrel{\sim }{r}}_{U,g}-\frac{1}{3}{\stackrel{\sim }{r}}_{U,n}\right)+{\stackrel{\sim }{k}}_f\stackrel{\sim }{w}-{\stackrel{\sim }{k}}_r\stackrel{\sim }{b}\stackrel{\sim }{a}-{\stackrel{\mathbf{\sim }}{\mathit{\lambda }}}_{B,\ell }{\mathcal{A}}_{B,\ell }(\stackrel{\sim }{\ell }-{\stackrel{\sim }{\ell }}_C),$$

where R_g,n = g_∞/n_∞ and adjustment factors ${\mathcal{A}}_i$ are given in Table 8. The transfer rate coefficients ${\stackrel{\sim }{\mathrm{\lambda }}}_{B,n}$, ${\stackrel{\sim }{\mathrm{\lambda }}}_{B,g}$, ${\stackrel{\sim }{\mathrm{\lambda }}}_{B,w}$, and ${\stackrel{\sim }{\mathrm{\lambda }}}_{B,\ell }$ follows the form

$${\stackrel{\sim }{\mathrm{\lambda }}}_{B,\sigma }={\stackrel{\sim }{\mathrm{\lambda }}}_{B,\sigma ,E}{Q}_3({\stackrel{\sim }{\varphi }}_E)+{\stackrel{\sim }{\mathrm{\lambda }}}_{B,\sigma ,C}\left[1-Q_3({\stackrel{\sim }{\varphi }}_E)\right],$$

$${\stackrel{\sim }{\mathrm{\lambda }}}_{B,\sigma ,C}={\stackrel{\sim }{\mathrm{\lambda }}}_{B,\sigma ,T}{Q}_3\left(\frac{{\stackrel{\sim }{\varphi }}_T}{{\stackrel{\sim }{\varphi }}_C}\right)+{\stackrel{\sim }{\mathrm{\lambda }}}_{B,\sigma ,H}\left[1-Q_3\left(\frac{{\stackrel{\sim }{\varphi }}_T}{{\stackrel{\sim }{\varphi }}_C}\right)\right].$$ (3.7.27)

The governing equations of tumorigenic species shown in Eqs. (3.5.1) – (3.5.3) are nondimensionalized and presented below:

$$0=\nabla \cdot ({\stackrel{\sim }{D}}_{\mathit{tgf}}\nabla \stackrel{\sim }{\mathit{tgf}})+{\stackrel{\sim }{S}}_{\mathit{tgf}}$$ (3.7.28)

$$0=\nabla \cdot ({\stackrel{\sim }{D}}_{\mathit{taf}}\nabla \stackrel{\sim }{\mathit{taf}})+{\stackrel{\sim }{S}}_{\mathit{taf}}$$ (3.7.29)

$$\frac{\partial \stackrel{\sim }{m}}{\partial \stackrel{\sim }{t}}=\nabla \cdot ({\stackrel{\sim }{D}}_m\nabla \stackrel{\sim }{m})+{\stackrel{\sim }{S}}_m$$ (3.7.30)

$$\frac{\partial ({\stackrel{\sim }{F}}_E)}{\partial \stackrel{\sim }{t}}+\nabla \cdot ({\stackrel{\sim }{F}}_E{\stackrel{\mathbf{\sim }}{\mathit{u}}}_E)=-\nabla \cdot ({\stackrel{\sim }{D}}_F{\stackrel{\sim }{F}}_E\nabla \stackrel{\sim }{\mathit{tgf}})+{\stackrel{\sim }{S}}_{FE}$$ (3.7.31)

and $\stackrel{\sim }{F}={\stackrel{\sim }{\varphi }}_E{\stackrel{\sim }{F}}_E$, ${\stackrel{\sim }{S}}_F={\stackrel{\sim }{\varphi }}_E{\stackrel{\sim }{S}}_{FE}$.

All diffusivity terms ${\stackrel{\sim }{D}}_i$ in Eqs (3.7.28) – (3.7.31) are written in the same form as Eq. (3.7.25). The source terms are expressed in the following dimensionless functions:

$${\stackrel{\sim }{S}}_{\mathit{tgf}}={\stackrel{\sim }{r}}_{V,\mathit{tgf}}+{\stackrel{\sim }{r}}_{B,\mathit{tgf}}+{\stackrel{\sim }{r}}_{L,\mathit{tgf}}+{\stackrel{\sim }{r}}_{F,\mathit{tgf}}+{\stackrel{\sim }{r}}_{de,\mathit{tgf}}+{\stackrel{\sim }{r}}_{U,\mathit{tgf}}={\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{tgf}}-({\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{tgf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{de,\mathit{tgf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{U,\mathit{tgf}})\stackrel{\sim }{\mathit{tgf}}$$

$${\stackrel{\sim }{S}}_{\mathit{taf}}={\stackrel{\sim }{r}}_{V,\mathit{taf}}+{\stackrel{\sim }{r}}_{B,\mathit{taf}}+{\stackrel{\sim }{r}}_{L,\mathit{taf}}+{\stackrel{\sim }{r}}_{F,\mathit{taf}}+{\stackrel{\sim }{r}}_{de,\mathit{taf}}+{\stackrel{\sim }{r}}_{U,B,\mathit{taf}}+{\stackrel{\sim }{r}}_{U,L,\mathit{taf}}={\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{taf}}-({\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{taf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{de,\mathit{taf}})\stackrel{\sim }{\mathit{taf}}+{\stackrel{\sim }{r}}_{U,B,\mathit{taf}}+{\stackrel{\sim }{r}}_{U,L,\mathit{taf}}$$ (3.7.32)

$${\stackrel{\sim }{S}}_m={\stackrel{\sim }{r}}_{V,m}+{\stackrel{\sim }{r}}_{B,m}+{\stackrel{\sim }{r}}_{L,m}+{\stackrel{\sim }{r}}_{F,m}+{\stackrel{\sim }{r}}_{de,m}={\stackrel{\sim }{\mathrm{\lambda }}}_m-({\stackrel{\sim }{\mathrm{\lambda }}}_m+{\stackrel{\sim }{\mathrm{\lambda }}}_{de,m})\stackrel{\sim }{m}-R_{\mathit{taf},m}{R}_{\mathrm{\lambda }}({\stackrel{\sim }{r}}_{U,B,\mathit{taf}}+{\stackrel{\sim }{r}}_{U,L,\mathit{taf}})$$

$${\stackrel{\sim }{S}}_{FE}={\stackrel{\sim }{r}}_{M,FE}-{\stackrel{\sim }{r}}_{A,FE}-{\stackrel{\sim }{r}}_{N,FE}={\stackrel{\sim }{\mathrm{\lambda }}}_{M,FE}{\mathcal{A}}_{M,FE}{\stackrel{\sim }{F}}_E-{\stackrel{\sim }{\mathrm{\lambda }}}_{A,FE}{\mathcal{A}}_{A,FE}{\stackrel{\sim }{F}}_E-{\stackrel{\sim }{\mathrm{\lambda }}}_{N,FE}{\mathcal{A}}_{N,FE}{\stackrel{\sim }{F}}_E$$

where R_taf,m = taf_sat/m_sat, R_λ = λ_U,V,n/λ_M,V, adjustment factors ${\mathcal{A}}_i$ are given in Table 8, and the transfer rate coefficient ${\stackrel{\sim }{\mathrm{\lambda }}}_{B,h}$ takes the same form as depicted in Eq. (3.7.27). Additional rate expressions are nondimensionalized as

$${\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{tgf}}={\stackrel{\sim }{\mathrm{\lambda }}}_{V,\mathit{tgf}}{\mathcal{A}}_{V,\mathit{tgf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{B,\mathit{tgf}}{\mathcal{A}}_{B,\mathit{tgf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{L,\mathit{tgf}}{\mathcal{A}}_{L,\mathit{tgf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{F,\mathit{tgf}}{\mathcal{A}}_{F,\mathit{tgf}}$$

$${\stackrel{\sim }{\mathrm{\lambda }}}_{U,\mathit{tgf}}={\stackrel{\sim }{\mathrm{\lambda }}}_{U,V,\mathit{tgf}}{\mathcal{A}}_{U,V,\mathit{tgf}}$$

$${\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{taf}}={\stackrel{\sim }{\mathrm{\lambda }}}_{V,\mathit{taf}}{\mathcal{A}}_{V,\mathit{taf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{B,\mathit{taf}}{\mathcal{A}}_{B,\mathit{taf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{L,\mathit{taf}}{\mathcal{A}}_{L,\mathit{taf}}+{\stackrel{\sim }{\mathrm{\lambda }}}_{F,\mathit{taf}}{\mathcal{A}}_{L,\mathit{taf}}$$

$${\stackrel{\sim }{\mathrm{\lambda }}}_m={\stackrel{\sim }{\mathrm{\lambda }}}_{V,m}{\mathcal{A}}_{V,m}+{\stackrel{\sim }{\mathrm{\lambda }}}_{F,m}{\mathcal{A}}_{F,m}$$ (3.7.33)

$${\stackrel{\sim }{r}}_{U,B,\mathit{taf}}=-{\stackrel{\sim }{\mathrm{\lambda }}}_{U,B,\mathit{taf}}\stackrel{\sim }{\mathit{taf}}{\stackrel{\sim }{B}}_{n}or{\stackrel{\sim }{r}}_{U,B,\mathit{taf}}=-\frac{{\stackrel{\sim }{k}}_{\mathit{cat},B}\stackrel{\sim }{\mathit{taf}}{\stackrel{\sim }{B}}_n}{{\stackrel{\sim }{K}}_{m,B}+\stackrel{\sim }{\mathit{taf}}}$$

$${\stackrel{\sim }{r}}_{U,L,\mathit{taf}}=-{\stackrel{\sim }{\mathrm{\lambda }}}_{U,L,\mathit{taf}}\stackrel{\sim }{\mathit{taf}}{\stackrel{\sim }{L}}_{n}or{\stackrel{\sim }{r}}_{U,L,\mathit{taf}}=-\frac{{\stackrel{\sim }{k}}_{\mathit{cat},L}\stackrel{\sim }{\mathit{taf}}{\stackrel{\sim }{L}}_n}{{\stackrel{\sim }{K}}_{m,L}+\stackrel{\sim }{\mathit{taf}}}$$

Adjustment factors ${\mathcal{A}}_i$ are given in Table 8.

Neo–blood and neo–lymphatic vessels, expressed in dimensionless densities, are governed by the following equations:

$$\frac{\partial {\stackrel{\sim }{B}}_n^E}{\partial \stackrel{\sim }{t}}+\nabla \cdot ({\stackrel{\sim }{B}}_n^E{\stackrel{\mathbf{\sim }}{\mathit{u}}}_E)=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{J}}}_{\mathit{BnE}}+{\stackrel{\sim }{S}}_{\mathit{BnE}}$$ (3.7.34)

$$\frac{\partial {\stackrel{\sim }{L}}_n^E}{\partial \stackrel{\sim }{t}}+\nabla \cdot ({\stackrel{\sim }{L}}_n^E{\stackrel{\mathbf{\sim }}{\mathit{u}}}_E)=-\nabla \cdot {\stackrel{\mathbf{\sim }}{\mathit{J}}}_{\mathit{LnE}}+{\stackrel{\sim }{S}}_{\mathit{LnE}}$$ (3.7.35)

Also, ${\stackrel{\sim }{B}}_n={\stackrel{\sim }{\varphi }}_E{\stackrel{\sim }{B}}_n^E$, ${\stackrel{\sim }{L}}_n={\stackrel{\sim }{\varphi }}_E{\stackrel{\sim }{L}}_n^E$, ${\stackrel{\sim }{S}}_{Bn}={\stackrel{\sim }{\varphi }}_E{\stackrel{\sim }{S}}_{\mathit{BnE}}$, and ${\stackrel{\sim }{S}}_{Ln}={\stackrel{\sim }{\varphi }}_E{\stackrel{\sim }{S}}_{\mathit{LnE}}$. The convective and diffusive flux terms for neovessels are nondimensionalized as

$${\stackrel{\mathbf{\sim }}{\mathit{u}}}_E={\stackrel{\mathbf{\sim }}{\mathit{u}}}_{\alpha }-\stackrel{\sim }{M}\nabla ({\stackrel{\sim }{\mu }}_E-{\stackrel{\sim }{\mu }}_H)$$ (3.7.36)

$${\stackrel{\mathbf{\sim }}{\mathit{J}}}_{\mathit{BnE}}={\stackrel{\sim }{\chi }}_{\mathit{che},\mathit{BnE}}{\mathcal{A}}_{\mathit{che},\mathit{BnE}}{\stackrel{\sim }{B}}_n^E\nabla \stackrel{\sim }{\mathit{taf}}+{\stackrel{\sim }{\chi }}_{\mathit{hap},\mathit{BnE}}{\mathcal{A}}_{\mathit{hap},\mathit{BnE}}{\stackrel{\sim }{B}}_n^E\nabla {\stackrel{\sim }{\varphi }}_E-{\stackrel{\sim }{D}}_{\mathit{BnE}}{\stackrel{\sim }{\varphi }}_E\nabla {\stackrel{\sim }{B}}_n^E$$ (3.7.37)

$${\stackrel{\mathbf{\sim }}{\mathit{J}}}_{\mathit{LnE}}={\stackrel{\sim }{\chi }}_{\mathit{che},\mathit{LnE}}{\mathcal{A}}_{\mathit{che},\mathit{LnE}}{\stackrel{\sim }{L}}_n^E\nabla \stackrel{\sim }{\mathit{taf}}+{\stackrel{\sim }{\chi }}_{\mathit{hap},\mathit{LnE}}{\mathcal{A}}_{\mathit{hap},\mathit{LnE}}{\stackrel{\sim }{L}}_n^E\nabla {\stackrel{\sim }{\varphi }}_E-{\stackrel{\sim }{D}}_{\mathit{LnE}}{\stackrel{\sim }{\varphi }}_E\nabla {\stackrel{\sim }{L}}_n^E$$

where diffusivities ${\stackrel{\sim }{D}}_{\mathit{BnE}}$ and ${\stackrel{\sim }{D}}_{\mathit{LnE}}$ are written as in Eq. (3.7.25) and adjustment factors ${\mathcal{A}}_i$ are found in Table 8.

Dimensionless source terms are listed in the following:

$${\stackrel{\sim }{S}}_{\mathit{BnE}}={\stackrel{\sim }{r}}_{m,\mathit{BnE}}+{\stackrel{\sim }{r}}_{de,\mathit{BnE}}+{\stackrel{\sim }{r}}_{\mathit{crush},\mathit{BnE}}={\stackrel{\sim }{\mathrm{\lambda }}}_{m,\mathit{BnE}}{\mathcal{A}}_{m,\mathit{BnE}}{\stackrel{\sim }{B}}_n^E-{\stackrel{\sim }{\mathrm{\lambda }}}_{de,\mathit{BnE}}{\mathcal{A}}_{de,\mathit{BnE}}\stackrel{\sim }{m}{\stackrel{\sim }{B}}_n^E-{\stackrel{\sim }{\mathrm{\lambda }}}_{as,\mathit{BnE}}{\mathcal{A}}_{as,\mathit{BnE}}{\stackrel{\sim }{B}}_n^E-{\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{crush},\mathit{BnE}}{\mathcal{A}}_{\mathit{crush},\mathit{BnE}}{\stackrel{\sim }{B}}_n^E$$ (3.7.38)

$${\stackrel{\sim }{S}}_{\mathit{LnE}}={\stackrel{\sim }{r}}_{m,\mathit{LnE}}+{\stackrel{\sim }{r}}_{de,\mathit{LnE}}+{\stackrel{\sim }{r}}_{\mathit{crush},\mathit{LnE}}={\stackrel{\sim }{\mathrm{\lambda }}}_{m,\mathit{LnE}}{\mathcal{A}}_{m,\mathit{LnE}}{\stackrel{\sim }{L}}_n^E-{\stackrel{\sim }{\mathrm{\lambda }}}_{de,\mathit{LnE}}{\mathcal{A}}_{de,\mathit{LnE}}\stackrel{\sim }{m}{\stackrel{\sim }{L}}_n^E-{\stackrel{\sim }{\mathrm{\lambda }}}_{as,\mathit{LnE}}{\mathcal{A}}_{as,\mathit{LnE}}{\stackrel{\sim }{L}}_n^E-{\stackrel{\sim }{\mathrm{\lambda }}}_{\mathit{crush},\mathit{LnE}}{\mathcal{A}}_{\mathit{crush},\mathit{LnE}}{\stackrel{\sim }{L}}_n^E$$

where adjustment factors ${\mathcal{A}}_i$ can be found in Table 8. Boundary conditions necessary to solve the set of governing equations listed here will be discussed in the following section.

3.8. Boundary Conditions

We model a tissue domain, Ω, bounded by an outer boundary, Σ. The tissue domain contains both tumor cell regions, Ω_T, and healthy host regions, Ω_H. A tumor region is defined by ${\mathrm{\Omega }}_T=\left\{\stackrel{\mathbf{\sim }}{\mathit{x}}|{\stackrel{\sim }{\varphi }}_T(\stackrel{\mathbf{\sim }}{\mathit{x}})>\frac{1}{2}\left[1-{\stackrel{\sim }{\varphi }}_E(\stackrel{\mathbf{\sim }}{\mathit{x}})\right]\right\}$ and is surrounded by a tumor boundary Σ_T, taken to be ${\sum }_T=\left\{\stackrel{\mathbf{\sim }}{\mathit{x}}|{\stackrel{\sim }{\varphi }}_T(\stackrel{\mathbf{\sim }}{\mathit{x}})=\frac{1}{2}\left[1-{\stackrel{\sim }{\varphi }}_E(\stackrel{\mathbf{\sim }}{\mathit{x}})\right]\right\}$ here. Naturally, a healthy host region is therefore defined by ${\mathrm{\Omega }}_H=\left\{\stackrel{\mathbf{\sim }}{\mathit{x}}|{\stackrel{\sim }{\varphi }}_T(\stackrel{\mathbf{\sim }}{\mathit{x}})<\frac{1}{2}\left[1-{\stackrel{\sim }{\varphi }}_E(\stackrel{\mathbf{\sim }}{\mathit{x}})\right]\right\}$.

Boundary conditions are not needed for the tumor boundary Σ_T. For outer boundary Σ, we define the following Neumann conditions for the cell volume fractions and Dirichlet condition for solid cell pressure:

$$\mathit{n}\cdot \nabla {\stackrel{\sim }{\varphi }}_V=\mathit{n}\cdot \nabla {\stackrel{\sim }{\varphi }}_D=\mathit{n}\cdot \nabla {\stackrel{\sim }{\varphi }}_E-\stackrel{\sim }{p}=0,$$ (3.8.1)

where n is the outward normal of the boundary. To allow cells to flow freely across the outer boundary, we set the conditions

$${\stackrel{\sim }{\mu }}_T={\stackrel{\sim }{\mu }}_E={\stackrel{\sim }{\mu }}_H=0.$$ (3.8.2)

For nutrients and waste products, Dirichlet conditions are imposed:

$$\stackrel{\sim }{n}=\stackrel{\sim }{g}=1,\stackrel{\sim }{w}=\stackrel{\sim }{\ell }=\stackrel{\sim }{b}=\stackrel{\sim }{a}=\stackrel{\sim }{s}=0.$$ (3.8.3)

For tumorigenic species, Dirichlet conditions are imposed, except for myofibroblastic cells, where Neumann condition is imposed:

$$\stackrel{\sim }{\mathit{tgf}}=\stackrel{\sim }{\mathit{taf}}=\stackrel{\sim }{m}=\mathit{n}\cdot \nabla \stackrel{\sim }{F}=0.$$ (3.8.4)

New vessels are assumed to be at ${\stackrel{\sim }{B}}_{\infty }$ and ${\stackrel{\sim }{L}}_{\infty }$ at all four boundaries.

The set of dimensionless governing equations listed here, combined with boundary conditions stated in the next section, will be solved using numerical methods described in Section 4.

4. Numerical Methods

The set of nondimensionalized governing equations are discretized implicitly in time using the Crank-Nicholson scheme as described in Wise et al. (2011). Spatial discretization methods employed are second order finite differences and central differences. In the computation of edge-centered approximation in the advection terms, both upwind donor-cell advection and third order upwind biased WENO scheme (Jiang and Shu, 1996; Liu et al., 1994) are used.

The discretized set is solved using a nonlinear full multigrid solver (Trottenberg et al., 2001) with self-adaptive mesh refinement. The nonlinear solver uses the full approximation scheme in V-cycles (Trottenberg et al., 2001; Wise et al., 2007), with Gauss-Seidel relaxations in red-black (odd-even) ordering. The block-structured composite Cartesian mesh consists of a hierarchy of levels with uniform grids that are increasing in their mesh spacings. In general, the composite mesh has a few adaptively refined finer levels sitting on top of several coarser global levels. Each global mesh level consists of one block that spans the entire domain. Each adaptively refined level may have one or more blocks generated during each time-step for areas where refinement is deemed beneficial. If the finest global level, also called the root level, is set as L₀ with grid spacing h₀, a subsequent coarser global level is set as L₋₁ with grid spacing h₋₁ = 2h₀, followed by another coarser level L₋₂ with grid spacing h₋₂ = 2h₋₁, and so on. Above the finest global level sits the first adaptively refined level L₁ with h₁ = h₀/2, followed by another adaptively refined level L₂ with h₂ = h₁/2, and so on.

A total of five levels of refinement is used here for the tissue domain Ω = (0,40)³. The mesh spacings for L₂ down to level L₋₂ are h₂ = 40/128, h₁ = 40/64, h₀ = h₁/32, h₋₁ = 40/16, and h₋₂ = 40/8, respectively. The root level has a grid size of 32×32×32. Several options for flagging cells for refinement are considered, ranging from the simple volume fraction test (Wise et al., 2008), undivided gradient test (Wise et al., 2007), and relative truncation error test (Trottenberg et al., 2001).

Simulations were performed on a node with 768 GB of RAM and 32 Intel Xeon 3.3GHz cores, running CentOS 6.7 ×86_64. The time step size was set to 1×10⁻². At t = 1, it took approximately 2.6 hrs to complete 100 time steps; at t = 10, the solver completed 100 time steps in about 3.5 hrs; at t = 20, 100 time steps were completed in roughly 4.7 hrs. The computation time for t = 10 was approximately 1 day and the total computation time to reach t = 20 was about 3 days. The algorithms were partially parallelized using OpenMP, and we expect further detailed parallelization work in the future to yield higher performance.

5. Computational Results

To gently perturb the symmetry of the mathematical model and to test the model’s ability to simulate a morphologically asymmetric system, the fraction of blood vessel species ℱ_Bn available for sprouting, remodeling, and taxis, as depicted in Eqs. (3.6.3), (3.6.4), (3.6.9), and (3.6.11), is set to a different constant for the eight equally-sized parts of the domain.

Figure 2 shows a sample of a desmoplastic tumor evolution in time through a cross-section in the index plane j = k = 58. The simulation parameters are as listed in Tables 2 through 6. Initially (t = 1), the tumor viable, dead, and ECM species are mostly symmetrical around the tumor center. There is a significant proportion of viable tissue that is hypoxic in the core (when the oxygen value < 0.3). The tumor essentially has a viable rim surrounding a mostly necrotic core (induced when oxygen value < 0.2). The ECM level is high, representing a fibrotic lesion. The pressure is high in the immediate surroundings of the lesion and significantly lower in the core in which there is little tissue proliferation. The diffusible substances driving the tumor evolution, including oxygen (O₂), glucose (Glu), carbon dioxide (CO₂), bicarbonate (Bic), lactate (Lac), and hydrogen ions (H⁺), reflect this symmetry in space. Oxygen and glucose experience a decreasing concentration into the core of the lesion, as their uptake by the viable tumor tissue depletes their concentration. The byproducts of glycolysis, carbon dioxide and bicarbonate, accumulate in the tumor tissue, with their diffusion outwards hindered by inadequate vascularization and adverse pressure gradients. Correspondingly, the concentration of lactate and hydrogen ions is significantly higher within the tumor tissue.

Figure 2.

Desmoplastic tumor evolution with regionally varied ${ℱ}_{Bn}$. Time progression from left to right for t = 1, 5, 10, 15, and 20, and plots are made for a cross section of the index plane j = k = 58. First row: tumor viable species ${\stackrel{\sim }{\varphi }}_V$, dead species ${\stackrel{\sim }{\varphi }}_D$, and ECM species ${\stackrel{\sim }{\varphi }}_E$. The overall tumor pressure is labeled by p_α. Second row: diffusible substances driving the tumor evolution, including oxygen (O₂), glucose (Glu), carbon dioxide (CO₂), bicarbonate (Bic), lactate (Lac), and hydrogen ions (H⁺). Third row: Concentration of myfibroblasts (myF), tumor growth factors (TGF), and matrix degrading enzymes (MDE). Fourth row: corresponding density of blood vasculature (Bn), lymphatic vasculature (Ln), and tumor angiogenic factors (TAF).

The tumor growth factor (tgf) and myofibroblast (myF) concentrations are also higher within the tumor, while the matrix degrading enzyme (MDE) concentration, produced by the expanding viable tumor tissue as well as the vasculature in response to tumor angiogenic factors released by the hypoxic tumor tissue, is slightly higher and asymmetrical within the core of the tumor, which reflects the asymmetry in the vascular layout due to some regions having a higher probability of endothelial tissue proliferation. The hypoxic tissue engenders a high level of tumor angiogenic factors (TAF) that diffuse outward from the tumor into the surroundings, and in turn drive higher the concentration of both blood and lymphatic vasculature. After 20 days of growth, the tumor has evolved into a heterogeneous system resembling a typical pancreatic cancer, which is mostly fibrotic, hypoxic, acidic, and with a low density of viable tissue spread throughout.

For comparison, Figure 3 shows the first five days of evolution for a perfectly spherical tumor (cross-section in the index plane j = k = 58), for which the percentage of proliferating vasculature is the same everywhere. Although in this case the tumor also represents a hypoxic, fibrotic lesion, the symmetric vasculature enforces a correspondingly symmetric MDE concentration. In time, however, fluctuations in the blood and lymphatic vasculature density are expected to disturb this symmetry and lead to a heterogeneous system as in Figure 2.

Figure 3.

Desmoplastic tumor evolution with uniform ${ℱ}_{Bn}$. Time progression is from left to right for t = 1 – 5, and plots are made for a cross section of the index plane j = k = 58. First row: tumor viable species ${\stackrel{\sim }{\varphi }}_V$, dead species ${\stackrel{\sim }{\varphi }}_D$, and ECM species ${\stackrel{\sim }{\varphi }}_E$. The overall tumor pressure is labeled by p_α. Second row: diffusible substances driving the tumor evolution, including oxygen (O₂), glucose (Glu), carbon dioxide (CO₂), bicarbonate (Bic), lactate (Lac), and hydrogen ions (H⁺). Third row: Concentration of myfibroblasts (myF), tumor growth factors (TGF), and matrix degrading enzymes (MDE). Fourth row: corresponding density of blood vasculature (Bn), lymphatic vasculature (Ln), and tumor angiogenic factors (TAF).

Figure 4 highlights the evolution of the velocity field along the pressure gradient in a sub-section of the x − z plane (at index j = 58). The velocity of solid phase components (viable and dead tumor, and ECM tissues) is represented by u_α, while the velocity of aqueous phase component (interstitial fluid) is represented by u_β, along with the solid pressure p and and hydrostatic pressure q contours. Figure 5 shows the viable tissue and ECM contours corresponding to the scenario in Figure 4, and highlights the heterogeneous growth-up of these two species in time. In these two figures, clockwise starting from the lower left quadrant (i < 65 and k < 65), ℱ_Bn is set to 0.8, 0.1, 0.2, and 0.15, respectively.

Figure 4.

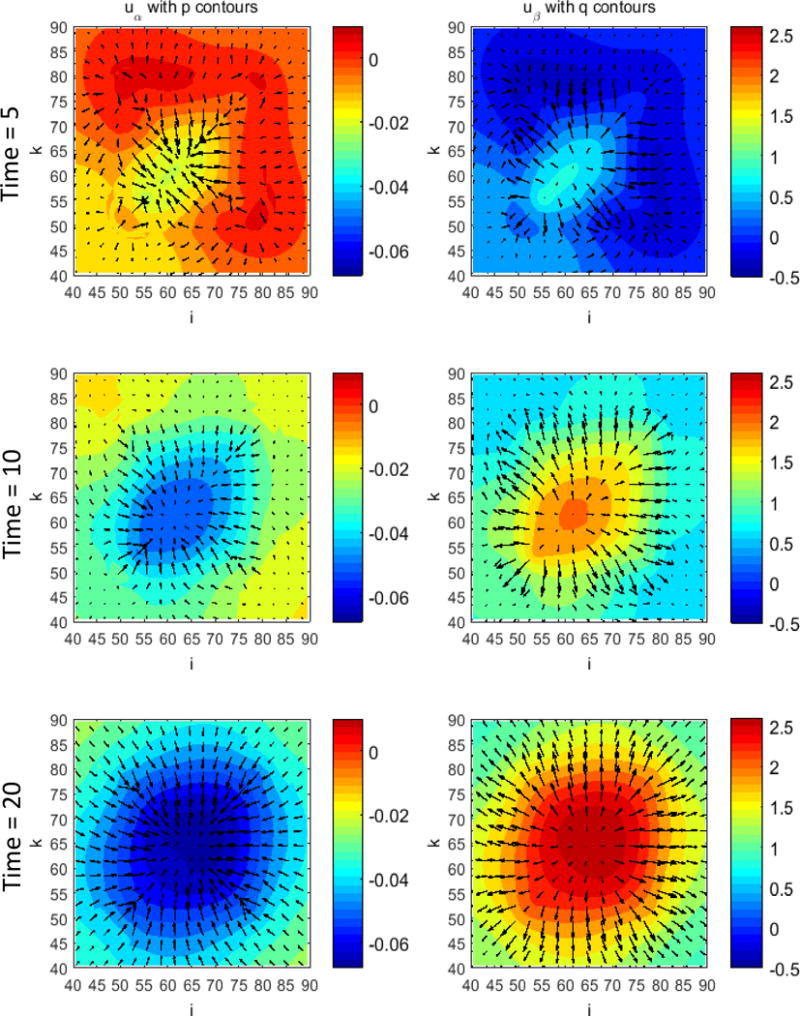
Evolution of the solid-ECM and interstitial fluid phase velocity fields along their corresponding pressure gradients. Plotted for t = 5, 10, and 20, in a sub-section of the x – z plane (at index j = 58). The arrows denote the velocity vectors, with longer arrows indicating a higher magnitude.

Figure 5.

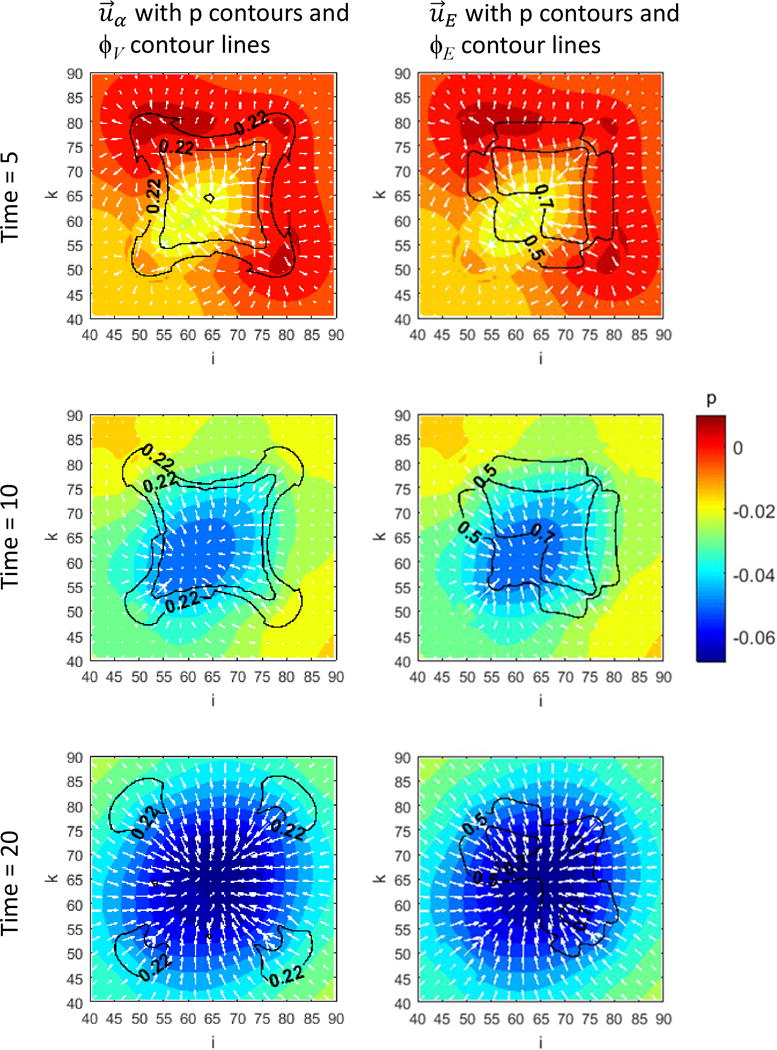
Evolution of viable tissue and ECM species (2D plot) with their corresponding velocity fields and pressure gradients. Plotted for t = 5, 10, and 20, in a sub-section of the x – z plane (at index j = 58). The arrows denote the velocity vectors, with longer arrows indicating a higher magnitude.

The evolution of the tumor in 3D space is presented in Figure 6. As time progresses the viable tissue tends to grow at the periphery, bulging out at the corners as has been previously reported with these types of mixture models (Frieboes et al., 2010; Wise et al., 2008). In the center of the tumor mass, oxygen and nutrient levels drop below the threshold necessary for viability, leading to tumor tissue becoming necrotic. Further, as TGF accumulates over time in the center due to its production by viable tumor tissue, thus drawing in myofibroblastic cells and upregulating their mitosis, more ECM is being secreted. As a result, the center of the tumor mass becomes denser with ECM (i.e., becomes fibrotic), while the viable tissue at the periphery, with access to higher nutrients levels from the surroundings, is able to continue growing. The dead tissue follows in structure the viable tissue, although in a smaller overall volume. The ECM species, initially mainly concentrated in the interior of the tumor, evolves non-uniformly to maintain a heterogeneous volume during the growth of the viable tissue. Figure 7 presents an alternate view of the viable, dead, and ECM species in 3D space (sliced through the center of the domain) at time t = 20 days, highlighting the heterogeneity of the structure in terms of the distribution of these species.

Figure 6.

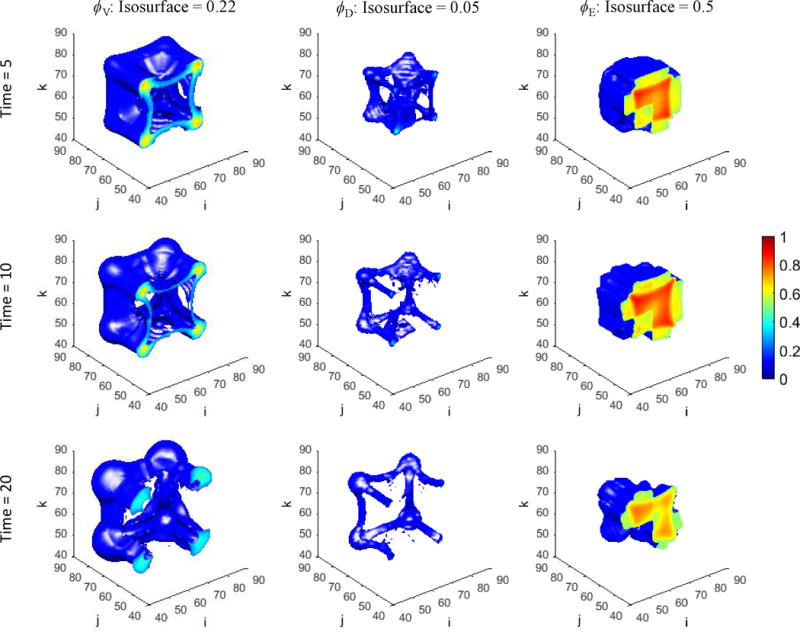
Evolution of the tumor viable, dead, and ECM species (3D plot) for t = 5, 10, and 20. Cross-sectional contours are on the x – z plane sliced at index j = 58. Highest density: red; lowest: blue.

Figure 7.

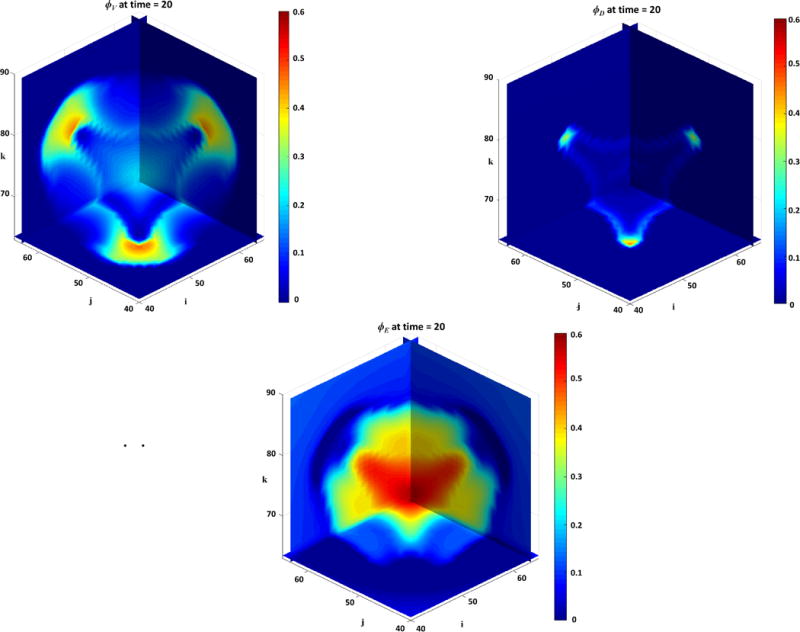
Tumor viable, dead, and ECM species at time t = 20 (3D plot). Cross-sectional contours are sliced at indices i = 58, j = 58, and k = 58. Highest density: red; lowest: blue.

The variation in the ECM species as a function of the elastic energy is shown in Figure 8. The interfacial strain energy coefficient ε_e as in Eqs. (3.2.16), (3.2.23), and (3.2.25), or the nondimensionalized form ${\stackrel{\sim }{\epsilon }}_e$ as in Eq. (3.7.11) is increased from ${\stackrel{\sim }{\epsilon }}_e=0.001$ for the base level ECM, to ${\stackrel{\sim }{\epsilon }}_e=0.01$ for 10 times the base level ECM, and to ${\stackrel{\sim }{\epsilon }}_e=0.1$ for 100 times the base level ECM. As the elastic energy contribution to the chemical potential increases over two orders of magnitude, the ECM species becomes more diffuse. For illustration, the ECM density at t = 2, initially with a high peak within the tumor region in the center of the x-dimension cross-section shown in the figure, decreases by about a third from the peak.

Figure 8.

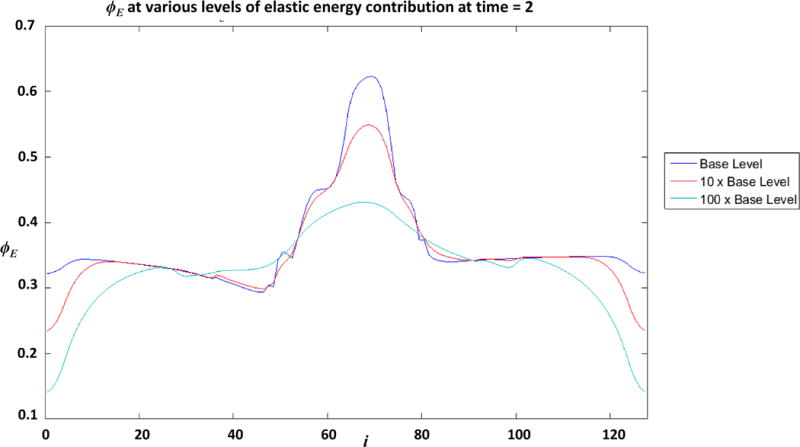
Variation in ECM species as a function of the elastic energy at t = 2. Blue: ${\stackrel{\sim }{\epsilon }}_e=0.001$; Red: ${\stackrel{\sim }{\epsilon }}_e=0.01$; Green: ${\stackrel{\sim }{\epsilon }}_e=0.1$.

We performed a sensitivity analysis using the glucose uptake rate constant of viable tumor cells. Values of the rate constant ${\stackrel{\sim }{\mathrm{\lambda }}}_{U,V,g}$ used are 10, 1, and 0.1. Simulation results at t = 20 are given in Figure 9. Profiles of volume fractions, species concentrations, and vessel densities in the center column are from the base case shown in Figure 2, where ${\stackrel{\sim }{\mathrm{\lambda }}}_{U,V,g}=1$. When the glucose uptake rate constant of viable tumor cells is increased to ${\stackrel{\sim }{\mathrm{\lambda }}}_{U,V,g}=10$, the higher uptake causes the glucose levels in the center of the domain (where viable tumor cells are seeded) to drop below the glucose viability limit of 0.1 very early during the simulation. Viable tumor cells in the center of the domain become necrotic, turning into dead cells and eventually lysed. The low levels of viable tumor cells in the center also results in lower levels of TGF and TAF being produced. Lower levels of TGF lead to lower levels of myofibroblastic cells, hence less ECM being secreted. Similarly, lower TAF levels result in lower vessel densities. However, when the glucose uptake rate constant of viable tumor cells is decreased to ${\stackrel{\sim }{\mathrm{\lambda }}}_{U,V,g}=0.1$, profiles of all volume fractions, species concentrations (except those involved in glycolysis), and vessel densities are the same as the base case. Since there is an abundance of glucose in the domain due to the low glucose uptake rate, oxygen is the limiting nutrient, as in the base case. Therefore, the system behavior is dictated by the same oxygen limitation and follows similar dynamics as in the base case.

Figure 9.

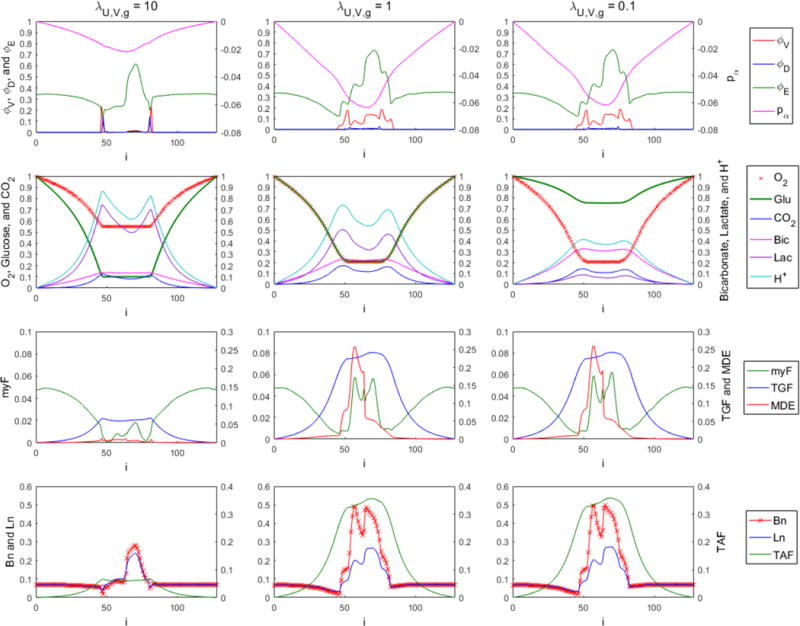
Desmoplastic tumor simulations at t = 20 for glucose uptake rate constants ${\stackrel{\sim }{\lambda }}_{U,V,g}=10$, 1 (the base case shown in Figure 1), and 0.1.

Lastly, we evaluated the effects of TGF on the tumor microenvironment. The levels of TGF are controlled through its secretion rate constant by viable tumor cells and degradation rate constant. Simulation results at t = 20 are plotted in Figure 10. Profiles of volume fractions, species concentrations, and vessel densities in the center column are from the base case shown in Figure 2, where ${\stackrel{\sim }{\mathrm{\lambda }}}_{V,\mathit{tgf}}=0.2$ and ${\stackrel{\sim }{\mathrm{\lambda }}}_{de,\mathit{tgf}}=0.05$. To simulate a case with lower TGF levels compared to the base case, a higher degradation rate constant ${\stackrel{\sim }{\mathrm{\lambda }}}_{de,\mathit{tgf}}=0.1$ is used. In the nutrient-starved tumor mass center, viable tumor cells undergo necrosis, followed by lysing of the dead cells. Since the mitosis rate of viable tumor cells is not sufficiently upregulated by the lower TGF levels, viable cells are mostly absent in the low-nutrient center region at t = 20, and they are mostly present outside the edge of the hypoxic core where they still proliferate. The low TGF levels also do not sufficiently upregulate myofibroblastic cells in the tumor region, resulting in low levels of myofibroblastic cells, and therefore little ECM is being secreted. The lack of viable tumor cells results in a dip in the TAF profile, causing insignificant angiogenesis in the core.

Figure 10.

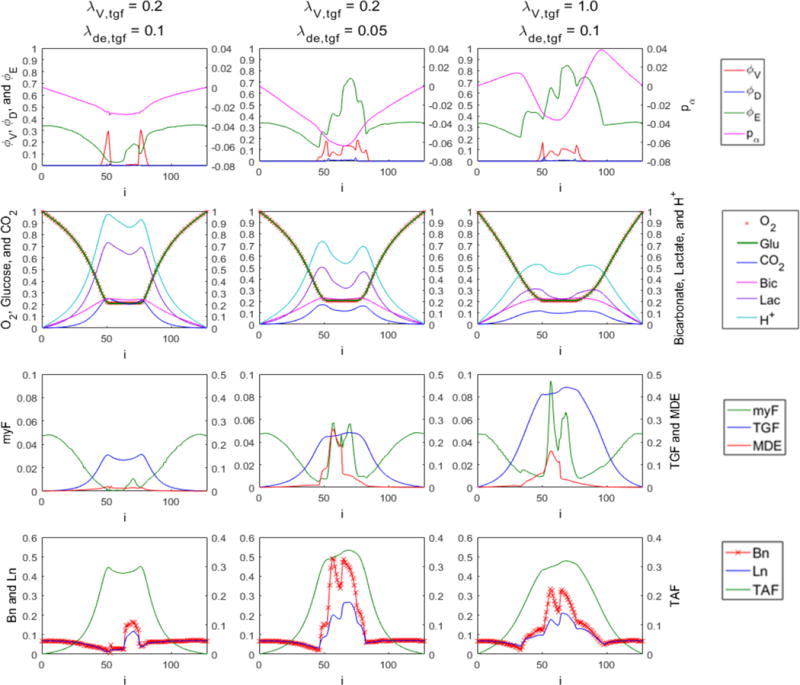
Desmoplastic tumor simulations at t = 20 for a decreased-TGF case ( ${\stackrel{\sim }{\lambda }}_{V,\mathit{tgf}}=0.2$ and ${\stackrel{\sim }{\lambda }}_{de,\mathit{tgf}}=0.1$), the base case shown in Figure 1 ( ${\stackrel{\sim }{\lambda }}_{V,\mathit{tgf}}=0.2$ and ${\stackrel{\sim }{\lambda }}_{de,\mathit{tgf}}=0.05$), and an increased-TGF case ( ${\stackrel{\sim }{\lambda }}_{V,\mathit{tgf}}=1.0$ and ${\stackrel{\sim }{\lambda }}_{de,\mathit{tgf}}=0.1$).

To achieve higher TGF levels compared to the base case, a higher production rate constant by viable tumor cells ${\stackrel{\sim }{\mathrm{\lambda }}}_{V,\mathit{tgf}}=1.0$ is used, accompanied by a higher degradation rate constant ${\stackrel{\sim }{\mathrm{\lambda }}}_{de,\mathit{tgf}}=0.1$. The higher level of TGF upregulates the proliferation of myofibroblastic cells. The increased density of myofibroblastic cells leads to increased amount of ECM secreted, hence the ECM-rich tumor mass as seen in the upper right plot in Figure 10. Moreover, in the TGF rich environment, the mitosis rate of viable tumor cells within the nutrient-starved center and surrounding areas is upregulated, resulting in a wider viable tumor area. The increase in viable tumor mass might not be reflected in the one-dimensional profile, but it is shown clearly in Figure 11. The higher amount of proliferating viable tumor tissue is also responsible for the broader region of higher TAF in the tissue. As a result of the higher TAF levels, there is a broader region of elevated blood vessel growth, as also evidenced by the relatively more relaxed curves of oxygen, glucose, and metabolic byproducts.

Figure 11.

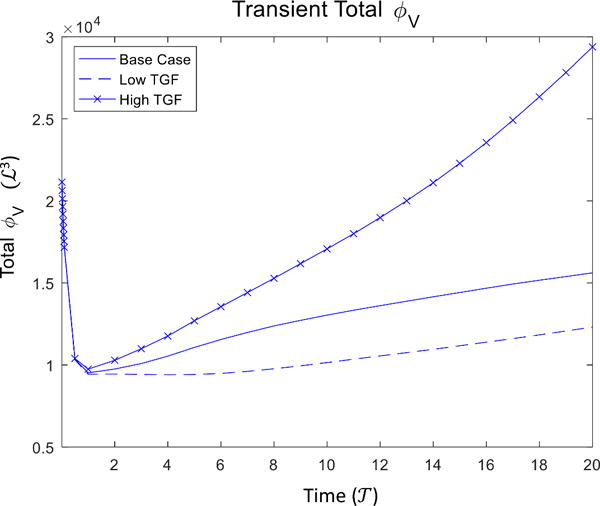
Transient total viable tumor volume corresponding to the three cases of different TGF levels in Figure 10.

6. Conclusion and Future Work

In this paper, we reviewed topics related to the study of the tumor microenvironment. We evaluated some of the key associated reactions and cell species, defined a scope that is sufficient for the purpose of simulating a vascular desmoplastic tumor microenvironment, and detailed the formulation of a mathematical model. We presented numerical simulations of symmetrical and nonsymmetrical desmoplastic tumor progression in 3D. We also showed that this model is capable of simulating an ECM-rich tumoral tissue and capturing complex morphological changes during growth of a tumor mass.

For future work, other forms of elastic energy contribution representing the mechanical behavior of biological tissues will be studied. The desmoplastic tumor growth could also include heterogeneous cell types such as mutated clones of tumor cells and cancer stem cells. To further approach a more complete tumor microenvironment, immune cell species could be included, as well as the tumor-associated inflammation response. Hormonal growth factors and chemoattractants can be incorporated in the model to drive the tumor growth and influence the migration of immune cells. We will obtain and make use of parameters and constants that are biologically appropriate. Reactions and responses in the model will also be studied in further detail, so that true dynamics can be captured in adjustment factors and modelled via empirical formulas obtained from experiments. As the model becomes more refined and well-tuned, the modelling of the transport and effects of anticancer drugs and nanovectors could be incorporated for evaluation of therapeutic efficacy.

Table 4.

Dimensionless Rate Constants.

Dimensionless Parameter	Biological Representation	Scaling Factor *	Value Assigned
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{M}\mathbf{,}\mathit{V}}$	Mitosis rate constant of viable tumor cells	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{A}\mathbf{,}\mathit{V}}$	Apoptosis rate constant of viable tumor cells	λM,V	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{N}\mathbf{,}\mathit{V}}$	Necrosis rate constant of viable tumor cells	λM,V	3.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{V}}$	Metastasis rate constant of viable tumor cells via blood vessels	λM,V	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{L}\mathbf{,}\mathit{V}}$	Metastasis rate constant of viable tumor cells via lymphatic vessels	λM,V	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{V}}$	Autophagy rate constant of viable tumor cells	λM,V	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{L}\mathbf{,}\mathit{D}}$	Lysis rate constant of dead tumor cells	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{V}\mathbf{,}\mathit{E}}$	ECM rate of secretion by tumor viable cells	λM,V	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{E}}$	ECM rate of secretion by ECs	${\stackrel{\sim }{\varphi }}_{\alpha }{\lambda }_{M,V}/B_{max}$	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{L}\mathbf{,}\mathit{E}}$	ECM rate of secretion by LECs	${\stackrel{\sim }{\varphi }}_{\alpha }{\lambda }_{M,V}/L_{max}$	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{F}\mathbf{,}\mathit{E}}$	ECM rate of secretion by myofibroblastic cells	${\stackrel{\sim }{\varphi }}_{\alpha }{\lambda }_{M,V}/F_{max}$	5.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{E}}$	Degradation rate of ECM	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{C}}$	Degradation rate of ECM macromolecules catalyzed by MDEs	${\lambda }_{M,V}{\stackrel{\sim }{\varphi }}_{\alpha }{C}_E$	5.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{n}}$	Apparent transfer coefficient of O2 via capillary network	λU,V,n	computed
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{n}\mathbf{,}\mathit{E}}$	Transfer coefficient of O2 via capillary network in ECM regions	λU,V,n	0.1
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{n}\mathbf{,}\mathit{T}}$	Transfer coefficient of O2 via capillary network in tumor regions	λU,V,n	0.001
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{n}\mathbf{,}\mathit{H}}$	Transfer coefficient of O2 via capillary network in host regions	λU,V,n	0.01
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{U}\mathbf{,}\mathit{V}\mathbf{,}\mathit{n}}$	Uptake rate constant of O2 by viable tumor cells	λU,V,n	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{U}\mathbf{,}\mathit{H}\mathbf{,}\mathit{n}}$	Uptake rate constant of O2 by healthy host cells	λU,V,n	0.0001
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{g}}$	Apparent transfer coefficient of glucose via capillary network	λU,V,n	computed
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{g}\mathbf{,}\mathit{E}}$	Transfer coefficient of glucose via capillary network in ECM regions	λU,V,n	0.1
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{g}\mathbf{,}\mathit{T}}$	Transfer coefficient of glucose via capillary network in tumor regions	λU,V,n	0.001
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{g}\mathbf{,}\mathit{H}}$	Transfer coefficient of glucose via capillary network in host regions	λU,V,n	0.01
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{U}\mathbf{,}\mathit{V}\mathbf{,}\mathit{g}}$	Uptake rate constant of glucose by viable tumor cells	λU,V,n	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{U}\mathbf{,}\mathit{H}\mathbf{,}\mathit{g}}$	Uptake rate constant of glucose by healthy host cells	λU,V,n	0.0001
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B},\mathit{w}}$	Apparent transfer coefficient of CO2 via capillary network	λU,V,n	computed
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B},\mathit{w}\mathbf{,}\mathit{E}}$	Transfer coefficient of CO2 via capillary network in ECM regions	λU,V,n	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B},\mathit{w}\mathbf{,}\mathit{T}}$	Transfer coefficient of CO2 via capillary network in tumor regions	λU,V,n	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B},\mathit{w}\mathbf{,}\mathit{H}}$	Transfer coefficient of CO2 via capillary network in host regions	λU,V,n	1.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{f}}$	Forward reaction rate of the dissolution of CO2 and H2O	λU,V,n	1.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{r}}$	Backward reaction rate of the dissolution of CO2 and H2O	λU,V,n/n∞	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\ell }$	Apparent transfer coefficient of lactate via capillary network	λU,V,n	computed
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\ell \mathbf{,}\mathit{E}}$	Transfer coefficient of lactate via capillary network in ECM regions	λU,V,n	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\ell \mathbf{,}\mathit{T}}$	Transfer coefficient of lactate via capillary network in tumor regions	λU,V,n	0.1
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\ell \mathbf{,}\mathit{H}}$	Transfer coefficient of lactate via capillary network in host regions	λU,V,n	0.5
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{V}\mathbf{,}\mathit{t}\mathit{g}\mathit{f}}$	Production rate constant of TGFs by viable tumor cells	λU,V,n	0.2
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{t}\mathit{g}\mathit{f}}$	Production rate constant of TGFs by ECs	λU,V,n	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{L}\mathbf{,}\mathit{t}\mathit{g}\mathit{f}}$	Production rate constant of TGFs by LECs	λU,V,n	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{F}\mathbf{,}\mathit{t}\mathit{g}\mathit{f}}$	Production rate constant of TGFs by MFCs	λU,V,n	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{t}\mathit{g}\mathit{f}}$	Degradation rate constant of TGFs	λU,V,n	0.05
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{U}\mathbf{,}\mathit{V}\mathbf{,}\mathit{t}\mathit{g}\mathit{f}}$	Uptake rate constant of TGFs by viable tumor cells	λU,V,n	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{V}\mathbf{,}\mathit{t}\mathit{a}\mathit{f}}$	Production rate constant of TAFs by viable tumor cells	λU,V,n	0.2
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{B}\mathbf{,}\mathit{t}\mathit{a}\mathit{f}}$	Production rate constant of TAFs by ECs	λU,V,n	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{L}\mathbf{,}\mathit{t}\mathit{a}\mathit{f}}$	Production rate constant of TAFs by LECs	λU,V,n	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{F}\mathbf{,}\mathit{t}\mathit{a}\mathit{f}}$	Production rate constant of TAFs by MFCs	λU,V,n	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{t}\mathit{a}\mathit{f}}$	Degradation rate constant of TAFs	λU,V,n	0.05
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{U}\mathbf{,}\mathit{B}\mathbf{,}\mathit{t}\mathit{a}\mathit{f}}$	Uptake rate constant of TAFs by proliferating ECs	λU,V,n/Bmax	0.0011574
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{U}\mathbf{,}\mathit{L}\mathbf{,}\mathit{t}\mathit{a}\mathit{f}}$	Uptake rate constant of TAFs by proliferating LECs	λU,V,n/Lmax	0.0011574
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{c}\mathit{a}\mathit{t}\mathbf{,}\mathit{B}}$	Rate constant for the loss of TAFs to the production of MDEs by proliferating ECs	$\frac{{\lambda }_{U,V,n}ta{f}_{\mathit{sat}}}{B_{max}}$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{c}\mathit{a}\mathit{t}\mathbf{,}\mathit{L}}$	Rate constant for the loss of TAFs to the production of MDEs by proliferating LECs	$\frac{{\lambda }_{U,V,n}ta{f}_{\mathit{sat}}}{L_{max}}$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{m}\mathbf{,}\mathit{B}}$	Michaelis constant for the uptake of TAF by proliferating ECs	tafsat	1.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{m}\mathbf{,}\mathit{L}}$	Michaelis constant for the uptake of TAF by proliferating LECs	tafsat	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{V}\mathbf{,}\mathit{m}}$	Production rate constant of MDEs by viable tumor cells	λM,V	0.2
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{F}\mathbf{,}\mathit{m}}$	Production rate constant of MDEs by MFCs	λM,V	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{m}}$	Decay rate constant of MDEs	λM,V	5.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{M}\mathbf{,}\mathit{F}\mathit{E}}$	Mitosis rate constant of MFCs	λM,V	0.1
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{A}\mathbf{,}\mathit{F}\mathit{E}}$	Apoptosis rate constant of MFCs	λM,V	0.1
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{N}\mathbf{,}\mathit{F}\mathit{E}}$	Necrosis rate constant of MFCs	λM,V	0.3
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{m}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}$	Maximum mitosis rate constant of ECs	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{c}\mathit{r}\mathit{u}\mathit{s}\mathit{h}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}$	Maximum degradation rate constant of new blood vessels due to cell pressure	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}$	Remodeling rate constant of new blood vessels by MDEs	λM,V/msat	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{a}\mathit{s}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}$	Anastomosis rate constant (periodic) of the new blood vessels	λM,V	0.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{m}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}$	Maximum mitosis rate constant of LECs	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{c}\mathit{r}\mathit{u}\mathit{s}\mathit{h}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}$	Maximum degradation rate constant of new lymphatic vessels due to cell pressure	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{d}\mathit{e}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}$	Remodeling rate constant of new lymphatic vessels by MDEs	λM,V	1.0
${\stackrel{\mathbf{\sim }}{\mathbf{\lambda }}}_{\mathit{a}\mathit{s}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}$	Anastomosis rate constant (periodic) of the new lymphatic vessels	λM,V	0.0

^*For example, ${\stackrel{\sim }{\lambda }}_{N,V}={\lambda }_{N,V}/{\lambda }_{M,V}$.

Table 5.

Mobility, Motilities, and Taxis Coefficients

Dimensionless Parameter	Biological Representation	Scaling Factor*	Value Assigned
$\stackrel{\mathbf{\sim }}{\mathit{M}}$	Mobility of cell species	ℳ	0.1
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{\alpha }}$	Motility of the solid phase (cells)	${\overline{\overline{k}}}_{\alpha }$	Computed†
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{T}}$	Motility of the tumor cell phase	${\overline{\overline{k}}}_{\alpha }$	10.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{E}}$	Motility of the ECM phase	${\overline{\overline{k}}}_{\alpha }$	10.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{H}}$	Motility of the healthy host cell phase	${\overline{\overline{k}}}_{\alpha }$	10.0
${\stackrel{\mathbf{\sim }}{\mathit{k}}}_{\mathit{\beta }}$	Motility of the fluid phase (interstitial fluid)	${\overline{\overline{k}}}_{\beta }$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{\chi }}}_{\mathit{c}\mathit{h}\mathit{e}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}$	Chemotaxis coefficient of ECs	${ℒ}^2/(\mathcal{T}ta{f}_{\mathit{sat}})$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{\chi }}}_{\mathit{h}\mathit{a}\mathit{p}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}$	Haptotaxis coefficient of ECs	${ℒ}^2/(\mathcal{T}{\stackrel{\sim }{\varphi }}_{\alpha })$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{\chi }}}_{\mathit{h}\mathit{a}\mathit{p}\mathbf{,}\mathit{B}\mathit{n}\mathit{E}}^{\mathit{m}\mathit{i}\mathit{n}}$	Minimum haptotaxis coefficient of ECs	${ℒ}^2/(\mathcal{T}{\stackrel{\sim }{\varphi }}_{\alpha })$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{\chi }}}_{\mathit{c}\mathit{h}\mathit{e}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}$	Chemotaxis coefficient of LECs	${ℒ}^2/(\mathcal{T}ta{f}_{\mathit{sat}})$	1.0
${\stackrel{\sim }{\chi }}_{\mathit{h}\mathit{a}\mathit{p}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}$	Haptotaxis coefficient of LECs	${ℒ}^2/(\mathcal{T}{\stackrel{\sim }{\varphi }}_{\alpha })$	1.0
${\stackrel{\mathbf{\sim }}{\mathit{\chi }}}_{\mathit{h}\mathit{a}\mathit{p}\mathbf{,}\mathit{L}\mathit{n}\mathit{E}}^{\mathit{m}\mathit{i}\mathit{n}}$	Minimum haptotaxis coefficient of LECs	${ℒ}^2/(\mathcal{T}{\stackrel{\sim }{\varphi }}_{\alpha })$	1.0

^*For example, ${\stackrel{\sim }{\chi }}_{\mathit{che},\mathit{BnE}}={\chi }_{\mathit{che},\mathit{BnE}}\mathcal{T}ta{f}_{\mathit{sat}}/{ℒ}^2$.

^†The solid phase motility ${\stackrel{\sim }{k}}_{\alpha }$ is computed from ${\stackrel{\sim }{k}}_E$, ${\stackrel{\sim }{k}}_T$, and ${\stackrel{\sim }{k}}_H$ using Eq. (3.7.25) by replacing ${\stackrel{\sim }{D}}_i$ with ${\stackrel{\sim }{k}}_i$.

Nondimensionalized chemotaxis and heptotaxis coefficients are set to 1 as an initial value in this study. A wider range of values will be tested and analyzed in future work.

Highlights.

• Created four-species model to simulate interactions between tumor and stromal cells

• Cellular metabolic processes are simulated, including respiration and glycolysis

• Growth-factor releasing fibroblasts are key contributors to abnormal ECM remodeling

• An elastic energy is implemented to provide elasticity to the connective tissue

• ECM remodeling simulates stromal desmoplasia in pancreatic ductal adenocarcinoma