Global transcriptional regulatory network for Escherichia coli robustly connects gene expression to transcription factor activities

Significance

While the transcriptional regulatory network (TRN) of Escherichia coli has expanded considerably in recent years through new chromatin immunoprecipitation (ChIP) data, an open question remains: Does the global TRN, reconstructed by combining ChIP data for individual transcriptions factors, consistently explain observed differential gene expression? We have reconstructed a high-confidence TRN, determined its consistency with transcriptomics and predictive capabilities across multiple conditions, extracted 10 functional regulatory modules, and characterized this network at the sequence and structural levels. Our multiomics algorithmic pipeline is expected to facilitate rigorous validation and prioritization of experiments to elucidate TRNs in other bacteria.

Abstract

Transcriptional regulatory networks (TRNs) have been studied intensely for >25 y. Yet, even for the Escherichia coli TRN—probably the best characterized TRN—several questions remain. Here, we address three questions: (i) How complete is our knowledge of the E. coli TRN; (ii) how well can we predict gene expression using this TRN; and (iii) how robust is our understanding of the TRN? First, we reconstructed a high-confidence TRN (hiTRN) consisting of 147 transcription factors (TFs) regulating 1,538 transcription units (TUs) encoding 1,764 genes. The 3,797 high-confidence regulatory interactions were collected from published, validated chromatin immunoprecipitation (ChIP) data and RegulonDB. For 21 different TF knockouts, up to 63% of the differentially expressed genes in the hiTRN were traced to the knocked-out TF through regulatory cascades. Second, we trained supervised machine learning algorithms to predict the expression of 1,364 TUs given TF activities using 441 samples. The algorithms accurately predicted condition-specific expression for 86% (1,174 of 1,364) of the TUs, while 193 TUs (14%) were predicted better than random TRNs. Third, we identified 10 regulatory modules whose definitions were robust against changes to the TRN or expression compendium. Using surrogate variable analysis, we also identified three unmodeled factors that systematically influenced gene expression. Our computational workflow comprehensively characterizes the predictive capabilities and systems-level functions of an organism’s TRN from disparate data types.

A transcriptional regulatory network (TRN) plays a major role in enabling an organism to modulate expression of thousands of genes in response to environmental and genetic perturbations (1). Escherichia coli’s TRN is probably the most extensively studied in any organism. However, the structure of even this TRN is still subject to considerable uncertainty, seriously limiting its utility for predicting gene expression or for interpreting disparate datasets. Indeed, over a decade ago, a combined metabolic and regulatory network model of E. coli could explain only 15% of differential gene expression in response to the major environmental change of oxygen deprivation (2). While much progress has been made since then (3–5), predicting global gene expression remains a fundamental challenge (6).

A global TRN can consist of regulatory interactions determined from a variety of data sources. These include direct and indirect experimental evidence or computational predictions (7). For the latter, reducing false-positive interactions remains challenging—the state of the art achieves 60% precision (8, 9). In recent years, improved chromatin immunoprecipitation (ChIP) methods have enabled precise characterization of transcription factor (TF) binding sites. Combining ChIP with transcriptomics for TF KO strains has yielded high-confidence regulatory interactions in the conditions studied. Such ChIP studies have now accumulated for over a dozen major TFs, with each study increasing the number of known binding sites of a TF by 74–400% (10–13).

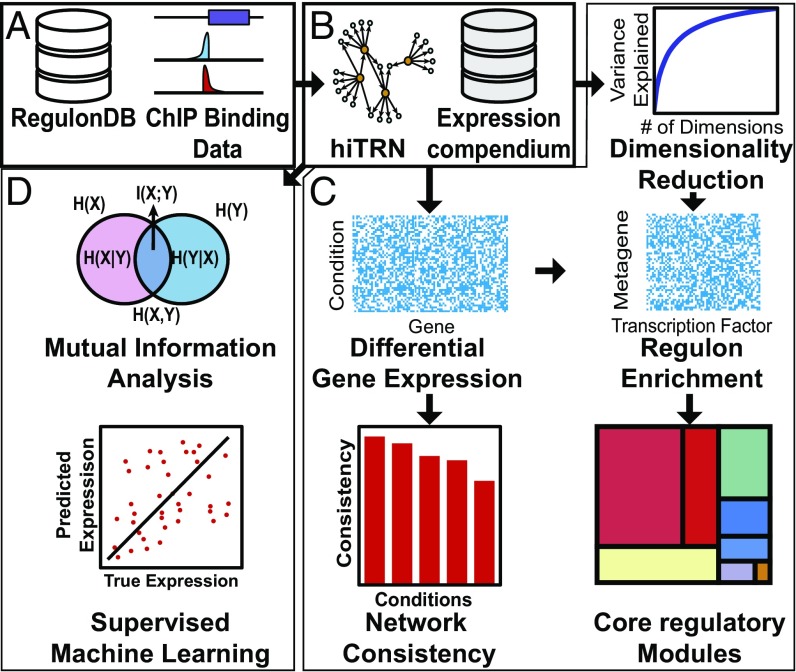
Here, we used this critical mass of data to perform a rigorous assessment of the latest high-confidence TRN (hiTRN) of E. coli that is devoid of uncertain regulatory interactions. We further examined this TRN’s ability to explain differential gene expression in response to genetic and environmental perturbations. The hiTRN was reconstructed by using published ChIP data for 15 TFs added to only high-confidence regulatory interactions from RegulonDB (7). We assessed our hiTRN using transcriptomics compendia (14–16) and multiple computational approaches: unsupervised and supervised machine learning, mutual information (MI) analysis, network topology analysis, integer programing, and community detection (Fig. 1).

Fig. 1.

Overview of our workflow. (A) RegulonDB (7) and additional published ChIP data were combined to reconstruct the hiTRN. (B) Using our hiTRN, we analyzed transcriptome shifts in expression compendia [EcoMAC (14), E. coli Expression 2 (15), and COLOMBOS (16)]. (C) We evaluated the completeness of our knowledge of our hiTRN on the basis of network consistency, dimensionality reduction, and detection of stable regulatory modules. (D) We assessed the ability of our hiTRN to quantitatively predict gene expression using MI and regression.

Results

The Coverage of the TRN Has Expanded, but Remains Incomplete.

Our reconstructed hiTRN consisted of 147 TFs, 1,538 transcription units (TUs), and 1,764 genes regulated by 3,797 high-confidence regulatory interactions (Dataset S1). We assessed the coverage of the hiTRN for explaining differential gene expression in three ways.

Completeness.

To assess hiTRN’s completeness, we computed what fraction of the 1,764 genes whose expression changed across 154 experimental conditions could be directly explained with the hiTRN (see Materials and Methods and SI Appendix, Fig. S1 for explanation of conditions analyzed). On average, 27% of differentially expressed genes (DEGs) in the set of 1,764 genes considered were enriched for at least one regulon, and 20% or more of DEGs were enriched for at least one regulon in 57% of the conditions.

Genetic Perturbations.

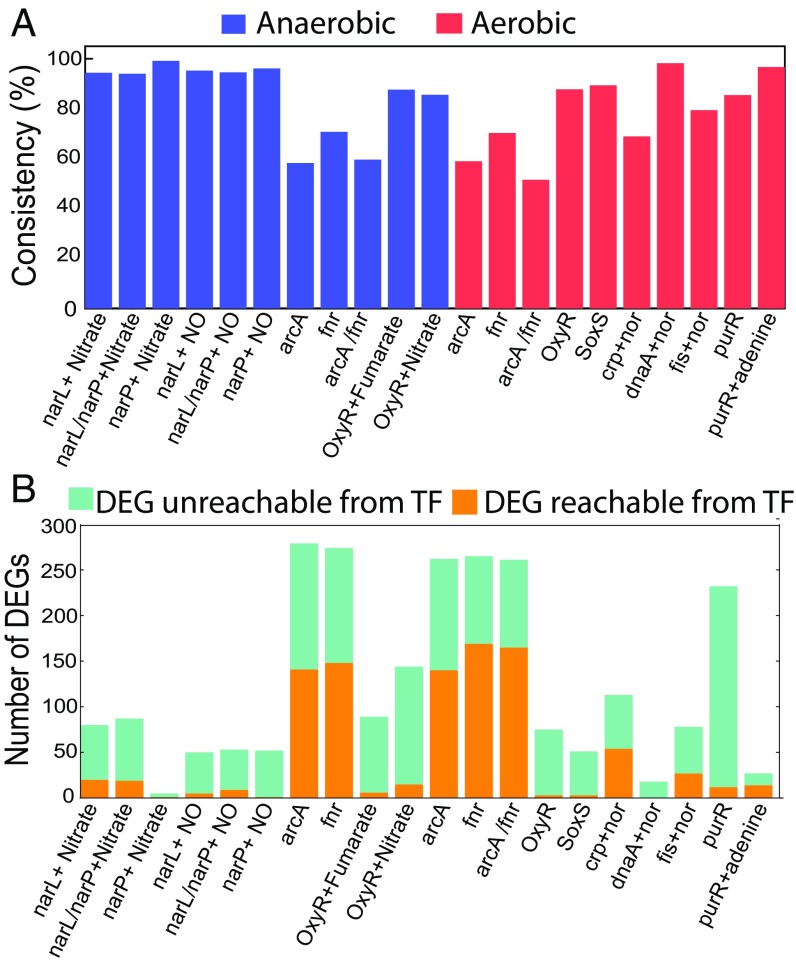
We then assessed whether differential gene expression could be traced through regulatory paths in our hiTRN to a knocked-out TF gene. We investigated 21 different sets of single or double TF KOs. We found that 0–63% of DEGs in the TRN were successfully traced to the knocked-out TF through one or more regulatory paths (Fig. 2B). We could best explain DEGs in the TRN (50–63%) for experiments $\mathrm{\Delta }arcA\mathrm{\Delta }fnr$ and $\mathrm{\Delta }purR$ (with adenine), while experiments $\mathrm{\Delta }narP\mathrm{\Delta }oxyR$ and $\mathrm{\Delta }soxS\mathrm{\Delta }purR$ (without adenine) were explained poorly. For comparison, we also extracted nine additional TF KO experiments from the COLOMBOS dataset (16) and performed the same analysis. For the four experiments that have DEGs identified, we found that $\sim$56% of the DEGs in the TRN could be successfully traced to the knocked out TF (SI Appendix, Fig. S2).

Fig. 2.

Consistency of hiTRN with observed differential gene expression in wild-type cells and in strains with a deleted TF gene. (A) Consistency of our TRN with observed differential and nondifferential gene expression accounting for regulatory bias (i.e., sign consistency). (B) Reachability (existence of contiguous regulatory paths in the TRN) from deleted TFs to DEGs in the TRN.

Regulatory Bias.

We then evaluated whether the regulatory bias (activation or inhibition) assigned to each regulatory interaction was consistent with DEGs given a TF KO. This “sign consistency” analysis was conducted by formulating the hiTRN as an influence graph (17), with edge signs reflecting activation (+) or repression (−). Overall, total sign consistency accounting for both DEGs and nondifferentially expressed genes was 51–99% consistent with the TRN (Fig. 2A). The highest consistency was observed for local TFs such as narL, narP, dnaA, and purR. Consistency was low for arcA/fnr under both conditions. We found a negative correlation between the number of genes regulated (both directly and indirectly) by a TF and the sign consistency between the TRN and experimental data (Pearson $r=-0.875$, $P=2.10\times {10}^{-7}$) (SI Appendix, Fig. S3). We also found a significant negative correlation between the longest regulatory path length of a TF and consistency (SI Appendix, Fig. S4). For the TF KO experiments from the COLOMBOS dataset, the overall consistency was similar (59–99%).

Not all DEGs could be traced to the deleted TF (Fig. 2B). Unreachable DEGs may indicate missing regulatory interactions, while low sign consistency suggests that additional factors influencing regulatory bias need to be explicitly modeled [e.g., effect of adenine on PurR binding (11)]. Additionally, some differential expression may have been due to growth rate-dependent global regulation (5, 18) (growth rates ranged from 2 to 37% of the wild-type, where these metadata were available).

Overall, the coverage of our hiTRN for DEGs varied across experimental conditions, with an average coverage of 26%, which was significant (permutation test, $P=3.91\times {10}^{-4}$; SI Appendix, SI Methods) and up to 63%. The low DEG coverage for individual TF KO experiments reflects the highly interwoven nature of many regulons. Thus, achieving 100% DEG coverage will likely require precise reconstruction of individual regulons, including mechanisms beyond TRN topology and regulatory bias.

The hiTRN Is Consistent with Major Modes of Changes in the Entire Transcriptome.

We evaluated our hiTRN in the context of transcriptomics data consisting of 4,189 genes $\times$ 441 samples. Transcriptomics data are difficult to interpret, in part because they are high-dimensional and noisy. We thus used nonnegative matrix factorization (NMF) (19) to identify major modes (i.e., important features) of transcriptome changes across conditions. NMF identifies cohesive subsystems from complex expression data set by reducing thousands of genes into several dozen metagenes, which represent the major modes (19–21). A metagene is a linear combination of the genes whose expression changes are correlated across conditions. Using NMF, we reduced the dimensionality of the expression data from 4,189 genes $\times$ 441 samples to 40 metagenes $\times$ 441 samples. We confirmed using principal component analysis (PCA) that 40 dimensions sufficiently explained (88%) of variance in the expression data (SI Appendix, Fig. S5).

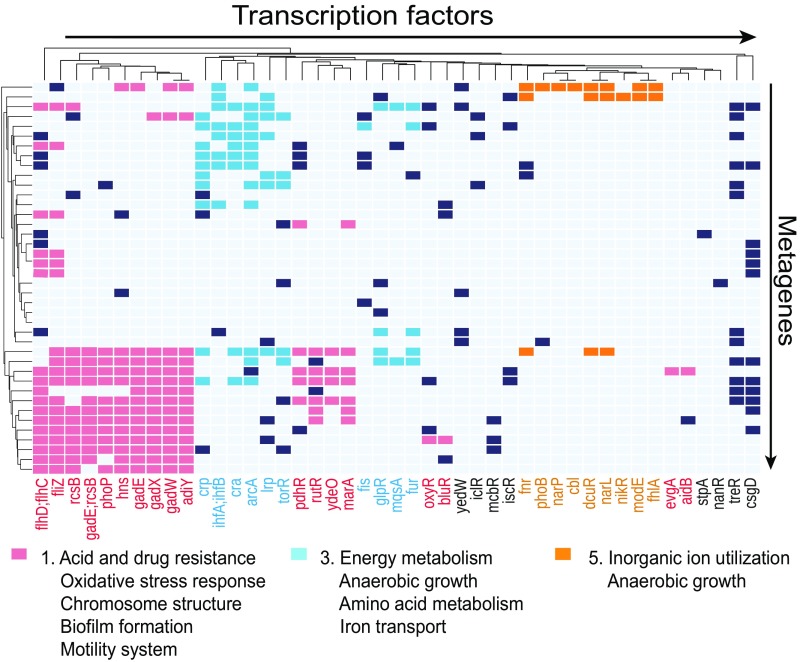
We then characterized the relationship between regulons and metagenes. To do so, we identified regulons that were enriched for genes that were determined to be major contributors within each metagene (i.e., genes that had large coefficients within a metagene). We found that all metagenes were enriched for at least one regulon (Fig. 3).

Fig. 3.

Regulon enrichment and functions of metagenes. Colors indicate functions of metagenes based on enriched regulons. Functionally related regulons are enriched in the same metagenes. Note that only TFs in modules 1, 3, and 5 are shown here. A full heatmap can be found in SI Appendix, Fig. S6.

Furthermore, metagenes tended to be enriched for hiTRN-regulons that shared related functions (Fig. 3). For example, some stress response TFs (rcsB, gadE, gadX, and gadW) were enriched simultaneously for several metagenes. This result is consistent with the hiTRN structure, which causally links these TFs: $rcsB\to gadX\to gadW\to gadE$ (7, 22). Overlapping regulons were also coenriched in the same metagene including narL and narP, or nrdR and dnaA.

These results demonstrate coverage and coherency in the hiTRN and consistency with high-dimensional transcriptomics data, albeit at a more coarse-grained level than the reachability and regulatory bias described above.

Robust Regulatory Modules Were Identified.

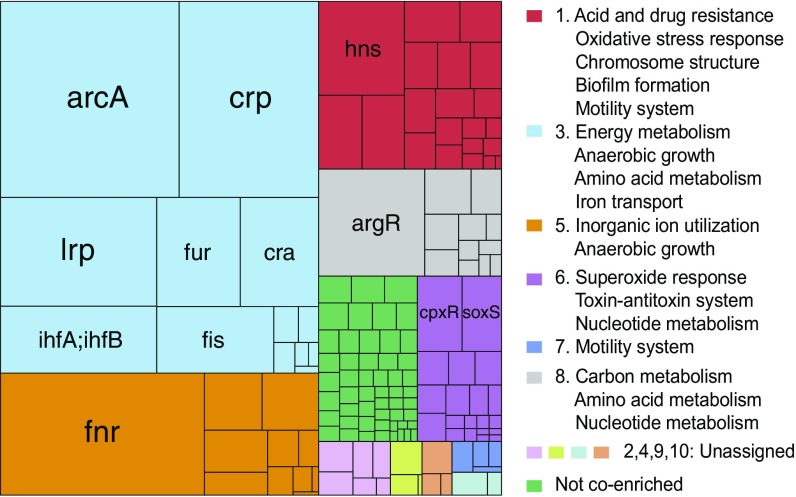
Next, we evaluated whether the organization of TFs in our hiTRN was consistent with the functional organization of regulons as derived from the transcriptome. We thus developed a computational pipeline to identify clusters of TFs (or modules) that were significantly and strongly coenriched across conditions (SI Appendix, SI Methods). We identified 10 coenriched modules (Fig. 4 and Dataset S2). Six modules in particular represented core biological functions. For example, module 6 included TFs and toxin–antitoxin pairs associated with multiple stress responses. Since the E. coli TRN is still expanding, we evaluated whether these modules would remain stable as new regulatory interactions are incorporated into the TRN. We randomly added up to 60 regulons and used our pipeline to identify new modules, which were compared against the original modules. The average Jaccard index (SI Appendix, SI Methods) between modules ranged from 0.34 to 0.81, and normalized variation of information (VI) (23) ranged from 0.025 to 0.34 (SI Appendix, Fig. S7). Module stability depended on which regulons were added, since even when 34 new TFs and 1,290 regulatory interactions were added, the clusters could be stable (Jaccard index = 0.55, normalized VI = 0.14). The modules were also relatively consistent when we used a different expression compendium, COLOMBOS (16). The normalized VI for the modules identified between the two compendia was 0.17, which was significant (permutation test, $P<{10}^{-4}$).

Fig. 4.

Ten functional regulatory modules for 147 TFs. Size of rectangles are proportional to the size of regulons (i.e., the number of regulated genes). The overlap between regulons is not shown. Modules are fully defined in Datasets S2 and S3.

Regulatory Modules Identified Have Broad Implications.

Next, we examined evolutionary characteristics of the regulatory modules at the DNA sequence and protein structure levels.

Evolutionary Conservation.

We hypothesized that modules associated with vital functions would be conserved across species, while organism-specific responses would not. We thus computed conservation of the 147 TFs in our hiTRN across Enterobacteriaceae and $\gamma$-, $\beta$-, $\alpha$-, and $\delta$-proteobacteria (SI Appendix, SI Methods). We found two conserved modules (modules 7 and 10) involved with motility, metal ion uptake, and DNA damage response (SI Appendix, Fig. S8). We also found one significantly less-conserved module (module 1), primarily involved with various stress responses, including acid stress. This result was consistent with availability of alternative pH stress response systems or alternative regulators of conserved proton consumption or generation genes (22).

Binding Motifs.

We investigated the sequence homology of DNA binding motifs of the 147 TFs. We found that the TFs in modules 1, 2, 3, 8, and 9 shared more similar binding motifs within the module compared with those in other modules (Mann–Whitney–Wilcoxon test $P<0.05$).

Protein Structure.

We explored the structural similarity between TFs in each module to identify whether a structure–function relationship existed within the modules. We aligned annotated DNA-binding domains and the full structures of TF pairs using the FATCAT structural alignment tool (24). The TFs in modules 4, 5, and 8 showed significantly higher structural similarity in both cases to TFs within the module compared with TFs in other modules. Specifically, module 8 was enriched for the periplasmic binding protein-like I domain (25).

The Expression of Most TUs Can Be Predicted Quantitatively from TF Expression.

We next asked whether gene expression could be quantitatively predicted as a function of TF expression levels across varying conditions and genetic perturbations. Eight potential model structures were explored to identify the best modeling procedure: four multiple linear regression models and four support vector regressors (SVRs). The model structures were similar to those described in the literature (14, 26–29).

Multivariate Linear Regression.

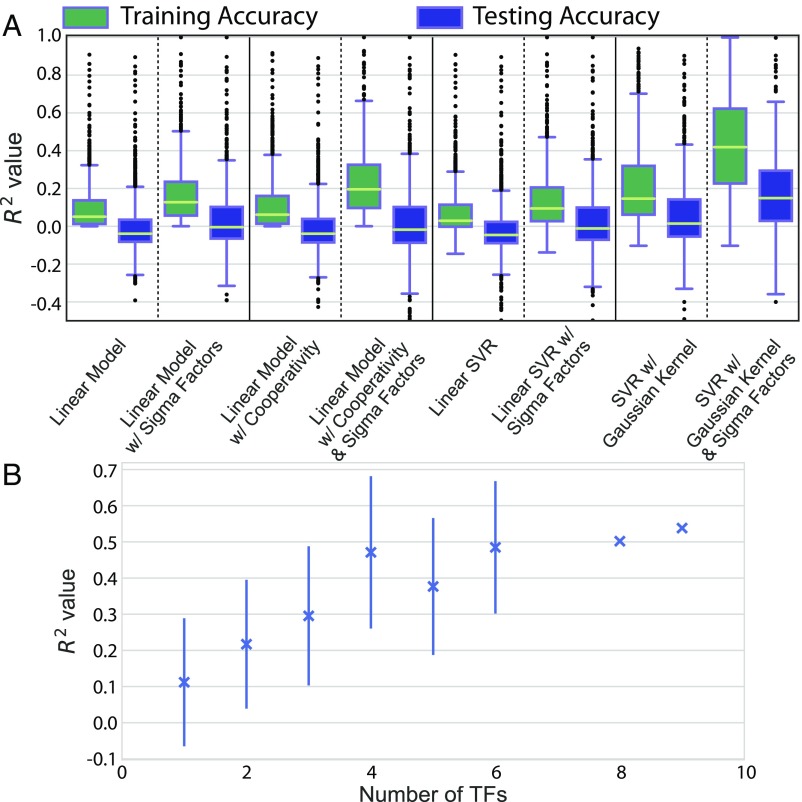
We used multivariate linear regression to predict the average expression of genes grouped by TUs from RegulonDB (7) (Materials and Methods). A total of 1,364 of the 1,538 identified TUs were measured in EcoMAC. We tested both TFs and sigma factors as regressors (30) and included a cooperativity term that allowed for bilinear interactions between TFs for each case (Fig. 5A). Using an F test of overall significance (31), we determined that in 77% (1,045 of 1,364) of TU-specific bilinear models, TFs significantly improved the fit of the models compared with intercept-only models under a false discovery rate (FDR) $<0.05$. However, sigma factors alone significantly improved the fit of 91% (999 of 1,093) of TUs with known sigma factors, highlighting the strong influence of sigma factors on TU expression.

Fig. 5.

Accuracy of expression predictions on training and held-out testing transcription units. (A) $R^2$ (coefficient of determination) of predicted expression profile vs. true expression profile using various regression models. (B) $R^2$ value of the testing dataset predicted by a Gaussian kernel SVR, grouped by number of known TFs. Error bars indicate SD for groups with $>$3 observations.

Nonlinear Interactions.

To better account for nonlinear regulatory interactions, we next trained SVRs with linear and Gaussian kernels, both with and without sigma factors. Not only did the Gaussian kernel SVR with sigma factors fit the training data better than the best-performing linear model ($P<.001$), but the SVR significantly improved the predictive power of the model when applied to the testing data ($P<.001$) (Fig. 5A). The coefficient of determination ($R^2$) of the SVR with sigma factors on the training data were correlated with the number of known TFs (Pearson $R=0.41$, $P<.001$) (Fig. 5B). Thus, as we discover more about the structure of the TRN, the predictive power of the TRN should increase. The regression was performed on COLOMBOS by using the hiTRN (SI Appendix, Fig. S9) and on both COLOMBOS and EcoMAC by using only strong interactions from RegulonDB (SI Appendix, Figs. S10 and S11), providing highly similar results (SI Appendix, SI Methods). Using this model, we also tested whether our predictions captured condition-specific effects by shuffling the TU expression profiles (predicted outputs) while maintaining the order of the TF expression profiles (features). A total of 86% (1,174 of 1,364) of TUs yielded significant differences between the shuffled expression profile regression and the original regression for the SVR (FDR-adjusted $P<0.05$).

Sensitivity of TU Expression to TRN Topology.

We next evaluated whether certain TUs were predicted more accurately using our hiTRN than random TRNs. We identified 193 of 1,364 TUs (14%) that were predicted significantly better than random TRNs for the best SVR (FDR-adjusted $P<0.05$). The random TRNs preserved the hiTRN’s distribution of the number of TFs regulating a TU (SI Appendix, Fig. S12). Also, TFs sharing high MI with known regulators of a TU were excluded (SI Appendix, Fig. S13).

MI Analysis.

We next investigated why predicting the expression of 86% of TUs was apparently insensitive to the exact TRN. Based on MI, we found that only 28% (39 of 137) of measured TFs shared significantly higher MI with genes inside compared with genes outside their regulons ($\text{FDR}<0.05$) (SI Appendix, Fig. S14). However, the average MI between genes within each regulatory module was significantly higher than the average MI between genes that did not share a regulatory module (SI Appendix, SI Methods). Furthermore, expression profiles of many TFs shared high MI with other TFs (SI Appendix, Figs. S15 and S16). Therefore, the expression of most TUs could be predicted from the expression of many alternate TFs, even if there was no evidence of TF binding. This result reflects known issues with nonidentifiability of the TRN from expression profiles (32). This issue is also encountered in other organisms (26) and reinforces the need for high-confidence regulatory interactions.

Other Cellular Processes Influence Gene Expression.

Unmeasured factors can affect gene expression, from batch effects pertaining to the experimental procedure to unmodeled cellular processes. Such systemic variables are not represented in the hiTRN and may pose difficulties for reconciling observed differential expression. Surrogate variable analysis (SVA) (33) determines the effect of such unmodeled variables directly from expression data. We applied SVA to EcoMAC, using the best model (i.e., SVR with sigma factors) to predict the primary expression signatures. We identified three surrogate variables, which were enriched in data from a single laboratory (SI Appendix, Fig. S17). These variables imply that unaccounted variation stemmed from this data source, potentially related to the use of a substrate not present in other sources (LB plus glycerol). Presence of three surrogate variables was consistent with clustering of data in the first two principal components (SI Appendix, Figs. S18 and S19) in PCA analysis.

Discussion

In this study, we answered three questions concerning the scope and gaps in our knowledge of the E. coli TRN and our ability to predict gene expression.

The hiTRN Explains Many Causal Connections Between Differential Gene Expression and TF Activation.

We found that across 21 different TF KOs, up to 63% (26% on average) of the resulting DEGs in the TRN were traced back to the knocked-out TF through regulatory cascades in our hiTRN. Compared with 15% coverage reported in an earlier assessment in 2004 (2), our result represents an increase in coverage ranging from 70 to 320%. Additionally, we found that when accounting for network topology and regulatory bias (i.e., inhibition or activation) (17), our hiTRN explained 51–99% of DEGs and nondifferentially expressed genes. Some of the unexplained differential expression was potentially related to unmodeled variables that systematically influenced gene expression. We identified three such surrogate variables, one of which corresponded to a single data source having a distinct media condition. Unmodeled variables may also be explained by systematic variation in other biological processes, including growth rate (34).

We Can Predict Expression for 86% of TUs, but only 14% of TUs Are Unambiguously Linked to Their Direct Regulators.

We could predict expression for 86% (1,174 of 1,364) of TUs significantly better than shuffled expression profiles (FDR-adjusted $P<0.05$). We found 193 TUs (14%) whose expression was predicted significantly better than random TRNs (FDR-adjusted $P<0.05$), indicating the critical importance of having a well-defined TRN for these TUs. This progress resulted from having high-resolution measurements for TF binding sites and knowing the occupancy of these sites in a context-specific manner. Thus, designing experiments to define high-confidence regulatory interactions should be prioritized when characterizing the TRN of an organism for which data are scarce. With the advances in ChIP-exo and transcriptomics methods, a much more comprehensive understanding of the TRN could be achieved in the near term. Furthermore, given recent progress in understanding dormant TF–DNA binding events (35, 36), it will be important to investigate diverse conditions for expanding the repertoire of high-confidence interactions, which involves observing a proximal effect of binding on gene expression.

We Robustly Understand Global TRN Function Within a Limited Scope.

We identified 10 regulatory modules representing core biological functions from two expression compendia using the hiTRN. These modules showed evolutionary conservation at the DNA sequence and protein structure levels and overlapped with previously identified clusters (37) (SI Appendix, SI Methods). Furthermore, the modules were consistent when the hiTRN was perturbed by adding random regulatory interactions from up to 60 regulons.

Together, these results indicate that core TRN functions are understood robustly, and gene expression can be predicted. To grow the scope of the hiTRN, new high-precision ChIP experiments en masse directed at unconfirmed TFs or TFs regulating uncharacterized genes are expected to greatly enhance the scope of understanding of E. coli’s TRN and can do so in the near term. Analyzing disparate data by using in silico models is likely to be important for guiding us through the selection and execution of the most informative experiments to fill gaps in our understanding and to design experiments to test its robustness.

Materials and Methods

High-Confidence Regulatory Network Reconstruction.

To reconstruct the high-confidence TRN (hiTRN), we combined strong evidence interactions from RegulonDB 9.4 (7) according to the RegulonDB Evidence Classification (38), with TF KO-validated ChIP-based interactions for 15 regulons from literature: arcA and fnr (10, 39, 40), argR (41, 42), trpR, lrp (42), fur (13), gadEWX (22), oxyR, soxRS (43), purR (11), crp (44), and cra (45). The regulatory direction ($+$ or $-$) was preserved from the original study. Both directions were added if the direction was uncertain.

Expression Compendium Preparation.

Experimental conditions from EcoMAC (14) were filtered to exclude nonrelevant conditions as described in Yang et al. (46), resulting in expression profiles for 4,189 genes $\times$ 444 samples. Three of these samples (wild-type E. coli MG1655 grown aerobically in M9 medium with glucose) were used as a reference.

Nonnegative Matrix Factorization.

We performed NMF using sklearn with “nnsvd” initialization (47). The top genes accounting for 15% of each metagene’s weight were used for regulon enrichment. We compared NMF with singular value decomposition to support our choice of 40 metagenes (20) (SI Appendix, Fig. S20). We also used nonsmooth NMF (nsNMF) to identify sparse metagenes (48) and removed genes from each metagene having coefficients <0.001 (attributable to numerical error). Since NMF solves a nonconvex optimization problem and requires multiple runs to ensure global optimality, we used two methods, by Kim and Tidor (20) and Wu et al. (21), to confirm that our NMF decomposition was stable (SI Appendix, SI Methods). Metagenes are defined in Dataset S4.

Regulatory Module Identification.

We compiled a network of TFs that were coenriched in a metagene, from 100 runs each of NMF and nsNMF (48). We kept only 522 TF pairs that were strongly coenriched ($\text{Jaccard index}>0.18$) and significant (permutation test, $P<0.05$, from 100,000 random networks sampled from the observed frequency of coenriched TFs). We then identified modules using multilevel modularity optimization (49). The modularity coefficient of 0.483 was above the recommended cutoff of 0.3 to indicate community structure by Clauset et al. (50). The functional labels of the modules were assigned by using DAVID (51) functional annotation, followed by manual curation.

DEG Identification.

DEGs were identified by using the R package limma in Bioconductor (52), with thresholds of $|{\log }_2(\mathrm{Fold}\mathrm{change}|>1$ and FDR-adjusted $P<0.05$. Three samples were used as the reference: wild-type MG1655 grown in M9 with glucose as carbon source under aerobic conditions. The resulting 441 samples of expression profiles relative to the reference corresponded to 174 experimental conditions. Of these conditions, 166 showed significant differential expression. In 162 of these 166 conditions, at least one regulon was enriched for DEGs.

Network-Expression Consistency Analysis.

We determined the consistency of DEGs with the hiTRN for 21 TF KO experiments. Network reachability was performed by using igraph in Python (49) and sign consistency by using SigNetTrainer in Matlab (17).

Expression Profile Regression.

We used supervised machine learning (multiple linear regression and support vector regression) to predict log-fold change in expression of 1,364 TUs having at least one known regulator. We compared eight model structures with features including known regulators of each TU, cooperation/competition terms for all pairs of TFs, and known sigma factors. Models were evaluated by using a stratified 10-fold cross-validation to reduce overfitting (Materials and Methods). We determined whether our models captured condition-specific effects by comparing them against models trained on 1,000 randomly shuffled TU profiles, while maintaining the order of regulator expression profiles. We further determined the significance of the TRN for predicting expression by comparing models trained on the known TRN against those trained on 1,000 random TRNs having random TFs assigned to each TU, preserving the distribution of regulators per TU. TFs having high MI with known TFs were not randomly assigned to the TU.

Information Analysis.

We computed MI between TFs and target genes using the NPEET Python package (53). As described in Faith et al. (9), we compared this MI to a background distribution of MI scores using the Wilcoxon rank-sum test ($\alpha =0.05$).