Significance
We have developed a model of T cell binding that accurately represents the influence of self-peptides on thymic negative selection. From this, we generated estimates for relevant antigen recognition rates. We found that negative selection only slightly interferes with a T cell’s ability to detect antigens that differ from self-peptide by a single amino acid and that these peptides may effectively be regarded as foreign. Moreover, negative selection thresholds chosen to reflect experimentally observed thymic survival rates result in optimal production of T cells that are capable of surviving selection and recognizing foreign antigen. Lastly, our model predicts empirically reasonable donor tissue recognition rates in the context of an HLA-matched transplant.
Keywords: neoantigen, T cell, immunotherapy, applied probability
Abstract
The advent of cancer immunotherapy has generated renewed hope for the treatment of many malignancies by introducing a number of novel strategies that exploit various properties of the immune system. These therapies are based on the idea that cytotoxic T lymphocytes (CTLs) directly recognize and respond to tumor-associated neoantigens (TANs) in much the same way as they would to foreign peptides presented on cell surfaces. To date, however, nearly all attempts to optimize immunotherapeutic strategies have been empirical. Here, we develop a model of T cell selection based on the assumption of random interaction strengths between a self-peptide and the various T cell receptors. The model enables the analytical study of the effects of selection on the CTL recognition of TANs and completely foreign peptides and can estimate the number of CTLs that can detect donor-matched transplants. We show that negative selection thresholds chosen to reflect experimentally observed thymic survival rates result in near-optimal production of T cells that are capable of surviving selection and recognizing foreign antigen. These analytical results are confirmed by simulation.
Immunotherapeutic strategies, which can, in principle, evolve with a growing malignancy, have gained recent popularity for treating a variety of cancer types (1, 2). Successful therapy depends on cytotoxic T lymphocyte (CTL) recognition of tumor-associated neoantigens (TANs) as well as nonmutated but misexpressed self-peptides to which T cells are intolerant. These antigens are displayed on the surface of cells via MHCs (3–8).
MHC-displayed TANs arising by somatic point mutations along with overexpressed or mislocalized self-peptides present in only minimal quantities during thymic negative selection carry antigenic potential (9–12). TANs resemble self-peptides, while overexpressed self-peptides may appear to CTLs as entirely foreign antigens that have never been selected against. Previous quantitative models of T cell receptor (TCR)–peptide interactions have succeeded in accurately characterizing many aspects of T cell immunology and thymic selection. Digit string representations have provided insight into foreign peptide recognition and MHC-unmatched alloreactivity rates as well as T cell specificity and cross-reactivity (13–17). Modeling TCRs and peptides as amino acid strings has also been successful in studying HIV (18–21). In the context of immunotherapy, characterizing recognition rates of TAN and overexpressed/mislocalized self-peptides is relevant to understanding CTL repertoire targeting efficiency. This recognition process has yet to be mathematically modeled; instead, nearly all attempts to understand CTL-based immunology have been empirical. Clearly, developing such a model is basic to achieving a fuller understanding of the overall functioning of the immune system.
Here, we began our analysis with a preexisting model adapted to isolate negative selection effects. We found anomalous behavior in the ability of this formulation to apportion the contributions of individual self-peptides to the overall selection process. In particular, a small number of “potent” thymic self-peptides dominated selection. We then formulated an alternative, more general approach for the TCR–peptide interaction that assigns random amino acid binding interactions in a position-independent manner as opposed to the fixed set of interactions between different amino acid pairs in the previous model. Despite exhibiting improvement, the problems discussed above still remained, rendering this model also unacceptable. This led us to consider a final approach that incorporates position dependence into the random interaction picture. This last model exhibits a realistic selection balance between individual self-peptides and allowed us to then consider issues of detection of altered peptides.
Using this model, we found that antigenic proximity to self-peptide only minimally reduced CTL recognition compared with recognition of foreign antigen. Moreover, we showed that TCR activation thresholds consistent with empirical selection rates resulted in a near-optimal production of T cells that both survive negative selection and identify foreign antigen. Lastly, we applied our model to the setting of transplantation, predicting alloreactivity (i.e., detection by host CTLs) rates consistent with empirical observations given known levels of host and donor single-nucleotide dissimilarity.
Model Development
We seek a model of negative thymic selection where the representation of self-peptides is defined explicitly by amino acid sequences and the survivors constitute a representative CTL repertoire. Most importantly, the model should exhibit reasonable selection behavior. That is, we require that a plurality of the thymic self-peptides, estimated to number around (16, 22) for each MHC class, nontrivially participate in negative selection. To this end, we started with a version of an existing model (18–21) built on the use of an amino acid binding matrix. We found that this model does not yield satisfactory behavior, and therefore, we considered, in turn, two alternative formulations for the TCR–MHC interaction. We studied the nature of thymic selection in each framework using both analysis and simulation. In each of these models, peptide-bound MHC (p-MHC) was represented by a sequence, , of amino acids; for definiteness, we chose . To facilitate analytical insight, we considered a single MHC type (in reality, there may be up to six) for each individual. Such a framework will allow us to determine the extent to which negative selection diminishes mutated self-peptide recognition. In the following, we did not focus on the precise physical mechanism by which TCRs recognize antigen (for example, affinity-driven vs. binding lifetime) (13, 23, 24) but instead, merely posit an interaction strength governing recognition; for simplicity, we will use throughout the language of binding energy.
Sequential Miyazawa–Jernigan.
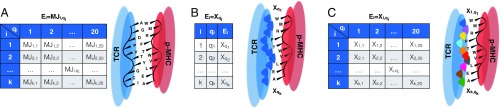
Our first formulation is an extension of the work by Chakraborty and coworkers (18–21), which has been successful in providing insight into HIV-immune dynamics. In their work, a TCR was represented by a string of amino acids that contact p-MHC, and the total binding interaction was the sum of a direct TCR–MHC interaction and pairwise amino acid binding interactions using the Miyazawa–Jernigan (MJ) matrix (25, 26) (Fig. 1A). The interaction between TCR and p-MHC was then given by
| [1] |
where represents the MJ interaction between amino acids and . Since plays no role when only one MHC class is present, we henceforth set it equal to zero.
Fig. 1.
Alternative TCR–MHC interactions formulations. (A) S-MJ. Each TCR is represented by a string of amino acids, and the binding energy with a self-peptide is the sum of pairwise binding energies between the TCR amino acids and those in corresponding positions along the peptides. (B) PIRA. TCR regions (shaded dark blue in the cartoon) that bind peptide are characterized by TCR-specific binding energies for each given amino acid type, all drawn from a standard Gaussian distribution. These binding energies are assumed to be position-independent. (C) RICE. The behavior of TCR contact regions is now position-dependent (hence represented by different colors in the cartoon). A TCR is represented by a 20 10 array of IID standard Gaussian random variables, indicating the binding energy contribution for each amino acid/contact position pair along the peptide.
Our extension, called the sequential Miyazawa–Jernigan (S-MJ) model, allows us to consider independently and sequentially the effects of positive and negative thymic selection on naïve T cell generation. The role of positive selection is to filter defective TCRs unable to properly interface with p-MHC (27, 28); this happens separately (both in time and space) from negative selection, which is our sole concern here (SI Appendix has more discussion of positive selection).
As we shall see, our analysis shows that this first model does not yield satisfactory behavior, and we are thus obligated to modify the model. In our alternate formulations, self-peptide sequences are represented in the same way as above, but we change the form of the interaction. In reality, the binding site for each amino acid on p-MHC is complex, and binding interactions represent the net effects of complicated TCR–p-MHC association in a binding groove. This affords TCRs with a large degree of freedom in their ability to interface with each amino acid in a given p-MHC. We, therefore, assume that individual amino acid interactions that comprise TCR–p-MHC interface are random variables, which we take to be Gaussian-distributed. To form a tractable model, we also assume that the binding energies attributed to each possible amino acid are independent and identically distributed (IID). This type of approach is reminiscent of the random energy model that was used to great effect in studies of protein biophysics (29).
Position-Independent Random Affinity.
In this first alternative model, we assume that TCR interactions with each amino acid are position-independent (Fig. 1B). That is, a given amino acid interacts with a given TCR identically, regardless of its position in the p-MHC. We refer to this as position-independent random affinity (PIRA). In this case, a TCR may be represented by its interactions with all amino acids and therefore, is described by a sequence of independent standard Gaussian random variables. The interaction function for negative selection is given by
| [2] |
Random Interaction Between Cell Receptor and Epitope.
More realistically, each 3D location in a given TCR handles amino acids very differently. For now, we neglect any correlation in binding interactions that might occur either because of amino acids with similar properties or through a dependence on adjacent amino acids. We characterize the binding energy of the peptide at the position of p-MHC as a function of itself in addition to the identity of the amino acid at this position (Fig. 1C). We refer to this approach as the random interaction between cell receptor and epitope (RICE) formulation. Here, we represent a TCR, , and all of its possible interactions by a array of IID standard Gaussian random variables, where denotes the interaction with which TCR binds amino acid located at position . The interaction function for negative selection is then given by
| [3] |
In SI Appendix, we analyze the alternate choice of IID uniform distributions and verify that the important results are independent of this level of detail.
Results
To study negative selection in these models, a given randomly constructed TCR was tested against a collection of randomly constructed self-peptides. For a given TCR to survive selection, the interaction energy between and each and every self-peptide must not exceed . Conversely, TCR recognizes (nonself-)peptide whenever the TCR–p-MHC interaction exceeds . Potency and recognition simulations use cohorts of TCRs.
In the following, we present the main findings of our analysis. Full mathematical derivations are provided in SI Appendix.
RICE Yields a Sensible Spectrum of Self-Peptide Contributions to Thymocyte Selection.
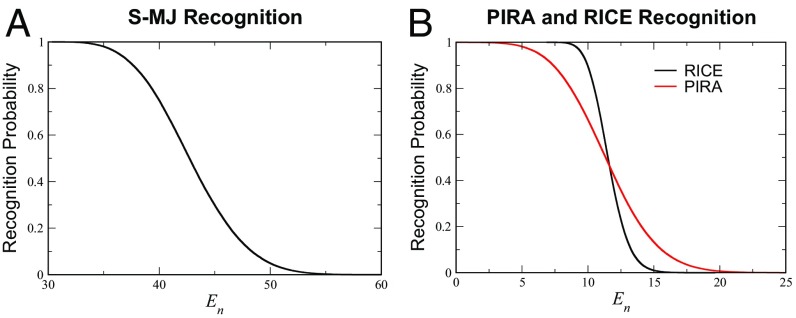
All three formulations described above exhibit similar empirical survival profiles with respect to the negative selection threshold (Fig. 2). However, in both S-MJ and PIRA, a very small number (1 in a typical simulation of S-MJ and 125 in PIRA, both with ) of potent self-peptides dominates nearly all of thymocyte selection as seen both in simulation and analytically (see Fig. 3; SI Appendix, Fig. S7). This feature does not depend on the assumed size of the training set (SI Appendix). One manifestation of a few peptides dominating the entire selection process is a much higher fluctuation in mean survival rates (SI Appendix, Fig. S14). More generally, we do not think that it makes sense for a system to use a large number of peptides for negative selection if only a very small fraction would achieve the same outcome.
Fig. 2.
TCR recognition probability for each model. Recognition occurs whenever the interaction energy is greater than an upper threshold, . Recognition rates as a function of threshold for (A) S-MJ as well as (B) PIRA and RICE. General recognition behavior is similar among all three formulations. In each case, thymocytes are simulated to undergo selection.
Fig. 3.
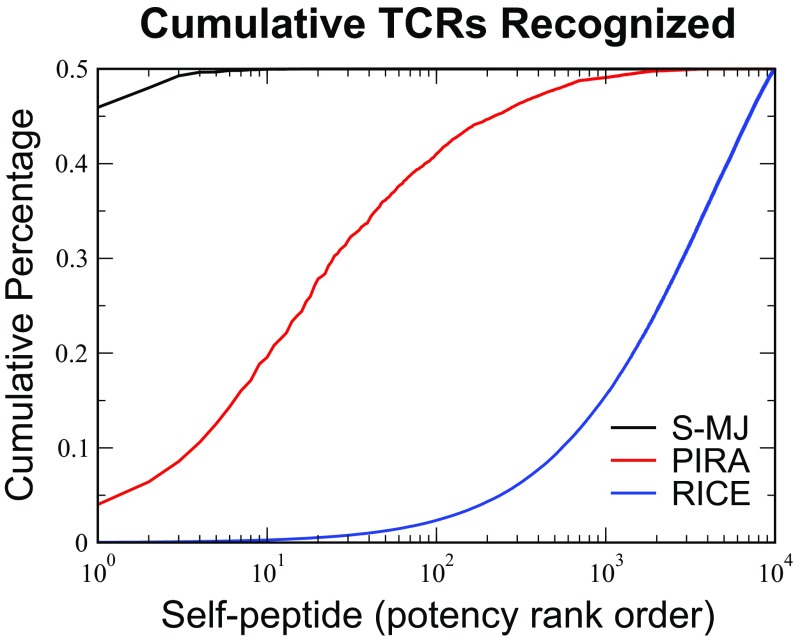
Peptide potency for each model. The self-peptides were ordered by “potency” or the fraction of (the ) thymocytes recognizing them during selection simulations. Potent self-peptides were those that were recognized most often by the TCRs. The cumulative contributions of each self-peptide to negative selection were plotted in decreasing order of self-peptide potency for the S-MJ, PIRA, and RICE models. In all cases, the selection thresholds are chosen to give survival. We see that, for the S-MJ model, the most potent self-peptide is responsible for roughly of the selection behavior, whereas for the PIRA (RICE) model, 200 (7,100) of self-peptides generate this level of selection.
In contrast, RICE results in a repertoire sculpted by all of the self-peptides (Fig. 3 and SI Appendix, Fig. S10). The extreme potency of some self-peptides in the S-MJ model is a result of the presence in these self-peptides of many amino acids with anomalously large average binding energy, which causes them to be recognized by a large number of TCRs. In PIRA, the potent peptides are those which have a large number of amino acid repeats, so that they are recognized by all TCRs that have a significant binding energy to those particular amino acids (SI Appendix has details). Since there are 20 different amino acids, it takes on the order of 20 self-peptides to accomplish the bulk of the negative selection (specifically, 25 peptides accomplish of the selection). Neither of these issues occur in RICE.
Given these findings, we have chosen to proceed with the RICE model. Current empirical observations of negative selection vary anywhere from to as high as (30–35). This defines an acceptable range, , for reasonable negative selection thresholds to be used in our analysis (Fig. 2B).
Thymic Selection Minimally Decreases Recognition of Point-Mutated Self-Peptide.
By construction, the binding interactions between TCR and self-peptide are sums of IID random variables. A given TCR survives negative selection against a collection of thymic self-peptides if all of its binding energies are below threshold. Under RICE, the survival probability may be approximated by neglecting similarities between self-peptides and noting that the amino acids comprising a self-peptide are IID:
| [4] |
The quantity is a sum of IID Gaussian random variables, and its distribution is given by
| [5] |
where is the cumulative distribution function (CDF) of the standard zero mean, unit variance normal distribution, and . The survival probability is then the probability that the maximum of over the set of amino acids is less than . The distribution of the maximum of a large number of Gaussian random deviates can be approximated by a Gumbel distribution with CDF (SI Appendix has details):
| [6] |
where
| [7] |
are the -dependent mode and width parameters of the Gumbel distribution, and is a parameter that is found by solving the implicit equation
| [8] |
This approximation for as well as more detailed analytic approaches, which also include the role of the variance of the mean energy for a given TCR caused by the finite number of amino acids, are compared with direct simulations of negative selection in SI Appendix.
We now wish to compare two cases of single-TCR recognition probabilities: one of a random peptide and one of a point-mutated self-peptide. For the random peptide, we denote this probability by . A simple analytical estimate is given by , the value for the recognition probability obtained by ignoring selection completely, as there are not likely to be any self-peptides close to one chosen completely at random:
| [9] |
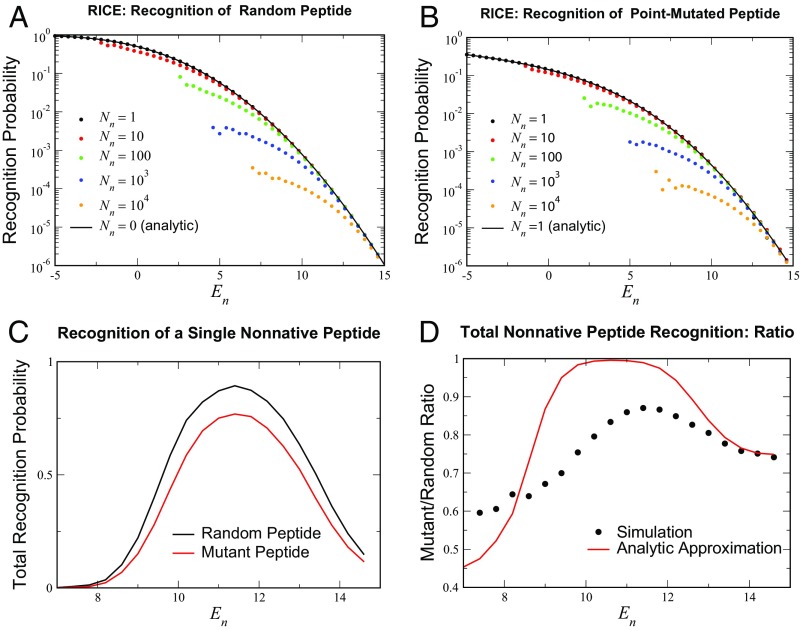
The subscript here denotes that no selection takes place (or equivalently, peptides) for this event. The analytic expressions for are compared with simulations for from to (Fig. 4A). Note that, in the selection threshold range of interest (), the agreement is semiquantitative, even for .
Fig. 4.
RICE recognition behavior. (A and B) Probabilities for a single selected TCR to recognize (A) random peptides and (B) point mutants of self-peptides for the analytically tractable limits and for higher values of . In both cases, the effect of increasing the number of negatively selecting self-peptides to has a relatively small effect on recognition rates in the range of relevant values (–) of . The simulation averaged over all of the surviving TCRs from the initial cohort of , a lower estimate of the mouse T cell diversity for a single MHC (36); random and point-mutant variants were tested. (C) The total recognition probability for the surviving () TCR cohort to recognize: a random peptide (black curve) and a single-site mutant of a native peptide (red). (D) The ratio of the two recognition probabilities in C; peptides of each class were tested. Included in D is the theoretical estimate of the ratio , where is the number of TCRs that survived selection.
One can similarly construct an analytic estimate for the single-TCR recognition probability for a point-mutated self-peptide, which we will refer to as a TAN, assuming that a tumor may be detected by its creation of singly mutated peptides. We will denote this TAN as , which is a mutated version of self-peptide , differing only at position . We let be the probability that TCR negatively trained on self-peptides would nonetheless recognize TAN . We estimate by evaluating the probability that TCR trained exclusively on the single (nonmutated) self-peptide can detect . We denote this probability by to indicate that it survived selection against a single self-peptide. This is motivated by the fact that is most closely related to and therefore, should account for a significant amount of the dependency of TCR recognition ability on ’s survival under full thymic selection. The probability, , that TCR recognizes , conditioned on surviving thymic selection by , is given by
This probability is computed in SI Appendix; the result is approximately
| [10] |
This expression for estimating the probability of TAN recognition is compared with simulations with ranging from to (Fig. 4B). We find that recognition estimates are again reasonably accurate even for large in the regime of realistic negative selection thresholds (), despite the potential influence of many negative selectors. This suggests that cross-dependencies between self-peptides caused by sharing amino acids in the same position have a weak effect on the overall selection of a repertoire. Moreover, reductions in the ability of a repertoire to detect closely related TAN peptides are quite modest compared with foreign or nonmutated self-peptides (Fig. 4C). The ratio ranges from to in the range . Also shown in Fig. 4 is the theoretical estimate deriving from and , which show the same trends, with slightly larger variation with . These findings support the hypothesis that TCR selection against self-peptides has a minimal influence on the recognition of peptides which are “close” to self and that these peptides are detected with rates similar to those of completely random (foreign) antigens. In the RICE model, the immune system seems to simply memorize the list of self-antigens and by doing so, generates a surprising level of immune protection against peptides not included on that precise list.
Observed Thymic Selection Is Close to Optimality for TCR Recognition Ability.
The above analysis provides a convenient context for framing negative selection as an optimization problem. Aside from maximally producing thymocytes, the immune system could be attempting to choose the TCR interaction threshold () in such a way as to encourage recognition of foreign antigen. In other words, the host benefits from producing TCRs that have the ability to survive negative selection and subsequently recognize random (currently unknown) foreign antigens. We again approximate the detection probability by the probability of recognition by TCRs undergoing no selection () and obtain
| [11] |
Then, existence of an extremum, , requires
| [12] |
Thus, at the optimal threshold,
| [13] |
The rate of optimal negative selection for large numbers of peptides () is characterized by
| [14] |
This value, consistent with the low end of measured survival probabilities, corresponds to a system optimized for recognition and agrees with an independent analysis that considered the optimal diversity of the T- and B-cell repertoires (16, 22). We should note, of course, that we expect there to be slight differences in the optimum threshold for case as opposed to our estimate based on . We do expect these to be close in general and in fact, can prove that the true maximum is always no less than (SI Appendix, Proposition S1) in selection regimes of interest.
Effects of Host–Donor Sequence Differences on Alloreactivity Percentages.
We now turn to the setting of transplants with MHC-matched host and donor. Even with the matching, there will be some SNPs between host and donor. These SNPS may give rise to amino acid differences that are detectable by the host T cells. We denote by the number of such differences. Since is the probability of a given TCR detecting a peptide with a single-amino acid difference, the probability of a host TCR recognizing a difference in the donor tissue (termed alloreactivity) is given by
| [15] |
We subsequently characterize the distribution of . We consider MHC-matched donor and host and use the frequency of SNPs in the genome (300/bp) (37) to estimate the number of 10-mer peptides which contain an SNP. Since each peptide comes from 30 bp of sequence, the chance that this sequence will contain a mutation is . Assuming that all donor peptides being probed by the immune system are contained in the size training set, the number of peptides that exhibit differences from the training set is distributed according to Poisson(. As alluded to above, a point mutation may or may not actually manifest as an amino acid difference between host and donor. We assume approximately equal frequencies of DNA base pairs and calculate the probability of an amino acid difference given an SNP as by considering the likelihood of missense mutations arising from DNA codons. Thus, , the number of self-peptides that actually manifest a different amino acid, is distributed as Binomial(). By use of the probability generating functions of , it can be shown that Poisson() (SI Appendix). From this, we may obtain the first and second moments of (i.e., the mean and variance of the fraction of TCRs exhibiting alloreactivity):
| [16] |
| [17] |
| [18] |
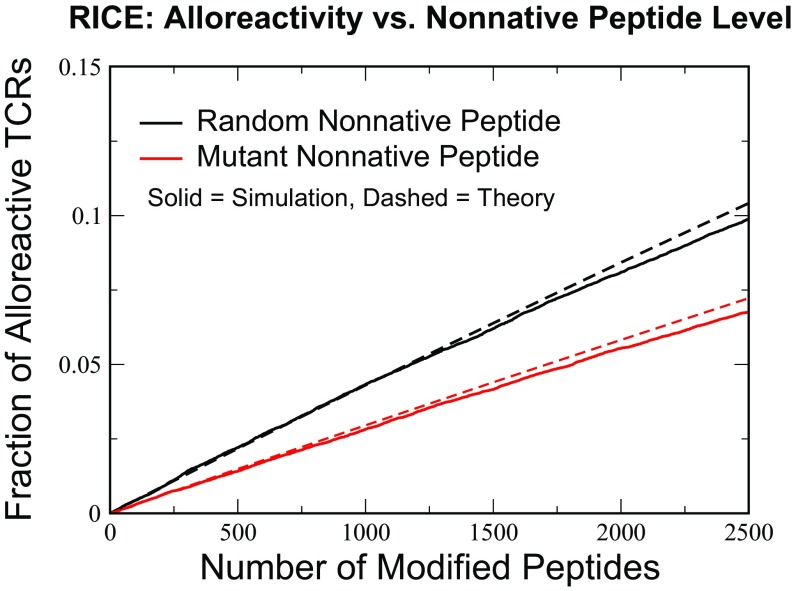
The percentage of alloreactive TCRs given by the above equations (in other words, the allogeneic CTL response) equals in MHC-matched host and donor pairs caused by SNPs (Fig. 5). This response is obtained from contributions of roughly 600 potential allogeneic p-MHCs. This number is on the low end of experimentally observed estimates of MHC-unmatched alloreactivity falling between 1 and 24% (13). We note in passing that the case of maximal single-amino acid sequence differences in our model with would correspond to an alloreactive rate of 26%, while maximal numbers of random peptides would correspond to rates as high as 38% (SI Appendix, Fig. S12).
Fig. 5.
The effects of increasing differences in host and donor thymic self-peptides on alloreactivity percentages in the RICE model. The simulation was performed with an original cohort of TCRs, of which survived selection under self-peptides (). Increasing numbers of nonnative peptides [either random (black curves) or single-difference mutants (red curves)] were introduced, and the numbers of TCRs reacting to these were recorded. The theoretical estimate is from Eq. 16, with single-TCR recognition probabilities for random and single-mutant peptide taken from Fig. 4 A and B.
Discussion
The development of a generative model relating T cell repertoires to thymic selection against individual self-peptides represents an important theory-driven milestone to better understand CTL cancer immunotherapy. Here, we were primarily interested in studying the influence of thymic negative selection on CTL repertoire recognition of relevant nonself-peptides with applications to TAN recognition and SNP recognition by MHC-matched CTLs. It was, therefore, important that the analysis be sensitive to small differences in individual thymic self-peptides that sculpt T cell repertoires. This, in turn, required that the model appropriately capture the behavior of thymic negative selection on an individual self-peptide level.
We started by comparing an adaptation of the previously proposed MJ discrete model of thymic selection, focusing on negative selection effects. We discovered that this model does not behave in a statistically reasonable manner. Specifically, single peptides can have inordinate consequences, including consequent fluctuations, on the selection behavior; these are the result of correlations in the MJ matrix. Instead of trying to modify the form of a peptide–peptide matrix, perhaps following the shape space ideas of refs. 13 and 38, we introduced a more general perspective on how the T cell sequence creates binding pockets for the p-MHC. This then allowed us to formulate two alternative models, PIRA and RICE, and found that widespread participation by thymic self-peptides action in T cell selection was observed only in the latter alternative, which supposed a position-dependent character of TCR–p-MHC interaction.
Using RICE, we analytically characterized events of relevance to the problem of immune action, including T cell survival during negative selection, SNP detection, and nonself-peptide recognition probabilities. We observed that TCR negative selection by host peptides has only a weak suppressive effect on detecting peptides which closely resemble self. This finding suggests that self-education during central tolerance in the thymus is a strategy that seeks to memorize as many of the self-peptides commonly found in the periphery (Fig. 1B) as possible as opposed to selection by a few self-peptides capable of mitigating autoimmunity and is a testament to the level of specificity exhibited by TCRs. Using the RICE model, we showed that parameter selection which generates realistic survival percentages also results in a near-optimal generation of thymocytes best suited to survive selection and to most effectively identify foreign peptides. Finally, the model produced realistic characterizations of alloreactivity when applied to the setting of MHC-matched individuals. A potential advantage of an immune system designed to follow the RICE model over MJ is that the latter presents only a static challenge that foreign peptides must undergo to evade detection; evasion of this detection might then be evolutionarily selected by pathogens. In contrast, there is no a priori strategy assumed within the RICE model, with its energy landscape that varies randomly from TCR to TCR.
We cannot expect a simple hypothesis, such as RICE, to fully capture every detail of actual TCR–p-MHC binding. In the absence of a quantitatively reliable molecular biophysics approach, we have chosen to work backward and illustrate the type of statistical model that makes functional sense and that allows for new questions (such as the penalty imposed by negative selection on tumor neoantigen detection) to be addressed. One criticism of RICE might be that it does not allow for similar peptide recognition by very similar TCRs or conversely, for TCR activation by very similar peptides. There are two reasons why this does not immediately concern us. First, coverage of the entire possible space of TCR sequences by actual TCR clones is so sparse that the chance of getting two TCRs with (nearly) identical chemical sequences should be very small. (Note that, if there are a few “public” clones, which are specifically programed into the TCR formation rules, these would presumably also be programed to automatically survive negative selection; our considerations apply to all of the others.) Second, the results of the RICE model are not significantly changed if we first group together chemically similar amino acids (39–41) (i.e., use a reduced amino acid alphabet) and then proceed with the repertoire construction (SI Appendix).
The overall objective of optimizing CTL therapy is complex and may require future analysis that incorporates additional relevant aspects of acquired immunity and T cell tolerance. Understanding this complex process holds the promise of, one day, optimizing and extending CTL immunotherapy to additional therapeutic contexts.
Methods
Selection behavior and peptide potency analyses were carried out for the three interaction formulations. In each case, randomly constructed TCR sequences were tested against thymic self-peptides, with a variable negative selection cutoff, , calibrated to give relevant selection rates. Thymic self-peptides were then ranked based on their individual ability to recognize TCRs; point-mutated and foreign peptides were then tested against surviving TCRs to estimate TAN and foreign recognition rates. To estimate alloreactivity, (donor) TCRs were challenged by varying numbers of (host) peptides by altering the number of nonself-peptides that each TCR faced. All simulations were compared with analytic estimations using probabilistic analysis. A complete description of all mathematical details may be found in SI Appendix.
Supplementary Material
Acknowledgments
We thank Philip A. Ernst for critical reading of the manuscript and Haven R. Garber and Jeffrey J. Molldrem for helpful discussions. J.T.G. is supported by National Cancer Institute of the NIH Grant F30CA213878. D.A.K. is supported by United States–Israel Binational Science Foundation Grant 2015619. H.L. is supported by Cancer Prevention and Research Institute of Texas Scholars Program R1111.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1708573114/-/DCSupplemental.
References
- 1.Couzin-Frankel J. Breakthrough of the year 2013. Cancer immunotherapy. Science. 2013;342:1432–1433. doi: 10.1126/science.342.6165.1432. [DOI] [PubMed] [Google Scholar]
- 2.McGranahan N, et al. Immune checkpoint blockade. Science. 2016;351:1463–1469. doi: 10.1126/science.aaf1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Robinson J, Soormally AR, Hayhurst JD, Marsh SGE. The IPD-IMGT/HLA database - New developments in reporting HLA variation. Hum Immunol. 2016;77:233–237. doi: 10.1016/j.humimm.2016.01.020. [DOI] [PubMed] [Google Scholar]
- 4.Ding L, et al. Clonal evolution in relapsed acute myeloid leukaemia revealed by whole-genome sequencing. Nature. 2012;481:506–510. doi: 10.1038/nature10738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gubin MM, Artyomov MN, Mardis ER, Schreiber RD. Tumor neoantigens: Building a framework for personalized cancer immunotherapy. J Clin Invest. 2015;125:3413–3421. doi: 10.1172/JCI80008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Verdegaal EME, et al. Neoantigen landscape dynamics during human melanoma-T cell interactions. Nature. 2016;536:91–95. doi: 10.1038/nature18945. [DOI] [PubMed] [Google Scholar]
- 7.Abbas AK, Lichtman AH, Shiv P. Cellular and Molecular Immunology. 8th Ed Elsevier Saunders; Philadelphia: 2015. [Google Scholar]
- 8.Schumacher TN, Schreiber RD. Neoantigens in cancer immunotherapy. Science. 2015;348:69–74. doi: 10.1126/science.aaa4971. [DOI] [PubMed] [Google Scholar]
- 9.Molldrem JJ, Komanduri K, Wieder E. Overexpressed differentiation antigens as targets of graft-versus-leukemia reactions. Curr Opin Hematol. 2002;9:503–508. doi: 10.1097/00062752-200211000-00006. [DOI] [PubMed] [Google Scholar]
- 10.Cai A, et al. Mutated BCR-ABL generates immunogenic T-cell epitopes in CML patients. Clin Cancer Res. 2012;18:5761–5772. doi: 10.1158/1078-0432.CCR-12-1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Restifo N, Dudley M, Rosenberg SA. Adoptive immunotherapy for cancer: Harnessing the T cell response. Nat Rev Immunol. 2012;12:269–281. doi: 10.1038/nri3191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Strønen E, et al. Targeting of cancer neoantigens with donor-derived T cell receptor repertoires. Science. 2016;352:1337–1341. doi: 10.1126/science.aaf2288. [DOI] [PubMed] [Google Scholar]
- 13.Detours V, Perelson AS. Explaining high alloreactivity as a quantitative consequence of affinity-driven thymocyte selection. Proc Natl Acad Sci USA. 1999;96:5153–5158. doi: 10.1073/pnas.96.9.5153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Detours V, Mehr R, Perelson AS. Deriving quantitative constraints on T cell selection from data on the mature T cell repertoire. J Immunol. 2000;164:121–128. doi: 10.4049/jimmunol.164.1.121. [DOI] [PubMed] [Google Scholar]
- 15.Chao DL, Davenport MP, Forrest S, Perelson AS. The effects of thymic selection on the range of T cell cross-reactivity. Eur J Immunol. 2005;35:3452–3459. doi: 10.1002/eji.200535098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.De Boer RJ, Perelson AS. How diverse should the immune system be? Proc Biol Sci. 1993;252:171–175. doi: 10.1098/rspb.1993.0062. [DOI] [PubMed] [Google Scholar]
- 17.Frankild S, De Boer RJ, Lund O, Nielsen M, Kesmir C. Amino acid similarity accounts for T cell cross- reactivity and for “Holes” in the T cell repertoire. PLoS One. 2008;3:e1831. doi: 10.1371/journal.pone.0001831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kosmrlj A, Jha AK, Huseby ES, Kardar M, Chakraborty AK. How the thymus designs antigen-specific and self-tolerant T cell receptor sequences. Proc Natl Acad Sci USA. 2008;105:16671–16676. doi: 10.1073/pnas.0808081105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chakraborty AK, Kosmrlj A. Statistical mechanical concepts in immunology. Annu Rev Phys Chem. 2010;61:283–303. doi: 10.1146/annurev.physchem.59.032607.093537. [DOI] [PubMed] [Google Scholar]
- 20.Kosmrlj A, et al. Effects of thymic selection of the T-cell repertoire on HLA class I-associated control of HIV infection. Nature. 2010;465:350–354. doi: 10.1038/nature08997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Košmrlj A, Chakraborty AK, Kardar M, Shakhnovich EI. Thymic selection of T-cell receptors as an extreme value problem. Phys Rev Lett. 2009;103:068103. doi: 10.1103/PhysRevLett.103.068103. [DOI] [PubMed] [Google Scholar]
- 22.Yates AJ. Theories and quantification of thymic selection. Front Immunol. 2014;5:13. doi: 10.3389/fimmu.2014.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Feinerman O, Germain RN, Altan-Bonnet G. Quantitative challenges in understanding ligand discrimination by T cells. Mol Immunol. 2008;45:619–631. doi: 10.1016/j.molimm.2007.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.François P, Voisinne G, Siggia ED, Altan-bonnet G, Vergassola M. Phenotypic model for early T-cell activation displaying sensitivity, speci fi city, and antagonism. Proc Natl Acad Sci USA. 2013;110:E888–E897. doi: 10.1073/pnas.1300752110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Miyazawa S, Jernigan RL. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules. 1985;18:534–552. [Google Scholar]
- 26.Miyazawa S, Jernigan RL. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J Mol Biol. 1996;256:623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 27.Hernandez JB, Newton RH, Walsh CM. Life and death in the thymus - cell death signaling during T cell development. Curr Opin Cell Biol. 2011;22:865–871. doi: 10.1016/j.ceb.2010.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Klein L, Kyewski B, Allen PM, Hogquist K. Positive and negative selection of the T cell repertoire: What thymocytes see (and don’t see) Nat Rev Immunol. 2014;14:377–391. doi: 10.1038/nri3667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bryngelson JD, Wolynes PG. Intermediates and barrier crossing in a random energy model (with applications to protein folding) J Phys Chem. 1989;93:6902–6915. [Google Scholar]
- 30.Sinclair C, Bains I, Yates AJ, Seddon B. Asymmetric thymocyte death underlies the CD4:CD8 T-cell ratio in the adaptive immune system. Proc Natl Acad Sci USA. 2013;110:E2905–E2914. doi: 10.1073/pnas.1304859110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Itano A, Robey E. Highly efficient selection of CD4 and CD8 lineage thymocytes supports an instructive model of lineage commitment. Immunity. 2000;12:383–389. doi: 10.1016/s1074-7613(00)80190-9. [DOI] [PubMed] [Google Scholar]
- 32.Merkenschlager M, et al. How many thymocytes audition for selection? J Exp Med. 1997;186:1149–1158. doi: 10.1084/jem.186.7.1149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ignatowicz L, et al. T cells can be activated by peptides that are unrelated in sequence to their selecting peptide. Immunity. 1997;7:179–186. doi: 10.1016/s1074-7613(00)80521-x. [DOI] [PubMed] [Google Scholar]
- 34.Tourne S, et al. Selection of a broad repertoire of CD4+ T cells in H-2Ma 0/0 mice. Immunity. 1997;7:187–195. doi: 10.1016/s1074-7613(00)80522-1. [DOI] [PubMed] [Google Scholar]
- 35.Zerrahn J, Held W, Raulet DH. The MHC reactivity of the T Cell repertoire prior to positive and negative selection. Cell. 1997;88:627–636. doi: 10.1016/s0092-8674(00)81905-4. [DOI] [PubMed] [Google Scholar]
- 36.Zarnitsyna VI, Evavold BD, Schoettle LN, Blattman JN, Antia R. Estimating the diversity, completeness, and cross-reactivity of the T cell repertoire. Front Immunol. 2013;4:270–280. doi: 10.3389/fimmu.2013.00485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kruglyak L, Nickerson DA. Variation is the spice of life. Nat Genet. 2001;27:234–236. doi: 10.1038/85776. [DOI] [PubMed] [Google Scholar]
- 38.Perelson AS, Oster GF. Theoretical studies of clonal selection: Minimal antibody repertoire size and reliability of self-non-self discrimination. J Theor Biol. 1979;81:645–670. doi: 10.1016/0022-5193(79)90275-3. [DOI] [PubMed] [Google Scholar]
- 39.Truong HH, Kim BL, Schafer NP, Wolynes PG. Funneling and frustration in the energy landscapes of some designed and simplified proteins. J Chem Phys. 2013;139:121908. doi: 10.1063/1.4813504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Murphy LR, Wallqvist A, Levy RM. Simplified amino acid alphabets for protein fold recognition and implications for folding. Protein Eng. 2000;13:149–152. doi: 10.1093/protein/13.3.149. [DOI] [PubMed] [Google Scholar]
- 41.Percus JK, Percus OE, Perelson AS. Predicting the size of the T-cell receptor and antibody combining region from consideration of efficient self-nonself discrimination. Proc Natl Acad Sci USA. 1993;90:1691–1695. doi: 10.1073/pnas.90.5.1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.