Evidence for a Low Bulk Crustal Density for Mars from Gravity and Topography

Abstract

Knowledge of the average density of the crust of a planet is important in determining its interior structure. The combination of high-resolution gravity and topography data has yielded a low density for the Moon’s crust, yet for other terrestrial planets the resolution of the gravity field models has hampered reasonable estimates. By using well-chosen constraints derived from topography during gravity field model determination using satellite tracking data, we show that we can robustly and independently determine the average bulk crustal density directly from the tracking data, using the admittance between topography and imperfect gravity. We find a low average bulk crustal density for Mars, 2582 ± 209 kg m⁻³. This bulk crustal density is lower than that assumed until now. Densities for volcanic complexes are higher, consistent with earlier estimates, implying large lateral variations in crustal density. In addition, we find indications that the crustal density increases with depth.

1 Introduction

The crust of a terrestrial planet is the result of differentiation processes in its early history, followed by magmatic evolution of the planetary surface [e.g., Wieczorek and Zuber, 2004]. Characterization of the crustal structure thus provides important constraints on a planet’s formation and subsequent evolution. The average bulk density of the crust is a fundamental parameter in geophysical studies, for example in determining the planet’s crustal thickness [e.g., Neumann et al., 2004], the mechanisms of its topographic support [e.g., Belleguic et al., 2005], and its thermo-chemical evolution [e.g., Schumacher and Breuer, 2006]. Yet even with in situ samples the crustal density is difficult to determine unambiguously, as exemplified by the Gravity and Interior Laboratory (GRAIL) mission [Zuber et al., 2013], which found an average crustal density for the Moon that was much lower than generally assumed [Wieczorek et al., 2013]. These results were possible owing to the combination of the high-resolution gravity data obtained by GRAIL, the high-resolution topography obtained by the Lunar Orbiter Laser Altimeter (LOLA) onboard the Lunar Reconnaissance Orbiter [Smith et al., 2016], and the high correlations between gravity and topography at short wavelengths.

For a geophysical model of a planet based on the spherical thin elastic shell approximation [Turcotte et al., 1981], the relation between gravity and topography, called admittance, can be expressed analytically. For such a model, the correlation between gravity and topography is 1 by definition, and it can be shown that for sufficiently high spherical harmonic degree, the dependence of the admittance on the elastic thickness vanishes and it approaches an asymptotic value that is only dependent on the crustal density [Wieczorek et al., 2013]. Currently, topography for Mars [Wieczorek, 2015] and the Moon [Smith et al., 2016] is nearly noise-free at the resolution of existing gravity field models. However, the resolution of gravity field models is often deemed too low for terrestrial planets such as Mercury, Venus, and Mars, for such a method based on admittance to be successful. We note that a pre-GRAIL estimate for the Moon using lower-resolution gravity actually hinted at a lower crustal density [Huang and Wieczorek, 2012]. As a consequence, densities covering a conservative range between 2700 kg m⁻³ and 3100 kg m⁻³ are usually adopted for the terrestrial planets [e.g., Padovan et al., 2015; James et al., 2013; Wieczorek and Zuber, 2004]. For Mars in particular, locally lower upper crustal densities [e.g., Nimmo, 2002] as well as higher crustal densities based on petrological considerations [e.g., Baratoux et al., 2014] have been advocated, resulting in an average value for crustal density of 2900 kg m⁻³ [e.g., Neumann et al., 2004]. To the extent that these results were based on gravity, they used earlier gravity field models with limited resolution [e.g., Nimmo, 2002]. In addition, known higher densities for the volcanoes [e.g., Belleguic et al., 2005] and low densities at the south pole [e.g., Wieczorek, 2008] indicate the possibility of significant lateral density variations, with most notably the dichotomy between the northern and southern hemispheres [e.g., Belleguic et al., 2005; Pauer and Breuer, 2008]. The presence of sub-surface loading further complicates the interpretation of admittance [e.g., McGovern et al., 2002, 2004; Belleguic et al., 2005; Grott and Wieczorek, 2012].

Planetary gravity field models are determined from satellite tracking data, and are usually expressed in spherical harmonics. These basis functions have global support, but because the spatial sensitivity of tracking data always varies, regularization is needed to ensure a smooth model without spurious power. In gravity field determination, the regularization (or constraint) of choice is often based on the Kaula rule [Kaula, 1966]: it forces the coefficients towards zero with an expectation according to the applied rule B/n², which counters the noise and suppresses power at higher spherical harmonic degrees n (Supplementary Information). The parameter B is a constant specific to the planet. Noise, more prevalent in the higher degrees, also naturally decreases correlations with topography [Wieczorek, 2015]. Consequently, for theoretical models where correlations are unity by definition, admittance modeling is only used in the degree range for which the correlations are deemed sufficiently high, and the model is robust. The generally low degree values used for terrestrial planets mean that the admittance for a given crustal density is not yet independent of the elastic thickness.

2 Methods and verification

Consider the covariance matrix (λP)⁻¹, where λ is a scale factor, applied as a constraint to the problem of determining a gravity field model from satellite tracking data (Supplementary Information). After the k-th iteration in a Gauss-Newton least-squares estimator [Seber and Wild, 1989], the solution using a standard Kaula constraint (which is diagonal) results in x_k+1 → 0 when λ → ∞since the preferred model state is chosen to be 0. However, we aim to construct a solution that correlates well with topography, without forcing the solution to be exactly the topography solution, i.e., we seek a constraint that leaves a part of the model space to be fully determined by the data, not the constraint. We assume some preferred a priori gravity model of M parameters, written as the vector x_a, with non-zero elements. Next, we assume that a bulk density of the crust ρ_c can describe most of the gravity signal, especially at higher degrees, so that for example x = x_a ρ_c, where in this case x_a are the coefficients of an expansion of gravity-from-topography. We can then choose the following attendant inverse-covariance matrix:

$$\mathbf{P}=\mathbf{F}\left(\mathbf{I}-\frac{1}{M}\mathbf{1}{\mathbf{1}}^{\mathrm{T}}\right)\mathbf{F},$$ (1)

where F is an M×M diagonal matrix such that F_ii = 1/(x_a)_i, I is an M×M identity matrix, and 1 is an M×1-vector of ones. We also note that we can write x_a ρ_c = F⁻¹1ρ_c. The corresponding P⁻¹ assigns infinite variance in the direction of x_a, whereas in all directions orthogonal to x_a the preferred model state is still 0. This constraint is chosen such that for λ → ∞, the k-th iteration for such a solution results in x_k+1 = α_kx_a, with α_k a scale factor that is completely determined by the data, and thus fully independent of the chosen constraint (Supplementary Information). In other words, our constraint can be seen as a transformation of the equation system from the spherical harmonic basis to a new system, where one basis vector of the new system is spanned by x_a. Our constraint affects all directions (the extent to which depends on the factor λ) except the x_a direction.

If we choose x_a to be the coefficients of an expansion in spherical harmonics of gravity computed from topography using some constant density ρ₀ [Wieczorek and Phillips, 1998], then it follows that for λ → ∞the correlations between the estimated gravity and gravity-from-topography will be ± 1. Moreover, if, as stated above, we assume that the estimated gravity can be expressed as the contribution of surface relief with the density ρ_estim, then for λ →∞it follows that ρ_estim = α_k · ρ₀ (Supplementary Information). In this way, our solution determines the density ρ_estim through the factor α_k (which is completely determined by the data). Therefore, our model density ρ_estim is independent of the density ρ₀ used for the constraint. In the limit of λ → ∞, our constraint thus equals the Bouguer correction [Wieczorek and Phillips, 1998], the first-order approximation of the gravity field at high degrees. Moreover, with our constraint the density for the Bouguer correction is determined directly from the data. This is different from the standard way in which crustal densities are determined from an already existing gravity field model (often derived using a Kaula constraint).

Next, we can compute the effective density spectrum, defined as the ratio of the cross-power between estimated gravity and gravity-from-topography, and the auto-power of gravity-from-topography [Wieczorek et al., 2013]. This spectrum represents the average crustal density as a function of spherical harmonic degree n, under the assumption of uncompensated topography. The scale factor λ determines the strength of the constraint. For reasonably small values of λ, the effective density spectrum will have variations, as we will show, from which laterally varying densities can be inferred, despite the assumption of constant density in the computation of x_a (used in both the constraint and computation of effective density). Lateral density variations were determined using GRAIL data in the exact same way [e.g., Wieczorek et al., 2013; Besserer et al., 2014]. These variations effectively mean that α_k varies per degree n for small values of λ: the estimated effective density varies per degree such that ρ_estim (n) = α_k (n) · ρ₀. For the case λ → ∞, the effective density collapses to one value for all degrees n, namely ρ_estim = α_k · ρ₀. We thus effectively estimate the asymptotic value of the admittance directly from the data. Because our constraint has one degree of freedom, i.e. α_k, we call these constraints “rank minus one” (RM1).

To verify that our constraint estimates the correct crustal density, we apply it to the data part of the least-squares system of the pre-GRAIL model SGM150J [Goossens et al., 2011]. This model uses tracking data from the Japanese Kaguya mission, and is valid globally up to degree n = 70. Its resolution thus falls short of the range used by GRAIL to determine the effective density [Wieczorek et al., 2013]. For our constraint, we chose x_a as the gravity computed from topography following Wieczorek and Phillips [1998], based on the LOLA data [Smith et al., 2016]. For simplicity, we use a “unit” density of 1000 kg m⁻³ for ρ₀, but we note that any other density would be translated into the same final model density ρ_estim when we compute the effective density spectrum. We apply the constraint for n ≥ 50. A model based on GRAIL extended mission data, GRGM900C [Lemoine et al., 2014], serves as truth given that it is constraint-free for the degree range of SGM150J.

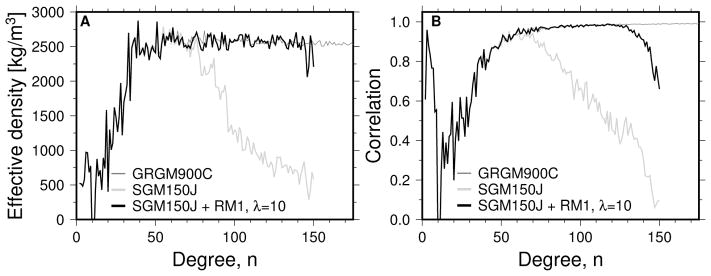
In Fig. 1A we show the effective density for several models. Our new model derived with the RM1 constraint follows the independent GRGM900C results very closely. The variations in the effective density spectrum are larger for the SGM150J with the RM1 constraint than those for GRGM900C. This is because the quality of the SGM150J and the GRAIL data sets is vastly different, with up to 3 orders of magnitude difference in the level of uncertainty [e.g., Lemoine et al., 2013]. Thus, even for systems that are not nearly as well-resolved as GRAIL’s, and therefore have an effective resolution well below the degree where the admittance becomes asymptotic, we can still obtain a reliable estimate of the bulk density. By taking the uniformly weighted average of the density between degrees n = 60 and n = 130, we find a value of 2587 ± 54 kg m⁻³ for GRGM900C, and 2579 ± 75 kg m⁻³ for the SGM150J model with the RM1 constraint. The uncertainties are obtained by averaging the variations in effective density around the obtained density value, using the same degree range. Both these values compare well to the GRAIL value of 2550 ± 18 kg m⁻³ from Wieczorek et al. [2013] which used a degree range of n = 150–310 for the averaging. We note that using the newer model GRGM900C over the same range results in a density of 2515 ± 25 kg m⁻³, slightly lower than the 2550 kg m⁻³ value, possibly due to an underestimation of the contribution from gravity-from-topography.

Figure 1.

(A) Effective density for various lunar gravity field models: a pre-GRAIL model (SGM150J), a GRAIL model with extended mission data (GRGM900C), and a model based on the SGM150J least-squares system using our new “rank minus one” (RM1) constraint. (B) Correlations between gravity models and gravity-from-topography.

In Fig. 1B we show the correlations between gravity and gravity-from-topography. The correlations with gravity-from-topography for the model with our constraint match the correlations of the GRAIL model very closely, despite the fact that the original SGM150J model only follows the GRAIL correlations up to n = 60. We further test our constraint on the GRAIL primary mission data system and obtain similar results (Supplementary Information and Fig. S1). The results in Fig. 1 use a damping factor λ = 10, and by increasing λ, the variations in effective density become smaller because we are moving towards estimating only a single scale factor, α_k, which then determines one effective density for the entire degree range over which the constraint is applied (Supplementary Fig. S2). Correlations become close to unity as λ increases (see also Fig. 2B below), but the path towards unity correlations is determined by both the data and constraint. For a factor λ = 10, the data still determine a large part of the solution (as indicated by the dropping correlations for high degrees in Fig. 1B), so it is an important result that the RM1 model with the SGM150J matrix matches the correlations of the independent GRAIL model with superior data (see also Supplementary Information and Fig. S3).

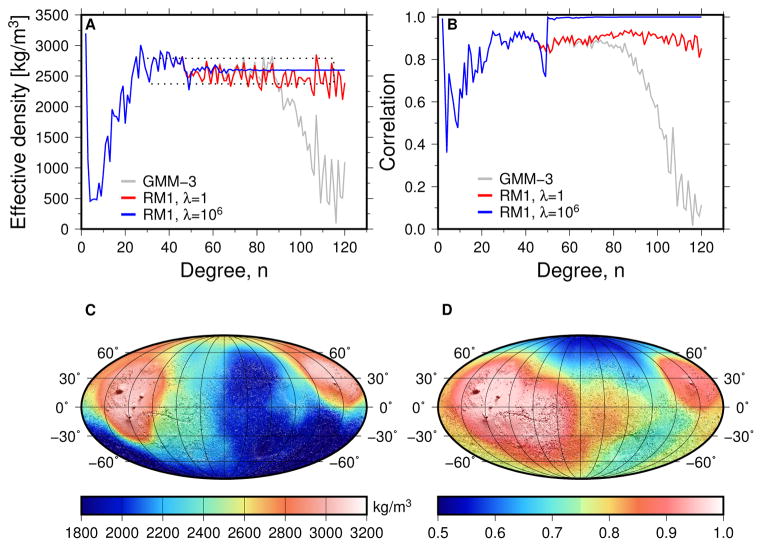
Figure 2.

(A) Effective density for the Mars model GMM-3, and for models using our constraint with different damping parameters. The dashed box indicates the minimum and maximum of the estimated density taken from the estimated errors, and the degree range over which the averaging was done. (B) Correlations between gravity and gravity-from-topography for the same Mars gravity models. (C) An example of how density on Mars can vary laterally, computed from localized effective density spectra averaged between degrees n = 50 and n = 85, using our degree and order 150 RM1 model based on GMM-3 data (See Supplementary Information). (D) Localized correlations between gravity and gravity-from-topography. The maps are in Mollweide projection centered on the prime meridian, shaded by topography.

3 Results for the crustal density of Mars

We now apply our method to determine the bulk crustal density of Mars. Recent global Mars models [Genova et al., 2016; Konopliv et al., 2016] are valid up to about degree and order 85. We use the data part of the least-squares system of the recent GMM-3 model, a gravity field model estimated to degree and order 120 [Genova et al., 2016]. For analysis purposes, we also generate partial derivatives of the Mars Reconnaissance Orbiter (MRO) measurements with respect to gravity coefficients up to degree and order 150, resulting in a data system of larger size (Supplementary Information). We exclude the Kaula constraint that was applied for n > 90 for this model. We compute gravity-from-topography using the MarsTopo2600 topography model [Wieczorek, 2015], again using a “unit” density of 1000 kg m⁻³. We apply the RM1 constraint for degrees n ≥ 50 (using the constraint for n ≥ 85 changes the correlation spectrum but not the effective density results, see Supplementary Fig. S4).

In Fig. 2A we show the effective density for GMM-3 and models using the RM1 constraint. While the GMM-3 model already shows a relatively constant effective density, it quickly decreases after degree n = 85. This is a result of the Kaula constraint which forces the solution to zero, especially at higher degrees where the data are not strong enough to fully determine the model. With our RM1 constraint we can extend the degree range over which the density is stable, which makes its estimate much more reliable. We further confirm this by comparing the effective density spectrum of these models with that resulting from the unconstrained GMM3 solution and with that of the additional degree and order 150 solution (Supplementary Fig. S5). While the unconstrained solution shows large, unrealistic variations, its average is followed closely by our RM1 solution, indicating that our RM1 solution is able to extract further information from the data which otherwise gets suppressed in standard models derived with a Kaula constraint. The RM1 result thus extends the density spectrum into the higher spherical harmonic degree range, where gravity is more and more expected to follow topography closely, and where the admittance is determined by the crustal density.

We find a bulk crustal density for Mars of 2582 ± 209 kg m⁻³. This value is determined as the average bulk density and its variation from a set of 1093 clone fields (Supplementary Information) over the degree range n=30–115 (different ranges do not affect the result within this uncertainty). The clone fields are an ensemble of solutions of the same statistical family [Lemoine et al., 2014], capturing the variations from the full covariance. The value of the asymptotic density (obtained for large λ, Fig. 2A) is 2597 kg m⁻³, consistent with our estimate.

In Fig. 2B we show the correlations per degree between gravity and gravity-from-topography. Correlations for the RM1 model are much higher and stable than those for GMM-3, and they increase steadily between n = 60 and n = 90. The sudden increase in the correlation values for large values of λ (for which correlations approach unity) does not influence the effective density, as was the case when applying the RM1 constraint for either n ≥ 50 or n ≥ 85 (Supplementary Fig. S3). The admittance reaches its asymptotic value at larger degrees n for Mars than for the Moon (Supplementary Fig. S6), and global admittance values for Mars become stable after around degree n = 25 [e.g., Konopliv et al., 2006], indicating that the admittance already is nearly independent of elastic thickness. The admittance spectrum for Mars is represented best by a theoretical model with high values for the elastic thickness T_e (Supplementary Fig. S7), which means that the asymptotic value is reached at lower degrees than it would be for low T_e values. Previous studies in general find values for T_e for Mars that are larger than 50 km, see Johnson et al. [2000]; Neumann et al. [2004]; Belleguic et al. [2005]; Audet [2014], and discussions and further references in Wieczorek [2015], although locally small values are possible [McGovern et al., 2004]. For large values of T_e the admittance is not dependent on T_e at high degrees. The asymptotic value of the admittance depends only on the crustal density (Supplementary Fig. S8), and it is this asymptotic value that we are estimating when we apply our constraint, further circumventing the dependence on elastic thickness.

We further investigate the influence of T_e on our density estimate by comparing theoretical admittance using the thin shell approximation [Turcotte et al., 1981] with measured admittance using the RM1 model. We assume a crustal thickness of 43 km (see also Section 4), and vary T_e and the crustal density. We compute the root-mean-square of the differences between measured and modeled admittance for a given range of degrees. If we include low degrees, n=10–115, we find a reasonably well-defined minimum in T_e-density space (Supplementary Fig. S9). If we do not include the lowest degrees, n=30–115, we find that the results become less sensitive to T_e. Results for both degree ranges indicate that low T_e values are unlikely (on the global scale that we are mostly considering), and both results produce density estimates that are consistent with what we obtain from the effective density spectrum, confirming that our bulk density value is mostly independent of T_e.

We prefer solutions with weaker constraints (lower values of λ) because those result in a more realistic effective density spectrum, as we have shown with our lunar test cases. The Mars results (Fig. 2A, and Supplementary Fig. S4 and Fig. S5) also indicate that the results using lower values of λ maintain the effective density spectrum up to higher degrees, extending the value and shape from the spherical harmonic range that was already fully determined by the data (up to n = 80), whereas the density for the Kaula model quickly decreases. The RM1 constraint thus makes the effective density spectrum more stable and the density value derived from it more robust (Supplementary Information). Low values for λ also mean that the resulting model is not forced to be equal to gravity-from-topography (which it will be for large values of λ), and this also allows us to perform an admittance analysis of the resulting model as described above. Our RM1 constraint still results in a meaningful density for large values of λ, because that allows us to estimate the asymptotic density value (Fig. 2A), in contrast to the Kaula constraint which would result in 0 for large values of λ.

We stress that our bulk crustal density estimate is a global average, a consequence of averaging a degree range in spherical harmonics which ignores lateral variations [e.g., Wieczorek et al., 2013]. This bulk density is important for global modeling, and we derive our value robustly from the available data and from geophysical considerations. Our value for the bulk crustal density of Mars falls below the wide conservative range of 2700 – 3100 kg m⁻³ that is generally used. Lower crustal densities for Mars have been advocated for local areas such as at the dichotomy [e.g., Nimmo, 2002], Valles Marineris [e.g., McGovern et al., 2002; Beuthe et al., 2012], and the Thaumasia highlands [e.g., Beuthe et al., 2012]. On the other hand, volcanic complexes on Mars such as the Tharsis province are considered to have higher densities [e.g., Belleguic et al., 2005; Beuthe et al., 2012], and known observations from wide-spread Martian meteorites and samples also favor higher densities [e.g., Baratoux et al., 2014], indicating that strong lateral density variations are likely.

The variations in the effective density spectrum are indicative of lateral density variations (Supplementary Information). The variations for Mars are larger than those for the Moon (see Fig. 1A). While part of this can be noise in the data (the variations in the SGM150J-RM1 spectrum are larger than those in the GRGM900C spectrum, see also Supplementary Fig. S3), we also note that these variations for Mars are already present in the degree range where the solutions are fully determined by the data (for n ≤ 80, see also Supplementary Fig. S5). By applying localized spectral analysis following Wieczorek and Simons [2005], we can explore local density variations. By localizing the gravity and gravity-from-topography coefficients over the Tharsis area, and by computing a localized effective density spectrum, we find a value of 3231 ± 95 kg m⁻³ using the same RM1 solution (Supplementary Information and Fig. S10), in agreement with earlier results: Belleguic et al. [2005] find 3266 kg m⁻³ and McGovern et al. [2004] find 3250 kg m⁻³, and these results are further confirmed by Beuthe et al. [2012]. This strengthens our confidence in the global result further: both the lower bulk crustal density and the expected higher densities over the volcanic complexes can be estimated from one and the same model using our RM1 constraint. We note that in this case the model with the Kaula constraint does not result in a stable effective density spectrum (Supplementary Fig. S10), but instead results in a divergent and unrealistic density.

We further explore lateral density variations by localizing the effective density spectrum (see Supplementary Information for details). Our local density results are limited however by the current resolution of the gravity field models, which does not allow a similar robust treatment as was possible with the GRAIL results [Besserer et al., 2014; Han et al., 2014]. Correlations with topography (Fig. 2D) are low in the northern hemisphere, which complicates the admittance interpretation due to the likely presence of bottom loading [e.g., McGovern et al., 2002]. We are most confident about our density estimates in areas with a correlation with gravity-from-topography larger than 0.8 (Supplementary Fig. S11), which covers mostly the volcanic complexes and parts of the southern hemisphere, possibly due to better data resolution there [Genova et al., 2016]. Because of limited resolution, our local analysis using multiple tapers often shows large oscillations in the effective density spectrum, resulting in relatively low densities in many areas (see also Supplementary Information). Our density map (Fig. 2C) thus only serves as an illustration of how density can vary laterally on Mars. Nonetheless, we find global density variations that are broadly consistent with earlier findings: densities over the volcanic complexes are relatively high, while the northern hemisphere is in general more dense than the southern hemisphere [e.g., Belleguic et al., 2005].

4 Discussion

The results for GRAIL indicated that at the Moon, density for the non-Mare regions increases with depth [Besserer et al., 2014; Han et al., 2014]. This was derived from the negative trend with increasing degree that the Moon’s effective density spectrum shows, and this is consistent with a decrease of porosity. For Mars, our results also show such a negative trend (Fig. 2A). This trend (fitted between n=40–100, Supplementary Fig. S12 and S13) is found to be consistent throughout our set of clone models, and it is consistent with various degree ranges. The trend is stronger than found with GRAIL for the Moon over the same degree range, perhaps due to Mars’ higher surface gravity, higher pressure gradients and larger crustal temperatures [e.g., Baratoux et al., 2014]. While we note that it is not clear that this trend will be the same at higher degrees (the resolution of GRAIL) due to the lower resolution of the Mars data, this would imply that large-scale porosity can play a role in determining the crustal structure of Mars [e.g., Pauer and Breuer, 2008] much in the same way that it does for the Moon. Our low bulk crustal density can then be explained through porosity, and with a grain density conservatively chosen at 3100 kg m⁻³ the resulting porosity varies between 10 % and 23 % (close to the lunar values). A bulk density lower than the mineral grain density can also be obtained when water or ice fills pore space. However, considering meteorite densities and a porosity of 12%, this would only reduce the crustal density by 200 kg m⁻³ [Pauer and Breuer, 2008; Baratoux et al., 2014].

With strong indications of varying crustal densities on Mars, it is to be expected that the increase of density with depth will also vary geographically. While our global effective density spectrum shows a negative trend, our local spectrum for Pavonis (Supplementary Fig. S10) is mostly flat, suggesting a mostly constant density in the crust in that location. We explored analytic models for the global admittance based on increasing density with depth [Han et al., 2014] (Supplementary Information and Fig. S14). While overall the results are consistent with models with porosity closure at depth, we found that the resolution of current gravity field models is not sufficient to unambiguously determine parameters such as the surface density, density gradient, or e-folding depth [Besserer et al., 2014; Han et al., 2014].

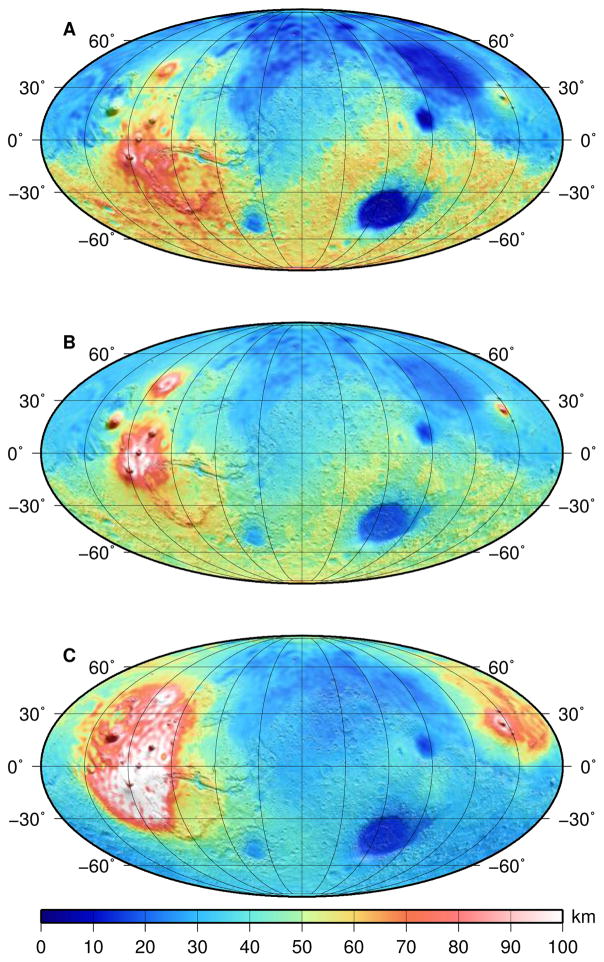
Crustal density is one of the driving parameters when determining the crustal thickness. To investigate the effects of a lower crustal density, we present two new crustal thickness models in Fig. 3, based on two different density maps, along with a model based on the standard density value of 2900 kg m⁻³ (Fig. 3A). Of our two new density models, one applies the global low value of 2582 kg m⁻³ and a higher value for volcanic complexes (Fig. 3B, and see Supplementary Fig. S15 for this density map), and the other applies our example of how density may vary laterally (Fig. 3C). Other parameters for our crustal thickness computations (Supplementary Information) are similar to those from earlier studies [Neumann et al., 2004; Wieczorek and Zuber, 2004; Genova et al., 2016]. We use uniform densities for the crust despite indications of depth-dependency, because we cannot estimate the parameters of such a model with confidence (see also Supplementary Information). All our models assume an average crustal thickness of 42 km. Because of the lower densities, variations at the crust-mantle boundary are generally smaller, resulting in a crustal thickness map that is smoother than that using a larger density. The minimum increases from close to 0 km for a constant density of 2900 kg m⁻³ to 13 km for the new density values. We note that these results thus indicate the possibility of a thinner mean crustal thickness for Mars, if one assumes that the minimum is likely to be close to 0 km.

Figure 3.

Crustal thickness for Mars: (A) applying a constant, standard density of 2900 kg m⁻³, (B) applying a laterally varying density using our new global density estimate of 2582 kg m⁻³, with a density of 2900 kg m⁻³ over volcanic complexes, (C) applying our example of laterally varying density as shown in Fig. 2C. The map projections are the same as the maps in Fig. 2.

5 Conclusions

We have shown how our RM1 constraints can be used to robustly and independently determine the bulk crustal density, and we applied it to current gravity field models for Mars based on satellite tracking data. Our lower crustal density for Mars is close to that obtained for the Moon, and our results indicate lateral variations in density. We found indications that density increases with depth, although the current model resolutions are too low to unambiguously determine parameters such as surface density or density gradients. A lower crustal density for Mars can be explained through the effects of porosity, for example obtained through impact cratering. Our RM1 constraint is also applicable to other celestial bodies for which we have knowledge of both the topography and gravity field.

Key Points.

• We estimate bulk crustal density directly from satellite tracking data using a constraint

• Mars has a lower bulk crustal density than assumed until now

• Densities for volcanic complexes are higher, implying large lateral variations in crustal density