Entropy-limited topological protection of skyrmions

Entropic effects counteract the topological protection of magnetic skyrmions, leading to faster decay rates than expected.

Abstract

Magnetic skyrmions are topologically protected whirls that decay through singular magnetic configurations known as Bloch points. We used Lorentz transmission electron microscopy to infer the energetics associated with the topological decay of magnetic skyrmions far from equilibrium in the chiral magnet Fe_1−xCo_xSi. We observed that the lifetime τ of the skyrmions depends exponentially on temperature, $\mathrm{\tau }~{\mathrm{\tau }}_0 \text{exp}\left(\frac{\mathrm{\Delta }\mathit{E}}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}\right)$. The prefactor τ₀ of this Arrhenius law changes by more than 30 orders of magnitude for small changes of the magnetic field, reflecting a substantial reduction of the lifetime of skyrmions by entropic effects and, thus, an extreme case of enthalpy-entropy compensation. Such compensation effects, being well known across many different scientific disciplines, affect topological transitions and, thus, topological protection on an unprecedented level.

INTRODUCTION

A question studied in many fields of the natural sciences concerns the lifetime of metastable states. Thermal activation across energy barriers governs (for example, chemical reactions) the lifetime of memory elements in computers and in hard disks and the transport of ions and electrons in disordered media. Often, these processes are controlled by a characteristic energy, the activation energy. However, it has also been established that a large number of different pathways across an activation barrier leads to a large entropic correction, reducing the lifetime of metastable states and, thus, the importance of the energy barriers. This effect is known as enthalpy-entropy compensation in the context of chemistry or the Meyer-Neldel rule in material sciences. Enthalpy-entropy compensation has, for example, been observed for catalytic reactions (1), transport in semiconductors (2, 3), biological processes (4), and in many other fields (5, 6).

In recent years, differences of the topology of physical states have been widely portrayed as providing exceptionally high stability. Topology represents a branch of mathematics concerned with those properties of geometric configurations that are unaffected by smooth deformations. Famous examples for topologically nontrivial objects include superconducting vortices, certain magnetic textures, structural defects and surface states of topological materials. However, despite this abundance of topologically nontrivial configurations in nature, an unresolved key question concerns their stability when being part of an ensemble far from equilibrium.

Skyrmions in spin systems with chiral interactions are particularly suitable to clarify this issue, because a well-founded highly advanced theoretical understanding exists in excellent agreement with the experiment. Representing topologically nontrivial spin whirls, skyrmions were experimentally first identified in the B20 compounds MnSi and Fe_1−xCo_xSi (7, 8), followed more recently by a wide range of bulk compounds (9–11), surface- and interface-based systems (10, 12–14), as well as hetero- and nanostructures (15, 16). With typical dimensions from a few up to several hundred nanometers, skyrmions in magnetic materials are accessible to a wide range of experimental techniques. Moreover, they are also of immediate interest for spintronics applications. At present, this concerns foremost memory elements (15, 17, 18), where lifetimes exceeding 10 years represent the technical requirement. In turn, the design of metastable states with long lifetimes is both mandatory and a major motivation for the study reported here.

RESULTS

Here, we have chosen the B20 compound Fe_1−xCo_xSi with x = 0.5, which displays a well-understood bulk phase diagram that is generic for this class of materials (7, 8, 19, 20). With decreasing temperature, a paramagnetic to helimagnetic transition occurs at T_c. A lattice of skyrmion lines forms in a small field and temperature window just below T_c, as first established by small-angle neutron scattering (SANS) (8). Lorentz force transmission electron microscopy (LTEM) in Fe_1−xCo_xSi provided real-space images of the skyrmions (21). Although the skyrmion phase in bulk materials is thermodynamically stable only in a small pocket of phase space, it was shown early on that the range of stability, albeit being hysteretic, increases markedly and extends down to zero temperature in ultrathin bulk samples (21–23). A typical phase diagram obtained from our sample when cooling at a fixed magnetic field and followed by an increase or a decrease of the field at a fixed low temperature is shown in Fig. 1A. In the red shaded region, the skyrmion lattice is stable on experimentally relevant time scales but decays when the magnetic field is increased or decreased further.

Fig. 1. Magnetic phases and skyrmion decay in Fe_1-xCo_xSi.

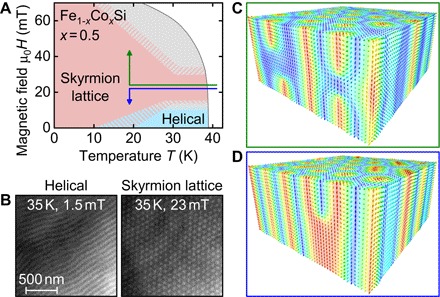
(A) Magnetic phase diagram of Fe_1−xCo_xSi with x = 0.5 obtained by first cooling the system at a fixed magnetic field, B ≈ 23 mT, and then raising or lowering the field at fixed temperature T. The decrease in the applied field triggers the decay into a helical configuration, whereas either a conical or ferromagnetic state is reached for an increase of the field. (B) Typical LTEM images of helical and skyrmion lattice order, respectively. (C) Schematic image of an early state of the decay of the skyrmion lattice toward a ferromagnetic state. The skyrmion splits by the formation of a pair of Bloch points located at the end of the skyrmion strings, which move toward the surface. (D) Decay of skyrmion lattice order toward the helical state. Neighboring skyrmions merge, and a Bloch point at the merging points moves toward the surface.

Schematic depictions of typical spin configurations during the early stages of the decay into a ferromagnetic state under increasing field or into a helical state under decreasing field are shown in Fig. 1 (C and D). The decay into the helical state was first addressed by means of magnetic force microscopy (MFM) of the surface of a bulk sample of Fe_1−xCo_xSi (x = 0.5) (24). Here, the decay was found to occur by a merging of skyrmions, implying the presence of a Bloch point that acts like a zipper between skyrmions, that is, a point of vanishing magnetization enabling the unwinding of the nontrivial topology (Fig. 1D). In comparison, the decay into the conical or ferromagnetic state is theoretically predicted to take place by a pinching-off through the creation of a pair of Bloch points, as shown in Fig. 1C, and the subsequent motion of the Bloch points toward the surface (23, 25).

Several studies had reported hysteretic and metastable skyrmion states. Early SANS studies on bulk samples of Fe_1−xCo_xSi revealed the possibility to super-cool the skyrmion lattice into a metastable state (8, 26). Detailed magnetization and ac susceptibility measurements combined with SANS showed (27) that the super-cooled skyrmion lattice order for temperatures below ~10 K may only be destroyed by means of an applied magnetic field exceeding the conical to ferromagnetic transition field, that is, at low temperatures, thermal activation is not sufficient to trigger a decay of the metastable skyrmion state. The observation of sizeable super-cooling effects in MnSi under pressure (28) or after violent quenches exceeding 400 K/min (29), and, in Cu₂OSeO₃, under electric field cooling (30), and the observation of slow relaxation at low temperatures in GaV₄S₈ (31) underscore the generic existence of supercooling effects noticed first in Fe_1−xCo_xSi. Several studies also investigated skyrmion generation and destruction triggered by electric currents (16, 32, 33). The energy barrier for skyrmion creation/annihilation in two dimensions was studied theoretically in the studies by Bessarab et al. and Hagemeister et al. (34, 35) and was extended to three dimensions by Rybakov et al. and Schütte et al. (23, 25). An elegant approach to explore the energetics requires time-resolved real-space imaging of large ensembles.

Here, we used time-resolved LTEM on thin bulk samples of Fe_1−xCo_xSi. On the one hand, this method provides the required spatial and temporal information, without driving the skyrmion decay. On the other hand, and as explained above, Fe_1−xCo_xSi represents an extremely well-understood and well-characterized material suitable to address these issues.

For our measurements, a sample with a thickness of d ≈ 240 nm was prepared using a focused ion beam (FIB) from the same optically float-zoned single crystal studied before (24, 26). The single crystal was cut such that a 〈100〉 axis was normal to the platelet. The magnetic field was applied along the same direction. As shown in Fig. 1B, for zero magnetic field and low temperatures, a well-defined helical order is observed with a modulation length λ ≈ 90 nm, in agreement with previous reports. Furthermore, under field cooling in an applied field of 23 mT, a well-defined hexagonal skyrmion lattice forms just below T_c. When reducing the temperature further, the same unchanged skyrmion lattice persists down to the lowest temperatures studied (12 K).

In our LTEM measurements, the evolution of the magnetic state was studied with a time resolution of ~100 ms, where movies were recorded after field cooling and a subsequent field change. We first investigate the destruction of the skyrmion state when the magnetic field is decreased. Shown in Fig. 2 are typical data for a decay into the helical state observed after field cooling at 23 mT down to T_m = 16.7 K and a reduction of the field to B_m = −2.6 mT. As illustrated in Fig. 2 (A to C) for patterns recorded at t = 0.1, 4.8, and 20.2 s after reaching B_m, respectively, the intensity pattern displays a merging of the skyrmions. This process corresponds accurately to the mechanism observed by means of MFM on the surface of bulk specimens cut from the same single crystal (24).

Fig. 2. Key characteristics of the decay of skyrmions into a helical order.

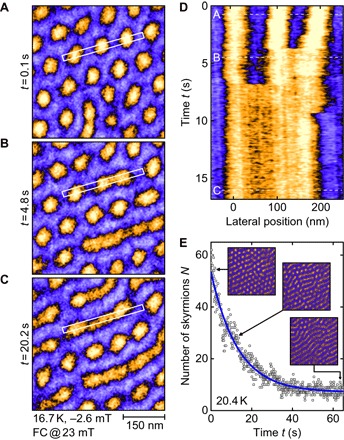
The sample was field-cooled (FC) from above the helical transition temperature (T_c ≈ 38 K) under an applied magnetic field B = 23 mT down to T_m, where the field was reduced to B_m and data recorded as a function of time t. (A to C) Typical LTEM patterns at T_m = 16.7 K after reaching B_m = −2.6 mT for t = 0.1 , 4.8, and 20.2 s, respectively. (D) Evolution of the intensity across the white box marked in (A), (B), and (C) as a function of time (vertical axis). (E) Typical time dependence of the number of skyrmions for T_m = 20.4 K and B_m = −2.6 mT. The blue curve represents an exponential fit.

The merging of skyrmions is additionally illustrated in Fig. 2D, which displays the intensity across the white box in panels (A) to (C) as a function of time along the vertical axis. Details of the merging cannot be resolved for the frame rate of our experiments, that is, the motion of the monopoles across the 250-nm thickness of the sample is faster than 100 ms corresponding to a speed greater than 2.5 × 10⁻⁶ m/s. However, by using a bespoke algorithm, we could track the number of skyrmions N for a given area as a function of time as illustrated in Fig. 2E. As a main new result, we observe an exponential time dependence, $\mathit{N}\approx {\mathit{N}}_0 \text{exp}(-\frac{\mathit{t}}{\mathrm{\tau }(\mathit{B},\mathit{T})})$ (blue line), from which we extract the lifetime, τ(B, T), as a function of field and temperature, analyzed further below. Note that N₀ is, in general, smaller than the initial number of skyrmions, because some skyrmions have already decayed during the field sweep when only blurred images are recorded because of image drifts.

The destruction of the skyrmion state after field cooling, when an increase in magnetic field triggers a decay into a conical (or ferromagnetic) state, is summarized in Fig. 3. Data shown were recorded after field cooling at 23 mT down to T_m = 18.5 K and an increase of the field to B_m = 57 mT. As predicted by theory (23), the decay pattern is characterized by the disappearance of individual skyrmions, as opposed to the merging observed for a decay into the helical state. Figure 3D displays the intensity across the white box in panels (A) to (C) as a function of time along the vertical axis. Using the same algorithm to track the number of skyrmions again, an exponential time dependence is observed for the entire parameter range accessible, as shown in Fig. 3E. Both the qualitative decay mechanism and the specific time dependence analyzed below represent the main results of our study.

Fig. 3. Key characteristics of the decay of skyrmions for increasing magnetic fields.

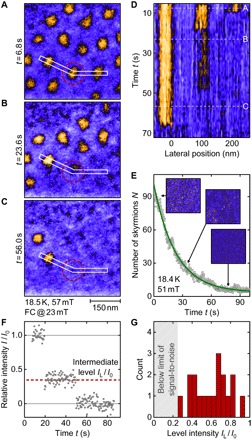
The sample was field-cooled (FC) from above the helical transition temperature (T_c ≈ 38 K) under an applied magnetic field B = 23 mT down to T_m, where the field was increased to B_m and the data were recorded as a function of time t. (A to C) Typical LTEM patterns at T_m = 18.5 K after reaching B_m = 57 mT, for t = 6.8, 23.6, and 56.0 s, respectively. (D) Evolution of the intensity across the white box marked in (A), (B), and (C) as a function time (vertical axis). (E) Typical time dependence of the number of skyrmions for T_m = 20.4 K and B_m = 57 mT, fitted by an exponential (green line). (F) Time dependence of the intensity within the red dashed circle in (A), (B), and (C). For a small number of skyrmions, a two-step decay via an intermediate state with lower intensity is observed. (G) Statistics of the intermediate-state intensities.

We note that for most of the decays, individual skyrmions vanish suddenly between two frames of our movies. However, for less than 10% of the skyrmions, the intensity does not vanish in a single step but exhibits a two-step process. An example is marked by the red dashed circle in Fig. 3 (A to C), corresponding to a diameter of ~100 nm in Fig. 3D. The relative change of intensity in this region, I/I₀, as a function of time is shown in Fig. 3F. The observation of the intermediate level implies that part of the skyrmion survives as an intermediate, metastable skyrmion string with a length shorter than the thickness of the sample. At least one end of the skyrmion string is, therefore, inside the sample, and topology enforces the presence of a Bloch point at this location. In turn, the metastable state consists of at least one Bloch point and a skyrmion string that either connects one Bloch point (or two) to the surface or connects a pair of Bloch points which each other.

One of the most likely mechanisms causing the metastable intermediate state is trapping of the Bloch points by local defects. As an interesting alternative, the metastable state may be a so-called chiral bobber, predicted theoretically by Rybakov et al. (23). The authors of this study pointed out that the surface energy of the skyrmion provides a repulsive potential for the Bloch point. Thus, a chiral bobber represents a Bloch point located immediately below the surface of the sample. To clarify the nature of the metastable states we observed, we analyzed the intensity of 18 of these inhibited decays (out of the 355 decays we investigated in detail). By plotting the number of inhibited decays as a function of relative intermediate intensity shown in Fig. 3G, we observe a very broad distribution. Taking these intensities as a measure of the length of the intermediate states, most of them are larger than expected theoretically for a single bobber located close to the surface. Hence, within our limited statistics, an interpretation in terms of Bloch points trapped by defects appears to be the most likely scenario.

DISCUSSION

Taking together all of our data, the lifetime τ(B, T) of skyrmions depends sensitively on the magnetic field and the temperature. Shown in Fig. 4A are typical decay times as a function of temperature for selected field values. The phase diagram shown in the background of that figure is identical to Fig. 1A. On a double-logarithmic scale, the decay times as a function of thermal energy display strong variations with magnetic field, where the decay into the conical and helical states is shown in Fig. 4 (B and C), respectively. As expected, the temperature dependence can be described approximately by an Arrhenius law, $\mathrm{\tau }(\mathit{B},\mathit{T})\approx {\mathrm{\tau }}_0(\mathit{B}){\mathit{e}}^{\mathrm{\Delta }\mathit{E}(\mathit{B})/{\mathit{k}}_{\mathrm{B}}\mathit{T}}$. However, the energy barriers vary strongly with the strength of the magnetic field, the largest being close to the stability regime of the skyrmion lattice. The energy barrier therefore drops for increasing field, for example, from ΔE = (199 ± 4) meV for B_m = 42.2 mT down to ΔE = (13 ± 1) meV for B_m= 56.8 mT. When the field is reduced and the skyrmions decay into the helical state, the activation energy ΔE = (32 ± 3) meV at B_m = 7.3 mT close to the stability region is again larger than that further away, where we find (15 ± 1) meV for B_m = −2.6 mT.

Fig. 4. Key characteristics of the decay rates of supercooled skyrmions in Fe_1−xCo_xSi (x = 0.5).

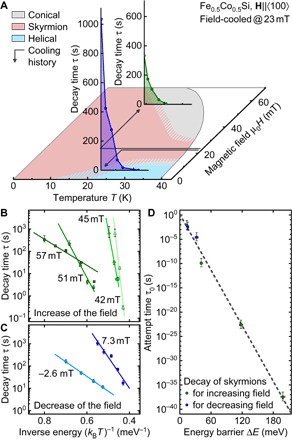
(A) Typical decay times τ after field cooling at B = 23 mT, followed by a decrease/increase to B_m. (B and C) Decay time τ as a function of thermal energy for increasing and decreasing magnetic fields, respectively, and various values of B_m. (D) Attempt time τ₀ as a function of energy barrier ΔE inferred from the exponential time dependence of the skyrmion decay. The variation of more than 30 orders of magnitude of τ₀ reflects the extreme enthalpy-entropy compensation.

This qualitative trend is consistent with existing theoretical predictions. Namely, in the study by Schütte and Rosch (25), stochastic micromagnetic simulations at finite temperatures were used to investigate the activation energy and magnetic field dependence for the decay of a single skyrmion into the helical state. Similar to our experiments, a strong dependence on the magnetic field B was found: Notably, the decay rate increases rapidly when the field is lowered. Furthermore, Rybakov et al. (23) used a variational approach at T = 0 to estimate activation barriers for a transition into a conical state. As in our experiments, theoretically predicted activation energies for this transition exceed those for the transition into the helical state. Using straightforward scaling arguments (see the Supplementary Materials) to extrapolate the calculated activation energies to the experimentally relevant parameter regime, we find, however, that the measured activation energies are about an order of magnitude smaller than the predicted ones. At present, we have no explanation for this substantial discrepancy; however, we speculate that it is connected with the large entropic effects discussed below, which become most pronounced for large activation barriers.

Surprisingly, measurements of the activation energies alone do not allow for the prediction of the lifetime of the metastable skyrmion state. Instead, we find that the prefactor τ₀(B)—the so-called attempt time—of the Arrhenius dependence assumes extremely small values and shows an unusually strong sensitivity to magnetic fields. This is emphasized in Fig. 4D, which shows that τ₀, as a function of the activation energy, changes from extremely low values, smaller than 10⁻³⁷ s, for the measurements at B_m = 42.2 mT, where the largest activation energy was measured, to almost macroscopic time scales ~10⁻² s at B_m = 57 mT. These values should be contrasted with typical microscopic time scales ~10⁻⁹ s commonly accepted for estimates of attempt times in magnetic materials (36–38).

To account for this extreme variation, we revisit the Arrhenius law used for fitting the decay times. At finite temperature, thermodynamics and transition rates are governed by the free energy F(T, B) = E(T, B) − T ∙ S(T, B). Thus, the Arrhenius-type decay law for a single energy barrier assumes the form $\mathrm{\tau }(\mathit{B})={\mathrm{\tau }}_{00} \text{exp}\left(\frac{\mathrm{\Delta }\mathit{F}(\mathit{T},\mathit{B})}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}\right)$, where ΔF = F_b − F₀ is the free-energy difference of the initial state, F₀, and a highly excited state, F_b, which defines the bottleneck of the skyrmion decay. Inserting the definition of the free energy one obtains

$$\mathrm{\tau }(\mathit{B})={\mathrm{\tau }}_{00} \text{exp}(-\frac{\mathrm{\Delta }\mathit{S}(\mathit{B})}{{\mathit{k}}_{\mathrm{B}}}) \text{exp}\left(\frac{\mathrm{\Delta }\mathit{E}(\mathit{B})}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}\right)$$ (1)

In turn, the high-energy offset of the decay time, given by ${\mathrm{\tau }}_0={\mathrm{\tau }}_{00} \text{exp}(-\frac{\mathrm{\Delta }\mathit{S}}{{\mathit{k}}_{\mathrm{B}}})$, depends exponentially on the entropy difference, ΔS, between the skyrmion state and the bottleneck state. A large positive value of ΔS leads to an exponential reduction of τ₀ and strongly increases the transition rates. Physically, this is due to the exponentially large number N_p of microscopic pathways across the energy barrier, ΔS = k_B ln[N_p], which increases the transition rate by the factor N_p. Similarly, a negative value of ΔS takes into account a reduction of the transition rate, which arises when the number of microscopic realizations of the initial state with skyrmion is much larger than the number of states close to the bottleneck.

Similar entropic effects as discussed here occur in many different systems in biology, chemistry, and physics. Because the high-energy states typically have a larger entropy, these entropic effects tend to partially counterbalance the energetic effects. Therefore, this phenomenon is often referred to as the “compensation effect.” Phenomenologically, linear relationships of activation energy and entropy are known as the Meyer-Neldel rule in the context of solid-state physics (2, 5, 6). In the limit where the activation energy is much larger than the typical microscopic energy scale E_m, they arise (5, 6) because the number of ways the activation barrier can be reached by microscopic processes varies exponentially in $\frac{\mathrm{\Delta }\mathit{E}}{{\mathit{E}}_{\mathrm{m}}},{\mathit{N}}_{\mathrm{p}}~\text{exp}\left(\frac{\mathrm{\Delta }\mathit{E}}{{\mathit{E}}_{\mathrm{m}}}\right)$ and hence $\mathrm{\Delta }\mathit{S}~{\mathit{k}}_{\mathrm{B}}\frac{\mathrm{\Delta }\mathit{E}}{{\mathit{E}}_{\mathrm{m}}}$. The fit in Fig. 4D shows that τ₀ follows the Meyer-Neldel rule approximately and exhibits an exponential dependence on the activation energy ΔE. From the fit, we obtain $\frac{{\mathit{E}}_{\mathrm{m}}}{{\mathit{k}}_{\mathrm{B}}}\approx 27\pm 3\mathrm{K}$, which is of the correct order of magnitude expected for our system where T_c ≈ 38 K. Remarkably, the approximate linear relation of ΔS and ΔE extends even in the regime where τ₀ is much larger than microscopic time scales, strongly suggesting a negative ΔS.

Our study reveals unprecedentedly large compensation effects by more than 30 orders of magnitude for the decay of topologically nontrivial spin configurations, notably skyrmions, as part of an ensemble far from equilibrium. This may seem particularly relevant in view of the technological impact expected of topological protection. It concerns, for instance, specifically the long-term stability of magnetic memory devices inferred from measurements of activation energies. Whereas typical values of τ₀ ~ 10⁻⁹ s are broadly accepted (36, 37), our results show that, especially for the large activation energies required for long-term stability, these estimates may overestimate the thermal stability of skyrmion-based memory devices by factors of the order of 10²⁰ and more. This illustrates that entropic effects will be very important for the technological exploitation of topologically nontrivial systems, such as memory technology based on skyrmions (39).

MATERIALS AND METHODS

Crystal growth and sample preparation

A large single crystal of Fe_1-xCo_xSi with x = 0.5 was grown by means of the optical floating zone technique under ultrahigh vacuum conditions (26, 39, 40). From the single-crystal ingot, we cut a bulk sample of 200 μm thickness along a 〈100〉 axis using x-ray Laue diffraction and a wire saw. This platelet was thinned by the FIB milling technique in plane-view configuration and subsequently polished by Ar ions at low voltages. The finished TEM lamella is shown in fig. S1A with dimensions of 10 × 10 μm. A TEM diffraction pattern in fig. S1B confirms the thinning of the specimen in the 〈100〉 direction. The thickness of the specimen was determined by high-angle annular dark-field scanning TEM imaging. The measured signal was normalized to the incoming beam intensity extracted from a detector scan (41). The normalized intensity was then compared with frozen phonon multislice simulations yielding the local specimen thickness. A thickness map is shown in fig. S1C. All measurements were performed in the marked area with a thickness of 241 ± 8 nm.

It is interesting to note that the thickness of our sample exceeds the modulation length of the helical state by a factor of 2.7. In comparison to bulk samples cut from the same ingot, which show a helimagnetic transition temperature of T_c = 47 K, the ordering temperature observed in the thin sample was T_c = 38 K. This reduction corresponds very well with a similar effect observed in MnSi, which was attributed to an enhancement of fluctuations with a reduction of sample thickness. Moreover, in a study on MnSi, a skyrmion lattice was observed across the entire magnetic phase diagram (42), consistent with LTEM studies in FeGe, where an increase of the temperature and field range of the skyrmion lattice was observed with a reduction of sample thickness (21, 43).

Magnetic imaging

Magnetic images were taken with an FEI Tecnai F30 transmission electron microscope in Lorentz mode (LTEM), where the magnetic field normal to the sample surface was tuned by the objective lens current. A defocused image was projected onto a phosphorescence screen, which is filmed by a high-speed camera through a lead glass window. We cooled and controlled the temperature of the specimen with a Gatan liquid helium holder.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/9/e1701704/DC1

section 1. Image processing for the skyrmion decay measurements

section 2. Evaluation of intermediate states

section 3. Scaling analysis of activation energies

fig. S1. Thickness determination of the FIB lamella.

fig. S2. Illustration of the evaluation of the skyrmion decay to the conical phase.

fig. S3. Illustration of the evaluation of the skyrmion decay to the helical phase.

fig. S4. Reduction of the skyrmion order deduced from the Fourier transform of the real-space data.

Reference (44)