On Estimation of Optimal Treatment Regimes For Maximizing t-Year Survival Probability

Summary

A treatment regime is a deterministic function that dictates personalized treatment based on patients’ individual prognostic information. There is increasing interest in finding optimal treatment regimes, which determine treatment at one or more treatment decision points so as to maximize expected long-term clinical outcome, where larger outcomes are preferred. For chronic diseases such as cancer or HIV infection, survival time is often the outcome of interest, and the goal is to select treatment to maximize survival probability. We propose two nonparametric estimators for the survival function of patients following a given treatment regime involving one or more decisions, i.e., the so-called value. Based on data from a clinical or observational study, we estimate an optimal regime by maximizing these estimators for the value over a prespecified class of regimes. Because the value function is very jagged, we introduce kernel smoothing within the estimator to improve performance. Asymptotic properties of the proposed estimators of value functions are established under suitable regularity conditions, and simulations studies evaluate the finite-sample performance of the proposed regime estimators. The methods are illustrated by application to data from an AIDS clinical trial.

1. Introduction

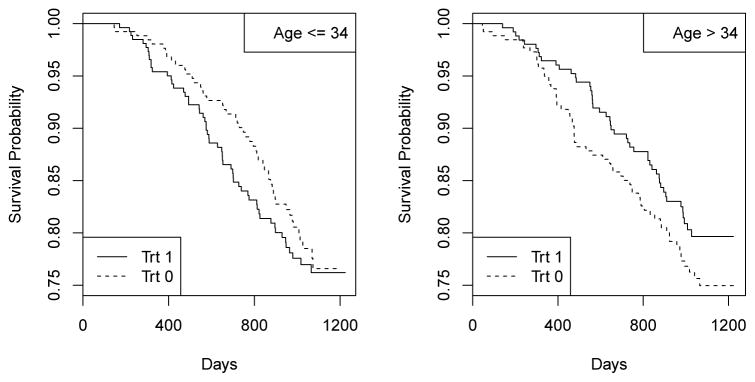
For many complex diseases, such as cancer, HIV infection, and mental disorders, there is generally not a uniformly best treatment for all patients. Rather, different patients may benefit from different treatments due to individual heterogeneity. For example, in AIDS Clinical Trials Group (ACTG) Study 175 (Hammer et al., 1996), the primary composite outcome of interest was time to having a larger than 50% decline in CD4 count, a measure of immunological status; progression to AIDS; or death. For the comparison of two treatments, zidovudine plus didanosine (coded as 1) and zidovudine plus zalcitabine (coded as 0), the data suggest that zidovudine plus zalcitabine leads to more favorable outcomes for younger patients than zidovudine plus didanosine. Figure 1 shows treatment-specific Kaplan-Meier estimates of the survival function for the two age strata defined by the observed median age, 34 years, in ACTG 175. It is clear that, among younger patients with age ≤ 34, those receiving zidovudine plus zalcitabine have almost uniformly larger survival probabilities those receiving zidovudine plus didanosine, whereas the situation is reversed for older patients with age > 34.

Fig. 1.

Treatment specific Kaplan-Meier curves by age.

This type of situation suggests that individual patient characteristics should be used when selecting treatments to maximize an expected long-term outcome of interest for which larger outcomes are preferred, such as t-year survival probability, and has heightened interest in derivation of optimal dynamic treatment regimes. Because in many chronic diseases treatment decisions may be made sequentially over time, a dynamic treatment regime is a set of one or more decision rules determine which treatment to give from among the available options based on accruing individual patient information, including baseline characteristics, intermediate outcomes between decisions, and previous treatments. An optimal regime is one that maximizes the expected outcome, or so-called value, if used by the entire patient population to select treatments.

There is a large literature on statistical methods to estimate an optimal treatment regime based on data from a clinical trial or observational study and non-survival outcomes. Q-learning (Watkins, 1989; Watkins and Dayan, 1992; Murphy, 2005; Zhao et al., 2009) and A-learning (Murphy, 2003; Robins, 2004) are two popular backward induction methods for estimating optimal dynamic treatment regimes based on regression-type modeling. The former involves positing parametric models for, roughly, the regression of outcome on accruing information and treatment, while the latter is based on semiparametric models in which only the part of the outcome regression representing contrasts among treatments is modeled parametrically, along with the propensity scores, the probabilities of observed treatment assignment given patient information at each decision point. Q-learning can be sensitive to misspecification of the required models, while A-learning enjoys the so-called double robustness property in that the corresponding estimating equations are asymptotically unbiased when either the propensity scores or main effects portion of the outcome models are correctly specified. An alternative class of approaches known as value or policy search methods is based on deriving and maximizing directly a consistent estimator for the value over a prespecified class of treatment regimes indexed by a finite-dimensional parameter. Zhang et al. (2012b) proposed inverse propensity score weighted (IPW) and augmented IPW (AIPW) estimators for the value in the case of a single decision point. Because the value estimator is nonsmooth, the optimization problem is challenging, and nonstandard optimization techniques are required. Zhao et al. (2012) and Zhang et al. (2012a) recast this approach as a weighted classification problem; the former refer to this method as outcome weighted learning. These approaches exploit approximations integrated into classification software to address the nonsmooth optimization problem, so that the class of regimes is dictated by a chosen classification method. Zhang et al. (2013) extended the value search methods of Zhang et al. (2012b) to more than one decision point, which share the computational challenges in the single decision case. Matsouaka et al. (2014) employed a kernel smoothing technique to nonparametrically estimate the conditional mean for the difference of the potential outcomes in a subgroup of patients and derived its associated treatment regime.

Although survival time is often the outcome of interest, to our knowledge there is relatively little development of methods for estimation of optimal treatment regimes where the goal is to maximize survival probability. Some work is focused on maximizing expected survival time. Goldberg and Kosorok (2012) developed a Q-learning method for censored survival data for estimating optimal dynamic treatment regimes and derived its associated finite sample risk bounds on the generalization error of the estimated regime, while Zhao et al. (2015) proposed a doubly robust estimator for expected survival time based on censored data and use outcome weighted learning to estimate an optimal regime. Bai et al. (2014) developed a locally-efficient doubly robust estimator for survival probability rather than mean survival time and estimate an optimal regime by extending the methods from a classification perspective of Zhang et al. (2012a). The latter two methods involve transforming maximization of the value to a weighted classification problem, which allows classification software to be used to address the optimization challenge and thus dictates the class of regimes. All of these methods are relevant to a single decision point only.

In this article, we propose a value search method for estimating an optimal treatment regime within a prespecified class for which the goal is to maximize survival probability that addresses the optimization challenges in a novel way and is relevant to more than one decision point. In particular, we develop a framework employing kernel smoothing techniques to smooth the estimator of the value prior to optimization, which we show greatly improves finite sample performance over the corresponding estimator with no smoothing. This approach is different from the smoothing technique used by Matsouaka et al. (2014), and, to the best of our knowledge, this is the first time smoothing has been integrated into estimation of the value function and its associated optimal treatment regimes in this way. Development of optimal treatment regimes for multiple decision points with censored survival data is challenging, as timing of observations, censoring, and events must be properly taken into account. In addition, we extend our smoothing approach to this setting.

In Sections 2 and 3, we introduce the statistical framework and estimators for a single decision point and multiple decisions, respectively. Asymptotic properties of the proposed estimators are given in Section 4. Finite sample performance is studied via simulation in Section 5, and Section 6 presents application of the methods to data from ACTG 175. Proofs are relegated to the Appendix.

2. Estimation of Optimal Treatment Regime for a Single Decision Time Point

2.1. Notation and Assumptions

Consider a study with two treatment options 𝒜; = {0, 1} given at baseline. For the ith patient, i = 1, …, n, let X_i denote the p-dimensional vector of baseline covariates taking values x ∈ 𝒳 and A_i denote the actual treatment received by the patient. Let T_i be the associated continuous survival time of interest, with conditional survival function S_T(t|a, x) ≡ P(T_i > t|A_i = a, X_i = x) and corresponding conditional cumulative hazard function Λ_T (t|a, x), where a = 0, 1. Let C_i denote right censoring time for patient i. The observed data are {(X_i, A_i, T̃_i, δ_i), i = 1, …, n}, independent and identically distributed (iid) across i, where T̃_i = min{T_i, C_i} and δ_i = I{T_i ≤ C_i}. We thus observe the counting process N_i(t) = I(T̃_i ≤ t, δ_i = 1) and the at risk process Y_i(t) = I(T̃_i ≥ t).

A treatment regime is a deterministic function that maps x ∈ 𝒳 to 𝒜;. For simplicity, we assume the regimes of interest are from 𝒢 = {g_η : g_η(x) = I{η^T x̃ ≥ 0}, ||η|| = 1}, where x̃ = (1, x^T )^T. However, the proposed method also applies to any other 𝒢 indexed by finite-dimensional parameters. Denote the potential survival time of a patient if he/she were given treatment a, which may be contrary to fact, as T^*(a). Accordingly, define the potential counting process N^*(a; t) and at risk process Y ^*(a; t) under treatment a, where N^*(a; t) = I{min(T^*(a), C) ≤ t, T^*(a) ≤ C} and Y ^*(a; t) = I{min(T^*(a), C) ≥ t}. If a patient follows a given regime g_η, we can write the corresponding potential survival time as T^*(g_η) = T^*(1)g_η +T^*(0)(1−g_η), whose survival function is given by S^*(t; η) = E(P[T^*{g_η(X)} > t|X]), as well as the potential counting process N^*(g_η; t) = N^*(1; t)g_η + N^*(0; t)(1 − g_η) and potential at risk process Y^* (g_η; t) = Y^* (1; t)g_η + Y^* (0; t)(1 − g_η). We wish to find an optimal treatment regime in 𝒢 that maximizes t-year survival probability; that is $g_{\mathit{\eta }}^{\text{opt}}(\mathit{x})\equiv g(\mathit{x};{\mathit{\eta }}^{\text{opt}})$, where η^opt = arg max_||η||=1 S^*(t; η). Here, t is a pre-determined time point.

To find an optimal treatment regime, we first derive consistent estimators of S^*(u; η) for any u. We make the uninformative censoring assumption: {T^*(1), T^*(0)} ⫫ C|A, X, where “⫫” means “independent of”. Let S_C(t|a, x) denote the survival function of the censoring time given A = a and X = x. If we were able to observe the g_η-specific potential counting process $N_i^{\ast }(g_{\mathit{\eta }};s)$ and at risk process $Y_i^{\ast }(g_{\mathit{\eta }};s)$, an intuitive estimator for S^*(u; η) is the inverse probability of censoring weighted Kaplan-Meier estimator

$${\widehat{S}}^{\ast }(u;\mathit{\eta })=\prod _{s\le u}\left(1-\frac{{\sum }_{i=1}^n[{dN}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}/S_C\{s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i\}]}{{\sum }_{i=1}^n[Y_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}/S_C\{s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i\}]}\right).$$ (1)

However, because $N_i^{\ast }(g_{\mathit{\eta }};s)$ and $Y_i^{\ast }(g_{\mathit{\eta }};s)$ are generally not observable, Ŝ^*(u; η) is not computable based on the observed data. To obtain proper estimators that are computable from the observed data, we make the following two assumptions, which are widely used in the causal inference literature (Rubin, 1974): (i) stable unit treatment value assumption (SUTVA); i.e. T = T^*(1)A+T^*(0)(1−A); and (ii) no unmeasured confounders assumptions; i.e. {T^*(1), T^*(0)} ⫫ A|X.

2.2. Estimation Procedure

Following Zhang et al. (2012b), we cast estimation of S^*(u; η) in a missing data framework. By SUTVA, for those patients whose actually received treatment matches the treatment dictated by g_η, $N_i^{\ast }(g_{\mathit{\eta }};s)=N_i(s)$ and $Y_i^{\ast }(g_{\mathit{\eta }};s)=Y_i(s)$, which are observed. For other patients, they are missing. This motivates us to modify the estimator given in (1) by incorporating inverse propensity score weighting. Formally, the weight for the ith patient is given by

$$w_{\mathit{\eta }i}=\frac{I[A_i=I\{{\mathit{\eta }}^T\stackrel{\sim }{\mathit{X}}\ge 0\}]}{\pi ({\mathit{X}}_i)A_i+\{1-\pi ({\mathit{X}}_i)\}(1-A_i)}=\frac{A_{i}I({\mathit{\eta }}^T\stackrel{\sim }{\mathit{X}}\ge 0)+(1-A_i)\{1-I({\mathit{\eta }}^T\stackrel{\sim }{\mathit{X}}\ge 0)\}}{\pi ({\mathit{X}}_i)A_i+\{1-\pi ({\mathit{X}}_i)\}(1-A_i)},$$ (2)

where π(X_i) = P(A_i = 1|X_i) is the propensity score. In practice, π(X_i) is known by design, as in a randomized clinical trial, or must be modeled and estimated from the data as in observational studies. In the latter case, a parametric model, say a logistic regression is usually used for estimating π(X_i), specifically,

$$\text{logit}\{\pi ({\mathit{X}}_i;\mathit{\theta })\}={\mathit{\theta }}^T{\stackrel{\sim }{\mathit{X}}}_i,$$ (3)

where logit(z) = log{z/(1−z)}. Let θ̂ denote the maximum likelihood estimator of θ, and define π̂ (X_i) = exp(θ̂^T X̃ _i)/{1 + exp(θ̂^T X̃_i)}. If the logistic regression model is correctly specified, θ̂ is a consistent estimator of θ.

To derive the estimator for S^*(u; η), we also need to estimate the censoring time survival function S_C(s|A_i, X_i). In many clinical studies with satisfactory follow-up, it is reasonable to assume that censoring times are independent of treatment assignment and covariates, i.e. independent censoring. Here, the Kaplan-Meier estimator for censoring times consistently estimates S_C(s|A_i, X_i). For some applications, the independent censoring assumption may be restrictive, but can be relaxed to a certain extent. For example, if censoring times are assumed to depend only on treatment assignment, the stratified Kaplan-Meier estimator can be used to estimate the treatment-specific censoring time survival function. For more general dependence, we can build a semiparametric model, say a proportional hazards model for censoring times, and obtain the model based estimator of S_C(s|A_i, X_i). For simplicity, from now on we make the independent censoring assumption and let Ŝ_C(·) denote the Kaplan-Meier estimator for censoring times.

Let ŵ_ηi denote the estimator of w_ηi obtained by replacing π(X_i) with π̂(X_i) in w_ηi. We propose the inverse propensity score weighted Kaplan-Meier estimator (IPSWKME) for S^*(u; η) given by

$${\widehat{S}}_I(u;\mathit{\eta })=\prod _{s\le u}\left\{1-\frac{{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}{dN}_i(s)}{{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}{Y}_i(s)}\right\}.$$ (4)

Note that the IPSWKME dose not depend on the Kaplan-Meier estimator Ŝ_C(·) for censoring times, as it cancels from numerator and denominator under the independent censoring assumption. In Section 4, we show that Ŝ_I (u; η) is a consistent estimator of S^*(u; η) under certain conditions. Based on Ŝ_I (u; η), the estimated optimal treatment regime to maximize t-year survival probability is given by $g(\mathit{x};{\widehat{\mathit{\eta }}}_I^{\text{opt}})$, where ${\widehat{\mathit{\eta }}}_I^{\text{opt}}=arg{max}_{\Vert \mathit{\eta }\Vert =1}{\widehat{S}}_I(t;\mathit{\eta })$.

The IPSWKME (4) relies on correct specification of the propensity score model. If it is misspecified, the IPSWKME is inconsistent. To improve the robustness of the IPSWKME, we propose augmented IPSWKME (AIPSWKME) by incorporating assumed model information. For example, we may posit a proportional hazards (PH) model (Cox, 1972) for the conditional cumulative hazard function of T by

$${\mathrm{\Lambda }}_T(t\mid A,\mathit{X})={\mathrm{\Lambda }}_0(t)exp\{{\mathit{\beta }}^T{({\mathit{X}}^T,A,A{\mathit{X}}^T)}^T\},$$ (5)

where Λ₀(t) is the baseline cumulative hazard function, and β is a (2p + 1)-dimensional parameter. The term $w_{\mathit{\eta }i}{dN}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}$ is augmented by

$$w_{\mathit{\eta }i}{dN}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}+(1-w_{\mathit{\eta }i})E[{dN}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}\mid {\mathit{X}}_i]=w_{\mathit{\eta }i}{dN}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}+(1-w_{\mathit{\eta }i})S_T(s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i)S_C(s)d{\mathrm{\Lambda }}_T(s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i),$$

where S_T (s|A_i, X_i) and S_C(s) are the conditional survival functions of T and C, respectively. Similarly, the term $w_{\mathit{\eta }i}{Y}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}$ is augmented by $w_{\mathit{\eta }i}{Y}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}+(1-w_{\mathit{\eta }i})S_T(s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i)S_C(s)$. It can be shown that the two augmented terms have the so-called double robustness property, i.e. they are unbiased for $E[{dN}_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}\mid {\mathit{X}}_i]$ and $E[Y_i^{\ast }\{g_{\mathit{\eta }}({\mathit{X}}_i);s\}\mid {\mathit{X}}_i]$, respectively, when either the propensity score model or the posited PH model is correctly specified. Therefore, we propose the AIPSWKME for S^*(u; η) as

$${\widehat{S}}_A(u;\mathit{\eta })=\prod _{s\le u}\left(1-\frac{{\sum }_{i=1}^n[{\widehat{w}}_{\mathit{\eta }i}{dN}_i(s)+(1-{\widehat{w}}_{\mathit{\eta }i}){\widehat{S}}_T\{s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i\}{\widehat{S}}_C(s)d{\widehat{\mathrm{\Lambda }}}_T\{s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i\}]}{{\sum }_{i=1}^n[{\widehat{w}}_{\mathit{\eta }i}{Y}_i(s)+(1-{\widehat{w}}_{\mathit{\eta }i}){\widehat{S}}_T\{s\mid g_{\mathit{\eta }}({\mathit{X}}_i),{\mathit{X}}_i\}{\widehat{S}}_C(s)]}\right),$$ (6)

where Ŝ_T (s|A_i, X_i) is the estimated survival function of T based on the fitted PH model and Ŝ_C(s) is the Kaplan-Meier estimator for censoring times. Based on Ŝ_A(u; η), the estimated optimal treatment regime to maximize t-year survival probability is given by $g(\mathit{x};{\widehat{\mathit{\eta }}}_A^{\text{opt}})$, where ${\widehat{\mathit{\eta }}}_A^{\text{opt}}=arg{max}_{\Vert \mathit{\eta }\Vert =1}{\widehat{S}}_A(t;\mathit{\eta })$. The asymptotic properties of Ŝ_A(u; η) and ${\widehat{S}}_A(t;{\widehat{\mathit{\eta }}}_A^{\text{opt}})$ are studied in Section 4.

2.3. Computational Aspects

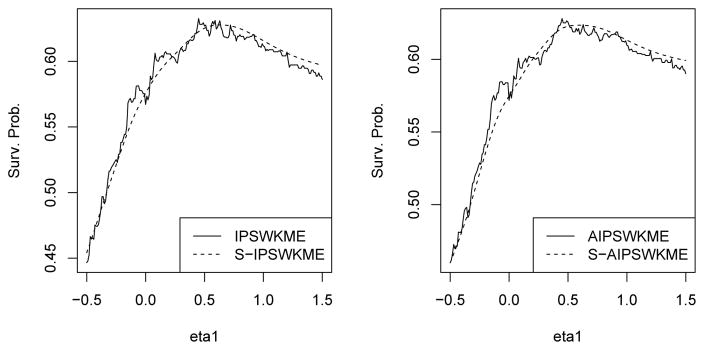
Note that Ŝ_I (t; η) and Ŝ_A(t; η) are not smooth functions of η. As an illustration, we plot Ŝ_I (t; η) and Ŝ_A(t; η) as functions of η₁ in Figure 2 for a simple example with one covariate and the intercept term in η being set as 1. The estimates are very jagged, and direct maximization of them with respect to η is challenging and may lead to local maximizers. From our simulation studies in Section 5, estimated survival probabilities following the obtained optimal treatment regimes may show substantial biases. As studied in Matsouaka et al. (2014), cross-validation may be used to correct the finite sample biases of the unsmoothed estimators, but it may increase the computational burden.

Fig. 2.

Plots for the original and smoothed estimates, where the original estimates are in black and the smoothed estimates are in red. In addition, the IPW and AIPW estimates are given in the left and right panels, respectively.

To reduce the biases of the estimators, we propose to smooth the estimators Ŝ_I (t; η) and Ŝ_A(t; η) using kernel smoothers. Specifically, we replace g_η(x_i) = I{η^T x̃_i ≥ 0} in Ŝ_I (t; η) and Ŝ_A(t; η) with g̃_η(x_i) = Φ(η^Tx̃_i/h) to obtain the smoothed IPSWKME (SIPSWKME) Ŝ_I (t; η) and smoothed AIPSWKME (S-AIPSWKME) Ŝ_A(t; η), where Φ(s) is the cumulative distribution function for the standard normal distribution, and h is a bandwidth parameter that goes to zero as n goes to infinity. For bandwidth selection, we set h = c₀n^−1/3sd(η^TX̃), where c₀ is a constant and sd(v) is the sample standard deviation of v. In our numerical studies, we found that c₀ = 4^1/3 generally gives good results for all scenarios. We plot in Figure 2 the smoothed estimates with the chosen bandwidth parameter for the same example. The smoothed estimates approximate the original estimates well and have unique maximizers around the true value η₁ = 0.5. Because the treatment regime I(η^T X̃ ≥ 0) remains the same when η is multiplied by k for any k > 0, choosing the bandwidth h to be a function of η, in particular, h being proportional to sd(η^T X̃), ensures the scale-free property of the regime, as the constant k cancels in Φ(η^T X̃/h). As shown in Figure 2, although the resulting smoothed value function is not convex in η, it generally has a unique mode, and the maximizer of the smoothed value function is much easier to obtain compared to the unsmoothed counterpart. In all our numerical studies, the non-convexity of the smoothed value function does not cause any difficulty in the maximization procedure. Such a bandwidth parameter has been widely used in the nonparametric smoothing literature and ensures that the original and smoothed estimators have the same asymptotic distribution (e.g. Heller, 2007). Let ${\stackrel{\sim }{\mathit{\eta }}}_I^{\text{opt}}$ and ${\stackrel{\sim }{\mathit{\eta }}}_A^{\text{opt}}$ denote the maximizers of Ŝ_I (t; η) and Ŝ_A(t; η), respectively. Then the associated estimated optimal treatment regimes are $g(\mathit{x};{\stackrel{\sim }{\mathit{\eta }}}_I^{\text{opt}})$ and $g(\mathit{x};{\stackrel{\sim }{\mathit{\eta }}}_A^{\text{opt}})$. In our implementation, we first conduct the optimization without the norm-one constraint. Instead, we search the maximizer in the domain −1 ≤ η_j ≤ 1 for all j’s and then we rescale η to have norm one. This does not change the estimated value function, Ŝ_I and Ŝ_A, and their smoothed counterparts.

3. Estimation of Optimal Treatment Regime for Multiple Decision Time Points

We now extend the foregoing methods to estimation of optimal dynamic treatment regimes incorporating multiple decision points. For simplicity, we illustrate for the case of two decision points. Specifically, treatments can be given at baseline and at a fixed interim time point s, 0 < s < t. For the ith patient, let X_0i denote his or her p₀-dimensional vector of baseline covariates and A_0i ∈ 𝒜;₀ = {0, 1} denote the initial treatment received at baseline. If the patient survives beyond s and is not censored before s, let X_1i denote his or her p₁-dimensional vector of intermediate covariates collected by s after assigning treatment A_0i and A_1i ∈ 𝒜;₁ = {0, 1} denote the follow-up treatment given at s. Thus, the observed data are {X_0i, A_0i, X_1iI(T̃_i > s), A_1iI(T̃_i > s), T̃_i, δ_i, i = 1, …, n} and iid across i.

As for a single decision point, we consider a class of linear dynamic treatment regimes for simplicity, i.e. 𝒢= {g_η = (g₀, g₁)}, where

$$\begin{array}{ll}\hfill g_0({\mathit{x}}_0;{\mathit{\eta }}_0)& =I\{{\mathit{\eta }}_0^T(1,{\mathit{x}}_0^T)\ge 0\},\hfill \\ \hfill g_1({\mathit{x}}_0,{\mathit{x}}_1;{\mathit{\eta }}_1)& =I\{{\mathit{\eta }}_1^T(1,{\mathit{x}}_0^T,g_0({\mathit{x}}_0;{\mathit{\eta }}_0),{\mathit{x}}_1^T))\ge 0\},\hfill \end{array}$$

η₀ is a (p₀+1)-dimensional parameter with ||η₀|| = 1, and η₁ is a (p₀+p₁+2)-dimensional parameter with ||η₁|| = 1. Here, a patient following a treatment regime g_η is given treatment g₀(X₀; η₀) at baseline, and, if he or she survives beyond s and is not censored before s, is given treatment g₁(X₀, X₁; η₁) at s. For patients whose initial treatments coincide with those assigned by g₀(X₀; η₀) and who die before s, their treatment assignments are consistent with the regime g_η. However, for patients whose initial treatments coincide with those assigned by g₀(X₀; η₀) but who are censored before s, it is not known whether their treatment assignments at the second decision follow the regime g_η. Let T^*(g_η) denote the potential survival time for a patient if he or she were given treatment according to g_η(X₀, X₁). We are interested in finding the optimal dynamic treatment regime ${\mathit{g}}_{\mathit{\eta }}^{\text{opt}}=\{g_0({\mathit{X}}_0;{\mathit{\eta }}_0^{\text{opt}}),g_1({\mathit{X}}_0,{\mathit{X}}_1;{\mathit{\eta }}_1^{\text{opt}})\}$ in 𝒢 that maximizes the t-year survival probability S^*(2)(t; η) = E(P[T^*{g_η(X₀, X₁)} > t|X₀, X₁]). As is standard in the causal inference literature for studying dynamic treatment regimes (e.g., Murphy, 2003), we assume: (i) SUTVA, i.e. a patient’s observed outcome agrees with the corresponding potential outcome if his or her actually received treatments are consistent with the assigned treatments and (ii) sequential randomization assumption (SRA), i.e. the treatment assignment at current stage only depends on the past received treatments and observed covariates, but not the potential outcomes. Under these two assumptions, the above defined t-year survival probability can be estimated from the observed data.

We propose a similar inverse propensity score weighted Kaplan-Meier estimator for the survival function S^*(2)(u; η) given any treatment regime g_η. However, the derivation of proper weights becomes more difficult, as some patients may be censored before s and whether their received treatments follow the regime g_η is unknown. To take this into account, we define the following new weight for patient i, i = 1, …, n:

$${\widehat{w}}_{\mathit{\eta }i}^{(2)}=\frac{I({\stackrel{\sim }{T}}_i\le s)\times {\delta }_i}{{\widehat{S}}_C({\stackrel{\sim }{T}}_i)}\times \frac{I\{A_{0i}=g_0({\mathit{X}}_{0i};{\mathit{\eta }}_0)\}}{{\pi }_{A_0}({\mathit{X}}_{0i})}+\frac{I({\stackrel{\sim }{T}}_i>s)}{{\widehat{S}}_C(s)}\times \frac{I\{A_{0i}=g_0({\mathit{X}}_{0i};{\mathit{\eta }}_0),A_{1i}=g_1({\mathit{X}}_{0i},g_0({\mathit{X}}_{0i};{\mathit{\eta }}_0),X_{1i};{\mathit{\eta }}_i)\}}{{\widehat{\pi }}_{A_0}({\mathit{X}}_{0i})\times {\widehat{\pi }}_{A_1}({\mathit{X}}_{0i},A_{0i},{\mathit{X}}_{1i})},$$

where π̂_A0 (X_0i) = π̂₀(X_0i)A_0i+{1− π̂₀(X_0i)}(1−A_0i), π̂_A1X_0i, A_0i, X_1i) = π̂₁(X_0i, A_0i, X_1i)A_1i+ {1 − π̂₁(X_0i, A_0i, X_1i)}(1 − A_1i), and π̂₀(X_0i) and π̂₁(X_0i, A_0i, X_1i) are the estimates of the propensity scores P(A_0i = 1|X_0i) and P(A_1i = 1|X_0i, A_0i, X_1i, T̂_i > s), respectively. In randomized studies, π̂₀ and π̂₁ are known by design, while in observational studies, they must be estimated, e.g. using logistic regression. The IPSWKME for S^* (u; η) is given by

$${\widehat{S}}_I^2(u;\mathit{\eta })=\prod _{v\le u}\left\{1-\frac{{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}^{(2)}{dN}_i(v)}{{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}^{(2)}{Y}_i(v)}\right\}.$$ (7)

Let ${\widehat{\mathit{\eta }}}_I^{\text{opt},(2)}=({\widehat{\mathit{\eta }}}_{I,0}^{\text{opt},(2)},{\mathit{\eta }}_{I,1}^{\text{opt},(2)})=arg{max}_{\Vert {\mathit{\eta }}_0\Vert =1,\Vert {\mathit{\eta }}_1\Vert =1}{\widehat{S}}_I^{(2)}(t;\mathit{\eta })$. Then the estimated optimal dynamic treatment regime is given by ${\widehat{\mathit{g}}}_{\mathit{\eta }}^{\text{opt},(2)}=\{g_0({\mathit{X}}_0;{\widehat{\mathit{\eta }}}_{I,0}^{\text{opt},(2)}),g_1({\mathit{X}}_0,{\mathit{X}}_1;{\widehat{\mathit{\eta }}}_{I,1}^{\text{opt},(2)})\}$.

To improve the finite sample performance of the IPSWKME, we again introduce kernel smoothing and replace the indicator functions g₀(X_0i; η₀) and g₁(X_0i, X_1i; η₁) in ${\widehat{S}}_I^{(2)}(u;\mathit{\eta })$ by $\mathrm{\Phi }\left\{{\mathit{\eta }}_0^T(1,{\mathit{X}}_{0i}^T)/h_0\right\}$ and $\mathrm{\Phi }\left[{\mathit{\eta }}_1^T\{1,{\mathit{X}}_0^T,g_0({\mathit{X}}_0;{\mathit{\eta }}_0),{\mathit{X}}_1^T\}/h_1\right]$, where the bandwidth parameters h₀ and h₁ are chosen as before. Let ${\stackrel{\sim }{S}}_I^{(2)}(u;\mathit{\eta })$ denote the resulting smoothed IPSWKME and ${\stackrel{\sim }{\mathit{\eta }}}_I^{\text{opt},(2)}$ denote the maximizer of ${\stackrel{\sim }{S}}_I^{(2)}(t;\mathit{\eta })$. To improve the robustness of IPSWKME, we can similarly derive the augmented IPSWKME based on a posited model for survival time, however, its formulation is very complicated and is not pursued here. Conceptually, the proposed IPSWKME can be generalized to accommodate more than two decision points. However, when there are more treatment decision points, the IPSWKME Optimal Treatment Regimes for Survival Endpoint may become less reliable because fewer patients will have assigned treatments consistent with a given dynamic treatment regime.

4. Asymptotic Properties

In this Section, we present the asymptotic properties of the proposed estimators in Theorems 1 – 3. Theorems 1 and 2 are for the cases with a single decision point while Theorem 3 is for the case with two decision points.

Theorem 1

Under conditions (A1)–(A6) in the Appendix, if the propensity score model (3) is correctly specified, for any regime g_η, we have, as n → ∞,

1. Ŝ_I (u; η) →^p S^*(u; η) for any 0 < u ≤ t;

2. $\sqrt{n}\{{\widehat{S}}_I(u;\mathit{\eta })-S^{\ast }(u;\mathit{\eta })\}$ converges weakly to a mean zero Gaussian process;

3. $\sqrt{n}\{{\widehat{S}}_I(t;{\widehat{\mathit{\eta }}}_I^{\text{opt}})-S^{\ast }(t;{\mathit{\eta }}^{\text{opt}})\}{\to }^{d}N(0,{\mathrm{\sum }}_I(t;{\mathit{\eta }}^{\text{opt}}))$, where the expression of Σ_I (t; η^opt) is given in the Appendix;

4. $\sqrt{n}\{{\widehat{S}}_I(t;{\widehat{\mathit{\eta }}}_I^{\text{opt}})-{\stackrel{\sim }{S}}_I(t;{\stackrel{\sim }{\mathit{\eta }}}_I^{\text{opt}})\}=o_p(1)$.

Theorem 2

Under condition (A1)–(A6) in the Appendix, if either the propensity score model (3) or the proportional hazard model (5) is correctly specified, we have, as n → ∞,

1. Ŝ_A(u; η) →^p S^*(u; η) for any 0 < u ≤ t;

2. $\sqrt{n}\{{\widehat{S}}_A(u;\mathit{\eta })-S^{\ast }(u;\mathit{\eta })\}$ converges weakly to a mean zero Gaussian process;

3. $\sqrt{n}\{{\widehat{S}}_A(t;{\widehat{\mathit{\eta }}}_A^{\text{opt}})-S^{\ast }(t;{\mathit{\eta }}^{\text{opt}})\}{\to }^{d}N(0,{\mathrm{\sum }}_A(t;{\mathit{\eta }}^{\text{opt}}))$, where the expression of Σ_A(t; η^opt) is given in the Appendix;

4. $\sqrt{n}\{{\widehat{S}}_A(t;{\widehat{\mathit{\eta }}}_A^{\text{opt}})-{\stackrel{\sim }{S}}_A(t;{\stackrel{\sim }{\mathit{\eta }}}_A^{\text{opt}})\}=o_p(1)$.

Theorem 3

Under certain regularity conditions, if the two propensity score models π₀(·) and π₁(·) are correctly specified, for any regime g_η, we have, as n → ∞,

1. ${\widehat{S}}_I^{(2)}(u;\mathit{\eta }){\to }^p{S}^{\ast (2)}(u;\mathit{\eta })$ for any 0 < u ≤ t;

2. $\sqrt{n}\{{\widehat{S}}_I^{(2)}(u;\mathit{\eta })-S^{\ast (2)}(u;\mathit{\eta })\}$ converges weakly to a mean zero Gaussian process;

3. $\sqrt{n}\{{\widehat{S}}_I^{(2)}(t;{\widehat{\mathit{\eta }}}_I^{\text{opt},(2)})-S^{\ast }(t;{\mathit{\eta }}^{\text{opt},(2)})\}{\to }^{d}N(0,{\mathrm{\sum }}_I^{(2)}(t;{\mathit{\eta }}^{\text{opt},(2)}))$, where ${\mathit{\eta }}^{\text{opt},(2)}=({\mathit{\eta }}_0^{\text{opt}},{\mathit{\eta }}_1^{\text{opt}})$;

4. $\sqrt{n}\{{\widehat{S}}_I^{(2)}(t;{\widehat{\mathit{\eta }}}_I^{\text{opt},(2)})-{\stackrel{\sim }{S}}_I^{(2)}(t;{\stackrel{\sim }{\mathit{\eta }}}_I^{\text{opt},(2)})\}=o_p(1)$.

Here the asymptotic variances Σ_I (t; η^opt), Σ_A(t; η^opt) and ${\mathrm{\sum }}_I^{(2)}(t;{\mathit{\eta }}^{\text{opt},(2)})$ can be consistently estimated from the observed data using the usual plug-in method. The proofs of Theorems 1–3 are given in the Appendix.

5. Simulation Studies

We examine the finite sample performance of the proposed estimators by simulation. We first consider scenarios with a single treatment decision time point at baseline. For each patient, baseline covariates X₁ and X₂ are independently and uniformly distributed on (−2, 2). Given X₁ and X₂, the binary treatment indicator A is generated from the logistic model logit{π(X₁, X₂)} = X₁ − 0.5X₂. The survival time T is generated from a linear transformation model (Cheng et al., 1995), h(T) = −0.5X₁ + A(X₁ − X₂) + ε, where h(s) = log(e^s − 1) − 2 is an increasing function, and the error term ε follows some known distribution, either the extreme value distribution or the logistic distribution, which corresponds to a proportional hazards and proportional odds model, respectively. The covariate-independent censoring time C is uniformly distributed on (0, C₀), where C₀ is chosen to achieve the censoring rate of 15% and 40%. The optimal treatment regime maximizing t-year survival probability is $g_{\mathit{\eta }}^{\text{opt}}(X_1,X_2)=I\{X_1-X_2\ge 0\}$ for any t. We search the optimal treatment regime in the class of regimes given by 𝒢 = {g_η : g_η(X₁, X₂) = I{η₀ + η₁X₁ + η₂X₂ ≥ 0}, η = (η₀, η₁, η₂)^T}, which contains the true optimal treatment regime with η^opt = (0, 0.707,−0.707).

To implement the proposed estimators, it is necessary to posit a model for the propensity scores. We consider both a correctly specified model, logit{π_A(X₁, X₂)} = θ₀+θ₁X₁+θ₂X₂, and a misspecified model, logit{π_A(X₁, X₂)} = θ₀. For the augmented estimators, we must posit a model for the survival time T. Here, we always use the proportional hazard model λ(t|X₁, X₂) = λ₀(t) exp{β₁₁X₁+β₁₂X₂+A(β₂₀+β₂₁X₁+β₂₂X₂)}. Note that when ε follows the extreme value distribution, the posited survival model is correctly specified. On the other hand, when ε follows the logistic distribution, this model is misspecified. We compare the performance of the IPSWKME (Ŝ_I ) and AIPSWKME (Ŝ_A), as well as their smoothed versions, S-IPSWKME (S̃_I ) and S-AIPSWKME (S̃_A), under different combinations of the assumed propensity score (PS) model, error term distribution, censoring rate, sample size (n = 250 or 500) and time point of interest (t = 1 or 2). For each scenario, we ran 1000 replications and used a genetic algorithm to do the optimization, which is implemented by the R function genoud within the package rgenoud (Mebane, Jr. and Sekhon, 2011).

We report results for the scenarios with n = 250 and t = 2, which are given in Tables 1 and 2 for the extreme value error and logistic error distributions, respectively. Results for other scenarios are similar. In the tables, we report the mean of estimated η^opt, the mean of estimated t-year survival probability following the estimated optimal treatment regime, namely the estimated optimal t-year survival probability (denoted by Ŝ(η̂^opt)), the mean of estimated standard error of Ŝ (η̂^opt) using the plug-in method based on the asymptotic variances established in Theorems 1–2 (denoted by SE), the empirical coverage probability of 95% confidence interval for the t-year survival probability following the true optimal treatment regime S(η^opt) (denoted by CP), the mean of simulated true t-year survival probability following the estimated optimal treatment regime (denoted by S(η̂^opt)), and the mean of misclassification rate by comparing the true and estimated optimal treatment regimes (denoted by MR). The numbers given in parenthesis are the standard deviations of the corresponding estimates. Here, S(η^opt) and S(η̂^opt) are computed using simulated survival times following the given treatment regime based on a large random sample of 5 × 10⁶ patients. We have S(η^opt) = 0.605 for the extreme value error distribution and S(η^opt) = 0.672 for the logistic distribution. The misclassification rate for one simulation is calculated as the proportion of patients for which the true and estimated optimal treatment regimes do not select the same treatment.

Table 1.

Simulation results for the extreme value error distribution with n = 250 and t = 2.

	PS	η̂0	η̂1	η̂2	Ŝ(η̂opt)	SE	CP	S(η̂opt)	MR
Censor Rate = 15%
ŜI	T	0.010 (0.298)	0.633 (0.192)	−0.665 (0.178)	0.645 (0.037)	0.040	0.839	0.590 (0.016)	0.118 (0.063)
S̃I	T	−0.005 (0.263)	0.652 (0.179)	−0.667 (0.171)	0.612 (0.036)	0.040	0.968	0.593 (0.014)	0.107 (0.057)
ŜA	T	−0.002 (0.287)	0.639 (0.171)	−0.676 (0.155)	0.639 (0.037)	0.040	0.866	0.592 (0.014)	0.109 (0.058)
S̃A	T	0.002 (0.256)	0.654 (0.169)	−0.675 (0.152)	0.609 (0.036)	0.040	0.969	0.594 (0.013)	0.102 (0.055)
ŜI	F	−0.031 (0.423)	0.408 (0.327)	−0.697 (0.249)	0.666 (0.036)	0.039	0.659	0.565 (0.040)	0.193 (0.100)
S̃I	F	−0.051 (0.403)	0.426 (0.285)	−0.714 (0.252)	0.643 (0.035)	0.039	0.844	0.569 (0.034)	0.184 (0.090)
ŜA	F	−0.014 (0.278)	0.660 (0.151)	−0.662 (0.161)	0.635 (0.038)	0.041	0.886	0.593 (0.012)	0.107 (0.055)
S̃A	F	−0.002 (0.246)	0.675 (0.141)	−0.665 (0.148)	0.607 (0.038)	0.041	0.968	0.596 (0.010)	0.096 (0.050)
Censor Rate = 40%
ŜI	T	0.008 (0.311)	0.616 (0.214)	−0.661 (0.202)	0.650 (0.041)	0.044	0.850	0.588 (0.019)	0.127 (0.068)
S̃I	T	−0.002 (0.285)	0.637 (0.202)	−0.660 (0.191)	0.613 (0.040)	0.045	0.958	0.590 (0.017)	0.118 (0.064)
ŜA	T	0.006 (0.310)	0.623 (0.203)	−0.663 (0.189)	0.645 (0.041)	0.045	0.879	0.589 (0.019)	0.123 (0.068)
S̃A	T	0.001 (0.282)	0.643 (0.192)	−0.661 (0.183)	0.612 (0.040)	0.044	0.965	0.591 (0.017)	0.115 (0.062)
ŜI	F	0.002 (0.448)	0.388 (0.349)	−0.676 (0.267)	0.671 (0.039)	0.043	0.677	0.560 (0.045)	0.206 (0.109)
S̃I	F	−0.024 (0.432)	0.403 (0.311)	−0.694 (0.271)	0.645 (0.039)	0.043	0.867	0.564 (0.038)	0.200 (0.095)
ŜA	F	−0.005 (0.299)	0.655 (0.169)	−0.650 (0.176)	0.641 (0.043)	0.046	0.896	0.591 (0.014)	0.115 (0.060)
S̃A	F	−0.005 (0.270)	0.664 (0.162)	−0.656 (0.173)	0.609 (0.041)	0.046	0.964	0.593 (0.012)	0.109 (0.054)

^†PS, the propensity score model. Here T means the correctly specified PS model while F means the misspecified PS model. Recall that S(η_opt) = 0.605.

Table 2.

Simulation results for the logistic error distribution with n = 250 and t = 2.

	PS	η̂0	η̂1	η̂2	Ŝ(η̂opt)	SE	CP	S(η̂opt)	MR
Censor Rate = 15%
ŜI	T	0.010 (0.370)	0.566 (0.272)	−0.641 (0.241)	0.716 (0.034)	0.038	0.791	0.652 (0.022)	0.155 (0.089)
S̃I	T	−0.004 (0.341)	0.593 (0.262)	−0.640 (0.235)	0.685 (0.034)	0.039	0.955	0.655 (0.020)	0.145 (0.082)
ŜA	T	0.007 (0.363)	0.578 (0.260)	−0.639 (0.240)	0.713 (0.034)	0.039	0.818	0.653 (0.020)	0.151 (0.084)
S̃A	T	−0.006 (0.341)	0.595 (0.251)	−0.642 (0.233)	0.684 (0.034)	0.039	0.962	0.655 (0.020)	0.143 (0.081)
ŜI	F	0.041 (0.461)	0.340 (0.389)	−0.662 (0.284)	0.729 (0.033)	0.037	0.649	0.632 (0.040)	0.224 (0.120)
S̃I	F	−0.001 (0.461)	0.375 (0.350)	−0.667 (0.283)	0.707 (0.033)	0.037	0.846	0.636 (0.035)	0.216 (0.107)
ŜA	F	−0.025 (0.337)	0.630 (0.198)	−0.637 (0.210)	0.723 (0.036)	0.040	0.753	0.658 (0.013)	0.133 (0.068)
S̃A	F	−0.029 (0.320)	0.633 (0.204)	−0.642 (0.204)	0.695 (0.036)	0.040	0.926	0.659 (0.012)	0.130 (0.064)
Censor Rate = 40%
ŜI	T	0.013 (0.395)	0.545 (0.293)	−0.625 (0.266)	0.721 (0.036)	0.041	0.785	0.649 (0.027)	0.168 (0.097)
S̃I	T	−0.008 (0.362)	0.581 (0.274)	−0.626 (0.255)	0.687 (0.036)	0.041	0.948	0.652 (0.022)	0.155 (0.087)
ŜA	T	0.004 (0.381)	0.558 (0.277)	−0.635 (0.255)	0.718 (0.036)	0.042	0.807	0.651 (0.023)	0.160 (0.089)
S̃A	T	−0.016 (0.361)	0.578 (0.270)	−0.634 (0.246)	0.686 (0.036)	0.042	0.955	0.653 (0.022)	0.153 (0.086)
ŜI	F	0.061 (0.471)	0.325 (0.413)	−0.640 (0.299)	0.733 (0.035)	0.039	0.661	0.628 (0.042)	0.235 (0.124)
S̃I	F	0.021 (0.482)	0.355 (0.370)	−0.639 (0.312)	0.709 (0.035)	0.040	0.842	0.631 (0.038)	0.229 (0.114)
ŜA	F	−0.012 (0.350)	0.625 (0.206)	−0.631 (0.217)	0.722 (0.038)	0.042	0.785	0.657 (0.014)	0.138 (0.070)
S̃A	F	−0.022 (0.331)	0.628 (0.214)	−0.634 (0.221)	0.692 (0.038)	0.043	0.939	0.658 (0.013)	0.136 (0.067)

^†PS, the propensity score model. Here T means the correctly specified PS model while F means the misspecified PS model. Recall that S(η_opt) = 0.672.

From the results, when the PS model is correctly specified, all estimators of η^opt have relatively small biases, in particular, the mean of ${\widehat{\eta }}_0^{\text{opt}}$ is close to zero while the mean ratio of ${\widehat{\eta }}_1^{\text{opt}}$ to ${\widehat{\eta }}_2^{\text{opt}}$ is very close to negative one. The means of simulated true t-year survival probability following the estimated optimal treatment regimes, i.e. S(η̂^opt), are all close to the true values. In addition, the estimates of η^opt based on the AIPSWKME and S-AIPSWKME of t-year survival probability generally have smaller standard deviation than those based on IPSWKME and S-IPSWKME. The unsmoothed IPSWKME and AIPSWKME of the optimal t-year survival probability have relatively large biases mainly due to the very jagged estimates of t-year survival probability, as illustrated in Figure 2, and as a consequence, the associated coverage probability of 95% confidence interval is much lower than the nominal level. The smoothed S-IPSWKME and S-AIPSWKME of the optimal t-year survival probability greatly reduce the biases and thus give the proper coverage probability. In addition, the unsmoothed and smoothed estimators of the optimal t-year survival probability have nearly the same standard deviation. When the PS model is misspecified, the IPSWKME and S-IPSWKME generally have relatively large biases as expected, while the AIPSWKME and S-AIPSWKME greatly reduce the biases and give much smaller MR. In particular, when the posited survival model is correctly specified under the extreme value error distribution, the S-AIPSWKME yields proper coverage probability. On the other hand, when the posited survival model is misspecified under the logistic error distribution, although the S-AIPSWKME is not consistent in general, it still gives small biases with reasonable coverage probability. Performance of the estimators improves as the censoring rate decreases and sample size increases.

We also compare the proposed method with the methods of Zhao et al. (2013) and Zhao et al. (2015). For the comparison with the method of Zhao et al. (2013), we consider randomized studies with known propensity scores, i.e. π_A ≡ 0.5, sample size n = 250, decision time point of interest t₀ = 2, and censoring rate of 15%. When implementing the method of Zhao et al. (2013), we set the threshold ξ = 0, 0.1, …, 0.6 and find the associated treatment regime for each ξ value.

Table 3 summarizes the simulation results for the extreme value and logistic error distributions based on 1000 replications. The performance of the method of Zhao et al. (2013) depends on the choice of the threshold value ξ. For the extreme value error distribution, the best choice is ξ = 0.4, while for the logistic error distribution, the best choice is ξ = 0.3. In practice, the best threshold value to use is unknown and must be estimated from data, which may not be straightforward. Moreover, even with the best choice of ξ value, the performance of the method by Zhao et al. (2013) is still worse than that of our proposed smoothed estimators, S-IPSWKME and S-AIPSWKME, under all the considered settings.

Table 3.

Results for comparison with the method of Zhao et al. (2013).

error	method	Surv. Prob.	MR
extreme value	Zhao et al. (2013) w. ξ = 0	0.445 (0.030)	0.467 (0.048)
	Zhao et al. (2013) w. ξ = 0.1	0.499 (0.046)	0.373 (0.089)
	Zhao et al. (2013) w. ξ = 0.2	0.555 (0.035)	0.245 (0.099)
	Zhao et al. (2013) w. ξ = 0.3	0.585 (0.027)	0.143 (0.091)
	Zhao et al. (2013) w. ξ = 0.4	0.590 (0.028)	0.112 (0.093)
	Zhao et al. (2013) w. ξ = 0.5	0.543 (0.066)	0.241 (0.162)
	Zhao et al. (2013) w. ξ = 0.6	0.542 (0.045)	0.275 (0.109)
	S-IPSWKME	0.594 (0.011)	0.107 (0.052)
	S-AIPSWKME	0.595 (0.009)	0.099 (0.047)
logistic	Zhao et al. (2013) w. ξ = 0	0.552 (0.028)	0.456 (0.061)
	Zhao et al. (2013) w. ξ = 0.1	0.606 (0.040)	0.323 (0.113)
	Zhao et al. (2013) w. ξ = 0.2	0.643 (0.029)	0.200 (0.111)
	Zhao et al. (2013) w. ξ = 0.3	0.650 (0.030)	0.164 (0.117)
	Zhao et al. (2013) w. ξ = 0.4	0.630 (0.037)	0.246 (0.132)
	Zhao et al. (2013) w. ξ = 0.5	0.590 (0.039)	0.373 (0.110)
	Zhao et al. (2013) w. ξ = 0.6	0.590 (0.030)	0.382 (0.079)
	S-IPSWKME	0.659 (0.012)	0.130 (0.063)
	S-AIPSWKME	0.660 (0.011)	0.126 (0.061)

^†Surv. Prob., the simulated survival probability at t₀ = 2; MR, the misclassification rate.

The true optimal survival probabilities are 0.605 and 0.672 for the extreme value and logistic error, respectively.

Values in the parenthesis are the standard deviations over 1000 simulations.

For the comparison with the method of Zhao et al. (2015), we consider the same simulation settings as in Tables 1 and 2 with sample size n = 250, decision time point of interest t₀ = 2, and censoring rate of 15%. For both methods, we consider the augmented estimation. Table 4 summarizes the simulation results based on 1000 replications. The proposed methods and the method of Zhao et al. (2015) lead to comparable survival probabilities under the estimated treatment rules, while the proposed methods yield smaller misclassification rates under all the considered settings. In summary, the proposed methods demonstrate very competitive performance compared with existing approaches.

Table 4.

Results for comparison with the method of Zhao et al. (2015).

error	method	PS	Surv. Prob.	MR
extreme value	Zhao et al. (2015)	T	0.587 (0.022)	0.136 (0.065)
	AIPSWKM	T	0.592 (0.014)	0.109 (0.058)
	S-AIPSWKM	T	0.594 (0.013)	0.102 (0.055)
	Zhao et al. (2015)	F	0.590 (0.008)	0.134 (0.044)
	AIPSWKM	F	0.593 (0.012)	0.107 (0.055)
	S-AIPSWKM	F	0.596 (0.010)	0.096 (0.050)
logistic	Zhao et al. (2015)	T	0.652 (0.027)	0.159 (0.090)
	AIPSWKM	T	0.653 (0.020)	0.151 (0.084)
	S-AIPSWKM	T	0.655 (0.020)	0.143 (0.081)
	Zhao et al. (2015)	F	0.659 (0.007)	0.141 (0.047)
	AIPSWKM	F	0.658 (0.013)	0.133 (0.068)
	S-AIPSWKM	F	0.659 (0.012)	0.130 (0.064)

^†PS, the propensity score model. Here T means the correctly specified PS model while F means the misspecified PS model.

^†Surv. Prob., the simulated survival probability at t₀ = 2; MR, the misclassification rate.

The true optimal survival probabilities are 0.605 and 0.672 for the extreme value and logistic error, respectively.

Values in the parenthesis are the standard deviations over 1000 simulations.

Next, we consider scenarios with two treatment decision time points, one at the baseline and the other at s = 1. The initial treatment assignment A₀ and the follow-up treatment assignment A₁, if applicable, are generated independently from a Bernoulli distribution with success probability of 0.5. A single baseline covariate X₀ is generated from a uniform distribution on (0, 4). To generate the survival time T, we first generate a time T₁ given A₀ and X₀ from an exponential distribution with the rate function λ₁(A₀, X₀). The censoring time C is generated from a uniform distribution on (0, C₀). If a patient is neither dead nor censored at time s = 1 (i.e. min(T₁, C) > 1), we generate a single intermediate covariate X₁ for this patient as X₁ = 0.5 X₀ − 0.4(A₀ − 0.5) + e, where e is uniformly distributed on (0, 2). Then we generate another time T₂ given A₀, A₁, X₀ and X₁ from an exponential distribution with the rate function λ₂(A₀, A₁, X₀, X₁). The survival time T of interest is defined as T = T₁ if T₁ ≤ 1 and T = 1+T₂ otherwise. The observed survival time is T̃ = min(T, C) with the censoring indicator δ = I(T ≤ C). Here, C₀ is chosen to achieve censoring rates of 15% and 40%. We consider three scenarios for the rate functions λ₁ and λ₂: (i) λ₁(A₀, X₀) = 0.5 exp{1.75(A₀ − 0.5)(X₀ − 2)} and λ₂(A₀, A₁, X₀, X₁) = 0.3 exp{2.5(A₁ − 0.4)(X₁ − 2) − A₀(X₁ − 2)}; (ii) λ₁(A₀, X₀) = 0.1 exp{2(A₀ − 0.5)(X₀ − 2)} and λ₂(A₀, A₁, X₀, X₁) = 0.2 exp{3(A₁ − 0.4)(X₁ − 2) − 3(A₀ − 0.5)(X₀ − 2)}; (iii) λ₁(A₀, X₀) = 0.2 exp{1.5(A₀ − 0.3)(X₀ − 3)} and λ₂(A₀, A₁, X₀, X₁) = 0.3 exp{2(A₁ − 0.5)(X₁ − 2) + 0.5(A₀ − 0.7)(X₀ − 1)}.

For the above three scenarios, the true optimal rule for maximizing t-year survival probability (t > 1) at time s = 1 is given by $g_1^{\text{opt}}(x_1)=I(2-x_1>0)$. However, the true optimal rule $g_0^{\text{opt}}(x_0)$ at time s = 0 is a complicated nonlinear function of x₀, which can be derived using backward induction as in Q-learning. In our implementation, for computation simplicity, we search for the optimal dynamic treatment regime in a class involving linear decision rules, specifically, 𝒢_η = {g₀(x₀) = I{η₁ + η₂x₀ > 0}, g₁(x₁) = I{η₃ + η₄x₁ > 0}, ||(η₁, η₂)|| = 1, ||(η₃, η₄)|| = 1}. Then, the true optimal rule $g_1^{\text{opt}}(x_1)$ at time s = 1 corresponds to $({\eta }_3^{\text{opt}},{\eta }_4^{\text{opt}})=(0.894,-0.447)$ for all three scenarios.

For scenarios (i) and (iii), we take t = 3, while for (ii) we take t = 6. We use simulation to find the true optimal rule at s = 0 in 𝒢_η to maximize t-year survival probability. Specifically, we first generate X₀, and for a given (η₁, η₂), we set A₀ by the regime g₀(X₀). Then, we generate X₁ given A₀ and X₀ the same way as in our design, and set A₁ by the optimal rule $g_1^{\text{opt}}$. Finally, we generate T₁ and T₂, and define T the same way as before. Using generated T’s for a large random sample of 5 × 10⁶ patients, we compute the associated empirical t-year survival probability. We find ( ${\eta }_1^{\text{opt}},{\eta }_2^{\text{opt}}$) to maximize the empirical t-year survival probability, which gives the true optimal rule $g_0^{\text{opt}}$ in 𝒢_η. Here, we use grid search method to find ( ${\eta }_1^{\text{opt}},{\eta }_2^{\text{opt}}$). Since $\Vert ({\eta }_1^{\text{opt}},{\eta }_2^{\text{opt}})\Vert =1$, we only need to do grid search for η₁. We have $({\eta }_1^{\text{opt}},{\eta }_2^{\text{opt}})=(0.890,-0.456)$ and S(3; η^opt) = 0.567 for scenario 1, $({\eta }_1^{\text{opt}},{\eta }_2^{\text{opt}})=(-0.891,0.454)$ and S(6; η^opt) = 0.624 for scenario 2, and $({\eta }_1^{\text{opt}},{\eta }_2^{\text{opt}})=(0.908,-0.419)$ and S(3; η^opt) = 0.702 for scenario 3. Here ${\mathit{\eta }}^{\text{opt}}={({\eta }_1^{\text{opt}},{\eta }_2^{\text{opt}},{\eta }_3^{\text{opt}},{\eta }_4^{\text{opt}})}^T$ and S(t; η^opt) is the t-year survival probability following the optimal dynamic treatment regime defined by η^opt.

We compare the unsmoothed and smoothed estimators. For both estimators, the propensity score models π₀ and π₁ are assumed known as for randomized clinical trials. Simulation results for 1000 replications are summarized in Table 3. From the results, we observe: (i) both unsmoothed and smoothed estimation methods give nearly unbiased estimators of η^opt, and the t-year survival probability following the estimated optimal treatment regime (denoted by S(η̂^opt) in the table) is very close to the t-year survival probability following the true optimal treatment regime η^opt; (ii) the mean of estimated standard error (SE) of Ŝ(η̂^opt) based on the established theory is close to the standard deviation of the estimates given in the parenthesis; (iii) The unsmoothed estimator for the t-year survival probability following the estimated optimal treatment regime (denoted by Ŝ(η̂^opt)) has relatively large bias and the associated coverage probability (CP) is below the nominal level; and (iv) the smoothed estimator for the t-year survival probability following the estimated optimal treatment regime has largely reduced bias and thus lead to proper coverage probability.

6. Application to ACTG 175

We illustrate the proposed methods for a single decision with the data from the ACTG Study 175 (Hammer et al., 1996). Subjects were randomized to four treatment groups with equal probability: zidovudine (ZDV) monotherapy, ZDV plus didanosine (ddI), ZDV plus zalcitabine (zal), and ddI monotherapy. A primary composite endpoint of interest is the time to having a larger than 50% decline in the CD4 count, or progressing to AIDS, or death, whichever comes first. From treatment-specific Kaplan-Meier curves, it can be clearly seen that treatments ZDV+ddI, ZDV+zal and ddI only are uniformly better than treatment ZDV only in terms of survival. In addition, treatments ZDV+ddI and ZDV+zal are overall the two best treatments giving the highest survival probabilities especially after day 400. For simplicity, we only consider two treatment options in our analysis, A = 1 for ZDV +ddI and A = 0 for ZDV+zal, which involves 1046 subjects. For each subject, there are 12 baseline clinical covariates; preliminary analysis results showed that Karnofsky score (Karnof), baseline CD4 count (CD40), and age (Age) are three important risk predictors and may have interaction effects with treatments. We include these three covariates in constructing treatment regimes. Our goal is to find the optimal treatment regime from the class of linear regimes defined by 𝒢 = {g_η = I(η₀ + η₁x₁ + η₂x₂ + η₃x₃ ≥ 0) : η = (η₀, η₁, η₂, η₃)^T, ||η|| = 1} to maximize t-year survival probability, x₁ is Karnof, x₂ is CD40, and x₃ is Age. Because the data come from a randomized study, we use a constant model for the propensity score and estimate this constant from data. For augmented estimation, we posit the proportional hazard model as given in (5). We estimate optimal treatment regimes at day t = 400, 600, 800 and 1000.

The estimated optimal treatment regimes and the associated t-year survival probabilities are presented in Table 6. We only present the results for S-IPSWKME and S-AIPSWKME, as they have better numerical performance than their nonsmoothed counterparts based on our simulation studies. The numbers in the columns of Intercept, Karnof, CD40 and Age are the parameter estimates η̃^opt defining the optimal treatment regimes, and S̃(t; η̃^opt) is the estimated t-year survival probability following the estimated optimal treatment regime. From the Table, the estimated optimal treatment regime for an earlier time may be different from that for a later time. For example, comparing the obtained optimal treatment regimes for t = 600 and t = 800, the S-IPSWKME assigns a set of 353 patients to treatment 0 and another set of 583 patients to treatment 1 for both time points. However, it assigns a set of 52 patients to treatment 0 for t = 600 but to treatment 1 for t = 800. On the other hand, it assigns another set of 58 patients to treatment 1 for t = 600 but to treatment 0 for t = 800. For the S-AIPSWKME, the findings are similar. S-IPSWKME and S-AIPSWKME yield very different parameter estimates η̃^opt. However, the corresponding optimal treatment regimes are similar. Using the results for day 600 as an example, among the 1046 subjects, there are only 57 subjects whose assigned treatments are different by the estimated optimal treatment regimes based on S-IPSWKME and S-AIPSWKME. In addition, the estimated t-year survival probabilities following the estimated optimal treatment regimes are nearly the same based on S-IPSWKME and S-AIPSWKME.

Table 6.

Estimation results for the ACTG175 data.

t	Method	Intercept	Karnof	CD40	Age	S̃(t; η̃opt)	CI1	CI0
400	I	−0.303	−0.340	0.024	0.890	0.965 (0.008)	(−0.002, 0.023)	(−0.003, 0.044)
	A	−0.729	−0.240	0.018	0.640	0.965 (0.008)	(−0.002, 0.022)	(−0.003, 0.043)
600	I	0.975	−0.082	0.001	0.206	0.923 (0.012)	(0.000, 0.045)	(−0.006, 0.052)
	A	0.909	−0.137	0.000	0.392	0.922 (0.012)	(0.000, 0.043)	(−0.009, 0.052)
800	I	0.871	−0.133	−0.010	0.473	0.887 (0.014)	(0.008, 0.058)	(−0.002, 0.069)
	A	0.874	−0.131	−0.009	0.469	0.886 (0.014)	(0.006, 0.057)	(−0.003, 0.068)
1000	I	−0.210	−0.185	−0.035	0.959	0.824 (0.017)	(0.004, 0.060)	(−0.006, 0.081)
	A	0.001	−0.187	−0.037	0.982	0.823 (0.017)	(0.002, 0.059)	(−0.007, 0.080)

^†I denotes the S-IPSWKME and A denotes the S-AIPSWKME; the numbers in the parenthesis are the estimated standard errors; CI₁ and CI₀ denote the 95% confidence intervals for the difference of the value functions obtained under the estimated optimal treatment regime and the simple treatment regime assigning all to treatment 1 and 0, respectively.

Next, we compare the estimated optimal regimes with the simple regimes that assign all subjects to the same treatment. Specifically, we construct 95% Wald-type confidence intervals for the difference between the estimated t-year survival probabilities under the estimated optimal treatment regimes and the simple regimes based on the derived asymptotic normal distribution. The results are also given in Table 6. The confidence intervals either stay above zero or zero is very close to the left end point of the intervals when it is contained. This implies that the increase in value realized by following the estimated optimal treatment regimes comparing with the simple regimes is significant or at least marginally significant. The Kaplan-Meier curves for patients following the estimated optimal treatment regimes (not shown here) are all uniformly better than those for each single treatment.

We have also estimated the optimal treatment regimes using the proposed methods based all twelve covariates when smoothing is and is not employed. We do not report on this here for brevity; however, we note that the results for smoothed estimators when using three versus twelve covariates are comparable, demonstrating the adaptivity of the smoothed estimators to incorporating relatively many covariates. The unsmoothed estimators can lead to slightly different optimal treatment rules but with similar estimated survival probabilities. In addition, the estimated survival probabilities show relatively larger differences between the cases with three and twelve covariates, which is likely due to the instability in maximizing the unsmoothed value functions.

7. Discussion

We have proposed Kaplan-Meier type estimators for the survival function of patients following a given (dynamic) treatment regime and introduce kernel smoothing to improve their performance. An optimal (dynamic) treatment regime within a class of prespecified treatment regimes may then be estimated by maximizing the estimator of the associated t-year survival probability. We consider the case when there are two treatment options at each decision time point. However, the proposed methods can be generalized to incorporate multiple treatment options at each decision by defining a treatment regime using multiple indexes instead of a single indicator function. In addition, current methods find the optimal (dynamic) treatment regime to maximize t-year survival probability, which can also be generalized to maximize other clinical outcomes of interest. Specifically, using the IPSWKME, Ŝ_I (·; η), as an illustration, we can find the optimal treatment regime to maximize f{Ŝ_I (·; η)}, where f is a specified function of interest; e.g., $f\{{\widehat{S}}_I(·;\mathit{\eta })\}={\int }_0^L{\widehat{S}}_I(u;\mathit{\eta })du$ corresponds to restricted mean survival time under a given treatment regime. Likewise f{Ŝ_I (·; η)} = sup{u : Ŝ_I (u; η) ≥ 0.5} corresponds to the median survival time under a given treatment regime.

In this paper, we study the asymptotic distributions of the estimated value function under the derived optimal treatment regimes. The asymptotic properties of η̂ in the treatment regime function are very challenging to obtain. The convergence rate of η̂ is slower than the classical n^1/2-rate due to the indicator function I(η^T X̃ ≥ 0), and the resulting limiting distribution is not standard. Matsouaka et al. (2014) studied a special case where the estimated value function depends on a single threshold value and showed that the estimator of the threshold that maximizes the estimated value function has the n^1/3-rate. We conjecture that our estimator η̂ should also have n^1/3-rate. This is an interesting problem that warrants future research.

Table 5.

Simulation results for estimating optimal dynamic treatment regimes.

C%	S	${\widehat{\eta }}_1^{\text{opt}}$	${\widehat{\eta }}_2^{\text{opt}}$	${\widehat{\eta }}_3^{\text{opt}}$	${\widehat{\eta }}_4^{\text{opt}}$	Ŝ(η̂opt)	SE	CP	S(η̂opt)	MR
Senario 1: ηopt = (0.890,−0.456, 0.894,−0.447); S(3; ηopt) = 0.567
15	F	0.881 (0.035)	−0.468 (0.062)	0.893 (0.017)	−0.449 (0.033)	0.591 (0.028)	0.030	0.887	0.559 (0.008)	0.107 (0.054)
	T	0.884 (0.029)	−0.463 (0.052)	0.894 (0.013)	−0.448 (0.026)	0.570 (0.028)	0.030	0.955	0.561 (0.006)	0.088 (0.048)
40	F	0.878 (0.042)	−0.471 (0.072)	0.890 (0.022)	−0.453 (0.042)	0.600 (0.036)	0.037	0.841	0.555 (0.011)	0.125 (0.061)
	T	0.884 (0.034)	−0.463 (0.061)	0.892 (0.018)	−0.450 (0.035)	0.574 (0.035)	0.038	0.955	0.558 (0.009)	0.108 (0.056)
Senario 2: ηopt = (−0.891, 0.454, 0.894,−0.447); S(6; ηopt) = 0.624
15	F	−0.888 (0.025)	0.456 (0.045)	0.891 (0.018)	−0.452 (0.035)	0.645 (0.025)	0.027	0.890	0.615 (0.008)	0.099 (0.052)
	T	−0.889 (0.018)	0.456 (0.034)	0.893 (0.014)	−0.450 (0.028)	0.624 (0.024)	0.027	0.967	0.618 (0.005)	0.079 (0.042)
40	F	−0.886 (0.030)	0.459 (0.053)	0.890 (0.020)	−0.453 (0.038)	0.650 (0.027)	0.029	0.855	0.613 (0.010)	0.110 (0.055)
	T	−0.888 (0.022)	0.457 (0.040)	0.892 (0.016)	−0.451 (0.032)	0.626 (0.027)	0.030	0.972	0.617 (0.007)	0.091 (0.048)
Senario 3: ηopt = (0.908,−0.419, 0.894,−0.447); S(3; ηopt) = 0.702
15	F	0.897 (0.037)	−0.434 (0.069)	0.892 (0.020)	−0.449 (0.039)	0.728 (0.026)	0.027	0.829	0.692 (0.009)	0.134 (0.067)
	T	0.900 (0.031)	−0.430 (0.060)	0.893 (0.016)	−0.448 (0.031)	0.707 (0.026)	0.027	0.952	0.695 (0.007)	0.116 (0.061)
40	F	0.895 (0.041)	−0.437 (0.075)	0.891 (0.023)	−0.451 (0.043)	0.732 (0.028)	0.029	0.809	0.691 (0.010)	0.142 (0.073)
	T	0.899 (0.035)	−0.431 (0.066)	0.893 (0.019)	−0.449 (0.036)	0.709 (0.028)	0.030	0.951	0.693 (0.008)	0.126 (0.066)

^†C% denotes the censoring rate; S indicates whether the smoothing technique is applied (T) or not (F).

A. Proof of Theorems

To establish the asymptotic results given in Theorems 1–2, we need to assume some regularity conditions. Recall that a working logistic model (3) is assumed for the propensity scores with parameters θ for the IPSWKME and a working proportional hazards model (5) is further assumed for the survival time T for the AIPSWKME with parameters β and Λ₀. Let ${\mathit{\nu }}_{Ai}={({\mathit{X}}_i^T,A_i,A_i{\mathit{X}}_i^T)}^T$ and ${\mathit{\nu }}_{\mathit{\eta }i}={({\mathit{X}}_i^T,g_{\mathit{\eta }}({\mathit{X}}_i),g_{\mathit{\eta }}({\mathit{X}}_i){\mathit{X}}_i^T)}^T$. Define

$$\begin{array}{l}{K}_1^I(\mathit{X},A,\stackrel{\sim }{T},\delta ;\mathit{\eta })={\int }_0^t\frac{(2A-1)dN(u)}{{\pi }^{\ast }E\{w_{\mathit{\eta }}^{\ast }Y(u)\}},\\ K_2^I(\mathit{X},A,\stackrel{\sim }{T},\delta ;\mathit{\eta })={\int }_0^t\frac{(2A-1)Y(u)E[\{(2A-1)g_{\mathit{\eta }}(\mathit{X})+(1-A)\}dN(u)]}{{[{\pi }^{\ast }E\{w_{\mathit{\eta }}^{\ast }Y(u)\}]}^2},\end{array}$$

where $w_{\mathit{\eta }}^{\ast }=[A{g}_{\mathit{\eta }}(\mathit{X})+(1-A)\{1-g_{\mathit{\eta }}(\mathit{X})\}]/{\pi }^{\ast }$ and π^* = π(X; θ^*)A+{1−π(X; θ^*)}(1−A). In addition, define

$$\begin{array}{l}{K}_1^A(\mathit{X},A,\stackrel{\sim }{T},\delta ;\mathit{\eta })={\int }_0^t\frac{J_1^A(u)-J_0^A(u)}{E[\{L_1^A(u)-L_0^A(u)\}{g}_{\mathit{\eta }}(\mathit{X})+L_0^A(u)]},\\ K_2^A(\mathit{X},A,\stackrel{\sim }{T},\delta ;\mathit{\eta })={\int }_0^t\frac{\{L_1^A(u)-L_0^A(u)\}E[\{J_1^A(u)-J_0^A(u)\}{g}_{\mathit{\eta }}(\mathit{X})+J_0^A(u)]}{{(E[\{L_1^A(u)-L_0^A(u)\}{g}_{\mathit{\eta }}(\mathit{X})+L_0^A(u)])}^2},\end{array}$$

where $J_k^A(u)=\frac{1-k-{(-1)}^{k}A}{{\pi }^{\ast }}dN(u)+e_k\left(1-\frac{1-k-{(-1)}^{k}A}{{\pi }^{\ast }}\right)exp\{-{\mathrm{\Lambda }}_0^{\ast }(u)e_k\}{S}_C(u)d{\mathrm{\Lambda }}_0^{\ast }(u),L_k^A(u)=\frac{1-k-{(-1)}^{k}A}{{\pi }^{\ast }}Y(u)+\left(1-\frac{1-k-{(-1)}^{k}A}{{\pi }^{\ast }}\right)exp\{-{\mathrm{\Lambda }}_0^{\ast }(u)e_k\}{S}_C(u)$e_k = exp {β^*T(X^T, k, kX^T)^T}, k = 0, 1. We assume the following conditions.

• A1The covariates X are bounded.
• A2The propensity score π(X) is bounded away from 0 and 1 for all possible values of X.
• A3The equation $E\left[\left\{A-\frac{exp({\mathit{\theta }}^T\stackrel{\sim }{\mathit{X}})}{1+exp({\mathit{\theta }}^T\stackrel{\sim }{\mathit{X}})}\right\}\stackrel{\sim }{\mathit{X}}\right]=0$ has a unique solution θ^*.
• A4
  The equation

  $$E\left({\int }_0^{\tau }\left[{\mathit{\nu }}_{Ai}-\frac{E\left\{Y_i(s)exp({\mathit{\beta }}^T{\mathit{\nu }}_{Ai}){\mathit{\nu }}_{Ai}\right\}}{E\left\{Y_i(s)exp({\mathit{\beta }}^T{\mathit{\nu }}_{Ai})\right\}}\right]\times {dN}_i(s)\right)=0.$$

  has a unique solution β^*, where τ > t is a prespecified time point satisfying P(T̃_i ≥ τ ) > 0. Let ${\mathrm{\Lambda }}_0^{\ast }(u)=E[{\int }_0^u{dN}_i(s)/E\{Y_i(s)exp({\mathit{\beta }}^{\ast T}{\mathit{\nu }}_{Ai})\}]$ and it satisfies ${\mathrm{\Lambda }}_0^{\ast }(\tau )<\infty$.

• A5 ${sup}_{\Vert \mathit{\eta }\Vert =1}E[{\{K_j^I(\mathit{X},A,\stackrel{\sim }{T},\delta ;\mathit{\eta })\}}^2]<\infty$ and ${sup}_{\Vert \mathit{\eta }\Vert =1}E[{\{K_j^A(\mathit{X},A,\stackrel{\sim }{T},\delta ;\mathit{\eta })\}}^2]<\infty$, j = 1, 2.
• A6nh → ∞ and nh⁴ → 0 as n → ∞.

Under assumed regularity conditions A1 – A4, we have the following asymptotic representations:

$$\begin{array}{c}\sqrt{n}(\widehat{\mathit{\theta }}-{\mathit{\theta }}^{\ast })=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\varphi }_{1i}+o_p(1),\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}^{\ast })=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\varphi }_{2i}+o_p(1),\\ \sqrt{n}\{{\widehat{\mathrm{\Lambda }}}_0(u)-{\mathrm{\Lambda }}_0^{\ast }(u)\}=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\varphi }_{3i}(u)+o_p(1),\sqrt{n}\{{\widehat{S}}_C(u)-S_C(u)\}=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\varphi }_{4i}(u)+o_p(1),\end{array}$$

where ϕ_1i’s and ϕ_2i’s are independently and identically distributed mean-zero vectors, and ϕ_3i(u) and ϕ_4i(u) are independent mean-zero processes. Moreover, consistent estimators ϕ̂_1i, ϕ̂_2i, ϕ̂_3i(u) and ϕ̂_4i(u) of ϕ_1i, ϕ_2i, ϕ_3i(u) and ϕ_4i(u) can be easily obtained.

In the following, we give a sketch for the proof of Theorem 1. The detailed proofs for Theorems 1–2 are provided in the Supplementary Appendix.

A.1. Proof of Theorem 1

For any given regime g_η, we first derive the asymptotic properties for the corresponding inverse propensity score weighted (IPSW) Nelson-Aalen estimator. Specifically,

$${\widehat{\mathrm{\Lambda }}}_I(u;\mathit{\eta })\equiv {\widehat{\mathrm{\Lambda }}}_I(u;\mathit{\eta },\widehat{\mathit{\theta }})={\int }_0^u\frac{{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}{dN}_i(s)}{{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}{Y}_i(s)}.$$ (A.1)

It is easy to show that Ŝ_I (u; η) and exp{−Λ̂_I (u; η)} are asymptotically equivalent for any given η. Therefore, the asymptotic properties of Ŝ_I (u; η) easily follows those of Λ̂_I (u; η).

When the propensity score model is correctly specified, we have θ^* = θ and $w_{\mathit{\eta }i}^{\ast }=w_{\mathit{\eta }i}$. Then $n^{-1}{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}{Y}_i(s){\to }_{p}E\{w_{\mathit{\eta }i}{Y}_i(s)\}=E[Y^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}]$ uniformly for s ∈ [0, τ] as n → ∞. Similarly, we have $n^{-1}{\sum }_{i=1}^n{\widehat{w}}_{\mathit{\eta }i}{dN}_i(s){\to }_{p}E\{w_{\mathit{\eta }i}{dN}_i(s)\}=E[d{N}^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}]$ uniformly for s ∈ [0, τ] as n → ∞. Therefore,

$$\begin{array}{c}{\widehat{\mathrm{\Lambda }}}_I(u;\mathit{\eta }){\to }_p{\int }_0^u\frac{E[d{N}^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}]}{E[Y^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}]}={\int }_0^u\frac{S_C(s)dP[T^{\ast }\{g_{\mathit{\eta }}(\mathit{X})\}\le s]}{S_C(s)P[T^{\ast }\{g_{\mathit{\eta }}(\mathit{X})\}\ge s]}\\ =-log\{S^{\ast }(u;\mathit{\eta })\}\equiv {\mathrm{\Lambda }}^{\ast }(u;\mathit{\eta }),\end{array}$$

which establish the consistency given in (i) of Theorem 1.

Next, we derive the asymptotic distribution of Λ_I (u; η). By applying the first-order Taylor expansion of Λ̂_I (u; η) with respect to parameter θ and some empirical process approximation techniques, we have

$$\begin{array}{l}\sqrt{n}\{{\widehat{\mathrm{\Lambda }}}_I(u;\mathit{\eta })-{\mathrm{\Lambda }}^{\ast }(u;\mathit{\eta })\}=n^{-1/2}\sum _{i=1}^n\left({\int }_0^u\frac{w_{\mathit{\eta }i}{dM}_i^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}}{E[Y^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}]}+D_1{(u)}^T{\varphi }_{1i}\right)+o_p(1)\\ \equiv n^{-1/2}\sum _{i=1}^n{\zeta }_i(u;\mathit{\eta })+o_p(1),\end{array}$$

where $M_i^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}=N_i^{\ast }\{g_{\mathit{\eta }}(\mathit{X});s\}-{\int }_0^s{Y}_i^{\ast }\{g_{\mathit{\eta }}(\mathit{X});v\}d{\mathrm{\Lambda }}^{\ast }(v;\mathit{\eta })$ is a mean-zero martingale process and D₁(u) = lim_n→∞ ∂Λ̂_I (u; η, θ)/∂θ. By delta method, we have $\sqrt{n}\{{\widehat{S}}_I(u;\mathit{\eta })-S^{\ast }(u;\mathit{\eta })\}=-S^{\ast }(u;\mathit{\eta })n^{-1/2}{\sum }_{i=1}^n{\zeta }_i(u;\mathit{\eta })+o_p(1)$, which converges weakly to a mean-zero Gaussian process by applying the empirical process theory. This proves (ii) of Theorem 1.

Since ${\widehat{\mathit{\eta }}}_I^{\text{opt}}$ is the maximizer of Ŝ_I (t; η) and η^opt is the maximizer of S^*(t; η), following the similar arguments in Zhang et al. (2012b), we have

$$\sqrt{n}\{{\widehat{S}}_I(t;{\widehat{\mathit{\eta }}}_I^{\text{opt}})-S^{\ast }(t;{\mathit{\eta }}^{\text{opt}})\}-\sqrt{n}\{{\widehat{S}}_I(t;{\mathit{\eta }}^{\text{opt}})-S^{\ast }(t;{\mathit{\eta }}^{\text{opt}})\}=o_p(1).$$

It follows that $\sqrt{n}\{{\widehat{S}}_I(t;{\widehat{\mathit{\eta }}}_I^{\text{opt}})-S^{\ast }(t;{\mathit{\eta }}^{\text{opt}})\}{\to }^{d}N(0,{\mathrm{\sum }}_I(t;{\mathit{\eta }}^{\text{opt}}))$, where ${\mathrm{\sum }}_I(t;{\mathit{\eta }}^{\text{opt}})={\{S^{\ast }(t;{\mathit{\eta }}^{\text{opt}})\}}^{2}E\{{\zeta }_i^2(t;{\mathit{\eta }}^{\text{opt}})\}$. This proves (iii) of Theorem 1.

Finally, we show that ${\widehat{S}}_I(t;{\widehat{\mathit{\eta }}}_I^{\text{opt}})$ and ${\stackrel{\sim }{S}}_I(t;{\stackrel{\sim }{\mathit{\eta }}}_I^{\text{opt}})$ are asymptotically equivalent. For any given η, we have

$$\sqrt{n}\{{\stackrel{\sim }{\mathrm{\Lambda }}}_I(t;\mathit{\eta })-{\widehat{\mathrm{\Lambda }}}_I(t;\mathit{\eta })\}=\sqrt{n}\times \frac{1}{n}\sum _{i=1}^n\left\{\mathrm{\Phi }\left(\frac{{\mathit{\eta }}^T{\mathit{X}}_i}{h}\right)-I({\mathit{\eta }}^T{\mathit{X}}_i\ge 0)\right\}\times K_1^I({\mathit{X}}_i,A_i,{\stackrel{\sim }{T}}_i,\delta ;\mathit{\eta })$$ (A.2)

$$\begin{array}{l}+\sqrt{n}\times \frac{1}{n}\sum _{i=1}^n\left\{\mathrm{\Phi }\left(\frac{{\mathit{\eta }}^T{\mathit{X}}_i}{h}\right)-I({\mathit{\eta }}^T{\mathit{X}}_i\ge 0)\right\}\times K_2^I({\mathit{X}}_i,A_i,{\stackrel{\sim }{T}}_i,\delta ;\mathit{\eta })\\ +o_p(1).\end{array}$$ (A.3)

Following the similar arguments in Heller (2007), we can show that sup_||η||=1 |(A.2)| = o_p(1) and sup_||η||=1 |(A.3)| = o_p(1). Therefore, we have $\sqrt{n}\{{\stackrel{\sim }{\mathrm{\Lambda }}}_I(t;\mathit{\eta })-{\widehat{\mathrm{\Lambda }}}_I(t;\mathit{\eta })\}=o_p(1)$ uniformly in η, which implies $\sqrt{n}\{{\stackrel{\sim }{S}}_I(t;\mathit{\eta })-{\widehat{S}}_I(t;\mathit{\eta })\}=o_p(1)$ uniformly in η. It follows that $\sqrt{n}\{{\stackrel{\sim }{S}}_I(t;{\stackrel{\sim }{\mathit{\eta }}}_I^{\text{opt}})-{\widehat{S}}_I(t;{\widehat{\mathit{\eta }}}_I^{\text{opt}})\}=o_p(1)$, which proves (iv) of Theorem 1.