Significance
While it is known that the shape and size of the cell nucleus change dramatically during the cell cycle, we find that the cell nucleus also exhibits subtle, but measurable, fast shape fluctuations at seconds. We find that the amplitude of these fluctuations systematically decreases during the cell cycle, thus serving as a reliable cell cycle stage indicator. Our findings show that the nucleus undergoes both thermally and actively driven undulations, the latter caused by forces from chromatin and cytoskeleton. Such undulations might affect gene regulation as well as aid the nuclear transport. Understanding the mechanism behind such undulations could prove critical for illuminating dynamic behavior of the nucleus in health and disease.
Keywords: nuclear envelope, chromatin, nuclear lamina, active materials
Abstract
The nuclear envelope (NE) presents a physical boundary between the cytoplasm and the nucleoplasm, sandwiched in between two highly active systems inside the cell: cytoskeleton and chromatin. NE defines the shape and size of the cell nucleus, which increases during the cell cycle, accommodating for chromosome decondensation followed by genome duplication. In this work, we study nuclear shape fluctuations at short time scales of seconds in human cells. Using spinning disk confocal microscopy, we observe fast fluctuations of the NE, visualized by fluorescently labeled lamin A, and of the chromatin globule surface (CGS) underneath the NE, visualized by fluorescently labeled histone H2B. Our findings reveal that fluctuation amplitudes of both CGS and NE monotonously decrease during the cell cycle, serving as a reliable cell cycle stage indicator. Remarkably, we find that, while CGS and NE typically fluctuate in phase, they do exhibit localized regions of out-of-phase motion, which lead to separation of NE and CGS. To explore the mechanism behind these shape fluctuations, we use biochemical perturbations. We find the shape fluctuations of CGS and NE to be both thermally and actively driven, the latter caused by forces from chromatin and cytoskeleton. Such undulations might affect gene regulation as well as contribute to the anomalously high rates of nuclear transport by, e.g., stirring of molecules next to NE, or increasing flux of molecules through the nuclear pores.
The cell nucleus changes its shape and size dramatically during the cell cycle (1, 2). Such changes correspond to, e.g., decondensation of chromosomes in a newly formed nucleus, or, later, chromosome duplication, and occur on time scales of hours (3). Recently, small oscillations of nuclear area were found for stem cells and fibroblasts at time scales of minutes and attributed to local changes in chromatin compaction and cytoskeletal forces (4, 5). Shape fluctuations at even shorter time scales, “flickering,” were previously studied only in membraneous systems, e.g., lipid vesicles, plasma membrane of red blood cells, and macrophages (6–8), where they were found to be largely thermally driven. Flickering of the cell nucleus, which has a more complex architecture, remains to be shown and characterized.
The shape of the cell nucleus is defined by the nuclear envelope (NE), a complex structure that confines chromatin, forming a physical boundary between the nucleoplasm and cytoplasm. NE comprises two lipid bilayers separated by a perinuclear space of 20 nm to 40 nm and supported from inside by nuclear lamina, a 50- to 80-nm-thick network formed by intermediate filament lamins (9, 10), which are presumed to provide NE with its structural support (11–13). Furthermore, NE is perforated by thousands of nuclear pores, gigantic protein complexes with diameter 120 nm and depth 45 nm, which aid the molecular transport into and out of the cell nucleus (14, 15). The presence of nuclear pores in the NE is integral to the NE’s mechanical properties (16, 17).
Since NE is sandwiched between two active systems inside the cell—cytoskeleton on the cytoplasmic side and chromatin on the nucleoplasmic side—both could contribute to the nuclear shape fluctuations. Moreover, cytoskeleton as well as chromatin maintain direct links with NE (e.g., LINC complex, emerin, MAN1) (19, 20). Recent studies in yeast showed that microtubules were involved in the nuclear shape fluctuations over minutes, while chromatin tethering to NE influences nuclear deformability (21). In mammalian cells, cytoskeletal perturbations lead to changes in nuclear deformability (5), whereas chromatin interacts with NE via hundreds of lamina-associated domains, which reshuffle stochastically inside the nucleus (22). In fact, chromatin’s interaction with NE is implicated in regulation of some genes (23–25).
Structural and functional errors of the NE lead to a large number of developmental and inherited disorders, so-called nuclear envelopathies, such as cardiomyopathy, muscular dystrophy, mandibuloacral dysplasia, and Hutchinson–Gilford progeria, as well as cancer (20, 26). Two major working hypotheses for these diseases are defects in gene regulation and abnormalities in nuclear architecture (27). Thus, elucidating mechanics of the nuclear shape fluctuations might contribute to the efforts to understand the NE in health and disease.
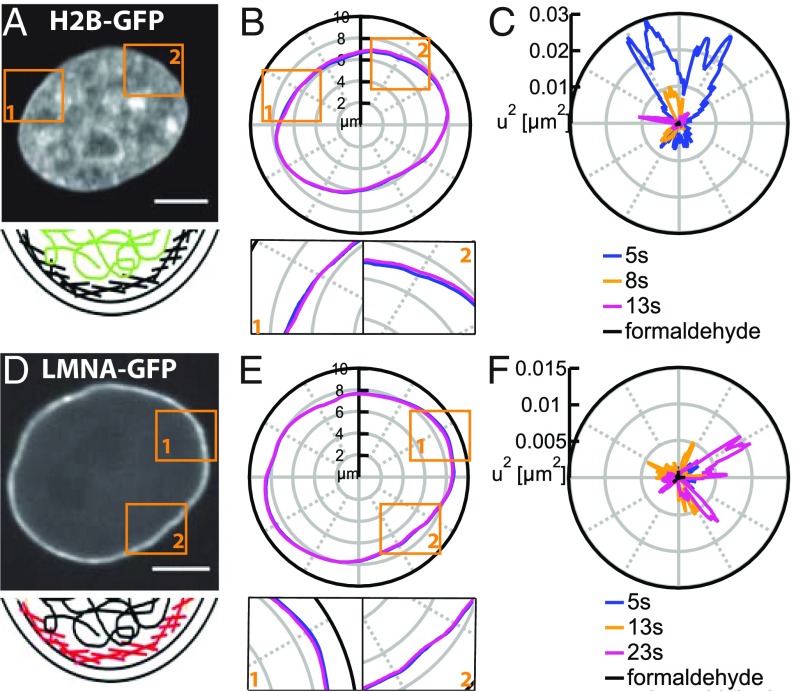
In this work, we study the flickering of the cell nucleus, i.e., nuclear shape fluctuations at short time scales of tens of seconds with temporal resolution of 250 ms. We monitor dynamics of both chromatin and nuclear envelope (NE) in live human cells. Using spinning disk confocal microscopy (Materials and Methods), we recorded high-resolution streams of live cells and studied the shape fluctuations for both the chromatin globule surface (CGS) visualized by GFP-tagged histone H2B (H2B-GFP) and the NE visualized by GFP-tagged lamin A (LMNA-GFP) (Fig. 1).
Fig. 1.
In vivo measurements of shape fluctuations of CGS and NE. (A) A micrograph of cell nucleus expressing H2B-GFP and schematics of the localization of chromatin (green) relative to the NE (black). (B) Contours of CGS at = 5 and 13 s. Insets 1 and 2 present a zoomed in view. (C) Fluctuations of CGS at = 5, 8, and 13 s and for nucleus fixed with formaldehyde (black dot at the origin) demonstrating that our measurements are well above the noise floor. (D) A micrograph of cell nucleus expressing LMNA-GFP and schematics of the localization of lamins (red) relative to chromatin (black) and two lipid bilayers (black) comprising the NE. (E) Contours of the NE at = 5 and 23 s. Insets 1 and 2 present a zoomed in view. (F) The of NE at = 5, 13, and 23 s. (Scale bar, 5 μm.)
Results and Discussion
In Vivo Measurements of Nuclear Shape Fluctuations.
To measure the shape fluctuations of CGS and NE as a function of time, we detected the contours of CGS (Fig. 1B) and NE (Fig. 1E) in every frame of the streams (Materials and Methods) and analyzed their dynamics. As shown in Fig. 1 B and E, Insets, the contours exhibit pronounced local shape fluctuations in time with amplitudes of 100 nm to 200 nm in both directions (Fig. S1). We calculated , which is the deviation of the instantaneous contour from the average contour , by at different times . To focus on the amplitude of both inward and outward fluctuations, we computed for CGS and NE, respectively. Fig. 1 C and F shows for CGS and NE at three different time points, demonstrating their dynamic behavior. As a negative control, we measured for cells fixed in formaldehyde and found the shape fluctuations to be eliminated (Fig. 1 C and F), showing that our measurements are well above the noise floor.
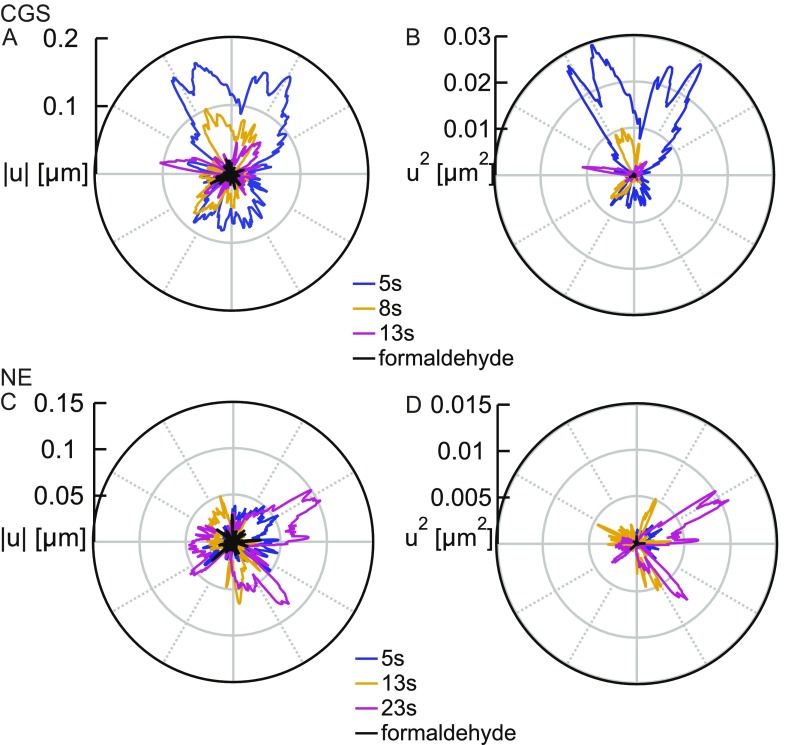
Fig. S1.
In vivo measurements of the shape fluctuations of the CGS and NE. (A) Fluctuations calculated for the contours of CGS from Fig. 1B at = 5, 8, and 13 s. (B) Fluctuations calculated for the contours of CGS from Fig. 1B at = 5, 8, and 13 s. (C) Fluctuations calculated for the NE contours from Fig. 1E at = 5, 13, and 23 s. (D) Fluctuations calculated for the NE contours from Fig. 1E at = 5, 13, and 23 s. In addition, in A–D, we plot and for samples fixed with formaldehyde (black), demonstrating that our measurements are well above the noise floor.
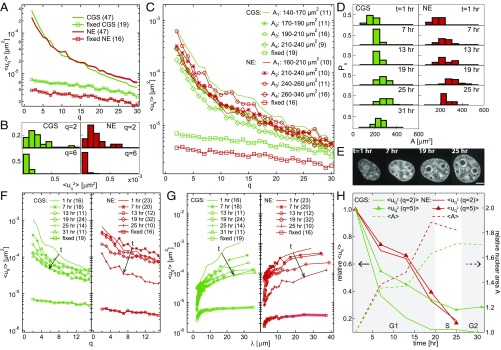
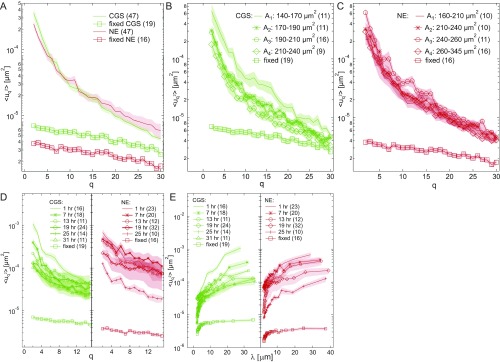
Further, to determine the wavenumber-dependent shape fluctuations of the CGS and NE, we performed the Fourier transformation of at every time following and calculated the mean-square amplitude as described in ref. 7 (SI Materials and Methods). We computed as a function of modal wavenumber for both CGS and NE. Fig. 2A shows averaged over 47 nuclei for both CGS and NE, which are similar in their amplitude and dependence (Fig. S2). As a negative control, we carried out the same calculation for cells fixed in formaldehyde (Fig. 2A), which shows elimination of shape fluctuations upon fixation.
Fig. 2.
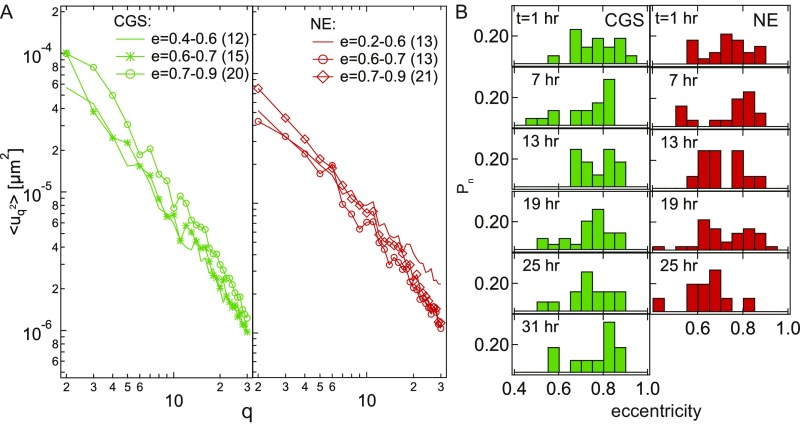
Shape fluctuations of CGS and NE are cell cycle-dependent. (A) Wavenumber-dependent fluctuations for CGS (H2B-GFP, green line, n = 47) and NE (LMNA-GFP, red line, n = 47). As a negative control, we calculated for both CGS (green square markers, n = 19) and NE (red square markers, n = 16) after fixing with formaldehyde. (B) Histograms of for CGS and NE, at = 2 and 6, respectively. (C) The of CGS and NE calculated separately for four groups based on their nuclear area for CGS (green) and NE (red); for CGS decreases with the increasing . (D) Histograms of nuclear area measured for a synchronized cell population at = 1, 7, 13, 19, 25, and 31 h after metaphase. The nuclear size increases for both CGS and NE with the progressing cell cycle. (E) Micrographs of the same nucleus at four different times, showing its size increase during the cell cycle. (Scale bar, 5 μm.) (F) The of CGS (green) and NE (red) measured at different times during the cell cycle; for both CGS and NE exhibits a monotonous decrease with increasing time (highlighted by the black arrow) with value less than 0.05 for = 1, 13, 25, and 31 h. (G) of CGS (green) and NE (red) from F plotted as a function of wavelength , where is the contour length. (H) Relative , i.e., at different times normalized by at = 1 h, for = 2 and 5, for CGS (green) and NE (red) decreases during G1, S, and G2 (timing from ref. 18), while the relative nuclear area , i.e., the nuclear area at different times normalized by the nuclear area at = 1 h, increases. Error bars for A, C, and F–G are shown in Fig. S2.
Fig. S2.
Shape fluctuations of CGS and NE are cell cycle-dependent. (A) Wavenumber-dependent fluctuations with error bars (SE) calculated for CGS (H2B-GFP, green solid line, n = 47) and NE (LMNA-GFP, red solid line, n = 47). (B) The of CGS calculated with error bars (SE) for four groups determined based on their measured nuclear area . (C) The of NE calculated with error bars (SE) for four groups determined based on their measured nuclear area . (D) Wavenumber-dependent fluctuations with error bars (SE) of CGS (green) and NE (red) measured at different times during the cell cycle; for both CGS and NE exhibits a monotonous decrease with increasing time during the cell cycle. (E) Wavenumber-dependent fluctuations as a function of wavelength with error bars (SE) of CGS (green) and NE (red) measured at different times during the cell cycle.
To gain insight into the population average from Fig. 2A, we reviewed the distribution at every separately. Fig. 2B shows examples of histograms for at and for both CGS and NE. We found the distributions to have quite complex shapes for both CGS and NE, suggesting a presence of more than one contributing population. For example, at for NE shows two modes, one at low and one at high . A careful inspection of the distributions revealed that different modes correspond to different sizes of the cell nuclei. To further explore this finding, we sorted the nuclei by their area into four groups (with n being the number of nuclei in the group) for CGS— = 140 m2 to 170 m2 (n = 11), = 170 m2 to 190 m2 (n = 11), = 190 m2 to 210 m2 (n = 16), and = 210 m2 to 240 m2 (n = 9)—and for NE— = 160 m2 to 210 m2 (n = 10), = 210 m2 to 240 m2 (n = 10), = 240 m2 to 260 m2 (n = 11), and = 260 m2 to 345 m2 (n = 16). Fig. 2C shows the average for all four groups for CGS (green) and NE (red). Remarkably, there was a clear decrease of with increasing nuclear size, while we found no correlation with the nuclear shape (Fig. S3). Thus, we hypothesized that, since the nuclear size is known to be cell cycle-dependent (1, 2), the is cell cycle-dependent.
Fig. S3.
Influence of average nuclear shape on the nuclear shape fluctuations. (A) Wavenumber-dependent nuclear fluctuations for nuclei of different eccentricity for both CGS and NE. (B) Histograms of nuclear eccentricity for CGS (green) and NE (red) measured at = 1, 7, 13, 19, 25, and 31 h after the metaphase. We find no correlation between the overall nuclear shape (described by eccentricity) and .
Nuclear Shape Fluctuations During Cell Cycle.
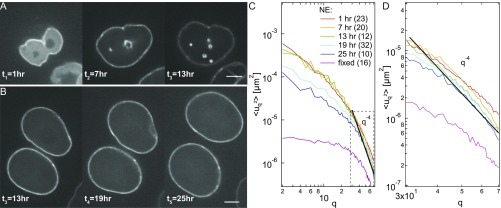
To test our hypothesis, we obtained as a function of cell cycle progression. We synchronized both HeLa H2B-GFP and HeLa LMNA-GFP cells (Materials and Methods) and measured as well as nuclear size for 31 h, where h corresponds to metaphase. We collected data at six time points: , and 31 h. Fig. 2D presents histograms of nuclear area for CGS and NE for different time points in the cell cycle, which clearly show the increase in the nuclear size with cell cycle progression. Fig. 2E presents four micrographs of the same HeLa H2B-GFP nucleus at four different time points, showing the monotonic increase in the size of the cell nucleus (corresponding data for HeLa LMNA-GFP are shown in Fig. S4). In addition, after we computed for the six time points, we found that clearly decreases with progressing cell cycle (Fig. 2 F and G), which is consistent with our original hypothesis. To quantify this phenomenon, we normalized at every time point by at , for = 2 and 5, for both CGS and NE. Fig. 2H shows a more than fivefold reduction of relative during the cell cycle for both CGS and NE, while the relative nuclear area , i.e., at different times normalized by at , shows almost a twofold increase, with the biggest changes found in G1 phase. Thus, strikingly, measuring allows us to determine the cell cycle stage in live cells. Using as a cell cycle stage reporter is noninvasive and requires only one fluorescent tag (labeling either NE or CGS).
Fig. S4.
Nuclear size increases with the cell cycle. (A) Micrographs of the same nucleus expressing LMNA-GFP taken at three different times during the cell cycle: = 1, 7, and 13 h (where t = 0 h corresponds to the metaphase), showing a monotonous increase in the nuclear size with progressing cell cycle. (B) Micrographs of two cell nuclei expressing LMNA-GFP taken at three different times during cell cycle: = 13, 19, and 25 h. (C) Wavenumber-dependent fluctuations of NE measured at different times during the cell cycle: = 1, 7, 13, 19, and 25 h. A black solid line, , indicates that follows this type of behavior at large values. (D) Inset from C shows that the part of spectra that follows the behavior decreases with time, suggesting stiffening of the NE. (Scale bar, 5 μm.)
The pronounced decrease of with the progress of cell cycle may be due to two main reasons: change of NE material properties (e.g., increase in its stiffness) or reduction of the forces driving the shape fluctuations. The former is consistent with our and others’ observations of gradual deposition of lamin A into NE over hours after mitosis, which would make NE stiffer (Fig. S4 and ref. 28). This is supported by an observed cell cycle-dependent decrease of at high , the part of the spectra that follows (Fig. S4), which would be expected from Helfrich theory for bending rigidity dominated thermal fluctuations (29). Furthermore, the forces driving the nuclear shape fluctuations might very well change with the cell cycle.
Coupling of CGS and NE Shape Fluctuations.
Similar dynamic behavior of CGS and NE as evidenced by suggests that CGS and NE are dynamically closely related, possibly coupled. To investigate how the dynamics of CGS and NE are related, we visualize the shape fluctuations of CGS and NE simultaneously by transfecting HeLa LMNA-GFP cells with H2B-mCherry (Fig. 3A and Materials and Methods). We evaluated the extent of fluctuations by calculating the ratio determined by counting the fluctuation sites , where or , along the contour and normalized by the length of the contour (i.e., total number of sites ); and are the shape fluctuations of CGS and NE, respectively. We find that, at a given time, two thirds of the contour exhibits shape fluctuations. We measured the duration of the fluctuation events and found two types of events: < 1 s and s to 5 s. Further, we computed the rate of the fluctuation activity for a fluctuation site to be, on average, , which we calculated as the time a fluctuation site is fluctuating per unit time, where is the length of the measurement (Fig. S5).
Fig. 3.
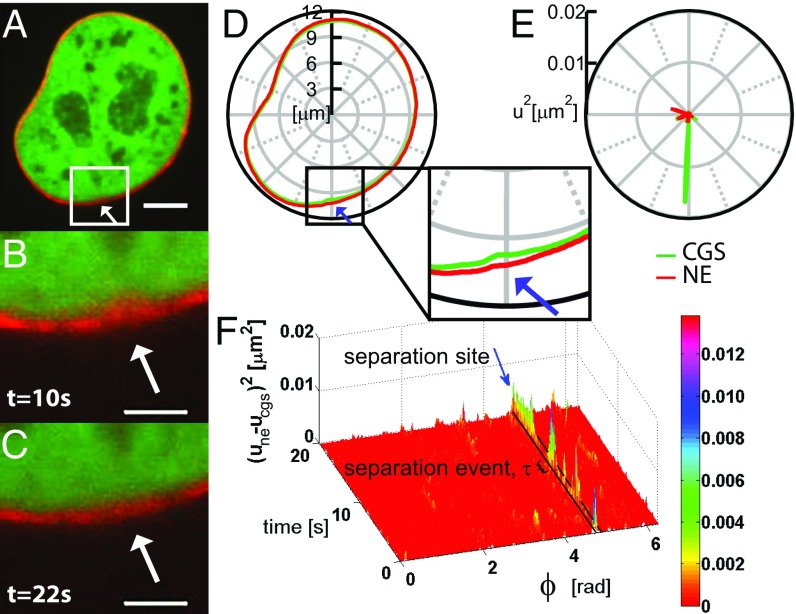
Simultaneous measurements of shape fluctuations of CGS and NE. (A) A micrograph of a nucleus expressing both H2B-mCherry (green) and LMNA-GFP (red) obtained using simultaneous two-color confocal microscopy. (B) Inset from A showing a site of local separation (highlighted by white arrow) of CGS and NE at = 10 s, which disappears by (C) time = 22 s. (D) Concurrent contours of CGS (H2B-mCherry) and NE (LMNA-GFP) obtained from A. (Inset) The region from B and C where CGS and NE locally separate (highlighted by blue arrow). (E) Fluctuations for the contours of CGS and NE from D. (F) Visualization of the separation sites of CGS and NE, by plotting as a function of polar angle and time ; and are the deviations of the NE and CGS contours from their respective average contours. The black box highlighted by blue arrow demarks the temporal evolution of the separation site from D. The black bracket shows one separation event of duration . [Scale bar, (A) 5 μm; (B and C) 2 μm.]
Fig. S5.
Analysis of fluctuation sites upon different perturbations. (A) Histogram of ratio of fluctuation sites for each condition. Ratio of fluctuation sites was determined by counting the sites with fluctuation () along the nuclear contour and normalized by its length. Green bars represent the fluctuations for CGS, where , and red bars represent the fluctuations for NE, where . (B) Histograms of fluctuation rate at each condition. The rate of a fluctuation site was calculated by counting the time points with fluctuations at that fluctuation site and normalized by the length of measurement (20 s). (C) Histogram of fluctuation duration for every condition; shows the region of short duration, and shows the region of long duration. (D) Histogram of ratio of separation sites for each condition. Ratio of separation sites was determined by counting the sites with separation along the nuclear contour and normalized by its length. (E) Histogram of the fraction of separation sites distribution calculated by normalizing data from D by the average value of obtained from A for each condition. (F) Histogram of separation rate at each condition. The rate of a separation site was calculated by counting the time points with separation at that separation site and normalized by the length of measurement (20 s). (G) Histogram of separation duration for every condition; shows the region of short duration, and shows the region of long duration. Green bars represent for , and red bars represent the for .
We found that, while CGS and NE typically fluctuate in phase, they do exhibit sites where they move out of phase, which we termed “separation sites.” Fig. 3 B and C shows an example of a separation site, which occurred at s, but is no longer present at s. The separation sites can be detected by comparing the simultaneous contours of CGS and NE (Fig. 3D, highlighted by blue arrow) as well as in the shape fluctuation amplitudes (Fig. 3E).
To analyze the extent and the temporal evolution of a separation site, we evaluated relative shape fluctuations of CGS and NE with respect to each other, which we defined as . Fig. 3F shows a plot of as a function of time and polar angle , which visualizes the temporal evolution of separation sites along the nuclear contour . The plot shows only the above the noise floor, which was determined by measurements in fixed cells. The separation sites undergo spurts of separation, which we named “separation events” and characterized by their duration time . The separation site in Fig. 3F shows several separation events of variable duration s to 5 s.
We evaluated two types of separation ratios, and , determined by counting the number of separation sites along the contour and normalized by and , respectively. We find that, at any given time, approximately 20% of the CGS and NE can fluctuate out of phase, as evidenced by , which corresponds to 30% of the fluctuation sites, as evidenced by . The rate of separation activity was found to be about 0.07, which we calculated as the time a separation site is actually separated ( above the noise floor) per unit time.
Origin of Nuclear Shape Fluctuations.
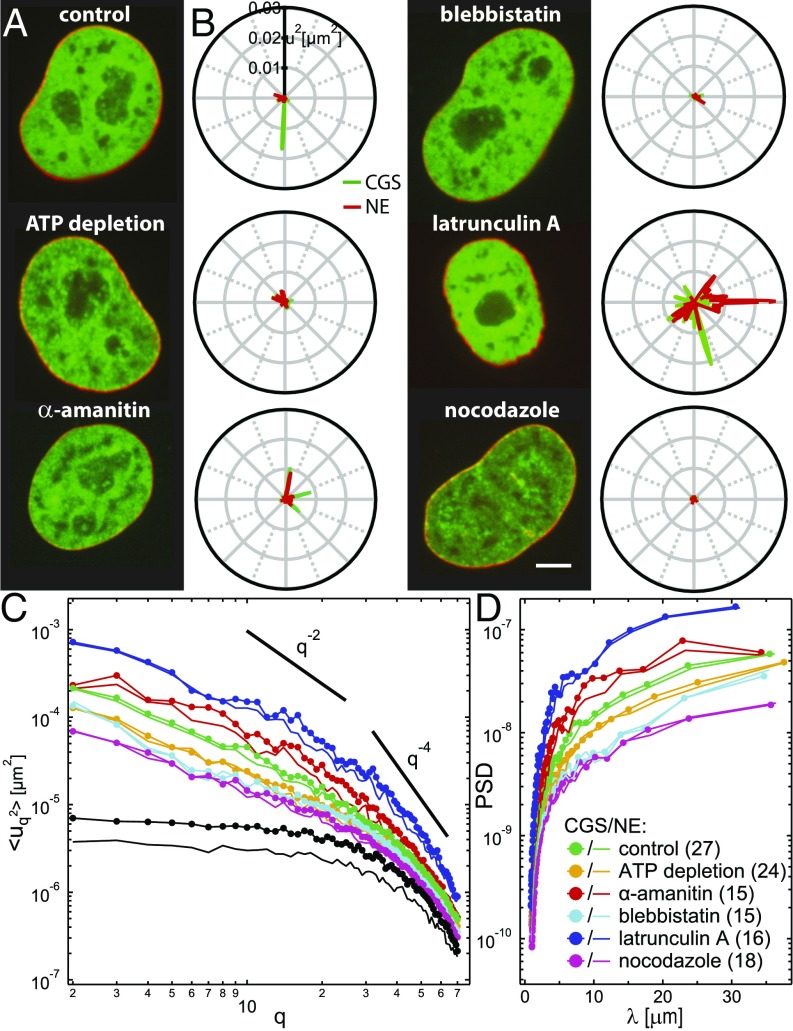
To elucidate the origin of the shape fluctuations of CGS and NE, we used biochemical perturbations (Fig. 4). Specifically, to determine whether the observed dynamics of CGS and NE are actively driven, we depleted ATP (Materials and Methods). We found that both (Fig. 4B) and (Fig. 4C) were strongly reduced (n = 24), confirming that active processes indeed contribute to nuclear shape fluctuations. Furthermore, we explored the involvement of the cytoskeleton in the CGS and NE dynamics by measuring the shape fluctuations of CGS and NE upon inhibition of microtubule polymerization by nocodazole (n = 18), actin polymerization by latrunculin A (n = 16), and myosin II activity by blebbistatin (n = 15). We found that both (Fig. 4B) and (Fig. 4C) decrease upon nocodazole and blebbistatin treatment, while they increase upon latrunculin A treatment, implicating cytoskeletal activity. Finally, we probed the involvement of the chromatin by measuring the shape fluctuations of CGS and NE upon inhibition of the polymerase II transcriptional activity by -amanitin (n = 15), which led to an increase in (Fig. 4B) and (Fig. 4C), implying chromatin’s participation. When compared against known dependencies for thermally driven systems, dominated by bending rigidity () and lateral tension () (29), shows new dependencies, which might be characteristic of nonequilibrium processes in our system.
Fig. 4.
Simultaneous measurements of shape fluctuations of CGS and NE upon biochemical perturbations. (A) Micrographs of cell nuclei expressing both H2B-mCherry (green) and LMNA-GFP (red) under the following conditions: control, after ATP depletion, and upon addition of -amanitin, blebbistatin, latrunculin A, and nocodazole. (B) Fluctuations of CGS (green) and NE (red) for each condition from A at one time point. Average and instantaneous contours for CGS and NE are shown in Fig. S6. (C) Wavenumber-dependent under the following conditions: control (n = 27), ATP depletion (n = 24), -amanitin (n = 15), blebbistatin (n = 15), latrunculin A (n = 16), and nocodazole (n = 18) treatment. Black curves represent negative control by fixation with formaldehyde for CGS (markers) and NE (no markers). Solid black lines illustrate slopes and . Error bars are shown in Fig. S6. (D) PSD of as a function of wavelength upon different perturbations. (Scale bar, 5 μm.)
To determine the dynamic contributions that became eliminated upon different perturbations, we computed the power spectral density (PSD) as a function of wavelength , where is the contour length (Fig. 4D). Inspection of PSD revealed that, for < 1.5 m, PSD remained unchanged after ATP depletion, nocodazole, blebbistatin, and -amanitin treatment, suggesting that these fluctuations are mostly thermally driven. This supports our finding that cell cycle-dependent decrease of at high is due to the NE stiffening, as this part of the spectra is dominated by thermal fluctuations and follows (Fig. S4 and ref. 29). For > 1.5 m, we found PSD reduced after ATP depletion, nocodazole, and blebbistatin treatment, while it increased after -amanitin treatment, suggesting that these fluctuations are actively driven, and thus sensitive to perturbations of involved activities. In contrast, PSD increased for all wavelengths after latrunculin A treatment. This is consistent with previous observations of dorsal actin cables, which were shown to hold the nucleus in place, while deforming it to its characteristic ellipsoid shape (30, 31). Hence, upon depolymerization of actin, the nucleus becomes more spherical and visibly softer (Fig. 5A).
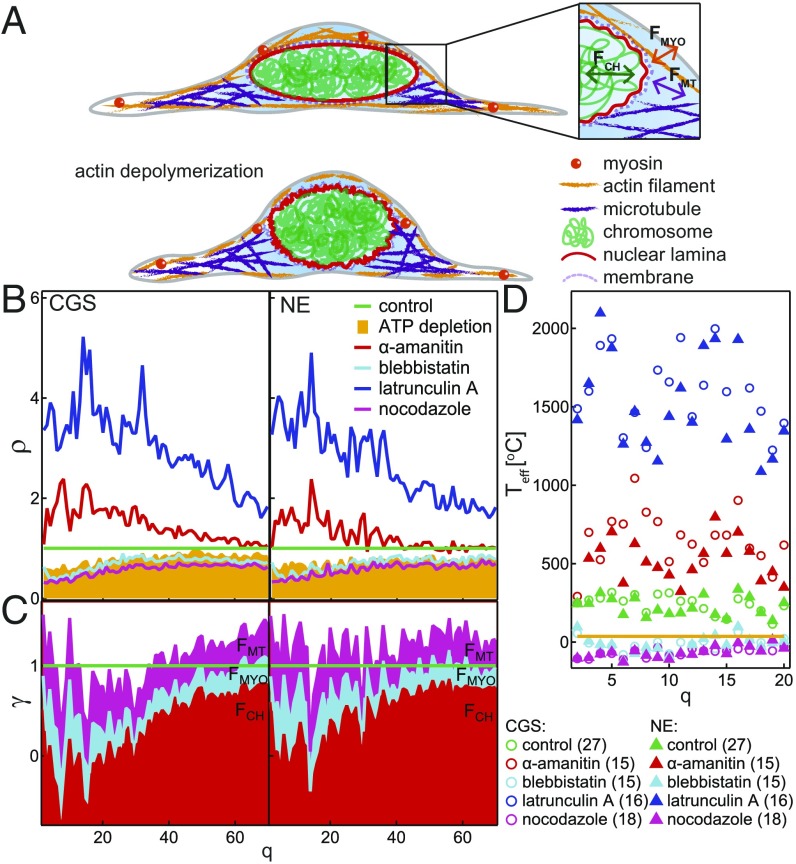
Fig. 5.
Active and passive dynamics of CGS and NE. (A) Cartoon of a control cell (Top) and after actin depolymerization (Bottom). Inset illustrates the fluctuations of the NE caused by chromatin, , microtubules, , and myosin II, . (B) The ratio shows the changes in fluctuations of CGS and NE upon different perturbations. (C) Cumulative plot of the passive contribution (baseline ) and relative active contributions of chromatin, microtubules, and myosin II amounts to 1. (D) for different perturbations.
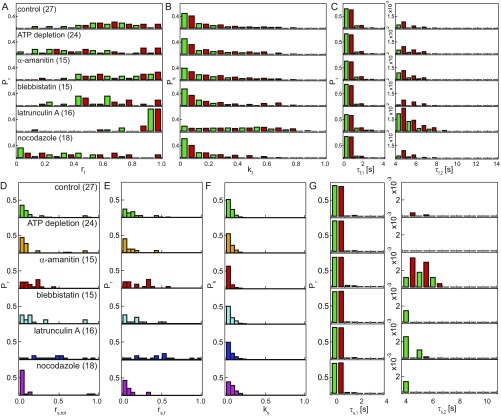
To gain insight into the molecular mechanism behind the shape fluctuations of CGS and NE, we analyzed the dynamic behavior of both fluctuation sites and separation sites upon all biochemical perturbations (Figs. S5–S7). A summary of and measured for all perturbations is provided in Table S1; here we review our main findings. We find that the fluctuations are driven both actively and passively, evidenced by a decrease in both and the number of fluctuation sites along the contour after ATP depletion. Furthermore, and the number of fluctuation sites along the contour decrease after blebbistatin and nocodazole treatment, respectively, suggesting that both microtubules and myosin II activity contribute to shape fluctuations. Conversely, we see an increase in both and the number of fluctuation sites, upon inhibiting transcriptional activity by -amanitin, implying chromatin’s involvement in shape fluctuations. In addition, while the amplitude of the fluctuations changes upon the perturbations as described above, inward and outward fluctuations remain equally likely. Based on these observations, we speculate that, while both cytoskeleton and chromatin are involved in driving the nuclear shape fluctuations, they might have opposing effects, with cytoskeleton acting as an amplifier and chromatin acting as a damper.
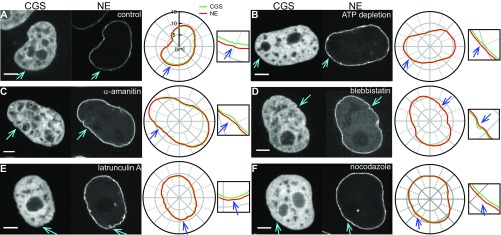
Fig. S7.
Example of separation sites exhibited upon different biochemical perturbations. Specifically, micrographs and instantaneous contours for CGS and NE are shown for (A) control, (B) after ATP depletion, and upon treatment with (C) -amanitin, (D) blebbistatin, (E) latrunculin A, and (F) nocodazole. The separation sites are highlighted by blue arrows in the CGS and NE images and contours. (Scale bar, 5 μm.)
Table S1.
Summary of fluctuation characteristics upon biochemical perturbations
| Condition | * | † | |||||||||
| Control | 0.66 0.04 | 0.22 0.04 | <1 s | 5 s | 0.18 0.05 | 0.28 0.08 | 0.07 0.02 | <1 s | — | 5 s | |
| ATP depletion | Decrease | 0.53 0.06 | 0.23 0.04 | <1 s | 5 s | 0.16 0.05 | 0.30 0.10 | 0.06 0.01 | <1 s | — | — |
| -Amanitin | Increase | 0.72 0.06 | 0.25 0.06 | <1 s | 5 s | 0.15 0.03 | 0.21 0.05 | 0.09 0.04 | <1 s | 6 s | 6 s |
| Blebbistatin | Decrease | 0.61 0.05 | 0.21 0.01 | <1 s | 5 s | 0.20 0.07 | 0.33 0.11 | 0.08 0.02 | <1 s | 5 s | — |
| Latrunculin A | Increase | 0.92 0.04 | 0.41 0.06 | <1 s | 6 s | 0.39 0.06 | 0.43 0.07 | 0.09 0.03 | <1 s | 5 s | — |
| Nocodazole | Decrease | 0.38 0.07 | 0.17 0.04 | <1 s | 5 s | 0.13 0.07 | 0.33 0.19 | 0.08 0.02 | <1 s | 5 s | — |
Ratio of the number of separation sites to the length of contour.
Ratio of the number of separation sites to the number of fluctuating sites.
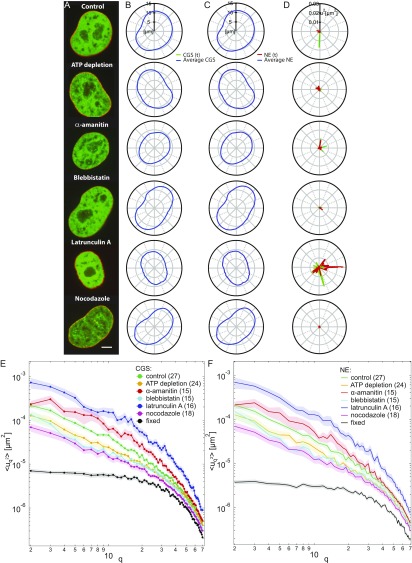
Fig. S6.
Simultaneous measurements of shape fluctuations of CGS and NE upon biochemical perturbations. (A) Micrographs of cell nuclei simultaneously expressing H2B-mCherry (green) and LMNA-GFP (red) depicting nuclear phenotypes under the following conditions: control, after ATP depletion, and upon addition of -amanitin, blebbistatin, latrunculin A, and nocodazole. (B) Average contour of CGS and instantaneous contour of CGS (H2B-GFP) at one time point for each perturbation. (C) Average contour of NE and instantaneous contour of NE (LMNA-GFP) at one time point for each perturbation. (D) Fluctuations of CGS (green) and NE (red) calculated for each condition at one time point; is strongly reduced upon ATP depletion as well as blebbistatin and nocodazole treatment, and increases upon addition of latrunculin A. (E) The for CGS plotted with error bars (SE). (F) The for NE plotted with error bars (SE).
This hypothesis is supported by the evidence that the number of separation sites of CGS and NE increases after ATP depletion, blebbistatin, and nocodazole treatment. In other words, when active fluctuations or cytoskeleton activity are suppressed, NE and CGS tend to move out of phase. In contrast, the number of separation sites decreases upon -amanitin treatment. This is consistent with previous observations of chromatin decondensation upon -amanitin treatment (32), effectively increasing the osmotic pressure inside the nucleus, which could lead to more in-phase movement of CGS and NE.
Interestingly, while the number of separation sites changes upon ATP depletion, as well as cytoskeletal and chromatin perturbations, the activity of a separation site remains unchanged under all of these conditions, suggesting that NE is a passive shell sandwiched between two active materials. This is further corroborated by our observation of two different types of activity of the separation sites: short events (<1 s) present under all conditions, including ATP depletion, suggesting these are thermally driven, and long events (>4 s), which are active, i.e., eliminated upon ATP depletion, reduced upon blocking cytoskeletal activity, and enhanced upon blocking the transcriptional activity of chromatin.
Active vs. Passive Fluctuations.
Our experiments demonstrate that nuclear shape fluctuations are both thermally and actively driven. The passive thermal fluctuations are visible after ATP depletion, when we find to be reduced by 50%. As evidenced by (Table S1), under physiological conditions, about 65% of the contour fluctuates, while it decreases to about 50% upon ATP depletion. These fluctuations are passive, with about one third having NE and CGS fluctuating out of phase (, Table S1).
From our observations, we can estimate the contribution of active vs. passive dynamics. First, the ratio of the fluctuations after a perturbation and the control sample provides a measure of the change in the shape fluctuations of CGS and NE with respect to those under physiological conditions (Fig. 5B). For latrunculin A, we find a large increase in , which refers to the flickering of the NE after the actin filament depolymerization. In this situation, the nucleus is not under the pressure of dorsal actin cables (30, 31), and thus the observed fluctuations might be informative of its true bending rigidity (Fig. 5A). After ATP depletion, we find reduced to about 40% at low and to about 50% at high , suggesting that up to one half of the observed dynamics is of thermal origin, i.e., passive. Computing for -amanitin, nocodazole, and blebbistatine, we find an estimate for dynamic contributions of chromatin, microtubules, and myosin II, respectively (Fig. 5B). To better visualize these estimates, we calculate their relative contributions and plot them cumulatively in Fig. 5C. The cumulative adds up to 1, confirming that we identified the major molecular players in the nuclear shape fluctuations. The ratio of their contributions might change during the cell cycle as their activity changes.
Another way to evaluate active fluctuations is to compute the effective temperature that our system would have, if in equilibrium (33). While this assumption is not correct, it allows us to assess how our system deviates from thermal equilibrium. Provided the excitations of active and passive fluctuations are driven independently, then can be expressed as a sum of active and passive fluctuations and (33). We find that, under physiological conditions C, while it increases to ∼500 °C upon inhibiting transcription and falls to 0 °C upon inhibition of microtubule polymerization and myosin II (Fig. 5D). Once the actin depolymerizes, both CGS and NE fluctuations are very high, with Teff≈1,000 °C to 2,000 °C. As a comparison, in red blood cells, was found to be about 3,000 °C at low (33, 34).
SI Materials and Methods
Contour Detection.
To detect a nuclear contour, we used a custom-written MatLab (The MathWorks) code. The contours were detected by watershed method. Since the images of CGS (H2B-GFP) and NE (LMNA-GFP) have two local minima, inside and outside the nucleus, for each image, we need to create a mask to implement watershed on these two regions. To create a mask, a preliminary edge was required and was determined via finding the local maximum of the gradient of the image. The preliminary edge was dilated to get the mask for outside the nucleus and was eroded to get the mask for inside the nucleus. These two masks were added to get the final mask for watershed. To obtain the contour, we needed to take the gradient of the original image, impose the mask on it, and apply watershed on the masked gradient. The contour was converted to binary image for the following analysis. The precision of this detection was estimated to be 20 nm.
Analysis of Contour Shape Fluctuations.
The following analysis was described in detail in ref. 7. After having determined the and coordinates of the contour in every frame (i.e., time point ) as described in Contour Detection, the center of mass of the contour was determined according to
where is the number of pixels in the contour. Further, we use the center of mass as an origin to describe the contour by polar coordinates . We divided the contour line equally into segments and calculated the average lying within each segment, thus obtaining 512 equidistant points. The noise was smoothed out by averaging over the values of lying within segments of to get a new set of 512 points. To provide a measure of the shape fluctuations of the contour, we calculated , which is the deviation of the instantaneous contour from the average contour , by at different time points .
Further, we performed the Fourier transformation of the using a Fast Fourier Transform procedure at every time following The Fourier transformation yields complex Fourier coefficients, , where runs from −255 to +255. Since the excitation modes are statistically independent, the time average of the contour is determined by averaging over the Fourier coefficients for M contours, Thus, a mean square amplitude of mode is given by
The PSD was calculated by , where is the Fourier coefficient at each q, and is the contour length of the nucleus.
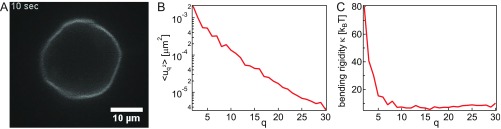
To test our analysis code, we computed for a vesicle (Fig. S8), which was analyzed and data provided in ref. 41, and we calculated the bending rigidity of the vesicle to be about 7 , where is the Boltzmann constant and is the temperature. This is in agreement with previous calculations, which obtain from 5 kBT to 30 (41, 42).
Fig. S8.
Control measurement of the contour fluctuations. (A) Image of the vesicle from ref. 41, which we used to test the correctness of our contour detection and fluctuation calculation algorithms (movie can be found in ref. 41). Adapted with permission from Loftus et al., Langmuir 29: 14588–14594, 2013. Copyright 2013 American Chemical Society. (B) Wavenumber-dependent fluctuations , which we measured for the vesicle from A. (C) Bending rigidity calculated for the vesicle from A.
Conclusions
Our findings reveal that NE flickers, i.e., undulates at time scales of seconds, with active undulations driven by both chromatin and cytoskeleton. The amplitude of these undulations provides us with an internal cell cycle stage indicator. The possible role of such undulations is yet to be revealed. Considering the complex structure of the NE, specifically its dense coverage with nuclear pores (five to seven pores per square micrometer) (35), we speculate that such undulations might aid nuclear transport. In fact, it has been shown previously that oscillating a membrane enhances flux through its pores (36, 37). Such undulations could facilitate a more effective stirring of the molecules in the NE vicinity, and thus their faster binding to importins/exportins. Also, the NE undulations could influence flows into and out of the cell nucleus and accelerate otherwise diffusion limited processes. Such flows, in turn, would lead to the transport of material that may cause osmotic pressure (and even Donnan potential) fluctuations across the NE. Such fluctuations are not considered in current models of nuclear transport (38–40).
Materials and Methods
Cell Culture and Cell Transfection.
HeLa cells (CCL-2) were cultured according to American Type Culture Collection (ATCC) recommendations. The stable HeLa LMNA-GFP and HeLa H2B-GFP cell lines were a gift from Tim Mitchison and James Orth, Harvard Medical School, Boston. Cells were cultured in a humidified, 5% CO2 (vol/vol) atmosphere at 37 °C in Gibco Dulbecco’s modified eagle medium supplemented with 10% FBS (vol/vol), 100 units per milliliter of penicillin, 100 mg/mL of streptomycin (Invitrogen), and 2.5 mg/mL of Plasmocin Prophylactic (Invivogen). Before the experiment, cells were plated on 35-mm MatTek dishes with glass bottom no. 1.5 (MatTek) for 24 h, and the medium was then replaced by Gibco CO2-independent medium supplemented with L-glutamine (Invitrogen). Cells were then mounted on the microscope stage kept in a custom-built 37 °C microscope incubator enclosure with 5% CO2 (vol/vol) delivery during the entire experiment. When specified, cells were synchronized using 10 M RO-3306 (ALEXIS), which arrests cells at the G2/M checkpoint of the cell cycle, and were released, 1 h before imaging, by washing with CO2-independent medium supplemented with L-glutamine. For fixation experiments, cells were fixed with 3.7% formaldehyde in PBS at room temperature for 20 min and then washed three times with PBS every 5 min. Coverslips were mounted on the glass microscope slides, using Prolong-Diamond antifade reagent (Invitrogen). HeLa cells expressing LMNA-GFP and H2B-mCherry were prepared by transient transfection of the stable HeLa LMNA-GFP cell line with H2B-mCherry plasmid using Lipofectamine 2000 (Invitrogen) following the manufacturer’s protocol.
Biochemical Perturbations.
To deplete ATP, cells were treated, 2 h before imaging, with 6 mM 2-deoxyglucose and 1 M trifluoromethoxy-carbonylcyanide phenylhydrazone dissolved in CO2-independent medium supplemented with L-glutamine. For cytoskeletal perturbations, 10 M latrunculin A, 10 M blebbistatin, or 10 M nocodazole, and, for chromatin perturbations, 20 g/mL -amanitin, in CO2-independent medium supplemented with L-glutamine, were added to cells 30 min before imaging. All chemicals are from Sigma-Aldrich.
Microscopy and Image Acquisition.
Images were taken with a Yokogawa CSU-X1 spinning-disk confocal head with an internal motorized high-speed emission filter wheel and Spectral Applied Research Borealis modification for increased light throughput and illumination homogeneity on a Nikon Ti-E inverted microscope equipped with a 100 Plan Apo NA 1.4 objective lens and the Perfect Focus System. The microscope was mounted on a vibration-isolation air table. LMNA-GFP and H2B-GFP fluorescence were excited by a 488-nm solid-state laser (controlled with an acousto-optic tunable filter) and collected with a 405/488/561/640 multiband-pass dichroic mirror (Semrock) and an ET525/50 emission filter (Chroma Technology). To image GFP and mCherry at the same time, we illuminated the sample simultaneously with two excitation wavelengths, 488 and 561 nm, produced by two distinct monochromatic solid-state lasers. The emission was separated by the W-View Gemini Image Splitter (Hamamatsu) using GFP/mCherry dichroic mirror (Chroma Technology), and further passed through an ET525/30 and an ET630/75m emission filter (Chroma Technology). The two fluorescent signals were allocated to the two halves of the image sensor, producing two distinct images. Images were obtained with a Hamamatsu ORCA-R2 cooled CCD camera controlled with MetaMorph 7 (Molecular Devices) software. The pixel size for the 100 objective was 0.065 m. The observation duration was 25 s, with an exposure time of 250 ms. The streams of 16-bit images were saved as multi-tiff stacks. Images were converted to single-tiff images and analyzed in MatLab (The MathWorks). To detect a nuclear contour and analyze its shape fluctuations, we used a custom-written MatLab code (see SI Materials and Methods and Fig. S8).
Acknowledgments
This research was supported by the National Institutes of Health (Grant R00-GM104152).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1702226114/-/DCSupplemental.
References
- 1.Steen H, Lindmo T. Cellular and nuclear volume during the cell cycle of nihk 3025 cells. Cell Tissue Kinet. 1978;11:69–81. doi: 10.1111/j.1365-2184.1978.tb00876.x. [DOI] [PubMed] [Google Scholar]
- 2.Fidorra J, Mielke T, Booz J, Feinendegen L. Cellular and nuclear volume of human cells during the cell cycle. Radiat Environ Biophys. 1981;19:205–214. doi: 10.1007/BF01324188. [DOI] [PubMed] [Google Scholar]
- 3.Alberts B, et al. Molecular Biology of the Cell. Garland Sci; New York: 2014. [Google Scholar]
- 4.Talwar S, Kumar A, Rao M, Menon G, Shivashankar G. Correlated spatio-temporal fluctuations in chromatin compaction states characterize stem cells. Biophys J. 2013;104:553–564. doi: 10.1016/j.bpj.2012.12.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Makhija E, Jokhun D, Shivashankar G. Nuclear deformability and telomere dynamics are regulated by cell geometric constraints. Proc Natl Acad Sci USA. 2015;13:E32–E40. doi: 10.1073/pnas.1513189113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brochard F, Lennon J. Frequency spectrum of the flicker phenomenon in erythrocytes. J Phys. 1975;36:1035–1047. [Google Scholar]
- 7.Duwe H, Sackmann E. Bending elasticity and thermal excitations of lipid bilayer vesicles: Modulation by solutes. Phys Stat Mech Appl. 1990;163:410–428. [Google Scholar]
- 8.Zidovska A, Sackmann E. Brownian motion of nucleated cell envelopes impedes adhesion. Phys Rev L. 2006;96:048103. doi: 10.1103/PhysRevLett.96.048103. [DOI] [PubMed] [Google Scholar]
- 9.Watson M. The nuclear envelope: Its structure and relation to cytoplasmic membranes. J Biophys Biochem Cytol. 1954;1:257–270. doi: 10.1083/jcb.1.3.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cohen A, Sundeen J. The nuclear fiburous lamina in human cells: Studies on its appearance and distribution. Anat Red. 1976;186:471–476. doi: 10.1002/ar.1091860402. [DOI] [PubMed] [Google Scholar]
- 11.Dahl K, Kahn S, Wilson K, Disher D. The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber. J Cell Sci. 2004;117:4779–4786. doi: 10.1242/jcs.01357. [DOI] [PubMed] [Google Scholar]
- 12.Lammerding J, et al. Lamins A and C but not lamin B1 regulate nuclear mechanics. J Biol Chem. 2006;281:25768–25780. doi: 10.1074/jbc.M513511200. [DOI] [PubMed] [Google Scholar]
- 13.Rowat A, Lammerding J, Ipsen J. Mechanical properties of the cell nucleus and the effect of emerin deficiency. Biophys J. 2006;91:4649–4664. doi: 10.1529/biophysj.106.086454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Davis L, Blobel G. Identification and characterization of a nuclear pore complex protein. Cell. 1986;45:699–709. doi: 10.1016/0092-8674(86)90784-1. [DOI] [PubMed] [Google Scholar]
- 15.Wente S, Rout M. The nuclear pore complex and nuclear transport. Cold Spring Harb Perspect Biol. 2010;2:a000562. doi: 10.1101/cshperspect.a000562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aaronson R, Blobel G. Isolation of nuclear pore complexes in association with a lamina. Proc Natl Acad Sci USA. 1974;72:1007–1011. doi: 10.1073/pnas.72.3.1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fowler P, et al. Membrane stiffness is modified by integral membrane proteins. Soft Matter. 2016;12:7792–7803. doi: 10.1039/c6sm01186a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McGarry TJ, Kirschner MW. Geminin, an inhibitor of DNA replication, is degraded during mitosis. Cell. 1998;93:1043–1053. doi: 10.1016/s0092-8674(00)81209-x. [DOI] [PubMed] [Google Scholar]
- 19.Wilson K, Foisner R. Lamin-binding proteins. Cold Spring Harb Perspect Biol. 2010;2:a000554. doi: 10.1101/cshperspect.a000554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Méjat A, Misteli T. LINC complexes in health and disease. Nucleus. 2010;1:40–52. doi: 10.4161/nucl.1.1.10530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schreiner S, Koo P, Zhao Y, Mochrie S, King M. The tethering of chromatin to the nuclear envelope supports nuclear mechanics. Nat Commun. 2014;6:7159. doi: 10.1038/ncomms8159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kind J, et al. Single-cell dynamics of genome-nuclear lamina interactions. Cell. 2013;153:178–192. doi: 10.1016/j.cell.2013.02.028. [DOI] [PubMed] [Google Scholar]
- 23.Kumaran R, Spector D. A genetic locus targeted to the nuclear periphery in living cells maintains its transcriptional competence. J Cell Biol. 2008;180:51–65. doi: 10.1083/jcb.200706060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Finlan L, et al. Recruitment to the nuclear periphery can alter expression of genes in human cells. PLoS Genet. 2008;4:e1000039. doi: 10.1371/journal.pgen.1000039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Reddy K, Zullo J, Bertolino E, Singh H. Transcriptional repression mediated by repositioning of genes to the nuclear lamina. Nature. 2008;452:243–247. doi: 10.1038/nature06727. [DOI] [PubMed] [Google Scholar]
- 26.Worman H, Ostlund C, Wang Y. Diseases of the nuclear envelope. Cold Spring Harb Perspect Biol. 2010;2:a000760. doi: 10.1101/cshperspect.a000760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Broers J, et al. Decreased mechanical stiffness in LMNA-/- cells is caused by defective nucleo-cytoskeletal integrity: Implications for the development of laminopathies. Hum Mol Genet. 2004;13:2567–2580. doi: 10.1093/hmg/ddh295. [DOI] [PubMed] [Google Scholar]
- 28.Moir R, Yoon M, Khuon S, Foldman R. Nuclear lamins A and B1: Different pathways of assembly during nuclear envelope formation in living cells. J Cell Biol. 2000;151:1155–1168. doi: 10.1083/jcb.151.6.1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Helfrich W. Steric interaction of fluid membranes in multilayer systems. Z Naturforsch A. 1978;33:305–315. [Google Scholar]
- 30.Khatau S, et al. A perinuclear actin cap regulates nuclear shape. Proc Natl Acad Sci USA. 2009;106:19017–19022. doi: 10.1073/pnas.0908686106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Burnette D, et al. A contractile and counterbalancing adhesion system controls the 3D shape of crawling cells. J Cell Biol. 2014;205:83–96. doi: 10.1083/jcb.201311104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zidovska A, Weitz D, Mitchison T. Micron-scale coherence in interphase chromatin dynamics. Proc Natl Acad Sci USA. 2013;110:15555–15560. doi: 10.1073/pnas.1220313110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gov N. Membrane undulations driven by force fluctuations of active proteins. Phys Rev L. 2004;93:268104. doi: 10.1103/PhysRevLett.93.268104. [DOI] [PubMed] [Google Scholar]
- 34.Rodríhuez-García R, et al. Direct cytoskeleton forces cause membrane softening in red blood cell. Biophys J. 2015;108:2794–2806. doi: 10.1016/j.bpj.2015.05.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Maeshima K, et al. Nuclear pore formation but not nuclear growth is governed by cyclin-dependent kinases (Cdks) during interphase. Nat Struct Mol Biol. 2010;17:1065–1072. doi: 10.1038/nsmb.1878. [DOI] [PubMed] [Google Scholar]
- 36.Gomaa H, Rao S. Analysis of flux enhancement at oscillating flat surface membranes. J Membr Sci. 2011;374:59–66. [Google Scholar]
- 37.Menais T, Mossa S, Buhot A. Polymer translocation through nano-pores in vibrating thin membranes. Sci Rep. 2016;6:38558. doi: 10.1038/srep38558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Milles S, et al. Plasticity of an ultrafast interaction between nucleoporins and nuclear transport receptors. Cell. 2015;163:734–745. doi: 10.1016/j.cell.2015.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Beck M, Hurt E. The nuclear pore complex: Understanding its function through structural insight. Nat Rev Mol Cell Biol. 2016;18:73–89. doi: 10.1038/nrm.2016.147. [DOI] [PubMed] [Google Scholar]
- 40.Raveh B, et al. Slide-and-exchange mechanism for rapid and selective transport through the nuclear pore complex. Proc Natl Acad Sci USA. 2016;113:E2489–E2497. doi: 10.1073/pnas.1522663113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Loftus AF, Noreng S, Hsieh VL, Parthasarathy R. Robust measurement of membrane bending moduli using light sheet fluorescence imaging of vesicle fluctuations. Langmuir. 2013;29:14588–14594. doi: 10.1021/la403837d. [DOI] [PubMed] [Google Scholar]
- 42.Lipowsky R. 1995. Generic interaction of flexible membranes, Structure and Dynamics of Membranes, Handbook of Biological Physics (Elsevier, AmsterdamVol 6, pp 521–602.