Quantitative Deformability Cytometry: Rapid, Calibrated Measurements of Cell Mechanical Properties

Abstract

Advances in methods that determine cell mechanical phenotype, or mechanotype, have demonstrated the utility of biophysical markers in clinical and research applications ranging from cancer diagnosis to stem cell enrichment. Here, we introduce quantitative deformability cytometry (q-DC), a method for rapid, calibrated, single-cell mechanotyping. We track changes in cell shape as cells deform into microfluidic constrictions, and we calibrate the mechanical stresses using gel beads. We observe that time-dependent strain follows power-law rheology, enabling single-cell measurements of apparent elastic modulus, E_a, and power-law exponent, β. To validate our method, we mechanotype human promyelocytic leukemia (HL-60) cells and thereby confirm q-DC measurements of E_a = 0.53 ± 0.04 kPa. We also demonstrate that q-DC is sensitive to pharmacological perturbations of the cytoskeleton as well as differences in the mechanotype of human breast cancer cell lines (E_a = 2.1 ± 0.1 and 0.80 ± 0.19 kPa for MCF-7 and MDA-MB-231 cells). To establish an operational framework for q-DC, we investigate the effects of applied stress and cell/pore-size ratio on mechanotype measurements. We show that E_a increases with applied stress, which is consistent with stress stiffening behavior of cells. We also find that E_a increases for larger cell/pore-size ratios, even when the same applied stress is maintained; these results indicate strain stiffening and/or dependence of mechanotype on deformation depth. Taken together, the calibrated measurements enabled by q-DC should advance applications of cell mechanotype in basic research and clinical settings.

Introduction

Eukaryotic cells are complex, viscoelastic materials that undergo changes in their mechanical phenotype, or mechanotype, during many physiological and disease processes. For example, pluripotent stem cells become more resistant to deformation as they differentiate (1, 2, 3, 4), and the deformability of cancer cells is associated with their invasive potential (5, 6, 7). Thus, cell mechanotype is emerging as a label-free biomarker for altered cell and pathological states. In addition, mechanotyping methods have demonstrated the potential for enhancing cancer diagnoses (8) and enriching stem cell populations (9). Rapid, calibrated measurements of cell viscoelastic properties could enable robust longitudinal and cross-study comparisons and thus further advance the utility of cell mechanotyping.

Standardized measurements of cell mechanical properties, such as elastic modulus, E, compliance, J, or viscosity, η, are acquired by probing cells with well-defined stresses and measuring the resultant deformations. Such measurements can be achieved using atomic force microscopy (AFM) (5, 10, 11), micropipette aspiration (12, 13, 14), optical stretching (2, 15, 16, 17), and microplate compression (18, 19), and can reveal physical principles that underlie cell mechanical properties, including viscoelastic and stress stiffening behaviors (20, 21, 22). Identifying such universal characteristics of cells can deepen our understanding of the role of mechanotype in physiology and disease. Moreover, standardized measurements enable accurate longitudinal and cross-study comparisons (11). However, measurements of mechanical moduli, for example, those obtained using AFM or micropipette aspiration, are typically acquired at rates of <1 cell/min. Higher throughputs are critical for measuring large numbers of single cells in clinical samples (23, 24) and elucidating the origins of phenotypic variability within a population.

Fluid-based deformability cytometry (DC) enables rapid single-cell mechanotyping at faster rates of 10²–10⁶ cells/min. Such DC methods demonstrate the potential of mechanotype for varying applications such as classifying cells at different stages of the cell cycle by their distinct mechanical properties (23) and enhancing the accuracy of clinical diagnoses by mechanotyping pleural effusions (8). In one DC method, the hydrodynamic forces of inertial flow deform cells on the microsecond timescale (25). Although this method facilitates the analysis of large populations, the external stresses on single cells are challenging to model and calculate. In the real-time DC method, the shear stresses of fluid flow induce cell deformations; as these shape changes are well described by a continuum elastic model (26), E can be measured for single cells on millisecond to microsecond timescales (23). With the transit DC method, cells are driven to deform and transit through microfluidic constrictions on millisecond timescales (16, 27, 28, 29, 30, 31, 32, 33, 34). The time required for cells to transit through microfluidic constrictions can depend on cell size, mechanical properties, and surface properties, but the initial deformation into microfluidic constrictions is dominated by cell deformability (32, 33, 35); cells and particles that have a higher E exhibit longer deformation timescales (16, 35, 36). Such transit experiments are widely used to mechanotype various cell types, from breast cancer cells to neutrophils, based on relative deformation timescales (27, 30). The average E of a population can be determined by driving cells through microfluidic constrictions with a range of pressures and fitting a viscoelastic model to the resultant strain and transit time data for thousands of cells (31, 34). However, single-cell analysis is critical for characterizing population heterogeneity (37).

Here, we demonstrate rapid, calibrated mechanical measurements of single cells using quantitative deformability cytometry (q-DC). We drive cells to deform through micron-scale constrictions at rates of thousands of cells per minute by applying a pressure gradient across the microfluidic device (29). To obtain quantitative measurements of cell mechanotype, we track the time-dependent strain of individual cells and calibrate the applied stresses using gel particles with well-defined elastic moduli. Our results show that the deformation response of single cells follows power-law rheology (PLR), which enables us to determine an apparent elastic modulus, E_a, and power-law exponent, β, or fluidity, for single cells. We validate our q-DC method by measuring E_a and β for human promyelocytic leukemia (HL-60) cells. We find that E_a increases with cell strain and applied stress on these time- and lengthscales. We also demonstrate that q-DC is sensitive to changes in HL-60 mechanotype after treatment with cytoskeleton-perturbing drugs. Differences in the mechanotype between human breast cancer cell lines, MCF-7 and MDA-MB-231 cells, can also be detected. Taken together, the q-DC platform enables rapid, calibrated mechanotyping, which should deepen our understanding of cells as materials.

Materials and Methods

Cell culture

Cells are cultured at 37°C with 5% CO₂. Cell media and L-glutamine are from Life Technologies (Carlsbad, CA) and fetal bovine serum (FBS) and penicillin-streptomycin are from Gemini BioProducts (West Sacramento, CA). Human promyelocytic leukemia (HL-60) cells are cultured in RPMI-1640 medium with L-glutamine, 10% FBS, and 1% penicillin-streptomycin. To perturb the cytoskeleton, cells are treated for 1 h with 2 μM cytochalasin D (Santa Cruz Biotechnology, Santa Cruz, CA), 100 μM blebbistatin (Santa Cruz Biotechnology), and 100 nM jasplakinolide (Life Technologies). Cell viability is determined using trypan blue staining (Table S1). Human breast cancer cell lines, MCF-7 and MDA-MB-231, are cultured in high glucose, L-glutamine, sodium pyruvate Dulbecco’s modified Eagle’s medium with 10% FBS and 1% penicillin-streptomycin. HL-60 cells and MCF-7 and MDA-MB-231 are from the American Type Culture Collection (Manassas, VA). The identity of each cell line is confirmed using multiplex short tandem repeat profiling (Laragen, Culver City, CA).

Fabrication of calibration particles

Silicone oil droplets and gel particles are fabricated using methods previously described (35). In brief, silicone oil droplets are formed by generating oil-in-water emulsions (Sigma-Aldrich, St. Louis, MO) where the dynamic viscosity of the silicone oil varies from 10⁻² to 10¹ Pa·s. Deionized (DI) water with silicone oil (1:5 v/v) and 4% (w/v) Tween 20 surfactant (Sigma-Aldrich) are vortexed for 1 min. The concentration of Tween 20 is significantly larger than the critical micelle concentration of 0.01% (w/v), such that the droplet surface is saturated with surfactant and the droplets are effectively stabilized while transiting through the microfluidic device. Before transit experiments, the emulsion is centrifuged at 157 × g for 3 min to remove air bubbles and filtered through a 35 μm mesh filter (BD Biosciences, Franklin Lakes, NJ) to create a size distribution of droplets that is similar to that of cells (35). To further ensure droplet stability during transit through the microfluidic devices, experiments are conducted within 1 h after plasma treatment to maintain hydrophilic surface properties. Channels are also filled with DI water 5 min after plasma treatment to reduce hydrophobic recovery.

To fabricate agarose microgels, water-in-oil emulsions are generated such that the aqueous phase contains the desired w/w percentage of low-gelling-temperature agarose (A4018-5G, Sigma-Aldrich). The agarose/DI water mixture is heated to 90°C on a heating block for 10 min until the agarose is fully dissolved. The liquid agarose solution is then vortexed with mineral oil (1:5 v/v) together with 1% w/w Span 80 for 30 s. After filtering the resultant emulsion through a 35 μm mesh filter (BD Biosciences), the sample is immediately placed on ice for 1 h to promote gelation and then stored at 4°C overnight. Thereafter, the microgels are removed from the oil phase by adding 5 mL of DI water and centrifuging at 157 × g for 10 min. To increase the yield, the samples are shaken vigorously after being removed from the centrifuge and spun down three more times, removing the oil from the top of the solution by pipetting. Washing steps are repeated three times to ensure sufficient separation of the water and oil phases. The suspension is filtered one last time through a 35 μm mesh filter.

Young’s modulus characterization of agarose calibration particles

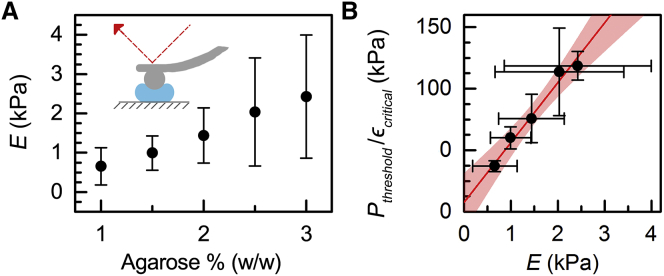
To determine the elastic modulus of microgels with varying compositions of agarose from 1 to 3% (w/w), particles are indented using an AFM (MFP 3D-BIO system, Asylum Research, Goleta, CA) that is mounted on an inverted microscope (Nikon Ti-E, Tokyo, Japan). To anchor the particles during AFM measurements, we incubate agarose microgels for 30 min on a glass substrate pretreated with 0.01% (w/v) poly-L-lysine overnight before AFM (Sigma-Aldrich, St. Louis, MO). AFM is performed using a silicon nitride cantilever with an attached 12-μm-diameter borosilicate glass sphere as an indenter (product no. HYDRA6R-200NG-BSG-B-5, AppNano, Mountain View, CA). The particles are probed using a 1 μm/s approach velocity. Thereafter, the AFM force curves are fit to the Hertz model with a spherical indenter to determine the Young’s moduli of the agarose microgels (Fig. 2 A). We use a Poisson ratio of 0.5. By brightfield imaging of each particle before AFM indentation, we measure particle size and confirm that there is no observable dependence of elastic modulus on particle size (Fig. S1 A).

Figure 2.

Stress calibration using agarose gel particles. (A) Elastic moduli of gel particles made with varying concentrations of agarose from 1.0 to 3.0 % (w/w) as measured by AFM. Data represent the average ± SD for N = 12–53 particles over two independent experiments. (B) Agarose calibration particles are used to determine the applied stresses in the q-DC device by measuring the minimum threshold pressure, P_threshold, required to induce a critical strain, ϵ_critical, for a particle to deform through a constricted channel. Shown here are representative data for N > 140 particles transiting through a 5 × 5 μm channel. Horizontal error bars represent the standard deviation of the elastic modulus, as indicated by the vertical error bars in (A). Vertical error bars represent the standard deviation of the threshold-pressure/particle-strain ratio. The line is the linear fit determined by the Deming method. The shaded region illustrates the 95% confidence interval of the fit. The inverse of the slope characterizes the calibration factor, A. To see this figure in color, go online.

Microfluidic device fabrication

Microfluidic devices are fabricated using standard soft lithography methods (38). To fabricate the master wafer, SU-8 3005 or 3010 (MicroChem, Westborough, MA) is spin-coated on a silicon wafer to a final thickness of 5 or 10 μm. A negative photomask is placed on the SU-8-coated wafer and the photoresist is cross-linked upon exposure to ultraviolet light with 100 mJ/cm² of exposure energy (35). The height of the resulting relief of the microfluidic channels is measured using a Dektak 150 surface profilometer (Veeco, Fullerton, CA). A 10:1 w/w mixture of base and curing agent for polydimethylsiloxane (PDMS) (Sylgard, Dow Corning, Midland, MI) is poured onto the master wafer. The mixture is degassed for 1 h under vacuum and cured in a 65°C oven for 2 h. Before bonding, inlets and outlets are excised using a biopsy punch with a 0.75 mm bore size. To bond the PDMS to a coverglass (no. 1.5 thickness), the complementary surfaces are exposed to plasma for 30 s and pressed together with light pressure. After bonding, the microfluidic devices are baked at 80°C for 20 min to further promote covalent attachment between PDMS and glass. To reduce possible measurement artifacts due to temporal changes in surface properties, devices are consistently used 24 h after plasma bonding (35).

q-DC device design

The q-DC microfluidic device consists of a bifurcating network of channels that extends into a parallel array of 16 channels that contain micron-scale constrictions (27, 28). To reduce the effect of transient channel occlusions as multiple cells transit simultaneously through the constriction region, a bypass channel is included in the device design and post-acquisition filtering is performed to exclude data when >10 channels, or 65% of the channels, are occupied (35). Below this cutoff, there are fluctuations in flow rate below 7% variability (35).

q-DC microfluidic experiment

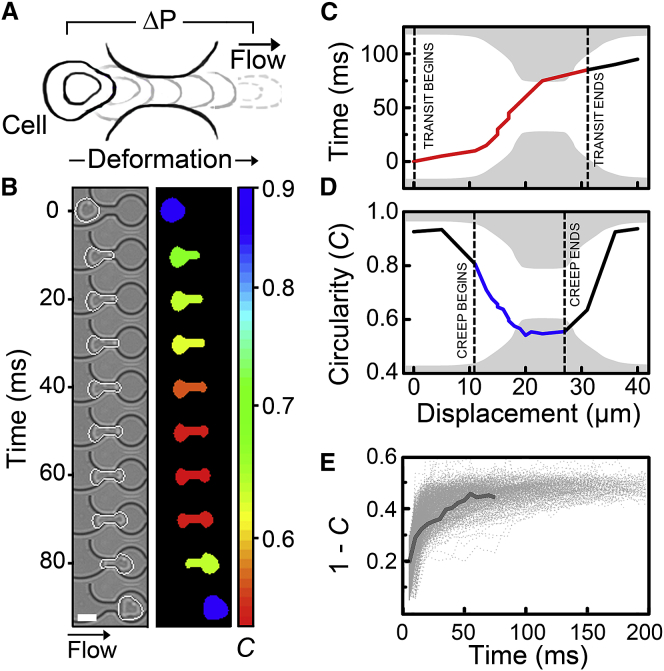
To perform q-DC experiments, microfluidic devices are mounted onto an inverted microscope (Zeiss Observer, Carl Zeiss, Oberkochen, Germany) that is equipped with a 20×/0.40 NA objective. To drive the suspension of cells through the channels, constant air pressure is applied to the device inlet, which is regulated using a pneumatic valve (OMEGA Engineering, Norwalk, CT). As cells flow into the device, a downstream filter traps foreign particles and cell aggregates that are >20 μm in size. As cells deform through the constrictions (29), brightfield images are acquired at rates of 200–2000 frames/s using a CMOS camera (MircoEx4; Vision Research, Wayne, NJ) to track cell shape and displacement (Fig. 1, A and B). This enables measurements of cell size, D_cell, time-dependent strain, ϵ(t), critical strain, ϵ_critical, creep time, T_c, and transit time, T_T. When a driving pressure of 28 kPa (4 psi) is applied to a cell suspension with a density of 2 × 10⁶ cells/mL, single-cell measurements can be acquired at rates of ∼10³ cells/min. For applied pressures of 69 kPa (10 psi), measurements can be acquired at ∼10⁴ cells/min.

Figure 1.

Cell-shape changes during transit through microfluidic constrictions. (A) Schematic of a single cell transiting through a micron-scale constriction by pressure-driven flow, where ΔP is the pressure drop across the cell. Cell shape is evaluated by measuring circularity, C(t) = 4πA(t)/P(t)², during transit, and the time-dependent strain, ϵ(t), is defined as 1 − C(t). (B) Time sequence of a representative HL-60 cell transiting through a microfluidic constriction that exhibits the median transit time and cell size of the cell population. The white border illustrates the cell boundary, as detected by our imaging algorithm. The color overlay illustrates the change in circularity, C, during deformation. Scale bar, 15 μm. (C and D) Timescale and shape change during transit through a microfluidic constriction. The x axis represents the position of the centroid of the cell. We extract (C) transit time, which is the time required for the leading edge of the cell to enter and exit the constriction region, and (D) time-dependent strain or creep, which is determined by the changes in shape (circularity) of the cell as it deforms into the pore. The creep time begins when the leading edge of the cell enters the constriction and ends when the centroid exits the constriction, as illustrated by the dashed lines. (E) Creep trajectories for the population of HL-60 cells (N = 550). The gray dotted lines represent data from individual cells. The solid gray line represents the creep trajectory of the representative HL-60 cell.

To minimize cell-surface interactions, measurements are conducted in the presence of 0.01% (w/v) Pluronic F-127 surfactant (Sigma-Aldrich). For some cell types, such as human pancreatic ductal epithelial cells, we qualitatively observe a decrease in cell-PDMS adhesion when Pluronic F-127 surfactant is added to the cell suspension (35); therefore, we consistently use this treatment across all cell types. There is no significant quantitative or qualitative effect of F-127 treatment on the E_a values of HL-60 cells (Fig. S2). Although cell-surface interactions can contribute to cell transit through long, narrow microfluidic channels, the timescale required by cells to enter microfluidic constrictions is largely determined by cell deformability (32, 33, 35).

Tracking of cell strain during deformation through microfluidic constrictions

To extract cell mechanical properties from transit experiments, cell position and shape are tracked by applying thresholding and morphological filters to the high-frame-rate images in a MATLAB code (The Mathworks, Natick, MA; code available online on GitHub). The creep function, J(t), is determined as the ratio between the observed strain and applied stress:

$$J\left(t\right)=\frac{\mathit{ϵ}\left(t\right)}{\overline{\sigma }},$$ (1)

where ϵ(t) is the strain and $\overline{\sigma }$ is the time-averaged stress. Here, the strain is measured as the change in circularity, C:

$$\mathit{ϵ}\left(t\right)=\frac{C_{\text{o}}–C\left(t\right)}{C_{\text{o}}},$$ (2)

where C(t) = 4πA(t)/P(t)². We find that circularity compared to length extension and width compression more robustly captures the deformation of cells through the curved microfluidic constrictions. Before entering the constriction, circularity values are ∼1, the value of a perfect circle. Therefore, the initial circularity is set to C_o = 1. As a cell deforms through a constriction, the strain reaches a maximum as the cell extends and deforms through the narrow gap (Fig. 1, B–D). The quantification of creep begins one frame after the leading edge of the particle reaches the constriction, which corresponds to the initial projection of the cell into the constriction, and ends when the centroid of the cell leaves the constriction (Fig. 1). We use a minimum of four frames to achieve sufficient fits for the creep trajectories of individual cells. Although fitting to a larger number of >15 frames can improve fitting accuracy, as indicated by the residuals (Fig. S3), this would exclude all cells that transit within <15 frames, or 7.5 ms. Increasing the frame rate captures cell deformations with higher temporal resolution, but the duration of the video is reduced to 3.7 s due to hardware limitations at the maximum frame rate of 3500 frames/s. Therefore, using a four-frame cutoff to acquire q-DC measurements enables us to resolve the power-law behavior of individual cells that are representative of the population by acquiring data across a range of cell-deformation timescales from milliseconds to seconds.

Calibration of time-averaged stress using gel particles

Since the device has a finite fluidic resistance, the stress applied to a cell as it deforms in the microfluidic constriction does not equate to the applied driving pressure, or P_applied, but rather scales with P_applied as

$$\overline{\sigma }=A{P}_{\text{applied}},$$ (3)

where $\overline{\sigma }$ is the time-averaged stress at the constriction region and A is the calibration factor. To determine A, we calibrate the system using agarose particles with elastic moduli (E) ranging from 660 ± 86 to 2.4 ± 0.44 kPa (average ± SE), as confirmed by AFM (Fig. 2 A); similar values are observed for agarose particles generated using droplet microfluidics (39).

To achieve particle transit through a fixed pore size, the applied stress must induce a minimum, critical strain, ${\mathit{ϵ}}_{\text{critical}}$, Assuming linear elastic behavior, the scaling factor, A, can be determined by the stress-strain relation at the threshold conditions where P_applied = P_threshold:

$$A=\frac{E{\mathit{ϵ}}_{\text{critical}}}{P_{\text{threshold}}}.$$ (4)

We define the threshold pressure as the minimum applied pressure needed to drive the transit of >∼80% of the particles through the constrictions. For example, when calibration particles with E = 1.5 ± 0.1 kPa are driven through a 5 × 5 μm device using an applied pressure below P_threshold = 41 kPa, the majority of particles occlude the microfluidic constrictions on the experimental timescale of 1 min. By contrast, with applied pressures above P_threshold, >80% of particles transit within this timescale. As we use a heterogeneous size distribution of particles, we determine P_threshold and ${\mathit{ϵ}}_{\text{critical}}$ for the largest (top 50th to 100th size percentile) gels that transit through the constriction for a given bead stiffness at P_threshold (Fig. S1 B). Here, we calculate the critical strain as ${\mathit{ϵ}}_{\text{critical}}=\left(D_{\text{agarose}}-w_{\text{constriction}}\right)/D_{\text{agarose}}$. Across the range of particle stiffnesses (0.6–2.4 kPa) and strains (40–60%) that we investigated, we find a linear relation between stress and strain (Fig. 2 B), which validates our assumption of linear elasticity.

By performing linear regression using the Deming method on ${\mathit{P}}_{\text{threshold}}/{\mathit{ϵ}}_{\text{critical}}$ versus E for our panel of calibration particles, we determine A for each device geometry (Fig. 2 B; Fig. S4) (40). We find that A is 0.021 ± 0.002, which yields $\overline{\sigma }\approx$ 568 ± 53 Pa for P_applied = 28 kPa in the 5 × 5 μm device geometry. Combining Eqs. 3 and 4, the resultant creep, J(t), for the 5 × 5 μm device is defined as

$$J\left(t\right)=\frac{\mathit{ϵ}\left(t\right)}{0.021P_{\text{applied}}}.$$ (5)

The Deming method also enables us to determine the error in A as it considers the error in both ${\mathit{P}}_{\text{threshold}}/{\mathit{ϵ}}_{\text{critical}}$ and E. In addition to any variability in elastic moduli of the calibration particles, error in A may arise due to fluctuations in applied stress as particles transit and occlude neighboring channels. In our previous analysis of cell transit times, we found that transit times significantly decrease when >10 neighboring lanes are occupied (35); therefore, we analyze data from particles and cells that transit when 10 or fewer neighboring lanes are occupied. Kirchoff’s law reveals that the flow rate can change by 7% within our experimental range of occluded neighboring lanes of 0–10 lanes; this is reflected in the error of applied stress of 10% (35).

Viscoelastic cell simulations

To provide insight into the stresses on cells as they deform through microfluidic pores, we use a three-dimensional multiphase flow algorithm in which each of the phases is modeled as a viscoelastic or Newtonian fluid. The viscoelasticity of the cells and walls of the microchannel are described by the Oldroyd-B constitutive model (41, 42). Similar to our experiments, cells flow through the microchannel of a PDMS device in response to an applied pressure (Fig. S6 A). The simulations determine the total stresses acting on cells, including fluid shear stresses and normal stresses that result from the pressure drop across the cell as it transiently occludes the pore. To reduce the computational expense of the simulations, cells are modeled to have E = 10 Pa and an apparent viscosity of 1.0 Pa·s. To maintain the same ratio between cell and PDMS stiffness as in our experiments (E_PDMS/E_cell ∼ 10³), the stiffness of the microchannel is modeled as E ∼ 10⁴ Pa. The carrier fluid of the cells during transit in the device is modeled as a Newtonian fluid.

Results and Discussion

Time-dependent cell strain follows PLR

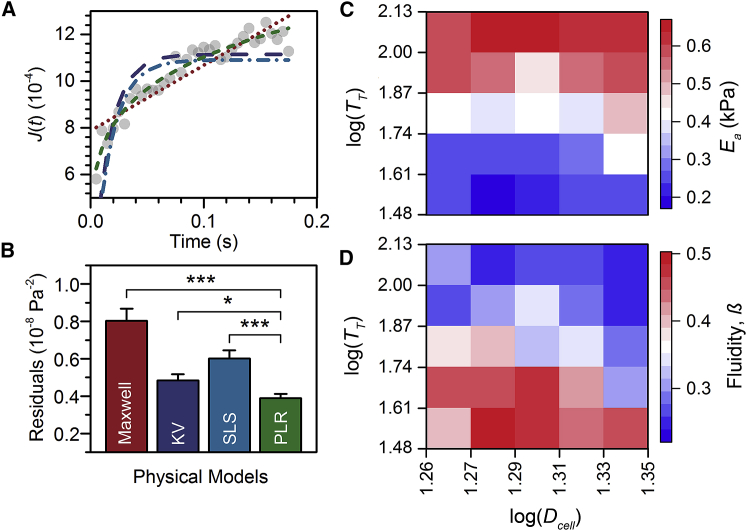
Determining the material properties of cells from transit experiments requires a physical model to describe the relationship between stress and strain. To simplify analysis, we consider the cell as a homogeneous, isotropic, and incompressible material. This enables us to fit mechanical models to the creep trajectories for individual cells, such as the liquid drop and Kelvin-Voigt models. The deformation of cells entering microfluidic constrictions can be assessed using models that describe cells as liquid droplets (32) or elastic solids (26), as well as viscoelastic (43) and soft glassy (31) materials. However, it is not a priori known which model best describes the deformations of cells into the microfluidic constriction and provides the most accurate measurement of cell mechanical properties. Here, we evaluate how effectively four viscoelastic models—the Maxwell solid, Kelvin-Voigt, standard linear solid (SLS), and PLR—describe cell creep through microfluidic constrictions. These models are described in greater detail in the Supporting Material.

Our analysis reveals that PLR provides the best fit to our data: the least-squares residuals are the lowest for PLR (3.9 ± 0.2 × 10⁻⁹ Pa⁻²), as compared to other standard viscoelastic models (4.8 ± 0.3 × 10⁻⁹ to 8.0 ± 0.2 × 10⁻⁹ Pa⁻²) (Fig. 3, A and B). Although an increasing number of fitting parameters can naturally result in reduced residuals, PLR has only two fitting parameters. By contrast, the SLS model has three fitting parameters, but the least-squares residuals are higher for SLS than for PLR (6.0 ± 0.1 × 10⁻⁹ Pa⁻², p ≪ 0.001). Our results are consistent with observations of PLR behavior in cells that are subjected to stresses by micropipette aspiration (44), optical stretching (2), transit DC (31, 34), AFM (20), and magnetic twisting cytometry (45).

Figure 3.

PLR for cell mechanotyping by q-DC. (A) Creep trajectory for a single, representative HL-60 cell (gray dots). Lines represent the least-squares fits of viscoelastic models to the creep data: Maxwell (red dotted line), Kelvin-Voigt (KV, purple long-dashed line), SLS (blue dot-dashed line), and PLR (green short-dashed line). (B) Residuals for the least-squares fits of the viscoelastic models to the creep trajectories of a population of HL-60 cells (N = 550), as shown in Fig. 1E. Shown here are the bootstrapped median residuals; error bars represent the bootstrapped confidence interval. ^∗p < 0.05, ^∗∗∗p$\ll$ 0.001. (C and D) Heat maps show (C) the apparent elastic modulus, E_a, and (D) the fluidity, β, of HL-60 cells as a function of transit time, T_T, and cell diameter, D_cell, which is measured in the microfluidic channel before the cell enters the constriction. Each bin represents the median E_a or β of N = 3–47 single cells.

Using PLR, we extract the mechanical properties of single cells as they deform through microfluidic constrictions by analysis of the time-dependent creep function,

$$J\left(t\right)=\frac{1}{E}{\left(\frac{t}{\tau }\right)}^{\beta },$$ (6)

where τ is the characteristic timescale, which is commonly set to 1 s; E is the elastic modulus when t = τ; and β is the power-law exponent that reflects the rate of stress dissipation and thus provides a measure of cell fluidity. When β = 0, the creep function describes a purely elastic material and Eq. 6 reduces to Hooke’s law; when β = 1, Eq. 6 reduces to the Newtonian liquid-drop model, reflecting a purely viscous material. Although our data are consistent with PLR, we refer to the elastic modulus that we measure using q-DC as the apparent elastic modulus, E_a, because of the potential nonlinear effects that may contribute to our measurements with the large 30–60% strains in q-DC.

We also recognize that these mechanical measurements assume constant stress during cell transit. As shown by the viscoelastic cell adhesion model simulations, the total stress on a cell varies as it deforms through a pore (Fig. S6). As the cell transits through the pore, there is a drop in the hydrodynamic forces on the cell, which are proportional to the cell velocity according to Stokes’ law (Fig. S6 B). In addition, there is a pressure drop across the cell, where the applied pressure, P_app, at the trailing edge is higher than the pressure at the cell’s leading edge, which is approximated by atmospheric pressure, P_atm (Fig. S6 C). Thus, when the cell is transiently occluding the pore, there are positive normal forces that deform the cell and that vary during cell translocation due to the curved geometry of the pore.

Validation of PLR using oil droplets

To validate the use of PLR in q-DC, we first quantify β, or fluidity, for droplets of silicone oil. We predict β = 1 for droplets of silicone oils, which are Newtonian fluids. We generate oil droplets that have a range of molecular weights, and thus dynamic viscosities, η, from 10⁻² to 10¹ Pa·s, and flow them through the constrictions at a constant driving pressure of 28 kPa. From 1000 random samplings of the β distributions, we obtain median bootstrapped values and confidence intervals of β. We observe β = 0.78 ± 0.08 for the lowest-viscosity silicone oil (η = 10⁻² Pa·s) (Fig. S4), which is close to purely viscous behavior. With increasing viscosity, we observe decreasing β, where the highest-viscosity oil droplets (η = 10¹ Pa·s) exhibit β = 0.54 ± 0.02. This decrease in β with increasing viscosity suggests a progressively increasing elastic response, which occurs due to the fast millisecond timescales of our measurements compared to the timescale of molecular rearrangements in the silicone oils that have increased molecular weight.

Single-cell measurements of elastic modulus and fluidity

To demonstrate the utility of q-DC for cell mechanotyping, we measure HL-60 cells, whose mechanical properties are well characterized using methods such as micropipette aspiration (46), AFM (47, 48), and optical stretching (16) (Table 3). Our results show that HL-60 cells have a median E_a and confidence interval of 0.53 ± 0.04 kPa (β = 0.29 ± 0.02), as measured by 1000 iterations of bootstrapped resampling (Fig. 3; Table S2); this is on the same order of magnitude as values obtained using AFM, where E = 0.9 ± 0.7 kPa (47) and E = 0.9 ± 0.2 kPa (48) (Table S3).

Since q-DC quantifies the mechanotype of single cells, the variability in mechanical properties across a cell population can be determined. To describe cell-to-cell variability, we use the interquartile range (IQR) as a quantitative metric. For HL-60 cells, the IQR spans half an order of magnitude, from 0.30 to 0.71 kPa, as measured by σ_{IQR_Ea} = log₁₀(75th/25th percentile) = 0.35 ± 0.06. We also find significant variability in β with σ_{IQR_β} = 0.25 ± 0.03.

By plotting E_a and β versus D_cell, we observe that larger cells tend to have higher E_a (Figs. 2 C and 3 A) and reduced β (Figs. 2 D and 3 A). For example, we find that for cells with D_cell = 18 ± 1 μm, E_a = 0.37 ± 0.06 kPa and β = 0.37 ± 0.04, whereas larger cells with D_cell = 22 ± 1 μm have E_a = 0.59 ± 0.04 kPa and β = 0.26 ± 0.02 (Fig. 2, C and D). Size dependence of cell mechanotype is also observed in other DC methods, where larger cells have longer transit times (31, 32, 33, 35) and exhibit more significant changes in shape due to forces exerted by fluid flow (23, 25). Although larger cells could be inherently stiffer than smaller cells, larger cells undergo larger strains as the constriction width is fixed (Fig. S7). Since cells are non-linear materials, the length- and timescales of deformation may influence their E_a, as observed in cells (20, 21, 22, 49, 50, 51, 52) and biopolymer networks (20, 49, 53, 54, 55).

Cell/pore-size ratio affects mechanotype

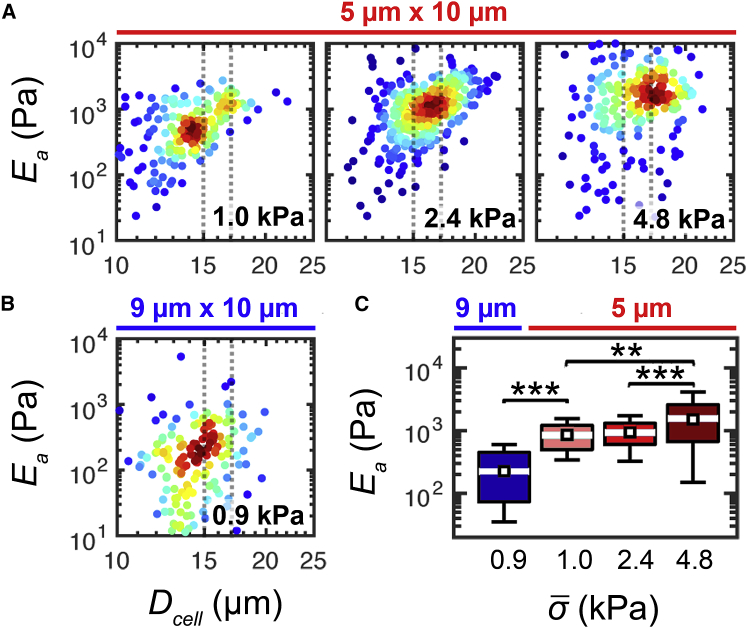
To further investigate the cell-to-pore-size dependence of E_a, we vary the constriction width from 5 to 9 μm while maintaining a constant constriction height of 10 μm; thus, we achieve median cell/pore-size ratios of ∼3 and 1.5. To ensure that cells are subjected to the same applied stress while undergoing different critical strains, we utilize the agarose calibration beads to determine the required applied pressures for each constriction geometry: P_applied = 14 kPa for 5 × 10 μm geometry and P_applied = 34 kPa for the 9 × 10 μm device (Table. S4). For cells of D_cell = 16 ± 1 μm, we observe a significant 70% decrease in E_a when measured using a 9-μm-width constriction (E_a = 230 ± 90 Pa), as compared to the 5-μm-width geometry (E_a = 860 ± 230 Pa; p ≪ 0.001). These results suggest that the magnitude of cell strain affects E_a, and they are consistent with observations of strain stiffening in mechanical measurements of cells and biopolymer networks (10, 54). Our findings of how mechanotype depends on cell/pore-size ratio also substantiates the comparison of cells of similar sizes across samples.

Cells are also spatially heterogeneous materials. Therefore, the magnitude of deformation depth, or strain, may impact the resultant mechanotype measurements. The nucleus is a major contributor to subcellular deformations: this organelle is typically 2–5 times stiffer than the surrounding cytoplasmic region (11) and rate limits the deformation of cells through microfluidic channels that are smaller than the diameter of the nucleus (28). HL-60 cell nuclei range in diameter from 5 to 14 μm and have an average size of 9.2 ± 2.0 μm (Fig. S9); thus, for most cells, the nucleus must deform when cells transit through a 5- or 9-μm-wide constriction. By quantitative image analysis, we find that larger HL-60 cells tend to have larger nuclei, as indicated by the positive correlation (R = 0.8) between nuclear and cellular diameter (Fig. S9 A). Thus, the increased E_a observed for larger cells could also result from the increased deformation of the nucleus that is required for transit. A similar increase in Young’s modulus is observed with increasing AFM indentation depth into the nucleus (11). The dependence of cell and nuclear size on the deformation response of cells as they deform through pores further underscores the importance of comparing q-DC data from cells that undergo a similar magnitude of strain (Fig. S7). These findings also provide a guide for establishing parameters in q-DC experiments: a cell/pore-size ratio of ∼2 ensures that cell deformation is required for transit through the pore and typically results in a strain of 35–40%, which is in the lower range of cell strains that can be achieved with q-DC and therefore minimizes strain-stiffening effects.

Stress-stiffening behavior of cells using q-DC

To determine the effects of applied stress on cell deformation behavior in q-DC, we drive HL-60 cells through 5 × 10 μm constrictions with increasing applied pressures from 14–69 kPa. From our calibration, we determine the corresponding range of applied stress to be $\overline{\sigma }$ = 1.0–4.8 kPa. With an increase in $\overline{\sigma }$ from 1.0–2.4 kPa, we find a small, not statistically significant 10% increase in elastic modulus (p = 0.34). Further increasing $\overline{\sigma }$ to 4.8 kPa, we observe a statistically significant stiffening reflected by the 60% increase in E_a (p < 0.001). From $\overline{\sigma }$ = 1.0–4.8 kPa we observe a significant 70% increase in E_a from 860 ± 230 to 1.5 ± 0.5 kPa (p = 0.003) (Fig. 4 A; Table. S4). Taken together, these results indicate stress stiffening response of HL-60 cells on these deformation timescales of milliseconds to seconds. The stress stiffening behavior of cells is observed across varying cell types from airway smooth muscle cells to fibroblasts (2, 20, 49, 56). Therefore, we consider cells of similar sizes when comparing between populations of single cells to minimize possible bias from strain and stress on q-DC measurements.

Figure 4.

Mechanotype of HL-60 cells depends on applied pressure and cell/pore-size ratio. (A) Density scatter plots show apparent elastic modulus, E_a, as a function of cell size. The cell diameter, D_cell, is measured in the microfluidic channel before the cell enters the constriction. Data represent the deformation response for HL-60 cells that are driven to deform through 5 × 10 μm constrictions with increasing applied pressure. The calibrated applied stress is shown on the bottom right corner of each plot. Dots represent single-cell data. Cell size, measured by q-DC, increases with applied pressure, as there is a higher probability that larger cells will transit at higher pressures; at lower pressures, larger cells have a higher probability of occluding constrictions. To compare data sets, we bin cells by the median cell diameter, as indicated by the gray dashed lines; the resultant size-binned data are shown in the boxplots in (C). (B) Density scatter plot illustrating the elastic modulus, E_a, as a function of cell size for HL-60 cells deforming through 9 × 10 μm constrictions. (C) Boxplots show the size-gated distributions of E_a for HL-60 cells with D_cell = 16 ± 1 μm. Cells are subject to varying applied stresses, $\overline{\sigma }$, and constriction geometries: white lines represent the median, boxes represent the interquartile ranges, whiskers represent the 10th and 90th percentiles, and white squares represent the bootstrapped median. N > 200 for each cell type. Statistical significance is determined using the Mann-Whitney U test: ^∗∗p < 0.01, ^∗∗∗p < 0.001. To see this figure in color, go online.

Validation of mechanical measurements using HL-60 cells

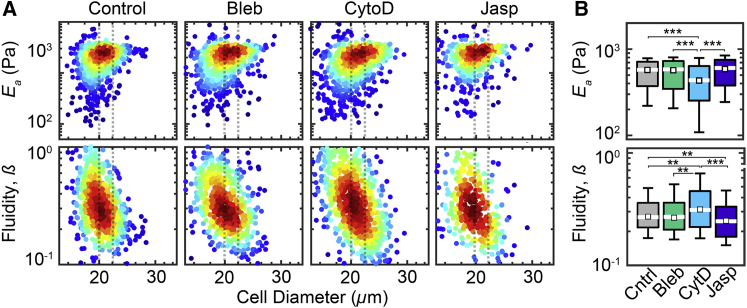
To demonstrate the sensitivity of q-DC to changes in cytoskeletal structure, we treat HL-60 cells with cytoskeleton-perturbing drugs, which are known to alter cell mechanical properties (10, 46, 57, 58). For example, treatment with cytochalasin D inhibits F-actin polymerization (27), whereas treatment with jasplakinolide inhibits F-actin depolymerization, thus stabilizing actin filaments. To compare cells of similar size, we size bin our data to investigate cells of the median diameter, D_cell = 21 ± 1 μm, of HL-60 cells across all drug treatments (Fig. 5 A). We find that treatment with cytochalasin D results in a small but significant decrease in E_a from 0.53 ± 0.04 to 0.39 ± 0.05 kPa, with an increase in cell-to-cell variability from σ_{IQR_Ea} = 0.35 ± 0.06 to 0.46 ± 0.08 (p ≪ 0.001) (Fig. 5). In addition, we observe that cytochalasin D treatment results in a marginal increase in cell fluidity from β = 0.29 ± 0.02 to β = 0.34 ± 0.03 (p = 0.006), as well as an increased variability in fluidity from σ_{IQR_β} = 0.25 ± 0.03 to σ_{IQR_β} = 0.33 ± 0.04 (Fig. 5 B). By contrast, stabilizing F-actin with jasplakinolide treatment insignificantly increases E_a to 0.54 ± 0.06 kPa and σ_{IQR_Ea} = 0.30 ± 0.06; we also observe a concomitant significant decrease in β to 0.27 ± 0.03 with σ_{IQR_β} = 0.27 ± 0.06 (Fig. 5 B). Our observations of the effects of cytochalasin D and jasplakinolide are consistent with previous studies investigating the contributions of F-actin to cell transit through micron-scale channels (27, 32, 59, 60). These results demonstrate the proof of concept and utility of q-DC to achieve mechanical measurements of single cells with increased throughput.

Figure 5.

Mechanotyping of HL-60 cells treated with cytoskeleton-perturbing drugs using q-DC. HL-60 cells are treated with blebbistatin (Bleb), cytochalasin D (CytoD), and jasplakinolide (Jasp). (A) Density scatter plots show apparent elastic modulus, E_a, and fluidity, β, as functions of cell size, which is measured in the microfluidic channel before the cell enters the constriction. The cell diameter shown here appears to be larger than unconfined cells (Fig. S8A), as well as cells in the 10 μm height devices (Fig. 4), due to axial compression that occurs when the cell diameter is larger than the device height. Each dot represents a single cell. To compare data sets, we bin cells by size, as depicted by the dotted lines. Cell-size distributions are shown in Fig. S8. (B) Boxplots represent the size-binned distributions of E_a and β for cells with D_cell = 21 ± 1 μm, white lines represent the median, boxes represent the interquartile ranges, whiskers represent the 10th and 90th percentiles, and white squares represent the bootstrapped median. N > 500 for each cell type. Statistical significance is determined using the Mann-Whitney U test: ^∗∗p < 0.01, ^∗∗∗p < 0.001. To see this figure in color, go online.

We also investigate the effects of blebbistatin, which inhibits myosin II activity and thus reduces cross-linking and actomyosin contractions. We observe no significant change in E_a after blebbistatin treatment as E_a = 0.52 ± 0.06 kPa and σ_{IQR_Ea} = 0.40 ± 0.09. We observe a slight increase in cell fluidity to β = 0.29 ± 0.02 and σ_{IQR_β} = 0.28 ± 0.05; however, this difference is not significant (Fig. 5, A and B). Previous observations show that blebbistatin treatment decreases the stiffness in adhered cells, as indicated by their reduced E (61), and suspended cells, as indicated by their reduced transit time (59). However, other measurements of suspended cells show increased stiffness with inhibition of myosin II (36). As minor differences in blebbistatin concentrations and treatment times across studies do not seem to explain the observed differences in the mechanotype of cells in suspension, we speculate that the varied results may be explained by considering deformation depth. In methods that deform cells by ∼5–6 μm (59), the nucleus may contribute more prominently to the deformation response; myosin II inhibition could cause softening of the “prestressed” nucleus as intracellular tension diminishes. By contrast, when cells are subjected to smaller, 1- to 3-μm deformations (36), the cortical region may dominate the response; a less deformable cortex may result from decreased turnover of actin due to blebbistatin treatment. We also acknowledge that differences in cell genotype, culture conditions, and passage number of cell lines may also contribute to the varied results observed between studies.

Mechanotyping cancer cell lines

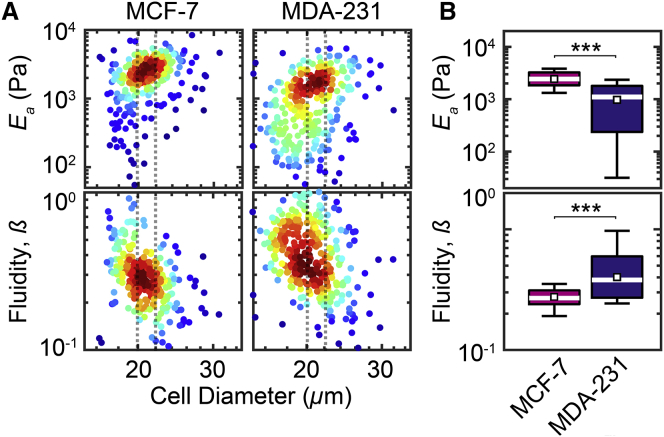
To further benchmark our q-DC method, we next investigate the human breast cancer cell lines MCF-7 and MDA-MB-231, whose mechanical properties are well characterized using methods including AFM and transit DC (Table S3). Since these breast cancer cells tend to be larger and stiffer than HL-60 cells (11), we use a 9 × 10 μm pore size with an applied stress of 2.2 ± 0.1 kPa, which ensures that >95% of cells transit through the pores on the experimental timescale (Fig. S3 B); this enables us to acquire single-cell measurements with a throughput of 10³ cells/min. For MCF-7 cells with D_cell = 21 ± 1 μm, we observe E_a = 2.4 ± 0.2 kPa (Fig. 6). We also measure MDA-MB-231 cells within the same size range, and find that E_a = 0.97 ± 0.50 kPa, which is 40% lower than MCF-7 cells (p ≪ 0.001). Our findings that MDA-MB-231 cells are more compliant than MCF-7 cells are in agreement with previous reports (62, 63) (Table S2). Using AFM and magnetic twisting cytometry, E values for MCF-7 cells typically range from 0.2 to 1 kPa (62, 64, 65, 66, 67), whereas for MDA-MB-231 cells, the E value varies from 0.2 to 0.69 kPa (11, 31, 62, 64, 65, 67). Considering the relatively higher 30–60% strains that are applied in q-DC compared to the local, less-than-micrometer indentations of AFM, the higher E_a values for MCF-7 cells that we observe are consistent with the dependence of E on deformation depth: MDA-MB-231 cells that are indented with 0.1 μm deformation depths that penetrate into the nuclear region exhibit a fivefold increase in Young’s moduli compared to 0.8-μm deformation depths (11, 62). Our measurements also reveal that E_a and β are inversely correlated for the breast cancer cells, where β = 0.28 ± 0.01 for MCF-7 cells and β = 0.40 ± 0.03 for MDA-MB-231 cells (p ≪ 0.001) (Fig. 4; Fig. S6 B); the inverse correlation is consistent with soft glassy rheology (2, 20, 31).

Figure 6.

Mechanotyping of human breast cancer cell lines using q-DC. (A) Density scatter plots show E_a and β as functions of cell size for MCF-7 and MDA-231 cell lines. To compare cell populations, we bin data by cell size, as depicted by the dotted lines. Cell diameter is measured in the microfluidic channel before the cell enters the constriction. (B) Boxplots represent the size-binned distributions of E_a and β for cells with D_cell = 21 ± 1 μm. White lines represent the median. Boxes denote the interquartile ranges and whiskers denote the 10th–90th percentiles. White squares represent the bootstrapped medians. N > 100 for each cell type. The Mann-Whitney U test is used to determine statistical significance: ^∗∗p < 0.01, ^∗∗∗p < 0.001. To see this figure in color, go online.

The differences in the mechanotypes of MCF-7 and MDA-MB-231 cells that we observe may reflect underlying molecular differences between these cell lines. These cell types also exhibit distinct invasive behaviors: MDA-MB-231 cells are more invasive than the MCF-7 cells (68). Although correlations between cancer cell invasive potential and mechanical properties are observed in other contexts (5, 7, 11, 69), the causal role of cell mechanotype in behaviors such as invasion is still unclear. The mechanotype of cancer cells could also have implications in how disseminated tumor cells resist shear forces during circulation and occlude narrow gaps, which is required for seeding metastatic sites. The ability of cells to transit versus occlude narrow capillaries is also critical for the deformability of blood cells (16, 28, 70, 71); in these contexts, changes in cell mechanotype have distinct biological implications. Furthermore, the evidence of stress and strain stiffening that we observe as cells undergo large, 40–60% strains through micron-scale gaps may be advantageous for cells in resisting significant deformations in vivo.

Although the biological relevance of mechanotype—which is most often measured in vitro—still remains an open question, it is notable that biological relevance is not a requisite to establish a valuable biomarker. For example, nuclear shape has been a diagnostic biomarker in breast and cervical cancers for decades (72), although the biological significance of the aberrant nuclear morphology of cancer cells remains unclear. Thus, robust differences in mechanotypes across cell types, which can be achieved using calibrated measurements, should have clinical value.

Conclusions

Here, we present a framework that uses calibration particles to quantify the external stresses in q-DC, a fluidic-based method that enables rapid measurements of cell mechanical properties. The use of calibration particles should ultimately enable standardized mechanotyping and longitudinal studies in clinical and research settings. To extract quantitative measurements of cell elasticity and fluidity, we use PLR, which is an effective analytical model for describing cell creep through microfluidic constrictions on timescales of milliseconds to seconds. Future studies will clarify the extent to which q-DC mechanotyping results add value as a biomarker, as well as the extent to which cell mechanotype impacts biological processes in physiology and disease.

Author Contributions

K.D.N. and A.C.R. designed research. K.D.N. performed all microfluidic experiments and analyses. K.D.N., K.H.H., S.H.K., and M.J.B. performed AFM experiments. D.B.K. performed simulations. K.D.N. and A.C.R. wrote the manuscript. All authors edited and approved the final manuscript.

Editor: Jochen Guck.