Irreversible particle motion in surfactant-laden interfaces due to pressure-dependent surface viscosity

Abstract

The surface shear viscosity of an insoluble surfactant monolayer often depends strongly on its surface pressure. Here, we show that a particle moving within a bounded monolayer breaks the kinematic reversibility of low-Reynolds-number flows. The Lorentz reciprocal theorem allows such irreversibilities to be computed without solving the full nonlinear equations, giving the leading-order contribution of surface pressure-dependent surface viscosity. In particular, we show that a disc translating or rotating near an interfacial boundary experiences a force in the direction perpendicular to that boundary. In unbounded monolayers, coupled modes of motion can also lead to non-intuitive trajectories, which we illustrate using an interfacial analogue of the Magnus effect. This perturbative approach can be extended to more complex geometries, and to two-dimensional suspensions more generally.

1. Introduction

Understanding the structure, dynamics and rheology of complex interfaces has become increasingly relevant in various fields of biology, technology and industry. Multiphase fluids are just about everywhere: in foams and emulsions [1]; in biological systems like the tear film and lung alveoli [2]; in food products [3]; and in the industrial processing of coatings and thin films [4].

Surface-active materials (surfactants) play a crucial role in the formation, flow and stability of these multiphase materials. Surfactants lower the surface tension of an interface, thereby reducing the energy required to create excess area. Surfactants are, therefore, prevalent in the form of soaps, emulsifiers, foaming agents and wetting agents [1,3].

Gradients in concentration of such surface species (and therefore in surface tension) lead to the well-known Marangoni stresses, which give rise to a wide variety of flow phenomena [5,6]. Additional stresses, beyond Marangoni stresses, may be required to deform the surfactant layer. That is, surfactants may exhibit a non-trivial surface rheological response [7,8]. The impact of interfacial rheology is more subtle than its three-dimensional analogue, particularly due to difficulties in clearly demarcating it from other sources of dissipation such as adsorption/desorption [9]. Interpretation of measurements is further complicated by surfactant-induced incompressibility [10], which fundamentally alters the boundary conditions obeyed by subphase flow as compared to a clean interface. Additional difficulties are associated with the design of microrheology tools that excite individual modes of deformation. Despite these challenges, recent years have seen the development of techniques [11–14] which have produced clear, quantitative and repeatable results that place interfacial rheology on a firm footing.

For surface rheology to play a non-trivial role, the excess interfacial stress must overwhelm viscous stress from the surrounding bulk phase. This is represented by the Boussinesq number,

$$Bo=\frac{{\eta }_{\mathrm{s}}}{\eta L},$$ 1.1

where η_s and η are surface and bulk shear viscosities of the surfactant and the subphase. Here L is the length scale over which gradients in surface stresses occur. The classic work of Saffman & Delbrück [15] regarding diffusivity of proteins within lipid membranes, for example, was in the regime of dominant surface viscosity (Bo≫1). In this limit, the interfacial layer is governed by the two-dimensional (2D) Stokes equations. However, there is no solution to steady flow past a cylinder in two dimensions that satisfies the boundary conditions far from the particle—the so-called Stokes paradox [6]. Saffman [16] showed that drag from the subphase ultimately regularizes the divergence at the root of this paradox. This transition from two to three dimensions beyond a Saffman–Delbrück length η_s/η has since been systematically measured [17]. In this work, we will assume interfacially dominant flows (Bo≫1) that completely decouple from the subphase, restricting our attention to distances within the Saffman–Delbrück length and, therefore, to 2D dynamics.

The standard framework for interfacial momentum balance is the Boussinesq–Scriven equation [18], which prescribes a general boundary condition for the bulk flow in the subphase. Viscous stresses within the interface are described by two viscosities, shear (η_s) and dilatational (κ_s), much like in bulk fluids, along with Marangoni stresses associated with gradients in surface tension, γ. Analogous to bulk pressure, one can define a surface pressure, Π, such that

$$\mathit{\Pi }(\mathit{\Gamma })={\gamma }_0-\gamma (\mathit{\Gamma })$$ 1.2

is the surface stress exerted by the surfactant against the surface tension γ₀ inherent in the clean interface. Here, Γ is the local surfactant concentration. The isotherm Π(Γ) can be measured experimentally [19,20] or specified using simple models.

The viscosities of bulk fluids typically change only under extreme pressure, if at all [21–23]. Departures from Newtonian solutions have been reported in the contexts of polymer melt processing [24,25] and lubricating oils [21], both under high pressures. The surface viscosity of surfactant-laden interfaces, by contrast, depends strongly on the surface concentration (and therefore on Π) of that surfactant. Surfactant monolayers are much easier to compress than three-dimensional (3D) fluids, and even a modest compression can force it to undergo phase transitions [26,7]. Consequently, surface viscosities change by orders of magnitude over relatively small changes in Π: in fact, η_s often increases exponentially with Π [19,20,27,28].

In a previous work [29], we illustrated the non-trivial consequences of surface pressure-dependent rheology by focusing on lubrication geometries on the interface. These geometries mimic thin gaps between particles (or between physical barriers) embedded within the monolayer. Not only do thin gaps naturally amplify surface pressures and therefore the effects of Π-dependent viscosity, but also the nonlinear governing equations turn out to have a separable solution within this approximation. Among other qualitatively new phenomena, this study revealed that the fluid stresses generated in response to the motion of a probe particle near a confining barrier break kinematic reversibility of Stokes flow. Such irreversible dynamics could have far-reaching consequences at the single-particle level, such as with interfacial microrheology, or more generally in the macroscopic behaviour of 2D suspensions.

In this work, we mathematically quantify the irreversible dynamics that break Newtonian symmetries and potentially affect the design and interpretation of high-Bo flows. Additionally, we move beyond the thin-gap regime of lubrication theory, and quantify the asymmetric forces and irreversible motion due to Π-dependent viscosity for arbitrary distances from confining walls. We appeal to asymptotic methods and develop a theory for ‘small’ departures from Newtonian behaviour. Similar methods have been previously used for spheres in weakly viscoelastic (second order) [30,31] and weakly inertial [32,33] 3D fluids, as well as with temperature-dependent viscosity [34]. In each of these cases, the leading-order correction to Newtonian behaviour is a lateral ‘lift’ force (or a reorienting torque) that breaks kinematic reversibility of Stokes flow.

This paper is organized as follows: in §2, we formulate a general expression for leading-order corrections to Newtonian behaviour using the Lorentz reciprocal theorem, and derive Newtonian solutions in bipolar cylindrical coordinates. We use this framework to study, in §3, the lateral force on a disc translating or rotating next to an interfacial boundary. We also show that the results are consistent with the predictions of a modified lubrication analysis for Π-dependent viscosity. In §4, we adapt the same method to the 2D journal bearing, which serves as a striking example of kinematically irreversible trajectories. As a final example, we illustrate the 2D analogue of the classic Magnus effect in §5, and conclude with suggestions for future problems and a note on the broader implications to 2D suspensions.

2. Problem formulation

(a). Governing equations

Let the x–y-plane represent a surfactant monolayer atop a bulk fluid (figure 1a). The quasi-steady Boussinesq–Scriven equation describes the interfacial stress balance [18]:

$${\mathbf{\nabla }}_{\mathrm{s}}\mathit{\Pi }={\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }[{\eta }_{\mathrm{s}}({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{\mathrm{T}})]+{{\mathbf{\nabla }}_{\mathrm{s}}[({\kappa }_{\mathrm{s}}-{\eta }_{\mathrm{s}}){\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}]-\eta \frac{\mathrm{\partial }\mathbf{\text{u}}}{\mathrm{\partial }z}|}_{z=0},$$ 2.1

where η_s and κ_s are the two surface viscosities, and η is the shear viscosity of the bulk fluid. The last term couples the interface to the subphase via the bulk viscous traction, which is determined by solving the Stokes equation for the bulk fluid flow u(x) with equation (2.1) as the boundary condition.

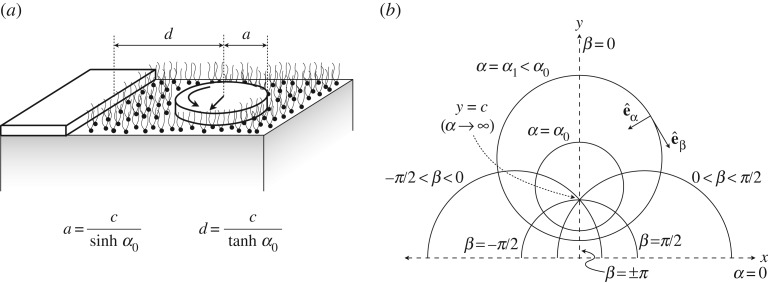
Figure 1.

(a) Typical geometry of a cylindrical disc embedded on a flat interface near an ‘interfacial wall’. (b) The bipolar coordinate system.

While surfactant monolayers are easier to compress than 3D fluids, Marangoni elasticity offers a restoring force against inhomogeneous compression. For example, a translating disc compresses the surfactant monolayer in front of it and dilates the monolayer behind it. This sets up surface concentration gradients that drive Marangoni flows from the front to the back of the disc, returning the surface species to a uniform concentration distribution. When Marangoni stresses are stronger than surface pressure gradients generated by fluid motion, the monolayer behaves like an incompressible 2D fluid [10,29]. The surface pressure in equation (2.1) then acts to enforce incompressibility, while the Π-dependence of viscosity is explicitly retained.

In the interest of highlighting the effect of Π-dependent viscosity, we will work in the mathematically simpler regime where Bo≫1. Non-dimensionalizing equation (2.1) over characteristic length L, velocity U and surface stress (which, in this regime, scales with the surface viscous term ∼η_sU), the last term is clearly $\mathcal{O}(1/Bo)$. While eliminating this coupling reintroduces the divergence associated with 2D Stokes flow at infinity, we will assume that all relevant length scales of interest lie within the Boussinesq length [17]. Then, the interface is decoupled from the bulk, and its dynamics follow the Stokes equations

$${\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }[{\eta }_{\mathrm{s}}(\mathit{\Pi })({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{\mathrm{T}})]={\mathbf{\nabla }}_{\mathrm{s}}\mathit{\Pi },{\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}=0,$$ 2.2

albeit with a surface pressure-dependent surface shear viscosity. The surface pressure, like the bulk pressure in 3D fluid dynamics, then acts to enforce surface incompressibility.

For most insoluble surfactants, a moderate change in Π drastically changes η_s. For example, a major constituent of pulmonary surfactant and cell membranes is the phospholipid dipalmitoylphosphatidylcholine (DPPC), which forms stable monolayers at air–water interfaces. Above a critical surface pressure (approx. 8 mN m⁻¹ at room temperature), DPPC undergoes a phase transition to a liquid-condensed phase [26], above which its surface viscosity grows exponentially with Π [20,28]. This can be qualitatively reasoned in terms of free-area theories of viscosity [27], and a good approximation for the surface viscosity of such a ‘Π-thickening’ monolayer is

$${\eta }_{\mathrm{s}}(\mathit{\Pi })=C\hspace{0.17em}{\mathrm{e}}^{\mathit{\Pi }/{\mathit{\Pi }}_{\mathrm{c}}}={\eta }_{\mathrm{s}}^0\hspace{0.17em}{\mathrm{e}}^{\mathit{\Pi }-{\mathit{\Pi }}_{\mathrm{\infty }}/{\mathit{\Pi }}_{\mathrm{c}}}.$$ 2.3

Here, C is a constant, Π is the ‘thermodynamic’ surface pressure from equation (1.2) and Π_c is the pressure scale over which this exponential change occurs. We define ${\eta }_{\mathrm{s}}^0=C\hspace{0.17em}{\mathrm{e}}^{{\mathit{\Pi }}_{\mathrm{\infty }}/{\mathit{\Pi }}_{\mathrm{c}}}$ as the reference or undisturbed surface viscosity of the monolayer. Then, $\mathit{\Pi }-{\mathit{\Pi }}_{\mathrm{\infty }}$ is the ‘mechanical’ surface pressure that enters equation (2.2).

For a Newtonian interface, ${\mathit{\Pi }}_{\mathrm{c}}\to \mathrm{\infty }$, while Π_c is measured to be approximately 6–8 mN m⁻¹ for DPPC. Certain surfactants (e.g. eicosanol [12]) exhibit ‘Π-thinning’ due to tilt transitions associated with an increase in surface pressure [26]. All results below are easily adapted to Π-thinning surfactants by inverting the sign of Π_c.

Consider the translation and/or rotation of a particle embedded within a bounded surfactant monolayer (figure 1a). The boundary conditions associated with such motion are

$${\mathbf{\text{u}}}_{\mathrm{s}}={\mathbf{\text{U}}}_{\mathrm{p}}+{\mathbf{\Omega }}_{\mathrm{p}}\times (\mathbf{\text{x}}-{\mathbf{\text{x}}}_0)\text{when}\hspace{0.17em}\mathbf{\text{x}}\in \ell$$ 2.4

and

$${\mathbf{\text{u}}}_{\mathrm{s}}=\mathbf{\text{0}}\text{when}\hspace{0.17em}\mathbf{\text{x}}\in {\ell }_w,$$ 2.5

where ℓ defines the boundary of the particle with centre of mass x₀, and ℓ_w represents a stationary ‘interfacial wall’. U_p and Ω_p are the imposed translational and rotational velocities of the particle, respectively.

Clearly, equation (2.2), in conjunction with equation (2.3), is extremely nonlinear. We approach this perturbatively, for small departures of η_s(Π) from η⁰_s. We set ${\mathit{\Pi }}_{\mathrm{\infty }}=0$ without loss of generality. Specifically, when |Π|≪Π_c, we rewrite the momentum equation in equation (2.2) as

$${\eta }_{\mathrm{s}}^0{\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }[\{1+\frac{\mathit{\Pi }}{{\mathit{\Pi }}_{\mathrm{c}}}+\mathcal{O}\left({\left(\frac{\mathit{\Pi }}{{\mathit{\Pi }}_{\mathrm{c}}}\right)}^2\right)\}({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{\mathrm{T}})]={\mathbf{\nabla }}_{\mathrm{s}}\mathit{\Pi }.$$ 2.6

Non-dimensionalizing over characteristic scales of a for length, U for fluid velocity and Π₀=Uη⁰_s/a for surface pressure, and retaining only terms to leading order in the ratio Π/Π_c gives

$${\mathbf{\nabla }}_{\mathrm{s}}^{\ast }\mathbf{\cdot }[(1+\zeta {\mathit{\Pi }}^{\ast })({\mathbf{\nabla }}_{\mathrm{s}}^{\ast }{\mathbf{\text{u}}}_{\mathrm{s}}^{\ast }+{\mathbf{\nabla }}_{\mathrm{s}}^{\ast }{\mathbf{\text{u}}}_{\mathrm{s}}^{\ast \mathrm{T}})]={\mathbf{\nabla }}_{\mathrm{s}}^{\ast }{\mathit{\Pi }}^{\ast }.$$ 2.7

For simplicity of notation, we drop the asterisks in dimensionless variables now. We have introduced the dimensionless group

$$\zeta =\frac{{\mathit{\Pi }}_0}{{\mathit{\Pi }}_{\mathrm{c}}}=\frac{U{\eta }_{\mathrm{s}}^0}{a{\mathit{\Pi }}_{\mathrm{c}}}\ll 1,$$ 2.8

which is a ratio of the characteristic surface pressure set up by particle motion to Π_c. Alternatively, ζ may be interpreted as a ratio of U to $U_{\mathrm{c}}\sim {\mathit{\Pi }}_{\mathrm{c}}a/{\eta }_{\mathrm{s}}^0$, where U_c is the surface velocity characteristic of surface pressure variations comparable to Π_c. In this sense, U has to be ‘small’ enough for the asymptotic expansion to remain valid.

Recasting equation (2.7) in terms of a stress tensor σ, the dimensionless governing equations read:

$${\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}=0,{\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }\mathit{\sigma }=\mathbf{\text{0}}$$ 2.9a

and

$$\mathit{\sigma }=-\mathit{\Pi }\hspace{0.17em}\mathbf{\text{I}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{\mathrm{T}}+\zeta \hspace{0.17em}\mathit{\Pi }({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{\mathrm{T}})+\mathcal{O}({\zeta }^2).$$ 2.9b

Then, expanding the fluid fields in powers of ζ as

$$\{{\mathbf{\text{u}}}_{\mathrm{s}},\mathit{\Pi },\mathit{\sigma }\}=\{{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)},{\mathit{\Pi }}^{(0)},{\mathit{\sigma }}^{(0)}\}+\zeta \{{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)},{\mathit{\Pi }}^{(1)},{\mathit{\sigma }}^{(1)}\}+\mathcal{O}({\zeta }^2)$$ 2.10

and substituting in equation (2.9), we find the zeroth (Newtonian) order to be 2D Stokes flow, as expected:

$${\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)}=0,{\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathit{\sigma }}^{(0)}=\mathbf{\text{0}}$$ 2.11a

and

$${\mathit{\sigma }}^{(0)}=-{\mathit{\Pi }}^{(0)}\mathbf{\text{I}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)}+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)})}^{\mathrm{T}}.$$ 2.11b

At first order in ζ, however, we have

$${\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)}=0,{\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathit{\sigma }}^{(1)}=\mathbf{\text{0}}$$ 2.12a

and

$${\mathit{\sigma }}^{(1)}=-{\mathit{\Pi }}^{(1)}\mathbf{\text{I}}+{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)}+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)})}^{\mathrm{T}}+{\mathit{\Pi }}^{(0)}({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)}+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)})}^{\mathrm{T}}).$$ 2.12b

Here, σ⁽¹⁾ is the stress associated with the leading effect of pressure-dependent rheology. We chose to set up the problem such that the particle is constrained to move with imposed velocities U_p and Ω_p, which are entirely accounted for by the leading-order flow. Any non-trivial effect of Π-dependent rheology, therefore, would yield a non-zero force F⁽¹⁾ or torque T⁽¹⁾ at $\mathcal{O}(\zeta )$. These can be computed as the moments of the stress tensor σ⁽¹⁾:

$${\mathbf{\text{F}}}^{(1)}=\int \widehat{\mathbf{\text{n}}}\mathbf{\cdot }{\mathit{\sigma }}^{(1)}\hspace{0.17em}\mathrm{d}\ell \mathrm{and}{\mathbf{\text{T}}}^{(1)}=\int \mathbf{\text{x}}\times {\mathit{\sigma }}^{(1)}\mathbf{\cdot }\widehat{\mathbf{\text{n}}}\hspace{0.17em}\mathrm{d}\ell ,$$ 2.13

where $\widehat{\mathbf{\text{n}}}$ is the normal pointing from the particle into the monolayer.

(b). A reciprocal approach

Solving the $\mathcal{O}(\zeta )$ equations of motion is at best tedious. However, the Lorentz reciprocal theorem [35] allows us to circumvent solving the inhomogeneous equation, using only solutions to homogeneous Newtonian problems. The reciprocal theorem, in its classic form, relates two different solutions to the Stokes equations in the same geometry, such that knowing one can provide useful information about the other. Generalizations of the reciprocal theorem beyond Newtonian problems have been successfully applied to evaluate perturbative solutions in both 3D [31,33,34] and 2D fluids [36].

To illustrate this, let us first consider an ‘auxiliary’ problem of a particle moving in a Newtonian 2D fluid (of constant surface viscosity η⁰_s) with translational and rotational velocities U_aux and Ω_aux, respectively. Let the associated fluid velocity, stress and hydrodynamics moments on the particle in the auxiliary problem be u_aux, σ_aux and {F_aux,T_aux}, respectively. Then, we have the vector identity

$${\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }({\mathit{\sigma }}_{\text{aux}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)})=({\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }{\mathit{\sigma }}_{\text{aux}})\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)}+{\mathit{\sigma }}_{\text{aux}}\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)}={\mathit{\sigma }}_{\text{aux}}\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)},$$ 2.14

where we have used the momentum equation, ∇_s⋅σ_aux=0. Similarly,

$${\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }({\mathit{\sigma }}^{(1)}\mathbf{\cdot }{\mathbf{\text{u}}}_{\text{aux}})={\mathit{\sigma }}^{(1)}\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\text{aux}}.$$ 2.15

Subtracting equation (2.15) from equation (2.14) and integrating over the entire fluid domain, we find

$$\int [{\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }({\mathit{\sigma }}_{\text{aux}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)})-{\mathbf{\nabla }}_{\mathrm{s}}\mathbf{\cdot }({\mathit{\sigma }}^{(1)}\mathbf{\cdot }{\mathbf{\text{u}}}_{\text{aux}})]\hspace{0.17em}\mathrm{d}S=\int [{\mathit{\sigma }}_{\text{aux}}\mathbf{:}({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)})-{\mathit{\sigma }}^{(1)}\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\text{aux}}]\mathrm{d}S,$$ 2.16

which is the general version of the reciprocal theorem. For Newtonian problems, the right-hand side vanishes.

The left-hand side of equation (2.16) can be simplified by applying the divergence theorem, and then using the boundary conditions on the disc, from equation (2.4). Then, applying the force and torque balances from equation (2.13), the left-hand side becomes

$$\begin{array}{rl}& \hspace{0.17em}-\int \widehat{\mathbf{\text{n}}}\mathbf{\cdot }{\mathit{\sigma }}_{\text{aux}}\mathbf{\cdot }{\mathbf{\text{u}}}_{\mathrm{s}}^{(1)}\hspace{0.17em}\mathrm{d}\ell +\int \widehat{\mathbf{\text{n}}}\mathbf{\cdot }{\mathit{\sigma }}^{(1)}\mathbf{\cdot }{\mathbf{\text{u}}}_{\text{aux}}\hspace{0.17em}\mathrm{d}\ell \\ & \hspace{0.17em}=-({\mathbf{\text{F}}}_{\text{aux}}\mathbf{\cdot }{\mathbf{\text{U}}}_{\mathrm{p}}^{(1)}+{\mathbf{\text{T}}}_{\text{aux}}\mathbf{\cdot }{\mathbf{\Omega }}_{\mathrm{p}}^{(1)})+({\mathbf{\text{F}}}^{(1)}\mathbf{\cdot }{\mathbf{\text{U}}}_{\text{aux}}+{\mathbf{\text{T}}}^{(1)}\mathbf{\cdot }{\mathbf{\Omega }}_{\text{aux}}).\end{array}$$ 2.17

We choose to constrain the particle to its leading-order motion and determine the external force or torque thus generated at $\mathcal{O}(\zeta )$; that is, ${\mathbf{\text{U}}}_{\mathrm{p}}^{(1)}={\mathbf{\Omega }}_{\mathrm{p}}^{(1)}=\mathbf{\text{0}}$. Simplifying the right-hand side of equation (2.16) using the definitions of the stresses and putting everything together yields

$${\mathbf{\text{F}}}^{(1)}\mathbf{\cdot }{\mathbf{\text{U}}}_{\text{aux}}+{\mathbf{\text{T}}}^{(1)}\mathbf{\cdot }{\mathbf{\Omega }}_{\text{aux}}=-\int {\mathit{\Pi }}^{(0)}[{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)}+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{s}}^{(0)})}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\text{aux}}\hspace{0.17em}\mathrm{d}S.$$ 2.18

Therefore, F⁽¹⁾ or T⁽¹⁾ can be evaluated using only the leading-order Newtonian solution {u⁽⁰⁾,Π⁽⁰⁾} and the flow field u_aux corresponding to another known Newtonian problem in the same geometry. Such a reciprocal formulation is therefore particularly appealing, and we use specific choices of U_aux and Ω_aux in the following sections to determine the $\mathcal{O}(\zeta )$ forces and torques in model problems. Note that the net force (or torque) at this order scales with the characteristic velocity as ζF⁽¹⁾∼U²: reversing the direction of velocity has no effect on the $\mathcal{O}(\zeta )$ force (or torque). This departure from Newtonian reversibility and its consequences are the central themes of this work.

(c). Newtonian solution in cylindrical bipolar coordinates

The flow and pressure fields required to evaluate the reciprocal integral in equation (2.18) are all Newtonian solutions to 2D Stokes flow with constant surface viscosity η⁰_s. For cylindrical discs embedded in the monolayer, it is convenient to work in the cylindrical bipolar coordinate system [37–39] as shown in figure 1b. In terms of Cartesian coordinates, the bipolar coordinates (α,β) are

$$\alpha +\mathrm{i}\beta =\log \frac{x+\mathrm{i}(y+c)}{x+\mathrm{i}(y-c)}.$$ 2.19

Equivalently, $x=h\sin \beta$ and $y=h\sinh \alpha$, where

$$h=\frac{c}{\cosh \alpha -\cos \beta }$$ 2.20

is a scale factor. Here, $0<\alpha <\mathrm{\infty }$, −π≤β<π and c is a positive number with dimensions of length. Particularly, curves of constant α correspond to non-intersecting, coaxial circles with centres along the y-axis. Curves of constant β correspond to intersecting circles with centres along the x-axis. We set α=α₀ to represent a circle of radius $a=c/\sinh {\alpha }_0$ at a distance $d=c/\tanh {\alpha }_0$ from the origin along the vertical axis (figure 1). Conversely, such a circle is described by ${\alpha }_0={\cosh }^{-1}(d/a)$ and then c²=d²−a². Also, we will use α₁<α₀ to represent a circle of a larger radius that will serve as the outer wall, such that the monolayer is confined to within α∈[α₁,α₀]. The limit of ${\alpha }_1\to 0$ corresponds to an outer wall of infinite radius, which represents a plane wall along the x-axis.

Defining a stream function Ψ in terms of the fluid velocities such that

$$u_{\alpha }=-\frac{1}{h}\frac{\mathrm{\partial }\mathrm{\Psi }}{\mathrm{\partial }\beta }\mathrm{and}{u}_{\beta }=\frac{1}{h}\frac{\mathrm{\partial }\mathrm{\Psi }}{\mathrm{\partial }\alpha },$$ 2.21

the Stokes equations can be recast as a biharmonic equation: ∇⁴Ψ=0. One way of writing the general solution of this equation that decays sufficiently rapidly at infinity is [37–39]

$$\begin{array}{rl}\frac{\mathrm{\Psi }}{h}& \hspace{0.17em}=A\alpha (\cosh \alpha -\cos \beta )+(B+C\alpha )\sinh \alpha -D\alpha \sin \beta \\ & \hspace{0.17em}+\sum _{n=1}^{\mathrm{\infty }}[\{a_n\cosh (n+1)\alpha +b_n\sinh (n+1)\alpha +c_n\cosh (n-1)\alpha +d_n\sinh (n-1)\alpha \}\cos n\beta \\ & \hspace{0.17em}+\{a_n^{\prime }\cosh (n+1)\alpha +b_n^{\prime }\sinh (n+1)\alpha +c_n^{\prime }\cosh (n-1)\alpha +d_n^{\prime }\sinh (n-1)\alpha \}\sin n\beta ],\end{array}$$ 2.22

where the coefficients are determined by the general boundary conditions:

$${\mathbf{\text{u}}}^{(0)}={\mathbf{\text{U}}}_{\mathrm{p}}+{\mathbf{\Omega }}_{\mathrm{p}}\times a(-{\widehat{\mathbf{\text{e}}}}_{\alpha })\text{at}\alpha ={\alpha }_0$$ 2.23a

and

$${\mathbf{\text{u}}}^{(0)}=\mathbf{\text{0}}\text{at}\alpha ={\alpha }_1.$$ 2.23b

The Cartesian unit vectors can be represented in terms of the bipolar unit vectors as

$$\begin{array}{rl}{\widehat{\mathbf{\text{e}}}}_x& \hspace{0.17em}=\frac{h}{c}[-(\cosh \alpha \cos \beta -1){\widehat{\mathbf{\text{e}}}}_{\alpha }-\sinh \alpha \sin \beta {\widehat{\mathbf{\text{e}}}}_{\beta }],\end{array}$$ 2.24a

$$\begin{array}{rl}{\widehat{\mathbf{\text{e}}}}_y& \hspace{0.17em}=\frac{h}{c}[-\sinh \alpha \sin \beta {\widehat{\mathbf{\text{e}}}}_{\alpha }+(\cosh \alpha \cos \beta -1){\widehat{\mathbf{\text{e}}}}_{\beta }]\end{array}$$ 2.24b

and ${\widehat{\mathbf{\text{e}}}}_z\times {\widehat{\mathbf{\text{e}}}}_{\alpha }={\widehat{\mathbf{\text{e}}}}_{\beta }$. Using these, and imposing the boundary conditions in equations (2.23), one can solve for the constants in the expression for the stream function in equation (2.22).

With the stream function known, the pressure field can be obtained from the Cauchy–Riemann equations [38,40]:

$$\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }\alpha }={\eta }_{\mathrm{s}}^0\frac{\mathrm{\partial }{\mathrm{\nabla }}^2\mathrm{\Psi }}{\mathrm{\partial }\beta }\mathrm{and}\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }\beta }=-{\eta }_{\mathrm{s}}^0\frac{\mathrm{\partial }{\mathrm{\nabla }}^2\mathrm{\Psi }}{\mathrm{\partial }\alpha }.$$ 2.25

Then, the Newtonian force (or torque) acting on the disc is obtained by integrating the traction $\widehat{\mathbf{\text{n}}}\mathbf{\cdot }{\mathit{\sigma }}^{(0)}$ (or its moment) over the cylinder surface [39]:

$${\mathbf{\text{F}}}^{(0)}=4\pi {\eta }_{\mathrm{s}}^0(C{\widehat{\mathbf{\text{e}}}}_x+D{\widehat{\mathbf{\text{e}}}}_y)$$ 2.26a

and

$${\mathbf{\text{T}}}^{(0)}=4\pi {\eta }_{\mathrm{s}}^{0}a(A\sinh {\alpha }_0+C\cosh {\alpha }_0){\widehat{\mathbf{\text{e}}}}_z,$$ 2.26b

where, again, α₀ represents the streamline corresponding to the edge of the disc.

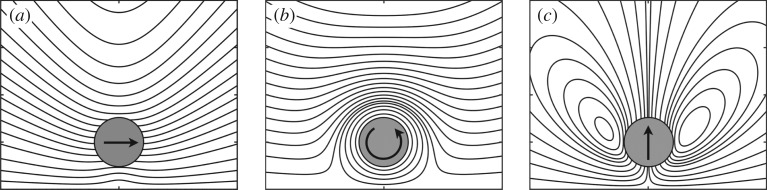
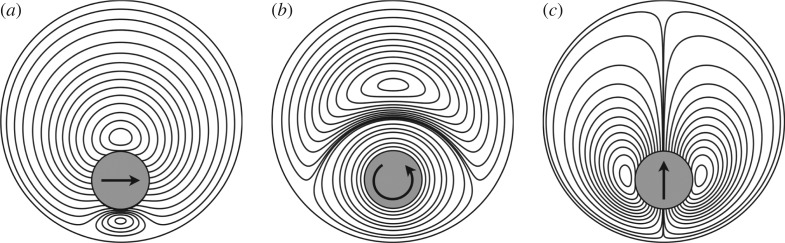
A surprising result [38,39] is that translation and rotation are decoupled for a cylinder moving next to a plane wall (i.e. ${\alpha }_1\to 0$). For instance, a torque-free cylinder sedimenting parallel to a wall will not rotate—unlike the corresponding case for a sphere. This is particularly convenient, as rotation and translation can be treated as independent $\mathcal{O}(1)$ problems in the reciprocal integration for plane walls. We will consider these problems first, which will serve to highlight the nature of the $\mathcal{O}(\zeta )$ force and its implications in breaking kinematic reversibility. The mathematical machinery is easily extendable to the case of coupled translation and rotation, as we shall then see with an interfacial ‘journal bearing’. In every case, we first seek the solution to three independent Newtonian problems: a cylinder translating parallel to the wall (${\mathbf{\text{U}}}_{\mathrm{p}}=U{\widehat{\mathbf{\text{e}}}}_x$), rotating next to the wall (${\mathbf{\Omega }}_{\mathrm{p}}=\mathrm{\Omega }{\widehat{\mathbf{\text{e}}}}_z$) and translating perpendicular to the wall (${\mathbf{\text{V}}}_{\mathrm{p}}=V{\widehat{\mathbf{\text{e}}}}_y$) (figure 2).

Figure 2.

The $\mathcal{O}(1)$ flow fields used to evaluate the lateral forces at $\mathcal{O}(\zeta )$ for a disc moving next to a plane wall. Streamlines correspond to the Newtonian solutions for a disc (a) translating parallel to the wall, (b) rotating adjacent to the wall and (c) translating perpendicular to the wall. The plane wall is the bottom edge of each panel.

3. Cylinder next to a plane wall

(a). Translation

A translating disc compresses the surfactant monolayer in front of it and expands it in the rear. When the interface is incompressible, the surface pressure responds by increasing (or decreasing) in front of (or behind) the disc. Consequently, η_s(Π) increases and changes the net force on the particle. For a disc moving quasi-steadily along a straight line in an infinite interface, however, the change in η_s preserves the dipolar symmetry of the surface pressure distribution, and generates no transverse forces. When near a barrier, however, this symmetry is lost and we expect a finite force in the direction perpendicular to the wall.

The force and torque on the disc at $\mathcal{O}(\zeta )$ can be obtained by appropriately choosing the auxiliary Newtonian solution in the reciprocal integration. Specifically, considering separately the cases $\{{\mathbf{\text{U}}}_{\text{aux}},{\mathbf{\Omega }}_{\text{aux}}\}=\{{\widehat{\mathbf{\text{e}}}}_x,\mathbf{\text{0}}\}$, $\{{\widehat{\mathbf{\text{e}}}}_y,\mathbf{\text{0}}\}$ and $\{\mathbf{\text{0}},{\widehat{\mathbf{\text{e}}}}_z\}$, equation (2.18) can be rewritten in bipolar coordinates as

$$\begin{array}{rl}{F}_{\parallel }^{\parallel }& \hspace{0.17em}={\mathbf{\text{F}}}_{\parallel }^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_x=-{\int }_{-\pi }^{\pi }{\int }_0^{{\alpha }_0}{\mathit{\Pi }}_{\parallel }[{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\parallel }+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\parallel })}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\parallel }{h}^2\hspace{0.17em}\mathrm{d}\alpha \hspace{0.17em}\mathrm{d}\beta ,\end{array}$$ 3.1a

$$\begin{array}{rl}{F}_{\parallel }^{\perp }& \hspace{0.17em}={\mathbf{\text{F}}}_{\parallel }^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_y=-{\int }_{-\pi }^{\pi }{\int }_0^{{\alpha }_0}{\mathit{\Pi }}_{\parallel }[{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\parallel }+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\parallel })}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\perp }{h}^2\hspace{0.17em}\mathrm{d}\alpha \hspace{0.17em}\mathrm{d}\beta \end{array}$$ 3.1b

$$\begin{array}{rl}\text{and}{T}_{\parallel }& \hspace{0.17em}={\mathbf{\text{T}}}_{\parallel }^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_z=-{\int }_{-\pi }^{\pi }{\int }_0^{{\alpha }_0}{\mathit{\Pi }}_{\parallel }[{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\parallel }+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\parallel })}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\circlearrowright }\hspace{0.17em}{h}^2\hspace{0.17em}\mathrm{d}\alpha \hspace{0.17em}\mathrm{d}\beta .\end{array}$$ 3.1c

The subscripts ∥, ⊥ and $\circlearrowright$ denote the velocity and pressure fields corresponding to translation parallel to the wall, perpendicular to the wall and rotation adjacent to the wall, respectively. The superscripts on the forces denote their directions.

The Newtonian velocity and pressure fields {u_∥(x),Π_∥(x)} are the $\mathcal{O}(1)$ solution to translation parallel to the wall with velocity U. We find that the only non-zero constants in equation (2.22) in the case of translation parallel to a plane wall are

$$A=-B=2b_1=\frac{U}{{\alpha }_0}\coth {\alpha }_0\mathrm{and}C=2a_1=-2c_1=-\frac{U}{{\alpha }_0}.$$ 3.2

The corresponding surface pressure distribution is then

$${\mathit{\Pi }}_{\parallel }=\frac{{\eta }_{\mathrm{s}}^{0}U}{c}\frac{\coth {\alpha }_0}{{\alpha }_0}[2\sin \beta \cosh \alpha +\sin 2\beta (\tanh {\alpha }_0\sinh 2\alpha -\cosh 2\alpha )].$$ 3.3

For the auxiliary flow field in equation (3.1a), the coefficients are the same as above. The only non-zero coefficients for the auxiliary flow field u_⊥(x) in equation (3.1b) (corresponding to a disc moving at velocity V perpendicular to the wall) are

$$D=2b_1^{\prime }=-\frac{V}{{\alpha }_0-\tanh {\alpha }_0}\mathrm{and}{a}_1^{\prime }=-c_1^{\prime }=-\frac{1}{2}D\tanh {\alpha }_0.$$ 3.4

Similarly, for the auxiliary solution ${\mathbf{\text{u}}}_{\circlearrowright }(\mathbf{\text{x}})$ in equation (3.1c) corresponding to rotation at angular velocity Ω, we have

$$A=-B=2b_1=-a\mathrm{\Omega }\frac{\coth {\alpha }_0}{\sinh {\alpha }_0}\mathrm{and}{a}_1=-c_1=a\mathrm{\Omega }\frac{1}{2\sinh {\alpha }_0}.$$ 3.5

We non-dimensionalize all variables as before and set V =U=aΩ=1. The integrals in equation (3.1) are cumbersome, but analytically tractable in terms of the streamline α₀ and the scale factor c that define a particular cylinder. It is illustrative to work with the dimensionless distance δ=d/a of the centre of the cylinder from the wall, such that ${\alpha }_0={\cosh }^{-1}\delta$ and $c/a=\sqrt{{\delta }^2-1}$.

The only non-zero integral at $\mathcal{O}(\zeta )$ corresponds to equation (3.1b), and results in a force in the direction perpendicular to the wall:

$$F_{\parallel }^{\perp }(\delta )=\frac{2\pi (2\delta {\cosh }^{-1}\delta -(1+{\delta }^2)\sqrt{{\delta }^2-1})}{{({\delta }^2-1)}^{3/2}{({\cosh }^{-1}\delta )}^2(\sqrt{{\delta }^2-1}-\delta {\cosh }^{-1}\delta )}.$$ 3.6

Both $F_{\parallel }^{\parallel }$ and T_∥ are identically zero at $\mathcal{O}(\zeta )$: corrections to the wall-parallel drag or torque arise at best at $\mathcal{O}({\zeta }^2)$. This can be rationalized in terms of the symmetries of the stresses around the inner disc. At $\mathcal{O}(1)$, the fluid stress is an odd function of x about the disc, and adds up to a net wall-parallel drag as expected. At $\mathcal{O}(\zeta )$, however, the stress is an even function around the disc, and the net result is only a force perpendicular to the wall. To clarify this, consider the net force on the disc:

$${\mathbf{\text{F}}}_{\mathrm{net}}=F_{\mathrm{d}}\hspace{0.17em}{\widehat{\mathbf{\text{e}}}}_x+\zeta (F_{\parallel }^{\parallel }{\widehat{\mathbf{\text{e}}}}_x+F_{\parallel }^{\perp }{\widehat{\mathbf{\text{e}}}}_y)+\mathcal{O}({\zeta }^2),$$ 3.7

where F_d is the Newtonian drag from equation (2.26). In dimensional terms, this reads

$${\mathbf{\text{F}}}_{\mathrm{net}}=-\frac{4\pi {\eta }_{\mathrm{s}}^{0}aU}{{\cosh }^{-1}(d/a)}{\widehat{\mathbf{\text{e}}}}_x+\frac{{({\eta }_{\mathrm{s}}^{0}U)}^2}{{\mathit{\Pi }}_{\mathrm{c}}a}(F_{\parallel }^{\parallel }{\widehat{\mathbf{\text{e}}}}_x+F_{\parallel }^{\perp }{\widehat{\mathbf{\text{e}}}}_y)+\mathcal{O}(U^3).$$ 3.8

The $\mathcal{O}(\zeta )$ corrections scale as U² and do not change sign upon reversing the direction of motion. Drag against translation (${\mathbf{\text{F}}}_{\mathrm{net}}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_x$) must be an odd function of U to reflect this change of sign, and therefore $F_{\parallel }^{\parallel }=0$. Corrections to wall-parallel drag or torque can thus appear at best at $\mathcal{O}(U^3)$, or equivalently, at $\mathcal{O}({\zeta }^2)$. This argument is illustrated further in §3c, where the stresses in a thin film are quantified to demonstrate these symmetries.

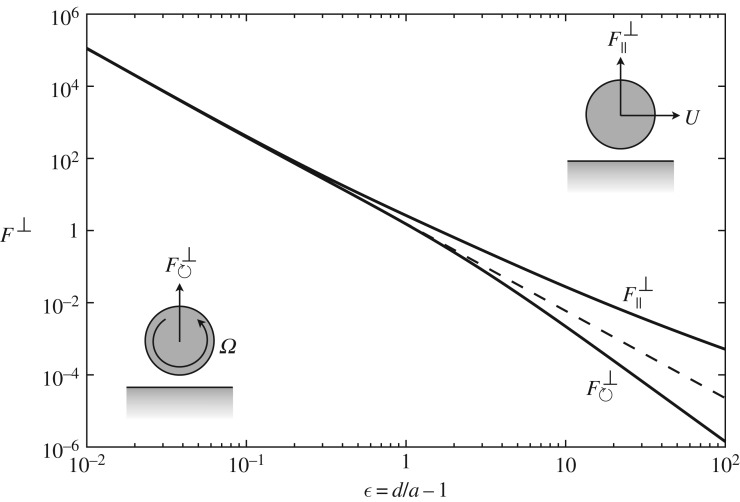
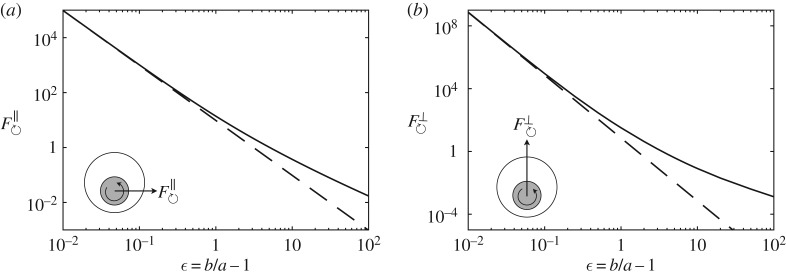
The force $F_{\parallel }^{\perp }$ is shown in figure 3 as a function of the separation ϵ=δ−1. For large distances from the wall, $F_{\parallel }^{\perp }$ decays to zero. This is expected from our discussion above regarding a cylinder in an infinite quiescent fluid, where symmetry dictates that the $\mathcal{O}(\zeta )$ contributions be zero. The more useful limit is when the disc is very close to the wall, whereupon equation (3.6) behaves as

$$F_{\parallel }^{\perp }(ϵ\ll 1)\sim \frac{\pi }{2\sqrt{2}}\hspace{0.17em}{ϵ}^{-5/2}+\mathcal{O}({ϵ}^{-3/2}).$$ 3.9

The effect of Π-dependent rheology is, therefore, more prominent as the fluid film between surface layers becomes thinner. Within this thin layer, a Π-dependent lubrication analysis [29] is possible, which, as we show in §3c, retrieves the same limiting behaviour as equation (3.9).

Figure 3.

Force on the disc due to Π-dependent η_s as a function of distance from the plane wall, following equations (3.6) and (3.12). This $\mathcal{O}(\zeta )$ force acts perpendicular to the wall and breaks the kinematic reversibility of Stokes flow. The dashed line is the ϵ^−5/2 behaviour predicted by the lubrication analysis (§3c).

The complementary case of a disc approaching (or departing) a wall along the y-direction is amenable to a simple symmetry argument. Such a flow is left–right symmetric about the disc, and there will not arise any stresses that result in a net force parallel to the wall. Indeed, it can be shown by integrating the corresponding velocity and pressure fields in place of equation (3.1) that this $\mathcal{O}(\zeta )$ force $F_{\perp }^{\parallel }={\mathbf{\text{F}}}_{\perp }^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_x$ is indeed zero.

(b). Rotation

As with translation, a disc rotating quasi-steadily in an infinite interface would not feel a net force. However, the surface pressure distribution changes in the proximity of a wall, which in turn changes the local surface viscosity to result in a net force perpendicular to the wall.

Consider a cylindrical disc rotating at angular velocity Ω near a wall (such that the characteristic fluid velocity scale is now U=aΩ). The only non-zero coefficients in the stream function corresponding to ${\mathbf{\text{u}}}_{\circlearrowright }(\mathbf{\text{x}})$ are the same as in equation (3.5), giving a surface pressure distribution:

$$\begin{array}{rl}{\mathit{\Pi }}_{\circlearrowright }& \hspace{0.17em}=-\frac{{\eta }_{\mathrm{s}}^{0}a\omega }{c}\hspace{0.17em}\frac{\coth {\alpha }_0}{\sinh {\alpha }_0}[2\sin \beta (\cosh \alpha -\tanh {\alpha }_0\sinh \alpha )\\ & \hspace{0.17em}+\sin 2\beta (\tanh {\alpha }_0\sinh 2\alpha -\cosh 2\alpha )].\end{array}$$ 3.10

Again, consider the auxiliary Newtonian flow field u_⊥(x) by setting Ω_aux=0 and ${\mathbf{\text{U}}}_{\text{aux}}={\widehat{\mathbf{\text{e}}}}_y$. The only non-trivial reciprocal integral is

$$F_{\circlearrowright }^{\perp }={\mathbf{\text{F}}}_{\circlearrowright }^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_y=-{\int }_{-\pi }^{\pi }{\int }_0^{{\alpha }_0}{\mathit{\Pi }}_{\circlearrowright }[{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\circlearrowright }+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\circlearrowright })}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\perp }\hspace{0.17em}{h}^2\hspace{0.17em}\mathrm{d}\alpha \hspace{0.17em}\mathrm{d}\beta ,$$ 3.11

where, like before, the subscripts refer to the modes of motion ($\circlearrowright$ for rotation) and $F_{\circlearrowright }^{\perp }$ is the $\mathcal{O}(\zeta )$ force on the disc in the direction perpendicular to the wall.

Performing this integral, and recasting in terms of the distance δ=d/a from the centre of the disc, the dimensionless vertical force at $\mathcal{O}(\zeta )$ is now

$$F_{\circlearrowright }^{\perp }(\delta )=\frac{2\pi (2\delta {\cosh }^{-1}\delta -(1+{\delta }^2)\sqrt{{\delta }^2-1})}{{({\delta }^2-1)}^{5/2}(\sqrt{{\delta }^2-1}-\delta {\cosh }^{-1}\delta )}.$$ 3.12

As shown in figure 3, $F_{\circlearrowright }^{\perp }$ decays with δ at a rate faster than due to a translating disc. More interestingly, the near-wall behaviour (ϵ=δ−1≪1) is identical to that of translation. In fact, expanding equation (3.12) in this limit, we find

$$F_{\circlearrowright }^{\perp }(ϵ\ll 1)\sim \frac{\pi }{2\sqrt{2}}{ϵ}^{-5/2},$$ 3.13

again suggesting that the problem is indistinguishable from the case of a disc sliding past the wall when the gap is very small.

A similar integral can be performed to evaluate the $\mathcal{O}(\zeta )$ force parallel to the wall on a rotating disc. The first-order problem maintains the symmetries of the Newtonian problem, and the force $F_{\circlearrowright }^{\parallel }={\mathbf{\text{F}}}_{\circlearrowright }^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_x$ evaluates to zero. Therefore, a cylinder rotating next to a wall in a pressure-thickening medium will experience a force solely in the direction perpendicular to the wall—if unconstrained, the cylinder will translate vertically away from the wall (see §4b) while maintaining its relative horizontal position.

(c). The lubrication limit

Thin gaps on the interface naturally amplify surface pressure fields, and therefore also the effects of Π-dependent surface viscosity as evinced by the behaviour of $F_{\parallel ,\mathrm{\Omega }}^{\perp }$ when $ϵ\to 0$. In thin gaps, momentum transport is predominantly in one direction, and the governing equations simplify significantly. In fact, it is possible [29] to obtain analytical solutions to flows within 2D lubrication geometries with Π-dependent η_s without resorting to asymptotic methods as we have done here.

Let h(x) be the profile of the thin fluid layer between a disc and a wall (figure 4a) such that the characteristic thickness of this gap, h₀, is much smaller that the size of the disc (h₀≪a). With the same assumptions as before (incompressible 2D flow; high Bo), the momentum equation equation (2.2) can be shown to simplify in thin gaps to [29]:

$$\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }x}={\eta }_{\mathrm{s}}(\mathit{\Pi })\frac{{\mathrm{\partial }}^2{u}_{\mathrm{s}}}{\mathrm{\partial }{y}^2},\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }y}=0.$$ 3.14

These equations take the same form as the Newtonian lubrication theory, albeit with a Π-dependent viscosity. Surface pressure (and therefore η_s(Π)) is constant along the y-direction within this approximation, and therefore the x-momentum equation can be integrated like in standard lubrication analysis. In a frame of reference moving with the particle, no-slip conditions are u_s(x,h(x))=0 on the particle surface and u_s(x,0)=−U at the wall. Then, the fluid velocity field and local flux are

$$u_{\mathrm{s}}(x,y)=U(\frac{y}{h(x)}-1)+\frac{1}{2{\eta }_{\mathrm{s}}(\mathit{\Pi })}\frac{\mathrm{d}\mathit{\Pi }}{\mathrm{d}x}y(y-h(x))$$ 3.15

and

$$Q={\int }_0^{h(x)}{u}_{\mathrm{s}}(x,y)\hspace{0.17em}\mathrm{d}y=-\frac{Uh(x)}{2}-\frac{h^3(x)}{12{\eta }_{\mathrm{s}}(\mathit{\Pi })}\frac{\mathrm{d}\mathit{\Pi }}{\mathrm{d}x}.$$ 3.16

Despite the strong nonlinearity due to an arbitrary functional form of η_s(Π), equation (3.16) can be rearranged to a separable ODE:

$$\frac{\mathrm{d}\mathit{\Pi }}{{\eta }_{\mathrm{s}}(\mathit{\Pi })}=-\frac{12}{h{(x)}^3}(Q+\frac{Uh(x)}{2})\mathrm{d}x.$$ 3.17

Remarkably, this relation can be integrated (at least in principle) for any given η_s(Π). Fluid incompressibility dictates that the flow rate Q be constant at every vertical section, and may be obtained by setting the pressure to be equal far away on either side of the particle in equation (3.17): $\mathit{\Pi }(x\to -\mathrm{\infty })=\mathit{\Pi }(x\to +\mathrm{\infty })=0$. We find

$$Q=-\frac{U}{2}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\mathrm{d}x}{h^2(x)}/{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\mathrm{d}x}{h^3(x)}.$$ 3.18

The above form is standard in lubrication theory for Newtonian fluids. The nonlinearity due to pressure-dependent viscosity enters only through the left-hand side of equation (3.17), allowing standard Newtonian results to be adapted in a straightforward manner.

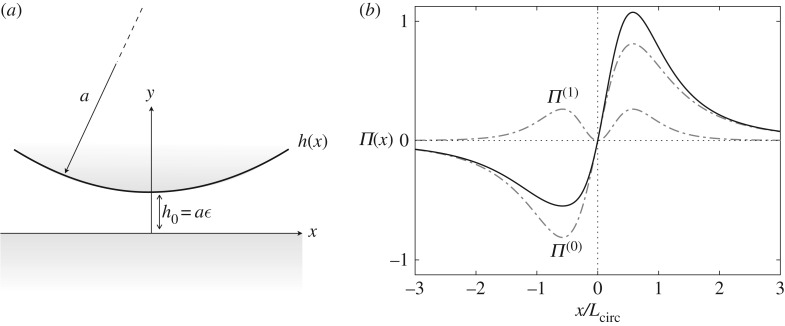
Figure 4.

(a) Geometry of the thin film between a disc and a wall. (b) Surface pressure distribution (in arbitrary units) in the thin gap (solid line) illustrating the Newtonian and $\mathcal{O}(\zeta )$ contributions (dashed-dotted lines) from equation (3.24).

Proceeding further needs an explicit expression for the gap profile. When the gap is small compared to the disc radius (h₀≪a), we can approximate the profile as

$$h(x)=h_0(1+\frac{x^2}{L_{\mathrm{circ}}^2}),$$ 3.19

where

$$L_{\mathrm{circ}}=\sqrt{2h_{0}a}.$$ 3.20

Then, Q=−2Uh₀/3, upon which equation (3.17) becomes

$${\int }_0^{\mathit{\Pi }(x)}\frac{\mathrm{d}{\mathit{\Pi }}^{\prime }}{{\eta }_{\mathrm{s}}({\mathit{\Pi }}^{\prime })}=\frac{6U}{h_0^2}{\int }_{-\mathrm{\infty }}^x(\frac{4}{3}\frac{1}{{(1+x^2/L_{\mathrm{circ}}^2)}^3}-\frac{1}{{(1+x^2/L_{\mathrm{circ}}^2)}^2})\mathrm{d}x.$$ 3.21

We now pick the same form of surface viscosity as before: ${\eta }_{\mathrm{s}}(\mathit{\Pi })={\eta }_{\mathrm{s}}^0\hspace{0.17em}{\mathrm{e}}^{\mathit{\Pi }/{\mathit{\Pi }}_{\mathrm{c}}}$. Performing the integration, the surface pressure distribution becomes

$$\mathit{\Pi }(x)=-{\mathit{\Pi }}_{\mathrm{c}}\ln [1-\frac{8{\eta }_{\mathrm{s}}^{0}U{a}^2}{{\mathit{\Pi }}_{\mathrm{c}}}\frac{x}{{(x^2+L_{\text{circ}}^2)}^2}].$$ 3.22

The logarithmic dependence imposes an upper bound on U: a unique feature of Π-dependent systems that we discuss at length in a previous work [29]. Here, however, we stay in the regime where the velocity is small enough such that ζ≪1. Upon non-dimensionalizing equation (3.22) as before and scaling lengths over L_circ, we have

$$\mathit{\Pi }(x)=-\frac{1}{\zeta }\ln [1-\frac{8\zeta a^3}{L_{\mathrm{circ}}^3}\frac{x}{{(1+x^2)}^2}].$$ 3.23

To compare with our asymptotic analysis from before, we expand equation (3.23) in a Taylor series for small ζ:

$$\mathit{\Pi }(x)=\frac{8a^3}{L_{\mathrm{circ}}^3}\frac{x}{{(1+x^2)}^2}+\zeta \hspace{0.17em}\frac{32a^6}{L_{\mathrm{circ}}^6}\frac{x^2}{{(1+x^2)}^4}+\mathcal{O}({\zeta }^2).$$ 3.24

Within the lubrication approximation, the net vertical force is simply $F^{\perp }=\int \mathit{\Pi }\hspace{0.17em}\mathrm{d}x$. The first term in the expansion in equation (3.24) corresponds to a Newtonian problem with constant surface viscosity η⁰_s, and the integrated vertical force at this order is zero. This is consistent with kinematic reversibility arguments, and from the shape of the pressure distribution at $\mathcal{O}(1)$ as shown in figure 4b. The $\mathcal{O}(\zeta )$ term, however, has a finite contribution resulting in a net ‘lift’ force away from the wall that breaks Stokesian reversibility. Using $L_{\mathrm{circ}}=\sqrt{2h_{0}a}$ and ϵ=h₀/a, we find

$$F^{\perp }\sim \zeta \hspace{0.17em}\frac{\pi }{2\sqrt{2}}{ϵ}^{-5/2},$$ 3.25

which is exactly the ϵ≪1 limit of equation (3.9).

This lubrication analysis not only verifies the thin-gap limit of the reciprocal theorem approach, but also illustrates the symmetries of the stresses at $\mathcal{O}(\zeta )$. The pressure distribution from equation (3.24) elucidates the origin of the $\mathcal{O}(\zeta )$ force perpendicular to the wall due to Π-dependent η_s, as shown in figure 4b. It is also evident from figure 4b that the leading-order correction to the drag on the particle in the direction parallel to the wall can occur only at $\mathcal{O}({\zeta }^2)$ due to the even symmetry of Π(x) at $\mathcal{O}(\zeta )$.

4. Cylinder within a cylinder

(a). The two-dimensional journal bearing

The framework of the bipolar cylindrical coordinate system and the reciprocal theorem developed here can be easily adapted to more complex geometries. Consider, for instance, a cylinder rotating within a cylindrical cavity, with a Π-thickening surfactant occupying the gap between them (figure 7a). The 2D journal bearing is a well-studied limit of this geometry when the fluid is Newtonian and the characteristic thickness of the fluid gap is small. Although our analysis is not restricted to thin fluid gaps, we shall again use results from lubrication theory [6,29] to compare our solutions in the appropriate limits. Notably, translation and rotation are now coupled, unlike in the case of a plane wall.

Figure 7.

(a) The interfacial journal bearing. When the disc is torqued, it spirals inward (or outward) in a Π-thickening (or -thinning) surfactant. (b–d) Trajectories obtained by time marching equation (4.10) to a finite time (when spiraling inward, in blue) or until the disc touches the outer wall (whenspiraling outward, in red). The three cases correspond to different values of ζ: (b) |ζ|=0.05, (c) |ζ|=0.1 and (d) |ζ|=0.5. (Online version in colour.)

Mathematically, the problem is identical to the previous sections, with the fluid now confined between α=α₀ and α=α₁. The inner cylinder, of radius a and identified by the streamline α₀, is translated and/or rotated by imposing an external force and/or torque. The external cylinder, of radius b>a corresponding to α₁<α₀, is held stationary.

The governing equation at $\mathcal{O}(1)$ is, again, ∇⁴Ψ=0, subject to boundary conditions now applied at a finite α₁≠0 (see electronic supplementary material). The Newtonian streamlines corresponding to different modes of motion of the inner cylinder are shown in figure 5.

Figure 5.

Newtonian streamlines corresponding to (a) azimuthal translation of the inner cylinder, (b) rotation and (c) radial translation.

It is useful to define a clearance ϵ and eccentricity λ such that the radius of the outer cylindrical wall is b=a(1+ϵ), and the distance between the centres of the cylinders is λaϵ. Written this way, λ=0 represents concentric cylinders, whereas the cylinders touch tangentially at λ=1. These geometric parameters then relate to α₀ and α₁ as

$$\sinh {\alpha }_0=\frac{(\lambda +1)(\lambda ϵ+ϵ+2)}{2\lambda }\sqrt{\frac{(\lambda -1)(\lambda ϵ-ϵ-2)}{(\lambda +1)(\lambda ϵ+ϵ+2)}}\mathrm{and}\cosh {\alpha }_1=\frac{{\lambda }^2ϵ+ϵ+2}{2\lambda (ϵ+1)}.$$ 4.1

In a Newtonian fluid, kinematic reversibility requires that the radial force (i.e. towards the centre of the outer cylinder) on a rotating disc be zero. The net hydrodynamic force generated by the no-slip condition on the inner cylinder, if at all, should act in the azimuthal direction (i.e. parallel to the outer wall). This Newtonian force is particularly significant when the fluid layer between the cylinders is thin, and the methods of lubrication theory may be used to evaluate this ‘journal-bearing force’ [6]:

$$F_{\text{lub}}=F_{\circlearrowright }^{\parallel }(ϵ\ll 1)=\frac{12\pi {\eta }_{\mathrm{s}}^0\mathrm{\Omega }a}{{ϵ}^2}\left[\frac{\lambda }{(2+{\lambda }^2){(1-{\lambda }^2)}^{1/2}}\right].$$ 4.2

The ϵ⁻² dependence on the clearance makes it particularly suitable for engineering applications, where a load balances this lubrication force in, say, a shaft rotating within a journal enclosing a thin film of lubricant.

We may readily compare the hydrodynamic force on the inner cylinder from the general Newtonian solution obtained in bipolar coordinates to this lubrication limit when the gap is thin. Following equation (2.26), the radial component (or F_y) is indeed zero, and the azimuthal component (or F_x) is

$$F_{\circlearrowright }^{\parallel }=\frac{8\pi {\eta }_{\mathrm{s}}^0\mathrm{\Omega }a\sinh ({\alpha }_1)\sinh ({\alpha }_0-{\alpha }_1)}{4\sinh ({\alpha }_0)\sinh ({\alpha }_1)\sinh ({\alpha }_0-{\alpha }_1)-({\alpha }_0-{\alpha }_1)[\cosh (2{\alpha }_0)+\cosh (2{\alpha }_1)-2]}.$$ 4.3

This is the Newtonian journal-bearing force without limitations on the thickness of the fluid layer. As expected, this relation limits to zero when ${\alpha }_1\to 0$ due to the decoupling of rotation and translation in two-dimensional Stokes flow next to a wall. Rewriting in terms of λ and ϵ, we can compare this force against the predictions of lubrication theory (figure 6a). When $ϵ\to 0$, equation (4.3) approaches the prediction from lubrication theory (equation (4.2)).

Figure 6.

Forces on a rotating disc in a journal-bearing geometry. (a) The Newtonian journal-bearing force (solid line) at $\mathcal{O}(1)$ and the prediction from standard lubrication theory (dashed line). (b) The $\mathcal{O}(\zeta )$ symmetry-breaking force (solid line) from the reciprocal theorem calculation and the prediction from Π-dependent lubrication theory (dashed line). In both cases, the eccentricity is λ=0.5.

Now, consider a fluid with Π-dependent viscosity filling the gap between the cylinders, as in figure 7a. Like with the motion of a cylinder near a plane wall, stresses generated in this geometry would result in a net force along the line connecting the centres of the cylinders. We will assume for now that the inner disc is constrained in the horizontal direction, so there is no azimuthal motion. The reciprocal integral then takes the form

$$F_{\circlearrowright }^{\perp }=-{\int }_{-\pi }^{\pi }{\int }_{{\alpha }_1}^{{\alpha }_0}{\mathit{\Pi }}_{\circlearrowright }[{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\circlearrowright }+{({\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\circlearrowright })}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\perp }\hspace{0.17em}{h}^2\hspace{0.17em}\mathrm{d}\alpha \hspace{0.17em}\mathrm{d}\beta ,$$ 4.4

where, like before, the subscripts denote the mode of motion (rotation corresponding to the $\mathcal{O}(1)$ solution and radial translation as the auxiliary solution), and the superscript on F denotes that this force is perpendicular to the outer wall.

The stream functions corresponding to this geometry are more involved than before, and a closed-form expression for the integral in equation (4.4) eludes us. However, a numerical integration is straightforward and $F_{\circlearrowright }^{\perp }$ is shown in figure 6b. As with translation/rotation near a plane wall, this regime can be interpreted to represent ‘small’ velocities such that the corresponding surface pressure is much smaller than Π_c. On the other hand, a separable solution valid for thin films but for arbitrary values of ζ can be found in a manner similar to §3c. The correction to the Newtonian pressure distribution again breaks the symmetry, generating a ‘lift’ force that is, to leading order [29],

$$F_{\circlearrowright }^{\perp }(ϵ\ll 1)\sim \frac{18\pi \zeta }{{ϵ}^4}\hspace{0.17em}\frac{{\lambda }^3(3-2{\lambda }^2)}{{(2+{\lambda }^2)}^2{(1-{\lambda }^2)}^{5/2}}.$$ 4.5

As shown in figure 6b, these two calculations are consistent in the regime where both the angular velocity (and therefore, ζ) and fluid layer thickness (or ϵ) are small.

(b). Irreversible trajectories

Both $F_{\circlearrowright }^{\parallel }$ and $F_{\circlearrowright }^{\perp }$ above were evaluated for a disc torqued such that it rotates at a constant angular velocity Ω at a fixed azimuthal location. If we relax this constraint on its position, one can expect the disc to move in both the radial (due to the $\mathcal{O}(1)$ Newtonian force $F_{\circlearrowright }^{\parallel }$) and the azimuthal (due to the $\mathcal{O}(\zeta )$ force $F_{\circlearrowright }^{\perp }$) directions. The net effect is a unique spiral trajectory that brings the inner cylinder closer to the centre of the outer cylinder in a Π-thickening fluid.

In order to obtain these trajectories, we consider a force-free inner cylinder imposed with an external torque T_e. Translation and rotation are now coupled, and we assume that the inner cylinder moves with angular velocity Ω, azimuthal velocity U and radial velocity V towards the centre of the outer cylinder, all of which are expanded as

$$\{U,V,\mathrm{\Omega }\}=\{U^{(0)},V^{(0)},{\mathrm{\Omega }}^{(0)}\}+\zeta \{U^{(1)},V^{(1)},{\mathrm{\Omega }}^{(1)}\}+\mathcal{O}({\zeta }^2).$$ 4.6

At $\mathcal{O}(1)$, the journal-bearing force $F_{\circlearrowright }^{\parallel }$ balances the hydrodynamic drag to azimuthal motion with velocity U⁽⁰⁾. Additionally, rotation as well as wall-parallel translation are both resisted by hydrodynamic torques, the sum of which should balance the applied torque T_e. It is also clear from the stream-function coefficients that radial motion is decoupled from azimuthal and rotational motion, and therefore V ⁽⁰⁾=0. The force and torque balances at $\mathcal{O}(1)$ are

$$\left(\begin{array}{cc}{\mathcal{R}}_{\parallel }^F& {\mathcal{R}}_{\circlearrowright }^F\\ {\mathcal{R}}_{\parallel }^{\mathrm{T}}& {\mathcal{R}}_{\circlearrowright }^{\mathrm{T}}\end{array}\right)\left(\begin{array}{c}{U}^{(0)}\\ {\mathrm{\Omega }}^{(0)}\end{array}\right)=\left(\begin{array}{c}0\\ -T_e\end{array}\right).$$ 4.7

Here, $\mathcal{R}$ is the resistance coefficient, with the superscript denoting the hydrodynamic moment (force or torque) and the subscript representing the mode of motion (wall-parallel translation or rotation). The $\mathcal{O}(1)$ flow fields are Newtonian, and these coefficients can be determined from equation (2.26) and the stream-function coefficients (see the electronic supplementary material) to give U⁽⁰⁾ and Ω⁽⁰⁾.

These $\mathcal{O}(1)$ modes of motion generate Newtonian fluid fields {u_∥,Π_∥} or $\{{\mathbf{\text{u}}}_{\circlearrowright },{\mathit{\Pi }}_{\circlearrowright }\}$ that in turn could result in $\mathcal{O}(\zeta )$ forces and torque on the inner cylinder. These corrections F⁽¹⁾ and T⁽¹⁾ can be determined by appropriately choosing the auxiliary flow field similar to equation (3.1). Stresses at this order follow the same symmetries along lines of constant α as with the case of a disc near a plane wall, and integrate to a non-zero force only in the direction perpendicular to the outer wall:

$$F_1^{\perp }=-{\int }_{-\pi }^{\pi }{\int }_{{\alpha }_1}^{{\alpha }_0}({\mathit{\Pi }}_{\circlearrowright }+{\mathit{\Pi }}_{\parallel })[{\mathbf{\nabla }}_{\mathrm{s}}({\mathbf{\text{u}}}_{\circlearrowright }+{\mathbf{\text{u}}}_{\parallel }){({\mathbf{\nabla }}_{\mathrm{s}}({\mathbf{\text{u}}}_{\circlearrowright }+{\mathbf{\text{u}}}_{\parallel }))}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\perp }\hspace{0.17em}{h}^2\hspace{0.17em}\mathrm{d}\alpha \hspace{0.17em}\mathrm{d}\beta ,$$ 4.8

where $F_1^{\perp }={\mathbf{\text{F}}}^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_y$. Similar integrations show that $F_1^{\parallel }={\mathbf{\text{F}}}^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_x$ and $T_1={\mathbf{\text{T}}}^{(1)}\mathbf{\cdot }{\widehat{\mathbf{\text{e}}}}_z$ are identically zero. As with a plane wall, corrections to U⁽⁰⁾ and Ω⁽⁰⁾ arise at best at $\mathcal{O}({\zeta }^2)$.

If the disc is not constrained, this force acts to push it closer to the centre of the outer cylinder. Like before, vertical translation decouples from rotation and horizontal translation. The $\mathcal{O}(\zeta )$ vertical force balance is simply

$${\mathcal{R}}_{\perp }^F{V}^{(1)}=-F_1^{\perp }.$$ 4.9

Between equations (4.7) and (4.9), the translational velocities of the inner disc are

$$U\approx U^{(0)}+\mathcal{O}({\zeta }^2)\mathrm{and}V\approx \zeta V^{(1)}+\mathcal{O}({\zeta }^2).$$ 4.10

Time-marching using these velocities, we obtain the trajectories in figure 7. As hypothesized, stresses generated at $\mathcal{O}(\zeta )$ in a Π-thickening surfactant lead to a spiral trajectory inward. When the surfactant is Π-thinning ($\zeta \to -\zeta$), these spiral trajectories bring the disc closer to the outer wall.

Indeed, when ${\alpha }_1\to 0$, rotation and wall-parallel translation decouple, and the calculations are simple enough to track analytically. The result is that a disc rotating adjacent to a plane wall drifts away from the wall (assuming positive ζ for Π-thickening) with a velocity V ≈ζV ⁽¹⁾ with V ⁽¹⁾ as in equation (4.9). The $\mathcal{O}(\zeta )$ force then is $F_1^{\perp }({\alpha }_1=0)=F_{\circlearrowright }^{\perp }$ as given in equation (3.12). The following limiting values can be easily obtained:

$$V(\delta \to 1)\sim \frac{\zeta }{12(\delta -1)}\mathrm{and}V(\delta \to \mathrm{\infty })\sim \frac{\zeta }{2{\delta }^3},$$ 4.11

where, like before, δ=d/a is the dimensionless distance of the centre of the disc from the wall and V is in units of the tangential velocity aΩ.

These transverse velocities are within experimentally accessible regimes for microfabricated ferromagnetic probes [11,12] of radius a∼50 μm on a DPPC monolayer (Π_c∼8 mN m⁻¹ and η⁰_s∼10 μNs m⁻¹). Obviously, thin gaps amplify the effect due to large lubrication pressures, and hence let such a disc placed at a distance of about half its radius from the wall (such that ϵ=δ−1∼0.5) be torqued to rotate at 3 Hz (Ω∼20 s⁻¹). The vertical velocity due to Π-dependence of viscosity is then V ∼5 μm s⁻¹. This drift is manifestly irreversible: flipping the direction of rotation, for instance, by imposing an oscillatory motion instead of constant rotation, does not reverse the direction of this drift and only continues to push the disc further away from the wall.

5. Interfacial magnus effect

More generally, the reciprocal theorem approach also applies to unconfined systems where Newtonian symmetries break as a result of Π-dependent viscosity. The integral in equation (2.18) is nonlinear in the $\mathcal{O}(1)$ pressure and velocity fields, and coupled modes of motion can also lead to non-zero forces. We illustrate this using an interfacial analogue of the Magnus effect in 3D fluids [32]. In the traditional Magnus effect, a rigid sphere simultaneously spinning and translating through a stationary fluid at finite Reynolds number experiences a ‘lift’ force, leading to a curved trajectory.

Consider the simultaneous translation and rotation of a disc of radius a on an unbounded interface. The disturbance velocity (figure 8a) induced by its translation at velocity U in a Newtonian monolayer is a superposition of a 2D Stokeslet and a 2D potential dipole [41]:

$${\mathbf{\text{u}}}_t(\mathbf{\text{x}})=[2(-\ln (r)\mathbf{\text{I}}+\frac{\mathbf{\text{x}}\mathbf{\text{x}}}{r^2})+a^2(\frac{\mathbf{\text{I}}}{r^2}-\frac{2\mathbf{\text{x}}\mathbf{\text{x}}}{r^4})]\mathbf{\cdot }\mathbf{\text{U}},$$ 5.1

where x is measured from the centre of the disc and r=|x|. The associated surface pressure distribution is

$${\mathit{\Pi }}_t(\mathbf{\text{x}})=\left[\frac{4{\eta }_{\mathrm{s}}^0\mathbf{\text{x}}}{r^2}\right]\mathbf{\cdot }\mathbf{\text{U}}.$$ 5.2

Similarly, the disturbance velocity corresponding to rotation (figure 8b) with angular velocity Ω is

$${\mathbf{\text{u}}}_r(\mathbf{\text{x}})=\left(\frac{a^2}{r^2}\right)\mathbf{\Omega }\times \mathbf{\text{x}},$$ 5.3

while the surface pressure remains unchanged due to rotation alone: Π_r(x)=0.

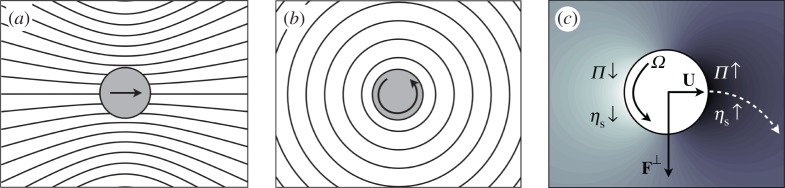
Figure 8.

Streamlines corresponding to a disc (a) translating and (b) rotating in an unbounded Newtonian monolayer. (c) Surface pressure contours due to translation (rotation does not alter the surface pressure). Darker shades correspond to a relative increase in Π ahead of the disc. The associated increase in η_s leads to the $\mathcal{O}(\zeta )$ force F^⊥ that ‘rolls’ the disc in a direction perpendicular to U, leading to a curved trajectory. (Online version in colour.)

These disturbance fields can be superimposed due to linearity of the $\mathcal{O}(1)$ equations. As the auxiliary Newtonian problem in equation (2.18), we use the solution u_aux corresponding to a disc translating with velocity U_aux. The correction at $\mathcal{O}(\zeta )$ then becomes

$${\mathbf{\text{F}}}_1\mathbf{\cdot }{\mathbf{\text{U}}}_{\mathrm{aux}}=-\int {\mathit{\Pi }}_t[{\mathbf{\nabla }}_{\mathrm{s}}({\mathbf{\text{u}}}_t+{\mathbf{\text{u}}}_r)+{({\mathbf{\nabla }}_{\mathrm{s}}({\mathbf{\text{u}}}_t+{\mathbf{\text{u}}}_r))}^{\mathrm{T}}]\mathbf{:}{\mathbf{\nabla }}_{\mathrm{s}}{\mathbf{\text{u}}}_{\mathrm{aux}}\hspace{0.17em}\mathrm{d}S.$$ 5.4

Neither translation nor rotation alone can generate a force at $\mathcal{O}(\zeta )$ in an infinite Π-dependent monolayer, due to physical symmetries as described earlier. The integral in equation (5.4) results in a non-zero force only due to the coupling between the two modes of motion. After some algebra, we find (in dimensional units)

$${\mathbf{\text{F}}}^{\perp }\approx 16\pi \frac{{({\eta }_{\mathrm{s}}^0)}^2}{{\mathit{\Pi }}_{\mathrm{c}}}\mathbf{\text{U}}\times \mathbf{\Omega },$$ 5.5

which acts perpendicular to the direction of motion.

The importance of the coupling between translation and rotation is depicted in figure 8c. Translation sets up a surface pressure distribution such that Π increases ahead of the disc and decreases in its rear. In a Π-thickening monolayer, η_s(Π) changes in the same sense as Π. Consequently, the surface-viscous resistance to rotation is larger in front of the disc as compared to its rear. The mechanism is similar to that of a ‘hot janus sphere’ in a 3D fluid with temperature-dependent viscosity [34]: a temperature dipole (as against a surface pressure dipole) then sets up a viscosity distribution and breaks spherical symmetry around the particle. In either problem, the disc (or the sphere) responds by ‘rolling’ on the more viscous side, moving in a direction perpendicular to U, leading to a curved trajectory (figure 8c). The direction of the curve is opposite that of the traditional Magnus effect in 3D inertial fluids, where the lift force on a sphere is F^⊥∝Ω×U [32].

6. Conclusion

We have illustrated the leading-order symmetry-breaking consequences of surface pressure-dependent surface viscosity, a feature of most insoluble surfactant monolayers. Working with incompressible monolayers with negligible bulk viscous stresses (‘high-Boussinesq’ limit), we applied the Lorentz reciprocal theorem to obtain perturbative corrections to Newtonian stresses when a disc is embedded in the monolayer. We focused primarily on bounded monolayers, which demonstrate the loss of Newtonian symmetries and reveal characteristic trends of the forces and torques generated by Π-dependent rheology. However, the formulation based on the reciprocal theorem is more general, as we illustrate with the interfacial Magnus effect.

We found that a disc translating parallel to (or rotating adjacent to) an interfacial barrier is subject to a force in the direction perpendicular to that barrier, leading to an evident loss of kinematic reversibility. The results are amplified in thin gaps, and are consistent with a lubrication theory adapted for η_s(Π). As a striking display of kinematic irreversibility, we solved for the trajectory of a force-free disc rotated within a cylindrical cavity. In this 2D ‘journal bearing’, forces perpendicular to the wall lead to unique spiral trajectories.

We have previously established the surprising consequences of Π-dependent viscosity in small fluid gaps [29], for any form of η_s(Π) and arbitrary velocities. The current work, on the other hand, focuses on ‘small’ velocities in a perturbative sense, without restrictions on the thickness of the fluid gap. Between these two works, we now have a clearer grasp of the impact of Π-dependent rheology, with quantitative predictions and qualitative insights into practically relevant situations. With the rising prominence and success of interfacial microrheology [11,12,14,28], these results are of particular experimental relevance due to their implications on the measurement and interpretation of surface rheology.

Even without wall effects, coupling different modes of motion can lead to non-intuitive trajectories, as evinced by the example of the interfacial Magnus effect. This also applies to the translation of a disc in a background surface flow with a rotational component [33]. Likewise, two discs translating at the same velocity perpendicular to the line of centres would repel (or attract) at $\mathcal{O}(\zeta )$ in a Π-thickening (or -thinning) monolayer, like in the analogous 3D viscoelastic problem [31]. Shape asymmetries can potentially introduce finite torques at $\mathcal{O}(\zeta )$, leading to reorientation of particles [42] either perpendicular or parallel to the direction of translation. This could probably enrich the applications of needle-shaped probes used to infer interfacial rheology [14]. Some of these results can be extended to finite Bo: while the corresponding auxiliary solutions are more involved [16], we expect the qualitative trends to remain unchanged.

Finally, the relative motion of force-free pairs of particles in an ambient flow, like its 3D analogue [43], sets the stage for a hydrodynamic theory of the rheology of 2D suspensions. Changes in local microstructure, guided by irreversible pair interactions due to η_s(Π), could lead to hydrodynamic aggregation or separation of particles, which in turn result in macroscopic shear-thickening or -thinning. The mathematical machinery developed here, and the qualitative insights gained, will inform these studies, which we leave for future work.

Data accessibility

This work does not have any experimental data. The coefficients in the expression for the stream function in equation (2.22) for a general geometry are provided in the electronic supplementary material.

Authors' contributions

H.M. and T.M.S. conceived the mathematical model, interpreted the results and wrote the paper. All the authors gave their final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Science Foundation (NSF) under grant no. CBET-1512833.