ALLELE-SPECIFIC COPY NUMBER ESTIMATION BY WHOLE EXOME SEQUENCING

Abstract

Whole exome sequencing is currently a technology of choice in large-scale cancer genomics studies, where the priority is to identify cancer-associated variants in coding regions. We describe a method for estimating allele-specific copy number using whole exome sequencing data from tumor and matched normal.

1. Introduction

Cancer is a disease characterized by gains and losses of segments of chromosomes. These somatic copy number alterations (CNAs) play critical roles in cancer progression, and their accurate detection and characterization is important for disease prognosis and treatment. Each person inherits two copies of the genome, one from each parent, and somatic CNAs that are acquired by a tumor can affect one or both inherited copies. A challenging problem in the analysis of tumor genomes is to accurately estimate the number of copies of each inherited allele, sometimes called the allele-specific copy number or the parent-specific copy number.

Methods for quantifying CNAs have evolved with the advance of technology, from traditional spectral karyotyping to array-based comparative genome hybridization (CGH), to single nucleotide polymorphism (SNP) genotyping arrays, and, more recently, to high-throughput sequencing-based methods. As one of the earliest high-throughput methods, CGH allows the genome-wide assessment of the sum of the copy numbers of the two inherited chromosomes. In contrast, genotyping microarrays, which have probes that separately target the different alleles at single nucleotide polymorphic sites, allow the estimation of allele-specific copy number. Allele-specific copy number estimation is especially important for detecting loss of heterozygosity, since there are common mutation processes that cause copy-neutral loss of heterozygosity where a region on one chromosome is replaced by the same region duplicated from the other homologous copy. For CNAs that do involve changes in total DNA copy number, it is often important to know whether one or both of the inherited alleles are affected. Thus, in addition to methods for total copy number estimation [see Lai et al. (2005), Willenbrock and Fridlyand (2005), Zhang (2010), Medvedev, Stanciu and Brudno (2009) for reviews], methods for allele-specific copy number estimation have received increasing attention [Chen, Xing and Zhang (2011), Olshen et al. (2011), Zhang, Lange and Sabatti (2012), Mayrhofer et al. (2013), Chen et al. (2014)].

High-throughput sequencing is a natural platform for allele-specific copy number estimation since at heterozygous loci both alleles will be sequenced and observed in the data. High-throughput sequencing can provide much finer resolution than genotyping microarrays, especially for allele-specific analysis. This is because most polymorphic loci have low minor allele frequency, and are not targeted by the probes on standard genotyping microarrays. Copy number estimation by high-throughput sequencing requires different statistical models from those designed for array-based technologies: The data is in the form of read counts, and many sources of experimental bias cause these counts to fluctuate wildly along the genome, even when copy number doesn’t change. Chen, Gunel and Zhao (2013), Chen et al. (2014) and Favero et al. (2015) proposed methods that utilize a matched normal sample, derived from normal tissue taken from the same patient, as the control for allele-specific copy number estimation. These methods have proven useful for whole genome sequencing, where DNA from the entire genome is sequenced.

In this paper, we focus on allele-specific copy number estimation from whole exome sequencing (WES) data. Only 1% of the human genome are protein coding. These regions are called exons or, collectively, the “exome.” Most cancer studies focus primarily on the exome because it is much more straightforward to assign functional relevance to mutations that are found in protein-coding regions. Since the target size (the size of the genome being targeted for sequencing) in whole exome sequencing is only 1% of the target size in whole genome sequencing, with the same cost one can afford to sequence at much higher coverage by WES. Such high coverage sequencing is crucial in cancer studies because mutations of clinical relevance may be present in only a small fraction of cells in the tumor, and thus are undetectable at low coverage. For these reasons, whole exome sequencing has become a platform of choice for many cancer studies.

Read coverage from whole exome sequencing data is much noisier than whole genome sequencing, with most of the noise coming from the step in the experiment where exons are selected and amplified. In whole genome sequencing, which does not involve this step, a matched normal sample serves in most cases as an adequate control for removing site-specific background bias, as shown in Chen et al. (2014). However, in whole exome sequencing, many studies [Fromer et al. (2012), Jiang et al. (2015)] have shown that experimental bias differs substantially across samples. In particular, Jiang et al. (2015) showed that simply comparing against a matched normal does not effectively remove the strong biases in whole exome sequencing. Several methods, including XHMM by Fromer et al. (2012), CoNIFER by Krumm et al. (2012), EXCAVATOR by Magi et al. (2013) and CODEX by Jiang et al. (2015), were proposed based on the idea of pooling data across a large cohort to estimate the biases caused by enrichment and amplification. However, these methods do not work for allele-specific copy number estimation since the set of heterozygous sites differ across individuals. Thus, it is still necessary to rely on the matched normal sample to identify heterozygous sites and to control for allele-specific experimental biases.

We propose a bivariate binomial mixture model with site-specific background bias to estimate allele-specific copy number from whole exome sequencing data. We describe a majorize-minimization (MM) algorithm for fast parameter fitting in this model. We also adapt the segmentation procedure from Chen et al. (2014) to this setting, and derive a new modified Bayes information criterion for model selection that builds on the framework developed in Chen et al. (2014), Zhang and Siegmund (2007) and Zhang and Siegmund (2012). The model and methods are described in Section 3. Performance is assessed on spike-in data in Section 4. The method is then applied to a breast and ovarian cancer data set in Section 5, where the improved accuracy of the new approach is shown by comparison to array-based results from The Cancer Genome Atlas Project.

The proposed method, which we call Falcon-X for finding somatic allele-specific copy number changes in whole exome sequencing, is implemented as an open source R-package falconx.

2. More background in biology

First, we summarize the concepts from biology that play a central role in this paper. This is not meant to be a comprehensive introduction to these subjects, but simply a definition of the key terms and a reference to the literature.

2.1. DNA variation, copy numbers and inherited heterozygous sites

Our genome, which is encoded by the four letter DNA code, encodes the instructions for the function of each cell in our body. Mutations are changes to the genome, and come in many sizes and types. Single nucleotide mutations are changes of one nucleotide, for example, a guanine to a cytosine. Copy number mutations are gains or losses of large segments of the genome. Normally, we have two homologous copies of each of the 22 autosomes, inheriting one from each parent. A heterozygous deletion is a deletion of one of the two parental copies, and a homozygous deletion is a deletion of both inherited copies. A gain in copy number may be a gain of either one or both of the two inherited copies. A loss of heterozygosity refers to a loss of one of the parental copies, which may or may not involve a change in total copy number; specifically, some mutation processes lead to a loss of one parental copy accompanied by a simultaneous gain of the other parental copy in the same region, thus leading to a loss of heterozygosity without changing total copy number, aka copy-neutral loss of heterozygosity.

We inherit many DNA variation from our parents, and these are carried by every cell in our body. Most inherited variants are population-level polymorphisms, that is, variation caused by mutations that are passed down from our evolutionary ancestors that are carried by many individuals in the current population. In addition, germ cells in each individual gain mutations, which can be passed along to the offspring and might not be shared within the population. The basic unit in our model for estimating allele-specific copy number is sequencing data at inherited heterozygous sites, where the variations/mutations (e.g., single-nucleotide variants, short insertions and deletions) hit one allele out of the two in the doploid genome. Somatic mutations occur sporadically during our lifetime to specific cell lineages within our body and are not passed to our offspring. Most of the mutations found in tumor genomes are somatic. The focus of this paper is detecting somatic copy number changes in tumors.

2.2. High-throughput sequencing

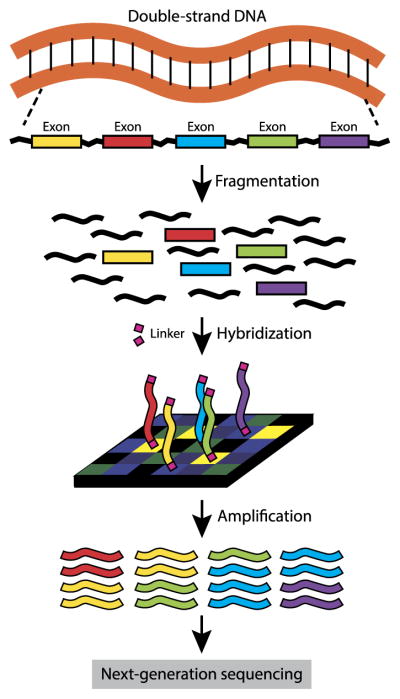
High-throughput short read sequencing, often referred to as “high-throughput sequencing” or “next-generation sequencing,” provides data for quantifying DNA, RNA, protein binding and many other genome-wide features in biology. A good overview of the technology and its applications can be found in three articles in the November 2009 issue of Nature Methods: Flicek and Birney (2009), Medvedev, Stanciu and Brudno (2009) and Pepke, Wold and Mortazavi (2009). In this paper, we focus on high-throughput whole exome sequencing (WES). Figure 1 shows an overview of a WES pipeline. First, DNA is extracted from the sample, fragmented, and the exon-regions are captured and enriched. This step, called target enrichment, may be achieved by several strategies including molecular inversion probes or microarrays. These exon regions are usually amplified by PCR, resulting in a sequencing library. The library can be sequenced by any of the existing strategies, including classical Sanger sequencing, Illumina Genome Analyzer or Life Technologies SOLiD.

Fig. 1.

Overview of a whole exome sequencing (WES) experiment.

In this paper, we consider mainly Illumina sequencing data, but our model can conceivably also be applied to other types of sequencing scenarios. The Illumina Genome Analyzer produces fixed length genome sequences, called reads, that cover the exon targets. These reads are mapped to a reference template, where the number of reads that cover a position is called the “coverage” at that position. At heterozygous positions, reads would reflect the alleles for that position that are present in the sample. For example, at a position that is heterozygous with the two alleles A and C, if there are no somatic mutations and the hybridization (and alignment) process is unbiased toward the haplotype with the A and the haplotype with the C, then approximately half of the reads should contain an A and half should contain a C. We define the allele-specific coverage to be the number of reads that contain a specific allele. At heterozygous positions, we should have two allele-specific coverage values, one for each of the two inherited alleles.

DNA sequencing has been used to detect copy number variation because coverage of any given region reflects the relative quantity of the DNA from that region in the sample. However, coverage is also influenced by many other features of the DNA sequence. For example, it has been shown that the local GC-content, defined as the proportion of the bases that are guanine (G) or cytosine (C), heavily influences coverage [Benjamini and Speed (2012)]. As mentioned earlier, such local biases are especially strong in whole exome sequencing, where the efficiency of target enrichment can vary dramatically from exon to exon. Careful modeling of the background biases are essential for accurate copy number estimation by whole exome sequencing data. Several algorithms have been developed for copy number estimation with whole exome data that uses latent factors estimated across many samples to remove the background bias [Krumm et al. (2012), Fromer et al. (2012), Jiang et al. (2015)]. Specifically, Jiang et al. (2015) showed that in matched case/control settings, such as a tumor sample with matched normal, cross-sample approaches are more effective than normalizing to the matched control. Jiang et al. (2015) proposed a method, CODEX, which estimates site- and sample-specific coverage bias. We will describe CODEX in more detail, and use its estimated bias values, in the next section.

3. Model and methods

3.1. Overview

The data input to our model consists of sequencing coverage for a tumor sample and its matched normal sample from the same patient. In addition, we assume that a large (>30) number of normal samples have been sequenced by the same laboratory protocols, which we call the “control cohort.” For example, in Section 5, the control cohort consists of the matched normal samples for all of the tumors in the study.

Figure 2 shows an overview of the analysis pipeline that we propose. First, in Step 1, sequenced reads are aligned to the reference template, resulting in bam files. In Step 2, the matched normal sample is used to identify all of the heterozygous sites in the individual, using existing software such as GATK [Auwera et al. (2013)]. These heterozygous sites are the inherited heterozygous sites and are the basic units in our model. Let T be the total number of heterozygous sites. In Step 3, the total and allele-specific coverage at these sites are extracted from the tumor sample as well as all of the samples in the normal control cohort. In Step 4, the matrix of total coverage at the union of all germline heterozygous loci across all samples is used by CODEX to estimate the background total coverage bias for the tumor and matched normal sample. For each t = 1, 2, …, T, we obtain from CODEX s(t) and s^*(t), the background total coverage bias for, respectively, the tumor sample and its matched normal control. In Step 5, the allele-specific coverage at these heterozygous positions in the tumor and the normal control, along with the total coverage bias estimates from CODEX, are taken as input to the Falcon-X model to estimate the allele-specific copy number at these heterozygous positions. Since GATK and CODEX are published methods, this paper focuses on Step 5 in the analysis.

Fig. 2.

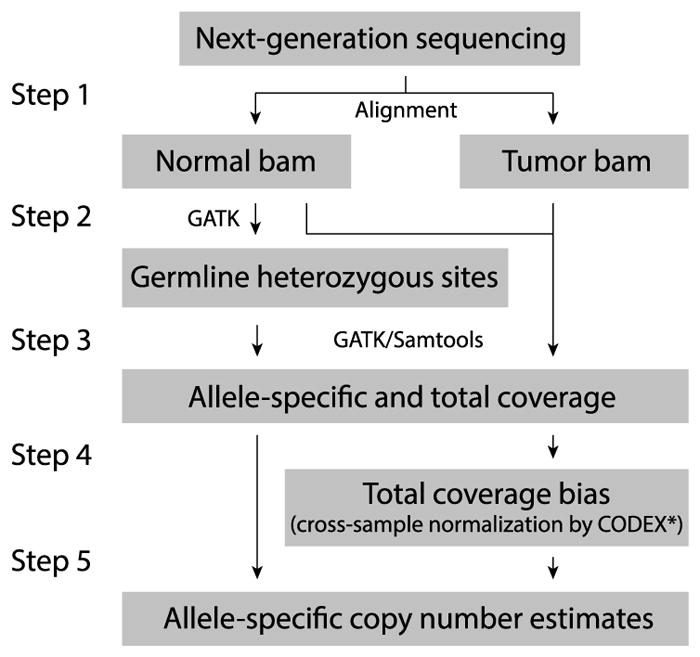
Overview of the proposed analysis steps for estimating allele-specific copy number from whole exome sequencing of tumor and matched normal samples^*CODEX is applied to the union of heterozygous sites across all samples using the tumor-normal option.

3.2. Model

We now describe the new model underlying Falcon-X. Let the two alleles at each bi-allelic loci be arbitrarily labeled A and B. At inherit heterozygous locus t ∈ {1, 2, …, T }, let Y_A(t) and Y_B (t) be the allele-specific coverage in the tumor sample, and let $Y_A^{\ast }(t)$ and $Y_B^{\ast }(t)$ be the allele-specific coverage in the matched normal sample. Notice that the tumor sample could be homogeneous at some inherited heterozygous loci due to somatic mutations. We label the two inherited homologous chromosomes arbitrarily by a and b, also called the two inherited haplotypes. A priori, we don’t know whether allele A is on inherited chromosome a or b. Let I (t) be a latent indicator variable that equals 1 if allele A is on inherited chromosome a, and 0 if it is on inherited chromosome b. Hence, I (t) is the same for the tumor sample and the normal sample from the same patient. Consider the hypothetical situation where we observe I (t); then we would know the haplotype-specific coverage, which we denote by Y_a (t) and Y_b(t) for the tumor sample and by $Y_a^{\ast }(t)$ and $Y_b^{\ast }(t)$ for the matched normal. The relationship between the haplotype-specific coverage and allele-specific coverage is

$$\begin{gathered} Y_a(t)=I(t)Y_A(t)+\left(1-I(t)\right)Y_B(t), \\ {Y}_b(t)=\left(1-I(t)\right)Y_A(t)+I(t)Y_B(t), \\ {Y}_a^{\ast }(t)=I(t)Y_A^{\ast }(t)+\left(1-I(t)\right)Y_B^{\ast }(t), \\ {Y}_b^{\ast }(t)=\left(1-I(t)\right)Y_A^{\ast }(t)+I(t)Y_B^{\ast }(t). \end{gathered}$$

Here, Y_a (t), Y_b(t), $Y_a^{\ast }(t),Y_b^{\ast }(t)$ can be modeled by independent Poisson random variables with location-specific means λ_a (t), λ_b(t), ${\lambda }_a^{\ast }(t),{\lambda }_b^{\ast }(t)$, respectively (the independence assumption is discussed in more detail in Section 3.5):

$$\begin{array}{ll}\hfill Y_a(t)~\text{Poisson}\left({\lambda }_a(t)\right),& Y_b(t)~\text{Poisson}\left({\lambda }_b(t)\right),\hfill \\ \hfill Y_a^{\ast }(t)~\text{Poisson}\left({\lambda }_a^{\ast }(t)\right),& Y_b^{\ast }(t)~\text{Poisson}\left({\lambda }_b^{\ast }(t)\right).\hfill \end{array}$$

The mean values depend on the true underlying haplotype specific copy numbers and other experiment and sequence-dependent variables. We use C_a (t), C_b(t) to represent the haplotype-specific copy numbers at loci t in the tumor; in normal we assume that both haplotypes have copy 1. Experimental variables that affect coverage include the following: the total number of reads sequenced for the sample, local biases in total coverage due to ease of fragmentation, mappability, and target enrichment and amplification, and allele-specific mapping bias. Let N and N^* be the total number of reads sequenced for tumor and normal, respectively. Let s(t) and s^*(t) be the site-specific biases in total coverage for normal and tumor, respectively, that are estimated by CODEX. Let b_A(t), b_B (t) be site-specific mapping biases for alleles A and B. Our model for the mean processes is

$$\begin{gathered} {\lambda }_a(t)=N{C}_a(t)s(t)b_A^{I(t)}(t)b_B^{1-I(t)}(t), \\ {\lambda }_b(t)=N{C}_b(t)s(t)b_A^{1-I(t)}(t)b_B^{I(t)}(t), \\ {\lambda }_a^{\ast }(t)=N^{\ast }{s}^{\ast }(t)b_A^{I(t)}(t)b_B^{1-I(t)}(t), \\ {\lambda }_b^{\ast }(t)=N^{\ast }{s}^{\ast }(t)b_A^{1-I_t}(t)b_B^{I(t)}(t). \end{gathered}$$

This model is similar to the model underlying Falcon, an allele-specific copy number estimation method proposed in Chen et al. (2014). The important difference between the two models is that, in this model, the total coverage bias values s(t) and s^*(t) vary between the tumor and normal samples, while Falcon assumes s(t) = s^*(t). For whole exome sequencing, the site-specific bias in total coverage varies substantially across samples, and the assumption of s(t) = s^*(t) in Falcon is not satisfied. On the other hand, the allele-specific mapping biases, b_A(t) and b_B (t), depend mostly on the mapping algorithm, and so it is reasonable to assume that they are shared across the tumor and matched normal samples.

Since copy number change is abrupt, it is appropriate to assume that C_a (t) and C_b(t) are piecewise constant functions of t. By a simple relationship between the Poisson and Binomial distributions, the model with K break points, which we denote by ℳ_K, can be written as

$$\left(Y_A(t),Y_B(t)\right)\mid \left(n_A(t),n_B(t)\right)~\frac{1}{2}\left(\text{Bin}\left(n_A(t),p_a(t)\right),\text{Bin}\left(n_B(t),p_b(t)\right)\right)+\frac{1}{2}\left(\text{Bin}\left(n_A(t),p_b(t)\right),\text{Bin}\left(n_B(t),p_a(t)\right)\right),$$ (3.1)

for t = τ_k + 1, τ_k + 2, …, τ_k+1, k = 0, 1, …, K, with

$$p_a(t)=\frac{w(t)C_{a,k}}{w(t)C_{a,k}+1},p_b(t)=\frac{w(t)C_{b,k}}{w(t)C_{b,k}+1},$$

where $n_A(t)=Y_A^{\ast }(t)+Y_A(t),n_B(t)=Y_B^{\ast }(t)+Y_B(t)$, (C_a,k, C_b,k) is the allele-specific copy number at segment k, and $w(t)=\frac{Ns(t)}{N\ast s\ast (t)}$.

Let τ_K = (τ₁, …, τ_K) be the change-points of this process. It is constrained to lie in the set

$${\mathcal{D}}_K=\{(t_1,\dots ,t_K):0<t_1<\cdots <t_K<T\}.$$

We augment τ_K by τ₀ = 0 and τ_K+1 = T to make the model complete.

We use a Minorize–Maximization (MM) algorithm to estimate the maximum likelihood estimators for the parameters C_a,k and C_b,k in each segment k (Section 3.3). As for searching the break points τ_k’s, we adapt Circular Binary Segmentation (CBS) [Olshen et al. (2004), Venkatraman and Olshen (2007)] to avoid the combinatorial problem of searching over all possible combinations of τ_k’s. To determine the number of break points K, we derived a modified BIC approach extended from Chen et al. (2014) and Zhang and Siegmund (2007) (for details see Section 3.4).

3.3. The estimation of C_a,k and C_b,k in segment k

We suppress the subscript k in this subsection. Algorithm 1 can be used to estimate the parameters. We next show that the algorithm is a valid MM algorithm.

This algorithm is modified from the conventional EM algorithm for mixture models. In the conventional EM algorithm, in the mth iteration, the missing data I (t) is estimated in the expectation step (line 4 in Algorithm 1), and is substituted into the log-likelihood function of the complete data [the observed data and missing data I (t)’s] by its estimate γ̂ (t):

$$\begin{gathered} Q_{(m)}(C_a,C_b)=h(X,Y,w)+\sum _t\left(Y_A(t)\widehat{\gamma }(t)+Y_B(t)\left(1-\widehat{\gamma }(t)\right)\right)log(C_a) \\ -\sum _t\left(n_A(t)\widehat{\gamma }(t)+n_B(t)\left(1-\widehat{\gamma }(t)\right)\right)log\left(w(t)C_a+1\right) \\ +\sum _t\left(Y_B(t)\widehat{\gamma }(t)+Y_A(t)\left(1-\widehat{\gamma }(t)\right)\right)log(C_b) \\ -\sum _t\left(n_B(t)\widehat{\gamma }(t)+n_A(t)\left(1-\widehat{\gamma }(t)\right)\right)log\left(w(t)C_b+1\right), \end{gathered}$$

where $h(X,Y,w)={\sum }_{t}log\left(\left(\begin{array}{c}{n}_A(t)\\ Y_A(t)\end{array}\right)\left(\begin{array}{c}{n}_B(t)\\ Y_B(t)\end{array}\right)w{(t)}^{Y_A(t)+Y_B(t)}\right)$. Then Q_(m)(C_a, C_b) is a minorization function of the log-likelihood on the complete data up to a constant that depends on (C_a,(m−1), C_b,(m−1)), the estimates of the parameters from the (m − 1)th iteration, and the equality achieves at (C_a,(m−1), C_b,(m−1)).

Since it is hard to maximize Q_(m) over C_a and C_b, we construct a new minorization function based on Q_(m). Let

$$\begin{gathered} Q_{(m)}^{\ast }(C_a,C_b)=h(X,Y,w)+\sum _t\left(Y_A(t)\widehat{\gamma }(t)+Y_B(t)\left(1-\widehat{\gamma }(t)\right)\right)log(C_a) \\ +\sum \left(Y_B(t)\widehat{\gamma }(t)+Y_A(t)\left(1-\widehat{\gamma }(t)\right)\right)log(C_b) \\ -\sum _t\left(n_A(t)\widehat{\gamma }(t)+n_B(t)\left(1-\widehat{\gamma }(t)\right)\right) \\ \times \left(log\left(w(t)C_{a,(m-1)}+1\right)+\frac{w(t)C_a+1}{w(t)C_{a,(m-1)}+1}-1\right) \\ -\sum _t\left(n_B(t)\widehat{\gamma }(t)+n_A(t)\left(1-\widehat{\gamma }(t)\right)\right) \\ \times \left(log\left(w(t)C_{b,(m-1)}+1\right)+\frac{w(t)C_b+1}{w(t)C_{b,(m-1)}+1}-1\right). \end{gathered}$$

Then $Q_{(m)}^{\ast }$ is a minorization function of Q_(m), and

$$Q_{(m)}^{\ast }(C_{a,(m-1)},C_{b,(m-1)})=Q_{(m)}(C_{a,(m-1)},C_{b,(m-1)}).$$

Thus, $Q_{(m)}^{\ast }(C_a,C_b)$ is a minorization function of the log-likelihood on the complete data up to a constant that depends on (C_a,(m−1), C_b,(m−1)), and the equality achieves at (C_a,(m−1), C_b,(m−1)). Solving for C_a and C_b that maximizes $Q_{(m)}^{\ast }$ gives Algorithm 1.

Algorithm 1.

MM Algorithm for Estimating C_a and C_b

1:	Take initial guesses for the parameters, such as C̃a = 0.95, C̃b = 1.05. (The initial values of Ca and Cb need to be different.)
2:	Set nIter=0, diff=0.
3:	while nIter==0 or diff > δ (δ can take value such as 10−5) do
4:	For every t,
	$$\widehat{\gamma }(t)=\frac{1}{1+{(\frac{{\stackrel{\sim }{C}}_b}{{\stackrel{\sim }{C}}_a})}^{Y_A(t)-Y_B(t)}{(\frac{w(t){\stackrel{\sim }{C}}_a+1}{w(t){\stackrel{\sim }{C}}_b+1})}^{n_A(t)-n_B(t)}}.$$
5:	Update the estimates of the parameters:
	$$\begin{gathered} {\stackrel{\sim }{C}}_{a,\mathit{new}}=\frac{{\sum }_t(Y_A(t)\widehat{\gamma }(t)+Y_B(t)(1-\widehat{\gamma }(t)))}{{\sum }_{t}w(t)(n_A(t)\widehat{\gamma }(t)+n_B(t)(1-\widehat{\gamma }(t)))/(w(t){\stackrel{\sim }{C}}_a+1)}, \\ {\stackrel{\sim }{C}}_{b,\mathit{new}}=\frac{{\sum }_t(Y_B(t)\widehat{\gamma }(t)+Y_A(t)(1-\widehat{\gamma }(t)))}{{\sum }_{t}w(t)(n_B(t)\widehat{\gamma }(t)+n_A(t)(1-\widehat{\gamma }(t)))/(w(t){\stackrel{\sim }{C}}_b+1)}. \end{gathered}$$
6:	$\text{diff}=\sqrt{{({\stackrel{\sim }{C}}_{a,\mathit{new}}-{\stackrel{\sim }{C}}_a)}^2+{({\stackrel{\sim }{C}}_{b,\mathit{new}}-{\stackrel{\sim }{C}}_b)}^2}$
7:	C̃a = C̃a,new, C̃b = C̃b,new.
8:	end while

3.4. Determining the number of break points

Because the site-specific biases in total coverage is different in the tumor and matched normal samples, p_a (t) and p_b(t) are not constants even within a segment. We extend the method in Chen et al. (2014) and Zhang and Siegmund (2007) to derive a modified Bayesian information criterion to choose the optimal K.

Let Z be the input data {Y_A(t), Y_B (t), $Y_A^{\ast }(t),Y_B^{\ast }(t)$, w(t): t = 1, …, T }. We reparameterize the parameters by letting

$$\begin{gathered} {\theta }_{a,k}=log{C}_{a,k},{\theta }_{b,k}=log{C}_{b,k}, \\ {\theta }_k=({\theta }_{a,k},{\theta }_{b,k}),{\mathit{\theta }}_K=({\theta }_{a,0},{\theta }_{b,0},\dots ,{\theta }_{a,K},{\theta }_{b,K}). \end{gathered}$$

Proposition 1

Let ℳ_K be the model defined in (3.1), assuming that (K, τ_K, θ_K) follows a uniform prior over 𝒵⁺ × 𝒟_K × ℝ^K; then when T is large, we have

$$log\frac{P({\mathcal{M}}_K\mid \mathbf{Z})}{P({\mathcal{M}}_0\mid \mathbf{Z})}\approx l\left({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K\right)-\frac{1}{2}\sum _{k=0}^{K}log\mid H_k\left({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K\right)\mid -l({\widehat{\mathit{\theta }}}_0)+\frac{1}{2}log\mid H({\widehat{\mathit{\theta }}}_0)\mid -\mathit{K}logT,$$ (3.2)

where τ̂_K = (τ̂₁, …, τ̂_K) = arg max_{0<τ1<⋯<τK<T} l(θ̂_K (τ_K)), θ̂_K (τ_K) are maximum likelihood estimates given break points τ_K, which can be estimated through Algorithm 1, and

$$\mid H_k\left({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K)\right)\mid ={\left[\frac{{\partial }^{2}l({\mathit{\theta }}_K({\widehat{\mathit{\tau }}}_K))}{\partial {({\theta }_{a,k})}^2}\frac{{\partial }^{2}l({\mathit{\theta }}_K({\widehat{\mathit{\tau }}}_K))}{\partial {({\theta }_{b,k})}^2}-{\left(\frac{{\partial }^{2}l({\mathit{\theta }}_K({\widehat{\mathit{\tau }}}_K))}{\partial {\theta }_{a,k}\partial {\theta }_{b,k}}\right)}^2\right]}_{{\theta }_k={\widehat{\theta }}_k},$$

with

$$\begin{gathered} \frac{{\partial }^{2}l({\mathit{\theta }}_K,{\mathit{\tau }}_K)}{\partial {({\theta }_{a,k})}^2}=\sum _{t={\tau }_k+1}^{{\tau }_{k+1}}\left(\frac{{(Y_A(t)-Y_B(t)-(n_A(t)-n_B(t))h_{w(t)}^{\prime }({\theta }_{a,k}))}^2{f}_1(t,{\theta }_k)f_2(t,{\theta }_k)}{{(f_1(t,{\theta }_k)+f_2(t,{\theta }_k))}^2}-\frac{h_{w(t)}^{″}({\theta }_{a,k})(n_A(t)f_1(t,{\theta }_k)+n_B(t)f_2(t,{\theta }_k))}{f_1(t,{\theta }_k)+f_2(t,{\theta }_k)}\right), \\ \frac{{\partial }^{2}l({\mathit{\theta }}_K,{\mathit{\tau }}_K)}{\partial {\theta }_{a,k}\partial {\theta }_{b,k}}=\sum _{t={\tau }_k+1}^{{\tau }_{k+1}}\frac{(Y_A(t)-Y_B(t)-(n_A(t)-n_B(t))h_{w(t)}^{\prime }({\theta }_{a,k}))f_1(t,{\theta }_k)}{f_1(t,{\theta }_k)+f_2(t,{\theta }_k)}\times \frac{(Y_B(t)-Y_A(t)-(n_B(t)-n_A(t))h_{w(t)}^{\prime }({\theta }_{b,k}))f_2(t,{\theta }_k)}{f_1(t,{\theta }_k)+f_2(t,{\theta }_k)}, \\ \frac{{\partial }^{2}l({\mathit{\theta }}_K,{\mathit{\tau }}_K)}{\partial {({\theta }_{b,k})}^2}=\sum _{t={\tau }_k+1}^{{\tau }_{k+1}}\left(\frac{{(Y_B(t)-Y_A(t)-(n_B(t)-n_A(t))h_{w(t)}^{\prime }({\theta }_{b,k}))}^2{f}_1(t,{\theta }_k)f_2(t,{\theta }_k)}{{(f_1(t,{\theta }_k)+f_2(t,{\theta }_k))}^2}-\frac{h_{w(t)}^{″}({\theta }_{b,k})(n_B(t)f_1(t,{\theta }_k)+n_A(t)f_2(t,{\theta }_k))}{f_1(t,{\theta }_k)+f_2(t,{\theta }_k)}\right), \end{gathered}$$

where h_w(t)(θ) = log(w(t)e^θ +1), and $h_{w(t)}^{\prime }(\theta )=\frac{w(t)e^{\theta }}{w(t)e^{\theta }+1},h_{w(t)}^{″}(\theta )=\frac{w(t)e^{\theta }}{{(w(t)e^{\theta }+1)}^2}$.

The proof of this proposition is in the Appendix. Based on the proposition, we choose K that maximizes

$$l\left({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K\right)-\frac{1}{2}\sum _{k=0}^{K}log\mid H_k\left({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K\right)\mid -\mathit{K}logT.$$ (3.3)

3.5. A discussion on the independence assumption

In whole exome sequencing, some nearby inherited heterozygous sites could be too close that they can be spanned by the same read for single-read sequencing or by the same pair of reads for paired-end sequencing. If this happens, the read counts for the nearby sites would be dependent, violating the independence assumption for model (3.1). Here, we discuss two approaches to get around the issue. The first approach (“combining”) treats the problem more completely but needs to start from the BAM file, while the second approach (“pruning”) can start from the raw read counts directly but is usually less efficient than the first approach.

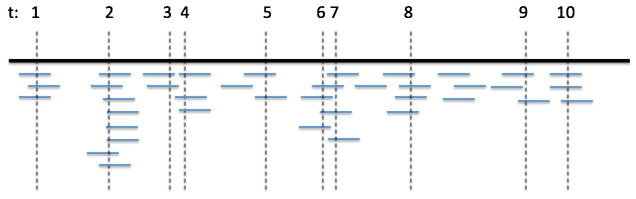
We first illustrate the two approaches for the single-read sequencing. Figure 3 is a schematic plot of reads over a stretch of a chromosome with 10 inherited heterozygous sites. We can see from the plot that if two sites are very close, they could be spanned by the same read. For example, there are two reads that span both site 6 and site 7. However, this does not necessarily happen to every pair of nearby sites. For example, sites 3 and 4 are close, but there is no read that spans both of them.

Fig. 3.

A schematic plot of reads over a stretch of a chromosome with 10 inherited heterozygous sites.

The combining approach is as follows: If two or more sites are spanned by the same read, then we view them all together as one site and the read count for the combined site is the number of distinct reads that cover at least one of the original sites contributing to the combined site. For example, sites 6 and 7 are viewed as one site and its read count is 6, while sites 3 and 4 are viewed as different sites and their read counts are 2 and 3, respectively. Then, in the example shown in the figure, there are 9 independent sites with one site being a combined site. To apply this approach, we need to know whether there is at least one read that spans the nearby sites. Hence, we need to start from the BAM file.

The pruning approach is easier to apply, and it can start from the raw read counts. For instance, the raw read counts for the 10 sites in the figure are 3, 8, 2, 3, 2, 3, 4, 4, 2 and 3, respectively. We then identify all combinations of sites that might be covered by one read, that is, identify the combinations of consecutive loci whose distances are less than the read length, such as 100 bp. In this example, we would identify two such combinations: {3, 4} and {6, 7}. We then randomly pick one site to keep for each combination. For example, keep site 4 from {3, 4} and keep site 7 from {6, 7}. This will lead to 8 sites—1, 2, 4, 5, 7, 8, 9, 10—and they are independent.

For paired-end sequencing, the two approaches can be adopted similarly by viewing the fragment spanned by the pair of reads as a “read” in the figure.

In the above discussion, we simplified the problem by only considering one sample. In practice, we need to consider the paired sample (tumor and matched normal samples). Then the criterion for the combining approach is slightly more complicated: If two or more sites are spanned by the same read in one or both samples, we combine these sites together.

Comparing the two approaches, it is clear that the combining approach loses less information but is more complicated in preparing the read counts, while the pruning approach is easier to implement but loses more information. If the BAM file is available, then the combining approach is recommended.

The R-package falconx takes read counts as input. If the combining approach was taken, then we can set the argument “independence = TRUE” (default) to let the function know that the input read counts are independent. Otherwise, we need to tell the function the length of read (or the maximal span of the read pairs for paired-end sequencing) and the pruning approach will be performed.

4. Spike-in experiment

We assess the accuracy of Falcon-X through a spike-in experiment, which allows us to systematically evaluate specificity and sensitivity for signals of varying size, purity and type. Sensitivity for copy number changes at low purity, that is, carried by a low proportion of cells in the sample, is especially desirable since tumor samples often have high normal cell contamination. To create the spike-in data sets, we started with real sequencing data from a normal sample and added signals of varying length at a fixed purity level by changing the coverage in the signal region commensurate with the given purity. As compared to simulating sequencing data in silico, adding signals to real sequencing data allows us to retain the noise properties of real data. For purity levels from 5% to 100% at 5% intervals, we created a total of 20 spike-in samples.

There are 6 possible configurations for allele-specific copy number aberrations listed in the rows of Table 1. All signals have width covering exactly 200 heterozygous sites, which on average corresponds to 26 Mb in the genome. For signals of this size, at 100% purity sensitivity is 100% for all aberration types for Falcon-X. We assessed sensitivity by recording, for each of the 6 types of aberrations, the lowest purity at which sensitivity rises above 95%. Falcon-X is compared to Falcon, an existing allele-specific method [Chen et al. (2014)], and CODEX, a total copy number estimation method [Jiang et al. (2015)]. Also shown for Falcon and Falcon-X, in parentheses, is the lowest purity at which not only the signal is detected but also the type of aberration is correctly identified. Note that, by modeling allele-specific changes, Falcon and Falcon-X significantly improve the sensitivity under low purity settings, as seen by the drop in purity level required for signal detection compared to CODEX. As previously shown in Chen et al. (2014), considering allele-specific information improves sensitivity, even for signals where the total copy number is changed. Also, by explicitly modeling the sample-specific biases in WES data, Falcon-X improves the aberration-type classification accuracy. For example, both Falcon-X and Falcon detect balanced Gain/Loss events at 15% purity; however, Falcon is able to correctly identify the event as balanced Gain/Loss only when the signal is present at 50%, whereas Falcon-X can do this when the purity is much lower, at 20%.

Table 1.

The smallest tumor purity under which the region of the change is found by Falcon-X, Falcon and CODEX. (The smallest tumor purity under which the type of aberration is correctly detected by Falcon-X and Falcon is shown in the parentheses)

Type of change	Falcon-X	Falcon	CODEX
Normal/Loss	15 (15)	15 (15)	30
Loss/Loss	15 (30)	10 (30)	15
Gain/Normal	15 (15)	20 (20)	35
Gain/Gain	15 (35)	15 (40)	20
Balanced Gain/Loss	15 (20)	15 (50)	–
Unbalanced Gain/Loss	10 (10)	10 (10)	35

Figure 4 shows the example of the true versus estimated signal for the 35% purity spike-in data. At this level, Falcon-X recovers the signal perfectly. Falcon also recovers a large part of the signal, but its segmentation is much less accurate and it makes some false positive detections as well.

Fig. 4.

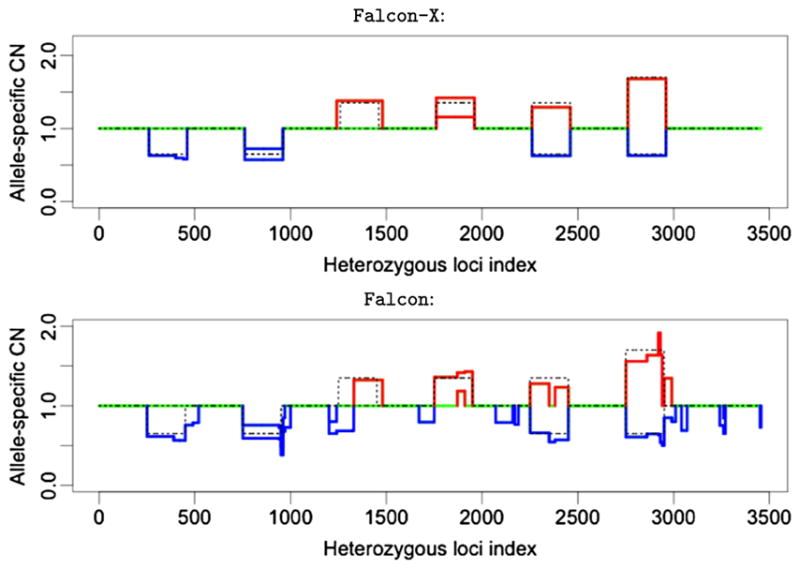
The allele-specific copy number estimates from Falcon-X (top panel) and Falcon (bottom panel) under 35% tumor purity with signals spanning 200 inherited heterozygous sites. The two colored lines represent the estimates of the two allele-specific copy numbers (C_a and C_b), and the two lines overlap when the two estimates are the same. Losses are shown in blue and gains are shown in red. Normal copy number is shown in green. Dotted black lines show the true allele-specific copy numbers in the spike-in set.

Figure 5 shows the specificity, as reflected by the percentage of loci where both alleles have copy number 1 that were not classified into any of the six aberration types. In all data sets, both Falcon and Falcon-X use a modified Bayes information criterion to determine the number of signals. Whereas Falcon makes a substantial number of false positives, the false positive rate of Falcon-X is much lower. This reduced false positive rate is due to the removal of sample-specific artifacts that are captured in the terms s(t) and s^*(t).

Fig. 5.

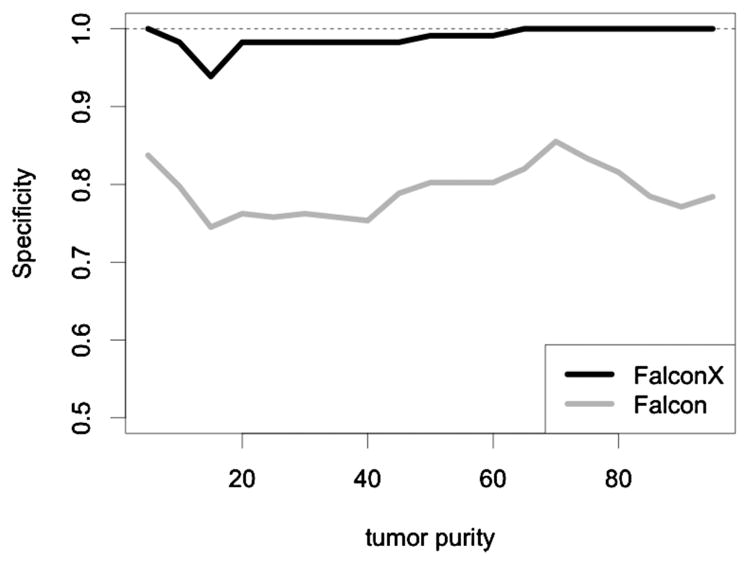
The percentage of loci where both alleles have copy number 1 that were not classified into any of the six aberration types for Falcon-X and Falcon.

To study the effect of the signal length on the performance of Falcon-X, we did spike-in simulations with shorter signal regions—signals spanning 40, 20 and 10 heterozygous sites, respectively. Table 2 lists the lowest purity at which the signal is detected, with the number in the parentheses the lowest purity at which the type of aberration is correctly identified by Falcon-X. We see that the performance of Falcon-X becomes slightly worse when the signal becomes shorter, while the sensitivity is overall quite good even for signals spanning only 10 heterozygous sites. Figure 6 plots the estimated and true ASCNs for 45% purity spike-in data with signals spanning 10 inherited heterozygous sites. We see that all signals are correctly identified.

Table 2.

The smallest tumor purity under which the region of the change is found by Falcon-X with different signal lengths (l: the number of heterozygous sites in each signal). (The smallest tumor purity under which the type of aberration is correctly detected is shown in the parentheses)

Type of change	l = 40	l = 20	l = 10
Normal/Loss	20 (20)	30 (30)	40 (40)
Loss/Loss	20 (25)	15 (25)	25 (25)
Gain/Normal	10 (10)	35 (35)	45 (45)
Gain/Gain	15 (35)	25 (35)	25 (30)
Balanced Gain/Loss	20 (20)	30 (30)	35 (35)
Unbalanced Gain/Loss	15 (20)	20 (25)	20 (20)

Fig. 6.

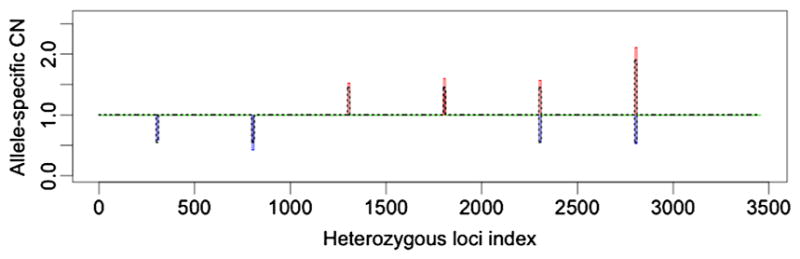
The allele-specific copy number estimates from Falcon-X under 45% tumor purity with signals spanning 10 inherited heterozygous sites. The two colored lines represent the estimates of the two allele-specific copy numbers (C_a and C_b), and the two lines overlap when the two estimates are the same. Losses are shown in blue and gains are shown in red. Normal copy number is shown in green. Dotted black lines show the true allele-specific copy numbers in the spike-in set.

5. Analysis of a breast cancer cohort of gBRCA1/2 carriers

Approximately 3–5% of breast and 20% of ovarian cancers arise in individuals carrying germline mutations in BRCA1 and BRCA2 [King et al. (2003)]. The main function of the BRCA1/2 proteins is the repair of double strand breaks in DNA. Mutations in these proteins lead to genome instability, facilitating the accumulation of somatic chromosome aberrations in tumorigenesis. Thus, BRCA1/2 mutation carriers have an increased risk for developing early onset breast and ovarian cancer.

Using Falcon-X, we analyzed WES sequencing data from 39 gBRCA1/2 breast and ovarian tumors with matched normal blood DNA. An in-depth study of these samples is described in Maxwell et al. (2016), where the goal is to delineate molecular mechanisms of tumorigenesis in gBRCA1/2 carriers and to identify potentially druggable alterations in these tumors. Whole exome sequencing on these samples was performed using the Agilent All-Exon Kit. Tumors were sequenced by Illumina Hi-Seq 2000 to an average depth of 141X and blood DNA to an average mean depth of 155X. The sequenced reads were aligned to the hg19 genome assembly using the Burrows-Wheeler Aligner (BWA) for short-read alignment. The aligned data was analyzed as described in Figure 2. Specifically, inherited heterozygous sites were called in the matched normal samples using GATK, the position-specific total coverage biases were estimated by CODEX, and allele-specific copy number was finally estimated through the Falcon-X model and algorithm. In this application, the pruning approach was used to avoid dependence issue.

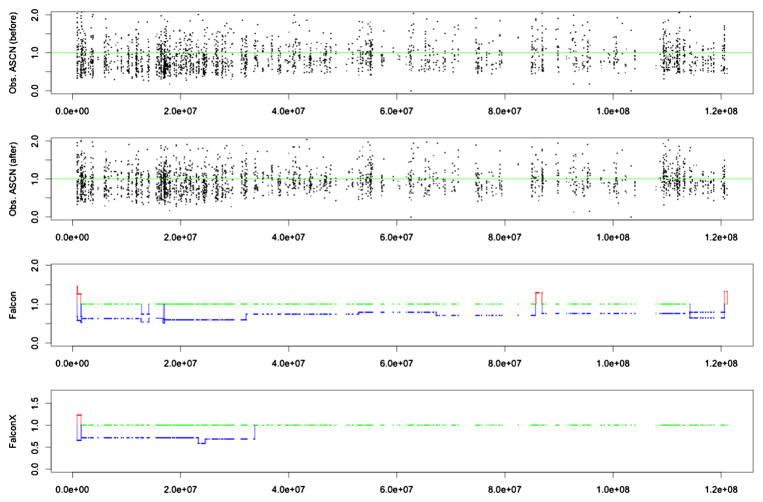
To illustrate the actual data that is used as input for our analysis, Figure 7 shows the raw values and estimated profiles from chromosome 1 p arm of one of the 39 samples. In the following, we refer to these samples as Basser gBRCA1/2 samples. The top plot shows the tumor to normal ratios of allele-specific coverage, that is, $Y_A(t)/Y_A^{\ast }(t)$ and $Y_B(t)/Y_B^{\ast }(t)$. The second plot shows the same ratios, after adjusting by the total coverage bias; that is, in the notation of Section 3.2, the second plot shows

Fig. 7.

Data from chromosome 1 p arm of a breast cancer patient (patient ID: Brca1Br10): The top plot shows the tumor to normal ratios of allele-specific coverage, that is, $Y_A(t)/Y_A^{\ast }(t)$ and $Y_B(t)/Y_B^{\ast }(t)$. The second plot shows the same ratios after adjusting by total coverage bias. In the first and second plots, a horizontal green line is plotted at value 1.0 for reference. The third and bottom plots show the allele-specific copy number estimates by Falcon and Falcon-X, respectively. Losses are shown in blue and gains are shown in red. Normal copy number is shown in green.

$$\frac{Y_A(t)/s(t)}{Y_A^{\ast }(t)/s^{\ast }(t)},\frac{Y_B(t)/s(t)}{Y_B^{\ast }(t)/s^{\ast }(t)}.$$

It is hard to detect by eye obvious change-points, and it is also hard to see the effect of bias correction, that is, the difference between the first and second figure panels. Statistically, however, there is a clear change-point at around position 3.3e7 indicated by both Falcon and Falcon-X results. Figure 8 shows the histograms of the tumor-to-normal allele coverage ratios for the two regions delineated in the Falcon-X result, where region 1 (from around 0.1e7 to around 3.3e7) contains a single copy deletion and region 2 (from around 3.3e7 to the end) is normal. Deletions cause allelic imbalance, that is, unequal copy numbers for the two alleles at heterozygote sites, and thus we expect the normal-to-tumor allele coverage ratios to be a two-component mixture for region 1, as opposed to a one-component mixture for region 2. In Figure 8, the histogram of these two regions look similar before the bias correction, but after the bias correction we indeed find, as expected, two peaks in region 1 and one peak in region 2. This example does not confirm the validity of our method, since we do not know the truth for this region, but is merely an illustration of the real data input and the empirical evidence that is used by Falcon-X to determine the change-points. As a contrast, the third plot from the top in Figure 7 shows the allele-specific copy numbers estimated by Falcon, which was not designed for whole exome sequencing and does not allow bias correction. It is clear that bias correction makes a difference, and we will next attempt to show that this difference is positive.

Fig. 8.

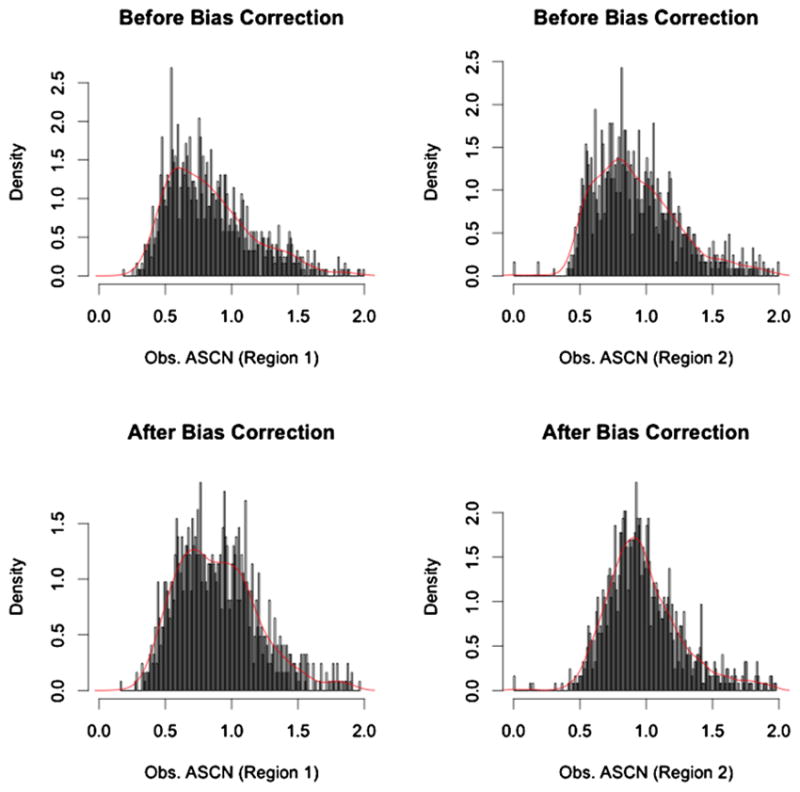
Histogram of tumor to normal ratios of allele-specific coverage before and after bias correction. These histograms summarize the values shown in the first and second plots of Figure 7, broken down by two regions, with region 1 including sites shown as Normal/Loss in the Falcon-X result and region 2 including sites shown as Normal/Normal in the Falcon-X result. The red curve is the kernel density estimated by the R function density() in package “stats.”

Allele-specific copy number estimates can be validated through procedures such as digital-droplet PCR or targeted sequencing, both of which are laborious procedures that are usually only applied to a small number of events. It is too costly to apply such validation techniques on the genome scale, and so, to assess the quality of Falcon-X estimates, we compare our analysis of the 39 breast cancer samples to an existing genotyping-array-based analysis of 47 gBRCA1/2 breast tumors from The Cancer Genome Atlas Project (TCGA). Since analysis methods for genotyping arrays are now more mature than those for high-throughput sequencing data, and since TCGA applied rigorous quality control to their data sets, we expect that high-level trends observed in the TCGA samples should be reproduced in our breast cancer cohort. Although no two cancer patients have the same chromosome copy number profile, it has been shown that breast cancer patients with gBRCA1/2 mutations, and similarly gBRCA1/2 ovarian cancer patients, often share recurrent gain and loss regions. We adopt that most of these recurrent CNAs have been seen in the TCGA cohort and we expect to observe similar recurrent gains and losses between the TCGA gBRCA1/2 breast cancer samples and our Basser gBRCA1/2 samples.

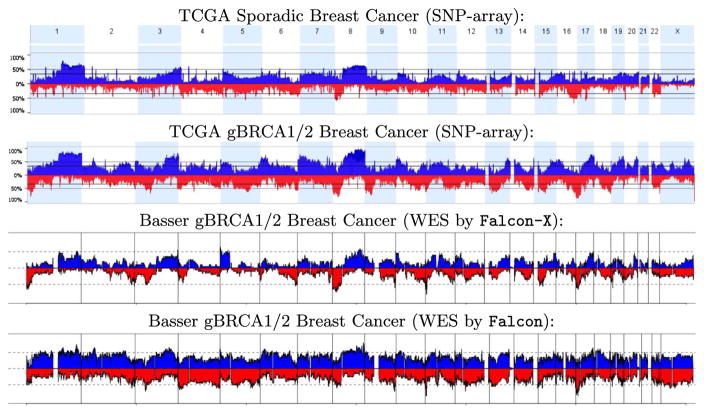
Figure 9 shows the frequency of detected gain and loss at each genome position for the TCGA gBRCA1/2 breast cancers as well as for the Basser gBRCA1/2 samples analyzed by Falcon-X and by Falcon. For each plot, blue bars in the “positive” direction show the proportion of the samples with a detected gain at the given position, and red bars in the “negative” direction show this proportion for losses. Since copy number changes are scattered somewhat randomly in the genomes of all gBRCA1/2 tumors due to genome instability, almost all positions are marked as gained or lost in at least some of the patients. Yet, the Falcon-X results clearly indicate that there are genome regions that are more frequently altered than others, such as loss of 8p and 17p and gain of 3q, 8q and 17q. This agrees with the recurrent regions reported in the literature on gBRCA1/2 breast tumors. Note that the recurrent regions found by Falcon-X are more similar to those found by TCGA, as compared to the Falcon results. Falcon analysis detects much more copy number events, as seen by the elevated occurrence of both gains and losses at all genome positions across the cohort. Against this uniformly elevated background of detections, Falcon results do not show marked evidence for recurrence at the known positions reported in the literature, which are found by Falcon-X. We believe many of the Falcon detections are false positives caused by the biases inherent in WES data.

Fig. 9.

Frequency of detected occurrence of gains (in blue, above the axis) and losses (in red, below the axis) of total copy number in three breast cancer cohorts: TCGA sporadic breast cancers, TCGA gBRCA1/2 breast cancers, and our Basser gBRCA1/2 breast cancers. The TCGA cohorts, shown in the top two plots, were profiled by the genotyping array. The Basser samples were profiled by WES and analyzed by Falcon-X, shown in the third plot from the top, and by Falcon, shown in the bottom plot. The horizontal axis shows genome location, and is aligned between the four plots. The vertical axis shows the proportion of samples where a call is made. Chromosome boundaries are marked by vertical lines or color shading.

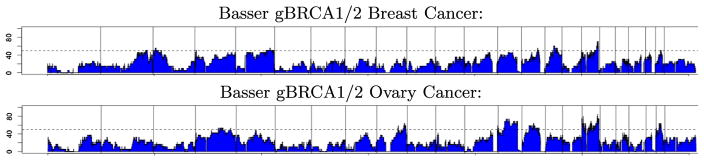
Figure 9 does not explicitly show the frequency of copy-neutral loss-of-heterozygosity (LOH) events, where one of the parental alleles have been lost and replaced by a duplication of the allele from the other parent. Figure 10, which plots the frequency of copy-neutral LOH events along the genome, shows that copy-neutral LOH events are frequent in the Basser gBRCA1/2 cancer data. These events would not have been detected if we only estimate total copy number. Using Falcon-X, we identified copy-neutral LOH that helped us better understand the initiation mechanism of BRCA1/2 tumors. These events are described and analyzed in Maxwell et al. (2016).

Fig. 10.

Frequency of occurrence of Copy-neutral loss of heterozygosity (LOH) found by Falcon-X in the Basser gBRCA1/2 breast cancer cohort and the Basser gBRCA1/2 ovarian cancer cohort. As in Figure 9, the horizontal axis shows genome location aligned between the two plots, and vertical axis shows percentage of samples where LOH is detected. Vertical lines denote chromosome boundaries.

6. Conclusion

We have proposed a statistical framework for allele-specific copy number estimation by whole exome sequencing. We focused specifically on the study design where a tumor sample and a matched normal control are both sequenced, and where a batch of normal tissue samples are also sequenced by the same protocol. Whole exome sequencing has become a commonly adopted approach to cancer genomics, and since experimental biases introduced by exon selection and amplification cannot be fully captured by simply comparing the tumor against its matched normal, more sophisticated statistical modeling is necessary. In the Falcon-X model, allele-specific sequencing coverage is represented by a binomial mixture process, where the binomial means depend on the copy numbers of the underlying haplotypes as well as site-specific sequencing bias. We showed using simulation spike-in data that, by controlling for these site-specific biases, Falcon-X allows more sensitive detection of allele-specific copy number change under high normal cell contamination. We also applied the new analysis approach to a set of BRCA1/2 breast and ovarian tumor samples, where the results we obtained are in good concordance with existing knowledge about this type of tumor.

The two technical challenges in the Falcon-X model are (1) fast and precise estimation of the parameters in the mixture model, and (2) determining the number of change-points, that is, the model complexity. For parameter estimation, we developed a majorization-minorization algorithm, described in Section 3.3. This fast algorithm allows the Falcon-X model to scale to large genomic studies (analysis of the 39 breast and ovarian tumors took less than one hour on a Macbook Air). This algorithm can potentially be used in other mixture deconvolution settings; for example, one can extend the Falcon-X model to allele-specific RNA expression analysis. For determining the number of change-points, we extended the modified Bayes information criterion of Chen et al. (2014) and Zhang and Siegmund (2007), which allows the method to be used off-the-shelf.

APPENDIX: PROOF OF PROPOSITION 1

The log-likelihood function of the observed data under the new parameterization can be written as

$$l({\mathit{\theta }}_K,{\mathit{\tau }}_K)=\sum _{k=0}^K\sum _{t={\tau }_k+1}^{{\tau }_{k+1}}log\left(f_1(t,{\theta }_k)+f_2(t,{\theta }_k)\right)+log\left(C(\mathbf{Z})\right),$$

where

$$\begin{gathered} C(\mathbf{Z})=\frac{1}{2^T}\prod _{t=1}^T\left(\begin{array}{c}{n}_A(t)\\ Y_A(t)\end{array}\right)\left(\begin{array}{c}{n}_B(t)\\ Y_B(t)\end{array}\right)w{(t)}^{Y_A(t)+Y_B(t)}, \\ {f}_1(t,{\theta }_k)=exp\left(Y_A(t){\theta }_{a,k}-n_A(t)log\left(w(t)e^{{\theta }_{a,k}}+1\right)+Y_B(t){\theta }_{b,k}-n_B(t)log\left(w(t)e^{{\theta }_{b,k}}+1\right)\right), \\ {f}_2(t,{\theta }_k)=exp\left(Y_B(t){\theta }_{a,k}-n_B(t)log\left(w(t)e^{{\theta }_{a,k}}+1\right)+Y_A(t){\theta }_{b,k}-n_A(t)log\left(w(t)e^{{\theta }_{b,k}}+1\right)\right). \end{gathered}$$

Fixing τ_K, we can expand the log-likelihood in a second order Taylor series around the maximum likelihood estimate:

$$l\left({\mathit{\theta }}_K({\mathit{\tau }}_K)\right)\approx l\left({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K)\right)+{\left({\mathit{\theta }}_K-\widehat{\mathit{\theta }}({\tau }_K)\right)}^{\prime }H\left({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K)\right)\left({\mathit{\theta }}_K-\widehat{\mathit{\theta }}({\tau }_K)\right)/2.$$

Under the uniform prior assumption for (τ_k, θ_K), we have

$$\begin{gathered} P(\mathbf{Z}\mid {\mathcal{M}}_K)={\int }_{{\mathcal{D}}_K}{\int }_{{ℝ}^{2K+2}}{e}^{l({\mathit{\theta }}_K({\mathit{\tau }}_K))}\frac{K!}{T^K}d{\mathit{\theta }}_{K}d{\mathit{\tau }}_K \\ \approx {\int }_{{\mathcal{D}}_K}{e}^{l({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K))}{\mid H\left({\widehat{\mathit{\theta }}}_K({\tau }_K)\right)\mid }^{-1/2}\frac{K!{(2\pi )}^{K+1}}{T^K}d{\mathit{\tau }}_K. \end{gathered}$$

Similarly, we have for K = 0

$$P(\mathbf{Z}\mid {\mathcal{M}}_0)={\int }_{{ℝ}^2}{e}^{l({\mathit{\theta }}_0)}d{\mathit{\theta }}_0\approx 2\pi {\mid H({\widehat{\mathit{\theta }}}_0)\mid }^{-1/2}{e}^{l({\widehat{\mathit{\theta }}}_0)}.$$

When K follows a uniform prior over ℤ⁺, we have

$$\begin{gathered} log\frac{P({\mathcal{M}}_K\mid \mathbf{Z})}{P({\mathcal{M}}_0\mid \mathbf{Z})}=log\frac{P(\mathbf{Z}\mid {\mathcal{M}}_K)}{P(\mathbf{Z}\mid {\mathcal{M}}_0)} \\ \approx l\left({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K\right)-\frac{1}{2}\sum _{k=0}^{K}log\mid H_k\left({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K\right)\mid -l({\widehat{\mathit{\theta }}}_0)+\frac{1}{2}log\mid H({\widehat{\mathit{\theta }}}_0)\mid -\mathit{K}logT+log{\int }_{{\mathcal{D}}_K}{e}^{l({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K),{\mathit{\tau }}_K)-l({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K)}\times \sqrt{\prod _{i=0}^K\frac{\mid H_k({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K\mid }{\mid H_k({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K),{\mathit{\tau }}_K)\mid }}d{\mathit{\tau }}_K. \end{gathered}$$

Based on the extension of Zhang (2005), it can be shown that

$${\int }_{{\mathcal{D}}_K}{e}^{l({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K),{\mathit{\tau }}_K)-l({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K)}\sqrt{\prod _{i=0}^K\frac{\mid H_k({\widehat{\mathit{\theta }}}_K({\widehat{\mathit{\tau }}}_K),{\widehat{\mathit{\tau }}}_K)\mid }{H_k({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K),{\mathit{\tau }}_K)}}d{\mathit{\tau }}_K$$

is uniformly bounded in T under the hypothesis of K change-points.

Notice that H (θ̂_K (τ_K)) is a block diagonal matrix with (K + 1) blocks and each block is a 2 × 2 matrix. Its (k + 1)th block is

$$H_k\left({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K)\right)=\left[\begin{array}{ll}{\frac{{\partial }^{2}l({\mathit{\theta }}_k,{\mathit{\tau }}_K)}{\partial {({\theta }_{a,k})}^2}|}_{{\theta }_k={\widehat{\theta }}_k}\hfill & {\frac{{\partial }^{2}l({\mathit{\theta }}_k,{\mathit{\tau }}_K)}{\partial {\theta }_{a,k}\partial {\theta }_{b,k}}|}_{{\theta }_k={\widehat{\theta }}_k}\hfill \\ {\frac{{\partial }^{2}l({\mathit{\theta }}_k,{\mathit{\tau }}_K)}{\partial {\theta }_{a,k}\partial {\theta }_{b,k}}|}_{{\theta }_k={\widehat{\theta }}_k}\hfill & {\frac{{\partial }^{2}l({\mathit{\theta }}_k,{\mathit{\tau }}_K)}{\partial {({\theta }_{b,k})}^2}|}_{{\theta }_k={\widehat{\theta }}_k}\hfill \end{array}\right].$$

Hence,

$$\begin{gathered} \mid H\left({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K),{\mathit{\tau }}_K\right)\mid =\prod _{k=0}^K\mid H_k\left({\widehat{\mathit{\theta }}}_K({\mathit{\tau }}_K),{\mathit{\tau }}_K\right)\mid \\ =\prod _{k=0}^K{\left(\frac{{\partial }^{2}l({\mathit{\theta }}_K,{\mathit{\tau }}_K)}{\partial {({\theta }_{a,k})}^2}\frac{{\partial }^{2}l({\mathit{\theta }}_K,{\mathit{\tau }}_K)}{\partial {({\theta }_{b,k})}^2}-{\left(\frac{{\partial }^{2}l({\mathit{\theta }}_K,{\mathit{\tau }}_K)}{\partial {\theta }_{a,k}\partial {\theta }_{b,k}}\right)}^2\right)|}_{{\theta }_k={\widehat{\theta }}_k}, \end{gathered}$$

and Proposition 1 follows.