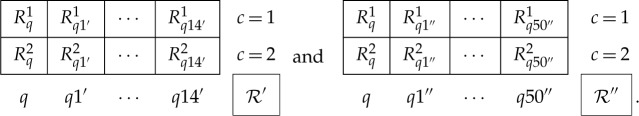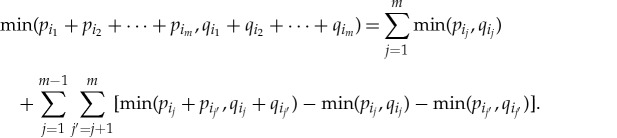Contextuality in canonical systems of random variables

Abstract

Random variables representing measurements, broadly understood to include any responses to any inputs, form a system in which each of them is uniquely identified by its content (that which it measures) and its context (the conditions under which it is recorded). Two random variables are jointly distributed if and only if they share a context. In a canonical representation of a system, all random variables are binary, and every content-sharing pair of random variables has a unique maximal coupling (the joint distribution imposed on them so that they coincide with maximal possible probability). The system is contextual if these maximal couplings are incompatible with the joint distributions of the context-sharing random variables. We propose to represent any system of measurements in a canonical form and to consider the system contextual if and only if its canonical representation is contextual. As an illustration, we establish a criterion for contextuality of the canonical system consisting of all dichotomizations of a single pair of content-sharing categorical random variables.

This article is part of the themed issue ‘Second quantum revolution: foundational questions’.

1. Introduction

We begin by recapitulating the basics of our theory of ‘quantum-like’ contextuality, and then explain how this theory is developed in this paper. The name of the theory is Contextuality-by-Default (CbD), and its recent accounts can be found in [1–3].

Remark 1.1 —

We use the following two notation conventions throughout the paper: (1) owing to its frequent occurrence, we abbreviate the term random variable as rv (rvs in plural); and (2) we unconventionally capitalize the words conteNt and conteXt to prevent their confusion in reading.

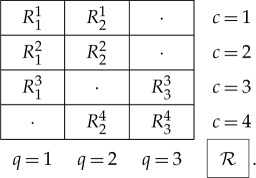
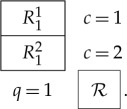
The matrix below represents the smallest possible version of what we call a cyclic system [4–7]:

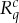Each of the rvs represents measurements of one of two properties, q=1 or q=2, under one of two conditions, c=1 or c=2. The ‘properties’ q can also be called ‘objects’, ‘inputs’, ‘stimuli’, etc. depending on the application, and we refer to q generically as the conteNt of the measurement . The superscript c in describes how and under what circumstances q is measured, including what other conteNts are measured together with q. We refer to c generically (and traditionally) as the conteXt of the measurement 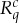. The conteNt–conteXt pair (q,c) provides a unique identification of 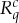within the system of measurements 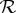. In addition, being an rv, 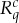is characterized by its distribution. In this paper, consideration is confined to categorical rvs, those with finite numbers of values. The term ‘measurement’ is understood very broadly, to include any response to any input or stimulus.

Let us begin with the simplest case of the system 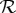, when all four rvs 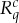are binary. In quantum physics, 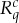may describe a measurement of spin along one of two fixed axes, q=1 or q=2, in a spin- 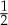particle. In psychology, 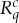may describe a response to one of two Yes–No questions, q=1 or q=2. In both applications, in conteXt c=1 one measures first q=1 and then q=2; in conteXt c=2 the measurements are made in the opposite order. The rvs sharing a conteXt c are recorded in pairs, 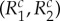, which means that they are jointly distributed and can be viewed as a single (here, four-valued) rv. No such joint distribution is defined for rvs in different conteXts, such as 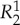and 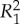. They are stochastically unrelated (to each other): one cannot ask about the probability of an ‘event’ 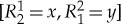, as no such ‘event’ is defined. In particular, two conteNt-sharing rvs, 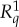and 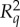, are always stochastically unrelated, hence they can never be considered one and the same rv, even if they are identically distributed (see [1] for a detailed probabilistic analysis).

In both applications mentioned, the distributions of 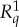and 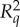are de facto different. In the quantum-mechanical example, the first spin measurement generally changes the state of the particle [8]. Assuming identical preparations in both conteXts c, therefore, the state of the particle when a q-spin is measured first will be different from that when it is measured second. In the behavioural example, one's response to a question asked second will generally be influenced by the question asked first [9,10]. This creates obvious conteXt-dependence of the measurements, but this is not what we call contextuality in our theory. The original meaning of the term in quantum mechanics, when translated into the language of probability theory (as in [1,3,11] and, with caveats, [6,12–17]), is that measurements of one and the same physical property q have to be represented by different rvs depending on what other properties are being measured together with q—even when the laws of physics exclude all direct interactions (energy/information transfer) between the measurements. By extension, when such direct interactions are present, as they are in our two applications of the system 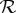, we speak of contextuality only if the dependence of 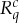on c is greater, in a well-defined sense, than just the changes in its distribution. Contextuality is a non-causal aspect of conteXt-dependence, revealed in the probabilistic relations between different measurements rather than in their individual distributions.

This is how this understanding is implemented in CbD. We characterize the conteXt-induced changes in the individual distributions, i.e. the difference between those of 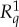and 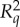, by maximally coupling them. This means that we replace 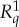and 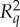with jointly distribute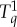d and 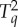that have the same respective individual distributions, and among all such couplings we find one with the maximal value of 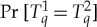. This maximal coupling 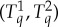always exists and is unique. The next step is to see if there exists an overall coupling S of 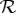, a jointly distributed quadruple with elements corresponding to those of ,

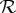such that its rows 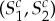are distributed as the rows of 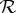and its columns 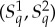are distributed as the maximal couplings 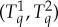of the columns of 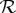. If such a maximally connected coupling S does not exist, one can say that the within-conteXt (row-wise) relations prevent different measurements of the same conteNt (column-wise) from being as close to each other as this is allowed by the direct influences alone. Put differently, the relations of 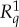and 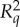with their same-conteXt counterparts force them, if imposed a joint distribution on, to coincide less frequently than if these relations are ignored. The system then is deemed contextual. Conversely, if the coupling S above exists, the within-conteXt relations do not make the measurements of 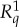and 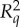any more dissimilar than required by the direct influences: the system is non-contextual.

The (non)existence of S is determined by a simple linear programming procedure [4,3]: in our example, S has 2⁴ possible values, and we find out if they can be assigned non-negative numbers (probability masses) that sum to the given row-wise probabilities 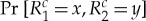and the computed column-wise probabilities 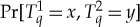. There is also a simple criterion (inequality) for the existence of a solution for this system of equations [4–6]. Using it one can show, e.g. that in our quantum-mechanical application the system 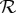is always non-contextual, and this is also true for the behavioural application if one adopts the model proposed in [9] (see [18] for details). Mathematically, however, the system 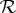can be contextual, and if it is, CbD provides a simple way of computing the degree of its contextuality [3]: one replaces the probability masses in the above linear programing task with quasi-probabilities, allowed to be negative, and finds among the solutions the minimum sum of their absolute values (see §2c).

Although most of these principles and procedures of CbD have been formulated for arbitrary systems of measurements [3,11], they only work without complications with systems that satisfy the following two constraints: (A) they contain only binary rvs, and (B) there are no more than two rvs sharing a conteNt (i.e. occupying the same column). What we propose in this paper is to always present a system of measurements in a canonical form, which is in essence one with the properties A and B. The cyclic systems form a subclass of canonical systems, rich enough to cover most experimental paradigms of traditional interest in quantum-mechanical and behavioural contextuality studies [3,4,6,11,18,19], but far from satisfactory generality.

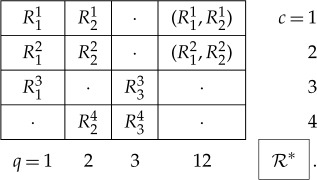
What are the complications one faces if a system does not satisfy the properties A and B? Consider the system below, with all its rvs binary but with three rather than two of them in each column:

How does CbD apply here? In the earlier version of the theory (summarized in [3,11]), we computed the couplings 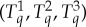of each column that maximize 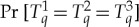. One problem with this approach is that the maximal coupling 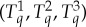, while it always exists, is not defined uniquely. What should be the contextuality analysis of 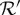if the within-conteXt (row-wise) distributions are compatible with some but not all combinations of the maximal couplings for the two columns? Shall one then speak of a partial (non)contextuality? Originally, we proposed to consider a system non-contextual if it is compatible with at least one of these pairs of maximal couplings, but in addition to being arbitrary, this leads to another complication: it may then very well happen that the system 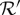is non-contextual but one of its subsystems, e.g. 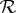, is contextual. This is contrary to one's intuition of non-contextuality.

In the most recent publications therefore [1,2], we modified our approach into ‘CbD 2.0’, by positing that a coupling for conteNt-sharing measurements should be computed so that it maximizes the probability of coincidence for every pair (equivalently, every subset) of them. In our case, this means maximization of 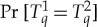, 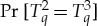and 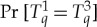(it is in fact sufficient to maximize only certain pairs rather than all of them, but this is not critical here). Such a coupling 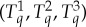is called multimaximal. With only binary rvs involved, a multimaximal coupling always exists and is unique; and a subsystem of a non-contextual system then is always non-contextual.

Returning to system 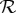, consider now the situation when the measurements involved are not dichotomous. For example, let the two successive spin measurements along axes q=1 and q=2 be made on a hypothetical spin-2 particle, with the measurement outcomes denoted by {−2,−1,0,1,2}. In the behavioural application, let the questions asked allow five answers each, labelled in the same way. A maximal coupling in this situation exists for each column of 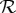, but not uniquely. This takes us back to the problem of what one should do if the row-wise distributions are compatible with some but not all pairs of these maximal couplings. Another problem is even harder. If the system is deemed non-contextual, one may consider it desirable that it remain non-contextual after some of the measurement outcomes are ‘lumped together.’ Thus, one may wish to consider {−2,−1,0,1,2} in terms of ‘negative-zero-positive’, lumping together −2 with −1 and 2 with 1. Or one may wish to look at the outcomes in terms of ‘zero-non-zero.’ As it turns out, a non-contextual system may become contextual after such coarsening of some of its measurements.

Both these problems can be resolved if we agree that every measurement included in the system, empirically recorded or computed from those empirically recorded, should be represented by a set of binary rvs. Let us denote by 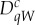the Bernoulli rv that equals 1 if the value of 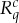is within the subset W of its possible values. We call 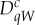a split (of the original rv). We posit that a measurement with k distinct values should always be represented by k ‘detectors’ of these values, i.e. the splits with one-element subsets W. Thus, in our system 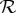, each measurement 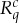should be replaced with the jointly distributed splits

If one is also interested in the coarsening of 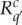into values ‘negative-zero-positive’, then the list should be expanded into

If one wishes to include all possible coarsenings of the original rvs in 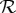, then the set of binary rvs should consist of all possible splits. As every dichotomization creating a split should be applied to all rvs sharing a conteNt, one ends up replacing the system 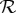with

There are (2⁵−2)/2=15 distinct dichotomizations of the set {−2,−1,0,1,2}, and the 15 subsets W in 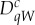should be chosen to avoid duplication, such as in D^c_q{0,1} and D^c_{q{−2,−1,2}}. Once duplication is prevented, however, all splits of all rvs one is interested in should be included. It is irrelevant that some of them can be presented as functions of the others. In fact, any split of our 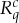can be presented as a function of just three splits, chosen, e.g. as

It is easy to show, however, that in the subsystem

of the system , the f-transformation of the maximal couplings of the first three columns, because these couplings are not jointly distributed, would not determine the coupling of the fourth column, let alone ensure that this coupling is maximal.

There is no general prescription as to which rvs should or should not be included in the system representing an empirical set of measurements: what one includes (e.g. what coarsenings of the rvs already in play one considers) reflects what aspects of the empirical situation one is interested in. Once a set of rvs is chosen, however, we uniquely form their splits and place them in a canonical system.

The remainder of the paper is organized as follows. In §2, we present the abstract version of CbD applicable to all possible systems of categorical (and not only categorical) rvs. In §3, we formalize the idea of representing any system of rvs by their splits and applying contextuality analysis to these representations only. In §4, we investigate the representation of all coarsenings of a single pair of conteNt-sharing rvs by all possible splits. In the concluding section, we explain why one might wish to consider only some rather than all possible splits.

Remark 1.2 —

The proofs of the formal propositions in the paper, unless obvious or referenced as presented elsewhere, are given in electronic supplementary material, file S, together with additional theorems and examples.

2. Formal theory of contextuality

(a). Basic notions

The definition of a system of rvs requires two non-empty finite sets, a set of conteNts Q and a set of conteXts C. There is a relation

2.1

such that the projections of into Q and C equal Q and C, respectively (this means that, for every q∈Q, there is a c∈C, and vice versa, such that 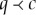). We read both 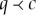and 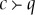as ‘q is measured in c’.

A categorical rv is one with a finite set of values and its power set as the codomain sigma-algebra. A system of (categorical) rvs is a double-indexed set (we use calligraphic letters for sets of random variables)

2.2

such that (i) any 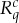and 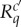have the same set of possible values; (ii) 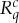and 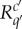are jointly distributed if c=c′; and (iii) if c≠c′, 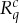and 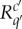are stochastically unrelated (possess no joint distribution). For any c∈C, the subset

2.3

of 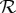is called a bunch (of rvs) corresponding to c. As the elements of a bunch are jointly distributed, the bunch is a (categorical) rv in its own right, so it can be also written as R^c. Note that we do not distinguish the representations of 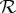as (2.2) and as

2.4

(See [1,3] for a detailed probabilisitic analysis.)

For any q∈Q, the subset

2.5

of 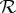is called a connection (between the bunches of rvs) corresponding to q. Any two elements of a connection are stochastically unrelated, so it is not an rv.

(b). General definition of (non)contextuality

A (probabilistic) couplingY of a set of rvs {X₁,…,X_n} is a set of jointly distributed {Y₁,…,Y_n} such that Y_i∼X_i for i=1,…,n. The tilde ∼ stands for ‘has the same distribution as’.

An (overall) coupling S of a system 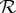in (2.2) is a coupling of its bunches. That is, it is an rv

2.6

(with jointly distributed components) such that S^c∼R^c for any c∈C. This implies that

2.7

is a set of jointly distributed rvs in a one-to-one correspondence with the identically labelled elements of .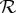

For a given q∈Q, a coupling T_q of a connection 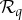is an rv

2.8

such that 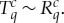In particular, if S is a coupling of 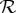, then

2.9

is a coupling of 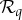for any q∈Q.

Definition 2.1 —

Given a set of couplings for all connections in a system , the system is said to be non-contextual with respect to if has a coupling S with S_q∼T_q for any q∈Q. Otherwise is said to be contextual with respect to .

Put differently, 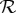is non-contextual with respect to if and only if there is a jointly distributed set

2.10

such that, for every c∈C, S^c∼R^c, and for every q∈Q, S_q∼T_q. A coupling S with this property is called 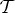-connected.

If the couplings T_q are characterized by some property C such that one and only one coupling T_q satisfies this property for any given connection 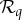, then the definition can be rephrased as follows.

Definition 2.2 —

is said to be non-contextual with respect to property C if it has a C-connected coupling S, defined as one with S_q satisfying C for any q∈Q. Otherwise is said to be contextual with respect to C.

Remark 2.3 —

In §3c, we will use the property of (multi)maximality to play the role of C, and the couplings in question then are referred to as (multi)maximally connected.

(c). Degree of contextuality

A quasi-distribution on a finite set V is a function 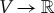(real numbers) such that the numbers assigned to the elements of V sum to 1. We will refer to these numbers as quasi-probability masses. A quasi-rv X is defined analogously to an rv but with a quasi-distribution instead of a distribution.

A quasi-coupling X of 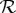is defined as a quasi-rv

2.11

such that X^c∼R^c for every c∈C. We have the following results.

Theorem 2.4 ([3, Theorem 6.1]) —

For any system and any set of couplings for the connections of , there is a quasi-coupling X of such that for any q∈Q.

The total variation of X is denoted by ∥X∥ and defined as the sum of the absolute values of the quasi-probability masses assigned to all values of X.

Theorem 2.5 ([3, Section 6.3]) —

The total variation ∥X∥ reaches its minimum in the class of all quasi-couplings X satisfying the conditions of theorem 2.4.

If 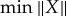is 1, then all quasi-probability masses are non-negative, and the system 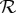is non-contextual with respect to 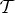. If 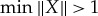, then the system is contextual with respect to 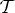, and 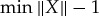can be taken as a (universally applicable) measureof the degree of contextuality.

3. Splits and canonical representations

(a). Expansions of the original system

One is often interested not only in a system of empirically measured rvs 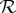but also in some transformations thereof. Each such a transformation F_q1,…,qk is labelled by a set of conteNts, q₁,…,q_k, and it takes as its arguments the rvs in each conteXt c such that 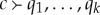. The outcome,

3.1

is an rv interpreted as measuring a new conteNt q* in the conteXt c. One is free to choose any such transformations and form the corresponding new conteNts, as there can be no rules mandating what one should be interested in measuring.

Using various transformations to add new conteNts and new rvs to the original system expands it into a larger system. Two types of expansions that are of particular interest are expansion-through-joining and expansion-through-coarsening. Joining is defined as

3.2

whereas coarsening is transformation

3.3

In fact any other transformation 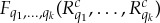can be presented as joining followed by coarsening.

Example 3.1 (joining) —

Consider the system

It contains the jointly distributed and also the jointly distributed , but in determining the maximal couplings of and of in the first and second columns, these row-wise joints are not used. In some applications, this would be unacceptable (e.g. in the theory of selective influences [20,21] and in the approach advocated by Abramsky and colleagues [22,23] this is never acceptable), and then the following expansion has to be used:

Example 3.2 (coarsening) —

If V is a set of possible values of , then U=F_q(V) is the set of possible values of the rv This rv is a coarsening of . Note that any rv is its own coarsening. As the way one labels the values of U is usually irrelevant, each such function F_q can be presented as a partition of V . Consider, e.g. the ‘mini’-system

and let the two rvs take values on {1,2,3,4,5}. If these values are considered ordered, 1<⋯<5, one may be interested in all possible partitions of {1,2,3,4,5} into subsets of consecutive numbers, such as {12|34|5}, {1|2345}, etc. There are 15 such partitions (counting {1|2|3|4|5} that defines the original rvs , but excluding the trivial partition {12345}). If the values 1,2,3,4,5 are treated as unordered labels, one might consider all possible non-trivial partitions, such as {{14},{25},{3}}, {{145},{23}}, etc. There are 51 such partitions. In either of these two coarsening schemes the partitions can be ordered in some way, and the respective expanded systems then become

Remark 3.3 —

Although the number of the states (combinations of the values of the elements) of the bunch R^c in and especially in is very large, the support of each bunch (the set of the states with non-zero probabilities) has the same size as that of the initial random variable in (i.e. in our example, it cannot exceed 5). This follows from the facts that each event uniquely defines the state of R^c in and in , and that .

(b). Dichotomizations and canonical/split representations

Definition 3.4 —

A dichotomization of a set V is a function . Applying such an f to an rv R with the set of possible values V , we get a binary rv f(R). We call this f(R) a split of the original R.

If 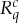is an element of a system 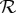, let us agree to identify 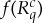as 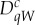, where W=f⁻¹(1), with the understanding that 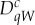and 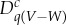are indistinguishable. To make the choice definitive, we always choose W as the smaller of W and V −W; in case they have the same number of elements, we order the elements of V , say 1<2<⋯<k, and then choose W as lexicographically preceding V −W.

With V ={1,2,…,k}, the jointly distributed set of splits

3.4

is called the split representation of 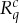. If k=2, then 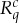is its own split representation, because D^c_q{1} and D^c_q{2} are indistinguishable.

Definition 3.5 —

The system obtained from a system by replacing each of its elements by its split representations is called the canonical(or split)representation of .

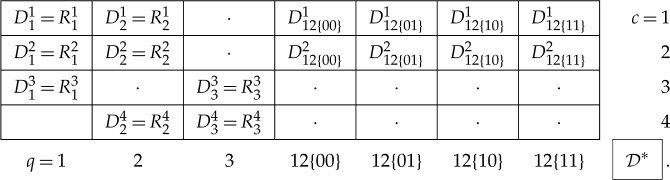
Example 3.6 (continuing example 3.1) —

Let all rvs in be binary, 0/1, whence and in have four values each: 00,01,10 and 11. Replacing them with the split representations and observing that the first three columns do not change, we get the following canonical representation of :

Example 3.7 (continuing example 3.2) —

For the system , it is clear that the split representations of the 15 coarsenings of variously overlap: e.g. D¹_q{3} belongs to the split representations of and of the coarsenings defined by the partitions {12 | 3 | 45}, {1 | 2 | 3 | 45} and {12 | 3 | 4 | 5}. Following our rules, W in the splits comprising the split representation of are (when written as strings) 1,2,3,4,5,12,23,34,45 and 15 (note that, e.g., the split of the coarsening {1 | 23 | 4 | 5} with W= {1,23} should be denoted as D¹_q{1,23} according to our definitions, but this is the same random variable as D¹_q{45} which we have included in the list). For the system the canonical representation, obviously, consists of all possible splits of . It will be the target of the analysis presented in §4.

(c). Multimaximality for canonical representations

If each connection in a canonical representation 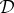contains just two rvs, one can compute unique maximal couplings for all of these connections. The determination of whether 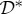is (non)contextual then can proceed in compliance with the general theory presented in §2b, and amounts to determining if 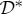has a maximally connected coupling S (see remark 2.3). If no such coupling exists, the computation of the degree of contextuality in 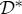can be done in compliance with §2c.

In a more general case, however, with an arbitrary number of rvs in each connection, maximal couplings should be replaced with computing what we call multimaximal couplings [1,2].

Definition 3.8 —

A coupling T_q of a connection of a split representation is called multimaximal if, for any c,c′∈C such that , is maximal over all possible couplings of . (If the connection contains two rvs, its multimaximal coupling is simply maximal.)

A multimaximal coupling is known to have the following properties.

• Multimax1: The multimaximal coupling exists and is unique for any connection ([2] Corollary 1).

• Multmax2: T_q is a multimaximal coupling of 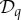if and only if any subset of T_q is a maximal coupling for the corresponding subset of 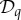([2], Theorem 5; [1], Theorem 2.3).

• Multimax3: In a connection 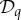, if {c₁,…,c_n} is the set of all 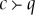enumerated so that

  

  then T_q is a multimaximal coupling of 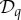if and only if 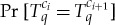is maximal for i=1,…,n−1, over all possible couplings of 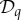([1], Theorem 2.3).

4. The largest canonical representation of a two-element connection

We consider here the case when one is interested in all possible coarsenings of the rvs in a system. The canonical/split representation of the system then contains all splits of all rvs. We will investigate in detail a fragment of the original (expanded) system involving just two k-valued rvs within a single connection:

The canonical system with all splits of these k-valued rvs is

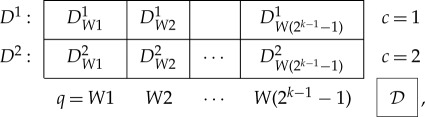
where W1, W2, etc. are the subsets f⁻¹(1) chosen as explained in §3b from the 2^k−1−1 distinct dichotomizations f of {1,…,k}. The number 2^k−1−1 is arrived at by taking the number of all subsets, subtracting 2 improper subsets, and dividing by 2 because one chooses only one of W and {1,2,…,k}−W. The goal is to determine whether 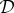is contextual. If it is, then any canonical system that includes 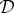as its subsystem (i.e. represents an original system with 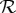as part of one of its connections) is contextual.

The two original rvs have distributions

4.1

A state (or value) of a bunch in the system is a vector of 2^k−1−1 zeroes and ones. However, the support of each of the bunches in system 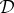consists of at most k corresponding states, and we can enumerate them by any k symbols, say, 1,2,…,k, as in the original variable:

4.2

As a result, 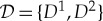has k² possible states that we can denote as ij, with i,j∈{1,2,…,k}. A coupling 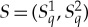of 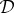assigns probabilities

4.3

to these k² states so that they satisfy 2k linear constraints imposed by (4.1),

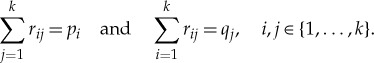4.4

If S is maximally connected, then it should also satisfy 2^k−1−1 linear constraints imposed by the maximal couplings of the corresponding connections. Specifically, if W={i₁,…,i_m}⊂{1,…,k}, then the maximal coupling 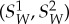of 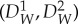is distributed as

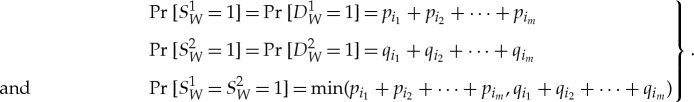4.5

Let us use the term m-split to designate any split D_W with an m-element set W (m≤k/2). Thus, D_W with W={i} is a 1-split, with W={i,j} it is a 2-split, and the higher-order splits appear beginning with k>5. Theorem 4.3 and its corollaries below show that in determining whether the system 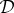is contextual, one needs to consider only the 1-splits and 2-splits. Let us use the term 1–2 system for this subsystem of 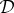. An overall coupling S of 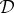contains as its part a maximally connected coupling of the 1–2 system if and only if the probabilities r_ij in (4.3) satisfy (4.5) for m=1 and m=2:

4.6

and

4.7

That is, a maximally connected coupling of the 1–2 system is described by the 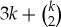linear equations (4.4), (4.6) and (4.7). We have therefore the following necessary condition for non-contextuality of .

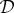Theorem 4.1 —

If the system is non-contextual, then the linear equations (4.4), (4.6) and (4.7) are satisfied.

Remark 4.2 —

Note that for k>5. (For completeness only, theorem S.1 in electronic supplementary material, file S, shows that the rank of this system of equations is .)

Theorem 4.3 —

In a maximally connected coupling S of with k>5, the distributions of the 1-splits and 2-splits uniquely determine the probabilities of all higher-order splits. Specifically, for any 2<m≤k/2, and any W={i₁,…,i_m}⊂{1,…,k}, the probability that the corresponding m-split equals 1 is

4.8

It is easy to find numerical examples of the distributions of 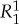and 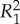for which (4.8) is violated (see example S.2 in electronic supplementary material, file S). As shown below, however, (4.8) cannot be violated if a maximally connected coupling for the 1–2 system exists. It follows from the fact that the statement of theorem 4.1 can be reversed: (4.4), (4.6) and (4.7) imply that 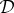is non-contextual. We establish this fact by first characterizing the distributions of 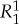and 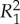for a non-contextual 1–2 system (theorem 4.4 with corollary 4.5), and then showing that (4.8) always holds for such distributions (theorem 4.6).

Theorem 4.4 —

A maximally connected coupling for a 1–2 system is unique if it exists. In this coupling, the only pairs of ij in (4.3) that may have non-zero probabilities assigned to them are the diagonal states {11,22,…,kk} and either the states {i1,i2,…,ik} for a single fixed i or the states {1j,2j,…,kj} for a single fixed j (i,j=1,…,k).

Assuming, with no loss of generality, that the single fixed i or the single fixed j in the formulation above is 2, the theorem says that the non-zero probabilities assigned to the states of the maximally connected coupling (shown below for k=4) could only occupy the cells marked with asterisks:

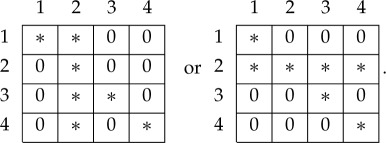
Corollary 4.5 —

The 1–2 system for the original rvs has a maximally connected coupling if and only if either p_i>q_i for no more than one i (this single possible i being the single fixed i in the formulation of the theorem), or p_j<q_j for no more than one j (this single possible j being the single fixed j in the formulation of the theorem), i,j∈{1,…,k}.

The relationship between (p₁,…,p_k) and (q₁,…,q_k) described in this corollary is some form of stochastic dominance for categorical rvs, but it does not seem to have been previously identified. We propose to say that 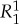nominally dominates 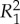if p_i<q_i for no more than one value of i=1,…,k (i.e. p_i≥q_i for at least k–1 of them). Two categorical rvs nominally dominate each other if and only if either they are identically distributed or k=2. Using this notion, and combining corollary 4.5 with theorems 4.1 and 4.4, we get the main result of this section.

Theorem 4.6 —

The system is non-contextual if and only if its 1–2 subsystem is non-contextual, i.e. if and only if one of the and nominally dominates the other.

5. Concluding remarks

Contextuality analysis of an empirical situation involves the following sequence of steps:

In the initial system, measurements are represented by rvs each of which generally has multiple values. Expansion means adding to the system new conteNts with corresponding connections (conteNt-sharing rvs) computed as functions of the existing connections. In a canonical representation of the system all rvs are binary, and the connections are coupled multimaximally, meaning essentially that one deals with their elements pair-wise. The issue of contextuality is reduced to that of compatibility of the unique couplings for pairs of conteNt-sharing rvs with the known distributions of the conteXt-sharing bunches of rvs. Coupling the connections multimaximally ensures that a non-contextual system has all its subsystems non-contextual too.

The canonical system of rvs is uniquely determined by the expanded system, but the latter is inherently non-unique; it depends on what aspects of the empirical situation one wishes to include in the system. Thus, it is one's choice rather than a general rule whether one considers a multi-valued measurement as representable by all or only some of its possible coarsenings. If one chooses all coarsenings, the split/canonical representation involves all dichotomizations, and then theorem 4.6 says that the canonical system is non-contextual only if, for any pair of rvs 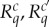in the expanded system, one of them, say 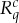, ‘nominally dominates’ the other. This domination means that 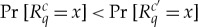holds for no more than one value x of these rvs: a stringent necessary condition for non-contextuality, likely to be violated in many empirical systems.

This is of special interest for contextuality studies outside quantum physics. Historically, the search for non-quantum contextual systems was motivated by the possibility of applying quantum-theoretic formalisms in such fields as biology [24], psychology [9,25,26], economics [26,27] and political science [28]. In CbD, the notion of contextuality is not tied to quantum formalisms in any special way. The possibility of non-quantum contextual systems here is motivated by treating contextuality as an abstract probabilistic issue: there are no a priori reasons why a system of rvs describing, say, human behaviour could not be contextual if it is qualitatively (i.e. up to specific probability values) the same as a contextual one describing particle spins. Nevertheless, all known to us systems with dichotomous responses investigated for potential contextuality (with the exception of one, very recent experiment) have been found to be non-contextual [18,19,29]. The use of canonical representations with dichotomizations of multiple-choice responses offers new possibilities.

In some cases, however, the use of all possible dichotomizations is not justifiable. Notably, if the values of an rv are linearly ordered, x₁<x₂<⋯ ,x_N, it may be natural to only allow dichotomizations f with f⁻¹(1) containing several successive values, {x_l,x_l+1,…,x_L}, for some l,L∈{1,…,N}. An even stronger restriction would be to only allow ‘cuts’, with f⁻¹(1)={x_l,x_l+1,…,x_N} or {x₁,x₂,…,x_l−1}.

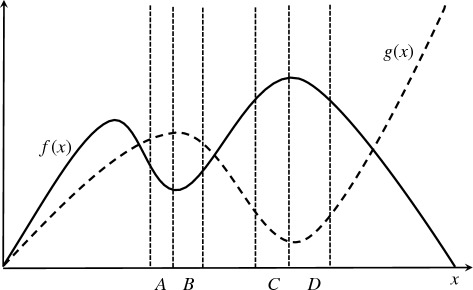Stronger restrictions on possible dichotomizations translate into stronger restrictions on the pairs 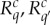whose canonical representation is contextual. This fact is especially important if one considers expanding CbD beyond categorical rvs. Thus, it is easy to see that if one considers all possible dichotomizations of two conteNt-sharing rvs with continuous densities on the set of real numbers, then the system will be contextual whenever the two distributions are not identical. Let the densities of these rvs be f(x) and g(x) shown in the graphic above. If the set of all splits of these rvs forms a non-contextual system, then any discretization of these rvs should satisfy corollary 4.5 to theorem 4.4. That is, for any k>2 and any partition H₁,…,H_k of the set of reals into intervals, we should have either

5.1

This is, however, impossible unless f(x)=g(x). If they are different, then f exceeds g on some interval, and g exceeds f on some other interval. If we take any two subintervals within each of these intervals (in the graphic they are denoted by A,B and C,D), any partition H₁,…,H_k that includes A,B,C,D will violate (5.1). The development of the theory of canonical representations with variously restricted sets of splits is a task for future work.

Data accessibility

See remark 1.2.

Authors' contributions

All authors significantly contributed to the development of the theory and drafting of the paper.

Competing interests

We declare we have no competing interests.

Funding

This research has been supported by AFOSR grant no. FA9550-14-1-0318 and Purdue Graduate School Summer Research Grant.