Recent theoretical work suggested that deleterious mutations could accumulate during the range expansion of a species, negatively affecting its fitness.
Keywords: range expansions, mutation load, experimental evolution
Abstract
Recent theory predicts that the fitness of pioneer populations can decline when species expand their range, due to high rates of genetic drift on wave fronts making selection less efficient at purging deleterious variants. To test these predictions, we studied the fate of mutator bacteria expanding their range for 1650 generations on agar plates. In agreement with theory, we find that growth abilities of strains with a high mutation rate (HMR lines) decreased significantly over time, unlike strains with a lower mutation rate (LMR lines) that present three to four times fewer mutations. Estimation of the distribution of fitness effect under a spatially explicit model reveals a mean negative effect for new mutations (−0.38%), but it suggests that both advantageous and deleterious mutations have accumulated during the experiment. Furthermore, the fitness of HMR lines measured in different environments has decreased relative to the ancestor strain, whereas that of LMR lines remained unchanged. Contrastingly, strains with a HMR evolving in a well-mixed environment accumulated less mutations than agar-evolved strains and showed an increased fitness relative to the ancestor. Our results suggest that spatially expanding species are affected by deleterious mutations, leading to a drastic impairment of their evolutionary potential.
Beneficial mutations are generally viewed as the main driver of evolution through adaptation, but most species harbor many deleterious mutations that have surprisingly not been eliminated by selection (Agrawal and Whitlock 2012). These deleterious mutations are known to affect the rate of adaptation in asexuals (Orr 2000; Denamur and Matic 2006; Lynch 2010), shape patterns of neutral genetic diversity (Charlesworth et al. 1995; Corbett-Detig et al. 2015), affect the evolution of recombination (Keightley and Otto 2006; Gordo and Campos 2008) and mutation rates (Lynch 2010; Sung et al. 2012), and can lead to the extinction of sexual or asexual populations (Haigh 1978; Lynch et al. 1993). Nevertheless, the effects of deleterious mutations are commonly ignored in studies of adaptation (Wilke 2004; Fogle et al. 2008; Good et al. 2012; Weissman and Hallatschek 2014), probably because deleterious mutations are expected to contribute little to the evolutionary dynamics of large populations [e.g., Blundell et al. (2015), but see Covert et al. (2013)].
Most individuals harbor deleterious mutations in their genome (Tennessen et al. 2012; Xue et al. 2012; Fu et al. 2014; Garcia-Alonso et al. 2014; Henn et al. 2015), making them incur a mutation load (Kimura et al. 1963). While a high mutation load is expected in small populations (Kimura et al. 1963; Lynch et al. 1993), deleterious mutations are not necessarily restricted to low frequencies in large recombining populations. In humans, for instance, recent genome sequencing studies have shown a surprisingly high number of deleterious mutations, including loss-of-function mutations (Sulem et al. 2015). The exact processes responsible for the creation and preservation of a mutation load in demographically successful organisms with large population sizes are still unresolved, and remain a hotly debated subject in human population genetics (Lohmueller 2008, 2014; Simons et al. 2014; Do et al. 2015; Henn et al. 2016; Simons and Sella 2016). A central theme in this controversy is the effect of past demographic processes on the efficacy of selection and on current patterns of mutation load (Lohmueller 2014; Henn et al. 2015).
Theoretical studies have recently proposed that spatially expanding populations should accumulate deleterious mutations, due to small effective size and inefficient selection on the range margins, a phenomenon that was called expansion load (Peischl et al. 2013). The fitness of individuals on the front of the expansion is predicted to decrease over time and space (Peischl et al. 2013; Peischl and Excoffier 2015), potentially affecting the speed of the expansion and imposing constraints on the limits of a species range (Peischl et al. 2015). Intuitively speaking, repeated cycles of founder events and population growth occurring at the front of a range expansion lead to an evolutionary dynamic that is like that expected for populations undergoing recurrent bottlenecks. Range expansions are in some sense similar to mutation accumulation experiments, which attempt to remove the effect of selection by imposing strong and regular bottlenecks, often though a single individual (Trindade et al. 2010); but, unlike mutation accumulation experiments, range expansions are a continuous process where low densities on the front naturally limit the effect of selection.
However, whereas the process and consequences of expansion load during range expansions have been well described (Peischl et al. 2013, 2015, 2016; Sousa et al. 2014; Peischl and Excoffier 2015), direct empirical evidence for it is still lacking. However, some theoretical predictions have been supported by the analysis of human exomes. For instance, one observes that there is a clear increase of the number of sites homozygous for predicted deleterious mutations along the expansion axis out of Africa (Henn et al. 2016; Peischl et al. 2016), suggesting that the expansion process led to an increased recessive mutation load. Contrastingly, the additive load, as measured by the total number of derived alleles, seems rather constant in all human populations (Simons et al. 2014; Do et al. 2015; Simons and Sella 2016), which is expected after range expansions (Peischl and Excoffier 2015; Peischl et al. 2016). Therefore, a more direct observation and clear measures of mutation load in successfully expanding species would be crucial to validate the theory.
Bacteria like Escherichia coli are an ideal candidate to directly test the prediction that expanding populations incur an expansion load. Indeed, E. coli growing on agar plates form sectors of low diversity where single mutants have fixed, which has been attributed to high rates of drift and low effective sizes on expanding wave fronts (Hallatschek et al. 2007; Korolev et al. 2010). Because E. coli expand radially on plates without much lateral movement, we expect strong differences between lines from different sectors. Furthermore, individual sectors should look like they were the product of one-dimensional expansions, for which theoretical predictions have been made (Peischl et al. 2016). Also, their haploid nature and asexual mode of reproduction simplifies the estimation of load, as no assumptions on the dominant–recessive status of harmful mutations are necessary, unlike in diploids (Simons and Sella 2016). Another advantage of E. coli is that strains with a defective mismatch repair (MMR) system have a very high mutation rate (HMR) (Barrick et al. 2009; Trindade et al. 2010; Lee et al. 2012; Tenaillon et al. 2016), increasing diversity and our ability to observe the evolution of bacterial growth and reproduction over a relatively short time. One would thus expect to be able to see if a prolonged period of bacterial expansions leads to a decrease in population fitness over time and space as predicted by theory (Peischl et al. 2013, 2015).
However, it is still unclear if rare beneficial variants could compensate the negative effects of more frequent deleterious mutations (Hallatschek and Nelson 2010; Lehe et al. 2012). Indeed, rare positively-selected mutations can increase in frequency on an expanding front more quickly than they would in a well-mixed population (Gralka et al. 2016b), and their recurrent fixation could potentially increase the fitness of front populations. Thus, evidencing the presence of an expansion load in naturally growing bacteria would oblige us to seriously reconsider the role that deleterious mutations play in the evolution and adaptation of living organisms.
Materials and Methods
Range expansion experiment
Bacterial strains:
We used E. coli K12 MG 1655 strains where the expression of the mutS gene is directly controlled by the arabinose promoter pBAD inserted in front of the mutS gene. In the absence of arabinose, mutS is not expressed, leading to a higher spontaneous mutation rate due to the inactivation of the methyl-directed MMR system (Yang 2000). Bacteria grown in the presence of arabinose express the mutS gene and thus have a lower spontaneous mutation rate. Additionally, our strain had a GFP marker located in the lac operon, which can be induced by IPTG (isopropyl β-D-1-thiogalactopyranoside) (see Supplemental Material, Figure S1 in File S1).
Growth on agar plates:
The growth of the mutator strain on agar plates was examined to find the time during which the colony is expanding with a constant velocity on an agar plate. The mutator strain was grown overnight in liquid culture at 37° in LB medium supplemented with 0.5% arabinose. One million cells were then deposited on five LB agar plates and incubated at 37° for up to 7 days and the colony size was measured every day. After a short period of exponential growth, the colonies were expanding at a constant velocity on an agar plate for up to 4 days, which then began to decrease.
All strains were grown on LB agar plates at 37° for a total duration of 39 days. More precisely, we transferred strains on a new plate every 3 days, thus before their growth rate would begin to decrease (Figure 1). An image of the colony was taken before transferring the cells to a new plate for later growth analyses. For each transfer, ∼100 million bacteria were sampled from the front using a sterile pipette tip and resuspended in 100 µl dilution solution (0.85% NaCl). The size of the sampling point to get ∼100 million bacteria was determined after an initial calibration. The number of sampled bacteria for different sampling sizes was first determined by plating serial dilutions on LB agar plates and incubation for 24 hr at 37°. The number of colony forming units (CFUs) were counted on plates where the range of CFUs was between 30 and 300. The CFUs were divided by the dilution factor to determine the number of bacteria present in the original solution. The location of the sampling point of each transfer was chosen at random on the periphery of the colony. New plates were then inoculated using 1 µl of this solution corresponding to ∼1 million cells. Note that this large initial population size guarantees that there is no bottleneck induced by the transfer itself, unlike what happens during mutation accumulation experiments, where bottlenecks are induced through a single clone. Selection, if any, should thus not be relaxed during this transfer, except for extremely mild mutations with selection coefficients smaller than 1/N or ∼10−6. Then, 43 µl glycerol (50%) was added to the remaining bacterial suspension and bacteria were stored at −80°. This range expansion experiment was done twice independently. The first experiment included the expansion of 48 HMR strains. The second experiment included the expansion of 10 HMR strains, and of 10 strains with a low mutation rate (LMR). In those LMR strains, the MMR mechanism was only partially induced by adding 0.2% arabinose. We excluded 1 out of 10 HMR strains due to contamination. The HMR lines from the first and second experiments were then analyzed jointly. Note that after the evolutionary experiments, all lines were handled in a medium containing 0.5% arabinose to fully induce mutS during DNA extraction and preparation of the competition experiments (see below).
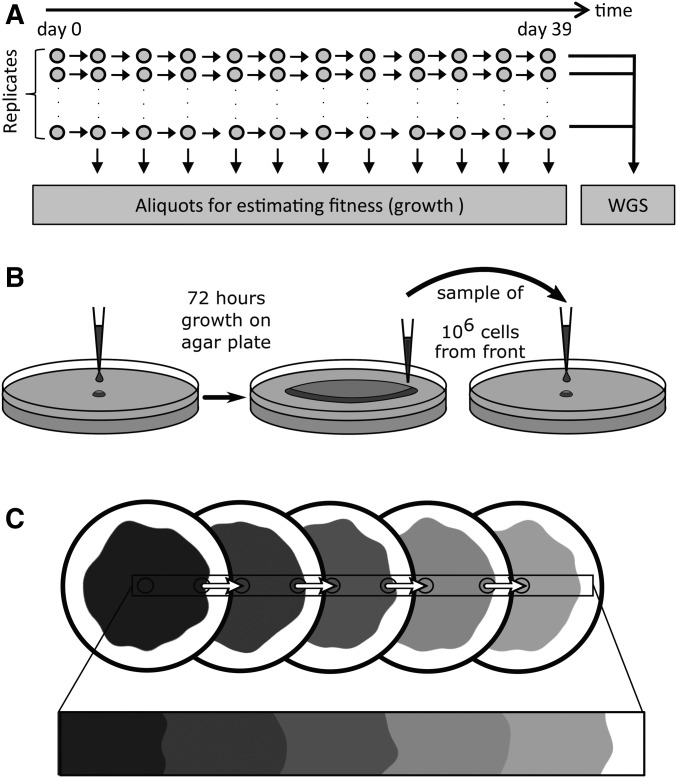
Figure 1.
Experimental setup. (A) mutS E. coli lines were grown on agar plates for a total of 39 days or ∼1650 generations assuming a generation time of 34 min (Figure S2 in File S1). (B) After 3 days of growth, ∼100 million bacteria are sampled on the edge of the colony, diluted in 1 μl LB medium, and ∼106 bacteria are deposited at the center of a new agar plate for a new 3-day growth cycle. This transfer should thus not impose any substantial bottleneck for the cells sampled on the edge of the colony that we are interested in following through time. This procedure was repeated 12 times for a total of 39 days of evolution for each line. (C) The expansion on several plates aims to mimic a continuous expansion. WGS, whole-genome sequencing.
Generation time on the wave front:
The generation time of bacteria at the front of the expanding colony was determined after 1 day of growth during the expanding phase with a constant velocity, by using a confocal microscope (Leica TCS SP5) (Figure S1 in File S1). Cells from −80° glycerol stock were grown in LB medium at 37° for 24 hr. Next, 1 µl of this culture was transferred to an LB agar plate containing 0.1 mM IPTG and incubated at 37° for 24 hr. A picture of the front of the colony was taken every 2 min for 1 hr with a 63× dry objective. The temperature during the measurement was set to 37° by using an incubation chamber. The images were analyzed by using the Fiji (Schindelin et al. 2012) image analysis software. The cell mass increase is directly proportional to the length of the cell (Kiviet et al. 2014), which was measured by analysis of fluorescence intensity profiles along the cell axis. This experiment was done three times independently. Overall, we measured the length increase of 49 individual cells. The growth rate was determined by calculating the elongation rate by using a linear mixed-effect model , where L is the length of the cell, is the length of the cell at time 0, t is the time in minutes, and r is the growth rate. The elongation dynamics of 16 cells is shown in Figure S2 in File S1. The average generation time corresponding to a doubling in cell mass estimated from the mixed-effect regression analysis is 34.2 min [95% C.I., 33.0 to 35.6)]. This generation time was used to estimate mutation rates per generation
Chemostat experiment:
The chemostat experiment was set up as described in Nanchen et al. (2006). Ten HMR samples were incubated in LB medium without arabinose at 37° for a total time of 39 days. The volume of the chemostat culture was 5 ml and the cultivation tube had a screw cap with an opening and a butyl rubber septum. The septum was pierced by three needles: one for medium supply, one for water saturated air supply, and one for removing bacterial suspension and air. Multichannel peristaltic pumps were used to supply the 10 replicates with LB medium. The growth rate of the continuous culture was adjusted to the estimated 34 min generation time of bacteria on the expanding front (see previous section) by calibrating the LB medium flow rate. A shaking incubator continuously mixed the samples during the experiment (600 rpm). An aliquot (100 μl) of the samples was taken every 3 days, and the samples were stored at −80° after adding 43 μl glycerol (50%). One million cells were transferred to a new cultivation tube with 5 ml fresh LB medium and incubated for the next 3 days. In total, there were 13 transfers in 39 days, and the strains thus evolved for a total of 1650 generations, like agar-grown strains. Three samples were excluded due to contamination during the experiment, leaving us with seven chemostat samples that were sequenced (see below).
Estimation of mutation rate with a fluctuation test
A fluctuation assay (Foster 2006) was used to calculate the mutation rate of the ancestral strain, three HMR strains, three chemostat strains, and three LMR strains. The rate at which mutations occur to enable cells to grow on selective agar (nalidixic acid) was calculated. For each strain, we used 45 independent cultures. The ancestor strain and the HMR strains were incubated in LB medium without arabinose and the LMR strain in LB medium with 0.2% arabinose. The starting concentration of the cultures was 5 104 CFU/ml, and the end concentration of the cultures was 1.5 109 CFU/ml. The bacteria (initially not resistant to nalidixic acid were then exposed to LB agar plates containing 100 μg/ml nalidixic acid. Resistant colonies were counted and the data were analyzed with the Ma-Sandri-Sarkar Maximum Likelihood Estimator Method using FALCOR (Hall et al. 2009).
DNA sequence analyses
DNA extraction:
After the range expansion experiment on agar, one million cells from the wave front were streaked out on an LB agar plate containing 0.5% arabinose and incubated for 24 hr at 37° to isolate single clones. A single colony was dissolved in 100 μl dilution solution (0.85% NaCl) and 1 µl was transferred to a new LB agar plate containing 0.5% arabinose. The plate was then incubated for 24 hr at 37°. Then, the entire colony was removed from the agar plate and resuspended in 1 ml dilution solution. Genomic DNA was extracted using the Wizard Genomic DNA Purification Kit (Promega, Madison, WI) following the manufacturer’s protocol. The integrity of the DNA was checked by gel electrophoresis. The DNA concentration was determined by fluorometric quantification (Qubit 2.0). After the chemostat experiment, one million cells for each sample were streaked out on an LB agar plate containing 0.5% arabinose and incubated for 24 hr at 37° to isolate single clones. A single colony was transferred to liquid LB medium containing 0.5% arabinose and incubated for 24 hr at 37°. Next, 1 ml of the culture was then used for DNA extraction. Genomic DNA was extracted using the Wizard Genomic DNA Purification Kit (Promega) following the manufacturer’s protocol. The integrity of the DNA was checked by gel electrophoresis. The DNA concentration was determined by fluorometric quantification (Qubit 2.0).
Whole-genome sequencing:
We sequenced DNA samples in three separate runs. Forty-eight HMR samples were first sequenced using a TruSeq DNA PCR-Free library (Illumina) on a HiSequation 2500 platform (Illumina), from which we obtained 100-bp end reads for all samples. Nine HMR strains and 10 LMR strains were then sequenced using a paired end NexteraXT DNA library (Illumina) on a MiSeq platform (Illumina). The MiSeq platform generated 300-bp end reads. Note that we did not find any differences between the average number of mutations () for HMR lines sequenced on the HiSeq2500 or MiSeq platforms ( = 113.8.4 vs. 121.4, respectively, t-test, P = 0.247). Finally, seven HMR chemostat samples were sequenced using a TruSeq DNA PCR-Free library (Illumina) on a HiSequation 3000 platform (Illumina).
Neighbor joining tree:
The phangorn R package ver 2.2 (Schliep 2011) was used to compute genetic distances between each pair of samples using point substitutions and Felsenstein’s K81 mutation model (Felsenstein 1981), as well as to compute a neighbor joining tree, which is repreented in Figure 2.
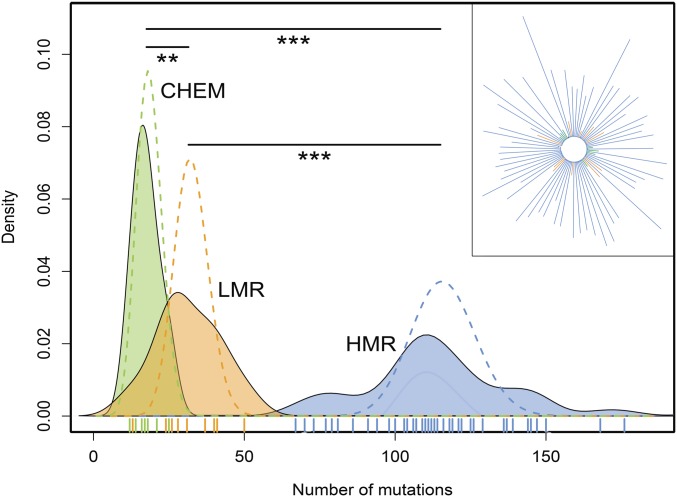
Figure 2.
Number of mutations in evolved strains. Distribution of the total number of observed mutations per strain. Dashed lines are Poisson distributions fitted to the mean of the observed distributions. The three means are significantly different by a Mann–Whitney test (HMR vs. LMR: P-value = 5.52 × 10−7; HMR vs. CHEM: P-value = 1.85 × 10−7; and LMR vs. CHEM: P-value = 0.0084). In the upper right inset we show a neighbor joining tree of the different strains (represented with the same color code as in the main figure). CHEM, chemostat; HMR, high mutation rate; LMR, low mutation rate; **, p < 0.01; ***, p < 0.001.
Variant calling:
We used Trimmomatic 0.32 (Bolger et al. 2014) to remove the adapter sequences from the reads and for quality trimming. Leading and trailing bases with quality < 3 were removed. The reads were scanned with a 4-bp sliding window, and cut if the average quality per base was < 15. Reads with a length < 36 were excluded from the analysis. Burrows–Wheeler Aligner 0.7.5 (Li and Durbin 2009) was used to map the reads to the E. coli K12 MG 1655 reference genome (National Center for Biotechnology Information Reference Sequence: NC_000913.3). Picard tool 1.99 was used to remove PCR duplicates and variant calling was performed with Genome Analysis Toolkit (GATK) 2.7 (McKenna et al. 2010). The SNPs were filtered based on the following variant call format (VCF) field thresholds: quality by depth (QD) < 2.0, Fisher strand (FS) > 60, and root mean square of the mapping quality (MQ) < 40. Indels were filtered based on the following VCF field thresholds: QD < 2.0 and FS > 200. Substitutions and small indels were also called using a modified version of a previously published pipeline (Tenaillon et al. 2012). We only kept mutations if the proportion of reads carrying the variant was > 75%. Substitutions and indels were retained as independent events if they could not be attributed to a gene conversion event. We used as a signal of gene conversion the presence of the mutated sequence (the mutated base and its 30-bp neighboring bases) somewhere else in the genome. Mutations within 200 bp of a gene conversion signal were also considered as gene conversion mutations. All mutations were manually validated thanks to a visual output and kept for further analysis if they were both detected with GATK and the pipeline described above. SnpEff 4.0 was used to annotate the variants (Cingolani et al. 2012; Foster et al. 2013).
Estimation of dN/dS ratio:
We computed the ratio of nonsynonymous over synonymous substitutions (dN/dS) for the bacterial lines by counting the number of nonsynonymous and synonymous substitutions accumulated in each line as compared to the reference sequence, as well as the number of nonsynonymous and synonymous substitutions expected if all codon positions in the reference sequence would mutate. dN/dS can then be written as , where and are the numbers of observed nonsynonymous and synonymous substitutions in a given line, and and are the total number of expected nonsynonymous and synonymous substitutions, respectively, over the whole bacterial genome. The observed and expected numbers of nonsynonymous and synonymous substitutions in each line were computed for each four possible transitions and two possible transversions, and summed across the six categories of mutations. We used a bootstrap approach to compute dN/dS C.I.s for each strain. Briefly, dN/dS was computed with the above-mentioned approach using randomized data sets in which the mutations were randomly sampled with repetition among the 12 observed categories of mutations (six types of synonymous and six types of nonsynonymous mutations). To test for differences between treatments, we used a permutation scheme to obtain the null distribution of the amount of differences in average dN/dS values between treatments, taking sample size differences into account.
PROVEAN scores:
We used PROVEAN (Protein Variation Effectve Analyzer) scores (Choi et al. 2012; Choi and Chan 2015) to compute the potential damaging effects of nonsynonymous substitutions and in-frame insertions and deletions observed in bacterial lines. PROVEAN scores are alignment-based scores measuring the change in protein sequence similarity before and after the introduction of the amino acid variation to the mutated sequence (Choi et al. 2012; Choi and Chan 2015). A threshold of −2.5 for PROVEAN scores has been shown to allow for the best separation between deleterious and neutral classes of variants in human and nonhuman UniProt protein variation (Choi et al. 2012). PROVEAN scores < −2.5 are thus indicative of a severe and thus potentially deleterious effect of the mutation (Choi et al. 2012; Choi and Chan 2015), even though we cannot dismiss the possibility that they might be advantageous in some lines. Conservatively, we have assumed that mutations with PROVEAN score < −2.5 have a strong phenotypic effect. The distribution of PROVEAN scores for HMR and LMR lines are shown in Figure S3 in File S1.
Measures of fitness
Expansion velocity on agar plate:
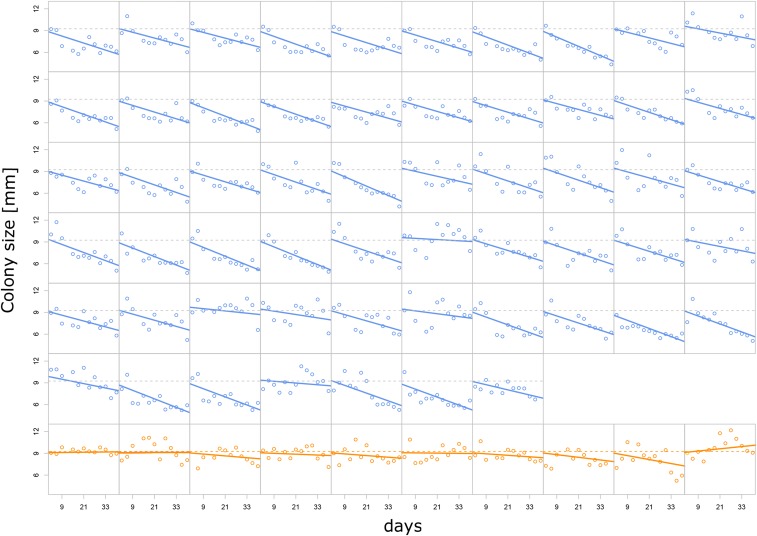
Images of the colony were taken during the experiments on agar plates (n = 57 for HMR lines and n = 10 for LMR lines) before transferring the cells to a new plate. We took a picture every 3 days for each line, and thus have a total of 13 pictures for each line. The images were analyzed with the Fiji package of the imageJ software (Schindelin et al. 2012). The radius of the colony was measured and plotted against time (Figure 3). Note that points for day 12 in HMR lines from the first experiment were not considered in further analyses due to a potential batch effect. The change in expansion velocity was then determined by fitting a mixed-effect linear model to the data. This model assumes that the growth rate of all lines changes due to a fixed effect common to all lines, but it considers line-specific variability in growth rates. The slopes of the regression lines plotted in Figure 3 for each line are obtained by adding the fixed and line-specific effects.
Figure 3.
Evolution of colony radius after 3 days of growth on agar. Blue, HMR lines; orange, LMR lines. The x-axis scale represents total days of evolution. Horizontal dashed lines represent the average colony size measured after the first 3 days of growth over all HMR or all LMR lines. Mixed-effect linear regressions have been performed separately for HMR and LMR strains. Solid lines represent strain-specific regression lines, with slopes obtained as the sum of fixed and line-specific effects. HMR change in growth rate per day: −78 μm, 95% C.I. (−85; −70), P-value < 2 10−16. LMR change in growth rate per day: −11 μm, 95% C.I. (−33; 10), P-value = 0.29 NS. HMR, high mutation rate; LMR, low mutation rate; NS, not significant.
Competition experiment on agar plates:
Linear growth of unmixed ancestral and evolved strains:
To determine the change of fitness on agar plates, we growth-competed our evolved lines and their ancestral strain against a reference strain where the lacZ was deleted. The evolved strains could thus be distinguished from the reference strain by adding X-gal to the cells. Bacteria with a functional lacZ gene turned blue within 15 min whereas the reference strain stayed white (see Figure S4 in File S1). An LB agar plate without arabinose was inoculated with an evolved strain and with the reference strain. The cells were deposited linearly on the agar plate with a razor blade dipped in the bacterial culture, with the reference strain being placed next to the evolved strain, without mixing. The plates were incubated at 37° for 3 days. After the growth, 0.1 M X-gal solution was sprayed on top of the agar plate and the plate was incubated for 15 min at 37°. Images were taken and analyzed with Fiji (Schindelin et al. 2012). If the two competing strains are equally fit, they should grow at the same speed and thus their boundary should be orthogonal to the inoculation line. On the contrary, if a strain is fitter than the other, it will grow faster, occupy more space than the less-fit strain, and their boundary will form an angle φ that will depend on the selective advantage of the fittest strain (see Figure S4 in File S1). Therefore, the relative fitness of an evolved strain can be estimated by measuring the angle of the boundary between its territory and that of a reference strain (Korolev et al. 2012) as
| (1) |
where s is the selection coefficient associated with the evolved strain and ϕ is the angle between the boundaries of the two strains (see Figure S4 in File S1). The selection coefficients of all evolved strains were then normalized by the mean selection coefficient of the ancestral strain, which was also competed against the reference strain. The results are shown in Figure 4B.
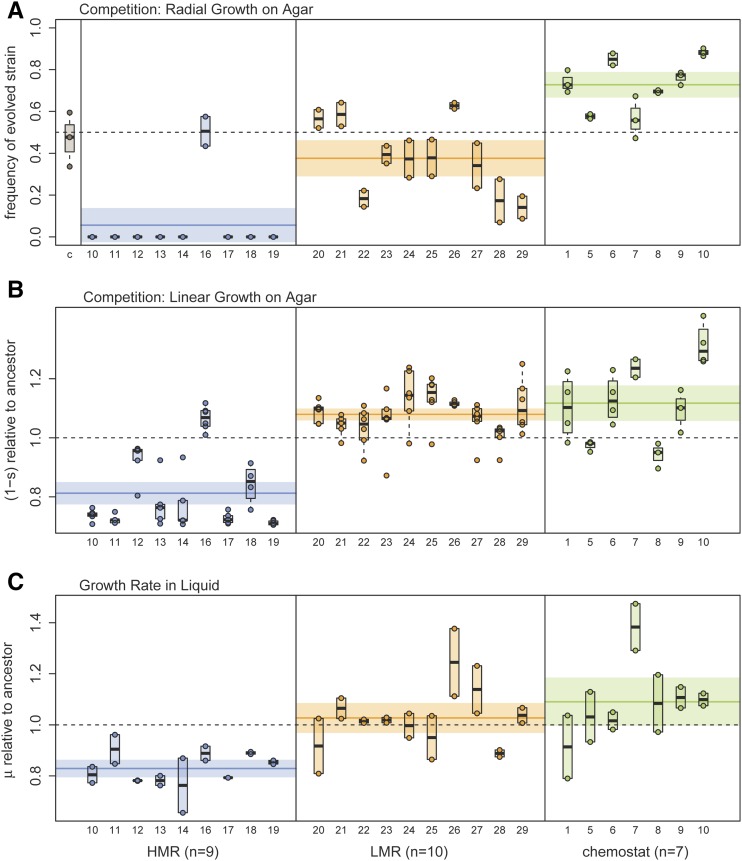
Figure 4.
Estimation of bacterial fitness. (A) Relative frequency of evolved strains on the edge of the colony after 3 days of radial growth on an agar plate, under conditions similar to those of our experiment of range expansion on agar (see Materials and Methods and Figure S5 in File S1). Note that this measure only gives a qualitative assessment of the relative fitness of two strains, as this proportion will quickly change over time in case of unequal fitness (Gralka et al. 2016b). The first column (c) of the leftmost pane represents the relative frequency of the ancestral strain containing the same plasmid as the evolved strains, showing that the incorporated plasmids do not induce any fitness difference between strains. (B) Competition on agar plate between a reference strain and evolved lines growing side-by-side for 3-days. The fitness of evolved strains (lines) is measured by the difference in growth rates at the contact zone between strains following Korolev et al. (2012). The angle formed by the contact zone between strains is indeed proportional to their fitness difference (see Materials and Methods). Each dot corresponds to one measure for a given strain. Note that the two HMR lines (12 and 16) with highest fitness both have a nonsynonymous mutation in the mlc (makes large colonies) gene. (C) Fitness of evolved strains relative to the ancestral strain, measured as growth rate in liquid culture. Note that labels on the x-axis represent line identifiers. HMR, high mutation rate; LMR, low mutation rate.
Radial growth of well-mixed ancestral and evolved strains:
The ancestor strain was labeled with either GFP- or mCherry-containing plasmids, each plasmid having an additional ampicillin resistance gene. The strains from experiment 2 (9 HMR and 10 LMR lines) and 3 (seven chemostat evolved lines) were labeled with mCherry plasmid. All strains were grown in LB medium with 0.5% arabinose and 50 μg/ml ampicillin at 37° for 24 hr. The density of the strains was adjusted by measuring the optical density and diluting the bacterial suspension with 0.85% NaCl solution to a final concentration of 109 CFU/ml. The evolved strains were mixed with the GFP-labeled ancestor strain in a 1:1 ratio. Additionally, we performed a control experiment where the mCherry-labeled ancestor strain was mixed with the GFP-labeled ancestor strain, where 1 μl of each mixture was put in the center of an LB agar plate with 50 μg/ml ampicillin and without arabinose, and the plates were incubated at 37°. After 3 days, a picture of the colony was taken and the fraction of the front occupied by the evolved strain was determined by using ImageJ, as shown in Figure S5 in File S1. This experiment was done three times independently for each sample. The results are reported in Figure 4A.
Growth rate in liquid medium:
Nine HMR, 10 LMR, and seven chemostat lines were pregrown in LB medium at 37° with 0.5% arabinose until they reached an optical density of 0.2. The cells were diluted in fresh LB medium 1:100 without arabinose, and transferred to a 96-well plate. A spectrophotometer (BioTek Eon Microplate Spectrophotometer) was used to measure the log transformed optical density of the cultures every 30 min for 24 hr at 37°. The exponential growth period was determined as the range where the logarithm of the optical density increased linearly (1–4 hr). The growth rate during this period was determined by computing the slope of a linear regression model. Four replicated measures were performed per line and reported in Figure 4C.
Estimation of the distribution of fitness effects (DFE):
Estimating the DFE from bacterial growth dynamics:
Peischl et al. (2015) developed an analytically tractable model for the evolution of mean fitness at an expansion wave front during a linear (one-dimensional) expansion along an array of discrete demes. One can use this model to predict the evolution of mean fitness and, assuming hard selection, also the evolution of colony size over time. Indeed, Peischl et al. (2015) showed that the change in mean relative fitness at the expansion front can be approximated using the following equation
| (2) |
where is the mutation rate of mutations with effect , is the effective population size at the expansion front at time , and is the fixation probability of mutations with effect at the front of an expanding population with an effective size of . The parameter measures genetic drift and corresponds to the compound parameter in Peischl et al. (2015), which is the product of the effective number of founders () and the time taken to fill an empty deme at the expansion front (). Note that is simply the inverse of the expansion speed. For definiteness and without loss of generality, we set the relative fitness at the onset of the expansion to Note that is a parameter that depends on the expansion speed as well as the rate of migration of individuals, and hence also depends on mean fitness and may change over time [see Peischl et al. (2015) for details]. Assuming exponential growth and that the growth rate is proportional to mean fitness, one can show that in this model
| (3) |
where and are the growth rate and effective population size at the expansion front at time . We have set , which simply defines the length of one generation as the time unit required for exponentially growing individuals to double their number.
We used a total mutation rate of 0.2 per individual per generation, as estimated by a fluctuation test (Table S4 in File S1). The DFE is conveniently modeled as a displaced γ distribution (Shaw et al. 2002), as such a distribution naturally arises under Fisher’s geometric model (Fisher 1930; Martin and Lenormand 2006). In addition to the shape and scale parameters and of a conventional γ distribution, this displaced distribution requires an additional parameter that represents the maximum effect of beneficial mutations, so that the distribution of individual mutation effects is given by
| (4) |
This leaves us with four unknown parameters to estimate: three parameters for the DFE and the effective population size at the expansion front at the beginning of the experiment, .
We then used the colony size trajectories (Figure 3) to estimate the unknown parameters of this model. More precisely, we used the theoretical model to predict the expected evolutionary trajectory of the colony size by iterating Equation (2), assuming that the mean fitness at the expansion front is proportional to colony size. We then calculated the sum of squared deviations (SSD) between each of the HMR lines and the theoretical expectation. A grid search over the parameter space was then used to determine the parameter combination that minimizes the total SSD of all 57 HMR lines. Note that we did not use the LMR lines here because the relatively small changes in colony size over time lead to numerical problems in the estimation procedure.
Building C.I.s for the DFE:
A C.I. for the DFE was obtained with a parametric bootstrap approach. For a given set of parameter estimates, we simulated trajectories of mean fitness using the individual-based simulation framework described in Peischl et al. (2015). We then reestimated the DFE from each bootstrapped data set using the procedure described above. This procedure was applied 1000 times to get 1000 bootstrapped DFEs, from which an empirical 95% C.I. was estimated (and shown in Figure 5).
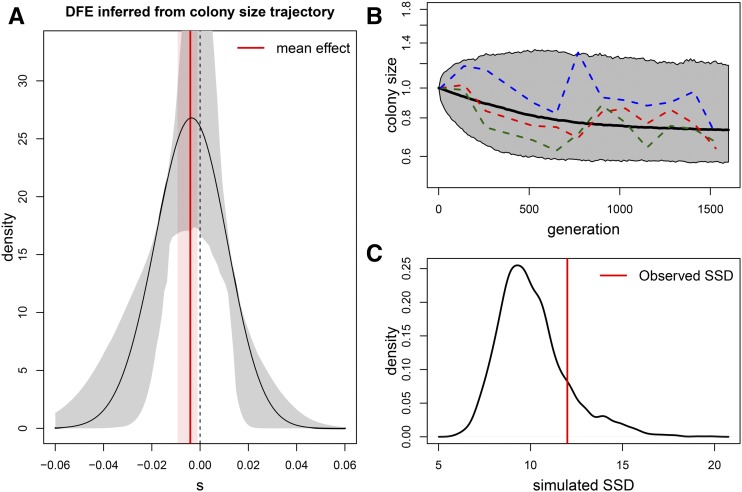
Figure 5.
Distribution of fitness effects (DFE). (A) DFE inferred from the evolutionary trajectory of colony size over time shown in Figure 3. Parameters were estimated by minimizing the sum of squared deviations (SSD) from the expectation of colony size obtained from the model described in Peischl et al. (2015). Estimated parameters of the displaced γ distribution: . The effective population size at the expansion front is estimated as , and the mean mutation effect is −0.00379. The gray area delimits an empirical 95% C.I. obtained from parametric bootstrap. The corresponding 95% C.I. for the mean mutation effect is shown in pink. (B) Evolution of colony size obtained by simulations using the estimated parameters. The solid line shows the average and the borders of the gray shaded area indicate the 0.5 and 99.5 percentiles of the simulated data, both estimated from 1000 simulations. The dashed lines show three randomly chosen examples of the observed colony size evolution of the high mutation rate strain. (C) Test of goodness of fit of the observed fitness under the estimated DFE shown in (A). The SSD between observed and expected fitness is compared to the distribution of SSD between the expected fitness and that simulated using the estimated parameters. The simulated SSD density was computed from 1000 simulations. The observed deviation between expected and observed fitness in (B) is thus not significant (P-value = 0.18).
Estimating the DFE from the number of observed mutations:
An alternative way to estimate the DFE is to use the relationship between the number of observed mutations and the fitness of the different lines. Assuming that mutation effects are additive, the total mutation effect of mutations that have accumulated in a bacterial strain and are thus equal to should also follow a displaced γ distribution similar to Equation (4), since the sum of γ variates also follows a γ distribution with rate parameter , displacement parameter , but with a new shape parameter . Therefore
| (5) |
The likelihood of a set of M lines having accumulated mutations is thus simply
| (6) |
where is a vector of the sum of mutation effects estimated as one minus the fitness of the different lines. Taking the derivative of the log likelihood for and equating it to zero allows us to get a maximum likelihood estimator of that only depends on and as
| (7) |
This maximum likelihood estimator can be reinserted into the log likelihood equation, which becomes
| (8) |
where and . The values of and maximizing can be found numerically, for instance by a simple grid search in the parameter space, from which Equation (7) can then be used to get the maximum likelihood estimate of .
This procedure was first applied to the change in colony size of evolved lines between day 3 and day 39. In that case, the total mutation effects were estimated as , where , and and are the colony sizes at day 3 and day 39 as predicted by a mixed-effect regression model, respectively (see Figure 3).
Building C.I.s for the DFE:
A C.I. for the DFE was obtained with a parametric bootstrap approach. For a given set of parameter estimates, we drew from the estimated DFE mutations for each of the M lines, and we reestimated the DFE from each bootstrapped data set using the procedure described above. This procedure was applied 2000 times to get the 2000 bootstrapped DFEs, from which an empirical 95% C.I. was estimated (and shown in Figure 6).
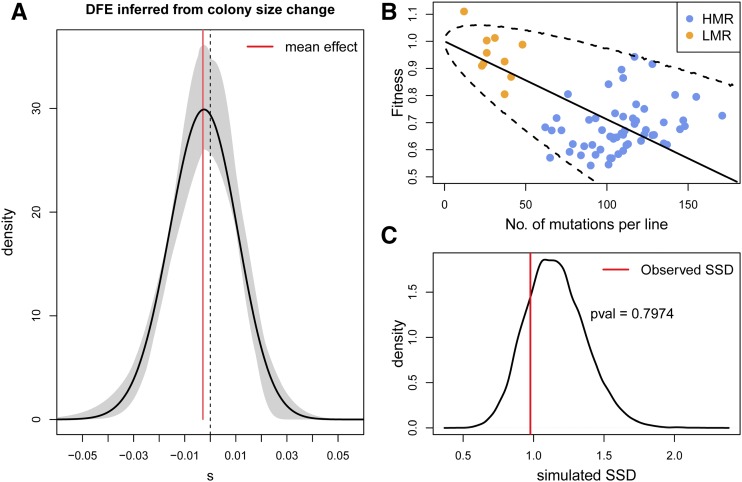
Figure 6.
Distribution of fitness effects (DFE). (A) Black line: DFE inferred from the change of colony size over time shown in Figure 3. Maximum likelihood parameters of the displaced γ distribution: . Mean mutation effect = −0.00288. The gray area delimits an empirical 95% C.I. obtained from parametric bootstrap. The corresponding 95% C.I. for the mean mutation effect is extremely narrow around the mean value (red vertical line) and shown in pink. (B) Fitness of bacteria as a function the number of observed mutations in HMR and LMR strains. The solid black line is the mean fitness decline expected under the DFE shown in (A), and the dashed lines represent limits of a 95% C.I. around the mean, both estimated from 50,000 simulations. (C) Test of goodness of fit of the observed fitness under the maximum likelihood DFE shown in (A). The SSD between observed and expected fitness is compared to the distribution of SSD between the expected fitness and that simulated under the ML DFE for the same numbers of mutations as those observed. The simulated SSD density was computed from 20,000 simulations. The observed deviation between expected and observed fitness in (B) is thus not significant (P-value = 0.80). HMR, high mutation rate; LMR, low mutation rate; ML, maximum likelihood; SSD, sums of square deviations.
Testing for differences between HMR and LMR DFEs:
We used a likelihood ratio test to test for potential differences between DFE’s separately estimated on HMR and LMR strains. If stand for the log-likelihood computed on both HMR and LMR strains, and and stand for the likelihood of HMR and LMR strains, respectively, then the statistic should be distributed as a with 3 d.f. under the hypothesis that the DFEs for HMR and LMR are identical.
Data availability:
Sequence data are available at Sequence Read Archive (SRA). The STUDY accession number is: SRP068347. The VCF files of the analysed strains are available in the GitHub repository, https://github.com/CMPG/ExpansionLoad_Bacteria
Results
We used the bacterium E. coli as a model system to test whether deleterious mutations can accumulate during the natural range expansion of an organism. We worked with a mutator (mutS-) strain in which we could experimentally modulate the mutation rates and thus analyze the evolutionary dynamics of mutation accumulation over a relatively short time (see Materials and Methods). We evolved replicated populations of E. coli for 39 days (∼1650 generations, Figure S2 in File S1) by letting them expand radially across a solid substrate for 13 periods of 3 days (Figure 1), mimicking a continuous expansion (Figure 1C). We performed this experiment with 57 lines having a HMR (HMR lines) and with 10 lines having a LMR (LMR lines) due to the addition of 0.2% arabinose in the LB agar lines (see Materials and Methods). Thus, LMR lines are initially genetically similar to HMR. Colony sizes of HMR and LMR lines were measured before each transfer and at the end of the 39 days, and aliquots of bacterial samples were preserved for whole-genome sequencing (Figure 1A). To compare the dynamics of mutation accumulation of HMR and LMR strains having expanded on a two-dimensional surface with a well-mixed high-density population, we have evolved the same ancestral strain with HMR for 39 days in a chemostat at high density, adjusting the generation time to 34 min as estimated from our analysis of bacterial mass doubling time on agar wave fronts (Figure S2 in File S1).
Genome-wide mutation patterns
We sequenced HMR, LMR, and chemostat lines at high coverage (> 100×, Table S1 in File S1) to detect any potential differences in the number and patterns of mutations. After 39 days of range expansion, HMR lines accumulated on average ∼3.7 times more mutations than LMR strains (115.0 vs. 31.5 mutations per line, respectively, P < 5.52 × 10−7, Mann–Whitney test, HMR range [67–204], LMR range [13–50], Figure 2 and Table S2 in File S1) and ∼6.12 more mutations than chemostat lines (115.0 vs. 17.57 mutations per line, P < 2.2 × 10−16, chemostat range [13.5–21.6], Figure 2 and Table S2 in File S1). When comparing substitutions between lines, we found that most of them (99.0%) occurred in distinct lineages and thus represent independent mutations (Figure 2). While showing fewer mutations, the mutation pattern of chemostat lines is similar to that of agar-grown lines, with a high transition bias and 2–3× higher proportions of A:T → G:C relative to G:C → A:T mutations (Table S3 in File S1), which is typical of defective MMR systems. Note that, at first sight, the mutation rate seems to have fluctuated along the genome (Figure S6 in File S1), which appears mainly due to positional constraints during chromosome replication (Figure S7 in File S1), suggesting that even though mutations are not randomly spatially distributed, they occurred randomly given local mutation rate constraints. Looking at the distributions of the number of mutations accumulated by each line, we observe that they are overdispersed as compared to Poisson expectations (Figure 2), suggesting that some mutator lines might have acquired genetic changes that further modify the mutation rate (Lee et al. 2012). We could confirm this hypothesis in the case of one HMR line containing ≥ 176 substitutions and 17 frameshift mutations. In this line, we indeed identified a frameshift mutation in the mutT gene, whose inactivation specifically increases otherwise rare A:T → C:G transversions (here n = 85) (Fowler and Schaaper 1997) that mostly lead to nonsynonymous changes (Table S3 in File S1). This could partly explain the strong bias toward nonsynonymous (n = 124) relative to synonymous (n = 25) mutations seen in this line. Moreover, this line had a nonsynonymous mutation in recC, which is involved in dsDNA repair and stress-induced mutagenesis (Al Mamun et al. 2012). Of note, a fluctuation test (Foster 2006) showed that the lines have retained their initial high (chemostat and HMR strains) or low (LMR strains) mutation rates at the end of the experiment (Table S4 in File S1).
An examination of the mutation pattern in coding regions with dN/dS ratio reveals no evidence for selection in both HMR and LMR lines (HMR lines: dN/dS = 1.014, site bootstrap 95% C.I. 0.962–1.065; LMR lines: dN/dS =1.093, site bootstrap 95% C.I. 0.812–1.354), and a permutation-based test revealed no significant difference in dN/dS ratios between HMR and LMR lines (P = 0.213). Contrastingly, the dN/dS ratio observed in chemostat lines (dN/dS = 1.334, 95% C.I. 0.69–2.14) was found to be significantly larger than that in agar-grown HMR lines (permutation test, P = 0.003), suggesting that positive selection has occurred in these lines. The use of PROVEAN scores (Choi and Chan 2015) to quantify the potential effects of amino acid substitutions and in-frame indels in coding sequences shows that a majority of nonsynonymous mutations have a potentially strong effect on protein function for both HMR and LMR lines (61.3 and 64.8%, respectively, t-test, P = 0.166, Figure S3 in File S1). It suggests that the observed dN/dS ratio close to 1 in both HMR and LMR lines is not due to the observation of phenotypically neutral mutations, but that it is rather including many nonsynonymous mutations that might impair cellular functions. Chemostat lines show a slightly larger (but not significant) proportion (70.4%) of nonsynonymous mutations with a strong functional effect (PROVEAN score < −2.5, see Figure S3 in File S1).
Evolution of colony expansion speed:
Theory predicts that an accumulation of deleterious mutations should lead to a reduction in expansion speed over time (Peischl et al. 2015). Indeed, we found that the colony size of HMR lines has significantly declined over time [−78 μm/day, 95% C.I. (−85; −70), P-value: < 2 × 10−16], whereas the colony size of LMR lines has not significantly changed [−11 μm/day, 95% C.I. (−33; 10), P-value = 0.29] (Figure 3). Using the individual linear regression lines to estimate the relative change in colony size over the course of the experiment, we found that the colony size of HMR lines after 3 days of growth has decreased by 33 ± 3% in 39 days (t-test, P-value < 2.2 10−16). In contrast, colony size of LMR lines after the same period of growth did not significantly change (P-value = 0.29), and the difference in colony size at day 39 is significant between the HMR and LMR lines (t-test, P-value = 4.16 × 10−7). The significant decrease in HMR colony size is not just due to the larger number of HMR than LMR lines analyzed. Indeed, we still find a significant decline of colony size over time for the HMR if we restrict our analysis to the nine HMR lines of the second experiment (−78 μm/day, 95% C.I. [−102; −53], P-value: <2 10−16), and this decrease is significantly different from that of the LMR lines (P-value = 2.0 10−4). Note however that we cannot completely exclude the fact that the growth reduction of LMR lines would be significant if we had studied a much larger sample size.
Reduced fitness of evolved strains:
While the observed reduction in colony size over time is consistent with an accumulation of deleterious mutations due to random genetic drift (Peischl et al. 2015), an alternative explanation would be the establishment of adaptive pleiotropic mutations that increase the ability of bacteria to end up at the expansion front, while at the same time have a negative effect on growth rates. Such antagonistic pleiotropy between motility and growth-related traits has recently been observed in experimental evolution studies of Pseudomonas aeruginosa (van Ditmarsch et al. 2013). Therefore, we evaluated the fitness of HMR, LMR, and chemostat lines as their ability to grow competitively on agar. We let them directly compete with the ancestral strain during a radial expansion on an agar plate, and thus measured their relative fitness under the exact same conditions as in the 39-day experiment shown in Figure 1 (Figure S5 in File S1). We found that the ancestral strain clearly outcompeted all but one HMR line (Figure 4A), providing strong evidence for an overall decrease in fitness during the 39-day experimental evolution on agar. The LMR strains showed similar patterns, with an overall reduced ability to compete with the ancestral strain on agar (Figure 4A). However, 3 out of 10 LMR lines showed signals of adaptation to growth on agar as they slightly outcompete the ancestral strain (Figure 4A). Importantly, these results demonstrate that adaptive processes involving trade-offs between growth and motility are unlikely to be the main reason for the decrease in colony size over time. Rather, our results indicate that accumulated deleterious mutations strongly reduced the fitness of bacteria in HMR lines, and to a lesser extent in LMR lines. Overall, the seven chemostat lines performed significantly better than the original strain (t-test, P-value = 5.3 10−7, Figure 4A), suggesting that their evolution in the LB medium chemostat has positively impacted their ability to grow on LB agar.
Alternative measures of fitness confirm predominant deleterious effects of mutations:
To test whether mutations accumulated in the HMR lines had any negative impact on biological processes and thus on cellular functioning, we assessed the fitness of our evolved bacterial lines in two additional ways, complementing the radial competition assay (Figure 4).
We first measured growth rate relative to a reference strain (different from the ancestral strain) during a linear expansion without any mixing (see Figure S4A in File S1). The advantage of this procedure relative to the radial growth competition described above is that one can directly transform differential growth rates into selection coefficients (Hosono et al. 1995; Korolev et al. 2012). One can thus more precisely assess the growth component of bacterial fitness than under radial expansion with mixed strains. However, note that with this measure of fitness we ignore another component of fitness, which is the ability to make it to the wave front where bacteria can grow and reproduce (Korolev et al. 2012). In any case, we find that the fitness as measured by the mean relative growth rate of the HMR lines is significantly lower than that of the ancestral strain ( = 0.81, t-test, P = 5.82 10−13, Figure 4B). We note that two out of the nine tested HMR lines (12 and 16) show no reduction in fitness despite having accumulated many mutations (128 and 142 mutations). Interestingly, these two lines have nonsynonymous mutations in the mlc (makes large colony) gene, known to enable prolonged growth on agar. Contrastingly, the average relative growth rate of LMR lines was significantly larger than that of the ancestral strain ( = 1.08, t-test, P = 1.44 10−10), with all lines showing an increase in relative growth rate. Importantly, HMR line 16, which shows a much higher fitness than the other HMR lines in the competitive radial growth assay (Figure 4A) also has an increased growth rate as measured by linear competition on agar (Figure S8 in File S1). This is again in contrast with a pleiotropic adaptation hypothesis for reduced colony size, under which we would expect to see lines showing a reduced growth rate measured by the linear growth experiment (Figure 4B) despite an increased overall fitness as measured by the radial competition experiments (Figure 4A). Note that the relative growth rate of chemostat lines is significantly larger than that of the ancestral strain ( = 1.08, t-test, P = 0.0008), and five out of seven chemostat lines show a larger fitness than the ancestral strain, in keeping with the results of the linear competition experiment.
We then estimated the fitness of bacteria as they grow in liquid batch culture (Figure 4C). In that case, the fitness of HMR lines in liquid culture was significantly decreased relative to the ancestral strain ( = 0.829, t-test, P = 8.52 10−9), whereas the fitness of the LMR lines remained identical ( = 1.027, t-test, P = 0.34), and that of the chemostat lines was slightly but not significantly increased ( = 1.091, t-test, P = 0.059) compared to that of the ancestral line.
DFE:
We first estimated the DFE and the effective population size at the expansion front by fitting an analytically tractable model for the evolution of mean fitness during range expansions (Peischl et al. 2015) to the colony size trajectories shown in Figure 3. The estimated DFE (Figure 5A) is almost symmetrical around zero, with an average negative effect of 0.00379 per mutation. Furthermore, we estimate an effective population size at the expansion front of = 14.6, very close to previous estimates suggesting an effective size on the wave front of the order of 10 cells (Hallatschek et al. 2007; Korolev et al. 2011), and indicating that evolution at the expansion front is largely determined by genetic drift. Figure 5B illustrates simulations of the estimated model with examples of observed data and reveals a good fit between theory and data. Further, Figure 5C shows that the difference between observed and expected fitness is not significantly greater than what would be expected by chance under our theoretical model of expansion load (P-value = 0.18).
The DFE estimated from the change in colony size over the 39 days of evolution as a function of the number of accumulated mutations is shown in Figure 6A. This DFE is almost symmetrical around zero, and very similar to that shown in Figure 5A, with an average negative effect of 0.0029 per mutation. This mean mutation effect is smaller than that shown in Figure 5, since this DFE is only based on observed mutations, i.e., that were not lost due to selection during the time of the experiment, whereas the DFE reported in Figure 5 considers all mutations, observed or not. Nevertheless, this DFE explains the data quite well, as shown on Figure 6B, where we report the decline in fitness expected for this DFE and its 95% C.I. under an additive model. Moreover, we see on Figure 6C that the difference between observed and expected fitness is not significantly greater than what would be expected by chance under our model (P-value = 0.80). We also tested whether the HMR and LMR lines have different DFEs using a likelihood ratio test, which reveals that it is not significant (, P-value = 0.269), suggesting that the DFE in Figure 6A can explain the dynamics of colony size change of both HMR and LMR lines.
Discussion
We provide here four lines of evidence that an accumulation of mutations during a range expansion leads to a decrease in fitness. We first observe that the ability to grow on agar of HMR lines significantly decreases, on average by 33%, over time, whereas that of LMR lines remains constant (Figure 3). This latter constancy is not due to the smallest number of LMR lines, as a similarly small sample of HMR lines shows significantly reduced growth after 39 days. Second, direct competition of evolved strains with ancestral strains during a radial expansion (exactly similar to what occurs in our experimental setup) reveals that 9/10 HMR lines and 7/10 LMR lines are outcompeted by the ancestral line (Figure 4A). Third, a linear competition experiment different from the evolution condition, but allowing us to directly estimate the fitness of the evolved strains relative to that of their ancestor on the expansion front, shows on average a significant 19% fitness reduction for HMR lines, and a significant increase in fitness for LMR lines (Figure 4B). Finally, a measure of the growth ability of evolved strains in a completely different and nutrient-wise richer liquid medium shows a significant 17% reduced growth rate for HMR lines and again no change in fitness for LMR lines (Figure 4C).
In comparison, bacteria having evolved at HMR in chemostat for 39 days have accumulated significantly fewer mutations than HMR and LMR lines (Figure 2) and retain high fitness. This result is in line with a previous experiment showing that yeast growing as a well-mixed population had a lower fitness loss than yeast growing on a flat agar (Lavrentovich et al. 2016). The fewer observed mutations in chemostat lines are thus probably due to an efficient removal of deleterious mutations by selection in well-mixed populations of large effective size. An alternative explanation would be that chemostat lines had a much lower mutation rate than HMR lines on agar. However, our fluctuation test experiment shows that chemostat evolved strains have retained the same HMR as the ancestral strain and the agar-grown LMR lines (Table S4 in File S1). Additionally, the chemostat lines still show the typical A:T → G:C transition bias typical of defective MMR systems (Lee et al. 2012) (Table S3 in File S1), suggesting that the MMR system was not fully functional in these lines. Since the dN/dS ratio is significantly larger in chemostat than in HMR lines (1.334 vs. 1.014, P = 0.003), positive selection could have been acting in the chemostat environment and recurrent selective sweeps could have also contributed to reducing diversity. Overall, we observe an approximately sixfold reduction in the number of mutations accumulated in chemostat lines as compared to HMR lines. A similar (around fivefold) reduction in number of accumulated mutations was found between studies of well-mixed batch cultures of a different mutator strain (mutL) (Barrick et al. 2009) and lines that evolved in a mutation accumulation experiment with strong recurrent artificial bottlenecks (Lee et al. 2012).
In addition to a dN/dS > 1, two other observations suggest that selection was more efficient in chemostat lines. First, chemostat lines have a higher fitness than other evolved or ancestral strains in the radial and linear competition assay (Figure 4C), indicative of potential adaptation to the LB medium. Second, the fact that we see fewer mutations in chemostat than in HMR and LMR lines, but that these mutations have a slightly higher (but not significant) associated PROVEAN score (Figure S3 in File S1), also suggests that they have been under strongly positive selection.
Overall, our observations are in line with theory, which predicts that natural selection is relatively inefficient during range expansions due to the low effective size prevailing on the wave front, such that most deleterious mutations are not purged on the wave front (Peischl et al. 2013, 2015). The use of this theoretical framework also allows us to directly infer the DFE from the reduction in growth rates of HMR lines over time under a hard selection model (Figure 5A). The resulting DFE suggests that 60.3% of mutations are deleterious, with a mean negative effect of 0.38% for new mutations. In addition, we have three lines of evidence suggesting that mutations have accumulated almost independently of their fitness effect. First, dN/dS ratios are not significantly different from one for both HMR and LMR lines, suggesting that nonsynonymous mutations have accumulated at the same rate as synonymous mutations. This would be expected if all nonsynonymous mutations were selectively neutral, even though most of them are predicted to have a phenotypic effect using PROVEAN scores (Figure S3 in File S1). Second, mutations have accumulated almost symmetrically along the genome on both sides of the origin of replication oriC (Figure S6 and Figure S7 in File S1), suggesting that the distribution of mutations along the bacterial genome reflects variable mutation rates that depend on positional constraints during chromosome replication (Foster et al. 2013) and not on local selective pressures. This wave-like distribution of mutations was described previously for both wild-type and MMR-deficient P. aeruginosa lines. Since this pattern is present in both P. aeruginosa lines, it is unlikely due to the disabled MMR system (Dettman et al. 2016). Note that this pattern has also been observed in a mutation accumulation experiment with E. coli (Foster et al. 2013), and therefore purifying selection is certainly not involved in this variable mutation rate across the genome (Foster et al. 2013). Third, the DFE inferred from the dynamics of colony size change as a function of the number of observed mutations per line is extremely similar to that inferred from all new mutations in HMR lines (compare Figure 5A and Figure 6A). This high similarity suggests that most new mutations have been retained during our evolutionary experiment, and that only highly deleterious mutations have been eliminated to lead to the 0.0009 shift between the estimated mean effects of new and observed mutations. The very low estimated effective size of ∼15 individuals on the wave front (Figure 5) indeed suggests that only mutations with negative effects of the order of 1/15 (∼6.7%) or higher have been deterministically eliminated by selection.
These lines of evidence for a predominantly neutral evolution of HMR lines argue against a possible adaptive explanation for their lower fitness assessed by direct competition between an ancestral strain and our evolved HMR strain. Indeed, one could hypothesize that growth on an agar plate implies the development of some gradient in nutrient concentration and toxic waste products, which could lead to the emergence of a complex system with the coexistence of several specifically adapted strains, and lead to frequency-dependent selection (Friesen et al. 2004). In this case, a single strain of this system would certainly be outcompeted by the ancestral strain as observed in Figure 4. However, this adaptive explanation does not appear parsimonious as it would require a high motility of the different strains to maintain a polymorphism on the edge and prevent the genetic surfing of a single variant. Moreover, under this hypothesis, we would not expect to see a continuous decrease in colony size over time (Figure 3), and we would also expect to see traces of these adaptations at the genomic level (e.g., dN/dS > 1), as in chemostat experiments.
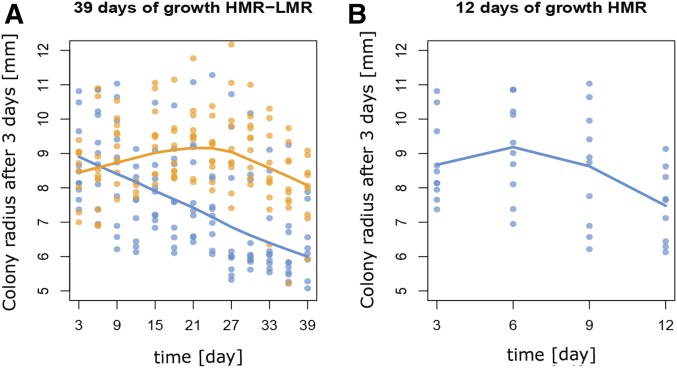
The fact that the fitness of most HMR lines has decreased during their range expansion does not mean that all observed mutations are necessarily deleterious or neutral, as some mutations adaptive for the wave front conditions could have occurred. The estimated DFEs suggest that many positively selected and thus potentially adaptive mutations have indeed occurred (see Figure 5A and Figure 6A). A closer examination of the early dynamics of the colony growths suggests that HMR and LMR lines could have adapted to life on wave fronts (Figure 7). Indeed, using nonlinear regression we observed that the colony size of LMR lines initially increases and then begins to decrease after 24 days of growth to reach levels similar to those observed at the onset of the experiment after 39 days of evolution (Figure 7A). A similar analysis of the growth rates in the first 12 days of evolution of HMR lines shows that they initially slightly increase before declining after 6 days (Figure 7B), in keeping with the potential occurrence of adaptive mutations in some HMR lines in the early phases of the experiment. For instance, some mutations could have potentially allowed some strains to preferentially occupy the wave front and thus access fresh nutrients. Such a positive selection of mutations allowing bacteria to occupy the expanding wave front has been recently described in several bacterial species (van Ditmarsch et al. 2013; Oldewurtel et al. 2015). Beneficial mutations could also increase the expansion speed of the colony, as was recently shown in P. aeruginosa (Madsen et al. 2015), and such beneficial mutations could be involved in the initial increase in colony size we observe for both HMR and LMR lines in the early phase of the experiment (Figure 7). In a different setting, it has also been shown that beneficial mutations can very quickly increase in frequency during range expansions on agar, and that this is significantly faster than in well-mixed populations, so that beneficial mutants present in some sectors can rapidly colonize a large proportion of the colony wave front by outcompeting mutants present in slow growing sectors (Gralka et al. 2016b). Such a competition between sectors occurring at the beginning of the experiments could explain the initial increase in fitness observed in LMR and HMR strains, which would be due to the rapid spread of beneficial mutations with large effects (Figure 7). Note that such initial increase in fitness is not observed in our simulations (Figure 5B), probably because they were performed in one-dimension, thus preventing competition between adjacent sectors. However, by overtaking the front, positively-selected bacteria would enter an environment where local population size is low (estimated here to be , Figure 5), genetic drift is high, and selection is inefficient, making it more difficult to purge further deleterious mutations (Hallatschek and Nelson 2010; Peischl et al. 2013, 2015). The evolution of E. coli strains during their growth on agar could thus result from a complex interplay between beneficial and deleterious mutations, but the effect of the latter ones seems to predominate in most HMR lines after 39 days. The estimated overall 19% fitness disadvantage of HMR lines relative to the ancestral strain (Figure 4B) makes them rapidly outcompeted by ancestral strains, and most of them entirely disappear from colonizing wave fronts during a radial competition experiment (Figure 4A). This strongly indicates that population expansions on solid surfaces are detrimental for mutator strains (Gralka et al. 2016a), which could explain why they are rarely seen in natural conditions (Matic et al. 1997; Tenaillon et al. 2000). Nonmutator spatially expanding bacterial populations would indeed be less likely to suffer from an accumulation of deleterious mutations, as shown by our results on LMR lines. However, we would expect that nonmutator strains expanding in one or two dimensions over longer periods (even interrupted by periods of well-mixed conditions and higher densities) should develop some degree of expansion load. Species having the possibility to purge this load (e.g., by recombination) would then be at some advantage, and it would be interesting to check if species expanding on one- or two-dimensional surfaces show reduced mutation and higher recombination rates as compared to others.
Figure 7.
Early growth dynamics of HMR and LMR lines. (A) Evolution of HMR (experiment 2) and LMR colony size after 3 days of growth over the course of the experiment. The average size of HMR colonies estimated by a LOESS regression linearly declines over time, whereas that of LMR colonies increases until day 24, and then declines until the end of the experiment. (B) Same as (A) but only for HMR lines during the first 12 days of growth, showing a pattern similar to that of LMR lines but on an ∼4× shorter timescale, which approximately corresponds to their ∼3.7× higher mutation rate (see Table S4 in File S1). HMR, high mutation rate; LMR, low mutation rate; LOESS, locally weighted scatterplot smoothing.
Since HMR lines show reduced growth abilities not only on agar but also in a well-mixed liquid culture (Figure 4C), some of the accumulated mutations are likely to be unconditionally deleterious. Thus, even though bacterial populations are generally considered to be able to adapt to almost any environmental conditions (Hindre et al. 2012), HMR strains seem to have accumulated deleterious mutations in a wide range of cellular processes. Our results thus imply that many mutations seen in natural bacterial populations are not necessarily adaptive and that populations of bacteria growing on two-dimensional surfaces can develop an expansion load (Peischl et al. 2015), even though the speed of this process should be slower for nonmutator strains. However, further studies are required to test if this pattern would also occur when conditions are different (e.g., a different growth medium). Theoretical results predict that more stringent conditions implying stronger selections against mutants should limit the accumulation of deleterious mutants (Peischl et al. 2013, 2015). Thus, if bacterial strains were in an environment to which they are badly adapted, beneficial mutations could be important at the beginning of the expansion (Barrick and Lenski 2013). Nevertheless, our results highlight the importance of considering the spatially explicit process of bacterial growth when studying bacterial adaptation and evolution.
The expansion load we demonstrate here in bacteria could also happen during the expansion of other populations, including humans (Henn et al. 2015) or plants (González-Martínez et al. 2017), potentially affecting their adaptive potential, but it could also affect other types of expansions, like the growth of solid tissues in eukaryotes. The analogy between the evolution of bacterial communities and the growth of eukaryotic tissue has recently been highlighted (Lambert et al. 2011). Indeed, multicellular organisms go through millions to trillions of cell divisions during their life span, accumulating somatic mutations at a rate ∼10× higher than germ line mutations (Lynch 2010; Shendure and Akey 2015), potentially contributing to cancers and other human diseases (Shendure and Akey 2015). In addition to having triggered the development of specific life-history traits in most organisms [reviewed in Charlesworth and Charlesworth (1998)], deleterious mutations and their evolutionary cost could have also led to the development of specific mechanisms preventing their accumulation during the growth of some organisms, as recently shown in a long-lived oak tree (Sarkar et al. 2017).
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300144/-/DC1.
Acknowledgments
We are grateful to Oskar Hallatschek, Mark Kirkpatrick, Sally Otto, and Olin Silander for constructive comments and critical reading of an earlier version of the manuscript, and to Jean-François Flot for discussions at various stages of this project. We also want to thank Tosso Leeb, Cord Drögemüller, and the Next-Generation Sequencing core facility of the University of Berne for their support. L.B., I.D., and S.P. were partly supported by Swiss National Science Foundation grants (31003A-143393 and 310030B-166605) to L.E. and M.A.
Footnotes
Communicating editor: L. Wahl
Literature Cited
- Agrawal A. F., Whitlock M. C., 2012. Mutation load: the fitness of individuals in populations where deleterious alleles are abundant. Annu. Rev. Ecol. Evol. Syst. 43: 115–135. [Google Scholar]
- Al Mamun A. A., Lombardo M. J., Shee C., Lisewski A. M., Gonzalez C., et al. , 2012. Identity and function of a large gene network underlying mutagenic repair of DNA breaks. Science 338: 1344–1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrick J. E., Lenski R. E., 2013. Genome dynamics during experimental evolution. Nat. Rev. Genet. 14: 827–839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrick J. E., Yu D. S., Yoon S. H., Jeong H., Oh T. K., et al. , 2009. Genome evolution and adaptation in a long-term experiment with Escherichia coli. Nature 461: 1243–1247. [DOI] [PubMed] [Google Scholar]
- Blundell J., Levy S., Venkataram S., Petrov D., Fisher D., et al. , 2015. Quantitative evolutionary dynamics of one million barcoded lineages. Bull. Am. Phys. Soc. Volume 60. [Google Scholar]
- Bolger A. M., Lohse M., Usadel B., 2014. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinformatics 30: 2114–2120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B., Charlesworth D., 1998. Some evolutionary consequences of deleterious mutations. Genetica 102–103: 3–19. [PubMed] [Google Scholar]
- Charlesworth D., Charlesworth B., Morgan M., 1995. The pattern of neutral molecular variation under the background selection model. Genetics 141: 1619–1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi Y., Chan A. P., 2015. PROVEAN web server: a tool to predict the functional effect of amino acid substitutions and indels. Bioinformatics 31: 2745–2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi Y., Sims G. E., Murphy S., Miller J. R., Chan A. P., 2012. Predicting the functional effect of amino acid substitutions and indels. PLoS One 7: e46688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cingolani P., Platts A., Wang le L., Coon M., Nguyen T., et al. , 2012. A program for annotating and predicting the effects of single nucleotide polymorphisms, SnpEff: SNPs in the genome of Drosophila melanogaster strain w1118; iso-2; iso-3. Fly (Austin) 6: 80–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett-Detig R. B., Hartl D. L., Sackton T. B., 2015. Natural selection constrains neutral diversity across a wide range of species. PLoS Biol. 13: e1002112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covert A. W., Lenski R. E., Wilke C. O., Ofria C., 2013. Experiments on the role of deleterious mutations as stepping stones in adaptive evolution. Proc. Natl. Acad. Sci. USA 110: E3171–E3178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denamur E., Matic I., 2006. Evolution of mutation rates in bacteria. Mol. Microbiol. 60: 820–827. [DOI] [PubMed] [Google Scholar]
- Dettman J. R., Sztepanacz J. L., Kassen R., 2016. The properties of spontaneous mutations in the opportunistic pathogen Pseudomonas aeruginosa. BMC Genomics 17: 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do R., Balick D., Li H., Adzhubei I., Sunyaev S., et al. , 2015. No evidence that selection has been less effective at removing deleterious mutations in Europeans than in Africans. Nat. Genet. 47: 126–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J., 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17: 368–376. [DOI] [PubMed] [Google Scholar]
- Fisher R. A., 1930. The Genetical Theory of Natural Selection. Oxford University Press, Oxford. [Google Scholar]
- Fogle C. A., Nagle J. L., Desai M. M., 2008. Clonal interference, multiple mutations and adaptation in large asexual populations. Genetics 180: 2163–2173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster P. L., 2006. Methods for determining spontaneous mutation rates. Methods Enzymol. 409: 195–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster P. L., Hanson A. J., Lee H., Popodi E. M., Tang H., 2013. On the mutational topology of the bacterial genome. G3 (Bethesda) 3: 399–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fowler R. G., Schaaper R. M., 1997. The role of the mutT gene of Escherichia coli in maintaining replication fidelity. FEMS Microbiol. Rev. 21: 43–54. [DOI] [PubMed] [Google Scholar]
- Friesen M. L., Saxer G., Travisano M., Doebeli M., 2004. Experimental evidence for sympatric ecological diversification due to frequency-dependent competition in Escherichia coli. Evolution 58: 245–260. [PubMed] [Google Scholar]
- Fu W., Gittelman R. M., Bamshad M. J., Akey J. M., 2014. Characteristics of neutral and deleterious protein-coding variation among individuals and populations. Am. J. Hum. Genet. 95: 421–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia-Alonso L., Jimenez-Almazan J., Carbonell-Caballero J., Vela-Boza A., Santoyo-Lopez J., et al. , 2014. The role of the interactome in the maintenance of deleterious variability in human populations. Mol. Syst. Biol. 10: 752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- González-Martínez S. C., Ridout K., Pannell J. R., 2017. Range expansion compromises adaptive evolution in an outcrossing plant. Curr. Biol. 27: 2544–2551 [DOI] [PubMed] [Google Scholar]
- Good B. H., Rouzine I. M., Balick D. J., Hallatschek O., Desai M. M., 2012. Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. Proc. Natl. Acad. Sci. USA 109: 4950–4955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordo I., Campos P. R., 2008. Sex and deleterious mutations. Genetics 179: 621–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gralka M., Fusco D., Hallatschek O., 2016a Watching populations melt down. Biophys. J. 111: 271–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gralka M., Stiewe F., Farrell F., Mobius W., Waclaw B., et al. , 2016b Allele surfing promotes microbial adaptation from standing variation. Ecol. Lett. 19: 889–898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haigh J., 1978. The accumulation of deleterious genes in a population–Muller’s ratchet. Theor. Popul. Biol. 14: 251–267. [DOI] [PubMed] [Google Scholar]
- Hall B. M., Ma C. X., Liang P., Singh K. K., 2009. Fluctuation analysis CalculatOR: a web tool for the determination of mutation rate using Luria-Delbruck fluctuation analysis. Bioinformatics 25: 1564–1565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallatschek O., Nelson D. R., 2010. Life at the front of an expanding population. Evolution 64: 193–206. [DOI] [PubMed] [Google Scholar]
- Hallatschek O., Hersen P., Ramanathan S., Nelson D. R., 2007. Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. USA 104: 19926–19930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn B. M., Botigue L. R., Bustamante C. D., Clark A. G., Gravel S., 2015. Estimating the mutation load in human genomes. Nat. Rev. Genet. 16: 333–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn B. M., Botigue L. R., Peischl S., Dupanloup I., Lipatov M., et al. , 2016. Distance from sub-Saharan Africa predicts mutational load in diverse human genomes. Proc. Natl. Acad. Sci. USA 113: E440–E449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindre T., Knibbe C., Beslon G., Schneider D., 2012. New insights into bacterial adaptation through in vivo and in silico experimental evolution. Nat. Rev. Microbiol. 10: 352–365. [DOI] [PubMed] [Google Scholar]
- Hosono K., Kakuda H., Ichihara S., 1995. Decreasing accumulation of acetate in a rich medium by Escherichia coli on introduction of genes on a multicopy plasmid. Biosci. Biotechnol. Biochem. 59: 256–261. [DOI] [PubMed] [Google Scholar]
- Keightley P. D., Otto S. P., 2006. Interference among deleterious mutations favours sex and recombination in finite populations. Nature 443: 89–92. [DOI] [PubMed] [Google Scholar]
- Kimura M., Maruyama T., Crow J. F., 1963. The mutation load in small populations. Genetics 48: 1303–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiviet D. J., Nghe P., Walker N., Boulineau S., Sunderlikova V., et al. , 2014. Stochasticity of metabolism and growth at the single-cell level. Nature 514: 376–379. [DOI] [PubMed] [Google Scholar]
- Korolev K. S., Avlund M., Hallatschek O., Nelson D. R., 2010. Genetic demixing and evolution in linear stepping stone models. Rev. Mod. Phys. 82: 1691–1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korolev K. S., Xavier J. B., Nelson D. R., Foster K. R., 2011. A quantitative test of population genetics using spatiogenetic patterns in bacterial colonies. Am. Nat. 178: 538–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korolev K. S., Muller M. J., Karahan N., Murray A. W., Hallatschek O., et al. , 2012. Selective sweeps in growing microbial colonies. Phys. Biol. 9: 026008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert G., Estévez-Salmeron L., Oh S., Liao D., Emerson B. M., et al. , 2011. An analogy between the evolution of drug resistance in bacterial communities and malignant tissues. Nat. Rev. Cancer 11: 375–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavrentovich M. O., Wahl M. E., Nelson D. R., Murray A. W., 2016. Spatially constrained growth enhances conversional meltdown. Biophys. J. 110: 2800–2808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H., Popodi E., Tang H., Foster P. L., 2012. Rate and molecular spectrum of spontaneous mutations in the bacterium Escherichia coli as determined by whole-genome sequencing. Proc. Natl. Acad. Sci. USA 109: E2774–E2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehe R., Hallatschek O., Peliti L., 2012. The rate of beneficial mutations surfing on the wave of a range expansion. PLoS Comput. Biol. 8: e1002447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R., 2009. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25: 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohmueller K. E., 2014. The distribution of deleterious genetic variation in human populations. Curr. Opin. Genet. Dev. 29: 139–146. [DOI] [PubMed] [Google Scholar]
- Lohmueller K. E., Indap A. R., Schmidt S., Boyko A. R., Hernandez R. D., et al. , 2008. Proportionally more deleterious genetic variation in European than in African populations. Nature 451: 994–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., 2010. Evolution of the mutation rate. Trends Genet. 26: 345–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., Burger R., Butcher D., Gabriel W., 1993. The mutational meltdown in asexual populations. J. Hered. 84: 339–344. [DOI] [PubMed] [Google Scholar]
- Madsen J. S., Lin Y. C., Squyres G. R., Price-Whelan A., de Santiago Torio A., et al. , 2015. Facultative control of matrix production optimizes competitive fitness in Pseudomonas aeruginosa PA14 biofilm models. Appl. Environ. Microbiol. 81: 8414–8426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin G., Lenormand T., 2006. A general multivariate extension of Fisher’s geometrical model and the distribution of mutation fitness effects across species. Evolution 60: 893–907. [PubMed] [Google Scholar]
- Matic I., Radman M., Taddei F., Picard B., Doit C., et al. , 1997. Highly variable mutation rates in commensal and pathogenic Escherichia coli. Science 277: 1833–1834. [DOI] [PubMed] [Google Scholar]
- McKenna A., Hanna M., Banks E., Sivachenko A., Cibulskis K., et al. , 2010. The genome analysis toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 20: 1297–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nanchen A., Schicker A., Sauer U., 2006. Nonlinear dependency of intracellular fluxes on growth rate in miniaturized continuous cultures of Escherichia coli. Appl. Environ. Microbiol. 72: 1164–1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldewurtel E. R., Kouzel N., Dewenter L., Henseler K., Maier B., 2015. Differential interaction forces govern bacterial sorting in early biofilms. Elife 4: e10811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr H. A., 2000. The rate of adaptation in asexuals. Genetics 155: 961–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peischl S., Excoffier L., 2015. Expansion load: recessive mutations and the role of standing genetic variation. Mol. Ecol. 24: 2084–2094. [DOI] [PubMed] [Google Scholar]
- Peischl S., Dupanloup I., Kirkpatrick M., Excoffier L., 2013. On the accumulation of deleterious mutations during range expansions. Mol. Ecol. 22: 5972–5982. [DOI] [PubMed] [Google Scholar]
- Peischl S., Kirkpatrick M., Excoffier L., 2015. Expansion load and the evolutionary dynamics of a species range. Am. Nat. 185: E81–E93. [DOI] [PubMed] [Google Scholar]
- Peischl S., Dupanloup I., Bosshard L., Excoffier L., 2016. Genetic surfing in human populations: from genes to genomes. Curr. Opin. Genet. Dev. 41: 53–61. [DOI] [PubMed] [Google Scholar]
- Sarkar N., Schmid-Siegert E., Iseli C., Calderon S., Gouhier-Darimont C., et al. , 2017. Low rate of somatic mutations in a long-lived oak tree. bioRxiv DOI https//.org/10.1101/149203. [DOI] [PubMed] [Google Scholar]
- Schindelin J., Arganda-Carreras I., Frise E., Kaynig V., Longair M., et al. , 2012. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9: 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schliep K. P., 2011. phangorn: phylogenetic analysis in R. Bioinformatics 27: 592–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw F. H., Geyer C. J., Shaw R. G., 2002. A comprehensive model of mutations affecting fitness and inferences for Arabidopsis thaliana. Evolution 56: 453–463. [DOI] [PubMed] [Google Scholar]
- Shendure J., Akey J. M., 2015. The origins, determinants, and consequences of human mutations. Science 349: 1478–1483. [DOI] [PubMed] [Google Scholar]
- Simons Y. B., Sella G., 2016. The impact of recent population history on the deleterious mutation load in humans and close evolutionary relatives. Curr. Opin. Genet. Dev. 41: 150–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons Y. B., Turchin M. C., Pritchard J. K., Sella G., 2014. The deleterious mutation load is insensitive to recent population history. Nat. Genet. 46: 220–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sousa V., Peischl S., Excoffier L., 2014. Impact of range expansions on current human genomic diversity. Curr. Opin. Genet. Dev. 29: 22–30. [DOI] [PubMed] [Google Scholar]
- Sulem P., Helgason H., Oddson A., Stefansson H., Gudjonsson S. A., et al. , 2015. Identification of a large set of rare complete human knockouts. Nat. Genet. 47: 448–452. [DOI] [PubMed] [Google Scholar]
- Sung W., Ackerman M. S., Miller S. F., Doak T. G., Lynch M., 2012. Drift-barrier hypothesis and mutation-rate evolution. Proc. Natl. Acad. Sci. USA 109: 18488–18492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon O., Le Nagard H., Godelle B., Taddei F., 2000. Mutators and sex in bacteria: conflict between adaptive strategies. Proc. Natl. Acad. Sci. USA 97: 10465–10470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon O., Rodriguez-Verdugo A., Gaut R. L., McDonald P., Bennett A. F., et al. , 2012. The molecular diversity of adaptive convergence. Science 335: 457–461. [DOI] [PubMed] [Google Scholar]
- Tenaillon O., Barrick J. E., Ribeck N., Deatherage D. E., Blanchard J. L., et al. , 2016. Tempo and mode of genome evolution in a 50,000-generation experiment. Nature 536: 165–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tennessen J. A., Bigham A. W., O’Connor T. D., Fu W., Kenny E. E., et al. , 2012. Evolution and functional impact of rare coding variation from deep sequencing of human exomes. Science 337: 64–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trindade S., Perfeito L., Gordo I., 2010. Rate and effects of spontaneous mutations that affect fitness in mutator Escherichia coli. Philos. Trans. R. Soc. Lond. B Biol. Sci. 365: 1177–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Ditmarsch D., Boyle K. E., Sakhtah H., Oyler J. E., Nadell C. D., et al. , 2013. Convergent evolution of hyperswarming leads to impaired biofilm formation in pathogenic bacteria. Cell Rep. 4: 697–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissman D. B., Hallatschek O., 2014. The rate of adaptation in large sexual populations with linear chromosomes. Genetics 196: 1167–1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke C. O., 2004. The speed of adaptation in large asexual populations. Genetics 167: 2045–2053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue Y., Chen Y., Ayub Q., Huang N., Ball E. V., et al. , 2012. Deleterious- and disease-allele prevalence in healthy individuals: insights from current predictions, mutation databases, and population-scale resequencing. Am. J. Hum. Genet. 91: 1022–1032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W., 2000. Structure and function of mismatch repair proteins. Mutat. Res. 460: 245–256. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Sequence data are available at Sequence Read Archive (SRA). The STUDY accession number is: SRP068347. The VCF files of the analysed strains are available in the GitHub repository, https://github.com/CMPG/ExpansionLoad_Bacteria