Prospects of Fine-Mapping Trait-Associated Genomic Regions by Using Summary Statistics from Genome-wide Association Studies

Abstract

During the past few years, various novel statistical methods have been developed for fine-mapping with the use of summary statistics from genome-wide association studies (GWASs). Although these approaches require information about the linkage disequilibrium (LD) between variants, there has not been a comprehensive evaluation of how estimation of the LD structure from reference genotype panels performs in comparison with that from the original individual-level GWAS data. Using population genotype data from Finland and the UK Biobank, we show here that a reference panel of 1,000 individuals from the target population is adequate for a GWAS cohort of up to 10,000 individuals, whereas smaller panels, such as those from the 1000 Genomes Project, should be avoided. We also show, both theoretically and empirically, that the size of the reference panel needs to scale with the GWAS sample size; this has important consequences for the application of these methods in ongoing GWAS meta-analyses and large biobank studies. We conclude by providing software tools and by recommending practices for sharing LD information to more efficiently exploit summary statistics in genetics research.

Introduction

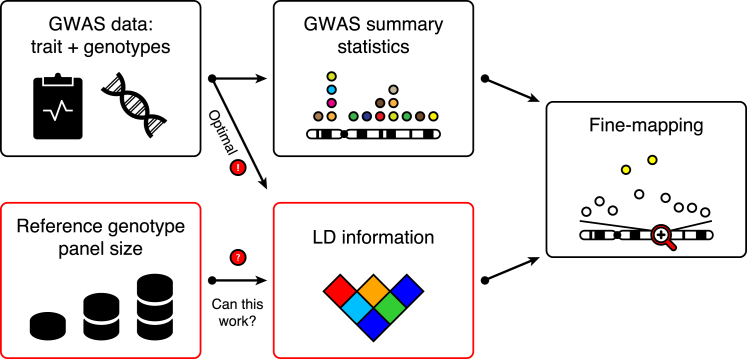
Public availability of summary statistics from genome-wide association study (GWAS) meta-analyses has recently generated exciting new opportunities to carry out various downstream analyses without access to the original genotype-phenotype data. This is a promising approach to utilizing the increasing GWAS sample sizes while avoiding privacy concerns and logistics of sharing individual-level genotype data. Typically, publicly available GWAS summary statistics originate from the standard additive model. Although this limits their use for modeling dominant, recessive, and interaction effects, they still provide a basis for a wide variety of important analyses. Examples include estimation of heritability^{1, 2} and genetic correlations,^{3, 4} gene-level tests,^{5, 6} risk prediction,⁷ Z score imputation,^{8, 9, 10} and fine-mapping^{11, 12, 13, 14, 15, 16, 17, 18, 19, 20} of causal variants. Common to all of these summary-statistical methods is that they require information about the linkage disequilibrium (LD) between the variants, and the hope has been that LD information from publicly available reference genotype panels could replace the original genotype data in these analyses.²¹ However, a thorough assessment of this topic is lacking in many application areas. In this work, we consider a central post-GWAS problem of fine-mapping causal variants by using summary statistics from GWASs and LD information from reference panels (Figure 1).

Figure 1.

Schematic of Fine-Mapping Causal Variants in Trait-Associated Genomic Regions by Using GWAS Summary Statistics and LD Information

Ideally, LD information is computed from the original GWAS data. LD information can, however, be obtained from a reference genotype panel when the original GWAS data are not available. An important open question is how large a reference genotype panel should be to nearly achieve the optimal fine-mapping performance given by the original GWAS data.

Fine-mapping aims to narrow the large set of variants associated with the trait down to a much smaller set of variants with a direct effect on the trait.²² This is a next step on the path from GWAS results to the molecular biology of complex traits and diseases and, eventually, to targets for therapeutic interventions. Even though establishing the biological mechanisms of the variants will require extensive experimental work,²³ initial fine-mapping can be done computationally through accounting for the complex correlation structure of the putative causal variants.²⁴

Recently, several software packages have been introduced for fine-mapping genomic regions by using GWAS summary statistics: Genome-wide Complex Trait Analysis (GCTA)’s conditional analysis,¹¹ CAVIAR,¹² PAINTOR,^{13, 14} CAVIARBF,^{15, 20} FINEMAP,¹⁶ JAM,¹⁷ RIVIERA,¹⁸ and RSS.¹⁹ All of these methods are able to run with LD information estimated from reference data, and an important question is how well this strategy performs in comparison with using the LD information from the original genotype data. To our knowledge, the most detailed analysis so far has been given by Yang et al.,²⁵ who used a reference panel of 6,654 individuals to carry out conditional analyses of height and body mass index (BMI) GWASs by using a stepwise regression method implemented in GCTA. On the basis of a simulation study, they concluded that a reference panel of at least 2,000 individuals is required and that little additional accuracy is gained beyond a size of 5,000. This advice has been followed by some other studies.¹⁷ However, a stepwise conditioning approach considers jointly only a handful of possible combinations of the variants, and therefore it is unclear how Yang et al.’s simulation study,²⁵ which used only two variants, represents the more general fine-mapping scenario where many more combinations of variants are evaluated. This question has not been carefully studied in conjunction with subsequent fine-mapping methods. Instead, typically public reference panels, such as the 1000 Genomes Project (1000GP),²⁶ have been suggested as the source of the LD information.^{12, 13, 15} However, given that alarming problems have already arisen from incompatibility between GWAS summary data and reference LD information,²⁰ it is important to make a comprehensive evaluation of the prospects of fine-mapping by using summary data and reference genotype panels, as well as create practical ways forward for the scientific community.

In this work, we evaluate how the size of the reference panel and the size of the GWAS affect the fine-mapping performance with and without the use of shrinkage methods^{19, 27} in LD estimation. As a motivation, we show how a proper fine-mapping analysis can refine the well-known association between the APOE (MIM: 107741) region and levels of low-density lipoprotein cholesterol (LDL-C), whereas estimation of LD from the 1000GP reference panel causes problems in the same context. Next, we carry out a comprehensive set of simulations on 100 GWAS regions by using Finnish genotype data and scale the results to biobank datasets by using UK Biobank data. We validate the earlier suggestion by Yang et al.²⁵ that a reference panel of a few thousand individuals from the target population is adequate also for fine-mapping as long as the GWAS sample size remains around 10,000. Importantly, we show that for fine-mapping, the size of the reference panel needs to scale with that of the GWAS sample. We conclude by providing the software tool LDstore to enable efficient sharing of LD information needed for accurate fine-mapping in the era of biobank-scale datasets.

Material and Methods

Cohorts

We used data from the FINRISK study,²⁸ the 1966 Northern Finland Birth Cohort (NFBC1966),²⁹ and the UK Biobank (UKBB).³⁰ FINRISK is a representative, cross-sectional survey of the Finnish working-age population. Since 1972, a random sample of 6,000–8,000 individuals has been collected every 5 years for the study of risk factors of chronic diseases. The study protocols of the FINRISK surveys used in this work (1992, 1997, 2002, and 2007) were approved by the ethics committee of the National Public Health Institute until 1997 and by the ethics committee of Helsinki and Uusimaa Hospital District after that. NFBC1966 is a longitudinal study of individuals from the provinces of Oulu and Lapland in northern Finland and was approved by the ethics committee of the Northern Ostrobothnia Hospital District Federation of Municipalities. The cohort was originally collected for the study of risk factors of birth-related complications and includes 12,068 mothers and 12,231 children. Genetically, NFBC1966 is not a perfect match to FINRISK, although both cohorts are collected within Finland (Figure S1). UKBB is a longitudinal study of individuals from 40 to 69 years of age in the United Kingdom and was approved by the North West Multi-center Research Ethics Committee. From 2006 to 2010, a sample of 500,000 individuals was collected for the investigation of genetic and environmental factors involved in disease development. All participants of FINRISK, NFBC1966, and UKBB have provided informed consent.

Genotype Data

In our analyses, we used genotype data on (1) 20,626 individuals included in the FINRISK surveys from 1992 to 2007, (2) 5,363 individuals from NFBC1966, and (3) 112,199 “white British” individuals from UKBB. For FINRISK and NFBC1966, we imputed 41 million variants separately with IMPUTE2 (see Web Resources) by using a combined 1000GP reference panel and low-pass Finnish whole-genome sequence data. For documentation about imputation of the UKBB genotype data, see the Web Resources. In each dataset, we removed variants with a minor allele frequency (MAF) below 1% and an imputation quality score below 0.5.

Fine-Mapping

Stepwise conditional analysis is a standard approach to fine-mapping a trait-associated genomic region. We performed stepwise conditioning implemented in SNPTEST2 (see Web Resources) by first conditioning on the variant with the lowest p value and then iteratively adding to the model the variant with the lowest conditional p value until no further variant reached the genome-wide significance threshold of 5 × 10⁻⁸. By jointly modeling the whole genomic regions, FINEMAP (see Web Resources) can potentially identify sets of variants with more evidence of being causal than those highlighted by a stepwise conditional analysis.¹⁶ The output from FINEMAP is (1) a list of potential causal configurations together with their posterior probabilities and Bayes factors and, (2) for each variant, the posterior probability and Bayes factor of being causal. We applied FINEMAP with its default settings while allowing for a maximum of ten causal variants.

In simulated datasets, where the causal status of each SNP was known, we computed the true-positive rate (TPR) and false-positive rate (FPR) by using the list of SNPs ranked by their posterior probability of being causal. Using the ROCR³¹ package in R, we compared the results obtained with different LD information according to their achieved TPR versus FPR through the partial area under the curve (pAUC).³² AUC is defined as the area under the TPR-versus-FPR curve and can be interpreted as the probability that a randomly chosen causal variant is assigned a higher posterior probability of being causal than a randomly chosen non-causal variant.³³ pAUC is defined as the area under the TPR-versus-FPR curve with a fixed FPR range. In our comparisons, we summarize the simulations by reporting the average pAUCs and vertically averaged TPR-versus-FPR curves over the set of replications.

We generated credible sets of causal variants³⁴ as the union of the variants included in the smallest set of causal configurations that already covered 90%, 95%, or 99% of the total posterior probability. For the credible sets, we calculated their size and coverage, defined as the proportion of causal variants that were included in the credible set.

Shrinkage Estimation of LD Information

We investigated shrinkage estimation³⁵ of Pearson correlations between pairs of variants from a reference panel; that is, we used a positive multiplicative factor < 1 to bring the correlation estimate toward 0. The simplest approach is to use the same constant shrinkage factor for all correlation estimates (“constant shrinkage”). A more advanced approach is to define the shrinkage factor for each pair of variants depending on their estimated recombination distance^{19, 27} (“recombination shrinkage”). For the recombination shrinkage, we used the recombination map from HapMap phase 2.³⁶

Association between LDL-C and APOE in Finnish Data

As a motivating example, we consider the association between LDL-C and the APOE region on chromosome 19. We used 15,626 individuals from FINRISK²⁸ and an additive linear model implemented in SNPTEST2 to test for associations with LDL-C (see Surakka et al.³⁷ for details about LDL-C measurements and covariate adjustment). The summary statistics from LDL-C GWASs were analyzed with FINEMAP and the LD information from the original genotype data on 3,078 variants with a MAF above 1% and covering 1 Mb around APOE. We also did two additional FINEMAP analyses with the 1000GP data to obtain LD information: first, we considered the Finnish reference panel with 99 individuals, and second, we extended the Finnish panel to the combined European panel with 503 individuals.

100 GWAS Regions in Finnish Data

To assess the effect of reference panels in a general fine-mapping setting by using a GWAS of about 5,000 individuals to represent a typical cohort that could be included in ongoing GWAS meta-analyses, we performed comprehensive simulations over 100 GWAS regions chosen from GWAS meta-analyses for coronary artery disease (CAD),³⁸ Crohn disease (CD),³⁹ lipid traits (LIPs),⁴⁰ schizophrenia (SCZ),⁴¹ and type 2 diabetes (T2D).⁴² For each study, we retained the lead SNPs outside the human leukocyte antigen (HLA) region with a marginal p value below 5 × 10⁻⁸ and selected 100 lead SNPs (18 from CAD, 20 from CD, 21 from LIPs, 21 from SCZ, and 20 from T2D) for further analyses. For each lead SNP, we defined genomic regions with 1,001 SNPs comprising 500 SNPs downstream and upstream of the lead SNP. Using genotype data on 5,363 individuals from NFBC1966, we generated 500 datasets (five replications per each region) according to the following linear model:

$$\mathit{y}=\sum _{c\in C}{\beta }_c{\mathit{g}}_c+\mathbf{ϵ},$$

where C is the set of causal SNPs, g_c is the vector of genotypes at the c^th causal SNP, β_c and f_c are the effect size and MAF, respectively, of the c^th SNP, and $\mathbf{ϵ}$ is Gaussian noise with mean 0 and variance

$${\sigma }^2=1-\sum _{c\in C}2f_c\left(1-f_c\right){\beta }_c^2.$$

In each dataset, the lead SNP and four randomly chosen other SNPs were causal. The effect sizes of the causal SNPs were specified so that the statistical power with 5,363 individuals was approximately 0.5 at a significance level of 5 × 10⁻⁸. We applied a linear model implemented in the lm() function in R (see Web Resources) to compute summary statistics (estimates of β and their standard errors). We then analyzed each set of summary statistics with FINEMAP and LD information either from the original NFBC1966 genotype data or from a subset of the reference genotype data on the FINRISK individuals to generate realistic reference panels that were not a perfect match to the target cohort but still originated from the same population (Figure S1).

ABO Region on Chromosome 9 in UKBB Data

The UKBB genotype data were split into two sets: 82,199 and 30,000 individuals. We extracted, from both datasets, 762 SNPs covering 100 kb around ABO (MIM: 110300). Using the genotype data on 82,199 individuals, we generated 100 datasets by applying the same additive linear model as we did for the simulations over 100 GWAS regions. To maintain comparability with our earlier simulations, we made sure that each dataset had five causal SNPs with effect sizes specified so that the statistical power with 5,363 individuals was approximately 0.5 at a significance level of 5 × 10⁻⁸. To systematically study the effect of the GWAS sample size, we computed summary statistics by using 5,363, 10,000, and 50,000 individuals from the set of 82,199 individuals. Each set of summary statistics was then analyzed with FINEMAP and LD information either from the original genotype data or from a subset of the reference genotypes of the 30,000 individuals.

Posterior Probability of a Pair of Variants

To illustrate the behavior of the posterior probability of the true causal configuration as a function of accuracy of LD information, we considered a simple setting of one causal (C) and one non-causal (N) SNP. In Appendix A, we give an explicit formula for the posterior odds between two configurations that we used to evaluate the posterior probability of the true causal configuration as a function of a correlation estimate from an external reference panel. We used simulations to define the sampling distribution of the pairwise correlation between variants given the sample size, true correlation between the SNPs (r = 0.37), and MAFs (0.02). The MAFs and the correlation were motivated by SNPs rs10418198 and rs61679753 in our APOE GWAS data. This pair was much more highly correlated in the Finnish panel of 1000GP (r = 0.86) and consequently created a false-positive causal configuration in our APOE analysis that used 1000GP. Therefore, we examined in more detail how different reference-panel sizes and different GWAS sizes affected the fine-mapping in this setting.

LDstore for Efficient Estimation and Storage of LD Information

A naive approach to estimating Pearson correlations between all imputed and genotyped variants on a chromosome incurs a cubic time complexity and quadratic space complexity in the number of variants. Run time can be reduced by (1) parallel processing and (2) a sliding-window approach that takes into account that the magnitude of LD between two variants decreases with their physical distance.²⁶ Space complexity can be reduced (1) by the symmetry property of Pearson correlation, (2) by the storage of correlations in an integer representation, and (3) by the storage of only values above a user-specified threshold.

Estimating correlations by using a sliding window has been implemented in the software packages PLINK^{43, 44} and RAREMETALWORKER (RMW).⁴⁵ RMW is a command-line tool for rare-variant association testing and is currently used for sharing whole-chromosome LD information via text files. PLINK differs from RMW by allowing LD information to be written in text or binary format. Although RMW and PLINK are very useful tools, we think that storing information (1) in text files (RMW), (2) on almost uncorrelated variants (PLINK and RMW), and (3) without variant information included in the same file (PLINK) is not the most practical way to share LD information files for the trait-associated genomic regions across cohorts of a GWAS consortium or to store whole-chromosome LD information.

We introduce LDstore, a software package for efficient estimation, storage, and seamless sharing of LD information. The sliding window of LDstore is similar to that of PLINK and RMW, whereas the important difference is (1) massively parallel processing using OPENMP or MPI (see Web Resources), (2) sparse estimation for achieving smaller file sizes, and (3) storage of the LD information with additional variant information in the same file. LDstore outputs LD information in an indexed binary file by using compressed row storage and hash tables to achieve fast lookups of LD information irrespectively of file size.

Results

Association between APOE and LDL-C in Finnish Data

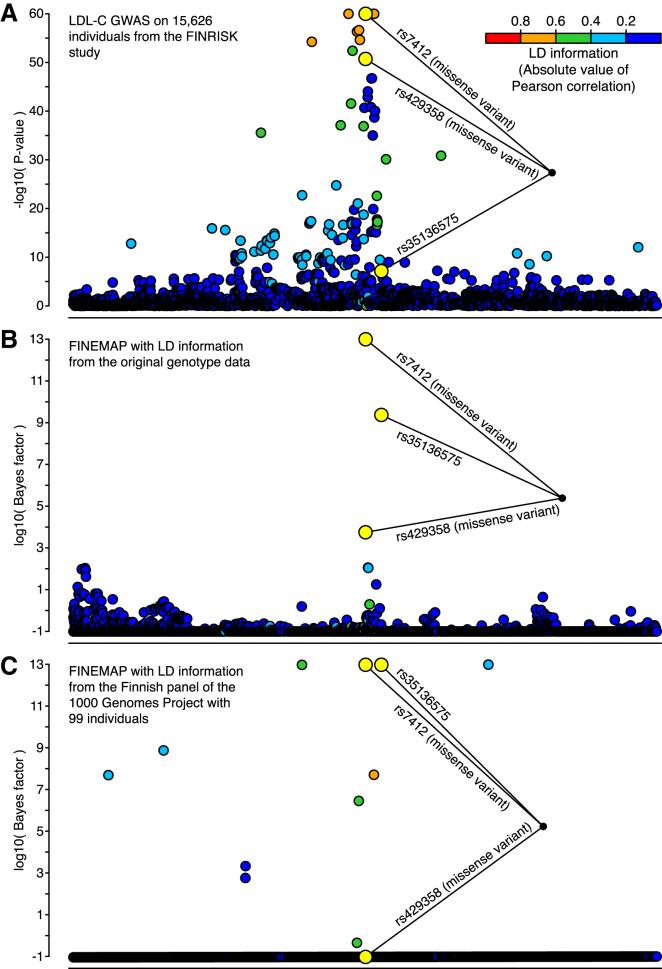
Recent fine-mapping efforts in Sardinians (n = 5,524)⁴⁶ and Finns (n = 12,834)³⁷ have concluded that the association is explained by the two well-known missense variants rs7412 and rs429358, which together define APOE ε-alleles. Our results (Figure 2A) suggest that in addition to the two known missense variants, a third SNP, rs35136575, is needed to explain the association (Figure 2B and Table 1), which agrees with an earlier study targeting the APOE locus.⁴⁷ The association pattern with three variants (rs7412, rs429358, and rs35136575) has the highest posterior probability (0.342) and is almost seven times larger than the second-most-probable (0.051) configuration, which included a fourth SNP (rs2722693). rs7412, rs429358, and rs35136575 have by far the most evidence of being causal (Figure 2B and Table 1). A standard conditional analysis identified the same association pattern with three variants, giving a conditional p value of 5.8 × 10⁻¹³ for rs35136575 when the two missense variants (rs7412 and rs429358) were included in the model and thus verifying the results of FINEMAP (the marginal p value of rs35136575 was 7.1 × 10⁻⁸; Table 2).

Figure 2.

Fine-Mapping the APOE Region Associated with LDL-C

Results are shown for 3,078 variants with a MAF above 1% and covering 1 Mb of the genome. Variants identified by a standard conditional analysis are highlighted in yellow. All other variants are colored with respect to their LD (absolute value of Pearson correlation) with the lead variant rs7412.

(A) Negative log₁₀ p values for each variant from a LDL-C GWAS on 15,626 individuals from the FINRISK study.

(B) Bayes factor (log₁₀) for assessing the causality of each variant by a FINEMAP analysis using the summary statistics from the LDL-C GWAS and the LD information from the original genotype data.

(C) Bayes factor (log₁₀) for assessing the causality of each variant by a FINEMAP analysis using the summary statistics from the LDL-C GWAS and the LD information from the reference genotypes of 99 Finns in the 1000GP.

Table 1.

Top Ten Variants from FINEMAP Analysis of the APOE Region with Summary Statistics from the LDL-C GWAS on 15,626 Individuals and Two Sources of LD Information

LD Information from Original Genotype Data		LD Information from the Finnish 1000GP Panel of 99 Individualsa
Variant	Posterior Probability of Being Causal	Variant	Posterior Probability of Being Causal
rs7412b	1.0000	rs7412b	1.0000
rs35136575b	1.0000	rs35136575b	1.0000
rs429358b	0.8255	rs117789739	1.0000
rs483082	0.0878	rs10418198	1.0000
rs438811	0.0853	rs75627662	1.0000
rs2722693	0.0833	rs11665929	1.0000
rs2571177	0.0740	rs141622900	1.0000
rs2734453	0.0690	rs111294029	1.0000
rs2734457	0.0663	rs61679753	0.9996
rs12984506	0.0342	rs8108277	0.6581

^aThe posterior probability that rs429358 is causal is smaller than 0.0004.

^bVariants identified by a standard conditional analysis.

Table 2.

Marginal and Conditional p Values from the LDL-C GWAS of the APOE Region with 15,626 Individuals from the FINRISK Study

Variant	Marginal p Value	p Value after Conditioning on rs7412	p Value after Conditioning on rs7412 and rs429358
rs7412	2.4 × 10−137	–	–
rs429358	1.9 × 10−51	8.2 × 10−36	–
rs35136575	7.1 × 10−8	1.4 × 10−17	5.8 × 10−13

Next, we assumed that we did not have access to the original genotype data, and we used the reference genotypes from the Finnish 1000GP panel with 99 individuals to obtain LD information. The Finnish 1000GP panel showed that the two most probable configurations included ten variants and already covered 99% of the total posterior probability (Figure 2C and Table 1). The posterior probability that rs7412 and rs35136575 were causal was still among the largest of all variants, but that of rs429358 was very small, and some low-frequency variants that showed little evidence from the original genotype data now showed decisive evidence (Figure 2C). Clearly, the Finnish 1000GP panel does not accurately approximate the LD information of the original genotype data, in that it causes several false-positive and one false-negative result in comparison with the original data. Similar problems remained when we extended the reference panel to contain all 503 European individuals of the 1000GP (Figure S2).

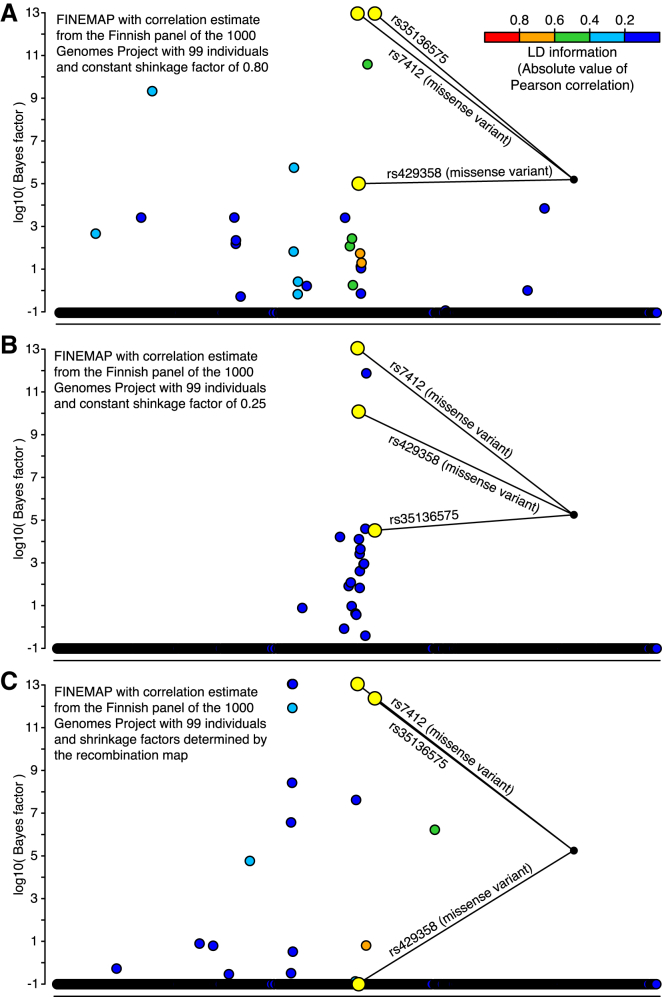
We also investigated shrinkage estimation of correlations from the Finnish 1000GP panel. Even though the constant shrinkage clearly increased detection of causal variants, it still led to an inflated FPR and therefore could not solve the problem of small panel size (Figures 3A and 3B). The recombination shrinkage had little effect on the correlation estimates of variants very close to each other and therefore did not improve the results in our fine-mapping application (Figure 3C). For example, with recombination shrinkage, we observed that the top configuration already covered 98% of the total posterior probability, and it included two SNPs (rs143695016 and rs2967668) that are very close to each other (111 bp). These two SNPs are much more highly correlated in the Finnish panel of 1000GP (r = 0.920) than in our GWAS data (r = 0.805). Recombination shrinkage had little effect on their correlation (shrinkage r = 0.919) because the SNPs are so close to each other. This explains why the fine-mapping model takes both SNPs as causal: it can make the observed summary statistics of the SNPs (Z scores of 1.9 and 10.0) consistent with the overestimated correlation from the panel only by stipulating that both SNPs have causal effects.

Figure 3.

Fine-Mapping the APOE Region Associated with LDL-C by Using Shrinkage Estimation of Correlations from the Finnish 1000GP Panel with 99 Individuals

Bayes factors (log₁₀) are shown from a FINEMAP analysis of 3,078 variants with a MAF above 1% and covering 1 Mb of the genome. GWAS summary statistics were computed with 15,626 individuals from the FINRISK study. Variants identified by a standard conditional analysis are highlighted in yellow. All other variants are colored with respect to their LD (absolute value of Pearson correlation) with the lead variant rs7412.

(A) The same constant shrinkage factor of 0.80 was used for all correlations.

(B) The same constant shrinkage factor of 0.25 was used for all correlations.

(C) Recombination distance was used to define the shrinkage factor for each pair of variants.

100 GWAS Regions in Finnish Data

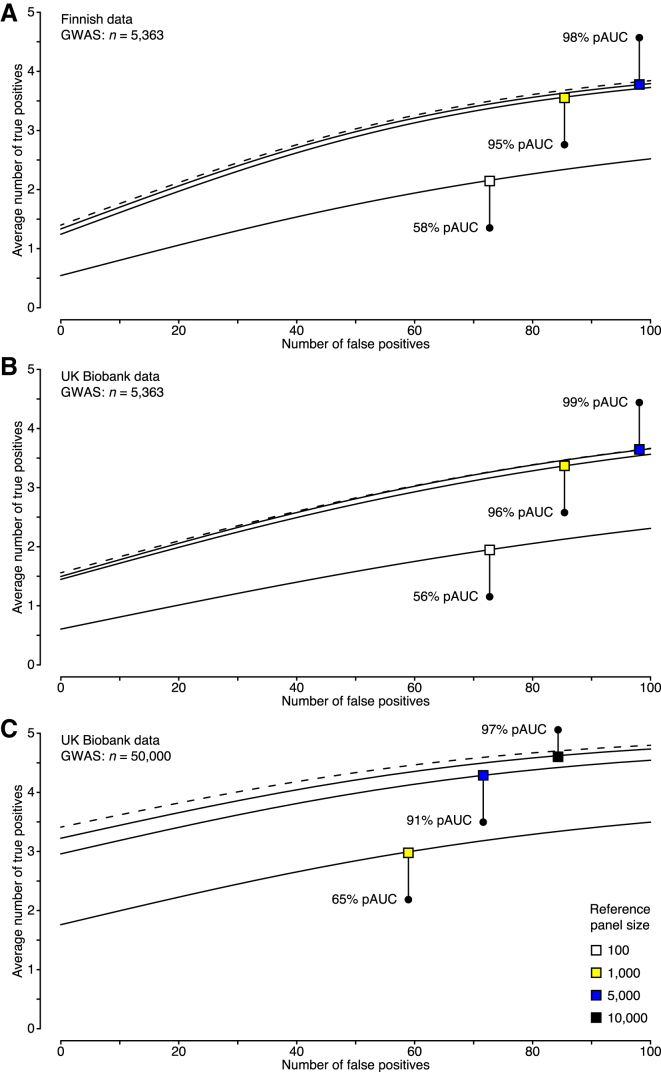
Using the datasets on the 100 GWAS regions, we evaluated how well the external FINRISK reference panels of different sizes performed in comparison with the original LD information from NFBC1966. Reference panels of 100 individuals achieved only 58% of the performance of the original genotype data, as measured by the relative pAUC measure, whereas panels of 1,000 individuals achieved very good performance (95% relative pAUC; Figure 4A). No considerable improvement was obtained with larger reference panels. These results suggest that a reference panel of 1,000 individuals is sufficient when summary statistics originate from a GWAS with a few thousand individuals, which is a typical sample size of an individual cohort in many current GWAS meta-analyses.^{48, 49}

Figure 4.

Fine-Mapping Accuracy on Simulated Data

In simulations with Finnish data, genotype data over 100 GWAS regions on 5,363 individuals from NFBC1966 were used for phenotype generation. In UKBB simulations, genotype data on 82,199 individuals covering the ABO region were used for phenotype generation. Each dataset included five causal SNPs with effect sizes that resulted in statistical power of 0.5 with 5,363 individuals at a significance level of 5 × 10⁻⁸. Results with different LD information are shown in plots of the number of selected causal SNPs (true positives) against the number of selected non-causal SNPs (false positives); the list of SNPs was ranked by their posterior probability of being causal. Reference genotype panels (solid line) are compared with the original genotype data (dashed line) with respect to the achieved partial area under the curve (pAUC). pAUCs and curves are averaged over the simulated datasets.

(A) Accuracy with NFBC1966 summary statistics from a GWAS on 5,363 individuals and LD information either from the original genotype data or from a subset of the reference genotype data on FINRISK individuals.

(B) Accuracy with UKBB summary statistics from a GWAS on 5,363 individuals and LD information either from the original GWAS data or from a subset of UKBB individuals not included in the GWAS.

(C) Accuracy with UKBB summary statistics from a GWAS on 50,000 individuals and LD information either from the original GWAS data or from a subset of UKBB individuals not included in the GWAS.

Although applying a constant shrinkage factor to correlation estimates from the reference panels with 100 individuals clearly increased detection of causal SNPs (from 58% up to 80% relative pAUC), it also led to an inflated FPR and therefore could not solve the problem of small panel size (Figure S3). For larger panels, the constant shrinkage factor did not improve performance and with large shrinkage factors even reduced it (from 95% to 85% relative pAUC; Figure S3). The shrinkage factors determined by the recombination map had little effect on the correlation estimates of SNPs very close to each other (see APOE results for an example) and therefore did not improve the results in our fine-mapping application in the way that has been reported among a sparser set of variants.¹⁹

UKBB Data

Our further investigations on large-scale biobank data revealed that the performance of fine-mapping does not only depend on the reference-panel size but also on the GWAS sample size, which to our knowledge is a new result. We used genotype data on up to 50,000 UKBB individuals to simulate phenotype data, and we used UKBB genotype data not included in the phenotype simulation as external reference panels of different sizes. Our results confirmed that reference panels of 1,000 individuals are large enough for a GWAS of about 5,000 individuals (Figure 4B) up to 10,000 individuals (Figure S4). For a GWAS of 50,000 individuals, reference panels of 1,000 and 5,000 individuals achieved, respectively, 65% and 91% relative pAUC (Figure 4C), whereas very good performance (97% relative pAUC) required reference panels of at least 10,000 individuals (Figure 4C). In particular, a reference panel of 1,000 individuals is not large enough for a GWAS of 50,000 individuals anymore, and this issue cannot be solved by shrinkage methods (Figure S5). Therefore, an important message for future fine-mapping efforts on large GWAS meta-analyses and biobank collections is that the size of the reference panel must scale with the GWAS sample size. Given that for identical GWAS sample sizes we achieved very similar fine-mapping performance with the UKBB data (Figure 4B), as with our earlier comprehensive simulation over 100 GWAS regions in the Finnish data (Figure 4A), we expect that our UKBB results represent well the average performance over the genome also for the larger sample sizes.

We also evaluated how the LD information affects the size and coverage of credible sets of causal variants. Table S1 shows that the small reference panels (d = 100 individuals) provide smaller credible sets than the larger reference panels or the original genotype data, and this phenomenon is amplified with increasing GWAS sample size. Importantly, the coverage of the credible sets from the small reference panels is much lower than the nominal coverage (Table S2). For example, with a GWAS sample size of n = 50,000 and reference-panel size of d = 100, the 99% credible sets cover on average only about 17% of the causal SNPs, which gives a misleading picture of fine-mapping accuracy. For larger reference panels (d = 5,000 individuals) and original genotype data, the coverage of credible sets is close to the nominal probability of the credible sets, indicating a good probabilistic calibration (all 90% credible sets have at least 90% coverage).

Consequences of Inaccurate LD Information

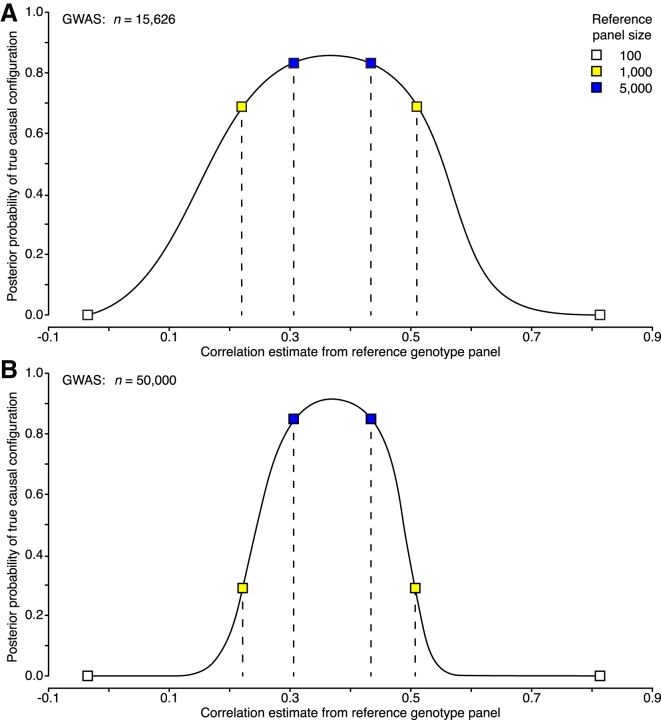
Thus far, we have empirically shown that inaccurate LD information can result in misleading inferences. In Appendix A, we also show theoretically why, for a fixed reference panel, this phenomenon gets more pronounced as the GWAS sample size grows and why the detrimental effect of growing GWAS sample size on fine-mapping could be compensated, at least asymptotically, if the size of the reference panel grew proportionally to the GWAS sample size. This theoretical result is empirically supported by the behavior of posterior probabilities for a pair of variants of which one is causal (C) and the other is non-causal (N). Figure 5 shows that for a reference panel of 1,000, with 95% probability, the posterior of the true causal configuration is above 0.7 for a GWAS size of 15,626 individuals (corresponding to our APOE dataset). Conversely, for a larger GWAS of 50,000 individuals, the corresponding lower bound for the probability of the true causal configuration has already dropped down to 0.3, leading to a wrong conclusion about the top causal configuration.

Figure 5.

Effect of Reference-Panel Size and GWAS Sample Size on Fine-Mapping Performance

Results are shown for a pair of variants (MAF of 2%) of which one is causal and the other is non-causal and whose correlation is 0.37. The effect size of the causal variant is such that the statistical power with 15,626 individuals is approximately 0.5 at a significance level of 5 × 10⁻⁸. The probability of the true causal configuration is plotted on the y axis. The x axis shows the estimated correlation of the variants from a reference genotype panel. The central 95% probability interval (dashed line) of the sampling distribution is shown for different reference genotype panels.

(A) GWAS summary statistics were computed with 15,626 individuals.

(B) GWAS summary statistics were computed with 50,000 individuals.

To explain the results of inaccurate LD information, consider first the case where the two variants are highly correlated in the GWAS data but the reference panel considerably underestimates their correlation. Then, the fine-mapping model takes the variants as almost independent and wrongly labels N causal as well. If their correlation is, however, accurately estimated by the reference panel, then by applying a large constant shrinkage factor, we will considerably underestimate the correlation and again cause a false positive. Second, if the two variants are only moderately correlated in the GWAS data but the reference panel considerably overestimates the magnitude of the correlation, then we can make the observed summary statistics of the variants consistent with their reference-panel correlation only by stipulating that both variants have causal effects, which again wrongly labels N as causal. In this case, if the two variants are very close to each other, then the shrinkage determined by a recombination map has little effect on the correlation estimate and does not remove the false positive.

LDstore

On the basis of our results, we expect that the biomedical research community needs to start sharing LD information in conjunction with GWAS summary statistics²¹ to fully exploit the rapidly growing GWAS sample sizes. To enable this, we introduce LDstore, a software tool for efficient estimation, storage, and sharing of LD information. LDstore uses parallel computing and sparse storage of LD information to achieve small file sizes. For example, processing a genomic region with 5,000 variants completed in less than 30 s on an off-the-shelf desktop computer and required less than 100 MB of disk space. Processing 500,000 variants completed in less than 10 min with 576 parallel processes and required 150 GB of disk space, whereas the naive approach required 1,000 GB. Importantly, LDstore outputs indexed binary files and uses hash tables to achieve fast lookups of LD information irrespectively of file size (it takes 1 min to lookup 5,000 variants from binary files that contain either 50,000 or 500,000 variants).

Discussion

A utilization of summary statistics from large international meta-analyses and biobanks has rapidly become an active research area in genetics.²¹ A good example is statistical fine-mapping, a central step for transforming GWAS results into molecular mechanisms behind the associations. Recently, several fine-mapping methods that can work on summary statistics have been proposed,^{11, 12, 13, 14, 15, 16, 17, 18, 19, 20} but their practical performance has not been thoroughly evaluated. In this work, we assessed the limits of reliable fine-mapping of causal variants from summary statistics by using an external reference panel as a source of LD information.

We established that for a typical GWAS cohort containing up to 10,000 individuals, a reference panel of 1,000 individuals from the study population (Finland or the UK in our examples) is adequate, whereas a reference panel of about 100 individuals from the study population (e.g., 1000GP data) is too small and should not be used. We demonstrated this by a comprehensive assessment of over 100 GWAS regions and by detailed fine-mapping of the association between the APOE locus and LDL-C, from which we identified an additional variant on top of the two well-known missense variants.

We also showed that the size of the reference panel must scale with the GWAS sample size. Although a panel of 1,000 samples is adequate for a GWAS sample size of 10,000, a panel of 10,000 samples is needed for a GWAS sample size of 50,000. This result has important consequences for ongoing large meta-analysis efforts and biobank studies. We confirmed the result in three ways: empirically through simulations, analytically through likelihood evaluations, and theoretically through mathematical derivation.

In our analyses, we used FINEMAP software,¹⁶ which is based on a stochastic search algorithm. We verified that the results of FINEMAP were consistent across separate runs when the LD information provided a good approximation of the LD information from the original genotype data. We also observed that inaccurate LD information or mismatches in the allele coding between the reference panel and GWAS data could lead to an inflation of false positives and also to an inconsistency between the FINEMAP results across separate runs. Such problems typically manifest when the posterior probability of the number of causal variants concentrates on the maximum value possible and can therefore be detected by comparison of several FINEMAP runs that allow for increasing numbers of causal variants.

All existing fine-mapping methods that use summary statistics,^{12, 13, 14, 15, 16, 17, 18, 19, 20} including GCTA’s conditional analysis,¹¹ share the challenges arising from inaccurate LD information. In several other contexts, shrinkage methods have proven useful for LD estimation.^{9, 19, 27} We evaluated both the constant shrinkage method and a recombination shrinkage method^{19, 27} that takes into account varying levels of LD between pairs of variants. Although the shrinkage methods did improve the performance of fine-mapping for small reference panels, a large number of false positives still remained, and we conclude that the current shrinkage methods do not solve the LD-estimation problem. Therefore, it is crucial that the biomedical research community start sharing LD information with GWAS summary statistics.²¹ We have introduced LDstore, a software tool for efficient estimation, storage, and sharing of LD information. Next, we briefly outline how sharing LD information could be implemented within a GWAS consortium and, more generally, publicly through existing web portals.

Consider first a GWAS meta-analysis. Until now, fine-mapping has been carried out (1) by meta-analysis of stepwise conditioning results from participating cohorts, which requires multiple rounds of time-consuming coordination between the cohorts;⁵⁰ (2) with the use of meta-analyzed summary statistics under the simplified assumption of a single causal variant in the genomic region;^{48, 49} or (3) with the use of an external reference panel for obtaining LD information,⁵¹ which, according to our results, might be inaccurate. Using LDstore to collect LD information for the trait-associated genomic regions across the cohorts only once could enable accurate fine-mapping from summary statistics and thus allow multiple causal variants without time-consuming communication and repeated analysis efforts across the participating cohorts.

Some consortia have already built web portals (e.g., Type 2 Diabetes Knowledge Portal or IBD Exomes Browser; see Web Resources) that allow an external researcher to browse and download the summary statistics. With LDstore, such web portals could further enable the researcher to download LD information for genomic regions by using either pre-computed or on-the-fly computed files. Similarly, with LDstore, large-scale multi-population reference collections of sequencing data (e.g., Haplotype Reference Consortium⁵² or Genome Aggregation Database⁵³) could extend their web services to provide LD information for researchers working with summary statistics without a possibility of accessing the original genotype data. Our results show that even though a reference panel will never achieve the optimal fine-mapping performance given by the original individual-level GWAS data, a reference panel can still perform well under the assumption that it originates from the relevant population and has a size comparable to the GWAS sample size.

On the basis of our results, we anticipate that widespread sharing of LD information will become crucial for the successful exploitation of rapidly accumulating GWAS summary statistics. With this in mind, we introduce LDstore and encourage additional concrete steps to make the sharing of LD information commonplace in genetics research.

Conflicts of Interest

C.B. and M.P. collaborated with Genomics plc (http://www.genomicsplc.com) when preparing this work. M.P. has provided consultancy services for Genomics plc.

Published: September 21, 2017

Appendix A

Here, we will show that the performance of fine-mapping depends not only on the reference-panel size d but also on the GWAS sample size n. Consider a pair of variants of which one is causal (C) and the other is non-causal (N). Following our earlier work,¹⁶ for a large GWAS sample size n, standardized genotypes, and small causal effects typical in GWASs, the maximum-likelihood estimator of the causal effects $\mathit{\lambda }$ is $\hat{\mathit{\lambda }}=\mathit{\lambda }+{\mathit{\epsilon }}_{\lambda }/\sqrt{n}$, where $p\left({\mathit{\epsilon }}_{\lambda }\right)=\mathcal{N}\left({\mathit{\epsilon }}_{\lambda }|0,{\hat{\mathit{R}}}^{-1}\right)$ and $\hat{\mathit{R}}$ is the empirical Pearson correlation matrix between the two variants estimated in the GWAS data. The Z scores of the two variants are computed as

$$\hat{\mathit{z}}=\left[\begin{array}{c}{\hat{z}}_C\\ {\hat{z}}_N\end{array}\right]=\sqrt{n}\hat{\mathit{R}}\hat{\mathit{\lambda }}=\sqrt{n}\left[\begin{array}{cc}1& \hat{\rho }\\ \hat{\rho }& 1\end{array}\right]\left[\begin{array}{c}{\hat{\lambda }}_C\\ {\hat{\lambda }}_N\end{array}\right].$$

We use a binary indicator vector $\mathit{\gamma }$ to indicate whether a variant is causal $\left(\gamma =1\right)$ and to define three causal configurations:

$${\mathit{\gamma }}_{10}=\left({\gamma }_C=1,{\gamma }_N=0\right),{\mathit{\gamma }}_{01}=\left({\gamma }_C=0,{\gamma }_N=1\right),\text{and}{\mathit{\gamma }}_{11}=\left({\gamma }_C=1,{\gamma }_N=1\right).$$

As in our earlier work,¹⁶ assume that, a priori,

$$\text{Pr}\left(\text{no}\text{.}\text{of}\text{causal}\text{variants}\text{is}1\right)=2/3$$

and

$$\text{Pr}\left(\text{no}\text{.}\text{of}\text{causal}\text{variants}\text{is}2\right)=1/3$$

and that the prior is divided equally among the configuration with the same number of causal variants $k={\gamma }_C+{\gamma }_N$. That is, $\text{Pr}\left({\mathbf{\gamma }}_{10}\right)=1/3$, $\text{Pr}\left({\mathit{\gamma }}_{01}\right)=1/3$, and $\text{Pr}\left({\mathit{\gamma }}_{11}\right)=1/3$.

We now derive an expression for the posterior odds, $\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)/\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)$, of the true causal configuration in relation to the configuration where both variants are causal when the correlation matrix $\tilde{\mathit{R}}$ between the two variants is estimated from a reference panel. The posterior odds are

$$\frac{\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)}{\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)}=\frac{\text{Pr}\left(\mathcal{D}|{\mathit{\gamma }}_{10}\right)}{\text{Pr}\left(\mathcal{D}|{\mathit{\gamma }}_{11}\right)}\frac{\text{Pr}\left({\mathit{\gamma }}_{10}\right)}{\text{Pr}\left({\mathit{\gamma }}_{11}\right)}=\frac{\text{Pr}\left(\mathcal{D}|{\mathit{\gamma }}_{10}\right)}{\text{Pr}\left(\mathcal{D}|{\mathit{\gamma }}_{11}\right)}=\frac{\text{BF}({\mathit{\gamma }}_{10}:{\mathit{\gamma }}_{00})}{\text{BF}({\mathit{\gamma }}_{11}:{\mathit{\gamma }}_{00})}=\frac{\mathcal{N}\left({\hat{z}}_C|\mathrm{0,1}+n{s}_{\lambda }^2\right)}{\mathcal{N}\left({\hat{z}}_C|\mathrm{0,1}\right)}\frac{\mathcal{N}\left(\hat{\mathit{z}}|0,\tilde{\mathit{R}}\right)}{\mathcal{N}\left(\hat{\mathit{z}}|0,\tilde{\mathit{R}}+n{s}_{\lambda }^2\tilde{\mathit{R}}\tilde{\mathit{R}}\right)},$$

where $s_{\lambda }^2$ is the prior variance for the causal effects; a derivation of the Bayes factor $\text{BF}\left(\mathit{\gamma }:{\mathit{\gamma }}_{00}\right)$ as a ratio of marginal likelihoods can be found in our earlier work.¹⁶ After both ratios are simplified, the logarithm of the posterior odds is

$$\text{log}\left\{\frac{\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)}{\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)}\right\}=-0.5\text{log}\left\{1+n{s}_{\lambda }^2\right\}+0.5\frac{{\hat{z}}_C^2}{1+1/\left(n{s}_{\lambda }^2\right)}+0.5\text{log}\text{det}\left({\mathit{I}}_2+n{s}_{\lambda }^2\tilde{\mathit{R}}\right)-0.5{\hat{\mathit{z}}}^{\text{T}}{\left({\mathit{I}}_2/\left(n{s}_{\lambda }^2\right)+\tilde{\mathit{R}}\right)}^{-1}\hat{\mathit{z}}.$$ (Equation A1)

We rewrite the third term by computing the determinant as follows:

$$\text{logdet}\left({\mathit{I}}_2+n{s}_{\lambda }^2\tilde{\mathit{R}}\right)=\text{logdet}\left(\left[\begin{array}{cc}1+n{s}_{\lambda }^2& n{s}_{\lambda }^2\tilde{\rho }\\ n{s}_{\lambda }^2\tilde{\rho }& 1+n{s}_{\lambda }^2\end{array}\right]\right)=\text{log}\left\{{\left(1+n{s}_{\lambda }^2\right)}^2-{\left(n{s}_{\lambda }^2\tilde{\rho }\right)}^2\right\}.$$

We also combine it with the first term:

$$\begin{array}{c}-\text{log}\left\{1+n{s}_{\lambda }^2\right\}+\text{logdet}\left({\mathit{I}}_2+n{s}_{\lambda }^2\tilde{\mathit{R}}\right)=\text{log}\left\{\frac{{\left(1+n{s}_{\lambda }^2\right)}^2-{\left(n{s}_{\lambda }^2\tilde{\rho }\right)}^2}{1+n{s}_{\lambda }^2}\right\}\\ =\text{log}\left\{1+n{s}_{\lambda }^2\left[1-\frac{{\tilde{\rho }}^2}{1+1/\left(n{s}_{\lambda }^2\right)}\right]\right\}\\ =\text{log}n+\text{log}\left\{\frac{1}{n}+s_{\lambda }^2\left[1-\frac{{\tilde{\rho }}^2}{1+1/\left(n{s}_{\lambda }^2\right)}\right]\right\}.\end{array}$$

Next, we simplify the quadratic form:

$$\begin{array}{c}{\hat{\mathit{z}}}^{\text{T}}{\left({\mathit{I}}_2/\left(n{s}_{\lambda }^2\right)+\tilde{\mathit{R}}\right)}^{-1}\hat{\mathit{z}}=\left[\begin{array}{cc}{\hat{z}}_C& {\hat{z}}_N\end{array}\right]{\left[\begin{array}{cc}1+\frac{1}{n{s}_{\lambda }^2}& \tilde{\rho }\\ \tilde{\rho }& 1+\frac{1}{n{s}_{\lambda }^2}\end{array}\right]}^{-1}\left[\begin{array}{c}{\hat{z}}_C\\ {\hat{z}}_N\end{array}\right]\\ =\left[\begin{array}{cc}{\hat{z}}_C& {\hat{z}}_N\end{array}\right]\left[\begin{array}{cc}1+\frac{1}{n{s}_{\lambda }^2}& -\tilde{\rho }\\ -\tilde{\rho }& 1+\frac{1}{n{s}_{\lambda }^2}\end{array}\right]\left[\begin{array}{c}{\hat{z}}_C\\ {\hat{z}}_N\end{array}\right]/\left({\left[1+\frac{1}{n{s}_{\lambda }^2}\right]}^2-{\tilde{\rho }}^2\right)\\ =\left({\hat{z}}_C^2+\frac{{\hat{z}}_C^2}{n{s}_{\lambda }^2}-2{\hat{z}}_C{\hat{z}}_N\tilde{\rho }+{\hat{z}}_N^2+\frac{{\hat{z}}_N^2}{n{s}_{\lambda }^2}\right)/\left({\left[1+\frac{1}{n{s}_{\lambda }^2}\right]}^2-{\tilde{\rho }}^2\right).\end{array}$$

Substituting all simplifications in Equation A1 results in the following expression:

$$2\text{log}\left\{\frac{\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)}{\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)}\right\}=\text{log}n+\text{log}\left\{\frac{1}{n}+s_{\lambda }^2\left[1-\frac{{\tilde{\rho }}^2}{1+1/\left(n{s}_{\lambda }^2\right)}\right]\right\}+\frac{{\hat{z}}_C^2}{1+1/\left(n{s}_{\lambda }^2\right)}-\left({\hat{z}}_C^2+\frac{{\hat{z}}_C^2}{n{s}_{\lambda }^2}-2{\hat{z}}_C{\hat{z}}_N\tilde{\rho }+{\hat{z}}_N^2+\frac{{\hat{z}}_N^2}{n{s}_{\lambda }^2}\right)/\left({\left[1+\frac{1}{n{s}_{\lambda }^2}\right]}^2-{\tilde{\rho }}^2\right).$$ (Equation A2)

For a large GWAS sample size n, $\hat{\rho }=\rho +{\epsilon }_{\hat{\rho }}/\sqrt{n}$, where ρ denotes the value of the correlation in the underlying population and $p\left({\epsilon }_{\hat{\rho }}\right)=\mathcal{N}\left({\epsilon }_{\hat{\rho }}|\mathrm{0,1}-{\rho }^2\right)$ with ${\epsilon }_{\hat{\rho }}/\sqrt{n}\to 0$, and we can approximate $\hat{\mathit{z}}\approx \sqrt{n}\mathit{R\lambda }$. For a large reference panel with size d, $\tilde{\rho }=\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}$, where $p\left({\epsilon }_{\tilde{\rho }}\right)=\mathcal{N}\left({\epsilon }_{\tilde{\rho }}|\mathrm{0,1}-{\rho }^2\right)$ with ${\epsilon }_{\tilde{\rho }}/\sqrt{d}\to 0$. We can therefore simplify the numerator in the last term in Equation A2 further:

$$\begin{array}{c}{\hat{z}}_C^2+\frac{{\hat{z}}_C^2}{n{s}_{\lambda }^2}-2{\hat{z}}_C{\hat{z}}_N\tilde{\rho }+{\hat{z}}_N^2+\frac{{\hat{z}}_N^2}{n{s}_{\lambda }^2}=n{\lambda }_C^2+\frac{{\lambda }_C^2}{s_{\lambda }^2}-2n{\lambda }_C^2\rho \left(\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}\right)+n{\lambda }_C^2{\rho }^2+\frac{{\lambda }_C^2{\rho }^2}{s_{\lambda }^2}\\ =n{\lambda }_C^2\left(1-[{\rho }^2+2\rho {\epsilon }_{\tilde{\rho }}/\sqrt{d}+{\epsilon }_{\tilde{\rho }}^2/d-{\epsilon }_{\tilde{\rho }}^2/d]\right)+\frac{{\lambda }_C^2}{s_{\lambda }^2}\left(1+{\rho }^2\right)\\ =n{\lambda }_C^2\left(1-{[\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}]}^2\right)+n{\lambda }_C^2{\epsilon }_{\tilde{\rho }}^2/d+\frac{{\lambda }_C^2}{s_{\lambda }^2}\left(1+{\rho }^2\right).\end{array}$$

Substituting this result into Equation A2 yields:

$$2\text{log}\left\{\frac{\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)}{\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)}\right\}=\text{log}n+\text{log}\left\{\frac{1}{n}+s_{\lambda }^2\left[1-\frac{{\left(\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}\right)}^2}{1+1/\left(n{s}_{\lambda }^2\right)}\right]\right\}+\frac{n{\lambda }_C^2}{1+1/\left(n{s}_{\lambda }^2\right)}-\frac{n{\lambda }_C^2\left(1-{\left[\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}\right]}^2\right)}{{\left(1+\frac{1}{n{s}_{\lambda }^2}\right)}^2-{\left(\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}\right)}^2}-\frac{n}{d}\frac{{\lambda }_C^2{\epsilon }_{\tilde{\rho }}^2}{{\left(1+\frac{1}{n{s}_{\lambda }^2}\right)}^2-{\left(\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}\right)}^2}-\frac{{\lambda }_C^2\left(1+{\rho }^2\right)/s_{\lambda }^2}{{\left(1+\frac{1}{n{s}_{\lambda }^2}\right)}^2-{\left(\rho +{\epsilon }_{\tilde{\rho }}/\sqrt{d}\right)}^2}.$$ (Equation A3)

For a large GWAS sample size n and reference-panel size d, we drop those terms in Equation A3 that remain bounded by a constant independent of n and d as n and d grow:

$$\text{log}\left\{\frac{\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)}{\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)}\right\}\approx \text{log}n-\frac{n{\lambda }_C^2{\epsilon }_{\tilde{\rho }}^2}{d\left(1-{\rho }^2\right)}.$$ (Equation A4)

When the error ${\epsilon }_{\tilde{\rho }}\approx 0$, the evidence in favor of the true causal configuration grows as logn. However, given the distribution of ${\epsilon }_{\tilde{\rho }}$, the expectation of ${\epsilon }_{\tilde{\rho }}^2$ is $\mathbb{E}\left[{\epsilon }_{\tilde{\rho }}^2\right]=\mathbb{V}\left[{\epsilon }_{\tilde{\rho }}\right]+\mathbb{E}{\left[{\epsilon }_{\tilde{\rho }}\right]}^2=1-{\rho }^2$, giving the expectation for the log posterior odds:

$$\mathbb{E}\left[\text{log}\left\{\frac{\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)}{\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)}\right\}\right]\approx \text{log}n-\frac{n}{d}\times {\lambda }_C^2.$$ (Equation A5)

We see that, asymptotically, the posterior probability $\text{Pr}\left({\mathit{\gamma }}_{10}|\mathcal{D}\right)$ of the true causal configuration is, on average, smaller than the probability $\text{Pr}\left({\mathit{\gamma }}_{11}|\mathcal{D}\right)$ that both variants are causal when the GWAS sample size n is much larger than the reference-panel size d. This indicates that false positives occur in this setting. On the other hand, if the reference-panel size is proportional to the GWAS sample size, then n/d is constant, and the probability of the true causal configuration becomes larger than that of the configuration with two causal variants as n grows. These properties of Equation A5 are in line with our results where the performance of correlation estimates from reference panels of 1,000 individuals is much worse for summary statistics from a GWAS on 50,000 individuals than for those from a GWAS on 5,363 individuals.

Web Resources

• FINEMAP, http://www.christianbenner.com

• FINRISK, https://www.thl.fi

• IBD Exomes Browser, http://ibd.broadinstitute.org

• IMPUTE2, http://mathgen.stats.ox.ac.uk/impute/impute_v2.html

• LDstore, http://www.christianbenner.com

• Northern Finland Cohorts, http://www.oulu.fi/nfbc

• OMIM, http://www.omim.org

• OpenMP, http://openmp.org

• Open MPI, http://www.open-mpi.org

• R, http://www.r-project.org

• SNPTEST2, http://mathgen.stats.ox.ac.uk/genetics_software/snptest/snptest.html

• Type 2 Diabetes Knowledge Portal, http://www.type2diabetesgenetics.org

• UKBB imputation, http://www.ukbiobank.co.uk/wp-content/uploads/2014/04/imputation_documentation_May2015.pdf