Abstract
A robust fully automated algorithm for identifying an arbitrary number of landmark points in the human brain is described and validated. The proposed method combines statistical shape models with trained brain morphometric measures to estimate midbrain landmark positions reliably and accurately. Gross morphometric constraints provided by automatically identified eye centers and the center of the head mass are shown to provide robust initialization in the presence of large rotations in the initial head orientation. Detection of primary midbrain landmarks are used as the foundation from which extended detection of an arbitrary set of secondary landmarks in different brain regions by applying a linear model estimation and principle component analysis. This estimation model sequentially uses the knowledge of each additional detected landmark as an improved foundation for improved prediction of the next landmark location. The accuracy and robustness of the presented method was evaluated by comparing the automatically generated results to two manual raters on 30 identified landmark points extracted from each of 30 T1-weighted magnetic resonance images. For the landmarks with unambiguous anatomical definitions, the average discrepancy between the algorithm results and each human observer differed by less than 1 mm from the average inter-observer variability when the algorithm was evaluated on imaging data collected from the same site as the model building data. Similar results were obtained when the same model was applied to a set of heterogeneous image volumes from seven different collection sites representing 3 scanner manufacturers. This method is reliable for general application in large-scale multi-site studies that consist of a variety of imaging data with different orientations, spacings, origins, and field strengths.
Keywords: Automated landmark detection, Morphometric measures, Statistical shape models, Principle component analysis
1. Introduction
Automated landmark detection can assist clinical procedures and accelerate research projects. In clinical applications, neurosurgeons often use landmarks from magnetic resonance imaging (MRI) data for planning a surgery. In research applications, a standardized orientation and placement of the anatomical objects (e.g., the anterior commissure (AC) and posterior commissure (PC)) is accomplished by rigid co-registration of landmarks (Horn, 1987). This initial registration step is critical in warping images to a common template space such as Talairach (Talairach and Tournoux, 1988) or MNI space (Mazziotta et al., 1995), that are frequently used in post-acquisition computerized image analysis. In automated image-processing schemes, anatomical landmarks are routinely used to run initial space normalization and obtain an initial linear transformation between a test volume and an atlas volume before performing high-dimensional nonrigid image registration (Kim and Johnson, 2013; Ghayoor et al., 2016; Kim et al., 2014; Pierson et al., 2011). The benefit of landmark initialization on high-dimensional warping has been reviewed in other works for both empirical registration results (Johnson et al., 2002, Christensen et al., 2003) and clinical relevance (Magnotta et al., 2003).
Manual identification of landmarks is labor-intensive, time-consuming, and suffers from intra-/inter-rater inconsistency. Consequently, several algorithms have been published for semi-automatic and automatic landmark detection (Bookstein, 1997; Frantz et al., 1999; Han and Park, 2004; Izard et al., 2006; Prakash, 2006; Vérard et al., 1997; Wörz and Rohr, 2005).
To overcome previous limitations, Ardekani and Bachman (2009) developed a fixed model-based algorithm for automatic AC and PC detection in 3D structural MRI scans that is not limited to operating on T1-weighted (T1W) images, and does not rely on successful localization of the corpus callosum and edge enhancement/detection, both of which can be problematic. Although an improvement on earlier approaches, their method relies on a narrowly defined a priori localization of the midbrain-pons junction (MPJ). An inaccurate a priori localization of the MPJ, a common issue in multi-site heterogeneous data sets, results in failure of this method.
This work presents automated steps to bypass the pitfalls of needing narrowly defined initial registration of the MPJ. The automatic method for landmark detection presented here combines flexible and scalable statistical shape models (Davies et al., 2010) and learned morphometric measures to provide reliable and accurate estimation of primary midbrain landmark points. This approach achieves robustness to large rotations in initial head orientation by extracting information regarding the eye centers using a radial Hough transform (Hough, 1959), and by estimating the centroid of head mass (CM) as described in a novel approach (Ghayoor et al., 2013).
Further, a linear model estimation using principle component analysis (Abdi and Williams, 2010) is employed to predict new landmarks using the knowledge of the already estimated primary landmarks. This model sequentially takes advantage of each additional landmark for a better prediction of the next landmark location, and it allows the localization of an arbitrary number of secondary landmarks in different regions of the human brain. Identification of additional landmarks directly benefit registration algorithms that use several manually identified cortical, cerebellar, and commissure landmarks for feature detection (Magnotta et al., 2003). Additional landmarks are also desirable in co-registration approaches. Kim and colleagues deomonstrated that having more automatically detected landmarks provide more accurate estimation of both linear transforms and low order spline-kernel transforms (Kim et al., 2011). Additionally, the ability to identify a large number of anatomical features provides alternative strategies for characterizing disease related morphometry (Toews et al., 2010). Automated landmark detection is also beneficial for initializing M-Reps (Pizer et al., 1999) and implicit surface initialization (Lelieveldt et al., 1999) by helping to find candidate edge points on boundaries, so as to automatically match the model to image data. All presented references have investigated the clinical importance of anatomical landmarks identification. As automated detection of landmarks has similar clinical benefits to manually selected landmarks, we do not explore the clinical relevance in this work but focused on evaluating comparisons of the automated method to the manual method.
The presented method was evaluated extensively using T1W MRI scans of the human brain and by comparison to localizations made by manual raters. The current implementation is specialized for landmark detection in MRI images of the human brain. However, the core algorithmic components of the presented constellation-based method would also be applicable for other modalities or can be customized for other landmark identification problems.
2. Materials and Methods
The method for automated landmark identification introduced in this paper makes no assumptions regarding the absolute intensity or sampling strategies used. Provided that the physical space meta data (i.e. spacing, voxel organization) is correct, no pre-processing is needed for model building data or test images.
In this section, first we present the details of the model building phase for generating statistical shape models, computing morphometric measures, and running a linear model estimation. Then, we follow with the details of the landmark detection phase for each of primary and secondary landmarks.
2.1 Model building phase
The model building phase of the proposed algorithm is an extension of the model-based training method described by Ardekani and Bachman (2009). The model building algorithm is applied to a set of representative model building datasets that include images and their respective manually annotated landmarks. The model building phase generates local intensity distribution surrounding each landmark in statistical shape models, which can be retrieved and applied later for the local search process during the detection phase. The model building extension involves two additional steps that collect complementary information to the intensity shape models. The proposed extensions improve the algorithm by providing more accurate and more robust search centers for the landmark detection before the intensity shape models are used for local search process.
First, morphometric measures and relationship information are collected for four mid-sagittal primary landmarks with prominent intensity localizations (Midpons junction-MPJ, Anterior Commisure-AC, Posterior Commisure-PC, and forth ventricle notch-VN4) and the left and right eyes. The extracted morphometric constrains are retrieved during the detection phase to provide robust initialization in the presence of large rotations in the initial head orientation.
The second step involves a linear model estimation using sequential principal components analysis (SPCA) for an arbitrary number of secondary landmark points. These secondary landmark points often have much larger intensity localization uncertainties (i.e. the precise location of the anatomical definition is not singularly obvious). The linear model finds principal components of each landmark and minimizes the least-squares estimation error. The “sequentially” aspect of SPCA indicates that this model uses the knowledge of all already estimated landmarks for a better prediction of additional landmarks. The model building steps are discussed in detail, as follows:
2.1.1 Building a statistical shape model for each landmark point
The mid-sagittal plane (MSP) is automatically estimated for each model building dataset by defining the plane that passes through annotated AC, PC, and MPJ landmarks, since these three non-collinear points are biologically defined as being close to the MSP.
A linear rigid-body transformation (rotation and translation) is applied to each of the model building datasets so that: a) the AC point is set as the origin, b) the AC to PC line lies on the image P-axis, c) the image S-axis points toward the top of the head, and d) the MSP lies on the L = 0 plane. At this step all model building datasets are aligned to a common space without resampling the original data (Lu and Johnson, 2010) by adjusting the image header physical space parameters (i.e., origin, and direction of the voxel lattice) in a new left-right, posterior-anterior, superior-inferior (LPS) coordinate system.
The linear rigid-body transformation, computed in step 2, is applied to all the manually identified landmarks.
-
A landmark template is a small cylindrical region that is centered on the position vector of the landmark point. The axes of these cylinders are parallel to the left-right axis to accommodate for increased locality uncertainty in the left-right direction. For each landmark (x), N cylindrical shape templates are created. First, the MSP-aligned model building images are rotated by N different angles (α) around the cylinder axis of the landmark template. Finally, for each angle of rotation, the average template vectors are computed over all model building images:
Where M is the number of model building datasets, and denotes the voxel values that fall in the cylindrical region centered around the xth landmark in ith model building image after undergoing a rotation of α degrees around the axis of the cylinder. The radius and height of each cylindrical template are specified as parameters to the model building program and should be customized for each landmark based on the landmark intensity localization uncertainty. Each template should be large enough to account for natural variations biological localization but should not be so large as to impede the computational efficiency or increase the false detection rate.(1) The extracted statistical shape information from the model building data is stored in a model file for use in the local search process during the detection phase. The statistical shape models are used for the local search around the landmark centers during the detection phase. The following two sections illustrate how the algorithm finds more promising search centers for the primary and secondary landmarks.
2.1.2 Storing morphometric measures for the primary landmark points
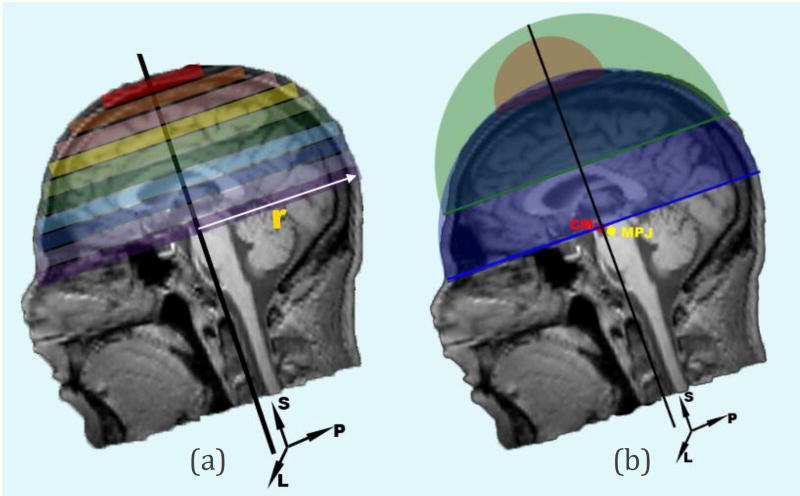
- Estimate the centroid of the head mass (CM) in the input model building images. This is estimated independently and needs no estimation of anatomical orientation. CM is estimated through a hemispherical approximation of the head volume after the tissue region is segmented from the noisy background using Otsu’s method (Otsu, 1979). The estimation process starts by scanning the foreground object slice by slice, superior to inferior. Then, for each slice, the volume of the hemisphere above the estimated cross section area as well as the foreground volume above the current slice are computed as shown in Figure 1. The process stops when the computed foreground volume above the current slice is greater than the estimated hemispherical volume:
Where Δ and ri are the thickness and the radius of each slice, respectively. Finally, CM is computed as the mass center of the last slice.(2) The midpoint of eye centers (MEC) is computed as the midpoint between the manually defined left eye (LE) and right eye (RE) landmarks.
The estimated CM and MEC points are transformed to the LPS coordinate system using the MSP-aligned transform computed in step two of section 2.1.1.
-
For each primary mid-sagittal landmark, the spatial relationship is represented by the mean of the displacement vectors between this landmark and the MPJ point in the estimated MSP-aligned space. Let denote the position vectors of the MPJ, CM, and the other primary landmarks, respectively, in the ith model building image after undergoing the MSP-aligned transform. These position vectors are measured in millimeters in the LPS coordinate system, with their origin at the AC point. Then, the mean displacement vectors between the MPJ and each landmark are computed over M datasets:
(3) (4) Additionally, the average angle between MEC to MPJ to AC/PC/VN4 is recoreded for use in the detection phase.
Figure 1.
Center of head mass (CM) is estimated through a hemispherical approximation of the head volume. (a) The estimation process starts by scanning the segmented head slice by slice, superior to inferior. (b) For each slice, the volume of the hemisphere above the estimated cross section area as well as the forground volume above the current slice are computed. The process stops when the computed foreground volume above the current slice is greater than the estimated hemispherical volume. Finally, CM is computed as the mass center of the last slice.
2.1.3 Linear model estimation of the secondary landmark points
Search centers for the secondary landmarks are detected one by one based on an sequentially approach such that each additional detected landmark contributes to finding the next landmark location. Therefore, a new linear estimation model is created for each landmark that utilizes the information of all the previously detected points. This implies ordering the landmarks before passing them through the model building phase, so that the most prominent and robust landmark is detected first, followed by the less robust landmarks. The sequential principle component analysis (SPCA) method consists of two model building phases: computing principal components and computing the linear model coefficients.
2.1.3.1 Phase One
The following information is collected from N model building datasets:
Landmark dimensions K (3D in this work).
Constellation of b primary landmarks .
Constellation of T secondary landmarks .
Where denotes landmark m from dataset n, and each is a K-by-1 vector; is the ith secondary landmark from nth the dataset.
A landmark vector space matrix X̌i is constructed for each secondary landmark:
| (5) |
| (6) |
Where si is the K-by-1 mean vector value of all vector elements, and Isi is a (b+i-2)-by-N matrix having all elements si.
Notice that is the reference landmark point that is subtracted from each to make the landmark vector space independent of the choice of reference frame in physical space. The midbrain-pons junction (MPJ) that is chosen as the reference landmark in this method due to the prominence of the MPJ as a brain landmark.
Isi regularizes the landmark vector space to have a zero mean to make the landmark vector space independent of the choice of model building dataset. For each landmark, si is saved to a file to be retrieved later in the detection phase.
PCA is applied to reduce the dimensionality of the landmark vector space X̌i, so that the representation is simplified and the processing time is reduced while essential basis is still preserved. Singular value decomposition (SVD) is used to compute the principle components of each X̌i matrix:
| (7) |
The columns of Wi represent the eigenvectors of X̌i. The objective is to reduced the dimensionality, so only first ri components are kept, where ri is set to the rank of the landmark vector space:
| (8) |
The output of this model building phase is a PCA-mapped landmark vector space Zi that is defined as:
| (9) |
Where is defined as a (b + i − 2) − by − ri matrix that is the first ri principal components of Wi, and Zi are denoted by an ri − by − N matrix.
Zi is passed to the second model building phase to compute the optimal linear model coefficients for each secondary landmark point.
2.1.3.2 Phase Two
First, for each secondary landmark, an N-by-K matrix Yi is defined as:
| (10) |
Where denotes the ith secondary landmark from the nth model building dataset. Again, the reference landmark is subtracted from the target landmark point in each dataset to make the vector space independent of the choice of physical reference frame. A linear relationship is computed between Yi and the corresponding PCA-mapped space for each secondary landmark point:
| (11) |
Where Ci is a ri − by − K matrix that can be optimized in terms of least squares:
| (12) |
The linear relationship matrix Mi is defined as:
| (13) |
Where Mi is a (b + i − 2)K − by − K matrix.
Finally, all the {Mi|i = 1, …, T} matrices corresponding to each secondary landmark are saved to a model file for use in the detection phase.
According to the matrices Mi and mean vector values si, the total number of parameters to be stored after the two model building phases is:
| (14) |
Which indicates a space complexity of the order O(k2T) scalars if the number of secondary landmarks is greater than the number of primary landmarks (T > b).
2.2 Landmark Detection Phase
Detection of landmarks is done by first identifying the primary landmarks, followed by identifying the secondary landmarks one by one in the same order as the SPCA model building process. In this work the MPJ was chosen as a reference point in estimation of the search center of other primary landmarks by a morphometric constraining approach. Once all primary landmarks are detected, they can be used as reference points to estimate secondary landmarks that have larger intensity localization uncertainties.
2.2.1 Primary Landmarks Detection
The centroid of the head mass (CM) is automatically detected using the same procedure as defined in 2.1.2, and acts as the search center for the MPJ landmark, MSP estimation process and eyes center detection.
-
MSP is automatically detected using a Powell’s optimizer (Powell, 1964) implemented by Brent’s method (Brent, 2013) to estimate parameters of a 3D rigid transform that maximize reflective correlation (RC) of the image intensity values across the MSP. A bounding box, centered on CM, is considered in the LPS coordinate system. If X and Y refer to all voxels in the left and right half of this bounding box, respectively, the voxel pairs xi ∈ X and yi ∈ Y satisfy (Lu, 2010):
Where ℒ, 𝒫, 𝒮 are the components of the voxel location in the LPS coordinate system, and PCM is the location of the centroid of the head mass. Then, the correlation between X and Y is:(14)
Where var(X) is the variance of X; var(Y) is the variance of Y; and cov(X, Y) is the covariance of X and Y.(15) Next, a Powell’s optimizer is used to find the parameter set with the maximum correlation coefficient. This parameter set consists of a translation t in the left-right direction, a rotation angle θ about the posterior-anterior direction, and a rotation angle ϕ about the superior-inferior direction. The MSP transform is used to find a roughly aligned image when there is little knowledge regarding most of the landmarks.
The input test image is respampled such that the detected MSP would lie on the L = 0 plane, and to have isotropic voxel dimensions matched to the dimensions used in the model building phase. This intermediate image is called the estimated image in MSP space or EMSP volume.
-
The MPJ landmark, is detected first by a local search around the CM point.
Local search
Each landmark location is finalized by a local search within a cylindrical region whose axis is parallel to the L-axis and is centered at the estimated search center of that landmark. The local search process is run in the Fourier domain.
First, extracting a region around the search center from the input EMSP volume forms a fixed image that is associated with a fixed mask defining the search bounds. In addition, the cylindrical templates of the target landmark are retrieved from the built model file and are used as moving template images.
Before computing the template matching, the intensities inside the masked regions of the fixed and template images are scaled to unity to reduce intensity heterogeneity across the test and model building MRI images and thereby improve numerical stability of the computations. The bounding masks are converted to label images (Lehmann, 2007); then, the image intensities are normalized within these labeled areas.
Finally, the best template matching is computed by finding the maximum correlation using a masked FFT normalized correlation method (Padfield, 2012).
Eye centers are detected by a radial Hough transform (Ballard, 1981). To detect adult human eyes, the estimated diameter of the eye is set to 24 mm (Rogers, 2010), and the normal adult inter-pupillary distance (IPD) is set to be between 40 mm to 80 mm (Dodgson, 2004). Eye centers are estimated as the locations with higher intensity values in an accumulator image generated over a region of interest that is defined as the region between two spherical sectors with the same center at the CM point and the same spread angle θ, but different radius, R1 > R2. By practical experiments, R1 and R2 are set to 120 mm and 30 mm respectively, and θ is set to 2.4 rad. This truncated sphere faces the anterior direction in the LPS coordinate system. After finding the first eye, a spherical exclusion zone is imposed around this point to avoid disturbance of the local maxima in the process of finding the other eye. Note that no local search is involved in estimating eye centers. Finally, MEC is computed as the midpoint of the estimated left and right eye landmarks.
-
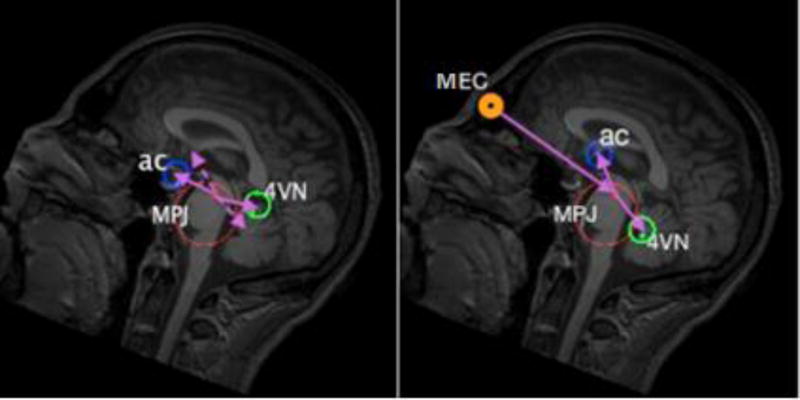
A morphometric constraining approach is used to estimate the search centers for the other primary landmarks (AC, PC, and VN4) from their morphometric relationships with MPJ and MEC. The mean displacement vectors P⃗mpj,x, x,∈{AC, PC, VN4}, computed in the model building phase, cannot be used immediately to find the search centers of the other primary landmarks because the computed displacement vectors are vulnerable to rotation differences between the test image space and the model building data space, as shown in Figure 2. To cancel the rotation error, the average angles subtended by MEC to MPJ to AC/PC/VN4 are computed from the average displacement vectors by the law of cosines (Heath, 1956).
This morphometric approach is performed based on anatomical relationships that all human brains share:- a similar angle subtended by MEC to MPJ to AC/PC/VN4.
- similar MPJ to AC/PC/VN4 landmark distances.
- VN4 is always inferior to the P⃗MPJ,MEC line on the estimated MSP plane, while AC and PC are always superior to this line.
- AC, PC, VN4, MPJ, and MEC are all very close to the MSP plane, so they have approximately the same L component in the LPS coordinate system.
The final location of AC, PC, and VN4 are found by a refinment local search (as described in step 4) around the preliminary estimated search centers.
Finally, to present the located landmarks in the coordinate system of the original test image, the inverse transformation of step (3) is applied to all detected landmarks and the MSP.
Figure 2.
Morphometric constraints provided by automatically identified eye centers and the center of the head mass provide robust initialization in the presence of large rotations in the initial head orientation. The average angles subtended by MEC to MPJ to AC/PC/VN4 are computed to cancel the rotation errors to provide an accurate estimation of the search centers for AC, PC and VN4. The left figure shows that the detected search centers for AC and VN4 (solid arrows) deviate from their anatomical locations (dashed arrows) because there is a rotation difference along the left-right direction between the test and model building image spaces (30 degrees in the presented image). This rotation difference has been compensated in the right figure, by considering the average MEC to MPJ to AC/VN4 angles.
2.2.2 Secondary Landmarks Detection
The search centers for the secondary landmarks are estimated by a linear model, using the knowledge of the current detected landmarks (including primary landmarks). The process is sequentially because each additional detected landmark is used to estimate subsequent landmarks. The sequential principle component analysis (SPCA) model created in the model building phase is used here to find the search centers of the secondary landmarks.
First, landmark search centers are estimated in the same order used in model building process:
| (16) |
Where the superscript t means that the landmark is related to the test image, and b is the number of midbrain primary landmarks (4 in this study). i varies from 1 to T according to T secondary landmarks.
Notice that Mi matrices are obtained from phase 2 of the model building process, and each Xi is a (b + i − 2)K − by − 1 matrix constructed as follows:
| (17) |
Where is a (b + i − 2)K − by − 1 vector having all elements si obtained in phase one of the model building process.
Finally, a local search is implemented around the estimated search centers to finalize the location of each secondary landmark, as described in step 4 of section 2.2.1. The search radius for each landmark is calculated as follows:
| (18) |
In this study the lower_bound is set to 1.6 mm by the experiments, and the upper_bound is set to maxerr, where meanerr, stderr, and maxerr are the mean, standard deviation and the maximum of the error distance between the estimated search centers and the locations of the landmarks in model building datasets in MSP-aligned space.
If the number of secondary landmarks is greater than the number of primary landmarks, the computation complexity is O(k2T2) scalar multiplications and O(k2T2) scalar additions, plus an additional time consuming T local search processes around each landmark search center.
3. Experiments and Results
3.1 Model building data
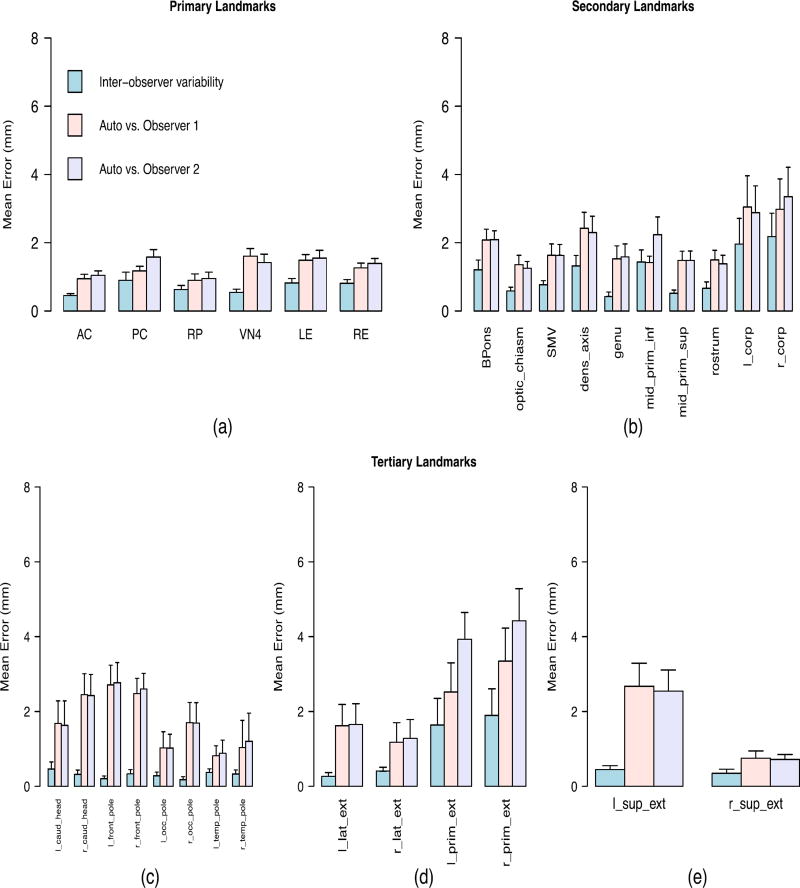
Model building process was run for a set of thirty landmarks, including 4 primary midbrain landmarks and the left and right eyes, that are mandatory in our implementation of this algorithm, and 24 arbitrary secondary landmarks annotated in different brain regions. All landmark names are depicted on the horizontal axis of Figure 3(a–e), and their full definitions can be found in the section A of the supplementary material.
Figure 3.
Inter-observer variability between the manual methods and discrepancy errors between the manually and automatically detected landmarks when the algorithm was applied to the single-site data that was collected from the same site as the training data. The full definition of all landmarks is presented in the first section of the supplementary material. (a) Primary landmarks: 3-D Euclidian distance was used as the error measurement. (b) Secondary landmarks with clear anatomical definitions: 3-D Euclidian distance was used as the error measurement. (c) Tertiary landmarks with high uncertainty in left-superior plane: Error was measured as distance in the anterior/posterior direction. (d) Tertiary landmarks with high uncertainty in posterior-superior plane: Error was measured as distance in the left/right direction. (e) Tertiary landmarks with high uncertainty in left-posterior plane: Error was measured as distance in the superior/inferior direction.
All model building image data were collected from a single site at the University of Iowa. All images were visually inspected and given a quality rating ranging from zero (unusable) to ten (best quality). Only images that received the best quality rating were included in the model building process. Each scan used for the model building was acquired from a different human subject. In total, 175 image datasets were selected for the model building process.
Manual identification of 30 landmarks in all model building images is very time consuming, so the model building datasets were created using an automated process. First, an expert rater manually annotated landmarks on an atlas (reference) image. Then, transformations from each model building image to the atlas image were derived using the symmetric image normalization (SyN) registration method (Avants et al., 2008). The inverse of the computed transformations were then used to propagate all manually annotated landmark points from the reference atlas space to each subject’s image space.
Theoretically, there is no limitation on the number of datasets needed to build the model file, but using more samples in model building process should help to reduce the average error in annotation of the landmarks locations that is caused by the human factor and by the registration error in propagating the annotated points.
Finally, a model was built using the provided datasets based on the process explained in section 2.1. To generate the statistical shape models, the radius and height of each template cylinder were set to 5 mm and 10 mm, respectively if the landmark has a clear anatomical definition (landmarks depicted on the x-axis of Figures 3a and 3b). Template sizes were set to 8 mm and 16 mm for the remainder of landmarks, which have larger intensity localization uncertainties.
3.2 Evaluation data
Thirty datasets were used to evaluate the method. Each evaluation dataset consisted of one imaging dataset and two sets of 30 landmarks annotated manually independently by two expertly trained raters. Evaluation images were acquired from different human subjects, and are mutually exclusive from the images used for the model building process. All imaging data were acquired via equivalent MRI protocols for the T1-weighted images. The images were considered as two categories: single-site data and multi-site data.
Single-site data consisted of 20 imaging datasets collected at the University of Iowa, all acquired from the same scanner with the same scanning protocol. Multi-site data consisted of 10 additional imaging datasets collected at 7 different collection sites with different scanner types. A detailed list of the collection sites and the scanning protocols for all the evaluation datasets is provided in the section F of the supplementary material.
3.3 Quantitative evaluation
Evaluation of accuracy used 20 single-site data collected from the same site and scanner protocol as the model building data. Evaluation of robustness used same generated model applied to a set of 10 heterogeneous data from external sites and scanners.
3.3.1 Accuracy evaluation
In order to evaluate the accuracy of the proposed method, the generated model was applied on the single-site data. Then, the average discrepancy was measured over all evaluation data between the locations of automatically detected and manually annotated landmarks. The computed error for each landmark was then compared with the inter-observer variability between the manual annotations. The error measurement criteria differed for different landmark types. Landmarks were considered in three categories in this regard:
The first category consisted of the primary landmarks that are anatomical points with high biologically relevant localization certainty. 3-D Euclidian distance in millimeters was used as the measure of error for the primary landmarks, which are listed on the x-axis of Figure 3(a).
The same measurement criterion was used for second category of landmarks, which have clear anatomical definitions but greater uncertainties than the primary landmarks. This consisted of those secondary landmarks listed on the x-axis of Figure 3(b).
The third category consisted of those secondary landmarks that are not uniquely definable in all directions, and which we henceforth refer to as tertiary landmarks. Each tertiary landmark points to an extreme boundary of a brain region in one direction, so its location along the other two coordinates is essentially a judgment call by an expert observer. Such landmarks can be used, for example, in the reference system to define the 3D bounding box of the corresponding brain region. The difficulties in picking the tertiary landmarks are explained in section B of the supplementary material. Tertiary landmarks are depicted in three groups on the x-axis of Figures 3(c–e), for which the measurement error is defined as the distance in millimeters in anterior/posterior, left/right, and superior/inferior directions respectively.
Figure 3 shows the average of error in mm with 95% confidence intervals for each landmark point when the algorithm was applied to single-site data. The accuracy evaluations are summarized in Table 1, which shows the overall average and maximum inter-observer variability, as well as the discrepancy between automatically and manually detected landmarks for each landmark category (primary, secondary, tertiary).
Table 1.
Overall average and maximum of the accuracy evaluation results for single-site data, for primary, secondary, and tertiary landmark categories.
| Landmark Type | Automatic vs. Manual Detection Error (mm) |
Inter-observer Variability (mm) |
Average algorithm- observer variablity vs. Average inter- observer variability |
||
|---|---|---|---|---|---|
|
|
|||||
| Average | Maximum | Average | Maximum | ||
| Primary landmarks | 1.27 | 1.60 | 0.69 | 0.89 | < 1 mm |
| Secondary landmarks | 1.97 | 3.34 | 1.10 | 2.17 | < 1 mm |
| Tertiary landmarks | 1.95 | 4.42 | 0.53 | 1.89 | < 2 mm |
3.3.2 Robustness evaluation
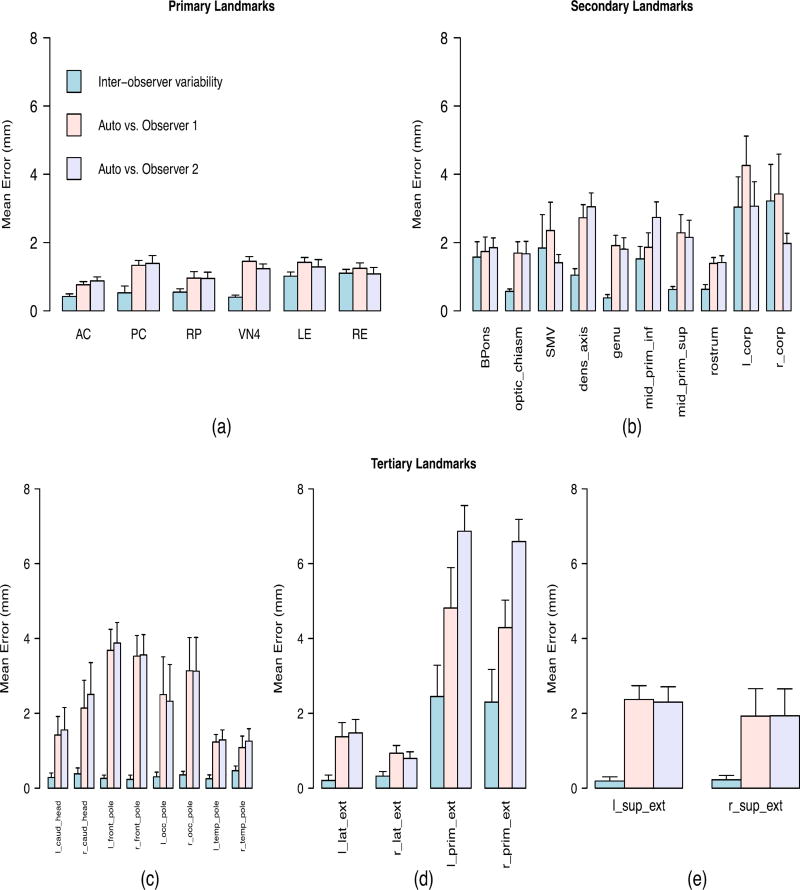
Without building a separate model, the robustness of the algorithm was evaluated via a multi-site data, which consisted of heterogeneous imaging data to demonstrate if the algorithm is reliable for general application in large-scale, multi-site studies. The measure of error was again selected based on the category of each landmark, as explained in section 3.3.1.
Figure 4 shows the results for each landmark point. Table 2 summarizes the robustness evaluation results for each landmark category by showing the overall average and maximum discrepancy between the automatically and manually detected landmarks, as well as the average and maximum inter-observer variability.
Figure 4.
Inter-observer variability between manual methods, and discrepancy errors between the manually and automatically detected landmarks, for multi-site data consisted of 7 different sites with different types of scanners. The full definition of all landmarks is presented in the first section of the supplementary material. (a) Primary landmarks: 3-D Euclidian distance was used as the error measure. (b) Secondary landmarks with clear anatomical definitions: 3-D Euclidian distance was used as the error measure. (c) Tertiary landmarks with high uncertainty in the left-superior plane: Error was the distance in the anterior/posterior direction. (d) Tertiary landmarks with high uncertainty in the posterior-superior plane: Error was the distance in the left/right direction. (e) Tertiary landmarks with high uncertainty in the left-posterior plane: Error was the distance in the superior/inferior direction.
Table 2.
Overall average and maximum of robustness evaluation results for multi-site data, for primary, secondary, and tertiary landmark categories.
| Landmark Type | Automatic vs. Manual Detection Error (mm) |
Inter-observer Variability (mm) |
Average of lgorithm- observer variablity vs Average inter- observer variability |
||
|---|---|---|---|---|---|
|
|
|||||
| Average | Maximum | Average | Maximum | ||
| Primary landmarks | 1.16 | 1.45 | 0.66 | 1.1 | < 1 mm |
| Secondary landmarks | 2.23 | 4.26 | 1.44 | 3.21 | < 1 mm |
| Tertiary landmarks | 2.63 | 6.86 | 0.58 | 2.45 | < 3 mm |
4. Discussion
The current work developed a novel, automated approach for estimating the position of the MSP and an arbitrary number of landmarks, including four prominent midbrain primary landmarks (MPJ, AC, PC, and VN4). The method exploits the centroid of head mass (CM) and locates the eye centers to provide a more reliable and accurate estimate of primary landmark positions, taking advantage of the morphometric constraints of extra landmarks. This method also extends the detection of landmarks to an arbitrary number of secondary landmark points in spaning all regions of the brain by applying a linear model estimation using sequential principle component analysis (PCA) that incorporates information regarding the already detected primary landmarks. The fidelity and reliability of our method was evaluated for 30 landmark points in two different test datasets that consisted of thirty MRI scans in total.
Figure 3(a) shows the accuracy results for primary landmarks. In addition to four prominent midbrain landmarks, we presented data on the left and right eye centers to demonstrate the reliability of the algorithm in detecting the eye centers, due to their important role in detecting the primary, mid-saggital landmarks. As shown by the first row of the Table 1, the average variability between the algorithm and each human observer differs less than 1 mm with the average inter-observer variability between two human raters (1.27 mm compared to 0.69 mm). Figure 4(a) does not show a significant change in the accuracy when the algorithm was applied to multi-site data. Again the average variability between the algorithm and each human observer differs less than 1 mm with the average inter-observer variability between two human raters (1.16 mm compared to 0.66 mm) as shown by the first row of the Table 2. The algorithm yields high accuracy and robustness in detecting the primary landmarks that are defined by having intensity patterns that are distinct from their surrounding points.
Figure 3(b) shows an increment in both inter-observer variability and discrepancies between automatic and manual methods for the secondary landmarks. However, the average difference between the two methods was still less than 1 mm (1.10 mm compared with 1.97 mm as shown in Table 1). The higher discrepancy is due to higher localization uncertainty compared with the primary landmarks. Figure 4(b) shows that the difference maintained (< 1 mm) when our algorithm was applied to multi-site data (1.44 mm compared with 2.23 mm as shown in Table 2). Although a decrease in the accuracy of the algorithm occurred when it was applied to multi-site data, the relative performance does not show a significant change due to the increasing discrepancy between the human observers.
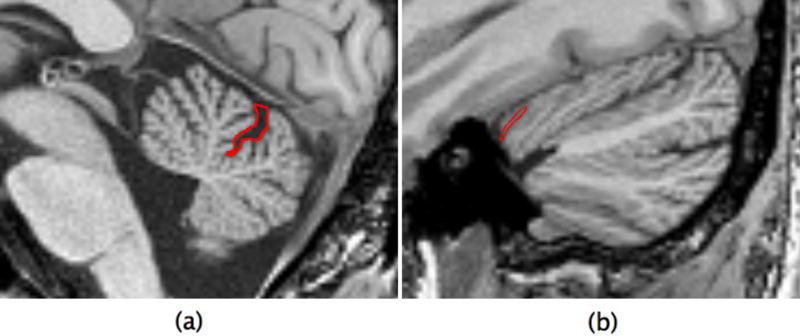
Figures 3(c–e) show the accuracy results for the third category of landmarks. As shown, the average discrepancy between the algorithm and each human rater differed by less than 2 mm versus the average inter-observer variability (0.53 mm compared with 1.95 mm). As shown in Figures 4(c–e), this average difference increased to less than 3 mm when the algorithm was applied to multi-site data (0.58 mm compared with 2.63 mm). There may be several reasons for higher error rate for the tertiary landmarks. It is informative to inspect the landmarks with highest error rate, namely the left/right lateral extremes of the cerebellar primary fissure (l/r_prim_ext) that are identified by following the primary fissure of the cerebellum to its most lateral aspects. As shown in Figures 3(d) and 4(d), even expert raters have an average disagreement of 2.07 mm regarding the final position of these landmarks because they may follow different branches of the primary fissure. Detecting these landmarks is even more challenging for an automatic algorithm because the surrounding region has very similar visual appearance and intensity distribution as can be observed in Figure 5. Although the primary fissure of the cerebellum is clearly distinguished from the other fissures in the mid-saggital plane (Figure 5a), all fissures have similar intensity patterns in the most lateral slice (Figure 5b). This makes searching for the maximum correlation similarity between the intensity values inaccurate when the algorithm tries to identify the exact location of the landmark in the local search procees.
Figure 5.
(a) Cerebellar primary fissure in mid-saggital plane (b) The right lateral extreme of the cerebellar primary fissure. Both defined by red boundaries.
Additionally, the algorithm detects the secondary landmarks in an sequential order, where detection of each landmark is based on the knowledge of all already estimated locations. Therefore, as the algorithm continues through the list of landmarks, the detection of each new landmark is negatively affected by the accumulated error resulting from the estimation errors in all previous iterations. This is another reason for the higher error rate for the tertiary landmarks versus primary and secondary landmarks.
The robustness of the method can be gleaned from comparison of the results in Figures 3 and 4, and their summary in Tables 1 and 2. When the algorithm was applied to multi-site data, that is, a collection of heterogeneous volumes, the difference between the average inter-observer variability and the average algorithm-observer variability was less than 1 mm for primary and secondary landmarks. The difference between the average variabilities increased for tertiary landmarks but was still less than 3 mm. Robustness of the results suggests this algorithm is a suitable candidate for large-scale multi-site studies, since a model can be built once on a selected set of data and thereafter be reliably applied on a variety of data with different resolutions and physical features, collected from different data sites, with different scanner types, and different scanning protocols.
The implemented method takes an average of 1 minute 30 seconds to be run on a test image volume using a 2 × 2.8 GHz Quad-Core Intel Xeon processor. About 50 percent of this time is spent on preprocessing operations, such as the Hough transform for eye detection. This step can be omitted if the user provides the coordinates of the eyes manually to the algorithm. This manual intervention is especially important when the algorithm needs to be applied to an input image that either has noisy eyes or does not meet the prerequisite field of view coverage incorporating the eyes. Optional steps for providing human intervention to manally identify eyes or primary landmark points is described in section E of the supplementary material.
The presented algorithm has been successfully incorporated into our routine data analysis pipeline (Kim et al., 2016) and has been fully automated applied to 4949 datasets acquired from approximately 1400 subjects across more than 40 different data collection sites with different scanning protocols and different scanner manufacturers at 3T and 1.5T data from both prospective and retrospective projects of data from over 15 years. The scans often had different physical space image orientation, spacing, origin, and field of view compared to the model building dataset. The results were visually inspected for a qualitative evaluation. The proposed algorithm succeeded without intervention in more than 90% of the cases. A trained observer inspected all the failed cases and confirmed that all the failures (414) were due to scans that did not meet the prerequisite field of view coverage of including the eyes. The algorithm succeeded on all the failed cases after manually providing the estimated coordinates of the eye centers through a manual intervention step. The method presented by Ardekani and Bachman (2009) does not rely on detecting the eye centers, so their method may detect the AC and PC points on these 414 failures without needing a manual intervention.
The “acpcdetect” method, presented by Ardekani and Bachman (2009), was run on 30 evaluation datasets to compare the results of their method with the presented auto constellation-based algorithm. The accuracy comparison is presented in the section G of the supplementary material. The “acpcdetect” tool failed to detect the AC point on one test case out of 30. Compared to our algorithm, the acpcdetect tool gets less accuracy (~0.5 mm) in detecting the AC point when evaluated on our heterogeneous evaluation datasets, but both automated constellation-based approach and the “acpcdetect” show similar results in detecting the PC point.
Also, a set of experiments were performed to compare the results of “acpcdetect” with manually inspected results of presented auto constellation-based algorithm on 3854 datasets. The results of this comparison is presented in the section H of supplementary document.
Furthermore, a registration-based landmark identification approach was performed on thirty evaluation datasets. It did not demonstrate improved results, but it took significantly longer than the presented algorithm. The details of this evaluation are presented in the section I of the supplementary document.
Although the presented work ran the model building and the evaluation processes only on T1-weighted MRI images, the same process could be followed to build a model for other image types such as T2-weighted images, which are of increasing importance in medical image processing, as long as the landmarks of interest have sufficient contrast profiles in those modalities.
As a future direction the training of statistical shape models can be replaced by feature point descriptors based on 3D local self-similarities that are used to characterize landmarks based on their surrounding structures (Guerrero et al., 2012). Then, in the local search process, a descriptor can be calculated for every voxel contained in the region of interest and the best possible match can be found for each of the training descriptors retrieved from the model file. This may be particularly helpful to obtain more accurate detection of secondary landmarks with higher intensity uncertainty, since feature point descriptors encode the intrinsic surrounding geometry of the point of interest, and not the intensity distribution.
The presented algorithm is implemented using the Insight Toolkit (ITK) libraries (Johnson et al., 2013) and conforms to the coding style, testing, and software license guidelines specified by the National Alliance for Medical Image Computing (NAMIC) group. The tool is also wrapped for use in the neuroimaging in python pipelines and interfaces (NIPYPE) (Gorgolewski et al., 2011) and is compatible as a 3DSlicer plugin module (Fedorov et al., 2012; Pieper et al., 2004). Section C of the supplementary material provides more information about building binaries from the source code repository (https://www.github.com/BRAINSia/BRAINSTools), implementation, and the usage of the tool.
Supplementary Material
Highlights.
A fully automated method to detect an arbitrary number of landmarks in human brain.
The method combines statistical shape models with brain morphometric measures.
Landmark detection is extended by applying a linear model estimation.
Once a model built, the method is reliably applicable to a variety of imaging data.
This method is reliable for general application in large-scale multi-site studies.
Acknowledgments
This research was supported by NIH Neurobiological Predictors of Huntington's Disease (PREDICT-HD; NS40068, NS050568), National Alliance for Medical Image Computing (NAMIC; EB005149 / Brigham and Women's Hospital), and Enterprise Storage in a Collaborative Neuroimaging Environment (S10 RR023392 / NCCR Shared Instrumentation Grant). Authors also wish to express their gratitude to The University of Iowa Scalable Informatics, Neuroimaging, Analysis, Processing, and Software Engineering (SINAPSE) laboratory team members for their all support, especially Wei Lu for his initial contribution to this work, and Kathy Jones and Eric Axelson for their technical contributions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abdi H, Williams L. Principle component analysis. Wiley Interdisciplinary Reviews: Computational Statistics. 2010;2:433–459. [Google Scholar]
- Ardekani BA, Bachman AH. Model-based automatic detection of anterior and posterior commissures on MRI scans. NeuroImage. 2009;46:677–682. doi: 10.1016/j.neuroimage.2009.02.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008;12:26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballard DH. Generalizing the Hough transform to detect arbitrary shapes. Pattern Recognit. 1981;13:111–122. [Google Scholar]
- Bookstein FL. Landmark methods for forms without landmarks: Morphometrics of group differences in outline shape. Med. Image Anal. 1997;1:225–243. doi: 10.1016/s1361-8415(97)85012-8. [DOI] [PubMed] [Google Scholar]
- Brent RP. Algorithms for Minimization Without Derivatives. Dover Publications; Mineola: 2013. [Google Scholar]
- Christensen GE, Johnson HJ. Invertibility and transitivity analysis for nonrigid image registration. J. Electron. Imaging. 2003;12(1):106–117. [Google Scholar]
- Davies R, Twining C, Cootes T, Taylor C. Building 3-D statistical shape models by direct optimization. IEEE Trans. Med. Imag. 2010;29:961–981. doi: 10.1109/TMI.2009.2035048. [DOI] [PubMed] [Google Scholar]
- Dodgson NA. Variation and extrema of human interpupillary distance. In: Woods AJ, Merritt JO, Benton SA, Bolas MT, editors. Proc. SPIE 5291. Stereoscopic Displays and Virtual Reality Systems XI. SPIE; San Jose: 2004. pp. 36–46. [Google Scholar]
- Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin JC, Pujol S, et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging. 2012;30:1323–1341. doi: 10.1016/j.mri.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frantz S, Rohr K, Stiehl HS. Improving the detection performance in semi-automatic landmark extraction. In: Taylor C, Colchester A, editors. MICCAI ’99, LNCS 1679. Springer-Verlag; Berlin: 1999. pp. 253–263. [Google Scholar]
- Ghayoor A, Vaidya JG, Johnson HJ. Development of a novel constellation based landmark detection algorithm. Proc. SPIE 8869, Med. Imaging: Image Proc. 2013 86693F (6 pages) [Google Scholar]
- Guerrero R, Pizarro L, Wolz R, Rueckert D. Landmark localisation in brain MR images using feature point descriptors based on 3D local self-similarities; IEEE International Symposium on Biomedical Imaging; 2012. pp. 1535–1538. [Google Scholar]
- Ghayoor A, Paulsen JS, Kim EY, Johnson HJ. Tissue classification of large-scale multi-site MR data using fuzzy k-nearest neighbor method. Proc. SPIE 9784, Med. Imaging: Image Proc. 2016:9784–66. (7 pages) [Google Scholar]
- Gorgolewski K, Burns CD, Madison C, Clark D, Halchenko YO, Waskom ML, Ghosh SS. Nipype: a flexible, lightweight and extensible neuroimaging data processing framework in Python. Front. Neuroimform. 2011;5:13. doi: 10.3389/fninf.2011.00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Y, Park H. Automatic registration of brain magnetic resonance images based on Talairach reference system. J. Magn. Reson. Imaging. 2004;20:572–580. doi: 10.1002/jmri.20168. [DOI] [PubMed] [Google Scholar]
- Heath TL. The Thirteen Books of Euclid's Elements. Dover Publications; Mineola: 1956. [Google Scholar]
- Horn BKP. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. 1987;4:629–642. [Google Scholar]
- Hough PVC. Machine analysis of bubble chamber pictures. Proc. Int. Conf. High Energy Accelerators and Instrumentation C50-09-14. 1959:554–558. [Google Scholar]
- Izard C, Jedynak B, Stark CEL. Spline-based probabilistic model for anatomical landmark detection. In: Larsen R, Nielsen M, Sporring J, editors. MICCAI 2006. LNCS. Vol. 4190. Springer; Heidelberg: 2006. pp. 849–856. [DOI] [PubMed] [Google Scholar]
- Johnson HJ, Christensen GE. Consistent landmark and intensity-based image registration. IEEE Trans. Med. Imaging. 2002;21(5):450–461. doi: 10.1109/TMI.2002.1009381. [DOI] [PubMed] [Google Scholar]
- Johnson HJ, McCormick S, Ibanez L. Updated for ITK 4. Insight Software Corporation; 2013. The ITK Software Guide. [Google Scholar]
- Kim EY, Johnson H, Williams N. Affine transformation for landmark based registration initializer in ITK. The MIDAS Journal - Med. Imaging Comput 2011 [Google Scholar]
- Kim EY, Johnson HJ. Robust multi-site MR data processing: Iterative optimization of bias correction, tissue classification, and registration. Front. Neuroinformatics. 2013;7:1–11. doi: 10.3389/fninf.2013.00029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim EY, Magnotta VA, Liu D, Johnson HJ. Stable atlas-based mapped prior (STAMP) machine-learning segmentation for multicenter large-scale MRI data. Magn. Reson. Imaging. 2014;32(7):832–844. doi: 10.1016/j.mri.2014.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim EY, Nopoulos P, Paulsen J, Johnson HJ. Efficient and extensible workflow: Reliable whole brain segmentation for large-scale, multi-center longitudinal human MRI analysis using high performance/throughput computing resources. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 2016;9401:54–61. [Google Scholar]
- Lehmann G. Label object representation and manipulation with ITK. The Insight Journal. 2007 URL: http://hdl.handle.net/1926/584.
- Lelieveldt PF, Boudewijn RJ, van der Geest MR, Rezaee JG, Bosch, Reiber JHC. Anatomical model matching with fuzzy implicit surfaces for segmentation of thoracic volume scans. IEEE Trans. Inf. Technol. Biomed. 1999;18:218–230. doi: 10.1109/42.764893. [DOI] [PubMed] [Google Scholar]
- Lu W. Unpublished Master’s Thesis. The University of Iowa; 2010. A Method for Automated Landmark Constellation Detection Using Evolutionary Principal Components and Statistical Shape Models. URL: http://ir.uiowa.edu/cgi/viewcontent.cgi?article=2036&context=etd. [Google Scholar]
- Lu W, Johnson H. Introduction to ITK resample in-place image filter. The Insight Journal. 2010 URL: http://hdl.handle.net/10380/3224.
- Magnotta VA, Bockholt HJ, Johnson HJ, Christensen GE, Andreasen NC. Subcortical, cerebellar, and magnetic resonance based consistent brain image registration. Neuroimage. 2003;19:233–245. doi: 10.1016/s1053-8119(03)00100-9. [DOI] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J. A probabilistic atlas of the human brain: Theory and rationale for its development. NeuroImage. 1995;2:89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- Otsu N. A threshold selection method from gray-level histogram. IEEE Trans. Syst. Man. Cybern. 1979;9:62–66. [Google Scholar]
- Padfield D. Masked object registration in the Fourier domain. IEEE Trans. Image Processing. 2012;21:2706–2718. doi: 10.1109/TIP.2011.2181402. [DOI] [PubMed] [Google Scholar]
- Pieper S, Halle M, Kikinis R. 3D Slicer. Proc. 1st IEEE Symposium Biomed. Imaging: Nano to Macro. 2004:632–635. [Google Scholar]
- Pierson R, Johnson H, Harris G, Keefe H, Paulsen JS, Andreasen NC, Magnotta VA. Fully automated analysis using BRAINS: AutoWorkup. NeuroImage. 2011;54:328–336. doi: 10.1016/j.neuroimage.2010.06.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pizer SM, Fritsch DS, Yushkevich PA, Johnson VE, Chaney EL. Segmentation, registration, and measurement of shape variation via image object shape. IEEE Trans. Med. Imaging. 1999;18:851–865. doi: 10.1109/42.811263. [DOI] [PubMed] [Google Scholar]
- Powell MJD. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comp. J. 1964;7:155–162. [Google Scholar]
- Prakash KN, Hu Q, Aziz A, Nowinski WL. Rapid and automatic localization of the anterior and posterior commissure point landmarks in MR volumetric neuroimages. Acad. Radiol. 2006;13:36–54. doi: 10.1016/j.acra.2005.08.023. [DOI] [PubMed] [Google Scholar]
- Rogers K. The eye: The physiology of human perception. The Rosen Publishing Group; New York: 2010. [Google Scholar]
- Talairach J, Tournoux P. Co-planar Stereotaxic Atlas of the Human Brain: 3-Dimensional Proportional System - an Approach to Cerebral Imaging. Thieme Medical Publishers; New York: 1988. [Google Scholar]
- Toews M, Wells W, Collins DL, Arbel T. Feature-based morphometry: discovering group-related anatomical patterns. Neuroimage. 2010;49:2318–2327. doi: 10.1016/j.neuroimage.2009.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vérard L, Allain P, Travère JM, Baron JC, Bloyet D. Fully automatic identification of the AC and PC landmarks on brain MRI using scene analysis. IEEE Trans. Med. Imaging. 1997;16:610–616. doi: 10.1109/42.640751. [DOI] [PubMed] [Google Scholar]
- Wörz S, Rohr K. Localization of anatomical point landmarks in 3D medical images by fitting 3D parametric intensity models. Med. Image Anal. 2005;10:41–58. doi: 10.1016/j.media.2005.02.003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.