Dye Diffusion at Surfaces: Charge Matters

Abstract

Fluorescence correlation spectroscopy and single molecule burst analysis were used to measure the effects of glass surface interactions on the diffusion of two common fluorescent dyes, one cationic and one anionic. The effects of dye–surface interactions on measured diffusion rates as a function of distance from the surface were investigated. Use of a three-axis piezo stage, combined with reference calibration measurements, enabled the accurate acquisition of surface-distance-dependent transport data. This analysis reveals attractive interactions between the cationic dye and the surface, which significantly alter the extracted diffusion values and persist in the measurements up to 1.0 μm from the surface. The Coulomb attraction between the cationic dye and the surface also results in rare, long-lived association events that lead to irreproducibility in extracted diffusion values. In addition to an assignment of the association lifetime for these events, this paper demonstrates that, if experiments must be performed with cationic probes near a glass surface, the use of solution electrolytes can eliminate deleterious dye–surface interactions, as the dyes were tested in a variety of environments. Finally, our data demonstrate that a better dye choice is an anionic probe, which exhibits no depth dependence of diffusion characteristics above a glass surface.

I. Introduction

In the present work, we report on the presence and extent of interactions between glass support substrates and two commonly used fluorescent probes of opposite charge, and the impact of these interactions on measurements of diffusion rates, as a function of distance from the support surface. The data presented are important because many photophysical experiments using a variety of molecular fluorescent dyes are performed on glass substrates. Although the objective of the aforementioned experiments-may not involve the glass–solvent interface, the presence of interfacial interactions can significantly perturb measurements up to distances of 1 μm from the surfaces and thus affect data interpretation. There are several phenomena that might influence data interpretation.

One property that can be affected significantly by surface interactions is dye photophysics. Both free and bound configurations of dyes have been used to probe kinetics, conformational dynamics, and the influence of surfaces on molecular photophysics. ^1–5 When experimental spectral or time windows overlap with surface-induced changes to photophysical lifetimes and spectral characteristics, data interpretation becomes complicated.

Another concern is surface chemical interactions that occur at an interface. In the case of the glass/water interface, it is well known that a charged double layer forms that can be nanometers thick depending on the ionic strength of the solute.^6,7 The electrical double layer can shield the dye from the surface, resulting in differences of behavior as a function of environment. Dynamic behavior of molecules at the surface can also exhibit dependence on the silica termination/silanol chemistry.⁸ This chemistry can be modified through oxygen plasma cleaning, which produces densely populated hydroxyl-terminated silica surfaces,⁹ as shown in Figure 1. The water solvent organization at the interfaces is significantly altered from that of bulk water.^10,11 Additionally, studies have shown that the translational diffusion of water is markedly different within confined regions, such as micelles and nanopores.^12,13 Furthermore, each of the previous factors can be drastically altered as a function of solution ionic strength.

Figure 1.

Illustration of plasma cleaned silica (glass) surface.

As stated, identifying and understanding these interactions is important because of their ability to alter the integrity of data analysis in the many experimental systems that are conducted close to surfaces.^14–17 Specifically, fluorescence correlation spectroscopy (FCS), although not designed to probe surface interactions, is frequently performed near a glass surface, and thus the surface interactions and their impact on the data must be understood. FCS and its more advanced cousins such as dual-focus FCS, scanning FCS, and two-photon FCS have recently developed in order to overcome some of the intrinsic limitations of conventional FCS.^18–24 These advances have allowed us to probe transport at and near membrane interfaces. Attempts to measure transport in such heterogeneous, crowded, or charged environments present their own innate challenges to data collection and analysis.^25–32 Since such environments also present an interfacial measurement to some degree, it becomes important to quantify the interaction of probes with the interfaces as a separate issue. Calibrating the focal volume for the objective, laser wavelength, the chemical makeup and thickness of the coverslip, and the medium are critical to acquiring accurate, reproducible diffusion data.^33,34 As we will demonstrate, choice of measurement distance from the support interface, dye charge, and solution electrolytic properties are other crucial factors.

Rhodamine 6G (R6G), a cationic dye, is common in fluorescence experiments,^35–41 and there have been several reports of its interfacial properties. For example, the probe has been shown to aggregate at the air/water interface using confocal fluorescence microscopy.^40,41 Further evidence has been reported that R6G is not only attracted to silica, but it also orders itself with respect to silanol groups.³⁵ In contrast, Boutin and co-workers did not observe attractive interactions in their study of hydrophilic surfaces.³⁶ Instead, those studies reported the largest attraction of R6G to hydrophobic surfaces. One purpose of the current work is to determine which of these earlier observations is correct, namely whether attractive interactions are observed between R6G and a hydrophilic glass surface when performing FCS and the extent of any interactions.

Other common dyes lack the extensive information on surface interactions that is present for R6G, and of particular interest are dyes with different charge value and distribution. The current work delves deeper into the effects of surface interactions by characterizing, as a function of distance from a hydrophilic glass interface, the mobility and local concentration of both cationic and anionic dyes using FCS and single molecule burst analysis. In order to extend previous studies and to provide a quantitative analysis of the depth dependence of measurements, the current work utilizes a three-axis piezo stage controller, which provides nanometer accuracy of the sample positioning.

In this study, we use confocal FCS to quantify the presence of dye–surface interactions between a glass surface and the cationic and anionic dyes R6G and AlexaFluor 555 (Alexa), respectively, as a function of distance from the surface. These studies are performed in aqueous media under a variety of electrolytic conditions. By comparing diffusion times for the two dyes under the various conditions, it was found that surface interactions with the cationic R6G contribute significantly to measured diffusion rates out to a focus position depth of 1.0 μm from the glass surface. Additionally, the surface interactions led to rare, but long-lived, association events that introduce irreproducibility in extracted diffusion constants. In contrast, the anionic dye did not exhibit surface interactions, and thus its measured diffusion rate was constant and reproducible at all distances measured. Single molecule burst analyses of single fluorescent events confirm that R6G is more concentrated near the surface and spends more time in the laser focal volume. The data acquired at various pH and electrolyte conditions support the hypothesis that the primary interactions betweenR6Gand the glass surface are Coulombic. The authors would offer the practical advice that if R6G is used in water, an electrolyte solution should be employed to eliminate surface interactions. Blip dwell-time analyses yield a characteristic association time for R6G at the surface of 0.71 ms.

II. Experimental Section

Materials and Sample Preparation

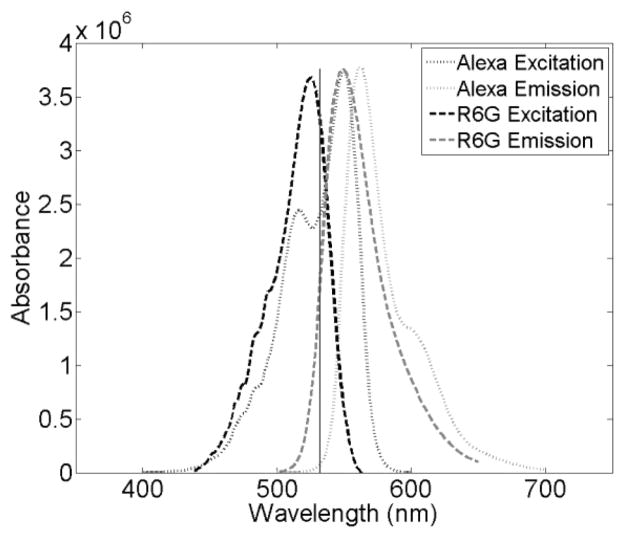
Many of the details of the sample preparation, setup, theory, data analysis, and acquisition have been previously reported.^24,31 Orange fluorescent carboxylate-modified FluoSphere beads (max abs/em: 540/560 nm) were used to calibrate the focal volume for the current FCS measurements at all depths measured. Both 40 and 100 nm beads were used; the 40nmbeadswere prepared at 1:10 000 dilution and the 100 nm beads were at 1:1000 dilution, in water. Both R6G (max abs/em: 530/566 nm) and Alexa (max abs/em: 555/565 nm) were diluted to ~100 pM for signal versus concentration optimization. ⁴² Figure 2 depicts the excitation and emission spectra of the two dyes, with the laser excitation line indicated. Because of differences in extinction and quantum yield at the excitation wavelength, the Alexa solutions were measured with a power density of ~2100 W/cm² and the R6G solutions were measured with a power density of ~800 W/cm².

Figure 2.

Absorption and emission spectra of Rhodamine 6G (solid) and Alexa Fluor 555 (dotted). The excitation source is also illustrated (vertical line).

NaCl (5 M, Sigma-Aldrich), KOH (85+%, Sigma-Aldrich), and spectroscopic gradeH₂SO₄ (J.T. Baker) were diluted to 0.001 N solutions serving as differing environments for the fluorescent dyes. The basic solution used was pH 11.0; the acidic solutions werepH1.0 and 3.0. Measurements were taken in each of the four solutions (aqueous, acidic, basic, and electrolytic) and at four depths (0.5, 1.0, 1.5, and 2.0 μm). No. 1 coverslips were rinsed in Hyclone Molecular Biology (MB) grade water (VWR) before undergoing oxygen plasma cleaning for 2 min. The coverslips were stored in a desiccator until use.

FCS Setup

A solid state laser was the excitation source (VERDI, Coherent). The 532 nm light was circularly polarized, filtered, and expanded to overfill the back aperture of an oil immersion microscope objective (FLUAR 100×, 1.3 NA, Carl Zeiss, GmBH). After excitation, the fluorescence was captured by the same objective⁴³ and isolated by a dichroic mirror (z532rdc, Chroma Technology) and a notch filter (NHPF-532.0, Kaiser). Fluorescence was then guided through a 50 μm pinhole to block out-of-focus light, increasing spatial resolution.^44,50 The resulting focal volume had a 1/e² beam radius of ~230 nm and height of ~1 μm.^44,50 Photons were detected by avalanche photodiodes (APD; SPCM-AQR-15, Perkin-Elmer). Apiezo stage (P-517.3CL Physik Instrumente) and controller (SPM100, RHK Technology) allowed the user to maneuver the sample in 3 dimensions. The output from the APDs was split to a photon counting board (PMS-400-A, Boston Electronics Corp.) and a 2Dimaging system (RHK Technology). All data were acquired by the photon counting board with a bin time of 10 μs. For each condition, the focal volume was calibrated in order to ensure that no experimental condition altered the confocal beam geometry. It was found that the beam geometry was consistent throughout the experiments.

FCS Theory

The utility of FCS methods arises from the Stokes–Einstein relation, which describes the rate of diffusion of particles as a function of particle characteristics:

$$D=\frac{k_{\mathrm{B}}T}{6\pi \eta R_{\mathrm{h}}}$$ (1)

Here, the diffusion coefficient, D, is proportional to the temperature of the solvent, T, and inversely proportional to the viscosity of the medium and the hydrodynamic radius of the particle, η and R_h, respectively.

The diffusion coefficient in eq 1 is related to the characteristic diffusion time, τ_D, through a laser beam focal volume by

$${\tau }_{\mathrm{D}}=\frac{{r_0}^2}{4D}$$ (2)

where r₀ is the beam waist radius, which can be determined through measurements of diffusion times through the volume for particles of known size.⁴⁶ It is important to note that these calibration criteria were employed to ensure that the confocal conditions were internally consistent throughout the experiment.

Through eqs 1 and 2, knowledge of characteristic diffusion times for a particle interacting in some system enables the extraction of specific information on environment and/or particle parameters. The diffusion times can be determined by FCS analysis. As measurements are taken, fluorescence signal fluctuates in accordance with the movement of a diffusing fluorescent molecule within the excitation focal volume. A simple autocorrelation of the fluorescence intensity signal can draw out the necessary information for the characterization of the molecule or environment. Elson and Madge, starting from a normalized autocorrelation function G(τ)

$$G(\tau )=\frac{\langle \delta F(t)\delta F(t+\tau )\rangle }{{\langle F(t)\rangle }^2}$$ (3)

derived an analytical expression relating the correlation function to the characteristic diffusion time.⁴⁶ In eq 3, 〈F(t)〉 is the average of the fluorescence signal over time, t, and δF(t)=F(t) − 〈F(t)〉 is the expression that describes the fluctuation of the signal around the mean value. The autocorrelation is a measure of self-similarity of the signal over a set of lag times, ranging from τ₀ to τ_max. (For representative autocorrelation curves for the samples measured for this study, see the Supporting Information.)

The initial findings of Elson and Madge derived the autocorrelation function for 2D diffusion within a detection volume with a Gaussian intensity profile for x and y. Aragon and Pecora expanded the expression to describe a detection volume with a Gaussian intensity profile for x, y, and z:⁴⁸

$$G(\tau )=\frac{1}{V_{\text{eff}}\langle C\rangle }\frac{1}{1+\frac{\tau }{{\tau }_{\mathrm{d}}}}\frac{1}{{\left(1+{\left(\frac{r_0}{z_0}\right)}^2\left(\frac{\tau }{{\tau }_{\mathrm{d}}}\right)\right)}^{1/2}}$$ (4)

where V_eff is the effective volume, 〈C〉 is the concentration of the dye, τ is the lag time, τ_d is the characteristic diffusion time, and z₀ is the beam height.

FCS To Measure Surface Interactions

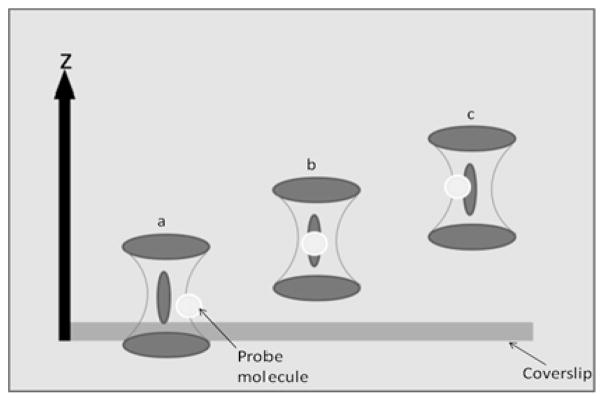
The fluctuating intensity characterized by FCS arises from the motion of fluorescent molecules as they pass through a tightly focused focal volume⁴⁹ as shown in Figure 3, which depicts our sample/observation volume geometry. For this study, measurements were acquired with the focal volume placed first at the surface of the coverslip (Figure 3a), corresponding to an offset of 0.5 μm of the beam waist from the surface, and at successively deeper positions within the bulk sample (Figure 3b,c). Therefore, the findings represent diffusion characteristics of the dyes in question as a function of distance from the coverslip surface.

Figure 3.

Placement of the bottom coverslip surface with respect to the focal volume.

There is some degree of uncertainty in the position of the focal volume with respect to the surface that can be quantified. Contributors to the uncertainty in position are the focus set point and focus drift. The focus set point was established prior to acquiring each sample by focusing the laser beam at the surface of the coverslip (i.e., at a depth of 0 μm into the sample). This focus set point was selected by adjusting the sample position along the z axis until the light scattered from the surface of the coverslip, as viewed on a CCD camera, was at its minimum area/maximum intensity. The uncertainty in setting the focus visually was determined to be ±75nm. This uncertainty arises from the limitation of visual discrimination of changes in the focusing spot within this 150 nm range. The second contributor to uncertainty is focus drift during the 5 min sample acquisition period. To minimize the effect of this source of error, the visual focus was checked at the conclusion of every measurement and its z axis location compared to the location recorded at the beginning of the measurement. The uncertainty associated with focus drift was ±0.17 μm; acquisition periods for which the drift was greater than this were resampled.

In considering the position of the focal volume with respect to the surface, and the resulting intersection of the focal volume with the surface/bulk portions of the sample, a discussion of the focal volume profile in z is also merited. Based on the work of Hess and Webb,⁵⁰ the focal volume profile for a high NA, overfilled (β<1, β=r_{microscope aperture}/r_pinhole), optical system with an aperture size of 7.68 ou (r_ou=r_pinhole × 2πNA/λM;M=magnification of the objective) is nearly Guassian in z over the 1/e² intensity range and has half length dimensions of ~0.5 μm which agrees with our estimated focal volume 1/e² dimensions. At these conditions, ~94% of signal is measured from the 1/e² focal volume and the remaining 6% occurs outside of these bounds. With these considerations, when setting the focus position (center of the focal volume along the z axis) to 0.5 μm above the surface of the coverslip, we are able to position the entire focal volume in the sample, while intersecting the surface region of interest. It is important to note that there is continuity to the measurements: since the focal volume is ~1 μm in the z dimension, taking measurements in 0.5 μm steps ensures that an overlap of data acquisition is present. All data presented in this article were averaged over three separate runs.

III. Results and Discussion

Depth Analysis

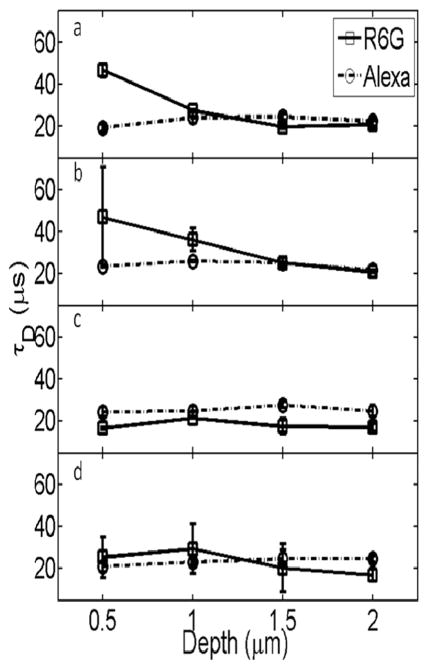
The depth dependence of the extracted diffusion time, τ_d, for the cationic R6G in water is shown in Figure 4a. The diffusion time for R6G is more than twice as long when measured close to the glass surface. For measurements taken further than 1 μm from the glass surface, the diffusion values converge to a diffusion time of 22 μs.⁵¹ In contrast, diffusion times for the anionic Alexa dye in water are not depth dependent, as is shown in Figure 4a. It should be noted that the self-consistent data obtained for Alexa diffusion at all depths establish that the slowed diffusion measured for R6G when close to the surface does not arise as an artifact of focal volume perturbation by the surface or from changes in the refractive index but from real perturbation of R6G diffusion. Thus, the longer R6G diffusion times close to the glass surface are clear evidence of attractive interactions between the cationic dye and the hydrophilic hydroxyl-terminated silica surface. They also provide at least partial insight into the wide range of reported values for the diffusion time of R6G.^2,42,51 Among the many possible explanations for these discrepancies are surface effects, as our results clearly demonstrate.

Figure 4.

Plots of the average τ_D vs depth for R6G and Alexa in aqueous (a), acidic (b), basic (c), and electrolytic (d) solutions. The spread in τ_D values at each depth reflects the reproducibility from multiple measurements. Lines between points are included only as a guide for the eye.

Because the focal volume encompasses the region close to the surface where attractive interactions may occur, and also extends into the bulk solution, fluctuations measured within this extended focal volume are expected to reflect both surface-hindered diffusion and bulk diffusion of the dyes. FCS analysis conducted with a two-component fit^52,53 was unable to reliably extract the two expected components, however. Limitations in resolving diffusion for two components can arise when diffusion times are similar and also when a second component is due to rare events that contribute to a small percentage of the total FCS signal.⁵⁴ Instead, other techniques, both chemical and analytical, are necessary to further test the hypothesis that our measurements are sensitive to attractive interactions, and to quantify these interactions, between the dye and surface.

Ionic Condition Analysis

The slow diffusion times measured for R6G close to the glass surface exhibited a strong dependence on the ionic conditions, as shown in Figure 4b–d. The depth dependence was observed in acidic conditions (pH 1.0 and 3.0) but not basic (pH 11.0) or electrolytic (0.001N NaCl) conditions. The pH 3.0 data are of particular significance. As shown in Figure 4b, there is a large standard deviation of extracted diffusion values closest to the glass surface under these conditions. Large standard deviations in FCS data suggest the presence of anomalous events such as aggregation or adsorption.³⁸ Wewould expect chemisorption events in the case of a Coulombic attraction between the cationic R6G and an anionic surface. The isolectric point (IEP) of silica is reported to be at pH 2.0 and can be dependent on the hydration of the surface.⁵⁵ Other studies have confirmed that below pH 2 glass coverslips are positively charged and from pH 2–5 the surface is negatively charged.³⁷ Thus, even under our acidic experimental conditions at pH 3, the negatively charged surface can be expected to attract the cationic R6G, leading to both to a slow diffusion time and a large spread in the error due to anomalous adsorption events. We performed additional depth-dependent experiments atpH1.0, below the reported isoelectric point⁵⁵ (data not shown), and our results differ from the findings of Chen and co-workers³⁷ in that surface interactions are not eliminated even at this pH. This can be explained by differences in the experimental conditions. The coverslips in our study were plasma cleaned, which increases surface hydration levels, and thus alters the surface IEP. There is experimental evidence that the IEP of a solid oxide/hydroxide is decreased when the level of surface hydration is increased.⁵⁵ According to this information, along with the data presented in Figure 4b and our findings during attempts to further acidify the surface (to pH 1.0), it is not practical to use acid to switch the surface charge when using plasma-treated glass coverslips.

Whereas measurements in aqueous and acidic solvent reveal a dependence of diffusion times on distance from the interface, neither the electrolytic nor basic conditions exhibit a comparable dependence. This reflects a lack of strong interfacial interactions between the dye and the surface in these conditions. Aligning the Gouy–Chapman and Stern models for the composition of ion concentration near a charged surface, we suggest that the differential behavior of R6G mobility we have observed near the interface in aqueous and acidic conditions as compared to basic and ionic solutions may be related to the identity of the counter-ions available to form the adsorbed and diffusive layers.⁵⁶ The use of MB water in all of the dye solutions ensures that the only ions present are those that have been purposefully introduced and the inherent hydronium/hydroxide pairs. In the case of the aqueous and acidic measurements, our data show that the cationic dye participates at the surface along with the expected hydronium ions in neutralization of the negative surface charges. However, in the case of the basic and ionic environments, the respective cations (Na⁺ and K⁺) are available to compose the Stern layer, and our data indicate that in this case there is significant inhibition of surface interactions for the cationic dye, perhaps due to exclusion from the surface by these cationic counterions.⁵⁷ The nature and composition of the physical ordering of ions at interfaces has been shown to be dependent on ion identity (and thus characteristics such as size of the ions), and our data support such a model with respect to the glass interface.^58,59

These data are supported by other studies that report attractive interactions between R6G and silica surfaces.^38,39 Of additional importance is a study in which attractions were observed in the case of hydrophobic surfaces, but not hydrophilic surfaces.³⁶ Our work demonstrates that attractive conditions are present in the case of the hydrophilic, polar SiOH surface.

It is important to note the lack of surface interactions under any conditions for the anionic Alexa dye. The lack of measurable effects on the behavior of anionic Alexa dye molecules can be attributed to charge exclusion from the negatively charged surface. This insensitivity to the glass surface makes Alexa a reasonable substitute for R6G in studies that require measurement close to this interface.

Frequency Analysis

A single molecule blip frequency analysis was performed to test the hypothesis that attractive forces are responsible for the slower R6G diffusion near the surface. If this hypothesis is correct, then we would expect to find a higher local concentration of R6G dye near the surface. Since our data are collected in the time domain rather than from an autocor relator acquisition board, it is possible to obtain data such as single event frequency, intensity, and duration values. Figure 5 displays the average number of events (with standard deviations over multiple samples) obtained from data binned up to 100 μs time bins versus the distance from the coverslip for the two dyes in aqueous solution. The increase in events observed near the surface arises from an increase in the average number of molecules in the focal volume per 100 μs bin time. The frequency trends shown here confirm that the local concentration of R6G is higher at the surface, as would be expected if there are significant attractive forces between the cationic dye and the coverslip surface. Similar trends are found in the case of the acidic condition and are reported in the Supporting Information.

Figure 5.

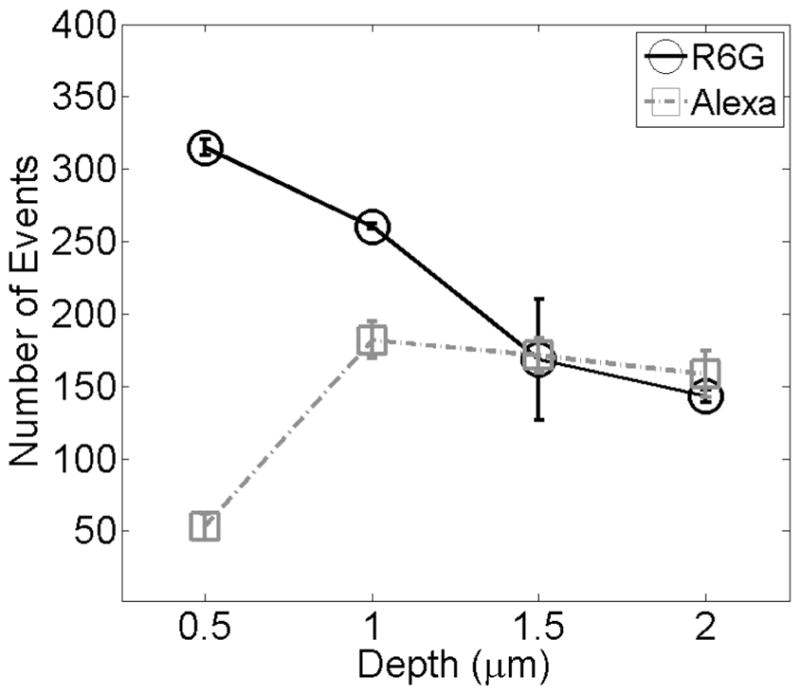
Mean events for R6G and Alexa in aqueous conditions. The spread in intensity values at each depth reflect reproducibility from multiple experiments. Lines are drawn as a guide for the eye.

Blip Dwell Time Analysis

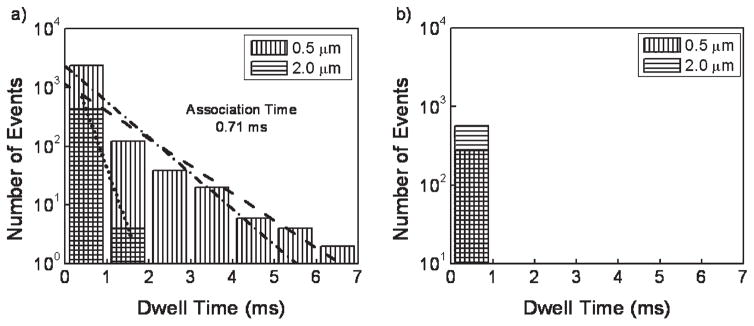
The blip frequency and FCS data both demonstrate attractive forces between the R6G dye and the surface that result in an overall measured slower diffusion time. An additional question about the extent of the attractive forces can be asked. Others have studied the orientational effects of silica on R6G and have found that the dye trapped in a silica cage rigidly orients itself with respect to the walls of the cage which are comprised of Si–OH bonds,³⁵ suggesting chemical coordination between the dye and the silica. In order to test for the presence of long-lived association events, we performed a blip dwell analysis. As shown in Figure 6, a fluorescence blip dwell time analysis was performed for each dye in water at 100 μs time bins (note that these bins are an order of magnitude larger than the 10 μs bins used for diffusion measurements) at 0.5 and 2.0 μm from the surface. In Figure 6a, at 0.5 μm, there are a large number of fluorescent events that are several milliseconds long for R6G. These dwell times are much longer than the diffusion time measured for R6G near the surface (~40 μs). It is also important to note that the measured number of events for these dwells represent minimum values because, despite the low excitation fluence in our FCS measurements, photobleaching limits detection of dwell times longer than several milliseconds. These observed long focal volume dwell times deviate considerably from those expected from a typical distribution, as evidenced by the bulk data displayed in Figure 6a. The dwell time distribution is significantly broadened near the surface when compared with diffusion in the bulk. These long dwell times are consistent with adsorption events. The present analysis reveals that there is a prolonged interaction of theR6Gwith the surface, consistent-with chemisorption events described earlier.³⁵ In conjunction with the frequency analysis data presented in Figure 5, and the large standard deviations shown in Figure 4, the dwell time data support the presence of rare, long-lived association events that are consistent with adsorption/desorption processes.⁶⁰ As shown in Figure 6b, and consistent with the FCS data, the Alexa dye conforms to a model of simple diffusion, even close to the coverslip.

Figure 6.

Dwell time histograms for R6G (a) and Alexa (b) in water. In (a) the 0.5 μm data was fitted to an exponential (dashed line) and decomposed into the IRF (dotted line) and the pure data (dot-dashed line).

One of the concerns in the study conducted by Schuster and co-workers³⁸ was their inability to determine the attachment times forR6Gto the surface. Using the dwell time analysis shown in Figure 6a, we were able to fit the bulk and close-to-surface data to exponential decay functions. The data measured close to the surface represents a convolution of long surface association events, bulk diffusion characteristics, and our instrument response function (IRF). To extract the characteristic association time for molecules at the interface from this data, the convoluted data (dashed line in Figure 6) was decomposed into two exponential functions (dotted and dot-dashed lines in Figure 6, respectively), representing the association data function and the combined bulk diffusion and IRF functions as obtained experimentally from measurements at 2.0 μm away from the surface. The association data function was extracted through Fourier deconvolutions of the two fitted exponentials. Fitting the resulting pure data function yielded an association time that was not resolvable from dual-component fitting of the FCS data. In this manner we establish that, in aqueous conditions, R6G shows a characteristic association time of 0.71 ms. Again, this is a low estimate of actual association lifetimes because detection of longer-lived events is reduced by photobleaching.

IV. Conclusions

The current studies offer evidence that R6G is attracted to a hydrophilic hydroxyl-terminated silica surface under aqueous and acidic conditions above the protonation point of the hydroxyl surface group. These studies suggest that, in order to avoid conditions in which surface interactions affect acquired data, diffusion studies using R6G should be performed at least 1 μm from the surface for confocal conditions, or salt should be added to shield the surface attraction when using the cationic R6G. Blip dwell time analyses yield an R6G surface association time of 0.71 ms. The anionic Alexa dye is not attracted to hydroxyl-terminated silica and thus presents itself as a good alternative to R6G as a diffusion probe when studies are to be performed near glass or hydrophilic substrates in aqueous conditions.