Manipulation of ionized impurity scattering for achieving high thermoelectric performance in n-type Mg₃Sb₂-based materials

Significance

Higher carrier mobility can contribute to a larger power factor, so it is important to identify effective means for achieving higher carrier mobility. Since carrier mobility is governed by the band structure and the carrier scattering mechanism, its possible enhancement could be obtained by manipulating either or both of these. Here, we report a substantial enhancement in carrier mobility by tuning the carrier scattering mechanism in n-type Mg₃Sb₂-based materials. The ionized impurity scattering in these materials has been shifted into mixed scattering by acoustic phonons and ionized impurities. Our results clearly demonstrate that the strategy of tuning the carrier scattering mechanism is quite effective for improving the mobility and should also be applicable to other material systems.

Abstract

Achieving higher carrier mobility plays a pivotal role for obtaining potentially high thermoelectric performance. In principle, the carrier mobility is governed by the band structure as well as by the carrier scattering mechanism. Here, we demonstrate that by manipulating the carrier scattering mechanism in n-type Mg₃Sb₂-based materials, a substantial improvement in carrier mobility, and hence the power factor, can be achieved. In this work, Fe, Co, Hf, and Ta are doped on the Mg site of Mg_3.2Sb_1.5Bi_0.49Te_0.01, where the ionized impurity scattering crosses over to mixed ionized impurity and acoustic phonon scattering. A significant improvement in Hall mobility from ∼16 to ∼81 cm²⋅V⁻¹⋅s⁻¹ is obtained, thus leading to a notably enhanced power factor of ∼13 μW⋅cm⁻¹⋅K⁻² from ∼5 μW⋅cm⁻¹⋅K⁻². A simultaneous reduction in thermal conductivity is also achieved. Collectively, a figure of merit (ZT) of ∼1.7 is obtained at 773 K in Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01. The concept of manipulating the carrier scattering mechanism to improve the mobility should also be applicable to other material systems.

Thermoelectric devices that can directly convert heat into electricity, and vice versa, can be used in waste heat recovery and cooling applications (1–3). This solid-state conversion technology has advantages in terms of its compactness for high power density, its capability to provide cleaner energy, and its long lifetime. However, the relatively low efficiency of thermoelectric modules has limited their application to niche markets. The efficiency of thermoelectric devices is determined by the Carnot efficiency and the material’s figure of merit (ZT), which is defined as ZT = (S²σ/κ)T, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity (κ = κ_ele + κ_lat, where κ_ele is the electronic part and κ_lat is the lattice part), and T is the absolute temperature (4–6).

The challenge of improving the ZT lies in the fact that the thermoelectric parameters S, σ, and κ_ele are strongly interdependent (7). Therefore, two basic approaches have been used to enhance the ZT via decreasing the relatively independent lattice thermal conductivity or increasing the power factor (i.e., S²σ). Phonon scattering via defect engineering [point defects (8–11), dislocations (12–15), and grain boundaries (16, 17)] or nanostructuring (18) has led to a significant reduction in lattice thermal conductivity. On the other hand, power factors have also been enhanced via different approaches such as band engineering (19–22), inducing resonant levels (23), the carrier filtering effect (24–27), ionized impurity scattering (28), and modulation doping (29, 30).

Generally, power factors have been optimized by tuning the carrier concentration so that a compromise between the Seebeck coefficient and the electrical conductivity is reached. Strategies for further improving power factors have mainly focused on enhancing the Seebeck coefficient (e.g., resonant levels, the carrier filtering effect, ionized impurity scattering), while a few have been aimed at boosting the mobility (e.g., modulation doping). However, Seebeck coefficient enhancement is usually accompanied by a noticeable reduction in carrier mobility (23, 28), which deteriorates the electrical conductivity, and therefore results in limited power factor improvement. In fact, the importance of increasing mobility to improve the power factor should be recognized. Its importance can be understood from the fact that since the Seebeck coefficient is strongly coupled with the electrical conductivity via carrier concentration rather than mobility, the improved mobility will monotonously increase the electrical conductivity without affecting the Seebeck coefficient, thus substantially improving the power factor.

The carrier mobility, µ, can be expressed as follows (31):

$$\mu =\frac{e\langle \tau \rangle }{m^{\ast }},$$ [1]

where e is the electron charge, m^∗ is the effective mass, and $\langle \tau \rangle$ is the average relaxation time. In the simplest case, the relaxation time is a function of carrier energy, E; temperature; and effective mass:

$$\tau \propto E^r{T}^s{\left(m^{\ast }\right)}^t.$$ [2]

Since τ varies for different scattering mechanisms, the mobility could be tuned by manipulating the carrier scattering mechanism.

Recently, a record high room temperature power factor of ∼106 μW⋅cm⁻¹⋅K⁻² was obtained in NbFeSb-based materials by optimizing the hot-pressing temperature (32). This high power factor originates from the noticeably improved mobility, which is due to the variation in the carrier scattering mechanism. Tamaki et al. (33) reported n-type Mg₃Sb₂-based materials with high thermoelectric performance via introducing extra Mg and Te doping, and similar results were also reported by Zhang et al. (34). Most recently, Shuai et al. (35) reported that substantial improvements in the room temperature Hall mobility and power factor were achieved in Nb/Te double-doped n-type Mg₃Sb₂-based materials. These materials showed mixed scattering due to ionized impurities and acoustic phonons, instead of being dominated by ionized impurity scattering. Therefore, these results unambiguously demonstrate that mobility can indeed be enhanced by tuning the carrier scattering mechanism.

The variation in the carrier scattering mechanism induced by Nb-doping in n-type Mg₃Sb₂-based materials is quite intriguing. It is natural to ask whether any other dopants have a similar effect and, more importantly, what are the underlying physics for such a phenomenon. Therefore, the motivation behind this work is to further investigate the carrier scattering mechanism in n-type Mg₃Sb₂-based materials. In the following discussion, it will be demonstrated that, in addition to Nb, transition-metal elements such as Fe, Co, Hf, and Ta show a similar effect in tuning the carrier scattering mechanism. In these cases, significant enhancements in the room temperature Hall mobility, µ_H (from ∼16 to ∼81 cm²⋅V⁻¹⋅s⁻¹), and power factor (from ∼5 to ∼13 μW⋅cm⁻¹⋅K⁻²) are observed. A simultaneous reduction in the thermal conductivity is also achieved, and, finally, a ZT of ∼1.7 is obtained in Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01.

Results and Discussion

Based upon the composition of Mg_3.2Sb_1.5Bi_0.49Te_0.01, which showed the best thermoelectric performance among the Mg₃Sb₂-based materials from the report by Tamaki et al. (33), doping on the Mg site by different elements (Hf, V, Ta, Mo, W, Fe, Co, Ni, and Zn) was investigated. Among these elements, Fe, Co, Hf, and Ta have shown an effect similar to that of Nb in tuning the carrier scattering mechanism (Fig. 1A). Detailed thermoelectric properties of Mg_3.1T_0.1Sb_1.5Bi_0.49Te_0.01 (T = V, Mo, W, Ni, and Zn) are shown in SI Appendix, Fig. S1. For clarity, Mg_3.1A_0.1Sb_1.5Bi_0.49Te_0.01 (A = Fe, Co, Hf, and Ta) will be referenced as double-doped specimens in the following discussion.

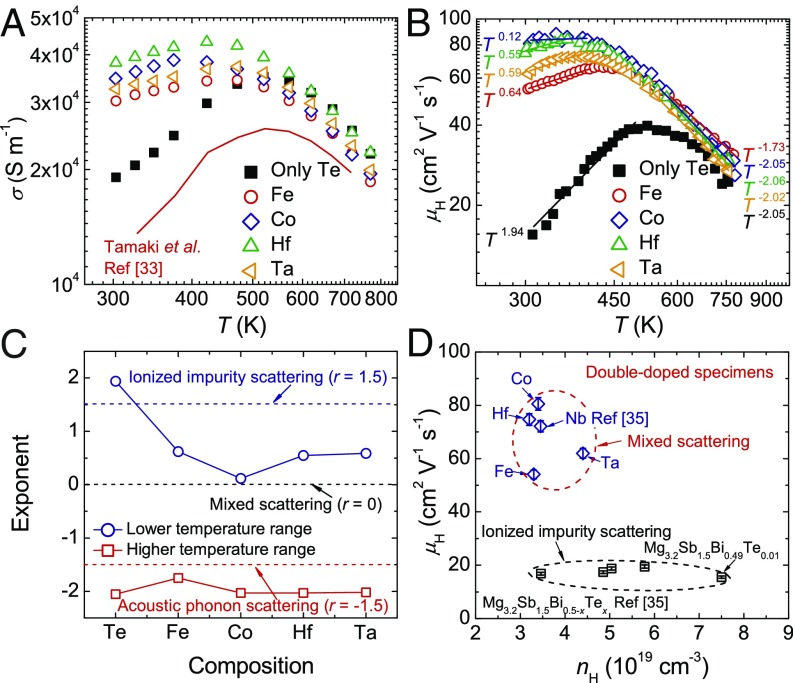
Fig. 1.

Temperature-dependent electrical conductivity of (A), temperature-dependent Hall mobility of (B), composition-dependent temperature exponent of (C), and relationship between Hall carrier concentration, n_H, and Hall mobility for (D) Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1A_0.1Sb_1.5Bi_0.49Te_0.01 (A = Fe, Co, Hf, and Ta). Data from ref. 33 in panel A and Nb data in panel D from ref. 35.

Although a slight difference in the magnitude of electrical conductivity is observed between Tamaki et al.’s results (33) and our data for Mg_3.2Sb_1.5Bi_0.49Te_0.01, the temperature dependences for the two specimens are quite similar. In sharp contrast, the temperature dependences at lower temperatures for double-doped specimens are noticeably different from that of Mg_3.2Sb_1.5Bi_0.49Te_0.01. Temperature-dependent Hall mobility is shown in Fig. 1B, where distinctly different temperature dependences at lower temperatures can be observed and a substantial difference in Hall mobility is noted. The room temperature Hall mobility is ∼16 cm²⋅V⁻¹⋅s⁻¹ for Mg_3.2Sb_1.5Bi_0.49Te_0.01, while it is more than ∼50 cm²⋅V⁻¹⋅s⁻¹ for the double-doped specimens. Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01 shows the highest mobility of ∼81 cm²⋅V⁻¹⋅s⁻¹, an increase of more than 400% compared with that of Mg_3.2Sb_1.5Bi_0.49Te_0.01. It is important to note that the Hall mobilities are quite comparable at higher temperatures, which should be ascribed mainly to the similar temperature dependence (i.e., the similar carrier scattering mechanism). This clearly indicates that the carrier scattering mechanism plays a critical role in the carrier mobility.

The relationship between the temperature exponent (derived from the Hall mobility) and composition is shown in Fig. 1C. In the lower temperature range, Mg_3.2Sb_1.5Bi_0.49Te_0.01 shows ionized impurity scattering, while the double-doped specimens are dominated by mixed scattering of ionized impurities and acoustic phonons. In the higher temperature range, all of the specimens are dominated by acoustic phonon scattering. The difference between the measured temperature exponent and the theoretical value for certain carrier scattering mechanisms (1.5 for ionized impurity scattering and −1.5 for acoustic phonon scattering) is noted, which could be partly ascribed to the assumptions involved in deriving the carrier scattering mechanism (e.g., it is usually assumed that the band is parabolic, but it could actually be a complex band structure). Fig. 1D shows the relationship between the Hall carrier concentration, n_H, and the Hall mobility. For Mg_3.2Sb_1.5Bi_0.5−xTe_x, where the ionized impurity scattering is dominant, the Hall mobility is quite low (less than ∼20 cm²⋅V⁻¹⋅s⁻¹) (35). Generally, the increased concentrations of ionized impurities and carriers will lead to enhanced ionized impurity scattering (36–38) and stronger electron-electron scattering (39–41), respectively. In other words, Hall mobility usually increases with decreasing the Hall carrier concentration. However, since the Hall carrier concentration of the double-doped specimens is similar to that of Mg_3.2Sb_1.5Bi_0.5−xTe_x (x < 0.01), the noticeable enhancement in Hall mobility after doping of transition-metal elements cannot be ascribed simply to the reduced Hall carrier concentration.

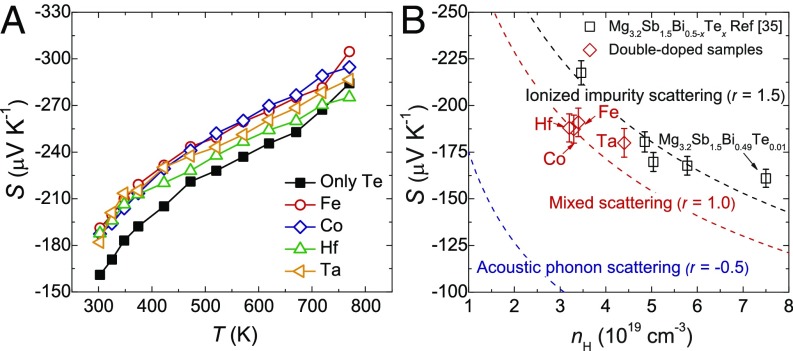
Fig. 2A shows the temperature-dependent Seebeck coefficient, indicating that all of the double-doped specimens show slightly higher Seebeck coefficients than that of the Mg_3.2Sb_1.5Bi_0.49Te_0.01. The relationship between the Seebeck coefficient and the Hall carrier concentration can be understood well from the Pisarenko plot, as shown in Fig. 2B. Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.2Sb_1.5Bi_0.5−xTe_x (x < 0.01) (35) show good agreement with the calculated Seebeck coefficient by considering the ionized impurity scattering. In contrast, all of the double-doped specimens deviate from this prediction but are close to the mixed scattering (r = 1) result. At identical Hall carrier concentrations, ionized impurity scattering shows the highest Seebeck coefficient, followed by mixed scattering, with acoustic phonon scattering showing the lowest Seebeck coefficient. However, the Hall carrier concentration for Fe-, Co-, Hf-, and Ta-doped specimens (in the range between ∼3 × 10¹⁹ cm⁻³ and ∼4.4 × 10¹⁹ cm⁻³) is lower than that of Mg_3.2Sb_1.5Bi_0.49Te_0.01 (∼7.5 × 10¹⁹ cm⁻³). This explains why slightly higher Seebeck coefficients are achieved in double-doped specimens. The difference in the Hall carrier concentration between Mg_3.2Sb_1.5Bi_0.49Te_0.01 and the double-doped specimens could be partially explained by the different amount of extra Mg. Our recent results indicate that extra Mg will change the carrier concentration in n-type Mg₃Sb₂-based materials, similar to the case of n-type Mg₂Sn-based materials (42), and detailed results will be reported elsewhere.

Fig. 2.

Temperature-dependent Seebeck coefficient of (A) and relationship between Hall carrier concentration, n_H, and the Seebeck coefficient for (B) Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1A_0.1Sb_1.5Bi_0.49Te_0.01 (A = Fe, Co, Hf, and Ta). The calculated density of states effective masses for all of the specimens are ∼0.5 m₀. Mg_3.2Sb_1.5Bi_0.5-xTe_x data in panel B from ref. 35.

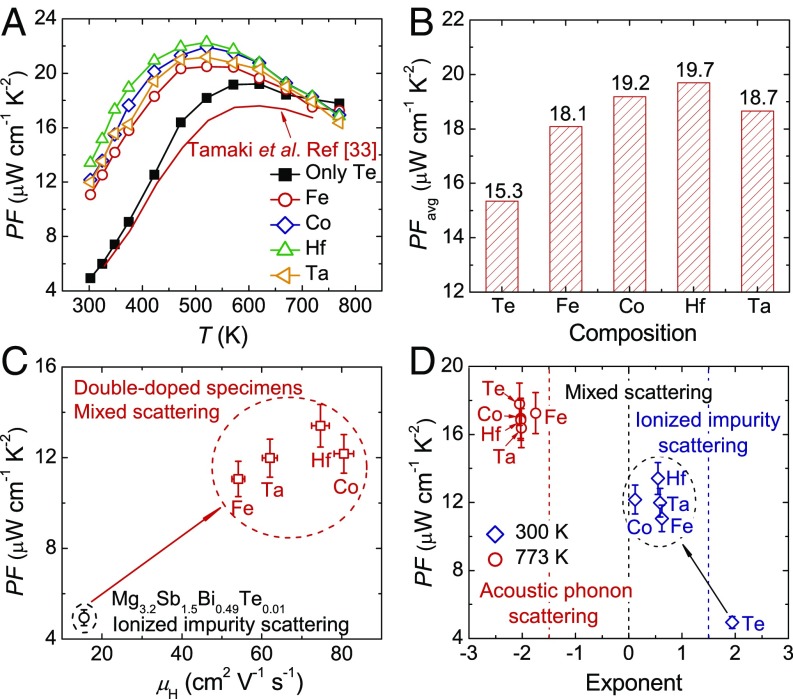
Due to the noticeably increased electrical conductivity and the slightly higher Seebeck coefficient, power factors are substantially improved for double-doped specimens at a lower temperature range (Fig. 3A). The room temperature power factor is ∼5 μW⋅cm⁻¹⋅K⁻² for Mg_3.2Sb_1.5Bi_0.49Te_0.01 but ∼13 μW⋅cm⁻¹⋅K⁻² for Mg_3.1Hf_0.1Sb_1.5Bi_0.49Te_0.01, an increase of ∼160%. A comparison of the average power factor (calculated by the integration method between the temperatures of 300 and 773 K) is further shown in Fig. 3B, where the double-doped specimens show noticeable enhancement. The average power factor of Mg_3.1Hf_0.1Sb_1.5Bi_0.49Te_0.01 is ∼19.7 μW⋅cm⁻¹⋅K⁻², which is ∼29% higher than that of Mg_3.2Sb_1.5Bi_0.49Te_0.01 (∼15.3 μW⋅cm⁻¹⋅K⁻²). The relationship between the room temperature Hall mobility and the power factor is shown in Fig. 3C, where the effectively enhanced power factor in double-doped specimens should be mainly ascribed to the improved Hall mobility. The temperature exponent-dependent power factor is further shown in Fig. 3D. At a lower temperature range, the power factor of Mg_3.2Sb_1.5Bi_0.49Te_0.01 is much lower than that of double-doped specimens, which should be mainly due to the difference in the temperature exponent (i.e., the carrier scattering mechanism). On the contrary, the power factors at higher temperatures are quite comparable for all of the specimens, and this could be explained by having similar carrier scattering mechanisms. This demonstrates that power factors are also strongly dependent on the carrier scattering mechanism. More specifically, the power factors of n-type Mg₃Sb₂-based materials increase through the range of states from those dominated by ionized impurity scattering to those dominated by acoustic phonon scattering.

Fig. 3.

Temperature-dependent power factor of (A), comparison of room temperature power factor among different specimens of (B), relationship between the Hall mobility and power factor for (C), and relationship between the temperature exponent and power factor for (D) Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1A_0.1Sb_1.5Bi_0.49Te_0.01 (A = Fe, Co, Hf, and Ta). Data from ref. 33 in panel A.

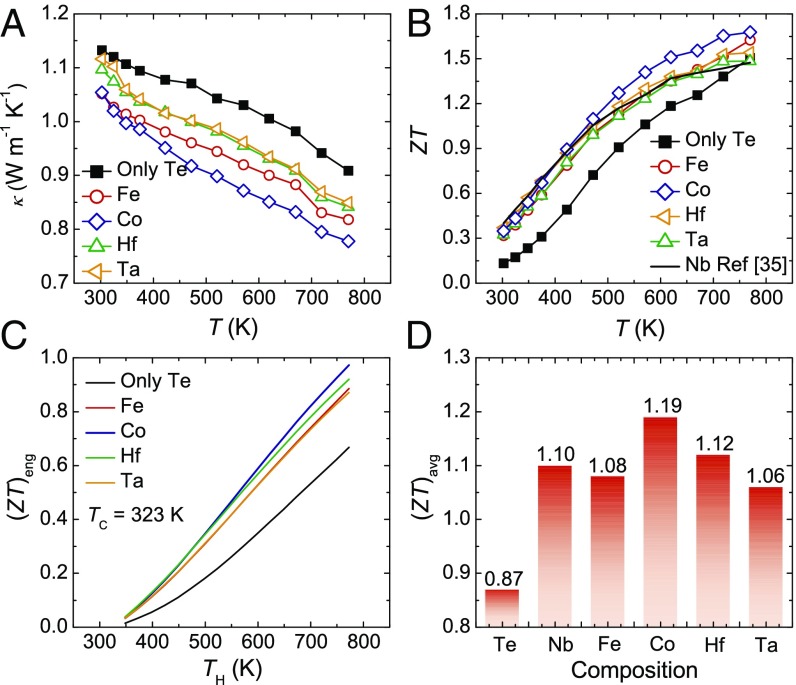
In addition to the enhanced power factors in doubled-doped specimens, lower thermal conductivity is achieved, as shown in Fig. 4A. The reduction in thermal conductivity could be partially ascribed to the phonon scattering by point defects. Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01 shows the lowest thermal conductivity, which could be due to the fact that Co has the highest solubility at the Mg site among all of the dopants (SI Appendix, Figs. S2 and S3). Owing to the substantially improved power factors and reduced thermal conductivities, ZTs have been effectively improved for the double-doped specimens, where a peak ZT of ∼1.7 is obtained in Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01 (as shown in Fig. 4B). The engineering dimensionless ZT [(ZT)_eng] can be used to reliably and accurately predict the practical conversion efficiency (43). Therefore, the hot-side temperature (T_H)-dependent (ZT)_eng is calculated as shown in Fig. 4C, where a noticeable increase in (ZT)_eng is observed for the double-doped specimens. The (ZT)_eng at the cold-side temperature (T_C) of 323 K and T_H of 773 K is ∼0.67 for Mg_3.2Sb_1.5Bi_0.49Te_0.01 but ∼0.97 for Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01, an increase of ∼45%. The average ZT [(ZT)_avg] is calculated by the integration method over the temperature range of 300 to 773 K. Comparison of the (ZT)_avg is shown in Fig. 4D, where the (ZT)_avg is ∼0.87 for Mg_3.2Sb_1.5Bi_0.49Te_0.01 but more than ∼1.05 for double-doped specimens. A high (ZT)_avg of ∼1.19 is obtained in Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01, an increase of ∼37% compared with Mg_3.2Sb_1.5Bi_0.49Te_0.01. Detailed composition-dependent thermoelectric properties of Mg_3.2−xCo_xSb_1.5Bi_0.49Te_0.01 (x = 0, x = 0.025, x = 0.05, x = 0.075, and x = 0.1) are also investigated, and an improvement in thermoelectric performance with an increased Co concentration can be observed (SI Appendix, Figs. S4 and S5).

Fig. 4.

Temperature-dependent thermal conductivity (A) and ZT of Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1A_0.1Sb_1.5Bi_0.49Te_0.01 (B) (A = Fe, Co, Hf, and Ta). Calculated (ZT)_eng at a cold-side temperature (T_C) of 323 K (C) and comparison of (ZT)_avg between Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1A_0.1Sb_1.5Bi_0.49Te_0.01 (D) (A = Nb, Fe, Co, Hf, and Ta). Nb data in panel B from ref. 35.

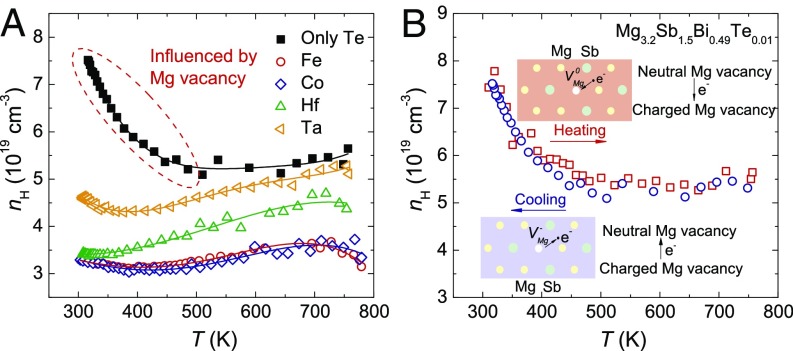
To understand the reason for the variation in carrier scattering mechanisms, temperature-dependent Hall carrier concentrations for different specimens are compared, as shown in Fig. 5A. The Hall carrier concentrations of the double-doped specimens are either nearly temperature-independent (Fe and Co) or increase slightly with temperature (Hf and Ta). In striking contrast, Mg_3.2Sb_1.5Bi_0.49Te_0.01 shows an anomalous temperature-dependent Hall carrier concentration that decreases with temperature in the range of 300–500 K. Such unusual temperature dependence of the Hall carrier concentration has rarely been reported. To confirm the obtained results, the Hall carrier concentration was measured during both heating and cooling cycles, and similar results were observed (Fig. 5B). Repeated measurements were also conducted, with similar results (SI Appendix, Fig. S6). It should be noted that our results are different from those of Tamaki et al. (33); however, the reason for such a difference is unclear at this stage.

Fig. 5.

Temperature-dependent Hall carrier concentrations of Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1A_0.1Sb_1.5Bi_0.49Te_0.01 (A) and the Hall carrier concentration of Mg_3.2Sb_1.5Bi_0.49Te_0.01 during heating and cooling cycles (B). (A = Fe, Co, Hf, and Ta) (Insets) Schematic views of ionization and deionization of the Mg vacancy.

For Mg_3.2Sb_1.5Bi_0.49Te_0.01, the ionized impurity scattering dominates in the same temperature range (Fig. 1B) in which the Hall carrier concentration decreases with temperature. Therefore, the ionized impurity scattering should be closely related to the anomalous temperature dependence of the Hall carrier concentration. More importantly, since the Hall carrier concentration of Mg_3.2Sb_1.5Bi_0.49Te_0.01 is highly reversible during the heating and cooling cycles, this suggests a thermodynamic reason for such a unique temperature dependence of the Hall carrier concentration.

According to the calculation by Tamaki et al. (33), in both the Mg-poor and Mg-rich conditions, negatively charged Mg vacancies are the most stable kinds of defects. It is worth noting that neutral-state vacancies can easily become charged due to their unsaturated bonding capabilities (e.g., dangling bonds). These capabilities facilitate the transfer of an electronic charge between the host matrix and the vacancy, and often occur to the point that the vacancy becomes fully ionized. The degree (different charge states) and direction of electron transfer (toward or away from the vacancy) naturally depend upon the electron richness of the host, as quantified by the host’s Fermi energy in the vicinity of the vacancy (44). The negatively charged Mg vacancy means that the neutral-state Mg vacancy always tends to acquire electrons from the host. In the Mg-rich condition of our specimens, −2 and −3 are the most stable charges for the Mg vacancy.

The ratio of charged Mg vacancy ($V_{Mg}^{2-}$ and $V_{Mg}^{3-}$) to neutral Mg vacancy $V_{Mg}^0$ can be described as follows (44, 45):

$$c_{V_{Mg}^{2-}}/c_{V_{Mg}^0}=\exp \left[-\left(E_{V_{Mg}^{2-}}-2E_F\right)/kT\right],$$ [3]

$$c_{V_{Mg}^{3-}}/c_{V_{Mg}^0}=\exp \left[-\left(E_{V_{Mg}^{3-}}+E_{V_{Mg}^{2-}}-3E_F\right)/kT\right],$$ [4]

where $c_{V_{Mg}^0}$ is the concentration of $V_{Mg}^0$, $c_{V_{Mg}^{2-}}$ is the concentration of $V_{Mg}^{2-}$, $c_{V_{Mg}^{3-}}$ is the concentration of $V_{Mg}^{3-}$, $E_{V_{Mg}^{2-}}$ is the acceptor level energy of $V_{Mg}^{2-}$, $E_{V_{Mg}^{3-}}$ is the acceptor level energy of $V_{Mg}^{3-}$, and $E_F$ is the Fermi level energy.

The thermal equilibrium concentration of the neutral Mg vacancy is expressed as follows (46):

$$c_{V_{Mg}^0}=c_0\exp \left[-g_{V_{Mg}^0}/kT\right],$$ [5]

where c₀ is the crystal atom density and $g_{V_{Mg}^0}$ is the Gibbs free energy of formation of $V_{Mg}^0$.

Therefore, the concentration of charged Mg vacancies is strongly temperature-dependent. In fact, the charged vacancies usually tend to increase with temperature. The charged Mg vacancies will inevitably change with the measured Hall carrier concentration according to the charge neutrality condition (45):

$$n=c_{\text{Te}}-2c_{V_{Mg}^{2-}}-3c_{V_{Mg}^{3-}}+p.$$ [6]

Clearly, the carrier concentration depends upon the concentrations of dopant (Te) and charged defects ($V_{Mg}^{2-}$ and $V_{Mg}^{3-}$), as well as minority carrier (hole) concentration. To explain the temperature dependence of the Hall carrier concentration in Mg_3.2Sb_1.5Bi_0.49Te_0.01, schematic views are shown in Fig. 5B. The neutral Mg vacancy captures the electron and becomes ionized during the heating process, and it releases the electron and returns to the neutral state during the cooling process. The reversible ionization and deionization of the Mg vacancy with respect to temperature will induce the corresponding variation in the Hall carrier concentration.

To prove the existence of Mg vacancies in the n-type Mg₃Sb₂-based materials, neutron powder diffraction was conducted for Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01. The Rietveld refinements for the two specimens are shown in the SI Appendix, Fig. S7. To achieve stable and converging refinement for the neutron powder diffraction of the samples, some assumptions were made, and the details can be found in SI Appendix. The refinement for Mg_3.2Sb_1.5Bi_0.49Te_0.01 indicates that the Mg1 site, [1/3, 2/3, 0.6292(7)], is 100% occupied, while the Mg2 site, (0, 0, 0), is only 89 ± 2% occupied. This implies that Mg vacancies indeed exist in Mg_3.2Sb_1.5Bi_0.49Te_0.01 and that they preferentially locate at the Mg2 site with a concentration of 11 ± 2%. Likewise, in Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01, the Mg1 site, [1/3, 2/3, 0.6236(9)], was found to be fully occupied. Co only dopes onto the Mg2 site, and the total occupancy of this site was found to be 91 ± 2% (SI Appendix, Fig. S7 and Table S1). This implies that the Co doping reduces the concentration of Mg vacancies, which could explain why the transition-metal–doped samples do not show the anomalous temperature dependence of the Hall carrier concentration (Fig. 5A). In addition, it is worth noting that a proposed Mg interstitial site, (0, 0, 1/2), (33) did not fit well to the data, and refinement of the occupancy tended toward zero. Therefore, the location of the extra Mg needs to be further investigated.

One critical question is how the unique temperature dependence of the Hall carrier concentration relates to the variation in the carrier scattering mechanism. In principle, the carrier mobility, when ionized impurity scattering is dominant, can be expressed as follows (39):

$${\mu }_{\mathrm{I}}=2^{7/2}/{\pi }^{3/2}{K}^2{\left(kT\right)}^{3/2}/{\left(m^{\ast }\right)}^{1/2}{e}^3{N}_{\mathrm{I}}{\left[\ln \left(1+b\right)-b/1+b\right]}^{-1},\hspace{0.17em}b=6/\pi K{m}^{\ast }{k}^2{T}^2/n{\hslash }^2{e}^2,$$ [7]

where K is the dielectric constant, N_I is the ionized impurity concentration, k is the Boltzmann constant, and ħ is the reduced Planck’s constant.

According to the Pisarenko plot (Fig. 2B), all of the specimens can be described well by considering different carrier scattering mechanisms with an identical m*, which means the m* should remain unchanged or quite similar after doping. It was previously assumed that the improved mobility is due to an increased dielectric constant after the transition-metal doping (35). Indeed, the dielectric constant is sensitive to the trace amounts of dopants in various material systems (47–53). However, this seems not to be the case for the n-type Mg₃Sb₂-based materials, where the calculated dielectric constants for Mg₃Sb₂ and Mg₃Sb_1.5Bi_0.5 are quite comparable considering the fact that up to 25% of the Sb has been replaced by Bi (SI Appendix, Table S2).

Therefore, the variation in the Hall mobility should not come from the variation in the material’s intrinsic parameters (m* and K). It should be noted that the ionized impurity concentration can be approximated to be the carrier concentration only when one type of dopant is present. In the case of multiple types of dopants, the ionized impurity concentration could be larger than the carrier concentration. In the n-type Mg₃Sb₂-based materials, the ionized impurities include both the ionized Te atoms and the charged Mg vacancies. The Rietveld refinement of neutron powder diffraction and the temperature-dependent Hall carrier concentration show that the double-doped specimens have lower concentrations of charged Mg vacancies. The noticeable difference in thermoelectric properties between the doubled-doped specimens and Mg_3.2Sb_1.5Bi_0.49Te_0.01 indicates that charged Mg vacancies play a central role in the carrier scattering mechanism, and hence the thermoelectric properties of n-type Mg₃Sb₂-based materials. In other words, by reducing the concentration of charged Mg vacancies, the ionized impurity scattering in Mg_3.2Sb_1.5Bi_0.49Te_0.01 changes to the mixed scattering in double-doped specimens.

In both NbFeSb (32) and n-type Mg₃Sb₂-based materials (35), the carrier scattering mechanism at a lower temperature shifted from extrinsic scattering mechanisms (i.e., grain boundary scattering, ionized impurity scattering) toward acoustic phonon scattering. Although different approaches (i.e., increasing hot-pressing temperature, doping) were used, the key idea of manipulating the carrier scattering mechanisms is identical, and relies on the control of defects (i.e., grain boundaries, Mg vacancies). Therefore, to apply this strategy to other material systems, it is first necessary to identify the defect that is responsible for the dominant carrier scattering mechanism and then to try to control it. In fact, since the dominant carrier scattering mechanism (especially in the lower temperature range) could be different for different materials, this concept should be applicable to a variety of other material systems for enhancing thermoelectric performance.

Conclusions

Ionized impurity scattering in the n-type Mg₃Sb₂-based materials is investigated further. Our results demonstrate that by doping transition-metal elements such as Fe, Co, Hf, and Ta at the Mg site of Mg_3.2Sb_1.5Bi_0.49Te_0.01, the dominant ionized impurity scattering at a lower temperature changes to a mixed scattering of acoustic phonons and ionized impurities, thus noticeably improving the Hall mobility and power factor. A simultaneous reduction in thermal conductivity is achieved, and, finally, a ZT of ∼1.7 is obtained in Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01. Our work demonstrates that the carrier scattering mechanism could play a vital role in the thermoelectric properties of the material, and the concept of tuning the carrier scattering mechanism should be widely applicable to a variety of material systems.

Experimental Section

Synthesis.

Mg turnings (99.98%; Alfa Aesar), Bi pieces (99.99%; Alfa Aesar), Sb shots (99.8%; Alfa Aesar), Te pieces (99.999%; Alfa Aesar), Hf crystals (99.9%; Altantic Metals & Alloys), V powders (99.5%; Alfa Aesar), Ta powders (99.9%; Alfa Aesar), Mo powders (99.95%; Alfa Aesar), W powders (99.9%; Alfa Aesar), Fe powders (99%; Alfa Aesar), Co powders (99.5%; Alfa Aesar), Ni powders (99%; Alfa Aesar), and Zn powders (99.9%; Alfa Aesar) were weighed according to the composition of Mg_3.2−xA_xSb_1.5Bi_0.49Te_0.01 (A = Hf, V, Ta, Mo, W, Fe, Co, Ni, and Zn). The elements were loaded into a stainless-steel ball-milling jar in a glove box under an argon atmosphere with an oxygen level below 0.1 ppm. The materials were ball-milled for 10 h and then loaded into a graphite die with an inner diameter of 12.7 mm. The graphite die with the loaded powder was then removed from the glove box and immediately sintered by hot pressing at 923 K under a pressure of ∼80 MPa for 2 min. The hot-pressed disks are about 2–3 mm thick.

Thermoelectric Property Characterizations.

All of the samples were cut into pieces with dimensions of about 2 mm × 2 mm × 12 mm for simultaneous electrical resistivity and Seebeck coefficient characterizations under an He atmosphere (ZEM-3; ULVAC Riko). Thermal conductivity, κ = dDC_p, was calculated using the measured density, d, (SI Appendix, Table S3) determined by the Archimedean method, thermal diffusivity, D, (SI Appendix, Fig. S8A) by determined by the laser flash method (LFA 457; Netzsch), and specific heat, C_p, (SI Appendix, Fig. S8B) by differential scanning calorimetry (DSC 404 C; Netzsch). The Hall coefficient, R_H, was measured at room temperature on a commercial system (PPMS; Quantum Design) using a four-probe configuration, with the magnetic field sweeping between +3 T and −3 T and an electrical current between 10 mA and 20 mA. The temperature-dependent Hall measurement was conducted under a reversible magnetic field of 1.5 T using the Van der Pauw technique from 300 to 773 K. The Hall carrier concentration, n_H, and the carrier mobility, μ, were calculated via the relations n_H = 1/(e·R_H) and μ = R_H/ρ. Thermoelectric properties show good thermal stability during the cooling and heating cycles (SI Appendix, Fig. S9).

Structure and Phase Composition.

The phase composition of the samples was characterized by X-ray diffraction (PANalytical X’pert PRO diffractometer with a Cu K_a radiation source).

Neutron Diffraction.

Neutron powder diffraction data were taken on samples of Mg_3.2Sb_1.5Bi_0.49Te_0.01 and Mg_3.1Co_0.1Sb_1.5Bi_0.49Te_0.01 in an ambient environment on HB-2A at the High Flux Isotope Reactor at Oak Ridge National Laboratory. A GE (115) monochromator (λ = 1.54 Å) and open – 21′ – 12′ collimation corresponding to before the monochromator, before the sample, and before the detector, respectively, were used. Pattern refinement was performed using the Rietveld method in FullProf (54), and the details for the refinement are shown in SI Appendix, Fig. S7 and Table S1.

First Principles Density Functional Calculations.

Dielectric tensors were calculated using the density functional perturbation theory as implemented in the VASP code (55). We used the generalized gradient approximation of Perdew et al. (56) and standard projector-augmented wave pseudopotentials. A planewave cutoff of 520 eV was used for the valence wavefunctions, and the Mg 2p and Bi 5d orbitals were included as valence states. We used relaxed lattice parameters and atomic coordinates for the calculations of dielectric tensors in both Mg₃Sb₂ and Mg₃Sb_1.5Bi_0.5.