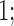Summary
Drawing causal inference with observational studies is the central pillar of many disciplines. One sufficient condition for identifying the causal effect is that the treatment-outcome relationship is unconfounded conditional on the observed covariates. It is often believed that the more covariates we condition on, the more plausible this unconfoundedness assumption is. This belief has had a huge impact on practical causal inference, suggesting that we should adjust for all pretreatment covariates. However, when there is unmeasured confounding between the treatment and outcome, estimators adjusting for some pretreatment covariate might have greater bias than estimators that do not adjust for this covariate. This kind of covariate is called a bias amplifier, and includes instrumental variables that are independent of the confounder and affect the outcome only through the treatment. Previously, theoretical results for this phenomenon have been established only for linear models. We fill this gap in the literature by providing a general theory, showing that this phenomenon happens under a wide class of models satisfying certain monotonicity assumptions.
Keywords: Causal inference, Directed acyclic graph, Interaction, Monotonicity, Potential outcome
1. Introduction
Causal inference from observational data is an important but challenging problem for empirical studies in many disciplines. Under the potential outcomes framework (Neyman, 1923 [1990]; Rubin, 1974), the causal effects are defined as comparisons between the potential outcomes under treatment and control, averaged over a certain population of interest. One sufficient condition for nonparametric identification of the causal effects is the ignorability condition (Rosenbaum & Rubin, 1983), that the treatment is conditionally independent of the potential outcomes given those pretreatment covariates that confound the relationship between the treatment and outcome. To make this fundamental assumption as plausible as possible, many researchers suggest that the set of collected pretreatment covariates should be as rich as possible. It is often believed that ‘typically, the more conditional an assumption, the more generally acceptable it is’ (Rubin, 2009), and therefore ‘in principle, there is little or no reason to avoid adjustment for a true covariate, a variable describing subjects before treatment’ (Rosenbaum, 2002, p. 76).
Simply adjusting for all pretreatment covariates (d’Agostino, 1998; Rosenbaum, 2002; Hirano & Imbens, 2001), sometimes called the pretreatment criterion (VanderWeele & Shpitser, 2011), has a sound justification from the viewpoint of design and analysis of randomized experiments. Cochran (1965), citing Dorn (1953), suggested that the planner of an observational study should always ask himself the question, ‘How would the study be conducted if it were possible to do it by controlled experimentation?’ Following this classical wisdom, Rubin (2007, 2008a, b, 2009) argued that the design of observational studies should be in parallel with the design of randomized experiments, i.e., because we balance all pretreatment covariates in randomized experiments, we should also follow this pretreatment criterion and balance or adjust for all pretreatment covariates when designing observational studies.
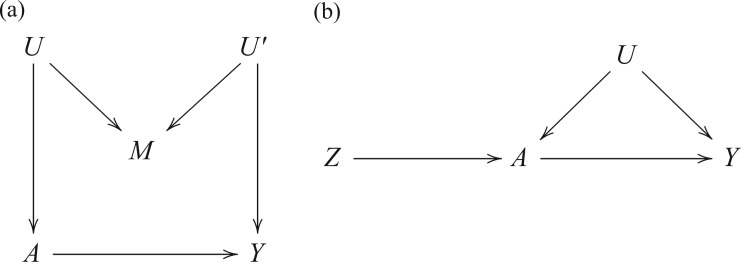
However, this pretreatment criterion can result in increased bias under certain data-generating processes. We highlight two important classes of such processes for which the pretreatment criterion may be problematic. The first class is captured by an example of Greenland & Robins (1986), in which conditioning on a pretreatment covariate invalidates the ignorability assumption and thus a conditional analysis is biased, yet the ignorability assumption holds unconditionally, so an analysis that ignores the covariate is unbiased. Several researchers have shown that this phenomenon is generic when the data are generated under the causal diagram in Fig. 1(a), in which the ignorability assumption holds unconditionally but not conditionally on  (Pearl, 2000; Spirtes et al., 2000; Greenland, 2003; Pearl, 2009; Shrier, 2008, 2009; Sjölander, 2009; Ding & Miratrix, 2015). In Fig. 1(a), a pretreatment covariate
(Pearl, 2000; Spirtes et al., 2000; Greenland, 2003; Pearl, 2009; Shrier, 2008, 2009; Sjölander, 2009; Ding & Miratrix, 2015). In Fig. 1(a), a pretreatment covariate  is associated with two independent unmeasured covariates
is associated with two independent unmeasured covariates 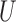 and
and  , but
, but 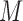 does not itself affect either the treatment
does not itself affect either the treatment 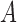 or the outcome
or the outcome 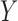 . Because the corresponding causal diagram looks like the English letter M, this phenomenon is called M-bias.
. Because the corresponding causal diagram looks like the English letter M, this phenomenon is called M-bias.
Fig. 1.
Two directed acyclic graphs, where 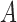 is the treatment and
is the treatment and 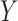 is the outcome of interest. (a) Directed acyclic graph for M-bias, where
is the outcome of interest. (a) Directed acyclic graph for M-bias, where 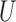 and
and 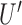 are unobserved and
are unobserved and  is observed. (b) Directed acyclic graph for Z-bias, where
is observed. (b) Directed acyclic graph for Z-bias, where 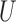 is an unmeasured confounder and
is an unmeasured confounder and 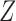 is an instrumental variable for the treatment-outcome relationship.
is an instrumental variable for the treatment-outcome relationship.
The second class of processes, which constitute the subject of this paper, are represented by the causal diagram in Fig. 1(b). Owing to confounding by the unmeasured common cause 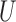 of the treatment
of the treatment 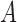 and the outcome
and the outcome 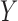 , both the analysis that adjusts and the analysis that fails to adjust for pretreatment measured covariates are biased. If the magnitude of the bias is larger when we adjust for a particular pretreatment covariate than when we do not, we refer to the covariate as a bias amplifier. It is of particular interest to determine the conditions under which an instrumental variable is a bias amplifier. An instrumental variable is a pretreatment covariate that is independent of the confounder
, both the analysis that adjusts and the analysis that fails to adjust for pretreatment measured covariates are biased. If the magnitude of the bias is larger when we adjust for a particular pretreatment covariate than when we do not, we refer to the covariate as a bias amplifier. It is of particular interest to determine the conditions under which an instrumental variable is a bias amplifier. An instrumental variable is a pretreatment covariate that is independent of the confounder 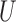 and has no direct effect on the outcome except through its effect on the treatment. The variable
and has no direct effect on the outcome except through its effect on the treatment. The variable 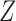 in Fig. 1(b) is an example. Heckman & Navarro-Lozano (2004), Bhattacharya & Vogt (2012) and Middleton et al. (2016) showed numerically that when the treatment and outcome are confounded, adjusting for an instrumental variable can result in greater bias than the unadjusted estimator. Wooldridge theoretically demonstrated this in linear models in a 2006 technical report finally published as Wooldridge (2016). Because instrumental variables are often denoted by
in Fig. 1(b) is an example. Heckman & Navarro-Lozano (2004), Bhattacharya & Vogt (2012) and Middleton et al. (2016) showed numerically that when the treatment and outcome are confounded, adjusting for an instrumental variable can result in greater bias than the unadjusted estimator. Wooldridge theoretically demonstrated this in linear models in a 2006 technical report finally published as Wooldridge (2016). Because instrumental variables are often denoted by 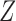 as in Fig. 1(b), this phenomenon is called Z-bias.
as in Fig. 1(b), this phenomenon is called Z-bias.
The treatment assignment is a function of the instrumental variable, the unmeasured confounder and some other independent random error, which are the three sources of variation of the treatment. If we adjust for the instrumental variable, the treatment variation is driven more by the unmeasured confounder, which could result in increased bias due to this confounder. Seemingly paradoxically, without adjusting for the instrumental variable, the observational study is more like a randomized experiment, and the bias due to confounding is smaller. Although applied researchers (Myers et al., 2011; Walker, 2013; Brooks & Ohsfeldt, 2013; Ali et al., 2014) have confirmed through extensive simulation studies that this bias amplification phenomenon exists in a wide range of reasonable models, definite theoretical results have been established only for linear models. We fill this gap in the literature by showing that adjusting for an instrumental variable amplifies bias for estimating causal effects under a wide class of models satisfying certain monotonicity assumptions. However, we also show that there exist data-generating processes under which an instrumental variable is not a bias amplifier.
2. Framework and notation
We consider a binary treatment  , an instrumental variable
, an instrumental variable 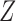 , an unobserved confounder
, an unobserved confounder 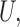 and an outcome
and an outcome 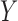 , with the joint distribution depicted by the causal diagram in Fig. 1(b). Let
, with the joint distribution depicted by the causal diagram in Fig. 1(b). Let  denote conditional independence between random variables. Then the instrumental variable
denote conditional independence between random variables. Then the instrumental variable 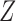 in Fig. 1(b) satisfies
in Fig. 1(b) satisfies 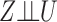 ,
, 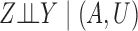 and
and 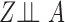 . We first discuss analysis conditional on observed pretreatment covariates
. We first discuss analysis conditional on observed pretreatment covariates 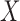 , and comment on averaging over
, and comment on averaging over 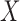 in § 6 and the Supplementary Material. We define the potential outcomes of
in § 6 and the Supplementary Material. We define the potential outcomes of 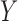 under treatment
under treatment 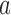 as
as 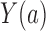
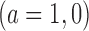 . The true average causal effect of
. The true average causal effect of  on
on  for the population actually treated is
for the population actually treated is
for the population who are actually in the control condition it is
and for the whole population it is
Define 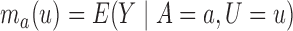 to be the conditional mean of the outcome given the treatment and confounder. As illustrated by Fig. 1(b), because
to be the conditional mean of the outcome given the treatment and confounder. As illustrated by Fig. 1(b), because 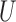 suffices to control confounding between
suffices to control confounding between 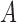 and
and 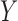 , the ignorability assumption
, the ignorability assumption 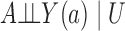 holds for
holds for 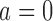 and
and 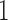 . Therefore, according to
. Therefore, according to 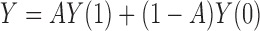 , we have
, we have
The unadjusted estimator is the naive comparison between the treatment and control means,
Define 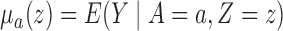 as the conditional mean of the outcome given the treatment and instrumental variable. Because the instrumental variable
as the conditional mean of the outcome given the treatment and instrumental variable. Because the instrumental variable 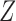 is also a pretreatment covariate unaffected by the treatment, the usual strategy to adjust for all pretreatment covariates suggests using the adjusted estimator for the population under treatment
is also a pretreatment covariate unaffected by the treatment, the usual strategy to adjust for all pretreatment covariates suggests using the adjusted estimator for the population under treatment
for the population under control
and for the whole population
Surprisingly, for linear structural equation models on  , previous theory demonstrated that the magnitudes of the biases of the adjusted estimators are no smaller than the unadjusted ones (Pearl, 2010, 2011, 2013; Wooldridge, 2016). The goal of the rest of our paper is to show that this phenomenon exists in more general scenarios.
, previous theory demonstrated that the magnitudes of the biases of the adjusted estimators are no smaller than the unadjusted ones (Pearl, 2010, 2011, 2013; Wooldridge, 2016). The goal of the rest of our paper is to show that this phenomenon exists in more general scenarios.
3. Scalar instrumental variable and scalar confounder
We first give a theorem for a scalar instrumental variable 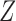 and a scalar confounder
and a scalar confounder 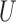 .
.
Theorem 1.
In the causal diagram of Fig. 1 (b) with scalar
and
, suppose that
(a)
is nondecreasing in
,
is nondecreasing in
, and
is nondecreasing in
for both
and
(b)
is nonincreasing in
for both
and
then
(1)
Inequalities among vectors as in (1) should be interpreted as componentwise relationships. Intuitively, the monotonicity in Condition (a) of Theorem 1 requires nonnegative dependence structures on arrows 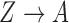 ,
, 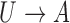 and
and 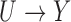 in the causal diagram of Fig. 1(b).
in the causal diagram of Fig. 1(b).
The monotonicity in Condition (b) of Theorem 1 reflects the collider bias caused by conditioning on 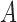 . As noted by Greenland (2003), if
. As noted by Greenland (2003), if 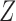 and
and 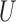 affect
affect 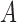 in the same direction, then the collider bias caused by conditioning on
in the same direction, then the collider bias caused by conditioning on 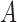 is often, although not always, in the opposite direction. Lemmas S5–S8 in the Supplementary Material show that if
is often, although not always, in the opposite direction. Lemmas S5–S8 in the Supplementary Material show that if 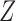 and
and 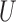 are independent and have nonnegative additive or multiplicative effects on
are independent and have nonnegative additive or multiplicative effects on 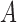 , then conditioning on
, then conditioning on 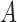 results in negative association between
results in negative association between 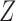 and
and 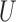 . This negative collider bias, coupled with the positive association between
. This negative collider bias, coupled with the positive association between 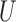 and
and 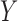 , further implies negative association between
, further implies negative association between 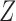 and
and 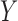 conditional on
conditional on 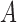 as stated in Condition (b) of Theorem 1.
as stated in Condition (b) of Theorem 1.
For easy interpretation, we will give sufficient conditions for Z-bias when there is no interaction of 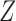 and
and 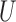 on
on  . When
. When 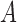 given
given 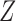 and
and 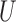 follows an additive model, we have the following theorem.
follows an additive model, we have the following theorem.
Theorem 2.
In the causal diagram of Fig. 1(b) with scalar
and
, (1) holds if
(a)
;
(b)
is nondecreasing in
,
is nondecreasing in
, and
is nondecreasing in
for both
and
;
(c) the essential supremum of
given
depends only on
.
In summary, when 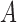 given
given 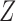 and
and 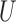 follows an additive model and monotonicity of Theorem 2 holds, both unadjusted and adjusted estimators have nonnegative biases for the true average causal effects for the treatment, control and whole population. Furthermore, the adjusted estimators, for either the treatment, the control or the whole population, have larger biases than the unadjusted estimator, i.e., Z-bias arises.
follows an additive model and monotonicity of Theorem 2 holds, both unadjusted and adjusted estimators have nonnegative biases for the true average causal effects for the treatment, control and whole population. Furthermore, the adjusted estimators, for either the treatment, the control or the whole population, have larger biases than the unadjusted estimator, i.e., Z-bias arises.
When both the instrumental variable 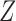 and the confounder
and the confounder 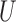 are binary, Theorem 2 has an even more interpretable form. Define
are binary, Theorem 2 has an even more interpretable form. Define 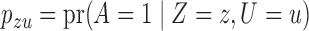 for
for 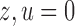 and
and 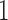 .
.
Corollary 1.
In the causal diagram of Fig. 1(b) with binary
and
, (1) holds if
(a) there is no additive interaction of
and
on
, i.e.,
(b)
and
have monotonic effects on
, i.e.,
and
, and
for both
and
.
When 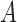 given
given 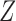 and
and 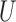 follows a multiplicative model, we have the following theorem.
follows a multiplicative model, we have the following theorem.
Theorem 3.
In the causal diagram of Fig. 1(b) with scalar
and
, (1) holds if we replace Condition (a) of Theorem 2 by
(a
)
.
When both the instrument 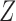 and the confounder
and the confounder 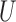 are binary, Theorem 3 can be simplified.
are binary, Theorem 3 can be simplified.
Corollary 2.
In the causal diagram of Fig. 1(b) with binary
and
, (1) holds if we replace Condition (a) of Corollary 1 by
(a
) there is no multiplicative interaction of
and
on
, i.e.,
.
We invoke the assumptions of no additive and multiplicative interaction of 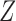 and
and 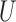 on
on 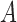 in Theorems 2 and 3 for easy interpretation. They are sufficient but not necessary conditions for Z-bias. In fact, we show in the proofs that Conditions (a) and (a
in Theorems 2 and 3 for easy interpretation. They are sufficient but not necessary conditions for Z-bias. In fact, we show in the proofs that Conditions (a) and (a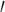 ) in Theorems 2 and 3 and Corollaries 1 and 2 can be replaced by weaker conditions. For the case with binary
) in Theorems 2 and 3 and Corollaries 1 and 2 can be replaced by weaker conditions. For the case with binary 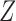 and
and 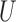 , these conditions are particularly easy to interpret:
, these conditions are particularly easy to interpret:
| (2) |
i.e., 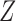 and
and 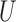 have nonpositive multiplicative interaction on both the presence and absence of
have nonpositive multiplicative interaction on both the presence and absence of 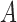 . Even if Condition (a) or (a
. Even if Condition (a) or (a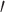 ) does not hold, one can show that half of the parameter space of
) does not hold, one can show that half of the parameter space of 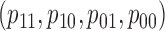 satisfies the weaker condition (2), which is only sufficient, not necessary. Therefore, even in the presence of additive or multiplicative interaction, Z-bias arises in more than half of the parameter space for binary
satisfies the weaker condition (2), which is only sufficient, not necessary. Therefore, even in the presence of additive or multiplicative interaction, Z-bias arises in more than half of the parameter space for binary 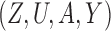 .
.
4. General instrumental variable and general confounder
When the instrumental variable 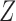 and the confounder
and the confounder 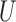 are vectors, Theorems 1–3 still hold if the monotonicity assumptions hold for each component of
are vectors, Theorems 1–3 still hold if the monotonicity assumptions hold for each component of 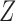 and
and 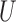 , and
, and 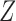 and
and 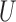 are multivariate totally positive of order two (Karlin & Rinott, 1980), including the case where the components of
are multivariate totally positive of order two (Karlin & Rinott, 1980), including the case where the components of 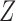 and
and 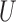 are mutually independent (Esary et al., 1967). A random vector
are mutually independent (Esary et al., 1967). A random vector 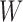 is multivariate totally positive of order two if its density
is multivariate totally positive of order two if its density 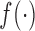 satisfies
satisfies 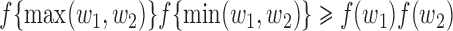 , where
, where 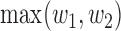 and
and 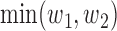 are the componentwise maximum and minimum of the vectors
are the componentwise maximum and minimum of the vectors 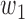 and
and 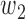 . In the following, we will develop general theory for Z-bias without the total positivity assumption about the components of
. In the following, we will develop general theory for Z-bias without the total positivity assumption about the components of 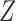 and
and 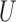 .
.
It is relatively straightforward to summarize a general instrumental variable 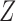 by a scalar propensity score
by a scalar propensity score 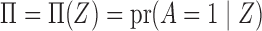 , because
, because 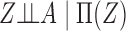 , as shown in Rosenbaum & Rubin (1983). We define
, as shown in Rosenbaum & Rubin (1983). We define 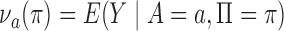 . The adjusted estimator for the population under treatment is
. The adjusted estimator for the population under treatment is
the adjusted estimator for the population under control is
and the adjusted estimator for the whole population is
When 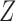 is scalar and
is scalar and 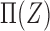 is monotone in
is monotone in 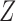 , then the above three formulas reduce to the ones in § 3.
, then the above three formulas reduce to the ones in § 3.
Greenland & Robins (1986) showed that for the causal effect on the treated population, 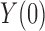 alone suffices to control for confounding; likewise, for the causal effect on the control population,
alone suffices to control for confounding; likewise, for the causal effect on the control population, 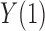 alone suffices to control for confounding. If interest lies in all three of our average causal effects, then we take
alone suffices to control for confounding. If interest lies in all three of our average causal effects, then we take 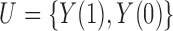 as the ultimate confounder for the relationship of
as the ultimate confounder for the relationship of 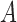 on
on 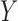 . Because
. Because 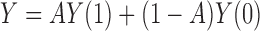 is a deterministic function of
is a deterministic function of 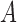 and
and 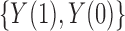 , this implies that
, this implies that 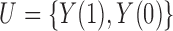 satisfies the ignorability assumption (Rosenbaum & Rubin, 1983), or blocks all the back-door paths from
satisfies the ignorability assumption (Rosenbaum & Rubin, 1983), or blocks all the back-door paths from 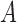 to
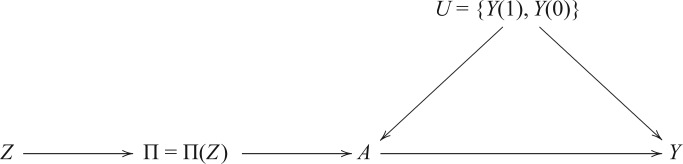
to 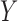 (Pearl, 1995, 2000). We represent the causal structure in Fig. 2.
(Pearl, 1995, 2000). We represent the causal structure in Fig. 2.
Fig. 2.
Directed acyclic graph for Z-bias with general instrument and confounder.
We first state a theorem without assuming the structure of the causal diagram in Fig. 2.
Theorem 4.
If for both
and
,
is nondecreasing in
, and
, then (1) holds.
In a randomized experiment 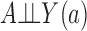 , so the dependence of
, so the dependence of 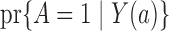 on
on 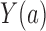 characterizes the self-selection process of an observational study. The condition
characterizes the self-selection process of an observational study. The condition 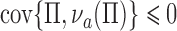 in Theorem 4 is another measure of the collider-bias caused by conditioning on
in Theorem 4 is another measure of the collider-bias caused by conditioning on 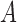 , as
, as 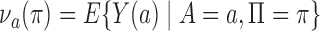 and
and 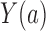 is a component of
is a component of 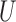 in Fig. 2. This measure of collider bias is more general than the one in Theorem 1. Analogous to § 3, we will present more transparent sufficient conditions for Z-bias to aid interpretation.
in Fig. 2. This measure of collider bias is more general than the one in Theorem 1. Analogous to § 3, we will present more transparent sufficient conditions for Z-bias to aid interpretation.
In the following, we use the distributional association measure (Cox & Wermuth, 2003; Ma et al., 2006; Xie et al., 2008), i.e., a random variable 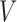 has a nonnegative distributional association on a random variable
has a nonnegative distributional association on a random variable 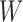 if the conditional distribution satisfies
if the conditional distribution satisfies 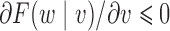 for all
for all 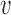 and
and 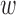 . If the random variables are discrete, then partial differentiation is replaced by differencing between adjacent levels (Cox & Wermuth, 2003).
. If the random variables are discrete, then partial differentiation is replaced by differencing between adjacent levels (Cox & Wermuth, 2003).
If there is no additive interaction between  and
and 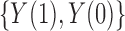 on
on 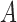 , then we have the following results.
, then we have the following results.
Theorem 5.
In the causal diagram of Fig. 2, (1) holds if
(a)
with
and
nondecreasing;
(b)
have nonnegative distributional associations on each other, i.e.,
and
for all
and
;
(c) the essential supremum of
given
does not depend on
, and the essential supremum of
given
does not depend on
.
Remark 1.
If we impose an additive model
then independence of
and
implies that
Therefore, we must have
and
.
When the outcome is binary, the distributional association between 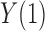 and
and 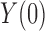 becomes their odds ratio (Xie et al., 2008), and nonnegative distributional association between
becomes their odds ratio (Xie et al., 2008), and nonnegative distributional association between 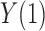 and
and 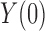 is equivalent to
is equivalent to
We can further relax the model assumption of 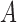 given
given 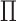 and
and 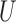 by allowing for nonnegative interaction between
by allowing for nonnegative interaction between 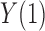 and
and 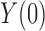 on
on 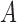 .
.
Corollary 3.
In the causal diagram of Fig. 2 with a binary outcome
, (1) holds if
(a)
with
;
(b)
.
Remark 2.
If we have an additive model of
given
and
,
then the functional form
imposes no restriction for a binary outcome. Furthermore,
implies that
and
, i.e.,
. Therefore, the additive model in Condition (a) of Corollary 3 is
If there is no multiplicative interaction of  and
and 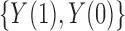 on
on 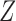 , then we have the following results.
, then we have the following results.
Theorem 6.
In the causal diagram of Fig. 2, (1) holds if we replace Condition (a) of Theorem 5 by
with
and
nondecreasing.
Corollary 4.
In the causal diagram of Fig. 2 with a binary outcome
, (1) holds if we replace Condition (a) of Corollary 3 by
5. Illustrations
5.1 Numerical examples
Myers et al. (2011) simulated binary 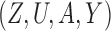 to investigate Z-bias. They generated
to investigate Z-bias. They generated 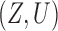 according to
according to 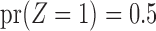 and
and 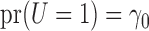 . The first set of their generative models is additive,
. The first set of their generative models is additive,
| (3) |
where the coefficients are all positive. The second set of their generative models is multiplicative,
| (4) |
where the coefficients in (3) and (4) are all positive. They use simulation to show that Z-bias arises under these models. In fact, in the above models, 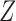 and
and 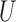 have monotonic effects on
have monotonic effects on 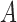 without additive or multiplicative interactions, and
without additive or multiplicative interactions, and 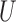 acts monotonically on
acts monotonically on 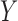 , given
, given 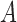 . Therefore, Corollaries 1 and 2 imply that Z-bias must occur. The qualitative conclusion follows immediately from our theory. However, our theory does not make statements about the magnitude of the bias, and for more details about the magnitude and finite-sample properties, see Myers et al. (2011).
. Therefore, Corollaries 1 and 2 imply that Z-bias must occur. The qualitative conclusion follows immediately from our theory. However, our theory does not make statements about the magnitude of the bias, and for more details about the magnitude and finite-sample properties, see Myers et al. (2011).
We use three numerical examples to illustrate the role of the no-interaction assumptions required by Theorems 2 and 3 and Corollaries 1 and 2. Recall the conditional probability of the treatment 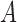 ,
, 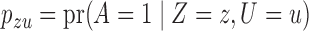 , and define the conditional probabilities of the outcome
, and define the conditional probabilities of the outcome 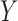 as
as 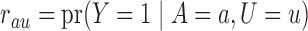 , for
, for 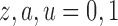 . Table 1 gives three examples where monotonicity on the conditional distributions of
. Table 1 gives three examples where monotonicity on the conditional distributions of  and
and  hold, and there are both additive and multiplicative interactions. In all cases, the instrumental variable
hold, and there are both additive and multiplicative interactions. In all cases, the instrumental variable  is Ber
is Ber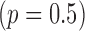 , and the confounder
, and the confounder  is another independent Ber
is another independent Ber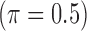 . In Case 1, the weaker condition (2) holds, and our theory implies that Z-bias arises. In Case 2, neither the condition in Theorem 1 nor (2) holds, but Z-bias still arises. Our conditions are only sufficient but not necessary. In Case 3, neither the condition in Theorem 1 nor (2) holds, and Z-bias does not arise.
. In Case 1, the weaker condition (2) holds, and our theory implies that Z-bias arises. In Case 2, neither the condition in Theorem 1 nor (2) holds, but Z-bias still arises. Our conditions are only sufficient but not necessary. In Case 3, neither the condition in Theorem 1 nor (2) holds, and Z-bias does not arise.
Table 1.
Examples of the presence and absence of Z-bias, in which
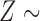 Ber
Ber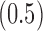 ,
, 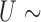 Ber
Ber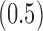 , the conditional probability of the treatment
, the conditional probability of the treatment 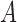 is
is 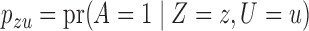 , and the conditional probability of the outcome
, and the conditional probability of the outcome  is
is 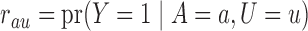
| Case |
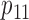
|
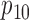
|
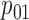
|
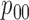
|
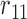
|
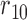
|
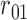
|
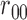
|
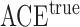
|
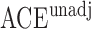
|
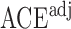
|
Z-bias |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 |
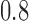
|
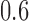
|
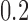
|
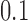
|
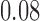
|
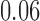
|
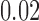
|
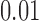
|
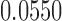
|
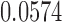
|
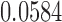
|
YES |
| 2 |
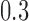
|
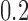
|
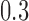
|
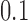
|
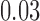
|
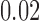
|
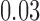
|
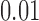
|
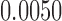
|
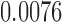
|
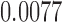
|
YES |
| 3 |
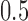
|
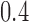
|
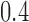
|
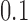
|
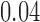
|
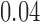
|
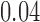
|
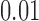
|
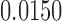
|
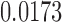
|
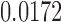
|
NO |
Finally, for binary 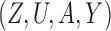 we use Monte Carlo simulation to compute the volume of the Z-bias space, i.e., the parameter space of
we use Monte Carlo simulation to compute the volume of the Z-bias space, i.e., the parameter space of 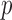 ,
,  ,
, 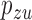 s and
s and 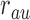 s in which the adjusted estimator has higher bias than the unadjusted estimator. We randomly draw these ten probabilities from independent Un
s in which the adjusted estimator has higher bias than the unadjusted estimator. We randomly draw these ten probabilities from independent Un random variables, and for each draw of these probabilities we compute the average causal effect
random variables, and for each draw of these probabilities we compute the average causal effect 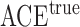 , the unadjusted estimator
, the unadjusted estimator 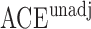 and the adjusted estimator
and the adjusted estimator 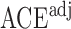 . We plot the joint values of the biases
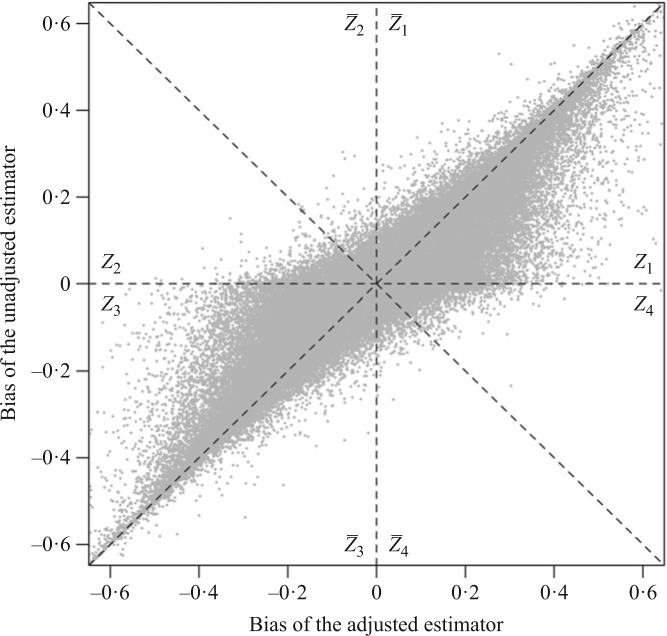
. We plot the joint values of the biases 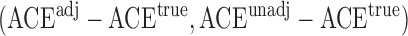 in Fig. 3. The volume of the Z-bias space can be approximated by the frequency that
in Fig. 3. The volume of the Z-bias space can be approximated by the frequency that 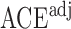 deviates more from
deviates more from 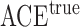 than
than 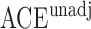 . With
. With 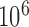 random draws, our simulation gives an unbiased estimate for this volume as
random draws, our simulation gives an unbiased estimate for this volume as 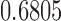 with estimated standard error
with estimated standard error 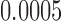 . Therefore, in about
. Therefore, in about 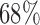 of the parameter space, the adjusted estimator is more biased than the unadjusted estimator.
of the parameter space, the adjusted estimator is more biased than the unadjusted estimator.
Fig. 3.
Biases of the adjusted and unadjusted estimators over 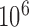 random draws of the probabilities. In areas
random draws of the probabilities. In areas  Z-bias arises, and in areas
Z-bias arises, and in areas 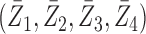 Z-bias does not arise.
Z-bias does not arise.
5.2 Real data examples
Bhattacharya & Vogt (2012) presented an example about the treatment effect of small classrooms in the third grade on test scores for reading, where the instrumental variable is the random assignment to small classrooms. Their instrumental variable analysis gave a point estimate of 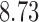 with standard error
with standard error 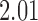 . Without adjusting for the instrumental variable in the propensity score model, the point estimate was
. Without adjusting for the instrumental variable in the propensity score model, the point estimate was 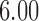 with estimated standard error
with estimated standard error 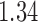 ; adjusting for the instrumental variable, the point estimate was
; adjusting for the instrumental variable, the point estimate was 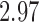 with estimated standard error
with estimated standard error 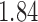 . The difference between the adjusted estimator and the instrumental variable estimator is larger than that between the unadjusted estimator and the instrumental variable estimator.
. The difference between the adjusted estimator and the instrumental variable estimator is larger than that between the unadjusted estimator and the instrumental variable estimator.
Wooldridge (2010, Example 21.3) discusses estimating the effect of attaining at least seven years of education on fertility, with the treatment 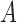 being a binary indicator for at least seven years of education, the outcome
being a binary indicator for at least seven years of education, the outcome 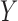 being the number of living children, and the instrumental variable
being the number of living children, and the instrumental variable 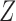 being a binary indicator of whether the woman was born in the first half of the year. Although the original dataset of Wooldridge (2010) contains other variables, most of them are posttreatment variables, so we do not adjust for them in our analysis. The instrumental variable analysis gives point estimate
being a binary indicator of whether the woman was born in the first half of the year. Although the original dataset of Wooldridge (2010) contains other variables, most of them are posttreatment variables, so we do not adjust for them in our analysis. The instrumental variable analysis gives point estimate 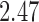 with estimated standard error
with estimated standard error 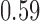 . The unadjusted analysis gives point estimate
. The unadjusted analysis gives point estimate 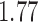 with estimated standard error
with estimated standard error 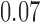 . The adjusted analysis gives point estimate
. The adjusted analysis gives point estimate 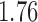 with estimated standard error
with estimated standard error 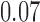 . Table 2 summarizes the results. In this example, the adjusted and unadjusted estimators give similar results.
. Table 2 summarizes the results. In this example, the adjusted and unadjusted estimators give similar results.
Table 2.
The example from Wooldridge (2010)
| Point estimate | Standard error | Lower confidence limit | Upper confidence limit | |
|---|---|---|---|---|
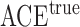
|
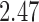
|
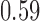
|
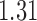
|
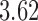
|
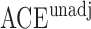
|
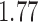
|
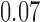
|
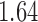
|
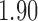
|
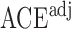
|
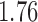
|
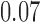
|
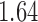
|
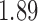
|
6. Discussion
6.1 Allowing an arrow from 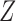 to
to 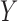
When the variable 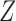 has an arrow to the outcome
has an arrow to the outcome  as illustrated by Fig. 4, the following generalization of Theorem 1 holds.
as illustrated by Fig. 4, the following generalization of Theorem 1 holds.
Fig. 4.
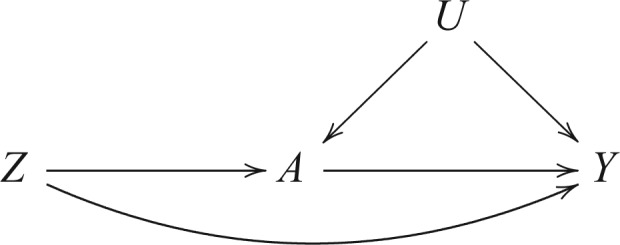
Directed acyclic graph for Z-bias allowing an arrow from 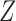 to
to 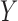
Theorem 7.
Consider the causal diagram of Fig. 4 with scalar
and
, where
and
for
and
. The result in (1) holds if we replace Condition (a) of Theorem 1 by
However, when there is an arrow from 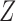 to
to 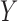 , Theorem 7 is of little use in practice without strong substantive knowledge about the size of the direct effect of
, Theorem 7 is of little use in practice without strong substantive knowledge about the size of the direct effect of 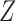 on
on 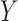 . In particular, neither Theorem 2 nor Theorem 3 is true when an arrow from
. In particular, neither Theorem 2 nor Theorem 3 is true when an arrow from 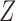 to
to 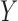 is added to Fig. 1(b). This reflects the fact that neither the absence of an additive nor the absence of a multiplicative interaction of
is added to Fig. 1(b). This reflects the fact that neither the absence of an additive nor the absence of a multiplicative interaction of 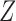 and
and 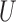 on
on 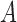 is sufficient to conclude that
is sufficient to conclude that 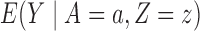 is nonincreasing in
is nonincreasing in 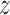 when
when 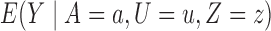 is nondecreasing in
is nondecreasing in 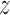 and
and 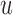 .
.
With a general instrumental variable and a general confounder, Theorem 4 holds without any assumptions on the underlying causal diagram, and therefore it holds even if the variable 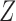 affects the outcome directly. However, Theorems 5 and 6 no longer hold if an arrow from
affects the outcome directly. However, Theorems 5 and 6 no longer hold if an arrow from 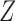 to
to 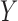 is added to Fig. 2. This reflects the fact that the absence of an additive or multiplicative interaction of
is added to Fig. 2. This reflects the fact that the absence of an additive or multiplicative interaction of 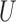 and
and 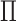 on
on 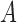 no longer implies
no longer implies 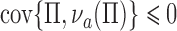 when
when 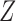 has a direct effect on
has a direct effect on 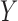 , even if the remaining conditions of Theorems 5 and 6 hold. Analogously, Theorems 5 and 6 no longer hold if there exists an unmeasured common cause of
, even if the remaining conditions of Theorems 5 and 6 hold. Analogously, Theorems 5 and 6 no longer hold if there exists an unmeasured common cause of 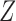 and
and 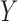 on the causal diagram in Fig. 2, even if
on the causal diagram in Fig. 2, even if 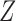 has no direct effect on
has no direct effect on 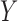 .
.
6.2 Extensions
In §§ 2–4, we discussed Z-bias for the average causal effects. We can extend the results to distributional causal effects for general outcomes (Ju & Geng, 2010) and causal risk ratios for binary or positive outcomes. Moreover, the results in §§ 2–4 are conditional on or within the strata of observed covariates. Similar results hold for causal effects averaged over observed covariates. We give more details in the Supplementary Material. In this paper we have given sufficient conditions for the presence of Z-bias; future work could consider sufficient conditions for the absence of Z-bias.
6.3 Conclusion
It is often suggested that we should adjust for all pretreatment covariates in observational studies. However, we show that in a wide class of models satisfying certain monotonicity conditions, adjusting for an instrumental variable actually amplifies the impact of the unmeasured treatment-outcome confounding, which results in more bias than the unadjusted estimator. In practice, we may not be sure about whether a covariate is a confounder, for which one needs to control, or perhaps instead an instrumental variable, for which control would only increase any existing bias due to unmeasured confounding. Therefore, a more practical approach, as suggested by Rosenbaum (2010, Ch. 18.2), Brookhart et al. (2010) and Pimentel et al. (2016), may be to conduct analysis both with and without adjusting for the covariate. If two analyses give similar results, as in the example in Table 2, then we need not worry about Z-bias; otherwise, we need additional information and analysis before making decisions.
Supplementary Material
Acknowledgement
Ding was partially supported by the U.S. Institute of Education Sciences, and VanderWeele by the U.S. National Institutes of Health. VanderWeele and Robins are also affiliated with the Department of Biostatistics at the Harvard T. H. Chan School of Public Health. The authors thank the associate editor and two reviewers for detailed and helpful comments.
Supplementary material
Supplementary material available at Biometrika online includes the proofs and extensions.
References
- Ali, M. S., Groenwold, R. H. & Klungel, O. H. (2014). Propensity score methods and unobserved covariate imbalance: Comments on “Squeezing the balloon”. Health Serv. Res. 49, 1074–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya, J. & Vogt, W. B. (2012). Do instrumental variables belong in propensity scores? Int. J. Statist. Econ. 9, 107–27. [Google Scholar]
- Brookhart, M. A., Stürmer, T., Glynn, R. J., Rassen, J. & Schneeweiss, S. (2010). Confounding control in healthcare database research: Challenges and potential approaches. Med. Care 48, S114–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks, J. M. & Ohsfeldt, R. L. (2013). Squeezing the balloon: Propensity scores and unmeasured covariate balance. Health Serv. Res. 48, 1487–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cochran, W. G. (1965). The planning of observational studies of human populations (with Discussion). J. R. Statist. Soc. A 128, 234–66. [Google Scholar]
- Cox, D. & Wermuth, N. (2003). A general condition for avoiding effect reversal after marginalization. J. R. Statist. Soc. B 65, 937–41. [Google Scholar]
- D’Agostino, R. B. (1998). Tutorial in biostatistics: Propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Statist. Med. 17, 2265–81. [DOI] [PubMed] [Google Scholar]
- Ding, P. & Miratrix, L. W. (2015). To adjust or not to adjust? Sensitivity analysis of M-Bias and Butterfly-Bias (with comments). J. Causal Infer. 3, 41–57. [Google Scholar]
- Dorn, H. F. (1953). Philosophy of inferences from retrospective studies. Am. J. Public Health Nations Health 43, 677–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esary, J. D., Proschan, F. & Walkup, D. W. (1967). Association of random variables, with applications. Ann. Math. Statist. 38, 1466–74. [Google Scholar]
- Greenland, S. (2003). Quantifying biases in causal models: Classical confounding vs collider-stratification bias. Epidemiology 14, 300–6. [PubMed] [Google Scholar]
- Greenland, S. & Robins, J. M. (1986). Identifiability, exchangeability, and epidemiological confounding. Int. J. Epidemiol. 15, 413–9. [DOI] [PubMed] [Google Scholar]
- Heckman, J. & Navarro-Lozano, S. (2004). Using matching, instrumental variables, and control functions to estimate economic choice models. Rev. Econ. Statist. 86, 30–57. [Google Scholar]
- Hirano, K. & Imbens, G. W. (2001). Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization. Health Serv. Outcomes Res. Methodol. 2, 259–78. [Google Scholar]
- Ju, C. & Geng, Z. (2010). Criteria for surrogate end points based on causal distributions. J. R. Statist. Soc. B 72, 129–42. [Google Scholar]
- Karlin, S. & Rinott, Y. (1980). Classes of orderings of measures and related correlation inequalities. I. Multivariate totally positive distributions. J. Mult. Anal. 10, 467–98. [Google Scholar]
- Ma, Z., Xie, X. & Geng, Z. (2006). Collapsibility of distribution dependence. J. R. Statist. Soc. B 68, 127–33. [Google Scholar]
- Middleton, J. A., Scott, M. A., Diakow, R. & Hill, J. L. (2016). Bias amplification and bias unmasking. Polit. Anal., 24, 307–23. [Google Scholar]
- Rothman, Joffe & Glynn]myers2011effects Myers, J. A., Rassen, J. A., Gagne, J. J., Huybrechts, K. F., Schneeweiss, S., Rothman, K. J., Joffe, M. M. & Glynn, R. J. (2011). Effects of adjusting for instrumental variables on bias and precision of effect estimates. Am. J. Epidemiol. 174, 1213–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neyman, J. (1923. [1990]). On the application of probability theory to agricultural experiments. Essay on principles. Section 9 Translated by Dabrowska D. M. and Speed T. P.. Statist. Sci. 5, 465–72. [Google Scholar]
- Pearl, J. (1995). Causal diagrams for empirical research (with Discussion). Biometrika 82, 669–88. [Google Scholar]
- Pearl, J. (2000). Causality: Models, Reasoning and Inference. Cambridge: Cambridge University Press. [Google Scholar]
- Pearl, J. (2009). Letter to the editor. Statist. Med. 28, 1415–6. [Google Scholar]
- Pearl, J. (2010). On a class of bias-amplifying variables that endanger effect estimates. In Proc. 26th Conf. Uncert. Artif. Intel. (UAI 2010), Grunwald P. & Spirtes, P. eds. Corvallis, Oregon: Association for Uncetainty in Artificial Intelligence, pp. 425–32. [Google Scholar]
- Pearl, J. (2011). Invited commentary: Understanding bias amplification. Am. J. Epidemiol. 174, 1223–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl, J. (2013). Linear models: A useful “microscope” for causal analysis. J. Causal Infer. 1, 155–70. [Google Scholar]
- Pimentel, S. D., Small, D. S. & Rosenbaum, P. R. (2016). Constructed second control groups and attenuation of unmeasured biases. J. Am. Statist. Assoc., 111, 1157–67. [Google Scholar]
- Rosenbaum, P. R. (2002). Observational Studies. New York: Springer, 2nd ed. [Google Scholar]
- Rosenbaum, P. R. (2010). Design of Observational Studies. New York: bSpringer. [Google Scholar]
- Rosenbaum, P. R. & Rubin, D. B. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika 70, 41–55. [Google Scholar]
- Rubin, D. B. (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. J. Educ. Psychol. 66, 688–701. [Google Scholar]
- Rubin, D. B. (2007). The design versus the analysis of observational studies for causal effects: Parallels with the design of randomized trials. Statist. Med. 26, 20–36. [DOI] [PubMed] [Google Scholar]
- Rubin, D. B. (2008a). Author’s reply. Statist. Med. 27, 2741–2. [Google Scholar]
- Rubin, D. B. (2008b). For objective causal inference, design trumps analysis. Ann. Appl. Statist. 2, 808–40. [Google Scholar]
- Rubin, D. B. (2009). Should observational studies be designed to allow lack of balance in covariate distributions across treatment groups? Statist. Med. 28, 1420–3. [Google Scholar]
- Shrier, I. (2008). Letter to the editor. Statist. Med. 27, 2740–1. [DOI] [PubMed] [Google Scholar]
- Shrier, I. (2009). Propensity scores. Statist. Med. 28, 1315–8. [DOI] [PubMed] [Google Scholar]
- Sjölander, A. (2009). Propensity scores and M-structures. Statist. Med. 28, 1416–20. [DOI] [PubMed] [Google Scholar]
- Spirtes, P., Glymour, C. N. & Scheines, R. (2000). Causation, Prediction, and Search. Cambridge: MIT Press, 2nd ed. [Google Scholar]
- VanderWeele, T. J. & Shpitser, I. (2011). A new criterion for confounder selection. Biometrics 67, 1406–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, A. M. (2013). Matching on provider is risky. J. Clin. Epidemiol. 66, S65–8. [DOI] [PubMed] [Google Scholar]
- Wooldridge, J. (2016). Should instrumental variables be used as matching variables? Res. Econ. 70, 232–7. [Google Scholar]
- Wooldridge, J. M. (2010). Econometric Analysis of Cross Section and Panel Data. Cambridge: MIT Press, 2nd ed. [Google Scholar]
- Xie, X., Ma, Z. & Geng, Z. (2008). Some association measures and their collapsibility. Statist. Sinica 18, 1165–83. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.