Super-swelled lyotropic single crystals

Significance

Lipids self-assemble in water into diverse polycrystalline mesophases. The swelling capacity of these superstructures is finite, specific, and traditionally dictated by lipid composition. Bicontinuous cubic phases have tremendous potential in drug delivery and protein crystallization. However, limited swelling caps unit cells at dimensions too small to encapsulate many drugs and most proteins. In this work, we discovered that bicontinuous cubic phase swelling is not solely determined by lipid composition. Self-assembly conditions yield stable unit cell sizes fourfold larger than usual. Unexpectedly, these conditions also dictate mesophase ordering resulting in X-ray and electron microscopy diffraction patterns that do not conform to polycrystallinity. Instead, macroscale super-swelled single crystals are encountered. This discovery highlights insights in understanding swelling and ordering of self-assembled materials.

Abstract

Lipids self-assemble into diverse supramolecular structures that exhibit thermotropic and/or lyotropic behavior. Lyotropic mesophases, where membranes conform to periodic minimal surfaces dividing two nonpenetrating aqueous subspaces, are arguably one of the most intriguing phases of lipid materials. Traditional 3D bicontinuous cubic lipid materials appear as a polycrystal of varying degrees of order. When exposed to water, the properties of the molecular building blocks of the membrane determine specific swelling limits setting the lattice dimensions at about 15 nm. This limited swelling severely impairs their application as delivery vehicles of large drugs or as matrices for guiding protein crystallization. We report the discovery of self-assembly strategies leading to the emergence of lipid bicontinuous single crystals with unprecedented swelling capacity. The conventional strategy to increase unit cell size is tweaking membrane composition to include charged building blocks, a process to achieve electrostatic-driven swelling. In this paper, we demonstrate that controlling self-assembly external conditions when coupled to membrane composition yields 3D bicontinuous cubic phases that swell up to lattice dimensions of 68 nm. Importantly, and contrary to what is perceived for soft lyotropic materials in general, the self-assembly methodology enables the development of large super-swelled monocrystals. Utilizing small-angle X-ray scattering and cryoelectron microscopy, we underpin three crucial factors dictating the stabilization of super-swelled lipid bicontinuous cubic single crystals: (i) organic solvent drying speed, (ii) membrane charge density, and (iii) polyethylene glycol-conjugated lipids amount.

Lyotropic lipid bicontinuous cubic phases are thermodynamically stable materials (1) described by periodic minimal surfaces (lipid bilayers) that divide the 3D space into two distinct water domains (2). In nature, lipid bicontinuous cubic phases have been identified in different cells and organelles such as mitochondria and the endoplasmic reticulum (3–8). In addition to biocompatibility, lipid bicontinuous cubic phases have several structural advantages, including isotropic molecular exchange, fusogenic ability, and high encapsulating power of hydrophilic and hydrophobic molecules (9–12). Important examples include nucleic acid loading for gene delivery applications (9, 13) and guiding of protein crystallization (14). Other applications, such as directed assembly of hard materials, have been recently proposed as well (15–17). Restrictions to the use of these lyotropic materials are small unit cells and concomitant narrow water channels (typical diameters, d_w = 5 nm) (18). Finding strategies to expand unit cells without compromising periodicity and ordering is a major challenge that a number of scientists are seeking to overcome (19–22).

The original modulator of unit cell sizes is based on electrostatic repulsion between lipid layers. This can be done by incorporating charged lipids (9, 23). In this case, unit cell dimensions double the size without loss of crystallinity (9). Another example is addition of lipids having headgroups covalently linked to polyethylene glycol (PEG-lipid) (13). Cholesterol alters the curvature at the bilayer−water interface through lipid tail ordering and increased hydration of headgroups (19, 24, 25). This molecular shape alteration changes curvature moduli in such a way as to increase the unit cell dimension by a few nanometers. Barriga et al. (20) recently reported a highly swelled 48-nm unit cell size bicontinuous primitive cubic phase through incorporation of negatively charged lipids and cholesterol into a glycerol monooleate (GMO) membrane at 54 °C.

Most soft materials self-assemble into polycrystalline mesophases yielding the typical X-ray ring diffraction patterns. However, several studies have reported that 3D bicontinuous cubic phases can exist as single crystals. This is possible for binary mixtures of water and ethylene oxide surfactants (26, 27). More recently, GMO lipids dispersed in a binary solvent (water/butandiol) displayed different degrees of ordering, depending on solvent ratio (28). In these well-ordered systems, the unit cell dimensions fluctuate between 10 nm (nonionic surfactants) and 15 nm (lipid case). In fact, Bruinsma (29) postulated a swelling limit for primitive bicontinuous cubic unit cells at finite temperature. It was predicted that, above a certain unit cell size (∼30 nm, depending on bilayer thickness, bending rigidity, and temperature), fluctuations would damp periodicity and order of the bicontinuous cubic matrix.

In this work, we discovered a lipid mixture processing method leading to super-swelled and stable bicontinuous cubic structures having unit cell dimensions (a) up to 68.4 nm at room temperature. The membranes are composed of GMO, charged lipids, and a few mol % of PEG-lipid. Importantly, these materials remain super-swelled and develop to large single-crystal monoliths.

Results and Discussion

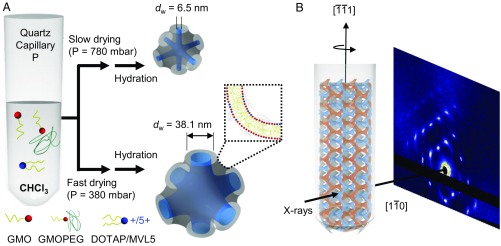
We report a nonequilibrium lipid self-assembly approach to generate bicontinuous phases with extremely large water channels with three kinds of minimal surfaces: primitive, Im3m; diamond, Pn3m; and gyroid, Ia3d. The process relies on fast organic solvent drying of a tricomponent lipid cake having GMOs, charged phospholipids, and PEG-lipids. Specifically, when chloroform is dried slowly at vapor pressure (P = 780 mbar) and the lipid cake is subsequently hydrated with excess water (30), the bicontinuous cubic phase obtained is a primitive lattice type of regular unit cell dimensions a = 16.6 nm, corresponding to water channels of d_w = 6.5 nm (31). Conversely, if the lipid cake is dried fast (P = 380 mbar), hydration yields unit cell dimensions reaching a = 68.4 nm, corresponding to water channels of d_w = 38.1 nm (31). The process is schematically represented in Fig. 1A. A single unit cell is sketched such that the water channels are represented in blue and the midplane of the lipid bilayer is represented as a gray minimal surface. We used a tricomponent lipid mixture (SI Appendix, Fig. S1 shows the chemical structures of each lipid) composed of (i) GMO, (ii) net positively charged lipid [1,2-dioleoyl-3-trimethylammonium propane (DOTAP) or N1-[2-((1S)-1-[(3-aminopropyl)amino]-4-[di(3-amino-propyl)amino]butylcarboxamido)ethyl]-3,4-di[oleyloxy]-benzamide (MVL5)], and (iii) custom-designed GMO lipid conjugated to 2 kDa PEG (GMOPEG). The calculated volume of a lipid chloroform solution to achieve the desired molar fraction of each lipid component is added directly to a 1.5-mm-o.d. quartz capillary. The samples are then dried in a rotary evaporator at the desired vapor pressures. We have previously established (13) that a GMO/DOTAP/GMOPEG lipid mixture at 95/4/1 mol ratios yields an equilibrium primitive bicontinuous cubic phase with lattice constant of a = 16 nm. However, if chloroform is dried fast (using vacuum or a rotary evaporator), rehydration results in the same type of phase but swelled up to 4.3 times at room temperature. After storage over a few weeks, it was found that super-swelled bicontinuous cubic phases develop as 1-mm³-sized single crystals, as shown in Fig. 1B. This indicates that it is possible to kinetically trap super-swelled states that remain stable and with maximum ordering. These results are in line with the general observation that metastability in lipid systems allows for additional control and diversity of the phase space (32).

Fig. 1.

Schematics of nonequilibrium lipid self-assembly and single-crystal scattering. (A) Lipids (GMO, a charged lipid, and a PEG-lipid) dissolved in chloroform are directly transferred to 1.5-mm quartz capillaries. The chloroform is extracted at specific pressures to control evaporation rate. Upon hydration, the systems where chloroform was quickly and fully extracted yield unit cell sizes expanded 400% compared with the equilibrium structure. (B) Schematics of a lipid super-swelled bicontinuous cubic single crystal and corresponding X-ray diffraction pattern.

Effect of Drying Speed.

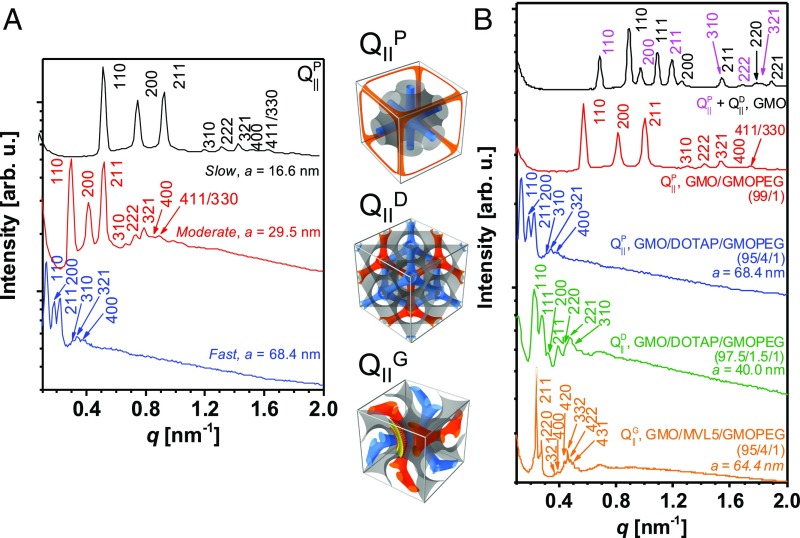
To explore the effect of organic solvent drying speed on unit cell dimensions, we dried lipid mixtures dissolved in chloroform at different conditions. Fig. 2A shows small-angle X-ray scattering (SAXS) data obtained for a ternary mixture of GMO/DOTAP/GMOPEG (95/4/1 mole ratio) at various drying conditions. Chloroform is dried off the lipid cake using a rotary evaporator operating at pressures of 780, 580, and 380 mbar, corresponding to ∼24, 17, and 12 h of drying time. All samples were further dried for over 48 h, and full solvent removal was confirmed by ¹H NMR (SI Appendix, Fig. S2). After drying, the lipid cake is exposed to excess water for at least 2 d at 45 °C before the structure is investigated by SAXS at room temperature. The SAXS I vs. q data reveal a series of structure factor peaks at relative positions that are conserved as a function of drying speed (black, slow; red, moderate; and blue, fast) but shift to lower q values for faster drying conditions. For the slow-drying sample, eight sharp Bragg reflections are observed, at the reciprocal lattice vectors q/(2π/a) = G_hkl/(2π/a) = (h² + k² + l²)^1/2 = √2, √4, √6, √10, √12, √14, √16, and √18, corresponding to the [110], [200], [211], [310], [222], [321], [400], and [411]/[330] reflections, respectively. These Bragg reflections are unequivocally matched with a primitive bicontinuous cubic structure (space group Im3m) with lattice constant a = 16.6 nm for slow drying (black line). This lattice structure and size are well matched with what was observed for the same system in our previous study (13). The peak indexes follow the Im3m structure rules: (i) hkl (h + k + l = 2n), (ii) 0kl (k + l = 2n), (iii) hhl (l = 2n), (iv) h00 (h = 2n), and (v) hkl (k, l = 2n) (with permutable h, k, and l and where n is an integer) (33). For the sample where chloroform was extracted at moderate speed (P = 580 mbar, red curve), upon water addition, eight Bragg peaks at the same relative positions were obtained, but the lattice spacing increased to a = 2√2π/q₁₁₀ = 29.5 nm. When we further increased the evaporation speed by reducing the pressure to 380 mbar, the Bragg peaks moved to even lower q values, q₁₁₀ = 0.13 nm⁻¹, corresponding to a = 68.4-nm lattice spacing. This surpasses the previously reported enlarged unit cell dimension (a = 48 nm) of a bicontinuous cubic phase (space group Im3m) composed of GMO/cholesterol/1,2-dioleoyl-sn-glycero-3-phospho-l-serine (65/30/5 mol ratio at 54 °C) (20). It is noteworthy that the Bragg reflections have analogous linewidth regardless of drying speed, indicating that the obtained bicontinuous cubic phases after hydration display similar and high degree of ordering.

Fig. 2.

Effect of drying speed and lipid composition. (A) Integrated SAXS data obtained for hydrated GMO/DOTAP/GMOPEG (95/4/1 mol ratio) lipid cakes where chloroform was previously dried at three different pressures (780, 580, and 380 mbar for black, red, and blue lines, respectively). The Bragg peaks correspond to the [110], [200], [211], [310], [222], [321], [400], and [411]/[330] reflections of a bicontinuous primitive Im3m cubic phase. The peaks shift to higher q as drying speed is increased, meaning largest unit cell size (a = 68.4 nm) obtained at the fastest drying speed (380 mbar, blue line). (B) Integrated SAXS data of hydrated lipid samples prepared by nonequilibrium assembly at different lipid compositions. In the GMO/water binary system (black line), primitive and diamond cubic phases (Q_II^P + Q_II^D) of regular spacings are observed. The Bragg peaks Q_II^P and Q_II^D phases are indexed in pink and black, respectively. A 1 mol % addition of GMOPEG induces a phase change into Q_II^P without super-swelling (red line). DOTAP addition (4 mol %, blue line) induces super-swelling of the primitive cubic phase. Decreasing DOTAP content (1.5 mol %, green line) results in a primitive to diamond (Q_II^P → Q_II^D) cubic phase change where both are super-swelled. When DOTAP is substituted with pentavalent lipid MVL5 (GMO/MVL5/GMOPEG 95/4/1, orange line), highly swelled and ordered gyroid phases (Q_II^G) with a = 64.4 nm are observed. A cartoon of the different unit cells (Q_II^P, Q_II^D, and Q_II^G) is represented by the midplane of a lipid bilayer (gray surface) separating two distinct water domains (orange and blue). arb. u., arbitrary units.

Effect of Lipid Composition.

Bicontinuous cubic gyroid phases composed of GMO and small amounts of DOTAP have been shown before to swell up to 23 nm (9). While a pure GMO lipid would only be stable in a gyroid phase at low water content and in the diamond phase at high water content (34), addition of charged lipid (DOTAP) enables the stabilization of the gyroid in excess water (9). The mechanism behind the additional swelling is electrostatic repulsion between positively charged membranes. To understand the effect of lipid composition, we fixed fast drying conditions using the rotary evaporator at P = 380 mbar and prepared hydrated lipid cakes with different lipid molar percentages. The obtained SAXS data are shown in Fig. 2B, corresponding to (i) GMO (black line), (ii) GMO/GMOPEG (99/1, red line), (iii) GMO/DOTAP/GMOPEG (95/4/1, blue line, sample as in Fig. 2A), (iv) GMO/DOTAP/GMOPEG (97.5/1.5/1, green line), and (v) GMO/MVL5/GMOPEG (95/4/1, orange line). Surprisingly, for the GMO−water binary system (Fig. 2B, black line), we found coexistence of primitive and diamond bicontinuous cubic phases (Q_II^P + Q_II^D) at fast chloroform drying conditions. For the diamond Pn3m cubic phase (Q_II^D), there are six sharp peaks found with ratios of √2, √3, √4, √6, √8, and √9, corresponding to the [110], [111], [200], [211], [220], and [221] reflections, respectively (indexed peaks in black color). These indexes also follow the Pn3m cubic structure rules: (i) hkl (h + k + l = 2n), (ii) hkl (h + k, h + l, k + l = 2n), (iii) 0kl (k + l = 2n), and (iv) h00 (h = 2n) (where h, k, and l are permutable and n is an integer) (33), with the additional primitive cubic phase (six Bragg peaks are indexed in pink color). It is noteworthy that the primitive bicontinuous cubic phase has not been observed previously in pure GMO−water binary systems and is not expected to occur as a thermodynamically stable phase in the GMO−water phase diagram (35). This indicates that the obtained primitive bicontinuous cubic phase is a kinetically trapped state arising from fast drying of chloroform. When we incorporate 1 mol % of GMOPEG into the GMO−water binary system, a pure primitive bicontinuous cubic phase (Q_II^P, Fig. 2B, red line) is observed, exactly matching what was observed in our previous study (13). In this case, it seems that the GMO/GMOPEG system is not affected by drying speed of the organic phase, and the unit cell dimensions are retained at a = 15.6 nm. This observation is consistent with a picture where sluggish PEG-lipids inserted in the membrane dampen any kinetic effects of fast drying.

The incorporation of DOTAP (4 mol %) (Fig. 2B, blue line) leads to a swelling of the primitive phase under fast organic solvent drying, as described in Fig. 2A. Interestingly, decreasing the amount of DOTAP to 1.5 mol % (Fig. 2B, green line) leads to a super-swelled phase with 40-nm unit cell dimension but of the diamond type Pn3m (Q_II^D). From these results, we can infer that the presence of charged lipids enhances the kinetic effects on establishing the swelling extent of lipid structures. Importantly, the membrane charge density seems to determine what type of unit cell is preferred. To test this hypothesis, we prepared a tricomponent lipid mixture where 4 mol % of the univalent charged lipid DOTAP is substituted by a multivalent (five positive charges) lipid MVL5. The SAXS scan for a GMO/MVL5/GMOPEG (95/4/1 mol ratio) sample (Fig. 2B, orange line) reveals a large unit cell bicontinuous cubic phase upon water addition (a = 64.4 nm). Interestingly, the Bragg peaks are consistent with a bicontinuous gyroid Ia3d cubic phase (Q_II^G). Eight intense Bragg reflections are observed at the ratios of √6, √8, √14, √16, √20, √22, √24, and √26, corresponding to [211], [220], [321], [400], [420], [332], [422], and [431] plane reflections, respectively. The observed X-ray reflections completely satisfy the gyroid bicontinuous cubic structure of Ia3d space symmetry rules: (i) hkl (h + k + l = 2n), (ii) 0kl (k, l = 2n), (iii) hhl (2h + l = 4n), and (iv) h00, h = 4n (where h, k, and l are permutable and n is an integer) (33). A cartoon of the Q_II^P, Q_II^D, and Q_II^G unit cells where a midplane of a lipid bilayer is represented by a gray surface separating two independent water domains (blue and orange) is represented in Fig. 2.

With these results, we have now established that the presence of a charged lipid determines the ability of a bicontinuous cubic phase to super-swell upon hydration of a lipid cake subjected to fast solvent extraction and that the symmetry of the bicontinuous cubic phase depends on membrane charge density. Higher charge density leads to gyroids being stable in excess water compared with neutral systems where they only exist at low water content. In our previous studies, we found that an increased fraction of charged lipids leads to the stabilization of the gyroid, due to larger unit cell size and higher membrane area per unit cell (13). The gyroid obtained with the pentavalent MVL5 (a = 64.4 nm) can be understood in a similar manner. At this stage, it is unclear why the drying speed of the organic solvent would have such a dramatic effect on the swelling ability of bicontinuous cubic phases, but our data support that it arises by combinatorial effects of the presence of PEG-lipids and charged lipids under fast drying of chloroform. One could suggest that membranes comprising these three components—(i) GMO, (ii) cationic phospholipid, and (iii) PEGylated lipids—are capable of yielding liquid−liquid phase separation (36–39). Upon dissolution of the lipid components in chloroform and subsequent fast drying, one can envisage that lipids partition unevenly in the membrane, leaving some areas of high cationic lipid concentration. This would lead to an enhanced swelling onset that then propagates to the overall structure. SAXS scans on both fast-dried and slowly dried lipid cakes (with no water) reveal no mesoscale structural differences (SI Appendix, Fig. S3), consistent with a picture of membrane domains at the nanoscale.

Using NMR and MALDI-TOF MS, we rule out the possibility of degradation of lipid components or chloroform contamination. SI Appendix, Figs. S4–S6 show ¹H NMR confirming the molecular integrity of all lipids, which eliminates the possibility of hydrolysis of ester groups and/or oxidation of olefins. In addition, the MALDI-TOF MS in SI Appendix, Fig. S7 validates the structure of GMOPEG. To eliminate concerns of degradation upon storage, we performed ¹H NMR of fresh, 3-, and 5-mo-old samples and found no signs of decomposition (SI Appendix, Fig. S8).

Stability of Super-Swelled Single-Crystal Lipid Bicontinuous Cubics.

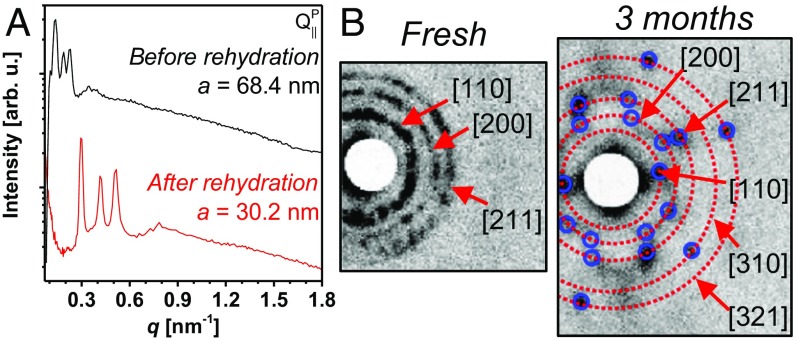
If the super-swelled bicontinuous cubic phase is a metastable state as we hypothesize, dehydration of the lipid structure followed by slow rehydration should result in rearrangements of the unit cell dimensions. We dried out a GMO/DOTAP/GMOPEG (95/4/1 mol ratio) with unit cell dimension of a = 68.4 nm for 7 d in a vacuum desiccator filled with dry desiccants. The loss of weight was about 9 mg, corresponding to 90% of original water weight. We rehydrated the dry lipid cake with Millipore water for 2 d before inspecting the structure by SAXS. Fig. 3A displays SAXS scans of a GMO/DOTAP/GMOPEG (95/4/1) system before desiccation and after rehydration. Both SAXS scans are consistent with a primitive bicontinuous cubic phase (Q_II^P) with different unit cell spacing. As expected, the unit cell dimension is dramatically decreased from 68.4 nm to 30.2 nm. There is a certain level of hysteresis, and the extent of swelling of the rehydrated sample is still higher compared with equilibrium (a = 16 nm). We believe that this hysteresis is a result of the difficulty of fully extracting water from the lipid matrix.

Fig. 3.

Metastability of super-swelled bicontinuous cubic phases. (A) Integrated SAXS data obtained for the GMO/DOTAP/GMOPEG (95/4/1) system at original hydration (black line). This sample is subjected to water removal and subsequent rehydration (red line). SAXS scans reveal that rehydration does not affect phase symmetry (Q_II^P), but it results in smaller unit cells, from a = 68.4 to a = 30.2 nm. (B) SAXS scans of a super-swelled primitive cubic phase (GMO/DOTAP/GMOPEG 95/4/1) showing increasingly ordered structures over time (fresh vs. 3 mo). arb. u., arbitrary units.

A natural follow-up question concerns the temporal stability of the super-swelled bicontinuous cubic phase, which will ultimately determine its practical use. To answer this, we stored a flame-sealed capillary containing the large bicontinuous cubic phase sample at 25 °C for 3 mo and performed SAXS structural investigations. Fig. 3B shows 2D SAXS scattering patterns of a fresh (Left) and a 3-mo-old (Right) sample. The fresh sample showed three clear polycrystalline rings corresponding to the [110], [200], and [211] primitive lattice plane reflections, and outer weak rings corresponding to higher-order diffraction peaks. To our surprise, the sample that was stored for 3 mo yields a diffraction pattern of crystalline spots instead of rings at the same q position. This indicates that the super-swelled bicontinuous cubic phase is stable with time and gets increasingly ordered with storage. Similar ordering in nonionic surfactant systems has been reported previously when samples are stored for several months (27).

Finally, one could argue that the presence of bulky PEG units could hinder the practical use of the super-swelled nanochannels for encapsulation. We challenged this argument by demonstrating a successful encapsulation of large inert solutes. Super-swelled bicontinuous phases encapsulate citric acid-capped 10-nm gold (Au) nanoparticles. This is demonstrated by SAXS and presented in SI Appendix, Fig. S9. Adding Au nanoparticles to the lipid matrix results in homogeneous highly ordered bicontinuous cubic phases. The Q_II phase accommodates Au nanoparticles by expanding unit cells and shifting crystal symmetry !(Q_II^D → Q_II^P → Q_II^G) as the concentration of Au increases (0.5 wt%, 1.5 wt%, and 3 wt%, respectively).

Single-Crystal Analysis.

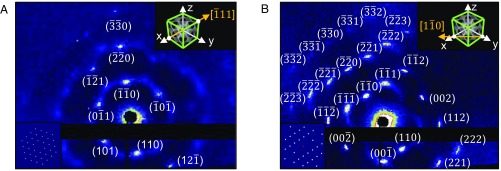
To evaluate the development of single-crystal-like diffraction patterns of the super-swelled bicontinuous cubic phases, we performed Synchrotron SAXS scans on samples that rested for extended periods of time. Fig. 4 displays the scattering patterns of a super-swelled bicontinuous diamond Pn3m cubic phase (Q_II^D) with the composition GMO/DOTAP/GMOPEG (97.5/1.5/1 mol ratio) that was examined after 6 wk storage. The scattering patterns observed are no longer consistent with a polycrystalline sample. Instead, a polygon pattern is clearly visible, with diffraction spots perfectly indexed to the Pn3m Miller planes, as indicated in the Fig. 4. These pattern features are present throughout the entire sample volume of ∼1 mm³, indicating the existence of a single crystal (SI Appendix, Fig. S10 shows diffraction patterns at different spatial locations and rotations). The 2D Synchrotron SAXS scan images from different locations of the single crystal are shown in Fig. 4. In Fig. 4A, nine intense Bragg peaks are indexed up to {330} through Ewald sphere construction (see SI Appendix for detailed indexing and orientation). The Fig. 4A, Top Right Inset schematics show the direct beam direction as [−1 1 1] in the unit cell, determined by plotting the scattered planes in reciprocal space (see SI Appendix for details). A simulated scattering pattern is also represented in the Fig. 4A, Bottom Left Inset, revealing a perfect match with the measured diffraction pattern. In Fig. 4B, 24 Bragg peaks up to {332} obtained with direct beam direction of [1 −1 0] unequivocally demonstrate the single-crystal nature of this sample. The simulated diffraction pattern on the Fig. 4B, Bottom Left Inset is also perfectly matched with the experimental diffraction pattern. One can note that, in between Bragg spots, there is a diffuse scattering streak that presumably arises due to dynamics in super-swelled single crystals (27). Exploring this diffuse scattering signal can yield invaluable information about membrane fluctuations in lipid bicontinuous cubic structures, which should have a determining role in establishing swelling limits.

Fig. 4.

Single-crystal diffraction: 2D SAXS scans obtained from 6-wk-old samples (GMO/DOTAP/GMOPEG 97.5/1.5/1). (A) Single crystal aligned with direct beam at [−1 1 1] direction showing nine sharp Bragg spots. A simulated scattering pattern (Bottom Left Inset) is well matched with the data. (B) Single crystal aligned with direct beam at [1 −1 0] direction displaying 24 intense Bragg peaks. (Bottom Left Inset) A simulated scattering pattern is also perfectly matched with the data. The directions of the direct X-ray beam are shown by the yellow arrows in the Top Right Insets of (A) and (B).

It is noteworthy that, while the observation of lyotropic bicontinuous lipid/surfactant single crystals in bulk (26, 28, 40, 41) as well as preferential alignment in films (11, 42–44) is not unprecedented, here, these single crystals are encountered in a dramatically swelled up state at room temperature. The unit cell dimensions of these single crystals are expanded 400% compared with previous reports, without any loss in crystallinity, confronting all predicted theories of membrane fluctuations impairing ordering of large bicontinuous cubic unit cells of lipids. Importantly, compared with previous efforts where single crystals are prepared from isotropic phases, our method has distinct differences. Through the SAXS scans of the entire capillary, we found that there is only a single phase with different orientations a few days following hydration. As the initial samples show diffraction patterns characteristic of partially ordered systems (SI Appendix, Fig. S11), we believe that our super-swelled bicontinuous cubic phase single crystals are not emerging from isotropic phases but rather from fusion of microcrystallites.

We have used Cryogenic Transmission Electron Microscopy (Cryo-TEM) to obtain real space imaging of the bicontinuous cubic phases (8). The results are shown in Fig. 5 for a super-swelled single crystal and regular spacing polycrystal. In Fig. 5A, highly swollen membranes elongated into one direction are observed. The lattice constant is measured at about 41 nm, which is well matched with the SAXS data. In addition, there is an indication of highly fluctuating membranes that is consistent with the SAXS diffraction patterns having diffuse scattering streaks. A Fourier transform to the large fluctuating unit cell yields a small reciprocal pattern that is not very informative. A simulation of the diamond Pn3m minimal surface in the [110] direction is shown in Fig. 5A, Right and is well matched with the Cryo-TEM result. Fig. 5B shows a Cryo-TEM image of a diamond Pn3m bicontinuous lipid cubic phase with regular unit cell dimensions. In this case, the image displays a polycrystalline pattern of regularly ordered membranes. Fourier transformation of one microcrystallite (red box region) yields a well-defined diffraction pattern analogous to that observed by SAXS, and the extracted unit cell size is a = 16.7 nm. Also, in this case, the simulated minimal surface in the [100] direction is well matched with the observed Cryo-TEM image (8). More Cryo-TEM images of these systems are available in SI Appendix, Fig. S12.

Fig. 5.

Cryo-TEM imaging of bicontinuous cubic phases. (A) Super-swelled Q_II^D single crystal showing fluctuating membranes with lattice parameter, a = 41 nm. A simulated image at the (110) plane is well matched with the data. (B) Regular sized Q_II^D polycrystal (a = 16.7 nm). A simulated image at the (100) plane is perfectly matched with the data. The simulated images in both A and B were generated in POV-Ray (Persistence of Vision Raytracer) (45) using the level-set equations (46) of a half unit cell thickness.

Conclusions

Through a thorough SAXS and Cryo-TEM study of lipid systems of varied compositions and conditions of organic solvent drying, we discovered a methodology to manufacture metastable super-swelled bicontinuous cubic single crystals. Under fast drying conditions of organic solvents, tricomponent lipid cakes containing GMO, a charged lipid, and a PEG-lipid swell up in excess water to dimensions never encountered before (unit cell dimensions a = 68.4 nm). Importantly, the super-swelled bicontinuous phases can develop perfect single crystals exceeding 1 mm³ in size. While the inclusion of charged lipids determines the super-swelling capacity, membrane charge density is a modulator of the symmetry of the phase. As a result, super-swelled lipid bicontinuous gyroids, which are traditionally found at very low water contents, can be stabilized in excess water for membranes with high charge density. At this time, we cannot fully identify the mechanism behind the extraordinary swelling capacity of lipid cakes subjected to fast organic solvent extraction, but it is noteworthy that a multicomponent lipid mixture is required. It is conceivable that lipids unevenly partition within the membranes upon drying, leaving highly charged regions that super-swell and epitaxially template the remaining structure.

Materials and Methods

The key feature of the methodology is fast organic solvent evaporation out of lipid mixtures prepared directly in a quartz capillary. We used >99.8% pure chloroform with negligible water content (SI Appendix, Fig. S13) to dissolve lipids. To ensure there is no residual lipids in the wall, quartz capillaries are centrifuged at 3,908.5 × g and 25 °C. The sample is then dried out while rotating inside a rotary evaporator at desired pressure and temperature. We fixed the temperature at 25 °C and varied pressures inside from 380 mbar to 780 mbar. To minimize residual chloroform in the dried lipid cakes, all samples are further dried for more than 2 d. Dried lipid cakes are half-transparent, with no visible lipid residue on the capillary wall. Fully dried samples are then hydrated by adding Milli-Q water to 0.1 M final concentration. This corresponds to a molar ratio–lipid/water weight fraction (wt/wt%) conversion as follows: GMO/DOTAP/GMOPEG (95/4/1–3.86, 97.5/1.5/1–3.78, 100/0/0–3.57, 99/0/1–3.73) and GMO/MVL5/GMOPEG (95/4/1–4.05). At these weight fractions, regular samples have about 7 μL of bulk water, and negligible amounts for super-swelled states. Samples are centrifuged at 3,908.5 × g for more than 10 min to ensure efficient water penetration through lipid cakes. Afterward, samples are incubated at 45 °C for more than 2 d. The fully hydrated samples are then stored at room temperature. The structure of the lipid phases was determined by SAXS in-house and at beamline 12-ID-B, Advanced Photon Source at Argonne National Laboratory. Cryo-TEM was used to further investigate structural features and diffraction patterns of bulk lipid cubic phase samples. More details on materials and methods can be consulted in SI Appendix.