Computational Population Biology: Linking the inner and outer worlds of organisms

Abstract

Computationally complex systems models are needed to advance research and implement policy in theoretical and applied population biology. Difference and differential equations used to build lumped dynamic models (LDMs) may have the advantage of clarity, but are limited in their inability to include fine-scale spatial information and individual-specific physical, physiological, immunological, neural and behavioral states. Current formulations of agent-based models (ABMs) are too idiosyncratic and freewheeling to provide a general, coherent framework for dynamically linking the inner and outer worlds of organisms. Here I propose principles for a general, modular, hierarchically scalable, framework for building computational population models (CPMs) designed to treat the inner world of individual agents as complex dynamical systems that take information from their spatially detailed outer worlds to drive the dynamic inner worlds of these agents, simulate their ecology and the evolutionary pathways of their progeny. All the modeling elements are in place, although improvements in software technology will be helpful; but most of all we need a cultural shift in the way population biologists communicate and share model components and the models themselves, fit, test, refute, and refine models, to make the progress needed to meet the ecosystems management challenges posed by global change biology.

Grounding and Motivation

This paper is about a vision for the future, but needs context and, hence, grounding in the past, as covered in various books (McIntosh 1985, Kingsland 1995). Here I provide only a very brief and selective review of material needed to develop my vision of Computational Population Biology (CPB) as a field in its own right. By virtue of its name CPB is a part of Computational Biology, but in this role it is distinct from Bioinformatics (Ouzounis 2012), Statistical Ecology, or even Ecoinformatics (Michener and Jones 2012): CPB essentially focuses on the construction of computationally intensive dynamical systems models of the emergent behavior, ecology, and evolution of heterogeneous collections of organisms with complex internal states rather than on issues of how to gather, store and manipulate data or fit model parameters to data. Of course, all these latter issues are of great relevance to CPB. At this time all the elements required for a quantum jump in the field of CPB are in place, except for two. What we have are: i) the necessary modeling experience to construct all the components of CPB models at both the agent-based and dynamical systems levels, ii) the required computational power and data handling capacities, iii) well-developed data collection and geographical information systems (GIS) processing technologies, and iv) a sophisticated understanding of computational methods needed to support statistical inference. What we still need are: i) better software technologies to rapidly and accurately code complex models and, ii) a cultural shift, which has to some extend begin with the adoption of the ODD (Overview Design concepts and details) protocol ((Grimm et al. 2006, Grimm et al. 2010)) in the way we communicate the structure, fit, and results of our models, and how we share model components and the models themselves.

Dynamic models in population ecology can either be Eulerian differential or difference equation descriptions of lumped or aggregated classes or groups of individuals—a class of models that I refer to as LDMs (lumped dynamic models)—or they can be Lagrangian descriptions of the behavior—a class of models that are referred to as ABMs (agent-based models, also individual-based models designated IBMs (Patterson et al. 2008, Hellweger and Bucci 2009)). The growing field of CPB is currently best epitomized by both stochastic simulations of LDMs (Costantino et al. 2005) and inherently stochastic ABMs; a distinction that Caswell and colleagues have cast in terms of so-called i-state distribution versus i-state configuration models (Maley and Caswell 1993).

During the first half of the 20^th Century, the foundations of population biology modeling were laid down through the development of a variety of LDMs of processes in demography, ecology, epidemiology, and evolution. Throughout the 1970s and 80s, a growing community of quantitative and mathematical ecologists crafted LDMs with increasing realism, as well as paying closer attention to using empirical data to estimate model parameters and validate model predictions. Only with the rise of powerful desktop computers in the late 1980s, however, did ABMs begin to take a foothold in population biology with calls to arms a number of researchers over the ensuing decade (Huston et al. 1988, Maley and Caswell 1993, Grimm 1999). Surprisingly, ABM studies in population ecology have been increasing only linearly (DeAngelis and Mooij 2005), and then at a paltry rate given the ubiquity of ABMs in other fields of science (Fig. 1).

Figure 1.

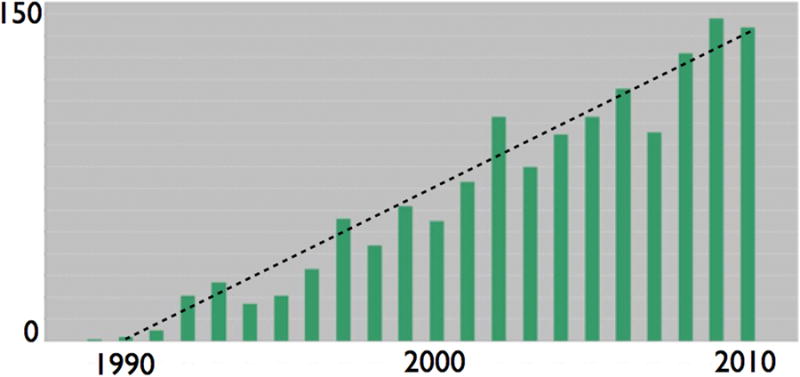
A Web-Of-Knowledge^SM search on the phrase “Individual-based model* OR Agent-based model*” for all years up until 2010 yields approximately 1.987 million hits that reduce to 1,561 once “AND Population Ecology” had been added. The first in this latter group of publications, as graphed here, appeared in 1989 with the number of ABM publications in population ecology increasing by an average of around 7-8 publications each year to an annual rate of around 150 in 2010.

The reason for the paltry rate could be that LDMs maintain many advantages over ABMs (Table 1) and large scale LDMs, particularly in modeling oceanic systems, can become rather large and computationally intensive (Espinosa-Romero et al. 2011). However, LDMs have severe disadvantages as well, the most crucial being their inability to take heterogeneity into account at the individual level (Table 1). This inability to account for the uniqueness of individuals greatly limits the kinds of questions that LDMs can be used to address. First, in trophic ecology, some individuals fortuitously or despotically have greater access to resources than other individuals (Revilla and Wiegand 2008), with the implication that populations are likely to resist negative impacts associated with a decline in resources than would be predicted by a mean-field LDM model. Second, in disease ecology, a full exploration of the impacts of superspreaders requires ABMs (Lloyd-Smith et al. 2005), particularly when disease processes have idiosyncratic contact network topologies (Eames and Keeling 2002, Keeling and Eames 2005). Third, processes in movement (Nathan et al. 2008) and behavioral ecology (Holmgren 1995, Hock et al. 2010) essentially act at the individual level, with effects that depend on the current, but dynamically changing, states of individuals. Fourth, although LDMs have proven to be invaluable in developing evolutionary ecology theory through the application inter alia of trait-for-allele multi-locus models, coalescence models (Rousset 2004), and evolutionarily stable strategy models (McGill and Brown 2007), genetic algorithms (Olden et al. 2008) applied to ABMs are needed to address the panoply of questions that can be posed with regard to heterogeneously rich systems (i.e. systems with at least many thousands of distinct individuals or a large number of heterogeneous groups of homogeneous individuals).

Table 1.

A limited list of the advantages and disadvantages of LDMs compared with ABMs in addressing questions in different subfields of ecology.

	LDM		ABM
Subfield	Advantage	Disadvantage	Advantage	Disadvantage
Demography	Stable stage-structure theory	Individual traits averaged	Relevant individual traits maintained	Lack of coherent theory
Disease Ecology	Coherent invasion and burnout theory	Limited account of superspreaders and variation in susceptibility	Unlimited account of variation in transmission and susceptibility	Difficult to generalize among diseases
Movement Ecology	Provides highly aggregated overview of population movement	Cannot account for movement at fine spatio-temporal scales	Can relate fine scale movements to local landscape factors	Theory of scaling up individual movements to population level needed
Behavioral Ecology	Simple fitness maximization theories possible: e.g. optimal foraging	Ignores fact that behavior is often highly heterogeneous at the individual level	Can account for heterogeneity of behavior at the individual level	More care is needed to handle the complexity of fitness maximizing theories
Trophic Ecology	Allows first order effects (averages) to be clearly assessed	Variation in resources available to individuals largely ignored	Critical effects due resource variation can be incorporated	Enormity of computations may be overwhelming if not handled carefully
Evolutionary Ecology	Well developed gene-for-trait and coalescence theory models exists	Links between genetic and ecological heterogeneity hard to make	Easy to link genetic and ecological heterogeneity	Hard to characterize emergent properties and processes responsible for speciation

From the above examples it follows that, although LDMs have provided and will continue to provide a powerful framework for addressing questions and developing theory in population biology, ABMs are needed to address questions beyond the capabilities of an LDM framework (Levin et al. 1997). To date, however, few LDM models have treated the individual agents themselves as complex dynamical systems within their own right: entities that grow, develop, reproduce and die, have physical, physiological, immunological, and neural states that affect these four processes through movement, interactions, and other behaviors. I will use the term CPM (computational population model) to distinguish an ABM in which the agents are represented by a finite number of discrete tags (species, gender, age, susceptible to disease, vaccinated, etc.) from an ABM in which agents are represented by internal dynamical system descriptions of inter alia consumption and growth, and possibly physiological, immunological, and neurological processes that are influenced by external factors and, in return, influence the way these agents dynamically interface with each other in their external worlds.

Apart from the data needed to parameterize the various modules that may make up a fully developed CPM, an important constraint in developing CPMs has been the computational resources needed to implement models consisting of thousands, or even tens of thousands, of agents. This constraint, however, is rapidly relaxing with the advent of parallel processing and cloud computing (Lee et al. 2011). An equally important constraint has been the challenge posed by the complexity of CPMs with regard to the scientists who have developed a particular CPM both 1.) communicating the details of the model in ways that enable others to understand how the model really works (Kettenring et al. 2006) and 2.) using the output of the model to obtain significant and deep insights in the behavior of the system the model is purported to represent. Taming the complexity of the CPMs needed to address global change biology problems is going to require the emergence of a much more sophisticated modeling culture than currently exists. This culture is not meant to dispense with LDMs in addressing theoretical questions or ABMs for modeling moderately complex systems, since Occam's principle that “ceteris paribus the simplest model should be selected” (Riesch 2010) must always be a central tenet of CPB. Rather this culture is meant to facilitate the development of new methods, as well as more powerful software platforms, to build a new generation of much more powerful ABMs—now called CPMs to distinguish them from their less complex progenitors—that are able to link the dynamic inner and spatially-detailed outer worlds of many different types of agents interacting in their tens of thousands (Fig. 2).

Figure 2.

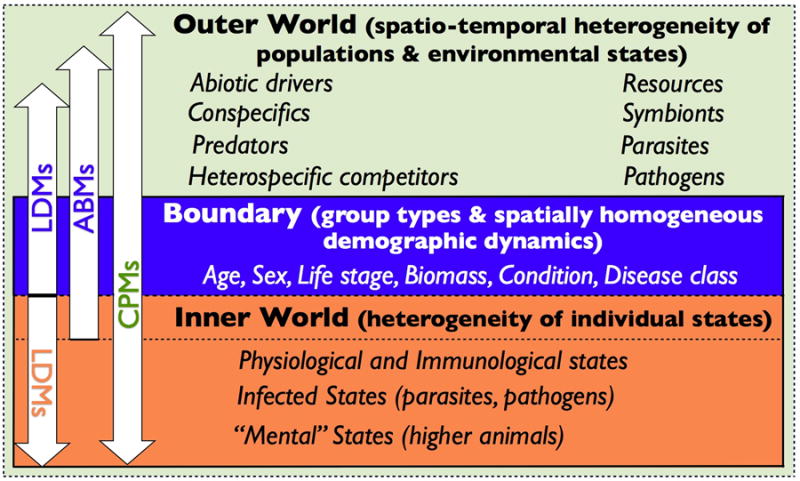
A depiction of the inner and outer worlds of individuals divides population models into kinds according to how the models span this universe: LDMs (lumped dynamics models), ABMs (agent-based models), and CPMs (computational population models). Agents at the boundary of the two worlds inherit their designated type from their internal state, with some designations, such as sex, being fixed early on, other designations, such as age class membership progressing linearly, and finally designations related to biomass and disease classes changing dynamically with food intake rates and immunological interactions. The internal states of individuals, however, are essentially driven by the inputs they receive from their external worlds (e.g. food intake, pathogen transmission, conspecific and heterospecific interactions).

LDM Mean-Field Models

Lumped dynamic models (LDMs, Fig. 2), sometimes referred to as mean-field population models (Ovaskainen and Cornell 2006), provide the foundational vocabulary for articulating dynamical systems theory in population biology. The vocabulary begins with Malthusian—that, is exponential—growth of the size of populations, either represented by the change over time t in the number N(t) of indistinguishable individuals, or the biomass x(t) of lumped homogeneous population. This vocabulary of exponential growth or decline, depending on whether or not the net growth rate r (births minus deaths in a closed population) of a particular population is respectively positive or negative was extended by the powerful concept of an environmental carrying capacity K. Since this concept is phenomenological, rather than mechanistic, the logistic growth model dx/dt=rx(-1-x/K) does not extend beyond the inner-outer world boundary (blue central strip in Fig. 2) even if K is made a function of time, unless K itself is mechanistically related to elements in the outer world of a population of agents through processes in the inner world of these agents. The outer-world includes resources needed for growth and other elements that drive the way agents interact among themselves and with their environment, while the inner-world processes include metabolism, respiration, and foraging efficiency (see (Kooijman 2010) and the references therein), where the latter may be influenced by memory (within lifetime learning) and genetics (evolution). Such links have been made (Getz 1991, 1993, South 1999, Johst et al. 2008), though the resulting extensions are within the LDM domain boundary if they do not deal with individual level heterogeneity in terms of the differential exposure of individuals to resources or genetic variation in the physiological and cognitive functions of individuals (Fig. 2).

The age-structured matrix model formulation of Leslie in the 1940's (Leslie 1945, 1948) has become the canonical stalwart of LDMs in nonhuman demography (Caswell 2001). With suitable modifications that phenomenologically account for density-dependent recruitment (Owen-Smith 2000, Ovaskainen and Cornell 2006, Abrams 2009), explicitly incorporate resource-dependent survival (Owen-Smith 2000, Wilmers and Getz 2004) or include environmental or demographic stochasticity (Lande et al. 2003), the Leslie framework has been used to assess and design harvesting policies in fisheries, forestry and wildlife management (Getz and Haight 1989) and to implement population viability analyses in conservation biology (Beissinger and Westphal 1998). In these cases, however, the LDM structure is maintained, albeit in a stochastic difference or differential equation framework.

The foundation for the boundary level canonical approach to modeling epidemiological processes—so-called SIR modeling—was laid by Kermack and McKendrick in the 1920's (Kermack and McKendrick 1927) (for modern expositions inter alia see (Anderson and May 1991, Hethcote 2000, Getz and Lloyd-Smith 2006)). These models have been greatly extended to address questions relating to multiple strain infections (White et al. 1998, Dawes and Gog 2002, Abu-Raddad and Ferguson 2005, Ackleh and Allen 2005), heterogeneity in susceptibility or infectiousness (Lloyd-Smith et al. 2005, Kenah and Robins 2007, Miller 2007, 2009), evolution of virulence (Porco et al. 2005, Osnas and Dobson 2012), and even to include internal host-immunity dynamics (Steinmeyer et al. 2010). However, the linking of internal host-pathogen dynamic processes with behaviorally detailed host contact processes has yet to be undertaken.

One lineage of LDMs is rooted in the competition and predation models of Lotka and Volterra (Lotka 1925, Volterra 1926) and their extensions to modeling interactions in multispecies assemblages (May 1973) and food webs (Hastings and Powell 1991, Ackland and Gallagher 2004), or including additional age or stage classes (Murdoch et al. 2003). A second lineage is rooted in the host-parasitoid models of Nicholson and Bailey (Nicholson 1933, Nicholson and Bailey 1935) and Thompson (Thompson 1924), with extensions to account for handling times (Hassell 1978, Getz and Gutierrez 1982), and egg versus search-limited tradeoffs (Getz and Mills 1996, Mills and Getz 1996) in parasitoid attack rates of hosts. Neither of these approaches provide explicit ways to link inner and outer world processes, unlike the metaphysiological (Getz 1993) approach that was explicitly formulated to provide a link between the outer world process of resource extraction and the inner world process of starvation, albeit at the population level. This approach has been recently refined at the multispecies level as the biomass transformation web (BTW) formulation (Getz 2011a), which differentiates between extraction (predation) and senescence (aging and starvation) type mortalities (Appendix A). Further, BTW has both population and individual level interpretations and provides a clear link between disease-induced mortalities (an inner-outer world immunology/physiology-epidemiology link) and the poor condition of individuals during starvation (an inner-outer world physiology-ecology link). The application of LDMs in describing the states of individuals also has a long and varied history, as elaborated in more detail in the subsection on an agent's inner world.

ABM Outer World Models

As illustrated in Fig. 1, the use of ABMs in population ecology (Grimm and Railsback 2005, Grimm et al. 2006, Railsback and Grimm 2011) has been growing slowly but surely over the past two decades. With the advent of cloud computing (Lee et al. 2011), the computational constraints are significantly reduced, thereby transferring the impediment of ABMs to issues of documenting and communicating the structure of models, exploring the behavior of models, and interpreting results following the ODD approach propounded by Grimm and colleagues ((Grimm et al. 2006, Grimm et al. 2010)). A first step to reigning in the complexity of ABMs is to understand the behavior of associated mean-field LDMs obtained through mathematical averaging and aggregating procedures (Durrett 1999, Johansson and Sumpter 2003, Ovaskainen and Cornell 2006, Adams et al. 2011). The behavior of mean-field LDMs provides a basis to understanding to what extent the behavior of related ABMs is determined by averages of processes and to what extend the behavior is due to the heterogeneity introduced through spatial variation and individual agency. Of course the relationship between LDMs and the ABMs from which they have been generated may diverge considerably when heterogeneity is large and idiosyncratic. The latter is the case for many disease processes where contact networks have nonrandom topologies (Grassly and Fraser 2008, Givan et al. 2011) or spatial peculiarities or irregularities (Hahn et al. 1999, Liu et al. 2009).

Until recently most ABMs focused more on the spatial heterogeneities of the external world (Travers et al. 2009) rather than on details of the internal dynamics of the agents themselves. The central component of these models is related to characterizing either the diffusion of individuals, or their propagules in the case of plants and sessile animals, through space (Turchin 1998), random walks of individuals over landscapes (Berg 1993, Edwards et al. 2007, Fryxell et al. 2008), the interactions of individuals or groups of individuals on contact networks (Hanski and Thomas 1994, Kretzschmar et al. 1995, Grassly and Fraser 2008), often reflecting social relationships (Zeggelink 1994) or interactions being spatial-scale dependent (Boots et al. 2009). Earlier movement studies focused on the statistical properties of elements in the movement tracks of individuals obtained by sampling the locations of individuals at different points in time (Berg 1983). Generally the properties of these tracks were expressed in terms of the distributions of step sizes and shifts in the directions of consecutive steps (Benhamou 2004, Edwards et al. 2007), and comparisons of these data with uncorrelated or correlated Gaussian and Lévy walks (Metzler and Klafter 2000, Edwards et al. 2007, Getz and Saltz 2008, Duffy 2011) or mixed-distribution walks (Morales et al. 2004, Fryxell et al. 2008). More recently individual movement has been related to structures on real landscapes (Gough and Rushton 2000, Clark et al. 2001, Harper et al. 2002, Macdonald and Rushton 2003, Wiegand et al. 2004, Bar-David et al. 2005, Bar-David et al. 2008, Elderd and Nott 2008), as well as and the presence of other organisms on the landscape (Getz and Saltz 2008, Willems and Hill 2009). In particular conspecifics influence the movement of individuals through herding, mating, and territoriality, while heterospecifics influence movement through foraging behavior, territoriality or predator avoidance, where the latter has been expressed in terms of the so-called “landscape of fear” (Laundre et al. 2001, Willems and Hill 2009, Laundre 2010).

An Agent's Inner World

The development of LDMs to characterize the dynamic state of populations has been paralleled by the development of LDMs to characterize the dynamic internal state of individual organisms. Some of the earliest models dealt with the growth of individuals (von Bertalanffy 1957, Turner et al. 1976) (i.e. the state variable was the organism's size or mass), including accounting for developmental and growth as a function of temperature (Chang et al. 2011) and energy intake (Mangel and Clark 1988, Clark and Mangel 2000, Nisbet et al. 2000, Jusup et al. 2011). Increasingly, however, quantitative descriptions of the biological state of individuals is being made more complex by moving from simple tags that denote gender, age, size or discrete disease class (e.g. susceptible, infectious, vaccinated, etc.) to dynamical systems representations of the physiological, neurological, immunological, serological and bacteremic or viremic states of individuals. Thus individuals are being associated with their own within-host pathogen-immunology models (Nowak and May 2000, Steinmeyer et al. 2010), neural cognitive and memory process models (Olsson and Holmgren 1998, Norrstrom et al. 2006, Holmgren et al. 2007, Dalziel et al. 2008), or dynamical systems formulations of individual level reproductive and physiological process models (e.g. see Individual Level Model in Appendix A).

The features required of any inner world model obviously relate to the problem at hand. Each agent would be associated with one or more modules, each of which is an LDM model of a particular subsystem (Appendix B), such as a growth module; a within-host disease module; one or more perceptual modules that gather information from the external world; one or more brain modules that use neural nets to process perceptual input (e.g. see (Holmgren and Getz 2000, Norrström et al. 2011) for the application of perceptron models (Haykin 1999) to habitat selection), one or more execution modules that instruct the agent how to behave (e.g. mate selection, path selection, direction of movement—see Appendix B, or decisions made during agonistic interactions). In addition, one or more developmental clocks will likely be included that either directly monitor the passing of time or calculate developmental rates as influenced by temperature (e.g. phenology models—see (Pau et al. 2011)) or other environmental drivers. The primary clock would determine the age or developmental stage of an individual beginning with its conception or its birth, and secondary clocks would determine periods elapsed since the occurrence of critical events such as mating or reproduction.

In closing this section we note two things. First, adhering to the principle of Occam's razor (Riesch 2010), only modules that are key to the behavior of the system in the context of addressing the specific question at hand should be incorporated——since otherwise the complexity of CPM behavior and output will ultimately lead to obfuscation in addressing the question at hand. The key challenge though is to know a priori what processes are indeed critical to incorporate in the model—a challenge that should not be underestimated and can be partially redressed using current methods in model selection theory (Burnham and Anderson 2002). Second, all modules that are used should be developed in a way that allows them to be linked to elements in the external world in a sensible way. Thus, for example, the BTW formulation presented in Appendix A, explicitly includes a resource variable R(t) that can be set to some constant or periodic function of time when exploring the affects that different extraction functions or model parameters have on the growth of individuals. This is equivalent to embedding the individual in a constant or idealized seasonal environment, but leaving open the option to of replacing R(t) with a dynamical systems module that computes a vector of resources available to each agent as time progresses, if there is a need to extend the model in this direction.

Merging the Inner and Outer Worlds with CPMs

In developing CPMs (Fig. 2, Table 2), the goal should be to create a powerful and comprehensive modularized software platform with toolboxes containing easily linkable, substitutable, and vetted procedures; the latter preferably through an open access participatory community resulting over time in a Darwinian selection of the most appropriate and computationally valid procedures and modules. The constituency served by this software is likely to include both students and professionals from a range of backgrounds and competences in the natural and engineering sciences. These users should be able to apply the contents of the toolboxes to rapidly and accurately assemble models capable of addressing both theoretical and applied questions in population ecology (see areas listed in Table 1), community ecology, systems ecology, and ecosystems and environmental sciences. Applications of the models would then include sustainable use of biological resources (fisheries, forests, regulated hunting), conservation of species and biological diversity in general, epidemiology (particular enzootic and plant diseases), biological remediation (pollution landscape restoration, river and wetlands restoration), and global change biology.

Table 2.

Computational Population Biology in a Nutshell.

A. Modeling Elements
Geographic information systems (GIS) foundation including complex environmental drivers Resource extraction, growth, and population interaction modules Demographic structure modules Epidemic structure modules Populations of agents that may include: internal states (physical/structural, physiological, immunological) connectance matrices (feeding, social, etc.) perceptual kernels (process specific: visual, olfactory, auditory, etc.) brain modules (input: perceptual, other neural modules, internal states, memory) behavioral modules (movement, consumption related, mate choice, mating etc.) reproduction modules (output of propagules, production of young, investment) genome modules (genetic mapping of parameters, inheritance processes, genetic algorithms) A simulation engine that has: Modularity (object oriented chip design) Hierarchical/nested scalability (unpacking parameters, packing models) Interchangeability (swapping chips doing the same task with differing complexity) Parameter estimation procedures for applying to both individual modules and full models Model selection procedures using information theory to minimize parameters Data manipulation and visualization procedures
B. Cultural Elements
Set up a user community (e.g. societies, journals, websites, workshops) to: set standards for publishing CPB studies develop protocols for naming modules and models develop protocols for sharing modules, models, data, and software Develop protocols for communicating model structure that include: a list of modules used with specification of their function, data developed and software implementation, as well as information on input and output structures connectance topologies, numbers of modules used, and a description of how module parameter values were specified or generated complete mathematical and coding details of new modules used specifications of GIS layers and environmental inputs Protocols for validating modules should include: a documented list of publications that have used the module. an associated file (e.g. a wiki) that documents the history of the module in terms of code quality and verification tests, modifications that have been made, etc. Efforts to facilitate comparative studies should include specifications for standardized output structures (in addition to study specific output) identification of existing and needed baseline studies documents (e.g. wiki) that contain a list of all modules performing a particular task, a comparative discussion of their relative complexity and input requirements More attention must be paid to developing software to fulfill educational needs and providing powerful tools for the CPB user community.

Implementation of CPMs involves simulating the internal dynamics of developmental, physiological, neural and immunological states dynamics of individuals (agents) and generating interaction and life history event lines, as the individuals move around theoretically constructed or empirically specified landscapes (Fig 3). Life-path constructions within CPMs require individuals to be generated de novo (birth, first event), be stationary (sessile phased) or allowed to move (vagile phases) across real landscapes (represented in geographic information systems layered data bases), interact with conspecifics (social behavior) and heterospecifics (commensal, predatory or avoidance), consume resources or be consumed by others, perceive their landscape and make decisions on where to move, remember landscape features, change their internal states (continuously or discretely), choose mates, reproduce, evolve and ultimately die (predation, starvation, senescence, accidents). A framework that includes this level of reality, generality, plasticity, and adaptability would need to consist of at least several linked computational modules coded in a way that allows for heritability and mutability of parameter values so that genetic algorithms can be implemented to simulate evolutionary processes as well (Eiben and Smith 2003, Olden et al. 2008, Clark et al. 2011).

Figure 3.

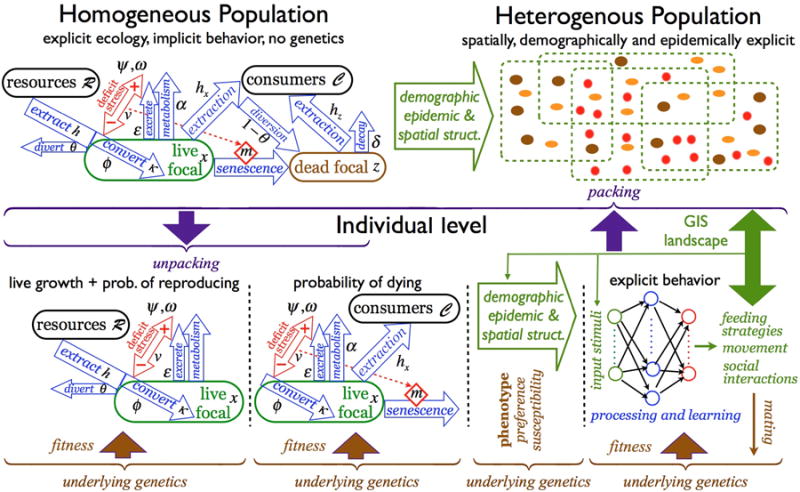
A pictorial representation of CPMs (lower half – see Appendix A for details on the consumer-resource interactions and Table 2 for a list of CPM modules) and how they relate to LDMs (upper right), or structurally elaborated LDMs and ABMs (upper left) where the latter do not account for the internal processes that take place within individual agents moving over landscapes, interacting with conspecifics and heterospecifics, extracting resources, growing, reproducing and evolving over generations.

The modular elements of a CPM framework are outlined in Table 2A. Underpinning all these elements is a GIS foundation that will provide the environmental details in terms of a series of geographic information system (GIS) landscape data layers (Skidmore et al. 2011). These layers will provide information on the placement of sessile agents or, at least suitable areas for the model to place sessile agents. The model will also initiate sites for the location of vagile agents and then move these agents over the landscape (Getz and Saltz 2008, Nathan et al. 2008) using modules listed in Table 2 to carry the behavioral, ecological and evolutionary processes that drive the model. Also underpinning all agent-related modules in the CPM (cf. Fig. 3) is a procedure for mapping parameter values onto genetic structures associated with each agent. Then through the application of genetic algorithms that carry out computations for expressing genetic traits through the setting of parameter values taking into account ploidy, dominance, mutations, and genetic crossover processes during zygote formation (Holmgren and Getz 2000, Holmgren et al. 2007), evolutionary processes can be simulated over multiple generations using individual fitness computations (Eiben and Smith 2003, Clark et al. 2011, Norrström et al. 2011).

A key module in many applications is modeling the process of converting resources extracted by each agent into agent biomass (growth) and condition (possible starvation), as well as life-history events (developmental life stages, reproduction and death). This enterprise has a considerable history (e.g. see (Kooijman 2010) and references therein). Resource extraction will typically include effects due to resource density, extraction efficiency, satiation, intraspecific competition and, where applicable, interspecific competition; although competition processes may be expressed at the resource location rather than extraction phase. One might expect that both the growth and condition of agents depend on their net converted intake (i.e. accounting for conversion efficiency, metabolism and excretion), while mortality depends on both condition (senescence) and predation (extraction). These ideas can applied at both the population and individual levels using the BTW approach outlined in Appendix A (Getz 2011b).

Linked to development are computations that will be carried out as individuals make transitions among various demographic classes (age, stage, sex), since many behavioral and ecological process are either age, size or sex-specific or proceed at age, size and sex-dependent rates. Beyond demographic classes, structured LDMs or ABMs that include infectious disease processes compute transitions among epidemiological classes (e.g. susceptible, exposed or infected, infectious individuals, and dead, and in some cases recovered individuals with some degree of immunity). On the other hand, CPMs that include infectious disease processes need to take a step beyond ABMs by including within-host pathogen-immune cell dynamics (Nowak and May 2000, Steinmeyer et al. 2010), thereby enabling CPMs to account for the following phenomena: i) dose-dependent initial infection effects, ii) infectiousness of individuals as a function of current pathogen levels, iii) risk of individuals dying as a function of current viremic or bacteremic, immunological and physiological states, iv) immunity/susceptibility as a function of the individual's history of exposure to pathogens.

Ultimately all ecological and epidemiological processes require assessments of interactions among individuals to compute rates of resource consumption, predation, and disease transmission, as well as outcomes of mate selection, agonistic interactions among agents for control of resources, and social interactions of importance to the fitness of individuals. These interactions can occur either due to encounters as individuals move over the landscape, or to deliberate interactions based on empirically determined or theoretically generated contact matrices (e.g. in epidemiology—see (Grassly and Fraser 2008)) or connectance topologies (e.g. food web ecology—see (Bersier et al. 2002)).

The way individuals move on landscapes can be characterized by distributions that provide information on directions taken and distances moved per unit time, as well as serial correlations among these data. Distributions derived from empirical movement data and their statistical properties (i.e. single and joint moments), however, depend on sampling frequency (Codling and Hill 2005, Codling and Plank 2011). The reason is that movement pathways are constructed from fundamental movement elements (sitting, walking, trotting, dashing, gliding, flapping) determined by the mechanical properties of the movement process, but understood from an ecological point of view in terms of the emergent canonical activity modes (CAMs: e.g. steadily heading to a distant location, milling around, grazing; (Morales et al. 2004, Fryxell et al. 2008, Getz and Saltz 2008)). It is insufficient for CPMs to simulate movement if the simulation does not produce the correct CAMs, which are usually influenced by either landscape structures or the internal states of the individuals (e.g. hunger or thirst, fear, and even memory of currently distant landscape features).

Movement models have been developed that incorporate elements of memory (Dalziel et al. 2008), as well as discrete internal states associated with fitting hidden Markov models to movement data (Patterson et al. 2008). Such models, however, have yet to combine continuously changing internal states driven by physiologically realistic dynamical systems models with externally detailed GIS landscape maps obtained using the latest remote sensing technology (e.g. lidar (Selkowitz et al. 2012)) to determine movement behavior. In a recent Kenyan elephant study (Boettiger et al. 2011), food resources (as represented by the NDVI greenness index obtained through remote sensing satellite data), aggregated over a radius of five miles from the center of the daily movements (cf. Appendix B) of individuals, were correlated, along with factors relating to the location of water and human habitation (roads and villages) to movement patterns; but this study did not include any information relating to the inner state of individuals (e.g. fear of humans).

CPM models that link the inner and outer worlds of individuals require that for each type of behavior (e.g., feeding, fleeing, heading to water or home) each individual is provided with a perceptual module that gathers and aggregates landscape information using kernel methods (Appendix B) to create redistribution kernels that contain the probabilities that individuals will next be move to or be located at particular points on the landscape (cf. Getz and Saltz 2008). Thus feeding behavior requires information on resources that for short time scales are within immediate sensory perception and for long time scales are within memory (learned experience or from parent) or instinctual (migrations), while herding behavior requires an assessment of where the herd leaders are or where some approximation of the geometric center of the herd, or a fragment of the herd, is located. Once all the relevant perceptual information has been collected with regard to a particular behavior (e.g. movement, or mate choice) and inputted along with relevant information on the internal state of the agent, a decision module is needed to determine the actual behavior to be implemented (Mueller et al. 2011). This module also needs to account for the fact that certain behaviors can only be performed sequentially and require fixed times for their execution. Decision modules can consist of a detailed set of rules. However, for many organisms, experience and learning play a central role (Appendix B), and neural network models or other types of learning machines have been used to model host selection (Norrstrom et al. 2006, Holmgren et al. 2007), movement (Dalziel et al. 2010), and mate selection (Ryan and Getz 2000) behavior.

Moving Forward

A cultural adjustment is needed for the field of Computational Population Biology (CPB) to develop in the same way that the field of bioinformatics (Ouzounis 2012) flowered over a decade-and-a-half ago (Fig. 4) and the new field of Ecoinformatics is beginning to flower now (Reichman et al. 2011, Michener and Jones 2012). Prior to 1995 only 14 publications were listed in 2012 in the Web-Of-Knowledge database under the topic “Bioinformatics”. Then in 1995 another 15 appeared with the numbers growing exponentially for the next decade but tapering off to just under 2000 publications by 2011. Currently several journals exist with “bioinformatics” or “computational biology” (with a bioinformatics mission) in their titles (Bioinformatics, BMC Bioinformatics, Briefings in Bioinformatics, Journal of Bioinformatics and Computational Biology, Journal of Computational Biology, and PLoS Computational Biology). Also, many undergraduate and graduate degree programs in bioinformatics are offered at major colleges and universities around the world. If CPB is to follow Bioinformatics in emerging as a recognized field of research in its own right—with its own societies, journals, and training programs—it needs to be clearly distinguished from the field of Bioinformatics, as well as the general field of Statistical Ecology, particularly since CPB, Bioinformatics, and Statistical Ecology are all parts of Computational Biology writ large. CPB is different from other parts of computational biology in that its primary focus is to build CPMs and use these as a way to better understand complex ecological systems and manage changes taking place in earth systems due to global anthropogenic forces (Barnosky et al. 2012). Of course, parameter estimation (Beeravolu et al. 2009 (Hartig et al. 2011)) and model selection methods, which are also being driven by the computational revolution, are critical handmaidens to CPM: they will be used to fit both module (some times prior to incorporation in models) and model parameters, as well as select among alternative modules in fitting models to real data. But again CPB is the model formulation and construction side of population biology, and CPB can only realize its full potential through being recognized as a field in its own right.

Figure 4.

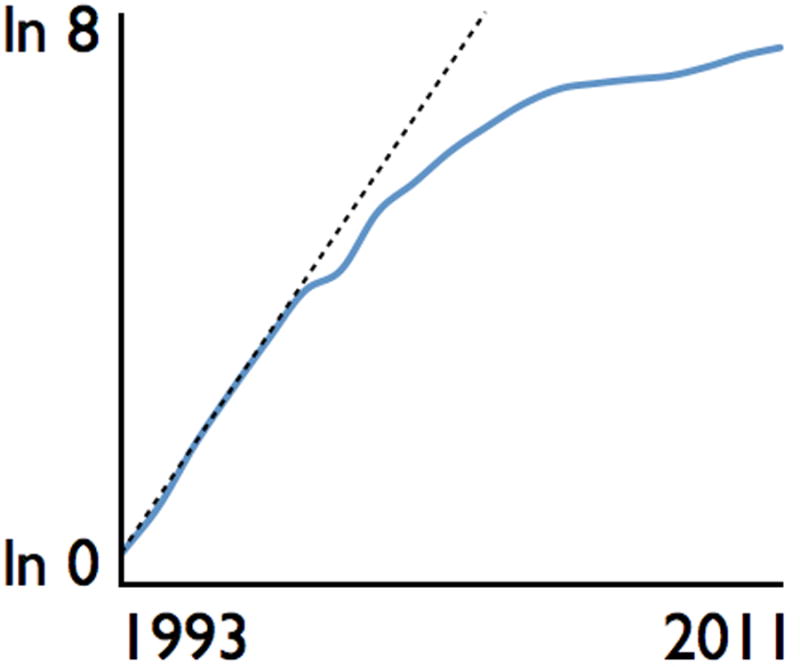
Number of publications, plotted on a natural logarithm scale (verticle axis: ln(1) = 0 to ln 8 = 2981), categorized by a Web-Of-Knowledge^SM search using the topic “Bioinformatics” for all year 1993 to 2011. Only three publications appear before 1992 (1 each in 1989, 1990, and 1991, 0 in 1992) and roughly each year (dotted line) from 4 in 1993 to 98 in 1998, and then tapering off to under 1920 in 2011.

At the time of writing this paper, Wikipedia had a page entitled “Bioinformatics Software” with hyperlinks to more than 150 Wikipedia pages describing specific bioinformatics software packages and platforms. Included on this list were packages for comparing strings of nucleotide and amino-acid sequences (e.g. BLAST (Mount 2007)) and for creating, handling and analyzing phylogenetic trees package (e.g. phyloXML (Han and Zmasek 2009). Also included was a page on an XML package called SBML (Systems Biology Markup Language, (Finney et al. 2001, Dada et al. 2010)) for storage and communication of computational models of biochemical and cellular systems, and on the software platform Galaxy (Goecks et al. 2010) for making computational biology methods accessible to scientists who have no model building or computer programming experience. Because building CPMs is at the heart of CPB, a Galaxy type platform for CPB would not have to cater to complete modeling neophytes. However, progress in and growth of CPB would be tied to the existence of software platforms and packages that facilitate the construction, classification, storage, analysis and comparisons of CPMs (cf. Table 2B, points 9-11) for individuals with minimal programming skills.

Software platforms for constructing CPMs are likely to be based on a scripting language that is able to seamlessly manage communication among computational procedures that have been written in any one of several mainstream computer languages. Beyond this multilingual object-oriented modularity of implementation, a suitable CPM platform would need to be flexible in the level of detail it incorporates at different levels of temporal resolution (cf. frame-based modeling pioneered by Starfield and colleagues: (Starfield et al. 1993, Hahn et al. 1999, Rupp et al. 2000)). It would also need to be scalable by being able to 1.) take any program that uses several or many of these independent procedures and wraps them up into a more complex procedure that then in its own right constitutes a new independent module or procedure (i.e. packing, or wiring chips together to create a more complex chip); 2.) take any parameter in any one of the procedures handled by the platform and replace it with a complete systems model that can be implemented as a module or chip in larger model. In the area of complex physical systems modeling “a non-proprietary, object-oriented, equation based language” called Modelica® exits that is used as a standard by both commercial and free physical systems simulation environments (Fritzson 2011). Modelica has its own association of users that runs regular symposia and workshops and publishers a newsletter¹. A similar type of platform and organization is needed to promote the growth of the CPB community.

Experienced scientists may initiate new fields of research, but the field can only grow if a cadre of young scientists are trained and cultivated. Thus the growth of a CPB user community would also be tied to the existence of software able to support educational activities in the field: classes, workshops, and online training. Further, in the same way that the above mentioned Galaxy platform (Goecks et al. 2010) serves computationally challenged researchers in the bioinformatics community, so would an especially user-friendly CPM software platform serve population biologists who have not been rigorously trained in dynamical systems modeling or do not have strong computer coding skills. One or more such software platforms, and I do not exclude the possibility of current platforms with active user communities (e.g. R in conjunction with a powerful front end) evolving to meet the needs articulated in Table 2, would facilitate rapid development of models. The most promising of these is NOVA (Salter 2013), a innovative platform for graphically constructing system dynamics, spatial, and agent-based models with automatic code generation—in this case NovaScript, which is an extension of the JavaScript language. Since much of Nova's code is contained in prefabricated “code chips,” Nova can be used to accurately and rapidly assemble NovaScript programs that are tens of thousands of lines long from code chips and other graphical elements that themselves have been thoroughly tested through constant reuse, with their history of use provided in accompanying documents. Such platforms would also facilitate the communication of model structure (Kettenring et al. 2006) in terms of modules used and module wiring diagrams, with coding details buried within the module documentation if closer examination is desired. Good communication of model structure is needed to promote the construction of ever more complex models, while retaining reliability, comparability and interpretability of model structures and output, as well as facilitating repeatability of studies (Ellison 2010) in which modeling has played a central role. Modularization and clear communication of model structure would also greatly facilitate assumptions analysis (Jarre et al. 2008, Starfield and Salter 2010, Starfield and Jarre 2011) by allowing modules representing different underlying assumptions to be easily exchanged and the effects of these exchanges coherently discussed.

The utility of CPM models, however, with their extensive numerical outputs, is predicated on the existence of powerful data manipulation and visualization tools that are needed to present and aid in interpreting results, and also to fitting modules to data. This challenge is epitomized by the problem of how to interpret both empirical and simulated animal movement data, with pattern-oriented methods (POM) providing a way forward for comparing data (Wiegand et al. 2003, Grimm et al. 2005) in ways that permit statistical inferences to be performed on such comparisons (Hartig et al. 2011). As already mentioned above, movement data can be characterized in terms of step size and direction distributions and their single and joint statistical properties. However, movement data with the same first and second order statistical properties may produce very different patterns on landscapes if these data differ in their higher order statistics due to the influence of landscape factors and internal agent states. Thus, CPMs that employ Monte Carlo methods to simulate empirical data must not only match the first and second order statistics of the empirical data, but must produce output that matches emergent landscape and spatio-temporal patterns in this data.

As an illustrative example of emergent spatio-temporal patterns in empirical data, Lyons and colleagues developed a method for identifying regions on a landscape that individuals visit for varying lengths of time at different times in the daily and seasonal cycles, and revisit at varying rates (Lyons et al. 2013). Plots of revisitation rates versus length of visits then produce a signature pattern, that can be more comprehensively understood in terms of plots of length of visits and revisitation rates versus time of day or day of year (Fig. 5 reproduced from Lyons et al. 2013). It is only once these kinds of patterns—diurnal, weekly/monthly, and seasonal spatial location and movement statistics—have been matched by CPM output that we can verify if the model indeed simulates the empirical data. Further it is only once we understand how various ecological factors, including projected temperature and precipitation shifts, affect these emergent patterns that we can claim to have models capable of evaluating the impacts of global change on ecosystems.

Figure 5.

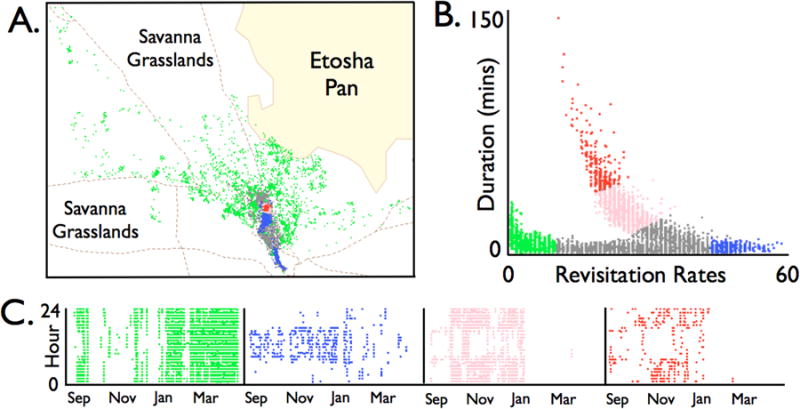
Points in panel A are the locations of a springbok male in the vicinity of the Okaukuejo research camp, Etosha National Park, collected every 30 minutes from early September 2009 to mid-April 2010. The points are color coded, as binned, in panel B according to the amount of time spent in a local neighborhood of the point and the number of times this local neighbor hood was revisit through the 7.5 month period (see Lyons et al in press for details). The four sections of panels C show how the binned points are distributed over the daily as the 7.5-month period progresses. (Reprinted with permission from Lyons et al. 2013.)

The problem of fitting CPMs to data is a field of research in its own right. Its methods apply to all types of models—LDMs, ABMs, phylogenetic tree models and other types of bioinformatics, ecoinformatics and computational biology models—and rely heavily on statistical and stochastic process theory, particularly hierarchical methods of analysis (Royle and Dorazio 2008). Methods both for estimating the value of the parameters in the various modules of CPMs and for validating model fits of empirical data, in terms of low order statics and emergent patterns, constitute fields of study with vast literatures of their own (Burnham and Anderson 2002, Royle and Dorazio 2008). Clearly CPMs rely on these methods as much as any other field of computational modeling, though a real challenge for CPMs will be to find the best way to handle the large number of repeated simulations needed to implement these methods. The central challenge for CPB, however, remains in finding ways for it to flourish and grow through the development of appropriate CPMs. The prescription for such CPMs is contained in Table 2, as well as suggestions for fostering a facilitating CPB culture. These prescriptions and suggestions outline the beginnings of a CPB program for constructing the computational tools needed to help us wisely manage earth systems during the global change upheavals we will face in the coming decades.

Appendix: Appendix A. A Biomass Transformation Web (BTW) Formulation

Definitions and Assumptions

Suppose at time t that

1. a consumer of biomass B(t) (this can either be and individual or a population) has access to resources at density R(t) (either a flux or pool),

2. a variable V(t)∈[0,1](V=1 is death from starvation) represents an average stress measure associated with each unit of biomass arising from a resource-intake deficit (individual or population average)

3. interference competition arises through a measure X(t) (=B(t) in a spatially lumped LDM or is a weighted sum of local competitors in an ABM)

4. F(R,B,X,t) is a function that specifies the resource extraction rate per-unit consumer B and per-unit resource R

5. ε(t) is a loss rate per unit B of biomass to the process of metabolism and excretion

6. is the proportion of extracted resource ingested

7. κ(t)∈[0,1] is the proportion of ingested resource converted to consumer biomass

8. the only source of non-extracted mortality (i.e. besides predation) is a senescence rate m(V,t), which includes death by starvation and disease (when the pathogen is included implicitly) and hence depends on V(t).

Mean Field Model

Under definitions and assumptions i)-viii) the total rate of biomass incorporation rate per unit B is on average:

Net biomass incorporation

$$\psi (R,B,X,t)=\theta (t)\kappa (t)F(R,B,X,t)R(t)-\epsilon (t)$$ (B1.1)

Thus growth at a population level is net resource incorporation minus mortality:

Population biomass growth equation

$$\frac{dB}{dt}=\psi (R,B,X,t)B-m(V,t)B$$ (B1.2)

Now assume that if ψ<0 then a resource stress-deficit accumulates at a rate wψ (w>0), but relaxes back to 0 at a rate rψ when ψ>0; that is, noting these equations hold only for V(t)∈[0,1]:

Stress-deficit state

$$\frac{dV}{dt}=\{\begin{array}{ccc}-w\psi & \text{for}& \psi <0\\ -r\psi & \text{for}& \psi >0\end{array}$$ (B1.3)

Individual Level Model

If the mean field mortality rate is m(V(t),t) then for an individual subject to this rate, the probability s(t) of surviving the interval [t,t+Δt] for small Δt is

Individual survival probability on [t,t+Δt]

$$s(t)=e^{-m(V(t),t)\mathrm{\Delta }t}$$ (B1.4)

Growth at the individual level represents both the growth of the individual given by

Individual growth equation

$$\frac{dB}{dt}=\psi (R,B,X,t)B$$ (B1.5)

For a point t_b at which reproduction of n offspring occurs, each of mass b_i, i=0,1,…n, where b₀ is the mass of the ‘after-birth,’ we have

Reproduction perturbation

$$B(t_b)=\underset{t\to t_b\text{in Eq}.\mathrm{B}1.5}{lim}B(t)-{\sum }_{i=0}^n{b}_i$$ (B1.6)

Appendix B. Perceptual Kernels and Brain Modules Perception Kernels

Kernels have many different meanings in mathematics. Our use is closest to the weighting function concept that tells us how to relate landscape information in the vector-valued function f(z|z′) at points z=(x,y) in the plane in the context of a designated point z′. If K_i(z,z′) represents the weighting function associated with the i^th element f_i(z|z′) of the landscape information vector f(z|z′), then the i^th element of an accumulated information vector F(z′) is

Informational input

$$F_i({\mathbf{z}}^{\prime })\underset{\text{plane}}{\int }{f}_i(\mathbf{z}|{\mathbf{z}}^{\prime })K_i(\mathbf{z},{\mathbf{z}}^{\prime })d\mathbf{z}$$ (B2.1)

Kernels often satisfy K_i(z,z′)>0 for all z, though asymptotically approach 0 as the distance (Euclidean) between z and z′ approaches infinity. In population biology compact kernels are more realistic: i.e. K (z,z′)=0 for z and z′ sufficiently far apart. Thus we naturally define an area of perception A_i(z|z′) associated with the i^th type of information such as the location of food resources, location of predators, or location of mates. The corresponding informational input may then be the center of mass of the resources, the location of the nearest predator, or the geometric center of the potential mates in A_i(z|z′). These areas of action could either be regular geometric shapes such as circles or ellipses covered by uniform height, conical-shaped or Epanechnikov-shaped kernels, or could be kernels constructed from the point of interest and its k nearest neighbors (e.g. LoCoH methods (Getz et al. 2007))

Brain Modules, Actions, and Teachers

A brain module is a vector-value function N that transforms the values of a perceptual input vector F, with elements possibly calculated using equation B2.1, an agent state vector v (inner dynamical system) and a brain state vector w (weighting parameters) into an output action vector a given by

Action output

$$\mathbf{a}=\mathbf{N}(\mathbf{z},\mathbf{v},\mathbf{w})$$ (B2.1)

If the action is implementation of a movement event, then a would contain the information on the direction of heading plus the step size to be taken, where this information my be distributional rather than a single value—in which case the action is a stochastic event associated with a draw from these distributions.

A teacher is a device that instructs an agent after an action a has been taken on what would have been the correct action a′ to take. The error E(a,a′) in this case is based on an appropriately defined measure of the distance between a and a′. Learning is then defined as an algorithm L for updating the brain state parameters w to w* such that

Learning

$${\mathbf{w}}^{\ast }=\mathbf{L}(\mathbf{w},E,\mathbf{a},{\mathbf{a}}^{\prime })\text{where}E({\mathbf{a}}^{\ast },{\mathbf{a}}^{\prime })<E(\mathbf{a},{\mathbf{a}}^{\prime })\text{for}{\mathbf{a}}^{\ast }=\mathbf{N}(\mathbf{z},\mathbf{v},{\mathbf{w}}^{\ast })$$ (B2.1)

Within the lifetime of an agent, a teacher could be a second agent able to make computations with lower errors (e.g. a mother instructing young) or an individual able to assess its own mistakes after the fact. For the case where N is a perceptron, an algorithm L called back-propagation exists to update the weights to improve the performance of N (Haykin 1999). Over evolutionary time, if the error is ultimately expressed in terms of the individual's fitness, then natural selection “teaches” the population of individuals over evolutionary time. (cf. (Norrström et al. 2011)).

Appendix References

Getz, W. M., S. Fortmann-Roe, P. C. Cross, A. J. Lyons, S. J. Ryan, and C. C. Wilmers. 2007. LoCoH: Nonparameteric Kernel Methods for Constructing Home Ranges and Utilization Distributions. Plos One 2.

Haykin, S. S. 1999. Neural networks: a comprehensive foundation. 2nd edition. Prentice-Hall, Upper Saddle River, N.J.; London.

Norrström, N., G. W. M, and N. M. A. Holmgren. 2011. Selection against accumulating mutations in niche-preference genes can drive speciation. Plos One 6:e29487.