We provide a framework to upscale biodiversity in tropical forests from local samples of species richness and abundances.
Abstract
The quantification of tropical tree biodiversity worldwide remains an open and challenging problem. More than two-fifths of the number of worldwide trees can be found either in tropical or in subtropical forests, but only ≈0.000067% of species identities are known. We introduce an analytical framework that provides robust and accurate estimates of species richness and abundances in biodiversity-rich ecosystems, as confirmed by tests performed on both in silico–generated and real forests. Our analysis shows that the approach outperforms other methods. In particular, we find that upscaling methods based on the log-series species distribution systematically overestimate the number of species and abundances of the rare species. We finally apply our new framework on 15 empirical tropical forest plots and quantify the minimum percentage cover that should be sampled to achieve a given average confidence interval in the upscaled estimate of biodiversity. Our theoretical framework confirms that the forests studied are comprised of a large number of rare or hyper-rare species. This is a signature of critical-like behavior of species-rich ecosystems and can provide a buffer against extinction.
INTRODUCTION
Tropical forests have long been recognized as one of the largest pools of biodiversity (1). Global patterns of empirical abundance distributions show that tropical forests vary in their absolute number of species but display surprising similarities in the distribution of individuals across species (2–4). For practical reasons, biodiversity is typically measured or monitored at fine spatial scales. However, important drivers of ecological change tend to act at large scales (5, 6). Conservation issues, for example, apply to diversity at global, national, or regional scales. Extrapolating species richness from the local to the whole-forest scale is not straightforward. A vast number of different biodiversity estimators have been developed under different statistical sampling frameworks (7–11), but most of them have been designed for local/regional-scale extrapolations, and they tend to be sensitive to the spatial distribution of trees (12–14), sample coverage, and sampling methods (15). A common statistical tool used to describe the commonness and rarity of species in an ecological community is the relative species abundance distribution (SAD or RSA), which is a list of species present within a region along with the number of individuals per species (16, 17). Typically, the SAD is measured at local scales (for example, in quadrats or transects; see Fig. 1), in which the identities of the individuals living in the area are known. The sampled SAD can be fit to a given functional form at that scale. However, that form may change at different spatial scales, thus hindering analytical treatment (18). Nonparametric approaches have also been proposed in the literature to infer species richness. Instead of assuming a specific functional form for the SAD and fitting data to arrive at the parameters, these methods are based on the intuitive idea that it is only the rare species that carry information on the undetected species in a sample. A successful example is the method introduced by Chao et al. (15, 19, 20), which takes into account only the number of singletons and doubletons (species with just one or two individuals) observed at the sample scale to infer the species richness of the whole forest.
Fig. 1. The challenge of estimating global tropical species richness.
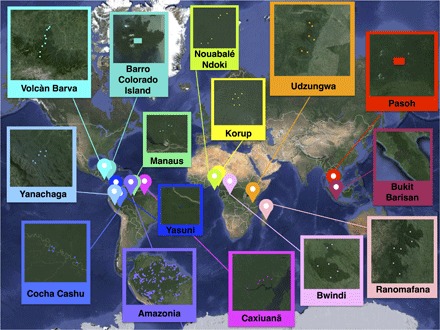
A map depicting the 15 forests in our data set in which the coordinates of each subplot (squares) are known. Our goal is to deduce the species richness and abundances of each entire forest on the basis of the very limited knowledge in the marked dots (see Table 1 and section S6 for a more detailed description of the data set).
Recently, a semianalytical method to upscale species richness based on a log series (LS) for the SAD has been proposed (section S1 and Fig. 2) (21–25). The LS distribution was obtained by Fisher et al. (26) as the limiting form of a negative binomial (NB) probability distribution (that is, the probability of observing n individuals when sampling from a population belonging to different species), excluding zero observations (no information on the number of missed species is available) and assuming that the distribution of individuals is known and simple (that is, Eulerian form). The LS distribution is often used to describe SAD patterns in ecological communities, including tropical tree communities. The robustness of the upscaling method relies on the stability property of Fisher’s α [approximately reflecting the number of observed singleton species (26)], which ought not to depend on the forest sample size and is given by
| (1) |
where Np and Sp are the total number of individuals and species, respectively, when sampling a fraction p of the forest (N1 = N and S1 = S corresponds to the total number of individuals and species when sampling the whole forest). Therefore, the LS method is composed of three main steps: (i) Fisher’s α is calculated, assuming that the species have an LS distribution (see Materials and Methods) and using the observed species Sp and number of trees Np as input. (ii) The total number of stems N for the whole area of interest is extrapolated [This is not a trivial task, and there is no consensus on the best methods to implement it. Generally, constant average stem density is assumed (24, 25).]. (iii) The number of species at the largest scale is estimated using the formula S = α ln (1 + N/α) (26). This method has been used to estimate the species richness of the Amazonia (24) and that of global tropical forests (25). For the latter case, Slik et al. (25) noted that when merging forests in different tropical regions, the value of Fisher’s α shows an asymptotic behavior for large areas, as if it is converging to its asymptote for each region. From this limiting value, it is then possible to infer the total species richness of the different tropical regions.
Fig. 2. Schematic presentation of our theoretical upscaling framework.
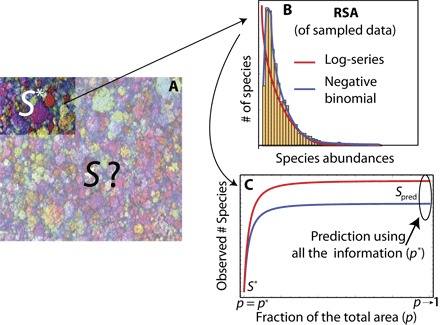
It consists of three steps. (A) We know the abundances of S* species within a given region covering a fraction p* of the whole forest. (B) We perform the best fit (maximum likelihood) of the SAD (an NB or an LS). (C) Using the best-fit parameters obtained in (B) and using our upscaling Eqs. 11 and 15, we predict the biodiversity Spred of the whole forest.
On the basis of theoretical and computational analysis as well as using the data from 15 tropical forests located all over the globe, we show that the LS method suffers from important limitations (see section S2, figs. S1 and S2, and table S1). Often, the SAD—especially at large scales or with increasing sampling effort (27)—displays an interior mode (14), which an LS cannot capture. The Fisher’s LS is not flexible enough (18) to describe different SAD patterns (14, 17, 28–32) found in tropical forests.
Here, we present a more general analytical framework to extrapolate species richness from local to whole-forest scales. This framework, derived from first principles on the basis of biological processes, is based on the fact that the functional form of any given SAD can be approximated to any degree of accuracy with a linear combination of NB distributions (see Materials and Methods), as long as the population sizes are smaller than some fixed, but otherwise arbitrary, threshold, as suggested by Nachbin’s theorem (see section S3) (33, 34). We will show that our method outperforms previously proposed methods and that the LS method turns out to be a special case of our framework.
RESULTS
Theoretical framework
The NB distribution arises naturally as the steady-state SAD of an ecosystem that undergoes simple birth-and-death dynamics, with an effective birth rate accounting for the effects of immigration events and/or intraspecific interactions (2, 14), and under the neutral hypothesis that individuals are demographically identical (see Materials and Methods) (31). This distribution is able to adequately fit the SADs of diverse ecosystems, such as tropical forests and coral reefs (14, 31). In particular, Eq. 2 below is the steady-state solution of the master equation governed by birth and death rates (see Materials and Methods). The continuum version of the NB (that is, the γ distribution) is also the stationary state of a model that captures the temporal turnover of species (35), an important aspect of tropical tree dynamics (36).
A single NB SAD is given by
| (2) |
which is normalized so that , where r > 0 and 0 ≤ ξ < 1 are the parameters accounting for immigration or intraspecific interactions and the ratio between the birth and death rates, respectively (see Materials and Methods). Fisher’s LS is obtained as the r → 0 limit of Eq. 2.
Owing to partial sampling, the empirical SAD of a small sample of a forest will likely show a monotonic decreasing behavior, because these samples contain many rare species with just a few individuals. However, a relatively larger sample may exhibit an internal mode, because relatively rare species are not found as the sampling effort increases (this happens, for example, if the SAD at the whole-forest scale is well described by a log-normal). Both situations are well captured by the NB distribution, whose functional form can accommodate both shapes, depending on the value of its different parameters (Fig. 3). When extrapolating to larger spatial scales (upscaling), a single NB distribution (Eq. 2) retains the same value of the parameter r—so we say that r is scale-invariant—whereas the parameter ξ depends on the sampling scale (see Materials and Methods). The same holds true for a linear combination of NB distributions with different values of r and the same ξ (see Materials and Methods).
Fig. 3. Versatility of the NB distribution.
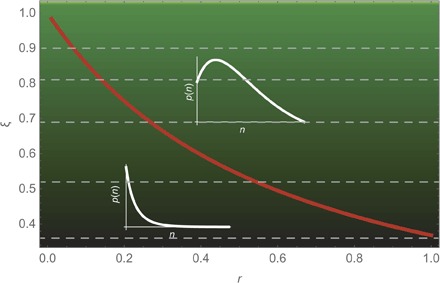
The NB distribution is a two-parameter distribution that shows self-similarity and can display both monotonic LS-like behavior (in the limit r→0, the NB tends to the LS distribution) and a unimodal shape, as a function of the scaling parameter ξ. The red curve represents the analytical threshold separating these two cases. The SAD, especially at large scales or with increasing sampling effort (27), often displays an interior mode that cannot be captured by the LS distribution but can be described by the NB. The NB distribution naturally arises as the steady-state SAD of an ecosystem undergoing generalized dynamics of birth, death, speciation, and migration processes (see Materials and Methods). Finally, any discrete probability distribution, such as the SAD, can be approximated to any degree of accuracy by a suitable linear combination of NBs that retains the self-similarity feature (see Materials and Methods). An example is shown of how the parameter ξ of the NB increases as the area of the forest doubles. Starting from ξ = 0.36, as the area doubles, the ξ value moves upward to the value corresponding to the successive (dashed) horizontal line in the upward direction.
We formulate our analytical framework on the basis of the following two steps: (i) Sample a fraction p* of the whole forest and then obtain the vector, , of the abundances of the S* sampled species. (ii) Use a linear combination of a suitable number of NBs with the same and different values of r to fit the empirical SAD at the desired degree of accuracy. This method is guaranteed to be effective according to Nachbin’s theorem (see section S3 and figs. S3 and S4) (33, 34). The NB does not change its functional form when sampling different fractions of areas—that is, distribution form invariance under different sampling efforts—although the parameters of the distribution do change. More precisely, the NB at different scales has the same r parameters, but different ξ, which is a function of the scale (see Materials and Methods). Thus, we obtain an analytical expression of the upscaled SAD at scale p from the data at scale p* in terms of the equation , defining in terms of p, p*, and (see Materials and Methods). Using the SAD at scale p*, a maximum likelihood method is used to estimate the parameters of the SAD, and the upscaling equations (see Materials and Methods) are used to predict the species richness of the entire forest, that is, p = 1. In particular, we found that the total number of species S at the largest scale (p = 1) is related to the number of species at scale p, Sp, by the following relation (see section S1 for detailed calculations)
| (3) |
where ξp and r are the NB-fitted parameters of the SAD at scale p. As noted above, r is scale-invariant and hence independent of p, whereas the parameter ξ at the largest scale, p = 1, is given by
| (4) |
The framework resembles the renormalization group technique in critical phenomena in which the behavior of a system at different scales is described in terms of equations for the model parameters, similarly to what has been suggested here (37). By using our framework (that we denote as the NB framework in the following sections), we were able to generate accurate and robust predictions for computer-generated forests and for 15 empirical tropical forests (Fig. 1 and Table 1).
Table 1. Predicting the biodiversity in tropical forests.
Predicted total number of species, Spred, at the whole-forest scale (corresponding to p = 1) for each of the 15 tropical forests in our database. Predictions are determined by using information on the sampled scale p* (fourth column), where we observe N* trees belonging to S* species (second and third columns). In the fifth column, we show the predictions obtained by using the NB framework with a single NB for fitting the sampled SAD. SEs were computed by propagating the errors in the fitting parameters of the SAD (obtained by the bootstrapping method) and of S*. The latter has been determined as follows: For each data set, we created the corresponding predicted forest at the scale p = 1 by generating Spred numbers distributed according to an NB with parameters (r, ξ). We then sampled the p% of the list of individuals, as in the original data. The last two columns show the predictions of the LS and Chao methods.
| Forest | S* | N* | p*% |
Spred (NB) |
Spred (LS) |
Spred (Chao) |
| Amazonia | 4962 | 553949 | 0.00016 | 13602 ± 711 | 14984 | 5561 |
| Barro Colorado |
301 | 222602 | 3.20513 | 366 ± 15 | 419 | 315 |
| Bukit Barisan |
340 | 14974 | 0.00169 | 471 ± 40 | 1020 | 346 |
| Bwindi | 128 | 18490 | 0.01813 | 163 ± 15 | 288 | 129 |
| Caxiuana | 386 | 32701 | 0.01818 | 437 ± 14 | 915 | 386 |
| Cocha Cashu | 489 | 16640 | 0.00035 | 731 ± 63 | 1674 | 501 |
| Korup | 226 | 17427 | 0.00473 | 282 ± 23 | 591 | 226 |
| Manaus | 946 | 38933 | 0.06000 | 1016 ± 14 | 2242 | 956 |
| Nouabalé- Ndoki |
110 | 7196 | 0.00143 | 125 ± 8 | 316 | 110 |
| Pasoh Forest Reserve |
927 | 310520 | 0.35714 | 1193 ± 36 | 1590 | 1049 |
| Ranomafana | 269 | 34580 | 0.01463 | 336 ± 22 | 620 | 269 |
| Udzungwa | 109 | 18447 | 0.00302 | 146 ± 20 | 269 | 114 |
| Volcan Barva | 392 | 44439 | 0.02025 | 448 ± 16 | 895 | 395 |
| Yanachaga | 209 | 2041 | 0.00372 | 802 ± 211 | 802 | 259 |
| Yasuni | 481 | 13817 | 0.61100 | 565 ± 20 | 974 | 484 |
Test on in silico forests
We first compared the results of our method applied to a computer-generated forest. In this in silico experiment, we fixed the number of species (S = 5000) and their abundance distribution a priori and then generated the forest accordingly. Species abundances were extracted from a log-normal SAD of mean, μ = 5, and SD, σ = 1, and the individual trees were located according to a modified Thomas process (see fig. S5 and section S4) (38, 39) with two distinct clustering coefficients (high and low clustering). The log-normal SAD, originally proposed by Preston (40), has been used to fit the SAD of several tropical forests (14, 41), whereas Thomas cluster models have reproduced empirical species-area curves with high fidelity (12, 42).
We then sampled nonoverlapping 1-unit plots at randomly chosen locations covering only a small fraction, p* = 5 %, of the area and attempted to predict S using only this partial information. We performed the estimation of the total species richness of the computer-generated forest by using a single NB distribution or a linear combination of two NB distributions, the LS method and the Chao estimator, based on sampling without replacement (see section S5 and table S3). For both clustering regimes, the prediction of the number of species using the NB framework with just one NB was already very good (error < 2%; high clustering, Spred = 5095; low clustering, Spred = 5067). The linear combination of two NBs increased the accuracy of the prediction at the whole-forest scale p = 1 (with two parameters, we obtained the following values: error < 0.2 %; high clustering, Spred = 4995; low clustering, Spred = 5011). Chao’s method gave results comparable to those with one NB (error < 2%; high clustering, Spred = 4938; low clustering, Spred = 4931) while underestimating the true number of species instead of overestimating it. In contrast, the LS method strongly overestimated the number of species (error > 56 %; high clustering, Spred = 7838; low clustering, Spred = 9036). We thus found that although the original forest had a log-normal SAD entangled with spatial correlations, a single NB or a linear combination of two NBs led to surprisingly good predictions and systematically outperformed the LS method; this result was also true for a computer-generated forest with an NB SAD and when a different sampling method was performed, consisting of collecting data within a unique spatial window covering the same percentage of the whole forest area (section S4 and table S2). Finally, we compared the results for an in silico LS forest. As expected, in this case, the LS method performed very well, predicting a species richness of 4930 against the true value of 5000 (error ~ 1.3%). The very same result was obtained by using the NB method. The best fit of the SAD with an NB led to an r parameter very close to zero (r ~ 10−5), so that the NB distribution was effectively converging to an LS. In contrast, the Chao method underestimated the number of species giving a prediction of 3878 (error ~ 22%). Previous results have shown (43) that the Chao estimator for upscaling species richness based on sampling with replacement perform poorly in hyperdiverse communities with many rare species. Here, we found that the very same result holds for the estimator based on sampling without replacement, an assumption consistent with the way empirical forests are sampled.
Test on empirical data
To test the accuracy of our method on more realistic distributions of trees (for example, habitat heterogeneity, species spatial distributions, etc.), we used subsamples taken from empirical forest data (see section S6 and table S6) and predicted the number of species at the corresponding largest empirically observable scale. That is, we extracted a fraction p of the data and applied our framework to infer the number of species at the scale p*. Moreover, we compared our results to those obtained with other methods to upscale species richness and abundances, previously proposed in the literature (see tables S3 to S5 and fig. S6) (19–21, 25). We found that our method outperforms that of Chao and Chiu (19, 20)—which typically overestimates the forest species richness—for Amazonia, Pasoh, and Yasuni (Fig. 4). For the remaining forests, the NB method performed better than the LS method, which overestimates the number of species at p*, and it was comparable to Chao’s (see section S5 for a detailed discussion). However, we remark that the accuracy in Chao’s predictions is due to the fact that, when sampling these forests at small scales, we found a low number of singleton and doubleton species. Therefore, Chao and Chiu (19, 20) conservatively gave the number of species at the observation scale itself as output, that is, (see section S5). This limitation is evident in Fig. 4, which shows the tropical forest species area relationship (SAR), that is, the number of observable species as a function of the fraction of the sampled area a, (p* ≤ a ≤ 1). Whereas LS and NB show the expected qualitative behavior, the method of Chao saturates almost immediately at a ≈ p*, which is clearly an artifact of the method. The same results were obtained when using Chao’s estimator based on sampling with replacement (43).
Fig. 4. Comparison between NB, Slik, and Chao estimators.
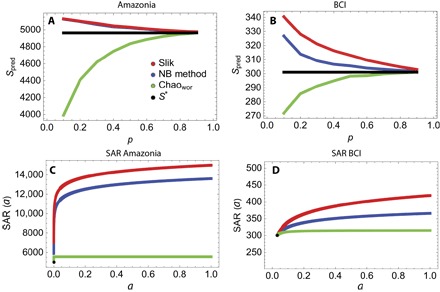
Top panels: Predictions at different subscales of the number of species (the number corresponding to p* = 1 is represented as a constant black line) of the Slik method (red line), the NB method (blue line), and the method of Chao (green line) for Amazonia (A) and BCI (B) forests. As can be seen, the first two methods perform better for the Amazon forest, where the number of singletons, on which Chao’s estimate is based, is high at every subscale but not enough to compensate the difference , at small scales (see section S5 for more details). In contrast, for the BCI forest, both the NB and the Chao methods give comparable predictions, because here the number of singletons is very small as is the difference between and Sp. Bottom panels: Amazonia (C) and BCI (D) SAR, that is, the predicted number of species at different normalized areas a (p* < a < 1) with the three methods. In the figures, the black dots are the number of species observed at the sample scale p*. In contrast with the canonical SAR obtained with the NB and LS methods, Chao’s prediction remains constant over a large part of the upscaling area range.
Biodiversity upscaling of tropical forest data
After testing our model on controlled computer-generated data and real forest subsamples, we applied our framework to predict the species richness and abundances of tropical forest data. Because of the good agreement between the predictions made with a single NB for the artificial forests, we chose to work again with a single NB. Such a form can be derived from basic ecological processes (14, 31), and it also permits an exact analytical treatment of the upscaling protocol. Although in few cases, using more than one NB improves the accuracy of the predictions, in general, it increases the likelihood that the empirical data are overfit at the sampled scale. Therefore, through the NB method, we attempted to predict the species richness at the whole-forest scale (p = 1) for each of the 15 tropical forests around the equatorial zone, and we compared our predictions with those of previous results based on the LS distribution (24, 25) and with that obtained with the method of Chao. We found that the LS method systematically led to higher estimates of the number of rare species and consequently of the forest species richness at the largest scale (see Table 1). Only for the Yanachaga Chemillén National Park, the two estimates with NB and LS were essentially the same. The discrepancies in the estimates increased to approximately 10% for Amazonia and Barro Colorado Island (BCI), reached 30 to 40% for Pasoh and Bukit Barisan and ranged between 72 and 152% for the remaining 10 forests. In contrast, Chao’s method predicted a much smaller number of species at the whole-forest scale. The errors in our estimates are also given in Table 1.
Our framework is also able to give a quantitative estimate of the sampling effort (ppred %; first column in Table 2) needed to achieve species richness predictions with error bars below approximately 5% (this percentage was arbitrarily chosen as an illustration, and our approach can be straightforwardly used for any other percentage of error). These estimates have been obtained through Monte Carlo simulations, which test the self-consistency of the NB method and allow us to infer these critical sampling thresholds (see section S7 and figs. S7 and S8). We found that for some forests (BCI, Caxiuana, Manaus, Volcan Barva, and Yasuni), the present sampling effort may be sufficiently informative and representative to characterize the biodiversity of the whole forest. In contrast, we propose an estimate of the further sampling required for all the other forests (Table 1). Amazonia, for example, would need approximately twice the current amount of sampling; Cocha and Nouabalé would need approximately 10 times; and Bwindi, Udzungwa, and Yanachaga would need several hundred times the current sampling (see the third column of Table 2 showing the ratio between the predicted needed sampling and the actual one).
Table 2. Sampling targets for forest percentage cover.
Using our results on upscaled forest species richness, it is possible to estimate the percentage ppred% of the forest that must be sampled to achieve an estimation error of approximately 5% with a certainty of 95%. We derived these values by creating the predicted forest at the whole-forest scale (we generated Spred numbers according to an NB with parameters r and ξ) and sampled it at increasingly larger scales until the desired accuracy in the estimation of the global species richness was reached (see section S7 for more details). The last column indicates how much extra sampling is needed (if the number is greater than 1) to reach 5% precision.
| Forest | ppred% | ppred/p* |
| Amazonia | 0.0003 | 1.875 |
| Barro Colorado | 3 | 1 |
| Bukit Barisan | 0.05 | 18 |
| Bwindi | 5 | 386 |
| Caxiuana | 0.01 | 0.55 |
| Cocha Cashu | 0.003 | 8.57 |
| Korup | 0.02 | 1.06 |
| Manaus | 0.02 | 0.17 |
| Nouabalé-Ndoki | 0.015 | 10.5 |
| Pasoh forest reserve | 0.5 | 1.4 |
| Ranomafana | 0.1 | 6.84 |
| Udzungwa | 1.5 | 497 |
| Volcan Barva | 0.02 | 0.25 |
| Yanachaga | 1 | 269 |
| Yasuni | 0.3 | 0.49 |
We also estimated the number of hyper-rare species, defined as species with fewer than 1000 individuals, and the number of hyperdominant species, defined as the most abundant species contributing approximately 50% to the total number of individuals of the forest (see Table 3) (24).
Table 3. Fisher’s paradox.
Hyper-rare species [defined as species with fewer than 1000 individuals (24, 25)] and hyperdominant species (the most abundant species, accounting for ≈ 50 % of the total number of individuals) percentages were predicted in the whole area of each tropical forest obtained by applying both the NB and LS methods. We found that by using our NB method, the number of hyper-rare species in most of the forests was drastically reduced with respect to the LS method, thus suggesting that the extremely high value of hyper-rare species predicted in previous studies (24, 25) is an artifact of the LS method. Nevertheless, we found that the hyper-rarity phenomenon is a genuine emergent pattern in tropical forests.
| Forest | Hyper-rare (%) | Hyperdominant (%) | ||
| NB method | LS method | NB method | LS method | |
| Amazonia | 33 | 37 | 2.2 | 2.0 |
| Barro Colorado Nature Monument | 47 | 60 | 5.5 | 4.8 |
| Bukit Barisan | 22 | 46 | 7.9 | 1.9 |
| Bwindi Impenetrable Forest | 15 | 48 | 7.4 | 3.5 |
| Caxiuana | 6 | 49 | 10.3 | 3.2 |
| Cocha Cashu Manu National Park | 7 | 41 | 8.4 | 2.5 |
| Korup National Park | 9 | 51 | 9.3 | 3.1 |
| Manaus | 6 | 59 | 14.5 | 2.8 |
| Nouabalé-Ndoki | 4 | 43 | 11.2 | 2.4 |
| Pasoh Forest Reserve | 34 | 55 | 6.5 | 3.1 |
| Ranomafana | 12 | 49 | 7.5 | 2.7 |
| Udzungwa Mountain National Park | 12 | 48 | 6.3 | 3.0 |
| Volcan Barva | 8 | 52 | 10.5 | 2.5 |
| Yanachaga Chemillén National Park | 54 | 56 | 3.0 | 2.7 |
| Yasuni National Park | 39 | 74 | 11.6 | 4.4 |
DISCUSSION
Our analysis shows that hyper-rarity, as also suggested by previous works (24, 25), is a recurrent pattern in large-scale tropical forests, which may suggest that these tropical forests are biodiversity hot spots (see also discussion below) (44). Focusing on Amazonia, we predict that roughly 4500 Amazon tree species are hyper-rare. If they could be found and identified, then this would automatically qualify them for inclusion in the International Union for Conservation of Nature’s Red List of Threatened Species. The NB upscaling for the entire Amazon forest predicts that half the total number of trees belong to just 300 hyperdominant species, whereas 33% of the 13,602 tree species are hyper-rare. In this way, ecologists would have an estimate of how many Amazon tree species face the most severe threats of extinction. These rare species in the Amazon forest (and our planet’s biodiversity) are like dark matter in cosmology, which accounts for much of the universe. Nevertheless, in most of the forests, we obtained a smaller number of hyper-rare species and a higher number of hyperdominant ones with respect to previous estimates (24, 25). This result is in agreement with the tests we performed both in silico and on empirical forest data. We believe that this is due to the fact that the asymptotic value of Fisher’s α in the LS method is strongly biased when a very small fraction of the forest is sampled (typically < 1%) (section S2).
As well as being a crucial and practical measure of fragile biodiversity in conservation ecology, hyper-rarity is also an important theoretically intriguing and open question that goes under the name of the “Fisher paradox” (43, 45). We still do not know why there is such a huge separation of population size scales between rare and hyperdominant species. Our framework provides a possible interpretation for this phenomenon and suggests that hyper-rarity could be a manifestation of criticality in tropical forests (37, 46). The parameters of the NB distributions that provided the best predictions of the upscaled species richness in tropical forests fall within a tiny region of parameter space: 0 < r < 0.7 and ξ ≈ 1. This result is surprising, because there are neither theoretical nor biological reasons why tropical forests should have their parameters localized within such a narrow region, especially when considering that they are in completely different geographical regions with differing evolutionary histories. However, a closer examination of the form of the NB distribution reveals that the relative fluctuation of abundances, that is, , diverges as ξ → 1 and r → 0 (see Fig. 5 and section S8). Thus, parameter values in the vicinity of this region allow an ecosystem to have the highest heterogeneity in its abundance distribution. The points shown in Fig. 5 correspond to the parameter values obtained for the 15 forests. A physical system, such as water and vapor, in the vicinity of its critical point, is characterized by density fluctuations that become very large, with droplets of water and bubbles of gas of all sizes thoroughly interspersed, and the system appears the same at different scales (that is, it is self-similar) (37). This scale invariance confers to the system an acute sensitivity to certain types of external perturbations or disturbances whose effects are realized at long distances. The observed large abundance fluctuations suggest that tropical forests may be critical systems and may be relatively reactive to disturbances (47, 48) and able to adapt optimally to new external conditions/constraints. Under a given set of environmental conditions, only a few species are best at exploiting the limited available resources (49). Because of environmental fluctuations, these conditions may not continue to remain advantageous for the existing very few abundant species. However, a large pool of species may serve as a reservoir of new opportunities and responses and as a buffer against newly changed conditions (49). According to this view, hyper-rarity is essential for an ecosystem to maintain its functions and react promptly to changes: Rare species may provide the key to an ecosystem’s future (50).
Fig. 5. Tropical forests are poised in the vicinity of criticality.
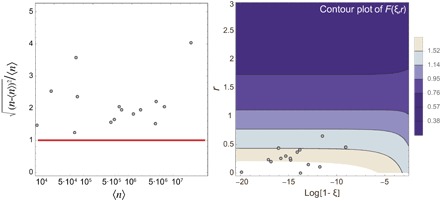
(A) Plot of the relative fluctuations of species abundances, , in linear scale versus abundances 〈n〉 at the logarithmic scale. The black dots represent the predicted values for each of the 15 tropical forests listed in Table 1 at the whole-forest scale, and the red line is the line of equation y = 1. All values are located above this line, thus indicating that the relative fluctuations in abundance are considerable for all the forests. (B) Contour plot of the relative fluctuation of abundances for an NB SAD . The black dots represent the pair (r, log [1 − ξ]), where r and ξ are the predicted parameters for each forest of our data set after upscaling at the whole-forest scale. These dots are all located in the region of the parameter space around which the function F(ξ, r) diverges, that is, ξ ≈ 1 and 0 < r < 0.7.
To summarize, we have presented a theoretical framework to upscale species richness and abundances in tropical forests from a limited number of samples. The advantage of our method mainly relies on two properties. First, it is flexible. The NB, depending on the value of its parameters, may display either an LS-like behavior or an interior mode, and it is therefore able to describe different SAD shapes. Thus, we can use the same functional form to reproduce different ecosystems’ SAD, as those observed in our data set. In contrast, an LS SAD predicts a very specific form for the SAD that is not flexible enough to describe any SAD with an interior mode. Furthermore, our approach, relying on an appropriate linear combination of NBs, can basically accommodate any type of complex SAD functional form.
Second, the NB (or a combination of them), besides being flexible, is also self-similar under different sampling intensities. This is the key feature that allows us to obtain an easy analytical formula to upscale the SAD from the sample scale to any arbitrary one. In the study of Harte et al. (21), despite the flexibility of the approach, the upscaling can be performed only by numerically solving a pair of analytical equations. In the study of Zillio and He (51), they proposed an iterative method for estimating the species richness and the abundance distribution. Again, this method is flexible, but no analytical treatment can be performed. Finally, in our framework, we only need the fraction of the sampled area with respect to the whole forest, whereas in other approaches, additional information on the upscaled forest is required [for example, the number of individuals of the most abundant species (52)].
These two properties allow our method to be applied on statistical upscaling problems beyond forest ecology. A possible application is, for example, in the field of metagenomics. Using recently developed DNA sequencing machines, it is possible to obtain the total genomic DNA directly from a macro fauna or flora environmental sample (that is, a macrobiome). This metagenomic (gene of genes) approach, together with taxonomic classification algorithms (53), allows a characterization of the biodiversity of the samples (typically prokaryotes). However, SAD curves built in this way describe the biodiversity only very locally (the scale of the given environmental sample). Nevertheless, by assuming well-mixed communities and finding an appropriate combination of NBs fitting the observed SAD, we can use our framework to upscale the microbiome SAD to a larger scale (for example, the whole gut), as would be measured if it were possible to survey the entire environment. It can also be applied to immunology for finding the number of T cell receptor clonotypes in a human body. These examples show the promising generality of our approach and open the possibility of new applications of the upscaling framework to other taxa or type of systems.
MATERIALS AND METHODS
Upscaling NBs
Here, we chose the NB distribution in Eq. 2 as the SAD. Apart from its simplicity and versatility, we chose this form for our analysis for four reasons:
(1) Any discrete probability distribution, such as the SAD, can be approximated to any degree of accuracy by a suitable linear combination of NBs (see section S3 for some examples and discussion). We made the parsimonious choice of a single NB function because it suffices to approximately describe the available tropical forest data, as discussed in the Results and Discussion.
(2) The NB distribution arises naturally as the steady-state SAD of an ecosystem with sufficiently weak interspecies interactions and undergoing generalized dynamics of birth, death, speciation, and immigration to and emigration from the surrounding metacommunity (see “Stochastic model leading to an NB SAD”).
(3) In the limit of r → 0, the NB becomes the well-known Fisher’s LS, which has been widely used to describe the patterns of abundance in ecological communities. Of course, because of the flexibility of choosing r to be nonzero, the NB distribution is always more versatile than the LS. The SAD, especially at large scales or with increasing sampling effort (27), often displays an interior mode that cannot be captured by an LS distribution. To assess whether the increased reliability of the NB method with respect to the LS method is only due to the introduction of the additional parameter r, we used the Akaike information criterion, which shows that the NB is the preferred model for all tropical forests in our data set except one for which r is very close to zero.
4. Finally and importantly, if one chooses two contiguous patches with NB as SADs characterized by the same parameters r and ξ ≡ ξ1/2 and combines the two, then remarkably, the resulting larger patch is also characterized by an NB distribution with the same scale-invariant value of r and a new scale-dependent parameter, ξ, given by the analytical expression in Eq. 4 below with p = 1/2. This special form-invariant property of the NB distribution, albeit with a scale-dependent parameter, makes it particularly well suited for our extrapolation studies.
When upscaling, we are interested in the SAD and in the total number of species, S, at the scale of the whole forest area A. We denote P(n|1) as the probability that a species has exactly n individuals at the whole-forest scale (here, 1 refers to the whole forest). Note that P(n|1) is defined only for n ≥ 1, because S is the total number of species actually present in the forest, thus each having at least one individual.
We assumed that the SAD has the functional form of an NB, , for nonzero populations, with parameters (r, ξ) (r is known as the clustering coefficient), that is
| (5) |
where c is the normalization constant. The constant c was determined by imposing , where the sum starts from n = 1, because species with zero abundance at the scale of the whole forest will be also absent in the subplots. Note that was normalized for n ≥ 0. In the subplots, there is a nonzero probability to find species, which are present in the whole forest, with n = 0 individuals, and thus it accounts for the number of missing species in the subplots.
Let us now consider a subsample of area a of the whole forest and define p = a/A as the scale of the sample, which is the fraction of the sampled forest. The goal is to compute the SAD in the subsample.
We assumed that the subsample SAD was not affected by spatial correlations due to both interspecific and intraspecific interactions. This hypothesis is well satisfied using in silico–generated forests with various degrees of spatial correlations (see section S4). Under this hypothesis, the conditional probability that a species has k individuals in the smaller area, a = pA, given that it has total abundance n in the whole region of area A is given by the binomial distribution
| (6) |
and if k > n. Now, we want to prove that the subsample SAD, P(k|p), is again an NB for k ≥ 1, with the rescaled parameter ξ and the same r. It can be shown that the probability, , to find a species with population k ≥ 0 in the subplot of area a = pA is
| (7) |
| (8) |
where
| (9) |
The method uses only the information that we can infer from a subsample at some scale p*. Therefore, we only have information on the abundances of the S*(≤S) species present in the surveyed area. By denoting with S*(k), the number of species of abundance k at scale p*, we obtained
| (10) |
which, from Eq. 5, is an NB normalized for k ≥ 1, whereas is normalized for k ≥ 0. We therefore obtained the key result that starting with an NB distribution for the SAD at the whole-forest scale, the SAD at smaller scales is also distributed according to an NB with the same clustering coefficient r and a rescaled parameter depending on both ξ and p*. A SAD with the property of having the same functional form at different scales is said to be form-invariant.
By fitting the SAD of the data at the scale p*, we can thus find both the parameters r and and, by inverting Eq. 9, we can obtain ξ
| (11) |
Using Eq. 9 to eliminate ξ from the last equation, one obtains the following relation for the parameter ξ at the two scales p and p* referred in the Results
| (12) |
from which, of course, one can recover both Eqs. 9 and 11, where .
We now wish to determine the relation between the total number of species at the whole scale p = 1, S, with the total number of species surveyed at scale p, Sp. Referring to the scale p*, in the following equation, we also used the notation . This can be simply obtained by observing that
| (13) |
| (14) |
Using Eq. 8, we finally found that the prediction for the total number of species in the whole forest, in terms of the data on the surveyed subplot, is given by
| (15) |
where ξ is given by Eq. 11.
Our framework holds exactly when species are spatially uncorrelated. However, our in silico experiments indicated that the framework is robust even in the presence of spatial correlations and for different sampling methods (section S4).
Stochastic model leading to an NB SAD
As explained in the Introductions, the NB distribution can be derived from first principles on the basis of biological processes. Let be the probability that, at time t, species s has exactly n individuals, where s ∈ {1, …, S}. We assumed that the population dynamics of each species is governed by two terms, bn,s and dn,s, which are the birth and death rates, respectively, for species s with n individuals. The master equation regulating the evolution of for n ≥ 0 is then
The above equation is also valid for n = 0 and n = 1 if we set b−1,s = d0,s = 0. The steady-state solution is
| (16) |
The term cs is a normalization factor found by imposing .
Let us assume that the birth term in the above equation depends on a density-independent term, bs, which is the per-capita birth rate, and on the term rs, which takes into account immigration events or intraspecific interactions
Analogously, let us suppose that the death term depends on a density-independent term, ds, which is the per-capita death rate
These suppositions are reasonable in ecology. By substituting in Eq. 16 and setting ξs = bs/ds, we obtained
| (17) |
The normalization constant can be easily found by imposing
Therefore, the probability that the sth species has n individuals at equilibrium is given by an NB with parameters (rs, ξs)
| (18) |
Under the neutral hypothesis, in which all species are considered to be equivalent, we can remove the species index s from the above equation, thus obtaining a negative binomially distributed SAD for the ecosystem under study.
Supplementary Material
Acknowledgments
We are indebted to S. P. Hubbell for his insightful comments. We also thank the Center of Tropical Research Science for providing the empirical data of the BCI and Pasoh forests. The BCI forest dynamics research project was founded by S. P. Hubbell and R. B. Foster and is now managed by R. Condit, S. Lao, and R. Perez under the Center for Tropical Forest Science and the Smithsonian Tropical Research in Panama. It has been funded by numerous organizations, principally the U.S. NSF, and hundreds of field workers have contributed. All other data in this publication were provided by the Tropical Ecology Assessment and Monitoring Network, a collaboration between Conservation International, the Missouri Botanical Garden, the Smithsonian Institution, and the Wildlife Conservation Society, and partially funded by these institutions, the Gordon and Betty Moore Foundation, and other donors. Funding: S.A. would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for the support and hospitality during the program “Stochastic Dynamical Systems in Biology: Numerical Methods and Applications,” where work on this paper was partially undertaken. This work was supported by Engineering and Physical Sciences Research Council grant no. EP/K032208/1. The authors acknowledge the Department of Mathematics “Tullio Levi-Civita” of the University of Padova and the Department of Applied Maths of the University of Leeds for financial support. Author contributions: S.A., J.R.B., A.M., and S.S. designed the work. A.T. and S.S. performed the numerical simulations and the data analysis and prepared the figures. S.A., A.T., M. Formentin, M. Favretti, I.V., and A.M. performed the analytical calculations. All the authors contributed to other aspects of the paper and the writing of the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: We use a global-scale compilation of 1248 local sites collected over 15 forests around the planet on different tropical field stations of the equatorial zone. All data are publicly available. See the Supplementary Materials for web links and a more detailed description of the data set. For numerical simulations performed in this study, we used standard commands and programming tools in R/Mathematica. A ready-to use code in R for predicting the upscaled SAD and total species richness and abundances is available at https://github.com/annatovo or in the web page of our group (www.pd.infn.it/~maritan). Requests for materials should be addressed to S.S. (suweis@pd.infn.it), to M. Formentin (marco.formentin@unipd.it), to J.R.B. (banavar@uoregon.edu), or to A.M. (maritan@pd.infn.it).
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/10/e1701438/DC1
section S1. Upscaling biodiversity
section S2. Limitation of the LS methods
section S3. Flexibility of NB distribution
section S4. Test on computer-simulated forests
section S5. Comparison with other popular estimators
section S6. Data set
section S7. Self-consistency and estimation of the critical p*: How much remains to be sampled?
section S8. RSA parameters maximize relative fluctuation in abundances
fig. S1. Assuming that the global RSA is distributed according to an NB, we can compute the probability that a species comprises a single individual at the scale p by using eq. S31.
fig. S2. Fisher’s α for three different rainforests: Amazonia, Barro Colorado Nature Monument, and Caxiuana.
fig. S3. Fit of an RSA consisting of a combination of an LS and a log-normal distribution.
fig. S4. We have generated synthetic data from a combination of discrete distributions (a binomial distribution of parameters r = 40 and ξ = 0.8, a geometric distribution of parameter μ = 0.15, and a Poisson distribution with parameter λ = 15) and fit these data with one, three, and six NBs, respectively.
fig. S5. Robustness of the method.
fig. S6. Comparison between biodiversity estimators for Amazonia and BCI forests.
fig. S7. Self-consistency test of our framework.
fig. S8. Plot, in logarithmic scale, of the percentage ppred% that one ought to sample to have a precision estimate of around 5% for the predicted percentage of hyper-rare species, that is, species with fewer than 1000 individuals at the global scale.
table S1. Predicted number of singletons in the whole area of each tropical forest obtained by applying our method (NB method).
table S2. Prediction of the total number of species obtained by applying both NB and LS methods to the forest generated according to an NB and distributed in 8900 × 8900 units according to two different modified Thomas processes with the same density of clusters ρ = 6 × 10−5 and different clump sizes σ = 15 and 200.
table S3. Summary table of the most popular biodiversity estimators.
table S4. Comparison between NB, LS, Chaowor, and the Harte methods on empirical data.
table S5. Comparison between the NB, LS, Chaowor, and Harte methods on BCI empirical data.
table S6. Number of species and singletons in 15 forests in our data set with the percentage p% (last column of the table) of surveyed area.
Reference (54)
REFERENCES AND NOTES
- 1.Crowther T. W., Glick H. B., Covey K. R., Bettigole C., Maynard D. S., Thomas S. M., Smith J. R., Hintler G., Duguid M. C., Amatulli G., Tuanmu M.-N., Jetz W., Salas C., Stam C., Piotto D., Tavani R., Green S., Bruce G., Williams S. J., Wiser S. K., Huber M. O., Hengeveld G. M., Nabuurs G.-J., Tikhonova E., Borchardt P., Li C.-F., Powrie L. W., Fischer M., Hemp A., Homeier J., Cho P., Vibrans A. C., Umunay P. M., Piao S. L., Rowe C. W., Ashton M. S., Crane P. R., Bradford M. A., Mapping tree density at a global scale. Nature 525, 201–205 (2015). [DOI] [PubMed] [Google Scholar]
- 2.Volkov I., Banavar J. R., He F., Hubbell S., Maritan A., Density dependence explains tree species abundance and diversity in tropical forests. Nature 438, 658–661 (2005). [DOI] [PubMed] [Google Scholar]
- 3.McGill B. J., Etienne R. S., Gray J. S., Alonso D., Anderson M. J., Benecha H. K., Dornelas M., Enquist B. J., Green J. L., He F., Hurlbert A. H., Magurran A. E., Marquet P. A., Maurer B. A., Ostling A., Soykan C. U., Ugland K. I., White E. P., Species abundance distributions: Moving beyond single prediction theories to integration within an ecological framework. Ecol. Lett. 10, 995–1015 (2007). [DOI] [PubMed] [Google Scholar]
- 4.Suweis S., Bertuzzo E., Mari L., Rodriguez-Iturbe I., Maritan A., Rinaldo A., On species persistence-time distributions. J. Theor. Biol. 303, 15–24 (2012). [DOI] [PubMed] [Google Scholar]
- 5.Alonso D., Ostling A., Etienne R. S., The implicit assumption of symmetry and the species abundance distribution. Ecol. Lett. 11, 93–105 (2008). [DOI] [PubMed] [Google Scholar]
- 6.Bertuzzo E., Carrara F., Mari L., Altermatt F., Rodriguez-Iturbe I., Rinaldo A., Geomorphic controls on elevational gradients of species richness. Proc. Natl. Acad. Sci. U.S.A. 113, 1737–1742 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bunge J., Fitzpatrick M., Estimating the number of species: A review. J. Am. Stat. Assoc. 88, 364–373 (1993). [Google Scholar]
- 8.Brose U., Martinez N. D., Williams R. J., Estimating species richness: Sensitivity to sample coverage and insensitivity to spatial patterns. Ecology 84, 2364–2377 (2003). [Google Scholar]
- 9.Mao C. X., Colwell R. K., Estimation of species richness: Mixture models, the role of rare species, and inferential challenges. Ecology 86, 1143–1153 (2005). [Google Scholar]
- 10.Wang J.-P. Z., Lindsay B. G., A penalized nonparametric maximum likelihood approach to species richness estimation. J. Am. Stat. Assoc. 100, 942–959 (2005). [Google Scholar]
- 11.Bunge J., Woodard L., Böhning D., Foster J. A., Connolly S., Allen H. K., Estimating population diversity with CatchAll. Bioinformatics 28, 1045–1047 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Plotkin J. B., Potts M. D., Leslie N., Manokaran N., Lafrankie J., Ashton P. S., Species-area curves, spatial aggregation, and habitat specialization in tropical forests. J. Theor. Biol. 207, 81–99 (2000). [DOI] [PubMed] [Google Scholar]
- 13.Carrara F., Altermatt F., Rodriguez-Iturbe I., Rinaldo A., Dendritic connectivity controls biodiversity patterns in experimental metacommunities. Proc. Natl. Acad. Sci. U.S.A. 109, 5761–5766 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Azaele S., Suweis S., Grilli J., Volkov I., Banavar J. R., Maritan A., Statistical mechanics of ecological systems: Neutral theory and beyond. Rev. Mod. Phys. 88, 035003 (2016). [Google Scholar]
- 15.Chao A., Colwell R. K., Lin C.-W., Gotelli N. J., Sufficient sampling for asymptotic minimum species richness estimators. Ecology 90, 1125–1133 (2009). [DOI] [PubMed] [Google Scholar]
- 16.MacArthur R., On the relative abundance of species. Am. Nat. 94, 25–36 (1960). [Google Scholar]
- 17.A. E. Magurran, Ecological Diversity and Its Measurement (Springer Science & Business Media, 2013). [Google Scholar]
- 18.Azaele S., Maritan A., Cornell S. J., Suweis S., Banavar J. R., Gabriel D., Kunin W. E., Towards a unified descriptive theory for spatial ecology: Predicting biodiversity patterns across spatial scales. Methods Ecol. Evol. 6, 324–332 (2015). [Google Scholar]
- 19.A. Chao, Species estimation and applications, in Encyclopedia of Statistical Sciences, S. Kotz, C. B. Read, N. Balakrishnan, B. Vidakovic, Eds. (John Wiley and Sons Inc., 2005), pp. 7907–7916. [Google Scholar]
- 20.A. Chao, C.-H. Chiu, Species richness: Estimation and comparison, in Wiley StatsRef: Statistics Reference Online (John Wiley and Sons, 2016), pp. 1–26. [Google Scholar]
- 21.Harte J., Smith A. B., Storch D., Biodiversity scales from plots to biomes with a universal species–area curve. Ecol. Lett. 12, 789–797 (2009). [DOI] [PubMed] [Google Scholar]
- 22.White E. P., Thibault K. M., Xiao X., Characterizing species abundance distributions across taxa and ecosystems using a simple maximum entropy model. Ecology 93, 1772–1778 (2012). [DOI] [PubMed] [Google Scholar]
- 23.Kitzes J., Harte J., Predicting extinction debt from community patterns. Ecology 96, 2127–2136 (2015). [DOI] [PubMed] [Google Scholar]
- 24.ter Steege H., Pitman N. C. A., Sabatier D., Baraloto C., Salomão R. P., Guevara J. E., Phillips O. L., Castilho C. V., Magnusson W. E., Molino J.-F., Monteagudo A., Núñez Vargas P., Montero J. C., Feldpausch T. R., Coronado E. N. H., Killeen T. J., Mostacedo B., Vasquez R., Assis R. L., Terborgh J., Wittmann F., Andrade A., Laurance W. F., Laurance S. G. W., Marimon B. S., Marimon B.-H. Jr, Guimarães Vieira I. C., Amaral I. L., Brienen R., Castellanos H., Cárdenas López D., Duivenvoorden J. F., Mogollón H. F., de Almeida Matos F. D., Dávila N., García-Villacorta R., Stevenson Diaz P. R., Costa F., Emilio T., Levis C., Schietti J., Souza P., Alonso A., Dallmeier F., Montoya A. J. D., Fernandez Piedade M. T., Araujo-Murakami A., Arroyo L., Gribel R., Fine P. V., Peres C. A., Toledo M., Aymard C. G. A., Baker T. R., Cerón C., Engel J., Henkel T. W., Maas P., Petronelli P., Stropp J., Zartman C. E., Daly D., Neill D., Silveira M., Paredes M. R., Chave J., Lima Filho Dde A., Jørgensen P. M., Fuentes A., Schöngart J., Cornejo Valverde F., Di Fiore A., Jimenez E. M., Peñuela Mora M. C., Phillips J. F., Rivas G., van Andel T. R., von Hildebrand P., Hoffman B., Zent E. L., Malhi Y., Prieto A., Rudas A., Ruschell A. R., Silva N., Vos V., Zent S., Oliveira A. A., Schutz A. C., Gonzales T., Trindade Nascimento M., Ramirez-Angulo H., Sierra R., Tirado M., Umaña Medina M. N., van der Heijden G., Vela C. I. A., Vilanova Torre E., Vriesendorp C., Wang O., Young K. R., Baider C., Balslev H., Ferreira C., Mesones I., Torres-Lezama A., Urrego Giraldo L. E., Zagt R., Alexiades M. N., Hernandez L., Huamantupa-Chuquimaco I., Milliken W., Palacios Cuenca W., Pauletto D., Valderrama Sandoval E., Valenzuela Gamarra L., Dexter K. G., Feeley K., Lopez-Gonzalez G., Silman M. R., Hyperdominance in the Amazonian tree flora. Science 342, 1243092 (2013). [DOI] [PubMed] [Google Scholar]
- 25.Slik J. W., Arroyo-Rodríguez V., Aiba S.-I., Alvarez-Loayza P., Alves L. F., Ashton P., Balvanera P., Bastian M. L., Bellingham P. J., van den Berg E., Bernacci L., da Conceição Bispo P., Blanc L., Böhning-Gaese K., Boeckx P., Bongers F., Boyle B., Bradford M., Brearley F. Q., Breuer-Ndoundou Hockemba M., Bunyavejchewin S., Calderado Leal Matos D., Castillo-Santiago M., Catharino E. L., Chai S.-L., Chen Y., Colwell R. K., Chazdon R. L., Clark C., Clark D. B., Clark D. A., Culmsee H., Damas K., Dattaraja H. S., Dauby G., Davidar P., DeWalt S. J., Doucet J.-L., Duque A., Durigan G., Eichhorn K. A. O., Eisenlohr P. V., Eler E., Ewango C., Farwig N., Feeley K. J., Ferreira L., Field R., de Oliveira Filho A. T., Fletcher C., Forshed O., Franco G., Fredriksson G., Gillespie T., Gillet J. F., Amarnath G., Griffith D. M., Grogan J., Gunatilleke N., Harris D., Harrison R., Hector A., Homeier J., Imai N., Itoh A., Jansen P. A., Joly C. A., de Jong B. H., Kartawinata K., Kearsley E., Kelly D. L., Kenfack D., Kessler M., Kitayama K., Kooyman R., Larney E., Laumonier Y., Laurance S., Laurance W. F., Lawes M. J., Amaral I. L., Letcher S. G., Lindsell J., Lu X., Mansor A., Marjokorpi A., Martin E. H., Meilby H., Melo F. P. L., Metcalfe D. J., Medjibe V. P., Metzger J. P., Millet J., Mohandass D., Montero J. C., de Morisson Valeriano M., Mugerwa B., Nagamasu H., Nilus R., Ochoa-Gaona, S. Onrizal, Page N., Parolin P., Parren M., Parthasarathy N., Paudel E., Permana A., Piedade M. T. F., Pitman N. C. A., Poorter L., Poulsen A. D., Poulsen J., Powers J., Prasad R. C., Puyravaud J.-P., Razafimahaimodison J. C., Reitsma J., Dos Santos J. R., Roberto Spironello W., Romero-Saltos H., Rovero F., Rozak A. H., Ruokolainen K., Rutishauser E., Saiter F., Saner P., Santos B. A., Santos F., Sarker S. K., Satdichanh M., Schmitt C. B., Schöngart J., Schulze M., Suganuma M. S., Sheil D., da Silva Pinheiro E., Sist P., Stevart T., Sukumar R., Sun I. F., Sunderland T., Suresh H. S., Suzuki E., Tabarelli M., Tang J., Targhetta N., Theilade I., Thomas D. W., Tchouto P., Hurtado J., Valencia R., van Valkenburg J. L. C. H., Van Do T., Vasquez R., Verbeeck H., Adekunle V., Vieira S. A., Webb C. O., Whitfeld T., Wich S. A., Williams J., Wittmann F., Wöll H., Yang X., Adou Yao C. Y., Yap S. L., Yoneda T., Zahawi R. A., Zakaria R., Zang R., de Assis R. L., Garcia Luize B., Venticinque E. M., An estimate of the number of tropical tree species. Proc. Natl. Acad. Sci. U.S.A. 112, 7472–7477 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fisher R. A., Corbet A. S., Williams C. B., The relation between the number of species and the number of individuals in a random sample of an animal population. J. Anim. Ecol. 12, 42–58 (1943). [Google Scholar]
- 27.Chisholm R. A., Sampling species abundance distributions: Resolving the veil-line debate. J. Theor. Biol. 247, 600–607 (2007). [DOI] [PubMed] [Google Scholar]
- 28.Chave J., Neutral theory and community ecology. Ecol. Lett. 7, 241–253 (2004). [Google Scholar]
- 29.Magurran A. E., Species abundance distributions: Pattern or process? Funct. Ecol. 19, 177–181 (2005). [Google Scholar]
- 30.Chave J., Alonso D., Etienne R. S., Theoretical biology: Comparing models of species abundance. Nature 441, E1 (2006). [DOI] [PubMed] [Google Scholar]
- 31.Volkov I., Banavar J. R., Hubbell S. P., Maritan A., Patterns of relative species abundance in rainforests and coral reefs. Nature 450, 45–49 (2007). [DOI] [PubMed] [Google Scholar]
- 32.Matthews T. J., Whittaker R. J., Neutral theory and the species abundance distribution: Recent developments and prospects for unifying niche and neutral perspectives. Ecol. Evol. 4, 2263–2277 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nachbin L., Sur les algebres denses de fonctions différentiables sur une variété. C. R. Hebd. Seances Acad. Sci. 228, 1549–1551 (1949). [Google Scholar]
- 34.J. G. Llavona, Approximation of Continuously Differentiable Functions, vol. 130 of North-Holland Mathematics Studies (Elsevier, 1986), pp vii–x. [Google Scholar]
- 35.Bertuzzo E., Suweis S., Mari L., Maritan A., Rodríguez-Iturbe I., Rinaldo A., Spatial effects on species persistence and implications for biodiversity. Proc. Natl. Acad. Sci. U.S.A. 108, 4346–4351 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Azaele S., Pigolotti S., Banavar J. R., Maritan A., Dynamical evolution of ecosystems. Nature 444, 926–928 (2006). [DOI] [PubMed] [Google Scholar]
- 37.Stanley H. E., Scaling, universality, and renormalization: Three pillars of modern critical phenomena. Rev. Mod. Phys. 71, S358–S366 (1999). [Google Scholar]
- 38.Azaele S., Cornell S. J., Kunin W. E., Downscaling species occupancy from coarse spatial scales. Ecol. Appl. 22, 1004–1014 (2012). [DOI] [PubMed] [Google Scholar]
- 39.Tovo A., Formentin M., Favretti M., Maritan A., Application of optimal data-based binning method to spatial analysis of ecological datasets. Spat. Stat. 16, 137–151 (2016). [Google Scholar]
- 40.Preston F. W., The commonness, and rarity, of species. Ecology 29, 254–283 (1948). [Google Scholar]
- 41.Magurran A. E., Henderson P. A., Explaining the excess of rare species in natural species abundance distributions. Nature 422, 714–716 (2003). [DOI] [PubMed] [Google Scholar]
- 42.Plotkin J. B., Chave J., Ashton P. S., Travis J., Cluster analysis of spatial patterns in Malaysian tree species. Am. Nat. 160, 629–644 (2002). [DOI] [PubMed] [Google Scholar]
- 43.ter Steege H., Sabatier D., Mota de Oliveira S., Magnusson W. E., Molino J.-F., Gomes V. F., Pos E. T., Salomão R. P., Estimating species richness in hyper-diverse large tree communities. Ecology 98, 1444–1454 (2017). [DOI] [PubMed] [Google Scholar]
- 44.Myers N., Mittermeier R. A., Mittermeier C. G., da Fonseca G. A. B., Kent J., Biodiversity hotspots for conservation priorities. Nature 403, 853–858 (2000). [DOI] [PubMed] [Google Scholar]
- 45.Hubbell S. P., Estimating the global number of tropical tree species, and Fisher’s paradox. Proc. Natl. Acad. Sci. U.S.A. 112, 7343–7344 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zillio T., Banavar J. R., Green J. L., Harte J., Maritan A., Incipient criticality in ecological communities. Proc. Natl. Acad. Sci. U.S.A. 105, 18714–18717 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hidalgo J., Grilli J., Suweis S., Muñoz M. A., Banavar J. R., Maritan A., Information-based fitness and the emergence of criticality in living systems. Proc. Natl. Acad. Sci. U.S.A. 111, 10095–10100 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hidalgo J., Grilli J., Suweis S., Maritan A., Muñoz M. A., Cooperation, competition and the emergence of criticality in communities of adaptive systems. J. Stat. Mech. 2016, 033203 (2016). [Google Scholar]
- 49.Grilli J., Suweis S., Maritan A., Growth or reproduction: Emergence of an evolutionary optimal strategy. J. Stat. Mech. 2013, P10020 (2013). [Google Scholar]
- 50.Hull P. M., Darroch S. A. F., Erwin D. H., Rarity in mass extinctions and the future of ecosystems. Nature 528, 345–351 (2015). [DOI] [PubMed] [Google Scholar]
- 51.Zillio T., He F., Inferring species abundance distribution across spatial scales. Oikos 119, 71–80 (2010). [Google Scholar]
- 52.Borda-de-Água L., Borges P. A. V., Hubbell S. P., Pereira H. M., Spatial scaling of species abundance distributions. Ecography 135, 549–556 (2012). [Google Scholar]
- 53.Menzel P., Ng K. L., Krogh A., Fast and sensitive taxonomic classification for metagenomics with Kaiju. Nat. Commun. 7, 11257 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Muneepeerakul R., Bertuzzo E., Lynch H. J., Fagan W. F., Rinaldo A., Rodriguez-Iturbe I., Neutral metacommunity models predict fish diversity patterns in Mississippi-Missouri basin. Nature 453, 220–222 (2008). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/10/e1701438/DC1
section S1. Upscaling biodiversity
section S2. Limitation of the LS methods
section S3. Flexibility of NB distribution
section S4. Test on computer-simulated forests
section S5. Comparison with other popular estimators
section S6. Data set
section S7. Self-consistency and estimation of the critical p*: How much remains to be sampled?
section S8. RSA parameters maximize relative fluctuation in abundances
fig. S1. Assuming that the global RSA is distributed according to an NB, we can compute the probability that a species comprises a single individual at the scale p by using eq. S31.
fig. S2. Fisher’s α for three different rainforests: Amazonia, Barro Colorado Nature Monument, and Caxiuana.
fig. S3. Fit of an RSA consisting of a combination of an LS and a log-normal distribution.
fig. S4. We have generated synthetic data from a combination of discrete distributions (a binomial distribution of parameters r = 40 and ξ = 0.8, a geometric distribution of parameter μ = 0.15, and a Poisson distribution with parameter λ = 15) and fit these data with one, three, and six NBs, respectively.
fig. S5. Robustness of the method.
fig. S6. Comparison between biodiversity estimators for Amazonia and BCI forests.
fig. S7. Self-consistency test of our framework.
fig. S8. Plot, in logarithmic scale, of the percentage ppred% that one ought to sample to have a precision estimate of around 5% for the predicted percentage of hyper-rare species, that is, species with fewer than 1000 individuals at the global scale.
table S1. Predicted number of singletons in the whole area of each tropical forest obtained by applying our method (NB method).
table S2. Prediction of the total number of species obtained by applying both NB and LS methods to the forest generated according to an NB and distributed in 8900 × 8900 units according to two different modified Thomas processes with the same density of clusters ρ = 6 × 10−5 and different clump sizes σ = 15 and 200.
table S3. Summary table of the most popular biodiversity estimators.
table S4. Comparison between NB, LS, Chaowor, and the Harte methods on empirical data.
table S5. Comparison between the NB, LS, Chaowor, and Harte methods on BCI empirical data.
table S6. Number of species and singletons in 15 forests in our data set with the percentage p% (last column of the table) of surveyed area.
Reference (54)


