Abstract
A key dilemma in global health is how to allocate funds between disease-specific “vertical projects” on the one hand and “horizontal programmes” which aim to strengthen the entire health system on the other. While economic evaluation provides a way of approaching the prioritisation of vertical projects, it provides less guidance on how to prioritise between horizontal and vertical spending. We approach this problem by formulating a mathematical program which captures the complementary benefits of funding both vertical projects and horizontal programmes. We show that our solution to this math program has an appealing intuitive structure. We illustrate our model by computationally solving two specialised versions of this problem, with illustrations based on the problem of allocating funding for infectious diseases in sub-Saharan Africa. We conclude by reflecting on how such a model may be developed in the future and used to guide empirical data collection and theory development.
Keywords: Global health, Health systems strengthening, Resource allocation, Cost effectiveness analysis, Economic analysis
1. Introduction
The notion of health system strengthening (HSS) has become increasingly important in global health discourse in recent years, manifest for example in a declaration at the 2008 G8 Toyako Summit (Takemi and Reich, 2009). This focus of attention arises from a recognition that attempts to implement disease-specific vertical projects often founder in the face of weak health systems: for example, a donor might purchase malaria medications or insecticide treated bednets for a low-income country, but the Ministry of Health as the implementing in-country partner is unable to deliver the medications before they expire or the bednets to the at-risk population before the end of the rainy season. Thus, the reasoning goes, funding for such vertical projects has to be complemented with funding for “horizontal” programmes which aim at strengthening the health system as a whole.
As Ellner et al. (2011) remark, although the label health systems strengthening is relatively recent, the dialectic between proponents of vertical and horizontal approaches is a defining feature of global health debate through much of its history. The eradication of smallpox in the 1960s and 70s is an example of a “vertical project” (as were the earlier, failed, attempts to eliminate malaria). On the other hand, the Alma-Ata declaration (WHO, 1978), with its stress on the role of primary healthcare, presents a holistic vision of health services and is often taken as a statement of the philosophy and principles of the horizontal approach. Hafner and Shiffman (2013) describe how the focus on HSS marks a renewed interest and engagement in horizontal approaches on the part of key actors, including international organisations such as the WHO, World Bank, and other international agencies and donors.
Evidence of the importance of HSS is provided by the wide variations in health system performance amongst Low and Middle Income Countries (LMICs). Balabanova et al. (2013) highlight six countries and regions – Bangladesh, Ethiopia, Kyrgyzstan, Thailand, and the Indian state of Tamil Nadu, which have achieved good health at low cost and stress the vital role of systems-level elements in delivering success in what can be extremely challenging environments. The achievements of these countries cannot be explained by increased funding alone and can to some extent be attributed to the strength of the health systems. Chowdhury et al. (2013) describe how Bangladesh, for example, has higher life expectancy and lower infant, under-5 and maternal mortality than its South Asian neighbours, India, Pakistan and Nepal, despite lower per head expenditure.
In this paper, we discuss a problem faced by donors who have a primary mandate to deliver vertical projects targeted at particular diseases, but at the same time, recognise the importance of (and seek to fund) HSS. Statements on the websites of the Global Fund, Global Alliance for Vaccines and Immunizations (GAVI) and President’s Emergency Plan for AIDS Relief (PEPFAR) indicate that many prominent donors meet this description. One problem such donors face is that of seeking an optimal balance of funding between disease specific programmes and HSS. Our paper attempts to address that question.
We organise our paper as follows. In Section 2, we provide an overview of the concept of HSS. In Section 3, we introduce our model through a motivating example. Section 4 presents our general model and shows how to efficiently solve a special case. In Section 5, we provide worked examples, based on the allocation of funds to infectious disease programmes in sub-Saharan Africa. Section 6 summarises our contributions and discusses implications for research and practice in this area.
2. Conceptual background
In this section to give the reader a clearer picture of what is captured in the concept of HSS, we present the WHO framework (WHO, 2007), which has played a key role in framing discussions of HSS. In this conception, the health system has six building blocks. These building blocks and the associated priorities are cited below.
Service delivery: packages; delivery models; infrastructure; management; safety and quality; demand for care;
Health workforce: national workforce policies and investment plans; advocacy; norms, standards and data;
Information: facility and population based information and surveillance systems; global standards, tools;
Medical products, vaccines, and technologies: norms, standards, policies; reliable procurement; equitable access; quality;
Financing: national health financing policies; tools and data on health expenditures; costing
Leadership and governance: health sector policies; harmonization and alignment; oversight and regulation (WHO, 2007).
This framework has been used by Warren et al. (2013) to track Global Fund expenditures, and similar frameworks have been suggested and used for expenditure tracking by Shakarishvili et al. (2011) and Goeman et al. (2010). Such expenditure tracking is clearly informative but limited. For example, it is impossible to infer whether funds are or are not optimally allocated across the building blocks without further information about cost-effectiveness. Note that a focus on HSS recognizes the importance of economies of scope that exist within any health system. In particular, resources such as service delivery platforms and information systems are shared by many interventions, and their nature and effectiveness will therefore be important determinants of cost structures within the system.
Investing in HSS presents a significant philosophical challenge from the point of view of economic appraisal. Of course, the difficulties of performing a sound economic analysis of the costs and benefits of a vertical project – delivering a course of TB treatment, or rolling out rotavirus vaccination – should not be underestimated. Obtaining reliable and useable empirical studies and transferring findings to a new setting with a different population, disease pattern, and service infrastructure requires considerable analytic capacity.
Nevertheless, appraisal of vertical projects falls squarely within the standard paradigm of economic analysis as it has developed over the last several years, and so can take place in a well developed theoretic framework according to clear standards (Drummond et al., 2005; Gold et al., 1996; Tan-Torres Edejer et al., 2003). In particular, because health benefits – whether measured in reduced number of infections, avoided mortality or gains in QALYs or decreases in DALYs – can be ascribed to a specific project, it is possible to assess their cost-effectiveness. The well-established decision rule of cost-effectiveness is to rank interventions in decreasing order of their benefit to cost ratios and proceed down the list from most to least cost-effective until the budget is exhausted (Weinstein and Zeckhauser, 1973; Weinstein, 2012).
Investments in HSS cannot be easily accommodated within this framework. Unlike funding vertical projects, funding HSS interventions such as policy development or information systems does not contribute to health directly, but is instead complementary to existing delivery systems. To take a concrete example, according to WHO (2007), in over 60 countries, less than a quarter of deaths are recorded by vital registration systems. Of course, vital registration by itself does not save lives. However, in such countries, if a system of vital registration existed, the ability of planners to target such medical resources as do exist on those in most needs may be massively improved. Yet such qualitative considerations do not help a decision maker with a mandate focused on (say) malaria control and elimination in deciding how much to invest in upgrading the system of vital registration.
Frenk (2010) has called for a “diagonal” approach to thinking about health systems, which recognises the complementarity between horizontal and vertical programmes. In this paper, we respond to that challenge. The way we think about this is as follows. We conceptualise the effect of a weak health system in terms of the gap between efficacy and effectiveness. In principle, one could estimate the effect which a treatment will have on a population by taking efficacy data from a laboratory study and multiplying up at the population level. In practice, of course, in all health systems, effectiveness in the field never attains the level of efficacy in the laboratory. In actual clinical practice, many of the population in need may not be able to secure access to medical care; they may be diagnosed wrongly or treated inappropriately; or they may refuse care, fail to comply with the treatment regime or terminate the course before completion – all of which may be consequences of a weak or failing health system. In other words, we conceptualise the impact that a weak health system has on the delivery of a vertical project as one of dilution of the health benefits.
3. Motivating example
In this section, we present a motivating example of a decision problem for a donor looking to allocate resources between different HIV prevention projects (with data based on Hutton et al., 2003). In Table 1 we present data for nine vertical projects on the total cost of full implementation, the number of infections averted and incremental cost-effectiveness ratios, ranked in descending order of cost-effectiveness.
Table 1.
Data for HIV prevention projects.
| Intervention | Total cost (US$) |
Number of infections averted |
Incremental cost-effectiveness ratio |
|---|---|---|---|
|
|
|
|
|
| 1 | 2 | 3 | |
| 1. Peer group education – sex workers | 39,575 | 2473 | 0.0625 |
| 2. Safe blood transfusion | 50,000 | 595 | 0.0119 |
| 3. Peer group education – young people | 423,500 | 799 | 0.00189 |
| 4. Mass media and social marketing of condoms | 1,300,000 | 2434 | 0.00187 |
| 5. Peer group education – high-risk men | 500,000 | 862 | 0.0017 |
| 6. Targeted AZT to pregnant women | 300,000 | 319 | 0.0011 |
| 7. Voluntary counselling and testing | 310,000 | 261 | 0.0008 |
| 8. Targeted advice for breast feeding | 150,000 | 62 | 0.00041 |
| 9. Targeted treatment of STIs | 560,000 | 204 | 0.00036 |
Assuming the projects are independent, the standard cost effectiveness rule for approaching this problem is to proceed down the table funding interventions until the budget b is exhausted. For example, if the donor has $2m, the optimal solution is to implement interventions 1–4 completely and then intervention 5 fractionally. This rule is the optimal solution to an implied mathematical program, the linear knapsack problem, (LK).
In (LK), I is the index set of projects (typical member denoted i); the ci terms are the monetary costs, the vi terms are the health benefits, i.e. the number of infections averted and the xi are the decision variables, indicating the proportion of project i implemented.
However, let us consider a variation on this problem (HV1) where the donor may also spend its money on health system strengthening as well as on vertical projects.
Compared to the previous decision problem, this program introduces a new decision variable y, representing the chosen expenditure on HSS. The effect of spending $y on health system strengthening is to scale the effectiveness of the HIV prevention projects by a dilution factor of yγ. For example in this context, health system strengthening may take the form of destigmatising HIV among health service workers, resulting in more effectively delivered interventions across the board. We enforce upper (P) and lower (p) bounds on the amount of expenditure that goes to health system strengthening. In practice, there may be reasons for limits on y, for example, policy limits set by a donor on the amount of budget which they are prepared to invest in HSS.
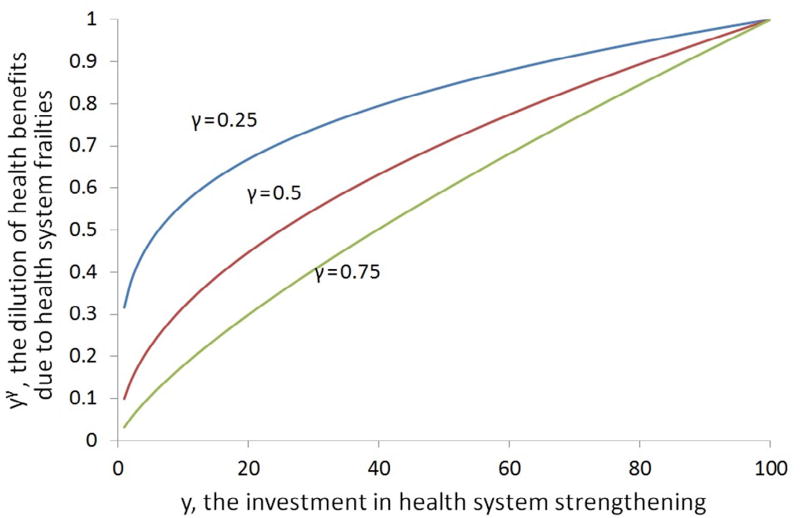
The chosen parameters γ > 0 allows us to model diminishing returns to HSS, as illustrated in Fig. 1 for three different values of γ, namely γ = 0.25, γ = 0.5, and γ = 0.75. For these values of γ the function is concave, reflecting that the first incremental dollar has greater impact on improving the health system than the last incremental dollar. As γ increases towards 1, the function becomes progressively more linear. A value of γ > 1 implies increasing returns to HSS.
Fig. 1.
Dilution of health benefits as a function of y for three different values of γ.
Intuitively, what is the solution to this mathematical program? For a given value of y = y0, the answer seems clear: we have a remaining budget of b − y0, and we should prioritise this budget by ranking the projects in descending order of cost-effectiveness and spending until we run out of money. The problem is that we do not know the optimal value of y. There is nevertheless a relatively simple way to identify an optimal solution, which is as follows.
Set y0 = p, rank the projects by cost-effectiveness, and proceed down the list until the residual budget b − y0 is exhausted. Calculate the value of this solution.
Set y0 = P, rank the projects by cost-effectiveness, and proceed down the list until the residual budget b − y0 is exhausted. Calculate the value of this solution.
Consider implementing project 1 completely and devote the residual budget to health systems strengthening; projects 1 and 2 completely and devote the residual budget to health systems strengthening; projects 1 to 3 completely and devote the residual budget to health systems strengthening; and so on. Eliminate infeasible solutions identified by this procedure (e.g. those in which the residual budget is negative) and calculate the value of the solutions which remain.
Consider implementing project 1 fractionally and devote the residual budget to health systems strengthening; project 1 completely and project 2 fractionally and devote the residual budget to health systems strengthening; projects 1 and 2 completely and project 3 fractionally and devote the residual budget to health systems strengthening; and so on. Eliminate infeasible solutions identified by this procedure and calculate the value of the solutions which remain.
Compare the values of the solutions identified by all the above four procedures and choose the one with the highest value.
The algorithm as outlined above is incompletely specified, as in step 4 there are multiple (actually infinite) possible fractions which can be chosen at each stage. In the ensuing technical discussion, we show how to specify this fraction so that we can guarantee that this algorithm does indeed return the optimal solution to problem (HV1).
4. Towards a more general model
4.1. The model (HV)
In this section, we develop a mathematical model that seeks to reflect the search for an optimal balance between vertical and horizontal programmes. By introducing more than one potential target of HSS, this model generalises the model of the previous section and provides a framework for analysing and discussing it.
In contrast to (HV1), we introduce the additional requirement that the projects can be clustered into programmes that rely on a common infrastructure, which may comprise factors such as workforce, capital, or information systems. These are indexed as j, so that we are considering a set of projects, clustered within programmes, which are referenced as (i, j). The important observation is that all projects i within a programme j benefit from the extent and quality of the common infrastructure, which can be thought of as the health system for that programme j. Thus, an investment in strengthening the programmes system will benefit all projects within the programme, without being assigned specifically to any one project.
As discussed in the previous section, the conventional decision maker’s problem is to decide which projects to fund. However, our reformulation extends the scope of decision making to include a choice of how much to invest in each programme’s infrastructure, in other words, strengthening elements of its health system. Such strengthening imposes costs, but also yields benefits, in the form of improved effectiveness of a range of projects. The model seeks an optimal balance between such strengthening and the direct expenditure on individual projects, subject to an overall budget constraint.
Our model requires the same estimates of project costs and benefits as conventional cost-effectiveness analysis. However, while CEA conventionally considers projects independently, our key additional information requirement is an estimate of the extent to which an investment in health system j will improve the effectiveness of each of the projects (i, j) within that programme. This allows us to model the impact of the health system on projects. Such information is traditionally not available. However, we argue that estimates of such impact are essential if informed decisions about health system strengthening are to be made.
Generalising the one-dimensional concept of the health system discussed in the previous section, our model is as follows:
The interpretation of this model is as follows:
J = {1, …, m} is an index set of programmes of projects, clustered according to whether they share the same underlying delivery system (for example countries may have highly integrated programmes for particular diseases which are separate from the rest of the healthcare system; the same vaccination programme may contain diphtheria, pertussis and measles projects; or in health systems with a strong regional tier, it may make sense to cluster disease projects by region).
I(j) = {1, …, nj} are a family of index sets of health projects at the population level within each programme j (e.g. a project to provide ACTs for malaria, a project to provide ART for HIV).
yj, j ∈ J are decision variables representing investment in health system strengthening within each programme j.
The functions , j ∈ J model the effectiveness of the health system for programme j given an investment of yj. This is a weighted power term: wj is a scaling factor and γ is an exponent. In terms of interpretation, wj may incorporate two elements: one is a normalisation to ensure that is less than 1 and hence can still be interpreted as a dilution of health benefits, and another is a weighting term which reflects the relative priority given to the programme j by the funder.
xi,j, j ∈ J, i ∈ I(j) are decision variables, indicating the extent to which the project i ∈ I(j) is funded with 0 indicating no funding and 1 indicating full funding.
ci,j, j ∈ J, i ∈ I(j) are (positive) coefficients representing the costs of the projects in the current planning period assuming full implementation. B is the overall budget.
vi,j, j ∈ J, i ∈ I(j) are (positive) coefficients representing the health benefits of the projects assuming full implementation and perfect operating conditions.
-
B represents a monetary budget. We assume that to ensure feasibility. We refer to as the “discretionary budget”.
This model makes the following major assumptions.
Vertical projects are characterised by constant returns to scale for a given level of HSS. Investment in HSS exhibits varying returns to scale as captured by the power function. This assumption is less strong than it might appear in that it is possible to break down projects into arbitrarily fine pieces (rather than “bednets in Mozambique”, one could have “bednets in Cabo Delgado”, “bednets in Nampula”, “bednets in Zambezia” and so on, or even down into the county level) – assuming that the data will allow such fine discrimination.
Vertical projects are independent for a given level of HSS. Vertical projects are assumed to have been selected from amongst mutually exclusive alternatives in a “competing choice” framework. The vertical projects can be seen as analogous to Weinstein’s shopping spree paradigm – where a decision maker with a fixed budget must choose to allocate funds amongst a set of interventions in a way that maximises health gains. Independence means that for a given level of HSS, there are well-defined costs and benefits which can be associated with a project, irrespective of what other projects are implemented. Failures of mutual exclusivity can be handled by augmenting the model with logical constraints which enforce relations of exclusion or precedence between alternatives for vertical projects. Failure of independence can be handled by augmenting the existing formulation by including “dummy” projects to represent the positive synergies or negative dis-synergies, and adding logical constraints to the model to enforce that if two projects are chosen, then their interaction is chosen also.
Costs can be disaggregated into project costs and system costs. This is a somewhat different cost definition to that usually used in applications, where the project costs used are often fully loaded unit costs. Fortunately over the last few years, costing data in global health is becoming better and more consistent across countries; thanks to greater use of tools such as the One health tool endorsed by the World Health Organization (WHO, 2015).
Costs are assumed to fall within a single time period. The time period is meant to be representative of national strategic plans of countries or funding agencies, typically around 3 to 5 years over which countries receive a fixed budget for implementation of vertical projects and HSS. The intertemporal trade-offs and associated uncertainties of irreversible investments that are characteristic of HSS expenditures and some vertical projects (such as life-long antiretroviral treatment for HIV positive individuals) are not explicitly modelled. However, the current assumption is often representative of the reality faced by either donors or countries who cannot make provision for financing for more than a few years due to uncertain revenue streams and have to make implementation decisions without explicit consideration of future uncertainties.
We make the following minor assumptions, which we label so we can refer to them later.
Assumption 1. Within each programme jo, projects are indexed in order of decreasing vi,jo/ci,jo.
Assumption 2. Within a given programme jo, all projects i differ in their cost-effectiveness ratio vi,jo/ci,jo.
- Assumption 3.
- Assumption 4.
- Assumption 5.
Assumptions 1–5 are not material assumptions and are made for presentation and computational convenience. In the case of Assumption 1, we can label the projects how we like. In the case of Assumption 2, if we have more than one project with identical cost effectiveness ratio we can bundle these projects together in a single project. Assumption 3 reflects the notion that it is necessary to spend something (at least one cent) on health systems before delivering vertical projects. Assumption 4 requires that we do not have enough money to implement all the vertical projects. Assumption 5 requires that investing in the health system has a positive impact on health system performance, but still admits considerable generality, e.g. it does not specify whether the function which models the efficacy of a given funding level is convex or concave.
The model (HV) thus captures the notion that the total health benefit is composed of health benefits from multiple health projects grouped in programmes. For each of these programmes, the health benefits arise from the combination of individual funded projects and the “health systems strengthening” investments in the programme as a whole. If no interventions are funded in some particular programme j, then there will be no health benefits, irrespective of whether there is investment in the health system: there is no point investing extensively in building a network of community health workers for finding TB cases if there are no funds for TB medication after cases are identified.
Math programming models have enjoyed some popularity in health economics in recent years as a way of providing a framework to discuss issues such as concerns about budgets, divisibility, and equity (Anand, 2003; Birch and Gafni, 1992; Birch and Gafni, 1993; Cleary et al., 2010; Earnshaw and Dennett, 2003; Epstein et al., 2007; Johannesson and Weinstein, 1993; Morton, 2014; Stinnett and Paltiel, 1996). The model (HV) is a quite different and specifically more complex model than any we have seen in the literature hitherto: as shown in Appendix A, it has a highly nonlinear and in fact nonconvex objective function. Our model is nevertheless developed according to the principles underlying the standard cost-effectiveness model in widespread use in health economics. The intention is to demonstrate the modelling implications of incorporating HSS into that model, and the feasibility of deriving optimal solutions.
While HV does echo some aspects of the Cobb–Douglas production function, it is mathematically more complicated (the Cobb–Douglas function is a product of powers; the function in HV is a sum of products, one of which is a power, but the other is a sum). In terms of economic interpretation, our model can be seen as capturing the concept of economies of scope (Panzar and Willig, 1981). This fundamental economic concept has been surprisingly neglected in health economics. Unlike the existing health economic literature on economies of scope (see Wholey et al., 1996 and Preya and Pink, 2006), we take a primarily theoretic rather than empirically driven approach in this paper. In Panzar and Willigs formulation, the concept is expressed through superadditivity of the cost function: the cost of saving x lives through an optimal mix of TB treatment and malaria treatment saving y lives from TB and z lives from malaria is less than the sum of the costs of saving y lives from TB plus the costs of saving z lives from malaria (see also Morris et al., 2007). In our analysis, we model the complementarity between different healthcare projects arising from the shared health system which is necessary for the delivery of both projects. This complementarity can be easily seen to imply the superaddivity of the cost function as described by Panzar and Willig.
Our problem is also reminiscent of certain models in the production optimisation literature where (in terms of the context of this model), there is a fixed charge (e.g. due to administrative overheads) associated with operating a disease programme, irrespective of what projects are implemented under that programme. In this setting, one has to decide both which programme to set up (and hence which fixed charges are incurred) and what is implemented under each programme. The structure of such models is well-understood (Hooker, 2012). However, these models are not really relevant in modelling investment in health system strengthening. Such investment is best understood as an investment in quality of the existing programmes of delivery (e.g. investing in education about the transmission mode of a disease may result in greater effectiveness of prevention activities across the board) rather than a precondition for investment in vertical programmes to take place.
Despite the complexity of this program (HV), it is possible to gain some insights into the structure of the optimal solution. Full details of the model and the proof of the optimization conditions are given in Appendix B. In particular, Theorem 6 in the appendix indicates that, at the optimum, there is within each programme a single critical project that is implemented wholly or in part. Projects with higher cost-effectiveness ratios than the critical project are rejected while projects with lower cost-effectiveness ratios are implemented in full. Thus, despite the additional complexity of our model, within each programme the core insight of Weinstein and Zeckhauser (1973) still holds – there is a unique “critical” intervention that separates the funded and unfunded interventions.
5. Examples
5.1. Preventing HIV infections: an algorithmic solution of (HV1)
The analysis of Appendix B also suggests an algorithmic solution to (HV1), the version of (HV) with just a single health system programme, as has already been sketched in Section 3. In this section, we present an example in which the optimal solution can be computed in this manner. Theorem 9 presents the technical details of calculating the optimal solution. The approach is summarized in the box Algorithm 5.1, yielding a set of ‘candidate solutions’ to the optimization problem. Those that do not satisfy the constraints on xi and y are deleted, and the remainder are chosen so as to maximise the value function. Note that computation time for the algorithm is a function of n the number of projects, so the algorithm is capable of yielding an exact optimal solution, even when n is large. Optimizing the general problem (HV) requires more complex solution concepts, and therefore we resort to a generic optimization routine, as discussed in the next section.
Here, we present a worked example of (HV1) as a decision problem for a donor looking to allocate resources between different HIV prevention projects (with data based on Hutton et al., 2003). We use Table 1 where we presented data for nine projects on total cost of full implementation, the number of infections averted, and the incremental cost-effectiveness ratios and ranked the projects in descending order of cost-effectiveness. In Table 2, we present values for the other inputs in our worked example.
Table 2.
HV1 Inputs.
| Value | |
|---|---|
| b | $2,816,537.5 |
| γ | 0.5 |
| p | $250,000 |
| P | $1,500,000 |
Algorithm 5.1 can be applied in the case of a single programme (disease) to recover the optimal solution. In the online supplementary materials, we demonstrate an application of the algorithm using data presented in the tables above. We begin by applying the four procedures presented in Algorithm 1 to calculate all candidates for the optimal solution (y*, ). Assuming a budget of approximately $2.8 million and a value of 0.5 for γ (later in this section we discuss sensitivity analysis around γ).
Algorithm 1.
Find candidate solutions.
| 1: | procedure A. Find y minimal candidate solution |
| 2: | for i ∈ I do |
| 3: | |
| 4: | ℐ ← 0 |
| 5: | while do |
| 6: | |
| 7: | ℐ ← ℐ + 1 |
| 8: | |
| 9: | procedure B. Find y maximal candidate solution |
| 10: | for i ∈ I do |
| 11: | |
| 12: | ℐ ← 0 |
| 13: | while do |
| 14: | |
| 15: | ℐ ← ℐ + 1 |
| 16: | |
| 17: | procedure C. Find whole number candidate solutions |
| 18: | for i″ ∈ I do |
| 19: | for i′ ∈ I do |
| 20: | if i′ ≤ i″ then |
| 21: | |
| 22: | else |
| 23: | |
| 24: | procedure D. Find fractional candidate solutions |
| 25: | for i″ ∈ I do |
| 26: | for i′ ∈ I do |
| 27: | if i′ ≤ i″ − 1 then |
| 28: | |
| 29: | if i′ ≥ i″ + 1 then |
| 30: | |
| 31: | |
| 32: |
Table 3 gives the level of expenditure in each of the projects in our optimal solution. In this example, the donor will spend approximately $1.46 million on health system strengthening and choose to implement interventions in order of cost-effectiveness until the remainder of the budget is spent. Following Theorem 6 in Appendix B, there is only one intervention (mass media and social marketing of condoms) in which there is fractional implementation and projects with higher vi/ci are fully implemented (vi′/ci′ > vi*/ci*) while projects with lower values receive no spending (vi*/ci* > vi″/ci″).
Table 3.
Optimal solution for HV1.
| Peer group education – sex workers | 1 |
| Safe blood transfusion | 1 |
| Peer group education – young people | 1 |
| Mass media and social marketing of condoms | 0.65 |
| Peer group education – high-risk men | 0 |
| Targeted AZT to pregnant women | 0 |
| Voluntary counselling and testing | 0 |
| Targeted advice for breast feeding | 0 |
| Targeted treatment of STIs | 0 |
In our example, we model the maximum output from spending in HSS through the γ parameter. γ influences the shape of the production function for HSS by altering its concavity. The health economics literature offers little evidence or insight on what the production function for HSS spending might look like. In our worked example above, we chose an arbitrary value of 0.5 for γ.
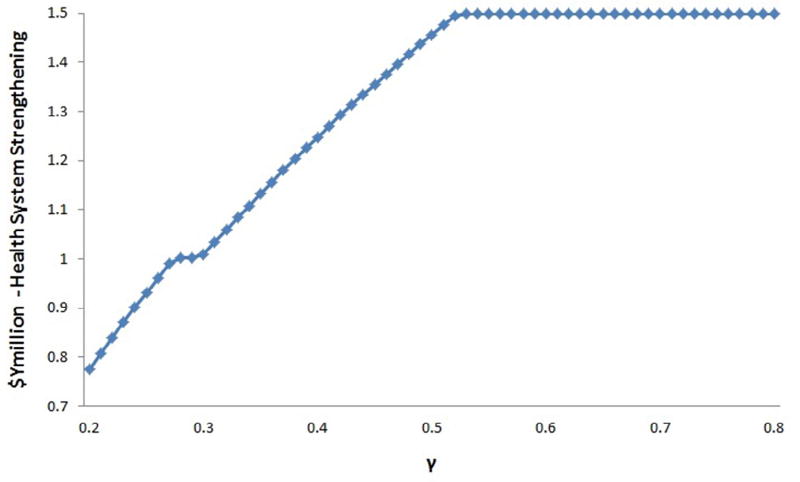
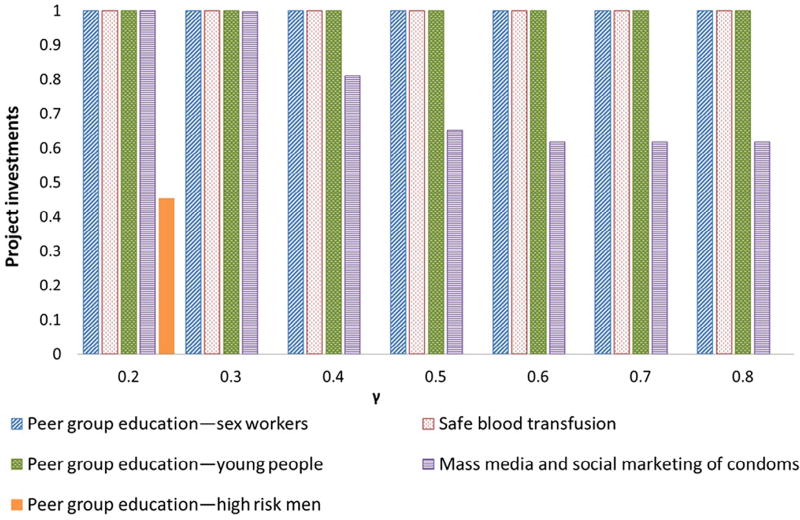
For illustration purposes, we simulate changes in the optimal solution and the expenditure on HSS by varying γ between 0.2 and 0.8. The results are presented in Figs. 2 and 3. Fig. 2 shows the optimal level of health system strengthening as a function of γ. Fig. 3 shows the optimal level of spending on each of the projects for different values of γ. Fig. 2 clearly shows nondecreasing expenditure on HSS as γ rises. Two things stand out in this graph. The first is the upper bound for expenditure on HSS occurs at γ = 0.5. In principle, the optimal level of expenditure on HSS will be either the level above which it is no longer efficient for a donor to increase expenditure in HSS for a given level of gamma or the upper bound of y, i.e. P, whichever is reached first. Second, at γ = 0.3, we see a plateau in the function values. Investigating this further in Fig. 3 shows that at this point peer group education for high risk men drops out of the optimal solution. In our simulation as γ increases, the optimal solution involves increasing levels of HSS while cutting spending on the least cost-effective projects.
Fig. 2.
Investment in HSS as function of γ.
Fig. 3.
Optimal solutions by gamma.
Our example highlights the importance of understanding the returns to spending on HSS and its effectiveness. Our data allow us to identify specific patterns for expenditure on HIV prevention and HSS, however we emphasize that the shape of the investment function for HSS is specific to the data we have used and the relationship between the optimal solution and γ might be different in other cases.
5.2. Balancing expenditures on HIV, TB, and malaria
In this section, we present a worked example of (HV) for a donor who wishes to support HIV, TB, and malaria vertical projects and also in HSS for these three diseases. (This is exactly the situation faced by, for example, the Global Fund). The data for our example is given in Table 4. In Table 5, we present two sets of input parameters (default and extreme) which we use in our example below. The data for vertical projects is notional but realistic, based on our consulting work (Thomas et al., 2013). The handling of the effects of HSS on outcomes is necessarily somewhat more sketchy, considering the lack of relevant quantitative evidence: in our model, for each of the three diseases, the funder has the opportunity to spend up to $10m in that disease and such spending will double the effectiveness of the vertical projects for that disease.
Table 4.
Data for HIV, TB, and malaria example.
| Intervention | Target population |
Unit cost of intervention (US$) |
Total cost (US$) |
$ per DALY | Adherence | DALYS averted |
Ratio of benefits to costs (cost-effectiveness) |
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| HIV | |||||||
| Testing | 1,700,000 | 17 | 28,900,000 | 38.27 | 0.39 | 294,512.67 | 0.0102 |
| ART first line treatment | 500,000 | 511 | 255,500,000 | 451.50 | 0.80 | 452,713.18 | 0.0018 |
| TB | |||||||
| DOTS treatment | 20,000 | 755 | 15,100,000 | 132.96 | 0.95 | 107,889.59 | 0.0071 |
| Diagnosis | 140,000 | 9.98 | 1,397,200 | 126.35 | 0.34 | 3759.78 | 0.0027 |
| MDR-TB treatment | 100 | 7595 | 759,500 | 521.96 | 0.80 | 1164.07 | 0.0015 |
| Malaria | |||||||
| Treatment with ACTs | 5,000,000 | 2.03 | 10,150,000 | 13.91 | 0.60 | 437,814.52 | 0.0431 |
| Intermittent preventive treatment in pregnancy (IPTp) | 945,000 | 0.30 | 283,500 | 25.68 | 0.40 | 4415.89 | 0.0156 |
Table 5.
HVQ inputs.
| Default parameters | Extreme parameters | |
|---|---|---|
| γ | 1 | 1 |
| B | $0 to $108,000,000 | $0 to $336,000,000 |
| p | HIV: $10,000,000 | HIV:$ 0 |
| TB: $10,000,000 | TB: $ 0 | |
| Malaria $10,000,000 | Malaria: $ 0 | |
| P | HIV: $20,000,000 | HIV: $ 56,880,000 |
| TB: $20,000,000 | TB: $ 3,451,340 | |
| Malaria: $20,000,000 | Malaria: $ 2,086,700 | |
| w | HIV: 0.6 | HIV: 0.6 |
| TB: 0.7 | TB: 0.7 | |
| Malaria: 0.5 | Malaria: 0.5 |
As Algorithm 1 only solves (HV1) rather than the more general (HV), we use the MATLAB nonlinear optimisation algorithm MultiStart (Ugray et al., 2007). We conducted preliminary testing which revealed that MultiStart performed consistently as well as or better than other nonlinear optimisation algorithms available for the MATLAB environment. In particular, optimisation algorithms that rely on techniques suitable (and indeed efficient) for convex problems such as those based on hill-climbing principles do not perform well on this problem due to the significant nonconvexities of the objective function. Such algorithms typically become trapped in a local optimum and give a misleading picture of the optimal solution. Our MATLAB code is provided in the supplementary online material to this paper.
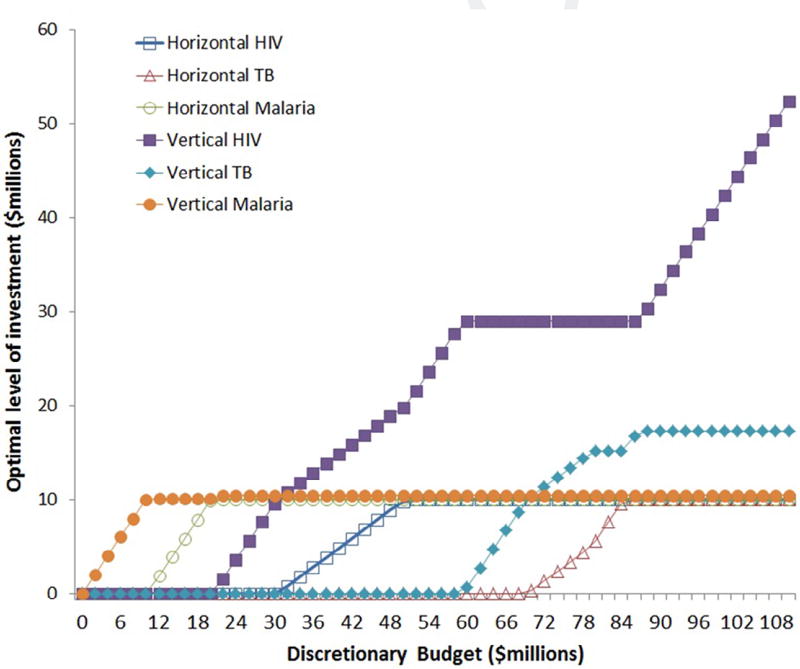
To give a sense of the performance of the model, we vary the discretionary budget between 0 and $110m and solve the model for increments of $2m. We track the optimal horizontal and vertical spending for the default parameter values in Fig. 4. Data points associated with HIV are marked with a square, TB with a triangle, and malaria with a diamond. The marker is empty for horizontal HSS and solid for vertical projects. The interpretation here is: first the decision maker should first fund ACTs (a malaria vertical project); then malaria health systems strengthening; then HIV testing and around the same time in IPT for malaria; once a testing project is in place, fund HIV HSS alongside scaling up testing; then around the $60m–$70m mark the decision maker should start funding the TB interventions, TB HSS and finally ARTs for HIV.
Fig. 4.
Investment in different diseases for different budget levels with default parameters.
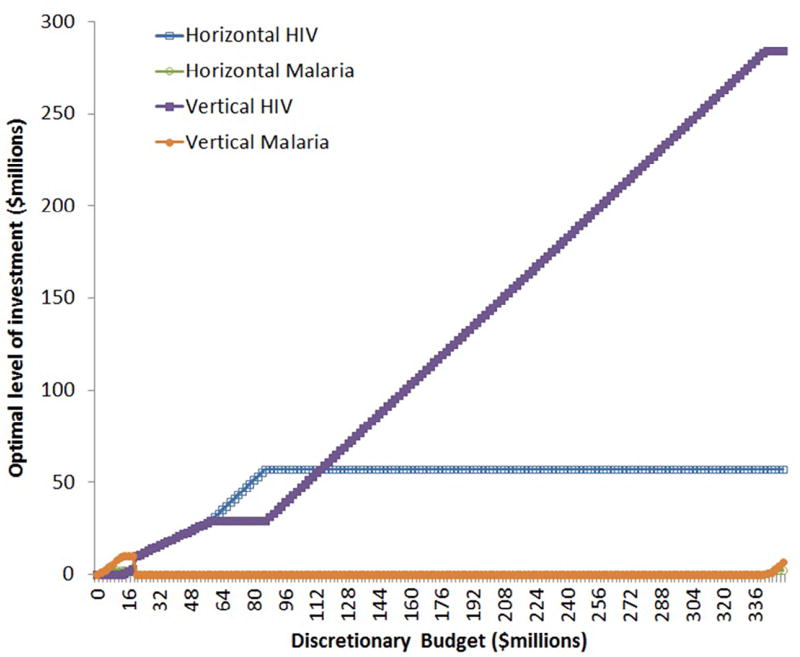
The graph presented in Fig. 4 shows expenditure on both horizontal and vertical programmes increasing as the budget increases. Because of the nonconvexity in the objective function, this behaviour, although intuitively sensible, will not always be exhibited. Consider the following example, with data as shown in the right hand column of Table 5 (the data are contrived to make a theoretical point about model behaviour – there is no suggestion that the following represents an actual policy recommendation). In this set up, being able to fund at scale in a programme is critically important, because by funding HSS we can radically scale up the effectiveness of a programme. When we run the algorithm for discretionary budgets between $0 and $350m we get results as shown in Fig. 5.
Fig. 5.
Funding in different diseases for different budget levels with extreme parameters.
The logic of the results is as follows: as long as the decision maker has a limited budget, she should fund malaria projects, because she can get health gains without a large outlay. But once the budget reaches about $20m, it is optimal to switch some expenditure from malaria to HIV, which is where the big gains are in this model (there are more DALYs to be gained from the vertical projects than for any other disease category). Intuitively, at this point she has the funds to build an HIV organisation which will have a transformative effect on a disease that has a massive associated burden of illness. Then, eventually at very high budget levels, the demand for HIV services is exhausted (since the entire HIV positive population is on ART) and it is optimal to start funding malaria again. Funding TB services is not optimal for any budget level in this model in the range considered here.
6. Conclusion
In this paper, we have shown how economic analysis of horizontal programmes – of Health Systems Strengthening – can be brought within the scope of analysis using principles that are consistent with standard cost-effectiveness analysis. We show that our models are computationally tractable and can provide insights that may not be immediately obvious. They illustrate the complexity of the task of prioritising HSS funding and underline that the choice of best distribution of expenditure for a given country is likely to be highly context dependent. Also in our formulation of the problem, the cost effectiveness ordering of projects is invariant with respect to global rescaling of assessments of benefits to reflect health system frailty. Our paper can be seen as an exploration of the neglected economic concept of economies of scope to better understand a key policy concept in the global health setting.
All health systems are different, and have different frailties. In some health systems, the priority should be on providing training for community health workers, in others on implementing hospital regulation, in others on providing data and analysis tools for local managers. We believe that the functional relationship between monetary investment and the strength of the health system will always have to be judgmentally assessed by local planners and policy makers based on their understanding of the particularities of their health system. However, we also believe that their task would be massively aided if there were a body of high quality and comparable empirical studies that show how particular spending on health systems have has improved the realised health gains from vertical projects. If one interprets the multiplicative rescaling of health benefits in our model as an efficacy – effectiveness gap, as we propose in the introduction, this suggests a possible approach to the empirical question: by calculating the ratio of health benefits from field studies and from clinical trials of the same interventions one could in principle assess the extent to which health system frailties (broadly conceived) dilute the maximum clinically realisable benefits.
In a recent book chapter (2012),Weinstein has reminded us that the linear knapsack problem, on which the models of this paper are based, requires restrictive assumptions, in particular on the absence of interdependencies between projects and multiple resource constraints, and the divisibility of projects. The models of the current paper suffer from some of the same limitations. But as explained by Weinstein (2012), some of these restrictions can be relaxed without abandoning the framework by redefining the vertical projects as combinations of projects or as different levels of individual vertical projects. Indeed, it is rather easy to formulate and (with today’s optimisation solvers) computationally solve still more general models which relax even the restrictions which remain. However, the models we present in the current paper are simple enough to have relatively easily characterised solutions, but also sufficiently complex to exhibit surprising and counterintuitive behaviour.
These limitations aside, we hope that our current paper will help focus and direct further empirical research in this area. Although as we note above, there are to our knowledge no current estimates to the parameter γ in our model, yet knowing this seems critical for making sensible decisions. Fortunately the availability, comparability, and quality of data in global health has been steadily improving over recent years, both in terms of relevant outcome measures (such as treatment completion rates) and in terms of detailed costings. We hope that it should soon be possible to make first-cut estimates of γ using standard econometric techniques for estimating productivity and growth.
We also consider that there are several interesting theoretic issues which could be usefully studied within an expanded version of the framework presented in this paper. For example, expenditure on HSS is a way of building sustainability into the health system: many of the assets that are created through horizontal programmes will persist over time. In a country that is making rapid (but hard-to-predict) progress through the development cycle, there is a real question about how best to frame the intertemporal tradeoff and handle the associated uncertainties. Another interesting and related issue is the alignment or non-alignment of donor and country objectives, particularly in the case where these two parties have different time preferences. Further, in a multi-donor environment, there is uncertainty about who should be the donor providing the funding for HSS – one can easily envisage a situation where a stand-off between donors may lead to underinvestment in HSS. However, addressing these questions would take us beyond the scope of this paper, and we leave them open for future investigators in this area.
Supplementary Material
Acknowledgments
Ranjeeta Thomas is supported by funding from the HIV Prevention Trials Network 071 Study (HPTN 071). HPTN 071 is funded by the National Institutes of Health (NIH), including the National Institute of Allergy and Infectious Diseases (NIAID), the National Institute of Mental Health (NIMH), the National Institute of Drug Abuse (NIDA), as well as the Office of the United Stated Global AIDS Coordinator (OGAC) and the Bill & Melinda Gates Foundation (BMGF). However, the views expressed in this paper are those of the authors, and do not necessarily reflect those of the funders or the HPTN 071 team. Peter Smith was in part funded by the International Decision Support Initiative (www.idsihealth.org), a global initiative to support decision makers in priority setting for universal health coverage. Alec Morton would like to thank the University of Science and Technology of China, City University of Hong Kong, and the Singapore University of Technology and Design for their hospitality while working on this paper, as well as the government of Anhui province for their support under the 100 Talents scheme, and Mara Airoldi, Sumitra Sribhashyam, Gwyn Bevan and the other members of his consulting team. The authors would also like to express thanks to the editor and two anonymous reviewers for their constructive comments, which helped us to improve the manuscript, Michael Borowitz and Shufang Zhang of the Global Fund for making us aware of this issue, Ashwin Arulselvan and Kerem Akartunali for helpful discussions on optimisation aspects, Jeremy Lauer for general encouragement and the participants at a meeting of the International Decision Support Initiative organised by Mark Sculpher in York for stimulating and constructive feedback.
Appendix
A Nonconvexity of HV
To see why HV is nonconvex, consider the following specialisation (HVQ).
In this new formulation (HVQ), γ is set to 1: thus each currency unit that is allocated to HSS for programme j within the prescribed limits improves the effectiveness of the health system by wj. (HVQ) is a quadratic program but its objective function is nonconcave, and so the Karush–Kuhn–Tucker conditions are necessary but not sufficient for a feasible point to be optimal. To see this, consider Example A.1.
Example A.1
Recall that for a function F(z) to be concave it must be the case that F (zα) ≥ αF (z′) + (1 − α)F (z″) where zα = αz′ + (1 − α)z″ for all points z′ and z″ in the domain of F and α ∈ [0,1]. Consider an instance of (HVQ) with J = {1} and I (1) = {1, 2} and w1 = v1,1 = v2,1 = 1. Consider the point defined by : the value of the objective function of (HVQ) for this point is 1 × 1/10 + 1 × 2/10 = 3/10. Consider the point defined by : the value of the objective function of (HVQ) for this point is 2 × 4/10 + 2 × 3/10 = 14/10. The average of the objective function values of these two points is thus 17/20. However, , and so the value of the objective function of (HVQ) for this point is 3/2 × 5/20 + 3/2 × 5/20 = 15/20. Since 15/2 < 17/2, the objective function of (HVQ) cannot be concave.
B Technical Appendix
Theorem 6
(i) For each jo ∈ J, there is at most one ijo ∈ each I (jo): xijo,jo ∈ (0, 1) (i.e. at most one intervention is fractionally implemented) – all other either = 0 or = 1. Moreover, (ii) vi′, jo /ci′, jo > vi″, jo /ci″, jo ∀i′ ∈ Ī (jo) and ∀i″ ∈ I̲ (jo) and if , then vi′, jo /ci′, jo > vijo,jo / ciijo,jo > vi″, jo / ci″, jo ∀i′ ∈ Ī (jo) and ∀i″ ∈ I̲ (jo).
We demonstrate this theorem through the proof of two Lemmata. To state the first Lemma, we introduce a formulation of a subproblem of (HV), which is the restriction of (HV) to a single programme jo. Note that we write this program as being parametric in the budget constraint b.
Now we are able to state our first Lemma.
Lemma 7
Given is an optimal solution to (HV), for each jo there exists a bjo such that is an optimal solution of (HVjo(bjo)).
Proof of Lemma 7
For given jo let b* be the value of . We claim that b* is the desired bjo of the statement of Lemma. To demonstrate this, suppose the contrary. In this case, there must be a solution which is feasible with respect to the constraints of (HVjo(b*)) such that . But then, we can define a new solution to the constraints of (HV) called which has and as defined above and and . This solution is guaranteed feasible in (HV) but must have strictly higher objective function value that that associated with the solution , which contradicts the assumed optimality of . Hence the claim is proved.
To formulate our second Lemma, we will find it useful to rewrite (HVjo (b)) as (HV1) to eliminate the now-redundant j subscript. This makes it less cumbersome to present the proof of the Lemma. We also take this opportunity to separate out the constraints representing the bounds on y and associate dual variables with the constraints.
(HV1) modifies (HV) by simply dropping the j subscripts (we presume it is not necessary to explain the notation again).
Analogously to (HV) we denote the values of an optimal solutions of (HV1) as (y*, ) and define and .
Lemma 8
(i) There is at most one i*: (i.e. at most one intervention which is fractionally implemented) – all other either = 0 or = 1. Moreover, (ii) vi′ / ci′ > vi″ / ci″ ∀i′ ∈ Ī and ∀i″ ∈ I̲ and if , then vi′ / ci′ > vi* / ci* > vi″ / ci″.
Proof of Lemma 8
The Lagrangean of problem (HV1) is as follows: .
The Karush–Kuhn–Tucker conditions for a local maximum are as follows (Jensen and Bard, 2003):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
with all of xi, y, λ, θ, Φ, μi non-negative ∀i ∈ I. A useful way to make these conditions easier to interpret is to rewrite constraints (1) to (6) using non-negative slack variables υ, χi, σ, Π, π, ζi, respectively, which case we get the following.
| (1’) |
| (2’) |
| (3’) |
| (4’) |
| (5’) |
| (6’) |
| (7’) |
| (8’) |
| (9’) |
| (10’) |
| (11’) |
| (12’) |
with all of xi, y, λ, θ, Θ, μi, υ, χi, σ, Π, π, ζi non-negative ∀i ∈ I.
Suppose in contradiction to part (i) of the Lemma, there were two projects i′ and i″ for which xi′ and ζi′ (resp. xi″ and ζi″) both ≠ 0. If there were such projects, then χi′ = μi′ = χi″ = μi″ = 0 (from (8’) and (12’)). But in this case, it follows from (2’) that , and this cannot be the case (as it contradicts Assumption 2). So there it is indeed the case that at optimality there is only one which is part (i) of the Lemma.
Forpart (ii)of the Lemma, observe that ∀i′ ∈ Ī, (8’) gives us χi′ = 0 and (2’) gives us wyγ vi′ − ci′ λ − μi′ = 0 ⇒ wyγ vi′ − ci′ λ ≥ 0 ⇒ vi′ / ci′ ≥ λ / wyγ. Similarly ∀i″ ∈ I̲, (12’) gives us μi″ = 0 and (2’) gives us wyγ vi″ − ci″ λ + χi″ = 0 ⇒ wyγ vi″ − ci″ λ ≤ 0 ⇒ vi″ / ci″ ≤ λ/wyγ. Hence, vi′ / ci′ ≥ vi″ / ci″ and Assumption 2 ensure that this inequality is strict. This gives us part (ii) of the Lemma.
The proof of Theorem 6 follows from Lemmata 7 and 8 in a straightforward way.
Theorem 9
The optimal solution can be identified by checking whether each of the candidate solutions identified by Algorithm 1 satisfies the constraints on the decision variables 0 ≤ xi ≤ 1 and p ≤ y ≤ P, deleting those which do not, and of the remainder selecting the candidate(s) which maximise(s) .
Now we make clear the utility of Algorithm 1. Recall that since we have a nonconvex program, the KKT conditions are necessary but not sufficient for optimality. We refer to such solutions as “candidate solutions” as they are candidates for optimality. We claim that the solutions identified by Algorithm 1 include all candidate solutions. We begin by recalling Assumption 1 (that projects are indexed in order of decreasing vi / ci) and making a couple of observations.
Observation 10
Assumption 4 in conjunction with constraint (3’) ensures that σ = 0 (otherwise we could reach a level of expenditure less than the budget constraint but with respect to which no further expenditure would yield additional value).
Observation 11
Assumption 3 in conjunction with constraint (7′) implies that υ = 0.
We now consider four cases.
Case 1: The candidate solution where y = p. Since we know the value of y (by assumption), σ (by Observation 10), constraint (3’) gives us an equality budget constraint on the xis. But Lemma 8 part (ii) also tells us that the xis of higher numbered projects cannot be made non-zero until the xis of all lower numbered projects have been made 1. Denote as io the minimal element of . Every project from 1 to io−1 must be implemented at optimum, or projects will have been chosen out of sequence and Lemma 8 will have been contradicted. No project with index higher than io can be implemented, otherwise the budget constraint would be broken; and io itself must be implemented fractionally in order that the budget constraint it met. The candidate solution characterised in this way is computed by procedure A.
Case 2: The candidate solution where y = P. By reasoning here exactly parallel to that of the previous case, procedure B. yields this candidate solution.
Case 3: The candidate solutions where y ∈ (p, P) and ∄i ∈ I : xi ∈ (0, 1). By Lemma 8 part (ii) the candidate solutions satisfying this condition are those where the lower indexed projects are 1 and the higher indexed projects are made 0. Constraint (3′) gives us the value of y for each of the candidate solutions which can be characterised in this way. Procedure C explicitly enumerates these solutions and computes the corresponding value of y.
Case 4: y ∈ (p, P) and ∃i ∈ I : xi ∈ (0, 1). Again by Lemma 8 part (ii) the candidate solutions are those where the projects indexed lower than the critical project are 1 and those indexed higher are 0. The problem here is we have two unknowns: we do not know the value of decision variable associated with the critical project, and we do not know the value of y. Fortunately, we are able to form two equations in these two unknowns. Call the index of the critical project i*. Now, because π and Π are both nonzero, (10’) and (11’) require that θ and Θ are zero, which means that (1’) gives us equation and since xi* ∈ (0, 1), (8”) and (12”) give us μi* and χi* = 0, hence yγ vi*/ci* = λ. Substituting out λ gives us and rearranging gives us . This is our first equation in y and xi*. The budget constraint (3’) gives us our second equation. According to this constraint (using Observation 10 again). Eliminating the ci*xi* terms, we can get and we can then solve the budget constraint equation for the value of xi*. Procedure D supposes that each project in turn is the critical project and then proceeds to compute corresponding values of y and xi*.
Since the KKT conditions are necessary for optimality (though not sufficient) and the above four cases are exhaustive, the solutions identified above include all solutions satisfying the KKT conditions and making the remaining feasibility checks against p ≤ y ≤ P and identifying the highest valued solution from the list remaining will produce an optimal solution to problem (HV1) (since the budget constraint is satisfied by construction).
Footnotes
Appendix: Supplementary material
Supplementary data to this article can be found online at doi:10.1016/j.jhealeco.2016.06.001.
References
- Anand P. The integration of claims to health-care: a programming approach. Journal of Health Economics. 2003;22:731–745. doi: 10.1016/S0167-6296(03)00024-9. [DOI] [PubMed] [Google Scholar]
- Balabanova D, Mills A, Conteh L, Akkazieva B, Banteyerga H, Dash U, Gilson L, Harmer A, Ibraimova A, Islam Z, Kidanu A, Koehlmoos TP, Limwattananon S, Muraleedharan VR, Murzalieva G, Palafox B, Panichkriangkrai W, Patcharanarumol W, Penn-Kekana L, Powell-Jackson T, Tangcharoensathien V, McKee M. Good Health at Low Cost 25 years on: lessons for the future of health systems strengthening. Lancet. 2013;381:2118–2133. doi: 10.1016/S0140-6736(12)62000-5. [DOI] [PubMed] [Google Scholar]
- Birch S, Gafni A. Changing the problem to fit the solution – Johannesson and Weinstein (Mis) application of economics to real-world problems. Journal of Health Economics. 1993;12:469–476. doi: 10.1016/0167-6296(93)90006-z. [DOI] [PubMed] [Google Scholar]
- Chowdhury AMR, Bhuiya A, Chowdhury ME, Rasheed S, Hussain Z, Chen LC. The Bangladesh paradox: exceptional health achievement despite economic poverty. Lancet. 2013;382:1734–1745. doi: 10.1016/S0140-6736(13)62148-0. [DOI] [PubMed] [Google Scholar]
- Cleary S, Mooney G, McIntyre D. Equity and efficiency in HIV-treatment in South Africa: the contribution of mathematical programming to priority setting. Health Economics. 2010;19:1166–1180. doi: 10.1002/hec.1542. [DOI] [PubMed] [Google Scholar]
- Drummond MF, Sculpher MJ, Torrance GW, O’Brien BJ, Stoddart GL. Methods for the Economic Evaluation of Health Care Programmes. OUP; Oxford: 2005. [Google Scholar]
- Earnshaw SR, Dennett SL. Integer/linear mathematical programming models – a tool for allocating healthcare resources. Pharmacoeconomics. 2003;21:839–851. doi: 10.2165/00019053-200321120-00001. [DOI] [PubMed] [Google Scholar]
- Ellner A, Bukhman G, Famer P. Routledge Handbook of Global Public Health. Routledge; Abingdon: 2011. Pathways to health systems strengthening for the bottom billion; p. 2011. [Google Scholar]
- Epstein DM, Chalabi Z, Claxton K, Sculpher M. Efficiency, equity, and budgetary policies: informing decisions using mathematical programming. Medical Decision Making. 2007;27:128–137. doi: 10.1177/0272989X06297396. [DOI] [PubMed] [Google Scholar]
- Frenk J. The global health system: strengthening national health systems as the next step for global progress. PLoS Medicine. 2010;7 doi: 10.1371/journal.pmed.1000089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goeman L, Galichet B, Porignon DG, Hill PS, Hammami N, Elouma MSE, Kadama PY, Van Lerberghe W. The response to flexibility: country intervention choices in the first four rounds of the GAVI Health Systems Strengthening applications. Health Policy Plann. 2010;25:292–299. doi: 10.1093/heapol/czq002. [DOI] [PubMed] [Google Scholar]
- Gold MR, Siegel JE, Russell LB, Weinstein MC. Cost-effectiveness in health and medicine. OUP; Oxford: 1996. [PubMed] [Google Scholar]
- Hafner T, Shiffman J. The emergence of global attention to health systems strengthening. Health Policy Plann. 2013;28:41–50. doi: 10.1093/heapol/czs023. [DOI] [PubMed] [Google Scholar]
- Hooker JN. Integrated methods for optimization. 2. Springer; New York: 2012. [Google Scholar]
- Hutton G, Wyss K, N’Diekhor Y. Prioritization of prevention activities to combat the spread of HIV/AIDS in resource constrained settings: a cost-effectiveness analysis from Chad, Central Africa. International Journal of Health Planning and Management. 2003;18:117–136. doi: 10.1002/hpm.700. [DOI] [PubMed] [Google Scholar]
- Jensen PA, Bard JF. Operations Research Models and Methods. Wiley; Chichester: 2003. [Google Scholar]
- Johannesson M, Weinstein MC. On the decision rules of cost-effectiveness analysis. Journal of Health Economics. 1993;12:459–467. doi: 10.1016/0167-6296(93)90005-y. [DOI] [PubMed] [Google Scholar]
- Morris S, Devlin N, Parkin D. Economic Analysis in Healthcare. Wiley; Chichester: 2007. [Google Scholar]
- Morton A. Aversion to health inequalities in healthcare prioritisation: a multicriteria optimisation perspective. Journal of Health Economics. 2014;36:164–173. doi: 10.1016/j.jhealeco.2014.04.005. [DOI] [PubMed] [Google Scholar]
- Panzar JC, Willig RD. Economies of scope. The American Economic Review. 1981;71(2):268–272. [Google Scholar]
- Preya C, Pink G. Scale and scope efficiencies through hospital consolidations. Journal of Health Economics. 2006;25:1049–1068. doi: 10.1016/j.jhealeco.2005.12.006. [DOI] [PubMed] [Google Scholar]
- Shakarishvili G, Lansang MA, Mitta V, Bornemisza O, Blakley M, Kley N, Burgess C, Atun R. Health systems strengthening: a common classification and framework for investment analysis. Health Policy Plann. 2011;26:316–326. doi: 10.1093/heapol/czq053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stinnett AA, Paltiel AD. Mathematical programming for the efficient allocation of health care resources. Journal of Health Economics. 1996;15:641–653. doi: 10.1016/s0167-6296(96)00493-6. [DOI] [PubMed] [Google Scholar]
- Takemi K, Reich M. G8 Summit Follow-up, Global Action for Health System Strengthening. Tokyo: Japan Center for International Exchange; 2009. The G8 and global health: emerging architecture from the Toyako Summit. [Google Scholar]
- Tan-Torres Edejer T, Baltussen R, Adam T, Hutubessy R, Acharya A, Evans DB, Murray CJL. WHO Guide to Cost-Effectiveness Analysis. World Health Organisation; Geneva: 2003. p. 2003. [Google Scholar]
- Thomas R, Smith P, Ezzati M, Hallett TB, Moreno-Serra R. A formula to support the Global Fund’s new funding model. The Global Fund to Fight AIDS, TB and Malaria; Geneva: 2013. [Google Scholar]
- Ugray Z, Lasdon L, Plummer JC, Glover F, Kelly J, Mart R. Scatter search and local NLP solvers: a multistart framework for global optimization. INFORMS Journal on Computing. 2007;19(3):328340. [Google Scholar]
- Weinstein M, Zeckhauser R. Critical ratios and efficient allocation. Journal of Public Economics. 1973;2:147–157. [Google Scholar]
- Weinstein MC. Decision rules for incremental cost-effectiveness analysis. In: Jones AM, editor. The Elgar Companion to Health Economics. second. Elgar; Cheltenham: 2012. p. 2012. [Google Scholar]
- Wholey D, Feldman R, Christianson JB, Engberg J. Scale and scope economies among health maintenance organizations. Journal of Health Economics. 1996;15:657–684. doi: 10.1016/s0167-6296(96)00499-7. [DOI] [PubMed] [Google Scholar]
- WHO. Declaration of Alma-Ata. 1978 [Google Scholar]
- WHO. WHO’s framework for actions. World Health Organization; Geneva: 2007. Everybody’s business – Strengthening health systems to improve health outcomes. [Google Scholar]
- WHO. World Health Organization; Geneva: 2015. [accessed 07.01.15]. OneHealth Tool. < http://www.who.int/choice/onehealthtool/en/>. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.