Mechanistic insights into electrochemical reduction of CO₂ over Ag using density functional theory and transport models

Significance

Chemical storage of solar energy can be achieved by electrochemical reduction of CO₂ to CO and H₂, and subsequent conversion of this mixture to fuels. Identifying optimal conditions for electrochemical cell operation requires knowledge of the CO₂ reduction mechanism and the influence of all factors controlling cell performance. We report a multiscale model for predicting the current densities for H₂ and CO formation from first principles. Our approach brings together a quantum-chemical analysis of the reaction pathway, a microkinetic model of the reaction dynamics, and a continuum model for mass transport of all species through the electrolyte. This model is essential for identifying a physically correct representation of product current densities dependence on the cell voltage and CO₂ partial pressure.

Abstract

Electrochemical reduction of CO₂ using renewable sources of electrical energy holds promise for converting CO₂ to fuels and chemicals. Since this process is complex and involves a large number of species and physical phenomena, a comprehensive understanding of the factors controlling product distribution is required. While the most plausible reaction pathway is usually identified from quantum-chemical calculation of the lowest free-energy pathway, this approach can be misleading when coverages of adsorbed species determined for alternative mechanism differ significantly, since elementary reaction rates depend on the product of the rate coefficient and the coverage of species involved in the reaction. Moreover, cathode polarization can influence the kinetics of CO₂ reduction. Here, we present a multiscale framework for ab initio simulation of the electrochemical reduction of CO₂ over an Ag(110) surface. A continuum model for species transport is combined with a microkinetic model for the cathode reaction dynamics. Free energies of activation for all elementary reactions are determined from density functional theory calculations. Using this approach, three alternative mechanisms for CO₂ reduction were examined. The rate-limiting step in each mechanism is **COOH formation at higher negative potentials. However, only via the multiscale simulation was it possible to identify the mechanism that leads to a dependence of the rate of CO formation on the partial pressure of CO₂ that is consistent with experiments. Simulations based on this mechanism also describe the dependence of the H₂ and CO current densities on cathode voltage that are in strikingly good agreement with experimental observation.

The electrochemical reduction of CO₂ to fuels is a subject of considerable interest because it offers a means for storing electricity from intermittent energy sources (e.g., wind and solar radiation) in the form of chemical bonds (1–3). An attractive strategy to this end involves the electrochemical production of CO by the CO₂ reduction reaction (CO₂RR) and the production of H₂ by the hydrogen evolution reaction (HER). Proper choice of catalyst and operating conditions (4, 5) enables attainment of optimal performance of the electrochemical cell for each of these reactions. Since CO and H₂ are insoluble gases, they can be readily separated from an aqueous electrolyte (6) and the resulting mixture, known as synthesis gas, can be converted to fuels such as methanol, dimethyl ether, or a mixture of hydrocarbons using known technologies (7). The overall kinetics of the CO₂RR depends on many factors (8), including details of the catalyst (9–12), electrolyte composition (13–16) and pH (17), the membrane separating the anolyte and catholyte, temperature (18, 19), CO₂ partial pressure (20), cell dimensions (19), and applied potential. Therefore, it is highly desirable to develop a model that can simulate the performance of the electrochemical cell so that the influence of each variable on cell performance can be identified. Such a model can also be used to assess whether the mechanism chosen to represent the kinetics of the CO₂RR is consistent with experimental data. The present work was undertaken for this purpose.

Electrocatalysts such as Au, Ag, Zn, Pd, and Ga are known to yield mixtures of CO and H₂ at varying ratios depending on the applied voltage (21–25). The electrocatalysts exhibiting the highest activity and selectivity to CO vs. H₂ are Au and Ag. Since Ag is much more abundant and less expensive than Au, Ag is the more promising electrocatalyst for large-scale production of CO. The CO₂RR to CO and H₂O requires two electrons and two protons, which are supplied by recombination of an electron with a proton or with water, in which case OH⁻ is also produced as a by-product (26). Although there exist low overpotential electrocatalysts for CO formation (12, 27), Ag was used in this study due to availability of (i) experimental data on current density of CO and H₂ versus applied potential and partial pressure of CO₂ and (ii) well-defined catalyst interface and cell parameters used in the experiments.

Various mechanisms for CO₂ reduction over Ag have been discussed in the literature. The earliest of these proposes that the first step of the reaction sequence involves the formation of a radical anion ($\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$) at the catalyst surface (28). While the onset potential for CO formation over Ag is higher (more positive) than the equilibrium potential of −1.9 V vs. NHE for $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$ formation (29), Hori et al. (28) have proposed that adsorbed $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$ could be stabilized at potentials higher than −1.9 V by back donation of electrons from the highest occupied d orbital of 1B elements such as Ag to the lowest unoccupied antibonding $\left({\pi }^{\ast }\right)$ orbital of $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$. They also noted that the adsorbed $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$ is chemically equivalent to adsorbed $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{-}$ (i.e., $\ast \mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{-}$), since the free electron associated with the radical anion will be donated to the unoccupied metal orbital. The bent structure of adsorbed $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$ not only lowers the energy for electron transfer but also facilitates hydrogenation of the O atom interacting with the catalyst surface to produce CO via the sequence of steps shown in reaction 1 (28):

$$\ast +\mathrm{C}{\mathrm{O}}_2\stackrel{{\mathrm{e}}^{-}}{\to }\ast \mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{-}\underset{-\mathrm{O}{\mathrm{H}}^{-}}{\overset{{\mathrm{H}}_2\mathrm{O}}{\to }}\ast \mathrm{COOH}\underset{-\mathrm{O}{\mathrm{H}}^{-}}{\overset{{\mathrm{e}}^{-}}{\to }}\ast \mathrm{CO}\to \ast +\mathrm{CO}\mathrm{.}$$ [1]

A reaction pathway to CO not involving *COOH has been proposed by Ikeda et al. (30) who envision that CO is produced over Ag by dissociation of adsorbed $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$:

$$\ast +\mathrm{C}{\mathrm{O}}_2\stackrel{{\mathrm{e}}^{-}}{\to }\ast \mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}\to \ast \mathrm{CO}+{\mathrm{O}}^{-}\stackrel{{\mathrm{H}}^{+}+{\mathrm{e}}^{-}}{\to }\ast +\mathrm{CO}+\mathrm{O}{\mathrm{H}}^{-}.$$ [2]

Another alternative for the path to CO has been proposed by Savéant and coworkers (31), who suggest that in nonaqueous electrolytes a $\mathrm{C}{\mathrm{O}}_2-\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$ adduct can form which upon disproportionation yields CO and $\mathrm{C}{\mathrm{O}}_3^{2-}$:

$$\ast +\mathrm{C}{\mathrm{O}}_2\stackrel{{\mathrm{e}}^{-}}{\to }\ast \mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}\stackrel{\mathrm{C}{\mathrm{O}}_2}{\to }\ast \mathrm{C}{\mathrm{O}}_2-\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}\underset{-\mathrm{C}{\mathrm{O}}_3^{2-}}{\overset{{\mathrm{e}}^{-}}{\to }}\ast \mathrm{CO}\to \ast +\mathrm{CO}\mathrm{.}$$ [3]

Mechanisms not involving the formation of $\mathrm{C}{\mathrm{O}}_{\mathrm{2}}^{•-}$ as the first intermediate have also been suggested for Ag. Kostecki and Augustynski (32) have proposed that hydrated CO₂ is reduced to dihydroxycarbene, which then undergoes dehydration to produce CO:

$$\ast +\mathrm{C}{\mathrm{O}}_2+2{\mathrm{H}}_2\mathrm{O}\underset{-2\mathrm{O}{\mathrm{H}}^{-}}{\overset{2{\mathrm{e}}^{-}}{\to }}\ast \mathrm{C}{\left(\mathrm{OH}\right)}_2\underset{-{\mathrm{H}}_2\mathrm{O}}{\to }\ast \mathrm{CO}\to \ast +\mathrm{CO}\mathrm{.}$$ [4]

Jiao and coworkers (33) have claimed that CO₂ can be electrochemically reduced with $\mathrm{HC}{\mathrm{O}}_{\mathrm{3}}^{-}$ to produce CO over Ag:

$$\ast +\mathrm{C}{\mathrm{O}}_2+\mathrm{HC}{\mathrm{O}}_{\mathrm{3}}^{-}\underset{-\mathrm{C}{\mathrm{O}}_3^{2-}}{\overset{{\mathrm{e}}^{-}}{\to }}\ast \mathrm{COOH}\underset{-\mathrm{O}{\mathrm{H}}^{-}-{\mathrm{H}}_2\mathrm{O}}{\overset{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\hspace{0.17em}+\hspace{0.17em}{\mathrm{e}}^{-}}{\to }}\ast \mathrm{CO}\to \ast +\mathrm{CO}\mathrm{.}$$ [5]

Additionally, Jaramillo and coworkers (9) have suggested that the simultaneous transfer of a proton and an electron to aqueous CO₂ produces *COOH on Ag, which in turn yields CO after another electron and proton transfer:

$$\ast +{\text{CO}}_2\stackrel{{\text{H}}^{+}+{\text{e}}^{-}}{\to }*\text{COOH}\underset{-{\text{H}}_2\text{O}}{\overset{{\text{H}}^{+}+\hspace{0.17em}{\text{e}}^{-}}{\to }}\ast \text{CO}\to \ast +\text{CO}.$$ [6]

A mechanism similar to reaction 6 but involving proton-coupled electron transfer to the adsorbed CO₂ has also been envisioned (26).

It is notable that the pathways for CO₂ reduction to CO over Ag discussed above are all based on chemical intuition, but for the most part, these schemes have not been validated by means of theoretical analysis, spectroscopic observations of proposed intermediates, or full microkinetic analysis. An exception to this perspective is the recent work of Nørskov and coworkers (34). Their density functional theory (DFT) calculations for the energetics of CO₂RR over Ag(111) support a scheme similar to reaction 1. Gas phase CO₂ is assumed to be in equilibrium with *CO₂ that reduces to *COOH, and the rate-limiting step is taken to be the reduction of *COOH. Operando spectroscopic support for the presence of the adsorbed species appearing in reactions 1–6 has proven to be very difficult due to the low coverages of these species and interference from gas bubbles; consequently, only limited information has been reported. Surface-enhanced Raman spectra of a polycrystalline Ag surface acquired during CO₂ reduction exhibit bands for adsorbed H₂O, CO, HCOO⁻, and Ag–CO₂ under reducing potentials. The frequency of these bands shift to lower wavenumbers and their intensity increases with decreasing applied potential (35, 36). Recently, IR spectroscopy has been used to observe the species present on polycrystalline Ag films during CO₂ reduction. Evidence for adsorbed $\mathrm{C}{\mathrm{O}}_2^{-}$, HCOOH, and CO has been obtained by this means (37). Although these findings support the presence of the carbon-containing species on polycrystalline Ag films during the electrochemical reduction of CO₂, the elementary steps by which they are formed were not revealed. Therefore, several open questions remain regarding the mechanism of the CO₂RR over Ag: (i) What are the key intermediates involved in the CO₂RR? (ii) How does the HER occur? (iii) Which hydrogen species participate in the CO₂RR? (iv) How do the free energies of adsorption and reaction, and the free-energy barriers for the elementary reaction involved in the CO₂RR vary with the applied potential? (v) How do the mass transport of species, such as $\mathrm{C}{\mathrm{O}}_2$, $\mathrm{HC}{\mathrm{O}}_3^{-}$, $\mathrm{C}{\mathrm{O}}_3^{2-}$, ${\mathrm{K}}^{+}$, ${\mathrm{H}}^{+}$, and $\mathrm{O}{\mathrm{H}}^{-}$, and cathode polarization affect the product distribution? (vi) How do rates of CO and H₂ evolution at the Ag cathode affect the coverages of adsorbates and hence the rate of reaction? (vii) What are the rate-limiting reactions for the CO₂RR and the HER over Ag?

The aim of the present study is to develop a multiscale, multiphysics model of the electrochemical reduction of CO₂ on Ag that can be used to predict the partial currents of CO and H₂ produced as functions of the applied potential and partial pressure of CO₂. The free energies of activation for each elementary step involved in three proposed pathways for CO₂ reduction are determined from DFT calculations. This information is used to determine the equilibrium constants and rate coefficients for each elementary step occurring on the cathode surface as a function of applied potential. The rate parameters, cathode CO₂ concentration, and cathode pH are used in a microkinetic model to calculate rates of formation of CO and H₂. The rates of reactant consumption and product formation obtained from a microkinetic model are used as boundary conditions for a continuum model describing the transport of all species through the electrolyte and to determine the concentrations of neutral and ionic species present at the cathode and anode surfaces. We demonstrate that, through the use of this multiscale, multiphysics model, it is possible to predict a dependence of the partial current densities of CO and H₂ on the cathode voltage and the CO₂ partial pressure that is in agreement with what is observed experimentally (9). We also demonstrate that, by simulating the full reaction dynamics, it is possible to identify which of the three proposed mechanisms for the electrochemical reduction of CO₂ on Ag is most physically consistent with experimental observations.

Theory

Continuum Transport Model.

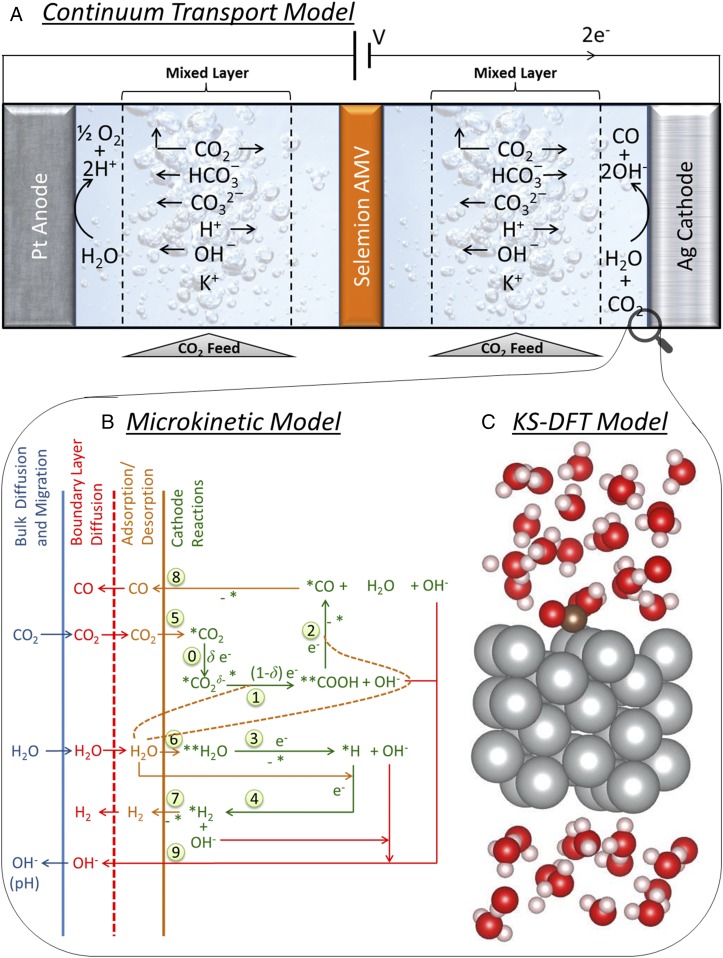
Fig. 1A shows a schematic of the electrochemical cell that was simulated. The cell dimensions and the compositions of the electrodes, electrolyte, and membrane separator were chosen to be identical to those used in the experimental work of Hatsukade et al. (9). The anode and cathode are Pt and Ag, respectively, and are separated by a distance of ∼3.56 cm. A 100-µm-thick anion-exchange membrane (Selemion AMV) is located halfway between the two electrodes. The electrolyte is 0.1 M KHCO₃ (pH 6.8) continuously sparged with 20 sccm of CO₂ gas at ambient conditions. Most aqueous-phase CO₂RR studies reported in the literature are conducted in 0.1 M KHCO₃ (pH 6.8) as higher concentrations of KHCO₃ favor HER over CO₂RR (38). This effect is due to screening of electric field in the concentrated electrolyte (8), which destabilizes the CO₂RR intermediates and thereby reduces the Faradaic efficiency (34). The anolyte and catholyte are assumed to be well mixed by the sparged CO₂ and to offer no diffusion resistances. The only resistances to mass transfer are assumed to occur in the ∼40-µm-thick hydrodynamic boundary layer present next to each of the electrodes and in the membrane separator. The hydrodynamic boundary layer was estimated based on the limiting current density of 22 mA⋅cm⁻² (8). Such small limiting current densities are a consequence of lower solubility of CO₂ (33 mM) and lower buffer concentration (0.1 M) in the aqueous electrolyte.

Fig. 1.

(A) Continuum model for species transport and reaction in a 1D electrochemical cell for CO₂ reduction. The electrochemical cell contains 8 mL of 0.1 M KHCO₃ on each side of a 100-µm-thick Selemion AMV membrane and is continuously sparged with 20 cm³⋅min⁻¹ of CO₂. The distance between the Pt anode and Ag cathode is ∼3.56 cm, and the boundary layer thickness is 40 µm. (B) Microkinetic model showing elementary processes for CO₂RR and HER over Ag(110), which is coupled with the continuum model. (C) Kohn–Sham (KS) DFT model with explicit water layers to calculate energies of adsorbates, intermediates, and reaction barriers, which are supplied to the microkinetic model.

Since the concentration of the electrolyte is <1 mol%, dilute solution theory was used in the Nernst–Planck equations to model diffusion, migration, and bulk reactions (water and buffer dissociation) of species in the electrolyte and the membrane. Ionic species, such as $\mathrm{HC}{\mathrm{O}}_3^{-}$, $\mathrm{C}{\mathrm{O}}_3^{2-}$, ${\mathrm{K}}^{+}$, ${\mathrm{H}}^{+}$, and $\mathrm{O}{\mathrm{H}}^{-}$, and the neutral species, such as $\mathrm{C}{\mathrm{O}}_2$, $\mathrm{CO}$, and ${\mathrm{H}}_{\mathrm{2}}$, were considered in the continuum model. The anion exchange membrane (AEM) was modeled as an electrolyte with fixed background positive charge concentration of ∼1 M, which is similar to ∼1.9 mequiv/g of ion exchange capacity of Selemion AMV (39). The diffusion coefficients of anions such as $\mathrm{HC}{\mathrm{O}}_3^{-}$, $\mathrm{C}{\mathrm{O}}_3^{2-}$, and ${\text{OH}}^{-}$ in a hydrated AEM is typically an order of magnitude lower than in an aqueous electrolyte (40). Since the diffusion coefficients of cations in an AEM are not available, we have assumed their values to be two orders of magnitude lower than those used for transport in the electrolyte. This assumption is based on experimental observation of similar order of magnitude reduction of counterion diffusion in a cation-exchange membrane (41, 42). The lower diffusion coefficient of ${\text{H}}^{+}$ in AEM does not affect the pH gradient in the electrolyte, since the majority charge carriers, such as ${\text{HCO}}_3^{-}$ and ${\text{CO}}_3^{2-}$, can be transported effectively through the membrane (8). The kinetics of water oxidation over Pt was modeled using the Butler–Volmer expression (43). The kinetics of CO₂RR was modeled using the microkinetic model described in Microkinetic Model. An overview of the continuum transport model is given in the SI Appendix, section S1. The continuum transport model was solved using COMSOL Multiphysics to obtain a concentration of CO₂ and pH at the cathode as a function of the product current densities.

Microkinetic Model.

Fig. 1B shows an example of the microkinetic model for CO₂RR and HER over Ag(110), which is the most active facet of Ag (10). The primary source of hydrogen for the HER is H₂O, as the concentration of H⁺ is at least eight orders of magnitude lower than the concentration of H₂O in neutral-pH electrolytes. The first elementary step of HER is taken to be the Volmer reaction, in which either free or adsorbed H₂O is reduced to an H atom adsorbed on Ag(110) and an OH⁻ anion released into the electrolyte. The second elementary step of the HER can occur via either the Tafel or the Heyrovsky reaction. The Tafel reaction involves reaction of two adsorbed H atoms to form H₂, whereas the Heyrovsky reaction involves the reaction of free H₂O with the adsorbed H atom to produce H₂ and the release of an OH⁻ anion into the electrolyte. The computed energy barrier for Tafel reaction was at least 0.4 eV higher than that for the Heyrovsky reaction. Therefore, the Volmer–Heyrovsky mechanism shown in Fig. 2 was used to model the HER.

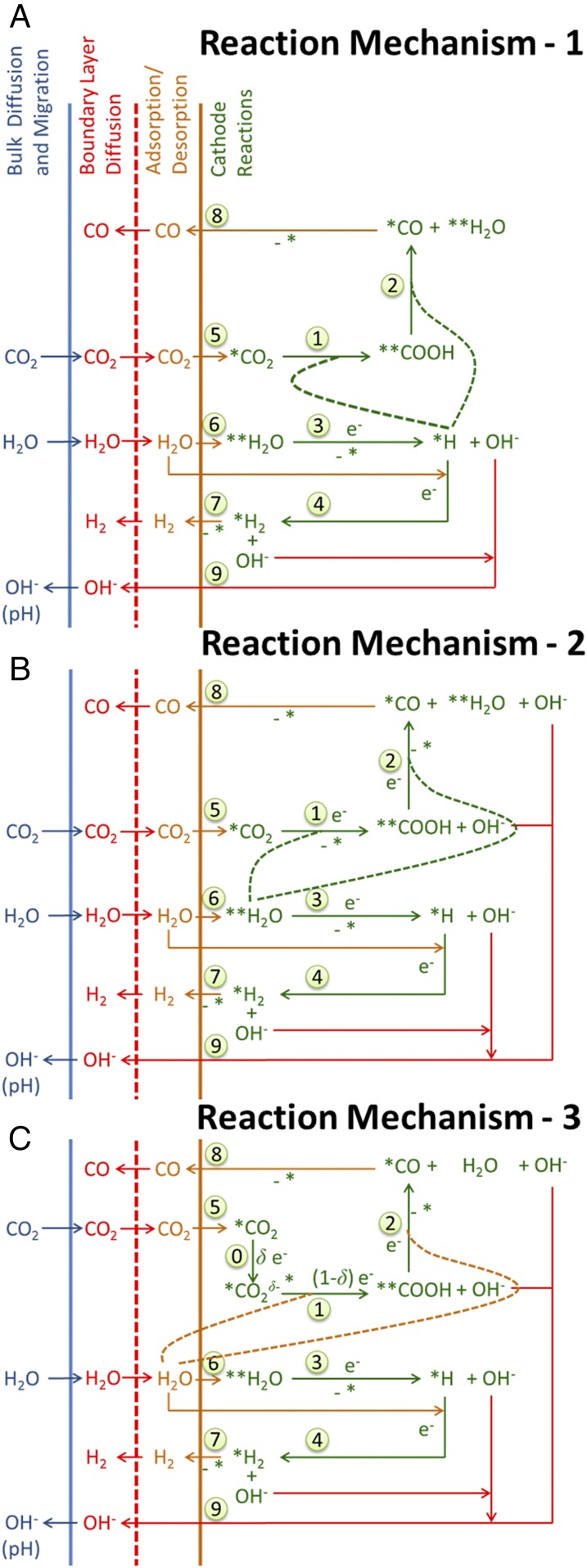
Fig. 2.

Three plausible reaction mechanisms (RMs) for the CO₂RR and one for the HER occurring over Ag(110). The HER follows the Volmer–Heyrovsky reaction, whereas CO₂RR can proceed via three different hydrogen donors such as *H (RM-1), **H₂O (RM-2), or free H₂O (RM-3). (A) RM-1 and (B) RM-2 have nine elementary reactions and seven species. (C) RM-3 has 10 elementary reactions and eight species. Reactions 0, 1, and 2 represent CO₂RR; reactions 3 and 4 represent HER; reactions 5, 6, 7, and 8 represent quasiequilibrated adsorption and desorption of reactants and products; and reaction 9 shows the direct release of OH⁻ to the bulk electrolyte, as it does not adsorb to the cathode.

The reduction of CO₂ to form CO occurs via two steps. In the first step, CO₂ adsorbs, so that the C atom binds with the Ag atom in the troughs of the (110) facets (SI Appendix, Fig. S5A). Adsorbed CO₂ (*CO₂) then reacts with an atom of H to form adsorbed COOH (**COOH). **COOH denotes twofold coordination to the surface, through C as in *CO₂ and also through H coordinated to another Ag site across the ridge. In the second step, **COOH reacts with a second H atom to form adsorbed CO (*CO), and H₂O. The C atom of *CO binds with a Ag atom, resulting in a vertical orientation. As shown in Fig. 2, the H atoms required for the reduction of CO₂ can come from adsorbed H (*H), from adsorbed H₂O [**H₂O, in which two H atoms bind with two Ag atoms across the trough of a (110) facet], or from free H₂O. Activation of *CO₂ to form $\ast \mathrm{C}{\mathrm{O}}_2^{-}$ before hydrogenation was also considered.

The rate coefficients for all elementary reactions were modeled using transition-state theory. The potential-dependent Gibbs free energies of adsorption for CO₂, CO, H₂, and H₂O, and the Gibbs free energies of activation for all elementary reactions were obtained from the DFT calculations described in Kohn–Sham DFT. Since the rates of electrocatalytic reactions are much lower than the rates of adsorption/desorption, the adsorbed reactants (CO₂ and H₂O) and the adsorbed products (H₂ and CO) are assumed to be in quasiequilibrium with their concentrations in the electrolyte. The activity of H₂O near the cathode was assumed to be 1.0 and the activity of dissolved CO₂ and OH⁻ are obtained from the continuum model. The activities of dissolved CO and H₂ near the cathode are determined from the fractional current densities of CO and H₂, respectively.

The microkinetic model considers adsorption and desorption of reactants and products, and the elementary surface reactions. Fig. 1B shows this model involves a total of 10 reactions and eight species. Therefore, the local concentration of CO₂ and pH near cathode need to be specified using the continuum model to fully describe the system. Given the initial concentration of CO₂ in the electrolyte and the bulk pH of the electrolyte, the microkinetic model predicts the partial current densities of products, which are then supplied to the continuum model to obtain the concentration of CO₂ and pH near the cathode. These calculations are repeated until species concentrations and current densities converge. Details of the microkinetic model are given in the SI Appendix, section S2. The equations representing the microkinetic model were solved using MATLAB.

Kohn–Sham DFT.

Fig. 1C shows the simulation cell used for the DFT calculations. It consists of a 3 × 3 × 4 atom cell representing the Ag(110) surface. This cell ensures that there is a minimum distance of 5 Å between adsorbates, which minimizes the interaction between periodic images. Free-energy calculations were performed in two steps. First, 5 ps of ab initio molecular dynamics were performed using 72 explicit water molecules, the reaction intermediate, and surface atoms to generate a reasonable water configuration. Subsequently, 36 of the water molecules were removed from the top layer and replaced by an implicit electrolyte. The solvent was treated as a continuum dielectric, and the electrolyte was described by a linearized Poisson–Boltzmann model (44, 45). The electrode potential was calculated from the Fermi energy. Since the Fermi energy can be varied by changing the number of electrons in the simulation cell, the electrochemical potential was set by calculating the number of electrons the simulation cell required for a specific Fermi energy. The simulation cell remains neutral as the linearized Poisson–Boltzmann model provides a charge compensation. Using this approach, the potential-dependent free-energy reaction barriers and free energy of reactions were calculated, following the procedure detailed in ref. 46. In our constant potential model, electrons are transferred when the atomic configuration dictates that an electron transfer (or partial electron transfer) needs to occur to maintain the applied potential. In essence, this assumes that electron transfer is not limiting the reaction and that a chemical step is the barrier to reduction. Therefore, only two types of steps need to be considered: (i) changes in the geometry of adsorbed species due to changes in the overpotentials, which result in activated adsorbed species before proton/hydrogen transfers, and (ii) proton/hydrogen transfers.

All calculations used the M06-L exchange-correlation functional as this functional provided good agreement between the calculated and measured heats of adsorption (47) of CO from the gas phase for small molecules on Ag(110) and has been shown to be reliable for barrier heights (48, 49). The energy profiles were obtained for potentials −0.0132 to −1.132 V vs. reversible hydrogen electrode (RHE) at an interval of 0.1 V using a modified version of Vienna ab initio simulation program (VASP). Since these energy barriers were obtained for a very low coverage, we have scaled the barriers to account for the effects due to adsorbate–adsorbate interactions at high coverages and errors intrinsic to the exchange/correlation functional used in the DFT calculations. The measured current densities from −0.6 to −0.65 V vs. RHE were used to scale the barriers such that the ratio of forward barriers of the two elementary reactions does not change. The scaled barriers were higher than the original barriers by ∼0.15–0.23 V, which is within the error of DFT calculations (50). Additional details are provided in the SI Appendix, section S3.

Multiscale Simulation.

Since simulation of the continuum model, the microkinetic model, and the DFT model require different software, we have used a look-up table approach to integrate these models and solve them iteratively to calculate surface coverages and partial current densities of CO and H₂. A table of pH and CO₂ concentration at cathode for a range of partial current densities was prepared using COMSOL Multiphysics. Another table of bonding energies of adsorbates and reaction barriers at different applied potentials was obtained from VASP. The multiscale simulations were performed in MATLAB where the microkinetic model was solved iteratively using these tables from COMSOL and VASP. The multiscale simulation scheme is discussed in the SI Appendix, section S4. The first step in the simulation was to obtain rate parameters at an applied potential using the DFT model. The initial concentration of CO₂ and pH at the cathode were assumed to be those in the bulk electrolyte and thereafter used in the microkinetic model along with the rate parameters to obtain the partial current densities of CO and H₂. These current densities were then supplied to the continuum model to obtain CO₂ concentration and pH at the cathode. All of the previous steps were iterated until the values of CO₂ concentration and pH at the cathode are converged. A convergence in the values of CO₂ concentration and pH of 1 × 10⁻³ was obtained in less than four iterations.

The current densities of CO and H₂ predicted over Ag(110) by multiscale simulation are compared with those measured experimentally over a polycrystalline Ag foil (9). The (110) facet of Ag was used in the multiscale simulation because it is the most active facet of Ag (10) and found in higher relative abundance than (111) facets on polycrystalline Ag foils (51).

Results and Discussion

Identification of Free-Energy Profile and Mechanisms for CO₂RR and HER.

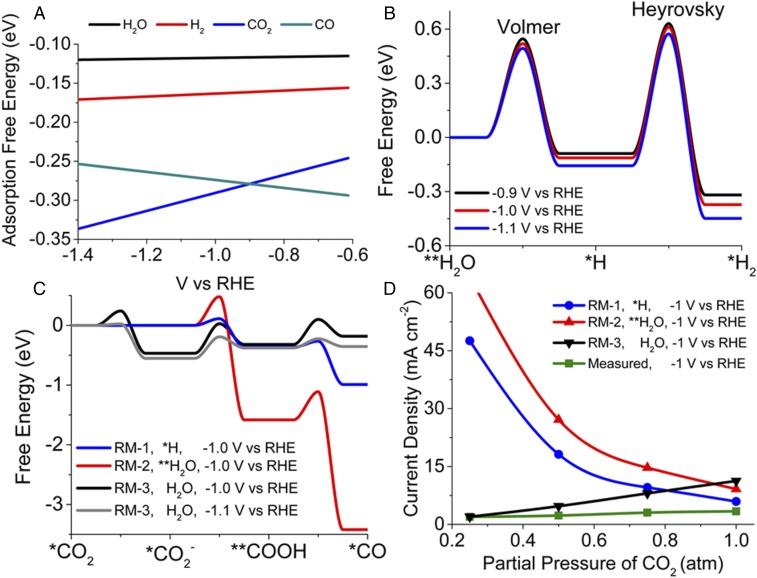
Fig. 2 shows three different reaction mechanisms for CO₂RR and HER over Ag(110). The mechanism of HER involves adsorption of H₂O followed by the transfer of one electron to **H₂O (Volmer step) to produce *H with the instantaneous release of OH⁻ and an Ag site. The second electron transfer to a free H₂O in association with *H (Heyrovsky step) releases another OH⁻ to produce *H₂ and an Ag site. H₂ desorbs into the electrolyte and phase separates to produce gas bubbles. The barrier for the Volmer step with adsorbed H₂O is lower than that with free H₂O. The Tafel step is not energetically favored due to the large interatomic spacing between *H and *H on Ag(110). Therefore, the rate of HER is dependent on the adsorption energies of H₂O and H₂, and the activation barriers for the Volmer and Heyrovsky steps. Fig. 3A shows that H₂ and H₂O are weakly bonded to Ag(110) with bonding energies −0.16 and −0.13 eV, respectively, at −0.6 V vs. RHE. Their absolute bonding energy increases by ∼0.02 eV upon decreasing the potential from −0.6 to −1.1 V vs. RHE. This small increase in bonding energy is due to the higher energies of the LUMO antibonding orbitals of H₂ and H₂O compared with those of CO and CO₂. Fig. 3B shows the free energies of intermediates and reaction barriers for the Volmer and Heyrovsky steps evaluated at −0.9, −1.0, and −1.1 V vs. RHE. At −1.0 V vs. RHE, the energy barrier for Volmer step is 0.52 eV and the Heyrovsky step is 0.72 eV. The calculated transfer coefficients (the slope of the free energy vs. potential plots) for the Volmer and Heyrovsky steps are 0.23 and 0.05, respectively. Since the Heyrovsky step has the highest free-energy barrier, it is the rate-limiting reaction for HER over Ag.

Fig. 3.

(A) Free energy of adsorption of H₂O, H₂, CO₂, and CO on Ag(110) as a function of applied potential. (B) Free-energy profile of the Volmer–Heyrovsky reaction to produce H₂ over Ag(110) at −0.9, −1.0, and −1.1 V vs. RHE. (C) Free-energy profile of the CO₂RR over Ag(110) at −1.0 V vs. RHE via three different reaction mechanisms (RMs). The hydrogen donors in RM-1, RM-2, and RM-3 are *H, **H₂O, and H₂O, respectively. The free-energy profile for RM-3 at −1.0 and −1.1 V vs. RHE is also shown. (D) Comparison of total current density simulated for RM-1, RM-2, and RM-3 over Ag(110) with the total current density measured over polycrystalline Ag foil at 0.25-, 0.5-, 0.75-, and 1-atm partial pressures of CO₂ in 0.1 M KHCO₃ electrolyte.

The CO₂RR begins with the diffusion of dissolved CO₂ across the hydrodynamic boundary layer and its adsorption via coordination of the C atom with the Ag atoms located at the trough sites of the (110) surface. The slightly distorted adsorbed CO₂ (*CO₂), shown in the SI Appendix, Fig. S5A, is stabilized by a donation from the highest occupied d orbital of Ag to the LUMO antibonding orbital of CO₂; this leads to a weakened C=O bond in which the oxygen participates in hydrogen bonding with water. Fig. 2 A and B show that *CO₂ is reduced to **COOH, which is then reduced to *CO using *H or **H₂O, respectively. Formation of a *CO₂ anion $\left(\ast {\text{CO}}_2^{\delta -}\right)$ was not considered in Fig. 2 A and B because the free-energy barrier for conversion of $\ast \mathrm{C}{\mathrm{O}}_2^{\delta -}$ to **COOH was at least 0.5 eV higher than the direct reduction of *CO₂ to **COOH. In the case of reaction mechanism 1 (RM-1), the two elementary reactions of CO₂RR compete with the Heyrovsky reaction for *H, whereas in RM-2 the CO₂RR competes with the Volmer reaction. RM-3 considers the formation of $\ast \mathrm{C}{\mathrm{O}}_2^{\delta -}$ (SI Appendix, Fig. S5B) by partial electron transfer to *CO₂ as the free-energy barrier for reduction of $\ast \mathrm{C}{\mathrm{O}}_2^{\delta -}$ is at least 1 eV lower than that for the reduction of *CO₂. The hydrogen donor in RM-3 is taken to be free H₂O. The CO desorbed from the Ag electrode is assumed to readily desorb and form gas bubbles. Therefore, the rate of CO₂RR is dependent on the adsorption energies of CO₂ and CO, and the free-energy barriers for the elementary reactions.

Fig. 3A shows that the adsorption free energy for CO₂ increases from −0.25 to −0.30 eV as the potential decreases from −0.6 to −1.1 V vs. RHE. However, the adsorption free energy (or bonding energy) of CO decreases from −0.29 to −0.27 eV over the same range of applied potentials. The small increase in CO₂ adsorption energy is due to stronger ${\pi }^{\ast }$ back-bonding, whereas the decrease in the bonding energy of *CO is due to the increase in the energy level of the ${\pi }^{\ast }$ orbital of CO. Such variation in the CO adsorption energy can be related to the measured low-wavenumber shifts in CO stretching frequency with decreasing potential (35). Fig. 3C shows the free-energy profiles for the elementary steps for the CO₂RR according to RM-1, RM-2, and RM-3 at −1.0 V vs. RHE. The highest barrier and hence the rate-limiting step in all three cases corresponds to the formation of **COOH. The energy barrier to produce **COOH is 0.11 eV for RM-1, 0.41 eV for RM-2, and 0.43 eV for RM-3. However, the predicted current density decreases in the order RM-3 > RM-2 > RM-1 (Fig. 3D) at 1 atm of CO₂, which is opposite to the expected order based on the values of the free-energy activation barriers for **COOH formation. The rate of reaction or current density is directly proportional to the concentration of hydrogen donor species and exponentially dependent on the energy barriers. At −1.0 V vs. RHE and 1 atm of CO₂, the coverage of *H in RM-1 is 1.6 × 10⁻⁸, the coverage of **H₂O in RM-2 is 1.2 × 10⁻³, and the concentration of H₂O in RM-3 is 55 M. The higher surface coverage of hydrogen donors in RM-3 offsets the higher free energy of activation to yield the highest current density among the three mechanisms.

Fig. 3D shows the variation in total current density with the partial pressure of CO₂. RM-3 follows the same trend as the experimentally measured values. However, RM-1 and RM-2 both show an unphysical increase in CO current density with decreasing partial pressure of CO₂. The rate of reaction is directly proportional to the product of the concentrations of *CO₂ and *H/**H₂O. Since *CO₂ is the majority species, a slight decrease in the CO₂ concentration and hence the coverage of *CO₂ can cause the coverage of minority species (<1 × 10⁻⁵) such as *H and **H₂O to increase by orders of magnitude, resulting in an overall increase in the rate of reaction. This result confirms that the highest energy pathway (RM-3) is the one that is consistent with experimental observation.

Intrinsic Kinetics of CO₂RR over Ag and the Consequences of Polarization.

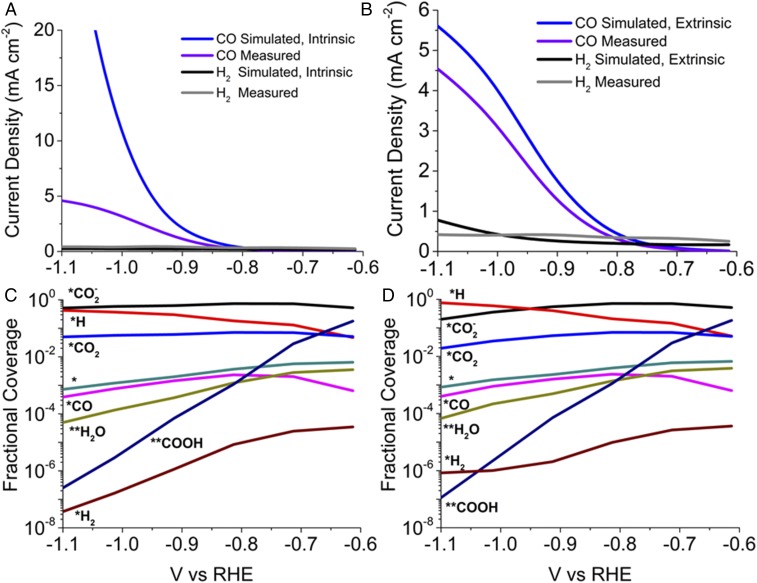
The dependence of the intrinsic current densities for CO and H₂ produced over Ag(110) as a function of applied potential is illustrated in Fig. 4A using RM-3. These calculations neglect the mass transfer resistances and assume that, for all potentials, the concentration of CO₂ near the Ag cathode is at equilibrium with 1 atm of gaseous CO₂. The intrinsic current density of CO is 12.3 mA⋅cm⁻² at −1.0 V vs. RHE, which is more than three times higher than that measured experimentally (3.5 mA⋅cm⁻²) (9). The intrinsic current density can be fitted to a Butler–Volmer expression for which the exchange current density is 1.71 × 10⁻⁵ mA⋅cm⁻², the anodic transfer coefficient is 0.17, and the cathodic transfer coefficient is 0.49. The fitted transfer coefficients are <0.5, which is within the range for most electrochemical reactions (52). The HER is completely suppressed during CO₂ reduction as the free-energy barrier for the Heyrovsky step is ∼0.3 eV higher than the barrier for $\ast {\text{CO}}_2^{\delta -}$ reduction reaction in RM-3. Fig. 3C shows potential-dependent fractional coverages of adsorbates and intermediates for intrinsic reaction conditions. The dominant species on the Ag(110) surface are $\ast {\text{CO}}_2^{\delta -}$ and *H, as species involved in the rate-limiting steps for CO and H₂ formation, respectively. As the potential decreases below −0.75 V vs. RHE, the fractional coverage of *H increases and all other species decreases. The sharp decrease in the coverages of **H₂O and **COOH is due to their consumption in the Volmer reaction and the reduction of **COOH, which are much faster than the rates of the Heyrovsky reaction and the $\ast {\text{CO}}_2^{\delta -}$ reduction reaction. The decrease in *CO coverage is due to the decrease in the adsorption energy of CO with decreasing potential (Fig. 3A).

Fig. 4.

Comparison of simulated (A) intrinsic (without mass transfer resistance) and (B) extrinsic (with mass transport effects) current densities for RM-3 with the measured current densities of CO and H₂ (9). The variation in the coverages of adsorbed and intermediate species with the applied potential under (C) intrinsic and (D) extrinsic conditions.

Fig. 4B shows the effect of mass transfer on the calculated current densities of CO and H₂ as a function of the potential applied to Ag(110). The current density for CO as shown in Fig. 4B is significantly lower than that calculated in the absence of mass transfer (Fig. 4A) due to cathode polarization. This effect is a consequence of the increase in the concentration of OH⁻ (pH) and the consequent decrease in the concentration of CO₂ during the CO₂RR (8). The partial pressure of CO₂ at the cathode decreases from 0.94 to 0.31 atm and the cathode pH increases from 6.8 to 7.5 as the potential decreases from −0.6 to −1.1 V vs. RHE. Fig. 4D shows the variation in the fractional coverage due to polarization. At higher negative potentials, the coverages of carbon species decrease and the coverages of the hydrogen species increase due to the polarization of the cathode. The majority species at lower negative potentials are $\ast {\text{CO}}_2^{\delta -}$ and **COOH, and at higher negative potentials are *H and $\ast {\text{CO}}_2^{\delta -}$. Our findings agree well with the recent IR spectroscopy of CO₂RR over Ag, which show **COOH as the majority species at lower negative potential and $\ast {\text{CO}}_2^{\delta -}$ as the major carbon-containing species at −1.0 V vs. RHE (37). The authors also report a very weak signal for *CO during CO₂RR, consistent with our simulation results. Fig. 4B shows a slight increase in H₂ current density at −1.1 V vs. RHE compared with the intrinsic current density due to the increase in the *H concentration caused by cathode polarization.

Effect of CO₂ Concentration and pH on the Kinetics.

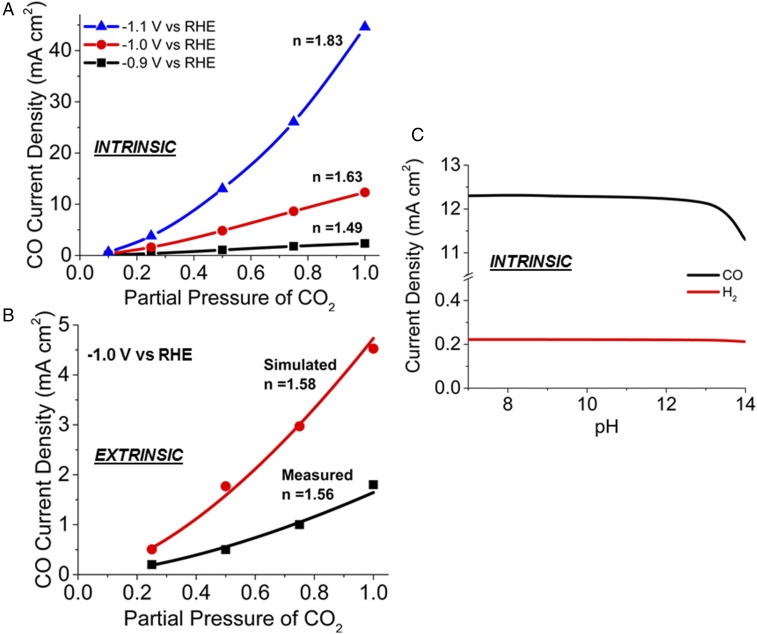
Fig. 5A shows the increase in the intrinsic current density of CO with increasing partial pressure of CO₂ at −0.9, −1.0, and −1.1 V vs. RHE. A power law fit to these curves indicates that the intrinsic reaction order with respect to CO₂ is 1.49 ± 0.30 at −0.9 V, 1.63 ± 0.19 at −1.0 V, and 1.83 ± 0.09 at −1.1 V. The intrinsic reaction order is greater than 1.0 because coverage of $\ast {\text{CO}}_2^{\delta -}$ (reactant for the rate-limiting step) increases nonlinearly with increasing concentration of CO₂. Since the adsorption free energy of CO₂ increases with decreasing potential (Fig. 3A), the reaction order increases with decreasing potential. The experimentally measured reaction orders are lower than the intrinsic reaction order due to the influence of mass transfer. Fig. 5B shows the extrinsic and measured current density of CO increases with increasing partial pressure of CO₂ at −1.0 V vs. RHE. The measured current density shown in Fig. 5B was obtained from the cyclic voltammograms for the CO₂RR over polycrystalline Ag for partial CO₂ pressures between 0.25 and 1 atm (9). These cyclic voltammograms were measured at a scan rate of 10 mV⋅s⁻¹ to obtain quasi–steady-state current densities. By contrast, the simulated current densities in Fig. 5B represents the steady-state product current densities for the CO₂RR over Ag(110) obtained at a constant potential of −1.0 V vs. RHE. The simulated apparent order is 1.58 ± 0.32 and the measured apparent order is 1.56 ± 0.23, indicating excellent agreement between the simulated and experimentally observed dependence on CO₂ partial pressure. Fig. 5C shows that the intrinsic current density of H₂ decreases very slightly for pH values between 7 and 14. The intrinsic current density for CO also changes very little for pH values between 7 and 13, but then declines when the pH is increased to 14. This result suggests that the pH of electrolyte does not have a direct effect on the rates of CO₂RR and HER in near-neutral pH electrolytes. However, the pH of the electrolyte can affect the solubility of CO₂ (8), which in turn affects the kinetics of CO₂RR. This trend has been observed experimentally for the CO₂RR over Cu (53) and Ag (9). The pH of the electrolyte may also affect the local orientation of H₂O near the cathode, which can, in turn, affect the free-energy barriers of CO₂RR and HER (54).

Fig. 5.

(A) Increase in the intrinsic CO current density with increasing partial pressure of CO₂. The intrinsic reaction order with respect to CO₂ is 1.49 at −0.9 V vs. RHE, 1.63 at −1.0 V vs. RHE, and 1.83 at −1.1 V vs. RHE. (B) Increase in the extrinsic CO current density with increasing partial pressure of CO₂. The measured current density was obtained from cyclic voltammogram of CO₂RR over polycrystalline Ag at −1 V vs. RHE. The simulated apparent reaction order of 1.58 agrees well with the measured apparent order of 1.56. (C) The decrease in the CO and H₂ current densities with increasing pH of the electrolyte.

Strategies to Increase Activity of CO₂RR over Ag.

The present analysis has shown that the rate-limiting step in CO₂RR over Ag(110) is the reduction of $\ast {\text{CO}}_2^{\delta -}$. $\ast {\text{CO}}_2^{\delta -}$ is stabilized by back-donation of electrons from highest occupied d orbital of the metal to the lowest unoccupied ${\pi }^{\ast }$ antibonding orbital of CO₂. The addition of electrons to the antibonding orbital weakens the C–O bond and facilitates the reduction of $\ast {\text{CO}}_2^{\delta -}$ to **COOH. The negative anion $\ast {\text{CO}}_2^{\delta -}$ can be stabilized by the electrostatic interactions with the cations (34). Although the magnitude of such interactions is limited by the size and the concentration of cations, it can boost the reaction rates by at least twofold (14). Another strategy to stabilize $\ast {\text{CO}}_2^{\delta -}$ is to create grain boundaries and under coordinated sites on the surface of the metal. Such strategies have shown much higher increase in the CO₂ reduction current densities over Cu (55).

Conclusions and Perspectives

This work clearly demonstrates that, to identify a physically correct mechanism for the electrochemical reduction of CO₂ and the dependence of the rate of product formation on the cathode voltage and partial pressure of CO₂, it is essential to simulate all aspects of the electrochemical system, and not just the cathode surface chemistry. Such a multiscale, multiphysics model was developed in the present study. Equilibrium constants and rate coefficients for processes occurring on the cathode surface were determined from DFT calculations of the free energies of adsorption and reaction, and the free energies of activation for all elementary processes. This information was used to determine equilibrium constants and rate coefficient for a microkinetic model that describes the current densities for H₂ and CO. The concentration of all species at the cathode and anode surfaces was determined from a continuum model that takes into account the transport of all neutral and ionic species by diffusion and migration as well as the inter conversion of anionic species.

The model developed here was used to predict the formation of H₂ and CO in an electrochemical cell that contains an Ag(110) surface as the cathode, a polycrystalline Pt foil as the anode, and a Seleminon, anion-conducting membrane separator. The lowest energy pathway for the HER was identified to be a Volmer–Heyrovsky sequence, for which the Heyrovsky is the rate-limiting step. Three different mechanisms for the CO₂RR were considered (RM-1, RM-2, and RM-3), which differ in the nature of the hydrogen donor—*H, **H₂O, and free H₂O. In all three cases, the hydrogenation of adsorbed CO₂ to produce **COOH is the rate-limiting step for producing CO. The barrier for this step increases in the order RM-1 < RM-2 < RM-3. Remarkably, while RM-3 exhibits the highest barrier for hydrogenation of adsorbed CO₂, this is the only mechanism that correctly predicts the dependence of the current density on the applied cathode voltage and the partial pressure of CO₂. It is notable that this unexpected finding would not have been possible without the use of a multiscale, multiphysics model to simulate the overall cell performance. The majority adsorbed species in RM-3 are predicted to be $\ast {\text{CO}}_2^{\delta -}$, **COOH, and *H; and the minority species are predicted to be *CO₂ and *CO. These predictions are in strong qualitative agreement with what has been recently reported in an in situ IR spectroscopic investigation of the CO₂RR over Ag (37). Previous theoretical efforts were able to predict only the onset potentials of the CO₂RR over Ag(111) using a pseudo–steady-state microkinetic model with rate parameters obtained from DFT calculations (34). Here, we have shown a full prediction of current densities, Faradaic efficiencies, and surface coverages as a function of applied potentials for CO₂RR over Ag. The predictions of these simulations compare very well with the experimental data because the multiscale model accounts for all essential physical phenomena, occurring over a wide range of length and time scales, that influence the dynamics of the CO₂RR. We also find that cathode polarization reduces the intrinsic current density significantly for cathode voltages above approximately −0.9 V vs. RHE. When the effects of cathode polarization are taken into account, the simulated extrinsic current density matches well with that measured experimentally, further validating the model (9). The simulated apparent order of CO₂RR with respect to the partial pressure of CO₂ at −1.0 V vs. RHE is 1.58, which agrees very well with the observed value of 1.56 (9). In summary, we have demonstrated that the multiscale approach developed in this study should be used to assess the validity of reaction mechanisms proposed for the CO₂RR under the circumstance where electrolyte polarization is unavoidable and can influence the pH and CO₂ concentration near the cathode surface.