Effects of Tissue-Specific Functional Magnetic Resonance Imaging Signal Regression on Resting-State Functional Connectivity

Abstract

Neuroimaging studies typically consider white matter as unchanging in different neural and metabolic states. However, a recent study demonstrated that white matter signal regression (WMSR) produced a similar loss of neurometabolic information to global (whole-brain) signal regression (GSR) in resting-state functional magnetic resonance imaging (R-fMRI) data. This was unexpected as the loss of information would normally be attributed to neural activity within gray matter correlating with the global R-fMRI signal. Indeed, WMSR has been suggested as an alternative to avoid such pitfalls in GSR. To address these concerns about tissue-specific regression in R-fMRI data analysis, we performed GSR, WMSR, and gray matter signal regression (GMSR) on R-fMRI data from the 1000 Functional Connectomes Project. We describe several regional and motion-related differences between different types of regressions. However, the overall effects of concern, particularly network-specific alteration of correlation coefficients, are present for all regressions. This suggests that tissue-specific regression is not an adequate strategy to counter pitfalls of GSR. Conversely, if GSR is desired, but the studied disease state excludes either gray matter or white matter from analysis (e.g., due to tissue atrophy), our results indicate that WMSR or GMSR may reproduce the gross effects of GSR.

Introduction

It is an axiom in neuroimaging that researchers measure brain activity from gray matter, whereas white matter is of interest either anatomically or as a “non-signaling” control region. However, a recent study published (Thompson et al., 2016) indicated that white matter shared signal-related characteristics with gray matter both in resting-state functional magnetic resonance imaging (R-fMRI) data and in fluorodeoxyglucose positron emission tomography (FDG-PET) data. These authors examined the state change between eyes open and eyes closed. They found that white matter showed an increase in glucose uptake in the eyes open state (measured by FDG-PET), similar to gray matter. This state change was homologous to a state change in functional connectivity density, a measure of hypothetical neural communication hubs calculated from R-fMRI (Tomasi and Volkow, 2011).

The authors of Thompson et al., 2016 observed that this homology was lost if global signal regression (GSR), removal of the mean from the whole brain, was used. Surprisingly, regression of the mean white matter signal caused a near-identical change to regression of the global signal. This result was unexpected as the loss of neurometabolic information within R-fMRI data due to regression would normally be attributed to the global signal correlating with neural activity in gray matter (Schölvinck et al., 2010).

As white matter signal regression (WMSR) has been suggested as an alternative or addition to GSR by many studies (Brown et al., 2014; Fox et al., 2005; Gotts et al., 2012; Patriat et al., 2013; Satterthwaite et al., 2013) and may potentially lack some of the GSR known drawbacks (Murphy et al., 2009; Schölvinck et al., 2010), Thompson and associates' observations [especially considering several recent studies suggesting functional activation in white matter (Astafiev et al., 2015; Ding et al., 2013, 2016; Gawryluk et al., 2014; Marussich et al., 2017; Wu et al., 2016)] suggest that the underlying assumption of white matter as nonsignaling may be incorrect. However, Thompson and associates were not able to address this in detail and, in addition, they used a combined PET/MRI scanner that may have influenced results.

To address this, we conducted a brief investigation into the effects of tissue-specific regression, including GSR, WMSR, and gray matter signal regression (GMSR), on several simple parameters that reflect gross effects on R-fMRI results using publicly available, standard R-fMRI data (Biswal et al., 2010). Small but significant differences existed between regressions regarding subject motion and intranetwork correlation, and specific tissue types are differentially affected (as expected). However, the gross effects of concern were omnipresent between GSR, WMSR, and GMSR. We thus suggest that WMSR is not a sufficient alteration to standard R-fMRI preprocessing to overcome known problems with GSR. We also suggest that if GSR is still needed, but white matter data are unusable (e.g., a clinical group is being studied where white matter is disrupted), GMSR may be a viable alternative, as long as the differences we discuss herein are considered.

Materials and Methods

Data acquisition

Datasets for this experiment were downloaded from the 1000 Functional Human Connectomes Project (Biswal et al., 2010). The datasets used herein were selected such that there was a spread of scanning parameters (e.g., gender and field strength) as shown in Table 1. To avoid possible comparison artifacts, datasets were also only used if the average root mean square of the percentage change of raw global signal was between 0 and 1. Only the first 20 subjects were used for the Beijing-Zang dataset, only the female subjects were used in the Saint Louis dataset, and only the first functional sessions were used from the New Haven B dataset. Subjects were excluded if any abnormalities were mentioned in the documentation (Ontario: two subjects missing anatomical scans). One subject (Saint Louis) was excluded because registration failed.

Table 1.

Details of All 1000 Functional Connectomes Project Datasets Used

Dataset	Magnet	N	Sex	Age range	TR	Time points	Eyes open vs. closed	Slice, acquisition order	Handedness
Beijing (Zang), China	3 T	20	11 F	18–26	2	225	Closed	Interleaved	Right-handed
								Ascending
New Haven (B)	3 T	16	8 F	18–42	1.5	181	Open, no projection	Interleaved Ascending	Right-handed
Saint Louis	3 T	16	16 F	21–29	2.5	127	Open, fixation	Interleaved Ascending	Right-handed
Ontario, Canada	4 T	9	\	\	3	105	Closed	Segmented Spiral, 2-shot Interleaved, descending	Mixed
Orangeburg	1.5 T	19	4 F	20–55	2	165	Closed	Interleaved Ascending	Mixed

A “\”denotes missing data. Sample sizes were calculated after subject exclusions.

TR, repetition time.

Data analysis

Standard R-fMRI preprocessing (for details, see Supplementary Data for Thompson et al., 2016; Supplementary Data are available online at www.liebertpub.com/brain) was performed, but the preprocessing was stopped after region-specific regression. This was done to prevent interaction effects between regression and further preprocessing steps. A summary of preprocessing follows.

All R-fMRI datasets except for Ontario were slice-time corrected, and all datasets were motion corrected using SPM8 (Statistical Parametric Mapping, The FIL Methods group, 2009, www.fil.ion.ucl.ac.uk/spm/software/spm8/). Ontario was not slice-time corrected as it used spiral acquisition. In SPM8, individual subjects' data were segmented to produce masks of gray matter, white matter, cerebrospinal fluid, and the whole brain. R-fMRI data were registered to each subject's gray matter mask. The data in anatomical space were registered to the Montreal Neurological Institute (MNI) template (2 mm, isotropic) using BioImage Suite (Yale School of Medicine, 2001, http://bioimagesuite.yale.edu/) and blurred with a Gaussian filter (full-width half-maximum 8 mm, kernel size 6 mm). Regression signals were calculated by averaging the time-series within a whole-brain mask for GSR, a gray matter mask for GMSR, or an eroded white matter mask for WMSR. The white matter erosion removed all voxels with at least one side facing a non-white matter voxel, thereby reducing the number of partial volume voxels. Regression signals were extracted from non-blurred data to avoid partial volume effects within our regression signals. All regressions were performed with a multivariate multiple least-squares linear regression. Experiments were done both with and without temporal filtering and motion parameter regression. Where applicable, a bandpass Fourier filter (0.01–0.08 Hz) was applied simultaneously with nuisance signal regression (Hallquist et al., 2013).

Blurred (not regressed) R-fMRI data in MNI space of all subjects in all datasets (also including two datasets that were not included herein due to root mean square of the percentage signal change of the raw signal exceeding 1) and the Group ICA of fMRI toolbox (GIFT; mialab.mrn.org/software/gift/) (Correa et al., 2007) were used to generate 20 networks. Two of the networks, the default mode network (DMN) (Binder et al., 1999) and task-positive network (TPN), were identified by visual inspection, comparing with Fox and associates (2005).

All significance testing presented in the results was corrected for multiple comparisons by holding the false discovery rate (FDR) under 5% (Benjamini and Hochberg, 1995).

All data processing was performed with MATLAB (version 9.0, The Mathworks, Inc., Natick, MA, USA).

Quality control

To ensure data quality, we assessed cross-modal registration by calculating the overlap of the whole-brain masks of T1 images and blood oxygenation level-dependent (BOLD) images (see Thompson et al., 2016, Supplementary Data for details). Mean overlap of all datasets exceeded 99% and datasets did not differ on their overlap (one-way ANOVA, p > 0.05). All white matter masks were visually inspected to confirm accurate segmentation.

Ethics statement

All data used in this study were anonymized before their uploading to the 1000 Functional Connectomes database. No identifying data were requested, and all data used are publicly available through the 1000 Functional Connectomes website [www.nitrc.org/projects/fcon_1000/ (Biswal et al., 2010)].

Results

Signal alteration due to regression

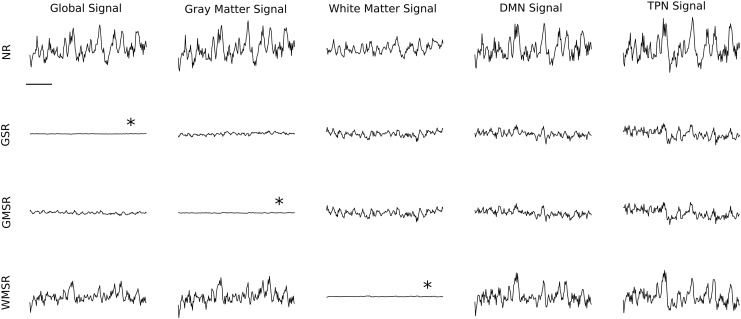
Regression methods are inherently designed to remove part of the signal. To estimate the amount of signal removed by a regression, the time-courses of a single representative subject (New Haven dataset) were brought to a similar scale by setting the signal's arbitrary mean to 1 and they subsequently represent the spontaneous BOLD signal fluctuations as fractional change (Fig. 1). After all regressions, a large drop in signal intensity occurs when compared with nonregressed (NR) signals, indicating that functional connectivity (after regression) is based on a relatively small part of the R-fMRI signal. For example, using GSR, the BOLD signal amplitude in gray matter drops by approximately a factor of 8, and using WMSR, the BOLD signal amplitude drops by approximately a factor of 2. While (relative to the white matter signal) the gray matter signal explains a larger part of variance of the global signal (Table 2), the variance explained of both signals is generally high across all sites (median >0.65), indicating that these signals, and by extension their regressions, may be quite similar to GSR. Filtering the data does not change this pattern (Table 2).

FIG. 1.

Effects of tissue-specific regression on BOLD signal amplitude. Data from a single subject (New Haven dataset). Averaged BOLD signal time courses in the (left to right) global signal (whole brain), gray matter signal, white matter signal, DMN signal, and TPN signal. The BOLD signal time courses shown are NR data before regression (first row), after GSR (second row), after GMSR (third row), and after WMSR (fourth row). The horizontal bar denotes 60 sec. All signals are scaled to represent fractional change (see the Results section), that is, vertical scales are arbitrary, but identical. Asterisks denote that these signals are expected to be flat because these were the regional signals that were regressed. BOLD, blood oxygenation level-dependent; DMN, default mode network; GMSR, gray matter signal regression; GSR, global signal regression; NR, nonregressed; TPN, task-positive network; WMSR, white matter signal regression.

Table 2.

Median Variance Explained of the Global Signal by the Gray Matter Signal and White Matter Signal With and Without Temporal Filtering

	Without temporal filter		With temporal filter
	Median GMS variance explained of GS	Median WMS variance explained of GS	Median GMS variance explained of GS	Median WMS variance explained of GS
Beijing (Zang)	0.98	0.78	0.98	0.62
New Haven (B)	0.98	0.69	0.99	0.78
Saint Louis	0.95	0.73	0.97	0.80
Ontario	0.97	0.76	0.98	0.76
Orangeburg	0.96	0.65	0.97	0.70

Generally, both signals explain a substantial amount of the GS, but the GMS variance explained is consistently higher than the WMS variance explained.

GS, global signal; GMS, gray matter signal; WMS, white matter signal.

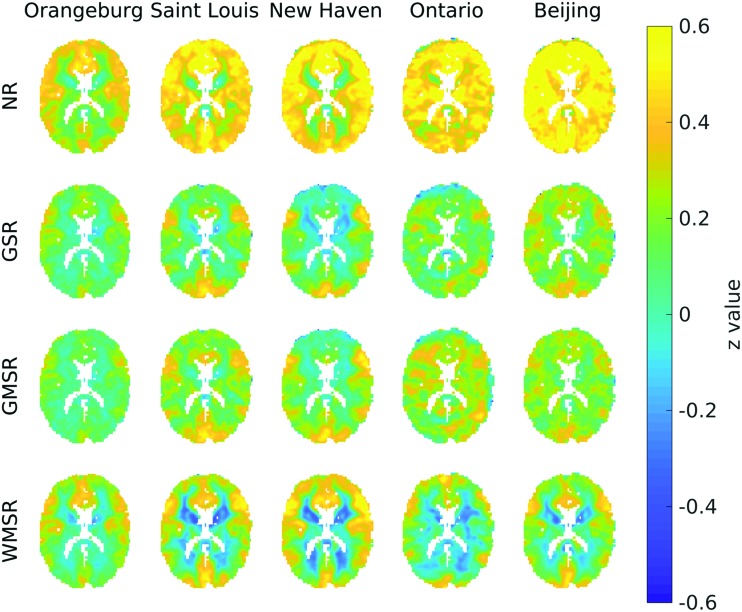
Correlation maps with the DMN were created by calculating the average time course within the DMN for each subject. The DMN time-course was Pearson correlated with the time-courses of all voxels of the same subject. Pearson correlations were converted to z values with a Fisher transformation. z Values of the same voxels were averaged across subjects within the same dataset. While regressions remove a large part of the signal, the resulting correlation maps are similar across all experiment sites (Fig. 2), although as expected, WMSR removes white matter correlations more consistently leaving GSR and GMSR appearing more washed-out across the brain. Despite their local differences, all regressions reduce correlations across the brain and generate correlation maps with comparable spatial distributions. The Ontario data set seems to be an exception, with its GSR and GMSR producing correlations throughout the brain rather than a DMN map. This may be due to a site-specific effect most likely arising from spiral acquisition, which could differentially affect the white and gray matter signals. Filtering the data does not change this pattern (Supplementary Fig. S1).

FIG. 2.

Effects of tissue-specific regression on appearance of negative functional connectivity. Single transverse slice is shown, nose up. Pearson correlations (expressed in z value) of all voxels' time-series with the DMN averaged signal are shown for all experimental sites (columns) in the NR data (first row) and after GSR (second row), after GMSR (third row), and after WMSR (fourth row). All z values are averaged across subjects for each dataset. Signal regressions reveal correlation and anticorrelation patterns across the five datasets. These observations shown for one slice are typical for all slices in the brain. Color images available online at www.liebertpub.com/brain

Effect on intranetwork correlation

The strength of correlation within resting-state networks has frequently been used as a biomarker of disease states and to predict performance in healthy individuals (Magnuson et al., 2015; Van Den Heuvel and Pol, 2010). Regression will always reduce intranetwork correlation, but the amount of reduction between GSR, WMSR, and GMSR has not been systemically tested. Thus, reduction of correlation within the DMN and TPN networks is used here as a basic measure of regression's effect on such biomarkers and performance indicators.

Pearson correlations of all voxels within the DMN and TPN with their respective averaged network signal were calculated after each regression. These correlations were converted to z values and averaged, separately for each network and regression, within subjects. One-tailed t-tests of the differences in z values were done in both directions for each network, site, and regression. Resulting p values in the same tail side of the same network and regression method were combined using Fisher's method and the combined p values were used to test for significance (p < 0.05, FDR corrected). All regressions reduce correlations within the DMN and TPN with their respective averaged time course (Fig. 3). While there are significant differences between regressions in both the DMN and TPN (DMN: NR>WMSR>GMSR>GSR; TPN: NR>WMSR≈GMSR>GSR), these differences are small compared with the difference between no regression and any other regression (Table 3A and B). Regressing motion signals, filtering the data, or both only changed results in the TPN (NR>WMSR>GMSR>GSR) (filtered data results shown in Supplementary Fig. S2 and Supplementary Table S1).

FIG. 3.

Change in voxels' correlation with their own network after regression. Pearson correlations (expressed in z value) of voxels in the DMN and the TPN with their respective averaged network signal are shown. Data are shown for the NR signal and for the signals after GSR, after GMSR, and after WMSR. Error bars represent standard deviation across subjects. Any regression reduces correlations by approximately a factor of 2. Small statistically significant differences exist (DMN: NR>WMSR>GMSR>GSR; TPN: NR>WMSR=GMSR>GSR). These differences are shown in Table 3A and B.

Table 3.

Effect of Signal Regression on (A and B) Intranetwork Correlation in the Default Mode Network and the Task-Positive Network and (C) Correlation with Motion Parameters

A	Default mode network				B	Task-positive network
	NR	GSR	GMSR	WMSR		NR	GSR	GMSR	WMSR
NR		226%	204%	184%	NR		196%	178%	184%
GSR	≈0*		90%	81%	GSR	≈0*		91%	94%
GMSR	≈0*	0.0009*		90%	GMSR	≈0*	0.0002*		103%
WMSR	≈0*	≈0*	0.0037*		WMSR	≈0*	0.0008*	0.1277

C	Motion correction
	Raw	GSR	GMSR	WMSR
Raw		356%	284%	490%
GSR	≈0*		80%	138%
GMSR	≈0*	0.0028*		172%
WMSR	≈0*	0.0131*	0.0008*

(A, B) The lower triangular half shows the lowest p value of the one-tailed two-sample t-tests between regressions. The upper triangular half shows the percentage difference between the z valued intranetwork correlations of all voxels within the network with the network's averaged signal. z Values were averaged over subjects within site first, and then across sites. (C) The lower triangular half shows the lowest p value of the one-tailed two-sample t-tests between motion parameters and all voxels' signals. The upper triangular half shows the percentage difference between the z valued correlations between motion parameters and all voxels' signals. Percentages in all tables are expressed as row variable divided by column variable. The differences between the raw correlations and any of the regressed correlations are far larger than any other difference. Asterisks denote significant p values after multiple comparison correction. “≈0” indicates smaller than resolvable by MATLAB.

GMSR, gray matter signal regression; GSR, global signal regression; NR, nonregressed; WMSR, white matter signal regression.

Spatial differences between regressions

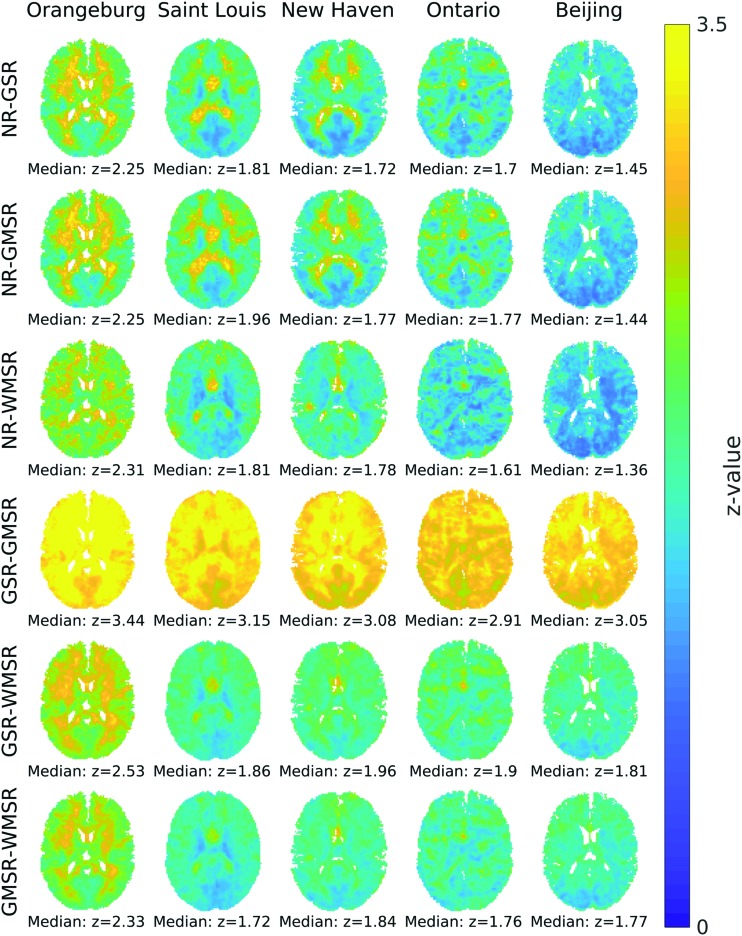
Figure 4 shows correlation between signals resulting from different regressions, spatially across the brain.

FIG. 4.

Spatial correlation of tissue-specific regressions. Single transverse slice is shown, nose up. Pearson correlations (expressed in z value, averaged across subjects for each dataset) of all voxels' time-series across regression pairs are shown for all experimental sites (columns) and all regression pairs. Median whole-brain z values are shown beneath each slice. Correlation is consistently positive and high (median z value >1.36), but in general, WMSR has a greater effect on white matter, while GSR and GMSR have a greater effect on gray matter. Color images available online at www.liebertpub.com/brain

First, as would be expected, sites that have a greater reduction in intranetwork correlation (Fig. 3) have less similarity between NR and any other regression. This is seen not only in gray matter, but in white matter as well. Second, WMSR and GMSR reduce correlation within their respective tissue type more than the alternative. This is likely due to differences in variance between gray matter and white matter being consistent across each tissue type. As expected from the similarity between the global and gray matter signals (Table 2), GSR and GMSR appear very similar, and when results are compared, GSR and GMSR are always the most correlated when compared with each other.

When comparing WMSR with GSR or GMSR, data are always more correlated in gray matter and less correlated in white matter than in WMSR versus NR. This suggests that there is some consistent variance within white matter that does not covary with gray matter. The Orangeburg site is an outlier here, possibly as regression had little effect on intranetwork correlation (Fig. 3), so WMSR, GMSR, and GSR are all highly correlated.

The Ontario data set appears to have small lines of high correlation tracing the innermost part of white matter and CSF regions, making it look visibly different from the other sites. This difference could be due to a site-specific artifact or due to the spiral acquisition altering sensitivity in the center of the brain.

However, despite these visible differences, GSR, GMSR, and WMSR in general are highly correlated, suggesting that gross effects are maintained across regression types (range of median Fisher z values = 1.72–3.44 across sites, corresponding r values = 0.94–1.0), whereas they are generally less correlated with NR (range of median Fisher z values = 1.36–2.31 across sites, corresponding r values = 0.88–0.98).

Effect on correlation with motion

GSR is claimed as advantageous as the global signal hypothetically conceals underlying neuroanatomical relationships (Fox et al., 2009). For example, subject motion in R-fMRI can add global correlation that is unrelated to underlying neural connections, altering measured functional connectivity (Power et al., 2014). Thus, GSR, WMSR, and GMSR were compared in terms of reducing the correlation between the R-fMRI signal and motion.

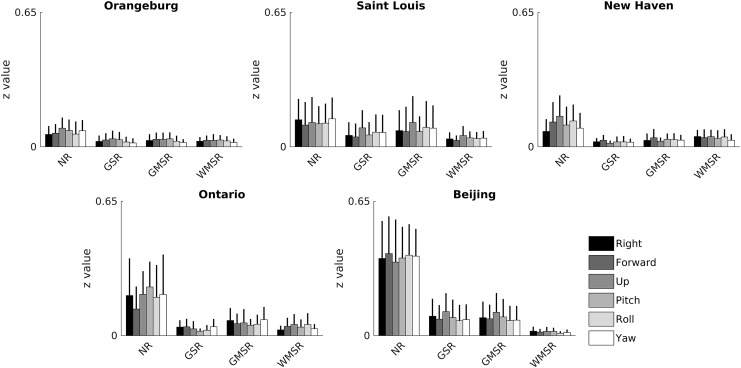
Correlation was calculated between six motion parameters and all voxels' time-series (Fig. 5). Motion parameters were three translations in mm (right, forward, and up) and three rotations in radians (pitch, roll, and yaw), calculated as deviation from the temporally central volume (e.g., for 300 sec of scanning, deviation from the volume at 150 sec) by SPM8. Time courses of all brain voxels after each regression method were correlated with all motion parameters. These correlations were converted to z values and averaged across voxels. Absolute z values of all motion parameters were averaged within subjects. One-tailed two-sample t-tests were performed for all pairs of regression methods in each experimental site and in both directions. p Values across experimental sites in the same tail side were averaged with Fisher's method. All regressions significantly reduced the averaged correlation of voxel time series with all motion parameters, and statistical differences between regressions exist (NR>GMSR>GSR>WMSR, p < 0.05, FDR corrected). However, the differences between regressions are small compared with the difference between no regression and any regression (Table 3C). Filtering the data (Supplementary Fig. S3 and Supplementary Table S1) reduced correlation with motion in all conditions and changed the significance of correlations substantially (NR>WMSR>GMSR>GSR, p < 0.05, FDR corrected). This may indicate that a temporal filter removes some motion artifacts that are differentially removed by regressions. Regressing the motion parameters left only a significant difference between GSR and WMSR (WMSR>GSR) and any regression versus no regression. Filtering and motion regressing the data removed all significant differences between tissue-specific regressions (NR>GMSR≈WMSR≈GSR), indicating that for purposes of motion correction, the effect of regressing motion parameters is far larger than the effect of nuisance regression (note that in the case of motion regression, we regress the same motion parameters that we correlate with, so all correlations are expected to approach 0).

FIG. 5.

Regressions correct for motion artifacts. Absolute Pearson correlations (expressed in z value) of all voxels' time series with rigid body motion parameters were averaged across subjects. Error bars represent standard deviations across subjects. Correlations between motion parameters and voxels' time series in the NR data are consistently larger than those after GSR, GMSR, and WMSR. Statistically significant differences between regressions exist (NR>GMSR>GSR>WMSR), shown in Table 3C, but are small compared with the difference between no regression and any other regression, indicating that for the purpose of motion correction, these regressions produce comparable results.

Discussion

Tissue-specific regression

While we were able to characterize key differences between GSR, GMSR, and WMSR (discussed in detail in the next section), in the context of prior work (Murphy et al., 2009; Power et al., 2012; Thompson et al., 2016), WMSR and GMSR produce similar global effects of concern as GSR (Table 3). While (as expected) tissue-specific differences exist, WMSR and GMSR still produce patterns of correlation and anticorrelation as GSR does (Fig. 2), which are held as physiologically relevant (Fox et al., 2009), although work beyond the present study is needed to establish the link between the BOLD signal and physiology. The global reduction in correlations observed in GSR by Murphy and associates (2009) was also observed here in WMSR and GMSR (Fig. 3). The reduction of motion effects through GSR observed by Power and associates (2012) was also observed here in WMSR and GMSR (Fig. 5).

These overall similarities between GSR, WMSR, and GMSR suggest that the use of WMSR instead of GSR is not a sufficient modification of the regression protocol to counter problems observed with GSR (Murphy et al., 2009; Saad et al., 2012; Schölvinck et al., 2010). This suggests that Thompson and associates' observation of WMSR removing neurometabolic information (Thompson et al., 2016) was not an artifact of the combined PET/MRI scanner, but is instead likely to translate to other studies that have used WMSR.

Despite the drawbacks, in many situations, researchers will wish to use GSR for its desirable effects, for example, Thompson and associates (2016) observed that performing regression improved network versus network differentiation for many R-fMRI metrics and Power and associates (2014) observed that GSR reduces motion-related signal changes. However, differences between white matter and gray matter in a disease of interest could preclude using particular regression techniques. The similarity of gross effects between GSR, WMSR, and GMSR we observed suggests that a regression method could thus be chosen based on such tissue-specific limitations. However, further validation of nuisance regressions in a disease population such as presymptomatic Huntington's disease, where the white matter signal may be altered (Ciarmiello et al., 2006), is needed to confirm this (in consideration of differences between regressions that we also characterized).

Advantages and disadvantages of each tissue-specific regression

While gross results are largely similar for any regression versus no regression (Table 3), there are important differences between regressions.

The most obvious difference observed was that tissue-specific regression creates a greater difference from NR within the specific tissue type regressed (Fig. 4). GSR, in this case, performs most similarly to GMSR probably due to the large number of high signal intensity gray matter voxels (Fig. 1) driving the global signal and the fact that gray matter contains networks of similarly behaving voxels.

WMSR reduced correlation with motion the most, GMSR the least. This is likely due to BOLD amplitudes being higher in gray matter than in white matter (Yu-Feng et al., 2007), thus if nonphysiological artifacts (e.g., motion) are uniformly added to both tissue types, it will differentially have a greater effect on white matter and a lesser effect on gray matter. Comparing regressions also suggests a small amount of variance that is specific to white matter itself (Fig. 4), which could also be linked to motion. When motion parameters are included in the nuisance signal regression, the motion-related difference becomes insignificant. Moreover, gray matter correlates higher with the cardiac rate time course than white matter (Shmueli et al., 2007), indicating that cardiac artifacts may conceal motion artifacts more in gray matter than white matter. GSR, using both white and gray matter, has an in-between effect. Overall, the relative amounts of observed correlation reductions mirror what was observed in a previous study that compared WMSR and GSR (Weissenbacher et al., 2009).

Filtering is expected to reduce motion correlation as the strongest temporal correlation between BOLD signals is expected to be under 0.1 Hz (Cordes et al., 2000), whereas most of the motion artifacts will fall outside this range. Indeed, a temporal filter reduced correlation with motion across all conditions (Supplementary Fig. S3). Simultaneous filtering and WMSR reduces correlation with motion the least and simultaneous filtering and GSR the most, suggesting that motion artifacts are still present within the 0.01–0.08 Hz frequency range. The differences between regression techniques may be because specific noise frequencies are more prominent in certain tissue types. Indeed, if part of the nonfiltered white matter signal represents motion outside the 0.01–0.08 Hz frequency band, then one would expect a reduced effect of WMSR on motion correlation when using filtered data.

GSR reduced intranetwork correlation the most. This may be because GSR includes the greatest number of voxels and thus was able to result in the greatest shift from positive to negative correlations (Murphy et al., 2009). Eroded white matter maps had the fewest voxels and thus had the smallest effect, with gray matter maps somewhere in-between.

Regardless of alterations to correlation coefficients, it should also be noted that regression removes a significant part of the spontaneous BOLD signal amplitude in every tissue type, but more so in gray versus white matter (Fig. 1).

Limitations and future work

Widely different groups of subjects were selected to demonstrate that the effects we observed were not due to being in a particular state (e.g., eyes closed vs. open) or being in a particular group (e.g., male vs. female subjects). However, this could obscure effects that only occur within one group or only occur within groups that have relatively low signal-to-noise ratio in the R-fMRI data. Furthermore, as the selected datasets sampled their functional data at relatively large voxel sizes (35–65 mm³), some partial volume effects may have occurred in our nuisance signal regression that may be prevented with modern high-resolution imaging.

Differences could exist between the effects of specific regressions on specific R-fMRI signal frequencies. While we have considered a standard temporal filter of 0.01–0.08 Hz and found a difference in motion correction, addressing the interaction between specific frequencies and regression methods was beyond the scope of this research. Future work can address this, in particular, if infraslow electrical recording is done to identify coherent frequency bands of R-fMRI data (Pan et al., 2013). As simultaneous recordings of infraslow electroencephalography and R-fMRI are now possible (Hiltunen et al., 2014), in the near future, it may be possible, noninvasively, to study the physiological basis of the spontaneous BOLD signal in human subjects.

While reductions in BOLD signal amplitude upon fMRI signal regression are within prior expectations (Hyder and Rothman, 2010), the metabolic and physiologic bases of the remaining fraction remain to be studied in further detail. To this end, a combination of fMRI and optical imaging methods (Sanganahalli et al., 2016) covering large swathes of the brain may prove useful.

Conclusion

GSR, WMSR, and GMSR all have similar effects in reducing BOLD amplitude, creating a pattern of correlations and anticorrelations, reducing intranetwork correlation and, reducing correlation with motion. Overall, our results suggest that WMSR, GMSR, and GSR affect R-fMRI time series in a similar, although not identical, manner. Thus, the use of tissue-specific regression is not recommended as an alternative to GSR if a researcher wants to avoid the undesired effects of GSR. However, if regression is to be used regardless of these effects, the gross similarity between regressions may be advantageous, and our work provides a characterization of the differences between regressions to expect. For example, if due to a study's constraints, white matter is unusable for regression (precluding GSR and WMSR), then GMSR might provide a reliable alternative.

Note

In an earlier version of this work, we assessed the effects of nuisance signal extraction before and after blurring the data without a temporal filter. We found that the spatial blur did not change the significance of any of our findings. Therefore, we expect our findings to extend to preprocessing pipelines that extract nuisance signals after spatial blurring.

Acknowledgments

Funding for this research included NIH P30 NS-052519 and NIH R01 MH-067528 to F.H. and a fellowship supporting G.J.T. from NIH 2T32DA022975-06A1. G.J.T. and F.H. would like to acknowledge Vinayak Mishra, a member of the National Junior Honors Society at Hill Regional Career High School, New Haven, CT, who worked on early aspects of this study through the Yale SSRI program. R.V. would like to thank Dr. Remco Renken for help in setting up the opportunity to work at Yale. The authors would like to thank Dr. Robert Fulbright for assisting with the forms for the Human Investigation Committee. The acknowledged funding sources were not involved in the design of this study.

Authors' Contributions

R.V., F.H., and G.J.T. designed the study. R.V. analyzed data. R.V., F.H., and G.J.T. wrote the article.

Author Disclosure Statement

No competing financial interests exist.