Distributed Intrinsic Functional Connectivity Patterns Predict Diagnostic Status in Large Autism Cohort

Abstract

Diagnosis of autism spectrum disorder (ASD) currently relies on behavioral observations because brain markers are unknown. Machine learning approaches can identify patterns in imaging data that predict diagnostic status, but most studies using functional connectivity MRI (fcMRI) data achieved only modest accuracies of 60–80%. We used conditional random forest (CRF), an ensemble learning technique protected against bias from feature correlation (which exists in fcMRI matrices). We selected 252 low-motion resting-state functional MRI scans from the Autism Brain Imaging Data Exchange, including 126 typically developing (TD) and 126 ASD participants, matched for age, nonverbal IQ, and head motion. A matrix of functional connectivities between 220 functionally defined regions of interest was used for diagnostic classification. In several runs, we achieved accuracies of 92–99% for classifiers with >300 features (most informative connections). Features, including pericentral somatosensory and motor regions, were disproportionately informative. Findings differed partially from a previous study in the same sample that used feature selection with random forest (which is biased by feature correlations). External validation in a smaller in-house data set, however, achieved only 67–71% accuracy. The large number of features in optimal models can be attributed to etiological heterogeneity under the clinical ASD umbrella. Lower accuracy in external validation is expected due to differences in unknown composition of ASD variants across samples. High accuracy in the main data set is unlikely due to noise overfitting, but rather indicates optimized characterization of a given cohort.

Introduction

Although autism spectrum disorders (ASD) are considered neurological, their diagnosis remains exclusively based on behavioral criteria (American Psychiatric Association, 2013). Despite thousands of neuroimaging studies of ASD, it is still not possible to pinpoint a brain finding as a diagnostic indicator of ASD. Part of the problem may be the great heterogeneity within the population, possibly reflecting hundreds of different neurodevelopmental etiologies (Geschwind and State, 2015). It is therefore possible that there may not be any uniquely sensitive and specific biomarkers of ASD and that any markers approaching this goal may be highly complex. However, given the relative specificity of diagnostic criteria primarily in the sociocommunicative domain (American Psychiatric Association, 2013), it is still probable that a well-defined set of brain features may achieve good classification of brains with and without ASD.

Numerous studies have shown aberrant anatomical (Ismail et al., 2016) and functional connectivity in ASD (Vissers et al., 2012). One method of choice in connectivity research is functional connectivity MRI (fcMRI) (Buckner et al., 2013; Van Dijk et al., 2010). This technique has been used for ASD diagnostic classification in several previous studies, mostly achieving 60–80% accuracy (Abraham et al., 2017; Anderson et al., 2011; Kassraian-Fard et al., 2016; Nielsen et al., 2013; Uddin et al., 2013; Yahata et al., 2016). One recent ASD diagnostic classification study using fcMRI achieved an accuracy rate of 91% (Chen et al., 2015). This study implemented random forest (RF)—a classification and regression tree model based on an ensemble of binary decision trees. Although the RF-based prediction model produced a high accuracy rate, there is concern that RF variable importance measures may suffer from a variable selection bias toward correlated predictor variables (Strobl et al., 2008). This is specifically an issue when using functional connectivity matrices, as connectivities may be extensively correlated. Hothorn and colleagues (2006) developed a conditional random forest (CRF) method addressing the problem of correlated predictor variables. The framework of CRF relies on measuring the association between responses and covariates via the conditional distribution of statistics. Theoretically, eliminating the variable selection bias should yield more interpretable and reliable results.

We therefore applied CRF feature selection to data from the Autism Brain Imaging Data Exchange (ABIDE) (Di Martino et al., 2014), which incorporates over 1100 resting-state functional MRI (rs-fMRI) data sets from 17 sites. As in the previous study by Chen and colleagues (2015), we only used a subset of highest quality low-motion data. Our study addressed four main questions: (1) Can CRF, due to its reduced feature selection bias, improve accuracy of diagnostic prediction? (2) Does the reduced selection bias result in a regional and network pattern of most informative features that differs from those previously reported for RF? (3) How well does CRF “out-of-bag” error correspond to validation in a truly novel external data set? And (4) how does extreme dimension reduction affect prediction accuracy (i.e., is it possible to find relatively simple connectivity patterns distinguishing ASD from TD participants)?

At the conceptual level, our study aimed to elucidate what findings from machine learning studies may imply for the ultimate goal of identifying a uniquely sensitive and specific ASD biomarker.

Materials and Methods

Data sets and participants

Data for building the model were selected from a high-quality (low-motion) subsample from the ABIDE (Di Martino et al., 2014). They included groups of ASD and typically developing (TD) participants, matched on head motion and demographic variables (as described in section “Head motion”). Data sets showing artifacts, signal dropout, suboptimal registration or standardization, or excessive motion were excluded from the study. Sites acquiring fewer than 150 time points were further excluded. Based on these criteria, a subset of 252 low-motion participants was selected. Groups were matched on age and motion to yield a final sample of 126 TD and 126 ASD participants, ages 7–36 years. The sample was identical to the one analyzed by Chen and colleagues (2015).

The classifiers were further validated using a separate in-house data set, with participants selected based on the same quality control and group matching criteria used for the ABIDE data set. Detailed information for both sample sets is shown in Table 1 (Supplementary Table S1 for fully detailed participant and site information; Supplementary Data are available online at www.liebertpub.com/brain).

Table 1.

Participant Information for the Full Sample from ABIDE and Validation Data Set from SDSU

	ASD M ± SD (range)	TD M ± SD (range)	p-value (2 sample t-test)
Full sample
N (female)	126 (18)	126 (31)
Age (years)	17.31 ± 6.0 (8.2–35.7)	17.12 ± 5.70 (6.5–34)	0.80
Motion (mm)	0.057 ± 0.020 (0.018–0.108)	0.058 ± 0.020 (0.020–0.125)	0.92
Nonverbal IQ	106.9 ± 17.0 (37–149)	106.3 ± 12.8 (67–155)	0.80
Validation sample
N (female)	42 (8)	30 (3)
Age (years)	13.30 ± 2.6 (9.2–18.0)	13.28 ± 2.9 (8.1–17.6)	0.98
Motion (mm)	0.074 ± 0.03 (0.02–0.15)	0.075 ± 0.05 (0.02–0.25)	0.92
Nonverbal IQ	105.1 ± 17.6 (67–145)	105.1 ± 9.9 (83–125)	1.00

ABIDE, Autism Brain Imaging Data Exchange; ASD, autism spectrum disorder; SDSU, San Diego State University.

Data preprocessing

Data were preprocessed and analyzed using AFNI (Cox, 1996) (afni.nimh.nih.gov) and FSL 5.0 (Smith et al., 2004) (www.fmrib.ox.ac.uk/fsl). The first 5 time points were discarded to allow for T1 equilibration. The remaining time series were motion, slice-time, and field-map corrected. Functional data were aligned to anatomical images using FLIRT with six degrees of freedom, resampled to 3.0 mm isotropic voxels using sinc interpolation, and standardized to the MNI152 template, using the FSL nonlinear registration tool, all in a single transformation step. Data were spatially blurred to a full-width at half-maximum of 6 mm. As traditional filtering approaches may cause rippling of motion confounds to neighboring time points (Carp, 2013), we used a second-order bandpass Butterworth filter (Power et al., 2013; Satterthwaite et al., 2013) to isolate low-frequency BOLD fluctuations (0.008 < f < 0.08 Hz) (Cordes et al., 2001). Average time series from trimmed white matter and ventricular compartments (from Freesurfer segmentation) as well as their derivatives were regressed from the data. All nuisance regressors (including motion regressors described below) were bandpass filtered using the same procedures as for BOLD time series (Hallquist et al., 2013). Data in the ABIDE and in-house validation sets were preprocessed in the same way except for regression of site, which was only applied to ABIDE data to control variability in multisite data sets (Power et al., 2014).

Head motion

Head motion was quantified as the Euclidean distance between consecutive time points. Motion regressors, including six rigid-body motion parameters and their derivatives, were removed from the time series. Time points with excessive head motion (root sum of squares ≥0.25 mm) were censored or “scrubbed” (Power et al., 2012), including one time point immediately preceding and following motion. Any time point that did not belong to a series of at least 10 consecutive time points remaining after censoring was discarded. Participants with fewer than 90% of time points or fewer than 150 total time points were excluded from the analysis. Runs were then truncated at the point where 150 usable time points were reached. Motion over the truncated run was summarized for each participant as the average Euclidean distance between time points (including censored segments) and was tightly matched between groups (p = 0.92).

Regions of interest and connectivity matrix

Our analysis implemented 220 of the 264 regions of interest (ROIs; each 10 mm spheres) from the meta-analysis of functional imaging studies by Power and colleagues (2011). Forty-four ROIs were excluded due to missing signal in two or more participants. For each participant, mean time courses of each ROI were extracted and a 220 × 220 connectivity matrix of Fisher-transformed Pearson correlation coefficients was generated. A 252 × 24,090 group-level data matrix was then generated with one row per participant and one column for each interregional connectivity. For interpretation of results, assignments of ROIs to functional networks were adopted from Power and colleagues (2011).

Data discretization and dimension reduction algorithm

Data discretization was necessary to minimize computational time. Correlation values of each feature (reflecting connections between ROIs) were sorted in descending order and segregated into 42 equally sized bins. Each value was then replaced by the median of its respective bin. This process limited the amount of possible correlation values and consequently reduced the number of possible splits to be considered when building binary trees. Overall, data discretization decreased computation time with only a minor loss in resolution.

We developed a CRF-based dimension reduction algorithm to increase computational efficiency, to eliminate noisy features, and to facilitate interpretation of results. The algorithm randomly partitioned the set of features into equally sized subsets and performed CRF, with 2001 trees on each subset. Each feature was evaluated for its conditional permutation importance, which reflects the impact of each predictor variable on the accuracy of the model (Strobl et al., 2008). A portion of the features with the highest conditional permutation importance values was retained and the process was repeated. In each run, initial dimension reductions produced many features that were discarded due to their negative variable importance measures. In subsequent dimension reductions, we retained between 50% and 80% of features, with higher retention rates in later iterations to mitigate the loss of informative features.

Beginning with the original discretized data set, we conducted this process three times to observe the effects of random partitioning. To ensure that our results would be reproducible, we used three unique seed numbers for the pseudorandom number generator in R. In run 3, dimension reduction was repeated until only 20 most informative features remained. This specifically served to examine the accuracy of an extremely simple classifier and for comparison with the recent study by Yahata and colleagues (2016).

Comparisons between CRF and RF

RF is an ensemble machine learning method often used for classification and regression analyses. RF grows many decision trees at training time with the aim to increase prediction accuracy via model averaging. The main principle behind the ensemble approach is to average many weak learners to form a strong classifier. In RF, training data are randomly drawn with replacement to construct binary decision trees and excluded data—termed out-of-bag (OOB) sample—are used for testing. As described by Breiman (2001), following Tibshirani (1996) and Wolpert and Macready (1997), OOB estimates can be used as an ingredient in the estimation of the generalization error. The OOB error estimate therefore removes the need for a set-aside test set (Breiman, 2001).

At each node, m variables are randomly selected for splitting, where m, for classification, is typically the square root of the total number of all predictors. This value remains fixed during the forest growing. After a forest is constructed, classifications are determined by majority vote in terminal nodes of each tree and then averaged over all trees in the forest. The percentage of votes for one class also represents the predicted probability. Subsequently, the OOB samples are run through the forest of binary decision trees and classifications are tallied. In the present study, we opted for 2001 trees to obtain reliable and unbiased OOB estimates. Misclassifications are averaged over all trees in the forest to assess the accuracy of the model via an OOB error rate. In addition, RF provides variable importance measures for feature selection. After training, features in the OOB sample are permuted and OOB errors are recomputed. The permutation importance is the average relative difference between OOB prediction accuracy before and after the permutation. Larger positive values of importance score signify greater importance.

It has been shown that RF variable importance becomes biased in the presence of highly correlated and continuous variables (Strobl et al., 2008), a concern likely to apply to fcMRI matrices. Consequently, it is important to distinguish between variables with conditional or marginal influences. A variable that appears marginally influential may be independent of the response when its conditional probability on another variable is considered. In other words, a variable that has no effect on its own but is correlated with a relevant predictor variable can receive a high importance score (Strobl et al., 2009). Two mechanisms are responsible for this bias: (1) a preference for the selection of correlated predictors in the tree building process and (2) the unconditional permutation scheme used to compute variable importance measures (Strobl et al., 2008).

CRF resolves these issues by using a conditional permutation scheme to measure variable importance. This approach more reliably reflects the impact of each predictor variable, compared to variable importance measures in RF. Our study used conditional variable importance to rank features after each dimension reduction, and ultimately to rank the final 20 features. Finally, classification trees were constructed without replacement to avoid the aforementioned bias and to promote accurate variable importance measures.

To examine the effects of reduced variable selection bias in CRF, we compared our results to those of the RF ASD classifier reported by Chen and colleagues (2015). Since we conducted three separate runs of our CRF dimension reduction algorithm, it was necessary to consolidate results before drawing comparisons. First, ROIs were categorized into functional brain networks based on Power and colleagues (2011) to improve the interpretability of the results. We then averaged the percentages of ROIs belonging to each brain network from the most accurate model in each run. This metric aimed to identify the brain networks most important in classifying ASD for each model, with percentages preferred to frequencies as the number of features varied across models.

The distribution of ROIs from Power and colleagues (2011) in each network is not uniform, and networks may be selected more frequently simply because they include more ROIs. We therefore further normalized the network percentages described above. We defined the normalized value as the percentage of selected ROIs belonging to a given network, divided by the percentage of the total ROIs belonging to that network. For example, if 10% of ROIs belonged to a given network before dimension reduction, and 16% of the ROIs afterward, the network would receive a normalized value of 1.6. Values above 1 imply that the network was favored by the dimension reduction process, while values below 1 imply that the network was disfavored.

Furthermore, we compared CRF to RF with regard to network-to-network connections selected as most informative by the respective classifier. For each model, we generated a matrix of values corresponding to the percentage of features connecting any two specific networks. The data for the CRF matrix were taken from the most accurate model (run 1, 400 features). Matrices were created for CRF and RF (from Chen et al., 2015), as well as for the differences between CRF and RF.

In addition, we mapped ROIs to anatomical locations for more anatomically specific comparisons between the models. For this comparison, we used the results from the CRF model that produced the overall highest accuracy. The most informative features for CRF were determined by conditional permutation importance measurements, while informative features in RF were determined by mean decrease in accuracy. A Circos connectogram (Krzywinski et al., 2009) was used for visualization of similarities and differences of most informative connections from each model.

There is tentative evidence suggesting that RF may be superior to CRF at the classification stage (Baayen, 2013), whereas CRF is preferable for feature selection. We therefore additionally performed classification with RF models, using the same feature sets resulting from CRF dimension reduction. This was done to compare classification accuracy between the methods and investigate the efficacy of using CRF for dimension reduction and RF for classification.

External and cross-validation of the CRF model

External validation gauges the generalizability of a model, testing whether features found most informative by CRF can be predictive of diagnostic status in an entirely novel data set. Breiman (1996) provides empirical evidence suggesting that the OOB estimate may be as accurate as using a test set of the same size as the training set, potentially eliminating the need for a set aside test set (Breiman 2001). Although bootstrapping in ensemble models is advantageous, it may not remove the necessity for confirmatory testing in independent samples, as suggested in a recent RF study using fMRI data by Ball and colleagues (2014).

Eleven different CRF models were trained using between 20 and 1254 features. The most accurate model using a specified number of features was selected for validation testing. For example, when examining models with 400 features, for which accuracy was 94% in run 1 and 92% in run 2, the model from run 1 was selected for validation. In addition, a model was trained with 100 features selected by RF dimension reduction (Chen et al., 2015). The external data set were drawn from a smaller sample of in-house data (Table 1).

Finally, we randomly partitioned the ABIDE data set into five separate bins, with four including 50 participants and one 52 participants (each bin including equal numbers of ASD and TD participants). We then created five data sets, each using four bins for training and the remaining bin for testing. We used the same dimension reduction algorithm on each training set as previously used with CRF. For the feature set selected based on a training set, we then ran RF classification on the corresponding testing set.

Results

Diagnostic prediction accuracies

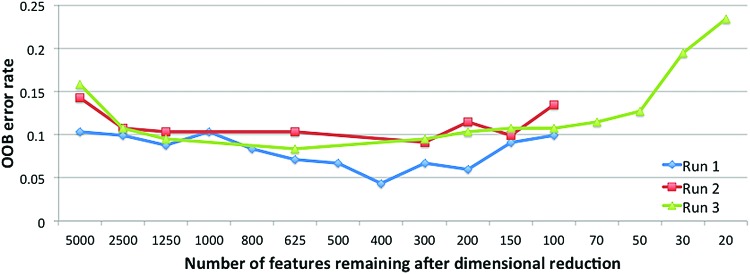
A series of CRF-based ASD classifiers was developed using progressively smaller numbers of features in each iteration of the dimension reduction algorithm. Depending on the seed used to initialize the pseudorandom number generator, peak diagnostic accuracy rates based on OOB error ranged from 91.7% to 95.6% for models with 308 to 627 features (Fig. 1). In further dimension reductions, accuracy plateaued around 90% and then decreased in models with fewer than 150 features. For run 3, dimension reduction was continued down to 20 features to explore accuracy of simpler models. Accuracy for this simple model was 77%.

FIG. 1.

OOB error rates were recorded after each dimension reduction. DR below 100 features was only continued in run 3, for exemplary purposes and comparison with Yahata and colleagues (2016). In all three runs, error rates decreased as the number of features was reduced. This trend was reversed when the models incorporated fewer than 200 features, suggesting that important diagnostic information is lost when models become oversimplified. The model that achieved the peak accuracy of 95.6% used 400 features. OOB, out-of-bag; DR, dimensional reduction. Color images available online at www.liebertpub.com/brain

Conditional variable importance measurements were taken at each dimension reduction step and their distributions are depicted in Supplementary Figure S1. The initial dimension reductions were skewed with the majority of features showing low variable importance. As the number of features was reduced, the distribution of variable importance shifted toward higher values.

Informative networks

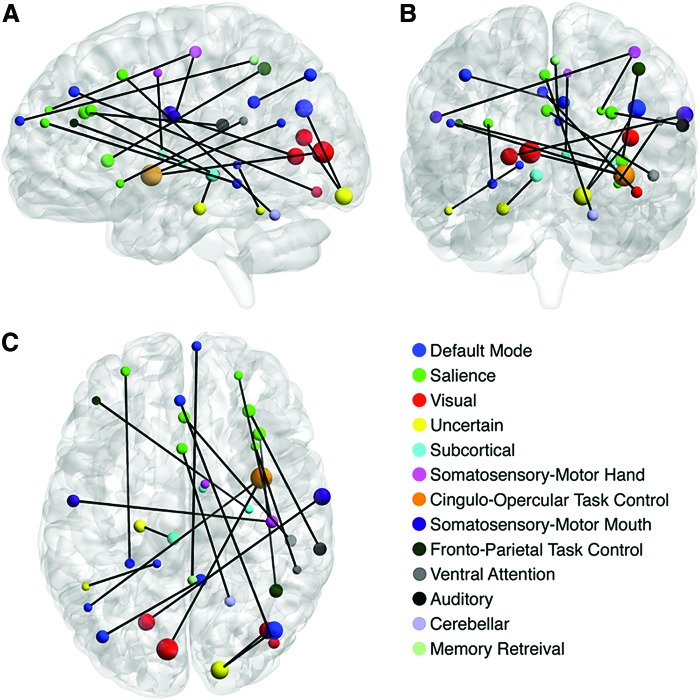
Based on frequency of ROI participation in features included in models that reached peak accuracy, the most informative features for diagnostic prediction were from the default mode, somatosensory-motor hand, visual, frontoparietal task control, and salience networks, with approximately 60% of selected features from these five brain networks (Supplementary Fig. S2A, C, E). After normalization [taking into account the variable number of ROIs per network among the total 24,090 connections adopted from Power et al. (2011)], a different pattern emerged. Prominent among most informative features were somatosensory-motor mouth and hand regions, as well as ROIs from ventral attention, salience, and cingulo-opercular task control networks (Supplementary Fig. S2B, D, F). Default mode, salience, and visual networks remained predominant in the simple model with only 20 features resulting from maximal dimension reduction in run 3 (Fig. 2).

FIG. 2.

Twenty most informative connections for predicting ASD (from maximal dimension reduction in run 3) in (A) sagittal, (B) coronal, and (C) axial views. The size of each node reflects the magnitude of conditional variable importance. Neural networks in the legend are sorted in descending order by frequency of occurrence. The majority of ROIs were selected from the default mode, salience, and visual networks. ASD, autism spectrum disorder; ROI, regions of interest. Color images available online at www.liebertpub.com/brain

As further shown in Supplementary Figures S2 and S3, changing the seed number for the pseudorandom number generator in R had no major effect on the pattern of results. The dimension reduction process was performed three times with different seeds, but error rates and the proportion of most informative networks selected remained largely consistent between runs.

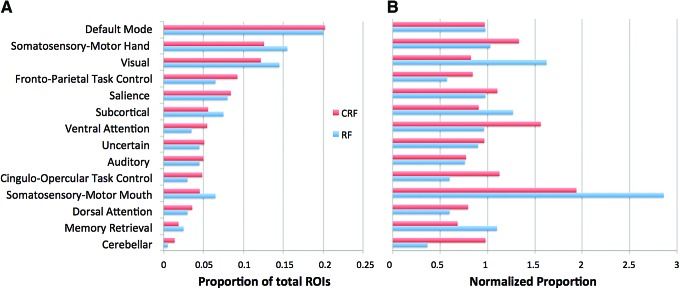
Comparisons between CRF and RF

Figure 3A shows how often a given network appeared among the most informative connections of the CRF models (averaged across all 3 runs), compared to RF. Before normalization, default mode, somatosensory-motor hand, and visual networks were predominant. After normalization (adjustment for variable number of ROIs per network across the entire 24,090 connections), the relative prominence of somatosensory-motor mouth and hand regions was highlighted (Fig. 3B). Although CRF findings were overall similar to RF findings, substantial differences (presumably due to reduced bias favoring correlated features in CRF) were also observed. The prominence of somatosensory-motor ROIs was reduced in CRF compared to RF for the mouth region, whereas it was increased for the hand region and for the ventral attention, frontoparietal task control, and cingulo-opercular task control networks. Cerebellar ROIs were also more prominent in CRF than in RF, but since the ROI scheme from Power and colleagues (2011) includes only three cerebellar ROIs, this difference must be viewed with caution.

FIG. 3.

ROI participation in most informative features, separated by network (from Power et al., 2011). CRF values are the average across all runs after dimension reduction resulted in peak accuracy (308, 400, and 627 features). RF values are taken from Chen and colleagues (2015) in a model containing 100 features. (A) Percentage of ROIs from each network. (B) Normalized percentages (adjusted for the variable numbers of ROIs per network among the total of 24,090 connections, before dimension reduction). CRF, conditional random forest. Color images available online at www.liebertpub.com/brain

We further compared CRF to RF at the level of network connections, again with respect to features remaining after the dimension reduction that resulted in peak accuracy. The heatmap in Figure 4A shows slight predominance of connections within the default mode network (DMN) and between DMN and frontoparietal task control, ventral attention, and visual networks. When compared to RF (Fig. 4B), the overall distribution of most informative features in CRF was relatively even across the network connection matrix. In particular, the findings suggest that the extremely informative value of connections between DMN and visual networks observed in RF may have been inflated by bias due to feature correlation, as also evident from Figure 4C, which shows the direct comparison between CRF and RF. Connections between these two networks comprised 13% of features in RF, but only 4.75% in CRF. Conversely, the informative value of connections between somatosensory-motor hand and visual networks detected by CRF (3.0%) remained undetected by RF (0.0%).

FIG. 4.

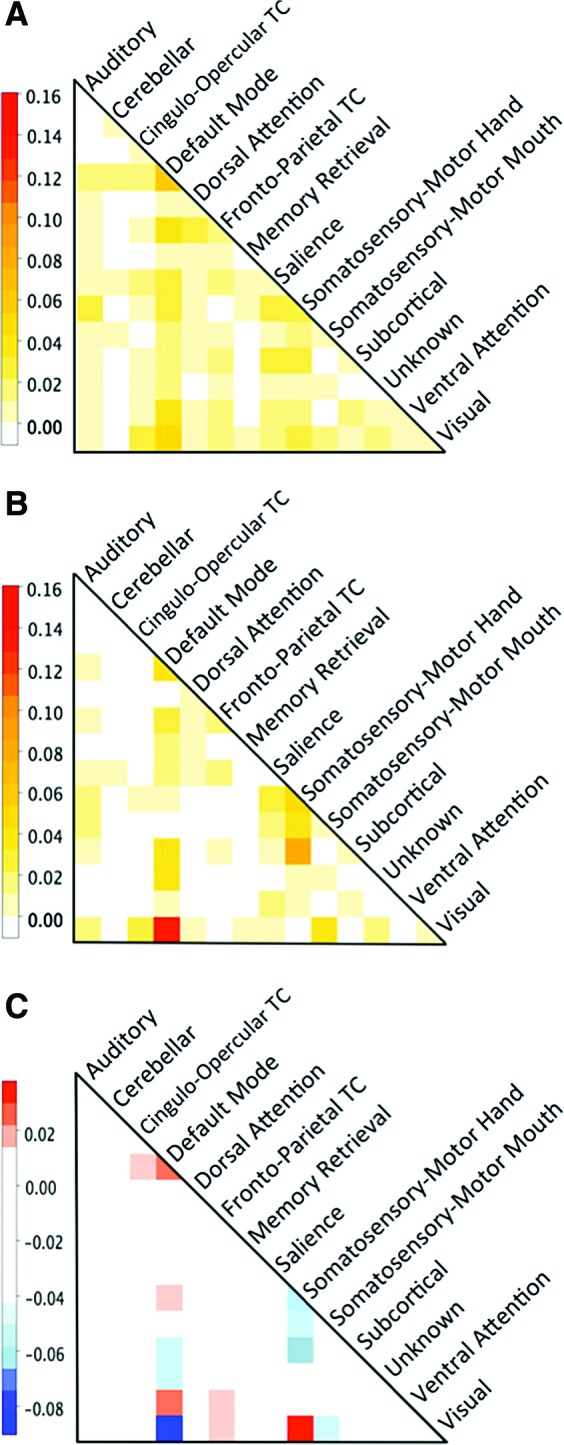
Heatmaps showing the proportion of brain network connections in (A) CRF model with 400 features and (B) RF model with 100 features. (C) Heatmap showing the difference between CRF and RF. Red values are positive and correspond to a connection favored by CRF. Blue values are negative and correspond to connections favored by RF. The largest difference in proportions (4.75% in CRF and 13% in RF, for a difference of −8.25%) between the two models occurred in default mode network to visual network connections. The CRF model favored visual to somatosensory-motor hand and default mode to ventral attention connections more than the RF model. TC, task control. Color images available online at www.liebertpub.com/brain

Substantial differences between CRF and RF were also observed when comparing findings at the level of unique ROI-to-ROI connections (rather than networks). Features from the most accurate model (run 1, 400 features) were sorted by their conditional variable importance and the top 100 were extracted for comparisons with RF. Among the top 100 features, only 32 connections were shared between CRF and RF. For comparison, the three CRF runs shared an average of 48 unique features (45–51) out of 100 when compared pairwise. Among the top 20 features from CRF (shown in Fig. 2), only 4 were shared with the top 20 from RF, again underscoring the effect of selection bias due to correlated features. Additional comparisons between CRF and RF results for 100 and 20 most informative features, sorted by anatomical location, are presented in Supplementary Figure S4.

We further tested whether RF may be preferable to CRF at the classification stage (Baayen, 2013). RF classification was indeed generally more accurate than CRF classification. RF achieved an average accuracy of 97.0%, compared to 92.7% for CRF. RF peak accuracy was 98.8%, in a model of 308 features (from CRF feature selection run 2).

External validation and cross-validation

For CRF, peak accuracy in the validation data set was 66.7%, achieved using a model of 200 features. Other diagnostic models that included 20–1254 features were also tested with the validation data set. Consistently, the specificity (TD accuracy rate) was much higher than sensitivity (ASD accuracy rate). Peak accuracy for RF was 70.8%, when using a model of 308 features. However, when all RF models were compared with their CRF counterparts, there was no consistent increase in classification accuracy. The RF model comprised of the features reported by Chen and colleagues (2015) yielded a classification accuracy of just 55.6%, further supporting the merit of CRF for dimension reduction. Detailed results of validation tests are listed in Supplementary Table S2.

Analyses splitting up the ABIDE data set into five bins (with one reserved for cross-validation) resulted in a mean accuracy of 65%, with peak accuracies per set ranging from 62% to 71% (Supplementary Table S3).

Discussion

Using whole-brain resting-state fcMRI data from large multisite cohorts and CRF, we were able to build classifiers for diagnostic prediction (ASD vs. TD) with >90% accuracy, peaking at 95.6% for one CRF classifier and at 98.8% for one RF classifier. CRF feature selection thus resulted in very high prediction accuracy compared to previous machine learning studies of ASD using fcMRI data (Abraham et al., 2017; Anderson et al., 2011; Kassraian-Fard et al., 2016; Nielsen et al., 2013; Uddin et al., 2013). Accuracy was also higher than in a previous study implementing RF feature selection in the identical data set (Chen et al., 2015). This suggests that reduced bias favoring correlated features (known to exist in fcMRI matrices) afforded by CRF feature selection improved results.

Many functional networks are informative, but somatosensory regions are prominent

Based on classifiers achieving peak accuracy in each of the three CRF runs, the percentage of informative features, including regions from default mode, somatosensory-motor hand, visual, frontoparietal task control, and salience networks, predominated. After normalization [adjusting for the highly variable numbers of ROIs included in different networks adopted from Power et al. (2011)], the somatosensory-motor mouth and ventral attention networks were particularly prominent. These patterns suggest that ASD, while diagnosed primarily with respect to sociocommunicative symptomatology, is characterized by neurofunctional features in many additional domains. Nonetheless, our findings are not unexpected, given evidence of atypical intrinsic functional connectivity of default mode (Doyle-Thomas et al., 2015; Jung et al., 2014), visual (Keown et al., 2013), and salience networks (Abbott et al., 2016; Odriozola et al., 2016), with additional findings of atypical activation from fMRI studies for frontoparietal task control (Just et al., 2007) and attention networks (Fitzgerald et al., 2015; Keehn et al., 2016).

The prominence of somatosensory-motor networks (both hand and mouth regions) was less expected from the available fcMRI literature on ASD. While for the hand region, connections involving pre- and postcentral gyri were informative at equal levels, this ratio was heavily tilted in favor of postcentral somatosensory cortex for the mouth region (with 89–96% of ROI participations among most informative features from this network, across the three CRF feature selection runs). There is indeed ample evidence of early-onset sensory anomalies in ASD (reviewed in Marco et al., 2011), which are so frequently observed as to warrant inclusion among most recent diagnostic criteria (American Psychiatric Association, 2013). These anomalies can also be observed in the somatosensory modality (Cascio et al., 2008; Puts et al., 2014; Riquelme et al., 2016). Recent magnetic resonance spectroscopy findings suggest that somatosensory impairments may be related to reduced bulk γ-aminobutyric acid (GABA) in the somatosensory cortex (Puts et al., 2017). A few fMRI (Cascio et al., 2012), magnetoencephalography (Khan et al., 2015), and diffusion tensor imaging (DTI) studies (Thompson et al., 2017) have also implicated somatosensory regions in ASD. Direct comparison of findings from the present study with those from Chen and colleagues (2015) in the same high-quality ABIDE subcohort suggests, however, that selection bias favoring correlated features may have inflated the informative role of the somatosensory hand region, whereas our three runs of CRF feature selection confirmed the relative importance of the somatosensory mouth region.

Best-performing classifiers include numerous features

In each CRF run, peak prediction accuracy was reached for models with over 300 features, with patterns optimally distinguishing ASD from TD cohorts, including connectivities across all forebrain lobes, subcortical structures, and cerebellum. This is in line with theoretical perspectives that view ASD as a disorder affecting multiple distributed brain networks (Menon, 2011; Müller, 2007; Wass, 2011). Given the breadth of empirical findings in the ASD neuroimaging literature, implicating large numbers of functional networks and brain loci (for reviews see Ismail et al., 2016; Philip et al., 2012; Vissers et al., 2012), it is expected that best-performing classifiers will be highly distributed, including features from as many networks and regions.

Our finding may appear to be inconsistent with some reports of relatively simple classifiers (with features from only a few networks and regions). Uddin and colleagues (2013) compared diagnostic prediction accuracy across multiple networks derived from independent component analysis and found that features from salience network alone achieved accuracy of 78–83%, with slightly lower accuracies >70% for primary visual and dorsal attention networks alone. Note that the sample sizes in this study were small (N = 70 for training and validation sets combined) and that the network scheme differed from the one used in the current study (Power et al., 2011).

More directly comparable to our investigation is a recent ASD study by Yahata and colleagues (2016) who reported 85% diagnostic prediction accuracy for a classifier of only 16 features. This classifier was dominated by features from the cingulo-opercular network, whereas our model of comparable simplicity (dimension reduction to 20 features) included mostly regions from default mode, salience, and visual networks (Fig. 2). This seeming discrepancy is easily explained. First, the classifier in Yahata and colleagues (2016) was trained exclusively on data from adults, whereas our samples were dominated by children and adolescents. Second, it is quite possible that the classifier (which used a different ROI scheme and was therefore not directly applicable to our analyses) would have reached accuracy levels similar to the relatively modest 75% reported by Yahata et al., if applied to an adult subsample from our selected high-quality ABIDE data set. Yahata and colleagues (2016) describe their classifier as “reliable” because it performed significantly above the chance level, but this criterion appears to set the bar for diagnostic classification rather low.

The reported accuracy of 85% in Yahata and colleagues (2016) was derived from leave-one out cross-validation (LOOCV) in the main sample (including 74 adults with ASD and 107 TD peers) and decreased to 75% when the classifier was applied to an external validation data set (N = 88 selected from ABIDE). The accuracy reached for the sample drawn from ABIDE was slightly higher than the 67–71% accuracy for the external validation set in the present study. Note that a high-quality (low-motion) external validation set was not available for the same age group in our study, which may account for relatively modest performance of the classifier (trained on a cohort aged 7–36 years, but validated against a cohort aged 8–18 years). Other implications will be discussed in the following sections.

The bogeymen of machine learning: Why are we obsessed with overfitting and external validation?

Our analyses and the discussion above relied to some extent on traditional doctrines of machine learning: to avoid overfitting to a training data set and to develop a classifier that will optimally perform in an external validation set. However, as sound as these principles may be from the methodological perspective, they ignore crucial challenges when viewed under the neurobiological lens. This also applies to the “peeking problem” (Kassraian-Fard et al., 2016), which occurs when feature selection is performed on an entire data set (including data used for validation).

The goal of optimal external validation requires that training and validation sets be matched. This may sound like a simple step, but it is actually an almost impossible one. Matching on easily available variables (e.g., age, sex, nonverbal IQ, diagnostic scores) will not suffice because it is likely that many other factors that are hard or impossible to match quantitatively (e.g., history of environmental interactions, interventions) will significantly affect the brain, either via neurotypical plasticity or disorder-specific mechanisms (Kolb and Gibb, 2014). Even if this hurdle could be taken with extensive effort, an even more intractable one will remain. A decade after the call “to give up on a single explanation for autism” (Happé et al., 2006), the field today agrees on the probable multitude of etiological variants (Betancur, 2011; Geschwind and State, 2015). However, the variants of idiopathic ASD are not known, and the growing evidence of many hundreds of somehow implicated genes and probably numerous additional epigenetic and environmental risk factors (Grayson and Guidotti, 2016; Hallmayer et al., 2011) suggests that they may not be well understood for years to come. This implies that on principle, training and validation data sets cannot be matched on one fundamentally important variable (etiological variant of ASD). It is therefore unrealistic to expect classifiers to perform optimally, especially in small validation data sets (where chance variations in subtype composition will have large effects on the accuracy of the classifier).

The relatively modest performance of our CRF and RF models in an external validation set of in-house data is thus not surprising. It contrasts with the very high accuracies up to 98.8% reached in the training data set. Our CRF approach avoided overfitting by numerous random divisions of the large data set into training and “out-of-bag” sets (each including about one-third of the data). However, the ubiquitous question about overfitting to a data set at hand misses a fundamental question related to the neurobiology of ASD.

There can be no perfect classifier for an imperfect construct

As already noted, there is consensus that the clinical construct of “autism spectrum disorder” probably applies to many etiologies. While these by definition [as per the diagnostic criteria of the DSM (American Psychiatric Association, 2013)] partially converge onto a common set of behavioral symptoms (mostly in the sociocommunicative domain), it is very likely that they differ heavily with respect to the underlying neurodevelopmental disturbances. To expect that children or adults who share a few diagnostic features would also share a specific set of anomalous connectivities is therefore unrealistic.

The very high accuracy reached with our CRF and RF classifiers needs to be considered on this background. What do the 308 features that resulted in an almost perfect OOB accuracy of 98.8% mean? Quite certainly, they do not imply that autistic symptomatology directly relates to each of these 308 functional connectivities, nor that every person with ASD will show some anomaly in each of these features. This was shown by the much lower accuracy in our external validation set. However, even within the large ABIDE sample, such uniform patterns of atypical connectivity cannot be expected, given etiological heterogeneity. Instead, the classifier can be interpreted as a set of features that in combination capture a large number of ASD variants, with each feature being affected in a subset of individuals, but possibly uninformative in others. The large number of informative features in the cohort classifier therefore does not necessarily imply equal complexity at the single-subject level, meaning that the set of distinctly anomalous functional connectivities in any given ASD participant may be much smaller.

Viewed from this perspective, it is possible that functional connectivity matrices carry some information about etiological variants of ASD. Although beyond the scope of the current study, unsupervised machine learning or other data-driven approaches may help identify variants of the disorder characterized by functional connectivity or other brain features that can be replicated across cohorts. However, a catalog of such variants may require much richer data (including genome, environmental risk factors, behavioral data, and multimodal brain imaging, ideally with history through longitudinal sampling), which are currently not available in large samples. Each of these variants may in turn lend itself to mechanistic etiological models and precision medicine, which are the ultimate goals of ASD research.

Limitations

Data included in our study were almost exclusively from high-functioning participants because fMRI data with minimal motion can rarely be acquired in lower functioning people with ASD. Findings may thus not generalize to the entire functional spectrum of ASD. We also did not include data from other developmental disorders and were therefore not able to directly test the specificity of atypical connectivities identified by CRF.

Conclusions

Combining CRF feature selection and RF classification, we achieved almost perfect diagnostic prediction accuracy in a large sample of children and young adults with ASD for models with >300 features. These models can be considered relatively accurate characterizations of the cohorts at hand, revealing patterns that may remain undetected in conventional statistics. However, they do not readily generalize to the population at large and to external validation sets (for which more modest accuracies were reached) because training and validation sets cannot be matched on crucial etiological variables. Furthermore, the large number of features in highest performing models probably reflects the multitude of etiological variants subsumed under the clinical label of ASD.

Acknowledgments

This study was supported by the National Institutes of Health R01 MH081023, R01 MH101173, and K01 MH097972 (PI: Inna Fishman). The authors thank the children and their parents who participated in the in-house study.

Author Disclosure Statement

None of the authors report any commercial associations that may create a conflict of interest.