Connectome-scale Functional Intrinsic Connectivity Networks in Macaques

Abstract

There have been extensive studies of intrinsic connectivity networks (ICNs) in the human brains using resting state fMRI in the literature. However, the functional organization of ICNs in macaque brains has been less explored so far, despite growing interests in the field. In this work, we propose a computational framework to identify connectome-scale group-wise consistent ICNs in macaques via sparse representation of whole-brain resting state fMRI data. Experimental results demonstrate that 70 group-wise consistent ICNs are successfully identified in macaque brains via the proposed framework. These 70 ICNs are interpreted based on two publicly available parcellation maps of macaque brains and our work significantly expand currently known macaque ICNs already reported in the literature. In general, this set of connectome-scale group-wise consistent ICNs can potentially benefit a variety of studies in the neuroscience and brain mapping fields, and they provide a foundation to better understand brain evolution in the future.

Introduction

We have witnessed extensive studies of functional networks, e.g., intrinsic connectivity networks (ICNs), in the human brains using resting state fMRI in the literature in the past decade (e.g., Fox et al. 2005; Greicius, et al. 2003; Damoiseaux, et al. 2006). Inspired by the great successes of fMRI in human brains, there has been growing interest to discover the functional organization of brain networks in macaque monkey based on fMRI due to at least three reasons (Vanduffel et al., 2014; Hutchison and Everling, 2012; Babapoor-Farrokhran et al., 2013; Hutchison et al., 2011a; Hutchison et al., 2011b; Hutchison et al., 2013; Maniti et al., 2007; Maniti et al., 2013; Margulies et al., 2009; Teichert et al., 2010). First, fMRI in the macaque monkey brain is a translational way to bridge the gap between human brain fMRI and invasive nonhuman primate studies in order to better understand the neuronal underpinnings of fMRI-derived BOLD signals; second, the identified functional networks based on fMRI in macaque monkey could guide the precise electrophysiological recordings in those networks for further investigation of cellular-scale properties of functional brain networks; third, fMRI data in macaque monkeys can provide invaluable insights for brain function and brain evolution studies (Vanduffel et al., 2014). Since the early applications of fMRI in nonhuman primate brain in 1998 (Dubowitz et al., 1998; Vanduffel et al., 2014), remarkable successes have been achieved in functional network analysis in monkeys. For example, the topographic organization and parcellation of visual cortex, and the mapping of the category-selective (e.g., faces, bodies, or places) regions, have been extensively investigated using fMRI (e.g., Arsenault et al., 2013; Brewer et al., 2002; Durand et al. 2007; Fize et al., 2003; Fogassi et al., 2005; Haxby et al., 2001; Janssen et al., 2000; Kolster et al., 2009; Ku et al., 2011; Smirnakis et al., 2005; Stefanacci et al., 1998; Vanduffel et al., 2001; Vincent et al., 2010). Moreover, the functional properties of parietal and frontal monkey cortices have been studied using fMRI during visual, motor, oculomotor, and cognitive tasks (e.g., Vanduffel et al., 2014; Guipponi et al., 2013; Baker et al., 2006; Nelissen et al., 2005; Nelissen and Vanduffel, 2011; Miyamoto et al., 2013; Nakahara et al., 2002; Wardak et al., 2010).

Meanwhile, considering that it can be time-consuming to train monkeys to fixate or perform specific tasks for fMRI experiments, identification of ICNs (i.e., resting state networks) based on fMRI in anesthetized or resting monkeys has received increasing interest (e.g., Vanduffel et al., 2014; Hutchison and Everling, 2012; Babapoor-Farrokhran et al., 2013; Hutchison et al., 2011a; Hutchison et al., 2011b; Hutchison et al., 2013; Maniti et al., 2007; Maniti et al., 2013; Margulies et al., 2009; Teichert et al., 2010). For example, Vincent et al., 2007 reported the intrinsic connectivity patterns within the well-known default mode network (DMN) and three other major systems (visual, somatosensory and oculomotor) in anesthetized monkeys. Another study compared the ICNs between monkeys and humans and reported nine common ICNs, including dorsal and ventral attention networks and the language network (Maniti et al., 2013). In a recent research report our group at Emory University, in collaboration with University of North Carolina, developed infant macaque monkey brain atlases to analyze postnatal brain development through 12 months (Shi et al., 2017). Although significant achievements have been obtained and reported in functional network identification in monkey brains based on fMRI, a possible limitation is that previous studies focused on the identification and functional properties of specific networks or regions (e.g., DMN, visual, attention, etc.), while the connectome-scale functional networks that are group-wise consistent across individual monkey brains are largely unknown.

As an attempt to address the abovementioned limitation and inspired by the success of our recent HAFNI (holistic atlases of functional networks and interactions) computational framework (Lv et al., 2015a, 2015b) in identification of consistent and concurrent connectome-scale functional networks in human brains, in this paper, we adopt the HAFNI methods on resting state fMRI data of macaque monkey brains to identify connectome-scale group-wise consistent ICNs. The basic idea of HAFNI is to aggregate dozens of thousands of rsfMRI signals within the whole brain of one subject into a big data matrix, and to decompose the data matrix into a dictionary matrix and a sparse coefficient matrix using the effective online dictionary learning algorithm (Mairal et al., 2010). A major difference between the dictionary learning/sparse representation approach and other matrix decomposition approaches (e.g., independent component analysis or ICA) is that ICA uses statistical independency of fMRI temporal patterns among different functional components as prior (Calhoun et al., 2009), while dictionary learning/sparse representation uses sparsity as prior (Mairal et al., 2010). Specifically, each column of the learned dictionary represents the temporal pattern of a functional network and the corresponding row of sparse coefficient matrix represents the spatial pattern of a functional network (Lv et al., 2015a, 2015b). By applying effective clustering methods on the functional networks’ spatial patterns of all subjects and age groups, those group-wise consistent functional networks are obtained. The major contributions of this work are two-fold. First, as far as we know, it is one of the early studies to identify the connectome-scale concurrent ICNs in macaques instead of focusing on specific networks, thus providing a holistic map of functional networks in macaque brains; second, we proposed a data-driven computational framework to identify connectome-scale ICNs that are consistent across different subjects and various age groups. In this paper, we concentrate on the identification for the common ICNs based on longitudinal rsfMRI signal obtained from macaque brain; we will discuss the potential developmental trajectories of connectome-scale group-wise consistent ICNs in future work. Currently, those identified connectome-scale group-wise consistent ICNs potentially provide a foundation for a variety of studies in the neuroscience and brain mapping fields in the future.

Experimental procedures

Our framework for identification of connectome-scale group-wise consistent ICNs in macaques includes three major steps (marked as 1–3 in Fig. 1): (1) identification of connectome-scale ICNs of each individual subject via dictionary learning and sparse representation of whole-brain rsfMRI data (Section ‘Identification of Connectome-scale ICNs within Individual Subject’), representation of the spatial pattern of each ICN via the ‘connectivity map’ model (Section ‘Representation of Spatial Pattern of ICN via Connectivity Map’), and identification of connectome-scale group-wise consistent ICNs across all subjects (Section ‘Identification of Connectome-scale Group-wise Consistent ICNs across Different Subjects and Scans’). The materials and methods section is organized by following the three major steps, respectively.

Fig. 1.

The pipeline of the proposed computational framework for identification of connectome-scale group-wise consistent ICNs in macaques. The three major steps are labeled as 1–3, respectively.

Data Acquisition and Preprocessing

The subjects used in this study were rhesus monkeys (Macaca mulatta) living in the breeding colony maintained at the Yerkes National Primate Research Center (YNPRC), Emory University (Lawrenceville, Georgia). A total of 10 subjects with longitudinal resting state fMRI (rsfMRI) scans collected during infancy and the juvenile period were used in this study (scans available at four different ages: 3-months: 10 subjects; 6-months: 10 subjects; 12-months: 8 subjects; 18-months: 5 subjects). The subjects represent typically developing, socially-housed rhesus monkeys, studied longitudinally as part of a larger study (Howell et al, 2016; McCormack et al, 2015). They were raised with their mothers and families for the entire duration of the study in large social groups and they span all social hierarchy strata (high, medium and low ranking families). Standard high fiber, low fat monkey chow and seasonal fruits and vegetables were provided twice daily, in parallel to enrichment items. Water was available ad libitum. All studies were performed in accordance with the Animal Welfare Act and the U.S. Department of Health and Human Services “Guide for the Care and Use of Laboratory Animals”, and approved by the Emory University Institutional Animal Care and Use Committee (IACUC).

Images were acquired on a 3T Siemens Trio scanner (Malvern, PA) at the Yerkes National Primate Research Center’s (YNPRC) Imaging Center using an 8-channel array, transmit and receive knee volume coil. The subjects were scanned supine under isoflurane anesthesia (standardized to the lowest possible - 0.8–1% isoflurane, inhalation- to minimize effects on functional connectivity). A custom-made head holder with ear bars and a mouth piece was used to secure and prevent movement of the head in order to avoid motion artifacts. Animals were intubated, administered dextrose/NaCl (I.V.) for hydration, placed over an MRI-compatible heating pad to maintain temperature and physiological measures monitored during the scans. After each subject was scanned and had completely recovered from anesthesia, it was returned to its mother, and mother-infant dyad returned to their social group.

The rsfMRI imaging was done using an echo planar imaging (EPI) sequence (repetition time (TR)=2060 msec, echo time (TE)=25 msec, and resolution/voxel size= 1.5×1.5×1.5 mm³, matrix is 85×104×65), and it included 2x15 min scans, with the total volume number (time points) of 400 per scan. The preprocessing of rsfMRI data includes skull removal, motion correction, slice timing correction, spatial smoothing, temporal pre-whitening, global drift removal, and band-pass filtering, which are similar as those in (Mantini et al., 2011) by using both publicly available FSL toolkit (http://fsl.fmrib.ox.ac.uk) and in-house tools (Li et al., 2016). Particularly, the INIA19 macaque brain atlas (Rohlfing et al., 2012) was adopted as the template space as an anatomic reference and all derived functional networks using the proposed computational framework in each individual fMRI space were aligned to the template space via linear registration (using FSL-FLIRT) for the identification of group-wise consistent functional networks among all of the available rsfMRI scans across different subjects and their multiple ages. That is, longitudinal rsfMRI scans were considered as separate data points and used independently to derive consistent ICNs. In our study, we adopted each individual macaque brain’ mask constructed by each individual’s mean functional image to extract the resting-state fMRI signals. The original matrix is 85×104×65, and the total number of macaque brain mask voxels is approximately from 34,000 to 45,000.

Identification of Connectome-scale ICNs within Individual Subject

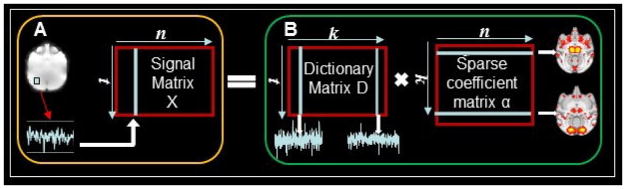
We identify the connectome-scale ICNs of each individual subject using our recent HAFNI approach (Lv et al., 2015a, 2015b) via dictionary learning and sparse representation of whole-brain rsfMRI data of each subject. Dictionary learning and sparse representation techniques have been successfully applied for brain fMRI time series analysis and functional brain network identification (e.g., Oikonomou et al., 2012; Abolghasemi et al., 2013; Zhao S et al., 2015; Zhang S et al., 2015; Jiang et al., 2014; Jiang et al., 2015a; Jiang et al., 2015b; Lv et al., 2015a; Lv et al., 2015b; Lv et al., 2015c; Makkie et al., 2015). In this work, the computational framework of identification of connectome-scale ICNs in each individual subject via dictionary learning and sparse representation is illustrated in Fig. 2. For each brain, first, we extract the rsfMRI signals of whole-brain voxels. After normalizing to zero mean and standard deviation of 1 (Lv et al., 2015a; Lv et al., 2015b), all normalized rsfMRI signals are aggregated into a big 2D signal matrix X ∈ R^t×n containing n rsfMRI signals of n voxels (Fig. 2A). Each rsfMRI signal has t time points. Then, X is decomposed into an over-complete dictionary matrix D ∈ R^t×k and a sparse coefficient matrix α ∈ R^k×n (Fig. 2B) (k is the dictionary atom number) so that X = D × α by applying the widely used effective online dictionary learning approach (Mairal et al., 2010). The vital concept for dictionary learning and sparse representation adopted in our paper is to decompose the input signal matrix X into D and α. Each element of X represents the measured functional activity of a brain voxel, and the element of D is the atom of dictionary. Here, each element of α represents the functional activity value for the certain identified spatial map of the brain, shown as the sparse coefficient matrix in Fig. 2B. Each column of D is a dictionary atom representing the temporal pattern of a ICN and the corresponding row of α can be mapped back to brain volume to obtain the spatial pattern of the ICN (Fig. 2B). In short, the proposed dictionary learning and sparse representation framework not only represents the whole-brain rsfMRI signals of one subject accurately and compactly, but also generates connectome-scale ICN patterns (the total number is k) whose temporal and spatial patterns can be assessed and interpreted in the neuroanatomic context.

Fig. 2.

The computational framework of identification of connectome-scale ICNs in each individual subject via dictionary learning and sparse representation of whole-brain rsfMRI signals. (a) The aggregated signal matrix X based on whole-brain rsfMRI signals of one subject. n is the number of voxels within the whole-brain and t is the rsfMRI time points. (b) The learned dictionary matrix D and sparse coefficient matrix α via sparse representation of X. Each column of D is a dictionary atom representing the temporal pattern of a ICN and corresponding row of α can be mapped back to brain volume to obtain the spatial pattern of the ICN. Each element of α is the functional activity value. k is the dictionary atom number.

To be self-contained, we briefly introduce the details of the dictionary learning and sparse representation framework to learn D and α. Since we aim to learn an over-complete dictionary matrix D ∈ R^t×k of which k>t and k≪n (Mairal et al., 2010), we define the empirical cost function f_n(D) of X considering the averaged loss of regression of all n rsfMRI signals as follows:

$$f_n(\mathbf{D})=\frac{1}{n}\sum _{i=1}^n\ell ({\mathbf{x}}_i,\mathbf{D})$$ (1)

where x_i is i-th rsfMRI signal. ℓ (x_i,D) is the loss function and defined as the optimal value of sparse representation:

$$\ell ({\mathbf{x}}_i,\mathbf{D})=min\frac{1}{2}{\Vert {\mathbf{x}}_i-\mathbf{D}{\mathbf{\alpha }}_i\Vert }_2^2+\lambda {\Vert {\mathbf{\alpha }}_i\Vert }_1$$ (2)

where α_i is i-th column of α. l₁-regularization is adopted to obtain a sparse solution of α. λ is used for adjustment of the trade-off between regression residual and sparsity. We adopt the publicly available online dictionary learning package (Mairal et al., 2010) to solve Eq. (2) to learn D. The basic idea is to alternate and minimize D and α over one while keeping the other one fixed to convert the problem to a convex optimization problem (Mairal et al., 2010). Because the sparse dictionary learning problem is a non-convex problem, we need to search the optimal solution both for dictionary D and coefficient matrix α at the same time. It is a very difficult issue to solve any kind of non-convex optimization problem in an effort to search the global optima. An efficient way to solve non-convex optimization problem is the alternative optimization which indicates one parameter such as dictionary D is fixed when α can be updated. This technique can convert a non-convex problem to a convex problem which can guarantee the solution is the global optima. The order of this alternation is depending on the method. For online dictionary learning method adopted in our paper, the D is trained at first, and then the α will be trained. The initialization for D and α is random, which is a popular technique for current numerical optimization algorithm (Mairal et al., 2010). Once D is learned and fixed, α is obtained by solving the l₁-regularized linear least-squares problem based on D (Mairal et al., 2010). Since we have demonstrated in (Lv et al., 2015a, 2015b) that there is not significant change in the obtained functional networks with the alteration of dictionary atom number k and parameter λ within a specific range.

For tuning the parameter dictionary atom number k and tradeoff λ, we employ two methods for the estimation of k and λ. At first, a rank estimation technique is adopted to estimate the number of dictionary atoms (Shen et al., 2014; Wen et al., 2012). An ideal estimation for the rank of X (input fMRI signal matrix), if denoted by k, is crucial to the success of the dictionary learning model in Eq. (2). Here we briefly introduce a rank estimation strategy proposed in (Shen et al., 2014), which adopts the strategy of rank-revealing by using QR factorization. In the beginning, we initialize the relatively large estimation k^* so that k^*≥ k and monitor the diagonal line of the upper-triangular matrix in the QR factorization of BV^T. We let QR = (BV^T)E be the economy-size QR factorization of D in Eq. (2) with permutation matrix E so that the diagonal matrix R is non-increasing in magnitude. By examining the diagonal elements of R, we search a large reduction in magnitude closing to zero which is the key technique for a rank estimation. It should be clear that if the iteration converges to a well-conditioned low-rank solution, and then QR factorization and rank-revealing will eventually provide a correct solution that a proper thresholding value is used in Eq. (6) for detecting the reduction in magnitude. Specifically, by detecting the diagonal line of R we compute two vectors ∈ ∈ R^k and r ∈ R^k−1:

$$\begin{gathered} d_i=\mid R_{ii}\mid \\ {r}_i=\frac{d_i}{d_{i+1}} \end{gathered}$$ (3)

and then examine the value:

$$\tau =\frac{(k-1)r(p)}{{\displaystyle \sum _{i\ne p}}{r}_i}$$ (4)

where r(p) is the maximum element of the vector r (with the largest index p if the maximum value is not unique). In the current implementation, we reset the rank estimate k top once τ > 2, and this adjustment can be successfully done only once. This efficient heuristic strategy appears to work well where the correct drops could usually be detected after a few iterations.

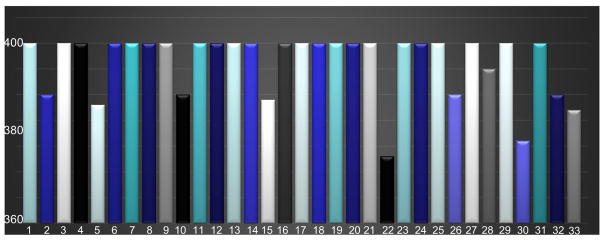
As discussed before, by using the default parameters in this rank estimation technique, we estimate the rank of each individual signal matrix X in Eq. (2) of each macaque brain. Since the dimension of X is about 400×32000; the initial estimated rank k^* is set as 400; Fig. 3 below shows the variance of the estimated rank k:

Fig. 3.

Illustration of statistical rank estimation for each individual resting-state fMRI signal matrix. As mentioned in Section 2.1, the total number of scans is 33. By using the rank estimation technique (Shen et al., 2014; Wen et al., 2012), the final rank estimation for most individuals is equal or very close to 400; only one rank estimation is 378 (less than 400). The statistical results of rank estimation indicate that the number of dictionary atom 400 is reasonable.

Moreover, empirically setting the same k=400 should be reasonable and our previous empirical experiments have also demonstrated that k=400 should be well justified (Lv et al., 2015a, 2015b). For the estimation of the tradeoff parameter λ, when λ → ∞, the Eq. (2) becomes an unconstrained optimization problem. Intuitively, there must exist λ_max (the maximal value for λ). We can follow the theorem and strategy proposed in (Liu et al., 2010).

The theorem in (Liu et al., 2010) is: we have the reformulated equivalent min-max problem for Eq. (2),

$$\underset{X\in R^n}{min}\underset{{\Vert Z\Vert }_{\infty }\le \lambda }{max}L(X,\mathbf{D},\alpha ,Z)=\frac{1}{2}{\Vert X-D\alpha \Vert }^2+\lambda \langle S\alpha ,Z\rangle$$ (5)

The linear system is:

$$S{S}^{T}Z=SX$$ (6)

Eq. (6) has a unique solution, denoted by Ẑ. Let

$${\lambda }_{\mathit{max}}={\Vert \widehat{Z}\Vert }_{\infty }$$ (7)

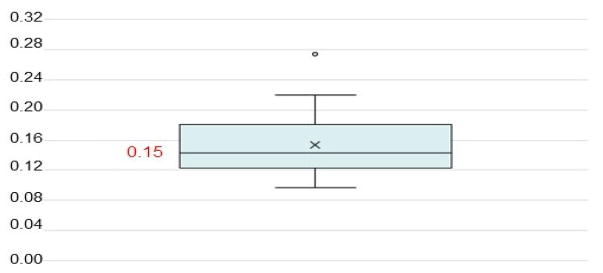
By using the Rose algorithm proposed in (Liu et al., 2010), and let SS^T be the Hessian matrix, we can estimate the maximal value for λ. An attenuation sequence in (Liu et al., 2010) as [10⁻³,10⁻²,10⁻¹] is adopted to obtain the value of λ, and λ = 10⁻³ × λ_max, since 10⁻³ can guarantee the fastest convergence velocity based on the extensive numerical experiments (Liu et al., 2010). In Fig. 4, we show all the values of λ calculated by the theorem and Rose algorithm statistically:

Fig. 4.

Illustration of the statistical analysis on the calculation of parameter λ. By using the theorem, Rose algorithm and attenuation value (Liu et al., 2010), the calculated value of λ is varied from 0.12 to 0.28. And most values of λ are close to 0.15. To avoid the heterogeneity caused by different values of λ, 0.15 can be utilized as the tradeoff parameter in our study to perform dictionary learning and sparse representation.

Representation of Spatial Pattern of ICN via Connectivity Map

We align all of the identified connectome-scale ICN spatial patterns within each individual subject to a common template space (the INIA19 macaque brain atlas (Rohlfing et al., 2012) was adopted in this study) via linear registration using FSL-FLIRT for the identification of group-wise consistent ICNs across different subjects. As shown in Fig. 2b as a schematic illustration, the spatial pattern of an ICN in brain volume is high-dimensional, i.e., a hundred of thousands of dimensional vectors which mean that the vector contains hundreds of thousands of elements (brain voxels) if we reshape all n voxels in the whole brain to one vector. Moreover, there are small noisy regions besides the major network pattern in the ICN which might affect the comparison across different ICNs. In order to represent the spatial pattern of ICN compactly and effectively and to alleviate the effect of the small noisy regions in the ICN, we adopt an “effective ‘connectivity map’ model” (Zhao et al., 2016) to represent the spatial pattern of ICN. Since the individual spatial map identified by dictionary learning and sparse representation contains the noise which can influence the performance of clustering for the individual spatial maps. In our prior research work (Zhao, Y. et al., 2016), the experiments have already demonstrated the alleviation for noisy regions can enhance the performance of construction of group-wised spatial maps.

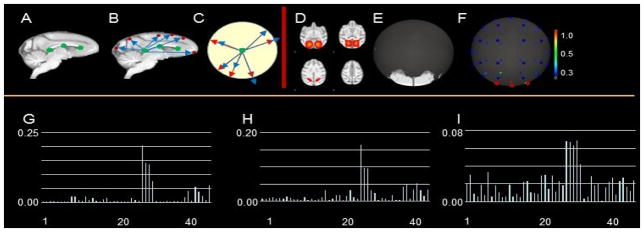
At the conceptual level, the ‘connectivity map’ model converts the spatial pattern of volumetric voxels to the projected points on a unit sphere, and generates a numerical vector via sampling the distribution of projected points on the unit sphere to describe the distribution pattern of the spatial pattern of ICN. This idea is inspired by our previous work on descriptor of fiber bundle shapes (Chen et al., 2013; Zhu et al., 2012). An illustration example of connectivity map is shown in Fig. 5. Specifically, first, we select the same three projection center voxels (green points in Fig. 5A) along the corpus callosum of INIA19 template image for all ICN patterns across all subjects (Zhao et al., 2016). The rationale is that we select the projection center in the relatively stable and identical white matter regions (corpus callosum) to reduce the potential inaccuracy of ‘connectivity map’ representation caused by individual variability and to avoid the situation that the projection center locates within the spatial pattern of a specific ICN. We select three different projection centers instead of one to increase the description power of ‘connectivity map’ so that different ICN spatial patterns will have different ‘connectivity map’ representations. Furthermore, our prior research works (Chen, et al., 2013; Zhu et al., 2012; Zhao, et al., 2016) demonstrated that the selected 3 points are qualified to provide the good projection, and adding more points will not improve the performance of projection substantially but increasing the computational complexity. In our investigation, each individual ICN spatial pattern has a connectivity map. For example, 400 individual ICN spatial patterns will generate 400 connectivity maps. Second, for each of the three projection centers, we calculate the vectors (blue arrows in Fig. 5B) from the projection center to each of the voxel involved in one ICN spatial pattern (red points in Fig. 5B). The vectors are normalized so that each normalized vector (red arrows in Fig.5C) is represented by a point on the unit sphere:

$$W=\{(i_j,\overrightarrow{u_j})\mid \overrightarrow{u_j}=(\overrightarrow{v_j}-\overrightarrow{v_0})/\mid \overrightarrow{v_j}-\overrightarrow{v_0}\mid ,j\in V\}$$ (8)

where W is a set of projected points on the unit sphere. v_j and v₀ are the coordinates of j-th voxel involved in one ICN spatial pattern and the projection center, respectively. V is a set of all voxels involved in one ICN spatial pattern. i_j is the functional activity value of j-th voxel. Third, we segment the sphere into 48 quasi-equal sized regions (Chen et al., 2013; Gorski et al., 2005) (the center points of each of 48 regions are represented as blue points in Fig. 5F). As mentioned before, for the reduction of high dimensional individual spatial pattern, each spatial pattern will be projected on 48 quasi-equal sized regions of a unit sphere. Specifically, the sphere is subdivided into 48 equal sized pixels as defined by construction with the Hierarchical Equal Area, iso-Latitude Pixelisation (HEALPix) of the sphere, which demonstrates that HEALPix is built geometrically as a self-similar, refinable quadrilateral mesh on the sphere (Gorski et al., 2005; Chen et al., 2012). The details of quasi-equal sized regions can be viewed in Fig. 4 in (Gorski et al., 2005). The functional activity values of all projected points within each of the 48 regions are accumulated and normalized:

$$P_m=\sum _{j\in W\cap R_m}{i}_j/\sum _{j\in W}{i}_j(m=1,\mathrm{..},48)$$ (9)

where P_m is the normalized density of functional activity values in m-th region. R_m is the area of m-th region. P = [P₁, P₂, ···, P₄₈] is a 48-dimensional vector (Fig. 5G) representing the ‘connectivity map’ of the volumetric spatial pattern of one ICN. The ‘connectivity map’ representation significantly reduces the dimension of spatial pattern of ICN and is less sensitive to those small noise regions in a meaningful network (Zhao et al., 2016). Moreover, these 48 points are good enough to convert a spatial pattern into a connectivity map. Since the connectivity map only concentrates on reduction of high dimensionality of individual spatial pattern rather than analyzing the brain cortical structural information, previous research works (Chen et al., 2013; Zhao et al., 2016; Zhu et al., 2012; Zhu et al., 2013) demonstrate that more points (>48) will further increase the computational complexity, are time-consuming, and will not provide better projection model.

Fig. 5.

Illustration of the ‘connectivity map’ for representation of spatial pattern of ICN. (A) 3 selected projection centers (green points) along the corpus callosum of INIA19 template image for all ICN patterns across all subjects; (B) 2-D spatial map. The red dots represent the activated areas; (C) projection of spatial map (B) to a unit circle; (D) an example of identified spatial map; (E) projection of spatial map in (C) to unit sphere; (F) connectivity map for (D); (G)-(I) present the distributions for spatial map (D) in a ‘connectivity map’ including 48 points on 3 different projection centers, respectively.

The measurement of the spatial pattern(s) of an individual ICN or among different ICNs is efficiently converted to quantitation of the 48 dimensional ‘connectivity map’ vector(s). First, the entropy of ‘connectivity map’ is adopted to measure the spatial pattern heterogeneity of one individual ICN:

$$H(S)={\displaystyle \sum _{m=1}^{48}}-P_m(S){log}_{48}{P}_m(S)$$ (10)

where H(S) is the entropy value of one ICN S ranging from 0 to 1. As shown in Fig. 6B the ICN with large entropy value is more likely to be a noise and less meaningful pattern with inhomogeneous spatial distribution. Second, the intersection between two ‘connectivity maps’ of two ICNs is adopted to measure the spatial pattern similarity between two ICNs:

$$I(S_{\mathrm{i}},S_j)={\displaystyle \sum _{m=1}^{48}}min(P_m(S_{\mathrm{i}}),P_m(S_j))$$ (11)

where I(S_i, S_j) is the intersection value of two ICNs S_i and S_j ranging from 0 to 1. It is straightforward that two ICNs with higher intersection value are more similar. Since we have three projection centers as mentioned before, we obtain three ‘connectivity maps’ for each of ICNs. The largest entropy value of the three ‘connectivity maps’ is adopted as the entropy of the ICN, and the smallest intersection value of the three pairs of ‘connectivity maps’ is adopted as the similarity between the two ICNs.

Fig. 6.

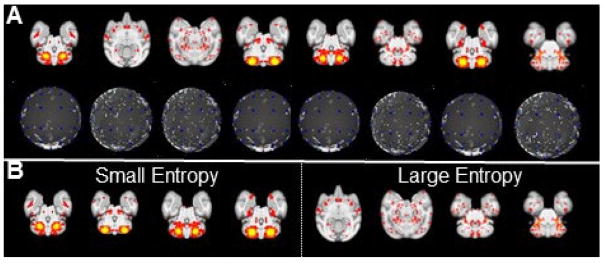
Examples identified as spatial patterns selected from individuals of ‘connectivity map’ representation of ICNs. (A) 8 example ICN patterns (first row) and corresponding ‘connectivity map’ representations (second row). (B) The four meaningful ICN patterns with small entropy values and the four ICN patterns with large entropy values which are more likely to be noise patterns.

Identification of Connectome-scale Group-wise Consistent ICNs across Different Subjects and Scans

In this section, as discussed in Section 2.3, the application of ‘connectivity map’ only concentrates on dimension reduction. Since we have already had a total of 33 scans from 10 macaques and each subject have 400 identified spatial pattern by dictionary learning and sparse representation (Section 2.3), it is absolutely time-consuming to calculate the similarity between two identified spatial patterns in a regular way. More specifically, a single spatial pattern registered into the INIA 19 standard space includes about 2,000,000 voxels. A very rough estimation of iteration is (400×33)²×2,000,000. The motivation to use ‘connectivity map’ is to effectively implement the similarity measurement by the estimation of iteration as (400×33)²×48, which dramatically reduces the dimension of spatial patterns.

Based on the identified connectome-scale ICNs within each individual subject’s rsfMRI scan (Section 2.2) and the ‘connectivity map’ representation of spatial patterns of all ICNs as feature vectors, we can identify connectome-scale group-wise consistent and meaningful ICNs across different subjects/scans from all 13300 ICN patterns based on the following six steps.

First, as demonstrated in Section 2.3 and Fig. 6, since the ICN patterns with large entropy values are more likely to be noise patterns, we eliminate those noise patterns using an empirical threshold entropy value 0.8 and further confirmed those eliminated noise patterns by visual inspection. Note that we choose a “safe” value (0.8) to avoid removing those meaningful ICN patterns, and other potential noise patterns which are not eliminated in this step will be examined in further steps.

Second, we adopt the widely-used k-means clustering approach to cluster similar ICNs among all remaining ICN patterns. We set the cluster number as 400 which is equal to the dictionary size in the previous dictionary learning step. Our rationale is that 400 is a reasonable estimate of the number of meaningful functional networks in the brain (Lv et al., 2015a; Lv et al., 2015b) and its justification has been discussed in the theoretical analysis and estimation in Section 2.1.

Third, we calculate the intra-cluster similarity using Eq. (11) to identify the outliers in the cluster and invalid clusters from all 400 clusters. Since the ICN patterns within the same cluster should have high spatial pattern similarity defined in Eq. (11) theoretically, for each cluster, we successively eliminate the ICN which has the lowest spatial pattern similarity with all other ICNs in the cluster until the intra-cluster spatial pattern similarity reaches a predefined threshold (0.6 is empirically set in this study). If the spatial pattern similarity is equal to or larger than 0.3, these two spatial patterns should be considered as the very similar component (Lv et al., 2015a, b, Smith et al., 2009). The empirically spatial similarity value 0.6 (>0.3) can maintain the better performance of the clustering. Those eliminated ICNs in this step which might belong to other clusters are moved to a temporary pool for further analysis in the next step. Fourth, we examine the spatial pattern similarity of each of the ICNs in the temporary pool with other clusters using the same approach in the third step. If the similarity to all ICNs in one cluster is larger than the threshold (0.6), we assign the ICN to that cluster. Otherwise all left ICNs in the temporary pool are eliminated. Fifth, since we aim to identify the consistent ICNs across all subjects, we adopt a relatively strict criterion to only keep those clusters that include at least one ICN pattern from each of all subjects. Finally, those retained clusters are further examined by two groups of experts in the case of potential noise patterns or artifacts. The clusters that are agreed by all experts are considered as the group-wise consistent and meaningful ICNs. We can obtain the spatial patterns of identified connectome-scale group-wise consistent ICNs by averaging all spatial patterns within each of the finalized clusters. The whole ICN identification framework is summarized below.

Algorithm 1.

Identification of connectome-scale group-wise consistent ICNs

1:	Input: All ICN spatial patterns across all subjects;
2:	Eliminate ICN patterns with a large entropy;
3:	Do k-means clustering for all remaining ICN patterns (cluster number equals 400);
4:	for m = 1 to 400 do
5:	for i = 1 to Nm (number of clustered ICN patterns in cluster m) do
6:	if I(Si,Sj) > 0.6 (j=1 to Nm, i ≠ j)
7:	Keep Si in the same class;
8:	else if
9:	Move Si to a temporary pool;
10:	end if
11:	end for
12:	end for
13:	for i = 1 to NP (number of ICNs in the temporal pool) do
14:	for m = 1 to 400 do
15:	Repeat 5–11;
16:	end for
17:	end for
18:	Delete the temporary pool;
19:	Only keep the clusters containing at least one ICN of each subject and double check by two groups of experts;
20:	Output: Finalized retained clusters representing group-wise consistent ICNs.

Results

Connectome-Scale Group-Wise Consistent ICNs in Macaques

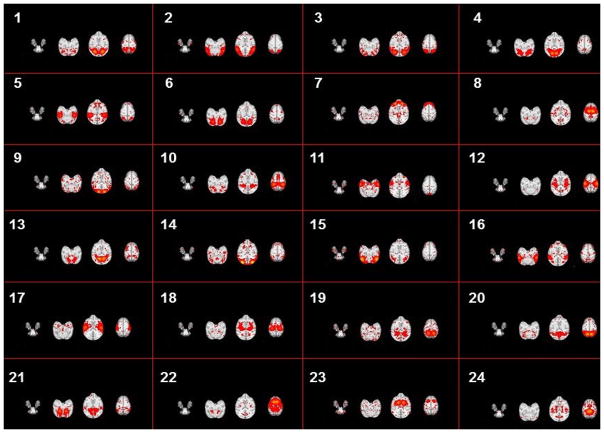
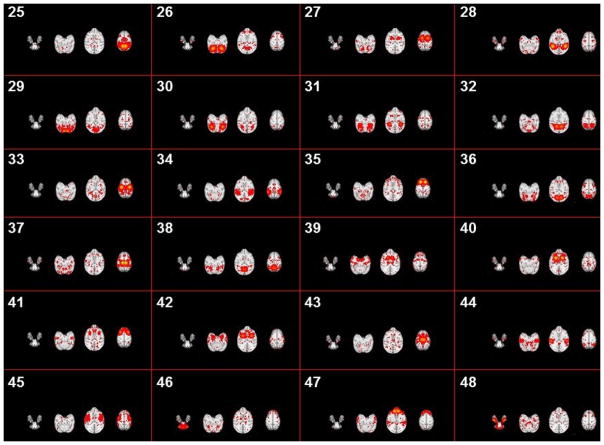
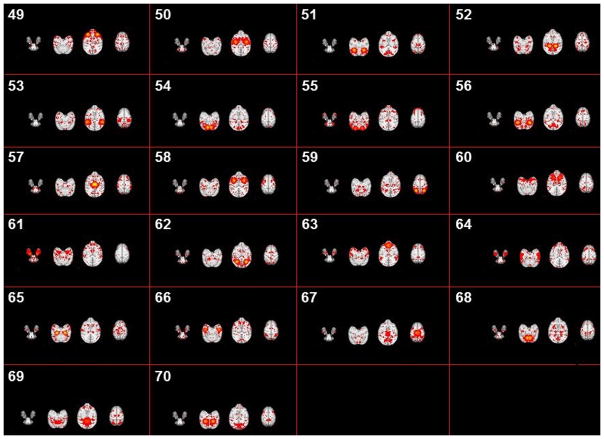
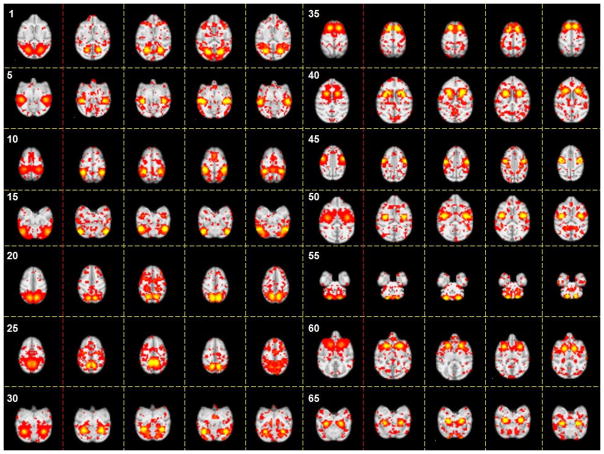
Based on the methods proposed in Sections 2.2 to 2.4, we successfully identified 70 group-wise consistent ICNs in macaques. All networks are arranged by using the descent average overlap rate, compared with 10 subjects’ corresponding networks at 4 different ages. For each of the 70 ICNs, the spatial pattern is averaged across all ICN patterns within the same cluster and visualized in Fig. 5. We name these averaged spatial patterns in the INIA19 space as ICN templates. Based on the previous studies on ICNs and their relationship with other functional networks/cognitions (e.g., Stefanacci et al., 1998; Vanduffel et al., 2014; Miyamoto et al., 2013; Nakahara et al., 2002; Nelissen et al., 2005; Seltzer et al., 1978; Seltzer et al., 1980; Seltzer et al., 1986; Margulies et al., 2009), to some extent, we demonstrate the meaningfulness of some of the identified ICNs. Since monkeys depend heavily on the vision system to interact with surrounding environment, previous reported ICNs are mainly related to visual areas (Stefanacci et al., 1998; Vanduffel et al., 2014). In general, a major part of our identified 70 ICNs are related to the occipitotemporal cortex, frontal lobe, prefrontal cortex (PFC), parietal cortex, frontal eye field (FEF) and temporal cortex. Among these areas, the occipitotemporal cortex is related to primary visual processing (through the so called “ventral object and motion pathways”), while the pathways involving frontal, PFC and parietal cortex mediate aspects of visual attention allocation, intention, understanding and memory (Miyamoto et al., 2013; Nakahara et al., 2002; Nelissen et al., 2005; Seltzer et al., 1978; Seltzer et al., 1980; Seltzer et al., 1986). Specifically, for example, ICN #22 includes a large area of frontal gyrus which is observed in multiple action representations (Nelissen et al., 2005). ICN# 10 contains a large area of precuneus involved in the widely-known default mode network (DMN), which has been demonstrated to have similar intrinsic functional architecture in both macaque and human brains (Margulies et al., 2009). ICN# 1, 2, 3 and 4 include the occipital gyrus which is the primary visual area of macaque (Vanduffel et al., 2014). Moreover, for the 12-macaque monkey ICNs reported in (Mantini, et al., 2013), we qualitatively find the reported networks #1-#3 in (Mantini, et al., 2013) correspond to #11, #2 and #24 in our identified ICNs, and networks #5-#12 in (Mantini, et al., 2013) correspond to our identified ICNs #26, #3, #9, #13, #17, #42, #53 and #66, respectively. There are also other ICNs containing the visual area such as #1, #2 and #3 but with different distribution patterns. ICN #49 represents a functional visual area-prefrontal cortex that is evolutionarily most developed in non-human primates and support high cognitive functions. This area in macaque monkey is detected by performing a cognitive set-shifting task (Nakahara et al. 2002). ICN #36 contains the area of posterior parahippocampal gyrus and fusiform gyrus. We will further interpret other ICNs using available parcellation maps and published references as detailed in Section 3.3.

Spatial Pattern Consistency of Connectome-scale ICNs across Different Subjects

We measure the spatial pattern consistency of each ICN across different subjects and age groups. Specifically, we measure the spatial pattern consistency by defining the spatial overlap rate between a specific ICN template pattern (Fig. 5) and an individual ICN pattern:

$$S(\mathit{IndividualMap},\mathit{Template})=\frac{{\displaystyle \sum _{k=1}^N}min(\mathit{Individua}{\mathit{lMap}}_k,\mathit{Template})}{{\displaystyle \sum _{k=1}^N}(\mathit{Individua}{\mathit{lMap}}_k,\mathit{Template})/2}$$ (12)

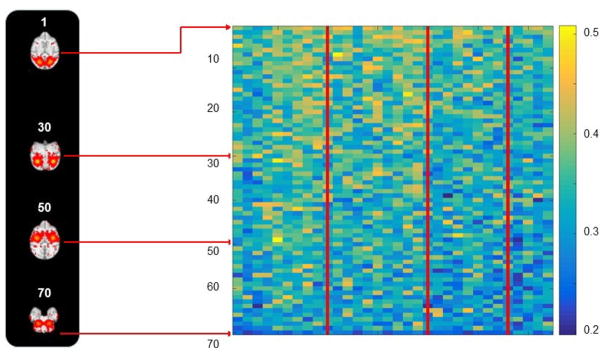
Note that both patterns are converted from continuous functional activity values to discrete labels (all functional activity values larger than 0 are labeled as 1, and the others are labeled as 0). For a specific ICN template, we calculate the spatial overlap rate with each of the 400 ICN patterns in one subject. The ICN pattern with the largest spatial overlap rate is considered as the corresponding specific ICN in this subject. Fig. 6 shows the spatial patterns of 20 examples of corresponding ICN templates in individual subjects. From visual inspection, we can see that each ICN has reasonable spatial pattern consistency across different subjects. Quantitatively, we calculate the spatial overlap rate (Eq. (12)) between an ICN template and corresponding ICN in all individual subjects. As shown in Fig. 7, we can see that the ICNs in all 10 subjects at 4 different ages have reasonably high spatial overlap rate values with the corresponding ICN template. For each of the 70 ICNs, one-sample t-test (p=0.01) based on the 33 spatial overlap rate values across 10 subjects at 4 different ages is performed and the p-values are reported in Fig. 8. We can see that there is no significant difference of spatial overlap rate across different subjects for all of the 70 ICNs. In short, the identified 70 connectome-scale ICNs have reasonable spatial pattern consistency across different subjects and age groups.

Fig. 7.

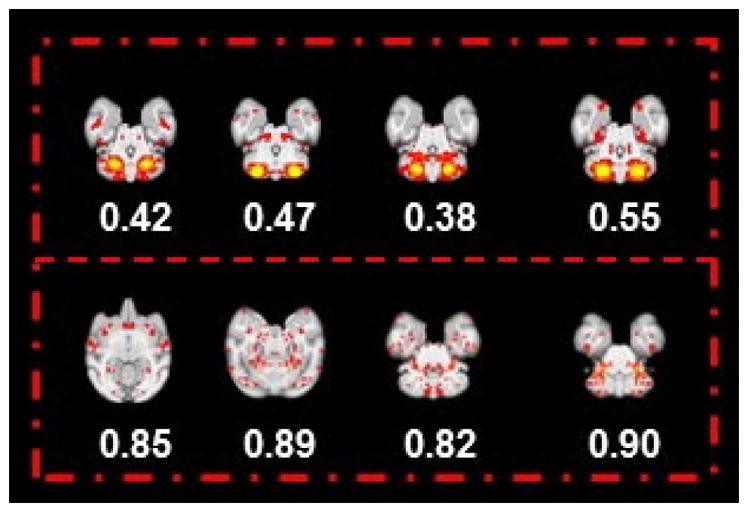
Eight examples identified as individual spatial patterns (the most informative slice) presented with their entropy values. The four representative slices in the first row indicate the meaningful spatial map with a relative smaller entropy value (<0.8); meanwhile, in the second row, another four representative slices are shown with the relative higher entropy value (>0.8). Obviously, by comparing the four slices in the second row with the first row, the spatial maps, in general, are much noisier with a larger entropy value. Based on our entropy analysis for 13,300 individual ICNs, we set the entropy threshold value as 0.6 in an effort to detect the noisy spatial patterns. Furthermore, experts’ manual examination for eliminated spatial pattern with larger entropy can guarantee that all spatial patterns used for clustering are meaningful.

Fig. 8.

The spatial patterns of identified #1-#24 connectome-scale group-wise consistent ICNs in the INIA19 template space. Each sub-figure shows one ICN which is averaged across all ICN patterns within the same cluster with three representative axial slices.

Interpretation of Connectome-scale Group-wise Consistent ICNs

In this section, we adopt two publicly available macaque brain parcellation maps INIA19 NeuroMaps (Rohlfing et al., 2012) and CBCatel15 (Calabrese et al., 2015) to interpret the identified 70 ICNs. These two parcellation maps have relatively finer-scale (INIA19 NeuroMaps provides ~1,200 parcellated regions, and CBCatel15 includes ~240 parcellated regions). Specifically, for the INIA19 NeuroMaps, because our identified 70 ICNs templates are already in the same INIA19 space, for each of the 70 ICN templates, the involved voxels within each of the ~1,200 regions are accumulated. After normalization to 0~1, we obtained a 1,200-dimensional INIA19 NeuroMaps distribution vector for the ICN. Each value represents the percentage of the ICN involved in the specific INIA19 Neuro Maps region. For the CBCatel15, after aligning all ICN templates to the same CBCatel15 space, we perform similar procedure to obtain the normalized 240-dimensional CBCatel15 distribution vector for each ICN. Fig. 9 shows the top five regions which have the highest percentages involved in 10 example ICNs based on INIA19 NeuroMaps/CBCatel15. The detailed names of those top five regions are reported in Tables 1 and 2. The top five regions which have the highest percentages in all 70 ICNs based on INIA19 NeuroMaps/CBCatel15 are reported at: http://hafni.cs.uga.edu/MonkeyNewICNs/All_70Templates_SpatialImg_NeuroMap_presentation.html and http://hafni.cs.uga.edu/MonkeyNewICNs/All_70Templates_SpatialImg_CIVMNeuroLabel__presentation.html; the visualizations of these maps support the consistency of the derived connectome-scale ICNs obtained by our framework.

Fig. 9.

The spatial patterns of identified #25-#48 connectome-scale group-wise consistent ICNs in the INIA19 template space. Each sub-figure shows one ICN which is averaged across all ICN patterns within the same cluster with three representative axial slices.

Table 1.

Top five regions which have the highest percentages in 7 example ICNs (Fig. 8–10) based on INIA19 Neuro Maps.

ICN #	Region #1	Region #2	Region #3	Region #4	Region #5
1	Occipital white matter	Cerebral white matter	Supramarginal gyrus	Cuneus	Angular gyrus
10	Cerebral white matter	Supramarginal gyrus	Superior parietal lobule	Postcentral gyrus	Superior temporal gyrus
20	Occipital white matter	Cerebral white matter	Superior parietal lobule	Precuneus	Supramarginal gyrus
30	Occipital white matter	Cuneus	Cerebral white matter	Lingual gyrus	Fusiform gyrus
40	Frontal white matter	Putamen	Caudate nucleus	Internal capsule	Cerebral white matter
50	Frontal white matter	Cerebral white matter	Precentral gyrus	Putamen	Postcentral gyrus
60	Putamen	Frontal white matter	Caudate nucleus	Fronto-orbital gyrus	Precentral gyrus

Table 2.

Top five regions which have highest percentages in 7 example ICNs (Fig. 8–10) based on CBCatel15.

ICN #	Region #1	Region #2	Region #3	Region #4	Region #5
1	Parietal area PEa	Parietal area PE	Parietal area PE, caudal part	Occipitoparietal area	Parietal area PF (cortex)
10	Parietal area PE	Parietal area PE, caudal part	Occipitoparietal area	Parietal area PEa	Porsal parietal area
20	Parietal area PEa	Parietal area PE, caudal part	Parietal area PE	Parietal area PF (cortex)	Occipitoparietal area
30	Parietal area PEa	Parietal area PF, opercular part	Parietal area PF (cortex)	Parietal area PE	Parietal area PFG
40	Occipitoparietal area	Dorsal parietal area	Parietal area PE	Depth intraparietal area	Parietal area PE, caudal part
50	Depth intraparietal area	Dorsal parietal area	Occipitoparietal area	Area 3b of cortex (somatosensory)	Parietal area PE
60	Parietal area PG, opercular part	Parietal area PG	Parietal area POa, external part	POa, internal part	Parietal area PFG

In this paper, since our major focus is to propose a computational framework to identify the connectome-scale group-wised consistent ICNs, hereby we will analyze the functions of these 70 ICNs briefly. More specific and further analyses of these 70 ICNs will be provided in our future research works. We have already pointed out that some of identified ICNs are very similar to certain reported macaque ICNs in Section 3.1. For our identified ICNs, in brief, some of them (#1, #4, #14, #15, #20, #29, #30, #31, #32, #35, #36, #43, #55, #62 and #64) are located in the occipital cortex and the frontal and parietal cortices (Vanduffel et al., 2014; Miyamoto et al., 2013; Seltzer et al., 1978; Seltzer et al., 1980; Seltzer et al., 1986; Margulies et al., 2009). Other interesting brain areas contain the thalamus (#57), putamen (#60) and temporal gyrus (#66 and #67). Our identified ICN #59 seems to include a large part of the frontal, temporal and parietal lobe areas of the macaque brain (Jones and Powell, 2016). In the following two tables, we provide a total of 14 examples with top five brain regions that have the highest percentages, compared with other brain areas. All details of these brain areas from the ICNs can be viewed on the two abovementioned websites.

Discussion

In this study, we proposed a computational framework to identify connectome-scale group-wise consistent intrinsic connectivity networks in macaques based on whole-brain resting state fMRI data. Hundreds of functional network patterns were firstly obtained within each subject by applying effective and efficient dictionary learning and sparse representation on the whole-brain rsfMRI data matrix of each subject. Then each functional network pattern was effectively represented as a ‘connectivity map’, and k-means clustering was performed on all ‘connectivity maps’ across all subjects and age groups to obtain group-wise consistent functional networks. The experimental results demonstrated that 70 ICNs were successfully identified via the proposed framework. Moreover, these 70 ICNs have reasonable spatial pattern consistency across different subjects and age groups based on both qualitative and quantitative measurements. The 70 ICNs were further interpreted based on two publicly available parcellation maps (Rohlfing et al., 2012; Calabrese et al., 2015) as a preliminary study.

This set of connectome-scale functional brain networks could potentially benefit a variety of studies in the neuroscience and brain mapping fields, and provide a foundation to better understand the brain evolution in the future. First, electrophysiological recordings have been widely adopted in macaque brains to link the activities in micro- and macro- circuitries to behavior and to study information transformation in specific brain regions/networks (e.g., Bosman et al., 2012), which can be adopted as a nonhuman primate model to understand the human brain. Under the guidance of the identified connectome-scale functional networks, the electrophysiological recordings can be relatively precisely performed on those brain regions of interest instead of on a coarse region covering a large part of brain (Bosman et al., 2012), thus improving the accuracy and reliability of studies. Second, there have been extensive comparative studies between monkey and human to investigate the homologies across the two species. For example, the correspondences of visual cortex, retinotopic regions, nonretinotopic regions, or parietal/frontal cortex have been studied between monkey and human brains (e.g., Van Essen et al., 2001; Van Essen et al., 2004; Vanduffel et al., 2014). For another example, researchers have compared specific resting state networks between monkey and human brains and found nine common networks (including dorsal and ventral attention network and language network) and three human-specific networks (Maniti et al., 2013). The identified connectome-scale functional networks in macaques in this work can provide a more fine-grained foundation with significantly more comprehensive information for comparative studies between monkey and human functions in order to yield crucial insights for the brain evolution given the explosively growing human brain fMRI datasets. Third, the identified connectome-scale functional networks based on fMRI in this work can be integrated with other meaningful characteristics such as retinotopic, connectional, and anatomical information to provide comprehensive insights or refines the publicly available macaque cortical parcellation maps based on different parcellation schemes (Van Essen et al., 2011).

In this study, we focused on the methodology development of identification of connectome-scale group-wise consistent ICNs in macaques. The potential applications of those ICNs in the brain mapping and neuroscience fields is relevant for future studies. First, in this study, to some extent, we interpreted the identified 70 ICNs using two publicly available parcellation maps since they provide relatively finer-scale parcellations (Rohlfing et al., 2012; Calabrese et al., 2015). In the future, we can adopt other publicly available parcellation maps (Van Essen et al., 2011) to further interpret these 70 ICNs, and to assess the regularity and variability among different parcellation maps. Second, in this study we identified connectome-scale group-wise consistent ICNs that are common across four age groups (3, 6, 12, and 18 months). These group-wise consistent ICNs essentially capture the relatively stable and less dynamically developing brain networks across these four ages. Or these group-wise consistent ICNs still exhibit similar global shape patterns across ages, despite certain levels of local developmental changes. In the future, we can perform the proposed computational framework to identify connectome-scale group-wise consistent ICNs within each age group, respectively. In addition, the developmental trajectories of those connectome-scale ICNs can be quantitatively assessed across different age points. In this way, both the global changes of more dynamically developing ICNs and the local changes of more temporally stable ICNs can be quantitatively measured. Third, we can apply the proposed framework to identify connectome-scale ICNs in the macaques with specific physiological conditions (e.g., early life stress (Howell et al., 2013)). Thus, the possible connectome-scale ICN disruptions compared with macaque normal control group can be assessed and adopted as potential biomarkers for further studies.

Fig. 10.

The spatial patterns of identified #49-#70 connectome-scale group-wise consistent ICNs in the INIA19 template space. Each sub-figure shows one ICN which is averaged across all ICN patterns within the same cluster with three representative axial slices.

Fig. 11.

The spatial patterns of 14 examples of corresponding ICN templates in individual subjects. For each ICN, the ICN template and the corresponding ICNs in four example individual subjects (one example subject for each of the four age groups, respectively) are shown with one representative axial slices. The indices of the 14 example ICNs are the same as in Fig. 5.

Fig. 12.

Spatial overlap rate between each of 70 ICNs template and corresponding ICNs in all 33 individual subjects. (a) 10 example ICN templates with one representative axial slice. (b) The spatial overlap rate matrix (70×33). The red lines separate the four age groups. Every identified 70 ICNs and 33 individual spatial map with the maximum overlap can be viewed by the web link: http://hafni.cs.uga.edu/MonkeyNewICNs/MonkeyBrain_NewTemplateComponentsSelectedByMeanStdOverlapSortMap_presentation.html. Most of the identified group-wised ICNs have a strong spatial overlap (>0.3) with individual spatial components (Lv et al., 2015 a, b; Smith et al., 2009), which indicates all identified group-wised ICNs are consistent.

Highlights.

1. A framework to identify connectome-scale group-wise consistent brain networks in macaques.

2. In total, 70 intrinsic connectivity networks (ICNs) are derived and interpreted.

3. Our work significantly expand currently known macaque ICNs reported in the literature.

4. All of these 70 ICNs are publicly released on our website.