Fundamental limitation of the instantaneous approximation in fold‐change detection models

Abstract

The phenomenon of fold‐change detection, or scale‐invariance, is exhibited by a variety of sensory systems, in both bacterial and eukaryotic signalling pathways. It has been often remarked in the systems biology literature that certain systems whose output variables respond at a faster time scale than internal components give rise to an approximate scale‐invariant behaviour, allowing approximate fold‐change detection in stimuli. This study establishes a fundamental limitation of such a mechanism, showing that there is a minimal fold‐change detection error that cannot be overcome, no matter how large the separation of time scales is. To illustrate this theoretically predicted limitation, the authors discuss two common biomolecular network motifs, an incoherent feedforward loop and a feedback system, as well as a published model of the chemotaxis signalling pathway of Dictyostelium discoideum.

1 Introduction

An important phenomenon in biology is that in which a physiological signal returns to a pre‐stimulus or ‘default’ value after a transient (impulse or pulse) input has been sensed. This input might be physical or biochemical, such as a light input to a photoreceptor, or a ligand to an olfactory receptor. Often, a return to such steady‐state values of outputs occurs even in the face of a sustained step or periodic excitation: the study of such exact (or at least approximate) adaptation to a persistent input has been the subject of extensive investigations in both the experimental and the modelling literature [1–3]. Physiological adaptation is a trait of many sensory systems, allowing them to accurately detect changes in input signals and distinguish meaningful information from background through a shifting of dynamic range. Thus, the human eye distinguishes features across nine orders of magnitude, even though its sensors can only detect a three order of magnitude contrast; this is achieved through both the pupillary light reflex and the adjustment of sensitivity of rods and cones [4]. Similarly, humans adapt to constant touches, smells or background noises, detecting new information only when a substantial change occurs. At a different scale of behaviour, a particularly well‐studied example of physiological adaptation is that of the response of the Escherichia coli (E. coli) chemotatic pathway response to stepwise addition and subsequent removal of attractant [3, 5]. In control theory, perfect adaptation is also called ‘disturbance rejection’ and is associated to ‘internal models’ of inputs and specifically, for linear systems, zero gain at zero or other frequencies [2, 6, 7]. For simplicity, we restrict to step responses in this paper, but similar questions can be studied for persistent oscillatory inputs.

1.1 Scale‐invariance

Specifically, we are interested here in a finer property than mere adaptation, namely scale‐invariance of responses. To explain this property intuitively (we later define what we mean by ‘input’ and ‘output’ precisely), consider two step inputs u ₁ and u ₂ which are scaled versions of each other: u ₂ (t) = pu ₁ (t), for some positive number or ‘scale factor’ p, see Fig. 1 a. Adaptation means that, whether excited by u ₁ or u ₂, the output signal will return to the same value, as shown in Fig. 1 b. On the other hand, scale‐invariance means that the entire actual transient response will be the same under either excitation, as shown in Fig. 1 d. An intermediate property between mere adaptation and scale‐invariance is the ‘Weber‐like’ property from biophysics and psychophysics [8–11], in which the temporal, transient response may be different, but the peak intensities are the same, as shown in Fig. 1 c.

Fig. 1.

Responses to scaled inputs

a Scaled step inputs and corresponding responses

b Perfect adaptation

c Weber‐like (same peak amplitude responses)

d Scale‐invariance (same transient responses)

Recent interest in scale‐invariance was triggered by a pair of papers [12, 13] published in late 2009, in which scale‐invariant behaviour was experimentally observed in a Wnt signalling pathway and an EGF pathway, respectively. These are highly conserved eukaryotic signalling pathways that play roles in embryonic patterning, stem cell homeostasis, cell division and other central processes, and their misregulation results in diseases including several types of cancer. Scale‐invariance is also found in certain bacterial signalling systems. A prediction, for the E. coli chemotaxis sensory circuit in response to the ligand α ‐methylaspartate, was made in [14], based on a model proposed by Tu et al. [15]. This prediction was later verified in a microfluics population experiment carried out in Stocker's lab as well as an in FRET measurements on genetically altered bacteria in Shimizu's lab [16].

1.2 Robustness to total protein levels is guaranteed by scale invariance of downstream components

Scaled inputs in molecular sensing may arise as follows. Suppose P is a signalling protein, whose total concentration P_T is assumed to be constant at the signalling timescale. This protein can be found in inactive or active forms P _i and P _a, respectively. The active form P _a is a transcription factor that controls the level of expression of a target gene and can be thus viewed as an input to a downstream system. The rates of transition between these two forms depend, in turn, on a signal w (t) (e.g. an extracellular ligand concentration) through functions k _on (w (t)) and k _off (w (t))

$$P_{\mathrm{i}}\underset{k_{\text{off}}(w(t))}{\overset{k_{\text{on}}(w(t))}{\rightleftharpoons }}{P}_{\mathrm{a}}$$ (1)

as shown in the diagram in Fig. 2.

Fig. 2.

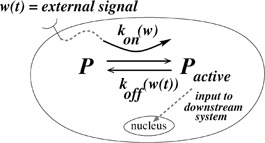
Activation and inactivation of a protein by an external signal

Active form is input to downstream gene expression

The simplest differential equation model describing the temporal dynamics of this process would be given by

$$\dot{u}(t)=k_{\text{on}}(w(t))(P_{\mathrm{T}}-u(t))-k_{\text{off}}(w(t))u(t)$$

(dot indicates time derivative), where we denote by u (t) the amount of active protein P _a at time t; we use this notation to emphasise that this function u (t) is what will be sensed by the downstream system as an input. The key observation is that, for any number p > 0, the function v (t) : = pu (t) satisfies

$$\dot{v}(t)=k_{\text{on}}(w(t))(p{P}_{\mathrm{T}}-v(t))-k_{\text{off}}(w(t))v(t)$$

which means that v (t) solves the new differential equation in which the total protein level P _T has been scaled by p. Another way to say this is that if P _T changes to some other value P′ _T, then the temporal signal u (t), the input to a downstream system, will be scaled by the constant factor p = P′ _T /P _T. This implies that the cell's response to w (t) will be robust to uncertainty in P _T provided that the response to u be scale‐invariant. (A similar discussion, but based on a much more restrictive Michaelis–Menten quasi‐steady‐state approximation, can be found in [17].) As total protein concentrations are highly variable from cell to cell, and even in the same cell over time [18–22], this robustness might explain the experimental results in [12, 13].

Scale‐invariance means that the downstream system cannot distinguish between an input u (t) and a scaled version pu (t). For step inputs that jump at t = 0, we can reformulate this property by saying that the response can only depend on the fold change of the input at time 0:

$$\frac{v(t)}{v(0)}=\frac{pu(t)}{pu(0)}=\frac{u(t)}{u(0)}$$

hence motivating the terminology ‘fold change detection’ (FCD), which we will use interchangeably from now on.

1.3 Feedforward circuits

Feedforward motifs have been the subject of extensive research in systems biology for the last decade [3]. They play a central role in metabolic pathways, signalling networks and genetic circuits in systems ranging from microRNA regulation [23] to bacterial carbohydrate uptake via the carbohydrate phosphotransferase system [24], and control mechanisms in mammalian cells [25] that regulate stress responses to free radicals, bacterial or viral infections and cancer, and in the regulation of meiosis, mitosis and post‐mitotic functions in differentiated cells, including, for example, the ATP‐induced release of intracellular calcium [26], the epidermal growth factor‐mediated activation of extracellular‐signal‐regulated kinases [27, 28], the activation of the NF‐κ B protein complex [29, 30], and the glucose‐induced release of insulin produced by β ‐cells of the pancreas, central to regulating carbohydrate and fat metabolism in the body [31, 32].

In particular, the IFFL (incoherent feedforward loop) motif, as represented generically by the directed graphs in Fig. 3, has been proposed as one of the two main biomolecular mechanisms (the other is integral feedback) that can help produce scale‐invariance or FCD [14, 17, 33].

Fig. 3.

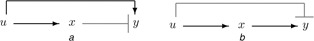
Two incoherent feedforward motifs

a Input activates and intermediate species represses output

b Input represses and intermediate species activates output

In IFFL's, an external cue or stimulus u activates a molecular species x which, in turn, activates or represses a downstream species y. Through a different path, the signal u represses or activates, respectively, the species y. This antagonistic (‘incoherent’) effect endows the IFFL motif with powerful signal processing properties [3].

The conceptual diagrams shown in Fig. 3 describe, in fact, various alternative molecular realisations. Different molecular realisations of the given motif can differ significantly in their dynamic response and, ultimately, biological function. Two realisations of the diagram in Fig. 3 b are shown in Fig. 4, and similar alternatives exist for the diagram in Fig. 3 a.

Fig. 4.

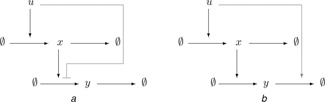
Two realisations of the ‘input repressing output’ motif in Fig. 3 b

a Input inhibits the formation of output

b Input enhances the degradation of output

These two realisations differ in a fundamental way in regards to their scale‐invariance (FCD) properties. The biological mechanism in Fig. 4 a exhibits FCD, but the one in Fig. 4 b does not. To be more precise, we study the simplest ordinary differential equation (ODE) models for these processes, in which the concentrations of the input u and species x and y are described by scalar time‐dependent quantities.

Suppose that (x (t), y (t)) is any solution corresponding to the input u (t), for the system described by Fig. 4 a. Then, (px (t), y (t)) is a solution corresponding to the input pu (t):

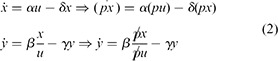
In particular, given a step input that jumps at time t = 0 and an initial state at time t = 0 that has been pre‐adapted to the input u (t) for t < 0 (i.e. x (0) = αu ₀ /δ, where u ₀ is the value of u for t < 0), the solution is the same as when instead applying pu (t) for t > 0, but starting from the respective pre‐adapted state pαu ₀ /δ. A simulation showing this effect is shown in Fig. 5.

Fig. 5.

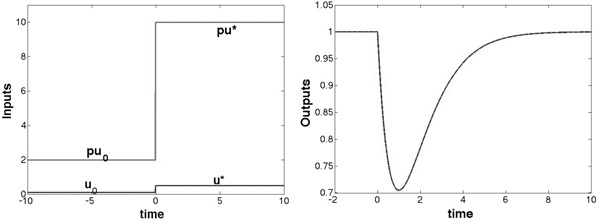
Dynamic response of the circuit in Fig. 4 a and described by the model (2) and all parameters set to 1

Pre‐adaptation value of input is u ₀ = 0.1, stepping to u * = 0.5 at t = 0

Original and p ‐scaled responses (p = 20) overlap perfectly

Here, α = β = δ = γ = 1

On the other hand, the FCD property fails for the system in which the input enhances the degradation of output, shown in Fig. 4 b. The same ‘trick’ of scaling states x by p does not work for this second system, when modelled in the obvious manner:

$$\begin{array}{rl}\dot{x}& =\alpha u-\delta x\\ \dot{y}& =\beta x-\gamma uy\end{array}$$

because the scaling $x\mapsto px\text{and}u\mapsto pu$ does not leave the y equation invariant. Moreover, one can prove that no possible equivariant group action on states is compatible with output invariance, which means that no possible symmetries are satisfied by the input/output behaviour of this system. These issues are carefully discussed in [14], which carried out a systematic analysis of the FCD property. (Presenting these results would entail formulating rigorously a general invariance problem, which is not needed for the purposes of this paper.)

1.4 Time‐scale separation provides approximate FCD

The above negative remarks notwithstanding, it has been observed that systems such as the one in Fig. 4 b satisfy an approximate FCD property provided that the parameters β and γ are large enough so that a time‐scale separation property holds. Multiple time scales, corresponding to slow and fast subsystems, are typically inherent in cellular systems [34, 35].

To introduce multiple time scales, corresponding to slow and fast subsystems, we carry out a standard non‐dimensionalisation procedure which is routinely used in chemical kinetic modelling to justify the validity of the quasi‐steady state assumption of enzyme kinetics [34, 35]

$$\begin{array}{rl}x& =X_0\overline{x},y=Y_0\overline{y},u=U_0\overline{u},t=\frac{X_0}{{\alpha }_0{U}_0}\overline{t},\alpha ={\alpha }_0\overline{\alpha },\\ \beta & ={\beta }_0\overline{\beta },\overline{\delta }=\frac{\delta X_0}{{\alpha }_0{U}_0},\overline{\gamma }=\frac{\gamma U_0{Y}_0}{{\beta }_0{X}_0},\epsilon =\frac{{\alpha }_0}{{\beta }_0}\cdot \frac{Y_0{U}_0}{X_0^2}\end{array}$$ (3)

Here, X ₀, Y ₀ and U ₀ are some mean or typical values of the variables x, y and u, respectively, and $\overline{x},\overline{y}\text{and}\overline{u}$ are the corresponding dimensionless variables. The parameters α and $\overline{\beta }$ can be interpreted as the dimensionless rates of formation or activation, while $\overline{\delta }$ and $\overline{\gamma }$ can be interpreted as the dimensionless rates of degradation or inactivation of the species x and y, respectively. In what follows, we omit the bar from all notations and think of $\overline{t}$ as our original time scale, so we simply write our system in the following singular perturbation form:

$$\begin{array}{rl}\dot{x}& =\alpha u-\delta x\\ \epsilon \dot{y}& =\beta x-\gamma uy\end{array}$$ (4)

Assuming that the corresponding pairs of kinetic parameters, α ∼ δ and β ∼ γ, are of the same order of magnitude, we can think of ε as a small parameter, that is, $0<\epsilon \ll 1$ in (3) and (4), where the remaining parameters are all O (1). Small values of ε can be attributed to various important factors. For example, suppose that the values of X ₀ and $\sqrt{U_0{Y}_0}$ are of the same order of magnitude in (3). Then $\epsilon \sim {\alpha }_0/{\beta }_0\ll 1$ means that the species y is activated much faster comparing with the rate of the activation of the species x. Another example corresponds to the situation where the rates of activation are of the same order of magnitude, that is, ${\alpha }_0\sim {\beta }_0$, while the concentrations of the corresponding species differ in several orders of magnitude, for example, $Y_0\ll X_0$ while U ₀ ∼ Y ₀ (or U ₀ ∼ X ₀).

When viewed at a slow time‐scale, we may assume that y (t) quickly equilibrates (set ε = 0 in the second equation) so that, in effect, the resulting system is given by a one‐dimensional (1D) differential equation together with a readout which is an instantaneous ratio of states and inputs:

$$\begin{array}{rl}\dot{x}& =\alpha u-\delta x\\ y(t)& \simeq \frac{\beta x(t)}{\gamma u(t)}\end{array}$$

(we include the time argument in y to emphasise the instantaneous nature of the quasi‐steady‐state dependence). Now a scaling $u\mapsto pu\text{and}x\mapsto px$ results in (approximately) the same output, since

The property of time‐scale separation for IFFL's can be traced back to work in [33, 36, 37], and systems of this form were theoretically analysed in [38]; see also the ‘sniffer’ circuit in [39]. We were particularly motivated to look at this question by the analysis in [40], which concluded, through a combination of theoretical analysis and numerical exploration that every three node enzymatic network (as studied in [41]) which has an approximate FCD property must rely upon this mechanism of time scale separation.

The study of this time‐scale separation for FCD, and the dependence of the magnitude of the FCD‐error on the input scaling, not only for feedforward systems but in a general context, is the topic of the current paper.

1.5 Limitations of time‐scale‐based scale‐invariance

Our main result is that, no matter how small ε is, there is always an irreducible minimal possible difference in instantaneous values of outputs when comparing the response to an input u (t) and to a scaled version of this input, pu (t).

This is illustrated by the simulation shown in Fig. 6.

Fig. 6.

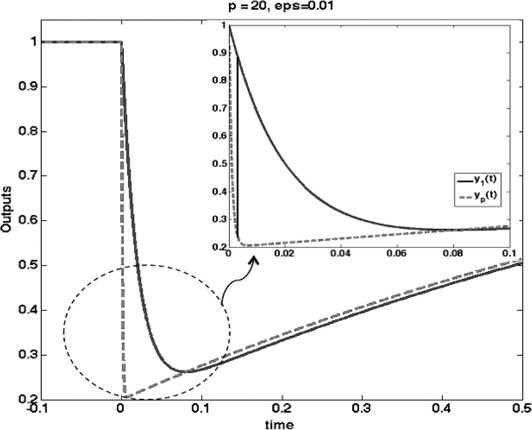
Dynamic response of the circuit in Fig. 4 b and described by the model (4) with all parameters except ε set to 1

Original (blue) and p ‐scaled (red) responses

Pre‐adaptation value of input is u ₀ = 0.1, stepping to u * = 0.5 at t = 0

The p ‐scaled output is denoted by y_p (t)

Here, ε = 0.01 and p = 20

Maximal magnitude of the FCD‐error is depicted by a black segment (inset)

Here, α = β = δ = γ = 1

We call such an irreducible difference an FCD‐error. As a matter of fact, one can show that the FCD‐error (difference between the original output y ₁ (t) and the output y_p (t) arising from a p ‐scaled input) is not merely non‐zero, but is in fact bounded below by a positive number that is independent of the value of the small parameter ε. Fig. 7 shows this effect.

Fig. 7.

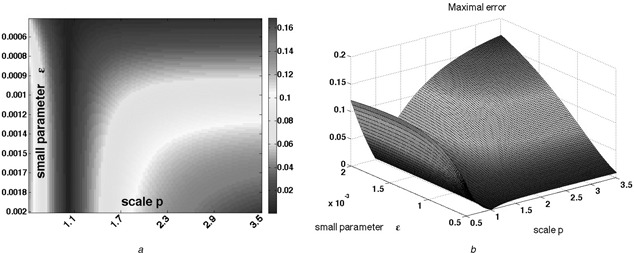
System with input‐dependent degradation

(a) Heat‐map and (b) 3D plot representing the largest absolute value of the difference between the two outputs y_p (t) and y ₁ (t)

Observe that, for any fixed p, except for the trivial case p = 1, the values approach a positive number as ε → 0

Pre‐adaptation value of input is u ₀ = 1, stepping to u * = 2 at t = 0

Parameter ε was sampled in the range [0.0005, 0.002]

Parameter p was sampled in the range [0.5, 3.5]

Hundred different samples for each were selected

Here, α = β = δ = γ = 1

An entirely analogous situation holds for systems in which the state degrades the output, modelled by switching the roles of u and x in the y equation

$$\begin{array}{rl}\dot{x}& =\alpha u-\delta x\\ \epsilon \dot{y}& =\beta u-\gamma xy\end{array}$$ (5)

and error behaviour is illustrated by Fig. 8.

Fig. 8.

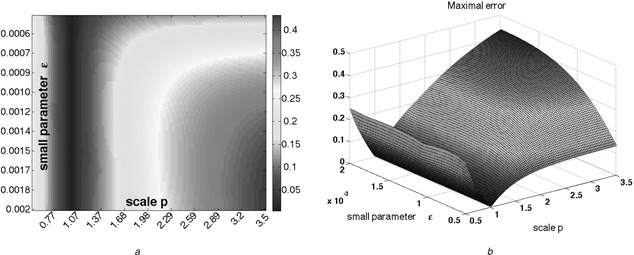
System with state‐dependent degradation

(a) Heat‐map and (b) 3D plot representing the largest absolute value of the difference between the two outputs y_p (t) and y ₁ (t)

Pre‐adaptation value of input is u ₀ = 1, stepping to u * = 2 at t = 0

Observe that, for any fixed p, except for the trivial case p = 1, the values approach a positive number as ε → 0

Parameter ε was sampled in the range [0.0005, 0.002]

Parameter p was sampled in the range [0.5, 3.5]

Hundred different samples for each were selected

Here, α = β = δ = γ = 1

This irreducible error, no matter how small ε > 0 is, establishes a fundamental limitation to fold‐sensing systems based on time‐scale separation, such as those proposed in the context of state‐degradation or input‐degradation feedforward systems. The existence of such an irreducible error can also be understood through a geometric interpretation based on singular perturbation theory [42–44]: a step change in the input changes the ODE, with the net result that, even though the output remains the same, the internal state, whose activity is hidden from the output measurement, has in fact ‘jumped’ away from the slow manifold. A derivation of estimates from that point of view, establishing asymptotic expansions to obtain precise bounds on the error for specific systems, will be conducted in future work. In this paper, we use more general techniques in order to rigorously prove the phenomenon in very general systems, and illustrate our results on examples of biological interest.

It is important to emphasise that scale invariance is by definition a transient notion. All the systems that we study in this paper have the perfect adaptation property, and thus, in particular, scale perfectly for large times. It is precisely the short‐term behaviour that is of interest in the study of the FCD property. That said, our results focus on the initial part of the response. This means that systems that are driven by the output of the system in question, but react slowly, might not be noticeably affected by this error. We present in the paper a basic mathematical principle, and make no claims regarding its relevance to specific biological systems. As the FCD field is rapidly developing, one may speculate, however, that examples will be discovered where this phenomenon is of importance.

The rest of this paper is organised as follows. In Section 2, we present rigorous results, using a general mathematical treatment without any a priori assumption on the smallness of the parameter ε. We first discuss an IFFL, for which explicit bounds can be given. That example reveals the complexity of the effect and motivates the need for general theory. We follow with a general comparison theorem for two arbitrary singularly‐perturbed systems. The theorem states that the maximal difference between the corresponding solutions of such singularly‐perturbed systems is always bounded below by a non‐zero quantity even though the value of the small parameter can be chosen arbitrarily small. In Section 3, we discuss several examples as illustrations of the main theorem. Finally, Section 4 contains details of proofs.

2 Lower bounds on scale‐invariance error

2.1 Concrete example

We start by considering the input‐induced degradation IFFL circuit under time‐scale separation described in (4), the ODE model which we repeat here for convenience:

$$\begin{array}{rl}\dot{x}& =\alpha u-\delta x\\ \epsilon \dot{y}& =\beta x-\gamma uy\end{array}$$

where α, β, δ and γ are the positive constants, and we think of ε as a small parameter. We wish to study the response of this system to a step input u (t) which switches from the value u (t) = u ₀ for t ≤ 0 to a different value u (t) = u * for t > 0, under the assumption (‘pre‐adaptation’) that the states x and y had converged to a steady state by time t = 0, and want to compare this response to the response to the input pu (t). In the first case, the steady state at time t = 0 can be found by setting αu ₀ − δx = 0 and βx − γuy = 0, and then solving for (x, y). The response for t > 0 will be, therefore given by the solution of the ODE with initial condition x (0) = (α /δ) u ₀ and y (0) = (αβ /δγ), and input u (t) ≡ u * for t > 0. In the second (p ‐scaled) case, the initial state will be x (0) = (α /δ) pu ₀, and the same y (0), now using the input u (t) ≡ pu * for t > 0. We will take α = β = δ = γ = 1 in our subsequent analysis. This involves no loss of generality, because a change of scale in x, u, y and time via: u = δu′ /γ, x = αx′ /γ, y = αβy′ /(δγ) and t = t′ /δ reduces to that case. The main result for this example given in Proposition 1.

We use the notation ${∥y-w∥}_{[0,T]}=ma{x}_{t\in [0,T]}\left|y(t)-w(t)\right|$ to denote the largest possible value of the difference |y (t) − w (t)| between two functions defined on an interval [0, T]. In particular, when quantifying FCD‐error, w will be the output when the input is scaled.

Consider solutions $(x_i^{\epsilon }(t),y_i^{\epsilon }(t))$ of the following two initial value problems

$$\begin{array}{cc}{\dot{x}}_1=u^{\ast }-x_1,x_1(0)=u_0& {\dot{x}}_2=p{u}^{\ast }-x_2,x_2(0)=p{u}_0\\ \epsilon {\dot{y}}_1=x_1-u^{\ast }{y}_1,y_1(0)=1& \epsilon {\dot{y}}_2=x_2-p{u}^{\ast }{y}_2,y_2(0)=1\end{array}$$ (6)

where ε, u *, u ₀ and p are non‐zero positive numbers, and we assume that p ≠ 1, u ₀ ≠ u *. Define M = M (u *, u ₀, p) > 0 by

$$M:=\left|1-\frac{u_0}{u^{\ast }}\right|p^{(p/(1-p))}\left|1-p\right|$$ (7)

Then, for any 0 < M′ < M < M′′, there exist two numbers ε ₀ = ε ₀ (u *, u ₀, p, M′, M″), and δ = δ (u *, u ₀, p, M′, M″) > 0, such that

$$M^{\prime }\le {∥y_1^{\epsilon }-y_2^{\epsilon }∥}_{[0,\delta ]}\le M^{\prime \prime },\forall 0<\epsilon \le {\epsilon }_0$$ (8)

The proof of Proposition 1 can be found in Section 4. Since M′ and M″ can be taken arbitrarily close to M, this result tells us, in particular, that ${∥y_1^{\epsilon }-y_2^{\epsilon }∥}_{[0,\delta ]}\simeq M$ for all $0<\epsilon \ll 1$, and δ small. In other words, the positive number given in formula (7), which does not depend on ε, provides a fundamentally irreducible error as ε → 0, for any non‐trivial scaling (p ≠ 1) and any nontrivial step input (u ₀ ≠ u *).

2.2 General comparison theorem

We now formulate a general comparison theorem that generalises Proposition 1 to arbitrary systems. The bounds obtained are not as explicit as with the example, yet they again show the existence of a positive number M that lower‐bounds the difference between outputs under scaling of inputs. To achieve the greatest possible generality, our theorem will be formulated and proved for two arbitrary singularly‐perturbed non‐autonomous initial‐value problems (IVPs), as follows:

$$\begin{array}{rl}(S_1)& \left\{\begin{array}{c}{\dot{x}}_1=f_1(x_1,y_1,t),x_1(0)={\xi }_1\\ \epsilon {\dot{y}}_1=g_1(x_1,y_1,t),y_1(0)={\kappa }_1\end{array}\right.\\ (S_2)& \left\{\begin{array}{c}{\dot{x}}_2=f_2(x_2,y_2,t),x_2(0)={\xi }_2\\ \epsilon {\dot{y}}_2=g_2(x_2,y_2,t),y_2(0)={\kappa }_2\end{array}\right.\end{array}$$ (9)

Here (x_i , y_i ), (ξ_i , κ_i ) ∈ X × Y, where X and Y are open sets, $X\subseteq {\mathbb{R}}^n\text{and}Y\subseteq {\mathbb{R}}^s$. The functions f_i and g_i are of class C ¹ with respect to x, y and t, i = 1, 2.

The main result will be that a minimal difference exists between y ₁ and y ₂, independently of ε > 0, provided only that the following two associated ODE systems

$$\begin{array}{rl}(A_1)Y_1^{\prime }& =g_1({\xi }_1,Y_1,0),Y_1(0)={\kappa }_1\\ (A_2)Y_2^{\prime }& =g_2({\xi }_2,Y_2,0),Y_2(0)={\kappa }_2\end{array}$$ (10)

have different solutions. These are the systems obtained when ε is ignored but x ₁ and x ₂ are replaced by their initial values ξ ₂ and ξ ₁ in S ₁ and S ₂, respectively. (We use primes ′ instead of dots to indicate time derivatives, for reasons to be clear below.) We now explain how we can apply the theorem to scale‐invariance. Suppose given a system of the generic form

$$\begin{array}{rl}\dot{x}& =f(x,y,u)\\ \epsilon \dot{y}& =g(x,y,u)\end{array}$$

where generally speaking, the input as well as the state vector (x, y) are of arbitrary dimensions. We think of the components of y as an output, and want to compare the outputs associated to two inputs u (t) and pu (t), for t > 0, when initial states might themselves depend on the values of u (t) and pu (t) for t < 0. This latter dependence is encapsulated in the initial states (ξ ₁, κ ₁) and (ξ ₂, κ ₂), respectively. To apply the theorem, we let f ₁ (x ₁, y ₁, t) := f (x ₁, y ₁, u (t)), g ₁ (x ₁, y ₁, t) := g (x ₁, y ₁, u (t)), f ₂ (x ₂, y ₂, t) := f (x ₂, y ₂, pu (t)) and g ₂ (x ₂, y ₂, t) := g (x ₂, y ₂, pu (t)). The systems considered are quite arbitrary, and allow for feedback and not merely feedforward structures, as will be evident when we study examples.

Our analysis starts from the observation that the transient FCD‐error occurs within a thin boundary layer adjacent to the perturbation moment t = 0, as can be seen in the example shown in Fig. 6. To analyse non‐linear effects occurring within small time intervals, it is convenient to use the stretched time τ = t /ε. Substituting t = ετ into (9), we obtain

$$\begin{array}{rl}(R_1)& \left\{\begin{array}{c}{X}_1^{\prime }=\epsilon f_1(X_1,Y_1,\epsilon \tau ),X_1(0)={\xi }_1\\ Y_1^{\prime }=g_1(X_1,Y_1,\epsilon \tau ),Y_1(0)={\kappa }_1\end{array}\right.\\ (R_2)& \left\{\begin{array}{c}{X}_2^{\prime }=\epsilon f(X_2,Y_2,\epsilon \tau ),X(0)={\xi }_2\\ Y_2^{\prime }=g(X_2,Y_2,\epsilon \tau ),Y(0)={\kappa }_2\end{array}\right.\end{array}$$ (11)

where (·) ′ = d(·)/dτ, and all functions are continuously‐differentiable with respect to the variables, the initial conditions and the parameter ε > 0 as discussed above.

In contrast to the singularly ‐perturbed systems (S ₁) and (S ₂), both systems (R ₁) and (R ₂) are regularly ‐perturbed with respect to ε. It follows that the FCD‐error should be already detected at ε = 0 in which case the systems (R ₁) and (R ₂) can be further reduced to the associated systems (10). Observe that the system (A_i ) is obtained from (R_i ), where X_i is replaced by its initial condition ξ_i , using the reference IVP X′_i = 0, X (0) = ξ_i at ε = 0, i = 1, 2. We will denote the solutions of the systems (R_i ) by $X_i^{\epsilon }(\tau )\text{and}{Y}_i^{\epsilon }(\tau )$, i = 1, 2.

Assume that the solution $(x_i^{\epsilon }(t),y_i^{\epsilon }(t))$ of the system (S_i ) is defined on [0, ∞) for all ε ∈ (0, ε ₀] with some ε ₀ > 0, i = 1, 2. Let $Y_i^0(t)$ be the solution of the associated system (A_i ), i = 1, 2. Then, for each ε ∈ (0, ε ₀] and each 0 ≤ τ ₀ < ∞, we have

$$M_{{\tau }_0}-\epsilon N_{{\tau }_0}\le {∥y_1^{\epsilon }-y_2^{\epsilon }∥}_{[0,\epsilon {\tau }_0]}\le M_{{\tau }_0}+\epsilon N_{{\tau }_0}$$ (12)

where $M_{{\tau }_0}\text{and}{N}_{{\tau }_0}$ are defined as follows:

$$\begin{array}{rl}& M_{{\tau }_0}=\left|Y_2^0({\tau }_0)-Y_1^0({\tau }_0)\right|,\\ & N_{{\tau }_0}=\underset{0\le \epsilon \le {\epsilon }_0}{\max }{∥\frac{\partial Y_1^{\epsilon }(\cdot )}{\partial \epsilon }∥}_{[0,{\tau }_0]}+\underset{0\le \epsilon \le {\epsilon }_0}{\max }{∥\frac{\partial Y_2^{\epsilon }(\cdot )}{\partial \epsilon }∥}_{[0,{\tau }_0]}\end{array}$$ (13)

Theorem 1, which is proved in Section 4, implies that if the solutions of the associated IVP (10) are different, that is, if $Y_1^0({\tau }_0)\ne Y_2^0({\tau }_0)$ for some τ ₀, then as ε → 0 there will always exist a minimal possible non‐zero difference (in supremum norm) between the solutions of the corresponding singularly‐perturbed problems (S ₁) and (S ₂), approximately equal to $M_{{\tau }_0}$. The effect is solely determined by the properties of the fast subsystem.

3 Examples

To illustrate Theorem 1, we consider three examples of increasing complexity: first, we revisit the example of an IFFL, then study a more complicated system in which there is feedback, and finally we look at a published model of the chemotaxis signalling pathway of Dictyostelium discoideum (D. discoideum).

3.1 Applying the general theorem to the IFFL

We begin our analytical study with the application of Theorem 1 to the input‐induced degradation IFFL circuit under time‐scale separation described in (4). To emphasise the value of the scaling p, we shall denote the solution of the p ‐scaled system by (x_p (t), y_p (t)). The systems (S ₁) and (S ₂) from (9) become, in this example

$$\begin{array}{rl}(S_1)& \left\{\begin{array}{c}{\dot{x}}_1=u^{\ast }-x_1,x_1(0)=u_0\\ \epsilon {\dot{y}}_1=x_1-u^{\ast }{y}_1,y_1(0)=1\end{array}\right.\\ (S_2)& \left\{\begin{array}{c}{\dot{x}}_p=p{u}^{\ast }-x_p,x_p(0)=p{u}_0\\ \epsilon {\dot{y}}_p=x_p-p{u}^{\ast }{y}_p,y_p(0)=1\end{array}\right.\end{array}$$ (14)

Here u ₀ = u (0⁻) and u * = u (0⁺) = u (t), t ≥ 0. The associated systems (A ₁) and (A ₂) in (10) are

$$\begin{array}{rl}(A_1)Y_1^{\prime }& =u_0-u^{\ast }{Y}_1,Y_1(0)=1\\ (A_2)Y_p^{\prime }& =p(u_0-u^{\ast }{Y}_p),Y_p(0)=1\end{array}$$ (15)

In what follows we will apply Theorem 1 to the systems (R ₁) and (R ₂) in (11) with the fixed values for ε ₀ and τ ₀ given by

$$\begin{array}{c}{\epsilon }_0=\min \{u^{\ast },u^{\ast }p\}/2,{\tau }_0=\frac{\ln p}{(p-1)u^{\ast }}\end{array}$$ (16)

The constants $M_{{\tau }_0}\text{and}{N}_{{\tau }_0}$ in (13) guaranteed by Theorem 1 satisfy, for these choices of ε ₀ and τ ₀

$$M_{{\tau }_0}=\left|1-\frac{u_0}{u^{\ast }}\right|\left|p-1\right|p^{(p/(1-p))}$$ (17a)

$$N_{{\tau }_0}\le {\tilde{N}}_{{\tau }_0}=\frac{4}{u^{\ast }}\left|1-\frac{u_0}{u^{\ast }}\right|\left(\frac{2(p+1)}{p}+\frac{\ln p}{p-1}\right)$$ (17b)

The expression for $M_{{\tau }_0}$ in (17a) is obtained in Lemma 1. Next we compute $N_{{\tau }_0}$, using the fact that, for this example, where the dynamics are linear, each system (R_i ) in (11) can be solved analytically.

Denote by (x ₁ (t; ε), y ₁ (t; ε)) and (x_p (t; ε, p), y_p (t; ε, p)) the solutions of the systems (S ₁) and (S ₂), respectively. We can find the solutions of (R_i ) as

$$\begin{array}{rl}& X_1^{\epsilon }(\tau )=u^{\ast }+(u_0-u^{\ast }){\mathrm{e}}^{-\epsilon \tau },\\ & Y_1^{\epsilon }(\tau )=1+\frac{(u_0-u^{\ast })}{u^{\ast }-\epsilon }({\mathrm{e}}^{-u^{\ast }\tau }-{\mathrm{e}}^{-\epsilon \tau })\end{array}$$ (18a)

$$\begin{array}{rl}& X_2^{\epsilon }(\tau )=p(u^{\ast }+(u_0-u^{\ast }){\mathrm{e}}^{-\epsilon \tau }),\\ & Y_2^{\epsilon }(\tau )=1+\frac{p(u_0-u^{\ast })}{p{u}^{\ast }-\epsilon }({\mathrm{e}}^{-p{u}^{\ast }\tau }-{\mathrm{e}}^{-\epsilon \tau })\end{array}$$ (18b)

Differentiating $Y_2^{\epsilon }(\tau )$ by ε yields

$$\frac{\partial Y_2^{\epsilon }(\tau )}{\partial \epsilon }=\frac{p(u_0-u^{\ast })}{p{u}^{\ast }-\epsilon }\left(\frac{{\mathrm{e}}^{-p{u}^{\ast }\tau }-{\mathrm{e}}^{-\epsilon \tau }}{p{u}^{\ast }-\epsilon }+\tau {\mathrm{e}}^{-\epsilon \tau }\right)$$ (19)

and hence when p = 1 we have

$$\frac{\partial Y_1^{\epsilon }(\tau )}{\partial \epsilon }=\frac{(u_0-u^{\ast })}{u^{\ast }-\epsilon }\left(\frac{{\mathrm{e}}^{-u^{\ast }\tau }-{\mathrm{e}}^{-\epsilon \tau }}{u^{\ast }-\epsilon }+\tau {\mathrm{e}}^{-\epsilon \tau }\right)$$ (20)

Observe that

$${∥\frac{\partial Y_1^{\epsilon }(\tau )}{\partial \epsilon }∥}_{[0,{\tau }_0]}\le \frac{\left|1-u_0/u^{\ast }\right|}{1-\epsilon /u^{\ast }}\left(\frac{2}{u^{\ast }(1-\epsilon /u^{\ast })}+{\tau }_0\right)$$ (21a)

$${∥\frac{\partial Y_2^{\epsilon }(\tau )}{\partial \epsilon }∥}_{[0,{\tau }_0]}\le \frac{\left|1-u_0/u^{\ast }\right|}{1-\epsilon /(p{u}^{\ast })}\left(\frac{2}{p{u}^{\ast }(1-\epsilon /(p{u}^{\ast }))}+{\tau }_0\right)$$ (21b)

Since ε ₀ is fixed according to (16), then, for all 0 ≤ ε ≤ ε ₀, we obtain 1 − ε /u * ≤ 1/2 and 1 − ε /(pu *) ≤ 1/2, and, hence, the estimates (21) can be simplified as

$${∥\frac{\partial Y_1^{\epsilon }(\tau )}{\partial \epsilon }∥}_{[0,{\tau }_0]}\le 2\left|1-\frac{u_0}{u^{\ast }}\right|\left(\frac{4}{u^{\ast }}+{\tau }_0\right)$$ (22a)

$${∥\frac{\partial Y_2^{\epsilon }(\tau )}{\partial \epsilon }∥}_{[0,{\tau }_0]}\le 2\left|1-\frac{u_0}{u^{\ast }}\right|\left(\frac{4}{p{u}^{\ast }}+{\tau }_0\right)$$ (22b)

Finally, we can use the sum of the right‐hand sides from (22) to obtain ${\tilde{N}}_{{\tau }_0}$ as

$$N_{{\tau }_0}\le {\tilde{N}}_{{\tau }_0}:=4\left|1-\frac{u_0}{u^{\ast }}\right|\left(\frac{2}{u^{\ast }}\frac{(p+1)}{p}+{\tau }_0\right)$$ (23)

Using (16) in (23) followed by simple algebraic rearrangements, we obtain (17b). Note that Theorem 1 gives ${∥y_1^{\epsilon }-y_2^{\epsilon }∥}_{\mathrm{\infty }}\ge M_{{\tau }_0}-\epsilon N_{{\tau }_0}\ge M_{{\tau }_0}-\epsilon {\tilde{N}}_{{\tau }_0}$.

Let us next analyse this example numerically, to see how tight the estimate from the theorem is. With the values of u ₀ and u * used in Fig. 5, we have

$$\begin{array}{rl}{M}_{{\tau }_0}& =0.2\text{and}{\tilde{N}}_{{\tau }_0}=23.636,\text{for}p=2\\ M_{{\tau }_0}& =0.64914\text{and}{\tilde{N}}_{{\tau }_0}=13.169,\text{for}p=20\end{array}$$ (24)

Tables 1 and 2 show numerically computed estimates of maximal error obtained by simulation of the system. This numerically computed magnitude of the FCD‐error belongs to the interval

$$M_{{\tau }_0}-\epsilon {\tilde{N}}_{{\tau }_0}\le E_{\epsilon }\le M_{{\tau }_0}$$ (25)

where E_ε is the magnitude of the FCD‐error, that is, $E_{\epsilon }={∥y_1^{\epsilon }-y_2^{\epsilon }∥}_{[0,T]}$ on a short time interval. We see that $E_{\epsilon }=M_{{\tau }_0}+\mathcal{O}(\epsilon )$. The theoretical prediction is seen numerically to be very tight.

Table 1.

Numerical estimation of the magnitude E_ε of the FCD‐error, as a function of the parameter ε, and its comparison with the theoretical prediction lower bound $M_{{\tau }_0}-\epsilon N_{{\tau }_0}$, where the values of $M_{{\tau }_0}\text{and}{N}_{{\tau }_0}$ are given in (24)

ε	Eε	M − Nε
10−2	0.19803	−0.03636
10−3	0.199800	0.176364
10−4	0.199980	0.197636
10−5	0.199997	0.199763
10−6	0.199999	0.199976

The scaling is p = 2

Table 2.

Numerical estimation of the magnitude E_ε of the FCD‐error, as a function of the parameter ε, and its comparison with the theoretical prediction lower bound $M_{{\tau }_0}-\epsilon N_{{\tau }_0}$, where the values of $M_{{\tau }_0}\text{and}{N}_{{\tau }_0}$ are given in (24)

ε	Eε	M − Nε
10−2	0.647580	0.517450
10−3	0.648983	0.635971
10−4	0.649124	0.647823
10−5	0.649138	0.649008
10−6	0.649139	0.649126

The parameter p is selected as p = 20

3.2 Simple feedback system

Our next example is the non‐linear system (26) obtained by adding a feedback term to the IFFL already analysed, in the form of a y ‐dependent degradation of x

$$\dot{x}=-xy+u^{\ast },x(0)=u_0$$ (26a)

$$\epsilon \dot{y}=x-u^{\ast }y,y(0)=1$$ (26b)

Since an analytical solution cannot be obtained for the non‐linear system (26), we perform a numerical study. We wish to compute the FCD‐error as a function of the parameter ε at the given fixed value of the scaling factor p. As the FCD‐error is a function of two equally important parameters ε and p, the values of ε and p have been sampled in the ranges [0.0005, 0.002] and [0.5, 3.5], respectively. The corresponding 2D and 3D plots are presented in Fig. 9.

Fig. 9.

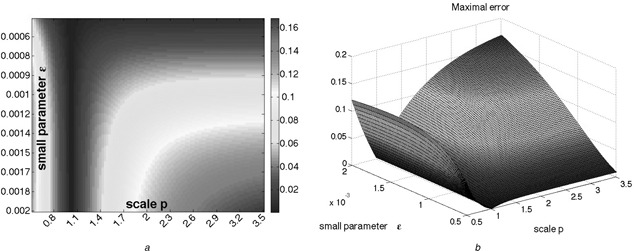
Simple feedback system

(a) Heatmap and (b) 3D plot representing the largest absolute value of the difference between the two outputs y ₂ (t) and y ₁ (t)

Parameter ε was sampled in the range [0.0005, 0.002] and p was sampled in the range [0.5, 3.5]

Hundred different parameters for each were selected

We observe from Fig. 9 that independently of the value of the parameter ε, the magnitude of the FCD‐error remains finite as ε → 0, as predicted by the theorem.

3.3 Chemotaxis signalling pathway of D. discoideum

The analysis of the approximate FCD property can also be carried out for a more complex mathematical model describing the adaptation kinetics in a eukaryotic chemotaxis signalling pathway of D. discoideum [45].

The authors in [45] analysed the dynamics of activated Ras (Ras‐GTP) to changes in chemoeffector cyclic adenosine monophosphate (cAMP), and then proposed alternative models for adaptation. The model that was identified as providing the best fit among several plausible models is given by the following system of six differential equations

$$\begin{array}{rl}{\dot{R}}_1& =k_{R_1}(v+r_1)(R_1^{\text{tot}}-R_1)-k_{-R_1}{R}_1\\ {\dot{R}}_2& =k_{R_2}(v+r_2)(R_2^{\text{tot}}-R_2)-k_{-R_2}{R}_2\\ \mathrm{G}\dot{\mathrm{E}}\mathrm{F}& =k_{\text{GEF}}(R_1+R_2)-k_{-\text{GEF}}\text{GEF}\\ \mathrm{G}\dot{\mathrm{A}}\mathrm{P}& =k_{\text{GAP}}(R_1+R_2)-k_{-\text{GAP}}\text{GAP}\\ {\mathrm{R}\dot{\mathrm{B}}\mathrm{D}}^{\text{CYT}}& =k_{\text{RBD}}^{\text{off}}({\text{RBD}}^{\text{tot}}-{\text{RBD}}^{\text{cyt}})-k_{\text{RBD}}^{\text{on}}{\text{Ras}}^{\text{GTP}}{\text{RBD}}^{\text{cyt}}\\ \mathrm{R}\dot{\mathrm{A}}{\mathrm{S}}^{\text{GTP}}& =k_{\text{RAS}}\text{GEF}({\text{RAS}}^{\text{tot}}-{\text{Ras}}^{\text{GTP}})-k_{-\text{RAS}}{\text{GAPRas}}^{\text{GTP}}\end{array}$$

The symbol v stands for the chemoeffector cAMP, and the authors assumed the existence of two different receptor populations (R ₁ and R ₂, with very different K_d 's) which when bound pool their signals to downstream components (through u). RBD‐GFP (the Ras binding domain of fluorescently tagged human Raf1), is a reporter for Ras‐GTP, and also shows almost perfect adaptation of previously unstimulated cells to cAMP concentrations ranging from 10 ⁻² nM to 1 μM. The constants r ₁ and r ₂ represent levels of constitutive activation. The variables GEF and GAP represent activation and deactivation of RasGEF and RasGAP, Ras^GTP represents the activated Ras and RBD^cyt describes the cytosolic reporter molecule RBD‐GFP.

The best‐fit parameters obtained in [45], and which we use in simulations, are as follows: $R_1^{\text{tot}}=0.1$, $R_2^{\text{tot}}=0.9$, r ₁ = 0.012 nM, r ₂ = 0.115 nM, $k_{R_1}=0.00267{\text{nM}}^{-1}{\mathrm{s}}^{-1}$, $k_{-R_1}=0.16{\mathrm{s}}^{-1}$, $k_{R_2}=0.00244{\text{nM}}^{-1}{\mathrm{s}}^{-1}$, $k_{-R_2}=1.1{\mathrm{s}}^{-1}$, k _GEF = 0.04 s⁻¹, k _−GEF = 0.4 s⁻¹, k _GAP = 0.01 s ⁻¹ , k _−GAP = 0.1 s⁻¹, RAS^tot = 1, k _RAS = 390 s ⁻¹ , k _−RAS = 3126 s⁻¹, RBD^tot = 1, $k_{\text{RBD}}^{\text{off}}=0.53{\mathrm{s}}^{-1}$ and $k_{\text{RBD}}^{\text{on}}=1.0{\mathrm{s}}^{-1}$. With these parameters, and cAMP concentrations which are small yet also satisfy $r_1\ll v(t)\text{and}{r}_2\ll v(t)$, it follows that ${\dot{R}}_1\simeq k_{R_1}{R}_1^{\text{tot}}v-k_{-R_1}{R}_1\text{and}{\dot{R}}_2\simeq k_{R_2}{R}_2^{\text{tot}}v-k_{-R_2}{R}_2$. Since R ₁ (t) and R ₂ (t) are linearly dependent on the external v (t), and hence scale in the same manner as v (t) (cAMP) does, we may think of u (t) = R ₁ (t) + R ₂ (t) as an input to the three‐variable system described by GEF, GAP and Ras^GTP. Since RBD^cyt depends only on Ras^GTP, we may view Ras^GTP as the output y (t). Based on the results from [40, 45], we expect scale‐invariant behaviour, provided that the dynamics of Ras^GTP are fast compared with GEF and GAP, which the identified parameters insure. Conceptually, and ignoring intermediates, we may think of this signalling pathway as an IFFL as shown in Fig. 10.

Fig. 10.

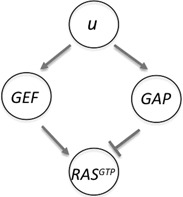
Simplified representation of the adaptation signalling pathway for D. discoideum

As the parameter ε is not explicitly given, we sampled parameters k _RAS and k _−RAS in the range [100, 5000] s ⁻¹ , and simulated the 6D system when using a step from 1 to 2 nM of cAMP, and also when stepping from 2 to 4 nM. For the sampled parameters, we computed |y ₁ (t) − y ₂ (t)|, where y ₁ (t) is a response of Ras^GTP when stepping from 1 to 2 nM and y ₂ (t) stepping from 2 to 4 nM (scale factor p = 2). The numerical results are shown on Figs. 11 and 12. Observe that, as expected from theory, there is a minimal value of the error, for each fixed p, as ε → 0.

Fig. 11.

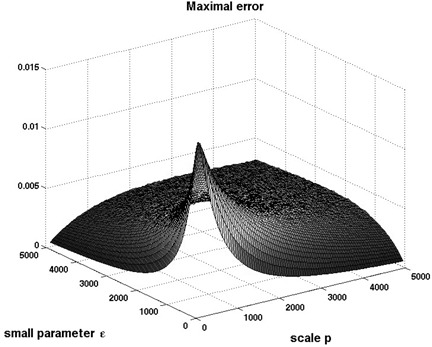
3D plot representing the largest absolute value of the difference between the two outputs y₁ (t) and y₂ (t)

Parameters k _RAS and k _−RAS were each sampled in a manner described in Fig. 12

Fig. 12.

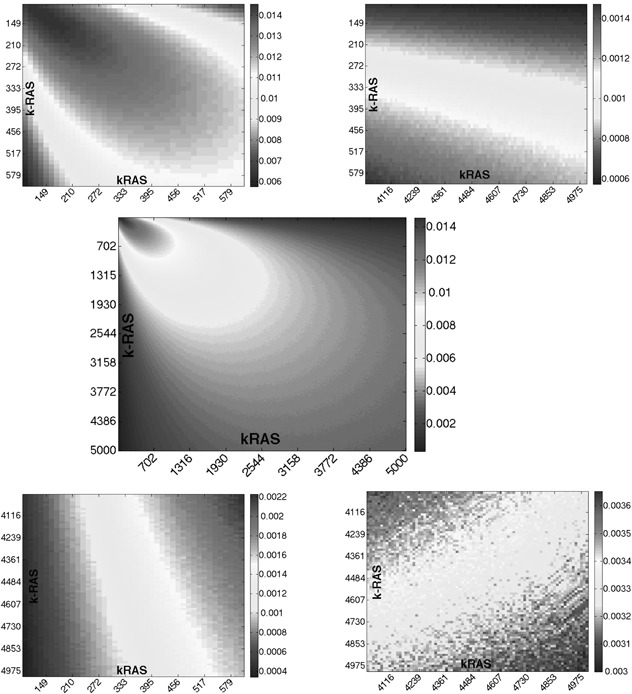
Heatmap representing the largest absolute value of the difference between the two outputs y₁ (t) and y₂ (t) (middle panel)

Top and bottom corners were plotted separately to demonstrate the effect of no‐zero FCD‐error

The parameters k _RAS and k _−RAS were each sampled in the range [100, 5000], with a sampling rate (5000 − 100/400)

4 Proofs

4.1 Proof of Proposition 1

We start with a number of technical results leading to the Proof of Proposition 1.

For any non‐zero positive numbers u *, u ₀, p such that p ≠ 1 and u ₀ ≠ u *, define M = M (u *, u ₀, p) > 0 and T = T (p, u *) > 0 by

$$M:=\left|1-\frac{u_0}{u^{\ast }}\right|p^{(p/(1-p))}\left|1-p\right|,T:=\frac{\ln p}{(p-1)u^{\ast }}$$ (27)

Consider the initial value problems:

$$\begin{array}{rl}\epsilon {\dot{w}}_1& =u_0-u^{\ast }{w}_1,w_1(0)=1\\ \epsilon {\dot{w}}_2& =p{u}_0-p{u}^{\ast }{w}_2,w_2(0)=1\end{array}$$ (28)

Then

$${∥w_1-w_2∥}_{\mathrm{\infty }}=\left|w_1(\epsilon T)-w_2(\epsilon T)\right|=M$$ (29)

The solutions of (28) can be found in an explicit form as

$$\begin{array}{rl}& w_1(t)=\frac{u_0}{u^{\ast }}+\left(1-\frac{u_0}{u^{\ast }}\right){\mathrm{e}}^{-u^{\ast }t/\epsilon },\\ & w_2(t)=\frac{u_0}{u^{\ast }}+\left(1-\frac{u_0}{u^{\ast }}\right){\mathrm{e}}^{-p{u}^{\ast }t/\epsilon }\end{array}$$ (30)

Using (30), we obtain

$$\left|w_1(t)-w_2(t)\right|=\left|1-\frac{u_0}{u^{\ast }}\right|\cdot \left|\phi (t;\epsilon ,p)\right|$$ (31)

where

$$\phi (t;\epsilon ,p)={\mathrm{e}}^{-u^{\ast }t/\epsilon }-{\mathrm{e}}^{-p{u}^{\ast }t/\epsilon }$$ (32)

We see that φ (0; ε, p) = 0 and φ (t; ε, p) → 0 as t → ∞. Then it follows that φ (t; ε, p) has its absolute extrema at 0 < t * < ∞ which can be found using the derivative tests, φ′ (t *; ε, p) = 0, and φ″ (t *; ε, p) ≠ 0.

From the first derivative test φ′ (t; ε, p) = 0, we obtain

$$\begin{array}{rl}{\phi }^{\prime }(t;\epsilon ,p)& =-\frac{u^{\ast }}{\epsilon }{\mathrm{e}}^{-u^{\ast }t/\epsilon }+\frac{p{u}^{\ast }}{\epsilon }{\mathrm{e}}^{-p{u}^{\ast }t/\epsilon }=0\\ t^{\ast }& =\epsilon \frac{\ln p}{(p-1)u^{\ast }}=\epsilon T\end{array}$$ (33)

Using the value for t * in (32), we obtain

$$\phi (t^{\ast };\epsilon ,p)=p^{(p/(1-p))}\cdot (p-1)$$ (34)

Using the second derivative test, we obtain

$${\phi }^{\prime \prime }(t^{\ast };\epsilon ,p)={\left(\frac{u^{\ast }}{\epsilon }\right)}^2{p}^{(1/(1-p))}\cdot (1-p)$$ (35)

From (35), it follows that φ″ (t *; ε, p) > 0 if p < 1, and φ″ (t *; ε, p) < 0 if p > 1, which correspond, respectively, to the absolute minimum, φ (t *; ε, p) < 0, and the absolute maximum, φ (t *; ε, p) > 0, of the function φ (t; ε, p). In both cases, |φ (t *; ε, p)| is the absolute maximum of φ (t; ε, p). □

The following two results allow one to obtain tighter bounds, for the special example of the IFFL in Proposition 1, and also for generalisations in which the scalar x ₁ subsystem is replaced by a generic linear system, than those assured by Theorem 1.

Consider a system

$$\begin{array}{rl}\dot{x}& =qAx+qBv,x(0)=0\\ y& =Cx\end{array}$$ (36)

where $A\in {\mathbb{R}}^{n\times n}$ is Hurwitz, $B\in {\mathbb{R}}^{n\times r}$, $C\in {\mathbb{R}}^{p\times n}$, q > 0, S > 0 and $\left|v(t)\right|\le \overline{\mathrm{\Delta }}$ for all t ∈ [0, S]. Then, there exists a c > 0 independent of q such that

$$\begin{array}{c}\underset{t\in [0,S]}{\max }\left|y(t)\right|\le \overline{\mathrm{\Delta }}\cdot c\end{array}$$ (37)

In fact, we may pick $c={\int }_0^{\mathrm{\infty }}∥C{e}^{As}B∥\mathrm{d}s$.

From (36)

$$\left|y(t)\right|\le \overline{\mathrm{\Delta }}{\int }_0^t∥C{\mathrm{e}}^{qA(t-\tau )}B∥q\mathrm{d}\tau ,\forall t\in [0,S]$$

Introducing the change of variables s = q (t − τ), the previous expression becomes

$$\left|y(t)\right|\le \overline{\mathrm{\Delta }}{\int }_0^{qt}∥C{e}^{As}B∥\mathrm{d}s\le \overline{\mathrm{\Delta }}{\int }_0^{\mathrm{\infty }}∥K(s)∥\mathrm{d}s=\overline{\mathrm{\Delta }}\cdot {∥K∥}_1$$

Define $c={∥K∥}_1<\mathrm{\infty }$. Then

$$\underset{t\in [0,S]}{\sup }\left|y(t)\right|\le \overline{\mathrm{\Delta }}\cdot c$$

as desired. □

For any non‐zero positive numbers u *, u ₀, r, p such that r < 1, p < 1 and u ₀ ≠ u *, let M = M (u *, u ₀, p) > 0 and T = T (p, u *) > 0 be as defined as earlier, and let δ = δ (u *, u ₀, p, r) > 0 be given by

$$\delta :=\left\{\begin{array}{cc}\min \left\{\ln \left(\frac{2\left|u^{\ast }-u_0\right|}{2\left|u^{\ast }-u_0\right|-M(1-r)u^{\ast }}\right),\frac{\ln p}{p-1}\right\},& \text{if}\frac{M(1-r)u^{\ast }}{2\left|u^{\ast }-u_0\right|}<1\\ \frac{\ln p}{p-1},& \text{otherwise}\end{array}\right.$$ (38)

Finally, define ε ₀ = ε ₀ (u *, u ₀, p, r) > 0 by

$${\epsilon }_0:=\delta /T$$

Consider any solution (x (t), y ₁ (t), y ₂ (t)), t ≥ 0, of the following initial‐value system of three differential equations

$$\begin{array}{rl}\dot{x}& =-x+u^{\ast },x(0)=u_0\\ \epsilon {\dot{y}}_1& =x-u^{\ast }{y}_1,y_1(0)=1\\ \epsilon {\dot{y}}_2& =px-p{u}^{\ast }{y}_2,y_2(0)=1\end{array}$$ (39)

where 0 < ε ≤ ε ₀. Then

$$rM\le {∥y_1-y_2∥}_{[0,\delta ]}\le (2-r)M$$

Consider the following equations

$$\begin{array}{rl}\epsilon {\dot{w}}_1& =u_0-u^{\ast }{w}_1,w_1(0)=1\\ \epsilon {\dot{w}}_2& =p{u}_0-p{u}^{\ast }{w}_2,w_2(0)=1\end{array}$$

By Lemma 1, ${∥w_1-w_2∥}_{\mathrm{\infty }}={∥w_1-w_2∥}_{[0,\epsilon T]}=M$, and, since εT ≤ ε ₀ T = δ, this implies that

$${∥w_1-w_2∥}_{[0,\delta ]}=M$$ (40)

as well. Let Δ(t) := x (t) − x (0) = x (t) − u ₀ on the interval t ∈ [0, δ], and $\overline{\mathrm{\Delta }}:={∥\mathrm{\Delta }∥}_{[0,\delta ]}$. Defining e ₁ (t) := y ₁ (t) − w ₁ (t), we have that

$$\epsilon {\dot{e}}_1(t)=\epsilon {\dot{y}}_1(t)-\epsilon {\dot{w}}_1(t)=-u^{\ast }{e}_1(t)+\mathrm{\Delta }(t)$$

or, equivalently

$${\dot{e}}_1(t)=-\frac{u^{\ast }}{\epsilon }{e}_1(t)+\frac{\mathrm{\Delta }(t)}{\epsilon }$$

Applying Proposition 2 with A = − u *, B = 1, C = 1, S = δ and q = 1/ε, we obtain: $\left|e_1(t)\right|\le \overline{\mathrm{\Delta }}/u^{\ast }$ for t ∈ [0, δ_r ], and thus

$${∥y_1-w_1∥}_{[0,\delta ]}\le \frac{\overline{\mathrm{\Delta }}}{u^{\ast }}$$ (41)

Similarly, to determine |y ₂ (t) − w ₂ (t)| we apply Proposition 2 with the same matrices A , B and C , and q = p /ε, and obtain

$${∥y_2-w_2∥}_{[0,\delta ]}\le \frac{\overline{\mathrm{\Delta }}}{u^{\ast }}$$ (42)

By the triangle inequality for norms

$${∥w_1-w_2∥}_{[0,\delta ]}\le {∥w_1-y_1∥}_{[0,\delta ]}+{∥y_1-y_2∥}_{[0,\delta ]}+{∥y_2-w_2∥}_{[0,\delta ]}$$

and therefore, using (40)–(42), we conclude

$${∥y_1-y_2∥}_{[0,\delta ]}\ge M-\frac{2\overline{\mathrm{\Delta }}}{u^{\ast }}$$ (43)

Similarly, from

$${∥y_1-y_2∥}_{[0,\delta ]}\le {∥y_1-w_1∥}_{[0,\delta ]}+{∥w_1-w_2∥}_{[0,\delta ]}+{∥w_2-y_2∥}_{[0,\delta ]}$$

we obtain that

$${∥y_1-y_2∥}_{[0,\delta ]}\le M+\frac{2\overline{\mathrm{\Delta }}}{u^{\ast }}$$ (44)

We next show that

$$\overline{\mathrm{\Delta }}\le \frac{M(1-r)u^{\ast }}{2}$$ (45)

which will imply that

$$\begin{array}{rl}rM& =M-M(1-r)\le {∥y_1-y_2∥}_{[0,\delta ]}\\ & \le M+M(1-r)=(2-r)M\end{array}$$

which is what the proposition asserts. To estimate $\overline{\mathrm{\Delta }}$, we compute the explicit solution x (t) = u * + (u ₀ − u *)e^{− t} , so that Δ(t) = x (t) − u ₀ = (u * − u ₀)(1 − e^{− t} ). This means that

$$\left|\mathrm{\Delta }(t)\right|=\left|u^{\ast }-u_0\right|(1-{\mathrm{e}}^{-t})$$

As |Δ(t)| is an increasing function on [0, δ], showing (45) is the same as showing that

$$\mathrm{\Delta }(\delta )=\left|u^{\ast }-u_0\right|(1-{\mathrm{e}}^{-\delta })\le \frac{M(1-r)u^{\ast }}{2}$$ (46)

hence we prove this last statement.

To prove (46), we first look at the case where δ = (ln p /p − 1), under the condition

$$\frac{M(1-r)u^{\ast }}{2\left|u^{\ast }-u_0\right|}\ge 1$$ (47)

Since 1 − p ^{(1/(1 −p))} < 1, indeed from (47), we have that

$$\begin{array}{rl}\frac{M(1-r)u^{\ast }}{2}& \ge \left|u^{\ast }-u_0\right|\ge \left|u^{\ast }-u_0\right|\left(1-p^{(1/(1-p))}\right)\\ & =\left|u^{\ast }-u_0\right|(1-{\mathrm{e}}^{-\delta })\end{array}$$

Next we consider the two cases for

$$\frac{M(1-r)u^{\ast }}{2\left|u^{\ast }-u_0\right|}<1$$ (48)

depending on what the minimum between

$$\ln \left(\frac{2\left|u^{\ast }-u_0\right|}{2\left|u^{\ast }-u_0\right|-M(1-r)u^{\ast }}\right)$$

and

$$\frac{\ln p}{p-1}$$

is. (Observe that (48) only plays a role in guaranteeing that the expression inside the logarithm is positive and hence the logarithm is well‐defined.) Consider first the case

$$\frac{\ln p}{p-1}\le \ln \left(\frac{2\left|u^{\ast }-u_0\right|}{2\left|u^{\ast }-u_0\right|-M(1-r)u^{\ast }}\right)$$ (49)

With δ selected as a minimum of these two expressions, we again have that Δ(δ) = |u * − u ₀ |(1 − p ^{(1/(1 −p))} ). Working with the condition (49) we have that

$$\begin{array}{rl}-\frac{\ln p}{p-1}& \ge \ln \left(\frac{2\left|u^{\ast }-u_0\right|-M(1-r)u^{\ast }}{2\left|u^{\ast }-u_0\right|}\right)\\ p^{(1/(1-p))}& \ge 1-\frac{M(1-r)u^{\ast }}{2\left|u^{\ast }-u_0\right|}\\ \left|u^{\ast }-u_0\right|\left(1-p^{(1/(1-p))}\right)& \le \frac{M(1-r)u^{\ast }}{2}\end{array}$$ (50)

which is exactly what we were supposed to prove. Finally, consider the case when

$$\begin{array}{c}\ln \left(\frac{2\left|u^{\ast }-u_0\right|}{2\left|u^{\ast }-u_0\right|-M(1-r)u^{\ast }}\right)<\frac{\ln p}{p-1}\end{array}$$ (51)

In this case

$$\begin{array}{rl}\left|\mathrm{\Delta }({\delta }_r)\right|& =\left|u^{\ast }-u_0\right|\left(1-{\mathrm{e}}^{-\ln \left(\left(2\left|u^{\ast }-u_0\right|\right)/\left(2\left|u^{\ast }-u_0\right|-M(1-r)u^{\ast }\right)\right)}\right)\\ & =\left|u^{\ast }-u_0\right|\left(1-\frac{2\left|u^{\ast }-u_0\right|-M(1-r)u^{\ast }}{2\left|u^{\ast }-u_0\right|}\right)\\ & =\left|u^{\ast }-u_0\right|\left(\frac{M(1-r)u^{\ast }}{2\left|u^{\ast }-u_0\right|}\right)=\frac{M(1-r)u^{\ast }}{2}\end{array}$$

which proves the claim (46). This completes the proof of the proposition. □

Proof

Without loss of generality, we may take p < 1. Indeed, if p > 1, we simply exchange the roles of y ₁ and y ₂, and the result is the same. Pick any r ∈ (0, 1) such that M′ < rM and (2 − r) M < M″. Such an r can be found because 2 − r → 1 as r → 1 and define ε ₀ (u *, u ₀, p, r) as in Proposition 3. Fixing any 0 < ε ≤ ε ₀, we have that $x_1^{\epsilon }=x\text{and}{x}_2^{\epsilon }=px$ in that proposition, so $y_1^{\epsilon }=y_1\text{and}{y}_2^{\epsilon }=y_2$ are as there. It follows that

$$rM\le {∥y_1-y_2∥}_{[0,\delta ]}\le (2-r)M$$

Thus, ${∥y_1-y_2∥}_{[0,\delta ]}\ge rM\ge M^{\prime }$ and ${∥y_1^{\epsilon }-y_2^{\epsilon }∥}_{[0,\delta ]}\le (2-r)M<M^{\prime \prime }$, as desired. □

4.2 Proof of the comparison theorem

Let $(X_i^0(\tau ),Y_i^0(\tau ))$ be the solution of the system (R_i ) in (11) at ε = 0. Then, obviously, $Y_i^0(\tau )$ is the solution of the associated system (A_i ) in (10). The following lemma, which will be used to prove Theorem 1, relates the solution of the associated system (A_i ) with the solution of the regularly‐perturbed system (R_i ), i = 1, 2.

Consider the solution $(X_i^{\epsilon }(\tau ),Y_i^{\epsilon }(\tau ))$ of the system (R_i ) in (11) on a closed interval [0, τ ₀] for some fixed τ ₀ > 0. Let $(X_i^{\epsilon }(\tau ),Y_i^{\epsilon }(\tau ))$ be continuously‐differentiable with respect to the parameter ε ∈ [0, ε ₀], ε ₀ > 0. Then

$$\parallel Y_i^{\epsilon }-Y_i^0{\parallel }_{[0,{\tau }_0]}\le N_{{\tau }_0,i}\epsilon$$ (52)

where

$$N_{{\tau }_0,i}:=\underset{0\le \epsilon \le {\epsilon }_0}{\max }{∥\frac{\partial Y_i^{\epsilon }(\cdot )}{\partial \epsilon }∥}_{[0,{\tau }_0]}$$ (53)

for all ε ∈ [0, ε ₀] and i = 1, 2.

The statement is an immediate consequence of the differentiability of solutions with respect to parameters, as a function with values in the space of continuous functions with supremum norm, which in turn follows from the Lagrange form of the mean value theorem, see for example, Theorem 1 in [46]. We provide the details to make the paper self‐contained. Fix any ε ₀ > 0. As the system (R_i ) is of class C ¹ with respect to x, y, ε and t, the solution of the system (R_i ) is also of class C ¹ with respect to ε, see for instance [47]. We have

$$Y_i^{\epsilon }(\tau )-Y_i^0(\tau )=\left({\int }_0^1\frac{\partial Y_i^{\theta \epsilon }(\tau )}{\partial \epsilon }\mathrm{d}\theta \right)\epsilon$$ (54)

Taking norms, and using that θε ∈ [0, ε ₀] when 0 < θ < 1

$$\left|\frac{\partial Y_i^{\epsilon }(\cdot )}{\partial \epsilon }\right|\le N_{{\tau }_0,i}$$

(54) yields (52). □

Using Lemma 2, Theorem 1 can now be proved as follows.

Consider solutions $\left(X_i^{\epsilon }(\tau ),Y_i^{\epsilon }(\tau )\right)$ of the system (R_i ), and the corresponding solutions $Y_1^0(\tau )\text{and}{Y}_2^0(\tau )$ of the associated systems (A_i ). Fix τ ₀ and ε ₀ > 0, and pick $N_{{\tau }_0,i}$, i = 1, 2, as in Lemma 2. Let $N_{{\tau }_0}=N_{{\tau }_0,1}+N_{{\tau }_0,2}$. Then, it follows from (52) that

$$\begin{array}{rl}& \parallel Y_1^{\epsilon }-Y_2^{\epsilon }{\parallel }_{[0,{\tau }_0]}\ge \parallel Y_1^0-Y_2^0{\parallel }_{[0,{\tau }_0]}-\parallel Y_1^{\epsilon }-Y_1^0{\parallel }_{[0,{\tau }_0]}\\ & -\parallel Y_2^{\epsilon }-Y_2^0{\parallel }_{[0,{\tau }_0]}\ge M_{{\tau }_0}-N_{{\tau }_0}\epsilon \end{array}$$ (55)

and also

$$\begin{array}{rl}& \parallel Y_1^{\epsilon }-Y_2^{\epsilon }{\parallel }_{[0,{\tau }_0]}\le \parallel Y_1^0-Y_2^0{\parallel }_{[0,{\tau }_0]}+\parallel Y_1^{\epsilon }-Y_1^0{\parallel }_{[0,{\tau }_0]}\\ & +\parallel Y_2^{\epsilon }+Y_2^0{\parallel }_{[0,{\tau }_0]}\le M_{{\tau }_0}+N_{{\tau }_0}\epsilon \end{array}$$ (56)

for all 0 < ε ≤ ε ₀. Let τ = t /ε, and let $(x_i^{\epsilon }(t),y_i^{\epsilon }(t))=(X_i^{\epsilon }(t/\epsilon ),Y_i^{\epsilon }(t/\epsilon ))$, where t ∈ [0, ετ ₀]. By uniqueness of solutions, we immediately obtain that $(x_i^{\epsilon }(t),y_i^{\epsilon }(t))$ is the solution of the singularly‐perturbed problem (S_i ) on the time interval [0, ετ ₀] for all ε ∈ (0, ε ₀], so ${∥y_2^{\epsilon }-y_1^{\epsilon }∥}_{[0,\epsilon {\tau }_0]}={∥Y_2^{\epsilon }-Y_1^{\epsilon }∥}_{[0,{\tau }_0]}$. It follows from (55) and (56) that

$$M_{{\tau }_0}-N_{{\tau }_0}\epsilon \le \parallel y_2^{\epsilon }-y_1^{\epsilon }{\parallel }_{[0,\epsilon {\tau }_0]}\le M_{{\tau }_0}+\epsilon N_{{\tau }_0}$$ (57)

for all ε ∈ (0, ε ₀]. □

5 Conclusions

Scale‐invariance, also called fold‐change detection, is a phenomenon that has been recently observed experimentally in systems ranging from the E. coli bacterial chemotaxis pathway to the eukaryotic Wnt and EGF pathways. These experimental observations have given rise to follow‐up modelling and theoretical research aimed at analysing systems that display the FCD property.

One of the mechanisms that have been proposed relies upon a time‐scale separation between internal variables and output variables. We have established, through a combination of theoretical and computational analysis, the existence of a fundamental limitation of such a mechanism for fold‐sensing, showing that there is a minimal error that cannot be overcome, no matter how large the separation of time scales is. This violation of the scaling behaviour always occurs at small times. For fast downstream processes, this initial fragility may result in unintended and potentially disruptive consequences.