Abstract
Mitochondrial metabolic function is affected by the morphology and protein organization of the mitochondrial inner membrane. Cardiolipin (CL) is a unique tetra-acyl lipid that is involved in the maintenance of the highly curved shape of the mitochondrial inner membrane as well as spatial organization of the proteins necessary for respiration and oxidative phosphorylation. Cardiolipin has been suggested to self-organize into lipid domains due to its inverted conical molecular geometry, though the driving forces for this organization are not fully understood. In this work, we use coarse-grained molecular dynamics simulations to study the mechanical properties and lipid dynamics in heterogeneous bilayers both with and without CL, as a function of membrane curvature. We find that incorporation of CL increases bilayer deformability and that CL becomes highly enriched in regions of high negative curvature. We further show that another mitochondrial inverted conical lipid, phosphatidylethanolamine (PE), does not partition or increase the deformability of the membrane in a significant manner. Therefore, CL appears to possess some unique characteristics that cannot be inferred simply from molecular geometry considerations.
Graphical abstract
INTRODUCTION
The mitochondrion is a double-membraned, energy generating organelle found in eukaryotes. The mitochondrial outer membrane provides an encompassing envelope with protein pores to control material flux into and out of the organelle. The inner membrane is the site of eukaryotic cellular respiration. It contains morphologically distinct domains: the flat inner boundary membrane, which maintains close proximity to the outer membrane, and the highly curved cristae membrane, which houses the oxidative phosphorylation machinery, as well as other protein complexes.1,2 The inner boundary membrane and cristae are contiguous membranes that are separated by highly curved tubular structures called cristae junctions. The morphology of the inner membrane allows for localization of the proton-motive force-generating machinery in close proximity to the proton-motive force-utilizing ATP synthase, and alteration of inner membrane morphology has been shown to affect metabolic function.3,4 Furthermore, the inner membrane can adjust its shape to account for ADP levels and oxidative stressors,5–7 effecting respiratory regulation through morphological changes. Thus, the mitochondrion must maintain inner membrane superstructure and protein organization within that superstructure, while being able to sense and respond to changing cellular conditions. Inner membrane morphology is maintained by several proteins, chief among them the MICOS complex, which maintains the cristae junction,8–10 and ATP synthase in the cristae. ATP synthase forms rows of dimers along curved regions of the cristae, imposing positive curvature on the matrix-facing leaflet.11–13 Additional proteins affecting morphology include the apoptotic factor tBID14 as well as mitofilin.15
Cardiolipin (CL) is a lipid-enriched in the inner membrane that also plays a role in morphology maintenance. CL is composed of two phosphatidyl groups joined by a central glycerol (Figure 1A). Recent experiments indicate that the two ionizable phosphates are both deprotonated at physiological pH,16–19 imparting a headgroup charge of −2, though other studies have suggested circumstances in which CL would carry a −1 charge.20–23 Under certain conditions, the effective size of the CL headgroup can be small relative to the volume occupied by its four acyl-chains. Lipids that have this molecular shape are referred to as having an inverted conical geometry, and these types of lipids will aggregate into inverse hexagonal (HII) phases. CL aids in assembly and stability of the respiratory complex24 and may affect inner membrane morphology in two ways. First, CL-containing bilayers are prone to adopt highly curved and nonbilayer structures in the presence of high ionic salt concentrations (particularly calcium) or low pH.25–32 A pair of studies have shown that cristae-like invaginations can be induced by directing a flow of protons at giant unilamellar vesicles containing CL, and that this effect is CL-dependent.33,34 Second, CL specifically binds or interacts with many mitochondrial proteins,35,36 and the partitioning of CL to regions of the inner membrane may influence the spatial organization of the proteins. This influence has been demonstrated by depletion of native CL by mutation of cardiolipin synthase or the CL-remodeling protein tafazzin in drosophila cells, which leads to disruption of the network of ATP synthase dimer rows and aberrant inner membrane superstructures.37,38
Figure 1.

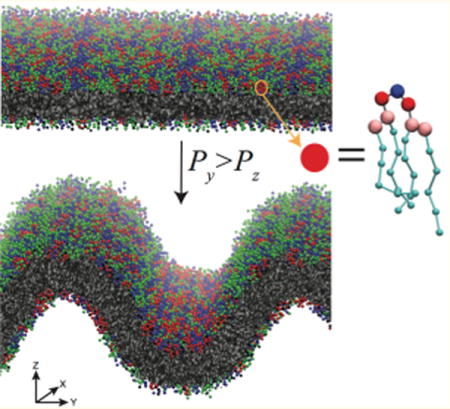
Coarse-grained representation of mitochondrial-mimicking membranes. (A) MARTINI representation of CL; blue = central glycerol, red = phosphate, pink = glycerol, cyan = acyl chains. Beads are not drawn to scale. (B) Side view of the transition from flat to buckled bilayer. Colored beads are the lipids in the main simulation cell, while the gray beads represent lipids in the neighboring periodic images.
CL-dependent protein organization implies that CL can self-organize in an otherwise homogeneously distributed bilayer. CL-enriched domains have been observed in bacterial cell membranes via specific staining with the fluorescent dye Nonyl Acridine Orange (NAO).39–41 These domains occur at the poles and fission sites of rod-like bacteria. The proposed mechanism of CL enrichment is lipid geometry-mediated: CL’s inverted conical shape minimizes curvature frustration in negatively curved regions of bilayers.
Curvature-driven partitioning has been explored in recent years for pure lipid systems42–46 as well as membrane embedded proteins,47–49 though CL has yet to be examined in this context. Molecular dynamics (MD) simulations have been used in several of the curvature-based partitioning studies and provide a powerful means to examine the molecular underpinnings of macromolecular behavior. Previous MD studies involving CL containing bilayers have been performed at both all-atom and coarse-grained modeling levels. One such study involved examination of how the number of acyl chains affects the phase behavior of homogeneous CL systems.50 Many other studies have examined the equilibrium structural properties of cardiolipin-containing bilayers in low curvature/flat geometries.51–55 No large-scale organization of CL has been demonstrated in these studies, although Dahlberg and Maliniak have shown very localized headgroup clustering in their work on coarse-grained CL-containing bilayers.54 In this work we have extended our understanding of CL-containing bilayers through coarse-grained (CG) MD simulations of highly curved systems. We assess the curvature-dependent mechanical properties and enrichment dynamics of CL in these highly curved (buckled) heterogeneous bilayers and demonstrate that CL has unique properties in its ability to promote curved phases and to laterally segregate to regions of high negative curvature. These observations are enabled by a curvature mapping analysis, where we show CL has a much stronger curvature-based segregation propensity than another inverted conical lipid, phosphatidylethanolamine (PE).
METHODS
Simulations were performed using the coarse-grained MARTINI 2.2 force-field with nonpolarizable water56 and implemented using the GROMACS 5 software package.57 A time step of 30 fs was found to be stable and used for all simulations. According to convention, reported simulation times are scaled by a factor of 4 to approximate experimental diffusion rates.56 Nonbonded interactions were calculated following the suggested parameters by de Jong and co-workers,58 where the Lennard-Jones interactions are shifted to zero at the cutoff distance of 1.1 nm using the potential-shift-Verlet modifier. Electrostatics were calculated with a relative dielectric constant of εr = 15 and the potential and forces were shifted to zero at the cutoff of 1.1 nm using the reaction field method. Temperature was maintained at 303 K using the v-rescale algorithm with a time constant of 1 ps. Solvent and lipids were coupled separately. Partitioning behavior of select bilayers was also assessed at 280, 320, and 350 K (see Figure S1).
Anisotropic pressure coupling was maintained using the Parinello–Rahman method59,60 with a time constant of 12 ps. In each system, pressure coupling was turned off in the short lateral dimension (X), fixing the box size in that dimension. To generate the initial buckled membranes, pressure in the membrane normal dimension (Z) was maintained at 1 bar, while pressure in the long lateral dimension (Y) was incrementally increased starting from 1 bar. In other simulations, frames were extracted from along the buckling trajectory and simulated in the NVT ensemble, to perform simulations at constant compressional strain (γ), which is a proxy for constant curvature simulations.
All simulations were carried out on the local UCONN high performance computing cluster (hornet). Simulations were run on compute nodes containing 24 Intel Haswell CPUs. Typical simulations would utilize 96 cores per job and would run at a rate of approximately 52 μs/day. Nodes in the cluster are connected with a high-speed, low-latency FDR infiniband network.
System Setups
All bilayer systems were generated using the CHARMM-GUI Martini Maker.61 The system dimensions were 10 nm by 30 nm in the X and Y directions (bilayer plane), respectively, and 30 nm in the Z direction (bilayer normal). To mimic mitochondrial membrane composition, bilayers were composed of 40% palmitoyl-oleoyl-phosphatidylcholine (POPC), 40% palmitoyl-oleoyl-phosphatidylethanolamine (POPE), and 20% tetraoleoyl cardiolipin (CL) to represent the IM or 50% POPC and 50% POPE with no CL to represent the outer membrane (OM). The effect of net headgroup charge on CL was investigated by performing simulations when the headgroup was both singly deprotonated (−1 charge, CL−1) and doubly deprotonated (−2, CL−2). In the CL−1 model, the headgroup charge was asymmetrically distributed on the phosphate beads, such that one phosphate carried a −1 charge and the other phosphate was neutral. In additional bilayer simulations, the concentration of POPC was increased to 80%, and the remaining fraction was composed of either POPE (PC/PE (4:1)) or CL−1 (PC/CL (4:1)). A full list of the bilayer systems studied including the compositions and total lipid count can be found in Table 1; all percentages indicate the mol %. Sodium ions were added to neutralize system charge. All systems were energy minimized and equilibrated as suggested by CHARMM-GUI, which involved energy minimization followed by five rounds of restrained MD, in which restraints on lipid headgroup beads were successively lowered, and the time step was incrementally increased starting from 2 fs.
Table 1.
Lipid Composition of Simulated Bilayers
| system name | % PC | % PE | % CL−1 | %CL−2 | # of lipids |
|---|---|---|---|---|---|
| PC/PE (1:1) | 50 | 50 | 0 | 0 | 948 |
| PC/PE (4:1) | 80 | 20 | 0 | 0 | 930 |
| PC/CL (4:1) | 80 | 0 | 20 | 0 | 750 |
| IM−1 | 40 | 40 | 20 | 0 | 810 |
| IM−2 | 40 | 40 | 0 | 20 | 810 |
Data Analysis
Simulations were analyzed using GROMACS Tools and custom scripts written in MATLAB 2016. The extent of bilayer compression was quantified by the compressional strain γ,
| (1) |
in which Ly,0 is the original box length in the dimension of compression (Y) and Ly,i is the current box length.62 Monolayer curvatures were calculated by extracting the lipid headgroup coordinates from individual leaflets in the Y (buckling) and Z (normal) directions. The monolayer Y–Z coordinates were fit by a series of cubic smoothing spline functions (see Figure S2). First and second spatial derivatives along the curve were calculated from the spline-fits and the pointwise curvature, C(y), was calculated from
| (2) |
where f′ and f″ are the first and second derivative of the monolayer height function with respect to the Y-dimension, respectively; C has units of inverse distance. The sign of curvature for the top leaflet was inverted to match the convention of curvature sign for a lipid monolayer. This approach allowed us to characterize lipid concentration with respect to curvature, since we can readily assign a local curvature to each lipid, based upon the headgroup position. These head-groups were then binned according to curvature, and relative concentrations at each curvature were calculated.
Ion binding calculations were performed using the gmx mindist tool in GROMACS, with the default cutoff value of 0.6 nm. Molecular packing was examined by considering several geometric properties of PE and CL lipids in nonbuckled states. The tail splay and the tail extension were measured by calculating the distance in the lateral (xy) plane (splay) or normal (z) direction (extension) between a reference bead in the headgroup and the terminal bead of the lipid chains. The phosphate bead was chosen as a reference for PE, and the central glycerol bead was chosen for CL. The area/headgroup was also computed by taking the simulation box dimensions and dividing by half the total number of head groups. CL was considered as having two head groups in this calculation.
RESULTS
To investigate the curvature-dependent properties of cardiolipin containing bilayers, we initially laterally compressed bilayers to generate buckled morphologies (Figure 1B). This was done to accomplish two goals: first to characterize the effect of CL on buckling propensity, and second to develop a system to study the dynamics of mitochondrial lipids in a curved environment. Table 1 describes the bilayer composition for each simulation. We focus first on bilayers mimicking mitochondrial compositions, PC/PE (1:1) is an equimolar binary system of PC and PE without CL and serves as an OM approximation, while our IM systems (inner membrane) refer to ternary systems containing 20% CL carrying either a −1 (IM−1) or −2 (IM−2) charge. We also examine two other binary systems (PC/PE (4:1), PC/CL (4:1)), which have a dominant composition of PC and a minor component of either CL−1 or PE, to evaluate differences between the inverted conical lipids PE and CL in the same background lipid environment. A CG representation of CL is shown in Figure 1A, and a schematic of the buckling procedure is presented in Figure 1B.
Effect of Bilayer Composition on Buckling Transition
Bilayer buckling was induced by applying pressure along the long axis (Y) in the plane of the bilayer, while fixing the box size in the short dimension (X). Pressure in the bilayer normal direction (Z) was maintained at 1 bar, while lateral pressure was initiated at 1 bar and increased in increments of 1 bar every 12 μs. In each simulation, lateral compression yielded a single buckle in the simulation box along the axis of compression (Figure 1B) All simulations reached a maximum compressional strain of roughly γ ≈ 0.6 (Figure 2) and displayed geometrically similar buckles. Once buckling occurred, application of greater lateral pressure did not result in further compressional strain. With pressure increments of 1 bar, transitions from flat to buckled states occurred rapidly at critical pressure differences (Figure 2B) and did not sample stable intermediate states between flat and strongly buckled states. Notably, CL-containing bilayers required lower pressures to induce buckling. The IM−1 bilayer buckled at 4 bar of applied pressure, the IM−2 bilayer at 5 bar, while the PC/PE (1:1) bilayer a required a 6 bar Y-pressure to buckle.
Figure 2.
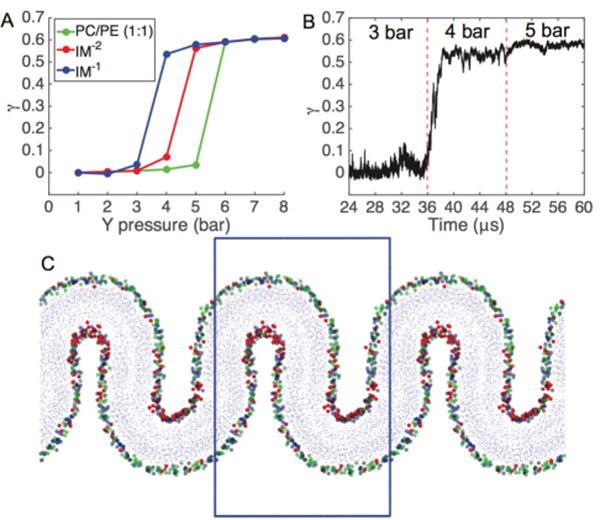
Pressure-induced buckling of mitochondrial membrane mimetic bilayers. (A) The compressional strain (γ) is plotted against the Y-dimension pressure. Each data point represents an averaging of the final 6 μs of a 12 μs simulation. (B) Time course of a buckling event for IM−1 system, which undergoes a buckling transition at the threshold lateral pressure of Py = 4 bar. (C) Snapshot of fully buckled state for IM−1. Head group beads are colored according to blue = PE phosphate, red = CL−1 central glycerol, green = PC phosphate; blue box represents the main simulation cell.
Molecular geometry theory predicts that the introduction of inverted conical lipids, like CL, leads to destabilization of bilayer integrity and a preference for curved environments. The destabilization energy is attributed to a curvature frustration, which is caused by a mismatch between the spontaneous curvature of a given lipid species and the actual monolayer curvature. The difference in behavior between charged CL variants can be explained in terms of headgroup electrostatics: charge repulsion at the level of the headgroup is increased in CL−2, increasing the effective headgroup area and imparting a more cylindrical lipid geometry, decreasing the curvature frustration. Our findings are in agreement with the experimental work of Nichols-Smith et al., who suggested that CL-containing bilayers have a propensity to create folds,63 and the computational work of Dahlberg and Maliniak,54 who showed that introduction of CL to PC and PE bilayers decreases the bending modulus, with CL−1 having a greater effect than CL−2.
Stability Modulation of Intermediate Curvatures
We next focused simulations near the buckling transition pressure difference to observe whether the system displayed the ability to maintain intermediate curvature states or if the system undergoes an abrupt buckling deformation once a critical pressure difference has been exceeded. For each bilayer, we repeated the previous compression procedure, though now using a finer pressure increment and longer simulation times to ensure intermediate states were not artifacts of insufficient sampling times. The pressure was increased in increments of 0.1 bar, along the previously discovered buckling ranges (3.1 to 3.9 bar, 4.1 to 4.9 bar, and 5.1 to 5.9 bar for IM−1, IM−2, and PC/PE (1:1) respectively). Each simulation at a given pressure was run for 36 μs, resulting in 324 μs of sampling for each system. IM−1 and IM−2 bilayers displayed plastic behavior in response to 0.1 bar pressure increases (Figure 3A–B), indicating these systems could be stable in intermediate curvature states in a precise pressure range. These intermediate states display greater curvature fluctuations compared to the stable flat or buckled states. For example, in the IM−1 bilayer system, the average standard deviation of γ (σγ) at pressures between 3.1 and 3.6 bar (calculated for each pressure, then averaged) was 0.064, whereas the stable unbuckled (3 bar) and fully buckled (4 bar) states displayed σγ values of 0.028 and 0.020, respectively.
Figure 3.
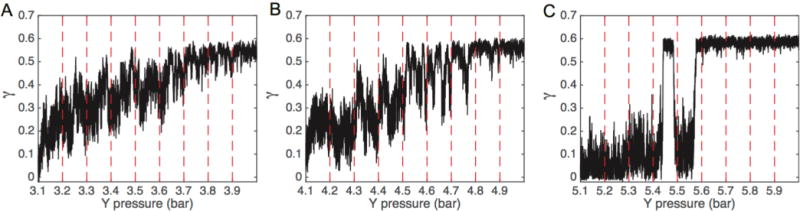
Compressional strain (γ) vs lateral pressure near the buckling transition point. The IM−1 (A), IM−2 (B), and PC/PE (1:1) (C) systems were evaluated by running 36 μs simulations at each pressure in 0.1 bar increments. The dashed red lines indicate points at which the pressure was incremented.
In contrast to the malleable CL-containing bilayers, the PC/PE (1:1) bilayer did not show any tendency to sample intermediate curvatures and displayed a two-state characteristic (Figure 3C). For the PC/PE (1:1) system, as the buckling transition point is approached the bilayer remains relatively flat, exhibiting γ < 0.2 between 5.1 and 5.3 bar. The simulation at 5.4 bar appears to be at (or very near) the critical buckling pressure, as the system jumps to the buckled state (γ ≈ 0.6) and then returns to the flat state within the same simulation. Stable buckled configurations were observed for pressures of 5.5 bar and above.
While a reduced bending modulus in CL-containing bilayers suggests they are more pliable than CL-lacking bilayers,54 one might still expect a CL-lacking bilayer to sample intermediately curved morphologies. Instead, in our systems only the IM−1 and IM−2 bilayers can tune the extent of curvature in response to pressure, whereas the PC/PE (1:1) bilayer samples only two states. One possibility is that a larger system size may allow for CL-lacking bilayers to bend more moderately in response to applied pressures, but we note that our compression dimension (30 nm) is roughly equivalent to the diameter of cristae tubules,64 so our simulations approximate the relevant biological system size magnitudes. These results indicate that CL not only enhances the ability of the mitochondrial IM to assume curvature that is consistent with cristae geometry, but also that CL allows bilayers to respond to more moderate physical stimuli, including the presence of curvature-inducing proteins. We note that, while a lateral applied pressure difference may not have a consistent physiological counterpart, it has been shown that exposure of retinal ganglion cells to elevated hydrostatic pressures leads to morphological changes in the mitochondrial which may be related to optic nerve impairment in glaucoma patients.65 Our observed curvature tuning capabilities of CL-containing bilayers may have significant implications for understanding the importance of CL in generating and maintaining curved morphologies in the mitochondria.
Curvature-Based Lipid Partitioning
We next examined lipid dynamics and clustering in the context of curved bilayers. To enforce a constant curvature environment for bilayers of different compositions, we extracted system configurations along the buckling transition corresponding to specific γ values. We then initiated new simulations in which we fix the box size (NVT) to control the extent of buckling, example configurations at various γ-values are shown in Figure 4A. In these fixed γ simulations, we were able to assign a curvature to each headgroup position, from derivatives of the spline fit function (eq 2) for each monolayer. This curvature mapping approach is illustrated in Figure 4B and Figure S2. The distribution of headgroup curvatures is dependent on the degree of buckling, but is generally characterized by a large peak at moderate positive curvature and a broad shoulder extending into the negative curvatures regions (Figure 5A). Asymmetry between positive and negative curvatures is a consequence of bilayer shape: every invagination with negative curvature has a corresponding patch of positive curvature in the opposite leaflet with a larger radius of curvature.
Figure 4.
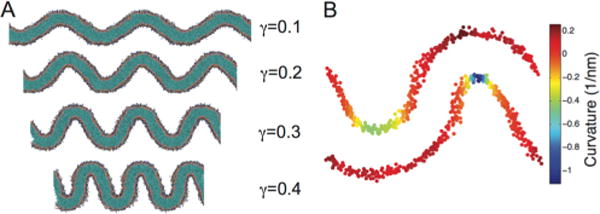
Buckling and curvature mapping. (A) Depiction of bilayers as a function of induced strain (γ). (B) Snapshot of the mapping of bilayer curvature onto the lipid headgroup positions for a γ = 0.3 system.
Figure 5.
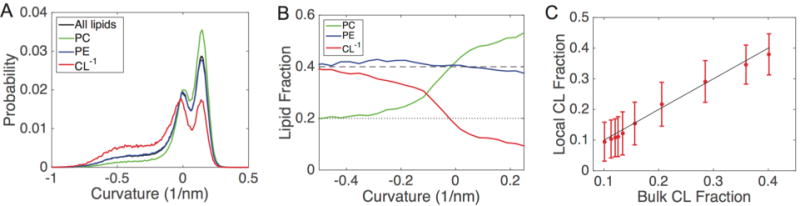
Curvature characterization in buckled bilayers; all data are shown for the IM−1 system at γ = 0.3. (A) Probability distributions of curvatures. Each distribution is normalized by the amount of each lipid type, such that the sum of probabilities for all curves equals one. (B) Lipid fractions as a function of curvature for the same system shown in panel A; the dashed line represents the bulk fraction of PC and PE (40%), and the dotted line represents the bulk fraction of CL−1 (20%). (C) Clustering analysis for CL−1. The system was subdivided based upon curvature, and the bulk fraction of CL−1 is compared with the percentage of CL nearest neighbors around each CL molecule. The solid line represents the well-mixed case (no clustering), where the local concentration matches the bulk concentration.
The lipid probability distributions for the IM−1 system at γ = 0.3 are shown in Figure 5A, where each distribution is normalized. This analysis allowed us to observe that CL−1 is enriched in the negative curvature regions and is suppressed in the positive regions (red curve), whereas PC has the opposite features of accumulating in positive curvatures and reducing in negative curvatures (green curve). Interestingly, PE does not show any curvature dependence, as the PE distribution (blue curve) matches that of the entire bilayer (black curve). To normalize for the asymmetric distribution of headgroup curvatures, we performed an additional analysis by calculating the relative fractional lipid concentration at different curvatures. Figure 5B presents the relative lipid fractions with respect to curvature for the IM−1 bilayer at γ = 0.3. Consistent with our visual inspections and the probability distributions (Figure 5A), this analysis again illustrates that CL−1 migrates to regions of negative curvature and depletes within positive curvature regions. PC shows an opposing trend, enriching at positive curvature and decreasing at negative curvature. This analysis also shows that PE is effectively insensitive to curvature variation in this system, showing only slight depletion at the highest negative curvatures. The IM−2 bilayer showed similar partitioning behavior to IM−1 (Figure 6), although the effect was less dramatic, especially at high γ values. An interesting feature of the lipid fraction analysis is that at zero curvature, we recover the bulk lipid factions for all species. The lipid fractions versus curvatures for all systems described in Table 1 for γ values ranging from 0.05 to 0.45 are presented in Figure S3–S7.
Figure 6.
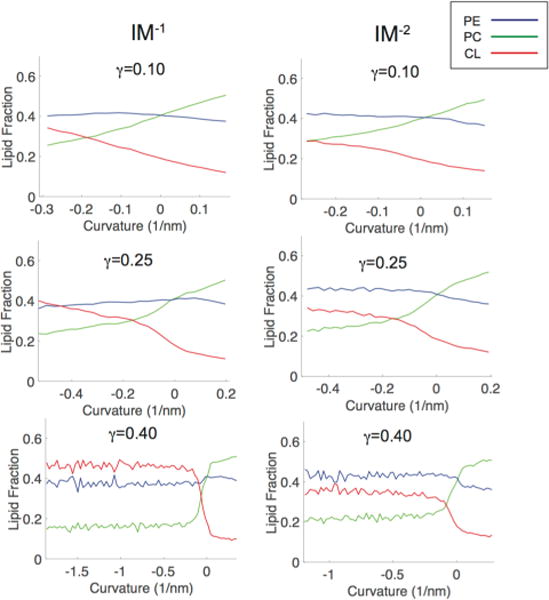
Curvature-based lipid partitioning comparison between ternary systems containing CL carrying either a −1 or −2 charge. The IM−1 systems are shown in the left column and IM−2 systems are shown on the right column. The partitioning curves are shown at three different compressional strain states (γ = 0.1, 0.25, 0.4).
We next addressed the degree to which CL self-associated (to form pure CL nanodomains) within regions of negative curvature. To analyze this, we subdivided the IM−1 system at γ = 0.3 into 10 regions based upon monolayer curvature. In each of these regions we computed the bulk fraction of CL, and also computed a local fraction of CL around each CL molecule. The local fractions were determined by considering the six nearest neighbors around each CL. At all curvatures, the local CL fraction matches the bulk fraction, and therefore CL is well-mixed and does not form self-associating clusters (Figure 5C).
Another analysis we performed was to track the lipid composition in regions of different curvatures as a function of compressional strain (γ). To reduce the dimensionality, we characterize membrane sections as negatively curved (C < −0.05 nm−1), neutral (−0.05 nm−1 ≤ C ≤ 0.05 nm−1) or positively curved (C > 0.05 nm−1). This coarse partitioning results in similar sampling statistics for the three curvature regions, due to the nonlinearity in the curvature-probability curve (Figure 5A). Accumulation of CL at negative curvatures was apparent at membrane strains as low as γ = 0.05 (Figure 7C), which has a mean unsigned curvature of 0.07 nm−1. Increasing γ enhanced lipid segregation at both positive and negative curvatures for both PC (Figure 7A) and CL−1 (Figure 7C) lipids. PE concentration was consistently unaffected by γ for IM−1 (Figure 7B) and IM−2 (Figure S8). The flat segments of every bilayer had fractional compositions equivalent to the bulk bilayer concentrations, a trend that was also independent of γ. The lipid fractions as a function of compressional strain for all other systems described in Table 1 are presented in Figures S8–S11.
Figure 7.
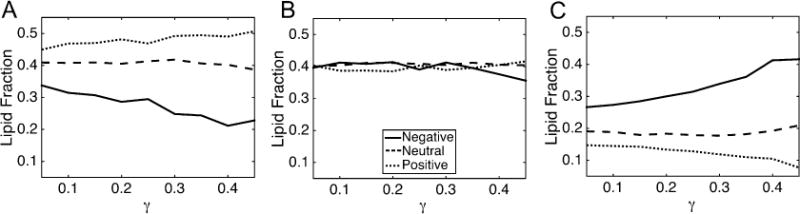
Lipid fractions as a function of compressional strain (curvature) for the IM−1 system. The lipid fraction of PC (A), PE (B) and CL−1 (C) are shown. The legend in B applies to all panels. The curvature regions were defined as follows: negative: C < −0.05; neutral: 0.05 ≤ C ≤ 0.05; positive: C > 0.05, where curvature units are nm−1.
The differential partitioning behavior of CL and PE cannot be explained simply by molecular geometry or a propensity for formation of inverted hexagonal phases (HII). PE is a highly inverted conical lipid with a more negative spontaneous curvature than CL66 and CG simulations have predicted similar bending moduli for pure PE and CL−2 bilayers.54 An explanation for the lack of PE accumulation in negatively curved regions could be that PE is outcompeted for negative curvature positions by CL. To investigate whether PE does have a propensity for negatively curved regions, we examined curvature partitioning in binary systems at γ = 0.30. We simulated binary lipid bilayers containing compositions of 80/20 PC/CL−1 and 80/20 PC/PE, to compare PE and CL−1 partitioning behavior in a background of PC lipids. As in the ternary bilayer systems, CL was found to be highly enriched within high negative curvature regions (Figure 8). In the absence of CL, PE showed a slight propensity for negative curvature, but even at the most negative curvatures, the enrichment was modest, increasing to a lipid fraction of 0.3 in a system with an overall 0.2 PE fraction. Stated another way, in the highest negative curvature regions, PE shows a 50% increase in concentration, while the CL−1 concentration increases by 150% over the bulk fraction. Our results regarding PE clustering is relatively consistent with a previous study examining DPPC/DOPE in a hemifusion system by CG-MD. In that work, 80% enrichment of DOPE was observed in the most negatively curved regions.67
Figure 8.
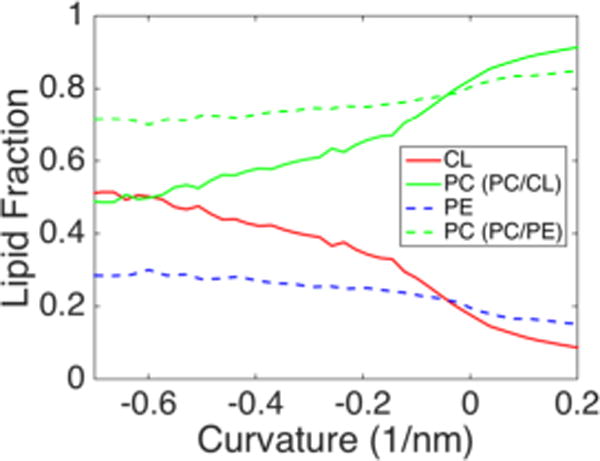
Curvature-mediated partitioning of inverted conical lipids in binary bilayer systems. The curvature-based lipid factions are presented for PC/CL−1 (4:1) (solid) and PC/PE (4:1) (dashed) systems.
Charge Effects
An interesting and perhaps unexpected finding is that CL−1 and CL−2 show similar partitioning behavior (see Figures S3 and S4), despite an expected difference in charge repulsion between head groups and resultant change in molecular geometry. A possible explanation for the lack of significant difference between CL−1 and CL−2 is that sodium ions have stronger binding to the IM−2 bilayer than the IM−1 bilayer, and provide more screening of the headgroup charges. We have examined the ion binding for γ = 0.30 and observe that the number of bound ions to IM−2 is more than double that of IM−1, and the surface charge density of the two systems are comparable. IM−1 has 100 ± 5.2 bound counterions and a surface charge density of −0.11 e/nm2, while IM−2 has 225 ± 7.4 bound counterions and a surface charge density of −0.17 e/nm2). In the absence of counterions, the surface charge density for the two systems would be approximately −0.27 e/nm2 for IM−1 and −0.54 e/nm2 for IM−2.
DISCUSSION
The motivations for conducting this study are numerous. The determination of mechanical properties of bilayers from molecular simulations have been a field of intense investigation for many years,68–71 including approaches that induce buckling to determine these properties.62,72,73 Understanding these properties in multicomponent systems, and particularly how concentration gradients may couple to curvature variations remains an area of open inquiry. In our approach, we are able to correlate curvature and concentration fields, which may provide an important advance for developing more refined theories on concentration effects on membrane properties.
Beyond the interesting and complex questions that arise in purely physical lipid bilayer systems, curved membrane environments can be used to model a number of biologically and physiologically relevant conditions as well. In this work, we have analyzed the effect of CL on bilayer buckling tendencies separately from partitioning behavior of CL in curved bilayers. However, the in-organello implications of these effects may be synergistic. A feedback-loop maybe at play, where CL partitioning can stabilize negative curvatures, which in turn may recruit more CL, which further stabilizes or increases the degree of curvature. Additionally, the role of curvature mediating proteins, such as ATP synthase dimers, likely contributes to this effect as well.12,74 ATP synthase dimers organization in mitochondrial is affected by depletion of CL,38 which may indicate its role to nucleate regions of high curvature, which promotes accumulation of CL, which facilitates further induction of curvature and more recruitment of ATP synthase dimers. The accumulation of these curvature-inducing proteins may relate to our simulations as a physical analogue to the pressure differential used to generate curved bilayers in silico.
Of particular interest is understanding mitochondrial morphology and how aberrant cristae morphology and protein organization may be the result of lipidic modifications.38 Other circumstances found in healthy mitochondria can also be examined in curved bilayers. For example, the transverse distribution of inner membrane CL has been shown to be asymmetric, with significantly more CL in the matrix-facing leaflet than the IMS-facing leaflet.75 The impact of this asymmetry in both buckling propensity and partitioning ability is well suited for the current approach and will be an avenue of future study. Another unique characteristic of the inner membrane is its extremely high protein density, and while some work has been done on the effect of dense protein concentrations on lipid diffusion in flat bilayers,76 we can extend these studies into curvature environments that more closely mimic the mitochondrial inner membrane.
Further work will be required to understand what are the driving forces, beyond molecular geometry/curvature matching, to induce lipid partitioning. As illustrated in our comparisons between PE and CL lipids, it is clear that equilibrium molecular packing considerations cannot predict the portioning properties. However, it is possible that when the bilayers are under an applied stress (nonzero surface tension), the lipid components could have a differential response to the applied stress. We have examined three molecular properties of PE and CL−1, in the background of 80% PC lipids. We calculated the lipid tail splay, tail extension, and mean headgroup area as a function of increasing applied lateral pressure (Figure S12). We only considered simulations in which the bilayer has not buckled. We find that CL−1 shows a greater response to applied pressure in that it both increases the tail splay and has a more dramatic reduction in headgroup area compared to the PE system. Taken together, this could imply that CL−1 is adopting a more inverted conical (negative curvature preferring) geometry. This could relate to a more negative spontaneous curvature, which in the Helfrich theory77 of membrane bending contributes quadratically toward the total bending energy, whereas the bending modulus only has a linear relationship with the bending energy.
In general, the extent of lipid partitioning arises from opposing forces of the energetic benefit of curvature matching and the demixing entropic cost. A theoretical model suggests these contributions are of the same order of magnitude.78 Huang and colleagues proposed that the energetic bonus of curvature matching for a single lipid at physiological curvatures is on the order of 1% of kBT, indicating that curvature preference alone is insufficient for significant partitioning at the cellular scale.79 Instead, clustering of self-interactive lipids is a prerequisite for significant curvature sensing, and that the aggregate cluster is then targeted to curved regions, as partitioning larger membrane components comes at a reduced entropic cost. For CL, short-range attractive forces (mediated by positive counterions) would be counterbalanced by long-range repulsive electrostatics, dictating cluster size. This view is supported by the observation that CL-localization to bacterial cell poles has a minimum concentration threshold.41
Our simulations, however, show CL accumulation at negative curvature, even without nanodomain formation (Figure 5C). The physical basis for this partitioning in the absence of thermodynamic benefits from clustering, as well as the differential behavior of PE and CL, are not yet understood and will require further analysis. However, we can speculate on a few factors that may be driving this partition effect. As suggested by Huang, partitioning a larger species comes at less entropic cost, and therefore the intrinsic larger size of CL relative to PE could play a role in the differential portioning characteristics. If we imagine there are a given number of sites available in the highly curved regions, CL would occupy two of these sites, while PE would only occupy one. The configurational entropy can be idealized as a product of the curved region multiplicity and the flat region multiplicity. Requiring fewer, larger CL lipids in the curved region to achieve a given lipid fraction (above the bulk lipid fraction), allows for a greater number of CL to be available to the flat region. Having a greater number of the minor component lipid in the larger flat region would have a multiplicative (entropic) benefit.
A final consideration is that we are generating curved phases that have zero Gaussian curvature (the product of the principal curvatures). Cristae morphology is highly varied, but our model approximates common cristae shapes having zero Gaussian curvature, such as tubular cristae and lamellar cristae with curved ridges. Membrane shapes exhibiting significant Gaussian curvature are possible in regions of the inner membrane, such as where tubular cristae junctions merge the cristae to the flat IBM. A possible driving force for our observed partitioning behavior is that CL has a preference for zero Gaussian curvature, possibly due to an asymmetric molecular geometry, whereas PE may have a stronger preference nonzero Gaussian curvature phases, such as the inner leaflet of highly curved vesicles. Such a preference could then impact membrane constituent organization between morphologically distinct domains with similar magnitudes of principal curvatures.
CONCLUSIONS
In this work we have examined the curvature-based partitioning of lipids, including cardiolipin, in mixed bilayer systems. From these studies, we have been able to draw several conclusions:
The presence of CL reduces the pressure difference required to generate buckled bilayers.
CL containing bilayers can sample a range of curvature states near the buckling transition pressure difference. This stands in contrast to PC/PE systems, which behave in a two-state fashion, adopting only flat or highly buckled states. This result is suggestive that the presence of CL creates bilayers that are more “tunable”, possibly in response to curvature inducing proteins, and can sample a greater range of morphologies.
CL accumulates in regions of negative curvature, while PE (which is also an inverted conical lipid), displays a much weaker propensity to aggregate in regions of negative curvature.
Understanding why CL has these unique properties may provide key insights into understanding mitochondrial organization and why disease states characterized by altered concentrations of CL and its variants lead to aberrant mitochondrial morphologies.
Supplementary Material
Acknowledgments
Computational resources for this project were provide by the University of Connecticut UITS through access to the Hornet HPC cluster.
Funding
This research has been supported by the NIH through grants R35-GM1197623 (EM), 1R01-GM113092 (NA), and the NSF through a graduate research fellowship, grant #1247393 (K.B.).
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.7b01185.
Additional figures (S1–S11), describing the temperature dependence of CL partitioning, the spline fitting to lipid head groups, the lipid fractions as a function of curvature, and the lipid fractions in different curvature regions as a function of compressional strain (PDF)
ORCID
Kevin J. Boyd: 0000-0002-1500-9062
Eric R. May: 0000-0001-8826-1990
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Notes
The authors declare no competing financial interest.
References
- 1.Vogel F, Bornhövd C, Neupert W, Reichert AS. Dynamic Subcompartmentalization of the Mitochondrial Inner Membrane. J Cell Biol. 2006;175(2):237–247. doi: 10.1083/jcb.200605138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gilkerson RW, Selker JML, Capaldi RA. The Cristal Membrane of Mitochondria Is the Principal Site of Oxidative Phosphorylation. FEBS Lett. 2003;546(2–3):355–358. doi: 10.1016/s0014-5793(03)00633-1. [DOI] [PubMed] [Google Scholar]
- 3.Cogliati S, Frezza C, Soriano ME, Varanita T, Quintana-Cabrera R, Corrado M, Cipolat S, Costa V, Casarin A, Gomes LC, et al. Mitochondrial Cristae Shape Determines Respiratory Chain Supercomplexes Assembly and Respiratory Efficiency. Cell. 2013;155(1):160–171. doi: 10.1016/j.cell.2013.08.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Song DH, Park J, Maurer LL, Lu W, Philbert MA, Sastry AM. Biophysical Significance of the Inner Mitochondrial Membrane Structure on the Electrochemical Potential of Mitochondria. Phys Rev E Stat Nonlin Soft Matter Phys. 2013;88(6):62723. doi: 10.1103/PhysRevE.88.062723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jendrach M, Mai S, Pohl S, Vöth M, Bereiter-Hahn J. Short-and Long-Term Alterations of Mitochondrial Morphology, Dynamics and mtDNA after Transient Oxidative Stress. Mitochondrion. 2008;8(4):293–304. doi: 10.1016/j.mito.2008.06.001. [DOI] [PubMed] [Google Scholar]
- 6.Tondera D, Grandemange S, Jourdain A, Karbowski M, Mattenberger Y, Herzig S, Da Cruz S, Clerc P, Raschke I, Merkwirth C, et al. SLP-2 Is Required for Stress-Induced Mitochondrial Hyperfusion. EMBO J. 2009;28(11):1589–1600. doi: 10.1038/emboj.2009.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Molina AJa, Wikstrom JD, Stiles L, Las G, Mohamed H, et al. Mitochondrial Networking Protects Beta Cells from Nutrient Induced Apoptosis. Diabetes. 2009;58:2303–2315. doi: 10.2337/db07-1781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Harner M, Körner C, Walther D, Mokranjac D, Kaesmacher J, Welsch U, Griffith J, Mann M, Reggiori F, Neupert W. The Mitochondrial Contact Site Complex, a Determinant of Mitochondrial Architecture. EMBO J. 2011;30(21):4356–4370. doi: 10.1038/emboj.2011.379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Horvath SE, Rampelt H, Oeljeklaus S, Warscheid B, van der Laan M, Pfanner N. Role of Membrane Contact Sites in Protein Import into Mitochondria. Protein Sci. 2015;24(3):277–297. doi: 10.1002/pro.2625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rabl R, Soubannier V, Scholz R, Vogel F, Mendl N, Vasiljev-Neumeyer A, Körner C, Jagasia R, Keil T, Baumeister W, et al. Formation of Cristae and Crista Junctions in Mitochondria Depends on Antagonism between Fcj1 and Su E/g. J Cell Biol. 2009;185(6):1047–1063. doi: 10.1083/jcb.200811099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Strauss M, Hofhaus G, Schröder RR, Kühlbrandt W. Dimer Ribbons of ATP Synthase Shape the Inner Mitochondrial Membrane. EMBO J. 2008;27(7):1154–1160. doi: 10.1038/emboj.2008.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Davies KM, Strauss M, Daum B, Kief JH, Osiewacz HD, Rycovska A, Zickermann V, Kuhlbrandt W. Macromolecular Organization of ATP Synthase and Complex I in Whole Mitochondria. Proc Natl Acad Sci USA. 2011;108(34):14121–14126. doi: 10.1073/pnas.1103621108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dudkina NV, Heinemeyer J, Keegstra W, Boekema EJ, Braun HP. Structure of Dimeric ATP Synthase from Mitochondria: An Angular Association of Monomers Induces the Strong Curvature of the Inner Membrane. FEBS Lett. 2005;579(25):5769–5772. doi: 10.1016/j.febslet.2005.09.065. [DOI] [PubMed] [Google Scholar]
- 14.Epand RF, Martinou JC, Fornallaz-Mulhauser M, Hughes DW, Epand RM. The Apoptotic Protein tBid Promotes Leakage by Altering Membrane Curvature. J Biol Chem. 2002;277(36):32632–32639. doi: 10.1074/jbc.M202396200. [DOI] [PubMed] [Google Scholar]
- 15.John GB, Shang Y, Li L, Renken C, Mannella CA, Selker JM, Rangell L, Bennett MJ, Zha J. The Mitochondrial Inner Membrane Protein Mitofilin Controls Cristae Morphology. Mol Biol Cell. 2005;16(3):1543–1554. doi: 10.1091/mbc.E04-08-0697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sathappa M, Alder NN. The Ionization Properties of Cardiolipin and Its Variants in Model Bilayers. Biochim Biophys Acta, Biomembr. 2016;1858(6):1362–1372. doi: 10.1016/j.bbamem.2016.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Olofsson G, Sparr E. Ionization Constants pKa of Cardiolipin. PLoS One. 2013;8(9):e73040. doi: 10.1371/journal.pone.0073040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Malyshka D, Pandiscia LA, Schweitzer-Stenner R. Cardiolipin Containing Liposomes Are Fully Ionized at Physiological pH. An FT-IR Study of Phosphate Group Ionization. Vib Spectrosc. 2014;75:86–92. [Google Scholar]
- 19.Kooijman EE, Swim LA, Graber ZT, Tyurina YY, Bayir H, Kagan VE. Magic Angle Spinning 31P NMR Spectroscopy Reveals Two Essentially Identical Ionization States for the Cardiolipin Phosphates in Phospholipid Liposomes. Biochim Biophys Acta, Biomembr. 2017;1859(1):61–68. doi: 10.1016/j.bbamem.2016.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kates M, Syz JY, Gosser D, Haines TH. pH-Dissociation Characteristics of Cardiolipin and Its 2′-deoxy Analogue. Lipids. 1993;28(10):877–882. doi: 10.1007/BF02537494. [DOI] [PubMed] [Google Scholar]
- 21.Nichols-Smith S, Kuhl T. Electrostatic Interactions between Model Mitochondrial Membranes. Colloids Surf, B. 2005;41(2–3):121–127. doi: 10.1016/j.colsurfb.2004.11.003. [DOI] [PubMed] [Google Scholar]
- 22.Hielscher R, Wenz T, Hunte C, Hellwig P. Monitoring the Redox and Protonation Dependent Contributions of Cardiolipin in Electrochemically Induced FTIR Difference Spectra of the Cytochrome bc1 Complex from Yeast. Biochim Biophys Acta, Bioenerg. 2009;1787(6):617–625. doi: 10.1016/j.bbabio.2009.01.006. [DOI] [PubMed] [Google Scholar]
- 23.Sidiq S, Verma I, Pal SK. pH-Driven Ordering Transitions in Liquid Crystal Induced by Conformational Changes of Cardiolipin. Langmuir. 2015;31(16):4741–4751. doi: 10.1021/acs.langmuir.5b00798. [DOI] [PubMed] [Google Scholar]
- 24.Pfeiffer K, Gohil V, Stuart RA, Hunte C, Brandt U, Greenberg ML, Schägger H. Cardiolipin Stabilizes Respiratory Chain Supercomplexes. J Biol Chem. 2003;278(52):52873–52880. doi: 10.1074/jbc.M308366200. [DOI] [PubMed] [Google Scholar]
- 25.Seddon JM, Kaye RD, Marsh D. Induction of the Lamellar-Inverted Hexagonal Phase Transition in Cardiolipin by Protons and Monovalent Cations. Biochim Biophys Acta, Biomembr. 1983;734(2):347–352. [Google Scholar]
- 26.Arslan P, Beltrame M, Muscatello U. Ultrastructural Characterization of Cardiolipin Liquid-Crystalline Structures in the Absence and the Presence of Divalent Cations. Micron (1969–1983) 1980;11(2):115–125. [Google Scholar]
- 27.Cullis PR, Verkleij AJ, Ververgaert PHJT. Polymorphic Phase Behaviour of Cardiolipin as Detected by 31P NMR and Freeze-Fracture Techniques. Effects of Calcium, Dibucaine and Chlorpromazine. Biochim Biophys Acta, Biomembr. 1978;513(1):11–20. doi: 10.1016/0005-2736(78)90107-4. [DOI] [PubMed] [Google Scholar]
- 28.de Kruijff B, Verkleij AJ, Leunissen-Bijvelt J, van Echteld CJA, Hille J, Rijnbout H. Further Aspects of the Ca2+-Dependent Polymorphism of Bovine Heart Cardiolipin. Biochim Biophys Acta, Biomembr. 1982;693(1):1–12. doi: 10.1016/0005-2736(82)90464-3. [DOI] [PubMed] [Google Scholar]
- 29.Antoinette Killian J, Koorengevel MC, Bouwstra JA, Gooris G, Dowhan W, de Kruijff B. Effect of Divalent Cations on Lipid Organization of Cardiolipin Isolated from Escherichia Coli Strain AH930. Biochim Biophys Acta, Biomembr. 1994;1189(2):225–232. doi: 10.1016/0005-2736(94)90069-8. [DOI] [PubMed] [Google Scholar]
- 30.Ortiz A, Killian JA, Verkleij a J, Wilschut J. Membrane Fusion and the Lamellar-to-Inverted-Hexagonal Phase Transition in Cardiolipin Vesicle Systems Induced by Divalent Cations. Biophys J. 1999;77(4):2003–2014. doi: 10.1016/S0006-3495(99)77041-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rand RP, Sengupta S. Cardiolipin Forms Hexagonal Structures with Divalent Cations. Biochim Biophys Acta, Biomembr. 1972;255(2):484–492. doi: 10.1016/0005-2736(72)90152-6. [DOI] [PubMed] [Google Scholar]
- 32.Vail WJ, Stollery JG. Phase Changes of Cardiolipin Vesicles Mediated by Divalent Cations. Biochim Biophys Acta, Biomembr. 1979;551(1):74–84. doi: 10.1016/0005-2736(79)90354-7. [DOI] [PubMed] [Google Scholar]
- 33.Khalifat N, Puff N, Bonneau S, Fournier J-B, Angelova MI. Membrane Deformation under Local pH Gradient: Mimicking Mitochondrial Cristae Dynamics. Biophys J. 2008;95(10):4924–4933. doi: 10.1529/biophysj.108.136077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Khalifat N, Fournier J, Angelova MI, Puff N. Biochimica et Biophysica Acta Lipid Packing Variations Induced by pH in Cardiolipin-Containing Bilayers: The Driving Force for the Cristae-like Shape Instability. Biochim Biophys Acta, Biomembr. 2011;1808(11):2724–2733. doi: 10.1016/j.bbamem.2011.07.013. [DOI] [PubMed] [Google Scholar]
- 35.Planas-Iglesias J, Dwarakanath H, Mohammadyani D, Yanamala N, Kagan VE, Klein-Seetharaman J. Cardiolipin Interactions with Proteins. Biophys J. 2015;109(6):1282–1294. doi: 10.1016/j.bpj.2015.07.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bajaj R, Munari F, Becker S, Zweckstetter M. Interaction of the Intermembrane Space Domain of Tim23 Protein with Mitochondrial Membranes. J Biol Chem. 2014;289(50):34620–34626. doi: 10.1074/jbc.M114.595702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Acehan D, Khuchua Z, Houtkooper RH, Malhotra A, Kaufman J, Vaz FM, Ren M, Rockman HA, Stokes DL, Schlame M. Distinct Effects of Tafazzin Deletion in Differentiated and Undifferentiated Mitochondria. Mitochondrion. 2009;9(2):86–95. doi: 10.1016/j.mito.2008.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Acehan D, Malhotra A, Xu Y, Ren M, Stokes DL, Schlame M. Cardiolipin Affects the Supramolecular Organization of ATP Synthase in Mitochondria. Biophys J. 2011;100(9):2184–2192. doi: 10.1016/j.bpj.2011.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mileykovskaya E, Dowhan W. Visualization of Phospholipid Domains in Escherichia Coli by Using the Cardiolipin-Specific Fluorescent Dye 10-N-Nonyl Acridine Orange. J Bacteriol. 2000;182(4):1172–1175. doi: 10.1128/jb.182.4.1172-1175.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kawai F, Shoda M, Harashima R, Sadaie Y, Hara H, Matsumoto K. Cardiolipin Domains in Bacillus Subtilis Marburg Membranes. J Bacteriol. 2004;186(5):1475–1483. doi: 10.1128/JB.186.5.1475-1483.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Romantsov T, Helbig S, Culham DE, Gill C, Stalker L, Wood JM. Cardiolipin Promotes Polar Localization of Osmosensory Transporter ProP in Escherichia Coli. Mol Microbiol. 2007;64(6):1455–1465. doi: 10.1111/j.1365-2958.2007.05727.x. [DOI] [PubMed] [Google Scholar]
- 42.Cooke IR, Deserno M. Coupling between Lipid Shape and Membrane Curvature. Biophys J. 2006;91(2):487–495. doi: 10.1529/biophysj.105.078683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Parthasarathy R, Yu C, Groves JT. Curvature-Modulated Phase Separation in Lipid Bilayer Membranes. Langmuir. 2006;22(11):5095–5099. doi: 10.1021/la060390o. [DOI] [PubMed] [Google Scholar]
- 44.Sorre B, Callan-Jones A, Manneville J-B, Nassoy P, Joanny J-F, Prost J, Goud B, Bassereau P. Curvature-Driven Lipid Sorting Needs Proximity to a Demixing Point and Is Aided by Proteins. Proc Natl Acad Sci USA. 2009;106(14):5622–5626. doi: 10.1073/pnas.0811243106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Liang Q, Ma YQ. Curvature-Induced Lateral Organization in Mixed Lipid Bilayers Supported on a Corrugated Substrate. J Phys Chem B. 2009;113(23):8049–8055. doi: 10.1021/jp9005789. [DOI] [PubMed] [Google Scholar]
- 46.Callan-Jones A, Sorre B, Bassereau P. Curvature-Driven Lipid Sorting in Biomembranes. Cold Spring Harbor Perspect Biol. 2011;3:a004648. doi: 10.1101/cshperspect.a004648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Reynwar BJ, Illya G, Harmandaris VA, Muller MM, Kremer K, Deserno M. Aggregation and Vesiculation of Membrane Proteins by Curvature-Mediated Interactions. Nature. 2007;447(7143):461–464. doi: 10.1038/nature05840. [DOI] [PubMed] [Google Scholar]
- 48.Parton DL, Klingelhoefer JW, Sansom MSP. Aggregation of Model Membrane Proteins, Modulated by Hydrophobic Mismatch, Membrane Curvature, and Protein Class. Biophys J. 2011;101(3):691–699. doi: 10.1016/j.bpj.2011.06.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wu QY, Liang Q. Interplay between Curvature and Lateral Organization of Lipids and Peptides/proteins in Model Membranes. Langmuir. 2014;30(4):1116–1122. doi: 10.1021/la4039123. [DOI] [PubMed] [Google Scholar]
- 50.Dahlberg M. Polymorphic Phase Behavior of Cardiolipin Derivatives Studied by Coarse-Grained Molecular Dynamics. J Phys Chem B. 2007;111(25):7194–7200. doi: 10.1021/jp071954f. [DOI] [PubMed] [Google Scholar]
- 51.Dahlberg M, Maliniak A. Molecular Dynamics Simulations of Cardiolipin Bilayers. J Phys Chem B. 2008;112(37):11655–11663. doi: 10.1021/jp803414g. [DOI] [PubMed] [Google Scholar]
- 52.Pöyry S, Róg T, Karttunen M, Vattulainen I. Mitochondrial Membranes with Mono- and Divalent Salt: Changes Induced by Salt Ions on Structure and Dynamics. J Phys Chem B. 2009;113(47):15513–15521. doi: 10.1021/jp905915m. [DOI] [PubMed] [Google Scholar]
- 53.Róg T, Martinez-Seara H, Munck N, Oresic M, Karttunen M, Vattulainen I. Role of Cardiolipins in the Inner Mitochondrial Membrane: Insight Gained through Atom-Scale Simulations. J Phys Chem B. 2009;113(11):3413–3422. doi: 10.1021/jp8077369. [DOI] [PubMed] [Google Scholar]
- 54.Dahlberg M, Maliniak A. Mechanical Properties of Coarse-Grained Bilayers Formed by Cardiolipin and Zwitterionic Lipids. J Chem Theory Comput. 2010;6(5):1638–1649. doi: 10.1021/ct900654e. [DOI] [PubMed] [Google Scholar]
- 55.Aguayo D, González-Nilo FD, Chipot C. Insight into the Properties of Cardiolipin Containing Bilayers from Molecular Dynamics Simulations, Using a Hybrid All-Atom/United-Atom Force Field. J Chem Theory Comput. 2012;8(5):1765–1773. doi: 10.1021/ct200849k. [DOI] [PubMed] [Google Scholar]
- 56.Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, De Vries AH. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J Phys Chem B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 57.Berendsen HJC, van der Spoel D, van Drunen R. ROMACS: A Message-Passing Parallel Molecular Dynamics Implementation. Comput Phys Commun. 1995;91(1–3):43–56. [Google Scholar]
- 58.De Jong DH, Baoukina S, Ingólfsson HI, Marrink SJ. Martini Straight: Boosting Performance Using a Shorter Cutoff and GPUs. Comput Phys Commun. 2016;199:1–7. [Google Scholar]
- 59.Parrinello M. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J Appl Phys. 1981;52(12):7182. [Google Scholar]
- 60.Nosé S, Klein ML. Constant Pressure Molecular Dynamics for Molecular Systems. Mol Phys. 1983;50(5):1055–1076. [Google Scholar]
- 61.Qi Y, Ingólfsson HI, Cheng X, Lee J, Marrink SJ, Im W. CHARMM-GUI Martini Maker for Coarse-Grained Simulations with the Martini Force Field. J Chem Theory Comput. 2015;11(9):4486–4494. doi: 10.1021/acs.jctc.5b00513. [DOI] [PubMed] [Google Scholar]
- 62.Diggins P, IV, Deserno M. Determining the Bending Modulus of a Lipid Membrane by Simulating Buckling. J Chem Phys. 2013;138(21):214110. doi: 10.1063/1.4808077. [DOI] [PubMed] [Google Scholar]
- 63.Nichols-Smith S, Teh S-Y, Kuhl TL. Thermodynamic and Mechanical Properties of Model Mitochondrial Membranes. Biochim Biophys Acta, Biomembr. 2004;1663(1–2):82–88. doi: 10.1016/j.bbamem.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 64.Lea PJ, Temkin RJ, Freeman KB, Mitchell Ga, Robinson BH. Variations in Mitochondrial Ultrastructure and Dynamics Observed by High Resolution Scanning Electron Microscopy (HRSEM) Microsc Res Tech. 1994;27(4):269–277. doi: 10.1002/jemt.1070270402. [DOI] [PubMed] [Google Scholar]
- 65.Ju WK, Liu Q, Kim KY, Crowston JG, Lindsey JD, Agarwal N, Ellisman MH, Perkins GA, Weinreb RN. Elevated Hydrostatic Pressure Triggers Mitochondrial Fission and Decreases Cellular ATP in Differentiated RGC-5 Cells. Invest Ophthalmol Visual Sci. 2007;48(5):2145–2151. doi: 10.1167/iovs.06-0573. [DOI] [PubMed] [Google Scholar]
- 66.Chen Y-F, Tsang K-Y, Chang W-F, Fan Z-a. Differential Dependencies on [Ca 2+ ] and Temperature of the Monolayer Spontaneous Curvatures of DOPE, DOPA and Cardiolipin: Effects of Modulating the Strength of the Inter-Headgroup Repulsion. Soft Matter. 2015;11(20):4041–4053. doi: 10.1039/c5sm00577a. [DOI] [PubMed] [Google Scholar]
- 67.Nishizawa M, Nishizawa K. Curvature-Driven Lipid Sorting: Coarse-Grained Dynamics Simulations of a Membrane Mimicking a Hemifusion Intermediate. J Biophys Chem. 2010;1(2):86–95. [Google Scholar]
- 68.Levine ZA, Venable RM, Watson MC, Lerner MG, Shea JE, Pastor RW, Brown FLH. Determination of Biomembrane Bending Moduli in Fully Atomistic Simulations. J Am Chem Soc. 2014;136(39):13582–13585. doi: 10.1021/ja507910r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Johner N, Harries D, Khelashvili G. Curvature and Lipid Packing Modulate the Elastic Properties of Lipid Assemblies: Comparing HII and Lamellar Phases. J Phys Chem Lett. 2014;5(23):4201–4206. doi: 10.1021/jz5022284. [DOI] [PubMed] [Google Scholar]
- 70.Khelashvili G, Kollmitzer B, Heftberger P, Pabst G, Harries D. Calculating the Bending Modulus for Multicomponent Lipid Membranes in Different Thermodynamic Phases. J Chem Theory Comput. 2013;9(9):3866–3871. doi: 10.1021/ct400492e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Hu M, Briguglio JJ, Deserno M. Determining the Gaussian Curvature Modulus of Lipid Membranes in Simulations. Biophys J. 2012;102(6):1403–1410. doi: 10.1016/j.bpj.2012.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Noguchi H. Anisotropic Surface Tension of Buckled Fluid Membranes. Phys Rev E - Stat Nonlinear, Soft Matter Phys. 2011;83(6):061919. doi: 10.1103/PhysRevE.83.061919. [DOI] [PubMed] [Google Scholar]
- 73.Wang X, Deserno M. Determining the Lipid Tilt Modulus by Simulating Membrane Buckles. J Phys Chem B. 2016;120(26):6061–6073. doi: 10.1021/acs.jpcb.6b02016. [DOI] [PubMed] [Google Scholar]
- 74.Davies KM, Anselmi C, Wittig I, Faraldo-Gomez JD, Kuhlbrandt W. Structure of the Yeast F1Fo-ATP Synthase Dimer and Its Role in Shaping the Mitochondrial Cristae. Proc Natl Acad Sci USA. 2012;109(34):13602–13607. doi: 10.1073/pnas.1204593109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Krebs JJR, Hauser H, Carafoli E. Asymmetric Distribution of Phospholipids in the Inner Membrane of Beef Heart Mitochondria. J Biol Chem. 1979;254(12):5308–5316. [PubMed] [Google Scholar]
- 76.Javanainen M, Hammaren H, Monticelli L, Jeon J-H, Miettinen MS, Martinez-Seara H, Metzler R, Vattulainen I. Anomalous and Normal Diffusion of Proteins and Lipids in Crowded Lipid Membranes. Faraday Discuss. 2013;161:397–417. doi: 10.1039/c2fd20085f. [DOI] [PubMed] [Google Scholar]
- 77.Helfrich W. Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z Naturforsch, C: J Biosci. 1973;28(11–12):693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 78.Derganc J. Curvature-Driven Lateral Segregation of Membrane Constituents in Golgi Cisternae. Phys Biol. 2007;4(4):317–324. doi: 10.1088/1478-3975/4/4/008. [DOI] [PubMed] [Google Scholar]
- 79.Huang KC, Mukhopadhyay R, Wingreen NS. A Curvature-Mediated Mechanism for Localization of Lipids to Bacterial Poles. PLoS Comput Biol. 2006;2(11):e151. doi: 10.1371/journal.pcbi.0020151. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


