The Timing of Reward-Seeking Action Tracks Visually Cued Theta Oscillations in Primary Visual Cortex

Abstract

An emerging body of work challenges the view that primary visual cortex (V1) represents the visual world faithfully. Theta oscillations in the local field potential (LFP) of V1 have been found to convey temporal expectations and, specifically, to express the delay between a visual stimulus and the reward that it portends. We extend this work by showing how these oscillatory states in male, wild-type rats can even relate to the timing of a visually cued reward-seeking behavior. In particular, we show that, with training, high precision and accuracy in behavioral timing tracks the power of these oscillations and the time of action execution covaries with their duration. These LFP oscillations are also intimately related to spiking responses at the single-unit level, which themselves carry predictive timing information. Together, these observations extend our understanding of the role of cortical oscillations in timing generally and the role of V1 in the timing of visually cued behaviors specifically.

SIGNIFICANCE STATEMENT Traditionally, primary visual cortex (V1) has been regarded as playing a purely perceptual role in stimulus-driven behaviors. Recent work has challenged that view by showing that theta oscillations in rodent V1 may come to convey timed expectations. Here, we show that these theta oscillations carry predictive information about timed reward-seeking actions, thus elucidating a behavioral role for theta oscillations in V1 and extending our understanding of the role of V1 in decision making.

Introduction

Timed responses to environmental stimuli are crucial for survival. Such stimulus-driven behaviors require knowledge of both what to expect and when and many high-level brain areas have been shown to report this information. Neurons in the striatum (Hikosaka et al., 1989; Apicella et al., 1992; Shidara et al., 1998; Tremblay et al., 1998), orbitofrontal cortex (Schoenbaum et al., 1998; Tremblay and Schultz, 1999; Hikosaka and Watanabe, 2000), and amygdala (Schoenbaum et al., 1998) have been found to express temporal predictions about outcomes, whereas dorsolateral premotor cortex (Okano and Tanji, 1987; Romo and Schultz, 1987; Kurata and Wise, 1988), prefrontal cortex (Watanabe, 1996), and distinct regions of the striatum (Schultz and Romo, 1988) have been implicated in translating this temporal information into action. Sensory regions such as primary visual cortex (V1), in which the earliest stage of cortical visual processing occurs, are typically regarded as contributing only to the first phase of such behaviors: perception (Hubel and Wiesel, 1962, 1965). However, recent work suggests that experience-dependent plasticity in V1 can also give rise to information about when to expect an outcome (Shuler and Bear, 2006; Sharma et al., 2015). It has even been shown that such sustained modulations in firing rate in V1 may be involved in visually timed behaviors (Namboodiri et al., 2015).

Oscillations in V1 local field potentials (LFPs) have also generally been interpreted as relaying perceptual information. One of the key roles for oscillations, particularly in the gamma range, may be to enhance binding of visual features to create a complete visual percept (Eckhorn et al., 1988, 1990). Another crucial function of oscillations is to facilitate anticipation of upcoming stimuli, though this type of predictive information is often reported as lasting on the order of only tens or hundreds of milliseconds (Engel et al., 2001; Arnal and Giraud, 2012; Gavornik and Bear, 2014). However, recent observations have also pointed to a role for oscillations in stimulus prediction on the order of seconds (Lima et al., 2011; Sharma et al., 2015), the temporal range that is crucial in many cognitive tasks. Moreover, it has been found that theta oscillations in the LFP of well trained rodents predict the expected delay to reward (Zold and Hussain Shuler, 2015). Although it is of interest that this LFP signal expresses temporal information, it is not known how it relates to interval timing activity expressed by V1 neurons nor to the performance of interval timing behavior.

To address this, we analyzed data from a task (Namboodiri et al., 2015) in which rodents with chronic electrode implants in V1 execute a timed action in response to a visual cue to achieve reward. Surprisingly, we found that these visual cues evoked theta oscillations in V1, the presence of which corresponded to improvement in timing accuracy and precision in the task. Further, the degree of this improvement was largest when the spatial extent of these oscillations was greatest. Importantly, we found that the duration of these oscillations covaried with the time of action on a per-trial basis and that this relationship evolved with training. This theta-oscillatory activity in the LFP was also found to be intimately related to the activity of single units, which were observed to spike at the frequency of the LFP oscillation and were themselves found to carry predictive information about the timing of the action. Interestingly, the likelihood of evoking these oscillatory states was found to depend on the rate of experienced reward, thus linking them to motivation and the balance between exploration and exploitation. Therefore, these findings further our understanding of sensory cortex's involvement during stimulus-driven behaviors, provide evidence for theoretical accounts of timing that implicate neuronal oscillators (Miall, 1989; Church and Broadbent, 1990; Buhusi and Meck, 2005), and extend our knowledge of the role for theta oscillations.

Materials and Methods

Behavioral task and neural recordings.

Experimental procedures were as described previously (Namboodiri et al., 2015). Briefly, water-deprived, adult, male, wild-type Long–Evans rats were trained to perform a visually cued timing task in which they entered a nose poke, waited a random delay without licking, received a 100 ms full-field monocular visual stimulus, executed a lick, and obtained a water reward (on 5/6 visually cued trials). The amount of reward available upon licking after the stimulus increased linearly up to 1.5 s, after which no reward was available (see Fig. 1a). After animals were sufficiently trained (average wait times exceeded one second for 3 consecutive days), they were stereotaxically implanted bilaterally with 2 × 8 electrode arrays (2.5 mm length; 0.5 mm width) targeted to the binocular zone of V1 (1.5 mm anterior and 4.2 mm lateral from lambda, at a depth of 1.0 mm). After recovery and water deprivation, animals performed the task while neural recordings were collected, amplified, and filtered by Neurlanyx hardware. For a different cohort of animals, referred to here as naive, implantation occurred before training (and the ramp of available reward extended only to 1 instead of 1.5 s). All procedures were conducted in accordance with the National Institutes of Health's Guide for the Care and Use of Laboratory Animals and were approved by The Johns Hopkins University Institutional Animal Care and Use Committee. Six spatially distant electrodes (three per hemisphere) were selected for LFP analysis to reduce redundancy in the signals.

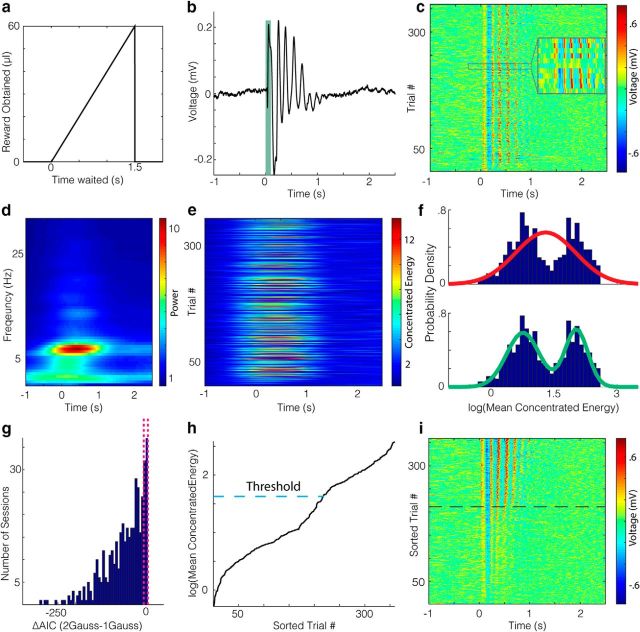
Figure 1.

Oscillatory states are present in V1 during a visually guided timing task. a, Schematic of the task reward structure in which waiting longer to lick after a visual stimulus (time 0) results in a larger volume of water delivery at the lick tube. Maximum delivery occurs at 1.5 s and drops to 0 thereafter, so that animals must time their lick. b, Average voltage trace in the LFP taken from an electrode in an example session, with a green bar overlaid to indicate when the visual stimulus was on. The voltage values seem to oscillate for ∼1 s poststimulus. c, Voltage traces per trial for the example session. d, Average time–frequency representation of the trials in c. e, Concentrated energy through time of the trials in c. f, Empirical probability density function (PDF) for the log(mean concentrated energy) scores on each trial shown in e are shown in blue. The mean concentrated energy is calculated in a 200–700 ms window poststimulus. A unimodal Gaussian fit is shown in red (top) and a bimodal Gaussian fit is shown in green (bottom). g, The distribution of the difference in AIC values for each model across all sessions is left shifted, indicating an overall preference for the bimodal model. The dotted lines around 0 are the bounds at which the relative likelihood of a model compared with another model is 5%. h, Sorted concentrated energy scores for the example session with a dotted line indicating the threshold used for determining whether a trial has an oscillation. If the concentrated energy score crosses this threshold during the 200–700 ms window poststimulus, it is considered to have an oscillation. I, Raw voltage trace in c sorted by the mean concentrated energy in the analysis window on a given trial. Oscillations were detected for trials above the dotted line.

LFP processing.

Neural signals were sampled continuously at 32 kHz, downsampled to 2.2 kHz, and band-pass filtered (1–400 Hz). This filtered LFP signal was then converted to concentrated energy scores by applying a methodology described previously (Zold and Hussain Shuler, 2015), which was chosen in that study because it provided a better agreement between quantitative analysis of signal duration and visual inspection than using energy alone. Here, concentrated energy is defined as the mean energy divided by the purity. To calculate the mean energy, we first generated a time–frequency representation from the filtered LFP by applying Gabor filters with frequencies from 4 to 9 Hz in 0.5 Hz steps (SD of Gaussian kernel = 0.5). The mean of this time–frequency representation across all frequency values for each point in time is defined as the mean energy. Purity, a measure of how concentrated the energy was among particular frequencies, was calculated as follows:

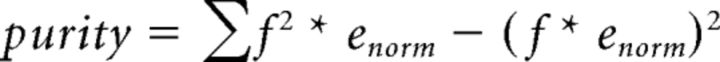where f is the frequency values and e_norm is the energy at each frequency at every point in time normalized to the total energy at that time. Importantly, to minimize the opportunity for bias, the parameters for this study were taken exactly from the prior study and were not adjusted across sessions or animals.

Oscillation detection and duration.

As done previously (Zold and Hussain Shuler, 2015), the concentrated energy scores during a session were used to detect the presence of an oscillation and duration. To categorize trials into oscillatory and nonoscillatory groups, we first created a threshold according to the following formula:

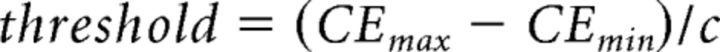where CE_max and CE_min are the maximum and minimum mean concentrated energy scores (taken from a 200–700 ms window following a visual stimulus) for any visually cued trial across the session, respectively, and c is a constant equal to 2.5. An oscillation trial is then defined as any trial in which the concentrated energy value crosses this threshold at any point in the 200–700 ms poststimulus window. For trials with an oscillation, the duration of the oscillation was the amount of time between when the concentrated energy exceeded this threshold to when it subsequently fell below the threshold.

Oscillation states.

To establish whether it is appropriate to treat trials as belonging to one of two classes (oscillatory or nonoscillatory), we modeled the poststimulus responses across trials. To do this, we took the mean concentrated energy from a 200–700 ms window poststimulus on each trial and attempted to find a good fit to this distribution. We started with the most straightforward hypothesis that the concentrated energy values across trials arose from a Gaussian process, (μ, σ) that would result in a unimodal distribution. This was tested against a mixed model in which two Gaussian processes are linearly combined, p * (μ1, σ1) + (1 − p) * (μ2, σ2), which would result in a bimodal distribution. To compare these “1-Gaussian” and “2-Gaussian” models, we calculated the corrected Akaike information criterion (AICc) values for each. The AIC takes into account the likelihood (derived from maximum likelihood estimation) and also the model complexity, such that models with more parameters are penalized. In this case, the 2-Gaussian model has 5 parameters, whereas the 1-Gaussian model has only 2 parameters. AICc is a correction for small samples and is calculated as follows: AICc = AIC + 2k(k + 1)/(n − k − 1). The difference in AICc values (or, more specifically, exp((AICc1 − AICc2)/2) thus provides a measure of the relative likelihoods of the models.

Because a unimodal Gaussian model is a simplistic alternative, we also tested against a variety of more plausible models. Specifically, we tried to find the best alternative to the 2-Gaussian model among 17 continuous distributions implemented in a custom MATLAB script by Mike Sheppard (including, among others, the following distributions: beta, exponential, gamma, generalized extreme value, inverse Gaussian, logistic, log-logistic, lognormal, normal, Rayleigh, and Weibull). Of these, 10 provided reasonable fits to the data in <30% of cases and thus were excluded from the data. Of the remaining seven candidates (which provided reasonable fits in 100% of cases), the generalized extreme value distribution had the lowest overall AICc value across sessions and therefore was chosen as the best alternative to the 2-Gaussian model. Unlike the unimodal Gaussian model, this model has skew and thus can fit the distribution of concentrated energies across trials better.

Visually evoked potential (VEP) correlation.

The acute response to the visual stimulus, termed the VEP, is defined here as the voltage modulation in the LFP during the first 200 ms poststimulus. To assess whether the correlation between the timed lick and oscillation can be explained by an earlier physiological event, we assessed whether the magnitude of the VEP (i.e., the absolute difference between the peak and the trough in the voltage trace during this 200 ms period) might be predictive of wait time. Specifically, we calculated the percentage of variance explained by a single variable (either oscillation duration or VEP amplitude) compared with a linear regression with both variables across all sessions and channels.

Spike-LFP phase locking.

Spiking data were sorted manually using Offline Sorter software from Plexon. Finding the phase of the oscillation at which these spikes occurred required converting the filtered LFP signal into a phase position at each time point. This was achieved, as described previously (Galiñanes, 2009; Zold and Hussain Shuler, 2015; Zold, 2007), by decomposing the signal with a discrete, Meyer-type wavelet transform into its 3.9–7.9 Hz components, applying a Hilbert transform on the reconstituted signal, and computing the angle of this result, z, with the following equation: angle(z) = imag(log(z)). Rayleigh's test for circular uniform distributions was then used to determine whether the phase angles at which the spikes occurred was isotropic.

Spike train analysis.

To compare the degree of rhythmic activity on oscillatory and nonoscillatory trials, we created the autocorrelation difference index (ADI). The ADI is the difference in the autocorrelation scores on oscillation and nonoscillation trials, which are defined as the sum of the sample autocorrelation function from 100–300 ms (which encompasses the range of the oscillatory periods) derived from the peristimulus time histogram (PSTH). Note that this range is distinct from the 200–700 ms range to determine the energy of the oscillation, which is a fixed window. This 100–300 ms range is not a fixed observation window, but rather a span over which the autocorrelation function is evaluated.

To separate trials based on their spike trains alone, we assessed whether the autocorrelation score defined above increased or decreased as each trial was removed from a session's overall PSTH. If removing a trial decreased the overall autocorrelation, then it was considered an oscillatory trial and vice versa. For the ensemble analysis, each neuron in the ensemble (i.e., the group of neurons recorded simultaneously during a session) was given a vote based on the aforementioned criterion and the majority vote determined whether a particular trial was labeled as oscillatory.

Oscillation prevalence modeling.

As stated, a 200–700 ms window poststimulus was used to determine whether an oscillation was present on each trial. To dissociate the contributions of various behavioral rates (reward, trial, and photic) to the likelihood of evoking an oscillation, we swept systematically through a parameter space of integration filters that incorporated past behavioral statistics. For completeness, we used both a uniform and exponential distribution as filters. The distribution of means tested for each filter type were identical, and were 2^x s, where x took on all integer values from 0 to 11, inclusive. The differentiability between the rates computed for all these parameters on oscillation and nonoscillation trials was measured on each session using the receiver operating characteristic (ROC). The mean ROC for a particular filter, mean parameter, and rate type was the average ROC value computed in this way across sessions and channels. We define the maximal mean ROC as the highest mean ROC for a given filter type (across all mean parameters and rate types).

Assessing the acute effect of licking.

We examined the possibility that the lick itself could affect an ongoing oscillation, thereby artificially creating a distinction between oscillatory and nonoscillatory states. Three analyses were brought to bear on this question. First, we investigated whether licking suppresses an oscillation acutely. To address this, we calculated the average difference in concentrated energy between a 50 ms window before and after a lick and compared it with the null distribution of concentrated energy differences obtained by repeatedly (n = 1000) shuffling the relationship between the wait times and trial number. Second, we investigated whether there was a phase relationship between licking and oscillations, in a manner similar to that described above in the “Spike-LFP phase locking” section but for licks. Third, we investigated whether there was a discernable difference in oscillatory power even before licking. To address this, we calculated the distribution of concentrated energy scores in 50 ms windows before the first lick on a given trial for oscillation and nonoscillation trials separately.

Experimental design and statistical analysis.

All of the above analyses were performed using MATLAB_R2015b. Experimental procedures were as described previously (Namboodiri et al., 2015) and were performed with eight wild-type adult male Long–Evans rats. In total, 150 experimental sessions, each consisting of 360 trials, were run (69 trained, 81 naive). Statistical tests and results are as reported in the Results section.

Results

Oscillatory states appear in V1 during a visually cued timing task

Eight wild-type rats were trained on a timing task (Namboodiri et al., 2015). In this task, the animal enters a nose poke to initiate a trial, waits a random delay without licking, receives a full-field monocular visual stimulus (100 ms, green LED, delivered through head-mounted goggles), and then licks at a chosen time. The time that the animal chooses to lick after stimulus determines the amount of reward it obtains on a given trial. Specifically, the amount of water reward available rises linearly with time up until 1.5 s, at which point it drops to and remains at zero (Fig. 1a). In this way, animals are encouraged to time their licks from the visual stimulus so that they fall near, but not past, the peak of the reward ramp.

Animals trained in this task exhibit cue-evoked theta oscillations in the LFP recordings from the V1. This theta oscillation can be seen in the average voltage trace across trials of a session when aligned to stimulus onset, as in Figure 1b. In this example, the average voltage trace exhibits appreciable oscillatory strength for ∼1 s after visual stimulation. Separating the responses per trial (Fig. 1c) reveals differences in the presence, amplitude, and duration of theta oscillations across trials (Fig. 1c, inset).

To quantify these across-trial differences in the presence, amplitude, and duration of oscillations, we transform this raw voltage signal into a metric of oscillation strength. We focus our analysis within a 4–9 Hz frequency range as the preponderance of the signal power falls within this range (Fig. 1d). Using this range, we generate a “concentrated energy” score, a measure of the power and purity of the oscillation (see Materials and Methods), for every time point within each trial, as done previously (Zold and Hussain Shuler, 2015; Fig. 1e). Note that, unlike for the raw voltage signal shown in Fig. 1c, the concentrated energy scores rise before stimulus onset due to the blurring in time that occurs when translating to a time–frequency representation. Qualitatively, trials with large oscillations in voltage (as in Fig. 1c) have high concentrated energy scores (as in Fig. 1e). Using these concentrated energy scores, we can investigate how the oscillation strength, defined as the mean concentrated energy within a 200–700 ms time window, varies across trials. By inspection, the probability density function (Fig. 1f) of the oscillatory strength (see Materials and Methods) is well described for this session by a bimodal fit (bottom), but not a unimodal fit (top), suggesting that there are distinct oscillatory states across trials. Therefore, we compared the quality of each fit by calculating the difference in the AIC scores (See Materials and Methods). For this example, the ΔAIC is large and negative (∼−99.76), which indicates that the bimodal model is heavily favored over the unimodal model. Applying this process across all sessions, we found that the bimodal model is overwhelmingly preferred (p = 6.87e-66, W₄₁₄ = 1186, z = −17.14; Fig. 1g, histogram) for a variety of metrics, including the median concentrated energy (ΔAIC = −27.78), mean concentrated energy in a later window from 0.5–1 s (ΔAIC = −49.33), and using raw energy scores (ΔAIC = −120.99), and when compared with a number of alternative models (p = 4.20e-33, W₄₁₄ = 13753, z = −11.99 for best alternative, generalized extreme value distribution; see Materials and Methods). Given that trials appear to have either a high- or low-power oscillation, a threshold (Fig. 1h) for sorting trials into “oscillation” and “nonoscillation” trials was lawfully applied (Zold and Hussain Shuler, 2015). Ordering the trials from Figure 1c by the strength of their oscillation makes the difference in oscillatory power across trials visually apparent (Fig. 1i). Finally, we define an oscillation's duration as the interval between the first moment postcue that the concentrated energy score surpasses this threshold for detection and the first moment it falls below it.

Lick-timing precision and accuracy improve during theta oscillation states

Having defined cue-evoked oscillations and their duration, we next addressed whether across-trial differences in the performance of the visually cued timing behavior tracks changes in the oscillatory state. To visualize whether performance is related to the presence/absence of cue-evoked theta oscillations, we plot, per trial, the time of the first lick poststimulus (the behavioral variable relevant for reward acquisition) atop the concentrated energy values (see Fig. 2a, top, for an example session). Viewed in this way, it is apparent that there is considerable variability in the time of the first lick (white squares), but challenging to see what, if any, relationship there is between concentrated energy and the delay to the first lick (the “wait time”). However, sorting trials by the strength of the oscillation (Fig. 2a, bottom) reveals that there is considerably greater precision in time to initiate licking on trials with higher oscillatory power. To quantify this difference, we compared the temporal distribution of wait times (<5 s poststimulus, >95%, to avoid outliers) on oscillation and nonoscillation trials (Fig. 2b, threshold shown by black dotted line). Wait times on oscillation trials tend to be more tightly packed (Fig. 2b, purple line) than on nonoscillation trials (Fig. 2b, green line). Indeed, this tends to be the case across all sessions recorded on this channel (Fig. 2c; p = 4.05e-11, W₆₆ = 2139, z = 6.60, two-tailed Wilcoxon signed-rank test against median = 0) and all channels (p = 4.8e-54, W₄₀₈ = 78618, z = 15.48). Moreover, the difference in variability across sessions from this channel tends to be more pronounced in well trained animals (i.e., rats performing at least 3 consecutive sessions with a median wait time of 1 s or greater) compared with naive on this channel (see Materials and Methods; p = 0.01, U = 5274, z = 2.43, n₁ = 66, n₂ = 75, two-sided Mann–Whitney U test) and across all channels (Fig. 2d; p = 1.4062e-15, U = 205955, z = 7.98, n₁ = 408, n₂ = 457). Because this increased variability on nonoscillation trials predominantly comes from a higher fraction of early licks, the central tendency of the wait times across sessions is significantly lower on nonoscillation trials (median of ∼1006 ms) than oscillation trials (median of ∼1103 ms; p = 1.51e-14, U = 193710, z = 7.69, n₁ = 409, n₂ = 410, two-sided Mann–Whitney U test). This means that, on average, licks on oscillation trials occur farther along the ramp, where more water is available and thus are more accurate. Therefore, the precision and accuracy of timed licks are considerably higher on trials with strong oscillations.

Figure 2.

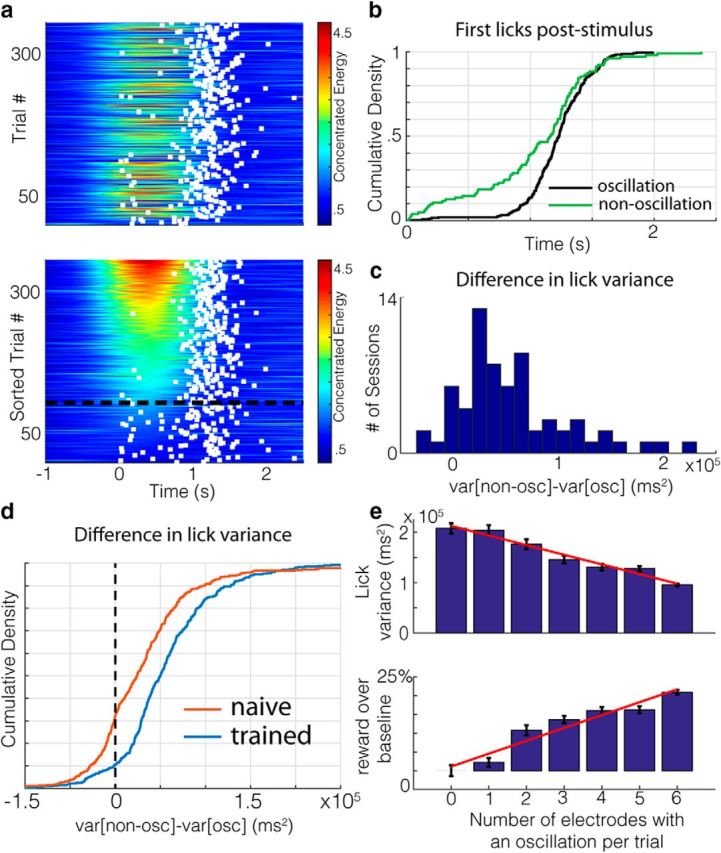
Wait time precision is higher during oscillatory states. a, Concentrated energy values with first wait times (white squares) poststimulus overlaid for each trial of an example session in chronological order (top) and sorted by oscillation duration (bottom). The dashed black line is the threshold for being categorized as oscillatory. b, Empirical cumulative density functions for the first lick times (wait times) poststimulus on oscillation (black) and nonoscillation (green) trials in a. c, Histogram of the difference in lick variability on oscillation and nonoscillation trials for each session recorded on a given electrode. d, Differences in wait time variability on oscillatory and nonoscillatory trials for all sessions and channels of trained (blue) and naive (red, animals. e, Top, Lick variability decreases as the number of electrodes on which an oscillation was detected increases for a given trial. Standard error bars are shown in black, with the regression line in red. Bottom, Percentage of water obtained over baseline (defined as trials in which no oscillations were detected on any electrodes) increases as the number of electrodes showing an oscillation increases. Standard error bars are shown in black, with the regression line in red.

Because the presence of an oscillation detected at a given electrode covaries with behavioral improvements, we hypothesized that there would be larger behavioral improvements during trials with more spatially widespread oscillations in V1. Because we analyzed LFP recordings from six channels (three per hemisphere) per session, we can assess how the timed lick behavior varies with the number of electrodes reporting an oscillation on a given trial. Variability decreases systematically (Fig. 2e, top; p = 8.27e-05, slope = −1.91e+04, r = 0.98) and the central tendency increases systematically (p = 0.020, slope = 23.78 ms, r = 0.83) as the number of electrodes reporting oscillations grows. These effects translate into a systematic increase in the amount of water obtained per trial (Fig. 2e, bottom; p = 4.9e-04, slope = 3.43, r = 0.96). Therefore, the greater the spatial extent of cue-evoked oscillations within V1, the greater the precision and accuracy of timed reward-seeking actions and the greater the obtained reward.

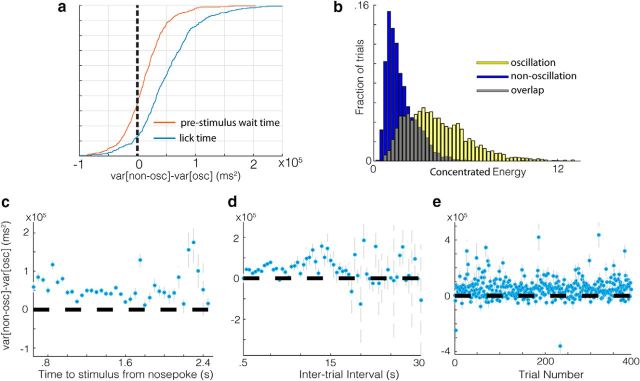
These observations suggest that cue-evoked theta oscillatory states observed in V1 may be effectors of timed behavior, but this relationship might arise from other sources. Because there is a random delay period between nose poke entry and visual stimulus onset, this higher variability in lick precision on nonoscillation trials might arise from higher variability in time waited before the stimulus (prestimulus wait time). Countering this hypothesis, we found that the difference in lick variability between oscillation and nonoscillation trials is considerably higher than the difference in prestimulus wait time variability (Fig. 3a; p = 3.94e-30, z = 11.4, U = 201251, n₁ = 414, n₂ = 414, two-sided Mann–Whitney U test) and that the lick variability is consistently higher on nonoscillation trials when holding the time waited since nose poke entry constant (Fig. 3c). The same is true when controlling for intertrial interval duration and trial number within session (Fig. 3d,e, respectively), indicating that these variables do not account for differences in timed licking. Although the distribution of oscillation strength scores from a given electrode are best described by a bimodal fit, oscillation and nonoscillation classified trials do not form fully separable distributions within a session. The distribution for oscillation strength scores for nonoscillation and oscillation classified trials are given in Figure 3b, showing the degree of overlap when collapsing across all recordings. Given this overlap, it is not surprising that the median difference in lick variance between nonoscillation and oscillation trials across sessions consistently increases as trials with more extreme strength scores are selected (p = 0.0021, r = 0.9625).

Figure 3.

Trial and session statistics do not account for differences in lick precision between oscillatory and nonoscillatory trials. a, Differences in wait time variability (blue) are considerably larger than differences in stimulus onset time (from nose poke entry) variability (red) on trials in which there was no licking prestimulus. b, Concentrated energy scores taken from a 50 ms window before the first lick on oscillation (blue) and nonoscillation (yellow) trials from all sessions and channels. c, Differences in lick variability between oscillatory and nonoscillatory trials for trials within a given range of times to stimulus onset (from nose-poke entry) from 0 to 2.5 s in 100 ms steps collapsed across all sessions and channels. d, Differences in lick variability between oscillatory and nonoscillatory trials for trials within a given range of intertrial intervals from 0 to 10 s in 100 ms steps collapsed across all sessions and channels. e, Differences in lick variability between oscillatory and nonoscillatory trials for a given trial number in a session collapsed across all sessions and channels.

Timed reward-seeking action tracks oscillation duration on a per-trial basis

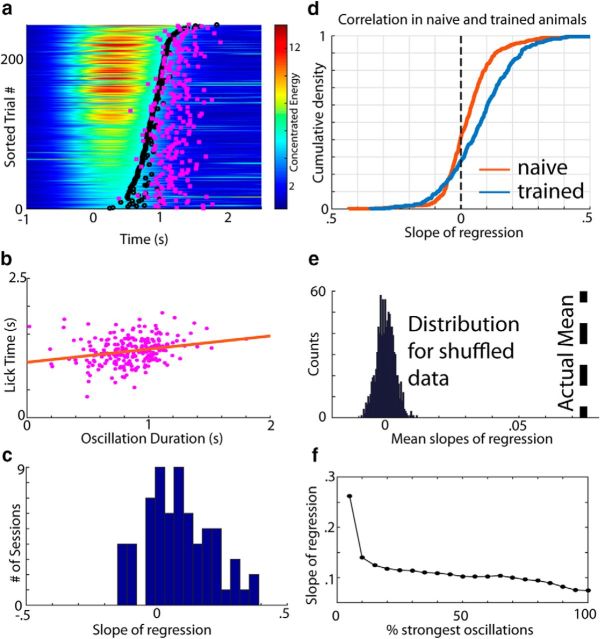
Given these differences in behavior with respect to the presence and spatial extent of cue-evoked theta oscillations within V1, we next assessed whether the duration of these oscillations is directly related to the timing of the reward-seeking action (lick initiation). Figure 4a shows the first lick time (wait time) per trial (pink squares) plotted over the concentrated energy values for an example session, sorted by oscillation duration. Lick initiation tends to follow the edge of the oscillations' termination (black circles). By transforming these data into a scatter plot (Fig. 4b), it appears that there is a positive relationship between wait time and oscillation duration (slope = 0.236, p = 1.49e-04, r = 0.240). Indeed, across all sessions from this electrode, the distribution of regression slopes is significantly right shifted (Fig. 4c, histogram; p = 3.29e-05, W₆₉ = 1902, z = 4.15, two-tailed Wilcoxon signed-rank test against median = 0), meaning that there tends to be a positive linear relationship between wait time and oscillation duration. This relationship holds across all sessions and channels (Fig. 4d, blue line; p = 3.43e-25, W₄₁₄ = 65641, z = 10.28) and is more pronounced in well trained compared with naive animals (Fig. 4d, blue vs red line; p = 3.72e-10, U = 196120, z = 6.27, n₁ = 414, n₂ = 486; two-sided Mann–Whitney U test). The same is also true when collapsing across channels per session (p = 0.0029, U = 5999, z = 2.98, n₁ = 69, n₂ = 81) and using a variety of other metrics/filters (using unrewarded trials only: p = 6.61e-08, U = 174568, z = 5.40, n₁ = 414, n₂ = 486) and using the correlation coefficient instead (p = 5.65e-07, U = 191575, z = 5.00, n₁ = 414, n₂ = 486). Moreover, the mean slope across sessions is significantly higher (p ≪ 0.05) than the distribution of mean slopes for shuffled wait time data (Fig. 4e; black dotted line is actual mean slope). Finally, as described previously (Zold and Hussain Shuler, 2015), the amplitude of the VEP (Fig. 5a), the acute response to the visual stimulus, is also related to the duration of the oscillation, but is a considerably worse predictor of wait time than oscillation duration (Fig. 5b).

Figure 4.

Wait time correlates with oscillation duration in trained animals. a, Concentrated energy values with first lick times (wait times) overlaid (pink squares) on trials sorted by oscillation duration. b, Scatter plot showing the relationship between oscillation duration and wait times for the trials in a with a regression line shown in orange. c, Distribution of the slopes of regression for each session recorded on a given channel. d, Empirical cumulative distribution of the slopes of regression for all sessions and channels from naive (red) and trained (blue) animals. e, Null distribution of slopes for the sessions taken from the trained cohort calculated by randomly shuffling the relationship between the wait time and oscillation duration 1000 times. The actual mean slope across session is shown by the black dotted line. f, Slope of regression decreases as the percentage of trials with the strongest oscillations is increased systematically. To do this systematic sweep, we sorted trials recorded on a given session/electrode by their mean concentrated energy and took the top x percentage of trials. Therefore, the x-axis ranges from 5% (in which only the trials in the top 5% of oscillation strength are included) to 100% (in which all trials are included).

Figure 5.

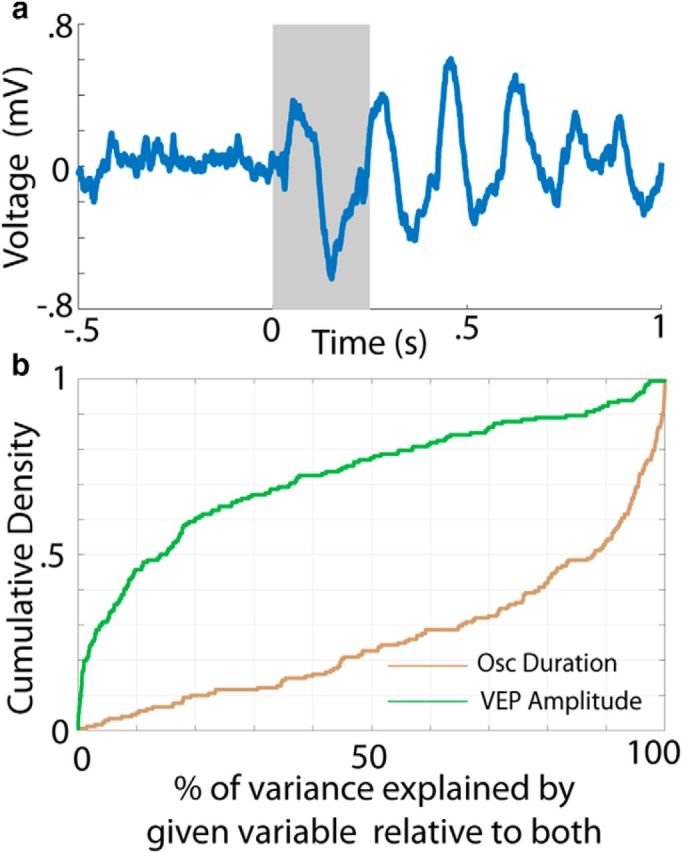
Wait time correlates with oscillation duration across a wide range of metrics and parameters. a, LFP trace from a single trial with a 250 ms gray bar overlaid to highlight the VEP. b, Percentage of variance explained by a regression of wait time against oscillation duration (brown) or VEP amplitude (green) relative to a model containing both variables.

Given these observations, we investigated whether the strength of the oscillation influences the relationship between wait time and oscillation duration. Because the oscillation would likely exert less influence over behavior the weaker it is, we hypothesized that the relationship between wait time and oscillation duration would degrade with oscillation strength (as appears to be the case in Fig. 4a). Indeed, filtering by trials with the strongest oscillations (i.e., taking the x percentage strongest oscillations, as defined by the mean concentrated energy in a 200–700 ms window poststimulus in a given session) yields the strongest correlations (Fig. 4f). Note that, whereas the largest drop occurs from the top 5% to the top 10% strongest oscillations (which may be due to nonlinear control over behavior by these strongest oscillations or to relatively low statistical power inherent in selecting a small subgroup), there is a consistent downward trend. Coupled with the observations above, this indicates that the duration of cue-evoked oscillations relates to the timing of reward-seeking actions.

Cue-evoked single unit oscillations are predictive of timing performance

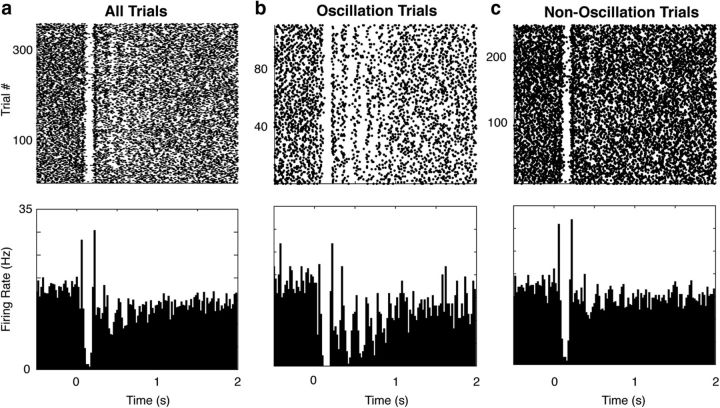
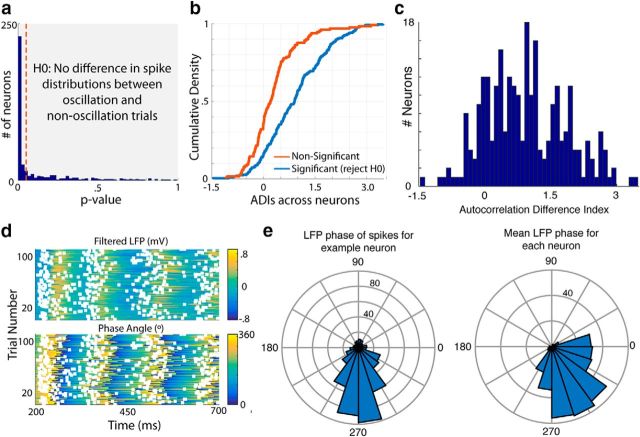
Having observed this timing-related activity at the level of the LFP, we sought to investigate the response patterns of single neurons recorded during this task. An example response is shown in Figure 6a. The spike raster (Fig. 6, top) and peristimulus time histogram (Fig. 6, bottom) across the whole session (i.e., all trials with a stimulus) suggest that this neuron primarily responds acutely to the visual stimulus (presented at time 0). However, separating each trial by whether an oscillation was detected in the LFP (for a given electrode within the same hemisphere) reveals that there are quite different response patterns during oscillation and nonoscillation trials (Fig. 6b,c). In particular, there is a long-duration oscillatory firing pattern on the oscillation trials, whereas there is predominantly an acute stimulus response on nonoscillation trials. Indeed, many neurons (∼66%) show a significant difference in their responses on oscillation and nonoscillation trials (Fig. 7a; see Materials and Methods). This difference is quantified as the ADI (see Materials and Methods; Fig. 7b), for which positive scores indicate more oscillatory spiking activity on LFP-identified oscillation trials. The ADI for this example neuron is ∼1.46 and the distribution of ADI's across all neurons is positively shifted (Fig. 7c, histogram; p = 5.27e-34, W₂₆₃ = 32152, z = 12.16, two-tailed Wilcoxon signed-rank test against median = 0).

Figure 6.

Neural oscillations occur during LFP oscillations. Spike rasters (top) for an example neuron on all trials (a), oscillation trials (b), and nonoscillation trials (c) of a session are shown. The PSTH for each group is shown below.

Figure 7.

Neurons spike at a consistent phase of the oscillations in the LFP. a, p-values for the null hypothesis that there is no difference in spike distributions between trials with and without an oscillation in the LFP for each neuron. The dotted red line indicates where p = 0.05. b, ADI, a measure of the difference in the level of autocorrelation between spike-separated oscillation and nonoscillation trials, is considerably higher in neurons for which the null hypothesis stated in a is rejected (blue) than in those for which it is not (red). c, Distribution of the ADI across all neurons is right shifted, indicating that the spike train autocorrelation is higher on LFP oscillation trials than nonoscillation trials. d, Heat maps showing the filtered LFP (top) and phase angle (bottom) on LFP oscillation trials, with spikes from the example neuron in Figure 7 overlaid (white squares). e, Polar plots indicating the distribution of LFP oscillation phase angles at which spikes occur for the example neuron (left) and the mean phase angle for each neuron in the population (right).

Given this rhythmic discharge pattern, we characterized how oscillatory single-unit activity was synchronized with the LFP signal. To assess this, we converted the LFP voltage into a phase angle at every point in time and investigated how well the spikes aligned to a particular phase of the signal (see Materials and Methods). For this example, the spikes (Fig. 7d, white squares) appear to be concentrated before the peak of the oscillatory envelope (Fig. 7d,e, left; p = 1.50e-88, z = 182.33, Rayleigh's test for nonuniformity). Indeed, the spikes from most neurons across the population cluster around this phase (Fig. 7e, right), indicating that these single units tend to be part of ensembles of neurons that are locked with one another.

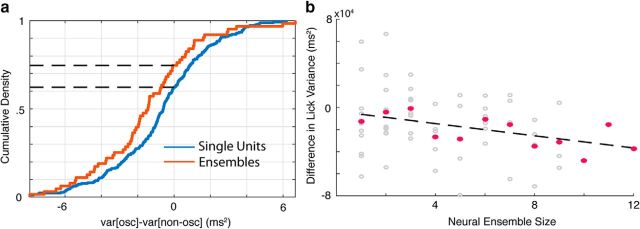
Given that the LFP oscillations are related to timing behavior and that single-unit activity is related to the LFP signal, we next assessed whether, and in what way, single-unit oscillatory activity could be related to timing behavior. We addressed this issue by restricting our analysis to the spiking activity for each recorded neuron, setting the categorization of trials on the basis of the LFP aside. For each neuron in a recording session, we categorized each trial as oscillatory or nonoscillatory on the basis of its spike train (see Materials and Methods) and then quantified the difference in first lick variance between these categories. As with categorizing trials on the basis of oscillations detected in the LFP, we found that sessions tended to have higher lick variance on nonoscillatory trials, which in this case corresponds to leftward-shifted scores (Fig. 8a, blue line; p = 6.49e-05, W₂₅₇ = 11812, z = −3.99). Further, given that neurons tended to be phase-locked to a particular phase of the LFP theta oscillation, we assessed whether aggregating evidence from multiple spike trains recorded simultaneously might boost the signal, improve classification, and consequently accentuate these behavioral differences. Indeed, by categorizing a trial based on the activity of multiple units, we found an even greater average difference in lick variance on oscillation and nonoscillation trials (Fig. 8b, red line; p = 4.06e-05, W₆₃ = 416, z = −4.05). In addition, the performance of timed reward-seeking behavior on oscillating trials improves with the size of the ensemble, as indexed by an increase in the difference of lick variance between oscillation and nonoscillation trials (Fig. 8b, sessions in gray, session averages in pink; p = 0.03, slope = −276, r = 0.28).

Figure 8.

Neural oscillations are predictive of timing performance. a, Empirical cumulative distribution functions for the difference in lick variance on spike-separated oscillation and nonoscillation trials (var[osc] − var[non-osc]) for individual neurons (blue) and neural ensembles (red). b, Relationship between neural ensemble size and difference in lick variance on each session (gray dots) shown with a regression line (dotted black line) and session means per ensemble size (pink dots).

Oscillation prevalence covaries with reward rate

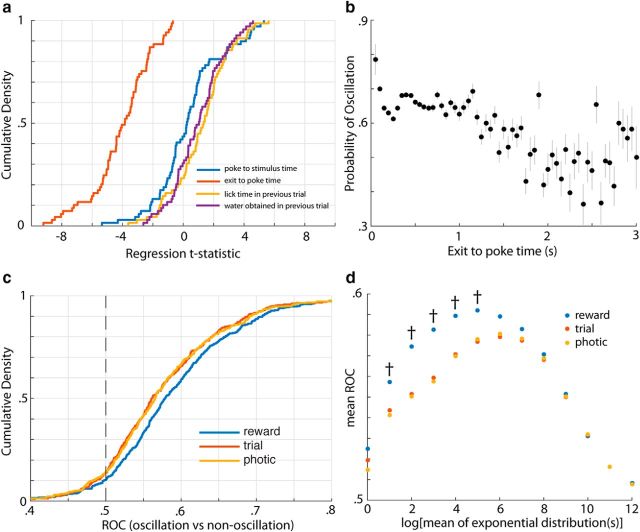
Because timing is more precise and accurate during oscillatory states in V1, we wondered what behavioral variable(s) might influence the likelihood of observing an oscillation on a given trial. To assess this, we created a logistic regression model with several candidate explanatory variables, in which the dependent variable was the fraction of channels detecting an oscillation (out of six). Of the variables tested, the intertrial interval (i.e., the time from nose poke exit to subsequent trial initiation) was consistently the most informative (i.e., the distribution of its t-statistic across sessions was shifted farthest from zero; Fig. 9a). Because the regression statistics can be influenced by extreme values, we probed this relationship further by plotting the likelihood of oscillation with respect to intertrial interval alone (Fig. 9b). It can be seen from this plot that longer intertrial intervals decrease the probability of evoking an oscillation. Such a relationship may arise if the cortical state was tracking some behavioral rate, such as the trial rate, photic rate (i.e., the rate of visual stimulation), or reward rate experienced by the animal. Therefore, we sought to dissociate these possibilities. Specifically, we compared the ROC values, a measure of the discriminability between two distributions (in this case the rates on oscillation versus nonoscillation trials), across all sessions. For the filter parameter (which sets the integration dynamics for calculating the behavioral rates) associated with the maximal mean ROC (see Materials and Methods), all three variables are good predictors of oscillation likelihood, but the experienced reward rate is the best predictor of the three (Fig. 9c). In fact, the reward rate was consistently the best predictor over the full range of time windows analyzed (i.e., the windows over which the rates were calculated; Fig. 9d). This suggests that oscillations are most prevalent during periods of high experienced reward rate in this behavioral timing task.

Figure 9.

Oscillation prevalence is related to experienced reward rate. a, Distributions of t-statistics across sessions for several variables in a logistic regression model in which the dependent variable is the fraction of electrodes displaying an oscillation on a given trial (of six). Of the variables considered here, the distribution of t-statistics for the intertrial interval (red line), the time between exit on the previous trial to subsequent trial initiation, is the farthest shifted from zero. b, Relationship between the probability of oscillation and the intertrial interval (exit to poke time). Probabilities are calculated by taking the number of oscillations divided by the total number of observations (i.e., all analyzed channels and trials) falling within a range of intertrial intervals 500 ms wide, sweeping from 0.5 to 30 s. c, Empirical cumulative distribution functions (CDFs) for the ROC values across sessions associated with the difference in various behavioral rates (reward, trial, and photic between oscillation and nonoscillation trials). These CDFs correspond to the exponential filter (used to calculate the rates) yielding the maximal mean ROC (see Materials and Methods). d, Mean ROC values for each rate variable across sessions for each exponential filter size tested. Daggers denote where the mean ROC value associated with reward rate is significantly different from that associated with trial rate.

Discussion

Appropriately timing actions in response to sensory stimuli is necessary for survival. Here, we show that oscillatory states evoked by reward-predicting cues in V1 may contribute to this ability. Specifically, we show that there is an enhancement of precision and accuracy of timed reward-seeking responses after a visual cue when that cue evokes theta oscillations in V1. The more widespread this theta oscillation across V1, the greater the improvement in timing performance. An appealing hypothesis to explain the difference in timed lick behavior between oscillatory and nonoscillatory states is that an ongoing oscillation in V1 exerts an influence on the animal's decision to lick (perhaps via a downstream motor region) by suppressing licking throughout its duration. Under this hypothesis, we would expect the time of the first lick to covary with the duration of the oscillation. Indeed, this relationship was stronger for well trained compared with naive animals, suggesting that the association between the oscillatory state and the timed behavior is learned. Furthermore, we found evidence for this oscillatory state in the spiking data of simultaneously recorded neurons. These oscillatory firing signals are related to enhanced timing precision, apparently acting in concert to boost the predictive signal. Together, these data suggest that there is a distinct oscillatory state in V1 that is related to the performance of visually timed actions.

An alternative to this interpretation is that lick initiation itself shuts down ongoing oscillations. If this were the case, then non-oscillation trials would appear to have earlier (and perhaps more variable) wait times because a lick during the scoring window would increase the likelihood of being categorized as a nonoscillation trial. However, this explanation is not satisfactory for a number of reasons. First, a prior study (Zold and Hussain Shuler, 2015) in which animals could lick freely poststimulus did not detect a suppression in ongoing oscillatory power. Consistent with this observation, we find that the first lick after a visual stimulus does not acutely suppress an ongoing oscillation (p = 0.90, by random shuffling; see Materials and Methods). Second, as shown previously (Zold and Hussain Shuler, 2015), we did not find any phase relationship between licking and oscillations, suggesting that the oscillation was not being driven by motor output (p > 0.05, Rayleigh's test for nonuniformity; see Materials and Methods). Third, we found that the distribution of oscillation strengths is already much lower for nonoscillation than oscillation trials before a lick (Fig. 3b; p < 0.001, U = 2.89e09, z = −261.86, n₁ = 59466, n₂ = 143514, two-sided Mann–Whitney U test; see Materials and Methods), indicating that these differences exist before the action. In sum, these observations suggest that the timing activity in V1 is not merely a consequence of the behavioral action itself.

Another interpretation of these data is that the oscillatory state is driven by some nonspecific variable such as arousal or motivation. Although this is plausible, it seems that the duration of the oscillation is specifically related to the wait times in the task and even when controlling for variables related to motivation, we still observe wait time differences between oscillation and nonoscillation trials. Specifically, the wait time differences are maintained when controlling for the time waited since nose poke entry, intertrial interval duration, and trial number within the session (Fig. 3d–f). Together, these results suggest that the theta oscillations in V1 carry timing information that is not explained by broad changes in behavioral state. Still, it is possible that this signal carries information about motivation or arousal (as addressed by the oscillation prevalence analysis and discussion below).

Our findings thus further our understanding of V1 's involvement during stimulus-driven behaviors. Traditionally, V1 was thought to contribute only to the first stage of such behaviors: sensation. Along these lines, V1 has been regarded as a feature detector that relays faithful representations of the visual world to downstream regions. This view has been challenged by recent work suggesting that V1 can actively generate predictions about visual input (Murray et al., 2002; Summerfield et al., 2008; den Ouden et al., 2009; Alink et al., 2010; Kok et al., 2012) and can be influenced by behavioral variables such as attentional states (Ahissar and Hochstein, 1993; Roelfsema et al., 1998; Gandhi et al., 1999; Somers et al., 1999; Fahle, 2004) and reinforcement (Serences, 2008; Seitz et al., 2009; Stănişor et al., 2013; e.g., water reward). Whereas these findings pertain to influences on perception, our findings provide evidence that V1 relates to the timing of behaviorally relevant actions. Specifically, we find that, after the acute visual response, V1 exhibits long-lasting theta oscillations that subtend the interval between stimulus and action during a timing task. Therefore, these oscillations in V1 may be a signature of V1's involvement beyond perception and into the decision-making phase of a timed, stimulus-driven behavior.

Nevertheless, it is likely that V1 does not act in isolation. Indeed, several studies have pointed to a top-down influence on intrinsic dynamics and expectancy signals in visual cortex (Engel et al., 2001). Given the breadth of evidence suggesting that timing emerges from interaction across multiple brain regions, it is likely that the contribution from V1 is part of a broader cortico-thalamic-basal ganglia (CTBG) loop (Merchant et al., 2013). In this view, the core CTBG-timing circuit, which is engaged across a broad range of behavioral contexts, interacts with a distributed network of local timing circuits that are involved in timing in a task- and modality-dependent manner. One influential model of timing in this vein, the striatal beat frequency model, posits that the striatum recognizes an interval of time by detecting that pattern of activation from a bank of cortical oscillators (Matell and Meck, 2004). In addition to top-down influence, V1 may also receive bottom-up expectation signals. Nonprimary thalamic neurons have been implicated in reward expectation in a modality-specific manner (Komura et al., 2001). In the future, it would be informative to make specific manipulations of the oscillatory activity in V1 and other regions implicated in timing to observe their influence on each other and their effect on timing behavior.

These observations also extend our knowledge about the role and behavioral significance of theta oscillations. In the hippocampus, theta oscillations have been implicated in several cognitive functions, including voluntary movement, learning, and memory processes (Hasselmo, 2005). This rhythm is believed to contribute to these processes partly through facilitation of information transfer with prefrontal cortex (Hyman et al., 2005; Siapas et al., 2005). Indeed, oscillatory synchrony is a common mechanism for interregional communication that has been shown in a number of circuits (Fries, 2005), including those involving visual cortex (Roelfsema et al., 1997; Bernasconi et al., 2000; von Stein et al., 2000; Siebenhuhner et al., 2016). In our visuomotor task, this mechanism may allow the output from V1 to be more effectively read out by a motor region that ultimately initiates the action. Within visual cortex itself, oscillations are often studied from a perceptual perspective and have been found to enhance responding to particular stimuli (Fries et al., 2001, 2002; Schroeder and Lakatos, 2009) and enable feature binding (Eckhorn et al., 1988, 1990). However, recent work has found that theta oscillations in V4 cortex may be important for the maintenance of information during the delay period of a working memory task (Lee et al., 2005) and that, in V1, LFP oscillations may be related to expectancy of future outcomes (Lima et al., 2011; Zold and Hussain Shuler, 2015). We extend these findings by showing that theta oscillations in V1 are related to the precise timing of visually cued behaviors. Although theoretical accounts of timing often implicate oscillatory processes in such timed behaviors (Buhusi and Meck, 2005), evidence supporting these theories has been lacking (Kononowicz and Wassenhove, 2016). Finding this kind of signal at as the earliest stage of cortical visual processing is particularly surprising and may suggest that such a mechanism is a common feature of local circuits. This view is supported by evidence that disruption of MT/V5 selectively impairs visual, but not auditory, timing (Bueti et al., 2008).

These findings also raise the question of why there are oscillatory and nonoscillatory states in V1 given that one appears to be behaviorally superior to the other. One straightforward possibility is that maintenance of an oscillatory response pattern is energetically taxing and therefore must be limited. Another, compatible possibility given the relationship between reward rate and oscillation prevalence (Fig. 9) is that animals performing the timing task are seeking to balance knowledge accumulation with reward accumulation (i.e., the exploration vs exploitation trade-off; Cohen et al., 2007). Under this construction, it may be advantageous for an agent to exploit its knowledge of the environment by tracking a theta oscillation and waiting a precise amount of time when the reward rate is high, but explore the environment otherwise. In support of this hypothesis, a prior study found that increasing the reward rate experimentally increased the likelihood of evoking an oscillation (Zold and Hussain Shuler, 2015). Future studies that manipulate reward rate precisely during a behavioral timing task will help to elucidate the role that this factor plays in governing cortical state and temporal decision making.