Parallel folding pathways of Fip35 WW domain explained by infrared spectra and their computer simulation

Abstract

We present a calculation of the amide I’ infrared spectra of the folded, unfolded, and intermediate states of the WW domain Fip35, a model system for β-sheet folding. Using an all-atom molecular dynamics simulation in which multiple folding and unfolding events take place we identify six conformational states and then apply perturbed matrix method quantum-mechanical calculations to determine their amide I’ infrared spectra. Our analysis focuses on two states previously identified as Fip35 folding intermediates and suggests that a three-stranded core similar to the folded state core is the main source of the spectroscopic differences between the two intermediates. In particular, we propose a hypothesis for why folding via one of these intermediates was not experimentally observed by infrared T-jump.

Introduction

Simple peptides that fold on a submillisecond timescale and contain a single secondary structural element are ideal model systems to understand early kinetic events in the folding pathways of more complex structures. These fast-folding peptides fold on a timescale only recently accessible by both experiment and computation. Advances in molecular dynamics (MD) simulation techniques have extended the reach of all-atoms simulations to periods on the order of a millisecond,¹ allowing fast-folding peptides to achieve their native states in silico. Direct comparison between experimental and simulated observables remains challenging because atomistic details obtained from MD simulations must be translated into experimental spectroscopic signals. Typically, atomistic simulations use structural order parameters to follow the folding process along the simulated trajectories. Instead, a rigorous test of the reliability of the structural information found in the simulations should require calculation of the actual experimental observables, for example the infrared (IR) signal in the amide I’ region or the fluorescence of aromatic side chains.

Here we apply the Perturbed Matrix Method (PMM)² to calculate the amide I’ IR spectra of a fast-folding β-hairpin peptide, the Fip35 WW domain, in different conformational states. The MD-PMM approach is based on the joint use of extended MD simulations and a mixed quantum/classical theoretical computational methodology (PMM),² and has been successfully used to model several relevant experimental observables such as absorption spectra,³ redox potentials,⁴ kinetic rates⁵ and the amide I′ spectra of helical^6;7 and β-sheet^5;6;8 peptides as well as amyloids⁹ and unfolded states.^5;6;8

WW domains consist of a three-stranded β-sheet with a small hydrophobic core,¹⁰ and have been extensively studied, both experimentally and computationally, as model systems for β-structures.^11–23. Their simple structure, small size, fast folding rate and resilience to mutation make them excellent model systems for β-sheet folding and stability. A large number of WW domain mutations have been found to speed up folding.^15;24;25 Among them is the 35-residue peptide Fip35 (Figure 1, sequence GSKLPPGWEKRMSR- DGRVYYFNHITNASQFERPSG), a variant of the human Pin1 WW domain. Fip35 was designed with a reduced five-residue (SR-DGS) loop 1,¹⁵ because formation of this loop is thought to be the rate-limiting step of WW domains folding.¹¹ The folding time of Fip35 is less than 14 µs at 72 °C, five times faster than the maximum folding rate, 69 µs, of the parent Pin1 WW domain.¹⁵

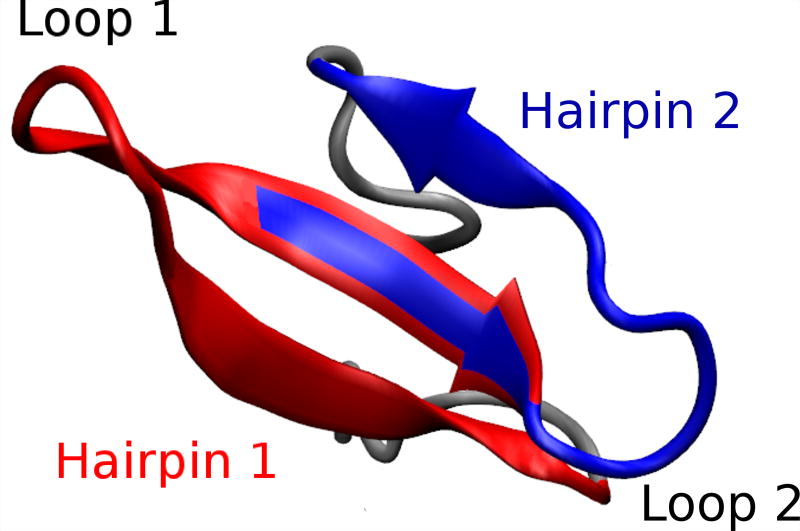
Figure 1.

Representative snapshot of the folded structure of Fip35. The two β-hairpins (hairpin 1, residues 8–22 and hairpin 2, residues 19–30) that form the three–stranded sheet are highlighted in red and blue, respectively, and the two loops (the shortened loop 1 and loop 2) are indicated.

Several computational and experimental studies have addressed the folding of Fip35, but the folding pathway(s) are still debated. In an experimental thermodynamic and kinetic survey of Pin1 loop 1 mutations, Fip35 was one of four mutants found to switch from two-state to downhill folding at temper atures below its melting temperature.¹⁵ Analysis of 100 µs MD trajectories of Fip35 initially supported this “downhill folding” mechanism,²⁶ but a number of independent analyses of the same trajectories hypothesized the presence of intermediate folding states.^18;27–30 Indeed, downhill and short-lived intermediate scenarios have been shown to be closely related.³¹ A number of independent MD folding trajectories of Fip35 also reported folding through an intermediate in which either hairpin 1 or hairpin 2 can fold first^{16;22;26;32;33}. Experimental studies on WW domains in general^21;34;35 and in particular on Fip35 using temperature-jump (T-jump) IR measurements in the amide I′ region,²³ predicted a folding mechanism where folding is initiated in the turn of the first hairpin. Recent experimental studies of Fip35 by pressure-jump have proposed a more heterogeneous mechanism, with folding proceeding through two alternative intermediates where either hairpin 1 or hairpin 2 is formed first.²²

We reconstruct the IR spectroscopic signal of the Fip35 conformational states by applying the MD-PMM approach to a 100 µs MD simulation previously performed on the massively-parallel special-purpose supercomputer Anton¹ by the D. E. Shaw Research group.^26;36 The MD simulations were performed at a temperature that was previously found to well reproduce the melting temperature of Fip35²⁶ allowing observation of spontaneous and reversible folding to the native structure. Because of the outstanding simulation length it is possible to not only sample the folded and unfolded states, but also a series of intermediate conformational states. Here we expand on previous analyses of this 100 µs trajectory by calculating the equilibrium IR spectra of these conformational states by means of the MD-PMM procedure.

The calculated IR spectra aid in the interpretation of ensemble experimental results where the spectra of individual intermediate states cannot be experimentally isolated. These calculations show that the various con formational states have different IR spectra that contribute to the observed ensemble IR spectrum. The results we present here can be useful for investigating IR spectra of WW domains in general, as these peptides show similar IR spectra.

Methods

MD-PMM calculations

In MD-PMM calculations, a portion of the system to be treated at the electronic level is pre-defined (the quantum center, QC). The rest of the system (i.e., the environment) is described at a classical atomistic level exerting an electrostatic effect on the QC. As the phase space sampling of the whole system (the QC and the environment) is provided by classical MD, the MD-PMM approach can be applied to a very large set of molecular configurations, hence providing the dynamic coupling of electronic properties with classical degrees of freedom. The fact that a statistically relevant sampling of the system configurations is achieved, essential for an accurate calculation of the spectra of complex systems, is the main strength of the MD-PMM approach. For the calculation of amide I′ IR spectra, trans-N-methylamide (NMA) is chosen as the QC model for each peptide backbone unit. The mass-weighted Hessian eigenvectors of the isolated trans-NMA molecule are calculated quantum chemically and provide the unperturbed vibrational modes of each pep tide backbone unit from which the amide I mode is selected. The electrostatic perturbation of the environment, including the solvent, is then included providing the perturbed frequencies for each backbone unit at each MD frame. Finally, coupling effects due to interacting vibrational centers (i.e., excitonic effects) are included in the calculations using the transition dipole coupling (TDC) approximation. More details of the quantum chemical calculations and of the theoretical background of the methodology used are provided in the Supporting Information (SI).

Results and discussion

Previous analyses^26;36 of the 100 µs MD simulation of Fip35 revealed the presence of a number of unfolding and refolding events. Here we characterize the conformations sampled by the peptide along this MD trajectory using the DSSP program³⁷ to extract the secondary structure of each residue at each MD frame. From this analysis, and using the crystal structure of a variant of the Pin1 WW domain with loop 1 shortened (PDB entry 2F21^36;38) as a reference structure for the folded state, six different states are defined as follows and schematically depicted in Table 1 together with the population of each state in the MD simulation.

Table 1.

Definition of the six states observed during the MD simulation. N is the number of residues with β-turn (T) or β-strand (E) secondary structure (according to the DSSP assignment) at the same position as the crystal structure. m is the number of residues with T, E or helical (H, G or I) secondary structure at a position different from the DSSP assignment for the crystal structure. Residue r belongs to hairpin 1 for 8≥r≤22 and to hairpin 2 for 19≥r≤30. In the Fip35 sequence which is given below the table, the β-strands are underlined.

State number	State abbreviation	Definition	Population (% of total)
1	F	N≥17	37
2	H1F	N≥10 for r∈hairpin 1	5
3	H2F	N≥9 for r∈hairpin 2	3
4	M	m≥17	2
5	PF	10≤N<17	23
6	U	N<10	30
	5 10 15 20 25 30
Fip35 sequence: GSKLPPGWEKRMSRDGRVYYFNHITNASQFERPSG

State 1 - Folded (F) The structure of Fip35 is considered folded at the nth frame of the MD simulation if 17 or more residues have the same secondary structure (either β-strand=E or β-turn=T in the DSSP assignment) as the corresponding residues in the crystal structure. Note that in the crystal structure there are 21 residues in E or T conformation.

State 2 - Hairpin 1 Folded (H1F) The nth frame belongs to state 2 if 10 or more residues in the first hairpin (from residue 8 to residue 22, see Figure 1) have the same E or T secondary structure as the corresponding residues in the crystal structure. Note that in the crystal structure there are 12 residues in E and T conformation in hairpin 1.

State 3 - Hairpin 2 Folded (H2F) The nth frame belongs to state 3 if 9 or more residues in the second hairpin (from residue 19 to residue 30, see Figure 1) have the same E or T secondary structure as the corresponding residues in the crystal structure. Note that in the crystal structure there are 11 residues in E and T conformation in hairpin 2.

As previously observed,³⁶ a number of non-native secondary structure elements are formed during the MD simulation. We have thus also defined a misfolded state as follows.

State 4 - Misfolded (M) The nth frame belongs to state 4 if 17 or more residues are present with secondary structure (E, T or any helix variant, H, G and I) at a position different from the one of the crystal structure.

State 5 - Partially folded (PF) The nth frame belongs to state 5 if some- where between 10 and 16 residues are present with E or T secondary structure at the same position of the crystal structure. Note that the frames that satisfy the above criterion but have already been identified to belong to state 2, 3 or 4 are not included in the partially folded state.

State 6 - Unfolded (U) The frames that do not satisfy any of the above criteria are representative of the unfolded state of Fip35. Note that such a definition includes in the unfolded state conformations in which up to 9 residues retain a well–defined secondary structure. The presence of residual secondary structure portions in the unfolded state has been recently dis cussed³⁹ and often peptide/proteins unfolded states are not considered as corresponding to pure random coil states.

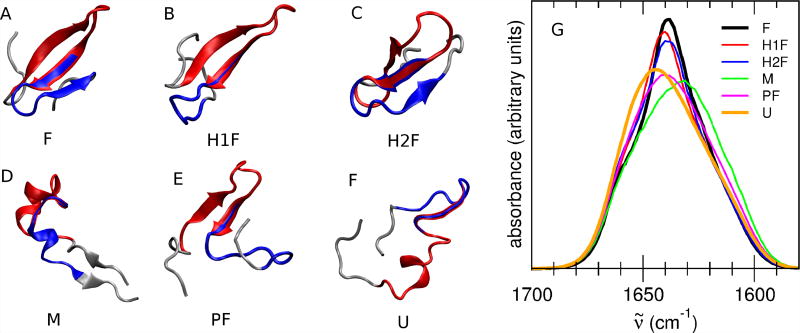
A representative structure of each of the six above defined states is reported in Figure 2. It must be noted that as most of the defined states show a high internal variability, the structures reported in Figure 2 are just examples of a highly heterogeneous population.

Figure 2.

A to F: Representative structure of Fip35 in each of the six states defined in Table 1. In each structure, the residues belonging to hairpin 1 are highlighted in red and the ones belonging to hairpin 2 are highlighted in blue. As most of the defined states show a high internal variability, the reported structures are just examples of a very heterogeneous population. G: Computed IR spectra in the amide I′ region of the six states defined from the MD simulation of Fip35. F state: black line, H1F state: red line, H2F state: blue line, M state: green line, PF state: magenta line, U state: orange line. All the spectra have been red-shifted by 83 cm⁻¹ to align the peak of the folded state spectrum with the peak of the experimental spectrum of Fip35 at low temperature.²³

The amide I′ region IR spectra of the defined conformational states of Fip35 are calculated and reported in Figure 2G. The calculated spectra are red-shifted by 83 cm⁻¹ to align the peak of the folded state spectrum with the peak of the experimental spectrum of Fip35 at low temperature.²³. Each conformational state shows a characteristic spectroscopic signature. The spectra of each of the six states differ from each other in the frequency and/or intensity of the main peak. Globally, the main features of the calculated spectra indicate the coexistence of folded and unfolded conformations, i.e., a blue-shift and decreased intensity of the main peak in the non-folded state spectra (H1F, PF, U) with respect to the F state (Figure 2G). However, there are two notable exceptions, namely the spectra of the M state and of the H2F state. The first is slightly red-shifted with respect to the folded state spectrum, and the second one does not show any frequency shift of the main peak but only a decreased intensity. The six states are thus investigated to clarify the origin of their spectroscopic differences. A special focus is placed on the states that have been previously identified as folding intermediates, i.e., only hairpin 1 (H1F) or hairpin 2 (H2F) folded, and that, according to our calculations, show peculiar differences in their spectroscopic features.

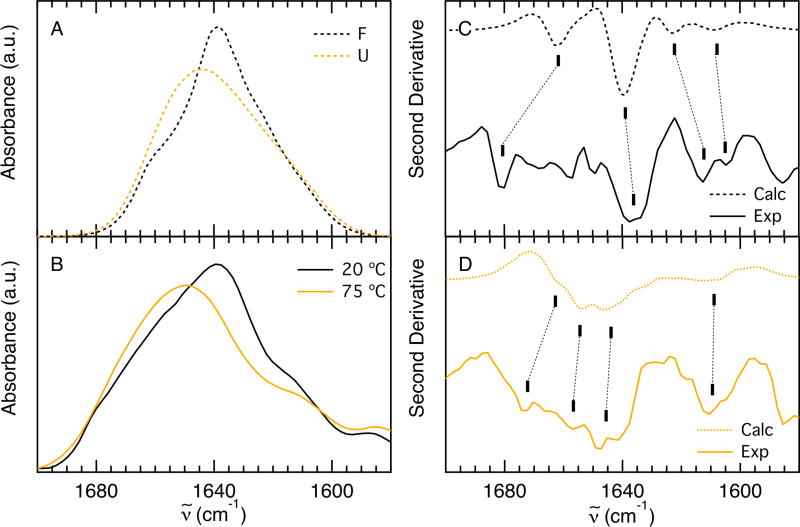
The shape and relative center frequency of the calculated F and U state spectra (black and orange lines, respectively, in Figure 3A) can be compared to the experimental spectra of Fip35 acquired at low (20 °C) and high (75 °C) temperature (Figure 3B). Frequency shift and change in subcomponent amplitudes agree well. The components of the amide I’ band are more easily resolved in the second derivative of the calculated and experimental IR spectra (Figure 3C and D, respectively). At 20 °C there are three main bands in the experimental second derivative (Figure 3C, solid), 1613 cm⁻¹, 1636 cm⁻¹ and 1680 cm⁻¹, that have been previously identified in other WW Domains.⁴⁰. The band at 1613 cm⁻¹ is commonly assigned to amide C=O groups in the turns of β-hairpins involved in hydrogen bonds with side-chain or backbone donors.^41;42 The band at 1636 cm⁻¹ arises from in-phase coupling of carbonyl groups in the sheet and the band at 1681 cm⁻¹ arises from out-of-phase coupling of carbonyls in the sheet⁴³. At 75 °C the experimental band at 1613 cm⁻¹ is maintained (Figure 3D, solid), indicating that the turns are still intact at this temperature. In addition, a broad band with a maximum at 1647 cm⁻¹ and a shoulder at 1674 cm⁻¹ can be observed in the second derivative of the high temperature spectrum. Typically, a broad random coil peak centered at 1660 cm⁻¹ is representative of unfolded carbonyl bonds hydrogen bonded to water.⁴⁴ As β-sheets melt, the in- and out-of-phase coupling of the carbonyl groups is reduced resulting in a decrease in intensity and splitting between the 1636 cm⁻¹ and 1680 cm⁻¹ bands. The maximum at 1647 cm⁻¹ and shoulder at 1674 cm⁻¹ suggest that there is still some residual structure from in- and out-of-phase coupling of the carbonyl sheets at 75 °C. The melt of Fip35 is broad and it is likely that residual structure exists at this temperature, in agreement with the definition of the unfolded state in the MD simulation. Experimental measurements were not conducted at higher temperature to avoid aggregation.

Figure 3.

A: Computed IR spectra in the amide I’ region in the folded (black dashed line) and unfolded (orange dashed line) states defined from the MD simulation of Fip35. B: Experimental absorption spectra in the amide I’ region, acquired at 20 °C (black line) and 75 °C (orange line) during the course of a thermal denaturation. The experimental spectra are taken from Davis and Dyer.²³ C: Second derivative of the computed (dashed line) and experimental (solid line) spectra of the folded states. D: Second derivative of the computed (dashed line) and experimental (solid line) spectra of the unfolded states. The experimental second derivative spectra were computed in IGOR PRO. Dashed lines connect the correlated bands discussed in the text.

The line shape of the computed second derivative of the folded state spec trum is in agreement with the experimental one at 20 °C, but spans an overall smaller frequency range: the same three bands can be observed, located at 1623 cm⁻¹, 1639 cm⁻¹ and 1660 cm⁻¹ (Figure 3C, dashed). An additional band at 1605 cm⁻¹ appears as a shoulder at 1607 cm⁻¹ on the 1613 cm⁻¹ band in the experimental data. The slight frequency disagreement between the cal culated and experimental bands arises from underestimation of the width of the calculated folded spectrum with respect to the low-temperature experimental spectrum (≈35 cm⁻¹ vs ≈50 cm⁻¹). This underestimation might be partly due to the frequency underestimation of the band at ≈1680 cm⁻¹ (≈1660 cm⁻¹ in the calculated spectrum). Previous PMM-MD calculations on β-proteins have shown that exclusion of excitonic coupling results in the disappearance of the band at 1660 cm⁻¹, so the calculated band at 1660 cm⁻¹ corresponds to the experimental band at 1680 cm⁻¹.^2;6 This assignment is supported by comparing the shape of the second derivative of the calculated and experimental bands (Figure 3C), which are both dominated by three bands. The underestimated width of the calculated folded spectrum also suggests a contribution from not fully folded states present in the experimental spectrum acquired at 20 °C, leading to a band-width equal to the one of the unfolded state spectrum. A contribution to the folded state spectrum of the not fully folded states we identify here (H1F, H2F and PF) would induce both an increased bandwidth and a decreased intensity. This hypothesis is supported by the observation that the peak intensity ratio of the calculated folded to unfolded state spectra is somewhat higher than the one of the experimental low- to high-temperature spectra (1.2 vs 1.1, Figure 3A, B). Furthermore, SVD analysis of the experimental temperature dependent FTIR of Fip35 identified a component with a broad transition and a T_m of 24 °C proposed to arise from melting of the sheets prior to the global transition.⁴⁰

The calculated second derivative of the unfolded state spectrum is also in agreement with the experimental one (Figure 3D). The band at 1613 cm⁻¹ and the maximum at 1647 cm⁻¹ are well reproduced in frequency, although the first is underestimated in intensity. Similar to the experimental spectrum, a shoulder at 1660 cm⁻¹ on the 1647 cm⁻¹ band indicates residual β-structure in the unfolded population. A small peak appears at 1654 cm⁻¹ in the calculated spectrum, but cannot be definitively assigned above the noise of the experimental data. The frequency shift between the 1647 cm⁻¹ and the 1654 cm⁻¹ bands is quite small and the two bands might be convoluted in the broad experimental band that arises from a wider ensemble of unfolded conformations.

The agreement between calculated and experimental line shapes of the second derivative of the spectra demonstrates that the calculation is able to capture most of the experimental spectral details and justifies the investigation of the IR spectra of the intermediate states that cannot be independently probed by experiment.

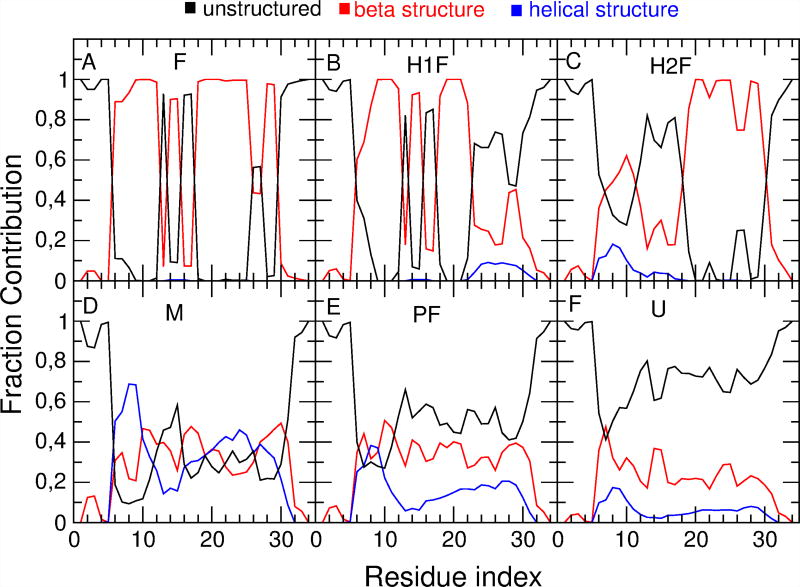
Both the H1F and the PF state spectra show a decreased intensity and a slight blue-shift of the peak with respect to the folded state spectrum. This is in agreement with previous experimental observations and discussions, in which similar frequency shifts (≈ 2–3 cm⁻¹) have been hypothesized to depend either on the loss of one of the three strands (as in the case of the H1F state) or on the presence of not fully folded structural elements in all the three strands (as in the case of the PF state).²¹ The PF state spectrum shows a more pronounced intensity decrease (coupled to a bandwidth increase) due to the higher structural variability with respect to the H1F state. This can be observed by comparing the secondary structure content of the PF state and the H1F state. The fraction of β-structure (red line), helical structure (blue line) and unstructured conformations (black line) sampled by each residue along the trajectory is reported in Figure 4 for all the above defined states. A decrease in β-structure content is localized in the second turn and in the third strand of the H1F state (Figure 4B). In the PF state (Figure 4E) a β-structure decrease can be observed across the entire peptide. In addition, the helical structure content of the PF state is increased with respect to both the F and the H1F state.

Figure 4.

Fraction of β-structure (red line), helical structure (blue line) and unstructured conformations (black line) sampled by each residue (indexed on the x axis) along the MD trajectory for the six states defined in Table 1.

The M state spectrum shows an intensity decrease and a bandwidth similar to that of the PF state spectrum. The definition of the M state allows for highly variable conformations, as no restrictions are given on the position of residues with a defined secondary structure. The conformations that are included in the M state thus show non-native secondary structure contacts in different portions of the peptide, leading to a very broad spectrum. Interestingly, the maximum of the M state spectrum is red-shifted with respect to the F state. Analysis of the conformations that populate the M state reveals an increase in helical conformations (Figure 4D). A deeper analysis of such he lical structures in the M state shows that at least one α-helix turn is present in 83% of the frames and at least one 3–10 helix turn is present in 67% of the frames, with an average number of turns equal to 1.99 for α-helix conformations and 1.63 for 3–10 helix conformations (see SI). This explains the shift to lower frequencies of the M state spectrum, as the amide I′ peak of helical peptides has been experimentally observed to be red-shifted with respect to that of β-peptides.^44;45 Helical states were previously observed in another independent trajectory of Fip35,⁴⁶ and, in general, it is not uncommon to find helical conformations in the folding process of small predominantly β-proteins.⁴⁷ While a non-negligible population of non-native helical structures is observed in the two heterogeneous states (M and PF) that are unlikely to be folding intermediates, only a small percentage of the two probable folding intermediates H1F and H2F have helical structure.

In the U state (Figure 4F) the unstructured conformations fraction increases, but according to our definition, a non-negligible amount of secondary structure is still present (up to 9 structured residues). The average population of helical and beta structures is equal to 5% and 20%, respectively. This primarily β-structure residual is mainly located in hairpin 1.

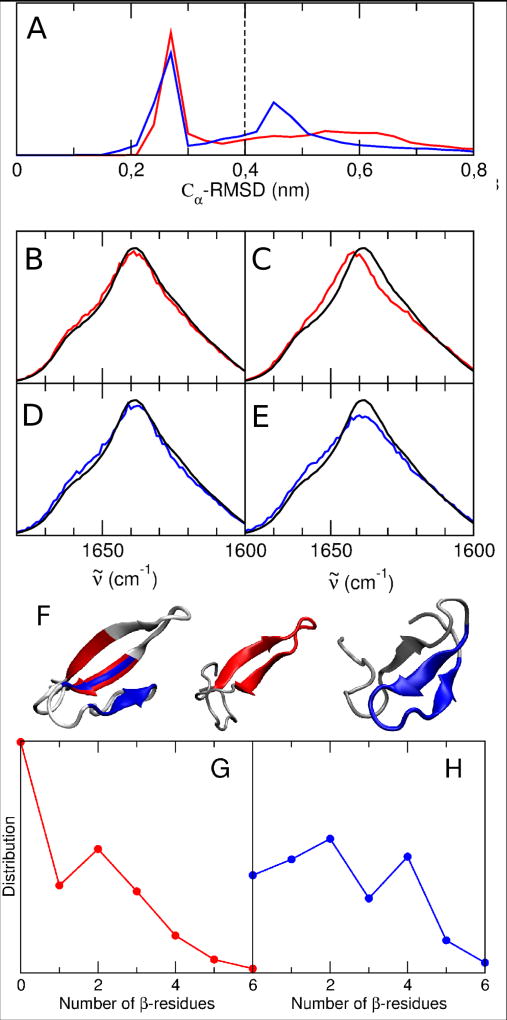
Comparison between the secondary structure content of the H1F and H2F states (B and C in Figure 4) shows a decrease in the β-structure content in the second hairpin in H1F state and in the first hairpin in H2F. However, the total β-structure content is almost identical in the two states (47%). To explain the previously mentioned different spectroscopic behavior of H1F and H2F, further analyses have been performed on the population of both states. In the F state hairpin 1 and hairpin 2 form a three-stranded core (residues 8 to 11, 19 to 22 and 27 to 30, see Figure 5F). The residues that constitute the three-stranded core behave differently in the H1F and H2F states. This can be observed by analyzing the RMSD of H1F and H2F with respect to the F state of the C_α atoms of the residues that belong to the three-stranded core. The normalized distribution of this RMSD, reported for both H1F and H2F in Figure 5A, shows a bimodal trend for both states. The low RMSD peak (at ≈0.3 nm) is similar for the two states and corresponds to structures in which the three-stranded core is formed (see SI for representative structures of the H1F and H2F states with low RMSD with respect to the F state). The calculated IR spectra of the sub-populations with low RMSD for both the H1F state (B, red line) and the H2F state (D, blue line) resemble the F state spectrum (black line). On the other hand, the high RMSD peak is different in the two states. The H1F state has a very broad distribution centered at ≈0.6 nm while the H2F state has a sharper peak centered at ≈0.45 nm. The high-RMSD spectrum of the H1F state is blue-shifted with respect to the folded state spectrum, while the high-RMSD spectrum of the H2F state is not shifted (Figure 5C, E). This can be ascribed to the presence of residual β-structure in hairpin 1 in the H2F state. Quantitative analyses of the residual β-structure content in H1F and H2F sub-populations with high RMSD with respect to the F state are reported in Figure 5G and H and are more exhaustively discussed in the SI. It shows that for H1F with high RMSD only 9% of the MD frames have the entire core formed (4 or more residues in β-sheet or β-turn in hairpin 2) while for H2F 28% of the MD frames have the entire core formed (4 or more residues in β-sheet or β-turn in hairpin 1). Note that such a residual β-content can be due to either a partial formation of native hairpin 1 or to the formation of nonnative contacts (e.g. register shifted contacts) in hairpin 1. A representative structure in which, besides the folded hairpin 2 (in blue), an additional non native strand can be observed is shown in Figure 5F, right. For high RMSD in the H1F state hairpin 2 assumes highly variable and mostly unstructured conformations, e.g. Figure 5F, center (folded hairpin 1 is highlighted in red). In agreement with the discussion above, the highest β-structure content in the part of the peptide corresponding to the first hairpin of the H2F state (see Figure 4C) is localized on the residues belonging to the three-stranded core (residues 8 to 11).

Figure 5.

A: normalized distribution of the C_α-RMSD of residues 8 to 11, 19 to 22 and 27 to 30 with respect to the folded state in the H1F (red) and H2F (blue) states. A bimodal distribution can be observed for both states: a first peak below ≈0.35 nm (low RMSD) and a second peak above ≈0.35 nm (high RMSD).

The spectra calculated on these two sub-populations for both states are reported in B, C, D, E and compared to the folded state spectrum (black lines): B, H1F state at low RMSD; C, H1F state at high RMSD; D, H2F state at low RMSD; E, H2F state at high RMSD.

F: Left, representative structure of the folded state in which the three stranded core (residues 8 to 11, 19 to 22 and 27 to 30) is highlighted. Center: representative structure of the H1F state (hairpin 1 is highlighted in red) at high RMSD. Completely unfolded hairpin 2 can be observed. Right: represen tative structure of the H2F state (hairpin 2 is highlighted in blue) at high RMSD. The formed three stranded core can be observed.

G: Normalized distribution of the number of residues in β-sheet or β-turn conformation in hairpin 2 fragment (residues 26 to 31) for the MD frames belonging to H1F with high RMSD with respect to the folded state. H: Nor malized distribution of the number of residues in β-sheet or β-turn conformation in hairpin 1 fragment (residues 7 to 12) for the MD frames belonging to H2F with high RMSD with respect to the folded state.

The H2F state would be difficult to detect from equilibrium experiments, because the frequency of the main peak is nearly identical to that of the folded state. FTIR ensemble measurements contain contributions from all of the conformational states at each frequency. Fip35 has an aspartic acid in the first turn that has a unique spectroscopic signature at 1713 cm⁻¹, so it was possible to probe the folding of that specific residue and compare it to the melt of the amide I’ band at 1636 cm⁻¹.²³ The melting transition of this single residue was more cooperative (two state-like) than that of the amide I’ band (β-sheet), which provided evidence for folding intermediates. SVD was then used to investigate these multiple conformations. This analysis identified three components: one arises from aggregation at high temperature, and the other two reflect the existence of at least one intermediate prior to the global transition at 74 °C. This does not preclude the existence of more than one intermediate, such as the multiple conformations predicted by IR calculations. In order for multiple intermediates to co-exist, they must have similar thermodynamic stability and kinetic accessibility. The SVD analysis relies on differences in thermodynamic stability of the spectra to separate individual conformations. Ensemble experimental measurements should be able to identify the presence of intermediate(s), but their similar stability and structural characteristics could make it difficult to differentiate the spectra of individual conformational states, such as H1F and H2F. However, inter mediates may still be distinguished by kinetic experiments. For example, the peaks associated with H2F (partially unfolded) and F (folded) are overlapped in the equilibrium spectrum, but they would have different time dependencies that could be resolved by a kinetic measurement. The experimental kinetics of Fip35 can be used to determine whether one of the previously identified kinetics phases involves only an intensity change and no spectral shift. For such cases, computation has the advantage over experiment that the IR signal of a single conformation or single residue can be analyzed independently from all others.

Conclusions

IR spectra in the amide I′ region are calculated for six conformational states of the WW domain Fip35 defined by analyzing a 100 µs long MD simulation. Among the states analyzed there are two states in which only one of the hairpins (hairpin 1 or hairpin 2) is fully folded. These states were previously identified as folding intermediates from the analysis of the same simulations. The IR spectra of these intermediate states show an interesting difference: the H1F state spectrum is blue-shifted with respect to the F state, while the H2F state spectrum is at the same frequency as the F state. This difference can be explained by investigating the conformations of the two states. Our results suggest that the main spectroscopic difference between H1F and H2F arises from the presence of a partially formed three-stranded core similar to the one of the F state. Conformations in which such a core is present are more populated in the H2F state than in the H1F state. The similarity between the IR spectra of the F and the H2F states explains why the H2F state has been detected as a folding intermediate from the analysis of MD simulations of the Fip35 peptide^{16;22;26;32;33} but not from experimental investigations based on IR spectroscopy that predict folding through the first hairpin only.²³ These results clarify the folding pathway of Fip35 and can aid interpretation of experimental IR spectra of this peptide and of WW domains in general.

Abbreviation

MD

molecular dynamics

PMM

perturbed matrix method

QC

quantum center

RMSD

root-mean-square deviation

TDDFT

time dependent density functional theory

trans-NMA

trans-N-methylamide