Sensitivity of Image Features to Noise in Conventional and Respiratory-Gated PET/CT Images of Lung Cancer: Uncorrelated Noise Effects

Abstract

The effect of noise on image features has yet to be studied in depth. Our objective was to explore how significantly image features are affected by the addition of uncorrelated noise to an image. The signal-to-noise ratio and noise power spectrum were calculated for a positron emission tomography/computed tomography scanner using a Ge-68 phantom. The conventional and respiratory-gated positron emission tomography/computed tomography images of 31 patients with lung cancer were retrospectively examined. Multiple sets of noise images were created for each original image by adding Gaussian noise of varying standard deviation equal to 2.5%, 4.0%, and 6.0% of the maximum intensity for positron emission tomography images and 10, 20, 50, 80, and 120 Hounsfield units for computed tomography images. Image features were extracted from all images, and percentage differences between the original image and the noise image feature values were calculated. These features were then categorized according to the noise sensitivity. The contour-dependent shape descriptors averaged below 4% difference in positron emission tomography and below 13% difference in computed tomography between noise and original images. Gray level size zone matrix features were the most sensitive to uncorrelated noise exhibiting average differences >200% for conventional and respiratory-gated images in computed tomography and 90% in positron emission tomography. Image feature differences increased as the noise level increased for shape, intensity, and gray-level co-occurrence matrix features in positron emission tomography and for gray-level co-occurrence matrix and gray-level size zone matrix features in conventional computed tomography. Investigators should be aware of the noise effects on image features.

Introduction

Clinical imaging by positron emission tomography (PET) and computed tomography (CT) is evolving into a quantitative discipline where a large number of metrics are computed in the intensity and gray-level matrix domains; this discipline has been termed as radiomics.^1,2 Radiomics of CT and PET images have shown promise as a diagnostic, prognostic, and predictive tool in the treatment of cancer.^1,3–6 It is also being combined with other “omics” (eg, genomics, transcriptomics, proteomics, metabolomics) into decision support systems.⁷ However, features are sensitive to various acquisition conditions (scanner type, image reconstruction algorithm, etc).^1,3–6,8 One major confounding factor introduced by these conditions is the presence of various random contributions to the signal, commonly referred to as noise. However, few authors have examined the impact that quantum or electronic noise can have on radiomic features. In this article, we examine the influence of electronic noise, a signal-independent contributor to image noise, on radiomics.

An image feature is a quantity that provides quantitative information about an image. It can be derived directly from the image (first order) or from heterogeneity matrices that are derived from the image (second order). Image features or “metrics” that describe image texture and heterogeneity analyze relationships between voxel pairs or groups of voxels. When noise is introduced into an image, the fundamental relationships between voxels are altered. As a result, the image metrics are also altered, and the texture or heterogeneity of the object may be misrepresented. If not accounted for, this noise can have significant implications on the clinical utility of image features. Although there are protocols for the standardization of PET/CT imaging, image noise varies between scanners, manufacturers, and institutions.^9–11 Thus, the impact of noise on image features may adversely affect multi-institutional studies involving radiomics.

Image noise is caused by a variety of modality-specific factors. The PET and CT images possess varying levels of image noise due to the different mechanisms of detection and image reconstruction. One of the most considerable sources of image noise (common to both PET and CT) is random variations in photon counting caused by the statistical nature of X-rays, which is related to the number of photons detected (correlated with signal and image texture). This is commonly referred to as quantum noise. Electronic noise, or “dark noise,” is another common source of image noise. This source of noise is inherent to the detector and independent of the number of photons detected. It is caused by the electronic components that make up the detector.

The CT image noise is mainly random, statistical noise caused by the finite number of X-rays in projection measurements¹² and the Poisson nature of X-rays.¹³ In CT, common sources of noise include body attenuation, detector inefficiency, electronic noise, round-off errors, artifacts, and structural noise (density variations in the object). On the other hand, PET image noise is caused by the random nature of radioactive decay.^13,14 The PET images are affected by partial volume effects, tumor motion, source to background ratio, patient weight, protocol (3-dimensional or respiratory gated), and signal loss (eg, induced by respiratory motion).¹⁵ Scattering coincidences, random coincidences, and the random corrections degrade the PET signal-to-noise ratio (SNR). Other contributors of image noise in PET images include detectors, electronics and recorder systems, reconstruction algorithms, convolution kernels, modes of attenuation correction, and radioactive decay correction.¹⁶ Electronic noise is a common source of noise in both PET and CT modalities. This particular source of noise is considered spatial frequency independent.¹⁷ It is typically considered uncorrelated noise.

Although the focus of this study is on image noise, motion is also a factor that affects image quality. It can affect standardized uptake values (SUVs) by up to 30% and can cause image artifacts because of registration mismatches in the attenuation correction (CT) and emission scans.^11,18 In PET, respiratory-gated (RG or 4-dimensional [4D]) images tend to have higher levels of noise because of the smaller number of counts (due to shorter acquisition times per bed position), but the quality of RG images are impacted less by motion. Both conventional (3-dimensional [3D]) and RG images are included in this study.

Image noise is an unavoidable component of medical imaging. Smoothing filters can be used to reduce noise, but they cannot eliminate noise completely, and may also reduce the signal of interest as well. Since the goal of radiomics is the clinical application of image features, it is important to carefully characterize image features and to understand how they might be influenced by various clinical situations with varying levels of noise. The goal of this study is to evaluate the effects of noise on image features.

Materials and Methods

Phantom Study

A standard American College of Radiology (ACR) accreditation phantom with a germanium (Ge)-68 cylindrical insert (Benchmark by RadQual LLC, Weare, New Hampshire, SN: BMCY06813067103) was placed on a motion table with 2.4 cm motion amplitude and a 4-second period to simulate lung tumor motion due to the respiratory cycle. The phantom was imaged with 3 protocols: (1) 3D PET/CT with motion, (2) 4D PET/CT with RG motion, and (3) 3D PET/CT without motion (static).

Noise Application

To assess the implications of electronic noise on image features, uncorrelated Gaussian noise (GN) with varying standard deviations was added to PET and CT patient and phantom images. A custom program was used to apply noise with varying standard deviation to phantom images using the following Gaussian function (p_g):

$$p_g\left(z\right)=\frac{1}{\text{σ}\sqrt{2\text{π}}}{e}^{-\frac{{\left(z-\text{μ}\right)}^2}{2{\sigma }^2}},$$ 1

where μ is mean noise added, σ is standard deviation, and z is gray level. The CT noise images were created with standard deviations of 10, 20, 50, 80, and 120 Hounsfield units (HU). These will be referred to as GN10, GN20, GN50, GN80, and GN120 henceforth. The PET noise images were created with standard deviations of 2.5%, 4.0%, and 6.0% of the maximum intensity (not SUV). These will be referred to as low noise, medium noise, and high noise. The PET images had varying standard deviations due to the variation in maximum intensities (not an issue in phantoms but very significant in patient images). Although the GN120 noise level may represent greater levels of electronic noise than expected in a scanner, we believe this was necessary to clearly distinguish noise-affected features. The low noise levels of GN10 and GN20 were included to demonstrate how small noise levels affect the image feature analysis. The higher noise levels were included to show the gross effects of noise on feature analysis. As demonstrated by Latifi et al, low-dose 4D CT settings sometimes involve high levels of noise.¹⁹

The specific activity (SA) of the ACR phantom was calculated using the activity on the date of source production (108 274.4 Bq/cm³ on March 20, 2013), the date of measurement (February 18, 2014), and the volume of the source (58.1 cm³). The measured SA was calculated using Mirada DBx (Mirada RTx; Mirada Medical, Oxford, United Kingdom). Mean counts (105 527 Bq/cm³) and standard deviation (2927.7 Bq/cm³) were obtained from the cylindrical region of interest (24.4 cm³) inside the volume of interest (VOI). The reciprocal of the coefficient of variation, or SNR, which was 2.7% from the noise contribution in the phantom data, was calculated.

Signal-to-Noise Ratio and Noise Power Spectrum

To understand the noise inherent in the images and to quantify the noise added to the images, the SNR and noise power spectrum (NPS) of the scanner was calculated. The NPS, representative of the noise texture of an image (used primarily in CT modalities), was calculated using the Ge-68 phantom. The SNR, representative of the amplitude of noise in an image, was also calculated on the phantom for both PET and CT modalities to verify and quantify the addition of noise to the images.

The SNR of a GE Discovery STE PET/CT scanner was measured with the Ge-68 phantom with activities of 0.62 and 0.79 mCi. The phantom was scanned with 70-cm field of view (FOV), 120 kV, 210 mA, 28 subsets, 2 iterations, and Full-Width-Half-Maximum (FWHM) of 7 mm for 3D PET/CT and 60-cm FOV, 120 kV, 200 mA, 28 subsets, 2 iterations, and FWHM of 7 mm for 4D PET/CT. To calculate the CT SNR, medical imaging software (Mirada RTx, Mirada Medical) was used to draw five 4-cm spheres onto the phantom image (Figure 1A). For PET SNR, two 4-cm spheres were drawn on the phantom image. One sphere was inside the Ge-68 source, and the other was in a nonradioactive region inside the phantom (Figure 1B). The SNR was calculated using Equations 2, 3, and 4:

Figure 1.

Method of SNR calculation for (A) CT and (B) PET using Ge-68 solid epoxy phantom. CT indicates computed tomography; Ge, germanium; PET, positron emission tomography.

$$Signal\to \left[s={\sum }_{i=1}^n\overline{H{U}_i}\right],$$ 2

$$Noise\to \left[\overline{\text{σ}}=\sqrt{{\sum }_{i=1}^n{\text{σ}}_i^2}\right],$$ 3

$$\text{SNR}\to \left[\text{SNR}=\frac{s}{\overline{\text{σ}}}\right],$$ 4

where s is the signal, ${\overline{HU}}_i$ is the mean HU for region i; n is the number of regions; is the mean standard deviation across all VOIs; and σ_i is the standard deviation for region i.

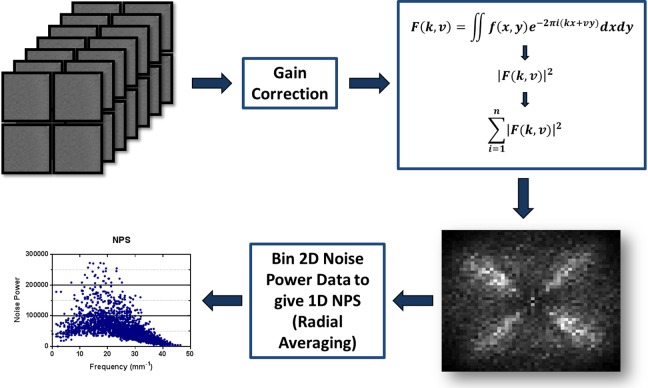
A CT image of the Ge-68 phantom was used to calculate the NPS of the GE PET/CT scanner at our institution. Ten axial slices, 4 regions per slice, were selected in the uniform region of the phantom. A gain correction was applied by subtracting the mean value of the regions, and the Fourier transform was applied to each region to create a 2-dimensional (2D) NPS. Forthwith, a 1-dimensional NPS was plotted from the 2D noise power data (Figure 2) by radial averaging.

Figure 2.

Method to measure CT noise power spectrum using Ge-68 solid epoxy phantom: (1) gather 4D independent images, (2) apply gain & offset correction and subtract mean, (3a) take 2D Fourier Transform of each image, (3b) take magnitude of results & square it, (3c) calculate Average of 40 results, (4) calculate 1D NPS by radial average of the 2D result.

Patient Study

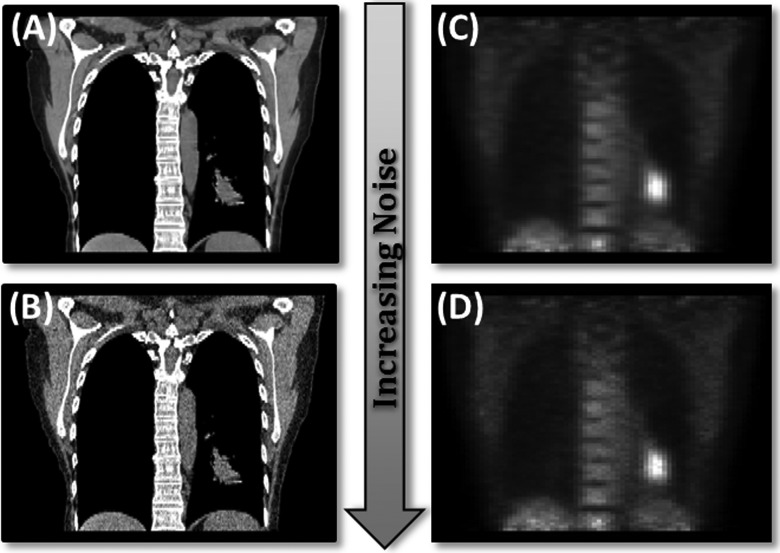
Thirty-one patients (13 males and 18 females) having non–small cell lung cancer with 3D and RG PET/CT images were retrospectively selected for this study with ages from 47 to 83 years. Thirty-two tumors were assessed. This study was approved with waived informed consent by the University of South Florida Institutional Review Board #105996. Standard of practice procedures at our institution were followed. Gaussian noise was applied to all 3D and 1 RG phase of PET and CT patient images according to the method described previously (Equation 1). Resulting PET and CT data sets consisted of 4 separate image sets for each patient, an original image data set, and image data sets of low, medium, and high noise for 3D PET, 4D PET, 3D CT, and 4D CT. Figure 3 demonstrates the noise levels for PET and CT for 1 case (coronal view).

Figure 3.

One coronal slice of a PET/CT image with and without noise. (A) Original image (B). The CT image with Gaussian noise (σ = 120 HU). (C) The PET image without noise. (D) The PET image with Gaussian noise (σ = 0.06 × maximum intensity). CT indicates computed tomography; HU, Hounsfield units; PET, positron emission tomography.

Feature Extraction

The original and noise-added image sets were imported, viewed, and contoured with Mirada DBx. Lung tumor contours were acquired separately for noise and original images. The PET image tumors were contoured at 40% maximum intensity inside a defined VOI. On CT images, tumors were contoured with CT region segmentation. An in-house program extracted image features for the region represented inside each contour. Eighty-one image features were extracted: 11 shape features, 22 intensity features, 26 gray-level co-occurrence matrix (GLCM) features, 11 run-length matrix (RLM) features, and 11 gray-level size zone matrix (GLSZM) features^20–23 (see the supplementary tables for a complete list of features and definitions). The dimension of the co-occurrence matrices were 128 × 128, calculated based on the 3D images with a step size of 1 voxel in 13 directions. The gray levels were binned into 128 levels with equal intensity intervals for the RLMs. The run length was calculated with the 3D images in 13 directions. These 13 directions are defined by Xu et al.^24,25

Statistical Analysis on Patient Data

Conventional and 4D PET and CT image feature differences were evaluated separately resulting in 4 data sets: 3D PET, 3D CT, 4D PET, and 4D CT. Features from the original images were compared to image sets with varying GN levels for each case. Percentage difference was used to compare image features extracted from noise images (low, medium, and high noise) and original images (Equation 5).

$$\%\text{Dif}{\text{f}}_{\text{ij}}^{\text{noise}}=100\times \left|\frac{N{V}_{ij}-O{V}_{ij}}{O{V}_i}\right|,$$ 5

where NV_ij is the value of feature j at noise level i, and OV_j is the value of feature j from the original image. The percentage differences were averaged for each level of noise across all patients. Features varying on average by more than 100% were considered “nonrobust” (those features that are not reliable or reproducible across noise). Those varying <10% were considered “robust.” Features were classified into 1 of 11 categories for CT: R1, R2, R3, R4, R5, NR1, NR2, NR3, NR4, NR5, and B and 7 categories for PET: R1, R2, R3, NR1, NR2, NR3, and B. These are defined in Table 1.

Table 1.

Computed Tomography (CT) and PET Feature Classifications.

Feature Classifications
R1	%Diff < 10% for CT noise level GN120 and PET highest noise level; robust 1
R2	%Diff < 10% for CT noise level GN80 and PET mid-noise level; robust 2
R3	%Diff < 10% for CT noise level GN50 and PET lowest noise level; robust 3
R4	%Diff < 10% for CT noise level GN20; robust 4
R5	%Diff < 10% for CT noise level GN10; robust 5
NR1	%Diff > 100% for CT noise level GN10 and PET lowest noise level; nonrobust 1
NR2	%Diff > 100% for CT noise level GN20 and PET mid-noise level; nonrobust 2
NR3	%Diff > 100% for CT noise level GN50 and PET highest noise level; nonrobust 3
NR4	%Diff > 100% for CT noise level GN80; nonrobust 4
NR5	%Diff > 100% for CT noise level GN120; nonrobust 5
B	10% < %Diff < 100% for CT noise level GN10 and PET lowest noise level

Abbreviations: GN, Gaussian noise; PET, positron emission tomography.

In addition to percentage difference, the concordance correlation coefficient (CCC) was calculated for each feature to assess whether feature values were reproducible at different levels of noise. The CCC provides the correlation between 2 readings by evaluating the deviation from the 45° line through the origin.²⁶ This technique has been used in other image feature analysis studies to quantify the reproducibility of image features and has been shown superior to the Pearson correlation coefficient for test–retest experiments.^2,26–30 A full description of the CCC can be found in the studies by Lin²⁶ and Balagurunathan et al.²⁷ A strength of agreement classification defined by McBride was used to classify CCC results (Table 2).³¹ The mean CCC for each feature subtype was calculated, and the median and range for each feature across noise levels were plotted.

Table 2.

Concordance Correlation Coefficient (CCC) Strength of Agreement Scale.^a

Strength of Agreement	CCC Score
High	>0.99
Substantial	0.95-0.99
Moderate	0.90-0.95
Poor	<0.90

^aThis scale originated from McBride.³¹

Results

Phantom Study

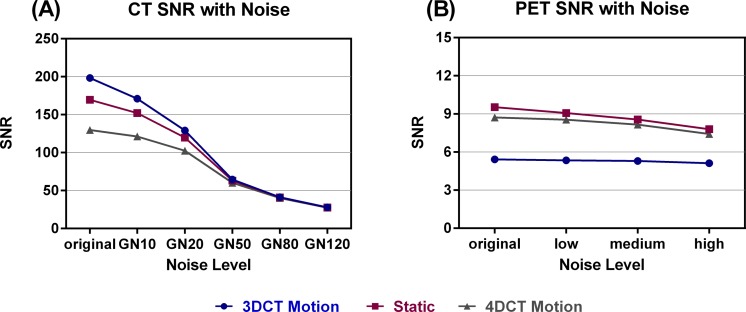
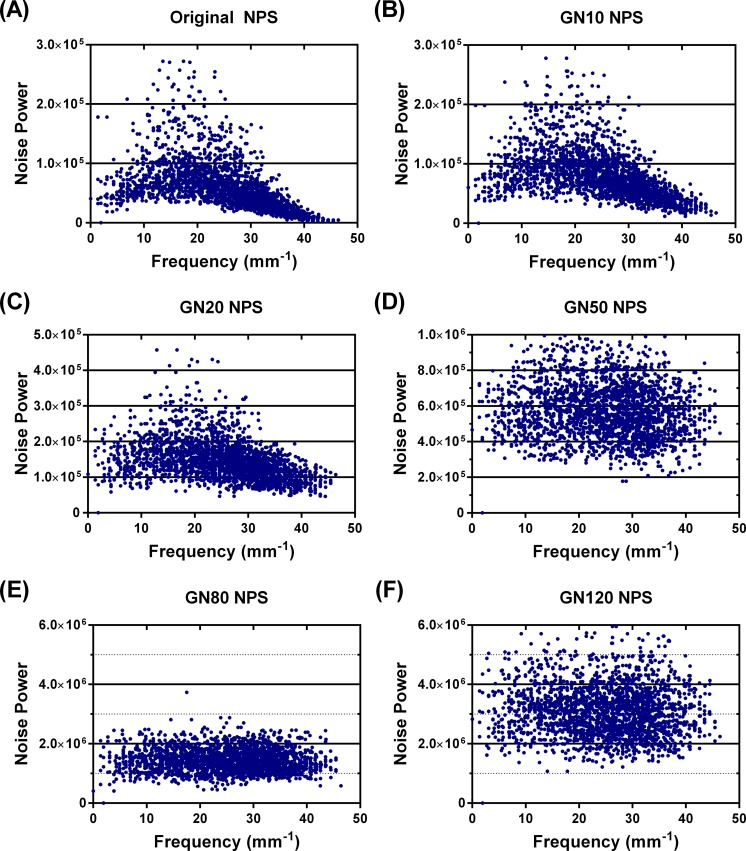
The SNR for PET and CT images behaved as expected by decreasing as the noise level increased (Figure 4), indicating that uncorrelated GN increased the image noise. The measured NPS (Figure 5) showed the noise texture associated with the scanner at our institution (using the phantom CT image). The NPS for the original CT image was spatial frequency dependent, indicating correlated noise texture (Figure 5A). Whereas, the noise power spectra of the CT images with high levels of added noise were spatial frequency independent, indicating that the addition of GN overwhelmed the correlated noise inherent to the image generation process (Figure 5D-F). The noise power spectra of the low noise level images, GN10, and GN20 (Figure 5B and C) were not completely spatial frequency independent, demonstrating that the inherent scanner noise power was still represented in part at these levels.

Figure 4.

Signal-to-noise ratios for: (A) 3D and 4D CT (1 phase) of phantom with motion table and static (3D only). (B) 3D and 4D PET phantom with motion table and static (3D only). CT indicates computed tomography; 3D, 3-dimensional; 4D, 4-dimensional; PET, positron emission tomography.

Figure 5.

Noise power spectrum (NPS) of Ge-68 solid epoxy phantom for GE Discovery STE PET/CT scanner with increasing image noise. A, Original NPS of CT image of phantom. B, The NPS of CT image with added Gaussian noise (σ = 10 HU). C, The NPS of CT image with added Gaussian noise (σ = 20 HU). D, The NPS of CT image with added Gaussian noise (σ = 50 HU). E, The NPS of CT image with added Gaussian noise (σ = 80 HU). F, The NPS of CT image with added Gaussian noise (σ = 120 HU). Y-scale changes from (A) to (F). CT indicates computed tomography; Ge, germanium; HU, Hounsfield units; PET, positron emission tomography.

Patient Study

The automatic contouring via intensity threshold in the lung was not significantly affected by the noise. The R1 (%Diff < 10% for highest added noise; Table 3) features with %Diff < 3% for 3D CT were peak intensity (<3%), mean intensity (<3%), root mean square (RMS; <3%, ), I30 (<2%, intensity ranging from lowest to 30% highest intensity volume), first-order entropy (<2%), inverse difference moment (<2%), and inverse difference (<3%). The results were comparable for 4D CT (see Table 3). In addition to the 3D CT R1 features, the 4D CT R1 features included surface area, sphericity, short axis, maximum intensity, V10 to V90 (percentage volume with at least 10% intensity minus percentage volume with at least 90% intensity), first-order contrast, histogram entropy, co-occurrence mean, sum average, and long-run emphasis. Minimum intensity, peak intensity, mean intensity, RMS, I30, first-order entropy, and inverse difference moment exhibited differences <1% for 4D CT. No features from the GLSZM were categorized as R1 features from 3D or 4D CT.

Table 3.

The R1 Features (%Diff < 10%) for CT and PET.

Subtype	Feature	3D CT	4D CT	3D PET	4D PET
Shape	Volume	✓	✓	✓	✓
	Surface area		✓	✓	✓
	Surface area/volume	✓	✓	✓	✓
	Sphericity		✓	✓	✓
	Compactness	✓	✓	✓	✓
	Spherical disproportion	✓	✓	✓	✓
	Long axis	✓	✓	✓	✓
	Short axis		✓	✓	✓
	Eccentricity			✓	✓
	Convexity	✓	✓	✓	✓
Intensity	Minimum intensity	✓	✓	✓	✓
	Maximum intensity		✓	✓	✓
	Peak intensity	✓	✓	✓	✓
	Mean intensity	✓	✓	✓	✓
	Standard deviation			✓	✓
	Coefficient of variation			✓	✓
	TGV (Total Summed Intensity)	✓	✓	✓	✓
	RMS	✓	✓	✓	✓
	I30	✓	✓	✓	✓
	I10-I90			✓	✓
	V10-V90		✓	✓	✓
	First-order energy		✓	✓	✓
	First-order entropy	✓	✓	✓	✓
	First-order contrast		✓	✓	✓
	First-order local homogeneity			✓	✓
	Histogram entropy		✓	✓	✓
	Uniformity			✓	✓
GLCM	Homogeneity			✓	✓
	Second-order entropy			✓	✓
	Dissimilarity			✓	✓
	Co-occurrence mean		✓	✓	✓
	Inverse difference moment	✓	✓	✓	✓
	Inverse difference	✓	✓	✓	✓
	Sum average		✓	✓	✓
	Sum entropy			✓	✓
	Difference average			✓	✓
	Difference variance			✓	✓
	Difference entropy			✓	✓
	Info correlation 1			✓	✓
	Info correlation 2			✓	✓
RLM	SRE	✓	✓	✓	✓
	LRE		✓	✓	✓
	HGRE				✓
	SRHGE				✓
	LRHGE
	GLNU			✓	✓
	RLNU			✓	✓
	RPC	✓	✓	✓	✓
GLSZM	ZP			✓	✓

Abbreviations: CT, computed tomography; 3D, 3-dimensional; 4D, 4-dimensional; GLCM, gray-level co-occurrence matrix; GLNU, gray level nonuniformity; GLSZM, gray-level size zone matrix; HGRE, high gray-level run emphasis; LRE, long-run emphasis; LRHGE, long-run high gray-level emphasis; PET, positron emission tomography; RLM, run length matrix; RLNU, run length nonuniformity; RMS, root mean square; RPC, run percentage; SRE, short run emphasis; SRHGE, short-run high gray-level emphasis; ZP, zone percentage.

Nonrobust features were defined as features that exhibited %Diff > 100% for the lowest level of added noise (NR1, Table 4). The 3D CT NR1 features included V40 (116%, percentage volume with at least 40% intensity), V70 (339%, percentage volume with at least 70% intensity), and V80 (447%, percentage volume with at least 80% intensity) from intensity features, as well as cluster shade (103%) and co-occurrence variance (151%) from the GLCM, and large-area emphasis (472%), low-intensity emphasis (LIE; 306%), low-intensity small-area emphasis (LISAE; 895%), low-intensity large-area emphasis (LILAE; 495%), high-intensity large-area emphasis (HILAE; 570%), and intensity variability (IV; 112%) from the GLSZM. The CT NR1 features for 4D CT included V40 (177%, percentage volume with at least 40% intensity) from the intensity features and small-area emphasis (1328%), LISAE (1699%), HISAE (2593%), and HILAE (370%) from the GLSZM.

Table 4.

The NR1 Features (%Diff > 100%) for PET and CT.

Subtype	Feature	3D CT	4D CT	3D PET	4D PET
Intensity	V40	✓	✓
	V70	✓
	V80	✓
GLCM	Co-occurrence variance	✓
	Cluster shade	✓
RLM	LGRE			✓
	SRLGE			✓
	LRLGE			✓
GLSZM	SAE		✓
	LAE	✓
	LIE	✓		✓	✓
	LISAE		✓	✓	✓
	HISAE		✓
	LILAE	✓		✓	✓
	HILAE	✓	✓
	IV	✓		✓

Abbreviations: CT, computed tomography; 3D, 3-dimensional; 4D, 4-dimensional; GLCM, gray-level co-occurrence matrix; GLSZM, gray-level size zone matrix; HILAE, high-intensity large-area emphasis; HISAE, high-intensity small-area emphasis; IV, intensity variability; LAE, large-area emphasis; LGRE, low gray-level run emphasis; LIE, low-intensity emphasis; LILAE, low-intensity large-area emphasis; LISAE, low-intensity small-area emphasis; LRLGE, long run low gray-level emphasis; PET, positron emission tomography; RLM, run length matrix; SAE, small-area emphasis; SRLGE, short run low gray-level emphasis.

For PET (3D and RG), shape features that depended solely on automatically drawn contours were the most stable. R1 features exhibiting %Diff < 2% included surface/volume, sphericity (RG only), spherical disproportion (RG only), compactness, mean intensity, RMS, first-order entropy (<1%), first-order local homogeneity, histogram entropy (3D only), second-order entropy (<2%), inverse difference moment (<1%), inverse difference (<1%), sum entropy (<2%), information measure of correlation 2 (<2%), and short-run emphasis (<0.5%). The R1 shape, intensity, GLCM, and GLSZM features were the same for both 3D PET and RG. The RLM R1 features for RG PET were the same as 3D PET but also included high gray-level run emphasis and short-run high gray-level emphasis. There was 1 GLSZM R1 feature: zone percentage.

The nonrobust features from the lowest level of noise (NR1) from 3D PET included low gray-level run emphasis (159%), short-run low gray-level emphasis (160%), and long-run low gray-level emphasis (156%) from the RLM and LIE (480%), LISAE (361%), LILAE (1796%), and IV (102%) from the GLSZM. There were fewer NR1 features from 4D PET. These features were from the GLSZM and included LIE (578%), LISAE (768%), and LILAE (758%).

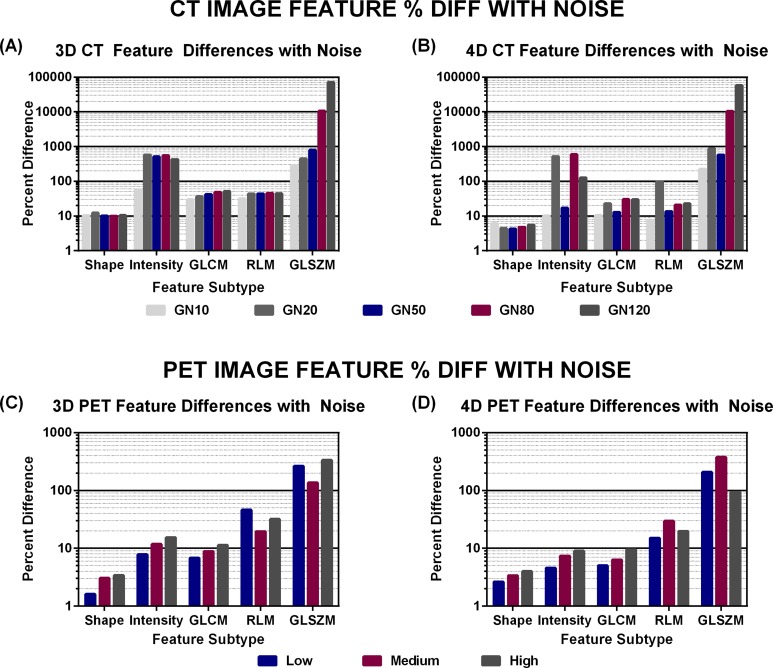
Figure 6 shows the trend between average percentage differences for feature subgroups. For PET, shape, intensity, and GLCM features demonstrate an increase in difference with added noise. In CT, this trend applied only to GLCM and GLSZM features, only with 3D CT. However, in both PET and CT, shape features exhibit the least change with uncorrelated noise (<4% average difference in PET and <13% average difference in CT), and GLSZM features were the most sensitive to uncorrelated noise.

Figure 6.

Average percentage differences between noise and original images across feature subtypes for low, medium, and high noise in (A) 3D CT, (B) 4D CT, (C) 3D PET, and (D) 4D PET. CT indicates computed tomography; 3D, 3-dimensional; 4D, 4-dimensional; PET, positron emission tomography.

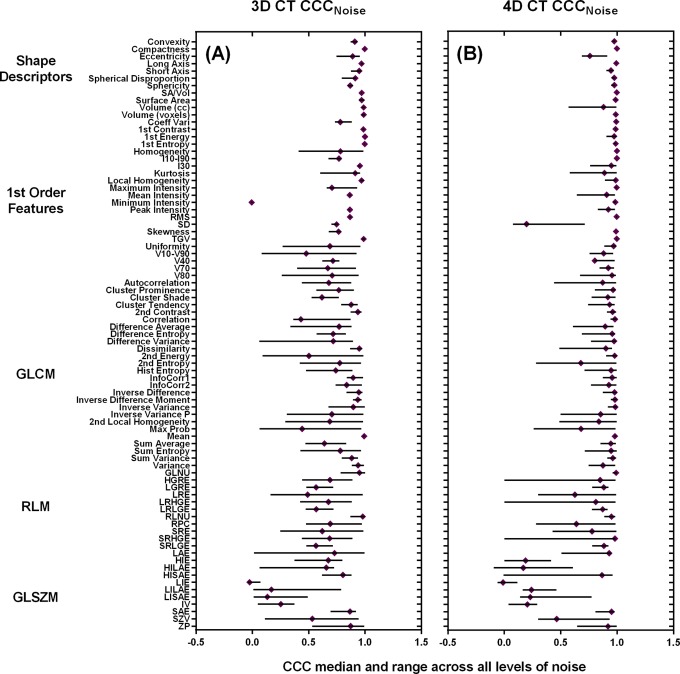
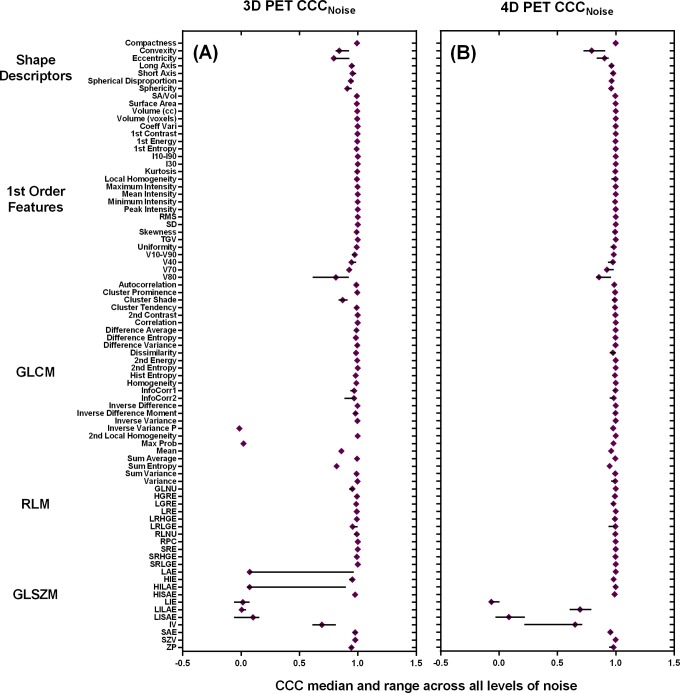
According to the CCC strength-to-agreement scale by McBride, feature subtypes responded differently to added noise. The GLSZM features demonstrated average CCCs below 0.90 for all modalities and all levels of noise (<0.70 for PET and <0.62 for CT). This demonstrated a poor agreement between the image features from noise and original images for GLSZM and supports our percentage difference results. There was a discrepancy between PET and CT with the RLM CCC scores. In 3D PET, the RLM features demonstrated the highest CCC values across noise levels, followed by the first-order features, shape descriptors, GLCM, and GLSZM. Although the feature subtypes had an order, the distinction was not pronounced. Besides the GLSZM features (all features) and GLCM features (highest level of noise only), all other average CCCs were >0.90, and thus, there was a moderate strength to agreement between these features derived from noise images and original images for feature subtypes excluding GLSZM and GLCM.

In 4D PET, the GLCM features demonstrated the highest CCC values across the highest noise levels, followed by the GLCM, first-order features, shape descriptors, and GLSZM. Although the feature subtypes had an order, the distinction was not pronounced. Besides the GLSZM, all other average CCCs were >0.95, and thus, there was a substantial strength to agreement between these features derived from noise images and original images for feature subtypes excluding GLSZM.

In CT, the average CCCs was highest for shape descriptors, followed by the first-order features, GLCM, RLM, and GLSZM. There was a clear distinction between the CCC values for the GLSZM versus all other feature subtypes. Figures 7 and 8 demonstrate the median CCCs for each feature across noise with the ranges (minimum to maximum) for 3D CT, 4D CT, 3D PET, and 4D PET.

Figure 7.

Median CCCs for all CT features—(A) 3D CT and (B) 4D CT—for the levels of noise including GN10, GN20, GN50, GN80, and GN120 ranges. CCC indicates concordance correlation coefficient; CT, computed tomography; 3D, 3-dimensional; 4D, 4-dimensional; GN, Gaussian noise.

Figure 8.

Median CCCs for all PET features—(A) 3D PET and (B) 4D PET—for the levels of noise including low, medium, and high levels of noise. CCC indicates concordance correlation coefficient; 3D, 3-dimensional; 4D, 4-dimensional; PET, positron emission tomography.

Discussion

We applied uncorrelated noise to phantom and patient images to analyze its effect on image features. We found that uncorrelated noise effects in GLCM, RLM, and GLSZM features were generally greater than those seen in shape features. Given what these texture features seek to measure, this finding is not surprising. Since GLCM, RLM, and GLSZM features measure the relationships between pixels and the addition of noise (correlated or uncorrelated) alters these relationships, these texture features would be affected more than shape features that depend mainly on the contour defining the tumor volume (VOI). Specifically, the GLCM measures spatial relationships between pixel pairs and the RLM measures runs of the same gray level across an image. The GLSZM, introduced by Thibault et al, is an advanced statistical matrix that measures homogeneity.^23,32 All matrices, except the GLSZM, were calculated along multiple directions. Shape features, however, are based on the size, shape, and convexity of VOI’s contour, which were essentially not affected by the addition of uncorrelated noise.

Adding uncorrelated noise to PET images with large areas of uptake in the tumor, brain, or bladder resulted in less significant effect from added noise. The large areas of high uptake created a bigger dynamic window of intensities, and thus, the added noise appeared to be less significant. For this reason, in situations where there are large tumors with high uptake, the uncorrelated image noise may not be a significant problem in feature analysis.

We discovered that the effects of Gaussian added noise in CT were usually smaller in 4D images than 3D images. We believe that since the original image noise of 4D images was greater than 3D images, the difference between original image features and noise image features was not as prominent. This also affected the CT SNR. The visible trend for PET wherein feature differences increased as noise increased was less distinguishable in CT, especially in 4D CT (Figure 6). The added noise appears to have altered the CT SNR to a greater degree than PET SNR (see Figure 4A and B). It is clear that at higher noise levels, beginning at the GN50 noise level, the CT SNR converges implying that the GN destroys the differences in SNR due to acquisition. Figure 4 demonstrates that at the GN50 noise level, the SNR for 4D CT had decreased by a factor of 2. At the GN120 noise level, the SNR for CT decreased nearly 5 times compared to PET where the SNR decreased by a factor of 1.

It is interesting that the SNR for 3D PET is lower than that of 4D PET, especially when compared to the CT SNR. This could be due to motion effects. The 4D PET accounts for motion. Since PET images are acquired over a long period of time (4 minutes per bed position), when motion is introduced into an image and not accounted for (as in 3D images) an averaging effect is introduced into the image and the true tumor location, size and shape is smeared. We believe this is why the static PET image and 4D motion images have similar SNRs, and 3D motion exhibits the lowest SNR. The SNR results in CT were drastically different from PET. To start, 3D motion had the highest SNR followed by static and finally 4D motion. Since CT images are acquired much faster than PET images, in the order of milliseconds and are much less sensitive to motion, it makes sense that the static and 3D motion images had the highest SNRs; they received a higher number of counts than 4D CT. It is also interesting that the PET SNR is considerably lower (40× for 3D motion) than the CT SNR even for the original images.

In PET images, the 3D and 4D image feature differences were comparable. Although there were fewer features in the NR1 category for 4D PET, differences were not consistently larger for 3D or 4D PET across all feature subtypes. In addition, the percentage difference in PET features did not always increase with respect to added noise. For instance, in the RLM and GLSZM features, average differences reached the maximum (4D PET) or minimum (3D PET) percentage difference at the medium noise level (Figure 6). This could be caused by the large pixel size in PET, the high level of noise in the image due to decreased counts, or simply a saturation of the uncorrelated noise in the image at the low or medium noise levels. Figure 4 demonstrates that the PET SNR did not decrease sharply for 3D motion, 4D motion, or 3D static PET indicating high levels of initial image noise.

The finding that shape descriptors were less affected by noise than GLCM, RLM, and GLSZM features is favorable for the field of radiation therapy. Increasingly common, the gross tumor volume (GTV) for radiation treatment planning is contoured using both PET and CT. The addition of PET as a diagnostic tool in radiation therapy has improved GTV definition and demonstrated a 21% to 100% change in tumor volumes.³³ The PET in radiation treatment planning improves the contouring accuracy of the GTV, which promotes decreased toxicity to healthy tissue.^34,35

The large differences in intensity, GLCM, RLM, and GLSZM features demonstrate that uncorrelated image noise affects the image feature analysis. The GLSZM features are highly unstable, particularly in 3D CT, with average values nearing 70 000% in some cases but as low as 270% in others. The full extent of this effect requires further investigation, but it is clear that image features, especially those from intensity, GLCM, RLM, and GLSZM are affected by uncorrelated noise. Investigators who are using large numbers of images from multiple scanners should be aware of the effects of image noise on image feature analysis. This was recently illustrated nicely for correlated noise by the work of Nyflot et al.³⁶ Although we did not compare results from multiple scanners, quantitative accuracy in PET/CT is still being established.³⁶ Multicenter PET/CT trials testing the stability and repeatability of PET data from different sites demonstrated that the quantitative PET measurement, SUVs, were within the PET Response Criteria in Solid Tumors limitations but were higher than in a previous study conducted in smaller single-center studies.³⁶ Even inside a single institution, patients imaged on the same scanner demonstrated SUV differences approaching 50% on test and retest analysis.³⁷ It is clear that studies involving multiple scanners should be aware of the effects of image noise on their features.

The noise texture, defined by the measured NPS, was uniform in shape for the highest levels of added noise demonstrating that we had indeed added uncorrelated noise to the images. This uncorrelated noise is commonly termed “white noise” and in this study is considered random noise of a Gaussian distribution. A distinct difference existed between noise phantom NPS and original phantom NPS due to the shift from the inherent correlated noise in the image to uncorrelated GN.

Uncorrelated noise is not the only criteria that affect PET/CT image features. Nyflot et al tested the effect of correlated (stochastic) noise on image features, as well as patient size, lesion size, and image reconstruction method. They determined how stochastic noise have various effects on different feature subtypes—what they term “classes of metrics”—concluding that additional standards are warranted for prospective PET image feature analysis studies toward predicting clinical outcome or treatment response.³⁶ Other studies have shown that motion, bin width, SUV discretization, acquisition modes, and reconstruction parameters also affect image features, and in some cases, the extent of these effects is feature dependent.^8,36,38,39 A common conclusion of these studies was that standardization of image feature analysis in radiomics is needed. We join in agreement with these studies that standardization is crucial as we look toward the application of radiomics in radiotherapy and other fields. We are also advocating for standardization of image feature analysis, especially in PET/CT, to promote accuracy and patient safety (if features are applied prospectively) when measuring image features for clinical purposes and to encourage accurate image feature study comparisons between scanners, institutions, and manufacturers.

There were limitations to this study. The major limitation of this study was that we did not have access to the prereconstruction PET/CT data due to proprietary reasons. This was a retrospective study; however, we wanted to determine the effect of noise on archived patient studies. These limitations affected the approach in which noise was added to the PET/CT images as typically done.^36,40 In typical imaging systems, PET and CT image noise is integrated into the reconstruction method and not necessarily additive, except in the case of electronic noise. Nevertheless, our method still allowed us to measure the sensitivity and degradation of radiomic features due to noise. Our statistical analysis was also a limit to the study. However, we applied the CCC that was sufficient to show feature reproducibility across noise levels. Percentage difference was sufficient to demonstrate feature differences across noise levels.

Conclusion

Uncorrelated noise was added to PET and CT images. Shape, intensity, GLCM, RLM, and GLSZM image features were extracted from VOIs, and image features that were nonrobust with respect to the additional noise were identified. Many intensity, GLCM, RLM, and GLSZM features varied significantly with noise. Percentage change between original and noise image features increased as noise level increased for intensity and GLCM features in PET and GLCM, RLM, and GLSZM features in CT. The GLSZM features were the most sensitive to noise both for CT and PET. A good understanding of feature sensitivity to noise is essential for image feature analysis and radiomics studies involving a large number of images from multiple scanners as would be the case in multi-institutional clinical trials. This study adds support to the proposal for standardization of clinical processes and analysis involved in radiomics.

Abbreviations

2D

2-dimensional

3D

3-dimensional

4D

4-dimensional

ACR

American College of Radiology

CCC

concordance correlation coefficient

CT

computed tomography

FOV

field of view

Ge

germanium

HILAE

high-intensity large area emphasis

HU

Hounsfield units

GLCM

gray level co-occurrence matrix

GLSZM

gray-level size zone matrix

GN

Gaussian noise

GTV

gross tumor volume

IV

intensity variability

LIE

low-intensity emphasis

LILAE

low-intensity large area emphasis

LISAE

low-intensity small area emphasis

NPS

noise power spectrum

PET

positron emission tomography

RLM

run length matrix

RMS

root mean square

SA

specific activity

SNR

signal-to-noise ratio

VOI

volume of interest

RG

respiratory gated

SUV

standardized uptake values.