Innovation and the growth of human population

Abstract

Biodiversity is sustained by and is essential to the services that ecosystems provide. Different species would use these services in different ways, or adaptive strategies, which are sustained in time by continuous innovations. Using this framework, we postulate a model for a biological species (Homo sapiens) in a finite world where innovations, aimed at increasing the flux of ecosystem services (a measure of habitat quality), increase with population size, and have positive effects on the generation of new innovations (positive feedback) as well as costs in terms of negatively affecting the provision of ecosystem services. We applied this model to human populations, where technological innovations are driven by cumulative cultural evolution. Our model shows that depending on the net impact of a technology on the provision of ecosystem services (θ), and the strength of technological feedback (ξ), different regimes can result. Among them, the human population can fill the entire planet while maximizing their well-being, but not exhaust ecosystem services. However, this outcome requires positive or green technologies that increase the provision of ecosystem services with few negative externalities or environmental costs, and that have a strong positive feedback in generating new technologies of the same kind. If the feedback is small, then the technological stock can collapse together with the human population. Scenarios where technological innovations generate net negative impacts may be associated with a limited technological stock as well as a limited human population at equilibrium and the potential for collapse. The only way to fill the planet with humans under this scenario of negative technologies is by reducing the technological stock to a minimum. Otherwise, the only feasible equilibrium is associated with population collapse. Our model points out that technological innovations per se may not help humans to grow and dominate the planet. Instead, different possibilities unfold for our future depending on their impact on the environment and on further innovation.

This article is part of the themed issue ‘Process and pattern in innovations from cells to societies’.

1. Introduction

The last 10 000 years in human history is unprecedented in terms of our success in overcoming ecological limitations and attaining inordinate population numbers. This is so to such an extent that we have become a geophysical force whose footprint on the planet marks a new geologic era (i.e. the Anthropocene) [1,2]. However, the question of to what extent are the current demographic and resource use trends sustainable is still unanswered. Mounting scientific evidence suggests, on the one hand, that our large-scale transformation of the biosphere has exceeded, or is close to exceeding, the limits of sustainability, which could have drastic consequences upon the dynamic state of the biosphere [3–5], diminishing our natural capital [6] and affecting our quality of life. On the other hand, innovation capacity, or the capacity to generate ideas or inventions that eventually diffuse within a human group, has been identified as the main process driving human demographic dynamics (e.g. [7,8]). This has led to the proposal that through innovations and investment in technology, it will be possible to solve potential constraints on population growth and resource use, making the human enterprise sustainable [9–11]. These later claims, however, rely on several assumptions such as no limits to growth, and that innovations have positive or neutral effects. These are at odds with available evidence pointing to the negative environmental impacts of some innovations, such as those that have abated the increasing resource demands of a growing population but generated negative externalities such as habitat loss and degradation, increased CO₂ emissions and pollution [4,12–18], and with the fact that our planet is finite and so are the natural capital and the ecosystem services it sustains. In this context, we focus on the alternative sustainability futures open to humans and, in particular, under which innovation scenarios can the human population continue to grow through continuous innovation (table 1).

Table 1.

Variables and parameters included in the model. CCE, cumulative cultural evolution.

parameter/variable	symbol	definition	dimensions
human biomass	ϕ	human biomass expressed as a proportion of the maximum that can be held in a finite habitat (planet Earth)	dimensionless
growth rate of human biomass	r	rate of growth in human biomass	T−1
habitat quality	ω	state of all ecosystem services required by humans expressed as a proportion of their maximum value for the habitat	dimensionless
habitat quality replenishment rate	λ	rate of supply of all ecosystem services that define the habitat quality	T−1
habitat quality basal maintenance requirements	B	basal maintenance requirements for human biomass expressed as a proportion of the maximum amount of ecosystem services available in the habitat	dimensionless
habitat quality social maintenance requirements	Bs	social maintenance costs or the extra ecosystem services requirements that arise as a consequence of living in a group of individuals innovating through CCE, expressed as a proportion of the maximum amount of ecosystem services available in the habitat	dimensionless
habitat quality reproduction requirements	E	proportional efficiency with which humans convert ecosystem services into human biomass	dimensionless
technological stock	μ	number of technological items or technologies, defined as any cultural device, tangible or not, that is the product of innovation driven by CCE and aimed at increasing the proportional supply of ecosystem services	number of technological items (n)
rate of technological innovation	ρ	per capita innovation rate	n × n−1 × T−1
rate of technology loss	l	per capita loss rate or rate at which technological items become obsolete. The reciprocal is the mean lifetime of a technology	n × n−1 × T−1
minimum technological stock	ɛ	minimum technological stock needed to ensure basic human well-being	number of technological items (n)
scaling parameter	α	parameter that determines the relationship between technological stock (μ) and supply of ecosystem services (λ)	dimensionless
scaling parameter	β	parameter that determines the relationship between technological stock (μ) and social maintenance costs (Bs)	dimensionless
normalization parameter	c1	normalization constant associated with the relationship between technological stock (μ) and supply of ecosystem services (λ)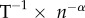
normalization parameter	c2	normalization constant associated with the relationship between technological stock (μ) and social maintenance costs (Bs)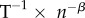
technological impact		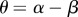net impact that technology has upon habitat quality	dimensionless
technological feedback		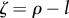net per capita impact that on average an extant technology has upon the production of new technologies before it disappears	n × n−1 × T−1
technological feedback		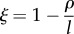normalized technological feedback	dimensionless

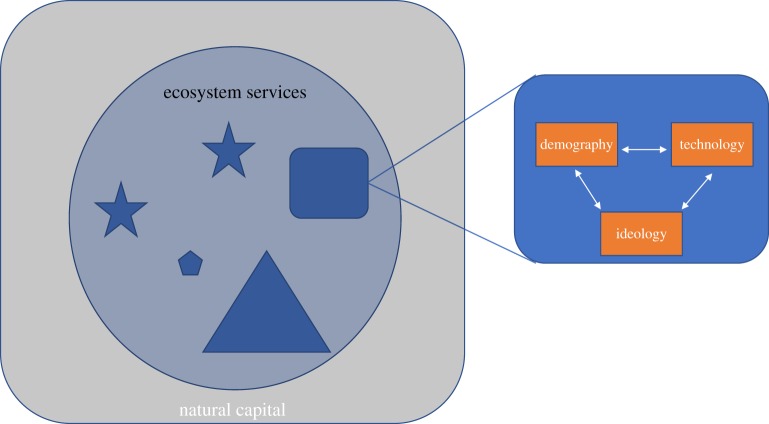
Different models have been developed to evaluate the sustainability of current human population growth dynamics, but none has explicitly determined whether innovations can sustain the future (increasing) demands of the growing human population on a finite planet. In this contribution, we develop a simple biological model aimed at explicitly evaluating how innovations expand natural population limits, determining the sustainability of the subsequent dynamics of a population. Starting from a general population growth model, we model innovations, through ‘cumulative cultural evolution’ (CCE), defined in our context as the transmission, modification and persistence of socially learnt technologies and other sources of cultural variation, which accumulate over many generations, leading to the evolution of technologies that no single individual could invent [19,20]. This is a salient trait of our species and a motor for innovations [21,22], through which humans have been able to maintain the flow of ecosystem services (i.e. the services provided by the biosphere and needed to sustain human life and its activities, [23]), at an adequate level for its continual exploitation. Continuous innovation is thus possible through CCE [24,25], and in the context of our model, this process increases the benefits that humans obtain from the environment by enhancing the flow of ecosystem services. These services not only sustain human numbers, but are also responsible for our well-being [26–29]. Innovations are essential to increase the flow of services and overcome ecological limits, but they can also bring about new social costs, ultimately setting a limit upon human population size. We summarize our views in the conceptual model presented in figure 1 [30].

Figure 1.

Conceptual model for the relationship between natural capital, ecosystem services and humans. The natural capital sustains the provision of ecosystem services. Different species, and humans in particular, can display different adaptive strategies to use available ecosystem services (depicted as geometric shapes within the space of ecosystem services). These strategies imply a particular interaction between demography (i.e. population size), technology production through innovation and ideology. These strategies redirect, through technological innovations, different proportions of the flow of ecosystem services to their own maintenance and growth, which is expressed by the size of the geometric shape in the space of ecosystem services.

The framework presented in figure 1 is rooted in simple biological reasoning; the persistence of humans, as any other species, is possible by the services provided by the ecosystem they inhabit, and whose flow affects their fitness. Human persistence is driven by continuous trial and error at the individual level, and by transmission through social learning and the persistence of innovations at the social level, and manifested in biological and technological evolution [31]. The flow of ecosystem services is sustained by the natural capital or stock of natural assets (soil, water, minerals, air and living entities) [27] and, for this reason, they are shown as embedded within the natural capital space in figure 1. Different species, and humans in particular, can display different adaptive strategies to use available ecosystem services (depicted as geometric shapes within the space of ecosystem services). These strategies imply a particular interaction between demography (i.e. population size), technology production through innovation and ideology. This latter component provides the narrative that sustains, and socially validates, the particular feedback between demography and technology associated with a given strategy. These adaptive strategies, or lifestyles, redirect through technological innovations different proportions of the flow of ecosystem services to their own maintenance and growth, which are expressed by the size of the geometric shape in the space of ecosystem services in figure 1. Using this conceptual model, we analyse the sustainability of our modern lifestyle and ask under what circumstances the maximization of our standards of well-being, propelled through increasing population size and increasing innovation (e.g. [10]), is feasible without compromising our survival and the environment.

2. General model

As a point of departure, we use the model proposed by Keymer et al. [32] (see equations (2.1)–(2.4)) below) to understand the dynamics of bacterial diversity and modify it according to the framework introduced in figure 1. These authors assume that any species is confined to a finite habitat, which in the case of humans is planet Earth. The finiteness of habitable habitat sets a limit to how much biomass can be packed inside it. We define ϕ as the proportion of human biomass in relation to the maximum that can be sustained on the planet. The dynamics of this human biomass can then be expressed as:

2.1

The logistic term on the right-hand side of equation (2.1) represents the spatial density dependence induced by the finiteness of the habitat. We make the per capita population growth rate (r) a function of ‘habitat quality’ (ω), which is a measure of the state of all ecosystem services required by humans and whose value is a function of the flow of those services [28]. Habitat quality affects r by modifying the fecundity and mortality of the population inhabiting it; therefore, we decompose r into its per capita birth (b) and death (d) rate components. Let us assume that there is a fixed level of mortality (d₀), which is biologically determined and would occur even in an optimal environment. Now assume that in addition, there is a mortality (d) that depends on the quality of the habitat as d(1 − ω), and thus tends to 0 when the quality of the habitat tends to 1. This implies

which is equivalent to

Making (b + d) = f and (d + d₀) = m, we arrive at

2.2

where f is the maximal fecundity rate that the species can achieve under ideal conditions, which is weighted by the habitat quality (ω). Mortality m, on the other hand, includes both a biologically determined rate (assumed fixed) and a habitat-dependent rate that varies according to habitat quality.

When habitat quality, 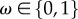, takes on the value of 1, the flux of all ecosystem services is at the maximal capacity for human use.

We model the habitat quality dynamics by considering that quality increases as the supply of ecosystem services in the habitat (λ) increases. Habitat quality decreases owing to the consumption of ecosystem services by the human population and is a function of maintenance needs (B) and the efficiency (E) with which an individual converts them, or uses them, to support offspring. Thus, the expression for habitat quality dynamics is as follows:

2.3

The first term on the right-hand side of equation (2.3) corresponds to the supply of ecosystem services affected by human actions in the habitat. The second term is ecosystem service consumption and/or use to fuel human population maintenance and growth.

The system of coupled equations can then be written as:

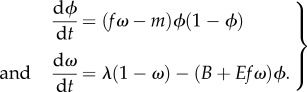2.4

This system has been studied by Keymer et al. [32] (see also [33]), with three known possible long-term behaviours, which in its current version correspond to: (1) the extinction equilibrium. Here, the human population goes extinct (ϕ* = 0) and the habitat quality, or flow of ecosystem services that sustain the human niche, stays at its maximal state (ω* = 1). (2) The Habitat Limitation equilibrium. This equilibrium is set by the balance between the consumption and supply of ecosystem services within the habitat, which reaches equilibrium at ω* = m/f, sustaining a population whose equilibrium biomass is given by 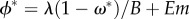. And, (3) the Space Limitation equilibrium. Here, the equilibrium is reached when the species fills the entire space with biomass ϕ* = 1, and habitat quality stays as 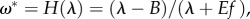which, in the human case, improves as humans decrease their maintenance needs (B) and increase the efficiency in converting ecosystem services to support offspring (E). The stability of the previous fixed points is provided in the electronic supplementary material.

With this model in hand, we evaluate how can it be used to explain the modern increase in human population numbers and ask about the sustainability of the process. We make the hypothesis that the human capacity for ‘CCE’ allows continuous improvement, through innovation, in the availability and flow of ecosystem services and therefore the maintenance of high habitat quality which ultimately allows higher population numbers to be reached (e.g. [34]).

3. Including innovation into the model

The ecosystem services replenishment rate (λ) is a key parameter in our general model, as it determines the final biomass that humans can attain under Habitat Limitation and, if great enough (i.e. λ > λ*), the final state of all ecosystem services or habitat quality that will support human biomass at planetary saturation (see the electronic supplementary material). Along these lines, it would always pay to invest in innovations that increase the replenishment rate of ecosystem services (higher λ). However, innovations necessarily entail costs [13,14,35,36], which need to be incorporated in the general model. The next sections discuss these processes and how they should be incorporated in the general model.

4. Cumulative cultural evolution as process in technological development

One definitive characteristic of humans is their enhanced capacity for cultural dynamics (e.g. [37]). Culture is defined as ‘information […] acquired from other conspecifics by teaching or imitation’ [38], and although what corresponds to culture is present in a number of species, humans are unique in their capacity to acquire and retain new cultural traits over generations and devise technologies that no single individual could invent [19,22,39]. This capacity of CCE allows continuous change or innovation of cultural features, generating extremely complex traits through time [21,22,40].

In our model, we are particularly interested in those cultural innovations that allow improvement of the flow of ecosystem services, which we will address as ‘Technology’ (μ). Defining technology is not an easy task, and it can be considered to encompass anything that is required to produce an ‘object of material culture’ that ‘fulfils a human purpose’ [41]. In the context of the current model, and for the sake of simplicity, we will consider technology as any cultural device, tangible or not, that is the product of innovation driven by CCE and whose direct effect is to increase the supply of one or more ecosystem services. This includes the knowledge base as well as the institutions that influence the effectiveness with which this knowledge is used [11].

A vast amount of literature analyses the processes behind technological/cultural innovation (e.g. [20,21,25,30,41–44]) and, although no complete consensus or an articulated theory exists [41], some principles of this process are well established. When modelling technological innovations, it is clear that: (i) a positive feedback exists with population size (e.g. [24,25,45–49]), because not only does having more individuals increase the chances that someone will come up with an invention, but also population size increases the rate of human interaction and social learning, and thus per capita invention probability and the production of complex innovations [24,25,30,31,42,44,46,50]. This is further augmented by the progressive trend in urban aggregation exhibited by our species [51]. (ii) There is a positive feedback with technological accumulation, because extant technologies can, through recombination, result in new technologies [21,31,41,52,53]. And (iii) CCE is the main mechanism for technological innovation, through the transmission, modification and persistence of socially learnt technologies. We suggest that at least some, if not all these processes, must be present when modelling innovations.

Considering the above, it becomes clear that the rate of ecosystem service provision should be a function of the technological stock aimed at improving its flow. This implies that λ in equation (2.4) should be λ(μ). Furthermore, based on the study of Enquist et al. [21], we can model the dynamics of technological stock as follows:

4.1

Here, the first term on the right side of equation (4.1) addresses invention mechanisms that produce new technological innovations through CCE, which depends on ϕ, and the impact of a per capita innovation rate ρ, which is modelled as a self-reinforcement process that is a function of the already accumulated technological stock μ. The second part of the right-hand side includes a rate of technology loss (l) due to chance events and/or technology deterioration over time. Finally, there is a minimum or basic technological toolkit (ɛ) associated with some basic knowledge and abilities (e.g. ability to find and gather water or food, to communicate, measure and calculate) that identify either a state characterizing early human societies or some other minimum technological toolkit to which humans have access.

5. Costs underlying technologically complex societies

The costs of technological innovation are associated with the conditions that foster their emergence such as large population size, usually in dense urban centres with augmented risks of epidemic outbreaks, increased waste production, pollution and violence, among others [54–56]. Urban centres are also loci for increased demand for ecosystem services [34] that result in environmental problems that can reach global extent (e.g. Global Change, [57]). While these costs could be abated through the creation and maintenance of social and physical infrastructure [44], it is unlikely that they will disappear, as the maintenance of such infrastructure necessarily increases the demands of individuals living in those settlements, as suggested by empirical data [13,14,34,36,58,59]. This, in our framework, translates into greater impacts upon the service provided by ecosystems.

To introduce this cost into the general model, we assume that the per capita maintenance requirements of human biomass are an increasing function of the accumulated technological stock. The logic behind this is that maintenance needs (B) increase owing to the added social costs of technological development B_s(μ), defined as the additional resources required by individuals to engage in fruitful teaching/learning dynamics, and thus innovation, in a given cultural group; hence 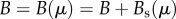. Furthermore, because 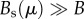(e.g. social costs are significantly greater than maintenance needs, see [34]), then 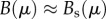, so we ignore the term Efω shown in equation (2.4).

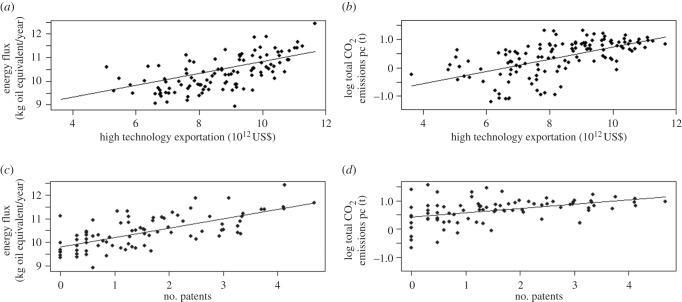
Finally, we need to specify suitable functions for λ(μ) and B(μ). Since technological development, innovation activity, inventions and ideas scale with population size (e.g. [8]), we assume that the increase in the technologically driven provision of supporting ecosystem services, and associated costs, scales with the amount of technological stock μ. Empirical evidence indicates that this may be a reasonable assumption. Figure 2 shows that the provision and the costs of primary energy increase with two proxies of innovation and technological development. Thus, we define both functions as simple scaling relationships of the form 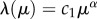and 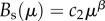, respectively, with normalization constants c₁ and c₂. After these considerations, we can now define the complete model, which links human biomass to habitat quality (i.e. the state of ecosystem services in the habitat) and then to technological innovations that increase the provision of the ecosystem services. The final, complete model is:

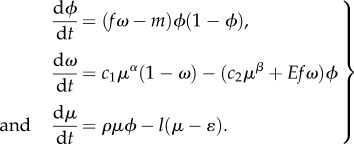5.1

Figure 2.

Relationship between energy flux (derived from oil, gas and coal) at the country level (a proxy for ecosystem service, (a,c)) as well as CO₂ emissions (b,d), a proxy for negative impacts, and two technological stock proxies (high technology exportation, based on the study of Hidalgo et al. [60], and number of patents, based on the study of Strumsky et al. [61]). Data come from the World Bank and the US Patent and Trademark Office for the year 2011. All relationships are significant and the slope values from (a–d) are 0.31, 0.22, 0.40, 0.15, respectively. 10¹² US$, trillion US dollars, pc, per capita; 1 t (tonne) = 10³ kg.

As with the previous model in equation (2.4), this model also has the analogous three equilibria (Extinction, Habitat Limitation and Space Limitation, see the electronic supplementary material), but their values and stability analyses are now functions of ‘technological impact’ 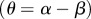and the strength of the ‘technological feedback’ 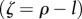(see the electronic supplementary material). Technological impact (θ) measures the net impact of technology upon the provision of ecosystem services, balancing the positive effect of technology on the increased supply of ecosystem services within the habitat (α) against the negative effect of technology due to an increased individual consumption (β) and/or ecosystem degradation. Positive technological impacts include ‘positive or green technologies' (α > β and therefore θ > 0), meaning that their effect on increasing the supply of ecosystem services is larger than the increase in individual consumption (the social cost of innovation as measured by B_s) or ecosystem degradation that they may accrue. On the other hand, negative values relate to ‘negative technologies' (α < β and therefore θ < 0), meaning that their adoption leads to an increase in individual consumption and indirect deterioration of ecosystem services in relation to their provision. Finally, ‘no-net-loss technologies’ have a net null impact on ecosystem services, because any technological increase in their flow is compensated by negative indirect effects or proportional costs in individual consumption (α = β and therefore θ = 0).

To exemplify our approach, consider technologies affecting the provision of freshwater ecosystems that provide a key service for humanity, and currently seriously affected by human population size and climate change (e.g. [62]). Relevant examples of green technologies include those that increase the efficiency of water reclamation (i.e. reuse of waste water) or exploit alternative water sources (i.e. fog), and are powered by energy from a grid based on photovoltaics and wind. An example of a negative technology is desalination plants powered by an energy grid heavily based on coal (see [63]), which fulfil the direct objective of providing water, but indirectly increase climate change impacts and thus negatively affect other ecosystem services (i.e. climate and wildfire regulation, and crop production, [64]). Increased climate change may also increase air temperatures, leading to a lower supply of water and an associated increase in water demand for agriculture (e.g. [65]).

The strength of the ‘technological feedback’ (ζ) measures the impact that a technology has on the production of new technologies before the former disappears or becomes outdated (see also [66]). As discussed previously, one technology can enhance further technological development through recombination, giving rise to positive feedbacks where technologies not only replace themselves through improvements in efficiency or design, but can also make possible the generation of new technologies during their lifetime (ρ > l and therefore ζ > 0). Continual technological development can only be achieved under this regime; otherwise, the technological stock will be reduced in size or slowly growing. On the other hand, neutral feedback refers to technologies that at the most only replace themselves, not leading to new innovations (ρ = l and therefore ζ = 0). Negative feedback (ρ < l and therefore ζ < 0) characterizes technology that does not importantly impact innovation dynamics. This regime could represent decreasing returns in innovation dynamics, implying the existence of limits to innovation, because the problems, and the technologies to solve them, become more complex and costly [61,67], or it could result when cutting edge technologies are so different from previous ones that the former's assimilation into existing technologies is difficult, generating an effect whereby their widespread adoption is challenging, and they may persist without diffusing for a long time [68].

For the complete model (equation (5.1)), once again, whenever mortality is greater than fecundity (m > f), the Extinction Equilibrium is the only stable scenario 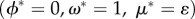, irrespective of other parameters. If this is not the case (and m < f), then either the Habitat or the Space Limitation scenarios can occur.

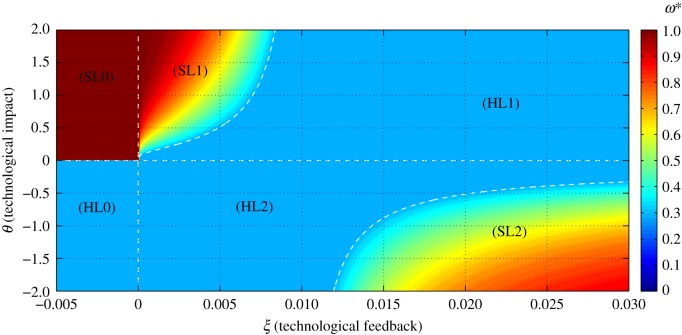
Figure 3 shows a phase-space diagram of technological impact (θ, where positive values identify green technologies) and technological feedback expressed as 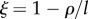(such that negative values imply a positive feedback), illustrating some of the possible dynamics of the model with habitat quality at equilibrium (i.e. ω*). The scenario where human biomass ‘fills up the world’ (ϕ* = 1) or Space Limitation equilibrium (areas labelled as SL0, SL1 and SL2 in figure 3) can only be sustained under (i) technologies with positive impact on ecosystem services (i.e. θ > 0, as in SL0 and SL1, see figures 3 and 4) or (ii) technologies that have a negative impact on ecosystem services (i.e. θ < 0), but at the cost of a reduced technological stock and a slow rate of technological accumulation (because the feedback is negative, as in SL2 in figures 3 and 4; see also electronic supplementary material). In scenario SL1 and SL2, habitat quality can be comparable (figure 4) and is a function of technological stock at equilibrium (see the electronic supplementary material), such that they satisfy 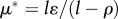and 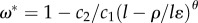. The SL0 case is different because the existence of a positive technological feedback (i.e. ξ < 0) makes the technological stock increase without bounds (i.e. it tends to infinity), which combined with a positive technological impact (θ > 0) results in ω* → 1 (figure 4 and Infinite technology analysis in the electronic supplementary material). As shown in the electronic supplementary material, for θ > 0, the SL1 equilibrium is stable if

5.2

Otherwise, the system moves to the Habitat Limitation equilibrium (HL1). Similarly, for 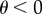, the stability condition for SL2 is

5.3

Otherwise, the equilibrium shifts from the SL2 to the HL2 equilibrium (figure 3).

Figure 3.

Phase-space diagram to classify the different types of dynamics exhibited by our model of human population growth coupled with innovation acting upon the provision of ecosystem services at equilibrium or habitat quality (ω*) of our planet. In this phase space, we represent the dynamics as driven by two key parameters, θ, which represents the net effect of technology upon ecosystem services (with θ < 0 implying that the costs of increasing the provision of ecosystem services, through technological innovation, are larger than the benefits accrued to humans), and the parameter 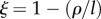, which represents the relationship between the lifetime of a technology 1/l and its impact upon fostering new technological advances mediated by the per capita innovation rate (ρ). A positive ξ means that ρ < l, implying that technologies tend to have little impact upon further technological innovation and long lifetimes. Regions identified with SL correspond to the Spatial Limitation equilibrium, whereas regions identified with HL refer to the Habitat Limitation one. Biomass saturation occurs in regions SL0, SL1 and SL2, and biomass collapse is likely in HL0 and HL1.

Figure 4.

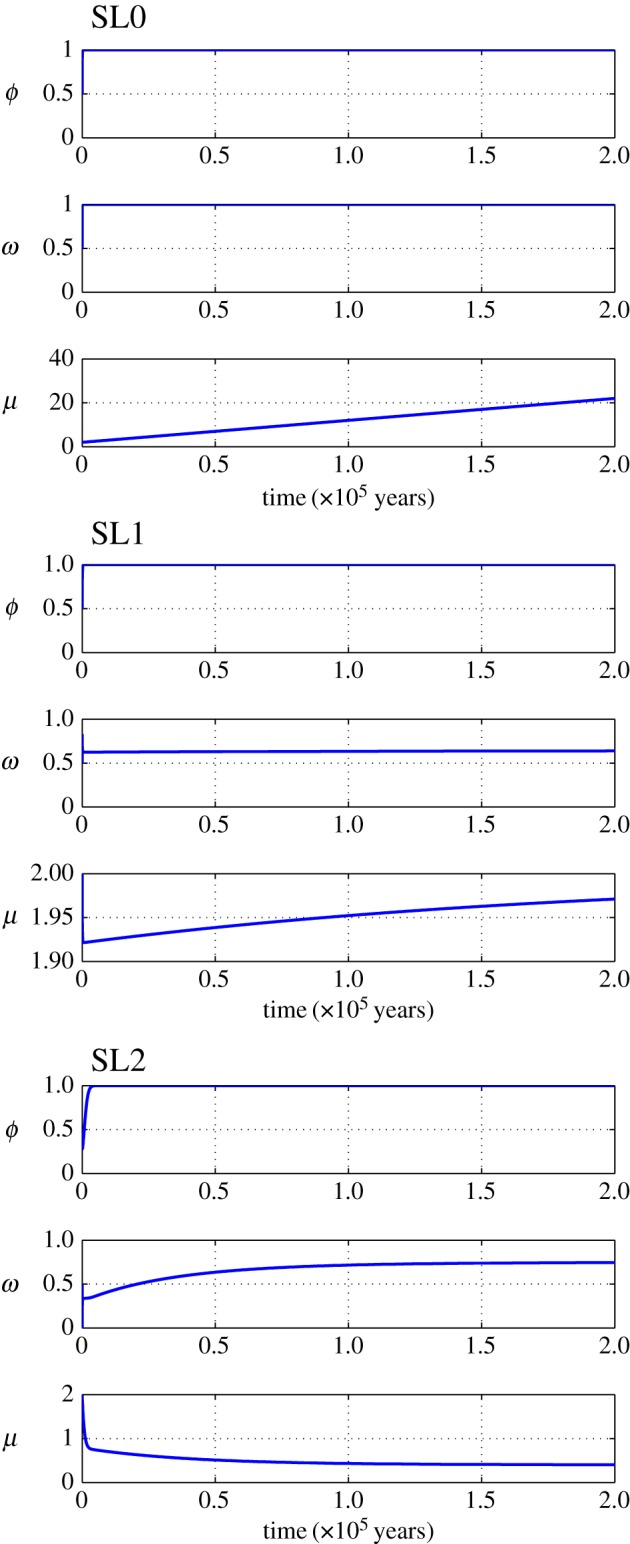
Simulation of representative trajectories for human biomass (ϕ), habitat quality (ω) and technological stock (μ) associated with different Spatial Limitation equilibrium regions in the phase space shown in figure 3. Parameters are as follows: SL0 (ξ = −0.0025, θ = 1.5), SL1 (ξ = 0.005, θ = 1.5), SL2 (ξ = 0.025, θ = −1.5). For all simulation parameters, values were set to m = 0.012, f = 0.04, ɛ = 0.01, l = 0.001, c₁ = c₂ = 1, β = 2, α = β + θ.

The Habitat Limitation scenario imposes a fixed habitat quality at 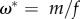, while equilibria for human biomass and technological stock cannot be explicitly listed because in this case one needs to know μ* to find ϕ* and vice versa (see the electronic supplementary material). Three important remarks for these equilibria arise: (i) technological stock is bounded within 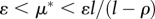; (ii) human biomass is bounded within 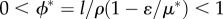and is prone to collapse to very low numbers as in HL0 and whenever the technological stock μ* < 1 in HL1 (figures 3 and 5). For HL1 and μ* > 1, it holds that 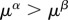and the benefits of technology are greater than the costs generated; however, when μ* < 1, 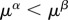making the costs of technology higher than the benefits, and the population collapses (figure 5).

Figure 5.

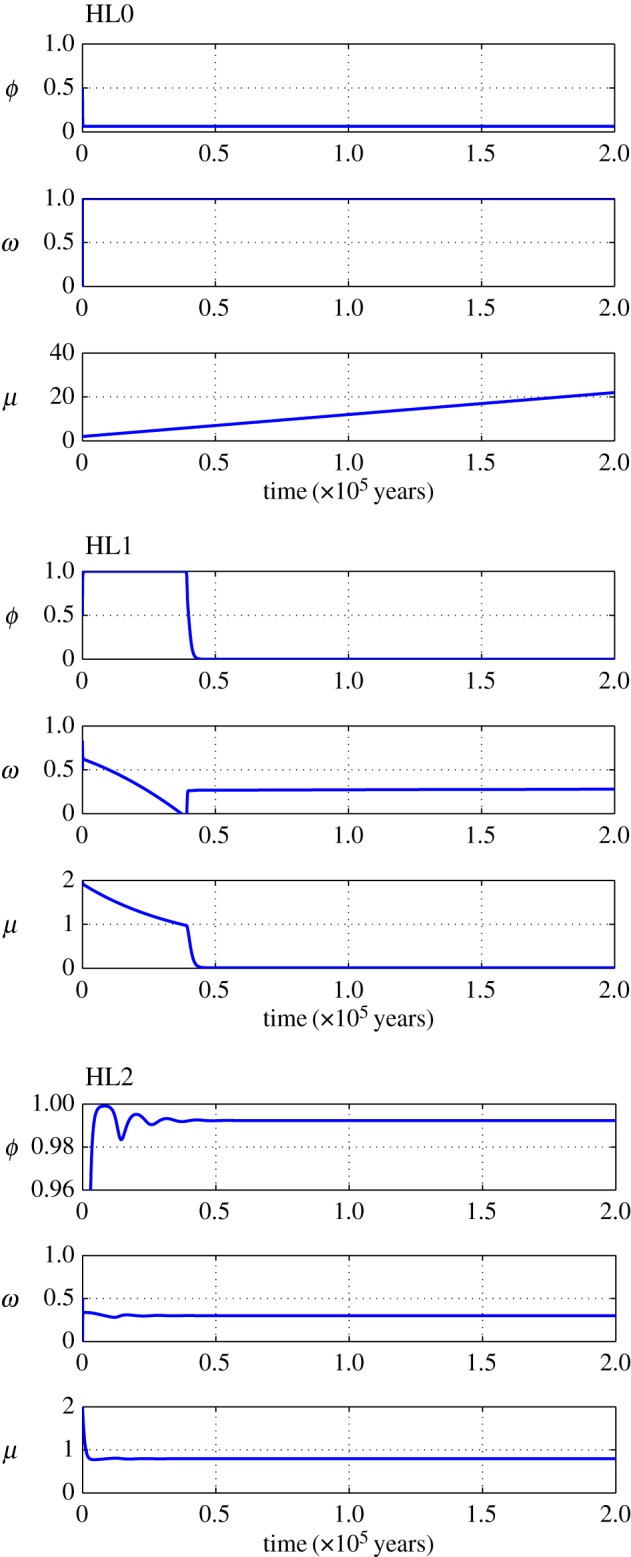
Simulation of representative trajectories for human biomass (ϕ), habitat quality (ω) and technological stock (μ) associated with different Habitat Limitation equilibrium regions in the phase space shown in figure 3. Parameters are as follows: HL0 (ξ = −0.0025, θ = −1.5), HL1 (ξ = 0.025, θ = 1.5), HL2 (ξ = 0.005, θ = −1.5). For all simulation parameters, values were set to m = 0.012, f = 0.04, ɛ = 0.01, l = 0.001, c₁ = c₂ = 1, β = 2, α = β + θ.

Finally, our model shows that whenever ρ > l, infinite technological stocks could be developed. A simplified analysis for this scenario shows that such an outcome can only be sustained under positive technological impacts (θ > 0) (see figures 3 and 4 and electronic supplementary material, figure S1).

6. Discussion

In theory, our model shows that the human population can fill the entire planet, while maximizing well-being and without exhausting ecosystem services, that is, in a sustainable way. However, this outcome necessarily requires a planet dominated by positive technologies that generate benefits surpassing their costs, and has positive feedbacks in terms of generating new technologies (figure 3). This is essentially the same as the technologically optimistic scenario dubbed ‘Star Trek’ by Robert Constanza [69]. However, we have shown that this scenario may not be robust should technologies suddenly become negative for the environment (see electronic supplementary material, figure S3).

Our model connects human population size with the demand and provision of ecosystem services and technological innovation. These connections, as well as the explicit inclusion of the environmental costs of innovation, are novel in the context of a model of human population growth, but have already been pointed out, at least conceptually, in the IPAT (environmental Impact = Population × Affluence × Technology) model developed by Ehrlich & Holdren [70], and included in the Limits to Growth project model [54]. In this context, our models provide theoretical evidence and mathematical arguments for the existence of alternative scenarios of sustainability, suggesting that collapse is a real possibility. Although our aim is to provide a model that improves understanding of how the factors outlined above interact in affecting sustainability, we think it is important to refine the model and estimate parameters in order to contrast it against real-world examples.

Importantly, our model may apply to both renewable and non-renewable ecosystem services. Humans have the capacity to affect the replenishment rate λ(μ) of both types of service through innovations that influence the efficiency of existing technologies, such as generating more efficient fishing gear to exploit fish populations, or by generating new ones that help us to use alternative ecosystem services such as artificially fixed nitrogen instead of natural nitrate deposits or guano. In an extremely deteriorated environment (i.e. ω* is very low), most of the remaining quality of the habitat for sustaining humans would reside in the potential to increase the provision of ecosystem services through innovation and technologies. Experiments such as Biosphere 2 have shown that this is a complicated task [71]. Furthermore, because in the Habitat Limitation scenario, habitat quality is determined by the relationship between fecundity and mortality, ω* = m/f, a limit to growth [54,70] should be part of a strategy to improve the provision of ecosystem services and thus the quality of life.

Our analysis begs the question of the extent to which our modern society can keep growing, not only without impacting the provision of ecosystem services, but also in improving them (i.e. positive sustainability). Available empirical data on modern human societies (e.g. [2,13,14,34,36,58,59]) indicate that we may well be in the dynamics associated with the equilibrium HL2 in figure 3. This is a situation that will be difficult to improve, resulting in a shift to the SL1 equilibrium, considering the accumulated cost already incurred, or the technological debt [3,12,17,72]. Thus, unless we drastically change our innovation ecosystem to one where new positive technologies become dominant, and the minimum technological stock that humans have access to (ɛ) increases (which would make the SL1 equilibrium more stable; see equation (5.2)), we could transit to a world saturated with people and a reduced technological stock (SL2, figures 3 and 4), or a world with very few people and moderate technology (HL0, figures 3 and 5). It is worth emphasizing that the only way of achieving saturation under technologies that generate a net negative impact upon ecosystem services (the SL2 equilibrium) is by sacrificing its stock, the rate of technological innovation (i.e. ρ < l, figure 3), and by decreasing the minimum technological stock to which humans have access (ɛ), so that the SL2 equilibrium is stable (see equation (5.3)), which we may equate with a decrease in the standard of living in modern societies. This scenario is similar to the ‘Mad Max’ scenario proposed by Constanza [69]. It is possible, however, that humans are on a course of imminent collapse in living standards and population size [73], suggesting that we may be in a transition to an SL2 or HL2 type of equilibrium, which implies a reduction in technological stock, and a decrease in habitat quality and population size.

One of the limitations of our approach lies in the mean field assumption whereby every human experiences the same average situation. The alternative is that some proportion of the saturating human biomass may experience different scenarios in figure 3, such that some may be living in a saturated world with a large technological stock while others live in an impoverished one. For the sake of simplicity and tractability, our model does not explore the impact of unequal access to technology or ecosystem services. Instead, we assumed that all human inhabitants equally share ecosystem services; however, inequalities in well-being and therefore ecosystem service access and demand exist among and within nations [74,75] and will likely increase [76]. Introducing these inequalities in the model may be important for determining whether technological stock is sufficient for coping with proposed well-being standards, or if ecosystem services are actually being sequestered mostly by one class of human beings to the detriment of the rest [12,77,78]. Some estimations show that sustaining a global population enjoying living standards similar to those of developed countries is not feasible, given the negative impacts of current technology on the supply of ecosystem services (e.g. [12–14,58]). However, inequality is not sustainable either, as it leads to social instabilities and conflicts. Further research of this topic in the context of the present model is required to illuminate the role of inequality in affecting the sustainability of human socio-ecological systems.

We assume that technological impacts remain constant in time, as if humans could continually maintain the ratio between technological benefits versus costs, but this is not necessarily so. This assumption comes from the implicit consideration of technological ‘instant adjustment’ to eventualities [79], constantly maintaining their benefits and costs. However, if we allow lags to occur between events (between the identification of a problem and its solution) as proposed by some technological theories (i.e. [80,81]), oscillations and therefore population crashes could occur ([82], see electronic supplementary material, figure S3). Also, given the context-dependent nature of ecosystem services [28], similar technologies can have different effects upon ecosystem services, depending on (among other things) the location where it is used. For instance, Polynesian cultures are known for their great navigation technology, conquering many Pacific islands [83,84]; however, the occupation of subtropical Easter Island implied a cooler, poorer and less diverse ecosystem for their standards [83]. And the same technologies that were sustainable in warmer climates led to the complete exploitation of the native forest, which had slower renewal times than the species they were accustomed to, leading to social collapse [83,85]. Similarly, technological innovations can directly affect fecundity and mortality through pollution for example, and tip the balance among the equilibria we found in our model (see equations (5.2) and (5.3)). It is worth noting that ρ/l is similar to the R₀ of epidemiological models, as it measures the amount of secondary technologies that a single technology influences during its lifetime.

Finally, we should acknowledge that ours is a closed system approach, where the environment is represented as natural capital that sustains the fluxes of services to humanity. However, under other types of environmental fluctuation, habitat quality may go through a threshold or abrupt transition in state with dramatic consequences upon human populations. Thus, the negative impacts of innovations can be amplified through positive feedbacks with other drivers such as climate fluctuations, societal instabilities, diseases and resource overexploitation, leading to population fluctuations and eventual collapse (e.g. [30,84–89]). Our simple model indicates that technological innovations are not the panacea that will help us to grow and dominate the planet by solving any problem that we may encounter. Far from that, different possibilities may unfold depending on their impact on the environment and on further innovation. In particular, we show the number of people that the planet can support will depend on the kind of technology, the living standard deemed acceptable and the impact of technologies on themselves and on the provision of ecosystem services [90]. Particularly worrisome, however, is the fact that over a large portion of parameter space, the collapse of the human population is likely; also likely is that our future is a world saturated with people on a planet where the provision of ecosystem services is low and the quality of life poor.

Data accessibility

This article has no additional data.

Author contributions

V.P.W., P.A.M. and C.Q. conceived the model, made the analysis and wrote the paper.

Competing interests

The authors declare no competing financial interests.

Funding

C.Q. was partially supported by CONICYT's Programa de Investigación Asociativa (PIA), Anillo SOC1405. V.P.W. is supported by Programa Capital Humano Avanzado from CONICYT. P.A.M. acknowledges support from projects CONICYT/SOC1405, ICM-MINECON P05-001 and PFB-CONICYT P-053 and the Santa Fe Institute.