Inferring processes of cultural transmission: the critical role of rare variants in distinguishing neutrality from novelty biases

Abstract

Neutral evolution assumes that there are no selective forces distinguishing different variants in a population. Despite this striking assumption, many recent studies have sought to assess whether neutrality can provide a good description of different episodes of cultural change. One approach has been to test whether neutral predictions are consistent with observed progeny distributions, recording the number of variants that have produced a given number of new instances within a specified time interval: a classic example is the distribution of baby names. Using an overlapping generations model, we show that these distributions consist of two phases: a power-law phase with a constant exponent of 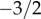, followed by an exponential cut-off for variants with very large numbers of progeny. Maximum-likelihood estimations of the model parameters provide a direct way to establish whether observed empirical patterns are consistent with neutral evolution. We apply our approach to a complete dataset of baby names from Australia. Crucially, we show that analyses based on only the most popular variants, as is often the case in studies of cultural evolution, can provide misleading evidence for underlying transmission hypotheses. While neutrality provides a plausible description of progeny distributions of abundant variants, rare variants deviate from neutrality. Further, we develop a simulation framework that allows the detection of alternative cultural transmission processes. We show that anti-novelty bias is able to replicate the complete progeny distribution of the Australian dataset.

This article is part of the themed issue ‘Process and pattern in innovations from cells to societies’.

1. Introduction

Most theoretical modelling frameworks to cultural evolution make the simplifying assumption that innovations are the product of erroneous cultural transmission resulting in the introduction of cultural variants not previously seen in the population at low abundances (e.g. [1,2]). But regardless of the mechanisms underlying the occurrence of any particular innovation, its subsequent fate (i.e. whether it goes extinct immediately or is able to spread through the population and reach a certain degree of visibility) provides a window into the processes of cultural transmission present in the population. For example, the ‘persistence’ of a large number of innovations might point to population-level preferences for novel or rare variants. As a large number of such cultural transmission hypotheses have been proposed in the literature (see [3]), the question whether we can develop systematic approaches to distinguish between different transmission hypotheses using aggregated population-level data has gained importance.

Seminal work by Bentley and colleagues (e.g. [4–6]) on this topic has focused on distinguishing broadly between neutral and non-neutral cultural transmission processes. Neutral models of cultural transmission make the assumption that there are no selective differences between variants, so that the dynamics of a new variant are not biased towards either proliferation or extinction. This hypothesis results in a particular kind of stochastic dynamics, known as drift. In balancing the utility and availability of cultural data, the studies mentioned above identified the progeny distribution as a way to distinguish the neutral hypothesis from others. The progeny distribution logs the abundances of cultural variant types which produce k new individuals over a fixed period of time. Bentley and colleagues have estimated the form of the neutral progeny distribution through simulation techniques (e.g. [4,5,7]), concluding that the progeny distribution takes the form of a power law. The exponent of this power law has been fitted as a function that depends on the innovation rate and the total population size. The theoretical predictions have been compared against empirical data for the choice of baby names, US patents and their citations or pottery motifs, and these analyses provided support for the neutral hypothesis [4,5]. Despite this progress, an analytical expression for the neutral progeny distribution has been lacking so far, which has limited further developments in understanding whether observed distributions are consistent with neutrality, or demand non-neutral explanations.

In this manuscript, we derive the first analytical representation of the neutral progeny distribution for large time intervals, using a neutral model where variants are not constrained to reproduce at discrete time points, known as an overlapping generations model. We show that the neutral progeny distribution consists of two phases. For small numbers of progeny there is a power-law phase. This is broadly consistent with the fits to earlier numerical simulations, but here we find that this power law has a fixed, universally applicable exponent of 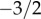. Following this power-law phase, for large enough numbers of progeny there is eventually an exponential drop-off in this distribution. The onset of the exponential decline depends on the innovation rate: the larger the rate, the earlier is the onset. The analytical representation of the progeny distribution allows for maximum-likelihood estimations of the model parameter and therefore provides a direct way of parametrizing neutral models using cultural data, and of subsequently evaluating the consistency between observed data and the neutral hypothesis. Importantly, we establish that analyses based on only the most popular variants, as is often the case in studies of cultural evolution, can provide misleading evidence for neutral evolution.

Further, we show that the progeny distribution represents a statistic that is able to detect alternative cultural transmission hypotheses, in particular bias for or against novelty, and therefore is potentially capable of distinguishing between different processes of cultural transmission based on population-level data. For that we develop a simulation procedure which includes pro- and anti-novelty bias. Anti-novelty bias is characterized as the preference for variants that have been present in the population for a long time (i.e. innovations possess an intrinsic disadvantage), while pro-novelty bias describes the preference for ‘young’ variant types that have only recently been introduced into the cultural system (i.e. innovations possess an intrinsic advantage). In general, we find that the progeny distribution reacts sensitively to those changes in the transmission process. Related results have been found by Mesoudi & Lycett [8], who concluded that strong frequency-dependent biases alter the shape of the progeny distribution. They also note that some transmission biases will generate population-level predictions indistinguishable from neutral predictions.

Following [5], we apply our framework to an Australian dataset recording the first names of newborns (The code of the simulation framework can be downloaded from https://github.com/odwyer-lab/neutral_progeny_distribution.). We demonstrate the importance of rare variants for reliable inference of processes of cultural evolution from aggregated population-level data in the form of progeny distributions. While the temporal dynamics of abundant names are consistent with neutrality, the analysis based on the complete distribution, including popular and rare names, provides evidence against neutral evolution. This means that progeny distributions generate reliable inferences only in situations where the complete dataset is available. We find that anti-novelty bias is able to replicate the complete progeny distribution of the considered Australian baby name data.

2. Neutral theory and innovation

Neutral models have provided basic null models in fields stretching from population genetics [9] and ecology [10–14], to cultural evolution and the social sciences (e.g. [4,15–17]). At the core of all varieties of neutral theory is a group of competing variants, and the assumption that selective differences between these variants are absent. In addition, most neutral models contain the possibility for innovation, i.e. the introduction of entirely new variants into the system. The most common approach to modelling an innovation event is to assume that with some rate a parent individual will produce an offspring of a new type instead of an offspring of the same parental type. This new variant then undergoes the same dynamics as all extant variants.

The assumptions of neutrality are often at odds with the vast stores of knowledge biologists and anthropologists have accumulated for natural and social systems. For example, we know that even closely related biological species differ in their phenotype, and we might expect that these differences are important for predicting and understanding the properties of ecological communities. And yet despite this obvious roadblock, neutral models in ecology have had some considerable success in predicting patterns of biodiversity observed at a single snapshot in time [18–29]. The same is true for cultural evolution, where humans are generally not thought of as making decisions at random. Neutrality would imply that individuals do not possess any preferences for existing cultural variants, nor does the adoption of a particular cultural variant provide an evolutionary advantage over the adoption of a different variant. While these inherent assumptions are likely to be violated in the cultural context (for detailed discussions see e.g. [15,16,30]), population-level patterns of various observed episodes of cultural change nevertheless resemble the ones expected under neutrality (e.g. [4,15,31]).

Statistical tests of neutral theory often focus on static patterns of diversity, observed at one moment in time, such as the balance of rare and dominant species in a population. It has been shown that neutral steady-state predictions for the distribution of species abundances often closely match observed distributions. By contrast, neutral theories in ecology have had less success in predicting the dynamics of diversity, from decadal-scale species abundance fluctuations to geological ages of species [32–36]. Similarly, recent work in cultural evolution has pointed to the importance of analysing temporal patterns of change as opposed to static measures of cultural diversity (e.g. [37–40]) and to the influence of aggregation processes particularly in archaeological case studies [7] when testing for departures from neutrality. At the very least, these discrepancies bring to light the importance of what statistics are chosen to test a hypothesis like neutral evolution. In this context, a recent study [41] analysed the patterns of frequency change, in particular, the kurtosis of the distribution of changes over time, of stable words in the Google Ngram database. Interestingly, this approach identified words under selection: kurtosis values close to zero signalled neutrality while deviations from zero were indicative of selection.

In this paper, we apply ecological neutral theory to cultural data. We use a model that allows for overlapping generations, an appropriate assumption when analysing distributions of cultural variants, and for an analytical representation of the progeny distribution. In the following, we provide a brief review of the characteristics of this model.

(a). Neutral theory in ecology

It is assumed that the temporal dynamics of species are governed by reproduction and competition, occurring in continuous time with a given set of rates. The full, interacting version of this model can be described by stochastic Lotka–Volterra systems (with either symmetric, pairwise competition between species where the strength of the competition is controlled by the constant α, or any related constraint on population size). Solving for the dynamics of these systems is, however, analytically intractable but a solvable mean field approximation has been found. This approximation is based on treating each species as interacting with the average state of all other species, rather than the specific configuration of abundances at any given moment in time [18,21,42]. In the limit of a large number of species this approach states that the correlation between the abundances of any two species is assumed to be small. In other words, the abundances of extant species are assumed to evolve independently of each other. Importantly, the resulting mean field description collapses nonlinear rates of competitive interaction into an increased, linear mortality rate for each species. This approximation of the overlapping generations neutral model is also known as the ‘non-zero-sum’ or NZS approximation, referring to the fact that the total population size may fluctuate over time, i.e. births and deaths do not sum to zero. It has been shown that this approach provides only a good approximation in populations with a large number of species, but in a less diverse population, where a handful of species are dominant, the mean field approximation is no longer a meaningful description.

In the mean field approximation, each species takes an independent, random walk, based on a linear stochastic process. Mathematically, this is described by a linear master equation for the probability P(n|t) that a species has abundance n conditioned on its age (i.e. time since introduction into the system)

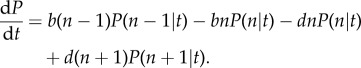2.1

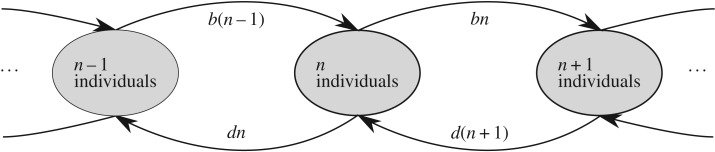
Here, t is the species' age, and for so-called ‘point’ speciation (where new species always have an abundance of 1) the initial condition is P(n|0) = δ_n,1 (see figure 1 for a schematic of the model dynamic).

Figure 1.

Schematic of the birth–death dynamic described in equation (2.1), where the variables b and d stand for birth and death rates, respectively.

The value d, which is always strictly larger than the birth rate, b, is a combination of intrinsic mortality and the effect of competition arising from all other species. For the point speciation process, this linear master equation has the time-dependent solution

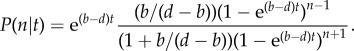2.2

For a more general initial condition, there is a correspondingly more general solution (see electronic supplementary material, §S2 for detailed mathematical derivation of these results).

Equation (2.2) describes the temporal dynamics of a single species, from its introduction into the system to (guaranteed) eventual extinction. Under the additional assumption that in the steady state, the rate of appearance of new species in a population of size J is given by νJ, it can be shown that the expected species abundance distribution (i.e. the number of species with abundance k) takes the form of a log series distribution

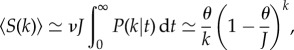2.3

where θ = (1 − b/d) J stands for the ‘fundamental biodiversity number’. Finally, there is a constraint relating speciation rate ν to b and d rooted in the mean field approximation. The parameter d is an effective parameter arising from the influence of the rest of the population, and therefore the per capita speciation rate ν is constrained to be related to these rates as

2.4

Summarizing, equation (2.2) gives a complete description of the non-spatial, NZS model that provides a good approximation to various neutral predictions in ecology when diversity is high [18,21,34,42,43].

To ensure consistent notation across different scientific disciplines, we will refer in the following to species as variants, to individuals as instances and to speciation as innovation. Further, birth and death rates describe the rates at which a cultural variant generates or loses an instance, respectively (see figure 1).

(b). Neutral theory in cultural evolution

Neutral theory in cultural evolution has been mainly modelled using the Wright–Fisher infinitely many allele model (see e.g. [44] for a review of the mathematical properties, [15] for its introduction to cultural evolution as well as e.g. [4,16,17,30] for further applications to cultural case studies). In general, this framework assumes that the composition of the population of instances of cultural variants at time t is derived by sampling with replacement from the population of instances at time t − 1 resulting in non-overlapping generations. We provide in electronic supplementary material, §S1 a brief review of the mathematical characteristics of this model.

3. The neutral progeny distribution

Datasets describing the accumulated appearances of cultural variants within a specific time interval, like the choice of baby names in human populations, have typically been summarized by the progeny distribution. This distribution logs the frequency of cultural variants with a total of k progeny, taken over a given, fixed duration, T. In part, this choice of distribution is pragmatic; data for baby names registered at birth are often more complete and more readily available than full censuses of names in a population, which would provide the analogue of a species abundance distribution given in equation (2.3). Additionally, the progeny distribution contains a temporal element, as in general the distribution will change with the duration, T, that the progeny counts are taken over. Finally, the progeny distribution is particularly useful for populations where the effective population size of reproducing individuals may be much smaller than the total population. The distribution directly probes the dynamics of transmission of cultural variants, whereas the species abundance distribution may be much more sensitive to the details of the age structure in the population.

In this section, we derive an analytical representation of the progeny distribution based on the overlapping generation NZS model for large, well-mixed populations. We show, in agreement with earlier work, that neutral theory generates a power-law progeny distribution but with a constant exponent of 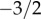(i.e. the power-law exponent does not depend on innovation rate or population). The power law is followed by an exponential cut-off, whereby the onset of this cut-off depends on the innovation rate. Further, we provide a method for identifying maximum-likelihood neutral parameters.

(a). Analytical results

Using the NZS approximation, the progeny distribution at late times T, i.e. under the assumption that sufficient time has passed that the distribution has reached stationarity, can be derived as

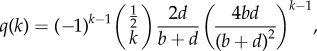3.1

where b and d, respectively, stand for the birth and death rates of the variants (see electronic supplementary material, §S3 for a detailed derivation). The term 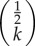is defined by

The function q(k) describes the frequency of cultural variants which generated exactly k instances, including its innovation event, within a time interval of length T. Equation (3.1) is valid only in the large T limit, but in electronic supplementary material, §S3 we also provide additional results for moments and generating functions of this distribution for arbitrary durations, T. The corresponding cumulative distribution (i.e. the fraction of variants with greater than or equal to k cultural variants generated within a time interval of length T) is given by

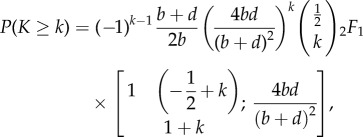3.2

with 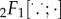representing the Gaussian hypergeometric function (see electronic supplementary material, §S3 for a detailed derivation).

Interestingly, the distribution q(k) fragments into two parts: one describes a power law and the other an exponential decay (see dotted and dashed lines in figure 2). For large enough values of k the first terms of equation (3.1) can be approximated by

3.3

which determines a power law with the exponent 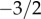. However, at approximately k = (b/(d − b))² = (b/ν)² the exponential decay starts dominating the distribution (see the red line in figure 2). In summary, the neutral progeny distribution tends towards a power law with a universally applicable exponent of 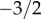(i.e. the exponent does not, as previously suggested, depend on the parameters of the neutral model) but shows an exponential cut-off at approximately k = (b/(d − b))² = (b/ν)². The larger the innovation rate, ν/d, the smaller are the values of k for which exponential decay dominates the progeny distribution.

Figure 2.

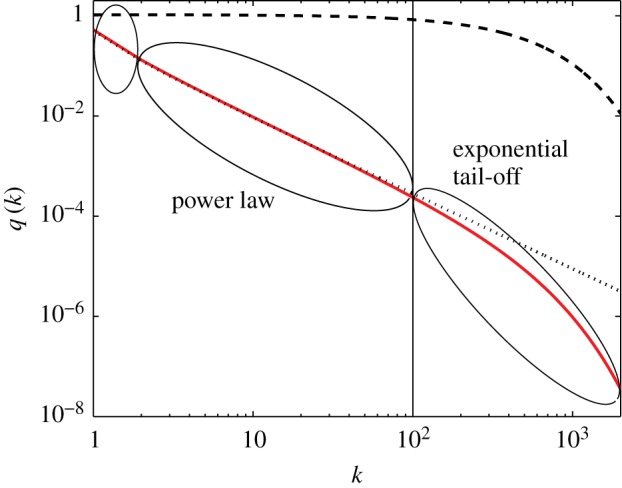
Illustration of the shape of the progeny distribution (3.1) with b = 1 and d = 1.1 (red solid line). The dashed line shows the term 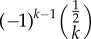and the dotted line the term 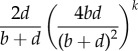. The black vertical line at (b/(d − b))² indicates the approximation of the transition point from the power-law behaviour to the exponential decay.

(b). Maximum-likelihood parameters

To fit the progeny distribution given in equation (3.1) to empirical data, we derive the maximum-likelihood estimate of the ratio η = d/b (as we show below that the shape of the progeny distribution depends only on the ratio of the death and birth rate).

The log likelihood of observing a given set of S cultural variants with abundances {k_i} at late times is given by

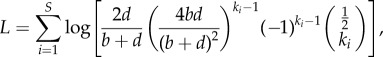which can be rewritten as

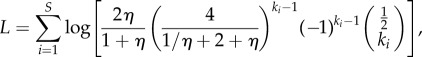by using the relation η = d/b. Maximizing this log likelihood with respect to parameter η provides the following point estimate

3.4

where K_total is the total number of instances observed in the data and S is the total number of variants (a detailed derivation can be found in electronic supplementary material, §S4).

(c). Comparison of analytical approximations with simulations

In this section, we ensure the validity of our approximations (in particular equations (3.1) and (3.2)) by comparing analytical and numerical results. To do so, we simulate the full, nonlinear model with overlapping generations. In detail, we generate the temporal frequency behaviour of a group of competing variants via the Gillespie algorithm and compute the resulting progeny distribution after a long time interval.

We use stochastic Lotka–Volterra systems, where variant i with current abundance n_i will undergo birth and death processes as well as be involved in competitive interactions with other variants. New variants are introduced at a rate νJ (J describes the total population size) with initial abundance 1, and are considered as an error in the birth process. Therefore, the effective per capita birth rate is given by b₀ − ν. The rates of these processes for variant i are as follows:

3.5

where the labels i and j refer to the extant variants in the system at any given point in time, and the sums are taken over all variants, including variant type i. The simulation of this population is based on the well-known Gillespie algorithm [45]. We provide a detailed description of the simulation procedure in electronic supplementary material, §S5.

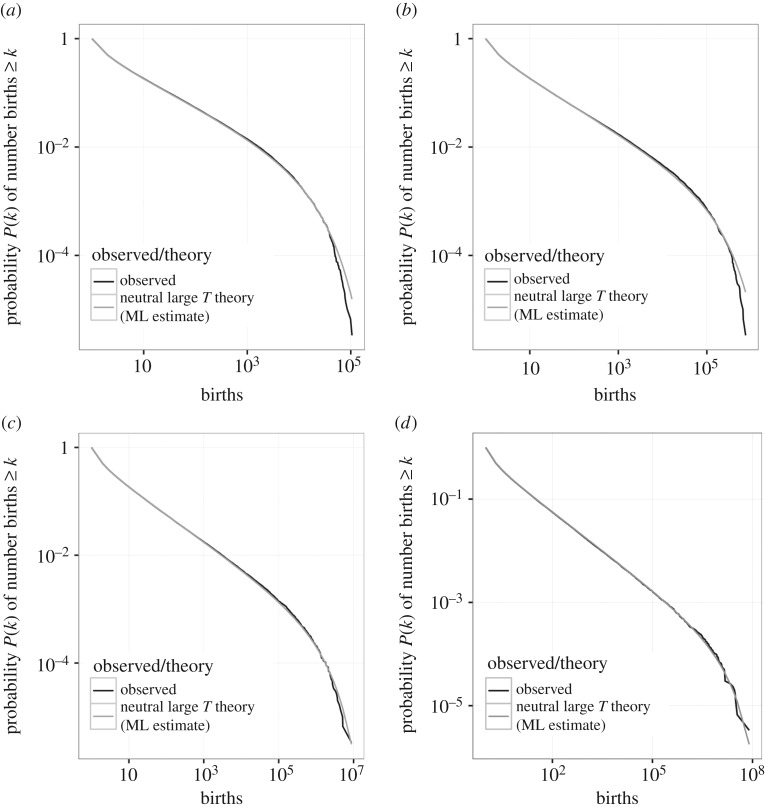
Figure 3 illustrates that the simulated cumulative progeny distributions based on competitive Lotka–Volterra interactions (black lines) coincide with their analytical counterparts given by equation (3.2) (grey lines) for long time intervals and various values of ν and J. In summary, equation (3.2) (and consequently equation (3.1)) provides an accurate description of the neutral predictions for a model with symmetric, competitive interactions and overlapping generations.

Figure 3.

Cumulative progeny distributions for long time intervals determined by simulated, neutral populations based on competitive Lotka–Volterra interactions with overlapping generations (black lines) match their mean field, non-zero sum approximations (3.2) (grey lines). We consider parameter values: (a) J = 300, ν = 0.01, (b) J = 1000, ν = 0.003, (c) J = 3000, ν = 0.01, (d) J = 10 000, ν = 0.0003. In all cases, the product Jν has been chosen to be ≃3, so that the mean field regime is reached, and in each case the simulated progeny distribution was logged for T = 100 000 generations. ML, maximum likelihood.

4. Novelty biases

So far we have assumed that there are no selective differences between the extant variants in the population. In this section, we generalize our framework to include selection for and against novel cultural variants (denoted as pro-novelty bias and anti-novelty bias, respectively), and explore the consequences of these selection biases on the shape of the progeny distribution.

In general, pro-novelty selection favours ‘young’ variants, i.e. variants that have been invented recently. By contrast, anti-novelty selection disadvantages ‘young’ variants and therefore favours the persistence of established cultural variants over a long time period. In cultural evolution, pro-novelty selection has been associated with fashion trends [40,46], i.e. the phenomenon where some cultural variants rapidly increase in frequency but also quickly fade away again after other variants have become fashionable. An ecological analogue to pro-novelty bias is the red queen effect which is well explored in the literature (e.g. [42]). While the red queen effect is typically thought to arise from the accumulation of selectively advantageous traits over time, the emergent effect is an advantage for new species.

(a). Pro-novelty bias

We model pro-novelty bias following earlier ecological theory developed in the context of the red queen hypothesis [42]. The only change relative to the simulation described in §3c is the form of the competition between older and younger variants. The rate α_ij now encodes the competitive effect of species j on species i, and depends on innovation times (i.e. the ages of the variants) τ_j and τ_i

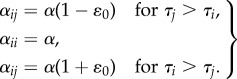4.1

This means we assume that new variants have the same competitive advantage over all extant variants and each variant interacts with three groups: newer, more advantageous variants, conspecifics and older, less advantageous variants [42]. The coefficient α characterizes the strength of competition, while ɛ₀ is a constant between 0 and 1 that introduces asymmetry in the competitive interactions.

Figure 4 shows the progeny distributions generated by neutral theory (grey line), and pro-novelty selection (green line) for the parameter constellation J = 300, ν = 0.01 and ɛ₀ = 1. It is obvious that pro-novelty bias leads to a higher number of variants with small and intermediate abundances and a lower number of variants with very high abundances. As expected, pro-novelty bias reduces the number of singletons, i.e. innovations that have never been transmitted and therefore remained at abundance 1.

Figure 4.

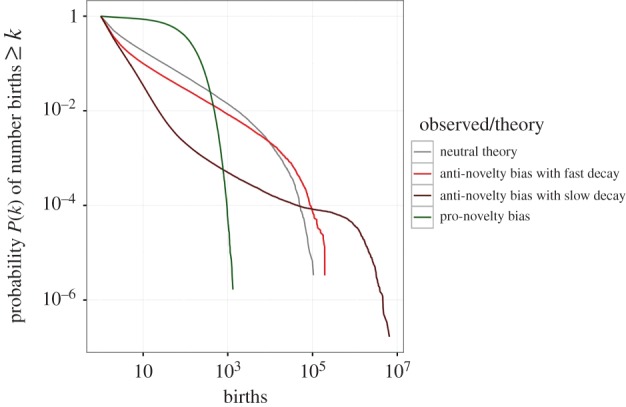
Cumulative progeny distributions generated by neutral theory (grey line), pro-novelty bias (green line) and anti-novelty bias (light red and dark red lines) for J = 300 and ν = 0.01. For pro- and anti-novelty bias the asymmetry parameter is set to ɛ₀ = −1. For anti-novelty bias, the decrease of the competitive difference is chosen to be λ = 0.3 (dark red) and λ = 3 (light red line). In each case, the simulated progeny distribution was logged for T = 100 000 generations.

(b). Anti-novelty bias

Modelling anti-novelty bias in a plausible way is not as straightforward as modelling pro-novelty bias. If we take the competition coefficients given in (4.1) and flip the signs, it is highly likely that, for realistic population sizes, we will end up with one, eternal, old variant, and all other variants that enter the system are driven to extinction over a relatively short time frame. While we would expect that anti-novelty bias should promote the persistence of older variants, with a strict competitive advantage of all older variants over all newer variants, these results are too extreme.

We therefore introduce the following rates α_ij for the competitive effect of variant j on variant i, which again depend on innovation times τ_j and τ_i but contain an additional exponential decay factor

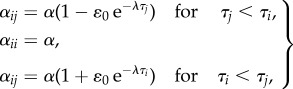4.2

where now we consider ɛ₀ < 0 and λ > 0. The effect of λ is that as a variant ages, competitive differences decrease and they begin to interact more and more symmetrically. This approach allows for the persistence of multiple, older variants, because once a type has survived for a time larger than 1/λ, it interacts almost neutrally with all other established variants.

Figure 4 shows the progeny distributions generated by neutral theory (grey line) and anti-novelty selection (light red and dark red lines) for the parameter constellation J = 300, ν = 0.01, ɛ₀ = −1, λ = 0.3 (dark red line) and λ = 3 (light red line). Anti-novelty bias leads to a lower number of variants with small and intermediate abundances and a higher number of variants with very high abundances. As expected, anti-novelty bias generates a large number of singletons. Further, the slower the decay of the bias, i.e the smaller λ, the more pronounced are the differences between neutral evolution and anti-novelty selection.

5. Empirical analysis for baby names

Starting with the work by Hahn & Bentley [5], data on the choice of baby names have been widely analysed in the literature using a variety of frameworks. For example, the authors in [47] analysed the spatial clustering patterns with regard to choices of baby names between US states (see also [48]) and those in [49] used turnover rates to detect transmission biases in US baby names. Further, Kessler et al. [50] aimed at disentangling stochastic and deterministic influences on the choice of first names. They suggested that the individual trajectories of name frequencies can be replicated by a deterministic dynamic governed by memory and delay processes.

Here, we apply our methodology to two datasets drawn from the state of South Australia, consisting of all boys' and girls' names registered from 1944 to 2013, respectively, and explore the conclusions about the evolutionary process that can be drawn from it. These datasets are included in electronic supplementary material, §S6 together with a general description and a justification of the application of the mean field approach.

(a). South Australia baby names, neutrality and novelty disadvantage

First, we calculate the maximum-likelihood estimate (3.4) of the neutral innovation rate, i.e. the rate that most closely explains the observed progeny distributions computed over the full time span of the datasets. We obtain

5.1

indicating a higher tendency for choosing a unique name for newborn girls than for newborn boys.

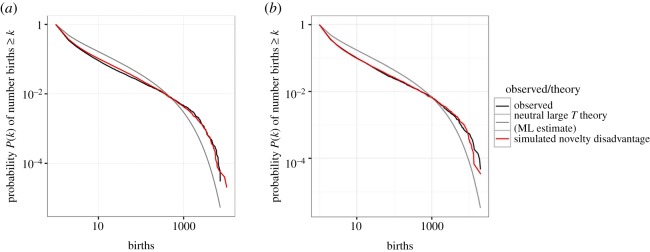
For both groups of names, we then plot the neutral progeny distribution with maximum-likelihood parameters alongside the empirical progeny distribution in figure 5. It is obvious that the neutral distribution (grey lines) produces too many names with intermediate numbers of progeny relative to singletons (i.e. names that have never been transmitted and therefore have an abundance of 1), and too few variants with very large numbers of progeny.

Figure 5.

Cumulative progeny distributions for South Australian girls' names (a) and boys' names (b). Black lines: empirical distributions over a 70-year span, grey lines: neutral progeny distribution with maximum-likelihood parameters, red lines: progeny distribution for novelty disadvantage. ML, maximum likelihood.

Given this discrepancy, we ask whether novelty bias can provide a better explanation. Any form of pro-novelty bias, however, will only increase the differences (cf. figure 4) and therefore we focus on anti-novelty bias. Figure 5 (red lines) shows the best fit over a discrete set of parameter values to the data. To replicate that only a relatively small (at least compared with the neutral predictions) number of innovations are transmitted at least once, we need to choose ɛ₀ = −1 in equation (4.2), so that new variants (initially) have zero competitive effect on any extant variant. We also choose λ ≫ b, so that if a variant survives (meaning is transmitted at least once), it quickly begins to interact neutrally with the rest of the population. We note that we are not seeking to rigorously fit the anti-novelty bias model, but it is apparent that with these choices anti-novelty bias provides a potential explanation for the phenomena we see in these data.

(b). Restricting to popular names

Our example dataset above contains every baby name registered over a 70-year period in a single region, leading to the potential conclusion that new, rare variants have a disadvantage. However, many available datasets for registered baby names in other regions are incomplete, providing only the most popular names owing to privacy considerations. Previous studies have often tested hypotheses for cultural evolution based on similarly incomplete data and in this section we explore how this incompleteness may alter conclusions about the existence of selection biases in the population.

In the following, we consider two common ways of preprocessing cultural frequency data, both of which amount to removing some subset of data. First, we only keep the most popular names over a given time span, removing any names with fewer appearances (in total, throughout the time interval) than a given threshold. Second, we remove any names with less than a given threshold in any given year.

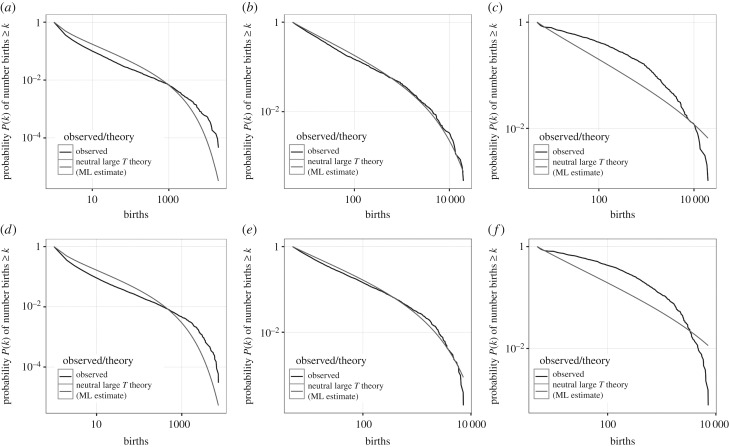
In figure 6, we show the results of three analyses of the South Australia baby name dataset (a,b,c: boys' names, d,e,f: girls' names). Alongside our analysis using the full dataset (a,d), we also (i) remove names containing fewer than 5 instances over the 70-year time span (b,e) and (ii) remove names from a given year that have fewer than 5 instances in that year (c,f). We call these a total threshold and a year-by-year threshold, respectively. The differences between the three approaches are stark.

Figure 6.

Empirical progeny distribution and maximum-likelihood neutral progeny distribution generated by (a,d) the full dataset as in figure 5; (b,e) imposing a threshold such that only names with five or more appearances are considered; (c,f) by imposing a year-by-year threshold, such that only names with five or more appearances in a given year are considered in that year. (a,b,c) boys' names, (d,e,f) girls' names. ML, maximum likelihood.

We have seen in §5a that the full progeny distribution can be replicated by assuming that innovations are strongly selected against but that this disadvantage fades away quickly, as soon as those novel names are transmitted. They then interact neutrally with the population and therefore we might expect that imposing the total threshold (i.e. in this case innovations are names whose progeny count exceeds this threshold) generates a distribution that is consistent with neutrality. However, if we impose the year-by-year threshold, the resulting progeny distribution changes substantially—if we treat these data as if all names were present, it would look consistent with a novelty advantage, rather than neutrality or novelty disadvantage. The effect of these preprocessings of names data, and the qualitative differences they make, demonstrate the need to be cautious about any conclusions drawn using incomplete data. Our results here mirror a long-standing debate in ecology on snapshots of species abundances, where a lack of sampling of rare species introduces what has been termed a ‘veil line’, and can alter the shape of the species abundance distribution [51,52]. In our case, the progeny distribution veil line can lead us to infer a purely neutral explanation, where in reality there is a strong bias against new names.

6. Discussion

Innovation is ubiquitous across biological and social domains, but in many cases we lack a direct way to characterize the mechanisms of the innovation process. This is particularly true in the realm of cultural evolution, where it is often not obvious what to look for or to measure in a new variant to describe the mechanism that gave rise to it. For example, the baby names considered in this paper have no direct analogue of beak size, body plan or carbon fixation pathways. Nevertheless, we know that in these domains new variants are ‘different’ from extant variants. In this paper, we assumed that variants are functionally equivalent but differ in their ages and abundances in the population, and aimed at understanding how these differences can affect the spread behaviour of the innovations. To this end, we analysed the characteristics of the progeny distribution, which aggregates the temporal dynamics of new variants across the population over a fixed time interval, under different assumptions of cultural transmission.

Using a mean field model drawn from ecology, we derived the first analytical representation of the progeny distribution under the hypothesis of neutrality. We showed that the neutral progeny distribution consists of two phases: a power-law phase for intermediate numbers of progeny with a universally applicable exponent of 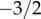, followed by an exponential decay phase for large numbers of progeny. The onset of the exponential phase is modulated by the innovation rate: the higher the rate, the earlier is the exponential cut-off. The analytical representation allowed us further to derive maximum likelihood estimates of the neutral model parameters, and therefore to establish whether observed empirical patterns are consistent with the hypothesis of neutrality.

To allow for selective differences between the cultural variants, we developed a simulation framework and analysed the effects of pro- and anti-novelty biases on the shape of the progeny distribution. These biases alter the shape of the progeny distribution, with pro-novelty biases increasing the occurrence of variants with a low or intermediate numbers of progeny and decreasing the occurrence of variants with high numbers of progeny. These results go hand-in-hand with decrease in the average lifetime of the individual variants. The reverse is true for anti-novelty bias.

In applying our methodology to baby names from South Australia, we found that the data showed at least two different regimes. First, we see the generation of a lot of variation. The datasets contain a large number of innovations with abundance 1, i.e. innovations that have never been transmitted. Second, we see the persistence of some names over a very long time. Our analysis showed that neutrality alone is not able to replicate these patterns, as it produces too many variants with intermediate numbers of progeny relative to singletons (i.e. names that have never been transmitted), and too few variants with very large numbers of progeny. The empirical progeny distribution of baby names is much more closely reflected by assuming an anti-novelty bias whereby the bias decays as soon as a variant survives long enough to become established. Importantly, we concluded that most new names do not proliferate, but if they are transmitted, their interactions with the other variants in the population quickly resemble those under neutrality (the code used for this analysis is available at https://github.com/odwyer-lab/neutral_progeny_distribution).

This result points to the crucial importance of rare variants for reliable inference of processes of cultural evolution from aggregated population-level data in the form of progeny distributions. Analyses based on incomplete datasets including only popular variants according to different threshold rules revealed consistency between the observed (incomplete) data and neutral evolution as well as pro-novelty bias. This is a powerful reminder that we need to be cautious with conclusions about underlying evolutionary processes drawn from incomplete data.

Lastly, we note that the result of this study is not to say that the choice of baby names is guided by anti-novelty bias but that anti-novelty bias is a potential cultural transmission process which could explain the observed, complete dataset of baby names, whereas neutral evolution and pro-novelty biases are not. There may be other, potentially more complex processes of cultural transmission that are able to replicate the observed progeny distribution equally well. For example, content bias might be producing a disadvantage for most new variants, leading to their early extinction, and leaving behind only those new variants which did not have this disadvantage. But the implication of this explanation is that content bias is fairly restrictive, with either a large negative, or neutral effect, but rarely (or never) a positive effect, a distribution that itself would require an explanation. The extension of our analytical approach to incorporate these processes, alongside the inherent variability over time of real systems, will help in shedding more light on this issue and be the focus of future research.

Data accessibility

The scripts to compute ML estimates and plot neutral progeny distribution curves are deposited at https://github.com/odwyer-lab/neutral_progeny_distribution.

Authors' contributions

J.P.O'D. and A.K. designed the study, analysed the model and wrote the paper.

Competing interests

We have no competing interests.

Funding

J.P.O'D. acknowledges the Simons Foundation grant no. 376199, McDonnell Foundation grant no. 220020439 and Templeton World Charity Foundation grant no. TWCF0079/AB47.