Modelling the effects of short and random proto-neural elongations

Abstract

To understand how neurons and nervous systems first evolved, we need an account of the origins of neural elongations: why did neural elongations (axons and dendrites) first originate, such that they could become the central component of both neurons and nervous systems? Two contrasting conceptual accounts provide different answers to this question. Braitenberg's vehicles provide the iconic illustration of the dominant input–output (IO) view. Here, the basic role of neural elongations is to connect sensors to effectors, both situated at different positions within the body. For this function, neural elongations are thought of as comparatively long and specific connections, which require an articulated body involving substantial developmental processes to build. Internal coordination (IC) models stress a different function for early nervous systems. Here, the coordination of activity across extended parts of a multicellular body is held central, in particular, for the contractions of (muscle) tissue. An IC perspective allows the hypothesis that the earliest proto-neural elongations could have been functional even when they were initially simple, short and random connections, as long as they enhanced the patterning of contractile activity across a multicellular surface. The present computational study provides a proof of concept that such short and random neural elongations can play this role. While an excitable epithelium can generate basic forms of patterning for small body configurations, adding elongations allows such patterning to scale up to larger bodies. This result supports a new, more gradual evolutionary route towards the origins of the very first neurons and nervous systems.

1. Introduction

To understand how the very first neurons and nervous systems evolved, we need an account of how each of neurons' most central characteristics came about: (a) their electrical signalling, (b) their synaptic connections, and (c) their elongations (axons and dendrites). These three features are essential for making a ‘full neuron’. All three features are central to nervous system functioning, and each has evolved into a wide variety of forms and modes of operation within the huge group of animals now known as the neuralia [1]. From these three characteristics, graded and action potentials go back to unicellular organisms [2–4], and the same applies to macromolecular components of both the pre- and postsynaptic organization [5,6].

More difficulties remain with explaining how separate pre- and postsynaptic components came together to form synapses between separate cells, as well as how neural elongations first evolved. Both are tied to the multicellular morphology and functionality of proto- and early neuralia. To understand such early multicellular organizations, genomic and molecular evidence gives insufficient guidance [7–9], while other evidence remains inconclusive. Fossils of neuralia go back to the beginning of the Cambrian, 542 Ma (Million years ago) [10]; therefore, synapses and neural elongations must have originated earlier. Body and trace fossils from the preceding Ediacaran (635–542 Ma) tend to be very different from modern animals and are difficult to interpret, although the presence of complex traces suggests the presence of some kind of nervous system at this time [11–13]. The first nervous systems may have evolved around this time, but molecular clock studies suggest the alternative option that the first neuralia evolved much earlier [14,15]. Leaving no fossils, such proto- and early neuralia could have lived as small meiofauna with sizes up to 1 mm [16,17]. It is also suggested that neurons and nervous systems evolved several times independently [18,19]. To conclude, at present very little can be said with certainty about the first neuralia, either their form, size or how and when they lived.

A systematic investigation and explication of potential evolutionary transitions from basic proto-neural configurations to neural ones will be beneficial here: this involves articulating possible trajectories that specify sequences of organismal organizations that span the transition from non-neural multicellular organizations to neural ones. Each step should consist of a functioning organism, while the consecutive steps from one organization to the next should be gradual, each one providing some improvement on the existing functionality [20–22]. Investigating specific hypothetical transition trajectories will aid in interpreting the limited empirical evidence and formulating more specific questions concerning this evidence.

A well-known example of such an idealized trajectory for nervous systems is provided by Braitenberg [23]. He formulated a sequence of configurations starting with a single neural connection between a sensor and an effector to which more connections could be added, eventually leading to increasingly complex neural circuits. Figure 1, for example, sketches a configuration with two connections. Braitenberg's proposed trajectory is based on an input–output (IO) view on (early) neural evolution [24]. IO views stress the functioning of neurons—and whole nervous systems—as connections between sensors and effectors. Initially, these connections may have been simple and direct, but over evolutionary time they have become increasingly complex neural circuits governing behaviour. Neural elongations function here as specific and often long-distance connections between specific loci within an organism (sensors, effectors or other neurons) [25]. While IO views seem well suited for modern nervous systems, they start with organizationally and developmentally complex bodily organizations, which raises doubts about their suitability as a primitive condition. In addition, an IO view does not readily fit the surface-distributed nerve nets that are generally considered to represent the most primitive kind of nervous systems [26], and which are found in cnidarians [27], ctenophores [28] and—possibly as a derived condition—in Acoelomorpha [9].

Figure 1.

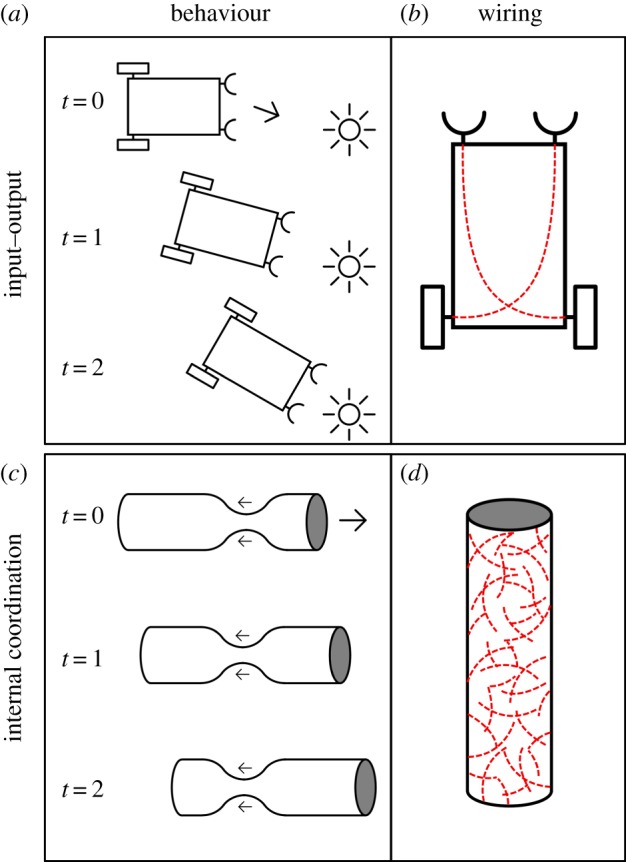
A comparison between an input–output (IO) view as exemplified by a Braitenberg vehicle (a,b) and an internal coordination (IC) view, represented by an excitable (myo)epithelium with short and random connections (c,d). (a,c) Behaviour of the respective systems and (b,d) the wiring. (Online version in colour.)

By contrast, we focus here on an alternative internal coordination (IC) view [24], which stresses the need to acquire multicellular (bodily) coordination as an initial key task for early—and modern—nervous systems. Coordinating contractile (muscle) tissue for motility and reversible changes in body shape is a central example here [29–31] that imposes different functional demands on early nervous systems and neural elongations. Rather than focusing on neural elongations as a way to provide specifically targeted connections, an IC view opens up the possibility of acquiring neural elongations in a more gradual way.

We performed a modelling study to test the IC idea that simple—short and randomly connected—neural elongations can have played a significant behavioural role for proto-neuralia. Focusing on the option that the first neuralia evolved early, we targeted systems of limited (meiofaunal) size that consist of a few hundred to thousands of cells. The starting point for this study consists of an excitable and contractile epithelium (a myoepithelium) that can provide primitive contractile motility [32]. Myoepithelia with direct electrical connections by means of gap junctions between the epithelial cells exist in various extant animals, such as cnidarians [33,34]. Here, we build on the hypothesis that proto-neuralia could have possessed myoepithelia with similar electrical connections or with chemical signalling to conduct electrical activity from one cell to the next, by either juxtacrine signalling or basic chemical synapses [30,35,36]. Importantly, this configuration could have provided a scaffold to bring separate pre- and postsynaptic elements in adjacent cells together as a full synapse. However, here we focus only on the impact of neural elongations on an excitable epithelium in which electrical activity is transmitted from cell to cell (figure 1).

The model consists of excitable cells connected to one another as a sheet to form an excitable epithelium in which active cells activate their neighbours; electrical excitability generic enough to represent either a calcium-based mechanism or a sodium-/potassium-based one, and abstract excitatory synaptic transmission to represent either electrical or chemical transmission. The sheet of cells is rolled into a ‘body-tube’ to provide a general body surface on which the activity takes place. This model does not include external senses, proprioception or pacemakers. A Poisson process randomly initiates activity in single cells. We take behavioural functionality to consist of travelling rings of activation along the tube that drive a form of muscle-based peristalsis as sketched in figure 1.

The model's ‘body-tube’ does not mimic any specific animal, such as Trichoplax or sponge larvae. Like Braitenberg's vehicles, the model is made as abstract and general as possible to investigate in a generalizable and systematic way under which conditions an excitable epithelium produces patterned activity across its surface. The model is also very different from the models of locomotion in modern animals (e.g. [37]) as it does not target motility itself but the evolutionary motivated question whether a very limited configuration of cells can potentially provide a basic controlling device for motility.

Earlier modelling showed that body topology is a crucial factor here [36]: body-tubes with a high length to width ratio enabled ring-shaped activity patterns travelling along the length of the tube, while a ring-shaped topology induced patterns travelling along the ring's circumference. In the present study, we only used a tube-shaped topology (a) as this particular configuration is generally plausible as a basic animal shape; (b) as a single example would be sufficient to make a case for the potential evolutionary relevance of short and random proto-neural elongations; and (c) by focusing on a single topology we could better focus on the relevance and impact of many different features of the elongations themselves, as will be discussed below.

For tube-shaped topologies, an excitable epithelium generates ring-shaped patterns of activation running along the long axis of a body-tube. These patterns are an emergent feature resulting from the topology of the system, the size measured in numbers of cells, random activations, and the refractionary nature of the cells. However, the occurrence of such patterns at the whole body scale depends on the size of the body-tube: ring-shaped activity occurs only for smaller tubes and is lost in larger ones [36]. For larger body-tubes, the speed of the travelling waves of activation is too slow to entrain activity at the level of the tube itself, giving local activations the opportunity to destroy global patterning. Also, signalling to adjacent cells provided only travelling wave-fronts that remain thin and insignificant on the scale of the body-tube.

While other modifications of the model could also have changed the characteristics of the patterning observed, the specific evolutionary question we aimed to address was whether adding neural elongations could provide a mechanism to overcome the limitations of nearest neighbour (NN) signalling. We hypothesized that the patterns of activation across a body-tube would change when neural elongations were added. To keep the change as generic and basic as possible, we focused on the effects of elongations that are relatively short—that is, connecting cells that have only a few intermediate cells between them—while the connections are made randomly. Such short and random connectivity is undemanding in terms of body morphology, cell differentiation and developmental patterning as it does not require preset destinations for these connections. Short and random elongations can, therefore, provide a small and plausible step in an evolutionary trajectory towards very primitive nervous systems.

To test the validity of this idea, we investigated a number of variations of randomly connected configurations: we varied the fraction of cells with elongations, the length of the elongations and the size of the body-tube. The ring-shaped patterns of excitation travelling along the length of the tube was used as a biologically plausible form of coordinated activity that also could be measured both qualitatively and quantitatively under various modelling conditions.

2. Material and methods

2.1. Computational model

We reimplemented the model of [36] using the brian2 package in Python [38]. All experiments use the following model:

• — A two-dimensional sheet of cells placed equidistantly in a triangular grid.

• — The sheet is rolled into a cylinder to create a tube.

• — Each cell is modelled by an integrate-and-fire model with a refractory period.

• — Each cell has superthreshold connections to its direct neighbours.

• — Each cell has a superthreshold per-cell Poisson process driver. In accord with [36], the rate of Poisson process is set at 0.1 Hz.

• — We used a tube as body topology. The length to circumference ratio of the folded tube was fixed at 4:1. While we varied overall size leading to length by circumference combinations, respectively, of 32 by 8, 64 by 16, 128 by 32, and 256 by 64.

• — A fraction of the cells were given straight elongations in random directions which provide them with connectivity to each cell visited by the elongation; details can be found in electronic supplementary material, S1. We performed a parameter scan over various elongation lengths: 1.5, 2, 2.5, 3, 3.5, 4, 6 and 10 grid spacings. Additionally, we included a condition without any elongations, but as in all cases above keeping NN connectivity.

• — Experiments have varying fractions of elongated cells. We performed a parameter scan over various elongated cell fractions. For fractions less than 1, cells to be elongated were picked randomly. The fractions used are 0.02, 0.05, 0.1, 0.2, 0.5, and 1.

• — All connections have a 2 ms synaptic delay. Transmission speed was not modelled explicitly as the delay used was assumed to incorporate a transmission delay that was plausible for the modelled system. For support for this assumption, see electronic supplementary material, S2.

2.2. Pattern quantification

The system as described above produces spatiotemporal patterns. Previous work shows that given suitable noise rates, NN connectivity, and activation with a refractory period, travelling ring-shaped activity patterns appear. To quantify the degree and relevance of ring-shaped activity on the surface of the animal, we developed a pattern detection method. We detect patternedness by comparing the activity in ring-shaped segments with average activity over all segments. The activity in a segment is simply the number of cells active in a given ring-shaped segment in a given time frame.

We summarize this activity for a given run as follows:

• — Divide the tube in n segments. A cell i is in segment s if (s − 1)/n · l_tube ≤ x_i < s/n.

• — A spike for a cell i in segment s takes place at a time t. The simulation is divided into time bins [jΔt, (j + 1)Δt).

• — For each segment and time bin, we can now count how many spikes take place: the matrix C_s,j indicates the number of spikes in segment s during time bin j.

We set Δt to 3 ms, larger than the average synaptic delay between cells (2 ms) but shorter than the refractory period (20 ms). Within a time bin, transmission between connected cells can occur, but a single cell cannot fire twice. Empty and incomplete intervals at the start and the end of each run are discarded. The number of segments (n) is set to 16 for all systems in order to be able to compare measurements between the various body dimensions.

The ratio T_end/Δt determines the number of intervals included in the analysis.

Visualizing C_s,j, as shown in figure 2, results in the condensed activity sequence plots found on the lower sides of figure 3a(i)–(iii), b(i)–(iii). Ring-shaped activity travelling down the tube shows up in this format as diagonal stripes, because a large amount of activation in a single ring-shaped segment travelling along the length of the animal and showing up in the next segment in a later time interval is a diagonal move.

Figure 2.

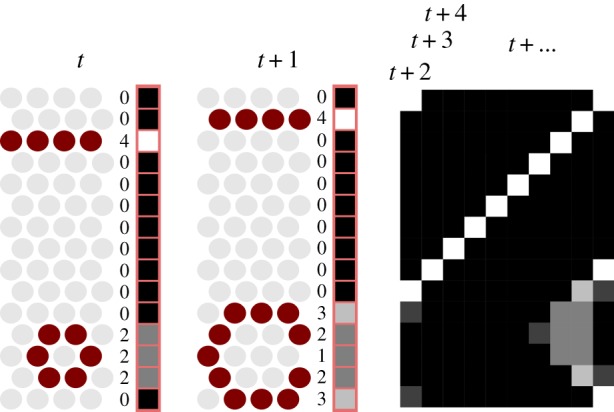
This graphic shows how a condensed activity representation is calculated. Time steps t and t + 1 show the process in detail. For each time step, the body-tube—cut open in grey on the left—is divided into 16 ring-shaped segments (in this case, all one cell wide) for each of which the number of active cells—emphasized—is tallied. This numerical score is translated to greyscale values ranging from white (maximum) to black (minimum), providing a single vector for each time step. (Online version in colour.)

Figure 3.

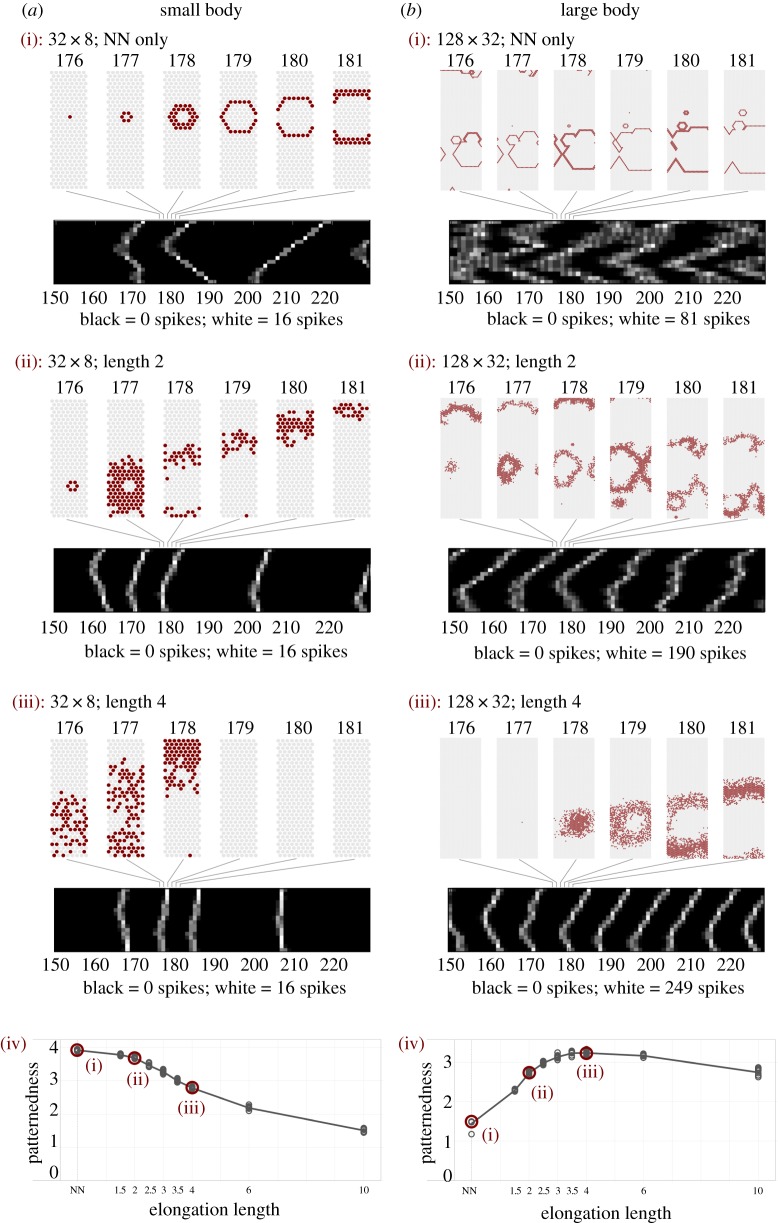
a(i)–(iii) and b(i)–(iii) Individual cases of sequences of activity across the body-tube for six different experiments (above), together with condensed representations spanning longer sequences (below). Individual time frames are identified by frame numbers, both above and below. a(i)–(iii) A small (32 by 8) body-tube, b(i)–(iii) a large one (128 by 32). Panes a(i) and b(i) represent nearest-neighbour connections only; panes a(ii) and b(ii) have in addition elongations of length 2; panes a(iii) and b(iii) have elongations of length 4. In all experiments shown, 50% of the cells have elongations. a(iv) and b(iv) The average patternedness for the conditions shown above them (marked in the graph) together with the results for five more elongation lengths. The points scattered around the graph represent the 10 individual model iterations which were performed for each condition. (Online version in colour.)

To quantify the deviation in activity, we performed the following steps. First, we define a per run normalized activity :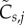

2.1

Using the normalized activities, we can define a new patternedness measure P, which detects how activity deviates from homogeneity during each time step and then calculates the root mean square:

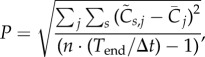2.2

where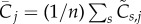

A high P implies low homogeneity over time and ring-shaped segments and thus strong patternedness over time and segments, allowing us to compare these values easily for various experimental conditions.

This measure compares the activity of a given segment not to the overall mean activity level but to the activity level in a particular time step. This way, we disqualify situations where the whole body shows high and homogeneous activity in one time interval and low homogeneous activity in other time intervals (‘flickering’ behaviour).

3. Results

Central examples of our main results are presented in figure 3. Figure 3a(i)–(iv) features small systems measuring 32 cells in length and 8 in circumference. Those on the right represent large systems of length 128 and circumference 32. All systems have NN signalling. Additionally, figure 3a(ii), b(ii) and a(iii), b(iii) have elongations of length 2 and 4, respectively. These lengths refer to each cell's elongation length, implying that cells up to maximally 4 and 8 cells apart can become connected. Figure 3a(i)–(iii), b(i)–(iii) provides a detailed picture of the randomly initiated electrical activity across the cut open body-tube during six time steps of 3 ms. Below is a condensed representation of this same activity across 100 time steps, providing a temporally extended overview of this activity by compressing all activity at a time step into a line of 16 segments, scaled to the size of the body-tube (figure 2). As white reflects high levels of activity, travelling waves are shown as diagonal lines, unpatterned activity as smudges, and synchronous activation of all cells as a vertical line. Together, these panes give an indication of both the details and the more abstracted differences between the patterning resulting from the various conditions.

In addition to these qualitative results, figure 3a(iv), b(iv) shows graphs for the same small and large body-tubes, representing more extensive parameter scans, involving the NN condition and eight different elongation lengths (on the x-axis). The y-axis shows the measure of patternedness calculated as outlined in the Pattern quantification section. The line represents the average patternedness for the given condition and the points the individual model runs. The conditions represented in detail in figure 3a(i)–(iii), b(i)–(iii) are marked as such within the two graphs.

As previously found [36], small systems without added elongations exhibit ring-shaped patterns (figure 3a(i)), while these patterns are lost when the system is larger (figure 3b(i)). As hypothesized, when neural elongations are added to such large systems, ring-shaped patterns return (figure 3b(ii)–(iii)). However, such elongations are detrimental for smaller systems (figure 3a(ii)–(iii)), where they have a negative effect on patternedness (figure 3a(iv)). This can be seen by inspecting the examples and the quantitative results presented in figure 3a(iv), b(iv).

The comparison between figure 3a(iv), b(iv) shows the main effect of elongations on different topologies: for the small systems, elongations lower the patternedness (figure 3a(iv)). For the large systems, elongations increase the patternedness, though returns do diminish for the longer elongations (figure 3b(iv)).

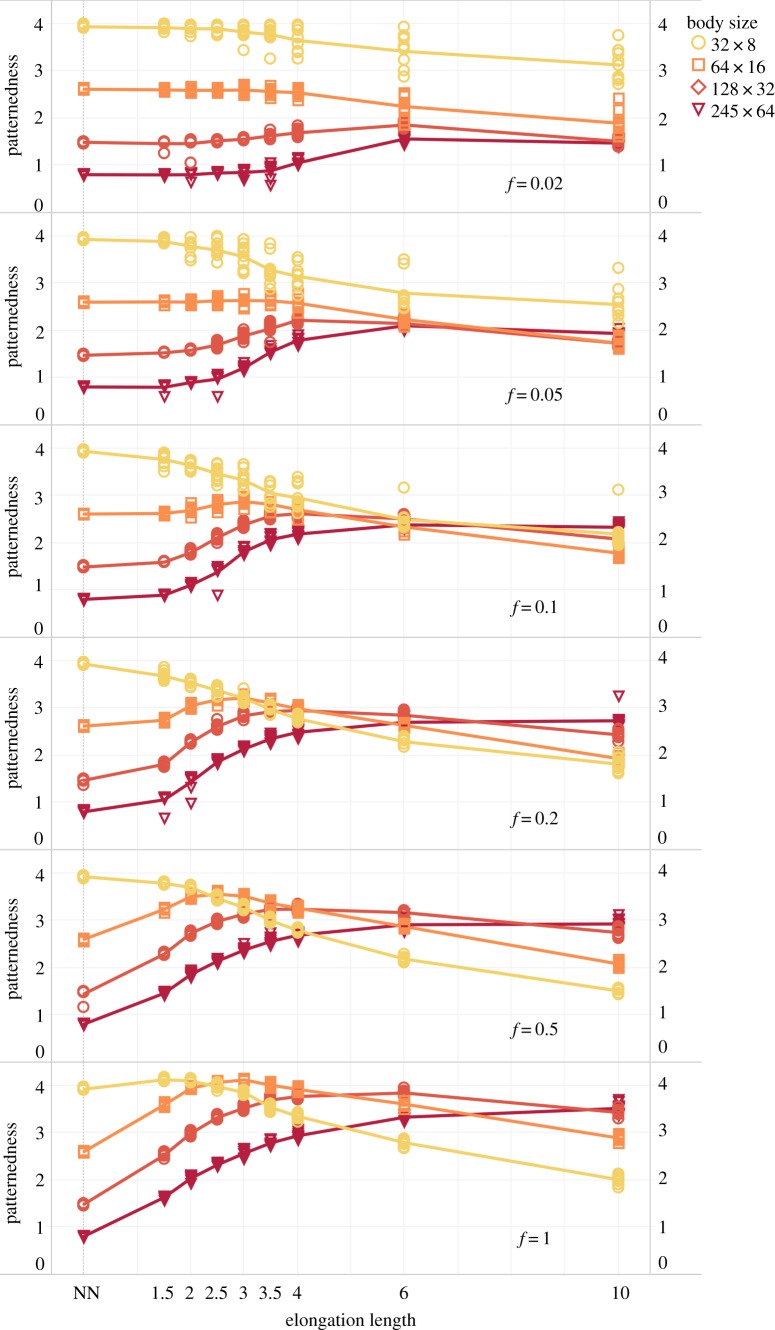
The results discussed so far are based on systems where the probability of each cell having an elongation is 0.5 (i.e. the chance that any given cell has an elongation on top of NN connectivity is 50%), while we focused on two sizes of the body-tube. To investigate the effect of various elongation fractions (hereafter referred to as f) on patternedness, we also compared elongation fractions f across various body sizes and elongation lengths as described above. We also did these experiments for two extra body sizes: 64 by 16 and 256 by 64. The results are presented in figure 4, which is similar to figure 3a(iv), b(iv) (included, respectively, as the lines marked with circles and diamonds in the pane marked ‘f = 0.5’) but with additional conditions regarding f and the additional body sizes.

Figure 4.

Comparison of the effect on patternedness of different elongation lengths and body sizes for six elongation fractions, f = 0.02 through f = 1.0. Line colour and point shape represent different body sizes. Patternedness is shown on the each individual y-axis, the different elongation lengths are on the x-axis and individual plots represent the various values of f. The points scattered around the graph line indicate the 10 individual model iterations which were performed for each condition and the line itself represents the average. (Online version in colour.)

Figure 4 shows the effect of f on patternedness. From top to bottom, f increases. For larger systems (darker red lines, marked with diamonds and triangles), having a higher fraction of cells with elongations improves patternedness. For the smallest system (yellow circles) elongations appear to be detrimental to patternedness. For the second-smallest system (orange squares), higher fractions (lower graphs) have a beneficial effect on patternedness for all but the longest two. However, low fractions (top graphs) show no such positive effect on patternedness—yet the low fractions also harm less for the longer elongation lengths.

Interestingly, for the larger body sizes, there appear to be diminishing returns to higher fractions. For the largest system (darkest line), patternedness for f = 0.5 is only marginally better than f = 0.2 for all elongation lengths.

4. Discussion

Our model represents an IC approach to early nervous system evolution (see figure 1). Our aim was to investigate IC scenarios that involve tissue configurations that are intermediate between non-neural and neural ones. In particular, we asked whether the presence of neural elongations providing random connections over very short distances could have functioned to enhance IC for comparatively small meiofaunal proto-neuralia. Our results show how such elongations can, indeed, enhance coordinated activity across very basic multicellular configurations. We discuss four specific implications of the modelling results.

First, short and randomly directed neural elongations allow patterned activity within larger multicellular organisms. Direct connections between adjacent cells within an excitable epithelium can provide a way to initiate and maintain coordinated patterns of excitability across a body surface. Such patterns could have enabled organized contraction. However, while this mechanism works for small body-sizes, such patterning deteriorates for larger bodies [36]. The model presented here shows that short and random neural elongations can support similar forms of patterning for increasingly larger multicellular organisms. Thus, such very primitive forms of neural elongations provide a mechanism for adapting patterned activity to changes in body-size.

Second, neural elongations provide a way to scale the activity patterns themselves with respect to the size of the organism. An epithelial configuration allows only the spread of activation to adjacent cells, which limits the width of the patterns in the travelling direction to one or two cells (figure 3a(i), b(i)). With elongations, the travelling patterns of activity can extend across more cells at every time step. This allows the patterns themselves to become wider and to scale up with larger body sizes (figure 3b(ii), b(iii)).

Third, for larger systems (figure 3b(iv)), patternedness tends to correlate positively with the length of the elongations, although even short elongations already provide an improvement of patterning. Thus, while even short elongations can be beneficial, lengthening them over evolutionary time provides a gradual path to further improve such patterning capabilities.

Fourth, while the influence of elongations on patterning tends to be more prominent when a larger fraction of cells have them, even a small fraction of cells with elongations can have significant effects depending on the size of the organism (see the top graph of figure 4). Again, this provides an evolutionary path for a gradual improvement of the system.

Together these results provide a proof of concept that an organismal configuration relying on patterned activity across an excitable epithelium can use very basic neural elongations to maintain and improve patterning capacity for larger body-sizes. These changes can occur in small incremental steps allowing for a gradual evolutionary route towards increasingly complex neural elongations.

These findings have a broad conceptual relevance for understanding the very early evolution of both neurons and nervous systems. Rather than assuming that neurons must have come first and by aggregating together came to constitute the first nervous systems, here the sequence is reversed. With the IC view developed here, ‘nervous system functioning’ can be produced without full modern neurons—combining electrical signalling, synapses and elongations—by epithelia acting as a ‘proto-nervous system’ and relying on electrical signalling alone. Such epithelia could have provided a scaffold for gradually evolving full neurons and nervous systems. In this way, tissue configurations spanning the gap between non-neural and neural tissues become conceivable. The model presented here shows that this speculative idea is indeed consistent and opens up new avenues for looking at the early evolution of nervous systems.

For example, the proposed outline of the piecemeal evolutionary assembly of neurons provides a new framework to make sense of the origins of nervous systems, which warrants further attention. Also, the focus on the intrinsic difficulties of evolving efficient muscle control provides a way to help explain the long cryptic evolutionary history of animals that is predicted by molecular clock studies [14,15] while also providing a scaffold for the Cambrian evolution of new senses such as eyes [39] and predatory behaviour [40]. Finally, the IC approach developed here predicts an intrinsic connection between muscle control and the evolution of nervous systems. While it is widely acknowledged that muscle and neurons systematically co-occur in extant animals [41] the connection is potentially much more significant, and could constitute a fundamental feature of the animal senses [31,35].

To conclude, in comparison to the standard IO view that assumes the beneficial presence of long and specifically targeted neural connections, the results from this IC-based model provide new evolutionary scenarios that bring the neuron's three main features—electrical signalling, synapses and elongations—together in a gradual and plausible way.

Data accessibility

The Python code of this model and its analysis will be made available on ModelDB (https://senselab.med.yale.edu/modeldb/) under accession number 231859.

Authors' contributions

All authors contributed to the text and the design of the experiments and the analysis. O.O.d.W. contributed to the implementation of the experiments and the implementation of the analysis. R.A.J.v.E. contributed to the implementation of the experiments.

Competing interests

The authors declare that they have no competing interests.

Funding

This work is partly financed by the Netherlands Organisation for Scientific Research (NWO), project no. 022.004.008.