Mechanical Properties of the Cytoskeleton and Cells

Microtubules, actin filaments, and intermediate filaments have different physical properties (e.g., stiffness) that confer on cytoskeletal networks a wide range of mechanical properties.

SUMMARY

The cytoskeleton is the major mechanical structure of the cell; it is a complex, dynamic biopolymer network comprising microtubules, actin, and intermediate filaments. Both the individual filaments and the entire network are not simple elastic solids but are instead highly nonlinear structures. Appreciating the mechanics of biopolymer networks is key to understanding the mechanics of cells. Here, we review the mechanical properties of cytoskeletal polymers and discuss the implications for the behavior of cells.

1. INTRODUCTION

Eukaryotic cells, especially those in multicellular organisms, are subjected to a variety of mechanical forces arising from effects such as gravity, fluid flow, and active contraction generated by neighboring cells or resisted by the extracellular matrix. These forces are large enough to significantly deform a viscous fluid surrounded by a lipid membrane such as a vesicle and, so, if the cell is to retain its original shape after the deforming force is released, or if it is to be able to maintain its shape in response to such a force, it must be at some level elastic. There are many molecular and structural mechanisms by which to make a cell-sized object elastic or viscoelastic (e.g., placing a finitely stretchable membrane around a purely viscous fluid), but most cell types are viscoelastic throughout their entire volume because they are filled with the three-dimensional network of protein filaments comprising the cytoskeleton (Schliwa 1986; Alberts 2015; Hardin et al. 2015). The filaments of the cytoskeleton are not simply mechanical supports but also the tracks along which motor proteins move, enzymes and substrates are localized, the lipid bilayers of the membrane are attached to the rest of the cell, and the assembly of signaling complexes is spatially organized (Wickstead and Gull 2011). Therefore, it is not always possible to isolate purely mechanical effects of cytoskeletal polymers from their biochemical activities, but, without these filaments, the eukaryotic cell would be too soft and fluid to maintain its shape and exert its function.

The protein filaments comprising the cytoskeleton have some similarities to the linear polymers within synthetic elastic materials such as the polyacrylamide in a gel or the polyethylene in a plastic bag, but two structural features that set them apart from synthetic polymers are a relatively large diameter and a much greater stiffness (MacKintosh and Schmidt 2010; Broedersz and MacKintosh 2014). Both the intracellular and extracellular spaces of most organisms contain highly flexible polymers such as glycosaminoglycans and other polysaccharides. The cell interior also contains other long flexible objects such as nucleic acid polymers and the membrane tubes of the endoplasmic reticulum, but the cytoskeleton is different in that its constituent filaments are orders of magnitude stiffer. The three major types of cytoskeletal polymer in most cells are microtubules (MTs), actin filaments (F-actin), and intermediate filaments (IFs); they each differ strongly in the magnitude of their stiffness, but they are all sufficiently rigid that they can be visualized as single extended filaments rather than tangled coils on the length scale accessible by light or electron microscopy, especially when they are arranged in filament bundles. In many cases, these filaments are long and straight enough to span nearly the entire dimension of the cell.

The length and stiffness of cytoskeletal polymers generates several features of the networks they form that appear advantageous from a biological perspective. For example, their elongated structure means that they can be assembled into three-dimensional networks at much lower volume fractions than are required to form gels from more flexible polymers (Mofrad 2009; Kollmannsberger and Fabry 2011; Broedersz and MacKintosh 2014). Consequently, a network with the same rigidity or elastic modulus (i.e., its resistance to deformation under applied force) as a 5% polyacrylamide gel can be made by cross-linked actin filaments with a concentration nearly two orders of magnitude lower. A second consequence of the length and rigidity of cytoskeletal polymers is that the viscoelasticity of the networks they make is different from those of gels formed by flexible polymers, especially when the networks are deformed to relatively large strains. One such difference is seen in the strain stiffening of cytoskeletal networks, in which the stiffness of these networks increases the more they are deformed—a feature that is lacking in flexible polymer gels such as polyacrylamide or gelatin and might help cells limit their deformation when they are subjected to abnormally large stresses. A further feature of cytoskeletal polymers is that they are all highly charged anionic polyelectrolytes (Janmey et al. 2014). The large surface charge density of actin filaments, MTs, and IFs does not by itself have a major effect on their rigidity, but it does influence the geometry of the networks that these polymers make and how they interact with filament binding proteins.

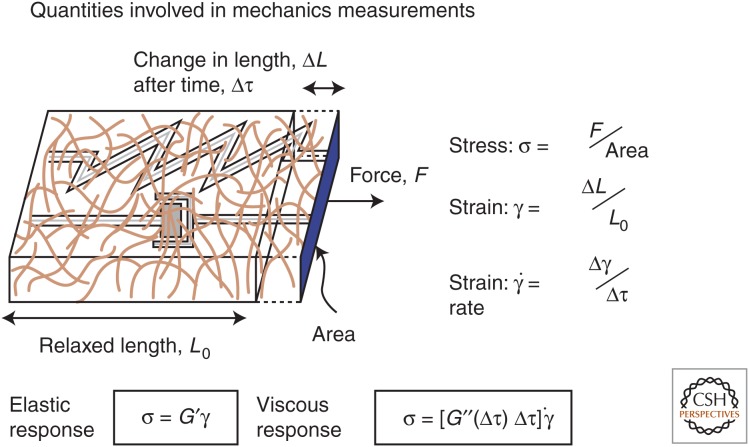
In addition to the creation of an elastic environment within the cell interior, the cytoskeleton also plays important mechanical roles in linking the plasma membrane of the cell, as well as interior membranes such as the endoplasmic reticulum, to the rest of the cell, in limiting the diffusive motions of intracellular polymers that are larger than the network mesh size, and possibly in controlling the permeation of water and small solutes through the cytoskeleton. A first approximation to modeling the mechanical properties of the cytoskeleton and cell mechanics in general is to consider the elements of the cytoskeleton as polymers, using experimental methods and theoretical models developed for traditional polymers but modified for the much larger, stiffer, and fragile biopolymers comprising the cytoskeleton. Within this framework, we use terms, concepts, and measurement techniques normally applied to inert material to describe the mechanical properties of these networks (Fig. 1). An important difference between the cytoskeleton and simple polymer networks is the presence of motor proteins that move along actin filaments and MTs to create active materials that are out of thermodynamic equilibrium (Mizuno et al. 2007; Guo et al. 2014). The degree to which the mechanics of live cells can adequately be modeled as polymer networks is by no means certain, but this analogy has potential to relate structural features of the cytoskeleton visualized by light, electron, and atomic force microscopy to the mechanical properties of the cell. This review will explore the mechanical properties of the cytoskeleton and cells from the perspective of polymer physics and soft materials, summarize the structural features of the three different cytoskeletal polymer types, and discuss how they can be assembled into passive and active networks that mediate cell mechanics.

Figure 1.

The terms applied to and the quantities measured in the study of rheology of biopolymer networks. G′, elastic response; G′′, the viscous response. Biopolymers are viscoelastic and both G′ and G′′ are significant. (Adapted from Kasza et al. 2007, with permission from Elsevier.)

2. MECHANICAL PROPERTIES OF THE THREE CLASSES OF POLYMERS

Like any system of polymers, the mechanical properties of cytoskeletal networks depend on the physical properties of the individual polymer strands, the structure and mechanical properties of the linkages between filaments, and the three-dimensional geometry of the filament arrangement (Fabry et al. 2001; Chen et al. 2010). In most cell types, the cytoskeleton is formed by a three-dimensional composite network of actin filaments (F-actin), MTs, and IFs, together with the host of proteins that bind to the sides or ends of these linear polymers. Binding proteins for actin, IFs, and MTs regulate filament length, cross-link filaments to each other, and apply forces to the filaments. The complex systems of cytoskeletal regulatory proteins have been extensively reviewed elsewhere.

The three types of cytoskeletal filaments differ from each other, both chemically and physically, in ways that permit a wide range of material properties in the networks they form. Among the most significant differences is the stiffness of each polymer type. The bending stiffness of cytoskeletal filaments, usually quantified by its persistence length, ℓ_p, ranges from a few hundred nanometers for IFs, to 10 μm for F-actin, to millimeters for MTs. Filament stiffness, filament length, and the geometry of cross-linking together determine the mechanical properties of cytoskeletal networks, and the unusually high stiffness of these polymers has motivated much theoretical and experimental work to relate the microscopic properties of the polymers to the macroscopic properties of the networks they form. The presence of molecular motors that can generate motions much larger than those produced by thermal energy and that can exert tension within networks creates new material properties that are only beginning to be experimentally measured and theoretically understood (Mizuno et al. 2007).

3. SINGLE-FILAMENT MECHANICS

The stiffness of polymer filaments can be quantified by their ℓ_p, which is defined as the length scale for the decay of the tangent–tangent correlation along the filament and is proportional to the stiffness of the polymer. This fundamental length has a simple physical interpretation: It is the typical range over which the orientation of an isolated polymer remains correlated along its length. It can also be thought of as the maximum length over which the polymer will appear to be straight in the presence of the constant Brownian forces it experiences because of thermal energy (kT) in a medium at finite temperature. If a polymer can be modeled as a uniform cylinder, ℓ_p = κ_B/kT, in which κ_B is the bending modulus of the filament. Usually ℓ_p is easier to measure than κ_B, and the force needed to deform a filament is inferred from ℓ_p, but recent studies of the coupling between bending or stretching and twisting of F-actin suggest that simultaneous application of torque, tension, or bending, as some actin-binding proteins appear to do, can have more profound effects on F-actin than suggested by ℓ_p alone (De La Cruz et al. 2010; Yamaoka and Adachi 2010). For complex filaments such as MTs, in which sliding between protofibrils can occur during MT bending, the relationship between ℓ_p and κ_B is not a simple proportionality, and some experiments and models predict a contour-length-dependent persistence length (Pampaloni et al. 2006; Heussinger et al. 2010).

The ratio between persistence length and the contour length (ℓ_c) differentiates the polymer filaments into three regimes. When ℓ_c > ℓ_p, the filaments are flexible (i.e., thermal energy can cause large transverse fluctuations), a filament then approximates a Gaussian polymer chain with a Kuhn length—the length over which the polymer is fixed and beyond which it is free to rotate—of 2ℓ_p. In the limit of ℓ_p > ℓ_c, filaments are stiff and do not show transverse thermal undulations but move in solution as rigid rods driven by thermal energy. Semiflexible filaments lie between these two limits, and ℓ_c and ℓ_p are on the same order of magnitude.

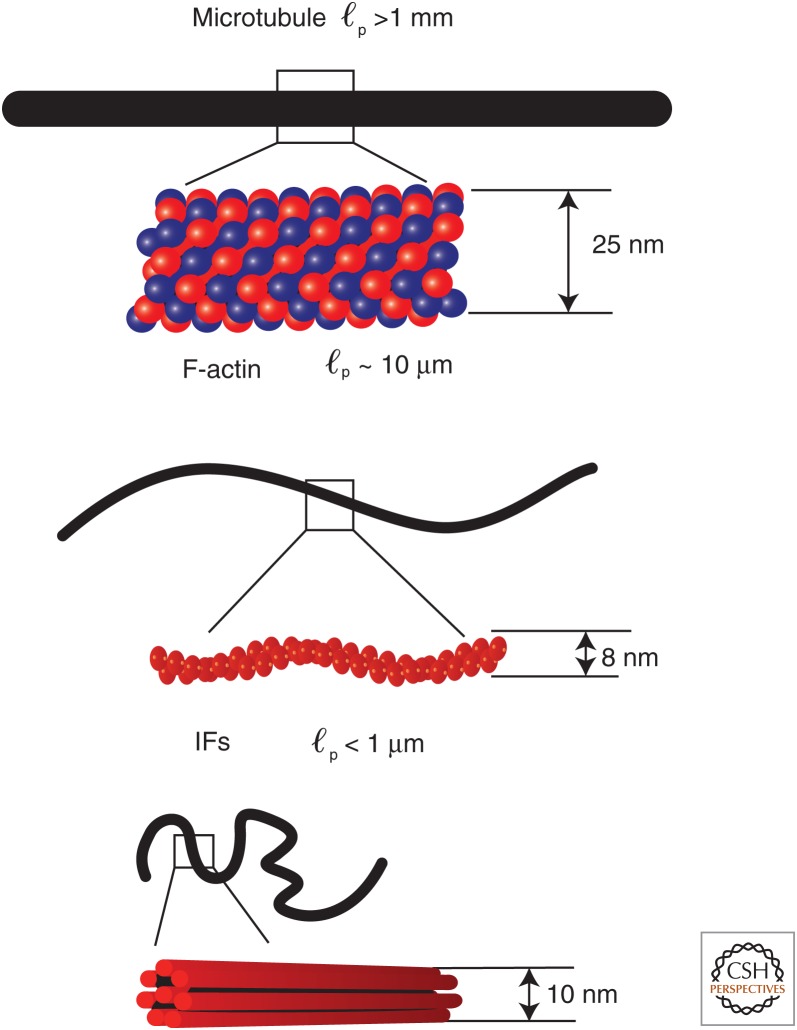
For filaments with a contour length of 10 µm, the three types of cytoskeleton filaments fall in these three stiffness regimes, respectively. Intermediate filaments are the softest among the three major types of cytoskeleton filaments. Their ℓ_p is reported to range from 200 nm to slightly more than 1 µm and is IF-type-dependent (Schopferer et al. 2009; Beck et al. 2010). The small persistence length of the 10-nm diameter IFs containing many coiled-coil dimer subunits per cross section is surprising as the persistence length of a single coiled-coil dimer such as tropomyosin is itself ∼100 nm (Sousa et al. 2010). The thinner, semiflexible F-actin is an order of magnitude stiffer than IFs and has a persistence length ranging from 3 µm to 17 µm (Gittes et al. 1993), which is comparable to the typical filament length. MTs are considered to be stiff polymers, with ℓ_p >1 mm (Gittes et al. 1993). The characteristic ℓ_p and diameter of the different types of cytoskeletal filaments are summarized in Fig. 2.

Figure 2.

Stiffness and structure of cytoskeleton filaments. Microtubules (MTs), F-actin filaments, and intermediate filaments (IFs) of diameter 10 µm are drawn on the same scale. Stiffer filaments with larger persistence length (ℓ_p) appear to be straighter. (Reprinted from Wen and Janmey 2013, with permission from Elsevier.)

Compared with IFs, MTs and F-actin are relatively brittle filaments and rupture under elongational strains less than ∼10% of their resting length. IFs, in contrast, can bear much larger extensional strain than MTs and F-actin. Several types of IFs have been stretched to >200% of their resting length without breaking (Qin et al. 2009; Qin et al. 2010). This large extensibility is thought to be attributable to the hierarchical structure of IFs that allows partial unfolding of subunits without breakage of the filament.

The mechanical and rheological properties of networks (i.e., filaments that are linked together with different types of cross-links) depend both on the response of individual polymers to forces at the molecular level and on the way in which these single polymers are connected or otherwise interact with each other. The uniquely extended form of cytoskeletal polymers results in a relationship between force and extension that is different from that of purely rigid rods or highly flexible coils. A single filament can respond to both transverse and longitudinal forces by either bending or stretching/compressing. On length scales shorter than the persistence length, bending can be described in mechanical (enthalpic) terms, as for elastic rods. In contrast, especially when the contour length is greater than the persistence length, stretching and compression can involve both a purely elastic mechanical response analogous to that of macroscopic elastic rods, and an entropic response related to that of purely flexible coils. This entropic elastic response comes from the thermal fluctuations of the filament. Perhaps surprisingly, the longitudinal response can be dominated by entropy, even on length scales that are small compared with the persistence length. Thus, it can be misleading to model a filament as truly rod-like, even on short length scales compared with ℓ_p.

The longitudinal single-filament response is often described in terms of a so-called force–extension relationship in which the force required to extend a filament is measured or calculated in terms of the degree of extension along a line. For filaments with the physical properties of cytoskeletal polymers, for which ℓ_p is on the order of ℓ_c, this relationship is not simple, especially at the large deformations that the cytoskeleton undergoes in vivo, and the full nonlinear force–extension curve has been calculated numerically (Storm et al. 2005). In the linear regime of relatively small extension, the force–extension relationships depend on whether the filament contour length is larger than the persistence length. For ℓ ≫ ℓ_p, the force–extension relationship is approximated well by

$$\tau \sim \frac{kT}{{\mathcal{l}}_{\text{p}}}\left(\frac{\delta \mathcal{l}}{\mathcal{l}}+\left[\frac{1}{4}\frac{{\mathcal{l}}^2}{{|\mathcal{l}-\delta \mathcal{l}|}^2}-1\right]\right)\text{for}\mathcal{l}\gg {\mathcal{l}}_{\text{p}},$$ 1

in which τ is the tensile force needed to extend the resting end-to-end distance of the filament by a length δℓ.

In contrast, for ℓ < ℓ_p,

$$\tau \sim \frac{kT{\ell }_{\mathrm{p}}}{{\ell }^2}\left(15\frac{\delta \ell }{{⟨\mathrm{\Delta }\ell ⟩}_0}+9\left[\frac{{⟨\mathrm{\Delta }\ell ⟩}_0^2}{{\left|{⟨\mathrm{\Delta }\ell ⟩}_0-\delta \ell \right|}^2}-1\right]\right)\mathrm{for}\ell \ll {\ell }_{\mathrm{p}}.$$ 2

A somewhat more accurate approximate form for the latter has also been derived (Palmer and Boyce 2008). A more tractable approximate analytic expression derived from this theory and applied to actin filaments concludes that the force–extension relationship can be expressed as

$$F\sim \frac{kT}{{\ell }_{\mathrm{p}}}\left(\frac{1}{4{(1-r/{\ell }_{\mathrm{c}})}^2}\right)\left(\frac{{\displaystyle \frac{{\ell }_{\mathrm{c}}}{{\ell }_{\mathrm{p}}}-6(1-r/{\ell }_{\mathrm{c}})}}{{\displaystyle \frac{{\ell }_{\mathrm{c}}}{{\ell }_{\mathrm{p}}}-2(1-r/{\ell }_{\mathrm{c}})}}\right),$$ 3

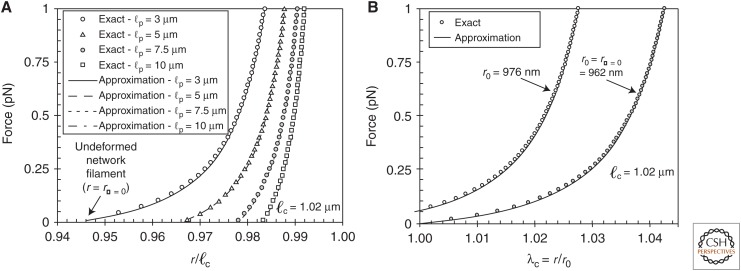
in which F is the force and r is the end-to-end distance of the filament. This expression agrees well with the more complete expression for extensions within the range 1–0.3 ℓ_c/ℓ_p < r/ℓ_c < 1. The success of these different models is evident in being able to capture single-filament responses, as shown in Figure 3. From the single-filament response, we can begin to understand the network response, in which geometry and filament connections play an important role in understanding how mechanics is determined for in vivo systems.

Figure 3.

(A) The effect of persistence length (ℓ_p) on filament force–extension behavior, as computed using numerical solutions of the model developed by MacKintosh and colleagues (Storm et al. 2005) (symbols) compared with an analytic model approximation (lines) (Palmer and Boyce 2008) fixing contour length (ℓ_c) to ℓ_c = 1.02 µm. (B) The effect of pretension on filament force–stretch behavior as computed by both methods. The end-to-end distance of a filament at a given condition is given by r. (Reprinted from Palmer and Boyce 2008, with permission from Elsevier.)

4. NETWORK MECHANICS

4.1. Strain Stiffening of Cytoskeletal Polymer Networks

The nonlinear force–extension relationship of semiflexible polymers, in which the force to extend the end-to-end distance of the filament increases the more the filament is stretched, suggests that networks made from such filaments will also become stiffer as they are deformed to larger strains.

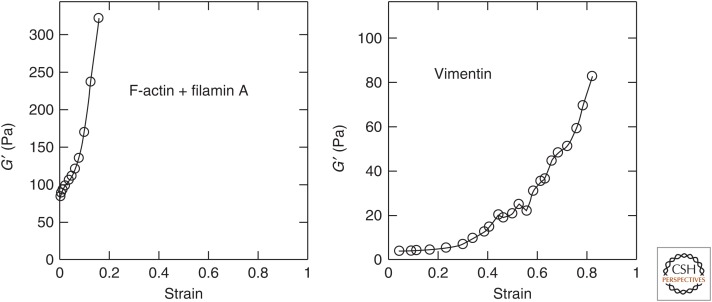
Networks formed by cross-linked actin or IFs show strain-dependent stiffening that is consistent with the nonlinear force–extension relationship of the individual polymers that make up the struts between nodes of such networks. To measure these mechanical properties, a network is formed between two plates in a shear rheometer; by rotating one while the other is kept fixed, a shear strain is applied to the network and the resultant restoring force can be measured. With the strain, plate area, and restoring force known, it is possible to measure the shear modulus of the material between the plates. When using biopolymer networks, they increase their shear moduli as the shear strain increases to relatively modest strains of a few percent for actin cross-linked by filamin A and 10%–20% for the softer vimentin IFs, as shown in Figure 4 (Storm et al. 2005; Wen and Janmey 2013). The magnitude of the shear modulus of a vimentin network increases by more than an order of magnitude between 1% and 80% strain (Lin et al. 2010b). The strain stiffening of these networks is reversible, with the modulus returning to low levels when the shear strain is reduced, unless the networks are strained to magnitudes large enough to break cross-links between filaments or break the filaments themselves. In many settings, the dependence of shear modulus on increased stress is perhaps more biologically relevant than its dependence on strain, and the dependence of shear modulus on imposed shear stress shows a characteristic power-law dependence that depends on the molecular mechanisms that lead to this nonlinear response (Fabry et al. 2001; Kollmannsberger and Fabry 2011).

Figure 4.

Strain stiffening of cytoskeletal networks in vitro. Shear storage modulus measurements of F-actin cross-linked by filamin A, and vimentin, measured at frequencies near 1 Hz and a range of strain magnitudes. Vimentin networks can be strained much more than actin networks and also strain-stiffen to a much larger degree. (Adapted from Storm et al. 2005; Wen and Janmey 2013, with permission from Elsevier.)

4.2. Mechanisms of Strain Stiffening

The molecular mechanism for strain stiffening in biopolymer gels (i.e., networks formed of cytoskeletal filaments) has been the subject of extensive theoretical work. Depending on the filament stiffness, network deformation can be accommodated by bending, stretching, and reorientation of individual filaments (Vahabi et al. 2016; van Oosten et al. 2016).

The strain stiffening of semiflexible polymer networks can, within a limited range of strain, be accounted for by an entropic model that assumes that network deformation is uniform throughout the sample owing to affine deformation of each semiflexible polymer; affine stretching assumes that the local strain at each point of the network matches the macroscopic strain of the network. The elasticity comes from the resistance of each thermally writhing polymer against the stretching, which effectively reduces the amplitude of thermal fluctuation and thus the thermal entropy of the filament (MacKintosh et al. 1995).

An alternative explanation for strain stiffening based on filament bending and enthalpic stretching has also been proposed for stiff filament networks (Onck et al. 2005; van Dillen et al. 2008; Zagar et al. 2011) and can arise in networks formed by filaments that themselves are linearly elastic. In this model, because it is easier to bend stiff filaments than to stretch them, the filaments initially bend at small network deformations. With increasing strain, the bent filaments reorganize so that more and more filaments align along the direction of shear. The network deformation then comes mainly from the enthalpic stretching of the aligned stiff filaments. This transition from bending to stretching gives rise to strain stiffening. The bending, buckling, and reorganization of filaments cause nonaffine deformations in the network (Onck et al. 2005).

These two strain-stiffening models predict different network deformations: The entropic model predicts uniform affine deformation, and the enthalpic model predicts heterogeneous nonaffine deformation in which individual filament deformation does not match the average macroscopic behavior. Which theory works depends on the network structure and filament stiffness. It has been shown that, as cross-linker concentration decreases, the deformation of an F-actin network transits from affine to nonaffine (Gardel et al. 2004). This change indicates that dense isotropic networks follow predictions of the entropic model, and the sparse networks follow predictions of the enthalpic model.

For entropic networks, the effective contour length of each filament is determined by the distance between cross-links; as the effective contour length decreases, network mechanics are increasingly dominated by the mechanical properties of the individual filaments. The contour length is determined by the concentration of polymer c_A and the density of cross-links, typically reported as the ratio R of cross-links to monomers. The shear modulus at low strain is indeed found to scale with polymer concentration and cross-link density in the case of permanent cross-links made using, for example, the tetrafunctional biotin-binding protein avidin as the cross-linker of filaments labeled with biotin, or an actin cross-linking protein such as scruin:

$$G^{\mathrm{\prime }}\sim c_{\mathrm{A}}^{11/2}{R}^{(6x+15y)/5},$$ 4

in which x characterizes how the cross-linker bundles the fibers, and y characterizes cross-linker efficiency. For these entropic networks, the differential shear modulus K′ increases dramatically beyond a critical stress and is expected to scale asymptotically as σ^3/2. This scaling derives from calculating the tension required to extend a single, thermally fluctuating filament—that is, the tension required to overcome the entropic motion of the fiber. Interestingly, the behavior of these entropic networks is self-similar; if the differential shear modulus is scaled by the zero strain shear modulus and the applied stress is scaled by the critical stress, all networks collapse onto a single universal stress-stiffening response curve. This universal curve is characteristic of affinely deforming networks of semiflexible polymers.

4.3. Effect of Cross-Links

The universal response curve and the predicted stress-stiffening behavior of entropic semiflexible polymers assumes that the system has rigid, permanent cross-links; however, many physiological cross-links are dynamic, forming only transient bonds and thus can change the behavior of biopolymer networks. For example, the binding affinity of α-actinin for F-actin is temperature-dependent; if the temperature of a cross-linked gel is increased from 8°C to 25°C, the network softens and becomes substantially more viscous as the effective number of cross-links is reduced owing to decreased binding (Tempel et al. 1996; Xu et al. 1998). The higher temperature leads to an increase in the rate of α-actinin unbinding from the F-actin network and allows cross-links to rearrange over time, enabling the network to remodel over long times when held at elevated temperatures (Sato et al. 1987). These dynamic cross-links that allow remodeling are crucial for the normal physiological function of the cell and enable the cell to reorganize its cytoskeleton. Indeed, changes in binding affinity, and thus the temporal dynamics of biopolymer cross-linkers, has been directly tied to disease—a mutation of α-actinin that causes an increase in binding affinity for actin has been found to be responsible for some types of kidney disease (Yao et al. 2004; Weins et al. 2005).

Although temperature is unlikely to be a large factor in determining cross-link behavior in vivo, cells are constantly exposed to varying mechanical forces in their environment. The mechanical loading of cytoskeletal networks can also change the binding dynamics of cross-links and thus affect cytoskeletal remodeling in response to force, as well as affecting force transmission through the cell. For example, in actin networks cross-linked with fascin, the forced unbinding of cross-links can occur at different rates of applied stress and therefore lead to mechanically induced softening of the system (Lieleg and Bausch 2007). Surprisingly, mechanical stress can also have the opposite affect—applied stress can increase the binding time of cross-links and thus delay network relaxation (Lieleg et al. 2009; Norstrom and Gardel 2011; Yao et al. 2013). This “catch-bond” behavior delays the onset of the gel-to-fluid transition and might be important for cells to resist mechanical deformation at physiological timescales.

Beyond changing the temporal dynamics of the system, cross-links themselves can also act like added mechanical elements and thus dramatically change the rheological properties of the network. For example, in the case of F-actin cross-linked with filamin A (FLNa), the cross-links themselves act as flexible, extensible elements in the network; essentially the network comprises two different semiflexible polymers. This has several consequences for network mechanics. The stiffness of the network is much more weakly dependent on cross-link concentration when compared with networks with fixed cross-links; indeed, at low stress, the elastic modulus of the network is only slightly above that of an uncross-linked solution of polymer (Gardel et al. 2006). Although an FLNa–F-actin network still strain-stiffens, it appears that the behavior is dominated by strain stiffening of the cross-links as opposed to stiffening of the actin elements in the network (Kasza et al. 2010). In this case, the actin has taken on the role of the cross-linker, and the FLNa cross-links are the polymer network and thus dominate network rheology. These networks fail at much higher strains than are achievable in actin networks with fixed cross-links. Additionally, the failure mechanism no longer involves actin rupture—instead, failure is caused by rupture of the cross-link elements (Kasza et al. 2010).

4.4. Active Versus Passive Systems

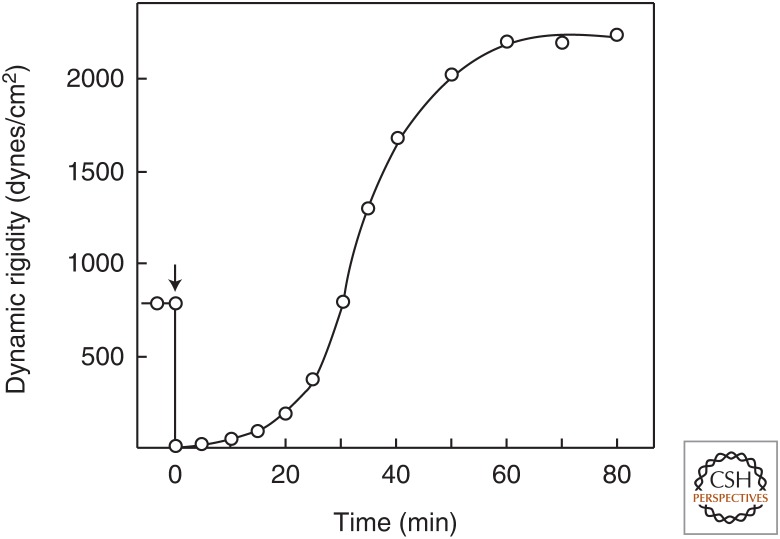
One of the major consequences of the strain-stiffening properties of cytoskeletal networks is that application of internal stresses such as those that are generated by the motor protein myosin on F-actin, or by the motors kinesin and dynein on MTs, leads to internal strains that have the same stiffening effect as external strains applied by rotational plate rheometers or neighboring cells. The fact that the active motion of myosin can alter the elastic properties of actin networks was shown in classic work from the laboratory of Maruyama in the 1970s (Abe and Maruyama 1971; Abe and Maruyama 1973). Figure 5 shows one example in which the shear storage modulus of a 4-mg/mL actin network, which was initially at a level of 800 dyne/cm², abruptly dropped when ATP was added to the network comprising actin and heavy meromyosin, demonstrating the fluidization effect that active motors have on otherwise non-cross-linked networks of actin filaments (Humphrey et al. 2002). However, at later times, as the myosin hydrolyzed the ATP that had been added and began to form rigor bonds with actin filaments, the shear storage modulus rose again and increased to levels that were much higher than those of the initial network that had formed without the prestress generated by the active motors. Numerous more recent studies have shown in further detail the effect of active motors to drive systems of actin filaments or MTs out of their equilibrium state, leading initially to increased motion and fluidization and followed, in some cases, by an abrupt increase in stiffness if the active motions are lost owing to ATP depletion and stable rigor-like cross-links are formed instead (Bruno et al. 2009; Mackintosh and Schmidt 2010; Soares e Silva et al. 2011; Khan et al. 2012; Schaller et al. 2012; Joanny et al. 2013; Henkin et al. 2014).

Figure 5.

The effect of ATP on the dynamic rigidity of a heavy meromyosin–F-actin gel (heavy meromyosin, 4.0 mg/mL; F-actin, 2.0 mg/mL). The arrow indicates the time of addition of 5 mm ATP, causing an instantaneous drop in rigidity that recovers with time as the myosin hydrolyzes the ATP. (Adapted from Abe and Maruyama 1971, with permission from Elsevier.)

These studies also laid the groundwork for quantitative estimates of the magnitude of the elastic modulus that could be generated by cytoskeletal polymers and their accessory proteins present within the cytoplasm. For example, early studies by Abe using 2.5 mg/mL of F-actin showed that, with appropriate molar ratios of myosin to actin, following the addition and hydrolysis of 1 mm ATP, the shear storage modulus of such myosin-cross-linked or α-actinin-cross-linked, prestressed actin networks could reach levels of 3500 dynes/cm² or equivalently 350 Pa (Abe and Maruyama 1971; Abe and Maruyama 1973). Many studies have shown that the shear modulus of cross-linked actin networks, like those of other networks formed by semiflexible polymers, scales with concentration to a power slightly greater than two. Therefore, at intracellular concentrations of actin that are often in the range of 10–20 mg/mL, the shear modulus of a prestressed and cross-linked actin cytoskeleton can reach magnitudes on the order of 10 kPa, even in the absence of MTs and IFs; this stiffness is consistent with that measured in cells. Such studies probably place an upper limit to the magnitudes of stiffness measured by atomic force microscopy and other methods suitable for single-cell measurements, and fluidization effects due to filament disruption or cross-linker release will decrease the levels of elastic moduli (Fig. 5).

5. RHEOLOGY OF NETWORKS ALONE

Considerable knowledge of the behavior of the cytoskeletal properties can be gleaned from studies of the rheology of reconstituted networks of pure filamentous systems (Janmey and McCulloch 2007; Broedersz and MacKintosh 2014). Reconstituted actin networks have been studied the most widely. In the absence of any cross-linkers, reconstituted actin networks can form weak elastic gels in which the solid nature of the structure is caused by the physical constraints of the entanglements of the filaments (Janmey et al. 1986; Hinner et al. 1998). Elastic moduli of the order of a few pascals are typically observed, with the modulus increasing as a power of the concentration, with an exponent of ∼2 (MacKintosh et al. 1995). These networks also show some strain stiffening. The behavior differs dramatically on the addition of actin cross-linking proteins. In this case, the networks become much more rigid solids, with elastic moduli several orders of magnitude greater (Gardel et al. 2004). If large, very flexible cross-linking proteins are used, such as filamin, the network shows similar behavior in the linear regime, but can become highly nonlinear, with the elastic modulus increasing very strongly with strain, and with the networks attaining elastic moduli as high as several hundred to even thousands of pascals. In fact, the behavior of such networks mimics the behavior of cells quite well (Gardel et al. 2006).

The elastic modulus of networks of MTs is less well studied, primarily because it is difficult to attain sufficient physical entanglement with filaments that are as individually stiff as MTs are. Some studies do measure a weak elasticity consistent with the small number of physical constraints (Sato et al. 1988; Lin et al. 2007; Pelletier et al. 2009). There are not many mechanically stable MT cross-linking proteins; thus, studies of cross-linked MTs are scarce (Yang et al. 2013).

Networks of pure IFs have been more generally explored (Janmey et al. 1991; Lin et al. 2010b). Although there are not many known cross-linking proteins for IFs, the large charges on their surfaces do cause significant cross-linking on addition of salt. Indeed, the elastic modulus of IF networks does show a large increase with increasing salt concentration, similar to the behavior of actin networks following the addition of cross-linking proteins (Lin et al. 2010a; Yao et al. 2010). Networks of IFs can also be strained to considerably larger values before they irreversibly break (Janmey et al. 1991).

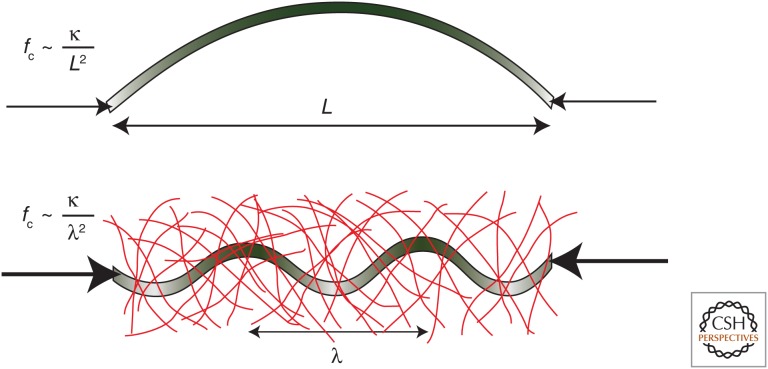
Perhaps even more interesting is the behavior of mixtures of proteins, in which interpenetrating reconstituted networks can be formed. When small amounts of MTs are added to actin networks, they have the effect of significantly increasing the elasticity of the actin networks. This is because the sparse, stiff MT rods lead to more affine deformation of the actin network at larger applied strains (Lin et al. 2007; Liu et al. 2007). It appears, therefore, that the MTs prevent bending deformations at larger scales because of their stiffness. Similarly, embedding MTs in an elastic actin network increases the energy of transverse deformation of the MTs (Brangwynne et al. 2006; Pelletier et al. 2009). As a result, the MTs behave dramatically differently under compression—isolated MTs are highly susceptible to buckling when they are compressed and hence cannot support compressive stresses. In contrast, when the MTs are embedded within an elastic actin network, longer-wavelength buckling, which corresponds to the entire MT bending and large lateral displacement, is suppressed because it is energetically too costly to elastically deform the elastic actin network (Fig. 6). Instead, buckling occurs at much shorter wavelengths such that many bends of short lateral displacement form along the length of the MT, and this significantly increases the capability of the MTs to support compressive loads. Actin networks can also be formed with interpenetrating IF networks. In this case, the elastic moduli of the individual networks is comparable, and the elastic moduli of the intermixed networks do not vary that much. However, there are some important changes to the behavior as the relative concentrations of the two proteins are varied, and this is because of the steric constraints that one network imposes on the formation of the second (Jensen et al. 2014).

Figure 6.

Buckling of stiff rods under compression, with and without a supporting elastic gel. A compressive force f_c is applied to a rod of unbent length L and bending modulus κ. For a free rod (upper image), large-scale bending is free to occur (bending exaggerated for clarity). In the presence of a surrounding gel (lower image), large displacements are suppressed and short-wavelength buckling occurs instead and the compressive force depends on the characteristic length scale of the buckling, given by λ. (Reprinted from Brangwynne et al. 2006.)

Reconstituted actin networks have also been studied with the addition of molecular motors (Mizuno et al. 2007; Koenderink et al. 2009). Typically, minifilaments of myosin II are added to the network. These minifilaments form dipolar structures that walk processively in opposite directions along two actin filaments. This results in an internal tension within the network. This leads to dramatic stiffening of the elastic modulus, in a fashion that can be directly mapped to the application of an external prestress. This also delays the onset of strain stiffening to much larger strains. However, once the stiffening does occur, the network reverts back to the behavior in the absence of the motors, as the externally applied prestress overcomes the internal tension of the motors.

6. MEASURING CELL STIFFNESS AND CAUTIONARY NOTES

Reconstituted biopolymer networks span a stiffness range from <1 Pa to >10 kPa, depending on the concentration of filaments, the presence of cross-links, and the prestress applied. Live, isolated eukaryotic cells span a similar stiffness range (Janmey and McCulloch 2007; Mofrad 2009); additionally, cells show a strain-stiffening behavior similar to that of biopolymer networks (Fernandez et al. 2006; Kollmannsberger and Fabry 2011). In practice, the reported mechanical properties of a cell depend on both the technique used and the model used to interpret the measurements. Indeed, several different techniques are available for measuring the stiffness of isolated cells, with the maximum measurable stiffness limited by the maximum applicable force. Regardless of the technique used, extracellular stiffness is found to vary from ∼0.1 to ∼10 kPa, and intracellular stiffness varies from ∼10 to ∼100 Pa.

The large difference between extracellular and intracellular stiffness highlights the highly heterogeneous nature of the cell; additionally, the locally measured stiffness can vary greatly, depending on parameters such as the local cytoskeletal structure or the distance from the nucleus. For these reasons, a variety of technologies have been developed to measure cellular mechanics, and these offer complementary approaches to studying cell behavior (Janmey and McCulloch 2007; Mofrad 2009; Kollmannsberger and Fabry 2011). Atomic force microscopy allows application of large forces, up to ∼100 nN, and can probe either local or global stiffness, depending on the tip geometry; the interpretation of the measured results is highly dependent on both the geometry used, be it a cone, colloidal probe, or flat plate, and the mechanical model used to recover cell stiffness from the actual measurement data (Guz et al. 2014; Gautier et al. 2015; Haase and Pelling 2015). Uniaxial stretching or compression of cells attached between two plates is essentially unlimited in the maximum force that can be applied; however, it is incapable of subcellular resolution (Fernandez et al. 2006). Uniaxial stretching can also be applied using an optical stretcher; cells in suspension are trapped between two laser sources, and the cell is stretched by means of the electric field gradient (Guck et al. 2001).

If particles are attached to the cell surface or embedded inside the cell, additional measurement techniques are possible. For particle-based techniques, the mechanism by which the particle interacts with the cytoskeleton significantly changes the stiffness measured; for example, particles can be coated with different binding proteins and, thus, are linked to the underlying cytoskeletal structure differently. In magnetic twisting cytometry, paramagnetic beads attached to the surface are magnetized in one direction and then are twisted by application of a perpendicular magnetic field; the resultant bead displacement can be tracked by optical microscopy (Fabry et al. 2001). The applied torque is limited to ∼140 Pa, and converting the measured displacement into absolute stiffness measurements relies on measuring bead embedding into the underlying structure. For optical and magnetic tweezers, the beads are uniaxially displaced by using electric and magnetic fields, respectively, with maximum forces of ∼500 pN and 100 nN, respectively. For optical tweezers, the maximum force can limit its applicability when measuring extracellular stiffness; however, intracellular stiffness is much lower and can be effectively measured when beads are embedded inside the cell (Guo et al. 2014).

Additionally, intracellular stiffness, in many instances, has been probed by measuring apparently spontaneous fluctuations of embedded particles. Although it is tempting to interpret these using the concepts of microrheology, from which mechanical properties are derived from fluctuations at thermal equilibrium, these interpretations are categorically wrong. The cell is not in equilibrium, and this form of microrheology cannot be used. Instead, the motion is driven by motor activity or other enzymatic processes within the cell; thus, instead, the motion can be used to probe the average enzymatic activity of the cell but cannot by itself be used to probe mechanical properties (Guo et al. 2014; Battle et al. 2016).

7. CONCLUSION

Cells are viscoelastic materials that exist under changing mechanical loads. For a cell, the origin of its mechanical properties and its response to load are predominantly determined by the cytoskeleton; these mechanical properties change in response to a cell’s environment and can be tied to both development and disease. For example, cell stiffness is correlated with stem cell differentiation, suggesting that cell mechanics is tied to transcriptional and translational changes within the cell (Engler et al. 2006; Chowdhury et al. 2010; Swift et al. 2013). Beyond single-cell properties, changes in the cytoskeleton are also related to tissue-level mechanics throughout the body, including in the central nervous system (Franze et al. 2013), kidneys (Yao et al. 2004; Weins et al. 2005), heart (Hein et al. 2000), smooth muscle (Gunst and Zhang 2008), and others (Omary et al. 2004; Fletcher and Mullins 2010).

Using reconstituted cytoskeletal biopolymer networks is one route to understanding the rheological properties of the cytoskeleton and has enabled the development of theoretical models to help understand these reconstituted networks and to build physical intuition about their behavior. Biologically relevant cross-links can dramatically change the mechanical response of biopolymer networks and introduce complex temporal dynamics into the system; understanding how these cross-links change network behavior is essential for understanding the processes by which cells sense and respond to force. Beyond systems of a single-biopolymer network, a clear understanding of mixed systems comprising different biopolymers is also essential. Fabrication of physiologically relevant mixed networks is challenging as intracellular polymerization of networks is under spatial and temporal control in a cell that is difficult to replicate in vitro. In addition, the active processes that control polymerization in the cell are essential to understand the contribution of enzymatic and motor activity to the mechanics of a cell. The cell and the cytoskeleton are far from thermal equilibrium, with many active processes directly altering the mechanical properties of the cell. Disentangling the role of active processes from the passive mechanical properties of the biopolymer networks is needed for understanding processes such as migration and cell division. The rich mechanical properties described here provide important physical concepts that will ultimately help in our understanding of the behavior of the cytoskeleton in cells.