How ecosystems recover from pulse perturbations: A theory of short- to long-term responses

Abstract

Quantifying stability properties of ecosystems is an important problem in ecology. A common approach is based on the recovery from pulse perturbations, and posits that the faster an ecosystem return to its pre-perturbation state, the more stable it is. Theoretical studies often collapse the recovery dynamics into a single quantity: the long-term rate of return, called asymptotic resilience. However, empirical studies typically measure the recovery dynamics at much shorter time scales. In this paper we explain why asymptotic resilience is rarely representative of the short-term recovery. First, we show that, in contrast to asymptotic resilience, short-term return rates depend on features of the perturbation, in particular on the way its intensity is distributed over species. We argue that empirically relevant predictions can be obtained by considering the median response over a set of perturbations, for which we provide explicit formulas. Next, we show that the recovery dynamics are controlled through time by different species: abundant species tend to govern the short-term recovery, while rare species often dominate the long-term recovery. This shift from abundant to rare species typically causes short-term return rates to be unrelated to asymptotic resilience. We illustrate that asymptotic resilience can be determined by rare species that have almost no effect on the observable part of the recovery dynamics. Finally, we discuss how these findings can help to better connect empirical observations and theoretical predictions.

1. Introduction

Ecosystem stability, in particular, the way ecosystems respond to perturbations, is a longstanding topic of interest in ecology (May, 1973; Pimm, 1984; Tilman and Downing, 1994). Ecologists have used a variety of procedures to quantify this type of ecosystem stability, differing in the characteristics of perturbations and in the way the system response is measured. A perturbation can consist of a change in an environmental parameter lasting for short or long times. It can correspond to biomass addition or removal, applied once or repeatedly. The ecosystem response can be assessed soon after the perturbation or much later, measuring the overall state of the ecosystem or an ecosystem variable of specific interest. This multitude of procedures has led to an overabundance of stability measures, whose relationships are often unclear (Donohue et al., 2013; Grimm and Wissel, 1997; Ives and Carpenter, 2007).

We focus here on measures based on an ecosystem’s response to pulse perturbations, i.e., perturbations of relatively short duration (Bender et al., 1984). We assume that after a sufficiently long time following a perturbation the ecosystem returns to the pre-perturbed state, which we call equilibrium. We posit that the faster the return the more stable the ecosystem is. Several stability measures can then be defined, differing in the time at which, and the ecosystem variable of which, the return to equilibrium is assessed. Terms used for these measures include return time, recovery rate, and resilience.¹

Quantifying ecosystem stability using the return to equilibrium is a common approach in both empirical and theoretical studies. Indeed, pulse perturbations are an appropriate model for many natural disturbances, such as floods, forest fires and disease outbreaks, and have been widely applied in experimental ecosystems. In the latter, it is typically the short-term return to equilibrium that is studied, due to practical difficulties of collecting long time series (e.g., Steiner et al., 2006; Downing and Leibold, 2010; Hoover et al., 2014; Wright et al., 2015). This stands in sharp contrast with theoretical work, in which the return to equilibrium is mainly studied at long time scales (e.g., Rooney et al., 2006; Loeuille, 2010; Thébault and Fontaine, 2010; Gellner and McCann, 2016). This is due to the fact that the long-term rate of return to equilibrium, known as asymptotic resilience, can directly be computed from the dominant eigenvalue of the community matrix (we revisit this theory in the next section).

The problem that ecological theory and data do not necessarily address the same time scales has been emphasized before (reviewed in Hastings, 2010). In particular, Neubert and Caswell (1997) argued that the initial response of an ecosystem to a pulse perturbation can strongly differ from its long-term response. They described ecosystems that eventually return to equilibrium for any perturbation but initially move away following some perturbations. Our work can be seen as an extension of Neubert and Caswell’s theory. Specifically, while their work dealt with the perturbation that causes the strongest response, we shall study the ecosystem average, or typical, response, and extend the analysis over all time scales.

We begin with a precise definition of return rates and return times covering the range between initial to asymptotic response to a perturbation. We show that short- and long-term return rates differ in their dependence on the perturbation direction, i.e., the way its intensity is distributed over species. This dependence can be strong for short times, but vanishes in the limit of very long times (i.e., asymptotic resilience). To compare short- and long-term return rates on an equal footing, we propose to summarize the distribution of return rates following different perturbations by its median, for which we present a simple and accurate approximation. Using this approach, we find that species abundance can play a predominant role in the recovery dynamics. In particular, rare species (that is, those with low abundance) often have a strong effect on the long-term response, while their effect on the short-term response is typically very weak. We describe the underlying mechanism, and illustrate its generality using a random model of many-species competitive communities.² Our results show that asymptotic resilience and short-term return rates are typically disconnected. While asymptotic resilience provides only a partial view on the recovery dynamics, empirically relevant predictions can be obtained from short-term return rates, such as those introduced and studied in this paper.

2. Defining return rates and return times

The study of the recovery dynamics starts by specifying the state from which the ecosystem is perturbed and to which it returns after the perturbation. Empirically, this reference state is a dynamic equilibrium, characterized by relatively small fluctuations around a fixed average. The pulse perturbation then induces a much larger displacement, such that the ecosystem leaves its reference state, thus initiating the recovery dynamics.

It is practically impossible to study the recovery once the displacement induced by the perturbation has become indistinguishable from the fluctuations of the dynamic equilibrium. This is a common problem in the analysis of empirical time series. Yet, almost all theoretical work focuses on the long-term return, which is, in principle, observable only if equilibrium fluctuations are absent. In other words, theory typically assumes the reference state to be a static equilibrium (May, 1973, 1974), a fixed point of a deterministic dynamical system. We also make this assumption, emphasizing however that our results on the short-term recovery also hold for a fluctuating reference state.

Denoting the vector of dynamical variables (e.g., the biomass of the species in the ecosystem) by N(t) and the equilibrium point by N*, we focus on the dynamics for the displacement vector x(t) = N(t) − N*. A pulse perturbation applied at time t = 0 to the ecosystem previously at equilibrium (i.e., x(t) = 0 for t < 0) is characterized by a vector u and describes the ecosystem’s state immediately after the perturbation (i.e., x(0⁺) = u). For pulse perturbations that are not too strong, a linearization of the dynamics around the equilibrium yields a qualitatively accurate, yet analytically tractable, picture of the recovery dynamics (we come back to this assumption and its limitations in the discussion). These linearized dynamics are governed by the community matrix A, that is, the Jacobian of the non-linear dynamical equations evaluated at N*,

$$\frac{\text{d}\mathit{x}}{\text{d}t}=A\mathit{\text{x}}.$$ (1)

Eq. (1) yields the recovery trajectory x(t) following the pulse perturbation,

$$\mathit{\text{x}}\left(t\right)={\text{e}}^{At}\mathit{\text{u}}\text{for}t>0,$$ (2)

where e^A denotes the matrix exponential of A. We assume the equilibrium to be stable in the sense of the stability criterion, so that the system returns to equilibrium following any sufficiently small displacement, so that lim_t→∞ x(t) = 0.

We are interested in quantifying how stable the system is, based on the idea that a more stable system returns faster to equilibrium. This general idea can be implemented in several ways. Here we introduce one classic measure that will serve as a reference throughout. It is based on the asymptotic return to equilibrium,

$${ℛ}_{\infty }=\underset{t\to \infty }{\text{lim}}-\frac{\text{ln}\Vert \mathit{\text{x}}\left(t\right)\Vert }{t},$$ (3)

where the Euclidean norm $\Vert \mathit{\text{x}}\left(t\right)\Vert =\sqrt{{\Sigma }_i{x}_i^2\left(t\right)}$ measures the phase-space distance to equilibrium. Eq. (3) states that ‖x(t)‖ decays asymptotically as e−^ℛ_∞t. In principle, ℛ_∞ could depend on the perturbation vector u. However, ℛ_∞ is in fact the same for virtually any perturbation u (see Appendix A). This common value, called asymptotic resilience, is equal to −ℜ𝔢(λ_dom (A)), where λ_dom (A) is the eigenvalue of A with the largest real part.³

Return rates

While the asymptotic return yields a stability measure with elegant mathematical properties, only the finite-time recovery is of practical interest. We define two finite-time return rates: the instantaneous return rate at time t,

$${ℛ}_t^{\text{ins}}=-\frac{1}{\Vert \mathit{\text{x}}\left(t\right)\Vert }\frac{\text{d}\Vert \mathit{\text{x}}\left(t\right)\Vert }{\text{d}t}=-\frac{\text{d}}{\text{d}t}\text{ln}\Vert \mathit{\text{x}}\left(t\right)\Vert ,$$ (4)

and the average return rate over the interval [0, t],

$${ℛ}_t^{\text{avg}}=-\frac{\text{ln}\Vert \mathit{\text{x}}\left(t\right)\Vert -\text{ln}\Vert \mathit{\text{x}}\left(0^{+}\right)\Vert }{t}.$$ (5)

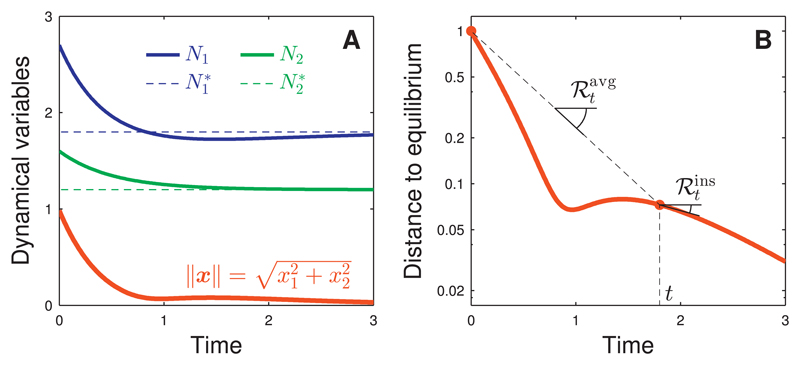
Definitions (4) and (5) are illustrated in Fig. 1, where we apply a pulse perturbation to a two-species community at equilibrium. From the recovery dynamics of variables N₁(t) and N₂(t), we deduce the distance to equilibrium ‖x(t)‖ as a function of time (panel A). To construct the return rates ${ℛ}_t^{\text{ins}}$ and ${ℛ}_t^{\text{avg}},$ we plot this distance on a logarithmic scale (panel B). The instantaneous return rate ${ℛ}_t^{\text{ins}}$ at time t is the slope (with opposite sign) of this curve at time t. The average return rate ${ℛ}_t^{\text{avg}}$ at time t is the slope (with opposite sign) of the segment connecting the distances to equilibrium at times 0 and t. Those rates can substantially differ; they can even have opposite sign. For example, in Fig. 1, at time t ≈ 1.2, we have ${ℛ}_t^{\text{ins}}$ < 0 and ${ℛ}_t^{\text{avg}}$ > 0 meaning that the trajectory moves away from equilibrium at that time, while having come closer to equilibrium since the end of the perturbation.

Fig. 1.

Definition of return rates. The response of an ecological system to a pulse perturbation contains information about the system’s stability, as illustrated here for a system of two interacting species. Panel A: We apply a pulse perturbation after which the species biomass N₁(t) (blue) and N₂(t) (green) return to their equilibrium values $N_1^{*}$ and $N_2^{*}.$ We monitor the recovery dynamics by the distance to equilibrium (red), $\Vert \mathit{x}\left(t\right)\Vert =\sqrt{x_1^2\left(t\right)+x_2^2\left(t\right)}$ with $x_i\left(t\right)=N_i(t)-N_i^{*}.$ Panel B: The relative rate at which the distance to equilibrium diminishes is a commonly used stability measure (note the logarithmic scale on the y-axis). Here we distinguish between the average rate of return ${ℛ}_t^{\text{avg}}$ over the period [0, t], and the instantaneous rate of return ${ℛ}_t^{\text{ins}}$ at time t. These two measures can largely differ, and can even have opposite sign. Parameter values: N*^⊤= (1.8, 1.2), $A=\left(\begin{array}{cc}-1& -4\\ 0& -2\end{array}\right)$ and u^⊤ = (0.9, 0.4) (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

It is instructive to compare the behavior of return rates ${ℛ}_t^{\text{ins}}$ and ${ℛ}_t^{\text{avg}}$ for very small and very large times t. It holds generally that ${ℛ}_0^{\text{ins}}={\text{lim}}_{t\to 0}{ℛ}_t^{\text{avg}}$ and that ${\text{lim}}_{t\to \infty }{ℛ}_t^{\text{avg}}={ℛ}_{\infty }.$ However, the analogous relationship ${\text{lim}}_{t\to \infty }{ℛ}_t^{\text{ins}}={ℛ}_{\infty }$ does not always hold. It does for the example of Fig. 1, but does not for the one of Fig. A.1 (Appendix A). In the latter, return rate ${ℛ}_t^{\text{ins}}$ continues to oscillate between positive and negative values for large time t, so that ${ℛ}_t^{\text{ins}}$ does not tend to a steady value. This is avoided when considering a time-average of ${ℛ}_t^{\text{ins}}$, such as ${ℛ}_t^{\text{avg}}.$ This is one reason why we shall focus on average return rates ${ℛ}_t^{\text{avg}}.$ Finally, it should be noted that while the theory in this paper is based on the distance to equilibrium, it can be extended to other ecosystem variables (see Appendix B).

Return times

While return rates measure the speed at which an ecosystem approaches equilibrium, it might be more interesting to consider the time it takes for an ecosystem to recover from a perturbation, i.e., its return time. Return rates and return times are clearly related. Return time is defined as the amount of time between the perturbation and the instant at which the distance to equilibrium becomes smaller than a prespecified bound. In Appendix C we show that this yields a family of return times parameterized by this bound, and we describe how these return times are related to average return rates ${ℛ}_t^{\text{avg}}.$ This provides another reason why we shall mainly focus on the latter. If the bound is chosen as the typical extent of the fluctuations in the equilibrium state, then the return time corresponds to the time during which the ecosystem response is distinguishable from equilibrium fluctuations.

In theoretical studies the return time is often approximated as the reciprocal of asymptotic resilience. This approach, initiated by Pimm and Lawton (1977, 1978), is not self-evident as it uses the asymptotic regime to describe the entire recovery dynamics. It implicitly assumes that the asymptotic return rate is a good proxy for the return rates at shorter times. As we argue extensively below, this need not be the case. It is in fact more appropriate to quantify the return time as the reciprocal of a finite-time return rate. For this matter the average return rate ${ℛ}_t^{\text{avg}}$ is particularly well suited, as it is based on the same part of the recovery that controls return times.

3. Return rates depend on perturbation direction

As mentioned above, virtually any pulse perturbation leads to the same asymptotic rate of return to equilibrium. Due to this remarkable property, asymptotic resilience has been called an intrinsic stability measure (Arnoldi et al., 2016). In contrast, finite-time return rates do depend on features of the perturbation; they are not fully determined by the system dynamics. Restricting to linear systems, we now investigate this qualitative difference.

A pulse perturbation along a perturbation vector u causes a displacement x(0⁺) = u. By linearity, the perturbation intensity, quantified by the norm ‖u‖, has a trivial effect: when the perturbation is multiplied by a constant factor, the response is multiplied by the same factor, which therefore does not affect return rates. We may thus restrict our attention to normalized vectors ‖u‖ = 1, i.e., perturbation directions. In ecological terms, the direction u defines the way the perturbation intensity is distributed over the constituent species of the ecosystem.

We focus on the average return rates ${ℛ}_t^{\text{avg}}$ but the results are similar for the other stability measures introduced in the previous section. Recall that ${\text{lim}}_{t\to \infty }{ℛ}_t^{\text{avg}}={ℛ}_{\infty },$ and let us denote the initial return rate by ${ℛ}_0={\text{lim}}_{t\to 0}{ℛ}_t^{\text{avg}}.$

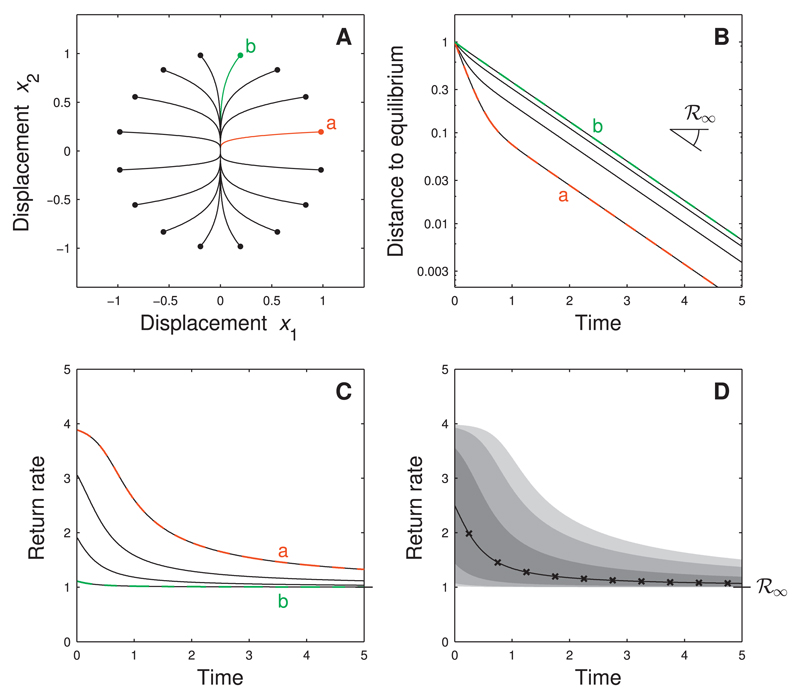
We start with a simple example of two non-interacting species (Fig. 2). The community matrix $A=\left(\begin{array}{cc}-4& 0\\ 0& -1\end{array}\right)$ indicates that the first species responds four times faster to a displacement than the second. The species with the slowest recovery determines asymptotic resilience ℛ_∞ = 1, thus following an arbitrary perturbation the system eventually returns to equilibrium with unit rate (Fig. 2B). This asymptotic rate is, however, not informative about the short-term recovery. In particular, the system absorbs a perturbation that mainly affects the first species (perturbation ‘a’ in Fig. 2) much faster than a perturbation that mainly affects the second species (perturbation ‘b’ in Fig. 2).

Fig. 2.

Return to equilibrium depends on perturbation direction - non-reactive case. Two-species system with community matrix $A=\left(\begin{array}{ll}-4\hfill & \hfill 0\\ 0\hfill & -1\hfill \end{array}\right),$ that is, species 1 responds four times faster than species 2. Panel A: phase-plane trajectories (lines) for several perturbations u = x(0⁺) (dots). For instance, perturbation ‘a’ (red) affects mostly species 1, while perturbation ‘b’ (green) affects mostly species 2. Note that all perturbations have the same intensity ||u|| = 1. Panel B: dynamics of distance to equilibrium ||x(t)|| for the perturbations of panel A. Perturbation ‘a’ in red, perturbation ‘b’ in green and the other perturbations in black (several of them coincide). The return to equilibrium is faster for perturbation ‘a’ than for perturbation ‘b’. For all perturbations the distance to equilibrium eventually decays at a rate given by asymptotic resilience ℛ_∞. Panel C: return rate ${ℛ}_t^{\text{avg}}$ as a function of time for the perturbations of panel A. As expected, the return rates are initially almost four times larger for perturbation ‘a’ than for perturbation ‘b’. Panel D: statistics of return rate ${ℛ}_t^{\text{avg}}$ for random perturbations (fixed intensity, uniformly distributed). Full line: median computed from simulations; × - marks: analytical approximation for median; shades of gray: 5%, 10%, 25%, 75%, 90% and 95% percentiles. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

As a result, at small t, the distribution of possible return rates ${ℛ}_t^{\text{avg}}$ (associated to all possible perturbation directions) is quite broad, but becomes increasingly narrow at longer times t (see Fig. 2D). Asymptotic resilience, which is the lower limit of each of these distributions, is not a good predictor of the short-term return rate for an arbitrary perturbation.

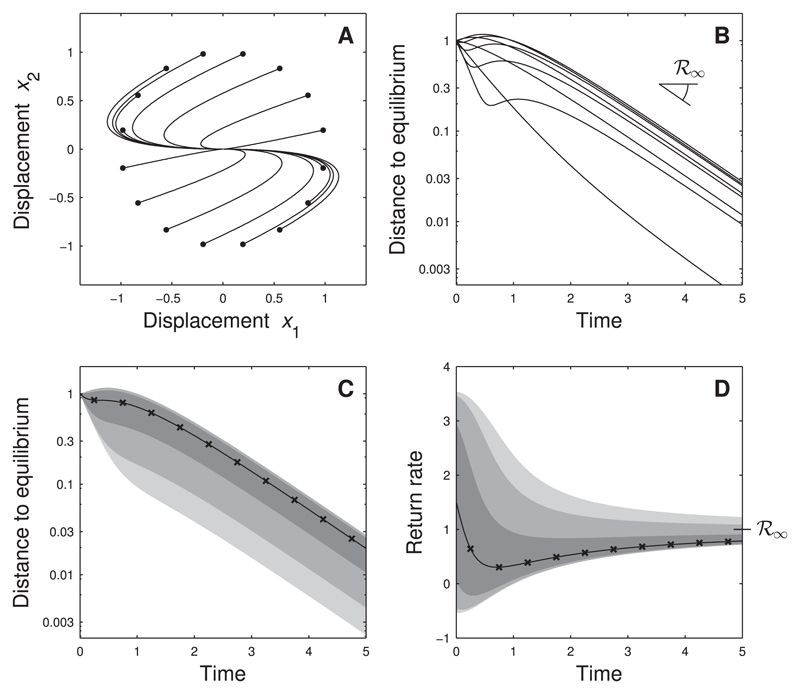
Consider now the asymmetric community matrix $A=\left(\begin{array}{ll}-1\hfill & -4\hfill \\ 0\hfill & -2\hfill \end{array}\right).$ Although all trajectories eventually return to equilibrium at a rate ℛ_∞ = 1, the short-term return to equilibrium has a much richer behavior (Fig. 3B). Many trajectories have short-term return rates either well above asymptotic resilience, or much smaller and even negative return rates (thus moving away from equilibrium). The latter phenomenon occurs because the system is reactive (Neubert and Caswell, 1997), which guarantees that there exist trajectories for which ℛ₀ < 0. However, it does not exclude that other trajectories display positive initial return rates. In fact, for the system in Fig. 3 the distribution of ℛ₀ is mainly concentrated on positive values (Fig. 3D).

Fig. 3.

Return to equilibrium depends on perturbation direction - reactive case. Two-species system with community matrix $A=\left(\begin{array}{ll}-1\hfill & -4\hfill \\ 0\hfill & -2\hfill \end{array}\right).$ Panel A: phase-plane trajectories for several perturbations u. Panel B: dynamics of distance to equilibrium. For some perturbations the system initially moves away from the equilibrium, but for all perturbations the distance to equilibrium eventually decays at a rate equal to asymptotic resilience ℛ_∞. Panels C and D: statistics of distance to equilibrium and of return rate ${ℛ}_t^{\text{avg}}$ for random perturbations (fixed intensity, uniformly distributed). Full line: median computed from simulations; × -marks: analytical approximation for median; shades of gray: 5%, 10%, 25%, 75%, 90% and 95% percentiles.

In general, the distribution of return rates ${ℛ}_t^{\text{avg}}$ over time has a funnel shape: a broad distribution for small times t and an increasingly narrow distribution for larger times. This can be understood from the initial and asymptotic return rates ℛ₀ and ℛ_∞. The distribution of ℛ₀ depends on all the eigenvalues of the symmetric part of the community matrix (Appendix D). Because these eigenvalues can span a large range, the distribution of ℛ₀ is typically wide. In contrast, ℛ_∞ only depends on one eigenvalue of the community matrix. The distribution of return rates ${ℛ}_t^{\text{avg}}$ for 0 < t < ∞ connects these two extremes, yielding the characteristic funnel shape. In Appendix D we show that other stability measures based on return rates exhibit similar patterns.

4. Averaging over perturbation directions

In practice, we can rarely know how a perturbation, whether natural or experimentally induced, will displace the ecosystem state variables. Here we propose a minimalistic way to deal with this uncertainty. We model the perturbation direction as a random variable, so that the return trajectories are also random. Each realization corresponds to a particular perturbation, which initiates a single return trajectory. To obtain a relevant prediction, we average the system response over the perturbation directions. Specifically, we construct a ‘typical’ return trajectory by taking, at each time after the perturbation, an average over the perturbation directions. This typical trajectory is not necessarily the response to a particular perturbation. Rather, it is the composition of the average displacements through time.

In Appendix D we derive simple and accurate formulas for the median system response, given a community matrix A and statistics of the random perturbation u encoded in a covariance matrix C. Component C_ii of this matrix is the variance of initial displacement u_i of species i. Component C_ij is the covariance of u_i and u_j; this covariance accounts for the fact that species i and j may undergo similar initial displacements. These formulas for median distance to equilibrium and return rate are

$$𝕄\left(\Vert \mathit{x}\left(t\right)\Vert \right)\approx \sqrt{\text{Tr}\left({\text{e}}^{At}C{\text{e}}^{A^{\top }t}\right)}$$ (6a)

$$𝕄=\left({ℛ}_t^{\text{avg}}\right)\approx -\frac{\text{ln}\text{Tr}\left({\text{e}}^{At}C{\text{e}}^{A^{\top }t}\right)-\text{ln}\text{Tr}\left(C\right)}{2t},$$ (6b)

where the symbol 𝕄 stands for the median over the ensemble of perturbation directions.

To illustrate their accuracy, we apply equations (6) to a few examples, first revisiting those of Figs. 2 and 3. We assume here that the perturbation directions are uniformly distributed. This assumption corresponds to setting the perturbation covariance matrix C proportional to the identity matrix (C_ii = 1/n and C_ij = 0, with n the number of species in the system; see Appendix E). The agreement between the numerically computed medians (full line) and their analytical approximations ( × -marks) is excellent (see Figs. 2D, 3C and 3D).

In the absence of additional information, the uniform distribution is an appropriate model for the perturbation randomness. As previously explained, in the linear regime, only the perturbation directions affect return rates and there is no reason to prefer one direction over another. However, additional information does exist in the form of the equilibrium biomasses $N_i^{*}.$ When species biomasses substantially differ, the distribution over perturbation directions should be non-uniform.

To make this point clear, let us take a numerical example. Suppose a perturbation acts on a two-species system, in which the first species is ten times more abundant than the second $\left(N_1^{*}=10N_2^{*}\right).$ Compare perturbation ‘a’ that mostly displaces species 1 (e.g., u₁ = 10 u₂) and perturbation ‘b’ that mostly displaces species 2 (e.g., u₁ = 0.1 u₂) as depicted in Fig. 2. Perturbation ‘a’ affects both species equally in relative terms, while perturbation ‘b’ has a very strong effect on the rare species (in relative but also in absolute terms). Clearly, perturbation ‘a’ is more likely than perturbation ‘b’. This implies that the distribution over perturbations directions should assign a larger weight to perturbation ‘a’ than to perturbation ‘b’. This requirement disqualifies the uniform distribution as a suitable perturbation model.

There is no unique perturbation model in the case of an un-even abundance distribution. Here we propose to take the expected displacement u_i of species i proportional to its equilibrium biomass $N_i^{*}.$ That is, all species are perturbed equally in relative terms. In Appendix E we prove that this assumption corresponds to setting the perturbation covariance matrix C to $C_{ii}={\left(N_i^{*}\right)}^2/\Lambda$ and C_i≠j = 0, with $\Lambda ={\Sigma }_i{\left(N_i^{*}\right)}^2.$ If all species have the same equilibrium biomass, we recover the formula for uniformly distributed perturbation directions. We use this biomass-dependent perturbation model in all the examples below.⁴

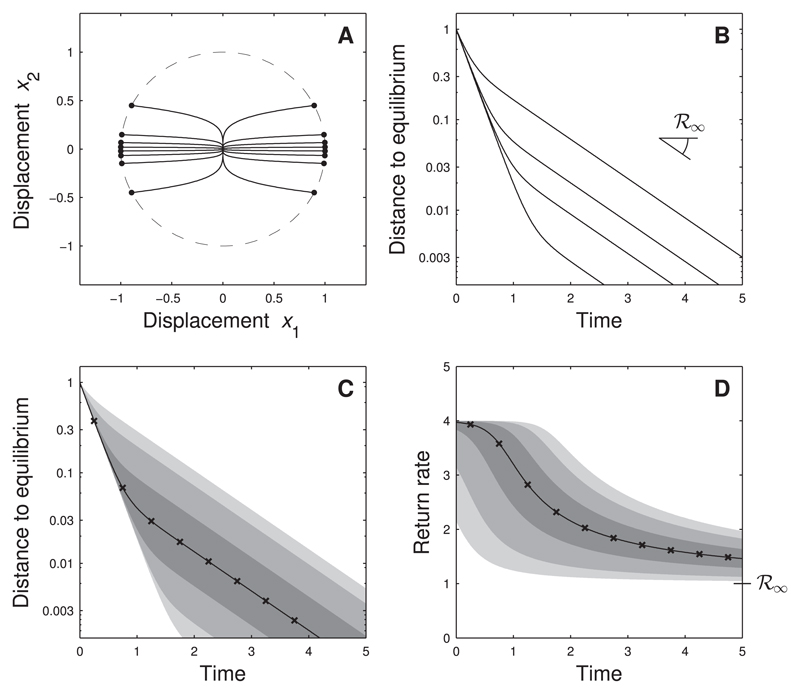
In Fig. 4 we revisit the example of Fig. 2, assuming that species have different equilibrium biomass. The biomass of species 1, which recovers four times faster than species 2, is ten times larger than the biomass of species 2. Due to its larger biomass, species 1 is typically displaced more strongly than species 2. Hence, the perturbations are no longer uniformly distributed (as was the case previously, see Fig. 2A), but are concentrated close to the x₁-axis corresponding to species 1 (see Fig. 4A). This implies that the fast recovery of species 1 has a much larger contribution to the average system recovery than in the previous scenario. For example, the median distance to equilibrium drops to about 5% of the initial displacement at the fast return rate of species 1 (Fig. 4C, for times t < 1). The slow return rate of species 2, equal to asymptotic resilience, governs the ecosystem response only later.

Fig. 4.

Return to equilibrium for biomass-dependent perturbations. Same system as Fig. 2, but here we take into account that perturbations affect abundant and rare species differently. Specifically, we assume that the equilibrium biomass of species 1 (the species with the fastest response) is ten times larger than the equilibrium biomass of species 2. Panel A: phase-plane trajectories for several perturbations u. Perturbations are no longer spread out on the unit circle (dashed line), but tend to be directed along the x₁ -axis corresponding to species 1 (dots). Panel B: dynamics of distance to equilibrium. For most perturbations the distance to equilibrium becomes small (below 10% of the pulse perturbation) at a rate equal to the return rate of species 1 (rather than the return rate of species 2, which is equal to asymptotic resilience). Panels C and D: statistics of distance to equilibrium and of return rate ${ℛ}_t^{\text{avg}},$ taking into account that perturbations tend to displace species 1 more strongly than species 2. As a result, perturbations like the one labeled ‘a’ in Fig. 2 contribute more strongly to the statistics than perturbations like the one labeled ‘b’ in Fig. 2.

5. Effect of rare species on recovery dynamics

As illustrated in Fig. 4, rare species can dominate the ecosystem response in the long term. This happens because rare species have the potential to introduce slow return rates in the system dynamics, and hence to determine asymptotic resilience. Here we explain why we expect this phenomenon to be common in real-world communities.

We emphasize that there is no mathematically inevitable link between species rarity and long-term return rates. This can easily be shown by considering a system of non-interacting species, whose biomasses N_i obey logistic growth with intrinsic growth rate r_i and carrying capacity K_i:

$$\frac{\text{d}{N}_i}{\text{d}t}=r_i{N}_i\left(1-\frac{N_i}{K_i}\right),$$ (7)

In the absence of interactions, each eigenvalue λ_i of the linearized community dynamics can be attributed to a different species as λ_i = −r_i. Hence different parameters determine equilibrium biomass (K_i) and eigenvalue (−r_i). By choosing parameters appropriately, any species can provide the dominant eigenvalue, irrespective of its abundance.

Thus, the claim that rare species govern the long-term recovery cannot hold in full generality. However, it can be expected as a common trend. To show this, we focus our attention on a particular type of rare species, namely those that play a minor role in the community. We call these species satellite, in opposition to core species, which constitute the bulk of the community biomass. This terminology is borrowed from Hanski (1982), who introduced it to describe the regional distribution of species, whereas we apply it to the local level. Removing satellite species does not impinge on community functioning. Satellite species do not affect core species, or only weakly, but can be strongly affected by them. In particular, competition with core species prevents them from reaching higher abundances. Natural communities almost always contain numerous rare species, and while some of them might be an essential part of the community, a large majority can be expected to be satellite.

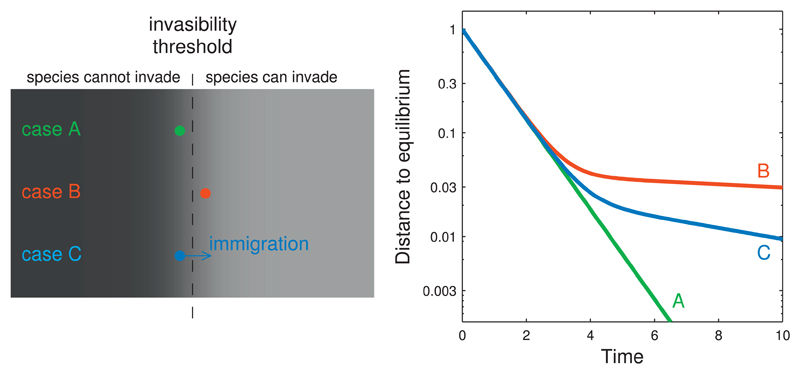
Despite their minor role in the community, satellite species can be predominant in the long-term return dynamics. To understand why this is the case, consider the following thought experiment, illustrated in Fig. 5. Suppose that all core species are aggregated into a single biomass variable coupled to a single satellite species (see Appendix F for details). If the satellite species is absent or cannot persist, the return rate is constant and determined by the core species (Fig. 5, green line, case A). If the satellite species can persist, however, it modifies the recovery dynamics (Fig. 5, red line, case B). The short-term recovery is not affected, but once the distance to equilibrium has decayed to a small fraction ( ≈5%) of the initial displacement, the return to equilibrium becomes much slower, corresponding to the asymptotic resilience of the coupled core-satellite system. In natural communities species are often maintained by immigration, especially rare ones. Thus, suppose that the satellite species is now maintained in the community by immigration (i.e., a sink population). As before, the presence of the satellite species does not affect the short-term recovery, but it drastically slows down the long-term recovery (Fig. 5, blue line, case C). Again, the part governed by asymptotic resilience sets in only very close to equilibrium, and is therefore of limited practical interest.

Fig. 5.

Effect of rare species on the long-term return to equilibrium. We study a simplified core-satellite competitive system, describing the introduction of a satellite species into an established community. Case A: if the introduced species has invasion fitness just below the invasibility threshold, it cannot persist and the dynamics are those of the core species alone (green line in right-hand panel). Case B: if the introduced species has invasion fitness just above the invasibility threshold, it persists at a small equilibrium biomass. Compared to the community without the satellite species, the short-term return to equilibrium does not change, but the long-term return to equilibrium becomes much slower (red line in right-hand panel). Case C: we assume weak immigration, maintaining the introduced species at a small equilibrium biomass (source-sink dynamics). As in case B, the long-term return to equilibrium is much slower (blue line in right-hand panel). Model details and parameter values are given in Appendix F. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

This thought experiment can be formalized in terms of the eigenvalues of the linearized dynamics, before and after introducing the satellite species. Because the satellite species has a negligible effect on the core community, the dynamics of the latter are essentially unaffected, and the eigenvalues of the core community alone are still eigenvalues of the coupled system. The latter has one additional eigenvalue, associated with the dynamics of the satellite species. This eigenvalue can introduce a slow return rate (i.e., have small negative real part), especially if the satellite species is close to the invasibility threshold (see Fig. 5 and Appendix F), and thus yield the dominant eigenvalue of the whole system. In this case, asymptotic resilience is determined by a single rare species and contains limited information about community stability.

Each satellite species can provide the dominant eigenvalue, and we expect that real-world communities contain many such species. Hence, the influence of rare species on the long-term recovery dynamics should be widespread. We provide support for this claim using a random model of many-species competitive communities. We impose that the equilibrium community has a realistic (log-normal) abundance distribution, with numerous rare species. The dynamics of species biomasses N_i are governed by Lotka–Volterra equations,

$$\frac{\text{d}{N}_i}{\text{d}t}=N_i\left(a_i-{\displaystyle \sum _{j=1}^n{b}_{ij}{N}_j}\right)\text{for}i=1,\dots ,n.$$ (8)

Parameter values of the n = 10 species are chosen as follows. First, we randomly generate the species biomasses $N_i^{*}$ using a broken-stick model (MacArthur, 1957; Sugihara, 1980). We divide the total biomass ${\Sigma }_i{N}_i^{*}=1$ over the species by first allocating a random fraction (uniformly in the interval [0, 1]) of the total biomass to the first species, then by allocating a random fraction (uniformly in the interval [0, 1]) of the remaining biomass to the second species, and so on. Second, we randomly draw the competition coefficients b_ij: the intraspecific competition coefficients b_ii from the uniform distribution on the interval [0.5, 1], and the interspecific competition coefficients b_ij with i ≠ j from the uniform distribution on the interval [0, 0.5]. Third, we determine the intrinsic growth rates a_i such that the species biomasses $N_i^{*}$ correspond to an equilibrium, that is, $a_i={\Sigma }_j{b}_{ij}{N}_j^{*}.$ We check whether this equilibrium is stable, and discard the model realization if this is not case⁵.

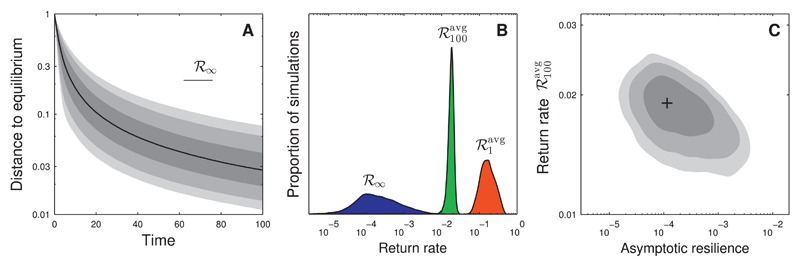
The distribution of the recovery trajectories are shown in Fig. 6A. At time t = 100 most trajectories have decayed to a small fraction ( ≈ 5%) of the initial displacement. This level of displacement is typically no longer observable in noisy time series. However, the return rate continues to decrease, from ${ℛ}_{100}^{\text{avg}}$ with median 0.02 to ℛ_∞ with median 0.0002 (Fig. 6B; note that the median ℛ_∞ corresponds to a horizontal line in Fig. 6A). By inspecting individual model realizations, we see that the disparity between ${ℛ}_{100}^{\text{avg}}$ and ℛ_∞ is often associated with a rare species. In particular, when removing this species, the recovery dynamics up to time t = 100 do not change, while asymptotic resilience does (Fig. F.1). This is consistent with case B of Fig. 5. Hence, asymptotic resilience is determined by the specificities of rare species, which have almost no effect on the observable part of the recovery dynamics. This is further illustrated in Fig. 6C, where we show that, surprisingly, return rates ${ℛ}_{100}^{\text{avg}}$ and ℛ_∞ have a weakly negative correlation. Although this negative correlation is due to the particular model parameterization (and is not generally valid), it clearly illustrates that asymptotic resilience is an unreliable predictor for empirically relevant return rates.

Fig. 6.

Return to equilibrium in a random community model. We analyze a Lotka–Volterra model with random competitive interactions. The equilibrium species biomass distribution is generated by the broken-stick model (see main text). Panel A: statistics of distance to equilibrium for random model realizations (averaged over perturbation direction). Black line: median; shades of gray indicate 5%, 10%, 25%, 75%, 90% and 95% percentiles. Median asymptotic resilience ℛ_∞ corresponds to a virtually horizontal line (represented in the top-right part of the panel). Panel B: probability distribution of return rates ${ℛ}_1^{\text{avg}},$ ${ℛ}_{\mathrm{100}}^{\text{avg}}$ and ℛ_∞ Asymptotic resilience ℛ_∞ is orders of magnitude smaller than the finite-time return rates. Panel C: joint probability distribution of return rates ${ℛ}_{\mathrm{100}}^{\text{avg}}$ and ℛ_∞. Black cross: maximum; shades of gray indicate regions of 50%, 80% and 90% probability (corresponding to contour lines of the probability distribution). Asymptotic resilience ℛ_∞ is unreliable as a proxy for return rate ${ℛ}_{\mathrm{100}}^{\text{avg}}.$ For this random community model there is even a (weakly) negative correlation between ${ℛ}_{\mathrm{100}}^{\text{avg}},$ and ℛ_∞. The probability distributions in panels B and C were reconstructed using kernel density estimation on 10⁴ simulations.

6. Discussion

The theory of ecosystems’ response to pulse perturbations developed in this article reveals a fundamental and generic interplay between time-scales and species abundances. While short-term recovery is typically governed by the more abundant species, the return dynamics for longer times tend to be determined by rare species. This shift from abundant to rare species follows from two observations. First, a pulse perturbation is expected to initially generate the largest biomass changes in the abundant species, simply because they have larger biomass to begin with. Second, after sufficiently long time, the recovery process becomes independent of the perturbation; it is then determined by the least stable species (in the sense of being closest to the invasibility threshold, see Fig. 5), which is often rare. The fact that distinct sets of species determine the short-term and long-term return rates implies that these two types of return rate are often unrelated, and that the asymptotic response can be determined by the specificities of rare species, which have almost no effect on the observable part of the recovery dynamics.

As a corollary, the asymptotic rate of return to equilibrium, or asymptotic resilience, should not be used as a proxy for the short-term recovery. Nevertheless, theoretical work on the return to equilibrium has focused almost exclusively on asymptotic resilience. For example, return time is often defined as the reciprocal of asymptotic resilience (a practice that dates back to Pimm and Lawton, 1977, 1978). But this theoretical construct need not be related to the actual return time, that is, the time it takes for the system to recover from a perturbation, which is mainly determined by the short-term response. Many ecologists seem to have built an intuition about the return to equilibrium based on very simple systems, such as single species, for which the return rate is constant over time. However, as illustrated by the examples in this paper, only slightly more complex systems exhibit much richer return dynamics, during which the return rate can change dramatically. We showed that in large, complex communities, due to the presence of species with very different abundances, asymptotic resilience need not even be a good predictor of return rates at longer times. Similarly, because asymptotic resilience does not depend on the perturbation direction, many ecologists seem to assume that the same holds for the entire recovery process. This intuition is erroneous because, as we have shown, the short-term return rates can, and often do, strongly depend on the perturbation direction.

Previous work has stressed that the asymptotic regime is often not representative of the short-time dynamics (Hastings, 2004, 2010). This issue has been particularly well studied in population ecology. It is generally recognized that depending on initial conditions the population dynamics can be governed by transient effects, which are missed out when analyzing the asymptotic regime alone (Caswell, 2001; Ezard et al., 2010). Practical tools are available to systematically investigate the transient dynamics of population models, and to incorporate these transient effects into predictions of future population dynamics (Caswell, 2007; Stott et al., 2011). Clearly, there are close parallels with the findings reported in this paper. It would be worthwhile to scrutinize whether theoretical insights and practical tools developed by population ecologists can enrich the study of ecosystem stability.

Because our work emphasizes the importance of the short-term recovery, it is closely related to the work of Neubert and Caswell (1997). They studied the instantaneous return rate immediately after a pulse perturbation, and showed that it can be negative even if the system is stable. They coined the term ‘reactive’ to denote systems for which this phenomenon occurs, and argued that many real-world systems can be expected to be reactive. However, we have shown that the initial return rate displays a particularly strong dependence on the perturbation direction. Therefore, the existence of a perturbation with a negative initial return rate does not imply that the initial return rate is negative for all or even most perturbations. For instance, in Fig. 3, the vast majority of perturbations are met with positive initial return rates, despite the system being reactive⁶. This suggests that the system property of being reactive does not provide much information about the initial return rate for an actual perturbation. The theory of reactive systems deals with the initial return rate for the worst-case perturbation, but does not tell us how the system typically responds to a perturbation. By studying this typical response, our paper can be interpreted as an extension of Neubert and Caswell’s theory.

This paper strives to develop theory for empirically relevant stability measures. The long-term return to equilibrum is of limited practical interest, because it corresponds to small displacements, which are often indistinguishable from inevitable fluctuations at the equilibrium state. Also, especially in field studies, the asymptotic response to a first perturbation might be concealed by the occurrence of a second one. Therefore, available empirical data are often restricted to the short-term recovery, which is explicitly addressed by our theory. Short-term responses depend on the perturbation direction, and we argued that the most relevant predictions are obtained by averaging over the perturbation distribution. We derived accurate formulas for the median return rate as a function of the time elapsed since the perturbation. These formulas can be evaluated as easily as asymptotic resilience, to which the median return rate converges in the limit of very long times. Thus, our work provides a theoretical framework to study the transient recovery following perturbations and to predict return times to equilibrium in community and ecosystem models.

This theoretical framework depends on a number of technical assumptions. First, we assumed that the reference state, i.e., the state in which the ecosystem settles at the end of the recovery process, is an equilibrium point. Alternatively, and more realistically, we could consider a fluctuating reference state. If the fluctuations are small compared with the displacement induced by the pulse perturbation, then they do not affect the analysis of the short-term recovery. More generally, we assumed that the recovery trajectories remain close to equilibrium. This allowed us to rely on the theory of linear dynamical systems, which are widely used by both theorists and empiricists to describe and interpret ecological dynamics (Caswell, 2001; Gurney and Nisbet, 1998). For sufficiently weak perturbations, the non-linear part of ecosystem dynamics is often an additional source of discrepancy between short-term and long-term responses. Indeed, non-linearities can have a strong effect on the short-term response, but leave the long-term response essentially unchanged, because the latter corresponds to small displacements for which the linear approximation is accurate. When allowing for stronger perturbations, the ecosystem might be pushed to a different state (e.g., to another equilibrium), and the notion of ecosystem recovery itself becomes meaningless (for concrete proposals of how to deal with this case, see Menck et al., 2013 and Lundström, 2017). Finally, it should be noted that ecosystem stability has also been analyzed in the absence of perturbations. For example, many studies have quantified stability based on the amplitude of endogenous oscillations (such as predator-prey cycles; e.g., Brose et al., 2006; McCann et al., 1998 and McCann, 2011), for which our work does not seem directly relevant.

The integration of theoretical and empirical approaches has been identified as one of the main challenges for research on ecological stability (Ives and Carpenter, 2007) and Donohue et al., 2016. This article attempts to make the theory of how ecosystems recover from pulse perturbations more practically relevant by emphasizing short-term responses. Future work could address how to translate our findings into concrete recommendations. While restricted to pulse perturbations, our paper might inspire analogous studies for other stability measures, such as the response to press perturbations and the temporal variability of ecosystems (see Arnoldi et al., 2016 and Haegeman et al., 2016 for first steps in this direction).