Abstract
Despite the many successes of genome-wide association studies (GWAS), the known susceptibility variants identified by GWAS have modest effect sizes, leading to notable skepticism about the effectiveness of building a risk prediction model from large-scale genetic data. However, in contrast to genetic variants, the family history of diseases has been largely accepted as an important risk factor in clinical diagnosis and risk prediction. Nevertheless, the complicated structures of the family history of diseases have limited their application in clinical practice. Here, we developed a new method that enables incorporation of the general family history of diseases with a liability threshold model, and propose a new analysis strategy for risk prediction with penalized regression analysis that incorporates both large numbers of genetic variants and clinical risk factors. Application of our model to type 2 diabetes in the Korean population (1846 cases and 1846 controls) demonstrated that single-nucleotide polymorphisms accounted for 32.5% of the variation explained by the predicted risk scores in the test data set, and incorporation of family history led to an additional 6.3% improvement in prediction. Our results illustrate that family medical history provides valuable information on the variation of complex diseases and improves prediction performance.
Keywords: family history, Genetic variability in complex binary traits, Liability threshold model, penalized prediction model, risk prediction in complex disease
DESPITE the existence of promising examples of genome-wide association studies (GWAS) findings that will or may soon be translated into clinical utility (Manolio 2013), many studies have shown that genetic screening to predict the risk of complex diseases currently has little value in clinical practice (Lyssenko and Laakso 2013) and only shows modest predictive power even if all relevant loci (including rare variants) were discovered (Clayton 2009). For example, heritability estimates of type 2 diabetes (T2D) from twin and familial studies range from 40 to 80% (Committee on Diabetic Twins, Japan Diabetes Society 1988; Kaprio et al. 1992), whereas the estimated heritability proportions explained by known susceptibility variants of T2D range from only 10 to 28%, indicating that most of the heritability remains unexplained (McCarthy 2010; So et al. 2011a,b). In addition to this so-called “missing-heritability” issue, GWAS-based common variants tend to only mildly predispose a carrier to a common disease (Wei et al. 2009), which generates some doubt about the overall value of the application of GWAS findings for risk assessment in clinical care (Manolio 2010).
The most popular approaches for disease risk prediction involve logistic regression analysis with genotype scores. With a training set, the regression coefficients of some significantly associated single-nucleotide polymorphisms (SNPs) (Miyake et al. 2009) are calculated, and the sums of the weighted genotype scores with their regression coefficients are incorporated as a single covariate to the logistic regression for the test set (Evans et al. 2009). However, the accuracy of these disease risk prediction models is generally much lower than what heritability estimates can provide.
To better convert heritability into prediction, several approaches have been proposed to include a large number of SNPs into the prediction model, including the use of penalized regression methods (Wu et al. 2009; Won et al. 2015) and random-effects models (Speed and Balding 2014). However, these attempts still have several limitations. The computational complexity linearly or quadratically increases with the number of SNPs depending on the algorithms, especially for the penalization approaches (Won et al. 2015). To reduce computational cost, it might be helpful to adopt a SNP-filtering strategy (filtering out less informative SNPs before building models). However, the performance of a prediction model based on this strategy largely depends on SNP-filtering methods.
An alternative is to incorporate family history. Family history reflects genetic susceptibility in addition to interactions between genetic, environmental, cultural, and behavioral factors (Macinnis et al. 2011; Do et al. 2012). Therefore, it has been repeatedly suggested that incorporation of family medical history into a risk prediction model might implicitly cover the effects of uncovered genetic risk factors and shared gene–environment interactions (Hariri et al. 2006; Cheng et al. 2015). Accordingly, family history is often expected to be an important risk factor in clinical assessment (Hariri et al. 2006). Moreover, a recent theoretical work shows that including family history decreases the effective population size in prediction designs, thus resulting in higher prediction accuracy (Lee et al. 2017). However, in spite of the known importance of family history, it is generally measured by an indicator variable (showing the existence of known affected relatives) and this simple indicator has been incorporated into the prediction models. There is usually a great amount of heterogeneity among subjects with respect to familial relationships of relatives with known disease status, which has thus far limited the utility of this simplified binary variable for disease prediction.
In this article, we propose a new disease risk prediction model based on penalized regression with the following features: (i) a certain number of SNPs selected according to the absolute value of the best linear unbiased prediction (BLUP), (ii) penalized logistic regression analyses were performed using a number of SNPs leaving important predictive clinical variables unpenalized, and (iii) a new method is applied to incorporate the general family history of diseases. Application of our model to T2D patients in a Korean population showed that incorporation of family history could improve the amount of variation explained in the model. The model and approach proposed highlight the importance of family history of diseases for disease prediction, and is expected to become a useful tool to explain the variation of complex diseases.
Methods
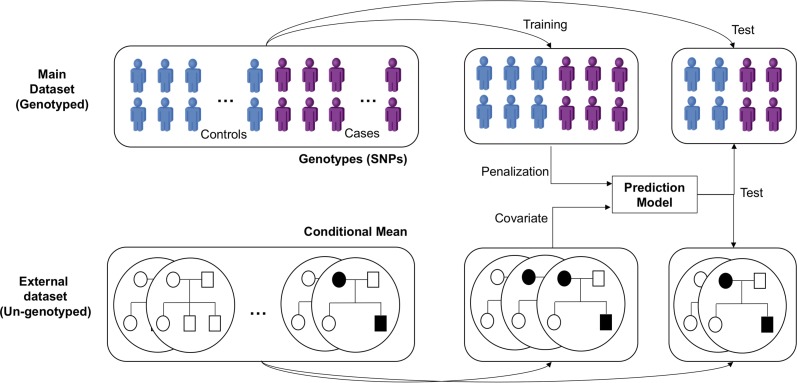
In this section, we first introduce the process by which we evaluated a subject’s conditional mean (CM) of disease risk using his/her family history and prescreened SNPs based on the BLUP (Figure 1). With these variables, we then present how sparse modeling can be applied to build a risk prediction model for complex disease. Finally, we introduce two SNP chip data sets used in this study and propose a method of estimating the variance for each variable in the prediction model.
Figure 1.
A schematic overview of the analysis. Individuals in the main data set include genotyped SNPs, while the external data set of those individuals includes relative’s relationship and disease status. A 10-fold cross-validation scheme was applied to build and test the performance of the prediction models
Evaluating the CM of disease risk using family history
Suppose there are n subjects whose genotypes are known and each subject has relatives whose genotypes are unknown, while disease status and relationship with subject are available. We began our model by evaluating the CM of disease risk using the standard liability threshold model (Falconer 1967). We assume that disease status is determined by the unobserved liabilities (denoted as ), and if they are larger than a threshold T, which is determined by the disease prevalence, a subject will become affected. We further assume that these liabilities are normally distributed. Here, , and , respectively, represent phenotypes, liabilities, and environment vectors of subject i and his/her family. For a given subject, we only use phenotypic information from their relatives, and we use subscript to indicate relative of subject We further denote by and the inbreeding coefficient for relative of subject and the kinship coefficient between two relatives and of subject respectively. It should be noted that is 0 if subjects and are in different families. We then define the kinship coefficient matrix as where is for and is otherwise. We denote a dimensional identity matrix by and dimensional column vector of which all elements are 0 by With these notations, we assume that
| (1) |
| (2) |
where indicates the coefficient vector of fixed effects, and and indicate the variances of the random polygenic effect and random residual effect, respectively.
As a way to include family history, we introduced a variable, CM, which is defined as an individual’s expected liability given case-control status of their relatives (Kim et al. 2017); CM reflects the likelihood of an individual to develop the disease (here, T2D) using only the knowledge of whether their relatives had the disease. Then, when comparing different regression methods, we included CM as we do other clinical covariates. To evaluate CM for each individual, it is necessary to integrate over all possible liabilities for the remaining individuals. Given an individual’s case/control status, their liability takes a truncated normal distribution, so CM represent an expectation of a multivariate truncated normal distribution, which can be evaluated in R by using the pmvnorm() function in the mvtnorm package (see Supplemental Material, Supplementary Note in File S1 for detailed methods). We implemented our method of evaluating familial risk in R and the source code and R package are available on Github (https://github.com/JungsooGim/familyRisk).
SNP prescreening
To select an effective list of SNPs to test the model, we considered the BLUP of SNP effects using GCTA (Yang et al. 2011), which is a mixed linear model with the random effects of SNPs; i.e., with and thus leading to the mixed model Here, is a genotype matrix in training sets. The variance components and are solved using restricted maximum likelihood, which also provides an estimate of each individual genetic random effect, From this, the BLUP of SNP effects can be obtained via and it can be simply obtained with GCTA (Yang et al. 2011). We ranked SNPs based on the absolute value of these estimated SNP effects. We also selected a list of SNPs based on the P-value from the univariate logistic regression for each SNP with age, sex, body mass index (BMI), systolic blood pressure (SBP), and diastolic blood pressure (DBP) adjusted.
Penalized regression method
Let and be a covariate vector and a dichotomous phenotype for subject and affected and unaffected subjects are coded as 1 and 0, respectively. We further denote and as coded genotypes of the th SNP and the th clinical covariate, respectively. The -dimensional coefficient vector consists of genetic variants and clinical variables. Under this model, can be estimated by minimizing the penalized negative log-likelihood:
| (3) |
where is a penalty function and is a vector of a tuning parameter that can be determined by a search on an appropriate grid. Note that only genetic variants are penalized in Equation 3.
For model analysis, Lasso (Tibshirani 1996), Ridge (Hoerl 1970), Elastic-Net (EN) (Zou and Hastie 2005), smoothly clipped absolute deviation (SCAD) (Fan and Li 2001), and Truncated Ridge (TR) (Chatterjee and Lahiri 2011) can be performed depending on the choice of penalty function. Lasso, Ridge, and EN were analyzed under the default settings of glmnet (Friedman et al. 2010). For SCAD, whose penalty is defined as we used for our own optimization algorithm. For TR estimates, we first obtained ridge estimates with tuning parameter and then truncated them with a level so that the coefficients with absolute values smaller than are set to zero. For the appropriate choice of a truncating level, 20 grid points (similar to EN) equally spaced in logarithmic scale from minimum to maximum ridge estimates were considered for All analyses were performed using R.
Building a disease risk model using the penalized regression method
In this section, we describe the brief steps for developing a disease risk model with the estimated CM score.
Covariates: age, sex, BMI, SBP, and DBP are considered as clinical covariates, and are included for all regressions.
Summarizing family history: calculate CM for all subjects with a familial history of disease.
Data preparation for cross-validation: conduct 10-fold cross-validation; that is, the data set is divided into 10 different subdata sets, one of which is used as a test set and the other nine are used as training sets.
SNP screening for the prediction model: using the training set in each cross-validation replicate, SNPs are prescreened with the different criteria (P-value and BLUP) as described in SNP prescreening in the previous section of Methods; for P-value criteria, SNPs with the top-k smallest P-values are selected, and for BLUP criteria, SNPs with the top-k largest absolute BLUP values are selected; here, we considered k = 100, 500, 1000, 5000, 10,000, and 20,000.
Model building: perform Lasso (Tibshirani 1996), Ridge (Hoerl 1970), EN (Zou and Hastie 2005), SCAD (Fan and Li 2001), and TR (Chatterjee and Lahiri 2011) for penalized regression; tuning parameters for each penalized regression are selected with an additional 10-fold cross-validation using the training set; the training set is divided into 10 different subdata sets, and for different choices of tuning parameters, the prediction model is obtained with the other nine subdata sets; the area under the curve (AUC) is then calculated with the remaining subdata set, and tuning parameters that result in the largest AUC are finally chosen.
Model validation: the prediction models for penalized regressions are applied to the test set, and the AUCs are calculated.
Performing cross-validation: repeat steps 4–6 for the different combinations of training and test sets.
Please note that ∼285k genotyped SNPs were used in this work by assuming less chance of linkage disequilibrium (LD) among prescreened SNPs in step 4. The assumption is likely to be falsified with a larger number of SNPs. In this case, an additional step of filtering SNPs within LD might be necessary.
Estimating variation in penalized logistic regression
To estimate the variation of each variable in the penalized regression model, we used the deviance calculated by comparing the predicted and true phenotypes in the test set. Specifically, we built the prediction model with a training set and the model was applied to predict the phenotypes of test samples. Then, the deviance was obtained by comparing the predicted phenotypes and the true phenotypes for those samples. If we denote the predicted and the true phenotypes by and respectively, the deviance is defined as
| (4) |
We used 10-fold cross-validation and the deviances for all subjects were evaluated by summing all deviances in the test set. Based on Equation 4, we defined the variation explained by the current model () using McFadden’s R2 (McFadden 1974)
| , |
where is the deviance of the null model. Then, the variation unexplained by the full model can be obtained by 1 − McFadden’s. If we denote the reduced model whose th element is excluded by and further defined the relative deviance explained by the th variables as
| (5) |
Equation 5 represents the relative deviance explained by the th variables among total variation.
Data description
To demonstrate the validity of our proposed model and to illustrate its application to disease risk prediction, we investigated T2D from two real data sets: KARE (Korea Association REsource) and SNUH (Seoul National University Hospital). Among the disease traits in KARE, T2D has the most well-investigated familial information, and additional T2D cases and their well-organized familial histories were available from SNUH. We merged the two data sets by adjusting for a platform difference (matching SNPs existing in both platforms and imputing missing genotypes using Shapeit). Overall, we analyzed the data of 3692 subjects (1846 cases and 1846 controls) with a total of 267,063 SNPs.
As a part of the Korean National Institute of Health (NIH)’s project, the KARE cohort was recruited to construct an indicator of diseases with a genetic component in an attempt to predict disease outbreaks. Genotype information for 8842 participants was received from the Korea Center for Disease Control and Prevention. For these participants, 440,794 SNPs were genotyped with the Affymetrix Genome-Wide Human SNP array 5.0 and 267,064 SNPs remained in our analyses after the following quality controls: (1) P-values for Hardy–Weinberg equilibrium of < 10−5, (2) genotype call rates < 95%, and (3) minor allele frequencies < 0.05. We also eliminated subjects with gender inconsistencies, whose identity in state was > 0.8, or whose call rates were < 95%. Participants were asked whether they have affected relatives and, if so, their ages and familial relatedness. The family histories of diseases, including T2D, are also available for the KARE data. Finally, we randomly selected controls to achieve the same number of cases and controls, and thus used 1846 T2D cases (1167 from KARE and 679 from SNUH) and 1846 randomly selected controls.
For SNUH data, T2D patients were diagnosed as T2D using the World Health Organization criteria for Seoul National University Hospital, and 681 subjects with a positive family history of diabetes in first-degree relatives were preferentially included. The family history of their relatives was based on the recall of the proband. However, family members were encouraged to perform a 75 g oral glucose tolerance test, and subjects that were positive for a glutamic acid decarboxylase autoantibodies test were excluded. In total, the disease statuses of 7825 relatives of 681 subjects were available, and 2875 of these relatives of the subjects had T2D. T2D patients originally diagnosed from Seoul National University Hospital were genotyped with the Affymetrix Genome-Side Human SNP array 5.0, and 480,589 SNPs were obtained. The same conditions for quality control with KARE were applied, and two subjects and 213,526 SNPs were excluded. In total, 679 T2D patients with 267,063 SNPs were used for the analysis.
Since these two data sets might be genetically distinct, the prediction is unduly driven by inclusion of the SNUH cases who (unlike the KARE individuals) do not have matched controls. Thus, we checked whether this was the case by drawing the multidimensional scaling plot and the minor allele frequency scatter plot and found no difference between these two data sets (Figure S1 and Figure S2 in File S1). We downloaded the data sets from www.nih.go.kr/NIH followed by an approval process from the Korean NIH (contact to biobank@korea.kr for further information).
Data availability
The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. All analysis scripts and the dataset used in the article are available upon request. R script and Shell script for the analyses performed in the article are also available at http://healthstat.snu.ac.kr/software/revealing_MH). Genotype datasets for KARE project can be downloaded from www.nih.go.kr/NIH followed by an approval process from Korean NIH. For more information about the approval process, please contact biobank@korea.kr.
Results
Characteristics of the variables
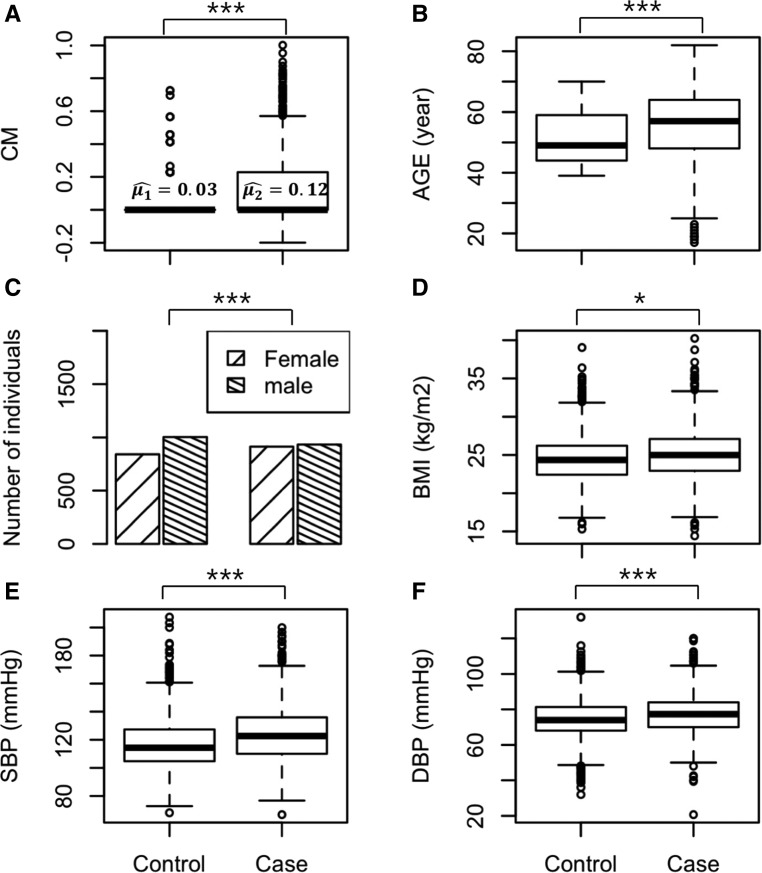
The methodology described earlier for estimating the CM for all subjects using their relatives in a pedigree was applied to the real data sets. Figure 2 shows the characteristics of six covariates included in the prediction model. As shown in Figure 2A, the mean values of CM are not much different between T2D cases and controls. However, more subjects with T2D had a significantly higher CM value compared to control subjects (mean values for cases and controls are 0.12 and 0.03, respectively, with P < E−10 from a two-sample t-test). Note that the individual with no family history has CM = 0. Similarly, all other clinical covariates are also significantly different between cases and controls (P < 0.05). The boxplots of other clinical covariates between cases and controls are shown in Figure 2, B–F. We also investigated the characteristics of both sets of SNPs selected according to the P-value and BLUP criteria, and found a similar pattern (Figure S3 in File S1).
Figure 2.
Clinical variables between cases and controls. Conditional mean (CM) (A), age (B), sex (C), body mass index (BMI) (D), systolic blood pressure (SBP) (E), and diastolic blood pressure (DBP) (F) are shown in boxplots. Two-sample t-test was performed to obtain P-values (* < 0.05; *** < 0.001). For sex, a χ2 test was conducted.
Comparison of the performance of the tested models
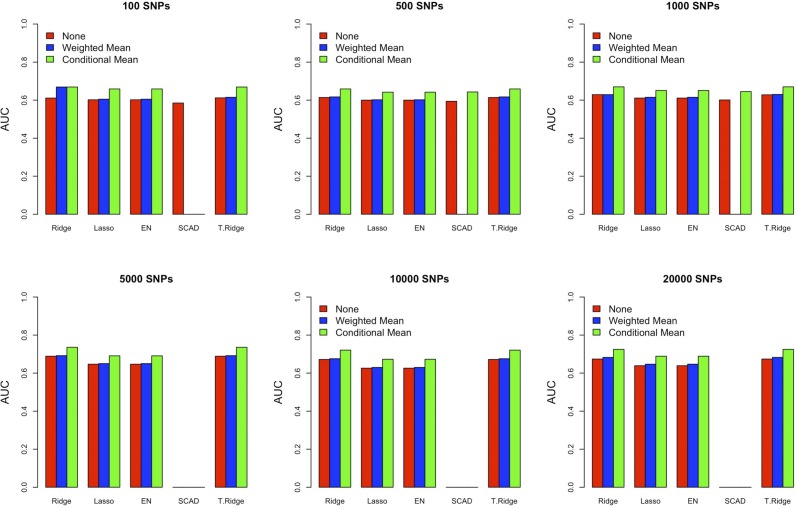
The purpose of this work was to investigate the performance of prediction models using family medical history and to construct the best T2D risk prediction model. For this purpose, we compared the performance of five different penalized regression methods by varying the number of SNPs with different measures of family history. To compare the performance of CM with other methods, we considered an alternative method, counting a weighted mean (WM) number of affected relatives in each pedigree, e.g., if individual one had six relatives of which three had T2D, a score of 3/6 is assigned. The key finding was that family history played a critical role in risk prediction for all methods (Figure 3 and Table S1 in File S1). Note that the performance tendency across different methods of considering family history, the number of SNPs, and the penalty can be more readily seen by bar plots (Figure 3), while the specific value can be found in the Table S1 in File S1.
Figure 3.
Model comparison with different family history measures. Prediction performance (AUC) is depicted without family history (red), with weighted mean (blue), and with conditional mean (green). AUC, area under the curve; EN, Elastic-Net; SCAD, smoothly clipped absolute deviation; T.Ridge, Truncated Ridge.
In the majority of cases, TR and Ridge revealed higher prediction performance compared to the other methods. Interestingly, similar behavior was observed between Ridge and TR, and between Lasso and EN. We also investigated the models with the SNPs filtered by P-value criterion and observed a similar result (Table S2 and Table S3 in File S1). For a small number of SNPs, use of the P-value criterion showed better performance. However, the difference became negligible (or even reversed in some cases) as the number of SNPs increased. Among all comparisons, the best performance (AUC = 0.736) was observed when using Ridge and TR with CM and 5000 SNPs selected by the BLUP criterion (Table S1 in File S1). The general performance of the model with the WM variable was much lower than that of the model with CM and the performance is slightly higher than that of the model without family history in terms of AUC (Figure 3). Note that the SD of the AUC was also evaluated and the range was 0.012–0.037. The best AUC value we obtained here is similar to that obtained previously (Aekplakorn et al. 2006; Lyssenko et al. 2008).
To further investigate the effect of the family history variable without SNPs, we built the logistic regression models without any SNPs. Based on the nested 10-fold cross-validation scheme, which was applied in the building steps of our model, we measured the performance of the logistic regression model without and with CM, or WM. Without CM, the AUC value was 0.672, but increased to 0.676 with WM included. When CM was included, AUC was 0.730. This value is similar to the highest AUC (0.736) obtained with 5000 additional SNPs. Taken together, the model including CM increased the prediction performance the best in terms of AUC.
We next measured the time taken for the analysis for each method, and the results are shown in Table 1. We used 10 cores [central processing units (CPU)] of our computing system (Intel Xeon CPU E5-2620 v2 @ 2.10 GHz). As can be seen, Ridge was the fastest method and truncated ridge followed. EN and SCAD were too slow to process the large genetic data sets even in our computing system. Note that unstable server usage might affect the time for each analysis but the tendency described here was steady.
Table 1. Analysis time.
| # of SNPs | Ridge | Lasso | EN | SCAD | T.Ridge |
|---|---|---|---|---|---|
| 100 | 15.6 sec | 13.2 sec | 4.7 min | 37 min | 1.9 min |
| 500 | 1.2 min | 1.2 min | 25.1 min | 5.2 hr | 6.0 min |
| 1,000 | 2.6 min | 2.2 min | 43.5 min | 12.2 hr | 11.1 min |
| 5,000 | 12.3 min | 53.7 min | 1.2 D | ∼3 daysa | 34.4 min |
| 10,000 | 24.3 min | 1.7 hr | 2.3 D | ∼6 daysa | 1.7 hr |
| 20,000 | 47.7 min | 3.4 hr | 3.61 D | ∼12 daysa | 3.3 hr |
, number; EN, Elastic-Net; SCAD, smoothly clipped absolute deviation; T.Ridge, Truncated Ridge.
Not measured but estimated.
Variation explained by each variable
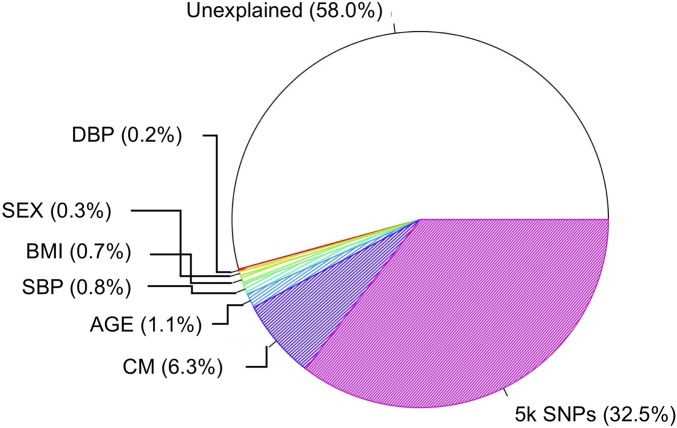
To estimate the variation explained by each variable, we investigated the model with 5000 SNPs selected by the BLUP (please see the File S2 for BLUP of the SNPs). As described in the Methods section, we fitted the reduced model to evaluate the residual deviance of each variable, calculated by comparing the predicted and true phenotypes in the data set, and the overall results are shown in Figure 4. Among the variation of the model including only an intercept, 42.0% of the total variation was explained by the full model, which includes all covariates (age, sex, BMI, SBP, DBP, CM, and 5k SNPs) (Figure S4 in File S1). The largest portion (58.0%) of the variation remained unexplained, indicating that the variables in the model are not sufficient to explain the data. The second largest portion (32.5%) was derived from the SNPs. Even though the prediction performance was not significantly increased with these SNPs, they nevertheless explained about one-third of the total variation. Genetic heterogeneity of the disease can be one possible reason for this seemingly inconsistent result. If a substantial proportion of variance is explained by a certain variable, it is usually expected to have a high predictive power. However, the better model fit does not always lead to the higher prediction performance in the existence of genetic heterogeneity of the disease.
Figure 4.
Proportion of variation explained by each variable in the final model. For six clinical variables [age, sex, body mass index (BMI), systolic blood pressure (SBP), diastolic blood pressure (DBP), and conditional mean (CM)], the individual proportions of variation are shown, whereas variation explained by the 5000 SNPs is shown according to their summed proportion.
In contrast, CM, which showed a dramatic increase in the prediction ability based on the AUC value, explained only 6.3% of the total variation. We also analyzed the model without incorporating family history to compare the effect of CM to the proportion of variation. We excluded the CM variable in the final model, and repeated the analyses to generate a pie chart. We found a ∼9% decrease (larger than the 6.3% CM proportion) from the total amount of variation explained with CM to that without (Figure S5 in File S1).
Discussion
Previous studies have documented the effectiveness of combining many SNPs using regularization methods or incorporating family history in improving the prediction performance of disease risk (Macinnis et al. 2011; Do et al. 2012; Won et al. 2015). However, these studies have either been one-sided designs or were not simultaneously focused on both sides; i.e., combining more SNPs and also incorporating family history. In this study, we tested the extent to which combining SNPs and incorporating family history could improve risk prediction, and applied this approach to a data set including a group of T2D patients and controls. We first developed a method to estimate the CM of being affected by a disease for subjects in a pedigree. We then compared the prediction performance of six different regularization methods using SNPs selected by the P-value obtained from logistic regression and the BLUP value obtained from a mixed-effects model. We adopted a nested cross-validation scheme, which is time-consuming but known to be more reliable (Varma and Simon 2006), to select the model showing the best prediction performance. Finally, we suggest a new method for estimating a variation explained by each variable in penalized regression models with a binary outcome (e.g., a case-control study).
In virtually all cases, the inclusion of family history (evaluated as CM) in the model greatly improved the prediction performance, while inclusion of SNPs showed only slight improvement. This finding indicates that proper incorporation of family history tends to produce a more effective genetic or environmental influence on the prediction results. Therefore, these benefits gained from incorporating CM might address the need for more rigorous investigations of gene–gene or gene–environmental interaction effects across a wide range of complex diseases. More importantly, a recent theoretical work has shown that using family information in training data would reduce the effective population size, which would lead to a better prediction model (Lee et al. 2017).
It has been thought that penalized regression models using all SNPs may simultaneously provide optimal performance even though it is infeasible in many cases because of the computational difficulty. Our results revealed that the additional power improvement is almost negligible if the number of SNPs is sufficiently large, compared to the scenario where all SNPs are used. Therefore, we can conclude that a well-developed feature selection method with a sufficiently large number of SNPs preserves the optimal prediction accuracy and is beneficial because computational burden can be drastically reduced (Fang et al. 2008). In this work, we identified the best-performed 5000 SNPs prescreened by the BLUP. The top 5000 SNPs that were prescreened by our BLUP-based selection method showed the highest AUC value. Note that we also analyzed the prediction model including all (∼300k) SNPs using MultiBLUP (Speed and Balding 2014) and the AUC was ∼0.6 regardless of CM inclusion. MultiBLUP assumes binary phenotypes as continuous values. This requires ridge penalty to be applied to the linear regression, not logistic regression, resulting in a likelihood that is quite different. Logistic regression is usually similar to the linear regression if the predicted probability is ∼0.5; yet, in our penalized regression model, there are many covariates that can push the probability away from 0.5, Thus, this may result from the less predictive performance of MultiBLUP. Interestingly, the variation explained by these BLUP-based 5000 SNPs (32.5%) was similar to the variance estimated by all SNPs (35%) reported to date (Speed et al. 2012).
However, there are some limitations of the study that are worth noting. First, we did not consider other types of structural variants such as copy number variations, which might also affect the risk of T2D, and their specific contribution is starting to be reported (Dajani et al. 2015). Second, it would be preferable to include rarer risk alleles with large effects and gene–gene or gene–environment interactions into the prediction model. More of the genetic risk can likely be explained as more causal risk variants are identified. However, rare variant analyses or interaction analyses require more complicated statistical methods to effectively analyze the effects. Also, gene–gene and gene–environmental interactions are important, but have not been clearly considered in this work. Note that the model might capture some familial phenotypic correlation due to environmental factors, which is likely proportional to kinship. Thus, genetic correlation can be distorted by environmental interaction. Therefore, the ultimate goal of future work is to integrate advanced statistical methods with accumulating genetic data, environmental effects, and biological knowledge to improve the efficiency of detecting complex interactions. In addition, no effect of LD among SNPs was considered here. However, if a prediction model includes many SNPs in high LD, the locus effect gets divided between many SNPs in LD and might affect the prediction performance, especially with the BLUP-filtering criterion. We assumed no such LD effect because a small set of SNPs were selected from only 285 k genotyped SNPs and they were all distant to each other (Figure S3 in File S1). However, an inclusion of the LD-pruning step is desirable with a larger number of genotyped SNPs or imputed SNPs. Also, there are number of measures of predictive performance, but we only considered AUC in this work. The main goal of this report was to compare the performance of the prediction model with and without family history (CM) using the AUC, and was not carefully stressed. However, it should be noted that for practical purposes, it is generally recommended that a prediction model provides both positive and negative results with the optimal threshold.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300283/-/DC1.
Acknowledgments
This research was supported by a grant from the Korea Health Technology R&D Project through the Korea Health Industry Development Institute, funded by the Ministry of Health and Welfare, Republic of Korea (HI15C2165). The authors declare no conflict of interest.
Footnotes
Communicating editor: N. Wray
Literature Cited
- Aekplakorn W., Bunnag P., Woodward M., Sritara P., Cheepudomwit S., et al. , 2006. A risk score for predicting incident diabetes in the Thai population. Diabetes Care 29: 1872–1877. [DOI] [PubMed] [Google Scholar]
- Chatterjee A., Lahiri S. N., 2011. Bootstrapping Lasso estimators. J. Am. Stat. Assoc. 106: 608–625. [Google Scholar]
- Cheng H., Treglown L., Montgomery S., Furnham A., 2015. Associations between familial factor, trait conscientiousness, gender and the occurrence of type 2 diabetes in adulthood: evidence from a British cohort. PLoS One 10: e0122701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton D. G., 2009. Prediction and interaction in complex disease genetics: experience in type 1 diabetes. PLoS Genet. 5: e1000540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Committee on Diabetic Twins, Japan Diabetes Society , 1988. Diabetes mellitus in twins: a cooperative study in Japan. Diabetes Res. Clin. Pract. 5: 271–280. [DOI] [PubMed] [Google Scholar]
- Dajani R., Li J., Wei Z., Glessner J. T., Chang X., et al. , 2015. CNV analysis associates AKNAD1 with type-2 diabetes in Jordan subpopulations. Sci. Rep. 5: 13391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do C. B., Hinds D. A., Francke U., Eriksson N., 2012. Comparison of family history and SNPs for predicting risk of complex disease. PLoS Genet. 8: e1002973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans D. M., Visscher P. M., Wray N. R., 2009. Harnessing the information contained within genome-wide association studies to improve individual prediction of complex disease risk. Hum. Mol. Genet. 18: 3525–3531. [DOI] [PubMed] [Google Scholar]
- Falconer D. S., 1967. The inheritance of liability to diseases with variable age of onset, with particular reference to diabetes mellitus. Ann. Hum. Genet. 31: 1–20. [DOI] [PubMed] [Google Scholar]
- Fan J. Q., Li R. Z., 2001. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96: 1348–1360. [Google Scholar]
- Fang L. H., Lv Y., Du G. H., 2008. Progress in study of pharmacological effect of Cortex Fraxini Zhongguo Zhong Yao Za Zhi 33: 2732–2736. [PubMed] [Google Scholar]
- Friedman J., Hastie T., Tibshirani R., 2010. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33: 1–22. [PMC free article] [PubMed] [Google Scholar]
- Hariri S., Yoon P. W., Qureshi N., Valdez R., Scheuner M. T., et al. , 2006. Family history of type 2 diabetes: a population-based screening tool for prevention? Genet. Med. 8: 102–108. [DOI] [PubMed] [Google Scholar]
- Hoerl A. E., 1970. Ridge regression. Biometrics 26: 603. [Google Scholar]
- Kaprio J., Tuomilehto J., Koskenvuo M., Romanov K., Reunanen A., et al. , 1992. Concordance for type 1 (insulin-dependent) and type 2 (non-insulin-dependent) diabetes mellitus in a population-based cohort of twins in Finland. Diabetologia 35: 1060–1067. [DOI] [PubMed] [Google Scholar]
- Kim W., Qiao D., Cho M. H., Kwak S. H., Park K. S., et al. , 2017. Selecting cases and controls for DNA sequencing studies using family histories of disease. Stat. Med. 36: 2081–2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. H., Weerasinghe W. M., Wray N. R., Goddard M. E., van der Werf J. H., 2017. Using information of relatives in genomic prediction to apply effective stratified medicine. Sci. Rep. 7: 42091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyssenko V., Laakso M., 2013. Genetic screening for the risk of type 2 diabetes: worthless or valuable? Diabetes Care 36(Suppl. 2): S120–S126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyssenko V., Jonsson A., Almgren P., Pulizzi N., Isomaa B., et al. , 2008. Clinical risk factors, DNA variants, and the development of type 2 diabetes. N. Engl. J. Med. 359: 2220–2232. [DOI] [PubMed] [Google Scholar]
- Macinnis R. J., Antoniou A. C., Eeles R. A., Severi G., Al Olama A. A., et al. , 2011. A risk prediction algorithm based on family history and common genetic variants: application to prostate cancer with potential clinical impact. Genet. Epidemiol. 35: 549–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio T. A., 2010. Genomewide association studies and assessment of the risk of disease. N. Engl. J. Med. 363: 166–176. [DOI] [PubMed] [Google Scholar]
- Manolio T. A., 2013. Bringing genome-wide association findings into clinical use. Nat. Rev. Genet. 14: 549–558. [DOI] [PubMed] [Google Scholar]
- McCarthy M. I., 2010. Genomics, type 2 diabetes, and obesity. N. Engl. J. Med. 363: 2339–2350. [DOI] [PubMed] [Google Scholar]
- Miyake K., Yang W., Hara K., Yasuda K., Horikawa Y., et al. , 2009. Construction of a prediction model for type 2 diabetes mellitus in the Japanese population based on 11 genes with strong evidence of the association. J. Hum. Genet. 54: 236–241. [DOI] [PubMed] [Google Scholar]
- So H. C., Gui A. H., Cherny S. S., Sham P. C., 2011a Evaluating the heritability explained by known susceptibility variants: a survey of ten complex diseases. Genet. Epidemiol. 35: 310–317. [DOI] [PubMed] [Google Scholar]
- So H. C., Kwan J. S., Cherny S. S., Sham P. C., 2011b Risk prediction of complex diseases from family history and known susceptibility loci, with applications for cancer screening. Am. J. Hum. Genet. 88: 548–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speed D., Balding D. J., 2014. MultiBLUP: improved SNP-based prediction for complex traits. Genome Res. 24: 1550–1557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speed D., Hemani G., Johnson M. R., Balding D. J., 2012. Improved heritability estimation from genome-wide SNPs. Am. J. Hum. Genet. 91: 1011–1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R., 1996. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B 58: 267–288. [Google Scholar]
- Varma S., Simon R., 2006. Bias in error estimation when using cross-validation for model selection. BMC Bioinformatics 7: 91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Z., Wang K., Qu H. Q., Zhang H., Bradfield J., et al. , 2009. From disease association to risk assessment: an optimistic view from genome-wide association studies on type 1 diabetes. PLoS Genet. 5: e1000678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Won S., Choi H., Park S., Lee J., Park C., et al. , 2015. Evaluation of penalized and nonpenalized methods for disease prediction with large-scale genetic data. BioMed Res. Int. 2015: 605891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T. T., Chen Y. F., Hastie T., Sobel E., Lange K., 2009. Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics 25: 714–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Lee S. H., Goddard M. E., Visscher P. M., 2011. GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88: 76–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H., Hastie T., 2005. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Series B Stat. Methodol. 67: 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. All analysis scripts and the dataset used in the article are available upon request. R script and Shell script for the analyses performed in the article are also available at http://healthstat.snu.ac.kr/software/revealing_MH). Genotype datasets for KARE project can be downloaded from www.nih.go.kr/NIH followed by an approval process from Korean NIH. For more information about the approval process, please contact biobank@korea.kr.