Estimation of Smooth ROC Curves for Biomarkers With Limits of Detection

Abstract

Protein biomarkers found in plasma are commonly used for cancer screening and early detection. Measurements obtained by such markers are often based on different assays that may not support detection of accurate measurements due to a limit of detection (LOD). The ROC curve is the most popular statistical tool for the evaluation of a continuous biomarker. However, in situations where LODs exist, the empirical ROC curve fails to provide a valid estimate for the whole spectrum of the false positive rate (FPR). Hence, crucial information regarding the performance of the marker in high sensitivity and/or high specificity values is not revealed. In this paper, we address this problem and propose methods for constructing ROC curve estimates for all possible FPR values. We explore flexible parametric methods, transformations to normality, and robust kernel-based and spline-based approaches. We evaluate our methods though simulations and illustrate them in colorectal and pancreatic cancer data.

1. Introduction

At the preclinical level, performing a research-grade biomarker assay might involve in vitro experiments and mass spectrometry techniques, among other procedures, with the objective of identifying genes or proteins that are over- or under-expressed in tumor tissue compared to control tissue (see [1]). Promising biomarkers obtained during that first phase are further explored using a clinical assay, which is usually developed by an industrial partner at great expense. It is common to have limited resources and technology at the preclinical level, which might impose detection limits (LODs), depending on the platform. Having to base conclusions on naive techniques that cannot accommodate such LODs might cause researchers to reject a promising biomarker at the early stage of biomarker discovery. Hence, it is crucial to properly evaluate biomarkers at the early stage of research. Furthermore, this will in turn result in decisions related to spending resources to improve technology for those promising biomarkers and eliminate these technical issues. Examples of biomarkers with such issues are not rare and might be related to colorectal cancer as well as pancreatic cancer among others.

Colorectal cancer is the third most common cancer diagnosed in both men and women in the United States. Early detection of colorectal cancer is key to successful treatment since it might be curable if detected at an early stage (see [2]). Carcinoembryonic antigen (CEA), normally produced in gastrointestinal tissue, is known to increase in individuals with colorectal carcinoma and to exhibit increased levels in individuals with pancreatic, lung and breast carcinoma as well. CEA is produced during the fetal period by endothelial cells, and postnatal by epithelial cells. Adenocarcinoma cells of the colon as well as fetal intestinal cells produce CEA, which is used as a biomarker for treatment monitoring purposes and to identify disease recurrence after surgical intervention. However, laboratory limitations play a role in measuring CEA, making its value undetectable below some LOD that may vary among different assay techniques. Carbohydate antigen 19-9 (CA19-9) is another well-known biomarker that is mainly used for diagnosis or monitoring response to therapy in pancreatic cancer. CA19-9 might also be subject to a lower LOD, the value of which depends on the assay. Although the most common situation is the existence of a lower LOD, there might be more rare cases that an upper limit of detection is present. An example is CA19-9. Its levels may be elevated in many types of cancer such as colorectal cancer, esophageal cancer, or hepatocellular carcinoma, as well as in pancreatitis and cirrhosis (see [3], [4], among others). Hence, it might not be safe to conclude that non-detected CA19-9 measurements above the upper LOD correspond to pancreatic cancer. More specifically, as pancreatic cancer is a rare disease and there is no suitable high-risk population for screening, any biomarker that identifies an average-risk population for screening will require very high specificity, which in turn will require unbiased estimators of the associated sensitivity. A very high specificity level of CA19-9 or the target biomarker, in cases where an upper LOD is present, could compromise the ability to derive an accurate estimate of the associated sensitivity. Likewise, when an accurate estimate of the specificity at a high sensitivity level (e.g., 95%) is required in a clinical context, the lower LOD will limit the ability to accurately estimate the desired specificity at the cutoff that corresponds to that sensitivity. It is common that a potential upper limit of detection might be resolved within the laboratory by dilution. However, such a strategy costs in time, resources and available samples that might be limited. This is the case presented in [5] that focuses on Hepatitis B and the Cobas Amplicor HBV Monitor test for which there is a limited range of detection due to an upper limit of detection. In that study even the dilution took place prior to the assay to avoid issues with the upper limit of detection, some sera had to be retested because they were still found to be above the upper limit of detection. However, such a retesting might cause a batch effect. Another example with an upper limit of detection is discussed in [6]. In that paper, the authors investigate kidney biomarkers for patients with cirrhosis and acute kidney injury. The measurements that correspond to the upper limit of detection are simply replaced by the exact value of the limit of detection and analysis is performed as if these measurements were exactly observed. Such an analysis might cause (downward) biased results. Therefore, the lower or upper LODs limit the ability to select candidate biomarkers for further development of clinical assays. We propose new approaches to address these issues.

The typical statistical tool to evaluate either continuous or ordinal biomarkers is the receiver operating characteristic (ROC) curve. If a lower LOD is present, clinicians cannot obtain exact measurements for patients whose measurements are below that lower LOD, d_L. It is also not possible to obtain exact measurements when they exceed the upper LOD, d_U. Hence, data that are left, right, or doubly censored arise in cases of a lower LOD, upper LOD, or both. We denote the biomarker measurements of healthy individuals as Y₀, and those of individuals with disease as Y₁. Assuming a continuous setting and that higher marker measurements are more indicative of the disease, we define sensitivity as P(Y₁ > c) and specificity as P(Y₀ < c), where −∞ < c < ∞ is a decision cutoff, above which we consider all measurements to be “positive.” For each cutoff value c, we obtain a pair of sensitivity and specificity values. The ROC curve is the plot of all possible pairs of sensitivity and specificity values obtained by scrutinizing all possible values of the cutoff c. Namely, ROC(c) = {FPR(c), TPR(c), c ∈ (∞, ∞)}. Let F₀(x) and F₁(x) be the distribution functions of the healthy and the diseased group respectively. The definition of the ROC curve as a function of the underlying distribution functions is

$$\mathit{\text{ROC}}(t)=S_1(S_0^{-1}(t)),t\in (0,1).$$ (1)

where S₀(x) = 1 − F₀(x) and S₁(x) = 1 − F₁(x) are the survival functions of the healthy and the diseased group respectively. For a detailed overview of the ROC curve, see [7] and [8]. When a lower and/or upper LOD is present, the construction of the ROC curve must account for the censored nature of the available data. Some practices in the setting of a lower LOD of a positively defined continuous biomarker involve ignoring the censored nature of the data and proceeding with the usual empirical ROC curve analysis (see [11] for an overview). This strategy is essentially equivalent to simply treating all left-censored measurements as if they were observed exactly at d_L, which is expected to result in bias. Other similar approaches might involve the replacement of these left-censored values with d_L/2 (see [12]) or d_L/√2 (see [13]). The first approach is based on the assumption that the distribution of the data is uniform in the interval [0, d_L]. The rationale for using d_L/√2 is a strategy that completes the tail of the underlying density with a straight line toward the (0,0) point, forming an orthogonal triangle with corners at the points (0, 0), (d_L, 0), (d_L, f(d_L)), where f is the underlying density function. It is not a surprise that the resulting empirical ROC curve remains the same regardless of which of these nave approaches one uses. This is due to the ranking of the data that remains unchanged no matter the replacement value used. The disadvantage of using such a replacement approach is threefold: (1) It only applies to positive supported marker measurements, which might not be the case even though it is common; (2) such an approach cannot be applied for the case of an upper LOD, as theoretically the interval of the true measurement in that case is [d_U, + ∞); and more importantly, (3) under the natural assumption of concavity of the ROC curve, the resulting ROC curve will most often be biased, which will result in downward bias of the targeted sensitivity and specificity values.

Some researchers have proposed parametric approaches. The use of the binormal model and the bigamma model was investigated in [14]. Mumford and others (2006) (see [15]) explored the binormal model as well, under a framework of taking random samples and pooling biospecimens. In [16] maximum likelihood ratio tests to compare biomarkers subject to LODs were considered. The multivariate normality assumption is employed in [17] for multiple biomarkers subject to an LOD. Maximum likelihood-based approaches under the normality assumption for making inference for optimal linear combinations of two biomarkers subject to LODs are discussed in [18]. They considered multiple biomarkers in the presence of lower LODs as well. However, such parametric approaches might be too restrictive. A spline-based approach was proposed in [19]. Their approach relaxes the need for common parametric assumptions; however, it cannot accommodate both upper and lower LODs.

The paper is organized as follows: In Section 2, we show that the naive empirical approach will provide a biased area under the ROC curve (AUC) estimate. We further show that, after the use of any replacement value, the empirical-based ROC curve will result in a biased estimate of the ROC(t). In Sections 3 and 4, we explore power transformations as well as the use of a flexible parametric model, the extended generalized gamma (GG) distribution (see [20] and [21]). In Sections 5 and 6, we investigate an imputation of kernel- and spline-based approaches to achieve robustness. We evaluate our approaches through simulations in Section 7, and apply them to colon cancer and pancreatic cancer data in Section 8. We close with a discussion.

2. Empirical ROC

A naive approach to the problem under study is to simply use the empirical ROC curve and ignore the censored nature of the data. The empirical-based ROC estimate for a continuous marker is obtained by all possible pairs of $T\widehat{P}R(c)={\sum }_{i=1}^{n_1}\frac{I(Y_1>c)}{n_1}$ and $F\widehat{P}R(c)={\sum }_{i=1}^{n_0}\frac{I(Y_0>c)}{n_0}$, −∞ < c < ∞. Some techniques (see Hughes, 2000 for a discussion) involve simply using a fixed replacement value for the censored data that are piling up on the lower LOD, d_L. Some replacement values discussed in the literature are a_L = d_L/2 or a_L = d_L/√2, and are used to attempt to reduce bias in terms of the estimated AUC, which in the case of a continuous marker corresponds to the probability P(Y₀ < Y₁). However, for any replacement value α_L < d_L and/or α_U > d_U, the empirical estimate of the ROC curve remains the same when it is obtained by an analysis that ignores the censored nature of the data. We show that any estimate based on a replacement value strategy induces bias. We generalize the result of [14] and show that the theoretical ROC curve in the presence of LODs d_L and d_U yields a biased estimate for any replacement value, both for the ROC(t) curve and for the AUC.

Proposition 1 Let the continuous marker that yields measurements for healthy individuals and those with disease be denoted by Y₀ and Y₁ from distributions F₀, F₁, respectively. Assume that the marker is subject to a lower LOD, d_L, and an upper, LOD d_U. Let a_L ≤ d_L and a_U ≥ d_U be the replacement values for the censored scores, which define the imputed scores M₀ and M₁ for the healthy and diseased, respectively. Denote with ROC_Y (t) the true unknown ROC(t) based on the unobserved scores Y₀ and Y₁, and denote with ROC_M(t) the ROC curve that is based on M₀ and M₁. It then holds that:

1. ROC_M(t) remains the same for any replacement values a_U and a_L. ROC_M(0) = 0, ROC_M(1) = 1, and ROC_M(t) = ROC_Y(t) for t ∈ [S₀(d_U), S₀(d_L)]. It is not defined elsewhere.

2. If we define ${\mathit{\text{ROC}}}_M^{\ast }(t)$ by linearly completing ROC_M(t), then we have ${\mathit{\text{ROC}}}_M^{\ast }(t)={\mathit{\text{ROC}}}_Y(t)$ for t ∈ (0, 1) if and only if $\frac{S_1(x)}{S_0(x)}=\frac{S_1(d_U)}{S_0(d_U)}x>d_U$, $\frac{F_1(x)}{F_0(x)}=\frac{F_1(d_L)}{F_0(d_L)}x<d_L$.

3. ${\mathit{\text{ROC}}}_M^{\ast }(t)={\mathit{\text{ROC}}}_Y(t)$ for t ∈ (0, 1) if and only if the following holds for the positive and negative predictive values of the (fully observed) marker: PPV_Y(c) = PPV_Y(d_U) c > d_U, NPV_Y(c) = NPV_Y(d_L) c < d_L.

4. If Y₀ is smaller than Y₁ in the hazard rate order (Y₀ ≤_hr Y₁), then ${\mathit{\text{ROC}}}_M^{\ast }(t)<{\mathit{\text{ROC}}}_Y(t)$ for t ∈ (0, S₀(d_U)). If Y₀ is smaller than Y₁ in the reverse hazard rate order (Y₀ ≤_rh Y₁), then ${\mathit{\text{ROC}}}_M^{\ast }(t)<{\mathit{\text{ROC}}}_Y(t)$ for t ∈ (S₀(d_L), 1). Equivalently ${\mathit{\text{ROC}}}_M^{\ast }(t)<{\mathit{\text{ROC}}}_Y(t)$ for t ∈ (0, S₀(d_U)) if PPV_Y(c) is increasing in c and ${\mathit{\text{ROC}}}_M^{\ast }(t)<{\mathit{\text{ROC}}}_Y(t)$ for t ∈ (S₀(d_L), 1) if NPV_Y(c) is decreasing in c. In particular, if ROC_Y(t) is concave (equivalent to Y₀ being smaller than Y₁ in the likelihood ratio order, Y₀ ≤_lr Y₁), then ${\mathit{\text{ROC}}}_M^{\ast }(t)<{\mathit{\text{ROC}}}_Y(t)$ for t ∉ [S₀(d_U), S₀(d_L)].

5. For the area under ${\mathit{\text{ROC}}}_M^{\ast }(t)$, ${\mathit{\text{AUC}}}_M^{\ast }=\frac{S_0(d_U)S_1(d_U)}{2}+{\int }_{S_0(d_U)}^{S_0(d_L)}\mathit{\text{ROC}}(t)\mathit{\text{dt}}+\frac{(1-S_0(d_L))(1-S_1(d_L))}{2}$, we have that ${\mathit{\text{AUC}}}_M^{\ast }<{\mathit{\text{AUC}}}_Y$, when the marker is subject to an upper LOD and PPV_Y(c) is increasing in c, or when the marker is subject to a lower LOD and NPV_Y(c) is decreasing in c, or when the marker is subject to both upper and lower LODs and with PPV_Y(c) increasing and NPV_Y(c) decreasing in c.

The proofs of the statements in the proposition are given in the Appendix. The first result in the proposition states that the ROC curve that corresponds to any replacement value strategy for the LODs is identical to the ROC curve obtained by setting all values outside the LODs equal to the LODs, and is a mixed-type ROC curve. In practice, one must be cautious with inference based on the empirical ROC since observed FPR and TPR values may not be attainable in the true ROC curve for the marker when specific LODs are set. Statements (ii) and (iii) of the proposition concern the common practice of replacing values outside the LODs and then proceeding to inference for accuracy measures while ignoring the LOD issue. In general, this practice results in biases. Strictly speaking, this practice is valid when one is willing to assume that, in terms of patient classification, knowledge of the actual marker measurement is useless when classifying a patient as healthy based on a value smaller than the lower LOD or when classifying a patient as having the disease based on a value larger than the upper LOD. We note here that there are some scenarios in which ${\mathit{\text{ROC}}}_M^{\ast }(t)$ may be close to ROC_Y (t). For example, consider the marker values for the diseased group being a mixture of a subpopulation identical to the values for the healthy group and another subpopulation of marker values that are well separated (in the ROC sense) from those for the healthy group. In the case of a reasonable lower LOD, d_L, based on the lower tail for the healthy group, we will have an approximately constant cdf ratio, resulting in ${\mathit{\text{ROC}}}_M^{\ast }(t)\approx {\mathit{\text{ROC}}}_Y(t)$. Statements (iv) and (v) of the proposition imply that the use of the empirical ROC in the presence of LODs results in the underestimation of the true ROC for markers that have desirable properties. Thus, LODs may lead to ‘good’ markers being ‘shortchanged’ on the basis of estimated accuracy measures when using the empirical ROC.

3. Box-Cox based ROC

The available data under the framework studied in this paper are of the form {Y_i, Δ_i}, i = 1, 2, 3, …, n where Y = [Y_0j, Y_1k] with j = 1, 2, …, n₀ with k = 1, 2, …, n₁, (n₀ + n₁ = n) and Δ_i is the censoring indicator that takes values -1, 0, and 1 for a left-censored, an exactly observed and a right-censored measurement, respectively. When common parametric models cannot be justified by the data at hand, power transformations are often employed. Such a transformation is the so-called Box-Cox transformation (see [22]). The Box-Cox transformation has been used under the ROC curve framework (see [8], [9], [10]). Its form is given by $Y^{(\lambda )}=\frac{Y^{\lambda }-1}{\lambda }$ if λ ≠ 0, and by Y^(λ) = log(Y) if λ = 0. The likelihood under this context is based on the power normal distribution implied for the original untransformed data:

$$f(y_i)=\frac{y_i^{\lambda -1}}{{\mathrm{\Phi }}_Y{\sigma }^{(\lambda )}}\varphi \left(\frac{y_i^{(\lambda )}-{\mu }^{(\lambda )}}{{\sigma }^{(\lambda )}}\right),$$

where ${\mathrm{\Phi }}_Y=\mathrm{\Phi }(\mathit{\text{sgn}}(\lambda )|\frac{\lambda {\mu }_1^{(\lambda )}+1}{\lambda {\sigma }_1^{(\lambda )}}|)$ if λ ≠ 0, and 1 otherwise. This is a truncation term often neglected by many authors, as discussed in [23]. However, as the support of the data must be positive in order for the Box-Cox transformation to be feasible, this truncation term must be taken into account when building the corresponding likelihood, which is given by

$$\begin{array}{ll}L(p)\hfill & =\prod _{i=1}^{n_0}{\left(\frac{1}{{\mathrm{\Phi }}_0}\right[\mathrm{\Phi }(\frac{y_{0i}^{\lambda }}{\lambda {\sigma }_0^{(\lambda )}}-\frac{1+\lambda {\mu }_0^{(\lambda )}}{\lambda {\sigma }_0^{(\lambda )}})-\mathrm{\Phi }\left(\frac{1+\lambda {\mu }_0^{(\lambda )}}{\lambda {\sigma }_0^{(\lambda )}}\right)\left]\right)}^{I({\delta }_i=-1)}{\left(\frac{y_{0i}^{\lambda -1}}{{\mathrm{\Phi }}_0{\sigma }_0^{(\lambda )}}\varphi \right(\frac{y_{0i}^{(\lambda )}-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\left)\right)}^{I({\delta }_i=0)}\hfill \\ & \times {(1-(\frac{1}{{\mathrm{\Phi }}_0}\left[\mathrm{\Phi }\right(\frac{y_{0i}^{\lambda }}{\lambda {\sigma }_0^{(\lambda )}}-\frac{1+\lambda {\mu }_0^{(\lambda )}}{\lambda {\sigma }_0^{(\lambda )}})-\mathrm{\Phi }(-\frac{1+\lambda {\mu }_0^{(\lambda )}}{\lambda {\sigma }_0^{(\lambda )}}\left)\right]\left)\right)}^{I({\delta }_i=1)}\hfill \\ & \times \prod _{i=1}^{n_1}{\left(\frac{1}{{\mathrm{\Phi }}_1}\right[\mathrm{\Phi }(\frac{y_{1i}^{\lambda }}{\lambda {\sigma }_1^{(\lambda )}}-\frac{1+\lambda {\mu }_1^{(\lambda )}}{\lambda {\sigma }_1^{(\lambda )}})-\mathrm{\Phi }\left(\frac{1+\lambda {\mu }_1^{(\lambda )}}{\lambda {\sigma }_1^{(\lambda )}}\right)\left]\right)}^{I({\delta }_i=-1)}{\left(\frac{y_{1i}^{\lambda -1}}{{\mathrm{\Phi }}_1{\sigma }_1^{(\lambda )}}\varphi \right(\frac{y_{1i}^{(\lambda )}-{\mu }_1^{(\lambda )}}{{\sigma }_1^{(\lambda )}}\left)\right)}^{I({\delta }_i=0)}\hfill \\ & \times {(1-(\frac{1}{{\mathrm{\Phi }}_1}\left[\mathrm{\Phi }\right(\frac{y_{1i}^{\lambda }}{\lambda {\sigma }_1^{(\lambda )}}-\frac{1+\lambda {\mu }_1^{(\lambda )}}{\lambda {\sigma }_1^{(\lambda )}})-\mathrm{\Phi }(-\frac{1+\lambda {\mu }_1^{(\lambda )}}{\lambda {\sigma }_1^{(\lambda )}}\left)\right]\left)\right)}^{I({\delta }_i=1)}\hfill \end{array}$$ (2)

where $p=({\mu }_0^{(\lambda )},{\sigma }_0^{(\lambda )},{\mu }_1^{(\lambda )},{\sigma }_1^{(\lambda )},\lambda )$, ${\mathrm{\Phi }}_k=\mathrm{\Phi }(\mathit{\text{sgn}}(\lambda )|\frac{\lambda {\mu }_k^{(\lambda )}+1}{\lambda {\sigma }_k^{(\lambda )}}|)$ if λ ≠ 0, and 1 otherwise with k = 0, 1. After maximizing likelihood (2), we obtain an estimate of all the underlying parameters $\widehat{p}=({\widehat{\mu }}_0^{(\lambda )},{\widehat{\sigma }}_0^{(\lambda )},{\widehat{\mu }}_1^{(\lambda )},{\widehat{\sigma }}_1^{(\lambda )},\widehat{\lambda })$. Note that I(A) = 1 if A is true, and 0 otherwise. Based on the estimate of the transformation parameter λ, λ̂, we then obtain the proposed estimate of the ROC curve by assuming that the transformed scores follow a truncated normal distribution, truncated at −1/λ. Namely, the cdf of the healthy is assumed to be

$$F_0(y)=\frac{\mathrm{\Phi }\left(\frac{y-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)-\mathrm{\Phi }\left(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)}{1-\mathrm{\Phi }\left(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)}\times I(x>-\frac{1}{\lambda }),$$ (3)

and this is similarly determined for the diseased. The inverse cdf function of the healthy is given by

$$F_0^{-1}(t)={\mathrm{\Phi }}^{-1}\left(\mathrm{\Phi }\right(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}})+t(1-\mathrm{\Phi }\left(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)\left)\right){\sigma }_0^{(\lambda )}+{\mu }_0^{(\lambda )}t\in (0,1).$$ (4)

Hence, the corresponding proposed ROC curve can be written in closed form based on the corresponding survival functions S₀ = 1 − F₀, S₁ = 1 − F₁, and is given by

$$\mathit{\text{ROC}}(t)=1-\frac{\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\mathrm{\Phi }\right(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}})+(1-t)(1-\mathrm{\Phi }\left(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)\left)\right){\sigma }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)-\mathrm{\Phi }\left(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)}{1-\mathrm{\Phi }\left(\frac{-\frac{1}{\lambda }-{\mu }_0^{(\lambda )}}{{\sigma }_0^{(\lambda )}}\right)}$$ (5)

where t ∈ (0, 1). An estimate of this ROC curve can then be obtained by simply plugging in the estimated parameters $\widehat{p}=({\widehat{\mu }}_0^{(\lambda )},{\widehat{\sigma }}_0^{(\lambda )},{\widehat{\mu }}_1^{(\lambda )},{\widehat{\sigma }}_1^{(\lambda )},\widehat{\lambda })$. The tails of the underlying density of the transformed scores are expected to conform with the tails of an estimated truncated normal distribution, and hence are nicely captured below the lower LOD and beyond the upper LOD in contrast to a naive approach that considers a simple replacement value.

4. Extended Generalized Gamma ROC

In case there are biological insights for speculating the shape of the tail of the underlying density of each group, and to allow for more flexibility in the tails, we explore a flexible parametric model known as generalized gamma (GG), which is based on the initial work of [20]. Extensions and computationally robust parameterizations for this model have proposed in [24]. For a thorough and elegant investigation of the extended GG model, we refer to [21]. Its density (see [24]) can be written as

$$f(x;\alpha ,\lambda ,\gamma )=\frac{|\alpha |}{\mathrm{\Gamma }(\gamma )}{\gamma }^{\gamma }{\lambda }^{\alpha \gamma }{x}^{\alpha \gamma -1}\mathit{exp}\{-\gamma {(\lambda x)}^{\alpha }\},$$

where α ≠ 0 and γ > 0 are the shape parameters, and λ > 0 is the scale parameter. When α = 0, the limiting case of the lognormal distribution is obtained. When γ = 1 or α = 1, we obtain the Weibull or the gamma distribution, respectively. Here, we denote the GG distribution by GG(α, λ, γ). The survival function is

$$S(x;\alpha ,\lambda ,\gamma )=\{\begin{array}{ll}I\{\gamma {(\lambda x)}^{\alpha },\gamma \},\hfill & \text{if}\alpha <0\hfill \\ 1-I\{\gamma {(\lambda x)}^{\alpha },\gamma \},\hfill & \text{if}\alpha >0.\hfill \end{array}$$

where I{·,·} is the incomplete gamma function. It is defined as $I(x,\theta )=\frac{1}{\mathrm{\Gamma }(\theta )}{\int }_0^x{t}^{\theta -1}{e}^{-t}\mathit{\text{dt}}$ and is also known as the regularized gamma function. This distribution provides a parametric platform under a survival analysis concept. Its hazard rate can take the form of the four most common types, i.e., increasing, decreasing, arc-shaped and bathtub-shaped. Even though the hazard rate under the ROC curve framework has no appealing interpretation, it loosely expresses the risk of having a measurement q + Δq given that the measurement is > q, and directly relates to the tails of the underlying densities, the form of which are of crucial interest in our setting. For example, a decreasing hazard rate refers to a heavy tail of the underlying density. Similarly, when the hazard rate is increasing, the tail of the density is light. The tails are of primary interest in our setting since it is the tails that are not ‘revealed’ due to the upper or lower LOD. We denote $I\overline{(x,\alpha )}=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_x^{\infty }{t}^{a-1}{e}^{-t}\mathit{\text{dt}}=1-\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^{\infty }{t}^{a-1}{e}^{-t}\mathit{\text{dt}}=1-I(x,\alpha )$ and let I⁻¹(x, α) and $I^{-1}\overline{(x,\alpha )}$ be the inverse functions of I(x, α) and $I\overline{(x,\alpha )}$, respectively. The proposed GG-based ROC curve can be derived after inverting the survival distribution of the healthy group. We denote the parameter vector of the GG that refers to the healthy group as (α₀, γ₀, λ₀), and the corresponding parameters for the group with disease as (α₀, γ₀, λ₀). The corresponding likelihood is given by

$$\begin{array}{c}L(p)=\prod _{i=1}^{n_0}{F}_0{(y_{0i};{\alpha }_0,{\gamma }_0,{\lambda }_0)}^{I({\delta }_i=-1)}{f}_0{(y_{0i};{\alpha }_0,{\gamma }_0,{\lambda }_0)}^{I({\delta }_i=0)}{S}_0{(y_{0i};{\alpha }_0,{\gamma }_0,{\lambda }_0)}^{I({\delta }_i=1)}\\ \times \prod _{j=1}^{n_1}{F}_1{(y_{1j};{\alpha }_1,{\gamma }_1,{\lambda }_1)}^{I({\delta }_j=-1)}{f}_1{(y_{1j};{\alpha }_1,{\gamma }_1,{\lambda }_1)}^{I({\delta }_j=0)}{S}_1{(y_{1j};{\alpha }_1,{\gamma }_1,{\lambda }_1)}^{I({\delta }_j=1)}\end{array}$$ (6)

where F₀(y; α₀, γ₀, λ₀) = 1 − S₀(y; α₀, γ₀, λ₀), and f₀(y; α₀, γ₀, λ₀) is the GG cdf and pdf that correspond to the healthy group. We note that δ_i is -1 if the i-th measurement is left censored, 1 if it is right censored and 0 if the measurement is exactly observed. The indicator function I(A) is 1 if A is true, and 0 otherwise. This is performed similarly for the group with disease. Hence, the proposed ROC curve under this parameterization is given by

$$\mathit{\text{ROC}}(t)=\{\begin{array}{ll}I\{{\gamma }_1{({\lambda }_1(I^{-1}\{{\gamma }_0{({\lambda }_{0}t)}^{{\alpha }_0},{\gamma }_0\}))}^{{\alpha }_1},{\gamma }_1\},\hfill & \text{if}{\alpha }_1<0,{\alpha }_0<0\hfill \\ 1-I\{{\gamma }_1{({\lambda }_1(I^{-1}\{{\gamma }_0{({\lambda }_{0}t)}^{{\alpha }_0},{\gamma }_0\}))}^{{\alpha }_1},{\gamma }_1\},\hfill & \text{if}{\alpha }_1>0,{\alpha }_0<0.\hfill \\ I\{{\gamma }_1{({\lambda }_1(I^{-1}\overline{\{{\gamma }_0{({\lambda }_{0}t)}^{{\alpha }_0},{\gamma }_0\}}))}^{{\alpha }_1},{\gamma }_1\},\hfill & \text{if}{\alpha }_1<0,{\alpha }_0>0\hfill \\ 1-I\{{\gamma }_1{({\lambda }_1(I^{-1}\overline{\{{\gamma }_0{({\lambda }_{0}t)}^{{\alpha }_0},{\gamma }_0\}}))}^{{\alpha }_1},{\gamma }_1\},\hfill & \text{if}{\alpha }_1<0,{\alpha }_0<0\hfill \end{array}$$ (7)

After maximizing the likelihood (6), the estimated ROC curve can be obtained by simply plugging α̂₀, γ̂₀, λ̂₀, α̂₁, γ̂₁, λ̂₁ into expression (7). The calculation of the incomplete gamma function as well as its inverse are built into software such as MATLAB (see gammainc and gammaincinv functions) and Mathematica (see GammaRegularized and InverseGammaRegularized). Furthermore, the fit of the GG model is readily available by using SAS (see LIFEREG procedure); a MATLAB routine named aft for the same purpose is available in the File exchange link of Mathworks provided by the first author.

5. Kernel-Imputation Based ROC

Here, we focus on a hybrid approach based on non parametric kernel based distribution estimates and parametric based imputation. A non parametric kernel based estimate of a density of a fully observed random variable X is given by:

$${\widehat{f}}_X(x)=\frac{1}{n_X{h}_X}\sum _{i=1}^{n_X}K\left(\frac{x-X_i}{h_X}\right),$$ (8)

where $K(t)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}$, and h_X is the bandwidth for which one can choose to use a simple plug in type equal to $h_X=0.9\mathit{\text{min}}(\mathit{\text{std}}(X_i),\mathit{\text{IQR}}(X_i))n_X^{0.2}$ (see [25]. When it comes to censored data the kernel estimate depends on the steps of the empirical survival curve that accommodates censoring. For example in the presence of right censoring the kernel based estimate depends on the steps of the Kaplan Meier estimate (see [26]). However, the Kaplan Meier survival estimate, and hence the kernel based distribution estimates, suffer from the ‘last is censored’ phenomenon. Namely, the Kaplan Meier step curve cannot provide a valid estimate beyond the last observation if that is right censored. The same problem persists for doubly censored data even if one decides to use Turnbull's algorithm (see [27]). That is, no valid estimate can be obtained before the first observation if that is left censored.

To overcome this problem we consider imputing the censored data by random draws of plausible parametric models in order to have some pseudodata in the tails of both distributions (of the diseased and the healthy) and then proceed with the non-parametric kernel based estimators for both distributions separately. For an overview regarding imputation see [28]. Assume that the number of left and right censored observations of the healthy are denoted with $n_{0L}^{\ast }$ and $n_{0U}^{\ast }$ respectively (notation is similar for the diseased related censored data). The proposed algorithm is:

• Step 1: Draw $n_{0L}^{\ast }$ data from a plausible parametric model f₀, $Y_{0Li}^{\ast }$, $i=1,\dots ,n_{0L}^{\ast }$ for which $Y_{0i}^{\ast }<d_L{\forall }_i$.

• Step 2: Draw $n_{0U}^{\ast }$ data from a plausible parametric model f₀, $Y_{0Ui}^{\ast }$, $i=1,\dots ,n_{0U}^{\ast }$ for which $Y_{0i}^{\ast }>d_U{\forall }_i$. The pseudodata set for the healthy is denoted with $Y_0^{\ast }=[Y_{0L}^{\ast },(Y_0:{\delta }_i=0),Y_{0U}^{\ast }]$. Namely $Y_0^{\ast }$ consists of all imputed data in place of the previously censored ones, and the exactly observed from the original Y₀.

• Step 3: Repeat the analogous Step 1 and 2 for the diseased group and obtain $Y_1^{\ast }$.

• Step 4: Obtain the kernel based distribution estimates based on $Y_0^{\ast }$ and $Y_1^{\ast }$ separately and hence obtain an estimate of the kernel based ROC, RÔC^j(t), t ∈ (0, 1).

• Step 5: Repeat Steps 1-4, 30 times, and obtain 30 smooth kernel based ROC curves.

• Step 6: The proposed kernel based ROC curve is the average of the ROC curves obtained in Step 5, namely $R\widehat{O}C(t)=\frac{{\sum }_{j=1}^{30}{R\widehat{O}C}^j(t)}{30}$.

The proposed estimate of Step 6 of the previous algorithm can be considered as a robust alternative to simply assuming a parametric model. It only uses the parametric assumption to fill in the data of the censored tails of each distribution while the main body of the distributions of both groups is estimated non-parametrically. This hybrid estimate has also the property of providing a smooth ROC curve which is a natural assumption for the true ROC curve. Here, based on the two previous sections, we consider two versions of this estimate: The kernel based BC ROC estimate (Kernel(BC)), and the kernel based GG ROC estimate where imputation is based on the GG model (Kernel(GG)). For the former, we first transform the data based on the maximum likelihood parameter estimates, and then imputation is done based on the obtained truncated normal distributions.

6. Spline Based ROC

Here we explore a spline based technique that is based on estimating the underlying survival functions of the healthy and the diseased, namely S₀(t) and S₁(t). We extend a monotone spline initially presented in [29]. Consider the K knots placed at τ₁ < … < τ_K and let the natural spline for the cumulative hazard which can be written as

$$H(x)={\theta }_1{(x-{\tau }_1)}_{+}^3+\dots +{\theta }_{K-2}{(x-{\tau }_{K-2})}_{+}^3+{\theta }_{K-1}{(x-{\tau }_{K-1})}_{+}^3+{\theta }_K{(x-{\tau }_K)}_{+}^3$$ (9)

$$\begin{array}{c}{\theta }_{K-1}=\frac{{\theta }_1({\tau }_1-{\tau }_K)+{\theta }_2({\tau }_2-{\tau }_K)+\dots +{\theta }_{K-2}({\tau }_{K-2}-{\tau }_K)}{{\tau }_K-{\tau }_{K-1}}\\ {\theta }_K=\frac{{\theta }_1({\tau }_1-{\tau }_{K-1})+{\theta }_2({\tau }_2-{\tau }_{K-1})+\dots +{\theta }_{K-2}({\tau }_{K-2}-{\tau }_{K-1})}{{\tau }_{K-1}-{\tau }_K}.\end{array}$$ (10)

The above model has the following appealing properties: (i) It is linearly extrapolated beyond the last knot τ_K, (ii) It equals to zero before the first knot τ₁, (iii) It is a smooth function since its first two derivatives are continuous. The number of parameters of interest θ₁, θ₂,…, θ_k, is K − 2 since the last two parameters are functions of all previous.

We attempt the fit of the above model to the cumulative hazard nonparametric step estimate. For that reason, monotonicity conditions must be imposed since the cumulative hazard is a non decreasing function. There is an implied region of monotonicity which is non-linear (see [29]). We employ an optimal polygon strategy to approximate linearly the nonlinear monotonocity region so that the minimization problem reduces to a least squares one with linear restrictions on the parameters (see [29]). We propose the use of six knots and regarding the knot placement we consider the following strategy: We derive the following 10 percentiles derived by the fully observed data: 0, 2.5th, 5th, 10th, 20th, 40th, 50th, 60th, 80th, and 100th. There are 10!/(6!4!) = 210 possible combinations, and thus 210 possible knot schemes. In a given application all 210 knot schemes are explored by fitting model (9) to the non-parametric maximum likelihood based cumulative hazard function. Finally, the knot scheme that results to the smallest distance from the corners of the step cumulative hazard function is the one chosen. That is, the knot scheme selection is based on the objective function for minimization:

$${\mathrm{\Psi }}_0({\widehat{\mathit{\theta }}}_0)=\sum _i{({\widehat{H}}_0(Y_{0i}|{\mathrm{\Delta }}_{0i}=0)-{\widehat{H}}_0^{\mathit{\text{KM}}}(Y_{0i}|{\mathrm{\Delta }}_{0i}=0))}^2,$$ (11)

where θ̂₀ is the estimated parameter vector of the spline related to the control group, Y_0i is the score of the i-th individual of the control group and Δ_0i refers to the censoring status of that individual (taking the value of 0 for an exactly observed score and the value of 1 for a right censored score), Ĥ₀ is the fitted model (related to the control group) defined in (9) under the appropriate constraints of monotonicity, and ${\widehat{H}}_0^{\mathit{\text{KM}}}$ is the Kaplan Meier based cumulative hazard estimator obtained by the biomarker data of the control group. The notation for the diseased group is similar. In the case of doubly censored data the above criterion is defined through Turnbull's non parametric cumulative hazard function estimate:

$${\mathrm{\Psi }}_0({\widehat{\mathit{\theta }}}_0)=\sum _i{({\widehat{H}}_0(Y_{0i}|{\mathrm{\Delta }}_{0i}=0)-{\widehat{H}}_0^{\mathit{\text{TB}}}(Y_{0i}|{\mathrm{\Delta }}_{0i}=0))}^2,$$ (12)

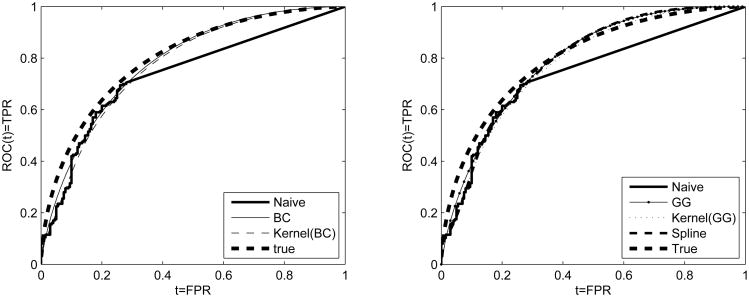
where ${\widehat{H}}_0^{\mathit{\text{TB}}}(\cdot )$ is Turnbull's estimate for H₀. Notation is similar for the diseased group. Resampling methods are feasible for inference. The proposed spline based ROC estimate is given by $R\widehat{O}C(t)={\widehat{S}}_1({\widehat{S}}_0^{-1}(t))$ where Ŝ_i(t) = exp(−Ĥ_i(t)), i = 0, 1 and Ĥ₀(t) and Ĥ₁(t) are the spline based cumulative hazard estimates for the healthy and the diseased whose forms are given by (9). We note here that the placement of the first knot in the case of doubly censored data can be derived with the help of the box-cox transformation and the first percentile of the underlying density estimate. Namely, for a given data set, we apply the box-cox transformation, estimate the first percentile of the implied truncated normal as discussed in section (3), and then back-transform on the original scale. This is done because the cumulative hazard is naturally assumed to be zero before the first knot. A simulated example that includes all methods discussed is given in Figure 1. In that figure we visualize how for a simulated example that is generated from two normal distributions, all methods approximate better the true underlying ROC curve compared to the Naive Empirical.

Figure 1.

Simulated data set of two normal distributions generated to attain true AUC=0.8 and expected level of censoring 50% due to a lower LOD. Left panel: Box-Cox (BC) and kernel(BC) based ROCs along with the true and the naive empirical. Right panel: Generalized gamma (GG), kernel(GG), and spline based ROCs along with the true and the naive empirical.

7. Simulations

To evaluate our approaches we conduct simulation studies for 105 different scenarios and use comparisons based on different ranges of the underlying integrated squared errors. The scenarios that generate the data depend on sample size, direction of censoring, level of censoring, AUC, and the true underlying model. We consider sample sizes fo (n₀, n₁) = (100, 100), (200, 200), and (500, 500). We generate data based on normal, gamma, and lognormal distributions with parameters set to achieve true values of the AUC equal to 0.7 and 0.8. All underlying true parameters for all scenarios are given in Table 1 of the Web Appendix (WA). Note that we consider scenarios that lie in the Box-Cox family as well as out of the Box-Cox (e.g. gammas). The levels of censoring we consider are 30% and 50% caused by a lower LOD, an upper LOD or both. The criterion on which we base our evaluation is the relative integrated squared error for different FPR ranges, namely ${\mathit{\text{rISE}}}_{a-b}=\frac{{\int }_a^b{({R\widehat{O}C}^{(\mathit{\text{naive}})}-\mathit{\text{ROC}}{(t)}^{\mathit{\text{true}}})}^2\mathit{\text{dt}}}{{\int }_a^b{({R\widehat{O}C}^{(\mathit{\text{proposed}})}-\mathit{\text{ROC}}{(t)}^{\mathit{\text{true}}})}^2\mathit{\text{dt}}}$. We consider exploring this criterion to intervals (a – b) = (0 – 0.2), (0 – 0.4), (0.6 – 1), (0.8 – 1) and the total (0 – 1). The value of our methods will be revealed in those cases that this criterion is > 1 and we are particularly interested in those areas where the tail of the true ROC is not supported by fully observed data. Namely, for lower LOD we do not fully observe the upper part of the ROC that corresponds to a high FPR (or equivalently high TPR range). Conversely, when an upper LOD is considered, particular interest in terms of performance lies in the part of the ROC estimate that corresponds to a range of low FPRs.

For the parametric approaches (see Tables 2 and 3(WA)) we observe the following: The BC approach appears to outperform the empirical naive estimate by far in all cases of the normal scenarios. For example, for the scenario of AUC = 0.8 and 50% censoring due to a lower LOD it provides rISE_0–0.2 = 3.1032, namely over three times smaller ISE. We observe that as we increase the sample size the gain is greater: (n₀, n₁) = (200, 200), and (500, 500) the rISE_0–0.2 equals to 5.6420 and 14.4367 respectively. The results of the lognormal related scenarios are equally impressive. The reason is that both the normal and the lognormal models are in the family of the Box-Cox. However, the BC approach demonstrates satisfactory robustness. For the gamma related scenarios we observe for AUC = 0.7, and 0.8 with 50% censoring due to an upper LOD rISE_0–0.2 = 4.1410 and 13.7343 respectively. As we increase the sample size, we outperform the naive empirical in almost all cases. The GG model seems to not provide so impressive results especially for smaller sample sizes. It seems, however, to outperfrom the naive empirical for larger sample sizes. For example it provides rISE_0–0.2 = 8.9095 for a lognormal related scenario with an upper LOD causes 50% censoring when AUC = 0.8. For the same scenario and a lower LOD it yields rISE_0.8–1 = 1.5484. The GG is a very flexible parametric model that contains as special cases the Weibull, the Lognormal, the Gamma, the log-logistic, the logistic, and the so called ‘ammag’ among other not so common parametric models as well (for a detailed discussion on this aspect see [21]). Due to its flexibility it seems that it requires a larger sample size to outperform the BC, which is also quite robust, but does not capture all these models theoretically within its family. In finite sample sizes, the BC seems to work well even for distributions like gamma which are out of the Box-Cox family. This is also stressed in [10]. However, as the sample size increases and of course asymptotically, being within the gamma family is in favor of the Generalized Gamma model. This is also verified by a large sample simulation we ran for n = (5000, 5000) where the GG outperforms the BC throughout. This result justifies the theoretical asymptotic expectation that as the sample size increases the GG will eventually outperform the BC when we lie within the GG family and outside the BC family. However, such huge sample sizes are not realistic in the early stage of biomarker discovery.

For the kernel based approach (see Table 4(WA)) we observe that when used in combination with the BC (Kernel(BC)), it performs nicely in all scenarios, outperforming the Naive empirical in nearly all cases. For larger sample sizes we achieve up to 27 times smaller rISE_0–0.2. The results of the Kernel(GG) approach are inconclusive for smaller sample sizes (see Table 5(WA)). For (n₀, n₁) = (500, 500) it seems to attain descent results in many cases, outperforming the Naive in the regions of interest as well as in terms of total rISE (rISE_0–1). Conclusions for the spline based approach are similar (see Table 6(WA)). We note, however, results for AUC = 0.8 are better compared to those that refer to AUC = 0.7. The explanation for that is the curvature of the underlying ROC curve. For poor biomarkers, it is a fact that the ROC near its tails is almost linear, hence the Naive empirical provides a computationally very effective approach for such cases. We additionally explore cases for which AUC = 0.6 and AUC = 0.9 that support this argument (see Tables 7-9(WA)).

In summary, the BC and the Kernel(BC) approaches perform nicely in all explored cases outperforming the Naive empirical. They provide satisfactory level of coverage for the underlying bootstrap based confidence intervals for the RÔC(t), while the Naive Empirical dramatically fails in that aspect yielding coverage close to 0 (see Table 10(WA)). The Kernel(BC) based approach is considered as a more robust alternative compared to the BC. The GG, Kernel(GG), and the spline approach should be used only in cases of very large sample sizes, and still they do not attain such a good performance compared to the BC and Kernel(BC). To further illustrate that we considered an additional simulation study for which the diseased group is generated from a bimodal normal mixture density. The results are given in Table 12 of the Web Appendix. In this scenario we observe that the BC under-performs as it fails to capture satisfactorily the true underlying density which is now bimodal. However, the Kernel(BC) as being more robust by construction is outperforms the Naive empirical in terms of rISE_(0–1) in all scenarios. The spline seems to generally be unstable and does not perform well in cases where the true AUC is not close to 0.8. The efficiency of all approaches depends heavily on the underlying curvature of that portion of the ROC curve that is undetected. In cases where the biomarkers under study have poor performance then the true ROC curve tends to be linear in the tails. Hence, for such cases the Naive empirical might have an advantage but these cases are unidentifiable in practice. We present an additional simulation for AUC = 0.6 for the normal related scenario for that purpose (see Tables 7-9 (WA)) in which we explore settings with AUC = 0.6 and AUC = 0.9. For the AUC = 0.9 the Box-Cox and the Kernel(BC) still perform nicely. It is a fact that below the lower LOD and above the upper LOD one deals with a ‘black box’ situation and caution is needed, since this is not a simple setting or random censoring out of which the pattern of the two underlying densities can be easily revealed. We observe that the Box-Cox based approaches tackle the problem nicely by extracting all information under its robust assumption, attempting to approximate the hidden tails. The notion of imputation under the same assumption is used for the Kernel(BC) which can be considered as a hybrid approach since it only uses the BC assumption to impute the censored data that only refer to the underlying tails of the corresponding densities.

As concluding remarks we provide the following guidance: (1) if the BC approach can be justified by the data at hand then it should preferred over all other explored approaches. (2) The spline based (HCNS) approach is not to be preferred over the other proposed approaches. It performs better than the Naive empirical when the sample size is large and the curvature allows it (around AUC=0.8). (3) When the available sample size is very large and the GG assumption can be justified by the data at hand then we propose the GG. Based on a large sample simulation (not presented here for brevity) for the gamma related scenario, where n = (5000, 5000), the GG outperforms the BC as expected. Such large sample sizes, however, are unrealistic in the early stage of biomarker discovery. (4) For any sample size, in case the BC assumption is not justified by the data at hand we propose the Kernel(BC) which performs satisfactorily in all cases illustrating robustness. The Kernel(BC) is the most robust alternative to the fully parametric BC method and is to be preferred when certain parametric assumptions cannot be justified by the data at hand.

8. Applications

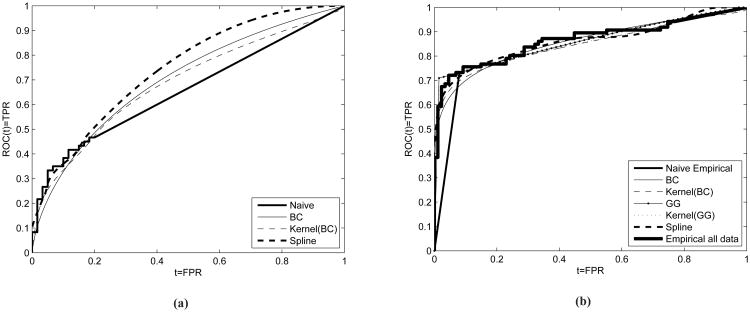
We employ our methods by using two examples that motivated our study. First, we use CEA measurements from a case-control validation study presented in Taguchi and others (2015). The purpose of the study is to determine the performance of biomarker MARPE1 in the presence of other biomarkers such as CEA in detecting early colorectal cancer and colon adenoma. Plasma samples are used from 60 patients with adenomas, 30 patients with early colorectal cancer, 30 with advanced colorectal cancer, and 60 individuals participating as controls. CEA plasma levels were measured based on ELISA. Here we focus on the performance of CEA in discriminating between subjects with either early or advanced colorectal cancer (n₀ = 60) from controls (n₁ = 60). The lower LOD as induced by the ELISA assay results in 66.67% left censoring. The empirical Naive AUC estimate is 0.6561 (see Figure 2). We illustrate the BC (AUC=0.7016), the Kernel-BC (AUC=0.6861), as well as the spline method (AUC=0.7440) since the generalized gamma did not converge for this data set. The LOD affects the Naive empirical for FPR > 0.2. We observe that all approaches yield a higher ROC(t) for t ∈ (0.2, 1) compared to the empirical naive. For the underlying AUC, we obtain 95% percentile bootstrap based confidence intervals see Table 1. We also focus on specific TPR values: 0.7, 0.8, and 0.9. For the sensitivity levels we calculate 95% confidence intervals for the associated FPRs (see Table 1). We observe that the confidence intervals obtained by the naive approach are narrower as expected since variability is reduced due to the linear part that is always used for estimation in that FPR range in all bootstrap samples. Narrow confidence intervals are indicative of the bias induced by the Naive empirical approach. The BC and Kernel(BC) yield fairly similar results. The spline based approach yields somewhat lower FPRs at the explored TPR values but with less certainty since all corresponding condidence intervals are wider. This is the price we pay for not making any parametric assumption at no stage. For this example we recommend the estimates obtained by the BC and Kernel(BC) since simulations have shown better performance of these approaches for scenarios related to AUCs approximately equal to 0.7. Based on the results for TPR=0.8 and 0.9 we observe that the point estimates of the Naive Empirical (0.7 and 0.85 respectively) barely make it to lie within the 95% confidence intervals as obtained by the BC and the kern(BC) method ([0.358-0.720] and [0.382, 0.738] respectively), giving evidence that conclusions based on the Naive approach might be deceiving.

Figure 2.

Figure (2a): ROC curves for CEA that refers to colon cancer. AUCs for the Box-Cox, Kernel(BC), HCNS (spline) and naive empirical are 0.699, 0.686, 0.744 and 0.6566 respectively. Figure (2b): ROC curves for CA19-9 that refers to pancreatic cancer. AUCs for the Box-Cox, Kernel(BC), GG, kernel(GG), spline and naive empirical are 0.8577, 0.8474, 0.8657, 0.8569, 0.8627, 0.8428. The corresponding AUC for the empirical when using all available data is 0.8651. We note that even though it seems so, the GG based ROC estimate does not exhibit a step on the right panel. It simply has a very steep curvature close to TPR = 0.7.

Table 1.

Results for the CEA and CA19-9 biomarkers.

CA19-9 related results
	Naive	Box-Cox	Kernel(BC)	GG	Kernel(GG)	Spline	Empirical using all data for CA19-9
FPR	TP̂R(95%CI)	TP̂R(95%CI)	TP̂R(95%CI)	TP̂R(95%CI)	TP̂R(95%CI)	TP̂R(95%CI)	TP̂R(95%CI)
0.01	0.091(0.052,0.219)	0.501(0.253,0.709)	0.515(0.255,0.686)	0.707(0.6406,0.8289)	0.710(0.614,0.781)	0.573(0.625,0.803)	0.384(0.291,0.674)
0.02	0.182(0.105,0.438)	0.554(0.339,0.741)	0.574(0.345,0.714)	0.711(0.6571,0.8327)	0.737(0.634,0.784)	0.617(0.641,0.806)	0.593(0.314,0.744)
0.04	0.364(0.209,0.756)	0.613(0.428,0.774)	0.637(0.456,0.746)	0.718(0.6776,0.8379)	0.767(0.656,0.789)	0.664(0.658,0.810)	0.686(0.500,0.802)
0.05	0.455(0.262,0.779)	0.633(0.463,0.785)	0.657(0.491,0.756)	0.722(0.6818,0.8401)	0.778(0.656,0.791)	0.680(0.664,0.811)	0.721(0.581,0.802)
0.10	0.756(0.524,0.837)	0.699(0.601,0.821)	0.712(0.594,0.790)	0.739(0.6981,0.8555)	0.813(0.676,0.796)	0.732(0.664,0.811)	0.756(0.651,0.826)
AUC:	0.795(0.773,0.898)	0.858(0.773,0.898)	0.846(0.773,0.898)	0.866(0.799,0.935)	0.906(0.729,0.832)	0.846(0.773,0.898)	0.865(0.816,0.917)
CEA related results
TPR	FP̂R(95%CI)	FP̂R(95%CI)	FP̂R(95%CI)	FP̂R(95%CI)	FP̂R(95%CI)	FP̂R(95%CI)
0.7	0.550(0.394,0.650)	0.417(0.235,0.591)	0.455(0.261,0.611)	-	-	0.364(0.193,0.993)	-
0.8	0.700(0.596,0.776)	0.561(0.358,0.720)	0.612(0.382,0.738)	-	-	0.473(0.236,0.999)	-
0.9	0.850(0.798,0.883)	0.748(0.535,0.857)	0.807(0.589,0.881)	-	-	0.618(0.306,1.000)	-
0.95	0.925(0.899,0.941)	0.863(0.686,0.928)	0.917(0.752,0.951)	-	-	0.723(0.356,1.000)	-
AUC:	0.656(0.577,0.735)	0.699(0.594,0.803)	0.686(0.584,0.786)	-	-	0.744(0.447,0.858)	-

As a second example we consider CA19.9 measurements from a study conducted at the MD Anderson Cancer Center ([30]). Plasma samples were obtained from the University of Michigan Comprehensive Cancer Center, the University of California San Francisco, the University of Utah School of Medicine and the University of Texas MD Anderson Cancer Center. The purpose of the study is the evaluation of candidate protein based biomarkers for the diagnosis of early stage pancreatic cancer. We focus only on the CA19-9 marker for which a lower LOD yields approximately 15% left censoring. Since in this example only a small portion of the empirical ROC estimate is affected by the lower LOD, we use it as illustration by artificially censoring more measurements and hence observe how our methods would have captured the empirical ROC based on all observed data, which is expected to be closer to the true and uknown ROC curve. We impose an upper LOD that along with the original lower LOD yields a total of 55% censoring (see Figure 2b). For this example we focus on very low FPR values (=0.01, 0.02, 0.04, 0.05, 0.10) and provide point estimates for the corresponding sensitivity as well as percentile bootstrap based 95% confidence intervals for all approaches. Results are given in Table 1. For this example, we have the luxury of a ‘substitute’ for the truth, and we are able to compare how all approaches perform at these low FPR values. We can observe how our approaches capture the empirical based ROC curve that uses all data as compared to the naive empirical. This is nicely visualized in Figure 2b. The fact that the Naive empirical approach can be misleading is evident in this example. For FPR=0.01, 0.02, and 0.05 we observe that the sensitivity point estimates, as are provided by the Naive empirical, fail to lie within the 95% confidence intervals of all methods, including the ‘full’ empirical which takes into account all available data. We observe that the point estimates of the Box-Cox and the Kernel(BC) approach are fairly close to the ‘full’ empirical that takes into account all available data. For example, the Kernel(BC) approach yields TP̂R = 0.554, 0.613, and 0.633 for FPR=0.02, 0.04, and 0.05 respectively. The corresponding sensitivity estimates based on the ‘full’ empirical are 0.593, 0.686, and 0.721, while for the Naive empirical we get 0.182, 0.364, and 0.455 respectively. Conclusions are similar for the confidence intervals as well. There is an impressive overlap of the CIs obtained by our approaches with those obtained by the ‘full’ empirical, as opposed to those that are obtained by the Naive empirical. Regarding the GG method we observe that is very close to the ‘full’ empirical for FPR=0.05, 0.05 and 0.10 yielding TP̂R = 0.686, 0.721, 0.756 that are fairly similar to the TPR estimates provided by the ‘full’ empirical: 0.686, 0.7210, and 0.756 respectively. The similarity is also epressed in terms of overlap of the corresponding 95% CIs. However, it seems that for even lower FPR values: FPR = 0.01 and 0.02 the GG has some discrepancies compared to the full empirical, a disadvantage that is not expressed by the kernelBC which generally performs better as shown in our simulation studies.

9. Discussion

Cancer screening is commonly based on biomarkers related to technology that includes gene expression profiles based on microarrays and protein expression profiles based on mass spectroscopy (see [1]). During a research based assay (Phase I of biomarker development) such technological resources might be limited due to technical reasons and as a result limits of detection might be present. Improper evaluation techniques at this stage might yield deceiving results against a promising biomarker. As a consequence, a potentially good biomarker might fail to pass the criteria of Phase I, since a clinical assay might be a very expensive step to undertake. When LODs are present, one has to take into account the censored nature of the data during the estimation of the underlying ROC. In the case of a lower LOD, d_L, many researchers refer to the replacement value technique that involves imputing all scores to a value less than d_L, typically d_L/2 or d_L/√2 (see [11] for a discussion). However, if one is based on these imputed scores to construct the empirical ROC curve, then the resulting empirical estimate remains unchanged regardless the actual replacement value used. We show that the naive empirical approach is biased both in terms of AUC and in ROC(t) for any pair of replacement values chosen. Even if one aims to build a parametric ROC curve based on some assumptions justified by the data, the rational of such an imputation technique is vague, and in that case building the underlying likelihood by taking into account the censored nature of the data is more appropriate. Furthermore, such an approach is inapplicable when the data lie on the real line, which often can be the case. This is due to transformations such as the log, that are typically employed in such settings, and project intrinsically positive scores on the real line. In addition, even if the scores are actually positive, an upper LOD is not bounded by an upper bound so as to justify any kind of replacement value.

We investigate flexible parametric, power transformations, as well as spline based techniques. More specifically, we explore the generalized gamma distribution which is an umbrella for many known distributions typically used in the ROC framework. The nature of censoring, however, is not random. Random censoring would allow at least some fully observed measurements to be available in the tails of the distributions of the healthy and the diseased. Under the investigated setting, all censored data pile up at the point of the LOD, resulting in a black box as far as the corresponding tails of the underlying densities concerns. An approach that deals nicely with this problem, is the proposed Box-Cox approach. The rational behind it is that it manages to transform the scores of the healthy and the diseased to exhibit an approximate known distribution. Hence, we attain some information regarding the tails of the underlying transformed densities, and thus construct the Box-Cox based ROC. One may argue that the Box-Cox assumption cannot be justified by the data at hand. For that purpose we also investigate a hybrid approach, that involves both the Box-Cox and kernel smoothers to non-parametrically estimate the fully observed measurements, and to only rely on the Box-Cox transformation to impute the censored data that lie on the tails of the underlying densities. Both approaches yield nice results and outperform the naive empirical approach throughout. An additional spline based approach is also explored. The latter does not make any distributional assumptions for the data and attempts to extrapolate the cumulative hazard of the measurements of the healthy and the diseased. The price to pay is that it is less efficient that the Box-Cox and the Kernel(BC) approach. Our simulation studies indicate that the Box-Cox based approaches are to be preferred over the others. We note also that the naive empirical might offer a nice robust and computationally simple strategy to deal with settings where very poor or very accurate biomarkers are under study. The reason is that the tails of the underlying true ROC are almost linear in those cases.

Once the ROC estimate is obtained any subsequent measures such as the AUC, the maximized Youden index or its associated cutoff point can also be straightforwardly derived. We stress that our approaches are mainly focused on the early stage of biomarker discovery in which it is usual that resources are an issue and hence technological limitations might impose limits of detection. At this early stage we attempt to explore the potential usefulness of a given biomarker so that further exploration can be suggested which would imply spending more resources in specific technologies in order to alleviate any similar limitations at subsequent stages of a biomarker study and thus be able to derive the ROC at the full spectrum of the FPR values. Estimation and inference with respect to other measures such as an optimal cut-off based on some criterion, is not generally appropriate at this early stage. Under a limit of detection framework such an optimal cutoff might lie at the undetected region of FPRs. Therefore, estimation of such a crucial index that might be used for clinical decision making should not be based on extrapolation of any kind and should generally be avoided under the studied framework.

Our proposed approaches, as shown in the simulation studies, clearly outperform the Naive empirical method which under some assumptions that are stated in our proposition is negatively biased. Thus, our approaches can provide the methodology framework to reveal potential markers that otherwise might have been ‘killed’ in the early discovery stage due to the Naive empirical estimate. As a referee pointed out, the followed methodology is appropriate only in the search and evaluation of biomarker potential. Use of our approaches is not recommended when interest lies in the actual discriminatory ability of the markers, or when interest lies in comparing the actual discriminatory capacity of two biomarkers. Our approaches are extremely useful in providing the biomarker potential, based on which subsequent decision making regarding the improvement of technology can follow. Once the actual measurements are technically possible, then the aforementioned issues of the actual accuracy of the biomarkers can be appropriately addressed. Without the proposed methods, useful biomarkers might have been totally missed and discarded as uninformative due to the Naive empirical method that most practitioners follow.