Nanoscopic control and quantification of enantioselective optical forces

Circularly polarized light (CPL) exerts a force of different magnitude on left- and right-handed enantiomers, an effect that could be exploited for chiral resolution of chemical compounds^{1, 2, 3, 4, 5} as well as controlled assembly of chiral nanostructures^{6, 7}. However, enantioselective optical forces are challenging to control and quantify because their magnitude is extremely small (sub-piconewton) and varies in space with sub-micron resolution². Here we report on a technique to both strengthen and visualize these forces, using a chiral atomic force microscope (AFM) probe coupled to a plasmonic optical tweezer^{8, 9, 10, 11, 12, 13}. Illumination of the plasmonic tweezer with CPL exerts a force on the AFM tip that depends on the handedness of the light and the tip. In particular, for a left-handed chiral tip, transverse forces are attractive with left-CPL and repulsive with right-CPL; additionally, lateral force differences between different-handed specimens exceed 10pN. The AFM tip can map chiral forces with 2 nm lateral spatial resolution, revealing a distinct spatial distribution of forces for each handedness.

Chiral structures, which are non-superimposable with their mirror images, abound in nature at every size scale ^{14, 15} and have distinct functions that emerge from their structure. In molecular biology, for example, enantiomers can exhibit distinct interactions with cellular binding sites, resulting in beneficial or detrimental effects based on the molecular handedness. Recently, it has been shown that formation and separation of chiral compounds can be controlled with light^{3, 7, 16}. However, enantioselective optical forces are exceedingly weak, scaling with the volume of the sample; for nano-scale specimens, the predicted forces are on the sub-piconewton scale. Moreover, enantioselective optical forces are often linked with evanescent^{3, 17} or superchiral¹⁸ fields, with rapidly-varying spatial distributions on the sub-micron scale. To strengthen and visualize these forces, we combine a plasmonic optical tweezer with a chiral AFM probe. Our technique, termed chiral optical force microscopy (COFM), is shown in Figure 1a. We illuminate the tweezer from the bottom with controlled polarization states of light and scan the chiral AFM tip across the top.

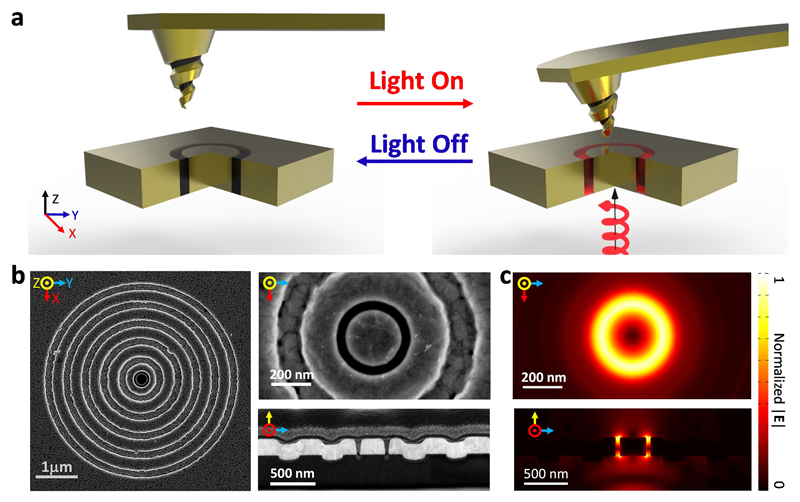
Figure 1. Schematic, microscopic images, and simulations.

a, Schematic illustration of enantioselective force mapping, where circularly polarized light illuminates a coaxial nano-aperture made of gold. b, Scanning electron microscope (SEM) images of grating-flanked coaxial nano-aperture. c, Finite difference time domain (FDTD, Lumerical) simulations of the field distribution on resonance.

In conventional AFM studies, force measurements are performed either with the tip in contact with the sample^{19, 20} or in tapping mode^{21, 22, 23, 24}. Instead, we use a quasi-noncontact method to increase the sensitivity and the range of forces that can be measured, as illustrated in Supplementary Fig. 1-2 (see Methods and Supplemental Note 1 for details). To locate the sample surface and thus fix the tip at a precise z-height above the tweezer, a non-oscillating tip first approaches the sample surface and then upon reaching the surface, retracts to a specified height. We then modulate the intensity of the incident light through the plasmonic tweezer at a frequency matching the cantilever’s natural resonance but much lower than the optical frequency of the illumination. This low-frequency modulation significantly improves the single-to-noise ratio and enables precise measurement of the cantilever deflection and thus the optical forces.

The coaxial plasmonic aperture functions as an optical tweezer which both enables precise control of the optical chirality density and enhances enantioselective optical forces^{25, 26,27}. Additionally, the resonance of the aperture can be easily tuned to the near infrared regime where biological samples have minimal absorption. We use numerical simulations (FDTD, Lumerical) to optimize the aperture geometry for transmission at ~770 nm, in the near-infrared window most desirable for potential bio-applications (Figure 1c and Figure 2a). As seen in Figure 1b, our optimized plasmonic nano-aperture consists of a 60 nm dielectric (air) ring embedded in a 220 nm thick gold film (see Methods for fabrication details). It is patterned with a concentric bull's eye grating to boost the transmission, thus increasing the near-field optical forces, and to narrow the angular spread of the transmitted beam^{25, 28}. White light transmission measurements confirm the transmission peak at ~770 nm, corresponding to the fundamental Fabry-Pérot resonance of the aperture (Figure 2a).

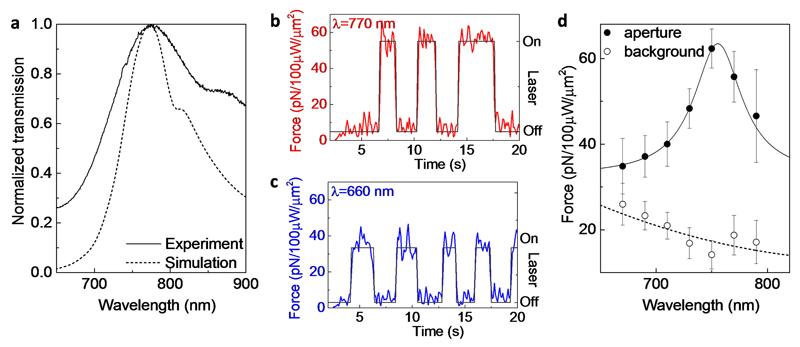
Figure 2. Spectroscopically measured optical forces with an achiral tip.

a, Normalized transmission spectra of the grating-flanked coaxial aperture shown in Figure 1b. The dotted curve is from numerical simulation (FDTD, Lumerical); the solid curve is from experimental measurement. The shoulder of the spectrum at longer wavelengths (~825-875 nm) comes from the converging beam interacting with the grating. The blue and red dashed lines highlight wavelengths of 660 nm and 770 nm, respectively. b, Measured optical force when the incident laser is at 770 nm, near the resonance of the coaxial aperture. The laser is manually toggled on and off (black line) to confirm the fidelity of the measurement. c, Measured optical force away from the coaxial resonance at 660 nm. d, Spectroscopic measurement of optical forces at the aperture and away from the aperture, where the on-aperture measurement follows the spectrum of the aperture. The error bars show standard deviations of measured forces at each wavelength. The solid and dashed curves are Lorentzian and polynomial fits, respectively.

Before probing the plasmonic tweezer with a chiral AFM tip, we use an achiral tip to measure the optical forces emanating from the aperture. With a fixed tip-aperture separation of 50 nm and the tip parked in one position over the dielectric channel (see Supplementary Fig. 3), we illuminate the tweezer at 770 nm with unpolarized light and toggle the source on and off with a rate far below that of the optical resonance. Forces of 55.3±3.9 pN are measured with an achiral silicon AFM probe and correspond with the on/off pattern of the laser, confirming their optical origin (Figure 2b). We then repeat the same measurement at an off-resonance wavelength of 660 nm (Figure 2c), and the measured force again follows the illumination pattern of the laser. However, this force has a mean value 35.8±4.7 pN, ~40% lower compared to forces on-resonance.

By sweeping the wavelength of the incident laser, we observe that the optical forces on the tip clearly follow the coaxial resonance (Figure 2d). To determine the background signal, we repeat the same measurement at a location away from the aperture on the gold surface. As expected, the background signal does not show any spectral peaks (Figure 2d). However, it does trend upwards at shorter wavelengths, corresponding to the optical absorption of the gold film. These results confirm that our spectroscopic force measurement has sufficient sensitivity to measure optical forces originating from our plasmonic optical tweezer.

To explore the effect of CPL, we illuminate our plasmonic optical tweezer with left- and right-handed CPL and then probe the transmitted near-fields as a function of tip-aperture separation with the same achiral AFM tip (Figure 3a). Figure 3c shows that the forces resulting from left- and right-CPL closely follow each other with the same spatial decay, indicating that the optical forces exerted on this AFM tip are nearly indistinguishable. The small difference between the forces induced by left- and right-CPL arises from the slightly asymmetric shape of the tip (Figure 3a), which imparts very weak chirality²⁹.

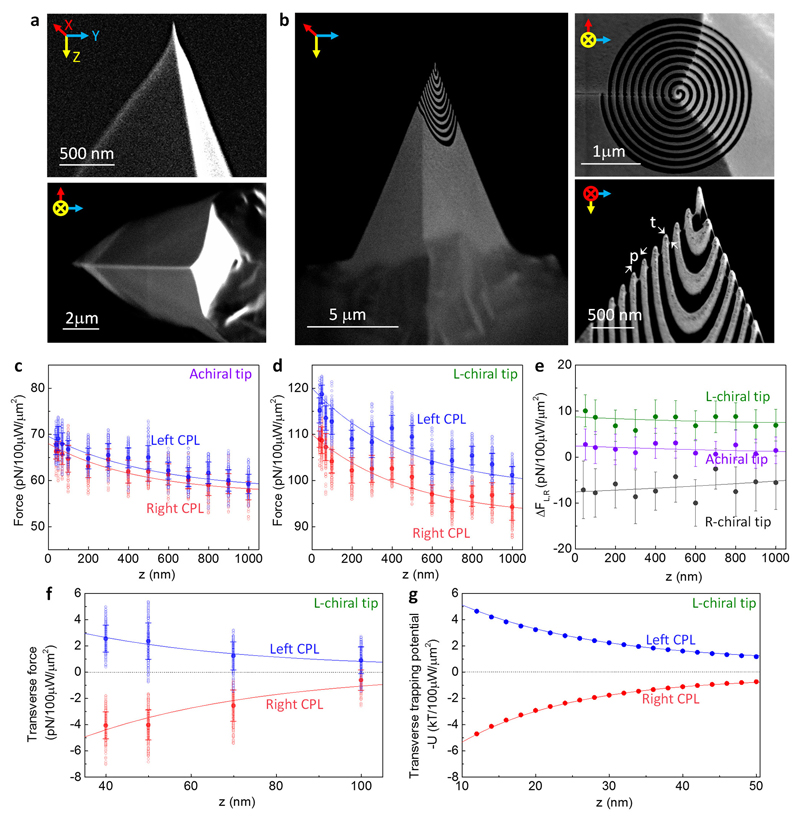
Figure 3. Enantioselective optical forces with achiral and chiral tips.

a, SEM images of an achiral silicon tip. b, SEM images of a chiral tip, which is made with focused ion milling (see Methods). “t” denotes thickness of the gold coating; “p” is the period of the spiral. c, Measured optical forces using the achiral tip with left-handed (blue) and right-handed (red) CPL, at 750 nm. d, Measured optical force using the chiral tip with left-handed CPL (blue), and right-handed CPL (red). e, Comparison of the enantio-selectivity in the measured force (difference in the forces with left- and right-handed illumination), with both achiral and chiral tips. f, Measured transverse forces with the chiral tip, with left-handed (blue) and right-handed (red) CPL illumination. In all panels, the void dots are raw data, the solid dots are mean values, and error bars show standard deviations. The solid curves in panels (c), (d), and (f) are fitted with exponential decay equations, while solid curves in panel (e) are fitted with polynomial equations. g, Simulated transverse trapping potentials exerted from the coaxial aperture on a chiral nanoparticle with size comparable to the AFM tip radius. Note that we plot the negative of the trapping potential to emphasize the similar trend as the measurements.

To quantify the enantioselective forces acting on a chiral specimen, we introduce structural chirality in the probe by first depositing a thin metallic film on the AFM tip and then using a focused ion beam to mill a spiral pattern with a period of p = 155 nm (Figure 3b). Both left-handed (L) and right-handed (R) tips are patterned. The results below describe the detail response of a gold L spiral tip, and the Supplemental Information describes the response of the R spiral tip as well as tips made of non-plasmonic materials (Supplementary Fig. 5-7). During the force measurement, the spiral tip acts as a chiral specimen that interacts with the local electromagnetic fields. Although the tip is inherently non-magnetic (i.e. relative permeability μ_r = 1), CPL induces a circulating current due to the structural chirality³⁰. The resulting magnetic dipole moment interacts with the electric dipole moment, giving rise to an additional force that is proportional to the chirality of the specimen. For left- versus right-handed enantiomers, this additional chiral force is opposite in sign (see Supplemental Note 8 for a full theoretical description).

To measure the enantioselective optical force on our L-chiral tip, we illuminate the aperture with left- and right-CPL and probe different z-heights above the sample. As seen in Figure 3d, the force resulting from left-CPL is significantly larger than that resulting from right-CPL. Our COFM setup enables us to quantify the enantiomeric force differences at each z-position over the sample: Figure 3e shows that a differential force of up to 10±3.5 pN is observed on the L-chiral tip, compared to 2.7±3.3 pN observed with the achiral tip and up to -9.9±5.1 pN with the R-chiral tip. Such differential forces also indicate that optical forces exerted through this achiral coaxial aperture can selectively trap a specimen based on its chirality.

We also find that the transverse forces exerted by left- and right-CPL have opposite signs as a function of z-height. Figure 3f shows that a chiral specimen placed at a given z-height above the aperture will be pulled towards the aperture when exposed to left-CPL, but pushed away when exposed to right-CPL. Indeed, finite-difference-time-domain (FDTD) simulations confirm that left- and right-CPL respectively give rise to attractive and repulsive trapping potentials (Figure 3g).

Next, we leverage our high-resolution COFM technique to directly visualize enantioselective optical forces. By scanning the chiral tip over a quadrant of our optical tweezer while illuminating with left- or right-CPL, we create full two-dimensional force maps, for each handedness, with 2 nm spatial precision. Figures 4a and b show that the normalized optical force exerted with left-CPL (Figure 4a) is substantially stronger than that with right-CPL (Figure 4b), and FDTD simulations (Figure 4c and d) corroborate this trend. These measurements confirm that the optical forces emanate from the dielectric channel of the coaxial aperture, and not simply from the gold film. Note that each force map is normalized to the mean force measured across an area of 70 × 70 nm² on the gold film in the center of the coax, highlighting the favorable signal-to-background ratio afforded by this technique.

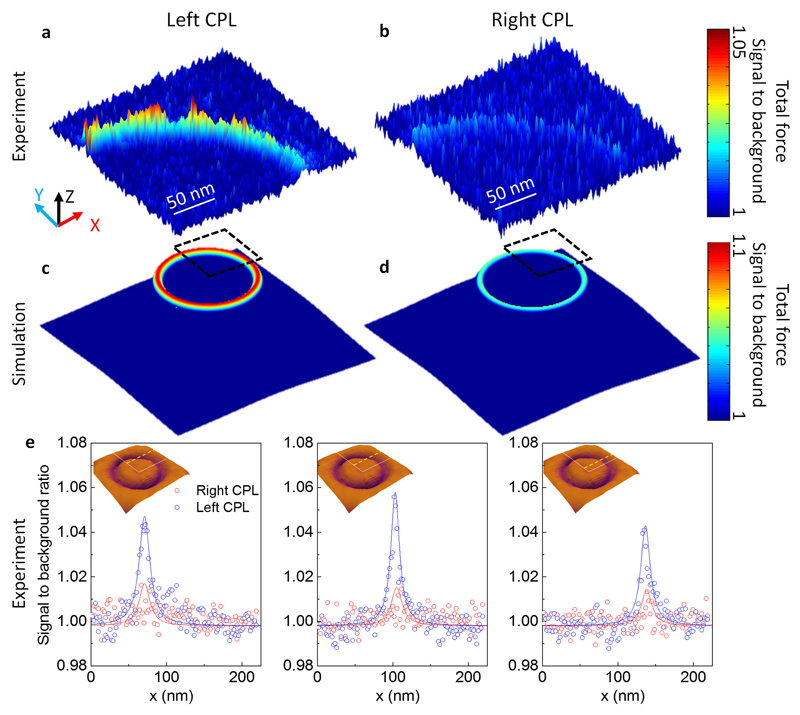
Figure 4. Enantioselective optical force map.

a, A quadrant of an experimental chiral force map on the coaxial nano-aperture with left-CPL illumination. b, Force map with the same chiral tip, but with right-CPL illumination. Both panels (a) and (b) are total forces normalized to the background signal, and plotted in linear scale with ranges indicated in the color bar to the right. c, Simulated optical forces with left-CPL and d, right-CPL illumination on the optical tweezer. The dashed square indicates the quadrant where the optical force map is experimentally measured. e, Normalized measured forces (signal-to-background ratio) in linear scale, along three horizontal locations across the coaxial aperture. The location of each line scan is indicated by the yellow dashed line in the inset, overlaid on the AFM topological map. The white lines in the inset indicate the quadrant of the coaxial aperture where the optical force maps are taken.

To further quantify the signal-to-background for both CPL illumination conditions, we take individual one-dimensional line scans across the dielectric channel. Three representative line-scans are shown in Figure 4e for left-CPL (blue dots) and right-CPL (red dots); the position of the scans is shown by dotted lines in the inset AFM topographical maps. As seen, near the aperture, the optical forces generated from left-CPL are 3 times stronger than those with right-CPL.

In summary, we have demonstrated a technique for enhancing and quantifying enantioselective optical forces. Using a chiral AFM probe to interrogate an achiral coaxial nano-aperture, we show that the optical forces are highly dependent on the handedness of the illumination as well as the chirality of the probe. Our control experiments with achiral probes demonstrate a negligible difference between the optical forces with left- and right-CPL illumination, confirming that the chirality-dependent optical forces arise both from the chirality of the probe as well as the local chirality density of the optical field. We envision that the capability to directly quantify and map piconewton chiral optical forces will enable new ways to study chiral materials and fields. For example, by functionalizing an achiral probe with a chiral molecule or nanoparticle, the optical forces exerted on that specimen could be measured. By monitoring changes in the force, conformational changes in the specimen might be detected in real time. Finally, measuring the force difference on enantiomeric pairs could lead to chiral sorting and optically-controlled enantiopure chemical syntheses.

Methods

Optical force measurement

The experimental schematic is shown in Supplementary Fig. 1 with additional detailed descriptions in the Supplemental Note 1. Briefly, the AFM (Asylum Research MFP-3D Bio) is integrated with an inverted microscope (Zeiss, Axio Observer Z1m). The unit is mounted within a temperature and vibration control chamber, where a temperature-stabilized heat reservoir is set to be ~5°C above room temperature with a temperature precision of 0.1°C and equilibrated with the sample for 10 hours before measurement; this setup is used to minimize expansion and contraction of the sample and the tip. A tunable laser source is fiber-coupled (multimode, Thorlabs) into the chamber, and then collimated with a reflective collimator (RC08APC-P01, Thorlabs). Circularly polarized light is created by passing the collimated beam through a linear polarizer (GT10-B Glan Taylor Polarizer, Thorlabs) and a quarter wave plate (AQWP05M-600, Thorlabs). The laser beam is focused with a 50x objective lens (NA=0.55, Zeiss) onto the glass substrate with the coaxial nano-aperture.

During the force measurement, we first locate a specific height above the surface by performing a force-distance curve. Then, at a designated height, we modulate the incident light through the coaxial aperture at a frequency that matches the cantilever's natural resonance (see Supplementary Fig. 2 and Note 1 for more details of the measurement). Light is modulated with an acousto-optic modulator (AOMO 3110-191, Gooch & Housego), where the modulation signal is connected to the reference of a lock-in amplifier (SRS 865, Stanford Research Systems). The cantilever deflection signal is routed from the AFM controller (ARC2), connected to the input of the lock-in amplifier. The measurement time frame is ~ 5 minutes for mapping in Figure 4, and ~10 seconds for single point force measurement in Figures 2-3. An uncoated silicon AFM tip is used for achiral force measurement (PPP-FM, Nanosensors) with a spring constant of 1.44 nN/nm and a fundamental resonance at 64.167 kHz (shown in Figure 3). Additional control experiments measured with silicon tip, achiral and chiral gold-coated tips, and chiral non-plasmonic tip under various illumination conditions are shown in Supplementary Notes 2 to 7.

Statistics of measurements: all measurements data are scaled to 100 μW/μm² input intensity for simplicity. Input intensity is monitored during the measurement with a beam-splitter and the mean value of the input intensity is used in the normalization. The actual input intensities range from 18 μW/μm² up to 53 μW/μm² during multiple sets of experiments. As seen in Figure 3, we display randomly down-sampled raw data during the measurements, with the standard deviation and mean values calculated from all the raw data over each tip-aperture separation.

Coaxial nano-aperture fabrication and chiral tip fabrication

Coaxial nano-aperture: we start with an optical flat glass substrate (C1737-1107, Delta Technologies). The substrate is first rinsed in deionized water and sonicated for 15 minutes, followed by a base piranha clean (5:1:1=H₂O:NH₄OH:H₂O₂) for another 15 minutes at 65 °C, then dried with compressed air. After cleaning, a 50 nm layer of chromium is sputtered on the substrate as a hard mask. Using focused ion beam (FIB) milling (Helios 660i, FEI) at 7.7 pA and 30 keV accelerating voltage, the peripheral grating is patterned into the glass coverslip, with a grating period of 500 nm, and depth of etching of 60 nm. After patterning, the chromium mask is removed through wet etching (Chromium Etchant 1020AC, Transene Company, Inc.). Titanium (3 nm) and gold (220 nm) are subsequently sputtered on the sample. Lastly, the coaxial aperture is fabricated at the center of the grating using FIB milling (1 pA, 30 keV). The coaxial aperture has an inner diameter of 270 nm and an outer diameter of 330 nm, with a 6º tapering angle that comes from the ion beam.

Chiral tip: Gold-coated silicon cantilevers are commercially available (Nanosensors, PPP-FMAu) with the same spring constant and shape as the uncoated silicon cantilever. The gold coating is ~35 nm thick (marked as "t" in the SEM in Figure 3b) and uniformly covers the front and back sides of the cantilever. The nano-spiral pattern has 10 spiral periods, and an edge-to-edge dimension of ~2.5 μm; if fabricated on a planner surface, within one period, the gold spiral has a width of ~74.2 nm and the gap between the gold spirals is ~38.2 nm. We pattern this nano-spiral on the AFM tip with focused ion beam milling (FEI Helios 660i), with a beam current of 1 pA and accelerating voltage of 30 kV for 1 minute and 55 seconds. When the pattern is transferred to the AFM tip, the spiral period is elongated due to the facet angle of the AFM tip; the final period is ~155 nm (marked as "p" in Figure 3b).