Abstract
Spectral imaging technologies have been used for many years by the remote sensing community. More recently, these approaches have been applied to biomedical problems, where they have shown great promise. However, biomedical spectral imaging has been complicated by the high variance of biological data and the reduced ability to construct test scenarios with fixed ground truths. Hence, it has been difficult to objectively assess and compare biomedical spectral imaging assays and technologies. Here, we present a standardized methodology that allows assessment of the performance of biomedical spectral imaging equipment, assays, and analysis algorithms. This methodology incorporates real experimental data and a theoretical sensitivity analysis, preserving the variability present in biomedical image data. We demonstrate that this approach can be applied in several ways: to compare the effectiveness of spectral analysis algorithms, to compare the response of different imaging platforms, and to assess the level of target signature required to achieve a desired performance. Results indicate that it is possible to compare even very different hardware platforms using this methodology. Future applications could include a range of optimization tasks, such as maximizing detection sensitivity or acquisition speed, providing high utility for investigators ranging from design engineers to biomedical scientists.
Keywords: Spectral, Spectroscopy, Microscopy, Linear Unmixing, Spectral Angle Mapper, Constrained Energy Minimization, Matched Filter
1. Introduction
Spectral imaging was developed by NASA and the DoD for remote sensing and aerial surveillance [1–7] and applications in the remote sensing field continue to comprise a large portion of the spectral imaging market. However, within the last 2 decades, many new applications of spectral imaging have been described, especially in the biomedical imaging field [8–12]. Microscope-based spectral imaging systems have been in use for use over a decade [9, 10, 13–18], while small in vivo animal imaging has also grown in use [19–25]. In fact, several commercial systems are now available (spectral microscope systems include, but are not limited to, those marketed by Nikon, Olympus, Zeiss, Lightform, and Cytoviva, which utilize spectral imaging detectors, while a subset of confocal spectral imaging microscopes also allow laser lines to be selected using an acousto-optic tunable filter, or AOTF). Potential use of spectral imaging for clinical applications has also been described, with great potential for detection of pathologic tissues such as cancer [26–30]. The focus of biomedical spectral imaging has been on the detection of either specific molecules (also called molecular imaging) or in detecting overall changes in a complex mixture (e.g., changes in spectral fingerprint of tissue autofluorescence).
A wide range of analysis approaches has been developed by the remote sensing field to understand, interpret, and classify spectral image data [3, 31–37]. These include approaches to assess pixel composition such as linear unmixing (also called sub-pixel analysis approaches) [38–40], supervised classification approaches such as neural networks [41–43] and machine learning [44–47], unsupervised classification approaches that include principle component analysis (PCA) and independent component analysis (ICA) –based approaches [4, 48, 49], and others [31, 50–53]. In addition, algorithms for pre-processing of spectral image data have also been developed to increase the effectiveness of target detection and composition assessment [54–56].
A range of analysis approaches have also been demonstrated for biomedical spectral imaging applications, including unmixing [8, 57–59], PCA and similar approaches [58, 60–62], and others [29, 63, 64]. However, only a limited amount of research has been performed to apply many of the spectral image processing algorithms developed by the remote sensing community to biomedical applications [10]. Even less work has been done to quantitatively assess the effectiveness of spectral image analysis algorithms as applied to biological image data or to compare algorithms or spectral imaging systems to each other [10, 65–67]. Hence, it is not always clear which spectral imaging platform or analysis algorithm should be used for a particular biomedical imaging application.
From this brief comparison of remote sensing and biomedical spectral imaging, two limiting and compounding issues are apparent. First, it is clear that the full range of possibilities for spectral analysis, as described in remote sensing literature, have not been evaluated or translated for use by the biomedical imaging community. A likely contributor to this issue is that most microscope applications and many of the proposed clinical applications use fluorescence, which is typically assumed to be a linear process with respect to molecular concentration [8, 57, 58, 68]. Hence, linear unmixing is assumed to be appropriate and has been extensively used as the approach of choice in biomedical spectral imaging. Second, the variability of biomedical spectral imaging applications and hardware has made it difficult to quantitatively compare the effectiveness of different analysis approaches. Hence, it may be difficult to assess which approach is best for a given biomedical spectral imaging scenario [65].
A complicating factor is that determination of ground truths in biological samples are often difficult (if not impossible) to make [69]. In remote sensing approaches, it is often straight-forward to evaluate one or several detection scenarios by simply placing or modifying ground truth objects. For example, if one would like to test the feasibility for detecting a vehicle when it is coated with different camouflage materials, it is easy to place several variations of camouflage side-by-side and then image them with a ground or aerial-based hyperspectral imager [70]. By contrast, it is very difficult to place a reference concentration of GFP molecules side-by-side with a reference concentration of RFP molecules within a single cell or tissue, so that one would know with absolute truth that the pixels corresponding to region 1 each represent 10 µM GFP and those corresponding to region 2 each represent 10 µM RFP. In microscopy, when external labels are used, it is possible to compile a library of all known labels added to a sample, but it is difficult to create a cellular sample where the composition of each pixel is known a priori. In addition, even in the case where the library is known a priori, unknown signatures may arise due to cellular autofluorescence [71–75], background or stray light, and modifications to the spectral properties of exogenous labels due to changes in pH, ROS, etc. [76–78]. Although techniques like fluorescence lifetime imaging (FLIM) can be used with specialized probes to measure changes in pH [79, 80], these techniques are also limited when a priori information is not available for all fluorophores in a sample. When imaging tissue preparations, either in microscopy or in pre-clinical or clinical applications, compiling an a priori spectral library becomes much more difficult as autofluorescence is usually variable and non-negligible [62, 71, 75, 81, 82]. In addition, for some scenarios, the autofluorescence signature itself is the parameter of interest, and it may be difficult to accurately assemble a spectral library containing either the signatures of all molecules that contribute to tissue autofluorescence or an accurate sampling of all of the possible autofluorescence spectral signatures that could be encountered. In these cases the spectral analysis problem may be overdefined and a unique solution may not be possible. In addition to the factors of ground truths and autofluorescence, biomedical preparations of tissues may be complicated by additional factors of light scatter and absorbance. These factors may create wavelength-dependent changes in the optical path-length or transmission properties of the sample, introducing optical non-linearities and complicating the separation of fluorescence optical properties from scatter- and absorbance-dependent optical properties [39, 83, 84].
The need for an objective methodology to evaluate and compare the effectiveness of spectral imaging and analysis approaches for biomedical applications is clear. Ideally, a standardized method would allow comparison and optimization of analysis algorithms, acquisition parameters, hardware systems, and effects of data pre-processing with objective and consistent parameters to evaluate the effectiveness of each option. Such a methodology would facilitate further translation of analysis approaches from the remote sensing to the biomedical imaging field and could be a critical tool for optimization of potential spectral imaging hardware or software.
In this paper, we present a method for theoretically assessing the experimental sensitivity of a spectral imaging approach for detecting a specific signature in biomedical spectral image data. This theoretical sensitivity analysis methodology allows quantitative assessment of the detection sensitivity and specificity using a set of standardized metrics that can be computed, regardless of the analysis algorithm or hardware used. This methodology allows quantitative characterization of the detection sensitivity and specificity for a given biological label or signature. In addition, we have designed the analysis to incorporate the natural biological variability in a sample, as the analysis is based not on purely theoretical estimates of signal and noise, but on image data acquired from biological control samples. As we demonstrate in the results of this study, the outcomes of the theoretical sensitivity analysis methodology can be used to provide a quantitative and objective comparison between different spectral analysis algorithms, different equipment settings, or even entirely different hardware configurations, all in terms of the ability to detect a specific molecular signature in a biomedical sample.
2. Methods
2.1. Theoretical background
The theoretical sensitivity analysis methodology described in this paper may be used to assess a wide range of scenarios, from comparing analysis algorithms to selecting an optimal spectral imaging platform and acquisition settings. As examples of how the methodology may be used, we have compared 4 spectral analysis algorithms that are well described in prior literature. These algorithms may present high potential interest for the biological spectral imaging community as they have either been extensively used within this community (linear unmixing), are very high speed and could be applied in real-time (spectral angle mapper), or may be able to more accurately separate unwanted background signatures such as autofluorescence from a desired target signature (constrained energy minimization and matched filter). Here, we give a brief theoretical overview of these algorithms, noting that more detailed descriptions are available in the original literature as well as several textbooks. Of particular interest is that, although these analysis algorithms have been well-documented for remote sensing applications, little work has been done to quantitatively compare the effectiveness of each algorithm for biomedical spectral image analysis.
2.2. Terminology
As the target audience for this paper crosses several interdisciplinary fields (remote sensing, biomedical imaging, microscopy, clinical imaging) we have added a brief description and table of spectral imaging terms and variables (Table 1). The following matrix nomenclature will be used: spectral image, x, with dimensions k × l × n (width × height × wavelength bands), where a single pixel spectrum (pixel vector) is denoted by of x⃗; spectral library r, with dimensions m × n (number of endmembers × wavelength bands), where a single component spectrum of the library is denoted by r⃗.
Table 1.
Nomenclature used in this manuscript
| Term | Description |
| Endmember | A spectral component of an image. This is often either an exogenously added dye, a fluorescent protein, or tissue autofluorescence. |
| Target | Target refers to a specific endmember of interest. This could be one fluorescent label, for which a particular study was designed to detect. |
| Signature, fingerprint | Both of these terms refer to the spectral shape of a given endmember. |
| Symbol | Variable |
| k | Image width (pixels) |
| l | Image height (pixels) |
| m | Number of endmembers |
| n | Number of spectral bands |
| w | Noise |
| I | Intensity |
| r⃗ | Endmember spectrum |
| r | Spectral library |
| x⃗ | Measured pixel spectrum |
| x⃗′ | Measured pixel spectrum for modified pixel within a region of interest (contains pixel + target endmember spectrum) |
| x | Spectral image |
| a | Abundance |
| Rcorr | Sample correlation matrix |
| U | Undesired spectra (spectral library with target endmember spectrum removed) |
| P | MTMF rejection operator |
| q⃗ | MTMF filter operator |
2.2.1. Linear Unmixing
Linear unmixing is the most common analysis technique used in biomedical spectral imaging applications. This is because linear unmixing calculates the abundance of each molecular species (endmember) in each pixel, assuming a linear mixing model[39]. For biomedical applications linear unmixing allows estimation of the relative concentration of each molecule in each pixel. Linear unmixing is typically implemented using a spectral library (acquired a priori from control samples) and using least-squares regression with a non-negativity constraint[39]. Historically, this technique was used in remote sensing to calculate abundances of vegetation, water, land, or other features in aerial images[85]. Linear unmixing has also been used in fluorescence microscopy and in vivo imaging[9]. An advantage of linear unmixing is that abundances can be obtained for all known endmembers. However, for linear unmixing to be effective, spectra from all endmembers must be known a priori, and error can arise if additional unexpected endmembers are present. Error may also be introduced if the spectrum of an endmember varies spatially, within the image. This is particularly relevant for cellular and tissue autofluorescence, where autofluorescence spectra may change dramatically from one tissue to another[86].
Non-negatively constrained linear unmixing was implemented using the “lsqnonneg” function in MATLAB (The MathWorks, Inc., Natick, MA). In brief, this function satisfies the following equation using a least-squares approach,
| (1) |
where x⃗ is the detected pixel spectrum vector and is a summation of the fractional abundance for each endmember (ai) multiplied by the respective endmember spectrum (r⃗i) plus the additive observation noise vector (w⃗).
2.2.2. Spectral Angle Mapper
Spectral Angle Mapper (SAM) is a classification algorithm that can be more insensitive to small spectral changes than linear unmixing [43]. SAM was first used for satellite image data analysis in the Spectral Image Processing System (SIPS) program in 1993 [3]. An advantage of SAM is that only the target endmember spectrum need be known. All pixels in the image are described based on their angular separation from the target endmember. This is especially useful in satellite imagery where endmember (e.g. vegetation) spectra can vary slightly depending on elevation, soil chemistry, moisture content, etc. [87, 88] SAM analysis produces angle images that show the variation between the target spectral signature and the measured signature of each pixel. A classification decision is then made, typically using a global threshold. The threshold is selected so that angles above the threshold are classified negative and angles below the threshold are positive. A receiver-operator curve (ROC) can be used to select threshold values [89, 90], and the theoretical sensitivity analysis shown here offers additional data that may be used for refining a classification threshold level.
SAM was implemented using a custom MATLAB script to calculate the arccosine between the measured pixel spectrum and the ith endmember spectrum [3].
| (2) |
2.2.3. Constrained Energy Minimization
Constrained Energy Minimization (CEM) applies a mathematical filter to amplify the desired spectral signature while minimizing background noise[50, 91]. This is done by applying an optical linear operator, LCEM that minimizes the intensity of unwanted signatures and amplifies the desired signatures.
| (3) |
where Rcorr−1 is the inverse of the sample correlation matrix of the observation pixel vectors[50], and was calculated as:
| (4) |
2.2.4. Mixture-Tuned Matched Filter
Mixture-Tuned Matched Filter (MTMF) partially unmixes one desired endmember from an image and maximizes its intensity while minimizing all other signatures [10, 92]. Similar to CEM, this technique is useful in quantifying the abundance of a known spectral signature where other spectral signatures may crowd the desired signal [93]. However, unlike CEM, MTMF magnifies the signal-to-noise ratio of the desired signature instead of only minimizing undesired signals. MTMF has been used in satellite imagery to determine the abundance of leafy spurge in aerial images [94]. While a small library of known spectra can be used to unmix the data with higher specificity than only using the target endmember, no prior knowledge of all constituent spectra is necessary[29]. Similar to CEM, MTMF may be advantageous for biomedical applications when a priori information is not known concerning all endmembers in the image, and for example, could allow screening for a specific biomolecule across a range of samples or tissue types.
The MTMF algorithm calculates a rejection operator, P, to increase SNR for a specific signature while minimizing background signatures, as described in [31]:
| (5) |
where U represents all signatures in the spectral library except the target signature (e.g., undesired signatures),
| (6) |
and U# is the pseudo-inverse of U,
| (7) |
The filter operator is calculated as,
| (8) |
and the product of the rejection operator and the measured pixel spectrum results in the matched filter estimated abundance,
| (9) |
2.3. Cell and Tissue Preparation
To demonstrate the theoretical sensitivity analysis methodology, several sets of previously-acquired spectral image data were used, acquired from samples demonstrating a common biomedical imaging problem – detection of a weak fluorescence signal (GFP-expressing cells) in the presence of high background autofluorescence (lung tissue). The cell and tissue preparation has been described in detail elsewhere[96, 97]. In brief, pulmonary microvascular endothelial cells (PMVECs) were isolated from CD rats. Cells were transfected for 48 hours with a lentivirus encoding GFP and further sorted by fluorescence activated cell sorting (FACS) to select GFP-expressing PMVECs. Both GFP-expressing and non-GFP expressing PMVECs were grown to confluency and suspended in phosphate-buffered saline (PBS) prior to use.
All animal and tissue resection procedures were carried out in accordance with Institutional Animal Care and Use Committee (IACUC) approved protocols and have also been described elsewhere[96–98]. In brief, male CD rats were anaesthetized and placed on mechanical ventilation. The pulmonary artery and left atrium were then cannulated and rinsed with 50 mL saline solution. Following rinse, a volume containing either 3 million GFP-expressing PMVECs or 3-million non-GFP-expressing PMVECs, suspended in PBS, was perfused into the lungs for 5 minutes. Perfused lungs were fixed in OCT, cryosectioned to 10 µm thickness, and mounted for imaging. A subset of slices were labeled with Hoechst 33342. For this study, spectral image data of control samples of lung perfused with non-GFP-expressing PMVECs were used, along with a library of pure spectra acquired from a confluent monolayer of GFP-expressing cells (GFP spectrum), from a confluent monolayer of non-GFP-expressing cells that were labeled with Hoechst 33342 (Hoechst spectrum) and from a tissue cryoslice of lung perfused only with PBS (autofluorescence spectrum).
To experimentally validate the results from the theoretical sensitivity curve analysis, a series of time-dependent update studies was conducted. HEK293 cells were grown to confluence on 25 mm round coverslips. Cells were labeled with 2 drops/mL NucBlue (Molecular Probes, ThermoFisher Scientific, Waltham, MA) and incubated for 20 minutes prior to imaging. During imaging, cells were labeled with 3.33 µM Calcein Green, AM (Molecular Probes, ThermoFisher Scientific) at a time point of 1 minute and time-lapse spectral image data were acquired for 30 minutes, as described below.
2.4. Hyperspectral Imaging Microscopy
Hyperspectral image data were acquired using several different spectral imaging microscope systems. For imaging of GFP-expressing cells in lung cryoslice preparations, images were acquired using a custom widefield inverted fluorescence microscope platform (TE2000-U, Nikon Instruments, Melville, NY) and 40× oil-immersion objective (S Fluor, 40×/1.30 Oil, DIC H/N2, Nikon Instruments). Custom long-pass fluorescence filter cubes were used to separate fluorescence excitation and emission, as are described in detail below. The microscope was configured in each of 3 ways to evaluate different equipment response characteristics.
An acousto-optic tunable filter (AOTF) based system (HSi-300 Hyperspectral Imaging System, ChromoDynamics, Orlando, FL) placed on the emission side of the microscope and coupled with an EMCCD camera (Cascade 512B, Photometrics, San Diego, CA). The AOTF system operates by deflecting a narrow portion of the spectrum via photon-phonon interactions, as has been described previously [24, 99–103]. This system was implemented with a 8.5 nm full-width at half maximum (FWHM) bandwidth and was sequentially tuned through emission wavelength bands, while the EMCCD camera acquired images at each wavelength band. Spectral image data were acquired from 450–700 nm, at 5 nm increments. A 458 nm long-pass filter cube was utilized that consisted of a long-pass dichroic beamsplitter (FF-458-Di02, Semrock, Inc., Rochester, NY) and long-pass emission filter (BLP01-458R, Semrock, Inc.). The wavelength accuracy, spectral resolution, and wavelength-dependent response of this system have been previously documented [96, 97]. In brief, this system provides accurate wavelength reproducibility and the ability to vary the bandwidth. When set to a bandwidth of 8.5 nm FWHM it achieved an average of 25% transmission and an out-of-band optical density (OD) ranging from 2 to 2.75.
A thin-film tunable filter (TFTF) based system (VersaChrome®, Semrock Inc.), placed on the emission side of the microscope and coupled with an EMCCD camera (Rolera EM-C2, QImaging, Surrey, British Columbia). The TFTF system operates by selecting an 18–20 FWHM band with a center wavelength that is dependent on the angle of incidence between the emitted light and the filter. An array of TFTF VersaChrome filters was utilized, each with a tuning range of approximately 50–60 nm, so as to be able to tune through a wide range of wavelengths. A 495 nm long-pass filter cube was utilized that consisted of a long-pass dichroic beamsplitter (FF-495-Di03, Semrock, Inc., Rochester, NY) and long-pass emission filter (BLP01-495R, Semrock, Inc.) [97, 104]. The wavelength accuracy, spectral resolution, and wavelength-dependent response of this system have been previously documented [97, 104]. In brief, this system provides accurate wavelength reproducibility, a bandwidth of 18–20 nm FWHM, an average of 80–95% transmission and an out-of-band optical density (OD) ranging from 2.5 to 3.
A thin-film tunable filter based system similar to #2, but placed on the excitation side of the microscope, directly coupled to a Xe arclamp (Titan 300, Sunoptic Technologies, Jacksonville, Florida) and coupled to the microscope using a liquid light guide (Sutter Instrument Company, Novato, CA). Images were acquired using an EMCCD camera (Rolera EM-C2) [67, 86].
For imaging of NucBlue and Calcein Green labeled HEK293 cells, coverslips were mounted in Attofluor Cell Chambers (ThermoFisher Scientific, Waltham, MA), maintained in 1× PBS, and imaged using a Nikon A1R spectral confocal microscope (Nikon Instruments) equipped with 60× water immersion objective (Plan Apo VC 60× DIC N2 WI NA - 1.2, Nikon Instruments) and 32 channel photomultiplier tube (PMT) array. The A1R spectral detector operates by selecting 1 of 3 available diffraction gratings and dispersing the fluorescence emission from the grating onto the 32 channel PMT. Fluorescence was excited using a 405 nm laser and spectral image data were acquired from 414–714 nm in 10 nm increments. For Calcein Green update studies, time-lapse image data of NucBlue labeled HEK293 cells were acquired every 30 seconds for 30 minutes with Calcein Green stain added at 1 minute.
2.5. Spectral Data Pre-Processing
Many spectral imaging systems have a wavelength-dependent transmission efficiency that produces spectral image data that is modified by the wavelength-dependent transfer function of the system. To correct for wavelength-dependent transmission artifacts, spectral image data were multiplied by a correction coefficient that was measured in reference to a NIST-traceable spectral illumination source. This was done by first measuring the wavelength-dependent system response using a fiber-coupled spectrometer (QE65000, Ocean Optics, Dunedin, FL) with integrating sphere and a NIST-traceable lamp (LS-1-CAL-INT, Ocean Optics), as described elsewhere[67, 96, 97]. In brief, the spectral response of either the emission-scanning or the excitation-scanning side of the microscope was measured and a correction factor calculated to correct image data to a flat spectral response. Raw spectral image data were corrected by first subtracting the background signal (to correct for stray or ambient light) and then by multiplying by the correction factor. All image correction was performed using custom scripts written in MATLAB. Spectral confocal image data were not corrected in this manner, as the spectral detector of the Nikon A1R microscope is marketed as NIST-calibrated.
2.6. Spectral Image Analysis
Custom MATLAB scripts were implemented for each of the 4 analysis algorithms described in the Theory section.
2.7. Theoretical Sensitivity Analysis Methodology
The theoretical sensitivity analysis methodology was implemented by first selecting a region of interest within a control spectral image that contained all spectral components except for the target endmember. A binary mask corresponding to the region was then created. The target endmember spectrum was then multiplied by a scalar, α, and added to each pixel in the region,
| (10) |
A range of scalar values (scaling factors) was used for each scenario, typically ranging from 0 (no target endmember added) to approximately the peak spectral value of other undesired signatures in the image (e.g., the maximum target endmember added was about the same level as tissue autofluorescence or other undesired signals). This operation resulted in a series of modified spectral images that were then analyzed using each algorithm described above. Results were used to construct 3 curves that form the main components of the theoretical sensitivity analysis methodology: Theoretical Sensitivity Curve (TSC), Thresholded Positive Pixel Curve (TPPC), and Receiver-Operator Curve (ROC).
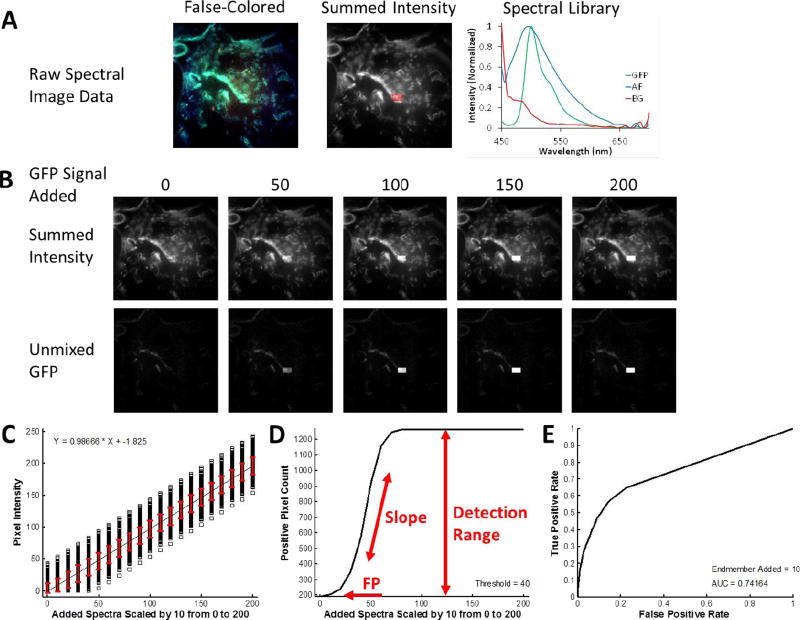
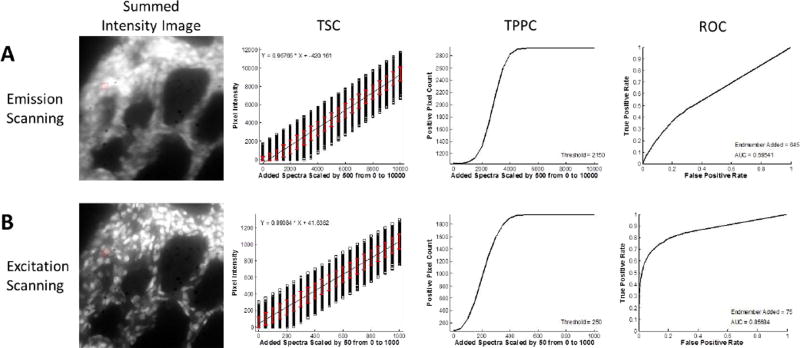
To demonstrate the theoretical sensitivity methodology, we characterized the sensitivity and specificity of several biomedical fluorescence microscopy case studies. In each case, a control sample was imaged that contained all of the fluorescent labels that would be present in the full biological assay except for the label of interest (the target endmember). Hence, the control sample included additional signals and variability from cellular or tissue autofluorescence and background signal sources. The first case study shown is that of detecting a localized and relatively weak signal – green fluorescent protein (GFP)-expressing microvascular endothelial cells – in the presence of a strong and broad lung tissue autofluorescence signal (Figure 1A). Single-labeled control samples were also prepared in order to construct a spectral library to be used for analysis. A region of interest, the test region, was then identified. The test region defined the pixels to which the target endmember spectrum was added, in order to test the response of the spectral analysis approach for detecting the target endmember in each pixel of the region. The target endmember spectrum was then added to the region in variable amounts, as specified by multiplying the target endmember spectrum by a scalar value (Figure 1B), producing a new spectral image that contained the control image data plus the additional target endmember spectrum added to selected pixels. This new image was then analyzed – for example, by using linear unmixing – and the target endmember image (in terms of abundance, spectral angle, etc.) was used for further analysis. Three plots were then constructed: a theoretical sensitivity curve (TSC - Figure 1C), a thresholded positive pixel curve (TPPC - Figure 1D), and a receiver-operator curve (ROC - Figure 1E).
Figure 1.
Overview of the Theoretical Sensitivity Curve procedure for determining the sensitivity of detecting a single endmember of interest. A) A raw spectral image that contains all endmembers except for the endmember of interest is acquired. For this example, a lung tissue slice that did not contain GFP-expressing cells (e.g., from a control animal) was imaged using the AOTF-based microscope system described in the Methods (instrument configuration #1). Spectral image data were acquired sequentially from 450–700 nm, in 5 nm increments. The false-colored image (left) displays the 610 nm (Red), 515 nm (Green), and 480 nm (Blue) bands as an RGB composite image. To visualize total fluorescence emission intensity, all wavelength bands are summed and a region of interest (ROI) is selected, as outlined shown in red. The spectral library used for analysis is also shown – in this case containing fluorescence emission spectra for green fluorescent protein (GFP), lung tissue autofluorescence (AF), and nonspecific instrument background (BG). These spectra were measured from single-label control samples: unlabeled lung tissue, GFP-expressing cells grown on coverslip, and a blank slide, respectively. B) The spectrum of the endmember of interest – in this case GFP – is added to the ROI in varying levels, where the number for GFP Signal Added indicates the intensity of the peak wavelength. The effect of adding the endmember signal can be visualized in the summed intensity image (the summed intensity across all wavelength bands) and in the spectrally analyzed image – in this case as analyzed using non-negatively constrained linear unmixing. C) The output of the theoretical sensitivity analysis methodology consists of 3 plots: the Theoretical Sensitivity Curve (TSC), the Thresholded Positive Pixel Curve (TPPC), and the Receiver Operator Characteristic Curve (ROC). These plots allow the user to assess the performance of the spectral imaging assay – including the sample characteristics, hardware configuration, and spectral analysis algorithm. The TSC is used to assess the linearity of response and to visualize the standard deviation of the analyzed (in this case, unmixed) spectral data. The TSC is generated by plotting the intensity of each pixel within the ROI after performing spectral analysis, for each amount of endmember signal added. Pixel intensities are shown as black squares, a linear regression to all pixel intensities is shown as a black line, and the red error bars indicate the standard deviation of pixel intensities. D) The TPPC is used to calculate the false positive detection rate at a given detection threshold, as well as to visualize the detection response slope (more vertical indicates increased ability to discriminate negative and positive pixels) and the detection range (which should equal the number of pixels within the detection region for a sufficiently high level of target endmember). The TPPC is generated by selecting a threshold for classifying positive pixels – in this case GFP-containing pixels. The number of pixels within the ROI above the threshold are counted and plotted as a function of endmember signal added. The ROC is used as an overall characterization of detection performance, where an area under the curve (AUC) of 1 represents an ideal discrimination between all positive and negative pixels. The ROC is also generated by assuming that any positive pixels detected within the ROI are true positive and that any positive pixels detected outside the ROI are false positive.
2.7.1. Theoretical Sensitivity Curve (TSC)
The TSC was constructed by plotting the analyzed intensity (e.g., abundance, spectral angle, energy) of each pixel within the region as a function of the scaling factor for the target endmember. The average analyzed intensity (averaged over all pixels within the region) was also plotted and used to regress a linear fit to assess the linearity of sensitivity response (Figure 1C, black line). The standard deviation of analyzed pixel values was also calculated and plotted for each scaling factor (Figure 1C, red error bars).
2.7.2. Thresholded Positive Pixel Curve (TPPC)
The TPPC was constructed by selecting a threshold for discriminating between positive and negative pixels. The number of positive pixels within the entire image was counted and plotted as a function of the scaling factor for the target endmember signal added. Positive pixels that were detected when a value of 0 target endmember was added were defined as false positive detections. True positive pixels can be visualized on the plot as an increase in the number of positive pixels, beyond the false positive number. The slope of the TPPC is an indicator of the intensity of target endmember signal that must be present in order to produce a positive detection event. A high slope indicates that only a small increase in the amount of target endmember signal is required to result in a pixel being detected as positive, whereas a low slope indicates that a large increase in the target endmember signal would be required for pixels to be detected as positive. The difference in the number of positive pixels detected for a specified level of target endmember signal added and the number of positive pixels detected for 0 target endmember signal added was defined as the detection range of the system (for well-performing classification the detection range should be the number of pixels within the region). This parameter could be used, with additional calculations, to estimate the minimum detectable limit of the spectral imaging approach for a given biomedical assay.
2.7.3. Receiver Operator Characteristic (ROC) Curve
The ROC was constructed by first defining a fixed scaling factor and a range of global thresholds to consider. For each threshold level, the number of positive pixels within the region and the number of positive pixels outside of the region were calculated. The true positive detection rate was defined by assuming that all pixels within the region should ideally be positive (e.g., the rate was calculated by the number of positive pixels detected within the region divided by the total number of pixels within the region). The false positive detection rate was defined by assuming that all pixels outside of the region should ideally be negative (e.g., the rate was calculated by the number of positive pixels outside of the region divided by the total number of pixels outside of the region). True positive rate – false positive rate data pairs were then plotted for each threshold level considered to construct the ROC curve. The area under the curve for the ROC was also calculated.
3. Results
The theoretical sensitivity analysis methodology we present here provides a means for assessing the sensitivity and specificity of a biomedical spectral imaging assay without the need to perform complex (sometimes impossible) experiments to measure the ground truth in a biological spectral imaging assay. This methodology combines experimental image data with a static sensitivity approach in a manner that maintains the high variability that is typically present in biological image data. Hence, the theoretical sensitivity analysis allows estimation of the detection sensitivity in the midst of highly variable and competing signals, such as cellular or tissue autofluorescence, stray light, and other background signals.
3.1. Experimental Validation
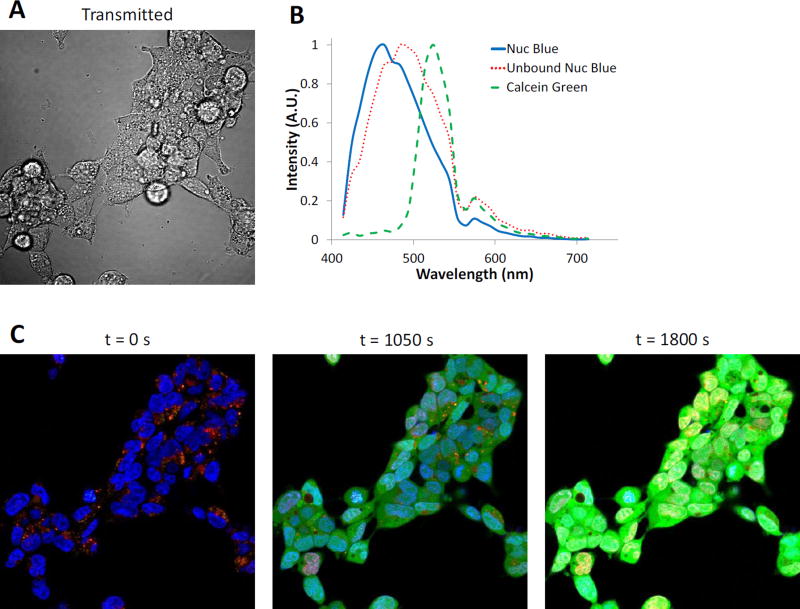
To determine whether the theoretical sensitivity analysis methodology represents an accurate depiction of equipment and sample response, an experimental sensitivity study was also performed and compared to the theoretical response. The uptake of Calcein Green, AM by HEK293 cells was monitored over time using a spectral confocal microscope, as the rate of cellular uptake and AM cleavage should be relatively linear for a fixed extracellular concentration (within a reasonable range of concentrations). Hence, the Calcein Green signal would be expected to increase linearly over time and could then be compared to linear response from the theoretical sensitivity analysis. NucBlue and Calcein Green concentrations and equipment parameters (laser power, detector gain, scan speed, etc.) were adjusted such that a small subset of pixels would become saturated prior to the 30 minute time course of the experiment (Figure 2). Regions of interest corresponding to pure NucBlue and unbound NucBlue signals were identified at a time point of 0 seconds (before Calcein Green addition), and the mean spectra from these regions used in the spectral library (ROIs shown in Figure 3C). A further cytosolic region containing no NucBlue label was used at a time point of 1050 seconds (after Calcein Green addition) and the mean spectrum from this region was used in the spectral library as the spectrum for Calcein Green.
Figure 2.
Experimental validation of the theoretical sensitivity analysis methodology was performed by measuring Calcein Green uptake in HEK293 cells labeled with NucBlue (nuclear marker) using a Nikon A1R spectral confocal microscope. A) Transmitted light image to visualize cellular outlines. B) Spectral library used for linear unmixing. C) Merged, false-colored composite of unmixed images for 3 selected time points: 0, 1050, and 1800 seconds. NucBlue labeling is shown as blue, non-specific NucBlue labeling as red, and Calcein Green as green. Note that by the final time point, several nuclear regions exhibit a bright yellow color, indicating pixels that are oversaturated on at least one wavelength band.
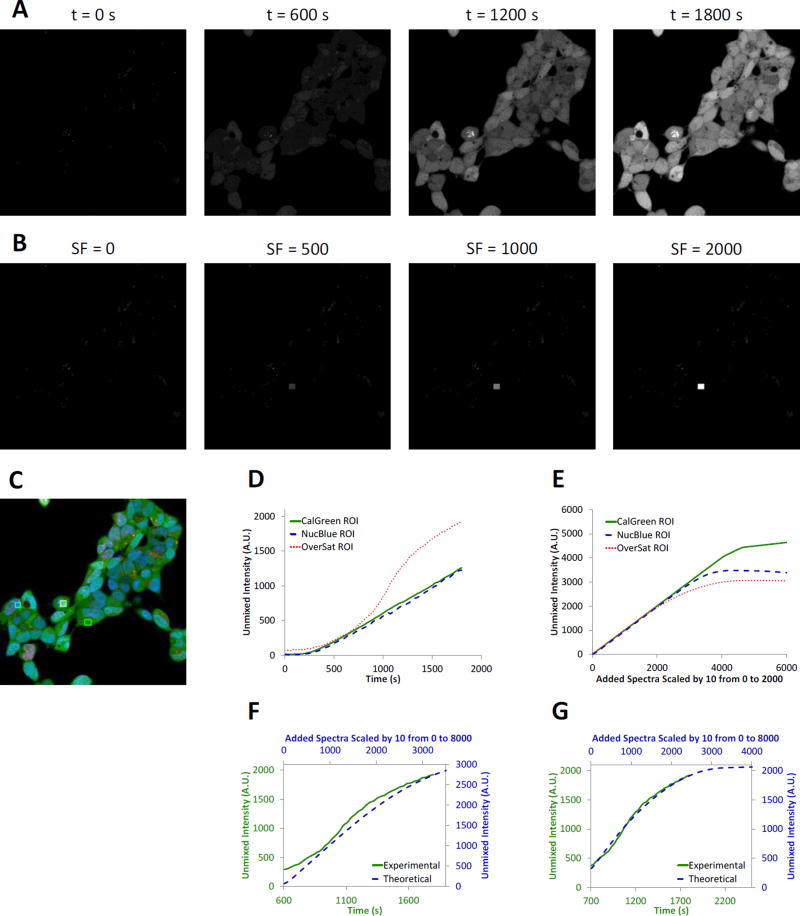
Figure 3.
The theoretical sensitivity analysis methodology provides similar signal response as experimental studies. A) Experimental time lapse image data of HEK293 cells labeled with NucBlue and Calcein Green (added at t = 60 seconds). The unmixed Calcein Green abundance is shown to visualize the increase in Calcein Green signal over time. Concentration and time-lapse parameters were adjusted so as to intentionally oversaturate the image data at later time points in order to evaluate the sensitivity response at saturated conditions. B) Theoretical sensitivity analysis of the initial time point from the same image set (t = 0 seconds). The spectrum of Calcein Green was added at varying scaling factors (SF) to a small region within the image prior to unmixing. The unmixed Calcein Green signal was then assessed, best visualized at a scaling factor of 2000 (SF = 2000). C) False-colored merged composite image of the 3 signals from the spectral library using experimental data from a time point mid-way through the experiment (t = 1050 seconds). NucBlue labeling is shown as blue, non-specific NucBlue labeling as red, and Calcein Green as green. Three regions of interest were selected to account for areas with high NucBlue intensity (cyan region), high Calcein Green intensity (green region), or a region with high intensities of both that became oversaturated at selected wavelength bands during later time points (yellow region). D) Experimental unmixed Calcein Green signal response from the 3 regions shown in Panel C. Note that the oversaturated region produced a highly nonlinear response indicating approach to a maximum achievable unmixed signal intensity (red dotted line). E) Theoretical unmixed Calcein Green signal response from the same 3 regions. Note that all 3 regions eventually reach a saturating signal level for very high Calcein Green scaling factors. F) Comparison of the experimental and theoretical responses using a 12-bit detector threshold in the theoretical sensitivity analysis demonstrated that the response curves are similar in shape, but that the theoretical response saturates at a higher unmixed Calcein Green signal intensity, as indicated by the blue dashed line and values on the secondary y-axis. E) Comparison of the experimental and theoretical responses using a 11.5-bit detector threshold in the theoretical sensitivity analysis demonstrated a greatly improved match of theoretical and experimental curves, as indicated by both the shape and magnitude of both responses.
Timelapse hyperspectral image data were unmixed using non-negatively constrained linear unmixing, resulting in a clear increase in Calcein Green signal over time (Figure 3A). The theoretical sensitivity analysis also showed an increase in Calcein Green signal as a function of scaling factor (Figure 3B). Several regions were selected to quantify signal response over time and to compare the results of the experimental and theoretical sensitivity analysis (Figure 3C). These regions included a region with only Calcein Green signal, a region with NucBlue and Calcein Green signal, and a region with strong NucBlue and Calcein Green signals where the average spectrum became oversaturated at later time points. The unmixed images from the experimental image data displayed a linear increase in Calcein Green signal after an initial delay, for both the Calcein Green region and the NucBlue region (Calcein Green was added at a time point of 60 seconds with a potential further delay introduced by mixing of solutions). However, for the oversaturated region, the unmixed Calcein Green signal displayed a non-linear response (Figure 3D, red line), indicating that one or more wavelength bands were saturating for pixels within this region and that the measured spectra of those pixels were no longer reflective of the real signal intensities. A theoretical sensitivity analysis was also performed using the oversaturated region, and when constrained to a maximum pixel intensity of 4095 (the A1R has a 12-bit detector), also displayed a non-linear response in unmixed Calcein Green signal, as a function of the scaling factor for Calcein Green (Figure 3E). However, the non-linear region for Calcein Green signal response occurred at a higher intensity in the theoretical model than in the experimental data (Figure 3F). This indicated that the experimental data was likely further limited by the detector performance of the system. To better account for detector performance, the theoretical saturation level was decreased to 11.5 bits of dynamic range (a maximum intensity of 2895), resulting in an accurate match to the experimental data (Figure 3G). Hence, results from the theoretical sensitivity analysis highly correlate with experimental data given the caveat that the full (claimed) dynamic range of a microscope system may not always be achievable (as has been documented elsewhere[105–107]).
3.2. Assessing Spectral Analysis Algorithms Performance
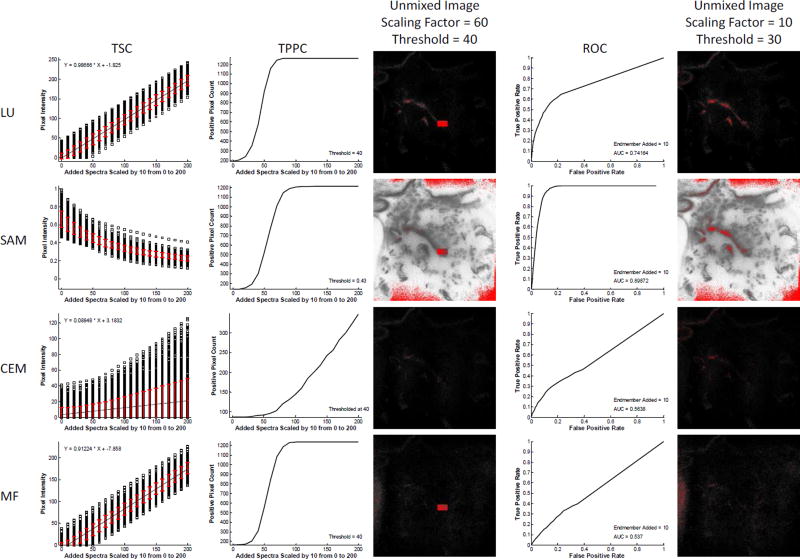
The theoretical sensitivity analysis methodology can be used to assess the effectiveness of different spectral analysis algorithms. Here, we provide an example comparing 4 common spectral analysis algorithms for the detection of GFP-positive pixels using the spectral image data shown in Figure 1. Results show widely varying effectiveness of the different algorithms for detecting GFP-positive pixels (Figure 4). From the TSC, it is clear that linear unmixing (LU) and matched filtering (MF) both provide a linear sensitivity to increasing levels of target endmember, while spectral angle mapper (SAM) and constrained energy minimization (CEM) are non-linear – this is as would be expected. In addition, each algorithm shows different effects of increasing target endmember levels on standard deviation of the detected level of the target endmember. For example, LU and MF algorithms produce a standard deviation of detected target endmember that is relatively insensitive to the amount of target endmember added. By contrast, SAM presents decreasing standard deviation of detected target endmember levels as a function of increasing target endmember added, while CEM presents increasing standard deviation of detected endmember levels. These results imply that SAM would have a high variation in detected endmember values if trying to identify a very weak target endmember signal in the presence of high background (tissue autofluorescence). However, for strong target endmember signals, SAM may present a smaller variation in detected signals.
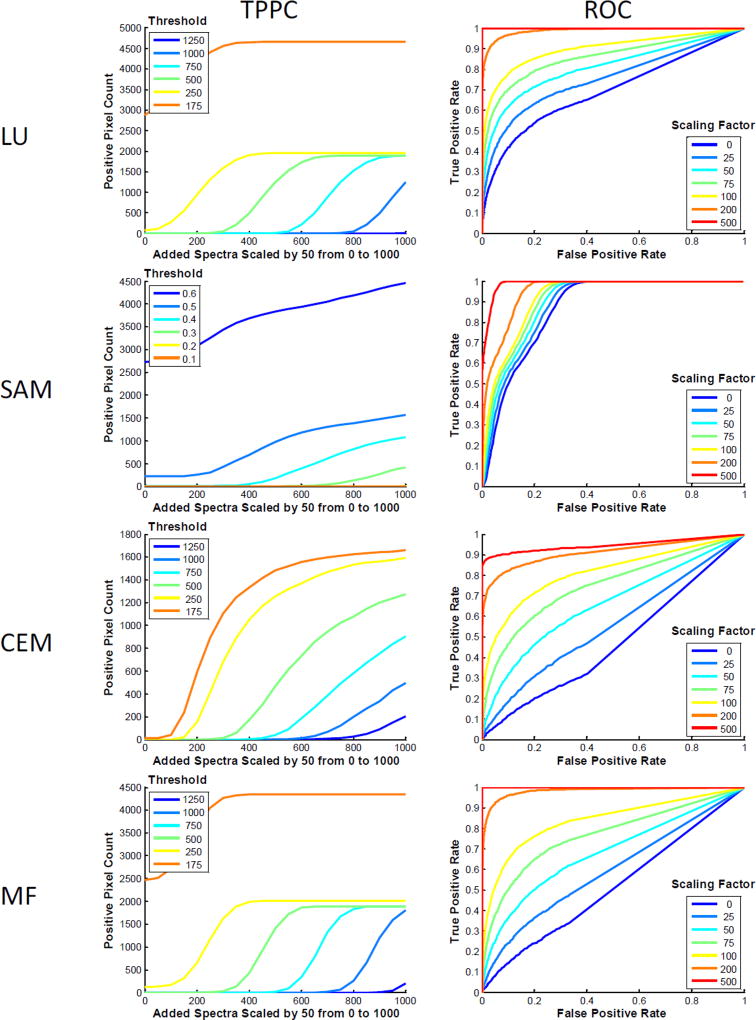
Figure 4.
The theoretical sensitivity analysis methodology can be used to compare the performance of different spectral analysis algorithms for endmember detection, and to select an optimal algorithm. The raw spectral image, region of interest (ROI), and spectral library from Figure 1 were evaluated with 4 analysis algorithms: Linear Unmixing (LU), Spectral Angle Mapper (SAM), Constrained Energy Minimization (CEM), and Matched Filter (MF). For each analysis algorithm, the Theoretical Sensitivity Curve (TSC), Thresholded Positive Pixel Curve (TPPC), and Receiver Operator Characteristic Curve (ROC) were calculated. To generate comparable results for the TPPC, a threshold for each analysis algorithm was selected that resulted in approximately 100–200 false-positive pixels detected (shown as the value of the TPPC at 0 added endmember spectra). Results from the TPPC curve show that LU, SAM, and MF algorithms provide similar response functions for detecting positive pixels. These results can be visualized in the spectrally analyzed target endmember image, generated at a scaling factor of 60 and identical threshold value (pixels above the threshold are false-colored red). Consistent with the TPPC results, a large percentage of pixels within the target region were identified as positive for the LU, SAM, and MF algorithms, but not for CEM. Note that the threshold value for SAM was 0.43 radians. Results from the ROC curve show that SAM provided the best ROC response, as measured by area under the ROC curve (AUC = 0.899), followed by LU (0.742), then CEM (0.564), then MF (0.537). These results were also visualized in the spectrally analyzed target endmember image, generated at a scaling factor of 10 and a threshold value of 30 (a threshold of 0.5 radians was used for the SAM algorithm). As can be seen for this very low level of target endmember added, SAM and LU were the only algorithms that identified even a subset of pixels within the region.
Results for the TPPC were also similar for LU and MF algorithms. The TPPC for SAM had a lower slope, indicating a larger increase in target endmember signature would be needed to cleanly separate between negative and positive pixels. The TPPC for CEM was very low, indicating that it would be difficult to detect all true positive pixels in the region while rejecting negative pixels outside the region, for the specified threshold.
Results from the ROC revealed additional information about the effectiveness of each algorithm. Interestingly, the ROC curves for LU and MF were not similar, with LU producing improved AUC (AUC = 0.742) when compared to MF (AUC = 0.537). SAM displayed the best ROC performance (AUC = 0.899). If based solely on ROC performance, SAM would be the algorithm of choice for detecting the GFP target endmember signal, as added to the image at a value of 10 intensity units (intensity at peak wavelength). However, it is worth noting that the performance of SAM in the TPPC was slightly poorer than that of LU or MF. This indicates that SAM may perform well for detecting a fixed level of target endmember added, but that the performance may be only equivalent with LU or MF when assessing the ability to discriminate between varying amounts of target endmember added for a given threshold.
Taken together, results from this analysis indicate that either LU or SAM would be preferable algorithms for detecting the GFP-positive pixels in lung tissues (using the specific hardware configuration and acquisition settings of this assay). LU would likely be the preferable choice if a quantitation of the amount of GFP added was being made, as the TSC for LU is linear. However, SAM may be preferable for a simple +/− classification scheme, especially if the level of target endmember that should be present in a positive pixel is relatively constant and is known a priori (e.g., a minimum detectible limit has already been established and all cells uniformly express approximately the same amount of GFP).
3.3. Comparing Equipment Platform Response
In addition to comparing the effectiveness of different spectral analysis algorithms, the theoretical sensitivity analysis methodology can be used to compare the performance of different hyperspectral imaging hardware. For this example, we have used a similar biological assay as was used in Figure 1, but have acquired image data using two different spectral imaging microscope systems: a fluorescence emission-scanning hyperspectral imaging system[97, 104] and a fluorescence excitation-scanning hyperspectral imaging system, both of which were previously developed in our lab[67]. In our prior work, we demonstrated that images acquired using the excitation-scanning system had significantly higher signal-to-noise ratios when all other imaging parameters were held constant (acquisition time, camera gain, etc.). Using image data from these experiments, we show here that the theoretical sensitivity analysis methodology allows extraction of much more detailed information regarding the effectiveness of each hardware system for detecting the target endmember. For consistency, spectral image data were acquired from the same field of view using both scanning modes: emission scanning and excitation scanning. The acquisition time of the emission scanning system was increased by a factor of 5 to produce a similar dynamic range of intensities as that of the excitation scanning system (we have previously demonstrated that the general approach of excitation scanning can produce higher signal strength than that of emission scanning). To compensate for the increased acquisition time required for the emission-scanning system, the variable levels of sensitivity, and the correction needed to achieve NIST-traceable response, target endmember levels added and detection thresholds were multiplied by a factor of 8.6 for the emission scanning images (8.6 was the ratio of the mean intensity of autofluorescence within the region for emission scanning divided by the mean autofluorescence intensity within the region for excitation scanning).
Results from the theoretical sensitivity analysis methodology using the LU algorithm demonstrate that the excitation-scanning system greatly outperforms the emission-scanning system (Figure 5). TSC results indicate that the standard deviation of detected intensities is 8–9 times higher in emission scanning than in excitation scanning. This is to be expected, as the acquisition time required to acquire comparable emission scanning images was 5 times higher than with excitation scanning. Investigation of the TPPC shows that, for comparable thresholding levels, the excitation-scanning system resulted in fewer false positive pixels (indicated by Figure 5, TPPC, by the positive pixel count at a value of 0 target endmember spectrum added). The ROC confirmed this result, showing that excitation scanning was much more effective at discriminating negative and positive pixels (AUC = 0.857) than emission scanning (AUC = 0.595).
Figure 5.
Theoretical Sensitivity Curve analysis can be used to compare the performance of different spectral imaging hardware or systems. Here, two different microscope configurations were compared: one which used a thin film tunable filter to scan the fluorescence emission spectrum[97, 104] and one which used a similar thin film tunable filter to scan the excitation spectrum[67]. A sample similar to that used in Figure 1 was used and the ability to detect green fluorescent protein (GFP) was assessed. A) The emission-scanning image was acquired using 1 s acquisition time per wavelength band. B) The excitation-scanning image was acquired using 200 ms acquisition time per wavelength band. By visual inspection of the wavelength-summed image data alone, it is clear that the excitation scanning system provides enhanced performance. This is likely due to the fact that the excitation scanning system has fewer optical elements to filter the emitted fluorescence, and thus allows a higher percent transmission of emitted fluorescence and corresponding higher detection sensitivity. Results from a theoretical sensitivity analysis methodology provide a quantitative metric for measuring the enhancement in performance – specifically the reduced false positive rate and the enhanced receiver operator characteristic performance. The theoretical sensitivity curve (TSC) and additional curves were calculated using a non-negatively constrained linear unmixing algorithm. The threshold for the thresholded positive pixel curve (TPPC) and the intensity of endmember added for the Receiver Operator Characteristic Curve (ROC) were scaled by the ratio of acquisition times to provide comparable results. Comparison of the TSC shows that both imaging modalities provide a linear response for detecting GFP. However, comparison of the TPPC for both images shows that detection of GFP-positive pixels is possible with fewer false positive pixels when using excitation scanning. Comparison of the ROC for both images shows that excitation scanning has a much higher area under the curve (AUC = 0.851) vs. emission scanning (AUC = 0.595).
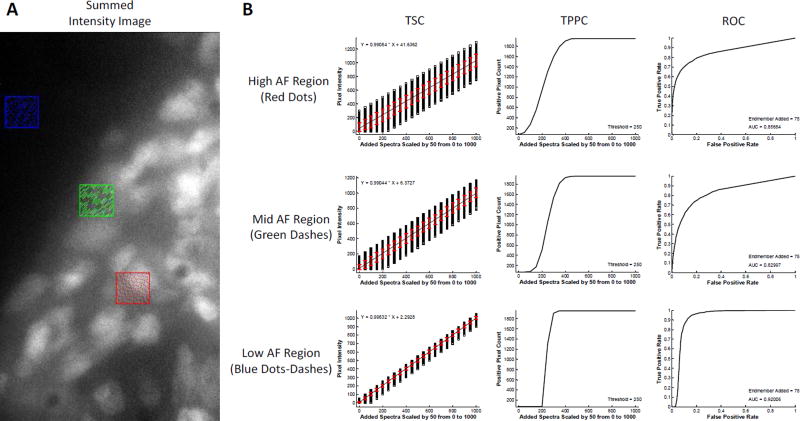
3.4. Effects of Region of Interest Selection
The selection of the region of interest can play a large role in theoretical sensitivity analysis methodology. To demonstrate this, the excitation-scanning image from Figure 5 was further investigated to assess the effects of selecting regions with low, medium, and high AF for analysis using the LU algorithm (Figure 6). When a region with high AF was selected (Figure 6, top row), the theoretical sensitivity analysis methodology produced degraded results as compared to when a region with low AF was selected (Figure 6, bottom row). The TSC indicated large standard deviation in the detected intensities of the target endmember. Similarly, the TPPC produced a low slope for discriminating among pixels with high and low target endmember signals, while the ROC produced a lower AUC (AUC = 0.857). When a region with low AF was selected, the TSC displayed reduced standard deviation, the TPPC slope was higher (allowing enhanced discrimination between high and low target endmember pixels) and the ROC curve was improved (AUC = 0.920). These results indicate that the placement of the region within an image can be used to provide additional information characterizing the effectiveness of the spectral imaging process as a whole. For example, what detection threshold is needed if the autofluorescence is low compared to if the autofluorescence is high?
Figure 6.
Comparison of theoretical sensitivity curve analysis performed in 3 regions of interest using non-negatively constrained linear unmixing analysis. A) Regions of interest correspond to high tissue autofluorescence (AF) – indicated by the red region, medium autofluorescence – green region, and low autofluorescence – blue region. In each case the endmember signal for GFP was added incrementally to each pixel in the region. B) Results from the theoretical sensitivity analysis show that incremental additions of GFP signal produce a linear response for all regions, shown by the Theoretical Sensitivity Curve (TSC). However, the standard deviation for detecting GFP signal is highest in the high AF region and decreases with decreasing AF, as shown by the red error bars. The Thresholded Positive Pixel Curve (TPPC) shows improved performance for detecting low GFP positive pixels in the low AF region. The high AF region resulted in a TPPC with a higher number of false positive pixels and a shallower slope. By contrast, the low AF region resulted in a TPPC with 0 false positive pixels and a steep slope, indicating that it is easier to discriminate between positive and negative pixels when AF is low. Finally, the Receiver Operator Characteristic Curve (ROC) produced increasing area under the curve (AUC) for decreasing autofluorescence, with AUC = 0.857 for the high AF region and AUC = 0.920 for the low AF region. Interestingly, the mid AF region resulted in AUC = 0.830, indicating reduced performance in the mid AF region.
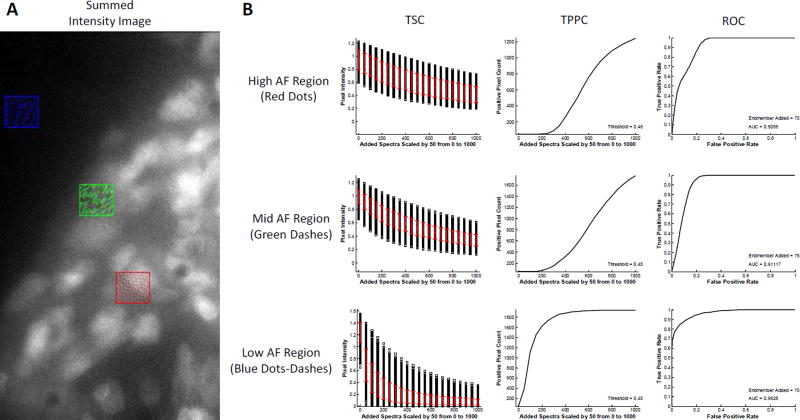
The analysis shown in Figure 6 was also performed using the SAM algorithm and the same regions (Figure 7). Interestingly, TSC analysis using the SAM algorithm produced a standard deviation of intensities of the target endmember that was smaller for the region with high AF than the region with low AF, when using low levels of target endmember added. When high levels of target endmember were added, the standard deviation for the low AF region became very small. This is likely due to the fact that SAM calculates a spectral angle based on normalized intensities (regardless of the magnitude of spectra being compared). Hence, for background pixels that are very weak, the main signal contributor will be instrument noise. When normalized, the instrument noise creates a widely varying spectral signature and the corresponding spectral angle between the target endmember (GFP) and the background pixels will also have high variance. When sufficient GFP signal was added to the pixels in the low autofluorescence region, the effects of background signal became negligible and the spectral angle decreased sharply, with a corresponding decrease in standard deviation. However, for the region with high AF, even high levels of GFP signal added produced a spectral angle of 0.4–0.6 radians, indicating that the AF signal played a role in limiting the minimum spectral angle that could be achieved.
Figure 7.
Comparison of theoretical sensitivity curve analysis performed in 3 regions of interest using spectral angle mapper analysis. A) Regions of interest correspond to high tissue autofluorescence (AF) – indicated by the red region, medium autofluorescence – green region, and low autofluorescence – blue region. In each case the endmember signal for GFP was added incrementally to each pixel in the region. B) Results from the theoretical sensitivity analysis show that incremental additions of GFP signal produce a non-linear and decreasing response for all regions, shown by the Theoretical Sensitivity Curve (TSC). The standard deviation for detecting GFP signal shows no immediate correlation to the level of AF in each region, as shown by the red error bars. Similar to linear unmixing analysis (Figure 6), the slope of the Thresholded Positive Pixel Curve (TPPC) becomes more vertical with decreasing AF, indicating that it is easier to discriminate between positive and negative pixels when AF is low. For the high AF region, the maximum value of the TPPC is 1243 and the minimum is 47, giving a range of 1196 positive pixels. For the mid AF region, the maximum value is 1768 and the minimum is 47, giving a range of 1721 positive pixels. For the low AF region, the maximum value is 1937 and the minimum is 47, giving a range of 1890 positive pixels, which is equal to the total number of pixels within the region (45×42 pixel region). Also similar to linear unmixing analysis, the Receiver Operator Characteristic Curve (ROC) produced increasing area under the curve (AUC) for decreasing autofluorescence, with AUC = 0.901 for the high AF region, AUC = 0.911 for the mid AF region, and AUC = 0.963 for the high AF region.
TPPC analysis showed that a large increase in target endmember signal was required to discriminate between negative and positive pixels for the regions with high and mid AF. However, for the low AF region, detection of positive pixels could be made at a much lower level of target endmember added, while still maintaining a low number of false positive pixels. ROC analysis confirmed the TPPC results with the curve for the low AF region displaying the best response (AUC = 0.963) while the high AF region had a reduced response (AUC = 0.906).
The theoretical sensitivity analysis methodology can also be “looped” or re-run to cover a range of possible scenarios. This allows for parameters to be tested for each analysis algorithm, hardware configuration, etc., or for optimization of specific parameters used in a spectral imaging assay (e.g., the threshold for discriminating positive and negative pixels). As an example, the image from Figure 5B was used and the theoretical sensitivity analysis methodology performed for a range of settings. The TPPC was evaluated at 6 threshold values for discriminating positive from negative pixels and the ROC was evaluated at 7 levels of target endmember added. Of note, a value of 0 target endmember added was also evaluated in the ROC response to assess ROC performance when the pixels within the region (defined as positive) do not contain the target endmember signature. Although a nontraditional use of the ROC, this allowed visualization of the classifier results and their dependence on high background signal within the region – and hence, the effect that this background signal had on subsequent trials with sequential levels of target endmember present. This was repeated for 4 different analysis algorithms: LU, SAM, CEM, MF.
Results from the TPPC show that a change in the global threshold level had varying effects in differentiating negative from positive pixels. For example, for thresholds that were sufficiently high as to result in 0 false positive pixels (number of positive pixels is 0 for a value of 0 endmember added), LU and MF both resulted in a shift of the positive pixel detection curve, but little change in the slope of the curve. This indicates that a thresholding decision based on LU or MF data will require the same approximate increase in unmixed signal detected, regardless of where the threshold cut-off is placed. By contrast, the TPPC for SAM changed in both horizontal and vertical position with even the least stringent threshold (0.6 radians) not detecting 100% of the pixels within the region for the highest scaling factor. This indicates that SAM had difficulty detecting all positive pixels due to the high tissue autofluorescence in the region. CEM presented a response that was intermediate of LU and SAM – for the lowest threshold tested, CEM detected >80% of the pixels in the region, and with a sufficiently high level of target endmember added would result in 100% detection.
Results from the ROC also showed a wide variation in algorithm sensitivity and specificity (all algorithms were assessed at identical levels of target endmember added). As in the TPPC results, LU and MF provided similar, though not identical, results. CEM performance was degraded, as compared to LU and MF. SAM produced the smallest change in ROC response as a function of change in target endmember added. Interestingly, the performance for SAM with 0 target endmember added is improved over that of the other 3 algorithms. This indicates that many of the pixels within the region (selected for high background autofluorescence) were classified as positive, even when no target endmember signature was present. The incremental improvements in SAM ROC performance for scenarios with increasing target endmember added were marginal, with only the highest level of target endmember added resulting in a large improvement in ROC performance. From this observation, it is likely that SAM provided improved ROC performance for low levels of target endmember added simply because the target endmember (GFP) spectrum was sufficiently similar to the tissue autofluorescence spectrum as to result in a low spectral angle when high levels of autofluorescence were present, and sufficiently dissimilar to the background (stray light + noise) signal as to result in a high spectral angle when low levels of autofluorescence were present. Hence, by selecting a region with high autofluorescence for the theoretical sensitivity analysis methodology, the ROC performance may be artificially biased towards a particular response (this observation is also supported by data shown in Figure 7).
3.5. Summary of Results and Impact on End Users
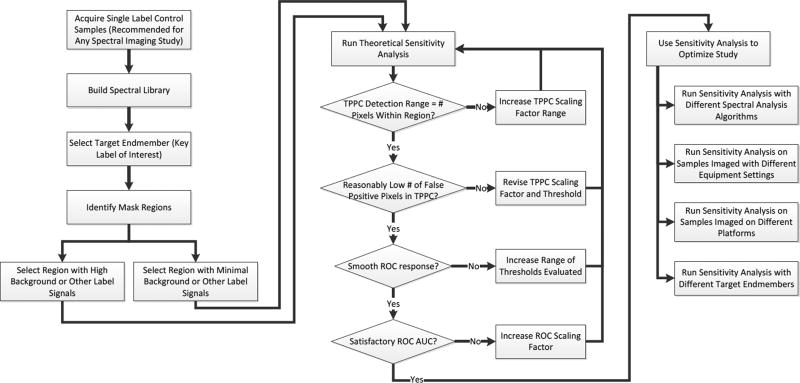
The theoretical sensitivity analysis methodology described here has high potential for improving the performance and experimental design of spectral imaging studies. The rationale for applying this methodology prior to conducting a full set of spectral imaging studies is that the results of the methodology can be used to inform and optimize several aspects of a study: the imaging platform selected, the equipment parameters used, and the analysis algorithm and threshold settings used. These parameters can be optimized with minimal reagent and instrument use costs, as only a simple set of single label controls needs to be run. The potential utility of the theoretical sensitivity analysis, and the results we have observed in applying it to detection of weak GFP signals in the midst of strong tissue autofluorescence is summarized in Table 2. Each of the outcomes of the sensitivity analysis (each type of curve) can be used to inform the user as to specific aspects of the spectral analysis detection sensitivity. We have summarized the responses that we have observed for four common spectral analysis algorithms, although this approach could easily be applied to a wide range of algorithms, equipment configurations, and instrument settings. We have also outlined a series of guidelines for applying this methodology to a generic spectral imaging study (Figure 8).
Table 2.
Summary of the effects of 4 common spectral analysis algorithms on the outcomes of the theoretical sensitivity analysis methodology, as applied to the example of detecting a weak fluorescence signal among strong background autofluorescence. The utility of each curve for providing information to the end user is summarized in the 2nd row. Each curve provides different information for examining the response and performance of the analysis algorithm.
| Measured Outcome | TSC (Theoretical Sensitivity Curve) |
TPPC (Thresholded Positive Pixel Curve) |
ROC (Receiver Operator Characteristic Curve) |
|---|---|---|---|
| Algorithm | |||
| Utility of Outcome | Valuable in visualizing the sensitivity linearity of the combined biological sample + imaging hardware + analysis algorithm, as well as potential error associated with measuring the target endmember. High standard deviation (error bars) indicates a high biological variability and potential for misclassification and false-positive detection. | Valuable in assessing the ability to detect positive pixels for a specified detection threshold. This is highly relevant to most biomedical spectral imaging assays, as the end result is often a quantified count (# of expressing cells, # of dividing cells, % of tissue that is pathogenic, etc.). For the majority of scenarios a global threshold is used to make the count, and the TPPC can be used to measure the number of false positive detections and the increase in target endmember signal that is required to detect all true positive pixels. | Valuable as a classical “gold-standard” approach for visualizing the sensitivity and specificity of a spectral imaging assay. The ROC characterizes the spectral imaging classification performance for one specified level of target endmember. |
| LU (Linear Unmixing) | Linear behavior Standard deviation insensitive to scaling factor | Reasonable detection slope indicates the ability to detect weak signals in high autofluorescence regions if the spectra of all endmembers are known a priori | |
| SAM (Spectral Angle Mapper) | Highly nonlinear behavior Standard deviation decreases with increasing scaling factor (as the angle between test pixels and the target endmember decreases) Standard deviation is very high for low background and low signal | Lower detection slope, especially for regions with high autofluorescenec, hence a higher scaling factor may be needed for accurate detection Threshold specified in radians | Improved performance, but may be skewed because SAM is insensitive to intensities |
| CEM (Constrained Energy Minimization) | Nonlinear behavior Standard deviation increases with increasing scaling factor | Much lower detection slope than LU and MF, hence a higher scaling factor will likely be needed for accurate detection and the threshold may need to be increased to compensate | Poor performance for weak signals |
| MF (Matched Filter) | Linear behavior Standard deviation insensitive to scaling factor | Similar detection slope as LU, but right-shifted, indicating a reduced ability to detect very weak signals | Poor performance for very weak signals |
Figure 8.
Flowchart for applying the theoretical sensitivity analysis methodology to optimize a hyperspectral imaging study. The process begins with a simple set of single-label control experiments, from which the spectrum of each label is extracted and stored in a spectral library. A target endmember is then selected and a region within which to evaluate the detection sensitivity is also selected. It is recommended to select 2 regions, one with a low level of other signals (autofluorescence or other labels) and one with the highest level of signals, so as to challenge the detection algorithm. The theoretical sensitivity analysis is then run and the parameters of the analysis adjusted to ensure that an appropriate range of scaling factors and thresholds are evaluated. The results of the sensitivity analysis are then used to select the analysis algorithm, equipment settings, equipment platform, and/or fluorescent labels that maximize detection performance.
The theoretical sensitivity analysis methodology starts with a set of basic single label control samples (Figure 8), which would be required to be run for most standard spectral imaging studies in order to perform spectral unmixing or analysis. Spectral image data acquired from each of the single label samples is used to construct a spectral library. An additional control sample should also be run that contains all of the fluorescent labels except for the label of interest. This control sample should be imaged using identical equipment settings as those of the final study. In addition, images over a range of acquisition settings (acquisition times, detector gains, illuminator intensities, number of wavelength bands, etc.) could be acquired to determine which settings optimize the detection performance. Two regions within the control sample should then be identified for conducting the sensitivity analysis: a region with low background signals (for characterizing the detection performance under “best case” conditions) and a region with high background signals (for characterizing the “worst case” or likely real-world detection performance). The theoretical sensitivity analysis is then run, allowing evaluation of the detection performance and comparison of different spectral analysis algorithms.
We suggest several error-checking steps during the theoretical sensitivity analysis process (indicated as diamonds in Figure 8). The first error check is to ensure that the range of scaling factors tested covers a range that allows positive identification of all pixels within the region for the TPPC. If all pixels are not identified as positive at the highest scaling factor tested, then the range of scaling factors should be increased, and possibly the detection threshold should be decreased. The second error check is to ensure that the TPPC does not produce a very high level of false positive pixels. If the number of false positive pixels is high (2–5× the number of pixels within the region may be considered high), this is an indication that the detection threshold for the TPPC is set too low, and the detection threshold should be increased and the analysis re-run. The third error check is to ensure that the ROC response is smooth. A discontinuous or highly discretized ROC curve likely indicates that a sufficient number of thresholds were not tested to obtain the ROC. If this is the case, then the threshold increment for the ROC, and possibly the upper-bound threshold value, should be increased so as to obtain a smooth ROC response. The fourth error check is to ensure that the target endmember pixels can be detected satisfactorily, as predicted using the ROC. In this case, the AUC of the ROC should be satisfactory. While the value of the AUC that is defined as satisfactory may vary, depending on the variation and nature of signals in a particular study, we have found that an AUC of ≥ 0.9 is desirable and that an AUC of ≥ 0.95 produces very good results. If the AUC is low, it is an indication that the detection sensitivity is poor for the scaling factor (amount of target endmember signal) used. In this case, the scaling factor should be increased so as to provide an adequate AUC, indicating that the minimum detectible signal is likely higher than was first thought. Alternatively, additional spectral analysis algorithms or varied equipment settings should be tested to optimize the ROC AUC. Once satisfactory settings have been achieved, the results of the theoretical sensitivity analysis should be run iteratively to optimize the study. This optimization could be used to select fluorescent labels to ensure ability to discriminate similar spectra and/or remove autofluorescence, select equipment parameters, select analysis algorithms, or evaluate the useable dynamic range of the assay, providing a wealth of valuable data prior to embarking on a set of biological spectral imaging experiments.
As described above, each type of curve can be used to evaluate a range of theoretical and/or experimental conditions to further optimize the study. As an example, we have iterated the TPPC and ROC curves over a range of threshold and scaling factor values to assess the range of responses (Figure 9). Interestingly, the TPPC for LU and MF shifts from left to right but maintains relatively constant slope with increasing threshold for cases when the threshold value is above the level needed to mitigate false positive pixels (a value of 250 for this example). This indicates that the step increase in analyzed pixel intensity required for all pixels to be detected as positive remains approximately equal at each threshold. When the threshold falls below this level, the curve shifts both left and vertically, indicating a rise in false positive pixels. By contrast, both the SAM and CEM algorithms display a horizontal and vertical shift in the TPPC for changes in threshold, indicating that a change in threshold will likely cause changes in both the detection sensitivity and the false positive detection rate. The ROC curve is perhaps most revealing as a characterization of each detection approach. ROC analysis indicates that all analysis algorithms have satisfactory performance for detecting high levels of target endmember (in this case, scaling factors ≥200). However, for weak levels of the target endmember, linear unmixing and SAM provided improved results over CEM and MF.
Figure 9.
Theoretical sensitivity analysis can be run for a range of scenarios, allowing optimization of image acquisition and analysis settings. The image from Figure 5B was used. Multiple Thresholded Positive Pixel Curves (TPPC) were constructed for different threshold values for each of 4 analysis approaches non-negatively constrained linear unmixing (LU), spectral angle mapper (SAM), constrained energy minimization (CEM), and matched filter (MF). TPPC analysis shows that, for decreasing threshold values, LU and MF allow weaker GFP endmember signals to be detected with no increase in false positives until a very low threshold is reached. However, decreasing the threshold in SAM analysis resulted in weaker endmember signals being detected at the expense of increasing false positive pixels, while CEM displayed decreased overall sensitivity in detecting positive pixels. ROC analysis shows that LU and MF also yield similar results, with CEM displaying reduced performance and SAM displaying only marginal improvements in performance with increasing levels of target endmember added.
4. Discussion
Spectral imaging technologies have been widely used by the remote sensing, aerial surveillance, and space exploration communities for many years. More recently, these technologies have been applied to biomedical imaging, where they have provided new possibilities for molecular analysis of cells and tissues. However, it has been difficult to objectively compare analysis approaches and hardware implementations, due to the high variability of biological samples and the limited ability to measure ground truths or to construct test samples.
The theoretical sensitivity analysis presented here is a methodology for characterizing the effectiveness of a biomedical spectral imaging assay for detecting a specific molecular signature. The advantages of this methodology are two-fold. First, it uses real image data acquired from biological control samples, thereby incorporating the biological variability, background signals, and noise properties of the spectral imaging assay. Second, the methodology has global applicability, in that the same characterization can be performed to compare different analysis algorithms, different equipment settings, or different hardware and system configurations. This standardized methodology could be used for a wide range of tasks: selecting an appropriate analysis algorithm, optimizing acquisition settings, optimizing the number and location of wavelength bands acquired[108], selecting a sufficient acquisition time, comparing the effectiveness of different spectral imaging platforms, comparing the effects of pre-analysis procedures (smoothing, de-noising, dimensionality reduction, etc.), and others. Without a standardized methodology, these tasks are difficult to perform. For example, selecting the optimal spectral microscopy platform for a given cellular experiment can be very difficult if based solely off of manufacturer specifications or prior “gut” experience. Questions such as “Does the 32 channel detector on a spectral confocal microscope provide comparable sensitivity to the AOTF-based system if I bin wavelength bands and open the confocal pinhole?” could require months of optical measurements and some system disassembly to answer. The methodology presented here offers an alternative approach to answer these questions, requiring only a few control samples to be imaged on the system(s) of interest, using the range of parameters of interest, and providing a consistent set of metrics that can easily be used to compare algorithm, setting, or system performance.
Experimental validation of the theoretical sensitivity analysis methodology demonstrated that the theoretical results can correlate well with experimental conditions, but for very high (saturating) signal intensities, it is necessary to estimate that useable dynamic range of the spectral imaging system, which is often less than the manufacturer-specified bit-depth of the detector. This experimental validation demonstrated that with appropriate constraints of dynamic range, the theoretical sensitivity analysis methodology can accurately reproduce nonlinear behavior of a spectral imaging assay. Another case to be considered is how a spectral imaging study would perform if excitation or emission wavelength bands were selected inappropriately, as this could lead to low or even negligible sensitivity of the spectral imaging system to a target endmember. In this case, for a system with greatly reduced sensitivity for a target endmember or reduced ability to excite fluorescence in a target endmember, the range of scaling factors representing the amount of target endmember signal added should be correspondingly reduced, resulting in reduced performance for a spectral detection algorithm. To verify such a case, the intensity of the target endmember as measured in the single label control experiment should be assessed, as it is likely that even for a single label sample, the intensity would be low with incorrect selection of excitation and emission wavelength bands.
The theoretical sensitivity analysis methodology could likely be extended to allow even more in-depth characterization of a spectral imaging assay, system, etc. For example, by evaluating regions with varying autofluorescence or other background signal levels (as demonstrated in Figure 6 and Figure 7), it may be possible to develop a correlation between the minimum target endmember signal that must be present for detection (minimum detectable signal) and the tissue autofluorescence or background signal present. This could be highly useful in characterizing the sensitivity of an imaging system for detecting a specific molecular signature across a range of environments or tasks – for example, the sensitivity for detecting indocyanine green (ICG)-labeled lymph nodes across a range of tissues or detecting NADH fluorescence in the upper versus lower esophagus. In this manner, the methodology described here could be useful in determining minimum detectable limits in a tissue-specific or location-specific manner, or as a function of the false positive detection rate that could be tolerated. This methodology could also be combined with a set of benchmark standards in order to fully maximize the dynamic range of the measurement while ensuring that the signal is not over-saturated and that a specified minimum detectible signal is achieved. Finally, this methodology could be extended to account for thick sample preparations and 3-dimensional spectral confocal image data. In this case, a 3-dimensional region would need to be specified, and the sensitivity analysis performed on all voxels within the region.
The advantage of the theoretical sensitivity methodology may also include some limitations, in that there is a requirement for a simple series of single label control samples to be imaged. It should be noted, however, that most standard spectral analysis algorithms such as linear unmixing or spectral angle mapper, require knowledge of the pure component spectra. Hence, single label samples must be run in most cases anyways. The theoretical sensitivity analysis might prove most advantageous for cases where it is very difficult to obtain a sample or to preserve a sample for imaging with two or more different settings or systems. In this case, the spectrum of the target endmember would only need to be imaged once, and then a series of optimization studies performed theoretically, using background or other label samples that were imaged under a range of equipment settings. A potential limitation could arise if a sample is used where there is no a priori information of the target endmember signature. This could be the case when attempting to analyze molecular composition of tissues from spectral autofluorescence image data or to classify tissue type based on overall autofluorescence spectrum. This case could also arise if the spectral properties of a fluorescent label or molecule were altered due to changes in environment, photobleaching, or other interactions. In such cases, a possible strategy could be to use this methodology to test the ability to detect one or a range of hypothetical target endmembers, assuming that one of them will be of interest. However, further work would likely need to be performed to confirm which of the hypothetical target endmembers is the real endmember of interest (e.g., the representative spectral signature of a specific unknown autofluorescence component, or of a pathologic region of tissue). Hence, this methodology would still be of utility, but would need to be run iteratively to evaluate different mixture scenarios.
5. Conclusion
Hyperspectral imaging approaches have been successfully translated to the research microscopy field and show great promise for clinical and other biomedical imaging systems. However, it has been difficult to quantitatively assess the effectiveness of biomedical spectral imaging approaches or to compare the response of one spectral imaging platform to another. This is likely due to the compounding factors of high biological variability and limited ability to construct biological samples that contain specific “known” concentrations or distributions of molecules (e.g., test scenarios where the ground truth is fixed). Here, we have presented an alternative methodology for performing a theoretical sensitivity analysis of biomedical spectral image data. This methodology has allowed us to compare the performance of different spectral analysis algorithms, system settings, or even different spectral imaging systems. We have validated this methodology using experimental data and shown that the theoretical sensitivity predictions track closely with experimental measurements. We then demonstrated the power of this approach using a classical biomedical imaging problem: detecting a desired fluorescence signal (target endmember signal) in the presence of high background autofluorescence. We have further demonstrated that this approach can be used to quantitatively compare different spectral imaging systems – here we have compared a system that scans the fluorescence emission spectrum with one that scans the fluorescence excitation spectrum. This methodology could be of high utility for any of the following tasks: selecting an optimal spectral analysis algorithm, optimizing equipment and acquisition settings, or selecting an optimal imaging platform.
In future work, this theoretical sensitivity analysis methodology could be extended to a wide range of spectral imaging scenarios, such as for minimizing the number of wavelength bands acquired while achieving a specified detection performance, resulting in increased imaging speed and data reduction. Similarly, the approach could be used as part of the system design process in order to assure system optimization for completing a specified biomedical image detection task.
Acknowledgments
The authors would like to acknowledge support from NIH grants P01 HL066299, UL1 TR001417, S10 RR027535, S10 OD020149, and the Abraham Mitchell Cancer Research Fund. The authors would like to thank Dr. T. Thomas (Electrical and Computer Engineering, University of South Alabama) for discussion of some of the theoretical sensitivity principles described. Drs. Leavesley and Rich disclose part ownership of a start-up company founded to commercialize hyperspectral imaging technology.
References
- 1.Fink DJ. Technology Review. 1973;75:32–41. [Google Scholar]
- 2.Goetz AFH, Vane G, Solomon JE, Rock BN. Science. 1985;228:1147–1152. doi: 10.1126/science.228.4704.1147. [DOI] [PubMed] [Google Scholar]
- 3.Kruse F, Lefkoff A, Boardman J, Heidebrecht K, Shapiro A, Barloon P, Goetz A. Remote sensing of environment. 1993;44:145–163. [Google Scholar]
- 4.Yesou H, Besnus Y, Rolet J. ISPRS journal of photogrammetry and remote sensing. 1993;48:23–36. [Google Scholar]
- 5.Landgrebe D. PE & RS- Photogrammetric Engineering & Remote Sensing. 1997;63:859–867. [Google Scholar]
- 6.Landgrebe D. IEEE Transactions on Geoscience and Remote Sensing. 2005 Mar.43 [Google Scholar]
- 7.Landgrebe D. A brief history of the laboratory for applications of remote sensing (LARS) 2007 Mar 15; [Google Scholar]
- 8.Dickinson M, Bearman G, Tille S, Lansford R, Fraser S. Biotechniques. 2001;31:1272–1279. doi: 10.2144/01316bt01. [DOI] [PubMed] [Google Scholar]
- 9.Zimmermann T, Rietdorf J, Pepperkok R. FEBS letters. 2003;546:87–92. doi: 10.1016/s0014-5793(03)00521-0. [DOI] [PubMed] [Google Scholar]
- 10.Harris AT. Cytometry A. 2006;69:872–879. doi: 10.1002/cyto.a.20309. [DOI] [PubMed] [Google Scholar]
- 11.Li Q, He X, Wang Y, Liu H, Xu D, Guo F. Journal of biomedical optics. 2013;18:100901–100901. doi: 10.1117/1.JBO.18.10.100901. [DOI] [PubMed] [Google Scholar]
- 12.Lu G, Fei B. Journal of biomedical optics. 2014;19:010901–010901. doi: 10.1117/1.JBO.19.1.010901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wachman ES, Niu W, Farkas DL. Biophysical journal. 1997;73:1215. doi: 10.1016/S0006-3495(97)78154-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schultz RA, Nielsen T, Zavaleta JR, Ruch R, Wyatt R, Garner HR. Cytometry. 2001;43:239–247. doi: 10.1002/1097-0320(20010401)43:4<239::aid-cyto1056>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 15.Hiraoka Y, Shimi T, Haraguchi T. Cell structure and function. 2002;27:367–374. doi: 10.1247/csf.27.367. [DOI] [PubMed] [Google Scholar]
- 16.Ecker RC, de Martin R, Steiner GE, Schmid JA. Cytometry Part A. 2004;59:172–181. doi: 10.1002/cyto.a.20053. [DOI] [PubMed] [Google Scholar]
- 17.Forest S, Grothaus J. Microsc. Microanal. 2004;10:1304–1305. [Google Scholar]
- 18.Papadakis A, Stathopoulos E, Delides G, Berberides K, Nikiforidis G, Balas C. Biomedical Engineering, IEEE Transactions on. 2003;50:207–217. doi: 10.1109/TBME.2002.807648. [DOI] [PubMed] [Google Scholar]
- 19.Zuzak KJ, Schaeberle MD, Lewis EN, Levin IW. Analytical Chemistry. 2002;74:2021–2028. doi: 10.1021/ac011275f. [DOI] [PubMed] [Google Scholar]
- 20.Ntziachristos V, Bremer C, Weissleder R. Eur.Radiol. 2003 Jan.13:195–208. doi: 10.1007/s00330-002-1524-x. [DOI] [PubMed] [Google Scholar]
- 21.Gao X, Cui Y, Levenson RM, Chung LW, Nie S. Nat. Biotechnol. 2004;22:969–976. doi: 10.1038/nbt994. [DOI] [PubMed] [Google Scholar]
- 22.Vo-Dinh T. Engineering in Medicine and Biology Magazine, IEEE. 2004;23:40–49. doi: 10.1109/memb.2004.1360407. [DOI] [PubMed] [Google Scholar]
- 23.Mansfield JR, Gossage KW, Hoyt CC, Levenson RM. Journal of biomedical optics. 2005;10:041207–041207. doi: 10.1117/1.2032458. [DOI] [PubMed] [Google Scholar]
- 24.Leavesley SJ, Jiang Y, Patsekin V, Rajwa B, Robinson JP. Rev. Sci. Instrum. 2008 Feb.79:023707–023710. doi: 10.1063/1.2885043. [DOI] [PubMed] [Google Scholar]
- 25.Leblond F, Davis SC, Valdés PA, Pogue BW. Journal of photochemistry and photobiology B: Biology. 2010;98:77–94. doi: 10.1016/j.jphotobiol.2009.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chwirot BW, Chwirot S, Redzinski J, Michniewicz Z. European Journal of Cancer. 1998 Oct.34:1730–1734. doi: 10.1016/s0959-8049(98)00210-x. [DOI] [PubMed] [Google Scholar]
- 27.Yaroslavsky AN, Neel V, Anderson RR. Journal of Investigative Dermatology. 2003;121:259–266. doi: 10.1046/j.1523-1747.2003.12372.x. [DOI] [PubMed] [Google Scholar]
- 28.De Beule P, Dunsby C, Galletly N, Stamp G, Chu A, Anand U, Anand P, Benham C, Naylor A, French P. Review of scientific instruments. 2007;78:123101. doi: 10.1063/1.2818785. [DOI] [PubMed] [Google Scholar]
- 29.Akbari H, Halig LV, Schuster DM, Osunkoya A, Master V, Nieh PT, Chen GZ, Fei B. Journal of Biomedical Optics. 2012;17:0760051–07600510. doi: 10.1117/1.JBO.17.7.076005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Leavesley SJ, Wheeler M, Lopez C, Baker T, Favreau PF, Rich TC, Rider PF, Boudreaux CW. Hyperspectral imaging fluorescence excitation scanning for detecting colorectal cancer: pilot study. presented at the SPIE BiOS. 2016:970315–970315. doi: 10.1117/12.2213153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Harsanyi JC, Chang C-I. IEEE Transactions on Geoscience and Remote Sensing. 1994;32:179. [Google Scholar]
- 32.Richards JA. Remote sensing digital image analysis: An introduction. 5. Springer-Verlag; 1999. [Google Scholar]
- 33.Chang C-I. Hyperspectral data processing: algorithm design and analysis. John Wiley & Sons; 2013. [Google Scholar]
- 34.Schowengerdt RA. Remote sensing: models and methods for image processing. Academic press; 2006. [Google Scholar]
- 35.Schott JR. Remote sensing. Oxford University Press; 2007. [Google Scholar]
- 36.Keshava N. Lincoln Laboratory Journal. 2003;14:55–78. [Google Scholar]
- 37.Keshava N, Mustard JF. Signal Processing Magazine, IEEE. 2002;19:44–57. [Google Scholar]
- 38.Boardman J, Kruse F, Green R. Mapping target signatures via partial unmixing of AVIRIS data. presented at the Summaries of JPL Airborne Earth Science Workshop. 1995 [Google Scholar]
- 39.Keshava N, Mustard JF. IEEE Signal. Process. Mag. 2002;19:44–57. [Google Scholar]
- 40.Keshava N. Lincoln Laboratory Journal. 2003;14:55–78. [Google Scholar]
- 41.Benediktsson J, Swain P, Ersoy O. IEEE Transactions on Geoscience and Remote Sensing. 1990;28:540–552. [Google Scholar]
- 42.Atkinson PM, Tatnall A. International Journal of remote sensing. 1997;18:699–709. [Google Scholar]
- 43.Shafri HZM, Suhaili A, Mansor S. Journal of Computer Science. 2007;3:419–423. [Google Scholar]
- 44.Huang X, Jensen JR. Photogrammetric engineering and remote sensing. 1997;63:1185–1193. [Google Scholar]
- 45.Melgani F, Bruzzone L. IEEE Transactions on geoscience and remote sensing. 2004;42:1778–1790. [Google Scholar]
- 46.Pal M, Mather P. International Journal of Remote Sensing. 2005;26:1007–1011. [Google Scholar]
- 47.Mountrakis G, Im J, Ogole C. ISPRS Journal of Photogrammetry and Remote Sensing. 2011;66:247–259. [Google Scholar]
- 48.Holden H, LeDrew E. Remote Sensing of Environment. 1998;65:217–224. [Google Scholar]
- 49.Li X, Yeh A. International Journal of Remote Sensing. 1998;19:1501–1518. [Google Scholar]
- 50.Harsanyi JC. Detection and Classification of Subpixel Spectral Signatures in Hyperspectral Image Sequences. UMI; 1993. [Google Scholar]
- 51.Chang CI. Hyperspectral imaging: Techniques for Spectral Detection and Classification. New York, NY: Kluwer Academy, Plenum Publishers; 2003. [Google Scholar]
- 52.Shafri HZM, Suhaili A, Mansor S. Journal of Computer Science. 2007;3:419–423. [Google Scholar]
- 53.Jia S, Qian Y. Geoscience and Remote Sensing, IEEE Transactions on. 2009;47:161–173. [Google Scholar]
- 54.Teillet P. International Journal of Remote Sensing. 1986;7:1637–1651. [Google Scholar]
- 55.Chavez PS. Remote sensing of environment. 1988;24:459–479. [Google Scholar]
- 56.Kaufman Y, Tanré D, Gordon H, Nakajima T, Lenoble J, Frouin R, Grassl H, Herman B, King M, Teillet P. Journal of Geophysical Research: Atmospheres. 1997;102:16815–16830. [Google Scholar]
- 57.Gu Y, Di W, Kelsell D, Zicha D. J. Microsc. 2004;215:162–173. doi: 10.1111/j.0022-2720.2004.01365.x. [DOI] [PubMed] [Google Scholar]
- 58.Chorvat D, Jr, Kirchnerova J, Cagalinec M, Smolka J, Mateasik A, Chorvatova A. Biophysical journal. 2005;89:L55–L57. doi: 10.1529/biophysj.105.073866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Leavesley S, Ahmed W, Bayraktar B, Rajwa B, Sturgis J, Robinson JP. Multispectral imaging analysis: spectral deconvolution and applications in biology. Proceedings of SPIE. 2005;5699:121. [Google Scholar]
- 60.Coghlan L, Utzinger U, Drezek R, Heintzelman D, Zuluaga A, Brookner C, Richards-Kortum R, Gimenez-Conti I, Follen M. Optics express. 2000;7:436–446. doi: 10.1364/oe.7.000436. [DOI] [PubMed] [Google Scholar]
- 61.Fox DJ, Jr, Velde HT, Preza C, O’Sullivan JA, Smith WH, Woolsey TA. Applied optics. 2006;45:3009–3021. doi: 10.1364/ao.45.003009. [DOI] [PubMed] [Google Scholar]
- 62.Liu L, Nie Y, Lin L, Li W, Huang Z, Xie S, Li B. Photodiagnosis and Photodynamic Therapy. 2012 doi: 10.1016/j.pdpdt.2012.07.003. [DOI] [PubMed] [Google Scholar]
- 63.Mansfield JR, Sowa MG, Payette JR, Abdulrauf B, Stranc MF, Mantsch HH. Medical Imaging, IEEE Transactions on. 1998;17:1011–1018. doi: 10.1109/42.746634. [DOI] [PubMed] [Google Scholar]
- 64.Ahmed WM, Leavesley SJ, Rajwa B, Ayyaz MN, Ghafoor A, Robinson JP. Proceedings of the IEEE. 2008;96:512–531. [Google Scholar]
- 65.Annamdevula NS, Sweat B, Favreau P, Lindsey AS, Alvarez DF, Rich TC, Leavesley SJ. Sensors. 2013;13:9267–9293. doi: 10.3390/s130709267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Favreau P, Hernandez C, Lindsey AS, Alvarez DF, Rich T, Prabhat P, Leavesley SJ. Journal of biomedical optics. 2014;19:011017–011017. doi: 10.1117/1.JBO.19.1.011017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Favreau PF, Hernandez C, Heaster T, Alvarez DF, Rich TC, Prabhat P, Leavesley SJ. Journal of biomedical optics. 2014;19:046010–046010. doi: 10.1117/1.JBO.19.4.046010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Thaler C, Vogel SS. Cytometry Part A. 2006;69:904–911. doi: 10.1002/cyto.a.20267. [DOI] [PubMed] [Google Scholar]
- 69.Sirkeci-Mergen B, Keralapura M, Coelho S, Leavesley SJ, Rich TC. Linear unmixing of hyperspectral images for analysis of fluorescently-labeled cellswith imperfect endmember spectra. presented at the 2013 IEEE 10th International Symposium on Biomedical Imaging. 2013:173–176. [Google Scholar]
- 70.Gupta N, Dahmani R, Gottlieb MS, Denes LJ, Kaminsky B, Metes P. Hyperspectral imaging using acousto-optic tunable filters. presented at the AeroSense’99. 1999:512–521. [Google Scholar]
- 71.Yuanlong Y, Yanming Y, Fuming L, Yufen L, Paozhong M. Lasers in surgery and medicine. 1987;7:528–532. [Google Scholar]
- 72.Hung J, Lam S, Leriche JC, Palcic B. Lasers in surgery and medicine. 1991;11:99–105. doi: 10.1002/lsm.1900110203. [DOI] [PubMed] [Google Scholar]
- 73.Pavlova I, Sokolov K, Drezek R, Malpica A, Follen M, Richards-Kortum R. Photochemistry and photobiology. 2003;77:550–555. doi: 10.1562/0031-8655(2003)077<0550:maboon>2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 74.Rocheleau JV, Head WS, Piston DW. Journal of Biological Chemistry. 2004;279:31780–31787. doi: 10.1074/jbc.M314005200. [DOI] [PubMed] [Google Scholar]
- 75.Mansfield JR, Gossage KW, Hoyt CC, Levenson RM. J. Biomed. Opt. 2005 Jul.10:41207. doi: 10.1117/1.2032458. [DOI] [PubMed] [Google Scholar]
- 76.Billinton N, Knight AW. Analytical biochemistry. 2001;291:175–197. doi: 10.1006/abio.2000.5006. [DOI] [PubMed] [Google Scholar]
- 77.Geddes CD, Lakowicz JR. Reviews in fluorescence. Springer; 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Rich TC, Webb KJ, Leavesley SJ. J. Gen. Physiol. 2014;143:17–27. doi: 10.1085/jgp.201311095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lin H-J, Szmacinski H, Lakowicz JR. Analytical biochemistry. 1999;269:162–167. doi: 10.1006/abio.1999.4011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Berezin MY, Achilefu S. Chemical reviews. 2010;110:2641–2684. doi: 10.1021/cr900343z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Alfano R, Tata D, Cordero J, Tomashefsky P, Longo F, Alfano M. Quantum Electronics, IEEE Journal of. 1984;20:1507–1511. [Google Scholar]
- 82.Richards-Kortum R, Sevick-Muraca E. Annu. Rev. Phys. Chem. 1996;47:555–606. doi: 10.1146/annurev.physchem.47.1.555. [DOI] [PubMed] [Google Scholar]
- 83.Tuchin VV, Utz SR, Yaroslavsky IV. Optical Engineering (Bellingham, Washington) 1994;33:3178–3188. [Google Scholar]
- 84.Tuchin VV. Tissue optics: light scattering methods and instruments for medical diagnosis. 2. SPIE press; Bellingham: 2007. [Google Scholar]
- 85.Chen X, Vierling L, Rowell E, DeFelice T. Remote Sensing of Environment. 2004;91:14–26. [Google Scholar]
- 86.Favreau PF, Deal JA, Weber DS, Rich TC, Leavesley SJ. Feasibility for detection of autofluorescent signatures in rat organs using a novel excitation-scanning hyperspectral imaging system. presented at the SPIE BiOS. 2016:971113–971113. doi: 10.1117/12.2213214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Lu D, Moran E, Batistella M. Remote sensing of environment. 2003;87:456–469. [Google Scholar]
- 88.Sohn Y, Morán E, Gurri F. Photogrammetric engineering and remote sensing. 1999;65:947–958. [Google Scholar]
- 89.Metz CE. Basic principles of ROC analysis. presented at the Seminars in nuclear medicine. 1978:283–298. doi: 10.1016/s0001-2998(78)80014-2. [DOI] [PubMed] [Google Scholar]
- 90.Reach G. Diabetes Care. 2001;24:803–804. doi: 10.2337/diacare.24.5.803. [DOI] [PubMed] [Google Scholar]
- 91.Du Q, Ren H, Chang C-I. IEEE Trans. Geosci. Remote Sens. 2003;41:1525–1529. [Google Scholar]
- 92.Manolakis D, Shaw G. Signal Processing Magazine, IEEE. 2002;19:29–43. [Google Scholar]
- 93.Boardman JW, Kruse FA. IEEE Transactions on Geoscience and Remote Sensing. 2011;49:4138–4152. [Google Scholar]
- 94.Williams P, Hunt A, R E., Jr Remote Sens. Environ. 2002;82:446–456. [Google Scholar]
- 95.Manolakis D, Shaw G. Signal Processing Magazine, IEEE. 2002;19:29–43. [Google Scholar]
- 96.Leavesley SJ, Annamdevula N, Boni J, Stocker S, Grant K, Troyanovsky B, Rich TC, Alvarez DF. J. Biophotonics. 2012;5:67–84. doi: 10.1002/jbio.201100066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Favreau PF, Hernandez C, Lindsey AS, Alvarez DF, Rich TC, Prabhat P, Leavesley SJ. Journal of biomedical optics. 2014;19:011017–011017. doi: 10.1117/1.JBO.19.1.011017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Sullivan L, Favreau P, Leavesley S, Alvarez D, Stringfellow A. Am J Respir Crit Care Med. 2012;185:A3663. [Google Scholar]
- 99.Chang IC. IEEE Transactions on Sonics and Ultrasonics. 1976;23:2–21. [Google Scholar]
- 100.Wachman ES, Niu W, Farkas DL. Biophysical journal. 1997;73:1215–1222. doi: 10.1016/S0006-3495(97)78154-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Romier J, Selves J, Gastellu-Etchegorry J. Rev. Sci. Instrum. 1998;69:2859. [Google Scholar]
- 102.Bei L, Dennis GI, Miller HM, Spaine TW, Carnahan JW. Progress in Quantum Electronics. 2004;28:67–87. [Google Scholar]
- 103.Hall H, Bridges M, Leavesley S, Robinson JP. Design of a wavelength-tunable light source using an acousto-optic tunable filter. Proceedings of SPIE. 2007;6668:66680W. [Google Scholar]
- 104.Favreau PF, Rich TC, Prabhat P, Leavesley SJ. Tunable thin-film optical filters for hyperspectral microscopy. presented at the SPIE BiOS. 2013:85890R–85890R. doi: 10.1117/12.2002469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Janesick JR. CCD transfer method: standard for absolute performance of CCDs and digital CCD camera systems. presented at the Electronic Imaging’97. 1997:70–102. [Google Scholar]
- 106.Janesick JR. Scientific charge-coupled devices. Vol. 83. SPIE press; 2001. [Google Scholar]
- 107.Halter M, Bier E, DeRose PC, Cooksey GA, Choquette SJ, Plant AL, Elliott JT. Cytometry Part A. 2014;85:978–985. doi: 10.1002/cyto.a.22519. [DOI] [PubMed] [Google Scholar]
- 108.Gruninger J, Sundberg R, Fox M, Levine R, Mundkowsky W, Salisbury M, Ratcliff A. Automated optimal channel selection for spectral imaging sensors. Algorithms for Multispectral, Hyperspectral and Ultraspectral Imagery VII. 2001;4381:68–75. [Google Scholar]