Moiré excitons: From programmable quantum emitter arrays to spin-orbit–coupled artificial lattices

Moiré pattern realizes programmable array of excitonic quantum emitters and exciton lattice with strong spin-orbit coupling.

Abstract

Highly uniform and ordered nanodot arrays are crucial for high-performance quantum optoelectronics, including new semiconductor lasers and single-photon emitters, and for synthesizing artificial lattices of interacting quasiparticles toward quantum information processing and simulation of many-body physics. Van der Waals heterostructures of two-dimensional semiconductors are naturally endowed with an ordered nanoscale landscape, that is, the moiré pattern that laterally modulates electronic and topographic structures. We find that these moiré effects realize superstructures of nanodot confinements for long-lived interlayer excitons, which can be either electrically or strain tuned from perfect arrays of quantum emitters to excitonic superlattices with giant spin-orbit coupling (SOC). Besides the wide-range tuning of emission wavelength, the electric field can also invert the spin optical selection rule of the emitter arrays. This unprecedented control arises from the gauge structure imprinted on exciton wave functions by the moiré, which underlies the SOC when hopping couples nanodots into superlattices. We show that the moiré hosts complex hopping honeycomb superlattices, where exciton bands feature a Dirac node and two Weyl nodes, connected by spin-momentum–locked topological edge modes.

INTRODUCTION

Artificial lattices of interacting particles offer a tunable platform for quantum information processing and quantum simulation of many-body physics, and have been extensively explored for atoms and electrons (1–3). Intrigued by the topological states of matter arising from spin-orbit coupling (SOC) as found in crystalline solids (4–6), a significant amount of effort has been devoted to synthesizing SOC in artificial lattices (2, 3), which is of great interest for simulating exotic quantum phases such as the topological superfluid.

Van der Waals (vdW) heterostructures of two-dimensional (2D) materials provide a new approach toward engineering artificial lattices, where the ubiquitous moiré pattern between different monolayers naturally endows quasiparticles with a nanoscale periodic landscape. The moiré modulation in electronic structures has led to exciting possibilities to engineer topological moiré minibands (7–11) and topological insulator superstructures (12). In 2D semiconductor vdW heterostructures, the interlayer exciton is a composite quasiparticle that can be most profoundly affected by the moiré because of the separation of its electron and hole constituents in two layers with interlayer registry varying from local to local (Fig. 1A). These interlayer excitons have demonstrated bright luminescence, ultralong lifetimes, robust spin-valley polarization, and spin-dependent interaction in transition metal dichalcogenide (TMD) heterobilayers (13–18), drawing remarkable interest for exploring new spin optoelectronics and high-temperature superfluidity (19).

Fig. 1. Moiré modulated local energy gaps and topographic height in the heterobilayer.

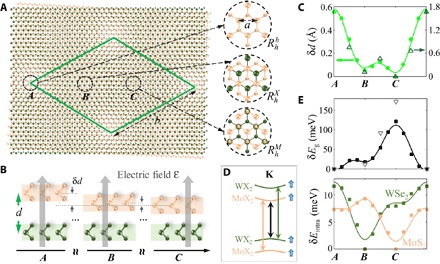
(A) Long-period moiré pattern in an MoX₂/WX₂ heterobilayer. Green diamond is a supercell. Insets are close-ups of three locals, where atomic registries resemble lattice-matched bilayers of different R-type stacking. (B and C) Dependence of interlayer distance d on the atomic registries. In (C), dots are our first-principles calculations for the MoS₂/WSe₂ heterobilayer, and triangles are the scanning tunneling microscopy (STM) measured variation of the local d values in a b = 8.7 nm MoS₂/WSe₂ moiré in the study of Zhang et al. (26). The variation in d then leads to laterally modulated interlayer bias (∝ d) in a uniform perpendicular electric field, as (B) illustrates. (D) Schematic of relevant heterobilayer bands at the K valley, predominantly localized in either the MoX₂ or WX₂ layer. (E) Top: Variation of the local bandgap E_g [black arrow in (D)] in the MoS₂/WSe₂ moiré. Bottom: Variation of the local intralayer gaps [denoted by arrows of the same color in (D)]. In (C) and (E), the horizontal axis corresponds to the long diagonal of the moiré supercell, and the vertical axis plots the differences of the quantities from their minimal values. The curves are fitting of the data points using eqs. S2 and S3 in section S1.

Here, we show that the moiré in vdW heterobilayers realizes superlattice potentials, in which the interlayer excitons have a unique spin-dependent complex hopping, leading to giant spin-orbit splitting in the exciton bands. In TMD heterobilayers, we show the presence of spin-orbit–coupled honeycomb superlattices, where the exciton bands feature Dirac and Weyl nodes and spin-momentum–locked edge states dictated by these magnetic monopoles. Hopping in the superlattice potentials can be switched off by a perpendicular electric field or by strain tuning of moiré periodicity, turning the superlattices into perfect arrays of nanodots that act as uniform quantum emitters. The electric field can also switch the positioning of the quantum emitters in the moiré, hence inverting their spin optical selection rules that are unique imprints of local atomic registries. These properties of moiré excitons point to exciting opportunities toward high-performance semiconductor lasers, single-photon emitter arrays, entangled photon sources, and a platform of versatile tunability for studying exotic quantum phases of matter with imaging possibilities.

RESULTS

Figure 1 (A to C) schematically shows a long-period moiré in heterobilayers of MX₂ (M = Mo,W; X = Se,S). MX₂ monolayers have conduction and valence band edges at K and −K corners of the hexagonal Brillouin zone, where large spin-orbit splitting leads to an effective locking of spin to valley, that is, the valence band edge at K (−K) has spin-up (spin-down) states only. Optically active excitons thus have a pseudospin-1/2 spanned by the spin-valley–locked band edges. The various MoX₂/WX₂ heterobilayers have the type II band alignment (Fig. 1D) (13–16, 18, 20–23), where electrons (holes) have lower energy in the MoX₂ (WX₂) layer. Excitons thus energetically favor the interlayer configuration, with electron and hole constituents in opposite layers.

The locally different interlayer registry in the heterobilayer moiré can be quantified by the in-plane displacement vector r₀ from a metal site in the hole layer to a near-neighbor metal site in the electron layer. Hopping and vdW interaction between the layers depend sensitively on r₀ (24, 25). The dependence of r₀ on location R in the moiré generally results in lateral modulation in the local bandgap (E_g) and interlayer distance (d) (26, 27). Thus, the interlayer excitons in the moiré experience nanopatterned periodic potential

$$\mathit{V}(\mathbf{R})={\mathit{E}}_{\mathrm{g}}({\mathbf{r}}_0(\mathbf{R}))+\mathit{e}\mathrm{\epsilon }\mathit{d}({\mathbf{r}}_0(\mathbf{R}))-{\mathit{E}}_{\mathit{b}}$$ (1)

where the second term is the Stark shift in a perpendicular electric field ε (16). In chemical vapor deposition–grown R-type MoS₂/WSe₂ heterobilayers, STM/scanning tunneling spectroscopy has revealed the laterally modulated local E_g and d in a moiré pattern with period b = 8.7 nm (26). In Fig. 1 (C and E), the measured local E_g and d values at different r₀ from Zhang et al. (26) are shown in comparison with our first-principles calculated values for the lattice-matched heterobilayer. The exciton binding energy E_b also depends on location R through d, but the dependence is expected to be weak because the variation in d is only a tiny fraction of the in-plane Bohr radius a_B (a few nanometers).

Nanopatterned spin optics and programmable quantum emitter arrays

The description of optical properties of the moiré excitons can be facilitated by wave packets moving adiabatically in the periodic potential. An exciton wave packet can be constructed using the basis of kinematic momentum eigenstates introduced for the lattice-mismatched heterobilayer (see section S2) (28), with a real-space extension being small compared to the moiré period b but large compared to the monolayer lattice constant a. When the wave packet falls on regions where the local atomic registries preserve the threefold rotational (${\widehat{\mathit{C}}}_3$) symmetry, the wave packet is an eigenfunction of the ${\widehat{\mathit{C}}}_3$ rotation about its center (see Fig. 2A). These high symmetry locals are located at A, B, and C points of the moiré supercell shown in Fig. 1A, corresponding to the ${\mathit{R}}_{\mathit{h}}^{\mathit{h}}$, ${\mathit{R}}_{\mathit{h}}^{\mathit{X}}$, and ${\mathit{R}}_{\mathit{h}}^{\mathit{M}}$ registries, respectively. Here, ${\mathit{R}}_{\mathit{h}}^{\mathrm{\mu }}$ denotes an R-type stacking, with the μ site of the electron layer vertically aligned with the hexagon center (h) of the hole layer. Upon fixing h as the rotation center, the hole Bloch function at K is invariant under ${\widehat{\mathit{C}}}_3$(29). The corresponding rotation center in the electron layer is then its h center, X (chalcogen) site, and M (metal) site, respectively, under ${\mathit{R}}_{\mathit{h}}^{\mathit{h}}$, ${\mathit{R}}_{\mathit{h}}^{\mathit{X}}$, and ${\mathit{R}}_{\mathit{h}}^{\mathit{M}}$ registries, about which the electron Bloch function has distinct ${\widehat{\mathit{C}}}_3$ eigenvalues, as shown in Fig. 2A. Hence, exciton wave packets $\mathcal{X}$ at these three locals have the following ${\widehat{\mathit{C}}}_3$ transformations (more details in section S2)

$${\widehat{\mathit{C}}}_3{\mathcal{X}}_{\mathit{A},\mathit{s}}={\mathit{e}}^{-\mathit{i}\frac{2\mathrm{\pi }}{3}\mathit{s}}{\mathcal{X}}_{\mathit{A},\mathit{s}}, {\widehat{\mathit{C}}}_3{\mathcal{X}}_{\mathit{B},\mathit{s}}={\mathit{e}}^{\mathit{i}\frac{2\mathrm{\pi }}{3}\mathit{s}}{\mathcal{X}}_{\mathit{B},\mathit{s}}, {\widehat{\mathit{C}}}_3{\mathcal{X}}_{\mathit{C},\mathit{s}}={\mathcal{X}}_{\mathit{C},\mathit{s}}$$ (2)

Fig. 2. Nanopatterned spin optics of moiré excitons.

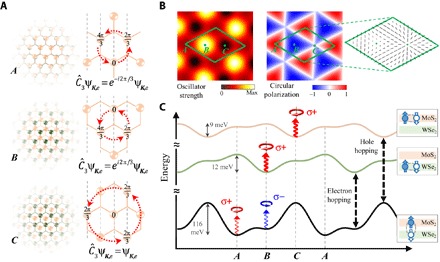
(A) Left: Exciton wave packets at the locals with ${\mathit{R}}_{\mathit{h}}^{\mathit{h}}$, ${\mathit{R}}_{\mathit{h}}^{\mathit{X}}$, and ${\mathit{R}}_{\mathit{h}}^{\mathit{M}}$ registries, respectively (see Fig. 1A). Right: Corresponding ${\widehat{\mathit{C}}}_3$ transformation of electron Bloch function ψ_K,e, when the rotation center is fixed at a hexagon center in the hole layer. Gray dashed lines denote planes of constant phases in the envelope part of ψ_K,e, and red arrows denote the phase change by ${\widehat{\mathit{C}}}_3$. (B) Left: Oscillator strength of the interlayer exciton. Right: Optical selection rule for the spin-up interlayer exciton (at the K valley). The distinct ${\widehat{\mathit{C}}}_3$ eigenvalues, as shown in (A), dictate the interlayer exciton emission to be circularly polarized at A and B with opposite helicity and forbidden at C. At other locals in the moiré, the emission is elliptically polarized (see inset, where ticks denote the major axis of polarization with length proportional to ellipticity). (C) Contrasted potential landscapes for the intra- and interlayer excitons, with the optical selection rule for the spin-up species shown at the energy minima. Transitions between the inter- and intralayer excitons (that is, via electron/hole hopping) can be induced by mid-infrared light with out-of-plane polarization.

Here, s is the spin-valley index: s = + (−) for the exciton at the K (−K) valley, which has up (down) spin. Photons convertible with excitons must have the same rotational symmetry. Thus, Eq. 2 dictates the optical selection rules: The spin-up exciton wave packet at A (B) couples to σ + (σ −) circularly polarized light only, whereas light coupling is forbidden at C.

The above spin optical selection rules imply the nanoscale patterning of spin optical properties in the moiré. Figure 2B plots the calculated oscillator strength and polarization of the optical transition dipole as the interlayer exciton wave packet adiabatically moves in the R-type MoS₂/WSe₂ heterobilayer moiré (see sections S1 and S2), consistent with the symmetry analysis. The optical selection rules cross between the opposite circular polarization at A and B via elliptical polarization at other locals, where the registry no longer has the ${\widehat{\mathit{C}}}_3$ symmetry.

The ${\widehat{\mathit{C}}}_3$ symmetry also dictates A, B, and C to be the energy extrema of the exciton potential V(R). For R-type MoS₂/WSe₂ heterobilayers at zero field, the global minima are the A points, around which the strong variation in V(R) (~100 meV) realizes perfect arrays of nanodot confinement (see Fig. 3A). The strong repulsive interactions (17) between interlayer excitons endow these nanodots with two desired functionalities (as single-photon emitters or as sources of entangled photon pairs) controlled by exciton number loaded per nanodot. As shown in Fig. 3D, the two-exciton configuration, energetically favored in antiparallel spins because of the repulsive on-site Coulomb exchange (U_ex), generates a polarization-entangled pair of photons at E_x and E_x + U_dd, respectively, where U_dd is the on-site dipole-dipole interaction. Figure 3F plots the estimated U_ex and U_dd in the nanodot confinement of the R-type MoS₂/WSe₂ heterobilayer moiré, both are orders larger compared to the radiative decay rate. Thus, cascaded emissions of multiple excitons have well-separated spectral resonances.

Fig. 3. Electrically tunable and strain-tunable quantum emitter arrays.

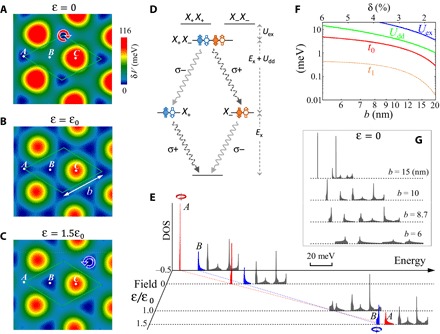
(A to C) Tuning of excitonic potential by perpendicular electric field (ε) in the R-type MoS₂/WSe₂ moiré. At zero field, nanodot confinements are at A points, realizing periodic array of excitonic quantum emitters, which are switched to B points at moderate field (see the main text). (D) Spin optical selection rule of quantum emitter at A. When loaded with two excitons, the cascaded emission generates a polarization-entangled photon pair. The optical selection rule is inverted when the quantum emitter is shifted to B [see (A) and (C)]. (E) Electric field tuning of exciton density of states (DOS) in the R-type MoS₂/WSe₂ moiré with b = 10 nm. The field dependence of V(A) and V(B) are denoted by the dotted blue and red lines on the field-energy plane. The colors of the two lowest energy peaks distinguish their different orbital compositions at A and B points in the moiré. (F) Exciton hopping integral between nearest-neighbor (NN) A and B dots in (B) (t₀), between NN A dots (t₁), and on-site exciton dipole-dipole (U_dd) and exchange (U_ex) interactions as functions of the moiré period b (see sections S4 and S5). The top horizontal axis is the corresponding lattice mismatch δ for rotationally aligned bilayer. (G) Exciton DOS at different b at zero electric field. The 20-meV scale bar applies for the energy axis in (E) and (G).

B points are also local minima of V(R), as shown in Fig. 2C. The different local interlayer distances at A and B (see Fig. 1C) make electric field tuning of their energy difference possible such that the nanodot confinement of the excitonic quantum emitters can be switched to the B points (see Fig. 3, A to C). The inversion of V(A) − V(B) happens at a modest field value of ε₀ = 0.36 V/nm [0.08 V/nm], taking first-principles calculated [STM measured (26)] δd in the R-type MoS₂/WSe₂ moiré, as plotted in Fig. 1C. Along with this electric switching in positions of the quantum emitters, their spin optical selection rules are inverted, and emission wavelength is continuously tuned over a wide range of ~O(100) meV (see Fig. 3E). Thus, the electric field (interlayer bias) can be used to program the spatial locations, optical selection rule, and emission wavelength of these quantum emitters on demand.

The heterobilayer moiré formed by different TMD compounds and the H-type stacking feature similar nanopatterned spin optics as the R-type MoS₂/WSe₂, whereas the potential profiles and their field dependence can have quantitative differences. Different compound combinations and stacking also lead to distinct emission lifetime of the interlayer exciton in nanodot confinement, offering choices on the photon bandwidth in the range of 0.01 to 1 GHz (see section S2 for an analysis on the interlayer exciton lifetime). Compared to monolayer TMD emitters (30–34), the wider range of choices on the heterobilayer bandgap (13, 15–17, 20–23, 26) and significant field tunability further promise applications of these moiré quantum emitters from the visible to the telecom wavelengths.

The lattice mismatch δ is ~ 4 % between disulfides and diselenides, and ~ 0.1 % between MoSe₂ and WSe₂ or between MoS₂ and WS₂. This allows choices on the moiré period b over a range up to ~10 nm in the M′S₂/MSe₂ bilayers and O(100) nm in the MoSe₂/WSe₂ or MoS₂/WS₂ bilayers. A differential strain between the two layers, applicable through a piezoelectric or flexible substrate, further allows in situ tuning of δ, which can be magnified into drastic change in the shape and period of the moiré (12), which can be exploited for programming the spatial pattern of the emitter array. Exciton hopping between the nanodots is an exponential function of the moiré period (Fig. 3F), whereas for large b or large Δ≡V(A) − V(B), the quench of hopping leads to the 0D spectrum of a uniform quantum emitter ensemble (see Fig. 3G). At b ≤ 10 nm and small Δ, hopping connects the A and B nanodots into an excitonic superlattice (see Fig. 3B).

Spin-orbit–coupled artificial lattices

Below, we focus on moiré excitons at relative small b and small Δ, where excitons can hop between the A and B dots, which form a honeycomb superlattice. The low-energy spectrum in this superlattice can be well described by a tight-binding model counting up to the third NN hopping (35). Distinct from graphene and other existing artificial honeycomb lattices (1), the hopping integrals of the interlayer excitons in this superlattice are complex numbers depending on exciton spin s and the orientation of the displacement vector between the sites. As illustrated in Fig. 4A, the NN and third NN hopping integrals are (see section S3)

$${\mathit{t}}_{\mathit{s}}({\mathbf{d}}_{0/2})={\mathit{t}}_{0/2},{\mathit{t}}_{\mathit{s}}\left({\widehat{\mathit{C}}}_3{\mathbf{d}}_{0/2}\right)={\mathit{t}}_{0/2}{\mathit{e}}^{-\mathit{i}\frac{4\mathrm{\pi }}{3}\mathit{s}},{\mathit{t}}_{\mathit{s}}\left({\widehat{\mathit{C}}}_3^2{\mathbf{d}}_{0/2}\right)={\mathit{t}}_{0/2}{\mathit{e}}^{\mathit{i}\frac{4\mathrm{\pi }}{3}\mathit{s}}$$ (3)

where ${\mathbf{d}}_0\equiv \frac{\mathit{b}}{\sqrt{3}}\widehat{\mathbf{x}}$ (${\mathbf{d}}_2\equiv -\frac{2\mathit{b}}{\sqrt{3}}\widehat{\mathbf{x}}$) is a displacement vector from A N (third NN) B site. These spin-dependent phases can be derived from the rotational symmetry of the exciton wave function at A and B sites, as given in Eq. 2. The second NN hopping integrals are also found to be complex: ${\mathit{t}}_{\mathit{s}}({\mathbf{d}}_1)={\mathit{t}}_{\mathit{s}}({\widehat{\mathit{C}}}_3{\mathbf{d}}_1)={\mathit{t}}_{\mathit{s}}({\widehat{\mathit{C}}}_3^2{\mathbf{d}}_1)={\mathit{t}}_1{\mathit{e}}^{\mathit{i}\frac{4\mathrm{\pi }}{3}\mathit{s}}$ (see section S3).

Fig. 4. Spin-orbit–coupled honeycomb lattices and Weyl nodes.

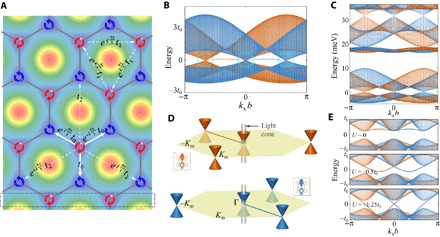
(A) Opposite photon emission polarization at A and B sites and complex hopping matrix elements for the spin-up exciton. (B) Exciton spectrum at V(A) = V(B) and moiré period b = 10 nm, from the tight-binding model with the third NN hopping. t₀ = 2.11 meV, t₁ = 0.25 meV, and t₂ = 0.14 meV. The bands feature a Dirac node and two Weyl nodes (highlighted by dotted circles). These magnetic monopoles are linked by an edge mode at a zigzag boundary, with spin polarization reversal at the Dirac node. Spin-down (spin-up) exciton is denoted by brown (blue) color. (C) Exact exciton spectrum in this superlattice potential (see section S4). Dirac/Weyl nodes are also seen in higher energy bands. (D) Schematic of the Dirac cones for the spin-up and spin-down excitons in the moiré–Brillouin zone (m-BZ), and edge modes at a zigzag boundary. Exciton-photon interconversion can directly happen within the shown light cone. (E) The Dirac and Weyl nodes are gapped by a finite A-B site energy difference Δ = 0.5t₀, whereas the edge band dispersion is tuned by changing the on-site energy of the dots on the zigzag boundary [enclosed by the dashed box in (A)] by the amount U.

Figure 4 (B and C) plots the exciton dispersion in such a complex hopping honeycomb lattice with Δ = 0, exhibiting a giant spin-orbit splitting comparable to the bandwidth. The exciton bands feature a Dirac node (fourfold degenerate) and two Weyl nodes (twofold degenerate) with opposite spin polarization. At a zigzag boundary, a nearly flat edge band connects the two Weyl nodes through the Dirac node at which the spin polarization of the edge band flips sign. These topological features originate from the spin-dependent hopping phases, which render the Hamiltonian of spin-s block a graphene model that shifted in the momentum space by sK_m, the wave vector at an m-BZ corner. The two spin-up Dirac cones now appear at the m-BZ center Γ and the m-BZ corner $-{\mathbf{K}}_{\mathit{m}}\equiv (0,-\frac{4\mathrm{\pi }}{3\mathit{b}})$, respectively (see Fig. 4D), whereas the spin-down Dirac cones are located at the Γ point and K_m corner, respectively.

The edge band has its topological origin from these Weyl nodes in the bulk bands. In each spin subspace, the pair of Weyl nodes is linked by an incomplete edge band, which is an analog of the surface Fermi arc in 3D Weyl semimetals (6) and has been addressed in graphene (36). The spin-up and spin-down edge bands now appear in conjugate moment space regions and are joined together at the Γ point by the coincidence of the spin-up and spin-down Weyl nodes that constitute a Dirac node. Observation of these spin-dependent excitonic edge modes can provide evidence of the topological nature.

The 2D Dirac/Weyl nodes will get gapped by a finite Δ, the Dirac mass, tunable by the electric field ε (Fig. 3, A to C). Interconversion between exciton and photon happens in a momentum space regime known as the light cone (see Fig. 4B), where the energy-momentum conservation can be satisfied. Because the light cone encloses only the Dirac cone at the Γ point, the tuning of the Dirac mass from zero to finite by the interlayer bias can drastically change the exciton DOS in the light cone and hence the radiative recombination rate of the moiré excitons.

Moreover, the edge modes connecting the 2D Dirac/Weyl nodes can be separately controlled by a potential localized to the boundary (37). Figure 4E shows an example of such a control, where the edge band can be continuously tuned from nearly flat band to the gapless helical states by tuning the magnitude of the on-site energy at the outermost column of A sites (see Fig. 4A). This points to interesting possibilities of experimental manipulation of topological exciton propagation and light coupling on the edge.

These band topological features, together with the observed spin-valley–dependent exciton interactions (17), further point to a unique Bose-Hubbard system for exploring many-body phenomena with the electric and strain tunability on the hopping and interactions (Fig. 3F).

DISCUSSION

Most of the properties discussed here are not limited to TMD heterobilayers and can be generally expected in other long-period heterobilayer moiré that host the interlayer excitons. The patterned optical properties are imprints on the excitons by their local atomic registries, which sensitively affect the interlayer hopping and hence the optical dipole moment of the exciton. The spin-dependent complex hopping is also a generic feature of the interlayer valley exciton in the heterobilayer moiré. Under proper gauge choice for the wave packet, the hopping matrix element from a site at R₁ to another site at R₂ in the moiré superlattices is of the form

$$\mathit{t}({\mathbf{R}}_1-{\mathbf{R}}_2)={\mathit{e}}^{\mathit{i}({\mathbf{Q}}_{\mathit{e}}-{\mathbf{Q}}_{\mathit{h}}^{\prime })({\mathbf{R}}_1-{\mathbf{R}}_2)}|\mathit{t}({\mathbf{R}}_1-{\mathbf{R}}_2)|$$ (4)

where ${\mathbf{Q}}_{\mathit{h}}^{\mathbf{\prime }}$ (Q_e) is the wave vector at the hole (electron) valley center, not necessarily high-symmetry points. The complex hopping phases are fully determined by ${\mathbf{Q}}_{\mathit{e}}-{\mathbf{Q}}_{\mathit{h}}^{\mathbf{\prime }}$, the momentum space displacement between the electron and hole valley centers due to the lattice mismatch. In the context of TMD heterobilayers, the displacement wave vector between the electron and hole K valleys corresponds to the corners of the m-BZ, and Eq. 4 reproduces all complex hopping integrals in the honeycomb superlattices given in Eq. 3 and Fig. 4A. In the presence of time-reversal symmetry, an exciton of valley configuration (${\mathbf{Q}}_{\mathit{h}}^{\mathbf{\prime }}$, Q_e) has a time-reversal counterpart at ($-{\mathbf{Q}}_{\mathit{h}}^{\mathbf{\prime }}$, − Q_e) with the opposite spin. Therefore, these two spin species have opposite complex hopping phases. This spin-dependent complex hopping, in general, leads to a large effective spin-orbit splitting in the exciton bands (see TMD examples in Fig. 4, B and C).

Both the complex hopping and the nanopatterned spin optics reflect the locally different rotational symmetries of exciton wave functions because of the locally different atomic registry in the moiré. These truly unique exciton physics enabled by the moiré pattern do not have a counterpart in other systems including the GaAs/AlGaAs quantum wells and individual TMD monolayers. Thus, the TMD heterobilayer moiré provides unprecedented opportunities to explore excitonic quantum emitters and exciton superlattices.

In the typical moiré pattern, the spacing of the nanodots ranges from several nanometers to several tens of nanometers, in the regime where a dense array of uniform exciton emitters can be collectively coupled to common optical modes. Thus, the moiré quantum emitter array can be exploited for a number of applications and studies, from quantum dot laser, entangled photon laser (38), and topological photonics (39) to the exploration of the seminal Dicke superradiance phenomena (40). Individual quantum emitters in the moiré superlattice can also be addressed using the spatially selective excitation of the moiré exciton, for example, using the nano-optical antenna tip (41).

It is worth noting that the intralayer excitons also experience moiré-patterned potentials (11), although much shallower, because of the dependence of the local intralayer gaps on the atomic registry (see Fig. 1, D and E). A comparison of the potentials and spin optical selection rules for the inter- and intralayer excitons in the R-type MoS₂/WSe₂ heterobilayer moiré can be found in Fig. 2C. The energy minima of the MoS₂ exciton are at C, the optically dark points and energy maxima for the interlayer exciton. In contrast, the WSe₂ exciton has its energy minima at B, where the spin-valley selection rules for the intra- and interlayer excitons have opposite helicities. These contrasts imply interesting possibilities of dynamic controls for loading the quantum emitter arrays.

MATERIALS AND METHODS

The first-principles calculations were performed using the Vienna Ab initio Simulation Package (42) based on plane waves and the projector-augmented wave method (43). The Perdew-Burke-Ernzerhof (44) exchange-correlation functional was used for all calculations, and the vdW interactions were considered in the DFT-D3 (dispersion-corrected density functional theory) (45) method. The experimentally measured bulk lattice constants are 3.288 Å for MoSe₂ (46), 3.160 Å for MoS₂ (46), and 3.282 Å for WSe₂ (47). Their average of 3.285 Å (3.221 Å) was used for the lattice-matched MoSe₂/WSe₂ (MoS₂/WSe₂) heterobilayer. Keeping the in-plane positions fixed, the out-of-plane positions were relaxed for all atoms until the energy difference of successive atom configurations was less than 10⁻⁶ eV. The out-of-plane force on each atom in the relaxed structure was less than 0.003 eV/Å. The cutoff energy of the plane-wave basis was set to 350 eV, and the convergence criterion for total energy was 10⁻⁸ eV. A Γ-centered k mesh of 15 × 15 × 1 was used for both the relaxation and normal calculations. The thickness of the vacuum layer was greater than 20 Å to avoid impacts from neighboring periodic images. SOC was taken into account for all calculations, except in structure relaxation.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/11/e1701696/DC1

section S1. Modulated electronic and topographic properties in the heterobilayer moiré

section S2. Nanopatterned optical properties of the interlayer excitons in the moiré

section S3. Complex hopping of the interlayer excitons in the moiré

section S4. Exciton bands in superlattice potential: Exact solution and tight-binding model

section S5. Exciton-exciton interactions in the superlattices

fig. S1. Schematic of how the interlayer translation vector r₀(R) (thick green arrows) changes as a function of in-plane position vector R.

fig. S2. The modulations of layer separation δd, interlayer bandgap δE_g, and intralayer bandgap δE_intra for H-type MoS₂/WSe₂, R-type MoSe₂/WSe₂, and H-type MoSe₂/WSe₂ lattice-matched heterobilayers of various interlayer atomic registries.

fig. S3. The potential profile of the interlayer excitons in the three types of TMD heterobilayers (see Eq. 1 in the main text).

fig. S4. The ab initio results of the optical matrix elements at various interlayer translations r₀.

fig. S5. The real-space form of an interlayer exciton wave packet $\mathcal{X}$, with width w ≪ b, corresponds to a Q-space distribution covering all the three main light cones (bright spots).

fig. S6. Nanopatterned spin optics of moiré excitons in an H-type MoS₂/WSe₂ moiré pattern.

fig. S7. The six reciprocal lattice vectors in the Fourier components of the excitonic potential, and the obtained hopping magnitudes t_0,1,2 as functions of the moiré period b or V/ER.

table S1. The parameters for fitting the first-principles results (symbols in fig. S2) with eqs. S2 and S3.

table S2. The ${\widehat{\mathit{C}}}_3$ quantum number of K-point Bloch function ψ_c or ${\mathrm{\psi }}_{\mathit{v}}^{*}$ for different rotation centers, taken from Liu et al. (29).

table S3. The estimated radiative lifetimes for the interlayer exciton wave packets at A or B site in different heterobilayers with b = 15 nm.

References (48–56)