Ordinal Convolutional Neural Networks for Predicting RDoC Positive Valence Psychiatric Symptom Severity Scores

Abstract

Background

The CEGS N-GRID 2016 Shared Task in Clinical Natural Language Processing (NLP) provided a set of 1000 neuropsychiatric notes to participants as part of a competition to predict psychiatric symptom severity scores. This paper summarizes our methods, results, and experiences based on our participation in the second track of the shared task.

Objective

Classical methods of text classification usually fall into one of three problem types: binary, multi-class, and multi-label classification. In this effort, we study ordinal regression problems with text data where misclassifications are penalized differently based on how far apart the ground truth and model predictions are on the ordinal scale. Specifically, we present our entries (methods and results) in the N-GRID shared task in predicting research domain criteria (RDoC) positive valence ordinal symptom severity scores (absent, mild, moderate, and severe) from psychiatric notes.

Methods

We propose a novel convolutional neural network (CNN) model designed to handle ordinal regression tasks on psychiatric notes. Broadly speaking, our model combines an ordinal loss function, a CNN, and conventional feature engineering (wide features) into a single model which is learned end-to-end. Given interpretability is an important concern with nonlinear models, we apply a recent approach called locally interpretable model-agnostic explanation (LIME) to identify important words that lead to instance specific predictions.

Results

Our best model entered into the shared task placed third among 24 teams and scored a macro mean absolute error (MMAE) based normalized score (100 · (1 − M M AE)) of 83.86. Since the competition, we improved our score (using basic ensembling) to 85.55, comparable with the winning shared task entry. Applying LIME to model predictions, we demonstrate the feasibility of instance specific prediction interpretation by identifying words that led to a particular decision.

Conclusion

In this paper, we present a method that successfully uses wide features and an ordinal loss function applied to convolutional neural networks for ordinal text classification specifically in predicting psychiatric symptom severity scores. Our approach leads to excellent performance on the N-GRID shared task and is also amenable to interpretability using existing model-agnostic approaches.

Graphical abstract

1. Introduction

The National Institute of Mental Health (NIMH) created the Research Domain Criteria (RDoC) framework to study mental health disorders from genetic to behavioral level aspects. It aims at developing a new nosology for mental disorders by also considering genetics, neuroimaging, and cognitive science for characterizing both normal and abnormal human behavior. This motivation deviates from the existing Diagnostic and Statistical Manual of Mental Disorders (DSM-5) framework that relies on presenting symptoms and signs [1]. While the RDoC framework evolves, transitioning into concrete approaches to assessing mental disorders according to it warrants development of informatics tools that can determine symptom severity scores based on RDoC dimensions and constructs. The CEGS N-GRID 2016 Shared Task in Clinical Natural Language Processing is a first step toward that goal. Specifically, the main prediction problem (track 2) in this shared task is to automatically determine ordinal symptom severity scores for the positive valence systems (PVS) using natural language processing (NLP) techniques applied to neuropsychiatric notes. Here, PVS refers to one of the five main domains under which different RDoC constructs are grouped. This particular domain refers to activities where individuals knowingly engage in harmful activities such as drug use, drinking, and gambling encapsulating positive motivational situations or contexts, such as reward seeking, consummatory behavior, and reward/habit learning [2]. The scores are ordinal levels, specifically, absent (0), mild (1), moderate (2), and severe (3) with integers shown in parentheses being used as numeric representations in both prediction and evaluation tasks. For details about the organizational aspects of the shared task including data collection and annotation, please refer to the overview paper [3]. Next, we outline the note structure and modeling choices for this task.

1.1. Neuropsychiatric Clinical Note Structure

The textual notes provided for this shared task are very different from other clinical notes such as discharge summaries and pathology reports typically used in text mining efforts. In fact, they are the first of their kind released to the NLP community and deserve some additional treatment. Several identifiers and other pieces of information that constitute private health information (PHI) have been changed to arbitrary values. Although the notes are in free text format, they still contain semi-structured information grouped under various headings. Furthermore, several portions of the note contain questions with Yes/No or categorical responses. When the response is affirmative, there is usually a brief text blurb elaborating relevant additional information for the corresponding question. Besides some essential PHI, the following psychopathology related fields are present in the notes.

1. The history of present illness is a text field averaging 300 words per note and is present earlier in the note describing initial assessment and observations made by the psychiatrist about the patient’s condition.

2. Additional information is available about histories of suicidal/violent behavior, prior inpatient/outpatient treatments, current alcohol/drug/caffeine/tobacco use, and family psychiatric history. For some themes, detailed information is collected. For instance, the AUDIT-C score [4] is computed based on answers to several questions on alcohol consumption patterns. For drug use, details about the use of specific types such as hallucinogens, marijuana, cocaine, stimulants, and opiates are recorded.

3. The psychiatric review of systems is a sequence of questions related to well known mental disorders and Boolean responses are recorded for each of them. For example, for depression, one of the questions is – “Has the patient had periods of time lasting two weeks or longer in which, most of the day on most days, they felt sad, down, or depressed”. There are 19 such questions covering conditions such as depression, bipolar disorder, anxiety disorders, dementia, eating disorders, and compulsive disorders.

4. Information about the patient’s medical history, medications currently being taken, and social aspects such as family and relationships, education, and employment are also included. An assessment of risk factors for mental disorders is also included.

5. The multi-axial diagnoses segment of the note is legacy information from the DSM-4 framework where different diagnoses (typically with ICD-9 codes) are listed along five different axes where the first axis is typically the main set of clinically diagnosed major psychiatric disorders including major depressive disorder, schizophrenic episodes, or panic disorder.

6. The final portion of note includes the formulation text field that describes the patient’s case and diagnosis, important etiological factors, plan of treatment, and prognosis.

Due to the free text nature of the notes, additional parsing is typically needed to collect the Boolean or categorical responses listed under several headings. These, in turn, can be used as additional features on top of the full-text note and its n-grams. For example, drug use can be treated as a Boolean variable and its subheadings corresponding to use of cocaine and opiates can also be incorporated as such features. On the other hand, smoker status has four categories: never, former, current some day, and current every day. Some of these features also include real number values such as the AUDIT-C score for alcohol consumption and numbers of cups of coffee for caffeine intake. All these features are henceforth called wide features given they are typically used as inputs to the final layer in a deep neural network, thus making the network wide in that sense, in contrast to the deep features that arise from transformations applied to word embeddings of n-grams in the full narrative.

1.2. Predictive Modeling Alternatives

Our main objective is to build supervised models to categorize each note into one of four ordered symptom severity degrees as mentioned earlier. There are two conventional approaches to modeling positive valence score prediction: as multi-class classification or regression problem. In a multi-class framework we would treat each class independently and all misclassifications are equally penalized. So a misclassification between absent and mild is equivalent to that between absent and severe in terms of the corresponding contribution to the cumulative error. Alternatively, we can use numeric {0, 1, 2, 3} representation of the four classes to model the task as a regression problem. In this case, the prediction outcome is typically a real number and will need to be projected back to one of the four original classes.

Contrary to both regular text classification and conventional regression methods, the RDoC score prediction problem exactly fits the ordinal regression modeling approach in statistical learning given we are to classify instances into a set of ordered classes where misclassifications are penalized differently depending on the distance between the correct label and the predicted one. Methodologically, this paper makes several contributions: successfully uses wide (auxiliary) features (based on categorical responses to questions outlined in Section 1.1) and an ordinal loss function (output layer) applied to a convolutional neural network for text classification. We present extensive quantitative and qualitative results on the N-GRID dataset, which includes interpretations of predictions made using our model.

We organize the remainder of this paper as follows: In Section 2, we discuss related work including relevant neural network and ordinal regression methods. In Section 3, we present technical details of our model including loss functions and regularization methods. Next, in Section 4 we assess our approach from both quantitative and qualitative perspectives and discuss results based on the evaluation metric used for the shared task.

2. Related Work

Given the recent widespread use and availability of electronic medical records and textual narratives included with them, it is now possible to apply state-of-the-art methods in machine learning and NLP to the biomedical domain. In this section, we review related work in the context of methods we propose in this effort: neural networks for natural language processing (Section 2.1) and prior work on ordinal regression problems (Section 2.2).

2.1. Neural Networks for Text Classification

A recent resurgence in neural networks has paved ways to more general alternatives to supervised learning, especially in object classification. Deep neural networks (deep nets) prevent the complicated process of feature engineering and take upon the burden of automatically learning high-level representations of input instances that are better suitable for the classification problem at hand. Deep nets have been initially applied to problems in computer vision but have recently been adapted to NLP tasks [5, 6, 7] especially through learning distributed representations of textual segments (words, sentences, documents) as vectors in ℝ^d. These vectors directly guide primitive natural language processing tasks such as part-of-speech tagging and statistical parsing as well as high-level tasks such as text classification and machine translation. Convolutional neural networks have been used in a wide array of natural language processing tasks including relation extraction [8], sentiment analysis [9], and other text classification tasks [10, 11, 12].

In this effort, we make use of recent advances in convolutional neural networks for text classification [9, 10]. Unlike previous work which focuses on standard classification tasks (multi-class and multi-label), we expand these models to ordinal regression tasks. Deep neural networks learn a suitable feature representation from the textual data. However, there are instances when we need to augment the neural network with structured information [10, 13] to achieve additional performance gains. Cheng et al. [13] show the usefulness of adding such auxiliary features (like those typically used for linear models) in conjunction with standard neural network inputs such as word vectors.

Unlike probabilistic models, neural networks suffer from the lack of a posterior predictive distribution. Recent work [14, 15] focuses on training probabilistic neural networks. Gal and Ghahramani [15] show that the dropout regularization approach can be used to approximate Bayesian techniques. Intuitively, by making multiple predictions per test instance with dropout activated, the predictions can be treated as samples to estimate a predictive distribution. We use these approaches to output probability estimates for our ordinal framework in this effort.

2.2. Ordinal Regression

Ordinal regression has a long history in statistical literature [16, 17, 18]. Specifically, Rennie and Srebro [16] modify multiple classical machine learning methods to ordinal regression problems. Many methods are threshold based; for example, logistic regression can be adjusted such that the score returned should fall within a particular range depending on the ordinal class. Other methods have been modified for ordinal regression [19, 20], including support vector machines modified by Herbrich et al [21].

In this work, we expand on recent work for estimating age in images [22]. Specifically, we adapt their multiple output ordinal regression layer to CNNs more appropriate for text. We also show how they can be added to an ensemble to improve performance as well as provide a method to convert the multiple outputs to a probability distribution over classes.

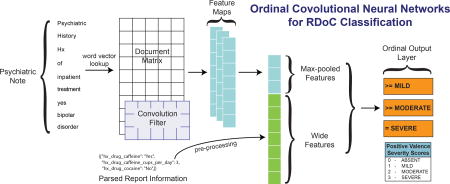
3. Methods: Ordinal Convolutional Neural Networks with Wide Features

In this section, we will describe a convolutional neural network (CNN) used in our prior work [10] and its adaptation to suit the current task with wide features and ordinal loss. Intuitively, a CNN will map each successive n-gram in a document to a real number. This mapping is accomplished using “convolutional filters” (CFs). Each CF will learn to extract informative n-grams from a document toward making the correct decision.

Word embeddings are dense vector representations that have been shown to capture both semantic and syntactic information of the corresponding language. A few recent approaches learn word vectors [5, 6, 7] (as elements of ℝ^d, where d is the dimension) in an unsupervised fashion from textual corpora. Henceforth, the input clinical note is represented by the corresponding document matrix where the i-th row corresponds to the word vector corresponding to the i-th word in the narrative.

3.1. Deep and Wide Neural Networks for Text Classification

The input to our CNN is a text document represented as a matrix, D ∈ ℝ^n×d, where each row represents a word vector, with n total words in the document, and the word vector has dimension d. CFs are defined as W_q ∈ ℝ^h×d, where h is the number of words we wish the convolution filter to span, that is, the length of the sliding window. Let the 2-D convolution operation * be defined as

$${\mathbf{W}}_q\ast {\mathbf{D}}_{j:j+h-1}=\sum _{i=j}^{j+h-1}\sum _{k=0}^{d-1}{\mathbf{W}}_{i,k}{\mathbf{D}}_{i,k}.$$

Next, we map a length h word window, D_j:j+h−1, of the document to a real number c_j ∈ ℝ using a non-linear function (rectified linear unit [23, 24]) f as

$$c_j=f({\mathbf{W}}_q\ast {\mathbf{D}}_{i,j:j+h-1}+b),$$

where b ∈ ℝ represents the bias term. After convolving over the entire document using W_q, we get the corresponding convolved feature map

$$\mathbf{c}({\mathbf{W}}_q)=[c_1,c_2,\dots ,c_{n-h+1}].$$

To overcome the issue of varying document lengths we perform a max-pooling [25] operation

$${ĉ}_{{\mathbf{W}}_q}=\underset{i}{\text{max}}\mathbf{c}{({\mathbf{W}}_q)}_i,$$

which gives a single feature ĉW_q corresponding to the feature map generated by W_q. However, several CFs will be trained, say k of them, ${\mathbf{W}}_q^1,\dots ,{\mathbf{W}}_q^k$, to create multiple feature maps leading to the corresponding single max-pooled features ${ĉ}_{{\mathbf{W}}_q^t},t=1,\dots ,k$. These form a final max-pooled feature vector

$${\mathbf{ĉ}}_{{𝒲}_q}={[{ĉ}_{{\mathbf{W}}_q^1},\dots ,{ĉ}_{{\mathbf{W}}_q^k}]}^T,$$ (1)

where ${𝒲}_q=\{{\mathbf{W}}_q^1,\dots ,{\mathbf{W}}_q^k\}$.

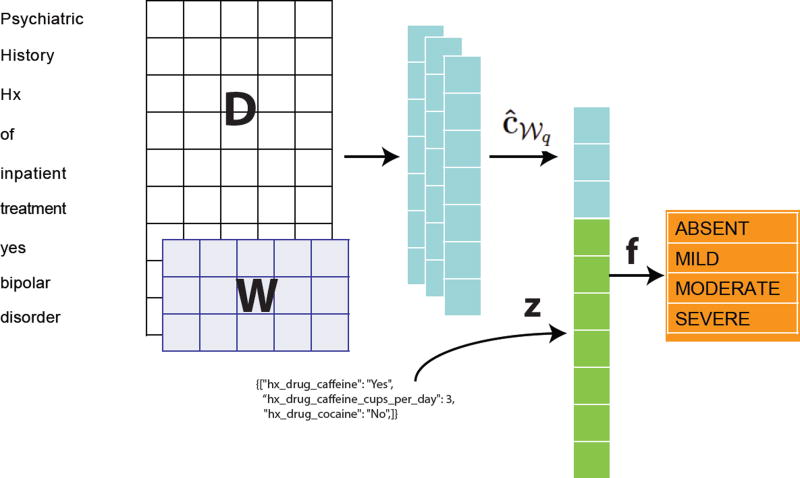
Given the question-answer structure of some portions of the note (as outlined at the end of Section 1.1), we want to explicitly leverage such information in the model. We parse this data from each psychiatric report. For example, we extract Boolean responses whether the patient takes drugs as mild as caffeine (hx_drug_caffeine in Figure 1) as well as extracting answers to questions about hard drugs, such as cocaine (hx_drug_cocaine in Figure 1). These form the wide features while the convolved full text provides deep features.

Figure 1.

This figure displays the overall architecture of our method. The input is a matrix, followed by a convolutional layer and max-over-time pooling. The max-pooled vector is concatenated with the wide features and passed to an output layer.

Let z ∈ ℝ^C represent a feature vector encoding all parsed information extracted from a note. For this current study we had C = 121 explicit structured features. Most of the information is represented as a categorical variable using a one-hot encoding scheme. A few variables are treated as real numbers (e.g., AUDIT-C score for alcohol consumption or number of cups of coffee) and represented as such in z. Both ĉ_𝒲q (from equation (1)) and z are combined

$$\mathbf{f}={\mathbf{ĉ}}_{{𝒲}_q}\Vert \mathbf{z}$$ (2)

where ‖ represents the concatenation operation such that f ∈ ℝ^C+k. f now gives a final representation of our document, including both the deep features ĉ_𝒲q and the engineered wide features z.

Overfitting is a major problem with deep neural networks. To alleviate this weakness, we utilize dropout [26] regularization. Instead of passing f from equation (2) directly to the output layer during training, we randomly let values of ĉ_𝒲 pass through to the output such that

$$\hat{\mathbf{f}}=({ĉ}_{𝒲}◦\mathbf{g})\Vert \mathbf{z},$$

where ◦ refers to element-wise multiplication and g ∈ {0, 1}^k is constructed with each g_i drawn from the Bernoulli distribution with parameter p (typically set to 0.5). Intuitively, this means that gradients are backpropagated only through unmasked elements where g_i = 1. During test time we scale the weights such that

$$\hat{\mathbf{f}}=p{ĉ}_{𝒲}\Vert \mathbf{z}.$$

This down weighting is essential since at training, on average, only half of the activations are non-zero, which is not true at test time.

The vector f̂ can now be passed to an output layer. Next we present two possible options for the output layer: softmax (Section 3.2) and ordinal output (Section 3.3).

3.2. Multi-class Output and Loss (CNN and CNN-Wide)

The easiest way to approach an ordinal regression problem is to treat it as a multi-class classification task. For example, in the case of positive valance classification, we can treat each class independently (absent, mild, moderate, and severe). This is a well studied problem and can be addressed by using a softmax layer.

After obtaining f̂, we transfer it to the softmax layer. Let U ∈ ℝ^4×(C+k) and b^U ∈ ℝ⁴ be the parameters of the softmax layer (assuming four classes) with weighted inputs

$$o_j={\mathbf{U}}_j\hat{\mathbf{f}}+b_j^U.$$

The corresponding output label probability estimates

$${ŷ}_j=P(y_j=1|D,𝒲,b,\mathbf{U},b^U)=\frac{e^{o_j}}{{\sum }_i{e}^{o_i}}$$

are calculated using the softmax function. Given ŷ_j the model can be trained by minimizing the multi-class log-loss

$$J(\theta )=-\sum _l{y}_l\mathit{\text{ log}}({ŷ}_l),$$

where y_l represents the true label; that is, y_l = 1 for the correct label and 0 otherwise.

3.3. Ordinal Regression Output and Loss (CNN-Ord and CNN-Ord-Wide)

Based on recent work by Niu et al. [22], we now formulate an ordinal output layer that maps the multi-class problem to have multiple outputs. In the case of positive valence, the problem is transformed from four to only three output units denoted by t₁, t₂, and t₃. Intuitively, we would like the j-th output unit to fire if the rank of the correct class r is equal or greater than j. That is,

$$t_j=\{\begin{array}{cc}1\hfill & j\le r,\hfill \\ 0\hfill & \mathit{\text{otherwise}};\hfill \end{array}$$ (3)

where r is the ordinal rank of the true class (0 for absent, 1 for mild, 2 for moderate, and 3 for severe). This means, when the level is absent, no units are expected to fire and when it is severe all units ought to fire. Thus, unlike Section 3.2, the ordinal layer can have multiple output units firing for an input instance.

What we show in equation (3) is the ground truth output expected. However, to approximate this using our CNN, for the ordinal regression output layer, we redefine U ∈ ℝ^3×(C+k) and b^U ∈ ℝ³, and output

$$o_j={\mathbf{U}}_j\hat{\mathbf{f}}+b_j^U,$$

where o_j is the score for the j-th output unit that is passed through a sigmoid unit to obtain the final firing probability estimate

$${\hat{t}}_j=P(j\le r|D,𝒲,b,\mathbf{U},b^U)=\frac{1}{1+e^{-o_j}}\in [0,1].$$ (4)

At test time, predictions are made by summing all activations that fire (based on equation (4))

$$\hat{r}=\sum _{j=1}^3𝟙({\hat{t}}_j>0.5),$$ (5)

where r̂ directly determines the corresponding severity class and 𝟙() evaluates to 1 if its parameter condition is true, and 0 otherwise. It should be noted that the threshold (0.5) can be tuned, but we found 0.5 to work well for our task.

We differ from Niu et al. [22] by using a multi-output loss function [27]. If there are γ ordinal classes, we use γ − 1 sigmoid units, while Niu et al. have γ − 1 binary softmax layers. Because of our use of sigmoid units, we train using a binary cross-entropy loss function

$$J(\theta )=-\sum _l(t_l\mathit{\text{ log}}({\hat{t}}_l))+(1-t_l)\mathit{\text{ log}}(1-{\hat{t}}_l)$$

summed over all three output units given γ = 4 for us.

Finally, we note that this approach predicts the correct ordinal class based on the number of units firing without actually computing a probability estimate. However, it is reasonable to want to have such an estimate for each class to have an explicit fine-grained representation rather than the coarser #units-firing. The ordinal output layer does not return such an estimate. We take advantage of recent work in approximating Bayesian models using dropout regularization [15]. Instead of using dropout only during the training process, we keep it activated at test time. However, instead of a single run of the test instance through the model, we make T different sample runs each time getting a potentially different outcome. We define the probability of an ordinal class

$$P(r|D,𝒲,b,\mathbf{U},b^U)=\frac{1}{T}\sum _{j=1}^T𝟙({\hat{r}}_j=r),$$

which counts the number of times we predict r over T trials and then normalizes to the [0, 1] range. Here 𝟙(r̂_i = r) determines cases when equation (5) evaluates to r for the i-th trial.

4. Evaluation

For evaluation, we wish to answer three questions. First, how does the the wide CNN model with ordinal loss compare against other common neural networks? Second, how does our method perform against other track 2 participants of the N-GRID shared task? Finally, can we qualitatively interpret how our model is making predictions?

4.1. Evaluation Measure

The evaluation measure used for the shared task was the macro mean absolute error (MMAE). Let A be the set of classes (absent, mild, moderate, and severe), 𝒪ⁱ be the index set of instances with ground truth class label i with 𝒪 = ∪_j𝒪^j, and M_i be the maximum ordinal difference for class i ∈ A. For the current problem we have M₀ = M₃ = 3 and M₁ = M₂ = 2 given predicting the opposite boundary generates maximum penalty of 3 for boundary classes and predicting farthest boundary produces the maximum error of 2 for the two middle classes. We now have

$$\text{MMAE}(\hat{r},𝒪)=\frac{1}{|A|}\sum _{i\in A}\frac{1}{|{𝒪}^i|M_i}\sum _{j\in {𝒪}^i}|{\hat{r}}_j-r_j|,$$

where |r̂_j − r_j| represents the absolute difference between the ordinal rank of the correct and predicted classes for the j-th instance. Intuitively, the mean absolute error is being calculated for each class independently, then all MAEs are averaged together. This approach weights each ordinal class equally, independently from the number of times it has occurred in the training dataset. For comparison purposes for the N-GRID shared task, the organizers scale MMAE to a normalized version

$$\text{NMMAE}=100\ast (1-\text{MMAE})$$

such that each score will be in the range 0–100 where 100 is the maximum possible score.

4.2. Implementation Details and Model Configurations

Our main approach presented in Section 3 involves the use of a CNN that operates on neural word embeddings with additional wide features and an ordinal loss function. We used the dataset of a total of 433 records (combining 325 with gold annotations and 108 annotated by a single annotator) supplied to all participants during the training phase to build our models. Because of the relatively small size of the dataset, the nonlinear models such as deep nets turn out biased toward certain classes. To address some of these issues, we also present ensemble models with a few simple rules that we outline in this section. The dataset has a few common question-answer pair patterns. Given this structure, we used a straightforward regular expression approach to extract structured features (Boolean, categorical, ordinal) from the text note component of the training XML files. These extracted components are used to supplement our method as wide features.

For the deep learning models outlined in Section 3, we ran Google’s word2vec [7] system on Medline citations (2014 PubMed baseline) to obtain 300-dimensional pre-trained word vectors, which are used as initial vectors to populate a document matrix. Note that these are also neural net parameters and are thus modified as part of the training process. The tokenizer used is a simple splitter on non-word characters (those excluding the English alphabet, ten digits, and underscore symbol). We used convolutional filters of three, four, and five tokens wide, and considered 300 feature maps per each fixed filter size. The initial convolution filter W values are drawn uniformly from [−0.1, 0.1]. The weights from the max-pooled output to the final sigmoid unit layer are initialized to values drawn from a normal distribution with mean 0 and standard deviation $\sqrt{2/\text{input}-\text{size}}$ where the input size is 900 given 300 feature maps for each of the three window sizes. This initialization is in line with standard practices used for initializing deep net parameters [28].

The models were trained using AdaGrad [29], an adaptive learning rate method for stochastic gradient descent with a maximum of 25 epochs per classifier. We also used mini-batches of size 5 and we zero-padded the document at the beginning and end as needed. The dropout regularization parameter was set to p = 0.5 as mentioned in Section 3.1. We also employed early-stopping to help combat overfitting. Typically early stopping is done by terminating the training of the model when the desired score on a held-out validation dataset does not increase in performance. However, we found this caused us to stop too early. To combat this, we stopped training if there were five consecutive epochs in the training procedure that did not increase the validation NMMAE score. We only saved the model on epochs that had an increase in NMMAE score on the validation dataset. Next, we outline various configurations we implemented.

1. CNN: This is the basic CNN model outlined in Section 3 with the multi-class loss from Section 3.2 and without the wide features. This model is typically used as the baseline in deep learning methods for text classification. For this method, we average the softmax layer outputs of 20 individual models trained on the entire dataset. This model averaging is mostly deemed indispensable with CNNs to achieve a more stable predictive model, especially for small training datasets owing to the randomized initialization of parameters.

2. CNN-Ord: This model is the basic CNN model listed above with the ordinal loss function described in Section 3.3. At test time, the ordinal class is equal to the number of units firing with none firing equivalent to the absent class prediction.

3. CNN-Wide: This is essentially the basic CNN model (the first one in this list) with additional wide features (outlined in Section 1.1).

4. CNN-Ord-Wide: This corresponds to the full model from Figure 1 with wide features (outlined in Section 1.1) and ordinal loss from Section 3.3. For both CNN-Ord and CNN-Ord-Wide, just like for the basic CNN, we averaged sigmoid output units (of 20 models) occupying the same position and determined whether a unit fired based on this average.

5. CNN-Wide-LIWC: This model is the basic CNN-Wide model with the addition of Linguistic Inquiry and Word Count (LIWC [30]) scores (generated from the psychiatric notes) as wide features. LIWC (http://liwc.wpengine.com/) is a licensed software program that analyzes free text documents and returns scores for various psychological and other types of dimensions. Employing peer reviewed linguistic research [31] on psychometrics of word usage, LIWC aggregates scores for different dimensions (e.g., negative emotions such as anxiety, anger, sadness; personal concerns; and cognitive processes) based on specific dictionaries with words that are pre-assigned (by linguistic experts) scores for each dimension. Given these dimensions are closely associated with mental health and given our prior experiences with exploiting them for text classification in the context of suicide watch [32], we included them as part of the wide features.

6. CNN-Ord-Wide-LIWC: Since the competition, we have improved CNN-Ord-Wide with the addition of LIWC scores as wide features as outlined earlier. The remaining details of this configuration are identical to that of the CNN-Ord-Wide model.

7. Lin-Ens: This model is based on averaging multiple linear models including support vector machines, logistic regression, ridge regression, and logistic ordinal regression, each of which is trained on TFIDF weighted uni/bigrams of the full psychiatric note and structured wide fields parsed from note text as mentioned earlier.

8. CNN-Ens-1: This ensemble prediction is essentially an average of the predicted classes 0–3 (not of sigmoid outputs) of constituent three models: CNN, CNN-Ord, and Lin-Ens. When the average has a fractional component, we round to the nearest integer to obtain the final class. Even with ensembling, due to the imbalanced nature of the dataset, mild and moderate predictions are more often than the boundary classes. To counter this we 15 devised a simple rule that is recall oriented. If the prediction is moderate, and the second best prediction (based on sigmoid output scores) from CNN and CNN-Ord models is severe, we change the prediction to severe. To avoid changing too many decisions, we do this to qualifying instances in the moderate class based on the descending order of scores from second best severe predictions; we stop the class changes if either the moderate class proportion goes below the training estimate or the severe class proportion goes above the corresponding training estimate. The intuition is that if the second best prediction is an infrequent class and the best prediction is an adjacent frequent class, in the interest of recall, it might be worth considering a change in the prediction to the infrequent class as long as the resulting proportions do not violate training estimates.

9. CNN-Ens-2: This is exactly like CNN-Ens-1 except we also add CNN-Ord-Wide, a fourth model, into the ensemble. With four models, unique rounding is not always viable, as the fractional value could be exactly 0.5 (e.g., an average of 1.5 can be rounded to mild or moderate). We break ties between the two classes by picking the more frequent one (in the training dataset). After this, similar to the rule in CNN-Ens-1, we move instances with moderate predictions to the severe class, if the newly added model CNN-Ord-Wide predicts moderate with the second best prediction being severe.

10. CNN-Ens-3: This is similar to CNN-Ens-2 where the CNN-Ord-Wide model is replaced with the CNN-Ord-Wide-LIWC model. The tie breaking is done as in CNN-Ens-2. As a post-processing rule, we move instances with moderate predictions to the severe class, if the newly added model CNN-Ord-Wide-LIWC predicts moderate with the second best prediction being severe.

4.3. Quantitative Evaluations

We present two sets of performance evaluations: comparisons against different neural network configurations from Section 4.2 and comparing against other track 2 competitors on the 2016 N-GRID shared task’s test set of 216 notes. We begin by comparing against multiple CNN variations and ensembles. The test set performances using CNN variations are shown in Table 1 where we show the NMMAE scores. The IDs of the models correspond to list position in the enumeration in Section 4.2. The systems we submitted as our final runs to the shared task correspond to models 1, 2, and 8 in the table and the ensemble model 8 is the best performer among them. We did not submit the CNN-Ord-Wide (model 4), CNN-Ord-Wide-LIWC (model 6), and the best performing ensemble models (IDs 9 and 10). This is because in our ten-fold cross-validation experiments using the training dataset, we did not obtain noticeable performance gains with the wide features. Given the cross-validation configuration leaves out a fold in each train-test split, 10% fewer training data points were used per fold than for building the final full models applied to test set. Given the relatively smaller size of the dataset, this could have masked the superior performance of CNN-Ord-Wide. We see that the addition of LIWC scores to the wide features makes a small improvement. Our best ensemble, CNN-Ens-3, achieves an NMMAE of 85.55 and seemed to benefit by involving the wide model CNN-Ord-Wide-LIWC as a component. This model when used without the post-processing rule described earlier, has a final score of 85.25. So using the rule has only benefited marginally in this case.

Table 1.

Final test set results for RDoC positive valence symptom severity classification

ID	Method	Absent	Mild	Moderate	Severe	NMMAE
1	CNN (Sys1)	90.32	90.12	75.00	78.624	83.51
2	CNN-Ord (Sys2)	84.95	90.12	79.35	80.50	83.73
3	CNN-Wide	90.32	89.53	69.57	84.90	83.58
4	CNN-Ord-Wide	84.95	91.28	81.52	79.24	84.25
5	CNN-Wide-LIWC	90.32	88.37	70.65	85.53	83.72
6	CNN-Ord-Wide-LIWC	84.95	91.86	81.52	80.50	84.71
7	Lin-Ens	73.12	90.12	81.52	79.87	81.16
8	CNN-Ens-1: Uses models 1, 2, and 7 (Sys3)	91.40	91.86	76.09	76.10	83.86
9	CNN-Ens-2: Uses models 1, 2, 4, and 7	84.95	94.19	78.26	83.02	85.10
10	CNN-Ens-3: Uses models 1, 2, 6, and 7	84.95	94.77	82.61	79.87	85.55

Interestingly, all CNN models involving ordinal formulation seem to perform more consistently across all classes than the standard CNN models. The ordinal models (models 2, 4, and 6) also outperform the corresponding regular CNN models (models 1, 3, and 5) in terms of overall NMMAE scores based on the first six rows of Table 1. Adding wide features seemed to help the ordinal models more than the vanilla CNN models. Furthermore, if we do not perform model averaging and simply look at the mean NMMAE scores of the 20 individual models, the CNN-Ord setup achieved a mean score of 81.23 but the plain CNN model scored 78.89. This further demonstrates that the ordinal formulation leads to more stable individual models when compared with conventional multiclass loss. We believe these desirable traits including consistency across classes, model stability, and overall superior performance are due the ability of models with ordinal loss to account for ordinal associations between classes. Thus, overall, incorporating the ordinal nature of the classification task into a deep architecture produced the best outcome for our team. Note that all scores reported here do not involve tweaking model parameters based on performance on the test set. As such, these scores are achieved without assuming any knowledge of the test set including class distributions.

Table 2 shows the competition results, where our ensemble model Sys3 (model 6 from Table 1) is placed third behind the top two teams: (1). SentiMetrix Inc. researchers use a large ensemble approach that also involves association rules learned from structured fields and (2). The University of Texas at Dallas participants use a pair-wise learning to rank approach combined with linear regression. The full details of methods used by these teams were not disclosed at the time of this writing. Our updated best ensemble (CNN-Ens-3) shown in the 2nd row of Table 2 performs on par with the top performer. Our single approach non-ensemble model (CNN-Ord-Wide-LIWC) shown in the third row of the table also does reasonably well without any additional ensembling.

Table 2.

Final results from the CEGS N-GRID 2016 NLP shared task (track 2).

Rank	Institutions	NMMAE
1	SentiMetrix Inc.	86.3019
new	CNN-Ens-3 (UKY)	85.5491
new	CNN-Ord-Wide-LIWC (UKY)	84.7079
2	The University of Texas at Dallas	84.0963
3	University of Kentucky (Sys3)	83.8615
4	University of Pittsburgh	82.5594
5	Med Data Quest Inc.	81.7474
6	Harbin Institute of Technology Schzhen Graduate	81.6844
7	University of Minnesota	81.4971
8	Antwerp University Hospital	80.6356
9	LIMSI-CNRS	80.1738
10	The University of Manchester	80.1143

4.4. Qualitative Analysis

Model interpretation is of great importance in the clinical setting beyond model performance. In this section, we use recent advances in the analysis of neural networks [15, 33] toward interpreting decisions made by the best single approach model CNN-Ord-Wide-LIWC from Section 4.3. Because we make use of wide features passed directly to the output layer, the interaction between each wide feature and the ordinal output unit is linear. We first discuss the influence of these wide features in the prediction process.

4.4.1. Wide feature significance

Table 3 shows the top ten coefficients among the 121 wide feature connections to each of the three ordinal output activation units. Each activation models the probability that the correct ordinal class rank is higher than or equal to the rank represented by the output unit. For example, unit-1 should fire for all instances where the correct class is at least mild, while unit-3 is expected to fire only when the actual class is severe. All numerical entries in Table 3 correspond to ICD-9-CM codes that are specified in the multi-axial diagnoses portion of the note. The largest coefficient for unit-1 is wide feature 303.9, which represents the ICD-9-CM code for alcohol dependence (but not involving acute intoxication). Intuitively, patients who use alcohol have a higher chance of being classified as at least mild for positive valence. It becomes more interesting as we study the differences between units 2 and 3. Specifically, ICD-9-CM code 305 (nondependent abuse of drugs) has a high weight for unit-2, while wide feature 304 (drug dependence) is an important code for unit-3. This means a patient may be misusing drugs, but if they are not dependent on them, then they are not as likely to be classified as severe. Usage of different drugs seems to be a general indicator across all three units. The flag for affirmative response for cocaine use for unit-1 indicates that such cases should at least be classified as mild. A relatively large negative coefficient for hx_drug_use=No in unit-3 denotes that without a history of drug use it is not as likely to be considered a severe case. The feature alcohol_six_use_occasion in the table refers to the real-valued answer to the question – “How often did you have six or more drinks on one occasion in the past year?”. This seems to play a major role in cases that are at least mild or moderate. Although all high coefficients may not lead to meaningful insights, from Table 3 we note that many are pertinent in the context of positive valence symptom severity.

Table 3.

Coefficients of connections between the wide features and the output layer for each of the three output units in the CNN-Ord-Wide-LIWC model.

Rank	Activation unit-1	Coef. wt.	Activation unit-2	Coef. wt.	Activation unit-3	Coef. wt.
1	303.9	0.219	300.3	0.251	300.21	−0.268
2	300.02	0.215	296.8	0.233	hx_drug_stimulants=Yes	0.240
3	hx_drug_use=Yes	0.201	304	0.218	207	0.227
4	hx_drug_stimulants=Yes	0.179	303.9	0.216	hx_drug_use=No	−0.225
5	315.9	0.168	hx_drug_opiates=Yes	0.206	295.7	0.167
6	296.32	0.162	hx_drug_stimulants=Yes	0.167	296.22	−0.149
7	hx_drug_sedative=Yes	0.159	alcohol_six_use_occasion	0.163	hx_drug_sedative=Yes	0.149
8	alcohol_six_use_occasion	0.145	305	0.159	hx_drug_smoker_status=Current	0.146
9	hx_drug_cocaine=Yes	0.145	207	0.155	304	0.142
10	hx_drug_use=No	−0.134	304.8	0.155	293.84	0.139

4.4.2. Instance specific interpretability

Besides gleaning model level insights, it is also important to obtain clues or explanations about why the model predicted a particular severity level for a specific input instance. This knowledge can inform a psychiatrist to appropriately vet the model’s decision before making a final call. These explanations can both expedite scoring and also identify any areas that might otherwise be ignored sometimes due to human error. When automating such severity score prediction to get rough aggregate estimates, this can be used for sampling and assessing a few reports for quality control. Linear models lend themselves to interpretability but do not perform as well relative to nonlinear models such as deep nets. However, deep nets suffer from interpretability issues and are often treated as black boxes leading to the well known trade off between interpretability and performance. We can analyze the wide features in our model but that alone would ignore the CNN aspect of the model.

Here we utilize recent work in interpreting neural networks and other nonlinear models to highlight text portions that led to particular decisions. The local interpretable model-agnostic explanations (LIME) framework by Ribeiro et al. [33] addresses this by approximating a linear model in the vicinity of the current instance for which interpretation is being sought. Intuitively, this is done based on features that are interpretable (such as words for text) rather than features that do not lend to such insights (e.g., word embeddings). The nonlinear model is still involved in making its predictions on a local training dataset of perturbed instances (obtained by removing certain words) in the vicinity of the current instance needing explanation. Finally, a linear model is fit to this perturbed dataset with local weighting of instances with more importance given to those that are more similar to the instance whose prediction needs interpretation.

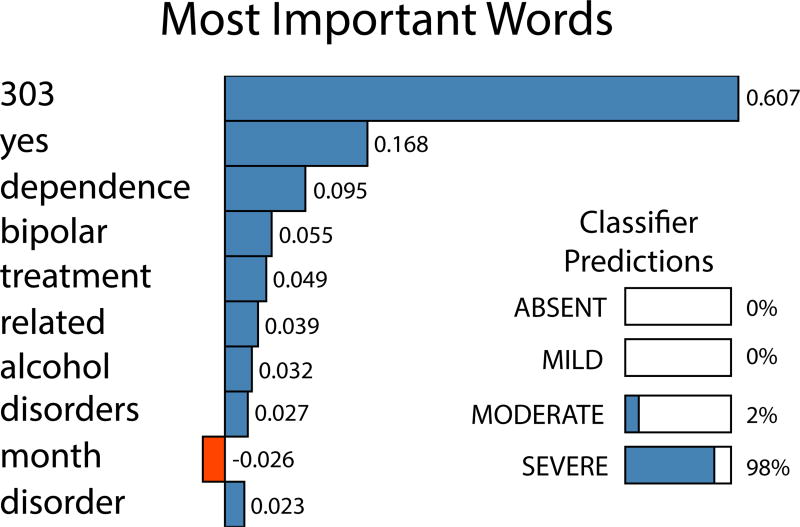
In Figure 2, on the left hand side we show an expert annotated sample note supplied to participants as part of the N-GRID shared task manual. Due to the portions highlighted in red color, experts classified this as a severe case. Our CNN-Ord-wide-LIWC correctly classified this sample but furthermore when we run our prediction through LIME, we obtain the blue colored highlighted terms shown in the right hand side of Figure 2. As we can see, there are nontrivial overlaps between text segments identified by experts and those identified through LIME, thus demonstrating the potential of LIME in generating instance specific interpretations. For this note, the words ranked in order of importance determined by LIME are shown in Figure 3. We see the word ‘yes’ has a relatively large weight. This LIME weight is because it is the answer to an inpatient history question in the report. Higher symptom severity scores align with more affirmative responses to several questions of this nature. We can also see that the severe alcohol dependence of the patient (seen with terms ‘alcohol’ and ICD-9-CM code 303) are predictive terms used by the model to make its prediction. The classifier prediction scores are also shown, where the probabilities per class are calculated using the dropout method as described in the last paragraph of Section 3.3.

Figure 2.

Expert vs LIME annotated sample note correctly classified by the CNN-Ord-Wide-LIWC model

Figure 3.

Top 10 words retrieved using LIME for the example shown in Figure 2.

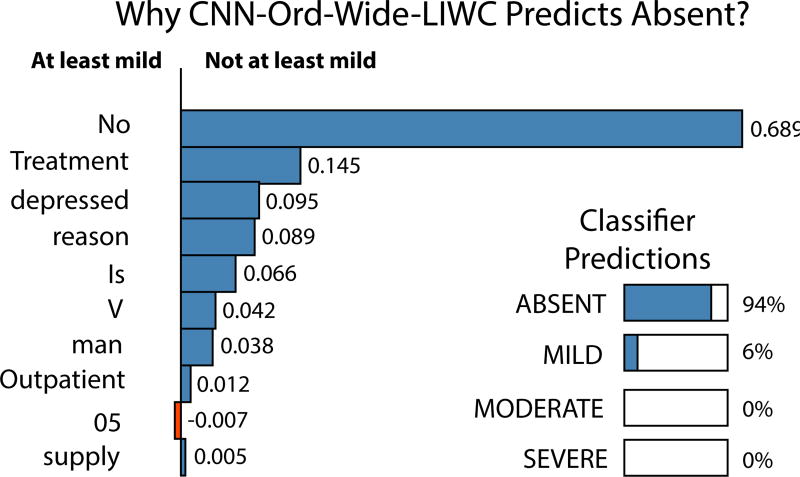
Our method misclassified five test notes (out of 216) with an ordinal error distance of two. Specifically, we incorrectly classified two reports as absent when the correct label is moderate. We classified three reports as mild when the true class was severe. CNN-Ord-Wide-LIWC did not misclassify any reports with an ordinal error distance of three. In Figure 4 we display our predictions along with the LIME based important features for one of the reports misclassified as absent when the correct class is moderate. When we manually examined the note, we notice that the patient had no prior psychiatric history, never drinks, never smokes, and has no history of drug use. Hence ‘no’ was an important word retrieved from LIME given most of the answers to positive valence related questions were negative. The patients’ lack of a drug history seemed to be the overwhelming reason why our classifier predicted absent. The main indication seemed to be social withdrawal following a surgery for meningioma. We hypothesize that given common causes for positive valence appear to be from the abuse of drugs, alcohol, and other addictions with reward seeking behavior, our model is not able to generalize to these types of atypical reports with no psychiatric history.

Figure 4.

Important words for an instance which we incorrectly predicted as absent with the correct score being moderate

5. Conclusion

In this paper, we presented a neural network architecture that combines recent advances in text classification based on max-pooled convolutions with a loss function that fits ordinal outcomes. We study the performance of this architecture and its variants through our participation in the CEGS N-GRID 2016 Shared Task in Clinical NLP (track 2) to predict RDoC positive valence symptom severity scores. Using a performance measure set by challenge organizers, our best model achieves a score that is within 1% of the highest score in the challenge achieved using a complex ensemble that also involves deep net models. Besides detailing our methods and results, we also present a qualitative analysis of our outcomes in terms of explainability of instance specific predictions for further examination. As such, we believe our effort demonstrates the potential of deep nets for superior performance in text classification with the application of additional approaches such as LIME to also support model interpretability.

Highlights.

RDoC positive valence symptom severity scores are predicted from psychiatric notes Ordinal convolutional neural networks outperform other supervised models in this task Ensemble approaches achieve a normalized macro mean absolute score of 85.55 Our performance is within 1% of best score reported on the CEGS NGRID 2016 dataset Deep nets with ordinal loss and wide features are suitable for ordinal text classification