Crimped Nanofibrous Biomaterials Mimic Microstructure and Mechanics of Native Tissue and Alter Strain Transfer to Cells

Abstract

To fully recapitulate tissue microstructure and mechanics, fiber crimping must exist within biomaterials used for tendon/ligament engineering. Existing crimped nanofibrous scaffolds produced via electrospinning are dense materials that prevent cellular infiltration into the scaffold interior. In this study, we used a sacrificial fiber population to increase the scaffold porosity and evaluated the effect on fiber crimping. We found that increasing scaffold porosity increased fiber crimping and ensured that the fibers properly uncrimped as the scaffolds were stretched by minimizing fiber-fiber interactions. Constitutive modeling demonstrated that the fiber uncrimping produced a nonlinear mechanical behavior similar to that of native tendon and ligament. Interestingly, fiber crimping altered strain transmission to the nuclei of cells seeded on the scaffolds, which may account for previously observed changes in gene expression. These crimped biomaterials are useful for developing functional fiber-reinforced tissues and for studying the effects of altered fiber crimping due to damage or degeneration.

Graphical abstract

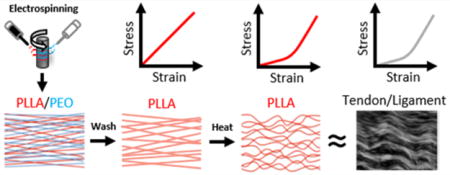
INTRODUCTION

Tendons and ligaments are composed of aligned collagen fibers that follow a sinusoidal waveform along the tissue length, which is termed collagen fiber crimping.^1,2 As these tissues are stretched, the crimped fibers progressively become straightened and bear load, which produces a nonlinear (i.e., strain hardening) mechanical behavior.^3–6 Because most tendons and ligaments experience in vivo loads within this nonlinear mechanical regime,^7–9 collagen crimping is believed to be an important structural feature underlying proper tissue function. This is further supported by the fact that collagen crimping is altered with tendon injury, degeneration, and healing.^10–15 Therefore, to fully replicate tendon/ligament structure-function relationships, there is a need to produce engineered biomaterials that contain similarly crimped fibrous structures.

Several methods, including weaving, braiding, and micro-molding, have been used to fabricate biomimetic scaffolds for tendon/ligament tissue engineering.^16–18 Although these approaches are capable of reproducing features of the nonlinear stress response, they fail to provide the nanoscale fibrous structures that cells encounter within these tissues. In contrast, electrospinning is a technique that can produce highly aligned arrays of polymer nanofibers that provide such nanotopographic cues.¹⁹ These highly aligned fibers direct cell shape and alignment, and lead to subsequent alignment of cell deposited extracellular matrix molecules, such as collagen.²⁰ Recently, a number of groups have further refined this process to generate crimped nanofibrous scaffolds via controlled heating above their glass-transition temperature, ethanol treatment, copolymer fiber formation, and other techniques.^21–29 Although these scaffolds replicate the microscale structure and nonlinear mechanics of tendon and ligament, they have a densely packed fibrous structure with small pores. This dense structure not only limits the degree to which the fibers can crimp, but also results in limited cellular ingress when these scaffolds are seeded with cells. In our previous work, accelerated cellular infiltration into these dense nanofibrous scaffolds was achieved by increasing scaffold porosity via inclusion of a water-soluble sacrificial poly(ethylene oxide) fiber fraction.²⁰ Inclusion of sacrificial fibers may provide both the high porosity required for cell infiltration, while at the same time increasing the degree to which crimping can occur, resulting in a more instructive and mechanically nonlinear scaffold.

Crimped scaffolds may also alter the instructive cues presented to cells, which deposit extracellular matrix molecules and drive scaffold maturation. Indeed, previous studies have demonstrated that crimped nanofibrous scaffolds alter gene expression compared to uncrimped material under both static and dynamic conditions.^26,28 Effects in the absence of applied strain suggest that the crimped topography intrinsically alters cell behavior. However, when the scaffolds are loaded, the uncrimping behavior of the individual fibers may also produce additional biophysical stimuli that increase cell mechanotransduction. Such mechanotransduction events can occur at the cell surface as well as deep within the cell, where intracellularly transmitted strains activate stretch sensitive cytoskeletal and nucleoskeletal associated molecules.^30–34 Our previous work has shown that both cell and nuclear deformation is highly dependent on fiber directionality with respect to the direction of applied strain in engineered nanofiber microenvironments.^35,36 Therefore, it is possible that the crimped micro-structure alters strain transmission to the nucleus, thereby altering cell mechanotransduction.

In this study, we investigated the effect of including a sacrificial fiber population on fiber crimp and scaffold mechanics. We hypothesized that increasing scaffold porosity prior to heating would increase scaffold crimp by providing increased space for crimped fiber formation. Additionally, we used a structural constitutive model to parameterize the scaffold bulk mechanics. Similar approaches have been used to investigate the mechanisms that underlie the mechanics of engineered scaffolds and biological tissues.^37–39 Our goal was to determine whether the nonlinear scaffold mechanics can be predicted by the degree of fiber crimping, which is useful for designing scaffolds with mechanical properties to match particular tissues. Finally, we investigated whether fiber crimping alters the strains transmitted to the nuclei of mesenchymal stem cells (MSCs) seeded on the scaffolds. We chose bone marrow-derived MSCs because they are a popular cell source for engineering orthopedic tissues and are highly responsive to topographical and mechanical cues, which both influence lineage commitment toward a tendon/ligament pathway.^40–44

METHODS

Scaffold Fabrication

Aligned nanofibrous scaffolds were generated, as described previously,^20,28 by electrospinning onto a rotating mandrel. Scaffolds were spun using an 8.5% w/v solution of poly-L-lactide (PLLA) in hexafluoropropylene either alone, or in combination with a second spinneret containing a 10% w/v solution of poly(ethylene oxide) (PEO) in 90% ethanol. The dual PLLA/PEO scaffolds contained 30.8 ± 5.3% PEO by weight. Based on the density of these polymers (PLLA: 1.25 g/mL, PEO: 1.13 g/mL), we can calculate the average volumetric ratio of PEO to be 33%. The two scaffold types (PLLA alone or PLLA/PEO dual component scaffolds) were washed with decreasing concentrations of ethanol (to hydrate and/or remove PEO) and heated to 85 °C for 15 min between two glass slides. Dual scaffolds were washed (DW), heated and then washed (DHW), or washed and then heated (DWH). This last group (DWH) is expected to produce the highest degree of crimp due to the increased porosity present during heating (see Figure S1). On the basis of methods used previously to weld polymer fibers (e.g., polycaprolactone, polyglycolic acid, nylon) together at their intersection points,^45–47 the pretreated scaffolds were immersed into 10% (w/v) poly(vinyl alcohol) (PVA) solution for 1 h and dried at 37 °C for 12 h to embed the PLLA fibers. The polymer composite was heated at 100 °C to increase the fiber crystallinity and fix their morphology. The PVA was then washed off in 50 °C water for 3 h. Fiber bonding was induced by heating the dried fiber samples to 175 °C for 10 min.

Surface Characterization

Following processing, scaffolds were dried by desiccation, mounted, and imaged at 1000× using a scanning electron microscope (SEM). Fiber morphology was characterized for each of the scaffold types by calculation of the fiber straightness, which was defined as the distance between the fiber ends divided by its contour length, which is the distance measured by tracing the fiber trajectory. Note that the stretch required to uncrimp the fibers (λ_c) is equal to the reciprocal of the straightness value.

Mechanical Testing

Scaffolds were cut into 40 × 5 mm² pieces and tested in air under uniaxial tension applied either parallel or transverse to the fiber direction using an Instron 5848 with a 50N load cell (Instron, Norwood, MA). Scaffold cross-sectional areas (100–200 μm thick) were measured using a noncontact laser transducer (optoNCDT1800, Micro-Epsilon, Raleigh, NC), loaded vertically into grips, and quasi-statically ramped at a rate of 0.05% strain/sec. Stress-strain curves were calculated and a bilinear fit (MATLAB, MathWorks, Natick, MA) was used to determine the transition strain and linear region modulus.⁴⁸

Constitutive Model Formulation

A structural hyperelastic model was used to investigate the effects of fiber crimping on the scaffold mechanics. The model was composed of aligned crimped fibers embedded in a neo-Hookean matrix.^37,38 Briefly, the fibers were assumed to bear no load until they became uncrimped at an uncrimping stretch (λ_c), which was represented by a gamma probability distribution parametrized by the mean uncrimping stretch ( ${\overline{\lambda }}_{\mathrm{c}}$) and standard deviation of uncrimping. $\left({\lambda }_{\mathrm{C}}^{\mathrm{S}\mathrm{D}}\right)$ Once the fibers were uncrimped, they were assumed to produce a linear stress response

$${\mathbf{P}}_{\mathrm{f}}=\frac{K}{2}{\displaystyle {\int }_1^{\lambda }G\left({\lambda }_{\mathrm{c}}-1\right)}\left(\frac{{\lambda }^2}{{\lambda }_{\mathrm{c}}^2}-1\right)\mathbf{F}\left[\mathbf{N}\otimes \mathbf{N}\right]\mathrm{d}{\lambda }_{\mathrm{c}}$$ (1)

where P_f is the first Piola—Kirchhoff stress tensor of the fibers, N is the unit vector along the fiber direction, K is the fiber modulus, G(λ_c − 1) is the gamma probability distribution of fiber uncrimping, λ is the applied scaffold stretch, and F is the deformation gradient tensor.³⁸ The matrix response was represented by the equation for a compressible neo-Hookean material

$${\mathbf{P}}_{\mathrm{m}}=\mu \left(\mathbf{F}-J^{-2\beta }{\mathbf{F}}^{-T}\right)$$ (2)

$$\beta =\frac{\nu }{1-2\nu }$$ (3)

where P_m is the first Piola—Kirchhoff stress tensor of the matrix, μ is the matrix shear modulus, J is the determinant of F, and ν is the matrix Poisson’s ratio.³⁷

Constitutive Model Fitting

To extract model parameters, the matrix shear modulus was first determined by fitting eq 2 to the experimental data obtained from tensile testing perpendicular to the fiber direction, with the matrix Poisson’s ratio set to the value obtained from separate testing of cell-seeded scaffolds (see eq 6 below). These values were then used as initial guesses for fitting the scaffold stress— strain curves obtained from tensile testing parallel to the fiber direction. The linear modulus and fiber straightness values were used as initial guesses for the fiber modulus and the parameters for the gamma probability distribution of uncrimping, respectively.

Cell Seeding

Bovine bone marrow-derived mesenchymal stem cells were isolated from the tibio-femoral joint of juvenile cows (Research 87, MA, USA), as described previously,⁴⁹ and expanded on tissue culture plastic for 2 passages in basal media (high glucose DMEM with 1% penicillin, streptomycin, fungizone and 10% fetal bovine serum). Scaffolds were cut into strips of 5 × 70 mm (static stretch) or 5 × 35 mm (immunostaining) with the long axis in the fiber direction and were hydrated and disinfected using decreasing concentrations of ethanol (100, 70, 50, 30, 0%; 30 min/step). Scaffolds were then soaked in a fibronectin phosphate-buffered saline solution (20 μg/mL, Sigma-Aldrich, St. Louis, MO) overnight at room temperature to enhance cell attachment. Fibronectin coated scaffolds were seeded with 1 × 10⁵ cells in 200 μL (5 × 70 mm) or 5 × 10⁴ cells in 100 μL (5 × 35 mm) of basal media. Cell seeded scaffolds were cultured for 2 days in basal media prior to static stretch or fixation.

Immunostaining

Two days after seeding, scaffolds were fixed with 4% paraformaldehyde overnight at 4 °C, washed three times and permeablized with 0.5% Triton X-100 in phosphate buffered saline (PBS) with 320 mM sucrose and 6 mM MgCl₂. Actin was stained using Alexa-fluor 488 phalloidin (1:1000, Molecular Probes, Eugene, OR) in PBS containing 1% w/v bovine serum albumin for 1 h at room temperature. Scaffolds were then washed 3 times with PBS and mounted on glass slides using ProLong gold antifade mounting media containing DAPI (Molecular Probes, Eugene, OR).

Static Tensile Stretch

Cells seeded on aligned scaffolds were stained with Hoechst (5 μg/mL, Molecular Probes, Eugene, OR) in high glucose phenol-free DMEM containing HEPES (Gibco, Carlsbad, CA) for 10 min at 37 °C. Samples were then loaded into a custom stepper motor driven tensile-device (n = 3–4/group) mounted on an inverted epi-fluorescence microscope (Nikon Instruments, Tokyo, Japan) and statically stretched (n = 3–4/group) to 8% strain in 1% increments with images being acquired at each strain level. Nuclear deformation was quantified (n > 45 cells/group) using a custom MATLAB program by calculating the ratio of the nuclear principal axis. Briefly, nuclear edges were detected using a Canny edge detection algorithm and used to calculate eigenvectors and eigenvalues for the groups of pixels associated with each nuclei. The first and second eigenvalue, which represent the length of the first and second principal axes, were then used to calculate a nuclear aspect ratio at each strain level for each nuclei. Additionally, the nuclei centroids were used as fiducial markers for calculation of microscale Lagrangian strains on the scaffold surface. First, the deformation gradient tensor was calculated for sets of 3 nuclei using their displacements at each strain level relative to the reference (0% strain) image by solving the equation

$$\left[\begin{array}{ccc}{x}_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right]=\left[\begin{array}{ccc}{F}_{11}& F_{12}& A_1\\ F_{21}& F_{22}& A_2\end{array}\right]\left[\begin{array}{ccc}{X}_1& X_2& X_3\\ Y_1& Y_2& Y_3\\ 1& 1& 1\end{array}\right]$$ (4)

where (x_i, y_i) (i = 1, 2, 3) are the positions of each nuclei in the deformed image, (X_i, Y_i) (i = 1, 2, 3) are the positions of each nuclei in the reference image, {F₁₁, F₁₂, F₂₁, F₂₂} are the components of F, and {A₁, A₂} are the components of a translation vector. This was then used to calculate the Lagrangian strain tensor (E) for each triad

$$\mathbf{E}=1/2({\mathbf{F}}^T\mathbf{F}-\mathbf{I})$$ (5)

Additionally, the effective Poisson’s ratio (ν) at each strain level was calculated for each triad

$$\nu =\frac{-E_{22}}{E_{11}}$$ (6)

Statistics

Statistical significance was set at p < 0.05 and statistical comparisons were made using a one-way ANOVA with Bonferroni post hoc tests. For analysis of data involving multiple strain levels, comparisons were made using a two-way ANOVA with Bonferroni post hoc tests. All data is presented as mean ± standard deviation unless otherwise noted.

RESULTS

Aligned nanofibrous scaffolds fabricated with two fiber populations (Dual PLLA/PEO, D) (Figure 1A) displayed an increased ability to crimp with heating (H) when the soluble fiber fraction (PEO) was removed via washing (W). This resulted in a significant decrease in fiber straightness (Figure 1B) quantified from SEM images of scaffold fiber topographies (Figure 1C). Dual scaffolds heated before washing (DHW) displayed a small decrease in fiber straightness whereas dual scaffolds heated after washing (DWH) displayed a significantly larger decrease in straightness.

Figure 1.

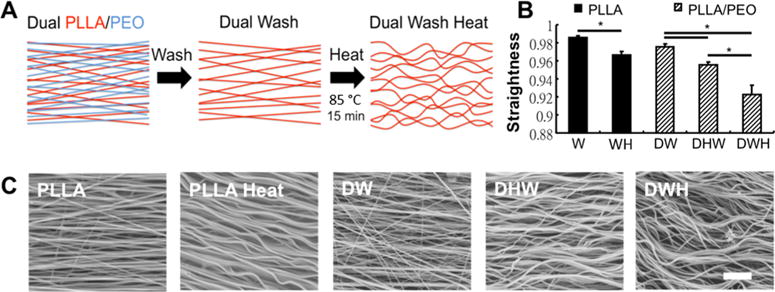
Inclusion of sacrificial fibers allows for increased fiber crimp and nonlinearity with heating. (A) Schematic of aligned nanofibrous material containing two fiber populations. For the Dual (D) PLLA/PEO scaffolds, the water-soluble PEO can be dissolved by washing with water (W), increasing porosity of the scaffold. Heating (H) the scaffolds (85 °C 15 min) increases fiber crimp by increasing PLLA fiber crystallinity. (B) Quantification of fiber straightness from SEM images shows that when heating is performed after scaffold porosity is increased (DWH), fibers display increased crimp (i.e., decreased straightness). (* p < 0.05) (C) Representative SEM images of fabricated scaffolds containing a single fiber population (PLLA) or two fiber populations (PLLA/PEO) (scale bar =1 μm).

This increase in crimped fibers influenced the scaffold mechanical properties. Tensile testing demonstrated that the DWH group, which had the greatest amount of crimping, was the only scaffold that exhibited a nonlinear (i.e., strain-hardening) mechanical response (Figure 2A). Quantification of the scaffold mechanics showed that single polymer PLLA scaffolds possessed a higher linear modulus than all other scaffolds, indicating that both heat treatment (WH) and increased porosity (DW) result in decreased stiffness (Figure 2B). Interestingly, washing out the PEO fibers produced a 78% decrease in the linear modulus (W vs DW), although the PEO fibers only accounted for ~33% of the scaffold volume. This suggests that the inclusion of PEO during electrospinning somehow altered the mechanics or connectivity of the PLLA fibers. Analysis of the transition strain, an important mechanical attribute of fibrous load bearing tissues, showed that the highly crimped dual wash heat (DWH) scaffolds achieved a significantly higher transition strain (Figure 2C). Additionally, these DWH scaffolds displayed a decreased Poisson’s ratio (Figure 2D).

Figure 2.

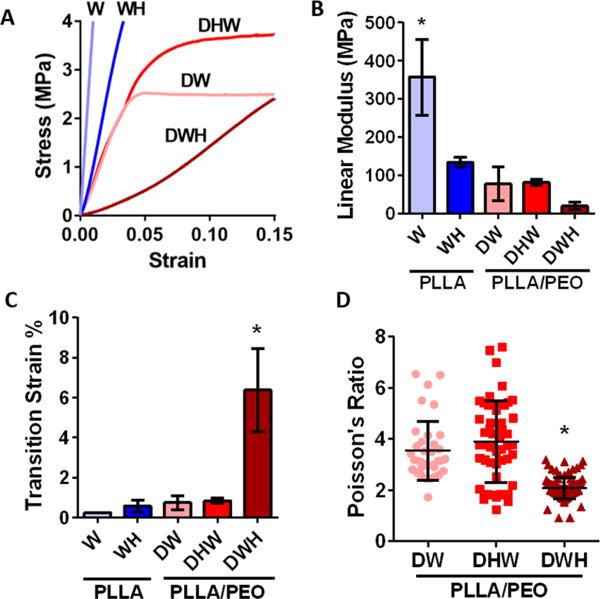
Crimped scaffolds have altered mechanics. (A) Average stress—strain curves for PLLA and PLLA/PEO scaffolds demonstrate only DWH group exhibited a nonlinear (i.e., strain-hardening) response. (B) Both heat-induced crimping (WH) and increased scaffold porosity (DW) reduced the scaffold linear modulus. (C) Increased fiber crimp in DWH scaffolds increased the transition strain and (D) decreased the Poisson’s ratio. (n = 4–5 per group, * p < 0.05 vs all other groups).

To further investigate the relationship between fiber crimping and scaffolds mechanics, we fit the experimental stress-strain curves with a structural constitutive model incorporating crimped fibers embedded in an isotropic matrix.^37,38 The model successfully fit all scaffold groups (minimum R² = 0.998); however, a nonzero matrix term was required to fit only the DWH samples (Figure 3A,B). The DW and DHW groups could be fit by the crimped fibers alone. While SEM measurements showed that fiber crimping increased for both the DHW and DWH scaffolds, the fiber uncrimping indicated by the model fits increased only for the DWH group (Figure 3C). The fiber modulus predicted by the model agreed with the measured linear modulus, which significantly decreased for both heat-processed groups (Figure 3D). The matrix shear modulus determined from testing perpendicular to the fiber direction was similar across all groups (Figure 3E); however, the matrix shear modulus determined from testing parallel to the fibers in the DWH group was significantly higher (3.0 ± 1.0 MPa; p < 0.05). This suggests that the matrix term is actually anisotropic and that load transmission to the fibers at low strains may contribute to the matrix term. Finally, the Poisson’s ratio predicted by the model was comparable with the experimental measurements of the DWH group (model: 2.9 ± 0.3, experiment: 2.1 ± 0.4).

Figure 3.

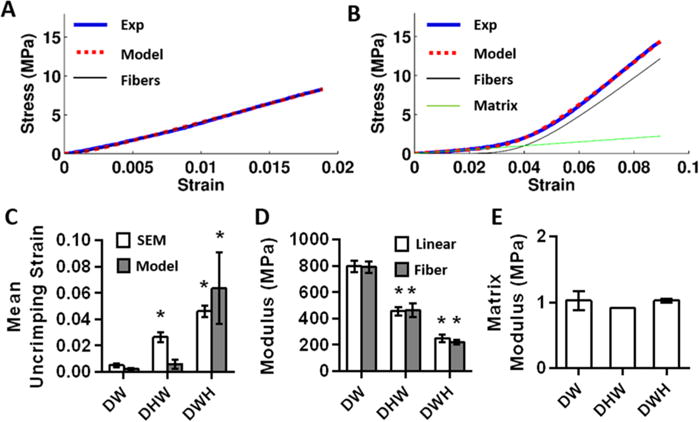
Constitutive modeling of scaffold mechanics. (A) Representative fit of DHW scaffold and (B) DWH scaffold. In general, fits of DW and DHW scaffolds could be fit by the fibers alone. (C) Only DWH scaffolds behaved mechanically as though they had crimped fibers, although fiber crimping was observed via SEM for both DHW and DWH scaffolds. (n = 3–4 per group, * p < 0.05 vs DW) (D) Fiber modulus matched the scaffold linear modulus and both decreased with heat treatment. (n = 3–4 per group, * p < 0.05 vs DW) (E) Matrix shear modulus determined from testing perpendicular to the fibers was similar between scaffolds.

To better understand the physical significance of the matrix term in the model and test whether it represented fiber-fiber interactions, we repeated the mechanical testing and analysis with PVA-treated scaffolds in which the fibers were physically bound together at their intersections. Tensile testing perpendicular to the fiber direction demonstrated that scaffolds with bound fibers had a higher matrix modulus compared to controls (Figure 4A). Testing parallel to the fiber direction showed that the fiber modulus was unchanged (Figure 4B). Furthermore, by measuring the fiber straightness in samples under a fixed strain applied parallel to the fiber direction, we confirmed that the fibers within the control DWH scaffolds became less crimped with strain (Figure 4C). However, the fiber straightness (and hence crimping) in the bound PVA-treated scaffolds remained constant. This suggests that the bound scaffolds behaved like an interconnected network of fibers rather than as a collection of individual crimped fibers. Finally, although fiber crimping was still evident under SEM, the PVA-treated DWH scaffolds lost all mechanical nonlinearity and behaved similar to the DW scaffold group. That is, the fibers were loaded immediately as a network, functioning as though they were not crimped (Figure 4D).

Figure 4.

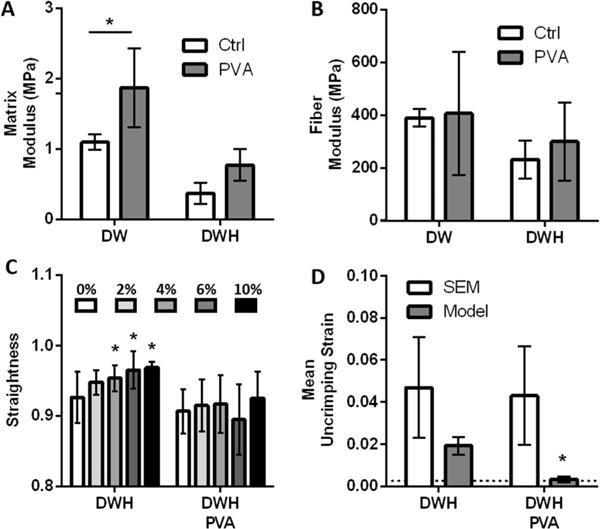
Effects of increased fiber—fiber interactions on scaffold mechanics. (A) Bonding fibers together at their intersection via PVA-treatment increased the matrix modulus determined from testing perpendicular to fiber direction. (n = 4 per group, * p < 0.05) (B) The fiber modulus was unaffected by PVA-treatment. (C, D) PVA-treatment of the crimped DWH scaffolds eliminated fiber uncrimping during tensile testing (C) as measured via SEM (n = 13-21, * p < 0.05 vs 0%) and (D) as predicted by the constitutive model. (n = 4 per group, * p < 0.05 vs DWH controls). Dotted line shows mean uncrimping strain predicted by the model for DW samples.

Finally, we investigated whether the crimped microstructure impacted cellular morphology and stretch induced nuclear deformation and reorientation. Staining of F-actin and DAPI after 2 days of culture showed cells were well attached and aligned in the fiber direction (Figure 5A). Autofluorescent fibers displayed crimp that was often followed by cell protrusions. Analysis of strain transfer to the cell nuclei indicated that all scaffolds induced significant nuclear deformation with applied stretch (Figure 5B). However, the nuclei of cells on crimped DWH scaffolds were less aligned in the fiber direction and this resulted in significantly more nuclear reorientation with applied strain (Figure 5C). Additionally, cells on crimped DWH scaffolds failed to reach the high nuclear aspect ratios observed in the other two groups (Figure 5B).

Figure 5.

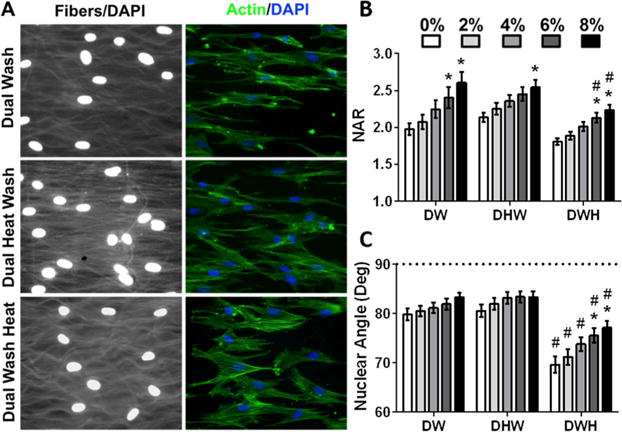
Crimped fibers alter cell morphology and stretch-induced nuclear reorientation. (A) Representative images of mesenchymal stem cell seeded scaffolds stained for F-actin (phalloidin, green) and nuclei (DAPI, blue), with autofluorescent fibers (white) displaying increased crimp in DWH scaffolds. (B) Quantification of nuclear aspect ratio (NAR) and (C) nuclear orientation with applied scaffold stretch. (mean ± SEM, n = 47– 99 cells/group, * p < 0.05 vs 0%, # p < 0.05 vs DW).

DISCUSSION

Fiber crimping is important for the appropriate function of fiber-reinforced soft tissues (e.g., tendon and ligament) and is the source of their mechanical nonlinearity. Further, this microstructure influences transfer of strain to cells within these tissues, which regulates cellular behavior. When engineering replacement tissues, recapitulation of this microstructure is important for both the bulk construct mechanics and cellular mechanotransduction. In this study, we found that a crimped nanofibrous structure could be engineered into aligned electrospun scaffolds, and that this crimp could be enhanced by inclusion of a sacrificial fiber fraction. Interestingly, only if the sacrificial fibers were removed prior to crimping (i.e., DWH group) did the scaffolds behave mechanically as though they were crimped and exhibit a nonlinear (i.e., strain-hardening) stress response with an increased transition strain (Figure 2A, C). Constitutive modeling demonstrated that the nonlinear response of the DWH scaffolds could be explained by fiber uncrimping (Figure 3C). Although inclusion of PEO fibers and heat-treatment (which alters PLLA crystallinity) reduces the scaffold modulus to values below that of native tissue,^7,50–52 they are still within a factor of 2 and can be adjusted by altering electrospinning parameters (e.g., polymer types, PEO ratio, etc.)^20,53 and with time in culture.²⁰ Additionally, the decreased Poisson’s ratio observed with the DWH scaffolds is consistent with modeling of native tissue, where increased crimp leads to lower Poisson’s ratios.⁵⁴ This suggests that fiber crimping affects the lateral contraction of scaffolds and native tissue during loading, which is an important determinant of the tissue time-dependent mechanical behavior.⁵⁵ Together, these results demonstrate that electospun PLLA scaffolds can be produced to mimic the fibrous microstructure and nonlinear mechanics of native tendons and ligaments.

Besides the mechanical contribution of the crimped fibers, the DWH scaffolds were unique in that they exhibited a nonzero stiffness at low strains (i.e., before fiber uncrimping). This response could not be explained by fiber uncrimping and was represented by the matrix term in the model. To test whether this matrix term represented fiber-fiber interactions, we bound the fibers together at their intersection points after inducing crimp. We found that fiber binding indeed increased the matrix stiffness measured during tensile testing perpendicular to the fibers (Figure 4A). Interestingly, it also eliminated the uncrimping of the fibers as the scaffolds were stretched along the fiber direction (Figure 4C, D). This suggests that fiber interconnections can transmit load between fibers before they are uncrimped and that partial loading of crimped fibers in the DWH scaffolds likely contributes to the matrix term in the model. This would also explain why the matrix modulus for the DWH scaffolds appeared greater when stretched parallel to the fiber direction, since the uncrimped fibers would be more efficiently loaded compared to testing perpendicular to the fiber alignment. Paradoxically, in the case of the PVA-treated DWH samples, where the fiber-fiber interactions are elevated, the matrix term is no longer needed to fit the scaffold mechanics. This is because the fibers are engaged immediately by the increased fiber interconnections, making the matrix and fiber terms effectively redundant. Similar to the PVA-treated scaffolds, the DHW scaffolds also lacked a nonlinear mechanical response despite observable fiber crimping under SEM (Figure 3C). This suggests that the linear response of the DHW scaffolds is also due to increased fiber binding generated by heating prior to removing the sacrificial PEO fibers.

Fiber crimping not only increases mechanical nonlinearity, but also results in microstructural changes that alter strain transfer to the cellular microenvironment. Given that micro-environmental strains are critical for tissue development and homeostasis,^56,57 it is important to investigate the effects of fiber crimping on the strain transfer from the scaffolds to the cells. Interestingly, we observed that cells seeded on DWH scaffolds displayed lower nuclear aspect ratios and less alignment in the fiber direction than the DW and DHW scaffolds. This resulted in increased nuclear reorientation with strain of the crimped scaffolds and nuclear aspect ratios that never reached the levels achieved on the less crimped scaffolds. Previous work demonstrated that fibroblasts seeded on crimped scaffolds increased expression of markers for tenogenesis (e.g., tenascin C, collagen I, collagen III), possibly due to altered nuclear morphology and/or strain transmission to cells.^26,28 Our current findings support this hypothesis by demonstrating that nuclear aspect ratios and nuclear reorientation during scaffold stretching are indeed sensitive to fiber crimping.

In summary, we developed a new method for generating aligned nanofibrous scaffolds with high porosity and crimp that mimic the microstructure and nonlinear mechanics of native collagenous tissues. Although fiber-fiber interactions appear to contribute to the scaffold stiffness at low strains, constitutive modeling demonstrated that the increase in stiffness at high strains can be predicted by the amount of fiber crimping. This is important for the rational design of engineered constructs for the replacement of diseased or damaged tissue. Additionally, we found that fiber crimping alters the nuclear morphology of cells seeded on nanofibrous scaffolds. This suggests that the crimped microstructure influences how strain is transmitted to cells during loading, which influences their gene expression and phenotype.^{34,35,58–61} These crimped biomaterials are useful for developing functional fiber-reinforced tissues as well as for studying the effects of altered fiber crimping due to damage or degeneration.