Abstract
We present estimates of ultimate tensile strength (UTS) for two engineered β-solenoid protein mutant fibril structures (spruce budworm and Rhagium inquisitor antifreeze proteins) derived from sonication-based measurements and from force pulling molecular dynamics simulations, both in water. Sonication experiments generate limiting scissioned fibrils with a well-defined length-to-width correlation for the mutant spruce budworm protein and the resultant UTS estimate is 0.66 0.08 GPa. For fibrils formed from engineered R. inquisitor antifreeze protein, depending upon geometry, we estimate UTSs of 3.5 3.2–5.5 5.1 GPa for proteins with interfacial disulfide bonds, and 1.6 1.5–2.5 2.3 GPa for the reduced form. The large error bars for the R. inquisitor structures are intrinsic to the broad distribution of limiting scission lengths. Simulations provide pulling velocity-dependent UTSs increasing from 0.2 to 1 GPa in the available speed range, and 1.5 GPa extrapolated to the speeds expected in the sonication experiments. Simulations yield low-velocity values for the Young’s modulus of 6.0 GPa. Without protein optimization, these mechanical parameters are similar to those of spider silk and Kevlar, but in contrast to spider silk, these proteins have a precisely known sequence-structure relationship.
Introduction
Bio-inspired nanoengineering relies on our ability to understand and control biological self-assembly processes. Several biologically inspired routes for self-assembly, including using viral capsids (1, 2), DNA (3, 4), and proteins (5, 6, 7), show promise and have been employed to template the growth of organic and inorganic materials (1, 2, 3).
One such approach we have recently developed uses the family of β-solenoid proteins (BSPs) for bottom-up protein engineering, where monomeric BSPs serve as programmable nanobricks that can self-assemble into fibrils and potentially into higher-dimensional structures (8). BSPs have practical advantages. The narrow, rod-like structure of the BSPs is advantageous for design and templating, whereas their thermal and chemical stability gives robust self-assembly into fibrils in extreme environments (to be published). More recently, we used molecular dynamics (MD) simulations to show that the BSPs are stiff to bend and twist, with bend/twist persistence lengths in the order of a few microns (9).
A potentially important application of the fibrils is to spin them into larger fibers, which can be readily processed into higher-order structures. For such applications, theoretical estimates of the tensile strength of the fibrils are very useful in design. Until now, there have been no measurements or simulations of their longitudinal breaking strength or Young’s (tensile) modulus.
In this study, we measure the tensile strength of fibrils of two engineered insect antifreeze BSPs, from R. inquisitor (10) and spruce budworm (8, 11), which we abbreviate as RiAFP and SBAFP, respectively, using both experimental and computational methods. The modified RiAFP is engineered to have one intermolecular disulfide bond, acting like a “staple” across the protein-protein interface. It can be removed by exposure to reducing agents such as dithiothreitol (DTT). For computational measurement of the tensile strength, we use nonequilibrium MD simulations (12, 13, 14, 15) and explore the dependence of these results on the rate of pulling. The computational measurement is validated against sonication experiments, where the high shear force generated by imploding bubbles in the cavitation process breaks the fibrils in solution, thereby allowing estimation of their ultimate tensile strength (16). Our results show that the tensile strengths of these proteins increase from 0.2 to 1.5 GPa over accessible pulling speeds in simulations, and from sonication we find mean values of 0.66 0.08 GPa and 1.6 1.5 to 2.5 2.3 GPa for the SBAFP and reduced RiAFP, and a correspondingly larger value of 3.5 3.2 GPA to 5.5 5.1 GPa for the RiAFP with the interfacial disulfide. Given the large error bars, these values are consistent with those of 1.4–1.5 GPa from simulation when extrapolated to the high velocities expected in sonication. Simulation also provides low-velocity estimates of the Young’s modulus of 6.0 GPa for both proteins.
Materials and Methods
Sonication experiments: expression and purification of recombinant proteins
The Escherichia coli-optimized RiAFP gene was synthesized by Thermo Fisher Scientific. The protein sequence and a structural model for RiAFP can be found in the Supporting Material. The gene was cloned into pET-28a using Gibson assembly (17, 18). Protein was expressed in E. coli BL21 (DE3) cells. Cultures were grown at 37oC with shaking at 250 Rpm until was 0.5–0.6. Isopropyl β-D-1-thiogalactopyranoside was added to a final concentration of 1 mM to induce expression. Four hours postinduction, cells were collected by centrifugation (4000 × g for 20 min). The cells were resuspended in lysis buffer (50 mM Tris-HCl, 200 mM NaCl, 10 mM β-mercaptoethanol, and 10 mM imidazole, (pH 8)) and were lysed by sonication. Soluble and insoluble proteins were separated by centrifugation (10,000 × g for 30 min). RiAFP was expressed in the soluble fraction and purified by nickel affinity chromatography. Purified RiAFP was dialyzed into 10 mM sodium phosphate, pH 7.4.
SBAFP was expressed and purified as previously published (8). The sequence for SBAFP can be found in the Supporting Material.
Amyloid fibril formation
To promote fibril formation, RiAFP was incubated for 6 days at 37oC at a concentration of 0.6 mg/mL, and SBAFP was incubated at a concentration of 0.5 mg/mL at 37oC for 10 days.
Sonication
A Heat System-Ultrasonics, Inc., model W-220F sonicator with a microtip was used for the sonication experiments. The output was set at sis (seven is the microtip limit). During these experiments, cavitation was evident in the samples. We sonicated both unreduced RiAFP fibrils and RiAFP fibrils treated with 10 mM DTT. Both reduced and unreduced RiAFP fibrils (2 mL; 0.6 mg/mL) and SBAFP fibrils (1 mL; 0.5 mg/mL) were sonicated in 15 mL conical Falcon tubes that were held in 1.2 L of water to mitigate sample heating from the sonication. After 20 h of sonication, a 10 μL sample was collected for transmission electron microscopy (TEM), whereas the rest of the protein was sonicated for another 20 h.
TEM imaging
After sonication (either after 20 or 40 h), the protein sample (∼10 μL) was loaded on a carbon-coated copper grid and incubated at room temperature for 2 min. Excess liquid was removed by filter paper and the sample was stained with 2% uranyl acetate at room temperature for 30 s. Excess stain was removed by filter paper and the grid was dried at room temperature. The specimen was imaged using a JOEL 1230 TEM with 100 kV of electron acceleration voltage.
Analysis of fibril widths and lengths
The lengths of fibrils were measured using ImageJ software. We measured 178 RiAFP fibrils after 20 (40) h of sonication. The lengths of 209(82) single RiAFP fibrils in DTT were measured after 20 (40) h of sonication. For the lengths of SBAFP fibrils, 200 (139) single fibrils were measured after 20 (40) h of sonication. Histograms of fibril lengths were analyzed using GraphPad Prism 5.01. The histogram bin width was set at 50 nm for RiAFP analysis and 20 nm for SBAFP analysis.
To assess the length versus width relationship of the fibrils we also used ImageJ to measure the width. We measured the widths of 61 single sonicated RiAFP fibrils, and of 89 sonicated RiAFP in DTT fibrils. We measured the widths of 185 unsonicated RiAFP fibrils with ImageJ. For SBAFP, we measured the widths for two independent syntheses of unsonicated fibrils, with 218 and 80 fibrils measured from the respective syntheses. For sonicated SBAFP, to assess the length versus width relationship, we simultaneously measured the length and width of 50 fibrils. For unsonicated SBAFP and for RiAFP, we analyzed the width histograms, and for sonicated SBAFP we carried out regression studies of length versus width and length2 versus width.
Calculation of ultimate tensile strength from results of sonication
The average and standard deviation of the final lengths of the proteins after 40 h of sonication were used to calculate the ultimate tensile strength (UTS) values for the two proteins generalizing a simple model for circular filaments previously proposed by Huang et al. (16). The UTS was calculated using
| (1) |
where is the mean limiting (final) length of the protein after prolonged sonication, C is the circumference of the fibril, r is the distance from the fibril axial center to the surface (the angular brackets denote a geometric average over ), A is the fibril cross-sectional area, is the rate of cavitation bubble expansion during sonication, is the cavitation bubble radius, and η is the solvent viscosity. Huang et al. (16) argue that the product should be approximately independent of solvent, reasoning that in a more viscous solvent the cavitation rate will be slower. In fact, the solvent used by Huang et al. (16) is 10 more viscous than ours (water). Using their estimated value for this product, the expression reduces to
| (2) |
As we show in the Appendix, the factor reduces to for a circular fibril, where d is the diameter. For an equilateral triangular fibril with edge size a, = . For a rectangular cross-section fibril with long edge b, short edge a, and aspect ratio , = .
Nonequilibrium pulling simulations
To estimate the ultimate tensile strengths of RiAFP (10) and SBAFP (8, 11) theoretically, classical MD simulations were used. The details of the simulation procedure were similar to (9). Briefly, we used Gromacs 4.6.5 (19), the Chemistry at Harvard Molecular Mechanics 27 force field (20), the transferrable intermolecular potential-three point water model (21), and periodic boundary conditions for all simulations. During the simulations, each protein was solvated in a box, with at least 1 nm distance between the protein and the box walls. The system was carefully equilibrated over many steps to remove any inherent stress in the protein structure and brought to a temperature of 300 K. These steps included energy minimization, heating the system to 300 K over a 50 ps period using a modified Berendsen temperature coupling scheme (22, 23), relaxation at constant volume and temperature again using the modified Berendsen temperature coupling scheme, and relaxation at constant pressure and temperature using Parrinello-Rahman pressure coupling (24). A simulation time step of 1 fs was used and coordinates were saved every 1 ps. After equilibration, the RiAFP system (the protein in a box of dimensions 12 × 6 × 4 nm, surrounded by water) had a density of 1017 kg/m3 and the SBAFP system (in box of dimensions 13 × 4 × 4 nm) had a density of 1045 kg/m3.
The protein was then subjected to stretching along its helical axis by treating it as a cantilever beam fixed at one end. The c-α atoms of the first turn of the protein were fixed with a strong harmonic constraint (spring constant k = 10,000 kJ/(mol-nm2)). The protein was pulled by attaching a stiff spring (spring constant k = 10,000 kJ/(mol-nm2)) to the center of mass of the last turn, and moving that spring along the helical axis of the protein at a constant speed. Various pulling speeds spanning over four orders of magnitude (0.01, 0.1, 0.5, 1.0, 5.0, 10.0, 30.0, 60.0, 80.0, and 100.0 nm/ns) were studied, and at each speed a minimum of 10 independent simulations were performed. For reference, pulling at 0.1, 1, and 30 nm/ns resulted in strain rates before breaking on the order of /ps, /ps, and /ps, respectively. All pulling simulations were done using a modified Berendsen temperature coupling (22) and Parrinello-Rahman pressure coupling (24). In each simulation, the protein was stretched until all the hydrogen bonds connecting the last turn to the second-to-last turn had been fully broken.
For calculating UTS and Young’s modulus (Y), it was necessary to estimate the length and cross-sectional area of both proteins. The length of each protein was estimated as the average distance between the center of masses of its first and last turns, over a 50 ps simulation. The cross-sectional area was calculated by treating the atoms of each turn as van der Waals spheres projected onto a plane perpendicular to the helical axis, and a grid of ∼0.3 Å was used to sample and measure the area of each projection. The average of the areas of each turn was used as the protein’s cross-sectional area. See Supporting Material for more details on area estimation.
Results and Discussion
The tensile strength of fibrils of two BSPs, SBAFP (8, 11) and RiAFP (10) (for sequences, see the Supporting Material), which have well-defined, helical, rod-like structures with different cross-sectional shapes (triangular and flat-rectangular, respectively) (Fig. 1), were measured using computational simulations and sonication experiments. Both proteins chosen for the study readily self-assemble in vitro into linear polymers, forming long (micron-length) nanowires (8) (Z.P., M.D.T, unpublished data on RiAFP).
Figure 1.
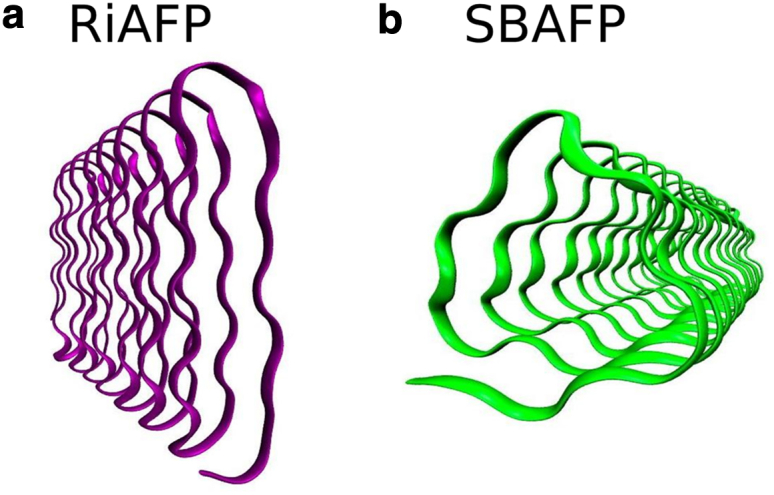
The backbone structure of the (a) RiAFP and (b) SBAFP studied in this work. The two proteins have distinct cross-sectional shapes (flat-rectangular for (a) RiAFP and triangular for (b) SBAFP). Images created using visual molecular dynamics (49). To see this figure in color, go online.
Results from sonication experiments
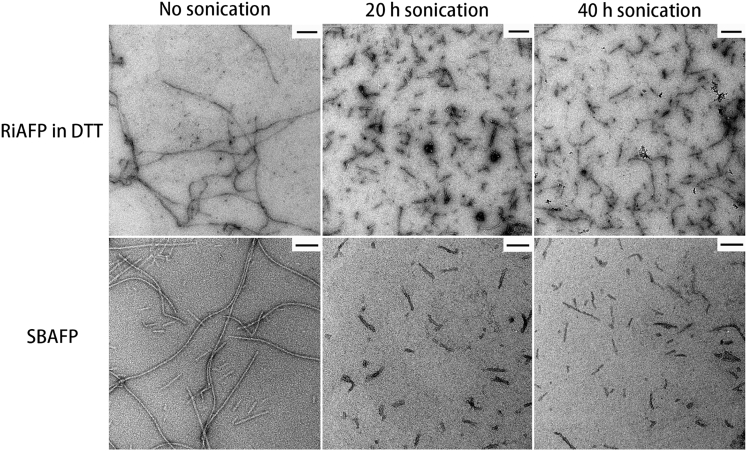
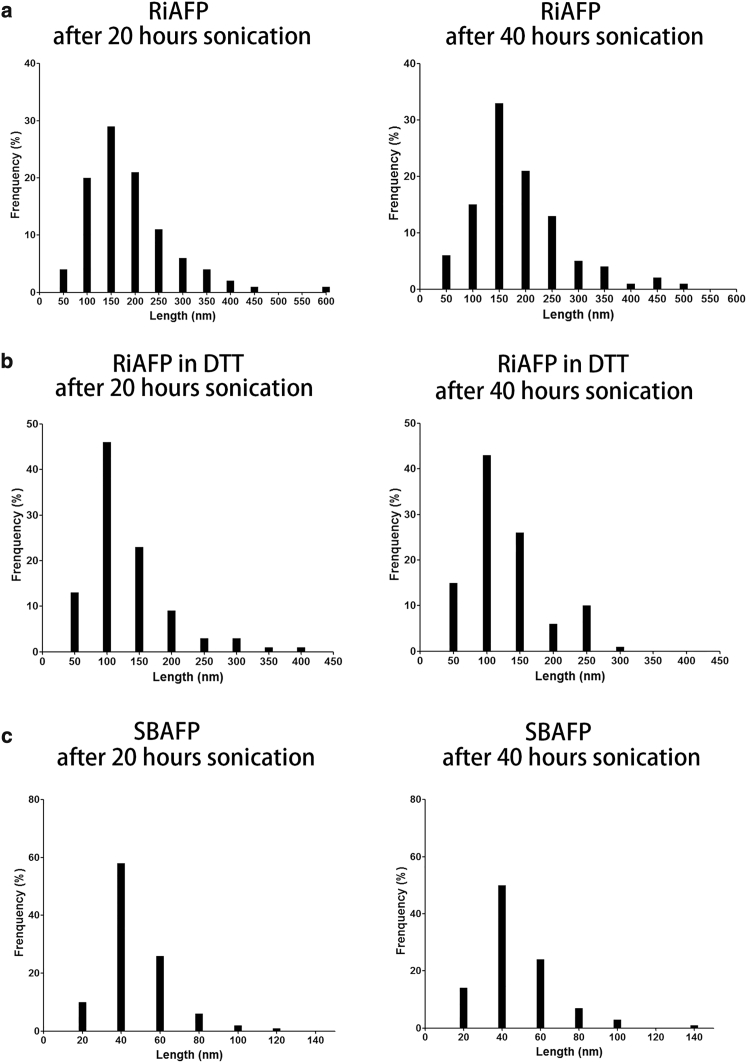
Both the RiAFP and SBAFP assemble into micrometer-long fibrils (Fig. 2). After 20 h of sonication, the mean length of oxidized (reduced) RiAFP fibrils is 186 86 nm (129 65 nm), and the mean length of SBAFP is 46 16 nm (Figs. 2 and 3). After an additional 20 h of sonication, the protein fibrils are not further shortened (Figs. 2 and 3). Fits to Gaussian- and γ-distributions at both 20 and 40 h gave very similar mean length and SD, though the skewed γ-distribution produces a somewhat better fit to the histograms.
Figure 2.
TEM images of fibrils, synthesized from RiAFP and SBAFP before and after sonication, are shown. Prolonged sonication-induced length reduction of fibrils is observed. The scale bars represent 200 nm for RiAFP and 100 nm for SBAFP.
Figure 3.
The frequency distributions of fibril lengths after sonication for 20 and 40 h are shown for (a) RiAFP, (b) RiAFP in DTT, and (c) SBAFP. In (a) and (b), the bin width is set at 50 nm. For (a), the average length after 20 (40) h is 186 87 nm (186 86 nm). For (b), the average length of RiAFP fibrils after 20 (40) h of sonication is 129 65 nm (130 60 nm). For (c), the bin width is set at 20 nm. The average length of SBAFP fibrils after 20 (40) h of sonication is 46 16 nm (47 19 nm).
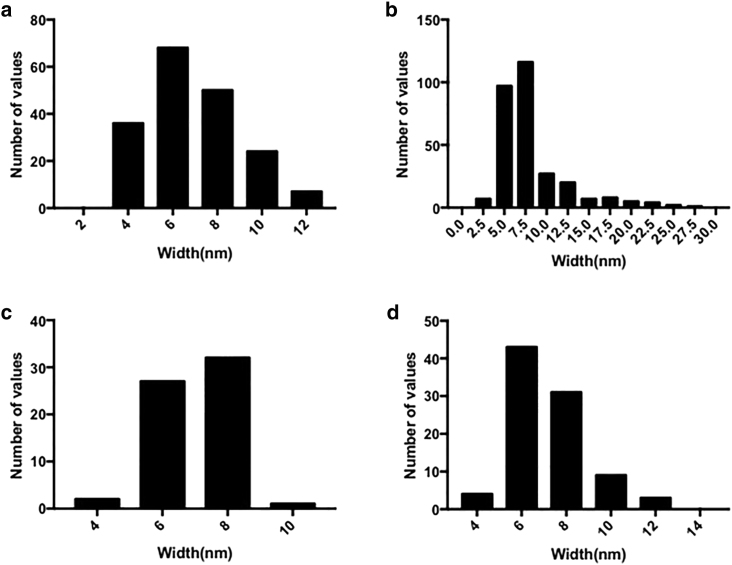
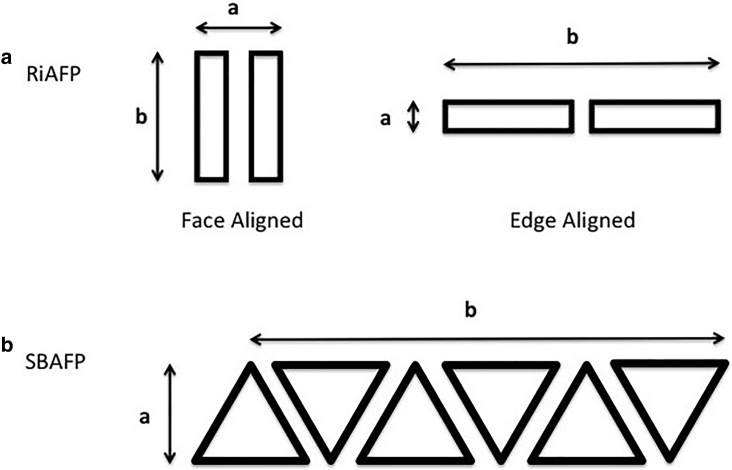
The widths of unsonicated and sonicated mutant RiAFP fibrils have narrow distributions centered around 7 nm, with similar distributions as shown in Fig. 4. This size is consistent with fibrils that are dimeric with two possible geometries as illustrated in Fig. 5 a. For the mutant SBAFP fibrils, the unsonicated distributions have long tails consistent with a distribution of multimers in one transverse dimension driven by lateral assembly of the individual (monomeric) filaments, as shown in Fig. 5 b. We have observed such lateral self-assembly in (8), and conjecture that the likely driver of lateral self-assembly are salt bridges between the added acidic and basic residues (relative to wild-type SBAFP) that reside mostly on two of the triangular facets of the engineered protein.
Figure 4.
Histograms of fibril widths (measured with ImageJ software). (A) Unsonicated mutant RiAFP fibrils. (B) Unsonicated mutant SBAFP fibrils. (C) Sonicated mutant RiAFP fibrils. (D) Sonicated mutant fibrils of RiAFP in DTT.
Figure 5.
Possible fibril cross-sections. (A) The observed widths of unsonicated and sonicated RiAFP fibrils are consistent with monomeric thickness in one transverse dimension and (most likely) dimeric thickness in the other. (B) SBAFP fibrils, both unsonicated and sonicated, show variable width. We assume it is most likely that they are of monomeric thickness in one transverse dimension and multimeric (with variable multimer number) in the other transverse dimension.
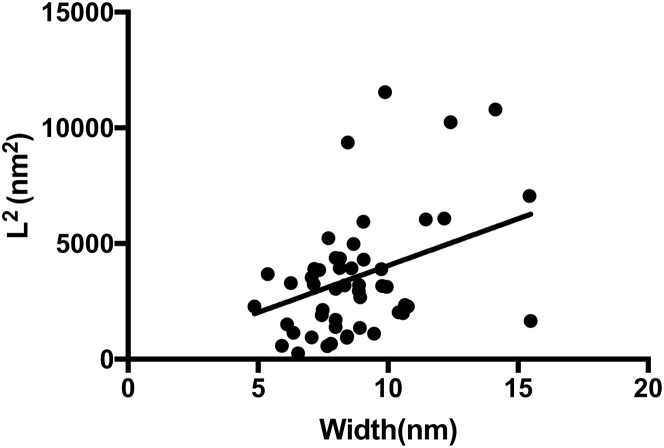
Because the mutant SBAFP fibrils have variable width, we can hypothesize that the ratio of length to width has a particular functional form to generate the same UTS value. For example, if the multiwidth fibrils were formed by radial accumulations of monomeric thickness polymers, we would expect the measured length L to width b ratio, , to be a constant. If, as we anticipate from the width histograms, they have a ribbon geometry with monomeric thickness in one dimension, we would anticipate that is constant, since the cross-sectional area of the fibril goes as , where W is variable but a is held fixed. A plot of versus b is shown in Fig. 6. The average value of for these fibrils is 1.06(0.07), and the height of SBAFP fibrils (8) is 2.6 nm, so this gives an estimate of the UTS as 0.66(0.08) GPa. The same versus W recession was observed for several fibrils of different proteins elsewhere (25).
Figure 6.
Regression of to fibril width b for engineered SBAFP fibrils after sonication, consistent with a ribbon geometry assumption per Fig. 5. We have assumed zero intercept, and obtain a slope of 404 (36) nm with an value of 0.71. The same regression of fibril squared length to width were observed in (25).
The correlation of length and width for the sonicated mutant SBAFP fibrils allows us to make a rather precise estimate of the UTS. For the mutant RiAFP sonicated fibrils, the uniform thickness does not allow this, and our estimates of UTS are intrinsically broad due to the breadth of the distributions. They are also dependent upon the assumed geometry of the fibrils per Fig. 5. We present the UTS estimates obtained from sonication for the mutant RiAFP fibrils in Table 1.
Table 1.
Parameter Values and Resulting UTS for RiAFP and RiAFP in DTT Assuming Either Edge Centered or Face-Centered Geometries, and for SBAFP
| Proteins | Area (nm2) | UTS (GPa) | ||||
|---|---|---|---|---|---|---|
| Edge RiAFP | 6.9(1.0) | 2.0 | 14 | 186 | 1.12 | 5.5(5.1) |
| Edge RiAFP(DTT) | 7.1(1.6) | 4.1 | 14.8 | 130 | 1.13 | 2.5(2.3) |
| Face RiAFP | 6.9(1.0) | 2.1 | 28 | 186 | 1.38 | 3.5(3.2) |
| Face RiAFP(DTT) | 7.1(1.6) | 4.2 | 29.6 | 130 | 1.41 | 1.6(1.5) |
| SBAFP | 4.9–15.5 | 2.6 | 1.06(07) | 0.66(0.08) |
UTS, ultimate tensile strength; RiAFP, insect antifreeze BSP from R. inquisitor; DTT, dithiothreitol; SBAFP, insect antifreeze BSP from spruce budworm.
Our approach for estimating widths suffers somewhat from potential artifacts of the negative stain in the TEM images (26, 27), which can include aggregation effects and flattening effects, as well as intrinsic image resolution limits. Although we cannot rule out the former, the latter is a problem with proteins that have hollow interiors; the tight hydrophobic packing of the BSPs makes flattening unlikely. More precise measurements of fibril heights using atomic force microscopy, as in (25), could help yield better estimates of geometric ratio used for estimating the UTS and will be considered in future studies.
Results from MD simulations
To measure the tensile strength of the solenoid proteins using MD simulations, we treated each monomeric protein as a cantilever beam fixed at one end, whereas the other end was pulled along the direction of the protein’s helical axis for a variety of pulling speeds (see Materials and Methods for details). Each simulation at a different pulling speed resulted in force-displacement curves similar to Fig. 7 a and b (purple and green curves for RiAFP and SBAFP, respectively). In our earlier study on bending and torsion of BSPs, we used quasi-equilibrium umbrella sampling simulations to estimate the mechanical properties (9). Unlike bending and torsion, the tensile strengths of solenoid proteins are not amenable to equilibrium measurements in MD simulations, owing to very little displacement along the pulling direction before breakage. Hence, we employed nonequilibrium measurements using forced pulling simulations to estimate the tensile strength and verified the results by running no less than 10 simulations at each speed.
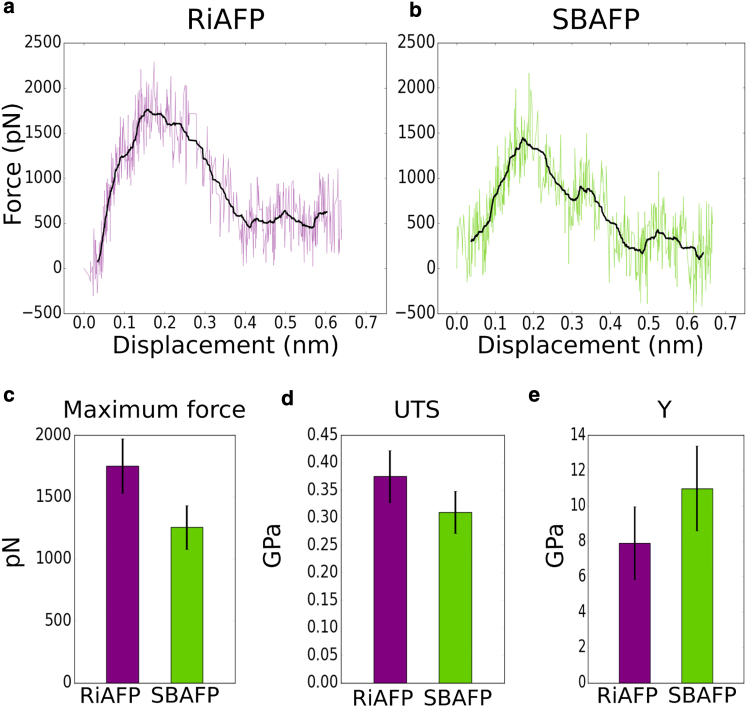
Figure 7.
Plots (a) and (b) show typical force-displacement curves for RiAFP and SBAFP (purple and green), respectively. In black, the smoothed curves are shown. Below, histograms show the mean and SD of the (c) maximum force, (d) UTS, and (e) Young’s modulus Y, for RiAFP and SBAFP (purple and green, respectively). The values shown in the histograms are as follows: (c) RiAFP: 1751.3 219.0 pN, SBAFP: 1256.3 177.8 pN; (d) RiAFP: 0.38 0.05 GPa, SBAFP: 0.31 0.04 GPa; and (e) RiAFP: 7.91 2.06 GPa, SBAFP: 11.00 2.41 GPa. To see this figure in color, go online.
To reduce the noise due to thermal fluctuation, the force-displacement curves were smoothed using a displacement window of ∼0.02 nm. It can be seen that the smoothed curves (black lines in Fig. 7) are roughly linear until the first peak, at which point the secondary structure of the protein breaks. By this we mean that the hydrogen bonds between the pulled turn and the turn adjacent to it are ruptured. This phenomenon can be seen in the trajectory visualizations, as well as in plots of the number of hydrogen bonds versus displacement. See Supporting Material for examples of the latter. For simulations at very high pulling speeds, there are fewer data points before breakage, necessitating smaller averaging windows. The peak value of the force is the maximum value of the smoothed force-displacement curves.
The average value of from 10 different simulation runs at pulling speed of 1 m/s are shown in Fig. 7 c. for RiAFP (1751.3 219.0 pN) is higher when compared to that of SBAFP (1256.3 177.8 pN), suggesting that in general RiAFP needs higher tensile force to break the self-assembly. This comparison holds true for other pulling velocities as well (see Fig. S3).
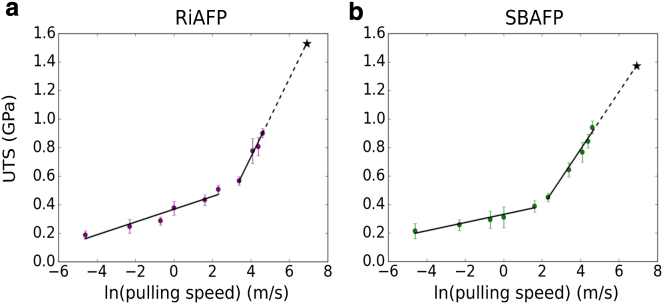
The UTS, obtained as the ratio of to the cross-sectional area of the peptide (see Supporting Material for details on the area measurement), was also calculated (Fig. 7 d). Unlike the maximum force, the UTS values for the peptides (at pulling velocity of 1 m/s) are comparable and within the measurement error (Fig. 2 d). This is true at most other pulling speeds as well (see Fig. 8). Note that Fig. 7 d shows UTS values for a single pulling speed (1 m/s) but, as noted earlier, these values vary with the pulling speed. Hence, the dependence of UTS on the pulling speed was also examined (Fig. 8 a and b). For both solenoid proteins, there is a clear increase in the average UTS (and ) with increasing pulling speed, as can be seen in Fig. 8 a and b. Over the four orders of magnitude in pulling speed (0.01–100 m/s), UTS varies between ∼0.2 and 1.0 GPa, showing the dependence of the measurements on the pulling speed.
Figure 8.
The ultimate tensile strength with respect to the natural log of the pulling speed is plotted for (a) RiAFP (purple) and (b) SBAFP (green). The errors are calculated using the SD of the maximum forces at each speed. For each protein, we note two distinct linear regimes, to which we fit two lines (black). For RiAFP, the lines are given by and . For SBAFP, the lines are given by and . To estimate the UTS at speeds achieved during sonication, we extrapolate to v = 1000 m/s, which gives a UTS of 1.5 GPa for RiAFP and a 1.4 GPa for SBAFP. To see this figure in color, go online.
Notably, we observe two different linear regimes in these plots with the slopes changing sharply at ∼10 m/s (black lines in Fig. 8 a and b). In general, the linear relationship between the natural logarithm of the pulling speed and is seen for many other materials, including composites (28), alloys (29), and steel (30). In the case of proteins, the two different linear regimes likely signify two different rupture mechanisms at different pulling speeds. Ackbarow et. al. (31) have also seen such behavior for simple α-helices and β-sheets, and they suggested that under slower pulling speeds, sets of hydrogen bonds within the protein secondary structure break in a concerted fashion, whereas at higher pulling speeds hydrogen bonds break serially, causing biphasic behavior. This idea is supported by the differences in energy barrier heights and barrier distances that need to be overcome to break the hydrogen bond structure at high and low pulling speeds.
A phenomenological kinetic transition model with an energy barrier (32) can be used to understand the mechanical breakage during pulling. In this model, the slopes and y-intercepts of the two linear regimes can be used to back-calculate the barrier height and bond-breaking length during the two different linear pulling regimes. This follows from the model’s assumption that the likelihood of transitioning through the energy barrier (for example, from folded to an unfolded, or broken, conformation) increases with an applied force along the reaction coordinate (31, 33). and for each regime can therefore be determined from the linear fits to the maximum force versus (Fig. S4), as done previously (31).
The results for our BSPs are very similar to those for β-sheet structures (31). For RiAFP, the values are = 8.05 kcal/mol, = 0.20 Å; = 1.27 kcal/mol, and = 0.03 Å. For SBAFP, the values are = 10.29 kcal/mol, = 0.34 Å; = 2.37 kcal/mol, and = 0.05 Å. Here, we have adopted the use of “slow” and “fast” to refer to the shallower and steeper slope regimes, respectively. A typical hydrogen bond disassociation energy is ∼2 kcal/mol (34), which is about the same as the energy barrier in the fast regime. In the slow regime, on the other hand, the energy barrier is about four or five times the energy required to break a single hydrogen bond, suggesting that to transition from the native to unfolded state, we must break multiple bonds simultaneously.
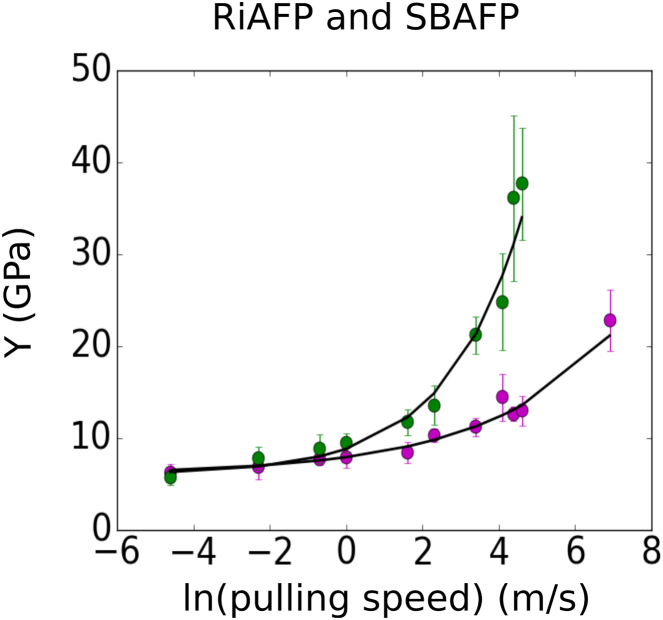
We also analyzed the relationship between Young’s modulus (Y) and pulling speed for the proteins. Y is given by , where is the original length of the protein, A is again the cross-sectional area, and is the spring constant of the protein. The slope of the linear fit to the smoothed force-displacement curves before breakage is used to obtain an estimate of the spring constant (k) for the proteins. The average and SD of the spring constant at any given pulling speed is measured from 10 independent simulations (for example, see Fig. 7 e), and the results are plotted against the natural logarithm of the pulling speed in Fig. 9.
Figure 9.
The average and SD of the Young’s modulus Y as a function of the natural logarithm of the pulling speed is shown. The results for RiAFP and SBAFP are shown in purple and green, respectively. The proteins have similar asymptotic values for Y at low pulling speeds of 6.0 GPa, which can be estimated by fitting exponentials (black) and extrapolating the fits to low speeds. At high speeds, Y for SBAFP increases more quickly than that of RiAFP. The value for Y of RiAFP at is plotted to more clearly illustrate its behavior as the speed increases. To see this figure in color, go online.
For both proteins, there is an increase in Y (and spring constant) with increasing pulling speed, as found with UTS values. The rate of increase is greater at higher speeds, and as the speed decreases, Y seems to be approaching an asymptotic value, suggesting that the slope of the force-displacement curve remains fairly constant at slow pulling speeds. Similar behavior was also observed for a tropocollagen molecule (35), and other polymer composites (36, 37) where the modulus increases with the strain rate. Here, the RiAFP and SBAFP clearly approach similar Y values at 0.01 m/s, and by fitting an exponential to each set of points and extrapolating to low speeds we find asymptotic values of 6 GPa for both proteins. For SBAFP, the Y value at 1 m/s is comparable to the bending and torsional moduli of the protein calculated earlier ( = 8.1 GPa and = 11.3 GPa). Although Y for the RiAFP and SBAFP approach similar values at low speeds, perhaps suggesting that their moduli, and therefore elastic behaviors, are similar under low mechanical loading conditions, they differ at higher pulling speeds. Thus, we view the theory results as lower bounds to the experimental ones, because the experimental values are for interface breakage whereas the theory values reflect intramolecular unraveling. Nevertheless, these two processes are very similar mechanistically.
Although both Y and UTS increase with pulling speed, there must be some difference in the origin of the increase, because Y is measured in the linear stress-strain region whereas UTS is measured close to rupture. In the case of silica glass, detailed MD simulations have revealed that the increase in modulus is associated with stress relaxation at high strain rates (38), but the mechanisms for relaxation in that solid-state system must be in detail different than what we have observed for our proteins here. This is an interesting and important question that is beyond the scope of our study.
Comparison of theory and experiment
The experimental values can be compared to the computational ones indirectly by extrapolating the pulling speeds to those expected in typical cavitation events in sonication. The typical speed of fluid propagation around cavitation bubbles in sonication is ∼1000 m/s. Extrapolating to those speeds on our simulation plot yields 1.5 GPa for RiAFP and 1.4 GPa for SBAFP (marked as stars in Fig. 8 a and b). We note that we overestimate the mutant SBAFP value found from the experiment and underestimate the RiAFP value (no DTT), although the latter agrees within the generous error bars engendered by the broad distribution of final lengths from the sonication. The values are certainly comparable. A key difference between theory and experiment is that the sonication experiments split the fibrils at interfaces, whereas the pulling experiments unravel the hydrogen bonds in a given layer at the UTS in a way restorable at equilibrium.
At least part of the discrepancy between theory and experiment might be related to the estimation of effective areas and diameters for the proteins. Calculation of UTS values from sonication experiments requires a diameter for the fibrils in the model of (16). The theory simulations are on individual filaments and, as noted, the data strongly suggests that the RiAFP and SBAFP fibrils studied here are not monomeric.
Separately, classical MD with the nonreactive CHARMM force field cannot directly model disulfide bond breakage in the unreduced RiAFP case. This is because the electronic structure is not being modeled directly, and the “bonded” interactions are fixed in the topology. Therefore, we can only capture the unraveling of hydrogen bonded structures. Sonication is expected to break all types of bonds, but is most likely to pull apart proteins at the weaker noncovalent interfaces. For the two cases here that lack an interfacial disulfide bond, fibril scission assuredly occurs at the noncovalent interface. The disulfide bond at the interface of the nonreduced RiAFP fibrils has a bond dissociation energy of 60 kcal/mol, which is significantly less than the covalent bonds of the polypeptide backbone (85 kcal/mol), and remains the weakest link in the polymer and the most likely point of scission.
Conclusions
In summary, we used nonequilibrium MD simulations of two BSPs, SBAFP and RiAFP, to extract theoretical estimates for UTS and Young’s modulus Y by averaging multiple runs over widely varying pulling speeds. Experimental UTS values were measured by sonication-induced scission. The extrapolated high pulling speed UTS values agree within error with the experimental values.
Our results are also consistent with those of other hydrogen-bonded structures. For example, the low pulling speed Y values derived from simulations here are a factor of two smaller than the 11–13 GPa cited for spider silk, whereas the UTS values estimated from sonication bracket those of spider silk (39). UTS values for a set of β-helical proteins of ∼0.5–0.7 GPa, and Young’s moduli of 13–27 GPa, have been found using similar theoretical methods (40), and a review of the mechanics of amyloid materials reports Young’s moduli of about 0.01–30 GPa and strengths of 0.1–1 GPa for amyloid fibrils (41). For a more thorough comparison to other studies of amyloid structures, see Supporting Material for a table in which we report other experimental and theoretical Young’s modulus and UTS values from the amyloid literature (16, 25, 40, 42, 43, 44, 45).
UTS values for our noncovalent fibrils are also similar to those for Kevlar (39, 46), although Kevlar-49 has a much higher Y value. A study of Kevlar using MD simulations on the nanometer length scale gives a UTS of 1.19 GPa for tension in the direction of the hydrogen bond network (47). In our case, the simple addition of a disulfide bridge across the RiAFP interface nearly doubles its UTS value.
Given the known sequence-to-structure match of BSPs, they appear to be strong candidates for engineering mechanically tough fibers for materials applications such as filtration meshes and high strength “smart” fabrics.
Author Contributions
Synthesis – Conducting, Z.P. and M.D.R.P.; Synthesis – Protocol Design, M.D.T.; Sonication, Z.P. and M.D.R.P.; TEM Measurements/Analysis, Z.P. (RiAFP) and M.P. (SBAFP); Simulation Studies, A.S.P. (conducting) and D.L.C. (supervision); Designed Engineered Fibrils and Developed the Sonication Protocol, M.D.T.; Image Analysis of Unsonicated Fibrils and Analysis of the Ultimate Tensile Strength from Sonicated Fibrils, D.L.C.; Writing, Z.P., A.S.P., M.D.T., and D.L.C.
Acknowledgments
The authors thank Dr. Fei Guo from the Electron Microscopy Imaging Facility of the Department of Molecular and Cellular Biology at the University of California, Davis for training and assistance with the TEM. We thank T.P. Knowles for a useful conversation.
We gratefully acknowledge the support of the University of California, Davis Office of Research RISE Program for support of the ANSWER project. We acknowledge support from the US National Science Foundation grant DMR-1207624 (A.S.P. and K.M.R.).
Editor: Elizabeth Rhoades.
Footnotes
Supporting Materials and Methods, five figures and three tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30988-8.
Appendix
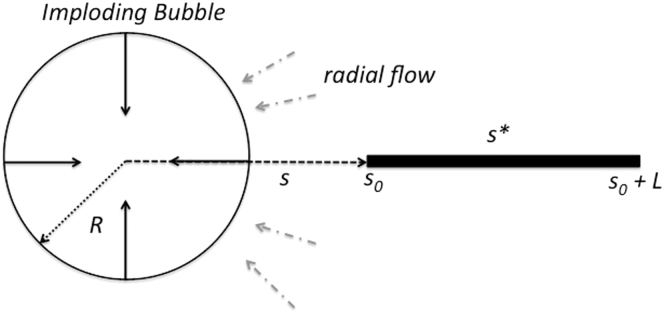
In this Appendix, we provide the analysis of the estimate of for fibrils of noncircular cross section. The basic model (before scission) is envisioned in Fig. 10.
Figure 10.
Model of prescission conditions for fibrils undergoing sonication. The picture is that fibrils of length L align radially in the vicinity of an imploding bubble of radius R thanks to the radial fluid flow. The radial coordinate from the center of the bubble is s and the fibril has an edge closest to the bubble of . The position denotes the radial distance at which the fixed fibril velocity matches the fluid velocity, so that the net viscous stress vanishes there. To see this figure in color, go online.
The imploding bubble sets up a radially inward velocity flow with solvent velocity
| (3) |
where is the velocity of the collapsing bubble surface. At a distance from the center of the bubble, the assumed uniform fibril speed matches the speed of the surrounding solvent, so that the fibril velocity is identified as
| (4) |
As clarified in (48), the viscous stress at a given distance s from the bubble center is given by
| (5) |
where is the distance from the center of the fibril to the surface of the fibril at arc position l on the fibril surface and η is the solvent viscosity. The total scission force is determined by identifying the distance where the fluid velocity equals the fluid velocity such that
| (6) |
where represents the end of the fibril of length L proximate to the bubble, s is integrated along the length of the fibril, and l is integrated around the fibril circumference. Note that the maximum scission force will be generated when , and this is assumed in (16, 48). Hence, it is very natural to introduce the factor
| (7) |
where is the circumference of the fibril.
The resulting cross-section fibril geometry influence on the force can be summarized in the factor , where A is the fibril cross sectional area. For a circle where d is the diameter, it is straightforward to evaluate the corresponding integral for triangular and rectangular geometry to obtain the results quoted in Calculation of ultimate tensile strength from results of sonication.
Supporting Material
References
- 1.Flynn C., Lee S., Belcher A. Viruses as vehicles for growth, organization and assembly of materials. Acta Mater. 2003;51:5867–5880. [Google Scholar]
- 2.Lee Y.J., Yi H., Belcher A.M. Fabricating genetically engineered high-power lithium-ion batteries using multiple virus genes. Science. 2009;324:1051–1055. doi: 10.1126/science.1171541. [DOI] [PubMed] [Google Scholar]
- 3.Seeman N.C. Nanomaterials based on DNA. Annu. Rev. Biochem. 2010;79:65–87. doi: 10.1146/annurev-biochem-060308-102244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Castro C.E., Kilchherr F., Dietz H. A primer to scaffolded DNA origami. Nat. Methods. 2011;8:221–229. doi: 10.1038/nmeth.1570. [DOI] [PubMed] [Google Scholar]
- 5.Chiti F., Dobson C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 6.Sára M., Sleytr U.B. Crystalline bacterial cell surface layers (S-layers): from cell structure to biomimetics. Prog. Biophys. Mol. Biol. 1996;65:83–111. doi: 10.1016/s0079-6107(96)00007-7. [DOI] [PubMed] [Google Scholar]
- 7.King N.P., Sheffler W., Baker D. Computational design of self-assembling protein nanomaterials with atomic level accuracy. Science. 2012;336:1171–1174. doi: 10.1126/science.1219364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Peralta M.D.R., Karsai A., Cox D.L. Engineering amyloid fibrils from β-solenoid proteins for biomaterials applications. ACS Nano. 2015;9:449–463. doi: 10.1021/nn5056089. [DOI] [PubMed] [Google Scholar]
- 9.Heinz L.P., Ravikumar K.M., Cox D.L. In silico measurements of twist and bend moduli for β-solenoid protein self-assembly units. Nano Lett. 2015;15:3035–3040. doi: 10.1021/nl5049719. [DOI] [PubMed] [Google Scholar]
- 10.Hakim A., Nguyen J.B., Meng W. Crystal structure of an insect antifreeze protein and its implications for ice binding. J. Biol. Chem. 2013;288:12295–12304. doi: 10.1074/jbc.M113.450973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Leinala E.K., Davies P.L., Jia Z. A beta-helical antifreeze protein isoform with increased activity. Structural and functional insights. J. Biol. Chem. 2002;277:33349–33352. doi: 10.1074/jbc.M205575200. [DOI] [PubMed] [Google Scholar]
- 12.Isralewitz B., Gao M., Schulten K. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol. 2001;11:224–230. doi: 10.1016/s0959-440x(00)00194-9. http://www.sciencedirect.com/science/article/pii/S0959440X00001949 [DOI] [PubMed] [Google Scholar]
- 13.Lu H., Isralewitz B., Schulten K. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation. Biophys. J. 1998;75:662–671. doi: 10.1016/S0006-3495(98)77556-3. http://www.sciencedirect.com/science/article/pii/S0006349598775563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Keten S., Xu Z., Buehler M.J. Nanoconfinement controls stiffness, strength and mechanical toughness of beta-sheet crystals in silk. Nat. Mater. 2010;9:359–367. doi: 10.1038/nmat2704. http://www.nature.com/nmat/journal/v9/n4/pdf/nmat2704.pdf [DOI] [PubMed] [Google Scholar]
- 15.Keten S., Buehler M.J. Asymptotic strength limit of hydrogen-bond assemblies in proteins at vanishing pulling rates. Phys. Rev. Lett. 2008;100:198301. doi: 10.1103/PhysRevLett.100.198301. http://journals.aps.org/prl/pdf/10.1103/PhysRevLett.100.198301 [DOI] [PubMed] [Google Scholar]
- 16.Huang Y.Y., Knowles T.P.J., Terentjev E.M. Strength of nanotubes, filaments, and nanowires from sonication-induced scission. Adv. Mater. 2009;21:3945–3948. [Google Scholar]
- 17.Gibson D.G.L., Young L., Smith H.O. Enzymatic assembly of DNA molecules up to several hundred kilobases. Nat. Methods. 2009;6:343–345. doi: 10.1038/nmeth.1318. [DOI] [PubMed] [Google Scholar]
- 18.Gibson D.G. Enzymatic assembly of overlapping DNA fragments. Methods Enzymol. 2011;498:349–361. doi: 10.1016/B978-0-12-385120-8.00015-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 20.Brooks B.R., Brooks C.L., III, Karplus M. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., L K.M. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 22.Berendsen H.J.C., Postma J.P.M., van Gunsteren W.F. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–36905. [Google Scholar]
- 23.Bussi G., Donadio D., Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 24.Martonák R., Laio A., Parrinello M. Predicting crystal structures: the Parrinello-Rahman method revisited. Phys. Rev. Lett. 2003;90:075503. doi: 10.1103/PhysRevLett.90.075503. [DOI] [PubMed] [Google Scholar]
- 25.Lamour G., Nassar R., Gsponer J.A. Mapping the broad structural and mechanical properties of amyloid fibrils. Biophys J. 2017;112:584–594. doi: 10.1016/j.bpj.2016.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sander B., Golas M.M. Visualization of bionanostructures using transmission electron microscopical techniques. Microsc. Res. Tech. 2011;74:642–663. doi: 10.1002/jemt.20963. [DOI] [PubMed] [Google Scholar]
- 27.Rames M., Yu Y., Ren G. Optimized negative staining: a high-throughput protocol for examining small and asymmetric protein structure by electron microscopy. J. Vis. Exp. 2014;90:e51087. doi: 10.3791/51087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Miwa M., Horiba N. Strain rate and temperature dependence of tensile strength for carbon/glass fibre hybrid composites. J. Mater. Sci. 1993;28:6741–6747. [Google Scholar]
- 29.Zinkle S.J., Eatherly W.S. Oak Ridge National Lab; Tennessee: 1997. Effect of Test Temperature and Strain rate on the Tensile Properties of High-Strength, High-Conductivity Copper Alloys; pp. 165–174. [Google Scholar]
- 30.Boyce B.L., Crenshaw T.B., Dilmore M.F. Sandia National Lab; California: 2007. The Strain-Rate Sensitivity of High-Strength High-Toughness Steels. [Google Scholar]
- 31.Ackbarow T., Chen X., Buehler M.J. Hierarchies, multiple energy barriers, and robustness govern the fracture mechanics of alpha-helical and beta-sheet protein domains. Proc. Natl. Acad. Sci. USA. 2007;104:16410–16415. doi: 10.1073/pnas.0705759104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 33.Kumar S., Li M.S. Biomolecules under mechanical force. Phys. Rep. 2010;486:1–74. [Google Scholar]
- 34.Sheu S.Y., Yang D.Y., Schlag E.W. Energetics of hydrogen bonds in peptides. Proc. Natl. Acad. Sci. USA. 2003;100:12683–12687. doi: 10.1073/pnas.2133366100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gautieri A., Buehler M.J., Redaelli A. Deformation rate controls elasticity and unfolding pathway of single tropocollagen molecules. J. Mech. Behav. Biomed. Mater. 2009;2:130–137. doi: 10.1016/j.jmbbm.2008.03.001. [DOI] [PubMed] [Google Scholar]
- 36.Jacob G.C., Starbuck J.M., Boeman R.G. Strain rate effects on the mechanical properties of polymer composite materials. J. Appl. Polym. Sci. 2004;94:296–301. [Google Scholar]
- 37.Wang Z., Zhou Y., Mallick P. Effects of temperature and strain rate on the tensile behavior of short fiber reinforced polyamide-6. Polym. Compos. 2002;23:858–871. [Google Scholar]
- 38.Chowdhury S.C., Haque B.Z., Gillespie J.W. Molecular dynamics simulations of the structure and mechanical properties of silica glass using ReaxFF. J. Mater. Sci. 2016;51:10139–10159. [Google Scholar]
- 39.Altman G.H., Diaz F., Kaplan D.L. Silk-based biomaterials. Biomaterials. 2003;24:401–416. doi: 10.1016/s0142-9612(02)00353-8. [DOI] [PubMed] [Google Scholar]
- 40.Solar M., Buehler M.J. Tensile deformation and failure of amyloid and amyloid-like protein fibrils. Nanotechnology. 2014;25:105703. doi: 10.1088/0957-4484/25/10/105703. [DOI] [PubMed] [Google Scholar]
- 41.Knowles T.P., Buehler M.J. Nanomechanics of functional and pathological amyloid materials. Nat. Nanotechnol. 2011;6:469–479. doi: 10.1038/nnano.2011.102. [DOI] [PubMed] [Google Scholar]
- 42.Adamcik J., Lara C., Mezzenga R. Measurement of intrinsic properties of amyloid fibrils by the peak force QNM method. Nanoscale. 2012;4:4426–4429. doi: 10.1039/c2nr30768e. [DOI] [PubMed] [Google Scholar]
- 43.Ruggeri F.S., Adamcik J., Dietler G. Influence of the beta-sheet content on the mechanical properties of aggregates during amyloid fibrillization. Angew. Chem. Int. Ed. Engl. 2015;54:2462–2466. doi: 10.1002/anie.201409050. [DOI] [PubMed] [Google Scholar]
- 44.Paul T.J., Hoffmann Z., Prabhakar R. Structural and mechanical properties of amyloid beta fibrils: a combined experimental and theoretical approach. J. Phys. Chem. Lett. 2016;7:2758–2764. doi: 10.1021/acs.jpclett.6b01066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Makky A., Bousset L., Melki R. Nanomechanical properties of distinct fibrillar polymorphs of the protein alpha-synuclein. Sci. Rep. 2016;6:37970. doi: 10.1038/srep37970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bunsell A. The tensile and fatigue behaviour of Kevlar-49 (PRD-49) fibre. J. Mater. Sci. 1975;10:1300–1308. [Google Scholar]
- 47.Chowdhury S.C., Sockalingam S., Gillespie J.W. Molecular dynamics modeling of the effect of axial and transverse compression on the residual tensile properties of ballistic fiber. Fibers. 2017;5:7. [Google Scholar]
- 48.Huang Y.Y., Terentjev E.M. Dispersion of carbon nanotubes: mixing, sonication, stabilization, and composite properties. Polymers (Basel) 2012;4:275–295. [Google Scholar]
- 49.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.