Abstract
Computational techniques are required for narrowing down the vast space of possibilities to plausible prebiotic scenarios, because precise information on the molecular composition, the dominant reaction chemistry and the conditions for that era are scarce. The exploration of large chemical reaction networks is a central aspect in this endeavour. While quantum chemical methods can accurately predict the structures and reactivities of small molecules, they are not efficient enough to cope with large-scale reaction systems. The formalization of chemical reactions as graph grammars provides a generative system, well grounded in category theory, at the right level of abstraction for the analysis of large and complex reaction networks. An extension of the basic formalism into the realm of integer hyperflows allows for the identification of complex reaction patterns, such as autocatalysis, in large reaction networks using optimization techniques.
This article is part of the themed issue ‘Reconceptualizing the origins of life’.
Keywords: graph transformation, graph grammars, reaction networks, hypergraphs, rule composition
1. Introduction
From a fundamental physics point of view, chemical systems, or more precisely molecules and their reactions, are just time-dependent multi-particle quantum systems, completely described by the fundamental principles of quantum field theory (QFT) [1]. At this level of description almost all questions of interest to a chemist are not tractable in practice, however. A hierarchy of approximations and simplifications is employed therefore to reach models of more practical value. These are guided at least in part by conceptual notions that distinguish chemistry from other quantum systems. Among these are constraints such as the immutability of atomic nuclei and the idea that chemical reactions comprise only a redistribution of electrons. On the formal side, the Born–Oppenheimer approximation [2] stipulates a complete separation of the wave function of nuclei and electrons and leads to the concept of the potential energy surface (PES) that explains molecular geometries and provides a consistent—if not completely accurate—view of chemical reactions as classical paths of nuclear coordinates on the PES. The PES itself is the result of solving the Schrödinger equation with nuclear coordinates and charges as parameters [3,4]. Quantum chemistry (QC) has developed a plethora of computational schemes for this purpose, typically trading off accuracy for computational resource consumption. Among them in particular are the so-called semi-empirical methods that use the fact that the chemical bonds are usually formed by pairs of electrons to decompose the electronic wave function into contributions of electron pairs.
Molecular modelling (MM) and molecular dynamics (MD) [5,6] abandon quantum mechanics altogether and instead treat chemical bonds akin to classical springs. Sacrificing accuracy, MM and MD can treat macromolecules and supramolecular complexes that are well outside the reach of exact and even semi-empirical quantum-chemical methods. For special classes of molecules, even coarser approximations have been developed. Many properties of aromatic ring systems, for instance, can be explained in terms of graph-theoretical models known as Hückel theory [7,8]. For nucleic acids, on the other hand, models have been developed that aggregate molecular building blocks (nucleotides) into elementary objects so that Watson–Crick base pairs become edges in the graph representation [9].
A common theme in the construction of coarser approximations is that more and more external information needs to be supplied to the model. While QFT does not require more than a few fundamental constants, nuclear masses and charges are given in practical QC computations. Semi-empirical methods, in addition, require empirically determined parameters for electron correlation effects. MM and MD models use extensive tables of parameters that specify properties of localized bonds as a function of bond type and incident atoms. Similarly, RNA folding depends on a plethora of empirically determined energy contributions for base pair stacking and loop regions [10]. A second feature of coarse-grained methods is that they are specialized to answer different types of questions, or that different classes of systems resort to different, mutually incompatible approximations.
This well-established hierarchy of internally consistent models of molecular structures is in stark contrast to our present capability to model chemical reactions. While transition state theory [11] does provide a means to infer reaction rate constants from PES, it requires the prior knowledge of the educt and product states.
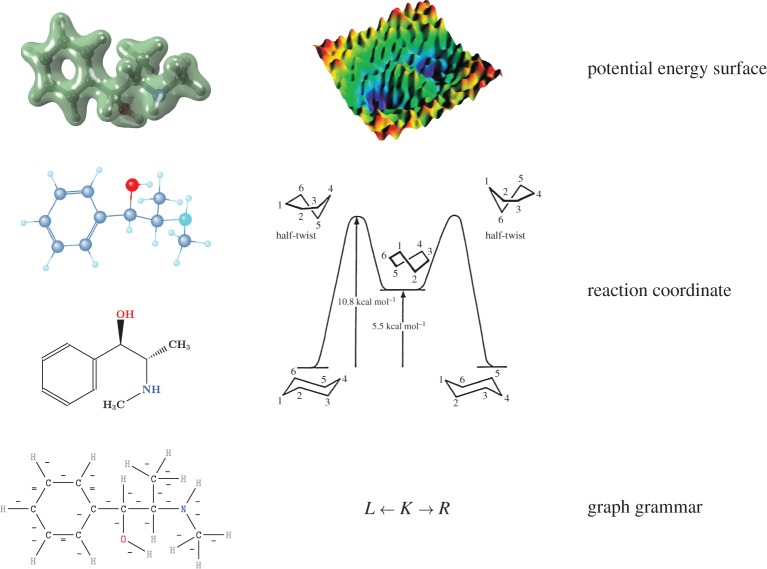
A systematic investigation of large chemical reaction systems requires the development of a theoretical framework that is sufficiently coarse-grained to be computationally tractable. Any such model must satisfy consistency conditions that are inherited from the underlying physics (figure 1). A study [12] on complex chemical reaction networks supports this view and concludes that, on the structure and reactivity level of small molecules, efficient quantum mechanics-based computational approaches exist, but on the large-scale network level heuristic approaches are indispensable. Here, we argue that chemistry offers a coarse-grained level of description that allows the construction of mathematically sound and consistent formal models that, nevertheless, are conceptually and structurally different from the formalism of QC. Much of chemistry is taught in terms of abstracted molecular structures and rules (named reactions) that transform molecular graphs into each other. In the following section, we show how this level of modelling can indeed be made mathematically precise and how it can accommodate key concepts of chemistry such as transition state theory and fundamental conservation laws inherited from the underlying physics.
Figure 1.
Levels of abstraction for computational approaches in chemistry. Shown is the hierarchy of approximations from quantum mechanics at the top to graph grammars at the bottom. The coarse-graining via the introduction of constraints (such as the Born–Oppenheimer approximation, or reducing coordinates of spatial objects to neighbourhood relations on graphs) is accompanied by a dramatic speed-up in computation time.
2. Graph grammar chemistry
The starting point of an inherently discrete model of chemistry is a simplified, graphical representation of molecules. This coarse-graining maps the atoms and bonds of a molecule to vertices and edges of the corresponding graph. All type information (atom types C, H, N, O, etc. and bond multiplicity single, double, triple bond) are mapped to labels on the respective vertices or edges of the graph. In this setting all information on properties which are tied to the three-dimensional space, such as chirality and cis/trans isomerism of double bonds, is neglected.
It is possible, however, to extend the model to retain the local geometric information and thus capture the part of stereochemistry which is tied to stereogenic centres. Helicity, for instance, cannot be expressed by the extended model because this property is generated by an extended spatial arrangement around an axis and not a single point or centre. The basis for the extended model is the valence-shell electron-pair repulsion (VSEPR) model, which, despite comprising a set of simple rules, has a firm grounding in quantum chemical modelling [13]. VSEPR theory determines approximate bond angles around an atom depending on the incident bond types, i.e. in terms of information conveyed by the labelled graph representation. Stereochemical information involving chiral centres as well as cis/trans isomerism thus can be encoded simply in the order in which bonds are listed, and augmenting the labelled graph with a permutation group on each vertex to describe geometric symmetries.
Nevertheless certain aspects of chemistry cannot be described in this form. For instance, the concept of bonds as edges fails in multi-centre bonds because three or more atoms share a pair of bonding electrons. These are frequently observed in boranes or organometallic compounds such as ferrocenes. Non-local chirality, found for instance in helical molecules, does not rely on local, atom-centred symmetries and thus is not captured by local orientation information.
With molecules represented as graphs, the mechanism of a chemical reaction is naturally expressed as a graph transformation rule. Graph transformation thus retains the semantics familiar from organic chemistry textbooks. As a research discipline in computer science, graph transformation dates back to the 1970s. Graph transformation has been studied extensively in the context of formal language theory, pattern recognition, software engineering, concurrency theory, compiler construction and verification among other fields in computer science [14]. Several formalisms have been developed in order to formalize and implement the process of transforming graphs. Algebraic approaches are of particular interest for modelling chemistry, where multiple variations based on category theory exist. For example, different semantics can be expressed using the single pushout approach, the more restrictive double pushout (DPO) approach or the recently developed sesqui-pushout approach [15].
In the context of chemical reactions, DPO graph transformation is the formalism of choice because it facilitates the construction of transformation rules that are chemical in nature. DPO guarantees that all chemical reactions are reversible [16]. The conservation of atoms translates to a simple formal condition (formally, the graph morphisms relating the context to the left-hand and right-hand side of a rule must be bijections for vertices). In turn, this requirement guarantees the existence of well-defined atom maps.
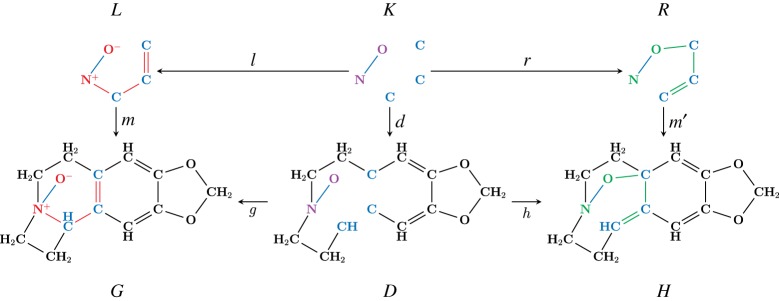
Figure 2 illustrates how the Meisenheimer rearrangement [17], a temperature-induced rearrangement of aliphatic amine oxides into N-alkoxylamines, translates to the DPO formalism. The reaction transforms educt graph G (amine oxide) into product graph H (N-alkoxylamine).
Figure 2.
Double-pushout (DPO) representation of the application of a graph transformation rule. The actual reaction (the top span 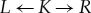 ) is the Meisenheimer rearrangement which transforms educt graph G into product graph H. All arrows in the diagram are morphisms, i.e. functions which map vertices/edges from the graph on the arrow tail to the graph at the arrow head. To be a valid transformation, the two squares of the diagram must form so-called pushouts.
) is the Meisenheimer rearrangement which transforms educt graph G into product graph H. All arrows in the diagram are morphisms, i.e. functions which map vertices/edges from the graph on the arrow tail to the graph at the arrow head. To be a valid transformation, the two squares of the diagram must form so-called pushouts.
All arrows in the diagram are morphisms. The reaction centre, i.e. the subset of atoms and bonds of the reactant molecules directly involved in the bond-breaking/-forming steps of the chemical reaction, is expressed as a graph transformation rule. The information of how to change the connectivity and the charges of the atoms is specified by three graphs (L,K,R). The left graph L (respectively, right graph R) expresses the local state of molecules before (respectively, after) applying the reaction rule. The context graph K encodes the invariant part of the reaction centre and mathematically relates L and R to each other. The left graph L is thus the precondition for application of the rule (i.e. it can only be applied if there exists a subgraph match m that embeds L in the host graph G; see the red and blue highlighted part of graph G in figure 2). In this case, L can be replaced by the right graph R (see the green and blue highlighted part of graph H in figure 2), which transforms the educt graph G into the product graph H.
A computationally very demanding step when performing graph transformation (e.g. for generating large chemical spaces) is the enumeration of subgraph matches. Deciding if a single subgraph match exists in a host graph is known to be an 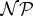 -complete problem [18,19]. Better theoretical results exist for certain classes of graphs, e.g. for the so-called partial k-trees of bounded degree (to which almost all molecule graphs belong [20–22]) where the subgraph matching problem can be solved in polynomial time [23,24]. In practice, it is however faster to use simpler algorithms, e.g. VF2 [25,26].
-complete problem [18,19]. Better theoretical results exist for certain classes of graphs, e.g. for the so-called partial k-trees of bounded degree (to which almost all molecule graphs belong [20–22]) where the subgraph matching problem can be solved in polynomial time [23,24]. In practice, it is however faster to use simpler algorithms, e.g. VF2 [25,26].
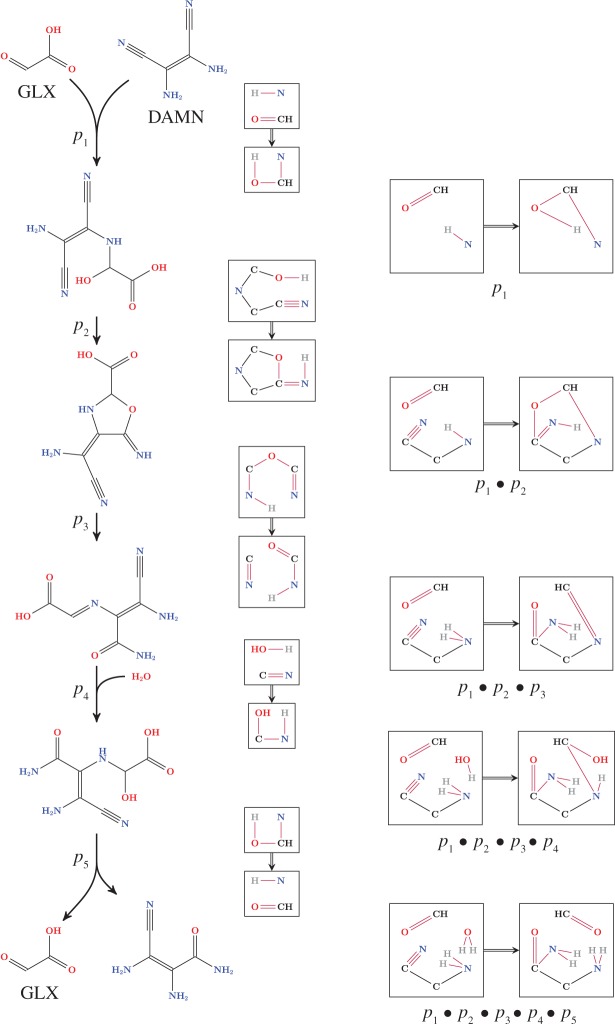
Chemical reactions are often compositions of elementary reactions. In the latter, the reaction centre can always be expressed as a cycle [27,28], with an even number of vertices for homovalent reactions and an odd number from ambivalent reactions, better known as redox reactions. Graph transformations have a natural mechanism for rule composition that allows the expression of multi-step reactions (e.g. enzyme-mediated reactions or even complete metabolic pathways) as compositions of elementary transformation rules. The properties of elementary rules in terms of mass conservation or atom-to-atom mapping nicely carry over to the composed ‘overall transformation rules’. As the action of chemical reactions is to redistribute atoms along complex reaction sequences, rule composition can be used to study the trace of individual atoms along these reaction sequences in a chemically as well as mathematically correct fashion. Rule composition can be completely automated and thus opens the possibility for model reduction (see [29] for further details). We illustrate rule composition in the context of prebiotic chemistry in figure 3.
Figure 3.
Automatic inference of an overall rule by subsequent composition of graph transformation rules. The example is based on a sequence of reactions from [30], in which Eschenmoser describes how aldehydes act as catalysts for the hydrolysis of CN groups of the HCN tetramer. The left column depicts the mechanism as presented in [30]. An automated approach will, based on graph transformation rules, first generate a (potentially very large) chemical space (not depicted here). The depicted mechanism is then found as one of the solutions for the general question of enumerating hydrolysis pathways of HCN polymers that use glyoxylate (GLX: glyoxylate, CID 760) as a catalyst. In the depicted pathway, the tetramer of HCN (DAMN: tetramer of HCN, CID 2723951) is hydrolysed. The middle column depicts the left and right graph of each transformation rule p1,…,p5 that models the generalized reactions. The subsequently inferred rules p1 (top), p1•p2,…, and the overall rule p1•p2•⋯•p5 (bottom) are depicted in the right column. Note that, in general, these can be several composed overall rules, each expressing different atom traces. In this example there is only a single one.
3. Network view of chemistry
Classical synthetic chemistry traditionally has been concerned with the stepwise application of chemical reactions in carefully crafted synthesis plans. In living organisms, by contrast, complex networks of intertwined reactions are active concurrently. These intricate reaction webs harbour complex reaction patterns such as branch points, autocatalytic cycles and interferences between reaction sequences. The emerging field of systems chemistry has set out to leverage the systemic, network-centred view as a framework also for synthetic chemistry. Consequently, large-scale chemical networks are no longer just a subject of analysis in the context of understanding the working of a living cell’s metabolism, but are becoming a prerequisite to understanding the possibilities within chemical spaces, i.e. the universe of chemical compounds and the possible chemical reactions connecting them. The formulation of a predictive theory of chemical space requires it to be rooted in a strict mathematical formalization and abstraction of the overwhelming amount of anecdotal knowledge, which has been collected on the single reaction and functional subnetwork level, into generalizing principles.
Graph transformation systems, as discussed earlier, provide the basis for such a formalism that allows for a systematic and stepwise construction of arbitrary chemical spaces. A chemical system is then specified as a formal graph grammar that encapsulates a set of transformation rules, encoding the reaction chemistry, together with a set of molecules which provide the starting points for rule application. The iteration of the graph grammar yields reaction networks in the form of directed hypergraphs as explicit instantiations of the chemical space. Usually a simple iterative expansion of the chemical space leads to a combinatorial explosion in the number of novel molecules. Therefore, a sophisticated strategy framework for the targeted exploration of the parts of interest of the chemical space has been developed [31]. Such strategies are indispensable if, for example, polymerization/cyclization spaces are the subject of investigation. These types of spaces are, for example, found in the important natural product classes of polyketides and terpenes, and in prebiotic HCN chemistry [32]. The strategy framework allows the guidance of chemical space exploration not only using physico-chemical properties of the generated molecules, but also using experimental data such as mass spectra. Importantly, the hypergraphs (reaction networks) are generated automatically annotated with atom-to-atom maps, as defined implicitly in the underlying graph grammar. For large and complex reaction networks it is thus possible to construct atom flow networks in an automated fashion, even including corrections for molecule and subnetwork symmetries, as required for the interpretation of isotope labelling experiments [33].
The origin of life can be viewed as an intricate process which has been shaped by external constraints provided by early Earth’s environment and intrinsic constraints stemming from reaction chemistry itself. Higher-order chemical transformation motifs, such as network autocatalysis, are believed to have played a key role in the amplification of the building blocks of life [34–36]. A combination of the constructive graph grammar approach with techniques from combinatorial optimization sets the proper formal stage for attacking some of these origin of life related questions. The key idea here is to rephrase the topological requirements for a particular chemical behaviour, e.g. network autocatalysis, as an optimization problem on the underlying reaction network (hypergraph). An example of this is the enumeration of pathways with specific properties, which can be formally modelled as a constrained hyperflow problem. Many of these problems are theoretically computationally hard [37], though in practice methods such as integer linear programming can be successfully used to identify such transformation motifs in arbitrary chemical spaces. The enumeration of transformation motifs is the first step in computer-assisted large-scale analysis of reaction networks. Other mathematical formalisms, such as Petri nets, and in general concurrency theory, can subsequently be used to model properties of chemical systems on an even higher level. Complicated chemical spaces, such as the one formed by the formose process [38], can thus be dismantled into coupled functional modules, advancing the understanding of how a particular reaction chemistry induces specified behaviour on the reaction network level. More generally speaking and emphasizing the need for new approaches, it is quite foreseeable that the future of chemistry is strongly bundled with a deeper understanding of complex chemical systems [39,40], and the necessary skills to analyse such systems will become more and more important.
4. Discussion and concluding remarks
Narrowing down potential pathways for prebiotic scenarios indispensably requires novel systemic approaches that allow for the investigation of large chemical reaction systems. While the development of mathematically well-grounded methods for abstraction and coarse-graining of (concurrent) systems is a very active research area in computer science, the interdisciplinary endeavour to integrate these approaches with chemistry is more often treated as a conceptual possibility rather than as a predictive approach. Many of the problems to be solved in this process are computationally hard (i.e. 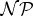 -hard) but still allow for practical in silico solutions. This discrepancy led to a relatively new and successful subfield in computer science called algorithmic engineering [41], in which one of the goals is to bridge the gap between theoretical results and practical solutions to hard problems. Clearly, results from that field should be taken into account when large chemical systems with a plethora of underlying hard problems have to be solved.
-hard) but still allow for practical in silico solutions. This discrepancy led to a relatively new and successful subfield in computer science called algorithmic engineering [41], in which one of the goals is to bridge the gap between theoretical results and practical solutions to hard problems. Clearly, results from that field should be taken into account when large chemical systems with a plethora of underlying hard problems have to be solved.
As an illustration of the integrative potential we sketch an example in figure 3 (see http://mod.imada.sdu.dk for further examples). It shows how graph transformation-based chemical space exploration (rooted in graph theory, category theory and concurrency theory) with subsequent solution enumeration (using diverse optimization techniques) can be applied to a reaction schema presented in [30], in which Eschenmoser describes how aldehydes act as catalysts for the hydrolysis of CN groups of the HCN tetramer. Given a set of chemical reactions p1,…,p5 (encoded as graph grammar rules) and a set of initial molecules, the iterative application of these rules (potentially with an underlying strategy for the space expansion) leads to a chemical space encoded as a hypergraph. This hypergraph is the source for solving the subsequent problem of inferring and enumerating declaratively defined reaction motifs or pathways. In figure 3, we do not illustrate the expansion step; the depicted mechanism (left column) is however found automatically as one of the potentially many solutions for the general question of enumerating hydrolysis pathways of HCN polymers that use glyoxylate (GLX: glyoxylate, CID 760) as a catalyst. Formally, such a solution is encoded as an integer hyperflow within the underlying hypergraph. Given the depicted reaction sequence, the possibility for transformation rule composition is utilized. The overall (more coarse-grained) rule p1•p2•⋯•p5 is thus automatically inferred by consecutive composition of the (simpler) transformation rules p1,…,p5. All intermediate steps are depicted in the right column of figure 3. Note that the automated coarse-graining implemented by rule composition allows for keeping track of the possibilities of different atom traces, expressed as the atom-to-atom mapping from educt to product in composed rules. An obvious reachable next step is therefore the analysis as well as the design of isotope labelling experimentation based on the in silico generative chemistry approach with subsequent trace analysis.
Clearly, the illustration in figure 3 serves only as an example. The modelling of essential chemical parameters including kinetic components and thermodynamics is still missing. Nevertheless, the approach is already highly automated, and will bring wetlab and in silico experiments closer together. We argue that the intermediate-level theory outlined here holds promise in many fields of chemistry. In particular, we suggest that it is a plausible substrate for a predictive theory of prebiotic chemistry.
Data accessibility
This article has no additional data.
Authors' contributions
All authors contributed equally to the paper.
Competing interests
The author(s) declare that they have no competing interests.
Funding
This work is supported by the Danish Council for Independent Research, Natural Sciences (grant no. DFF-7014-00041), the COST Action CM1304 ‘Emergence and Evolution of Complex Chemical Systems’ and the ELSI Origins Network (EON), which is supported by a grant from the John Templeton Foundation.
Disclaimer
The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.
References
- 1.Weinberg S. 2005. The quantum theory of fields. Cambridge, UK: Cambridge University Press; (doi:10.1017/CBO9781139644167) [Google Scholar]
- 2.Born M, Oppenheimer JR. 1927. Zur Quantentheorie der Molekülen. Ann. Phys. 389, 457–484. (doi:10.1002/andp.19273892002) [Google Scholar]
- 3.Mezey P. 1987. Potential energy hypersurfaces. Amsterdam, The Netherlands: Elsevier. [Google Scholar]
- 4.Heidrich D, Kliesch W, Quapp W. 1991. Properties of chemically interesting potential energy surfaces. Lecture Notes in Chemistry, vol. 56. Berlin, Germany: Springer.
- 5.McCammon J, Gelin B, Karplus M. 1977. Dynamics of folded proteins. Nature 267, 585–590. (doi:10.1038/267585a0) [DOI] [PubMed] [Google Scholar]
- 6.Burkert U, Allinger N. 1982. Molecular mechanics, vol. 177 Washington, DC: American Chemical Society. [Google Scholar]
- 7.Hückel E. 1931. Quantentheoretische Beiträge zum Benzolproblem. I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. Z. Phys. 70, 204–286. (doi:10.1007/BF01339530) [Google Scholar]
- 8.Hoffmann R. 1963. An extended Hückel theory. I. Hydrocarbons. J. Chem. Phys. 39, 1397–1412. (doi:10.1063/1.1734456) [Google Scholar]
- 9.Zuker M, Stiegler P. 1981. Optimal computer folding of larger RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 9, 133–148. (doi:10.1093/nar/9.1.133) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Turner D, Mathews D. 2010. NNDB: the nearest neighbor parameter database for predicting stability of nucleic acid secondary structure. Nucleic Acids Res. 38, 280–282. (doi:10.1093/nar/gkp892) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Eyring H. 1935. The activated complex in chemical reactions. J. Chem. Phys. 3, 107–114. (doi:10.1063/1.1749604) [Google Scholar]
- 12.Rappoport D, Galvin CJ, Zubarev DY, Aspuru-Guzik A. 2014. Complex chemical reaction networks from heuristics-aided quantum chemistry. J. Chem. Theory Comput. 10, 897–907. (doi:10.1021/ct401004r) [DOI] [PubMed] [Google Scholar]
- 13.Gillespie R. 2008. Fifty years of the VSEPR model. Coord. Chem. Rev. 252, 1315–1327. (doi:10.1016/j.ccr.2007.07.007) [Google Scholar]
- 14.Rozenberg G. (ed.). 1997. Handbook of graph grammars and computing by graph transformation. Singapore: World Scientific. [Google Scholar]
- 15.Corradini A, Heindel T, Hermann F, König B.2006. Sesqui-pushout rewriting. In Graph transformation, Proc. 3rd Int. Conf., ICGT 2006, Natal, Brazil, 17–23 September 2006. Lecture Notes in Computer Science, vol. 4178, pp. 30–45. Berlin, Germany: Springer.
- 16.Andersen JL, Flamm C, Merkle D, Stadler PF. 2013. Inferring chemical reaction patterns using graph grammar rule composition. J. Syst. Chem. 4, 4 (doi:10.1186/1759-2208-4-4) [Google Scholar]
- 17.Meisenheimer J. 1919. Über eine eigenartige Umlagerung des Methyl-allyl-anilin-N-oxyds. Chem. Ber. 52, 1667–1677. (doi:10.1002/cber.19190520830) [Google Scholar]
- 18.Cook SA. 1971. The complexity of theorem-proving procedures. In Proc. of the 3rd Annu. ACM Symp. on Theory of Computing, STOC ’71, Shaker Heights, OH, 3–5 May 1971, pp. 151–158. New York, NY: ACM.
-
19.Garey M, Johnson D.
1979.
Computers and intractability. A guide to the theory of
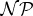 completeness. San Francisco, CA: Freeman. [Google Scholar]
completeness. San Francisco, CA: Freeman. [Google Scholar] - 20.Yamaguchi A, Aoki KF, Mamitsuka H. 2004. Finding the maximum common subgraph of a partial k-tree and a graph with a polynomially bounded number of spanning trees. Inf. Proc. Lett. 92, 57–63. (doi:10.1016/j.ipl.2004.06.019) [Google Scholar]
- 21.Horváth T, Ramon J. 2010. Efficient frequent connected subgraph mining in graphs of bounded tree-width. Theor. Comput. Sci. 411, 2784–2797. (doi:10.1016/j.tcs.2010.03.030) [Google Scholar]
- 22.Akutsua T, Nagamochi H. 2013. Comparison and enumeration of chemical graphs. Comput. Struct. Biotechnol. J. 5, e201302004 (doi:10.5936/csbj.201302004) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Matoušek J, Thomas R. 1992. On the complexity of finding iso- and other morphisms for partial k-trees. Disc. Math. 108, 343–364. (doi:10.1016/0012-365X(92)90687-B) [Google Scholar]
- 24.Dessmark A, Lingas A, Proskurowski A. 2000. Faster algorithms for subgraph isomorphism of k-connected partial k-trees. Algorithmica 27, 337–347. (doi:10.1007/s004530010023) [Google Scholar]
- 25.Cordella LP, Foggia P, Sansone C, Vento M. 2001. An improved algorithm for matching large graphs. In Proc. of the 3rd IAPR-TC15 Workshop on Graph-based Representations in Pattern Recognition, Ischia, Italy, 23–25 May 2001, pp. 149–159. CUEN. [DOI] [PubMed]
- 26.Cordella L, Foggia P, Sansone C, Vento M. 2004. A (sub) graph isomorphism algorithm for matching large graphs. IEEE Trans. Pattern Anal. Machine Intell. 26, 1367–1372. (doi:10.1109/TPAMI.2004.75) [DOI] [PubMed] [Google Scholar]
- 27.Hendrickson JB. 1997. Comprehensive system for classification and nomenclature of organic reactions. J. Chem. Inf. Comput. Sci. 37, 852–860. (doi:10.1021/ci970040v) [Google Scholar]
- 28.Hendrickson JB. 2010. Systematic signatures for organic reactions. J. Chem. Inf. Model 50, 1319–1329. (doi:10.1021/ci1000482) [DOI] [PubMed] [Google Scholar]
- 29.Andersen JL, Flamm C, Merkle D, Stadler PF.2014. 50 Shades of rule composition: from chemical reactions to higher levels of abstraction. In Proc. of the 1st Int. Conf. on Formal Methods in Macro-Biology, Noumea, New Caledonia, 22–24 September 2014 (eds F Fages, C Carla Piazza). Lecture Notes in Computer Science, vol. 8738, pp. 117–135. Berlin, Germany: Springer.
- 30.Eschenmoser A. 2007. On a hypothetical generational relationship between HCN and constituents of the reductive citric acid cycle. Chem. Biodivers. 4, 554–573. (doi:10.1002/cbdv.200790050) [DOI] [PubMed] [Google Scholar]
- 31.Andersen JL, Flamm C, Merkle D, Stadler PF. 2014. Generic strategies for chemical space exploration. Int. J. Comp. Biol. Drug Des. 7, 225–258. (doi:10.1504/IJCBDD.2014.061649) [DOI] [PubMed] [Google Scholar]
- 32.Andersen JL, Andersen T, Flamm C, Hanczyc M, Merkle D, Stadler PF. 2013. Navigating the chemical space of HCN polymerization and hydrolysis: guiding graph grammars by mass spectrometry data. Entropy 15, 4066–4083. (doi:10.3390/e15104066) [Google Scholar]
- 33.Buescher JM, et al. 2015. A roadmap for interpreting 13C metabolite labeling patterns from cells. Curr. Opin. Biotechnol. 34, 189–201. (doi:10.1016/j.copbio.2015.02.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kauffman S. 1995. At home in the universe: the search for the laws of self-organization and complexity. Oxford, UK: Oxford University Press. [Google Scholar]
- 35.Kauffman S. 2007. Question 1: origin of life and the living state. Orig. Life Evol. Biosph. 37, 315–322. (doi:10.1007/s11084-007-9093-2) [DOI] [PubMed] [Google Scholar]
- 36.Ulanowicz R. 1997. Ecology, the ascendent perspective. New York, NY: Columbia University Press. [Google Scholar]
- 37.Andersen JL, Flamm C, Merkle D, Stadler PF. 2012. Maximizing output and recognizing autocatalysis in chemical reaction networks is NP-complete. J. Systems Chem. 3, 1 (doi:10.1186/1759-2208-3-1) [Google Scholar]
- 38.Butlerov A. 1861. Einiges über die chemische Structur der Körper. Z. Chem. 4, 549–560. [Google Scholar]
- 39.Whitesides GM. 2015. Reinventing chemistry. Angew. Chem. Int. Ed. 54, 3196–3209. (doi:10.1002/anie.201410884) [DOI] [PubMed] [Google Scholar]
- 40.Gothard CM, Soh S, Gothard NA, Kowalczyk B, Wei Y, Bilge Baytekin BAG. 2012. Rewiring chemistry: algorithmic discovery and experimental validation of one-pot reactions in the network of organic chemistry. Angewandte Chemie 51, 7922–7927. (doi:10.1002/anie.201202155) [DOI] [PubMed] [Google Scholar]
- 41.Sanders P.2009. Algorithm engineering—an attempt at a definition. In Efficient algorithms. Lecture Notes in Computer Science, vol. 5760, pp. 321–340. Berlin, Germany: Springer. ( doi:10.1007/978-3-642-03456-5_22)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This article has no additional data.