Summary measures of agreement and association between many raters’ ordinal classifications

Abstract

Interpretation of screening tests such as mammograms usually require a radiologist’s subjective visual assessment of images, often resulting in substantial discrepancies between radiologists’ classifications of subjects’ test results. In clinical screening studies to assess the strength of agreement between experts, multiple raters are often recruited to assess subjects’ test results using an ordinal classification scale. However, using traditional measures of agreement in some studies is challenging due to the presence of many raters, the use of an ordinal classification scale and unbalanced data. We assess and compare the performances of existing measures of agreement and association as well as a newly developed model-based measure of agreement to three large-scale clinical screening studies involving many raters’ ordinal classifications. We also conduct a simulation study to demonstrate the key properties of the summary measures. The assessment of agreement and association varied according to the choice of summary measure. Some measures were influenced by the underlying prevalence of disease and raters’ marginal distributions and/or were limited in use to balanced data sets where every rater classifies every subject. Our simulation study indicated that popular measures of agreement and association are prone to underlying disease prevalence. Model-based measures provide a flexible approach for calculating agreement and association and are robust to missing and unbalanced data as well as the underlying disease prevalence.

1. Introduction

Studies of agreement between expert raters are often conducted to assess the reliability of diagnostic and screening tests. Many screening and diagnostic test results are classified using an ordered categorical scale. For example, radiologists use the BI-RADS (Breast Imaging Reporting and Data System) scale to classify breast density from mammography screenings. BI-RADS is an ordinal classification scale with four categories ranging from A (almost entirely fatty) to D (extremely dense) to reflect increasing breast density [1]. Measures of agreement and association provide useful summaries for ordinal classifications. Measures of agreement focus on assessing the levels of exact concordance (i.e. where raters assign the exact same category to a subject’s test result), while measures of association also take into account the degrees of disagreement among raters’ classifications. For example, the level of disagreement is higher between two raters who each independently classify the same mammogram into categories A and D respectively, compared to the level of disagreement between two raters who each independently classify the same mammogram into categories A and B. Measures of association are sometimes considered as weighted measures of agreement in which higher weight (“credit”) is assigned to pairs of raters’ classifications that are more similar.

Cohen’s kappa statistic is a popular summary measure of agreement, but is limited to assessing agreement between two raters’ ordinal classifications [2,3]. However, various extensions of Cohen’s kappa that provide summary measures of agreement (and association) among multiple raters have been developed. These include Fleiss’ kappa for multiple raters [4], the intra-rater correlation coefficient, also known as the ICC [5], and weighted (and unweighted) kappas by Meilke et al. [6] Despite the availability of these extended measures, many agreement studies report the average or the range of pairwise Cohen’s kappas and weighted kappas when assessing the agreement and association respectively among more than two raters [7–12]. This can lead to complexities in interpretation and is infeasible in studies with a large number of raters.

A model-based approach can flexibly accommodate ordinal classifications of many expert raters and can provide a comprehensive summary agreement measure. Results can be extended to the general populations of raters and subjects. Nelson and Edwards [13,14] recently proposed a population-based measures of agreement and association for ordinal classification. Their model-based approach is based on the observed agreement between raters (where raters assign a subject’s test result to the same category) from a generalized linear mixed model (GLMM), while minimizing the impact of chance agreement (where raters assign the same category to a subject’s test result due to pure coincidence). Their approach produces easily interpretable single summary measures of agreement and association over all raters’ classifications, and unbalanced and missing data can be flexibly accommodated [14]. Furthermore, Cohen’s kappa and its variants have several vulnerabilities including susceptibility to extreme prevalence of the underlying disease rate (where prevalence is defined as the probability of being classified into each disease category) while the model-based approach is robust to these effects. Although restricted to small number of raters, other model-based approaches based on the generalized estimating equations (GEE) also provide summary measures of agreement and association [15]. In contrast, Nelson’s model-based approach is applicable to small (at least three) and large numbers of raters.

In this paper, we demonstrate how various agreement and association measures can be applied in three real large-scale screening test studies, each based on incorporating many raters’ ordinal classifications. Specifically, we apply average pairwise weighted and unweighted Cohen’s kappas, Fleiss’ kappa, ICC, Mielke’s weighted and unweighted kappa for multiple raters, and Nelson and Edwards’ model-based measures of agreement and association to three clinical screening test studies of breast cancer, uterine cancer and skin disease. The rest of the paper is constructed as follows: In section 2, we provide a brief description of some of the existing summary measures of agreement and association. In section 3, we demonstrate how these summary measures can be implemented in three screening test studies and present results from a simulation study. Finally, in section 4, we provide a discussion and recommendations.

2. Methods

2.1. Measures of agreement

The conventional interpretation of an agreement or association measure according to Landis and Koch [16] is as follows; < 0.00 indicate poor agreement, 0.00–0.20 indicate slight agreement, 0.21–0.40 indicate fair agreement, 0.41–0.60 indicate moderate agreement, 0.61–0.80 indicate substantial agreement, and 0.81–1.00 indicate almost perfect agreement.

2.1.1. Cohen’s kappa

Cohen’s kappa [2] is a popular measure of agreement between a pair of raters classifying I subjects into C categories adjusting for chance agreement, i.e. the chance probability that two raters independently classify subjects into the same category by pure coincidence [2]. The general formula of Cohen’s kappa is

$$\kappa =\frac{p_0-p_c}{1-p_c}$$

where p₀ is the proportion of observed agreement between the two raters and p_c is the proportion of chance agreement. The statistic ranges from −1 to 1 where 1 indicates complete agreement, −1 indicates complete disagreement, and 0 indicates agreement that is no better than chance. Cohen’s kappa is easy to compute and is widely used in agreement studies. However, it has been noted to be vulnerable to extreme prevalence of the underlying disease rate and the marginal distribution of raters (raters’ tendencies to classify the test results in a certain way) [17]. Because Cohen’s kappa is designed for measuring the agreement between two raters, many authors report the average or the range of the $\left(\begin{array}{c}J\\ 2\end{array}\right)$ kappa statistics computed from each possible pair of raters when a study involves multiple raters (J > 2) [7–12]. However, such range or average of many kappa statistics can be complicated and difficult to interpret, and is impractical in studies with a large number of raters, say J ≥5. In R [28], the psych package can be used to compute Cohen’s kappa and in SAS (SAS Institute Inc. Cary, NC), the FREQ procedure has options to compute Cohen’s kappa.

2.1.2. Fleiss’ kappa

Fleiss extended Scott’s pi statistic [18] to account for the case of more than two raters classifying multiple subjects using a scale with more than two categories [4]. Fleiss’ kappa is also a function of observed agreement corrected for chance agreement. Let I be the total number of subjects, K be the number of ratings for each subject and C be the number of categories in the ordinal classification scale. Also, let n_ic be the number of raters who assign the ith subject to the cth category. Then, Fleiss’ kappa is defined as

$${\kappa }_F=\frac{{\sum }_{i=1}^I{\sum }_{c=1}^C{n}_{ic}^2-IK[1+(n-1){\sum }_{c=1}^C{p}_c^2]}{IK(K-1)(1-{\sum }_{c=1}^C{p}_c^2)}$$

where $p_c=\frac{1}{IK}{\sum }_{i=1}^I{n}_{ic}$.

A formula to calculate the corresponding variance of Fleiss’ kappa is also available [19]. Due to a multiplicative factor of the sample sizes of raters and subjects on the denominator of this formula, the variance yields disproportionately small values, consequently producing an extremely narrow 95% confidence interval for Fleiss’ kappa, and increasingly so for large sample sizes of raters and subjects. Fleiss’ kappa ranges from 0 to 1 where 0 indicates no agreement and 1 indicates perfect agreement. Fleiss’ kappa is straightforward to compute but is limited to balanced data where each subject’s test result is classified by the same number of raters [20], which can be problematic in many real life studies where the ratings of some subjects test results are missing. Similar to Cohen’s kappa, Fleiss’ kappa is also vulnerable to extreme prevalence of the underlying disease rate. To compute Fleiss’ kappa in R, the irr package can be used and in SAS, there is a user-written macro, MKAPPA [21].

2.1.3. Model-based kappa statistic

The model-based kappa statistic, which is based on a generalized linear mixed model (GLMM) was recently introduced by Nelson and Edwards [13]. Suppose, we have a sample of J (j = 1, …, J) raters each independently classifying a sample of I (i = 1, …, I) subjects using an ordered classification scale with C (c = 1, …, C) categories. We denote the rating on the ith subject’s test result classified by the jth rater into the cth category as Y_ij = c. An ordinal GLMM with a probit link and a crossed random effect structure can be used to model the cumulative probability that a subject’s test result, Y_ij, is classified as category c or lower. Then the probability that a subject’s test result is classified as category c can be computed by

$$P\left(Y_{ij}=c|u_i,v_j\right)=\mathrm{\Phi }\left({\alpha }_c-(u_i+v_j)\right)-\mathrm{\Phi }\left({\alpha }_{c-1}-(u_i+v_j)\right)$$ (1)

where Φ is the cumulative distribution function of the standard normal distribution, α₀, …, α_c are the thresholds that estimate the cutoffs between the C categories (with α₀ = −∞ and α_C = +∞), and u_i and v_j are random effects for each subject and each rater respectively. The subject random effect, u_i, represents the heterogeneity of the subjects’ test results and is distributed normally with mean 0 and variance ${\sigma }_u^2$. The rater random effect, v_j represents the heterogeneity of the raters’ tendencies to classify test results and is also distributed normally with mean 0 and variance ${\sigma }_v^2$. A large positive value of u_i indicates a test result that is more likely to be classified into a higher disease category. A large positive value of v_j indicate a rater who liberally classifies subjects into higher disease categories.

Due to recent advances in statistical software, fitting an ordinal GLMM with a probit link and crossed random effects has become relatively straightforward. We used the ordinal package in R, in particular, the clmm function, which is one of the software packages that can be used to fit such forms of GLMMs efficiently and quickly [22]. Once the model is fitted, we can use the parameter estimates obtained for (α₀, …, α_C, ${\sigma }_u^2,{\sigma }_v^2$) to compute the model-based kappa statistic (κ_m) as follows

$${\kappa }_m=\left(\frac{C}{C-1}\right)\times \underset{-\infty }{\overset{+\infty }{\int }}\left\{\sum _{c=1}^C{\left[\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c-1}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]}^2\right\}\varphi (z)dz-\frac{1}{C-1}$$

This model-based kappa statistic appropriately corrects for chance agreement and takes values between 0 and 1, interpreted in a similar way to Fleiss’ kappa where 0 indicates agreement no better than chance and 1 indicates perfect agreement among the raters. The variance, calculated using the delta method, is

$$\begin{gathered} \mathit{var}({\widehat{\kappa }}_m)=\left(\frac{C}{C-1}\right)\times \mathit{var}(\widehat{\rho }) \\ \times \{\underset{-\infty }{\overset{+\infty }{\int }}\sum _{c=1}^{C}2\times \left[\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c}{C}-z\sqrt{\rho }\right)}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c-1}{C}-z\sqrt{\rho }\right)}{\sqrt{1-\rho }}\right)\right] \\ \times [\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c}{C}-z\sqrt{\rho }\right)}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c}{C}\right)-z\sqrt{\rho }}{2{(1-\rho )}^{\frac{3}{2}}}\right) \\ -\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c-1}{C}-z\sqrt{\rho }\right)}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\mathrm{\Phi }}^{-1}\left(\frac{c-1}{C}\right)-z\sqrt{\rho }}{2{(1-\rho )}^{\frac{3}{2}}}\right)]\varphi (z){dz\}}^2 \end{gathered}$$

where $\rho ={\sigma }_u^2/({\sigma }_u^2+{\sigma }_v^2+1)$ and $\mathit{var}(\widehat{\rho })=\frac{2{\left({\sigma }_u^2\right)}^2{\left({\sigma }_v^2+1\right)}^2}{I{\left({\sigma }_u^2+{\sigma }_v^2+1\right)}^2}+\frac{2{\left({\sigma }_v^2\right)}^2{\left({\sigma }_u^2\right)}^2}{J{\left({\sigma }_u^2+{\sigma }_v^2+1\right)}^2}$. Further details regarding κ_m and var(κ_m) can be found in Nelson and Edwards [13].

There are several advantages in using a model-based measure of agreement over simpler summary statistics. One is the ability to accommodate missing or unbalanced data, a common occurrence in large-scale studies when not every subject is rated by each rater [23]. Another is the option to include covariates in the GLMM to evaluate the effects of raters’ or subjects’ characteristics (such as rater experience or subject age) on agreement and to calculate summary measures of subgroups of raters and subjects [24]. Currently, three packages in R (ordinal, lme4, and MCMCglmm) can be used to fit ordinal GLMMs with crossed random effects. In SAS, the GLIMMIX procedure can be used for classification scales with two categories only. We provide the R code to compute the model-based measures of agreement and association using the estimates from the GLMM as supplementary material.

2.2. Measures of association

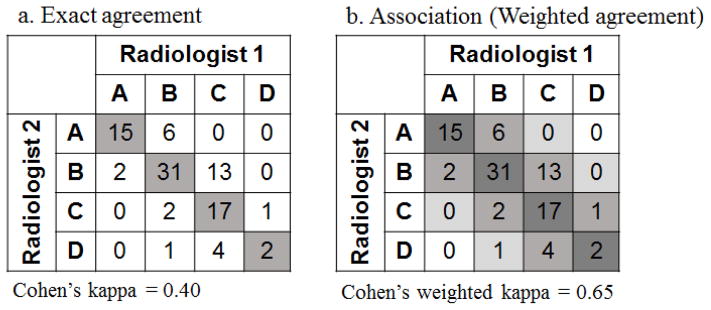
For ordinal classifications, measures of association are often preferred to, or used in conjunction with measures of (exact) agreement. Association measures take into consideration the level of disagreement among the raters with stronger credit given to pairs of raters’ classifications which concur more closely. Figure 1 depicts the difference between agreement and association. In measuring agreement, only exact concordance in classifications by raters is considered (any discordant classifications receive no “credit”) [Figure 1a]. In measuring association, exact concordance between raters receives highest “credit” while classifications that differ by one scale receive the second highest “credit and classification that differ by two scales receive the third highest “credit”, etc. [Figure 1b] As a result, the association measure is typically larger than the agreement measure. In the example depicted in Figure 1, the Cohen’s kappa for agreement between the two raters is 0.40 while the Cohen’s weighted kappa for association is 0.65.

Figure 1.

Differences in weight (“credit”) assigned when measuring agreement vs. association

2.2.1. Cohen’s weighted kappa

In 1968, Cohen introduced a weighted kappa, which is the proportion of weighted observed agreement corrected by chance agreement [25]. The general form of the statistic is similar to the unweighted version:

$$\kappa =\frac{p_{0w}-p_{cw}}{1-p_{cw}}$$

where p_0w is now the weighted proportion of observed agreement and p_cw is the weighted proportion of chance agreement. Typically, quadratic weights (also referred to as squared error weights) or linear weights (also referred to as absolute error weights) are used with lower “credit” assigned to pairs of ratings in high discordance [26]. The quadratic weights and linear weights take the form w_rs = 1−(r−s)²/(C−1)² and w_rs = 1−|r−s|/(C−1) respectively where C is the total number of categories and r and s are the category levels (r,s = 1, …, C). Many authors compute the average pairwise weighted kappas when more than two raters are involved in a study. Cohen’s weighted kappa can also be computed using the psych package in R and the FREQ procedure in SAS.

2.2.2. Intraclass correlation coefficient (ICC)

The intraclass correlation coefficient (ICC) is a measure of association that can accommodate many raters’ ordinal classification derived from the components of an analysis of variance (ANOVA) model. There are several versions of the ICC depending on the design and the purpose of the study [5]. In this paper, we focus on the version which assumes that each subject is classified by the same set of raters who were randomly selected from a larger pool of raters (Case 2 in Shrout and Fleiss [5]). The ICC based upon this assumption requires fitting a two-way ANOVA model where raters are considered as random:

$$Y_{ij}=\mu +a_i+b_j+{(ab)}_{ij}+e_{ij}$$

where Y_ij is the rating given to subject i (i = 1, …, I) by rater j (j = 1, …, J), μ is the overall population mean of the ratings, a_i is the difference between μ and the mean ratings of the ith subject, b_j is the difference between μ and the mean ratings of the jth rater, (ab)_ij is the difference between the jth rater’s typical ratings and his or her rating given on the ith subject, and e_ij is the random error of the jth rater’s rating on the ith subject. This model produces the following three sources of variation; between subjects sum of squares (df = I – 1), between raters sum of squares (df = J – 1) and an error sum of squares (df = (I – 1)(J – 1)). The mean squares used to compute the ICC are; mean squared sum of squares between subjects (MSB), mean squared sum of squares between raters (MSJ) and mean squared error (MSE). The ICC is given by

$$\mathit{ICC}=\frac{\mathit{MSB}-\mathit{MSE}}{\mathit{MSB}+(J-1)\mathit{MSE}+(J/I)(\mathit{MSJ}-\mathit{MSE})}$$

The ICC ranges from 0 to 1Koo and Li provide an interpretation for ICC as the following: <0.5 indicate poor reliability, 0.5–0.75 indicate moderate reliability, 0.75–0.9 indicate good reliability, and >0.90 indicate excellent reliability [27]. For more detail, see Shrout and Fleiss [5]. The ICC has been demonstrated to be equivalent to Cohen’s weighted kappa with quadratic weights for the case of two raters [3,26,28]. The ICC can be easily calculated using most statistical software packages including the irr package in R and the official INTRACC macro in SAS.

2.2.3. Weighted kappa by Mielke and Berry

Mielke et al. published a weighted kappa statistic for multiple judges using an ordinal classification scale [6]. Their method relies on constructing a contingency table with J dimensions, where J is the number of independent raters. Suppose we have a sample of J = 3 raters (rater X, rater Y, and rater Z) each independently classifying subjects into an ordered scale with C=4 categories. We can construct a 3-dimensional contingency table where each cell frequency, n_ijk, corresponds to the number of subjects that were classified as the dimensional position by the first, second, and third rater. The first step in computing the weighted kappa is to sum up all the cell frequencies in this contingency table, denoted by N. The next step is to compute the marginal frequency for each row, column and slice of the contingency table. Let X_i, Y_j, and Z_k denote the marginal frequency of the ith row, jth column and kth slice respectively. Then, the weighted kappa introduced by Mielke is given by

$${\kappa }_w=1-\frac{N^2{\sum }_{i=1}^C{\sum }_{j=1}^C{\sum }_{k=1}^C{w}_{\mathit{ijk}}{n}_{\mathit{ijk}}}{{\sum }_{i=1}^C{\sum }_{j=1}^C{\sum }_{k=1}^C{w}_{\mathit{ijk}}{X}_i{Y}_j{Z}_k}$$

where w_ijk is the linear or quadratic weight assigned to each cell for i = 1, …, C, j = 1, …, C, k = 1, …, C, with w_ijk = |i −j| + |i−k| + |j−k| for linear weights and w_ijk = (i −j)² + (i−k)² + (j−k)² for quadratic weights. By assigning binary weights (w_ijk = 0 if i = j = k and 1 otherwise), the weighted kappa reduces to an unweighted version for measures of agreement.

Mielke et al. also demonstrated an approach to compute the exact variance of the weighted kappa statistic, which is computationally very intensive [29]. The above formula can be extended to cases with J > 3 raters. The method is conceptually simple and does not require fitting a complicated statistical model. However, when J is large (J > 4 or 5), the computation of Mielke et al.’s weighted kappa becomes unwieldy because the number of dimensions of the contingency table increases exponentially with J (dimension = C^J).

2.2.4. Model-based kappa statistic for association

Nelson and Edwards also introduced a model-based measure of association by incorporating weights (quadratic or linear) that place more emphasis on categories that are closer than categories that are far apart. The formula for the weighted kappa, κ_ma, and its variance var(κ_ma) can be found in Appendix I and full details can be found in Nelson and Edwards [14]. R code is available as supplementary material to efficiently and quickly calculate this measure of association.

3. Results

We now demonstrate the use of these existing summary measures to assess the strength of agreement and association between many raters in three diverse medical studies. We used the psych package in R to compute Cohen’s kappa and the irr package in R to compute Fleiss’ kappa and the ICC [30]. For the Nelson approaches, we used the clmm function in the ordinal package in R to obtain the parameter estimates for the GLMM, then used our own R script to compute the measures of agreement and association. The R script for fitting a sample of the data set from one of the examples (Example Three, Holmquist) is provided as supplementary material online. We show

3.1. Example One (AIM)

The Assessing and Improving Mammogram (AIM) study is a large-scale cancer screening study conducted by the Breast Cancer Surveillance Consortium (BCSC) where a sample of 130 mammograms was obtained from six breast imaging registries in the United States [31]. A total of 119 radiologists each classified 109 mammograms from the sample of 130 mammograms into a four-level BI-RADS density assessment scale [31]. The BI-RADS density scale classifies breast density into four ordinal groups ranging from least to most dense:

1. Almost entirely fatty

2. Scattered fibroglandular densities

3. Heterogeneously dense

4. Extremely dense

Mammographic breast density is an important risk factor for breast cancer. Multiple studies have shown that women with dense breasts have at least a slight increased risk of developing breast cancer [9–12]. Furthermore, mammographic breast density is linked to decreased mammographic sensitivity because small malignant lesions are difficult to detect in subjects with high breast density [8,10].

Various agreement measures applied to the AIM study are presented in Table 1, including the average pairwise Cohen’s kappa, Fleiss’ kappa, Nelson and Edwards’ (abbreviated as Nelson’s in this section) model-based measure for agreement, and average pairwise weighted Cohen’s kappa, the ICC, and Nelson’s model-based measure for association. Due to the large number of raters (J = 119), we were unable to apply Mielke et al.’s weighted (and unweighted) kappa to this data set. The average pairwise Cohen’s kappa and Fleiss’ kappa yielded similar agreement measures (0.438 and 0.434 respectively) [Table 1]. Based on these two measures, there was moderate agreement among raters [16]. The 95% confidence interval (CI) for Fleiss’ kappa was extremely narrow due to the large sample of subjects and raters for this data set (I = 109, J = 119) which leads to a disproportionately small standard error term for Fleiss’ kappa. Nelson’s model-based approach produced a kappa estimate that was slightly lower than the average pairwise Cohen’s kappa and Fleiss’ kappa indicating slightly decreased agreement among raters (0.388).

Table 1.

Agreement and association measures for the AIM data set

Measure	Method	Estimate (95% CI)
Agreement	Average pairwise Cohen*	0.438 (0.309, 0.567)
	Fleiss*	0.434 (0.432, 0.435)
	Model-based Kappa	0.388 (0.350, 0.427)
Association	Average pairwise weighted Cohen*	0.726 (0.641, 0.811)
	ICC*	0.721 (0.661, 0.783)
	Model-based Weighted Kappa	0.587 (0.543, 0.631)

^*Based on a subset of 84 subjects who were classified by all 119 raters.

All of the association measures were larger than any of the agreement measures which usually occurs because credit is also assigned for discordant pairs of classifications. Estimates of the average pairwise weighted Cohen’s kappa and the ICC both indicated a substantial association [16] between the radiologists (0.726 and 0.721 respectively). Nelson’s model-based approach yielded a much smaller measure of association (0.587) compared to the other two approaches. In this data set, not all subjects were rated by J = 119 raters. Therefore, we had to use a subset of 84 subjects who were classified by all 119 raters (66.2% of all subjects) in order to compute Cohen’s kappa, Fleiss’ kappa and the ICC. Nelson’s model-based measures of agreement and association when applied to this subset of subjects were identical to the second decimal place to their corresponding measures when applied to the entire data set. The probability of disease for the AIM study was moderately low with 15%, 43%, 31% and 11% of the classifications falling in the four ordinal categories of increasing breast density.

3.2. Example Two (Gonin and Lipsitz)

Faust et al. describe a dermatology index of disease severity (DIDS) used to classify the severity of inflammatory skin disease [32]. DIDS is composed of five ordinal categories with increasing disease severity:

1. No evidence of clinical disease

2. Limited disease

3. Mild disease

4. Moderate disease

5. Severe disease

Twelve raters (seven dermatologists and five staff including residents and nurses) were recruited to assess 38 subjects. An interesting feature of this study is that each rater classified only a small subset of the 38 subjects inducing missing/incomplete data. The resulting data set, presented in Gonin et al. [15] in its entirety, is highly sparse. Cohen’s kappa, Fleiss’ kappa, the ICC and Mielke’s method all require data to be balanced (each subject is rated by the same number of raters), thus could not be used to assess agreement and association for this study. Motivated by this data set, Gonin et al. developed a model-based weighted kappa statistic based on the generalized estimating equations which considers each rater as a “fixed” effect and is thus limited to a small to moderate number of raters [15]. The measure of association reported in their paper, 0.868 (95% CI = 0.751–0.932), is comparable to the result obtained using Nelson’s model-based approach for measure of association, 0.878 (0.841, 0.915) [Table 2] reflecting almost perfect agreement and association [16] between raters’ classifications of the subjects’ skin condition using the DIDS scale. This is an example where only model-based measures of agreement and association can be applied due to the highly unbalanced nature of the data set. The probability of a subject’s test result classified into the more severe disease categories were high with 11%, 14%, 9%, 34% and 33% of the classifications falling in the five ordinal categories of increasing severity of inflammatory skin disease.

Table 2.

Agreement and association measures on Gonin data set

Measure	Method	Estimate (95% CI)
Agreement	Model-based Kappa	0.746 (0.699, 0.793)
Association	Gonin method	0.868 (0.751, 0.932)
	Model-based Weighted Kappa	0.878 (0.841, 0.915)

3.3. Example Three (Holmquist)

In an earlier study, Holmquist et al. investigated the variability in agreement of the classification of carcinoma in situ of the uterine cervix [33]. Seven pathologists each independently classified 118 histological slides into one of five ordinal categories of increasing disease severity:

1. Negative

2. Atypical squamous hyperplasia

3. Carcinoma in situ

4. Squamous carcinoma with early stromal invasion

5. Invasive carcinoma

This data set is regarded as a classic example to evaluate agreement between multiple raters each classifying a sample of subjects’ test results according to an ordinal classification scale [34]. It serves as an ideal data set because each of the 118 subjects’ histological slides is rated by each of the seven raters, providing a balanced (or complete) data with a relatively small number of raters (J = 7). We were able to apply all methods to this optimal data set (subset shown in Appendix II). All agreement measures ranged between 0.127 and 0.366 indicating slight to fair agreement [16]between the seven pathologists. [Table 3] Again, average pairwise Cohen and Fleiss’ kappa produced comparable estimates (0.366 and 0.354, respectively). Mielke’s method produced a much lower estimate of agreement (0.127) and Nelson’s model-based approach produced an estimate (0.266) that was lower than Cohen’s and Fleiss’ kappas but higher than Mielke’s indicating poor agreement among the seven pathologists. The weighted Cohen’s kappa, ICC and weighted Mielke’s method all yielded comparable measures of association (0.657, 0.644, and 0.647 respectively), indicating substantial association [16] between the seven pathologists, while Nelson’s model-based method yielded a lower estimate (0.509), a similar pattern observed in Example One. In their paper, Mielke et al. provided an example of calculating the exact variance for the case of three raters [29]. However, the formula was too unwieldly to extend to the case of seven raters and hence we omit the 95% CI for Mielke’s methods. The probability of a subject’s test result classified into a higher diseased category in the Holmquist study was small (i.e. 28%, 28%, 32%, 8%, and 4% of the classifications in the five ordinal categories of increasing disease severity), reflecting a low prevalence of cervical cancer in this sample of subjects.

Table 3.

Agreement and association measures for the Holmquist data set

Measure	Method	Estimate (95% CI)
Agreement	Average pairwise Cohen	0.366 (0.256, 0.476)
	Fleiss	0.354 (0.331, 0.378)
	Unweighted Mielke	0.127
	Model-based Kappa	0.266 (0.204, 0.328)
Association	Average pairwise weighted Cohen	0.657 (0.547, 0.767)
	ICC	0.644 (0.575, 0.712)
	Weighted Mielke	0.647
	Model-based Weighted Kappa	0.509 (0.421, 0.598)

In the following section, we describe a simulation study aimed to explain the varying agreement and association measures observed in the three studies.

3.4. Simulation study

3.4.1 Motivation

To better understand why the different existing summary measures of agreement and association vary across approaches, we conducted a simulation study to explore the performance of each approach. We randomly generated 1000 data sets for each simulation scenario. For each simulated data set, we generated random effects for 250 subject 100 raters from N(0, 5) and N(0, 1) distributions respectively. Following Equation (1), we used the cumulative distribution function of the standard normal to generate the probability of each subject being assigned to category c for c=1, …, 5. Using these probabilities, the classification of each subject’s test result was randomly assigned into one of the c=1, …, 5 categories. We simulated seven scenarios where each scenario varied by the underlying prevalence of the disease ranging from low prevalence of disease with 80% of subjects in category 1 and 5% in category 5, to high prevalence of disease with 5% of subjects in category 1 and 80% of subjects in category 5. The prevalence for each of the seven scenarios are listed in Table 4. The following measures of agreement and association were calculated for each simulated data set: the average pairwise Cohen’s kappa, Fleiss’ kappa and Nelson’s model-based measure for agreement, and the average pairwise Cohen’s weighted kappa (with quadratic weights), the ICC, and Nelson’s model-based measure (with quadratic weights) for association. Mielke’s method was not applied due to the large number of raters (J=100).

Table 4.

True prevalence (%) used in simulation study

Probability of disease	Category (% of subjects in each category)
	1	2	3	4	5
Low ↓	80	5	5	5	5
	60	10	10	10	10
	40	15	15	15	15
Medium ↓	20	20	20	20	20
	15	15	15	15	40
	10	10	10	10	60
High	5	5	5	5	80

3.4.2. Simulation results

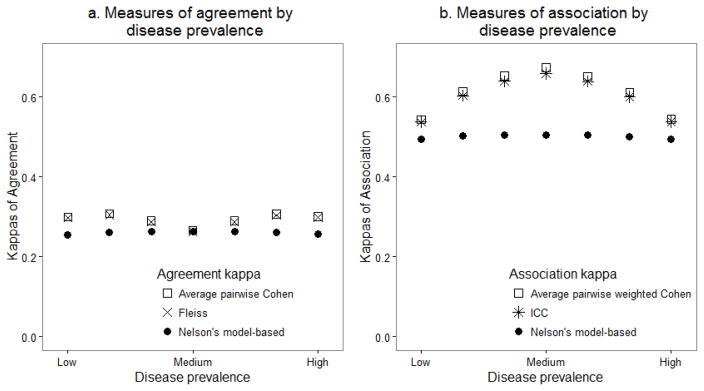
Simulation results are presented in Figure 2, where Figures 2a and 2b depict the mean measures of agreement and association respectively based on the 1000 simulated data sets for each approach.

Figure 2.

Average summary measures over 1000 simulated data sets by varying prevalence of underlying disease

Figure 2a depicts the mean measures of agreement over the 1000 simulated data sets from average Cohen’s kappa, Fleiss’ kappa and Nelson’s model-based approach as the prevalence of disease increases from low (fewer subjects classified with disease) to high (many subjects classified with disease). Nelson’s model-based approach remained unchanged and was robust to varying disease prevalence. The other two measures of agreement (Cohen’s kappa and Fleiss’ kappa) overestimated the agreement for more extreme levels of prevalence compared to Nelson’s model-based approach [Figure 2a]. The three agreement measures were most similar in the scenario with medium disease prevalence where the probability of disease was equally distributed across the five classified categories.

Figure 2b depicts the mean measures of association over the 1000 simulated data sets from Cohen’s kappa, ICC and Nelson’s model-based approach as the prevalence of disease increases from low to high. Nelson’s model-based measure for association was also unaffected by the changes in level of disease prevalence whereas the average Cohen’s weighted kappa and the ICC were impacted by the underlying disease prevalence and generally overestimated the association regardless of the prevalence level compared to Nelson’s approach. [Figure 2b] However, the three association measures were most similar when the prevalence was extreme (both highest and lowest prevalence). We also computed the coverage probabilities for Nelson et al’s model-based measure of association based upon the simulation study. The results are presented in Appendix III. We observe that when disease prevalence is extreme (low or high), coverage probabilities for Nelson’s model-based method were below the expected 95%. When the disease prevalence is even across the categories, the coverage probabilities were close to 95%. The coverage probabilities for the Cohen’s kappas and Fleiss’ kappa could not be computed because these are usually considered to be strictly data-driven statistics for assessing agreement and association [35]. To provide some insight of the performance of Cohen’s kappas and Fleiss’ kappa, we present the distributions of the 1,000 simulated agreement and association values in the Supplementary material online.

3.4.3. Conclusions based on the simulation study

The simulation study provided valuable insight into possible reasons for the range of values of the agreement and association measures across the different approaches in each of the three studies described in Sections 3.1–3.3. In a manner consistent to the simulation study results, the average Cohen’s kappa and Fleiss’ kappa applied to Holmquist data were larger than that of Nelson model-based measure of agreement. This can be attributed to the low prevalence of disease in the Holmquist study [Table 3]. Although not as extreme as one of our simulation scenarios, the Holmquist data set indicated a low prevalence with 28%, 28%, 32%, 8%, and 4% of the classifications in the five ordinal categories of increasing disease severity.

The probability of disease for the AIM study was also moderately low with 15%, 43%, 31% and 11% of the classifications in the four ordinal categories of increasing breast density. Based on the results from the simulation study, the low disease prevalence in the AIM study possibly explains why the model-based approaches yielded lower measures of agreement and association compared to the other approaches [Table 1].

4. Discussion

Strong agreement and association between expert raters’ subjective classifications of test results are essential components of effective diagnostic and screening tests. However, many studies report variability in agreement and association [7–9,11]. In this paper we demonstrate how various summary measures of agreement and association can (or cannot) be applied to three real large-scale screening test studies where an ordinal classification scale is used by expert raters to subjectively classify each subject’s disease condition. In each study we examined, there were noticeable discrepancies between the measures of agreement and association. An important limitation of the more commonly used measures of agreement and association (Cohen’s kappa, Fleiss’ kappa, and the ICC) is that they cannot be applied to unbalanced data sets where not all raters classify each subject. This was most apparent in the Gonin data set where no two raters classified the same set of subjects resulting in extremely sparse data. For the AIM data set, we were able to apply the three aforementioned methods on a subset of the subjects that were classified by the same number of raters. On the other hand, Nelson and Edwards’ model-based agreement is robust to missing and unbalanced data and could be implemented in all three studies. Another advantage of Nelson and Edwards’ model-based approach is the option to include covariates in the GLMM. Although not demonstrated in this paper, the model-based approach can be used to compute the agreement (and association) among a subset of raters or a subset of subjects by including a rater- or subject-specific covariate in the GLMM. For example, by including a covariate that represents the experience level of the raters, we can compute the agreement (and association) among experienced raters and among inexperienced raters. See Nelson and Edwards for more details [14].

Mielke’s unweighted and weighted kappas were not suitable for large-scale studies involving many raters because the computation becomes too unwieldly with a large number of raters. For small-scale studies with five or fewer raters, Mielke’s method provides a reasonable measure of association, though, as an extension of Cohen’s kappa, is also prone to similar issues including prevalence and missing data.

We also showed, through simulation, that some of the more commonly used measures of agreement and association are susceptible to the disease prevalence level of the underlying disease. Under the simulation scenario with medium prevalence, average weighted Cohen’s kappa and the ICC overestimated the strength of association. Both Cohen’s kappa and Fleiss’ kappa have previously been noted to have issues such as the susceptibility to the level of prevalence [17]. Despite this, Cohen’s kappa remains a popular choice for assessing agreement, perhaps because it can easily be implemented due to the availability in most statistical software such as SAS and R. We observed through our simulation study that ICC was also susceptible to the prevalence level which is not surprising, given its equivalence to the weighted Cohen’s kappa for two raters. We also observed that Nelson and Edwards’ model-based approach was the most robust to the underlying disease prevalence, and generally provided reasonable 95% coverage probablities with some decreased coverage probability observed in Nelson and Edwards’ model-based measures of agreement and association when disease prevalence is extreme (Appendix III). The results from our simulation study demonstrated that some of the discrepancies observed between the various measures of agreement applied to the three examples may be attributed to the underlying disease prevalence.

Existing summary measures, Cohen’s kappa, Fleiss’ kappa and ICC, can easily be implemented in existing software packages including R and SAS. Nelson and Edwards’ model-based summary measure can quickly be calculated using R. In the supplementary materials, we provide the R code to compute the model-based agreement and association measures for the Holmquist data set (Example Three). We anticipate that users will be able to apply the program to their own data set.

We recommend that researchers estimate the disease prevalence in their study by calculating the proportion of all test results assigned to each classification category. For agreement, if the test results are fairly evenly distributed over the classification categories, then each approach (Cohen’s kappa, Fleiss’ kappa, ICC, and Nelson and Edwards’ model-based summary measure) produces similar summary measures. If the subjects’ test results are unequally distributed across the ordinal categories, resulting in high or low disease prevalence, we recommend Nelson and Edwards’ model-based approach to measure agreement. When measuring association in large-scale studies, we would generally recommend the use of a model-based summary measure such as that developed by Nelson and Edwards to appropriately account for disease prevalence effects.

List of abbreviations

BI-RADS

Breast Imaging Reporting and Data System

ICC

Intra-class Correlation Coefficient

GLMM

Generalized Linear Mixed Model

GEE

Generalized Estimating Equations

ANOVA

Analysis of Variance

AIM

Assessing and Improving Mammogram

DIDS

Dermatology Index of Disease Severity

Appendix I

Model-based kappa for association and its variance

As with agreement, the parameter estimates obtained from fitting the model

$$P(Y_{ij}\le c|u_i,v_j)=\mathrm{\Phi }({\alpha }_c-\left(u_i+v_j\right))$$

are (α₀, …, α_C, ${\sigma }_u^2,{\sigma }_v^2$).

Let $\rho ={\sigma }_u^2/({\sigma }_u^2+{\sigma }_v^2+1)$ and ${\alpha }_c^{\ast }={\alpha }_c/({\sigma }_u^2+{\sigma }_v^2+1)$ with ${\alpha }_0^{\ast }=-\infty$ and ${\alpha }_C^{\ast }=+\infty$. Also, let ${\alpha }_{min,1}^{\ast },\dots ,{\alpha }_{min,C}^{\ast }$ be the values that minimize chance association. For pairs of classifications in the rth and sth categories respectively (r, s = 1, …, C) by two independent raters, we can define the quadratic weight as w_rs = 1−(r−s)²/(C−1)² and the linear weight as w_rs = 1−|r−s|/(C−1). Then,

$$\begin{gathered} {\kappa }_{ma}=2\times \underset{-\infty }{\overset{+\infty }{\int }}\sum _{r=1}^C\sum _{s=1}^C{w}_{rs}\left[\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{r}}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{r}-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right] \\ \times \left[\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{s}}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{s}-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]\varphi (z)dz-1,0\le {\kappa }_{ma}\le 1 \end{gathered}$$

Where Φ and ϕ are the cumulative distribution function and the probability distribution function of the standard normal respectively.

$$\begin{gathered} var({\widehat{\kappa }}_{ma})=4\times var(\widehat{\rho }) \\ \times \left[\underset{-\infty }{\overset{+\infty }{\int }}\sum _{r=1}^C\sum _{s=1}^C{w}_{rs}\right\{\left[\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{r}}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{r}-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right] \\ \times [\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{s}}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,\mathrm{s}}^{\ast }-z\sqrt{\rho }}{2{(1-\rho )}^{3/2}}\right) \\ -\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{s}-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,\mathrm{s}-1}^{\ast }-z\sqrt{\rho }}{2{(1-\rho )}^{3/2}}\right)] \\ +\left[\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{s}}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{s}-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right] \\ \times [\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{r}}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,\mathrm{r}}^{\ast }-z\sqrt{\rho }}{2{(1-\rho )}^{3/2}}\right) \\ -\mathrm{\Phi }\left(\frac{{\alpha }_{min,\mathrm{r}-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\alpha }_{min,\mathrm{r}-1}^{\ast }-z\sqrt{\rho }}{2{(1-\rho )}^{3/2}}\right)]\}\varphi (z){dz]}^2 \end{gathered}$$

where

$$var(\widehat{\rho })=\frac{2{({\sigma }_u^2)}^2{({\sigma }_v^2+1)}^2}{I{({\sigma }_u^2+{\sigma }_v^2+1)}^4}+\frac{2{({\sigma }_v^2)}^2{({\sigma }_u^2)}^2}{J{({\sigma }_u^2+{\sigma }_v^2+1)}^4}$$

R code to compute the association and its variance is available as supplementary materials.

Appendix II. Classifications of pathologists for Holmquist data set (118 subjects and 7 raters)

Subject	Rater
	A	B	C	D	E	F	G
1	4	3	4	2	3	3	3
2	1	1	1	1	1	1	1
3	3	3	3	3	3	3	3
4	4	3	3	4	3	3	3
5	3	3	3	3	3	3	3
6	2	1	2	1	1	1	1
7	1	1	1	1	2	1	1
8	3	3	2	3	2	2	3
…	…
118	2	3	1	1	2	1	2

Appendix III

Table 1A.

Simulation Estimates and Coverage Probability of Model-based Kappa Agreement

	Simulation Scenario A (Used in manuscript)		Simulation Scenario B (Additionally conducted)
	${\sigma }_u^2=5,{\sigma }_v^2=1$, True κm = 0.264		${\sigma }_u^2=1,{\sigma }_v^2=1$, True κm = 0.090
Prevalence of disease	Model-based Kappa Agreement Estimate	Coverage Probability	Model-based Kappa Agreement Estimate	Coverage Probability
Low ↓	0.256	0.831	0.090	0.933
	0.262	0.903	0.091	0.931
	0.264	0.929	0.091	0.943
Medium ↓	0.263	0.933	0.090	0.946
	0.262	0.896	0.090	0.929
	0.262	0.918	0.091	0.940
High	0.256	0.861	0.090	0.923

Table 1B.

Simulation Estimates and Coverage Probability of Model-based Kappa Agreement

	Simulation Scenario A (Used in manuscript)		Simulation Scenario B (Additionally conducted)
	${\sigma }_u^2=5,{\sigma }_v^2=1$, True κm = 0.506		${\sigma }_u^2=1,{\sigma }_v^2=1$, True κm = 0.216
Prevalence of disease	Model-based Kappa Association Estimate	Coverage Probability	Model-based Kappa Association Estimate	Coverage Probability
Low ↓	0.495	0.866	0.216	0.933
	0.503	0.937	0.218	0.930
	0.506	0.944	0.218	0.943
Medium ↓	0.505	0.952	0.217	0.945
	0.504	0.924	0.216	0.929
	0.504	0.936	0.218	0.939
High	0.496	0.892	0.216	0.920