A parallel adder coordinates mycobacterial cell cycle progression and cell size homeostasis in the context of asymmetric growth and organization

Summary

In model bacteria, such as E. coli and B. subtilis, regulation of cell cycle progression and cellular organization achieves consistency in cell size, replication dynamics, and chromosome positioning [1–3]. Mycobacteria elongate and divide asymmetrically, giving rise to significant variation in cell size and elongation rate among closely related cells [4, 5]. Given the physical asymmetry of mycobacteria, the models that describe coordination of cellular organization and cell cycle progression in model bacteria are not directly translatable [1, 2, 6–8]. Here we used time-lapse microscopy and fluorescent reporters of DNA replication and chromosome positioning to examine the coordination of growth, division, and chromosome dynamics at a single-cell level in Mycobacterium smegmatis (M. smegmatis) and Mycobacterium bovis Bacillus Calmette–Guérin (BCG). By analyzing chromosome and replisome localization, we demonstrated that chromosome positioning is asymmetric and proportional to cell size. Furthermore, we found that cellular asymmetry is maintained throughout the cell cycle and is not established at division. Using measurements and stochastic modeling of mycobacterial cell size and cycle timing in both slow and fast growth conditions, we found that well-studied cell size control models are insufficient to explain the mycobacterial cell cycle. Instead, we showed that mycobacterial cell cycle progression is regulated by an unprecedented mechanism involving parallel adders (i.e. constant growth increments) that start at replication initiation. Together, these adders enable mycobacterial populations to regulate cell size, growth, and heterogeneity in the face of varying environments.

In Brief

Logsdon et al. study cell cycle dynamics of asymmetrically growing mycobacteria and show how cell cycle, chromosome organization, and division are coordinated in single cells. A parallel adder model, where cells add a constant length between initiations and initiation to division, describes cell size control in M. smegmatis and BCG.

Results and Discussion

M. smegmatis chromosome positioning is proportional to cell length

Chromosome subcellular positioning is highly organized yet variable among bacterial species [2, 9, 10]. In E. coli, the origin is located midcell with left and right chromosome arms symmetrically positioned on either side [2, 11]. We hypothesized that mycobacteria cannot fit this model because of asymmetry and aimed to determine chromosome positioning throughout the cell cycle. We developed a fluorescent repressor operator system (FROS) in M. smegmatis to label the origin of replication (ori) and track its movement using time-lapse microscopy (Figures 1A–1B & S1D; Movie S1).

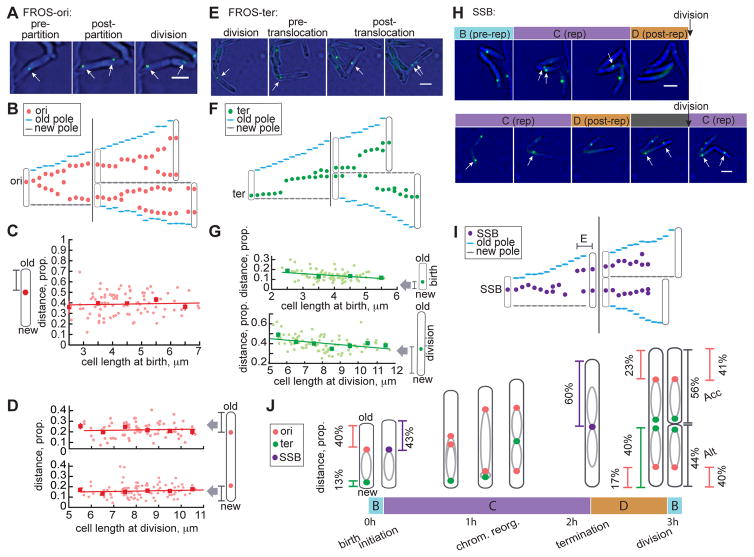
Figure 1. M. smegmatis chromosome localization is proportional to cell length.

(A) 60 minute interval image sequence of single M. smegmatis FROS-ori reporter cells. Oris are indicated with white arrows. Scale bar=2 μm. (B) Representative (of n=101) single-cell traces of FROS-ori localization every 15 min for one mother and two daughter cells. (C–D) Scatter plots of proportion of cell length from the ori to the nearest cell pole at birth (C) or division (D) versus cell length at birth (C) or division (D). Linear regression lines are plotted in red and red squares display mean values for cells binned by birth length in 1 μm increments with red SEM bars (n=101). (C) Pearson correlation r=0.0403, p=0.7124; (D, top) Pearson correlation r=0.0688, p=0.5602; (D, bottom) Pearson correlation r =−0.0272, p=0.7957. (E) Image sequence as in (A) of FROS-ter reporter in M. smegmatis. (F) Representative (of n=85) single-cell traces as in (B) of FROS-ter foci. (G) Scatter plot as in (C–D) of proportion of cell length from ter to the new cell pole at birth versus birth length (top, Pearson correlation r=−0.29, p=0.009; see Figure S1G&S1H) or division versus division length (bottom, Pearson correlation r=−0.31, p=0.004; see Figure S1I&S1J). (H) Image sequence of SSB-GFP reporter in M. smegmatis showing phases of the cell cycle in cells without (top) and with (bottom) an E period. Replisomes are indicated with white arrows. Cells of interest are indicated with white asterisks when not replicating DNA. Scale bars=2 μm. (I) Representative (of n=280 cells) single-cell traces as in (B) of SSB-GFP foci. (J) Model of M. smegmatis chromosome organization and replisome localization throughout the cell cycle. Inferred positioning of left and right arms of the chromosome is depicted with grey ovals.

See also Figure S1, Movies S1, S2 & S3

In most cells, ori localization is approximately midcell, slightly closer to the old pole at birth (Figures 1B&S1K). The average distance from the ori to the old pole at birth is 1.8 μm±1.2 μm. This large variation led us to re-examine localization as a proportion of cell length (Figure S1A). We found that the ori was located a constant proportion (39%±11%) of the cell length from the old pole (Figures 1C&S1A; STAR Methods) in agreement with previous studies [13, 14]. As the cell cycle progresses, the ori remains closer to the growing old pole (Figures 1B&S1K). Before replicated oris partition, they shift midcell (55%±14% of cell length from old pole; Figure S1B). Timing of partitioning correlates with cell length (Figure S1E) and may be caused by forces applied to the ori region by the ParABs segregation system [13–15].

Ori positioning is also proportional to cell size before division. The ori nearest the old pole is slightly further from this pole than the ori nearest the new pole preceding division (23%±9% vs. 17%±7%, respectively; Figure 1D). At division, the daughter inheriting the older pole is termed the accelerator cell because it is born larger and elongates faster than the sister inheriting the new pole, termed the alternator cell because it is born smaller and elongates more slowly [4]. The average division ratio for accelerator and alternator sister cells is 44%/56% (Figure 1J). Therefore, the 23%/17% ori position pre-division gives rise to localization at ~40% of cell length in both newly-born accelerator and alternator cells (Figure 1J). Ori positioning is asymmetric, reflecting a positioning mechanism that prepares oris for consistent localization at birth within daughter cells of unequal sizes.

To gain a more complete understanding of subcellular chromosome positioning we adapted the FROS system to tag the chromosomal terminus (ter). The terminus is located near the new pole at birth and translocates midcell partway through the cell cycle (Figures 1E–1F, S1C, S1G–S1H&S1L). Both ori partitioning and ter translocation occur later in smaller cells (Figures S1E–S1F). The ter translocation event from the new pole to midcell is rapid, typically completing in 15–30 minutes (Figures 1F&S1L; Movie S2). The distal attB chromosome site (245° from ori) was also reported to translocate rapidly to the replisome, indicating that the replisome “reels in” chromosomal loci before they are replicated [10]. Ter positioning is approximately proportional to cell length at birth and division (Figures 1G, S1G–J). The pre-division asymmetric midcell positioning of the terminus (40%±8% cell length from new pole) corresponds to the site of septum formation (Figures 1G, 1J&S1I; Movie S2) [4].

Together, our data suggest that M. smegmatis chromosome positioning is asymmetric, proportional to cell size, and arranged in an ori-ter-ter-ori orientation (Figure 1J). The ori and ter are positioned closer to the new pole before division so asymmetric division gives rise to identical chromosome locations in unequally sized daughter cells (Figure 1J). M. smegmatis chromosome subcellular organization has been previously explored, however orientation and symmetry conclusions were inconsistent between studies [10, 13, 14]. Our finding of ori-ter-ter-ori orientation is similar to the longitudinal pattern of chromosome organization of C. crescentus and M. xanthus [9, 16] and reported for M. smegmatis [14], but unlike the L-ori-R chromosome organization and midcell localization of E. coli [2] also suggested for M. smegmatis [10, 13]. We speculate that the lack of a chromosome terminus reporter previously obscured patterns of chromosome localization in M. smegmatis.

Replisome localization is proportional to cell length

To understand the coordination of chromosome organization with cell cycle progression, we measured the timing and subcellular location of DNA replication using a M. smegmatis strain expressing a fluorescently tagged single stranded binding protein reporter SSB-GFP [17]. Using time-lapse microscopy, we observed one to two SSB-GFP foci during DNA replication (“C”) but none during pre- (“B”) and post- (“D”) replication periods (Figure 1H). We and others have observed M. smegmatis subpopulations that begin new rounds of replication after completing the first round but before division [10, 12, 17, 19]. We identified this additional replication period (“E”) in 54% of cells by observing SSB-foci near poles pre-division (Figures 1H, 1I&S1P). Throughout replication, the replisome remains primarily midcell (Figures 1I&S1M). Although both SSB-GFP foci are generally co-localized, we observed transient foci splitting and rejoining in most cells (Figures 1H, 1I&S1M; Movie S3). M. smegmatis replisome dynamics therefore resemble the “hybrid” dynamics of Myxococcus xanthus [2, 9].

Replisome localization is proportional to cell size, positioned 38%±12% of cell length from the old pole at initiation (Figure S1N). This distance corresponds to FROS-ori positioning at birth, confirming that initiation is proximal to the ori in our reporter strains (Figures 1C, 1J&S1N). At termination, the replisome is localized 60%±17% of the length from the old pole, corresponding to ter positioning at division (Figures 1G, 1J, S1I&S1O). Together, measurements of chromosome and replisome positioning throughout the cell cycle suggest that mycobacterial asymmetry is not established at division but is maintained throughout a cell’s life (Figures 1J&S1P).

M. smegmatis division timing is inconsistent with the division adder

We next sought to investigate how mycobacteria control cell size in the context of underlying growth and size heterogeneity. We used time-lapse imaging to measure cell size and cell cycle timing in SSB-GFP M. smegmatis cells. Several studies recently developed a division adder model (also called an incremental model) of cell size control, in which bacteria add a constant length (Δl_bd) from birth to division regardless of birth size (Figures 2A, S2D&S4; STAR Methods) [6, 8, 20–23]. Because Δl_bd is not correlated to birth length, we found that M. smegmatis is consistent with this aspect of the division adder model (Figure 2B) [4, 6, 19].

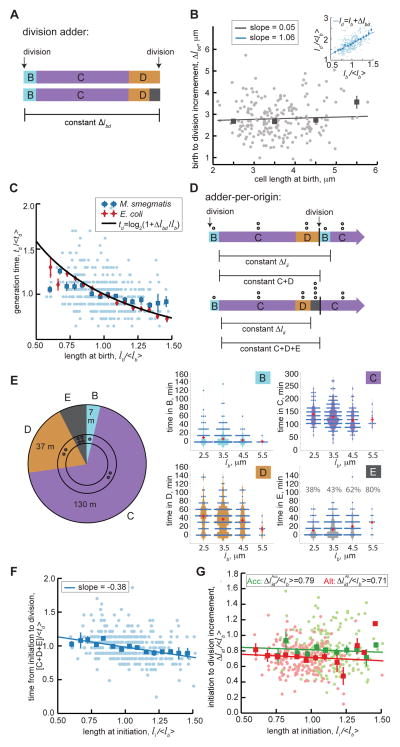
Figure 2. M. smegmatis growth and cell cycle timing in rich medium, n=380.

(A) Schematic representation of the division adder model of cell size control in cells with (bottom) or without (top) E period. Δl_bd is the growth increment between birth and division events. (B) Scatter plot of birth length compared to growth from birth to division (Δl_bd). Light grey dots are individual data points and grey squares are averages of data binned in 1μm increments with SEM bars. The linear regression line is plotted in grey. Inset shows normalized birth size vs. division size with Pearson correlation r=0.65±0.06 95% CI. (C) Scatter plot as in (B) of normalized initiation size (l_i/<l_b>) vs. normalized generation time (t_d/<t_d>). Red diamonds are binned E. coli data from [22]. (D) Schematic representing the adder-per-origin model of cell size control in cells with (bottom) or without (top) E period. Δl_ii is the growth increment between replication initiation events in mother and daughter cells and C+D or C+D+E is the time between initiation and division. Open circles represent number of origins (O) present in different phases of the cell cycle. (E) Pie chart of average time spent in each phase of the M. smegmatis cell cycle. Open circles represent number of origins present in different phases of the cell cycle. Violin plots of cell phase timing are binned by cell size at birth (bin ranges span 1μm, centered as indicated on the axes), red bars denote mean and SEM. The E period violin plot also displays the percentage of cells per bin that experience E period. (F) Scatter plot as in (B) of initiation to division timing (C+D+E periods/<t_d>) vs. cell length at initiation (l_i/<l_b>). Pearson correlation r=−0.35±0.09 95% CI. (G) Normalized initiation to division increment vs. normalized cell length at initiation, plotted for accelerator (Acc; green) and alternator (Alt; red) subpopulations. Linear regression lines are fit to data of each cell type with Acc Pearson correlation r=−0.06±0.09 95% CI and Alt Pearson correlation r=−0.08±0.07 95% CI. See also Figures S2&S4.

There is a proportional relationship between birth length and interdivision time expected in exponentially growing cells that are division adders: t_d∝log₂(1+Δl_bd/l_b) (Figure 2C; STAR Methods) [22]. We found that M. smegmatis data are consistent with exponential growth (Figures S2A&S2B; STAR Methods). Whereas birth and increment size data from E. coli fit the expected proportional relationship between birth length and interdivision time, M. smegmatis measurements systematically deviate (Figure 2C) [22]. These data suggest a more detailed model is needed to explain coordination of division and size.

M. smegmatis division timing is inconsistent with the adder-per-origin model

We therefore considered whether M. smegmatis chromosome replication and cell division are consistent with size control models that couple division to initiation timing [3, 7, 24, 25]. The recent adder-per-origin model, an adaption of the Cooper-Helmstetter model, postulates that: (i) the time from initiation to division is constant regardless of cell size, and (ii) initiation occurs after a constant growth increment measured from the previous initiation (Figures 2D&S4; STAR Methods) [3, 7, 26]. Models that include initiation timing must account for the number of origins, because cells may initiate multiple rounds of replication before division. In the adder-per-origin model, the growth increment scales with the number of origins to ensure cell size homeostasis when there are re-initiation events (STAR Methods). Thus, the adder-per-origin model achieves size homeostasis by implementing the adder mechanism at initiation [21].

In this and previous studies we used the SSB-GFP reporter to characterize the timing of M. smegmatis DNA replication (Figure 2E) [12, 17]. We found that the frequency and duration of E period correlates positively with birth length (Figure 2E) [7]. We also found a negative correlation between cell size at initiation and time from initiation to division (slope of −0.38±0.09 95% CI; Figure 2F). Because timing from initiation to division is not constant, the adder-per-origin model is inconsistent with regulation of cell size and DNA replication in M. smegmatis.

Parallel adder model of initiation and division timing

Instead of a constant time, we observed a constant growth increment between initiation and division. This increment is maintained in accelerator and alternator subpopulations, despite their distinct size and growth properties (Figure 2G). We sought to reconcile this initiation-to-division adder with the birth-to-division adder behavior observed in M. smegmatis. Because an initiation-to-initiation adder mathematically reduces to an emergent birth-to-division adder in E. coli [3, 21], we reasoned that cell cycle control and the constant division increment in M. smegmatis may be due to parallel adders: one from initiation-to-division and another from initiation-to-initiation (Figure 3A).

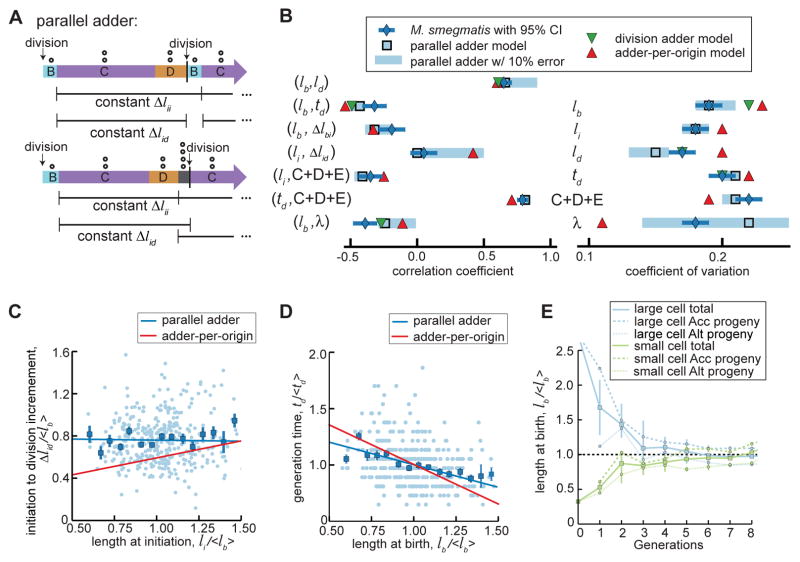
Figure 3. Parallel adder model of mycobacterial cell size control, n=380.

(A) Schematic of parallel adder model of cell size control in cells with (bottom) or without (top) E period. Δl_ii is the growth increment between two initiation events and Δl_id is the growth increment between initiation and division. Open circles represent number of origins (O) present in different phases of the cell cycle. (B) Chart of cell cycle correlation coefficients and CVs comparing M. smegmatis measurements normalized to population mean (blue diamonds with 95% confidence interval bars) to parallel adder model simulations (light blue squares), adder-per-origin model simulations (red triangles), and division adder model simulations (green triangles). Parallel adder simulations with 0% measurement error prediction are represented with open light blue squares and simulations with 10% measurement error prediction are represented with light blue bars. Variables represented are l_b = birth length, l_d = length before division, l_i = length at initiation of DNA replication, t_d = interdivision time, Δl = length increment between the b=birth, i=initiation, and d=division events indicated in the subscripts, C+D+E = total time spent initiation to division, and λ = growth rate. (C) Scatter plot of normalized initiation length (l_i/<l_b>) vs. normalized initiation to division increment (Δl_id/<l_b>). Light blue dots are individual data points and blue squares are binned data with SEM bars. Simulated correlations from parallel adder and adder-per-origin model simulations are plotted, as blue (parallel adder) and red (adder-per-origin) lines. (D) Scatter plot as in (C) of normalized birth length (l_b/<l_b>) vs. normalized generation time (t_d/<t_d>). (E) Plot showing parallel adder simulations for progeny of hypothetical cells born extremely large (blue) or small (green). The average cell birth length with SEM bars over 8 generations is plotted for a hypothetical cell (accelerator) born 2.5x the population average and a hypothetical cell (alternator) born 0.3x the population average. Average sizes of accelerator and alternator cell progeny from each hypothetical progenitor cell are also plotted with SEM bars over 7 generations.

See also Table S1 and Figure S4.

The difference between parallel adder and adder-per-origin models is how division is coordinated with initiation. In the adder-per-origin, a constant time elapses between initiation and division. In the parallel adder, cells grow a constant length initiation to division (Figure S4). Parallel adder and adder-per-origin models are similar in that the constant initiation-to-initiation is scaled to the number of origins (Figures 2D, 3A&S4) thereby achieving size homeostasis in cells with E period. Similarly, the parallel adder can allow multifork replication, a phenomenon recently reported in M. smegmatis [27].

M. smegmatis initiation and division timing is consistent with a parallel adder

To test the hypothesis that mycobacteria use a parallel adder, we constructed a computational model in which cells add a constant increment initiation-to-initiation and initiation-to-division (Figures 3A&S4; STAR Methods). A model simulation approach enables comparison of measurements against models of size control. Simulation allows integration of data stochasticity into a quantitative framework to evaluate size control in the context of cell-to-cell heterogeneity. Because most parameters could be extracted from our data, only two free parameters in the parallel adder model were calibrated (standard deviation of interdivision timing and growth rate; STAR Methods).

Using simulation, we calculated thirteen correlation coefficients and coefficients of variation (CVs) for cellular parameters (Figure 3B). To compare coefficients from simulation to data, we simulated the parallel adder with 10% error in size measurements (STAR Methods). We observed that many coefficients are relatively insensitive to stochasticity while others (such as growth rate) exhibit a broad range of values with this modest error model, indicative of the sensitivity of some parameters to stochasticity that may be amplified from multiple sources (Figure 3B). A stochastic modeling approach provides information about which parameters are most robust to variation and therefore appropriate to be compared to experimental data.

We simulated the division adder, adder-per-origin, and parallel adder models of cell size regulation (Figures S2C–S2I; STAR Methods). All three models account for accelerator and alternator size and growth differences (Figures S2G–S2I; STAR Methods) [4, 28]. Simulations demonstrate that correlation coefficients and CVs from M. smegmatis measurements are consistent with calculated coefficients from the parallel adder model while inconsistent with either the division adder or the adder-per-origin model (Figure 3B). The fit of M. smegmatis measurements to parallel adder model simulation is insensitive to the method used to determine cell division (Table S1). Additionally, the time-resolution of imaging does not affect comparison of measurement to simulation (Figures S3F–S3H). Importantly, the parallel adder model simultaneously captures correlations between Δl_id and initiation size and between birth length and interdivision time, which cannot be explained by the adder-per-origin model (Figures 3C–3D). Parallel adder model simulations demonstrate population size convergence in hypothetical cells born very large or small (Figures 3E, S2C&S2F) as well as accelerator and alternator subpopulations, despite larger accelerator cells adding larger increments than smaller alternator cells (Figures 2G, 3E, 4C&S2I; STAR Methods).

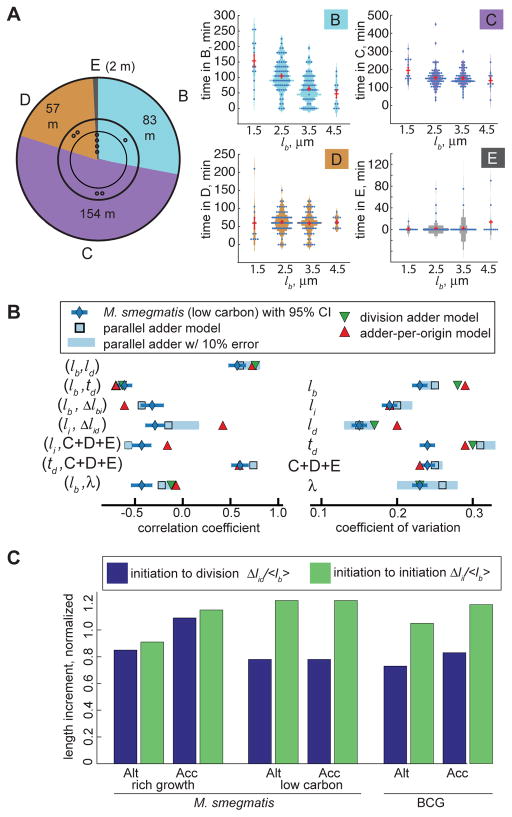
Figure 4. Cell cycle timing and growth of M. smegmatis under carbon limitation, n=160.

(A) M. smegmatis cell cycle timing during carbon limitation, as in Figure 2E. (B) Chart of carbon limited M. smegmatis cell cycle correlation coefficients and CVs comparing measurements normalized to population mean to model simulations, as in Figure 3B. (C) Average normalized accelerator and alternator Δl_id and Δl_ii growth increments for M. smegmatis in rich and carbon limited media and BCG in rich medium.

See also Figure S3.

A parallel adder model describes mycobacterial cell cycle progression in slow growth

We next evaluated whether the parallel adder was consistent with M. smegmatis size control in carbon limited slow growth conditions and with slow growing species BCG (Figure S3B). BCG exhibited an interdivision time of 15–20 hours while the average carbon limited M. smegmatis interdivision time was 4.9 hours, in contrast to 3.1 hours in rich medium (Figures 2E, 4A, S3C&S3D). We identified differences in BCG and carbon limited M. smegmatis cell cycle timing compared to rapidly growing M. smegmatis. B period was disproportionatly extended in slow growth, particularly in small cells (Figures 4A&S3D). Additionally, BCG spent an average of 9.4 hours in C, similar to previous measurements in Mycobacterium tuberculosis (Figure S3D)[29]. BCG and carbon limited M. smegmatis birth lengths were more variable than M. smegmatis growing in rich medium, with CVs of 20% and 22%, respectively, compared to 19% for M. smegmatis in rich medium (Figures 3B, 4B, S3A&S3E), and 12% for E. coli [8].

We compared simulations of parallel adder, adder-per-origin, and division adder models to measurements from slow growth (STAR Methods). We observed that a parallel adder describes these data well, in contrast to adder-per-origin and division adder models (Figures 4B&S3E). Whereas the length increments to division and initiation are similar in rich growth conditions, Δl_id is much longer than Δl_ii for M. smegmatis in carbon limited medium and BCG (Figure 4C). Within the context of the parallel adder model, this difference in increments explains the observation that E period is rare and B is extended during slow growth (Figures 2E, 4A&S3D). This provides one example of how the parallel adder model offers flexibility to shift and capture cell cycle and division coordination in varying growth conditions.

We conclude that mycobacteria utilize a parallel adder at initiation to control cell size in the context of deterministic growth and size variation. This cellular mechanism enables mycobacteria to control both size and variability in an environment-specific manner. Thus, variation in cell cycle timing is adaptable, which may play a role in stress tolerance. We have yet to fully understand mechanisms by which mycobacteria implement a parallel adder and maintain an asymmetric, yet ordered, chromosome subcellular localization, but our study informs the search for the molecular basis of these processes. Given the important role of mycobacterial growth and variation on disease and treatment outcome, we anticipate the further understanding of these fundamental processes may give rise to new therapeutics against mycobacterial diseases, such as tuberculosis.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Bree Aldridge (bree.aldridge@tufts.edu)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Growth conditions

M. smegmatis cells were grown to log phase overnight with shaking at 37°C in rich (7H9 supplemented with 0.05% sterile tween 80, 10% ADC (albumin, dextrose, catalase), 0.2% glycerol) or carbon limited (7H9 supplemented with 10% modified AC (albumin concentration reduced to 1% standard concentration), 0.05% Tyloxapol) media. BCG cells were grown and passaged to log phase in at 37°C in 7H9 medium supplemented with 0.25% sterile 20% tween 80, 10% OADC (oleic acid, albumin, dextrose, catalase), 0.2% glycerol. FROS-ori and ter growth medium was supplemented with 25 μg/ml kanamycin. SSB strain growth medium was supplemented with 50 μg/ml hygromycin.

METHOD DETAILS

Generation of reporter strains

To create FROS-ori and FROS-ter strains, M. smegmatis mc²155 was first transformed with the KanR attBL5 integrating plasmid that expressed lacI-gfp fusion construct under the control of the pMOP promoter. These KanR strains were checked under the microscope to confirm the expression of lacI-GFP in a non-localized manner. The 120 repeat lac operator array containing plasmid pLAU37 was used as a backbone to create the FROS plasmids by cloning in a hygR marker for selection in mycobacteria and one of the mycobacterial attP sites and the corresponding integrase to facilitate site-specific integration within the mycobacterial genome [30, 31]. The FROS-ori plasmid carried the BP attP-integrase that integrated at the attB-6 site located near the chromosomal origin of replication [30], and the FROS-ter plasmid carried the Omega attP-Integrase that integrated at the attB-11 site located near the chromosomal replication terminus [31]. To create FROS-ori strains, M. smegmatis mc²155 was co-transformed with the attBL5-lacI-GFP-Kan plasmid and the FROS-ori plasmid, and the transformants were selected on 7H10 agar medium supplemented with 25 μg/ml kanamycin and 50 μg/ml hygromycin. The FROS-ter strains were created following sequential transformation of the attBL5-lacI-GFP-Kan plasmid and then the FROS-ter-HygR plasmid. Upon integration of the lac operator arrays, microscopic examination was performed to confirm that GFP foci localized at discrete locations within the bacterial cell corresponding to the ori and ter proximal regions of the chromosome. Growth defects were not detected in FROS strains (Fig. S1D). SSB-GFP M. smegmatis and BCG were transformed with a hygromycin resistant single-stranded binding green fluorescent protein (SSB-GFP) replicating plasmid [17].

Live-cell microscopy

M. smegmatis cells were filtered through a 10μm filter to remove clumps before being loaded into a custom polydimethylsiloxane (PDMS) microfluidic device, as in [32]. The viewing device contained a main microfluidic medium feeding channel, with a height of approximately 10–17μm, and viewing chambers with a diameter of 60 μm and a height of 0.8–0.9μm. 2% DMSO and 0.0625 mg/ml FM4-64 were added to media to stain septal membranes in the FM4-64 experiment. Fresh medium was delivered to cells using a microfluidic syringe pump.

The microfluidics device was placed on an automated microscope stage housed within an environmental chamber maintained at 37°C. M. smegmatis cells were imaged for 26 hours using a widefield DeltaVision PersonalDV (Applied Precision, Inc.) with a hardware-based autofocus. Cells were illuminated with an InsightSSI Solid State Illumination system every 15 minutes: SSB and FROS foci were visualized with 475nm excitation and 525 emission wavelengths, FM4-64 was visualized with 475nm excitation and 679 nm emission wavelengths, and cells were additionally imaged using transmitted light brightfield microscopy.

BCG cells were filtered through a 10μm filter to remove clumps before loading into a PDMS microfluidic device. Culture supernatant was filtered through a 0.2 μm filter to generate sterile spent media. Fresh 7H9 media was supplemented with sterile spent medium (60:40) and flowed through the microfluidic device at a rate of 5 μl/min. BCG cells were imaged every 45 min for a course of 86 hours using the system described above. 475 nm excitation and 525 nm emission wavelengths were utilized for SSB foci visualization. Cells were also imaged using transmitted light brightfield microscopy.

Mode of Growth at the Single Cell Level

Most models of bacterial cell size control are based on the assumption that cells grow exponentially in volume over time. However, single cell traces cannot distinguish between linear and exponential modes of growth in M. smegmatis (Figure S2A). We therefore evaluated cell growth parameters from numerous cells to determine whether normalized cell generation time (i.e., generation time divided by the mean generation time) was proportional to the natural log of the ratio of division length to birth length (ln(l_d/l_b)), as is expected for exponential growth or comparable to the linear growth expectation of total elongation (l_d−l_b) (Figure S2A). Overall, we found that M. smegmatis measurements were consistent with the exponential model of cell growth in bulk compared to a linear growth model (Figure S2B). Cells with the longest generation times (the largest two binned data points) deviate slightly from exponential growth, however the effect on the overall fit of the data to the ln(l_d/l_b)=λt_d line and subsequent comparison of models is not significant because they contain very few data points (6/391 cells or 1.5% of the data) (Figure S2B). Determining the growth mode directly at the single cell level requires more advanced techniques [33]. Nevertheless, the agreement with exponential growth is strong enough that we modeled cells growing exponentially with growth constant λ.

Models

We consider three models of cell size regulation: the division adder, the adder-per-origin, and the parallel adder (see also Figure S4). In all three models, we distinguish between alternator and accelerator cells. Accelerator cells are, barring noise, the larger cells upon asymmetric division with ratio r (r = 0.5 corresponds to symmetric division), and may have different requirements than alternator cells for replication initiation and division, as discussed below. The three models each maintain cell size homeostasis, as illustrated with simulation in Figures 3E & S2C–I and also explained with derivations below.

Division Adder Model

In the division adder, cells attempt to add a constant size increment from birth to division. The increment may be different between alternator and accelerator cells. This model does not consider replication initiation, and can be summarized as

$$l_d^z=l_b+\mathrm{\Delta }{l}_{bd}^z$$

where l is the cell length at the event denoted by the subscripts b and d, for birth and division. The superscript z = acc, alt denote alternator (Alt) or accelerator (Acc). Given exponential growth (Figure S2B; l_d = l_be^λt_d where λ is the growth constant and t_d, is the generation time), a division adder (l_d = l_b + Δl_bd) may be rewritten in terms of t_d, by a log transformation and substitution, as follows and described also in [22]:

$$\begin{gathered} ln(l_d)=ln(l_b{e}^{\lambda t}d), \\ ln(l_d)-ln(l_b)=\lambda t_d, \\ ln(l_d/l_b)=ln((l_b+\mathrm{\Delta }{l}_{bd})/l_b)=\lambda t_d, \\ {t}_d=\frac{1}{\lambda }ln(1+\mathrm{\Delta }{l}_{bd}/l_b). \end{gathered}$$

The convergence property of the “basic” division adder without distinction between accelerators and alternators has been rigorously investigated and is well understood [9, 11, 14]. In summary, the division adder converges because a cell adds a constant size regardless of its size at birth. Following this strategy, cells smaller than average will increase in size and cells larger than average will decrease in size until they reach the average size over several generations [9, 11, 14].

With the additional consideration of accelerators and alternators, a similar reasoning applies. In this model, the growth increment may be different for the accelerator and alternator subpopulations. We show by model simulation that even when accelerator and alternators cells do have different requirements for the growth increment between division events, the birth length of the population converges (Figure S2D). In this simulation, a large accelerator cell (purple) and a small alternator cell (red) each seed a population in which the average cell lengths at birth converge over several generations.

To understand the theoretical basis for convergence, it is helpful to consider what happens to the birth lengths of “pure” subpopulations of accelerator cells (from a lineage of all accelerator cells) and “pure” subpopulation of alternator cells (from a lineage of all alternator cells) separately, as they represent the extremes of large and small cell subpopulations, respectively. We note that these pure subpopulations do not exist naturally because they consider only one of two daughter cells at each division. In reality, every division gives rise to one accelerator and one alternator cell. Consider an accelerator cell from this artificial pure subpopulation lineage. Its size at division is on average

$$\langle l_d^{\mathit{acc}}\rangle =\langle l_b^{\mathit{acc}}\rangle +\mathrm{\Delta }{l}_{bd}^{\mathit{acc}},$$

Hence for a division ratio r, we find that:

$$\begin{gathered} \langle l_b^{\mathit{acc}}\rangle /r=\langle l_b^{\mathit{acc}}\rangle +\mathrm{\Delta }{l}_{bd}^{\mathit{acc}},\text{or} \\ \langle l_b^{\mathit{acc}}\rangle =\frac{r}{1-r}\mathrm{\Delta }{l}_{bd}^{\mathit{acc}}. \end{gathered}$$

Cells in the pure accelerator subpopulation are the largest cells on average, and their sizes converge to the above expression. Similarly, the average size of a pure alternator cell is

$$\langle l_b^{\mathit{alt}}\rangle =\frac{1-r}{r}\mathrm{\Delta }{l}_{bd}^{\mathit{alt}}.$$

We illustrate the convergence of both pure lineages by simulation (Figure S2G). In the longest cell subpopulation possible (the pure accelerator cells), the lineages from a large cell and a small cell each converge to $\frac{r}{1-r}\mathrm{\Delta }{l}_{bd}^{\mathit{acc}}$. Similarly, the lineages of alternator cells (the shortest cell subpopulation) converge to $\frac{1-r}{r}\mathrm{\Delta }{l}_{bd}^{\mathit{alt}}$. Because the accelerator and alternator subpopulations each converge, the entire population must also converge. An expression for the population averaged size at birth can be derived by considering the target size at division $l_d^z$ of a cell of type z, not necessarily from a pure lineage. Summing the target sizes for the two types,

$$l_d^{\mathit{acc}}+l_d^{\mathit{alt}}=l_b^{\mathit{acc}}+l_b^{\mathit{alt}}+\mathrm{\Delta }{l}_{bd}^{\mathit{acc}}+\mathrm{\Delta }{l}_{bd}^{\mathit{alt}}.$$

Because the two types exist in equal numbers in a population, the population averaged size at birth and division can be approximated as $\langle l_b\rangle =(\langle l_b^{\mathit{alt}}\rangle +\langle l_b^{\mathit{acc}}\rangle )/2$ and $\langle l_d\rangle =(\langle l_d^{\mathit{alt}}\rangle +\langle l_d^{\mathit{acc}}\rangle )/2$, respectively. Because cell size homeostasis requires that 〈l_d〉 = 2〈l_b〉, the above expression reduces to $\langle l_b\rangle =(\mathrm{\Delta }{l}_{bd}^{\mathit{acc}}+\mathrm{\Delta }{l}_{bd}^{\mathit{alt}})/2$. We verified this convergence with stochastic population simulation (see above and Figure S2D).

Adder-per-Origin Model

In the adder-per-origin model, cells attempt to add a constant size increment per origin of replication between replication initiations, and a round of replication initiation triggers cell division after a constant time initiation to division. The model can be summarized as

$$\begin{gathered} {(l_i^{\prime })}^{\text{total}}=l_i^z+O\mathrm{\Delta }{l}_{ii}^z, \\ {l}_d=l_i{e}^{\lambda (C+D)}. \end{gathered}$$

Here, ${(l_i^{\prime })}^{\text{total}}$ is the total cell length for the next (indicated by ′) round of initiation. If the cell divides before this next initiation, than the total length is the summation of lengths of both daughters. z (for Acc or Alt) corresponds to the cell type at the first initiation (e.g. the mother and not each daughter). O is the number of origins in the cell. The number of origins O is not set by hand, but is a dynamic variable. For example, in cases without E period where there are no ongoing replication forks after division, the number of origins is equal to one before initiation and is equal to two after initiation (Figures 2D & S4).

Note that because the number of origins per cell is halved at division, the growth required until initiation must be recalculated as follows. Each daughter cell must accumulate a size increment $O\mathrm{\Delta }{l}_{ii}^z/2$. But each daughter will inherit a different cell length accumulated after the mother’s initiation because of asymmetric division so the initiation length for the sister accelerator and alternator cells will be adjusted according to the division ratio. Consider the accelerator daughter: it has already accumulated a length r(l_d − l_i) towards the requirement, and will initiate once it has accumulated the remaining length. Therefore, the accelerator daughter will initiate replication at size

$${\left(l_i^{\prime }\right)}^{\mathit{acc}}={\left(l_i^{\prime }\right)}^{\text{total}}/2+(r-1/2)l_i.$$

Similarly, the alternator daughter will initiate replication at size

$${\left(l_i^{\prime }\right)}^{\mathit{alt}}={\left(l_i^{\prime }\right)}^{\text{total}}/2-(r-1/2)l_i.$$

For simulations, it is useful to express ${\left(l_i^{\prime }\right)}^{\mathit{acc}}$ in terms of total requirement and the previous size at initiation.

It is important that a cell attempts to add a constant size increment per origin. This is because cells may initiate an extra round of replication due to stochasticity in cell cycle timings. In these cases, adding not just a constant size increment, but a size increment per origin allows the cell to maintain size homeostasis [3]. Due to these extra rounds of replication initiating before division (i.e. E period) a sequential adder model where cells grow a constant increment from birth to initiation and another constant increment from initiation to division was also ruled out. In a sequential adder model, every initiation is uniquely coupled to a division event (Figure S4). Thus, a sequential adder model does not allow a cell cycle in which two initiations occur, in contradiction to our experimental findings that cell cycles with an “E period” do occur.

Expressions for the average size at birth of cells in pure lineages can be found as follows. Because the regulation at initiation in the adder-per-origin model is the same as that in the parallel adder model, the result at initiation is the same as that derived in section 6.3. The average size at division of a pure accelerator/alternator cell is simply

$$\langle l_d^z\rangle =e^{\lambda (C+D)}\langle l_i^z\rangle ,$$

where 〈 $l_i^z$〉 is the same as in the next section.

The adder-per-origin model achieves size homeostasis by implementing the adder mechanism between replication initiations. Its convergence has been shown theoretically and experimentally [10]. Briefly, the per-origin requirement is necessary for convergence because of the possibility of extra rounds of initiation within a division cycle or E periods. The per-origin requirement allows the model to recover from these stochastic events. We show by simulation that cell size converges even when the growth increment between initiations is larger for accelerator cells than alternator cells (Figure S2E). As in the division adder model, we also show in Figure S2H that the largest and smallest subpopulations (the pure lineages of accelerator and alternator cells, see Section 6.1 above) converge. Because the accelerator and alternator subpopulations each converge, the entire population must also converge.

The population averaged cell size at birth can be derived as follows. As will be derived in the next section, the target size at initiation $l_i^{zy}$ of a cell of type y whose mother is of type z is

$$l_i^{zy}=s(z)l_i^z+\mathrm{\Delta }{l}_{ii}^z,$$

where s(z) = r or 1 − r for accelerator and alternator cells, respectively. The four types of target size at initiation then lead to four types of target size at division via multiplication by a factor e^{λ(C + D)}. Because these four types of cells exist in equal numbers in the population, the population averaged cell size at birth can be approximated as $\langle l_b\rangle =({\sum }_{zy}{l}_d^{zy})/8$. After simplification, $\langle l_b\rangle =\left(\mathrm{\Delta }{l}_{ii}^{\mathit{alt}}+\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}\right)e^{\lambda (C+D)}/2$. Simulations confirm this result (Figure S2E).

Parallel Adder Model

In the parallel adder model, cells attempt to add a constant size increment per origin between initiations, and from initiation to division. The increments may be different between initiations and from initiation to division. The model can be summarized as

1. ${(l_i^{\prime })}^{\text{total}}=l_i^z+O\mathrm{\Delta }{l}_{ii}^z$,

2. $l_d^z=l_i^z+O\mathrm{\Delta }{l}_{id}^z$.

where l_i is the cell size at initiation, ${(l_i^{\prime })}^{\text{total}}$ is the total combined cell size of the daughter cells at the next initiation as described in section 6.2 above for the adder-per-origin model, l_d is the cell size at division, and O is the number of origins of replication. O is typically two at the beginning of C period, because C+D is often less than the average doubling time, but is four if the cell experiences re-initiation at E period (Figures 3A & S4). $\mathrm{\Delta }{l}_{ii}^z$ is the size increment required per origin between successive initiations, while $\mathrm{\Delta }{l}_{id}^z$ is the increment required from initiation to division. There is a cell type dependence on increments in the parallel model such that the superscript z = acc, alt denotes alternator (Alt) or accelerator (Acc) cell types and these different increments capture the asymmetric growth rates and different lengths of accelerator and alternator cells. The increments are set in part by measured population averaged values, because

$$\begin{gathered} \langle l_b\rangle \approx ({\mathrm{\Delta }}_{id}+{\mathrm{\Delta }}_{ii})/2, \\ \langle l_i\rangle \approx {\mathrm{\Delta }}_{ii}, \end{gathered}$$

where ${\mathrm{\Delta }}_{ii}=\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}+\mathrm{\Delta }{l}_{ii}^{\mathit{alt}}$ and ${\mathrm{\Delta }}_{id}=\mathrm{\Delta }{l}_{id}^{\mathit{acc}}+\mathrm{\Delta }{l}_{id}^{\mathit{alt}}$. This result is derived below. Although the ratios between the accelerator and alternator increments can be chosen arbitrarily, numerical simulations described below show that the parallel adder best describe the data when the increments are either equally distributed or distributed in proportion to the asymmetry ratio r. Simulations of the model best capture data from M. smegmatis and BCG growing in rich medium when the increments are proportioned between alternator and accelerator cell types per the asymmetry ratio r and best capture data from M. smegmatis growing in carbon limited medium when the increments are equally distributed between alternator and accelerator cell types.

When increments are proportioned between the alternator and accelerator cell types per the asymmetry ratio r, the average size of pure accelerator and pure alternator cells can be derived as follows. To derive 〈 $l_b^{\mathit{acc}}$〉 for a pure accelerator cell, write the average size at birth in terms of the average size at initiation

$$\langle l_b^{\mathit{acc}}\rangle =r\langle l_i^{\mathit{acc}}\rangle +2r\mathrm{\Delta }{l}_{id}^{\mathit{acc}}.$$

For simplicity, consider the case without an extra round of initiations so that O = 2. As discussed above, an accelerator cell inherits a fraction r of the size accumulated between initiation and division towards the size $\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}$ required for the next initiation. In other words,

$$2r\mathrm{\Delta }{l}_{id}^{\mathit{acc}}+(l_i^{\mathit{acc}}-l_b^{\mathit{acc}})=\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}.$$

The size at next initiation is therefore

$$l_i^{\mathit{acc},\mathit{next}}=r{l}_i^{\mathit{acc}}+\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}.$$

Stationarity then implies that the average size at initiation of a pure accelerator cell is

$$\langle l_i^{\mathit{acc}}\rangle =\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}/(1-r).$$

This expression allows us to express 〈 $l_b^{\mathit{acc}}$〉 in terms of model parameters $\mathrm{\Delta }{l}_{ii}^{\mathit{acc}},\mathrm{\Delta }{l}_{id}^{\mathit{acc}}$, and r. The same reasoning leads to the average size at birth for a pure alternator cell, but with r replaced by 1 − r and accelerator increments replaced by alternator increments, giving

$$\langle l_b^{\mathit{acc}}\rangle =2r\mathrm{\Delta }{l}_{id}^{\mathit{acc}}+\frac{r}{1-r}\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}$$

and

$$\langle l_b^{\mathit{alt}}\rangle =2(1-r)\mathrm{\Delta }{l}_{id}^{\mathit{alt}}+\frac{1-r}{r}\mathrm{\Delta }{l}_{ii}^{\mathit{alt}}.$$

The parallel adder converges because of the same principle as the adder-per-origin model (e.g. convergence occurs because of the constant growth increment between initiation events per origin). We show by simulation that cell size converges even when the growth increment between initiations is larger for accelerator cells than alternator cells (Figures 3E & S2F). We illustrate the convergence of both pure accelerator and alternator lineages by simulation (Figure S2I). In the largest subpopulation possible (the pure accelerator cells), the lineages from a large cell and a small cell each converge to $2r\mathrm{\Delta }{l}_{id}^{\mathit{acc}}+\frac{r}{1-r}\mathrm{\Delta }{l}_{ii}^{\mathit{acc}}$. Similarly, the lineages of alternator cells (the smallest subpopulation) converge to $2(1-r)\mathrm{\Delta }{l}_{id}^{\mathit{alt}}+\frac{1-r}{r}\mathrm{\Delta }{l}_{ii}^{\mathit{alt}}$. These simulations did not include any fitting parameters and verify convergence the pure accelerator and alternator subpopulations. Because the accelerator and alternator subpopulations each converge and are the subpopulations with the longest and shortest cells, respectively, the entire population must also converge.

The population averaged cell size at birth can be derived as in the adder-per-origin model. In this case, each of the four types of target size at initiation leads to the following target size at division

$$l_d^{zy}=l_i^{zy}+\mathrm{\Delta }{l}_{id}^y.$$

Here, the superscripts zy denote a cell of type y whose mother is of type z. Because these four types exist in equal numbers in the population, the population averaged cell size at initiation and at birth can be approximated as $\langle l_i\rangle ={\sum }_{zy}\langle l_i^{zy}\rangle /4$ and $\langle l_b\rangle ={\sum }_{zy}\langle l_d^{zy}\rangle /8$. Simplification leads to the result quoted above (〈l_b〉 = (Δ_id + Δ_ii)/2 and confirmed in simulations (Figure S2F).

The parallel adder model also predicts that the mean growth increment from birth to initiation (<Δl_bi>) can be calculated from both of the constant growth increments (Δl_ii and Δl_id), below

$$<\mathrm{\Delta }{l}_{bi}>=<l_i>-<l_b>=\mathrm{\Delta }{l}_{ii}-\frac{\mathrm{\Delta }{l}_{ii}+\mathrm{\Delta }{l}_{id}}{2}=\frac{\mathrm{\Delta }{l}_{ii}-\mathrm{\Delta }{l}_{id}}{2}.$$

Because the B period is so short in rich growth conditions (<4% of the length of the cell cycle, on average), we evaluated the increment during the B period in slow (carbon limited) conditions. The average normalized growth increment in B, 0.24 +/− 0.026 95% CI, was very similar to the value (0.22) calculated using the parallel adder model (Supplemental Experimental Procedures section 6.4). The growth increment during B is correlated with birth length because the longer accelerator cells inherit more of the mother’s cell body, and therefore more of the accumulated length since the last initiation. Simulation of the parallel adder model predicts a slope of −0.28 (normalized to average l_b) for Δl_bi vs. l_b, in agreement with (and within the 95% confidence interval of) our measurement of −0.24 +/− 0.092 95% CI.

Numerical Simulation

We use numerical simulations to compare division adder, adder-per-origin, and parallel adder models (section 6.1–6.3) to measurements. We consider sources of stochasticity that are important to describe measurements: a time-additive noise between successive initiations with standard deviation σ_t, an asymmetric and noisy division ratio with mean r and standard deviation σ_r, and a noisy growth rate with mean λ and standard deviation σ_λ. Noise in cell cycle timings is implemented as a time-additive noise onto the size required at initiation. In the division adder, a size-additive noise gives size and time distributions of slightly different shapes, but does not change the correlation coefficients compared to a time-additive noise [21]. We therefore focus on time-additive noise onto the size required at initiation, so that

$${\left(l_i^{\prime }\right)}^{\text{total}}=\left(l_i^z+O\mathrm{\Delta }{l}_{ii}^z\right)e^{\lambda {\xi }_t}.$$

At division, a cell divides according to a noisy ratio

$$r+{\xi }_r,$$

where r is the average asymmetry ratio. The newborn cell is also given a noisy growth rate

$$\lambda +{\xi }_{\lambda },$$

where λ = ln 2/τ is the average growth rate. ξ_t, ξ_r, and ξ_λ are random variables with zero mean and standard deviations σ_t, σ_r, σ_λ. Because all other parameters can be extracted, there are only two free parameters in the parallel adder model: −σ_t and σ_λ.

Simulations begin with one accelerator and one alternator cell, although the initial condition does not matter because the average cell size achieves stationarity (Figures 3E & S2D–F). The simulations advance in time for twelve generations and track all cells in the population. Initiation and division events are dictated by the models. The simulations also mimic measurement errors by adding to the recorded cell size at birth a random noise with standard deviation σ_e. Measurement errors are assumed to be multiplicative in size, so that the noise has magnitude 2σ_e at division. The single-cell statistics of the population are used to calculate the coefficients of variation and Pearson correlation coefficients, which we compare to measurements. In particular, because σ_t, σ_λ, and σ_e are fitting parameters, we can determine the best fit by minimizing the residue between the measured and simulated coefficients of variation of cell size at birth, at division, and interdivision time.

Because measurements were taken at discrete time intervals (every 15 minutes for M. smegmatis, every 45 min for BCG), the average cell size at division is slightly less than twice the average size at birth. This affects the mean behavior when comparing the measured correlation between v_d − v_i and v_i. Hence, the simulated size at divisions are multiplied by a corrective factor equal to 〈v_d〉/〈v_b〉/2. Note that this correction does not affect the correlation coefficient.

To test if experimental imaging frequencies were too long to compare to model simulations, we sampled model simulations in which correlation coefficients were collected at limited time resolution, ranging from 0–30% interdivision time (Figures S3F–H). We observe noticeable changes in correlation coefficients when time resolution is over 25% of the cell cycle, whereas M. smegmatis experiments in rich medium have a time resolution of 8% interdivision time (Figures S3F–H), M. smegmatis experiments in carbon limited medium have a time resolution of 5% interdivision time, and BCG experiments have a time resolution of 4% interdivision time. Because experimental resolutions are much shorter than the resolution threshold obtained from model simulations, we conclude that experimental imaging frequencies do not affect the evaluation of the parallel adder model against experimental data.

QUANTIFICATION AND STATISTICAL ANALYSIS

Image Annotation and Analysis

Images were saved in the SoftWoRx format (Applied Precision, Inc.) and annotated in ImageJ (version 1.49e) with an ObjectJ plug-in. Cell poles and any visible foci were annotated each frame. In the majority of experiments, cell division was defined as “v-snapping” or “pinching”, as in [27, 32]. FM4-64 was also evaluated as a division determinant in Table S1. FM4-64 division was defined as the appearance of a visible FM stained septum, which occurs 0–30 minutes before cell wall pinching. All but one correlation coefficient remained consistent (within the 95% confidence interval) between pinching/v-snapping division and FM septum formation division data sets (Table S1). The correlation between cell size at initiation (v_i) and time spent from initiation to division (C+D+E) was less negative in FM division data versus pinching/v-snapping division data, which was expected when using the earlier septation event to determine division (Table S1).

Locations of cellular components were analyzed and plotted using MATLAB (version R2015b). Single cell foci localization traces were manually analyzed and used to assign cell cycle timing of each cell’s growth from birth to division. The SSB-GFP reporter forms a clear fluorescent focus at site(s) of active DNA replication and diffuses in the cytoplasm after termination of DNA replication. Initiation was defined as appearance of GFP foci after division. Termination was defined as disappearance of GFP foci after the replication period. If foci disappeared for a frame or two due to focus or cell overlap and then reappear, we assumed replication continued until the last foci disappears. SSB-GFP often exhibits diffuse background fluorescence when cells are not replicating DNA [2, 10, 12, 17, 18]. Cells within a microcolony can have varying levels of background SSB-GFP. Cells expressing either very bright (showing fluorescence throughout cytoplasm) or very dim (showing no foci) SSB-GFP were excluded from analysis. Mother/daughter cell relationships and accelerator/alternator status of cells was collected from cell pedigree trees.

Statistics

Statistical analysis was performed using MATLAB 2015b. Sample size (n=) refers to the number of individual cells measured and can be found in figure legends. Scatter plots were presented as binned data averages (squares) with SEM bars plotted over individual data points. Lines were fit to individual data points and not to binned data. Pearson correlations with an r value > |0.1| and p value < 0.05 were considered significantly correlated. Correlations that showed an r value < |0.1| and p value > 0.05 were considered to show no significant relationship between the two variables, and thus had a constant relationship. Two component relationships were assessed using the likelihood-ratio test. This test compares goodness of two models (in our case, one versus two component lines) and uses residuals and standard deviation values in order to reject the null model, e.g. the less complex one-component line. The ratio of the two competing models needs to be larger than a critical chi squared value, based on the difference between degrees of freedom in the two competing models. All reported two component relationships meet this level of significance. Violin plots were generated using the distributionPlot MATLAB function written by Jonas Dorn. The histograms were lightly smoothed using a histogram.m-determined ksdensity, causing <0 tails for some cell cycle timing distributions. Individual data points were plotted on top of this distribution and show that there were no negative timing measurements. Bin widths were normalized across all birth sizes for each plot. The red cross demarks the mean and SEM.

DATA AND SOFTWARE AVAILABILITY

Model simulation code: https://sites.tufts.edu/aldridgelab/LogsdonHoSimulationCode2017/

Supplementary Material

1

Movie S1. Time-lapse microscopy of FROS-ori M. smegmatis growth in a microfluidics device. Related to Figure 1.

2

Movie S2. Time-lapse microscopy of FROS-ter M. smegmatis growth in a microfluidics device. Related to Figure 1.

3

Movie S3. Time-lapse microscopy of SSB-GFP M. smegmatis growth in a microfluidics device. Related to Figure 1.

Highlights.

• The M. smegmatis chromosome is asymmetric in cells and oriented ori-ter-ter-ori

• M. smegmatis adds a constant length between initiations and initiation to division

• A parallel adder model describes M. smegmatis asymmetry and cell size control

• The parallel adder model also describes BCG and nutrient limited M. smegmatis