Revealing dynamics of helicase translocation on single-stranded DNA using high-resolution nanopore tweezers

Significance

DNA helicases are enzymes that use energy from ATP hydrolysis to move along nucleic acid tracks and unwind double-stranded DNA. Helicases are involved in every aspect of DNA metabolism and are therefore vital to maintaining genomic integrity. Using the single-molecule technique single-molecule picometer-resolution nanopore tweezers (SPRNT), which measures the position of DNA through the biological membrane protein MspA as an enzyme moves along the DNA, we monitored the kinetics of the helicase Hel308 at 1,000 times better temporal resolution than was previously possible. We derived a detailed mechanism for how ATP hydrolysis coordinates the motion of Hel308 along single-stranded DNA that can likely be applied to other structurally similar helicases and showed that the DNA sequence in Hel308 affects its kinetics.

Abstract

Enzymes that operate on DNA or RNA perform the core functions of replication and expression in all of biology. To gain high-resolution access to the detailed mechanistic behavior of these enzymes, we developed single-molecule picometer-resolution nanopore tweezers (SPRNT), a single-molecule technique in which the motion of polynucleotides through an enzyme is measured by a nanopore. SPRNT reveals two mechanical substates of the ATP hydrolysis cycle of the superfamily 2 helicase Hel308 during translocation on single-stranded DNA (ssDNA). By analyzing these substates at millisecond resolution, we derive a detailed kinetic model for Hel308 translocation along ssDNA that sheds light on how superfamily 1 and 2 helicases turn ATP hydrolysis into motion along DNA. Surprisingly, we find that the DNA sequence within Hel308 affects the kinetics of helicase translocation.

Enzymes, such as helicases, polymerases, translocases, and ribosomes that move along DNA or RNA, perform the core functions of replication and expression in all of biology. Helicases are molecular motors that catalyze the unwinding of double-stranded DNA or RNA powered by ATP hydrolysis. Due to helicases’ vital role in genome maintenance, helicase defects are specifically linked to various cancers (1–3) and aging disorders (4). Helicases are divided into six superfamilies (SFs) based on structure and function. SF1 and SF2 are composed of the monomeric helicases (5–7). Structural studies of SF1 and SF2 helicases have revealed many conserved residues and motifs involved in walking along DNA and ATP binding and hydrolysis. Hel308 is a representative of the SF2A DNA helicases/translocases and possesses structure that is highly conserved in both archaea and eukarya, including humans (8). It has been proposed that Hel308 is recruited to stalled replication forks to restart the replication process (9, 10). Hel308 is an interesting system because it requires the coordination of several protein domains in addition to the Walker motifs (8) that are ubiquitous in SF1 and SF2 helicases, and can be used to develop general models for how SF1 and SF2 helicases move along ssDNA. Hel308 has been primarily studied by bulk assays, which cannot directly probe the mechanisms by which it walks on and unwinds DNA.

Single-molecule technologies that monitor the kinetics of single enzymes at high resolution in real time have enhanced mechanistic understanding of helicases and other motor enzymes. Techniques such as optical tweezers (11), magnetic tweezers (12), and Förster resonance energy transfer (13) have been used to infer kinetic mechanisms of helicases such as UvrD (14, 15), PcrA (16), Hepatitis C NS3 helicase (17, 18), RecQ (19), and XPD-like helicases (20). It has been shown that SF1 and SF2 helicases step in single-nucleotide steps and that ATP binding causes a conformational change followed by ATP hydrolysis and ADP release; at some point in this cycle, a conformational change back to the original state results in the completion of a single-nucleotide step along the DNA (14, 16, 18, 21, 22). During this cycle, changes in how tightly the two RecA-like domains hold onto the DNA backbone enable processive, inchworm-like motion of the helicase along the DNA. While much is known, the exact timing and choreography of these events are unclear (5). To fully understand the exact mechanism by which ATP hydrolysis coordinates the directed motion of the helicase along DNA, a technique with the ability to resolve kinetic substeps of the hydrolysis cycle is required.

Recently, nanopore-sensing experiments have emerged as a powerful tool for single-molecule detection (23–29). Here, we applied a nanopore-based single-molecule technique that we developed (26, 27), called single-molecule picometer-resolution nanopore tweezers (SPRNT), to analyze the kinetic mechanism of translocation by the helicase Hel308 on single-stranded DNA (ssDNA). SPRNT has the spatiotemporal resolution necessary to resolve kinetic substates of the ATP hydrolysis cycle (27), and by directly observing these kinetic substates we have constructed a detailed kinetic model of Hel308 translocation on ssDNA.

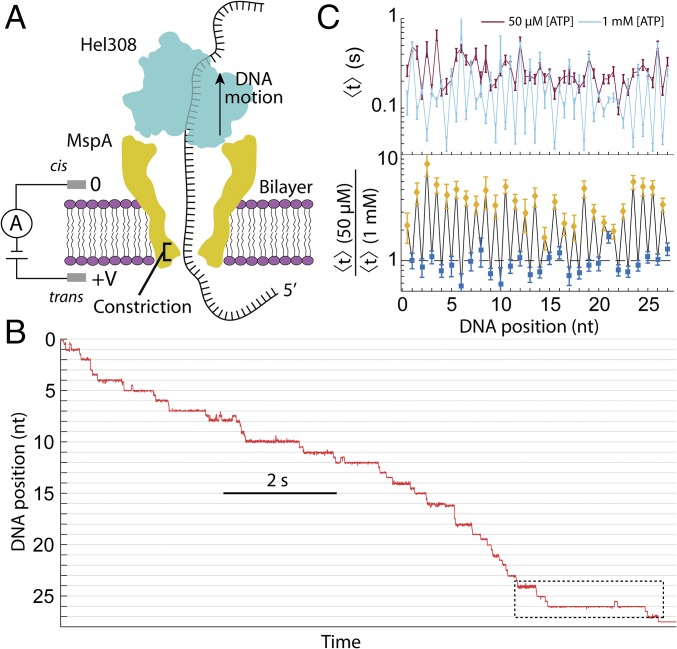
SPRNT is an in vitro single-molecule technique for monitoring the motion of DNA through a motor enzyme with unprecedented spatiotemporal resolution. In SPRNT, a single Mycobacterium smegmatis porin A (MspA) nanopore in a phospholipid bilayer forms the only electrical connection between two salt solutions (Fig. 1A). A voltage applied across the pore causes an ion current to flow through the pore. Negatively charged ssDNA bound to the motor enzyme is attracted to the pore and is then drawn through the pore by the electric field. Once the motor enzyme comes to rest on the rim of MspA, it controls the progression of the DNA through the pore. The DNA bases in the pore modulate the ion current through the pore depending on the base sequence, resulting in a highly reproducible succession of discrete ion current amplitudes (SI Appendix, Fig. S1). The ion current amplitudes indicate the DNA sequence, and thereby provide a single-molecule record of an enzyme’s progression along the DNA (28, 29). The ion current is converted to a measurement of DNA position with subangstrom spatial resolution on millisecond timescales (27) (Fig. 1B and SI Appendix, Fig. S1). Because DNA position and sequence are simultaneously measured at submillisecond resolution, SPRNT is ideal for analyzing how DNA sequence affects enzyme translocation activity. For full details of the SPRNT methodology, we refer the reader to refs. 26 and 27.

Fig. 1.

Schematic of SPRNT and Hel308 helicase. (A) A schematic of Hel308 translocase experiment. A single Hel308 molecule on an MspA pore draws the ssDNA out of the pore. The DNA in the pore modulates the ion current through the pore depending on the bases in the constriction, enabling measurements of enzyme position. (B) Position versus time trace for a single Hel308 molecule moving on ssDNA. The section of data in the dashed box will be examined in Fig. 2. These data are sampled at 500 Hz. (C, Top) The average dwell time of Hel308 enzyme states versus DNA position at [ATP] = 50 µM (dark red) and [ATP] = 1,000 µM (light blue). (C, Bottom) The ratio of the two curves from above for [ATP]-dependent steps (yellow) and [ATP]-independent steps (blue).

Using SPRNT, we established that the helicase Hel308 from Thermococcus gammatollerans moves in two steps per nucleotide translocated along ssDNA. These steps are likely the combined result of conformational changes of Hel308 on the rim of MspA and motion of the DNA through the enzyme that result in our observation of two ∼1/2-nt movements of the DNA through the pore per nucleotide translocated (27) (Fig. 1B). Increasing [ATP] caused the average dwell time of steps at half-integer nucleotide positions to decrease, while the average dwell time of steps at integer nucleotide positions did not change, demonstrating the presence of two observable substates of the Hel308 ATP hydrolysis cycle (Fig. 1C). We call the half-integer DNA positions “[ATP]-dependent steps” and the integer DNA positions “[ATP]-independent steps.” Here, we used SPRNT recordings of thousands of Hel308-ssDNA translocations (SI Appendix, Table S1) to pursue two major goals: first, to develop a kinetic model that places known chemical processes such as ATP binding, ATP hydrolysis, and ADP release in the context of the [ATP]-dependent and [ATP]-independent steps. Second, we analyzed the dwell times at each DNA position separately to look for sequence-dependent translocation of Hel308 on ssDNA.

Kinetic Methods

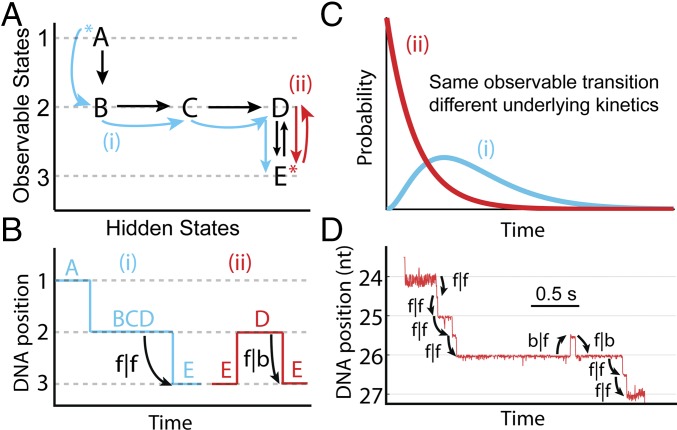
Because helicases and other enzymes operate at energy scales similar to the thermal energy, they move both forward and backward along nucleic acid tracks. With SPRNT, it is possible to resolve these quick forward (Hel308 movement from 3′ to 5′) or backward (5′ to 3′) transitions at saturating [ATP]. We analyzed the properties of forward and backward steps as a function of experimental conditions and DNA position, and considered the initial conditions of each enzyme step (30, 31). As an example, Fig. 2A shows a hypothetical kinetic model. The different rows represent observable states (labeled observable states 1, 2, and 3). Transitions within the rows do not cause enzyme progression along the DNA and cannot be directly observed, but their existence can be inferred by analyzing dwell time distributions at each DNA position (SI Appendix, Fig. S2). We call transitions within rows “hidden chemical transitions.” The two paths (red and blue, Fig. 2A) both pass through observable state 2 and conclude in observable state 3 (Fig. 2B). However, because the two paths proceed through different hidden chemical transitions within observable state 2, the underlying dwell time distributions for observable state 2 are different (Fig. 2C). In this article, we use the following notation for transitions between observable states: f|f for a forward step following forward step (the enzyme’s “normal” step), f|b for a forward step following a backward step, and b|f for a backward step following a forward step. Backward steps following backward steps (b|b) were rare, and we did not analyze them in detail. We studied the kinetics of f|f, f|b, and b|f steps for both of Hel308’s observable states ([ATP]-dependent and [ATP]-independent) to determine the kinetic pathway of Hel308 translocation. Examples of these step types are shown in Fig. 2D.

Fig. 2.

Kinetic methods. (A) A hypothetical kinetic model, with two possible enzyme paths through the model. In path i (blue), the progression of chemical states is A → B → C → D → E, resulting in three observed steps in SPRNT (1–3). In path ii (red), the progression of chemical states is E → D → E, resulting again in three observed steps (3, 2, 3). The asterisk (*) indicates the initial kinetic state. (B) Hypothetical DNA position vs. time trace for the two paths shown in A. On average, the dwell time of the second step is longer in path i because that path goes through multiple hidden kinetic steps, whereas in path ii the dwell time is determined by D → E alone, resulting in a short average dwell time. (C) Hypothetical probability distribution of dwell times for paths i and ii (blue and red, respectively). (D) Raw DNA position vs. time data trace for Hel308 on ssDNA (dashed box in Fig. 1B), with step classifications indicated.

Results

ATP and ADP Binding to Hel308.

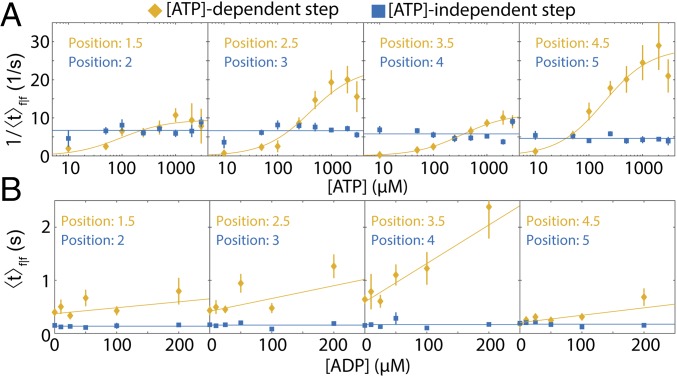
We varied [ATP] and [ADP] independently to analyze their effects on Hel308 translocation. Fig. 3A shows the reaction rates for f|f [ATP]-dependent and f|f [ATP]-independent steps at several DNA positions as a function of [ATP] at [ADP] = 0. The data were binned by DNA position to probe for potential sequence-dependent kinetics. Unsurprisingly, rates of the individual f|f [ATP]-independent steps are unchanged over this [ATP] range. The rate of each f|f [ATP]-dependent step is well described by the Michaelis–Menten kinetics with V, the reaction rate at saturating [ATP], in the range of 10–34 s⁻¹ and with Michaelis constant, K, spanning the range of 66–412 μM. (SI Appendix, Fig. S3 and Table S2). V and K are related to the underlying chemical rate constants. The large variation of V and K at different DNA positions suggests that the Hel308 stepping behavior depends on the DNA sequence in Hel308.

Fig. 3.

ATP and ADP binding to Hel308. (A) The average rate of reaction for four sequential f|f [ATP]-dependent steps (yellow) and four sequential f|f [ATP]-independent steps (blue) as a function of [ATP] ([ADP] = 0). The rate is calculated by taking the reciprocal of the arithmetic mean dwell time. The DNA positions from Fig. 1B are displayed above. The x axis is logarithmic. The yellow lines represent the best-fit Michaelis–Menten equation to the [ATP]-dependent data. The blue lines are the weighted average of the [ATP]-independent data. (B) The mean dwell time for the same f|f [ATP]-dependent steps (yellow) and [ATP]-independent steps (blue) as in A, as a function of the [ADP] ([ATP] = 50 µM). The yellow lines are the best linear fit to the data, while the blue lines are weighted average of the [ATP]-independent data. All error bars are SEM.

Fig. 3B shows the average dwell time of f|f steps for the same DNA positions as in Fig. 3A, but with constant [ATP] = 50 μM and varying [ADP]. The average dwell time of f|f [ATP]-dependent steps increases linearly with [ADP], implying that ADP acts as an inhibitor to the forward progression of Hel308 in the [ATP]-dependent step (SI Appendix, Fig. S4). The dwell time of f|f [ATP]-independent steps is unaffected by the presence of ADP, implying that ADP binding/unbinding to Hel308 does not occur during the [ATP]-independent step.

Changing the kinetic state that an enzyme reaction starts in can provide additional information about the underlying kinetic mechanism. To determine whether the initial conditions affected the [ATP]-dependent step kinetics, we compared the rate of f|f [ATP]-dependent steps to f|b [ATP]-dependent steps as a function of [ATP] for several DNA positions at which the following [ATP]-independent step moved backward often enough to collect significant statistics (SI Appendix, Fig. S5). Surprisingly, the kinetics of f|f and f|b [ATP]-dependent steps are nearly identical, with f|b steps following Michaelis–Menten kinetics with very similar values of V and K. The underlying dwell time distributions were also indistinguishable (eight of eight tested steps with P > 0.05, SI Appendix, Fig. S5). The similarity of these distribution functions can be used to constrain the parameters of the underlying kinetics (SI Appendix).

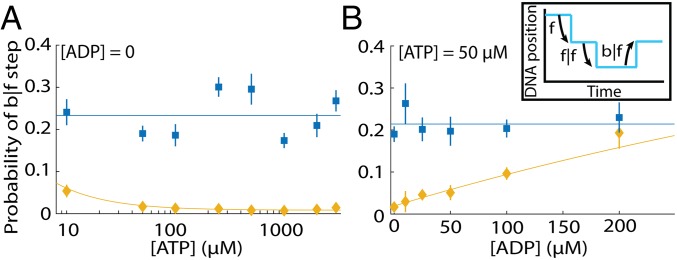
Next, we analyzed b|f steps to understand backward motion of Hel308. We first noticed that the probability of a b|f [ATP]-independent step varies with DNA position, ranging from ∼1 to ∼60% (SI Appendix, Fig. S6), suggesting that the energetics landscape of Hel308 stepping is modified by the DNA sequence. Fig. 4A shows the probability of a b|f step at varying [ATP] ([ADP] = 0) for both [ATP]-dependent and [ATP]-independent steps, averaged over DNA position to accumulate sufficient statistics (n = 21 DNA positions, with n = 30,417 time intervals evaluated). We found that the probability of a b|f [ATP]-independent step is independent of [ATP]. For the [ATP]-dependent step, the probability of a b|f step increases slightly at low ATP concentrations. Fig. 4B shows the probability of b|f step at varying [ADP] ([ATP] = 50 µM). The probability of a b|f [ATP]-independent step is independent of [ADP]; however, the probability of a b|f [ATP]-dependent step grows with [ADP] from ∼2% at [ADP] = 0 to ∼20% at [ADP] = 200 µM, demonstrating that ADP helps to drive Hel308 backward along the DNA.

Fig. 4.

Hel308 backward steps. (A) The probability of a b|f [ATP]-independent step (blue) and [ATP]-dependent step (yellow) at varying [ATP] and fixed [ADP] = 0, averaged over all DNA positions. The weighted average of the [ATP]-independent data are plotted on Top. The yellow line is fit based on our kinetic model for Hel308 (Fig. 6A and SI Appendix, Eq. S45). The x axis is logarithmic. (Inset) An illustration of b|f steps. (B) The probability of a b|f [ATP]-independent step (blue) and [ATP]-dependent step (yellow) at varying [ADP] and fixed [ATP] = 50 µM. The blue line is the weighted average of the [ATP]-independent data. The yellow line is fit based on our kinetic model for Hel308 (Fig. 6 and SI Appendix, Eq. S45). All error bars are SEM.

Analysis of f|f, f|b, and b|f [ATP]-Independent Dwell Time Distributions.

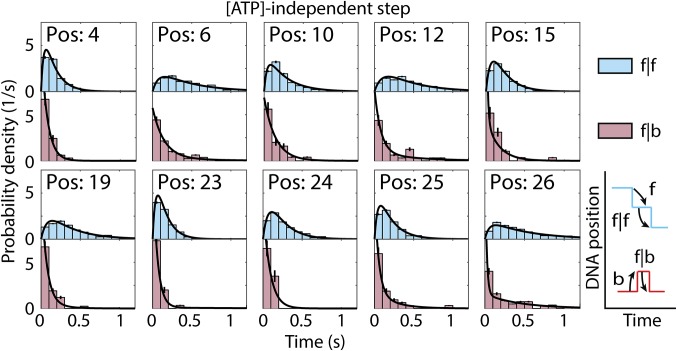
Because the average dwell time of f|f [ATP]-independent steps is independent of both [ATP] and [ADP] (Fig. 3), we assumed that the underlying dwell time distributions for each step were also unaffected by [ATP] and [ADP]. This allowed us to combine our data at various [ATP] and [ADP], yielding large statistics for each step. Fig. 5 shows the dwell time distributions for f|f and f|b [ATP]-independent steps for each DNA position with n > 20 counts of the f|b step. We compared these distributions with several classes of exponential distribution functions to probe the minimum number of hidden chemical transitions in the [ATP]-independent step (SI Appendix, Table S3). We found that the dwell time distributions of f|f [ATP]-independent steps are best described by the convolution of two exponential distributions, implying the existence of at least one hidden chemical step in the forward progression of the [ATP]-independent step. In contrast, for f|b steps the dwell time distributions are best described by the sum of two exponentials (SI Appendix, Table S4), which could be caused by one of several effects. First, if following a backward step the reaction can be further reversed, then we would expect the dwell time distribution to be the sum of exponentials (SI Appendix). It could also suggest that following a backward step that there are two possible pathways from which the [ATP]-independent step can then go forward to the [ATP]-dependent step. Because the f|f [ATP]-independent steps are well modeled by the convolution of two exponentials, this would then suggest that there are multiple pathways through which the [ATP]-dependent step can go backward to the preceding [ATP]-independent step. As with the [ATP]-dependent steps, we find that the [ATP]-independent dwell time distributions depend on the position of Hel308 along the DNA, suggesting that the DNA sequence also modifies the kinetics of the [ATP]-independent step.

Fig. 5.

[ATP]-independent step dwell time distributions. Probability distribution of dwell times for f|f [ATP]-independent steps (Top, light blue) and f|b steps (Bottom, light red). The black lines drawn on the histograms are maximum-likelihood estimates for two convolved exponential distributions (f|f steps, SI Appendix, Eq. S17) or a mixed two-exponential distribution (f|b steps, SI Appendix, Eq. S19). Only DNA positions with n > 20 measurements of the f|b step are included. Error bars are SEM.

We similarly compared the dwell time distributions of f|f to b|f [ATP]-independent steps. SI Appendix, Fig. S6C shows the dwell time distributions for f|f and b|f steps for each DNA position with n > 50 counts of the b|f step. Surprisingly, we found that the f|f and b|f dwell time distributions were very similar (31), and for some DNA positions were statistically indistinguishable (8 of 16 DNA positions with P > 0.05, SI Appendix, Fig. S6C). This suggests either that the rate constants are finely tuned to produce similar histograms, or that some population of b|f steps follow a chemical pathway parallel to f|f steps, which instead results in an unproductive forward step, stepping a half-nucleotide backward instead. Interestingly, in each of the histograms in SI Appendix, Fig. S6C, the b|f step has a higher fraction of short dwell time steps compared with the f|f step, suggesting that at least some population of the b|f steps are the reverse process of the previous f|f [ATP]-dependent step, or what we call an on-pathway backstep. This is similar to the logic presented in Fig. 2B: for an on-pathway f|f [ATP]-independent step, Hel308 must go through multiple hidden chemical transitions to reach its final state, but for an on-pathway b|f step, Hel308 may only go through one kinetic step to move backward, leading to a larger fraction of short dwell times compared with f|f steps. Because we cannot determine whether these b|f steps are on-pathway or off-pathway, interpretation of the f|b [ATP]-dependent step data are more complicated, since we cannot know if the initial conditions of the [ATP]-dependent step are truly modified.

Variation of Voltage and Temperature.

SPRNT permits force spectroscopy by varying the voltage across the pore. Because force coupling in some mechanochemical kinetic models depends on the substrate concentration (32), we calculated the mean dwell time of both f|f [ATP]-dependent and f|f [ATP]-independent steps at nearly saturating ([ATP] = 500 µM) and subsaturating ([ATP] = 50 µM) conditions at [ADP] = 0, averaged over DNA position (SI Appendix, Fig. S7 and Table S5). For both [ATP]-dependent and [ATP]-independent steps, we found that the average dwell time is independent of the applied voltage in the range of 140–280 mV (force estimated as ∼30–65 pN) (27).

Changing the temperature of the solution can yield further insight into the energetics of helicase motion (SI Appendix, Fig. S7). We varied the temperature of the reaction volume from 22 to 45 °C while maintaining [ATP] = 500 µM and [ADP] = 0, and found that the average dwell time of both f|f [ATP]-dependent and f|f [ATP]-independent steps are well described by an exponential function of the reciprocal temperature, consistent with Arrhenius’ equation (SI Appendix). Because the kinetics are independent of the applied force, the activation energy is determined by fitting to Arrhenius’ equation. We found the activation energies for the [ATP]-dependent and [ATP]-independent steps were 60 ± 11 and 77 ± 15 kJ/mol, respectively. Because there are hidden chemical transitions in both the [ATP]-dependent and [ATP]-independent steps and because we averaged over DNA position, the calculated activation energies are the average activation energy for the rate-limiting substep of each observable step type.

Development of Hel308 Kinetic Model.

We sought to construct the simplest possible kinetic model of Hel308 translocation consistent with each of the above observations. Because the [ATP]-independent step kinetics were independent of [ATP], [ADP], and applied force (Fig. 3 and SI Appendix, Fig. S7), we focused on developing a model of the [ATP]-dependent step, and then hypothesized what processes occur during the [ATP]-independent step. We had established that ADP binding to Hel308 caused an increase in the average dwell time of f|f [ATP]-dependent steps (Fig. 3B), implying that the ADP unbinding/binding is a hidden chemical transition within the [ATP]-dependent step. Similarly, we knew that ATP binding must occur during the [ATP]-dependent step. Because the average dwell time of [ATP]-independent steps did not change when varying either [ATP] or [ADP], neither ATP nor ADP binding should occur in our model during the [ATP]-independent step.

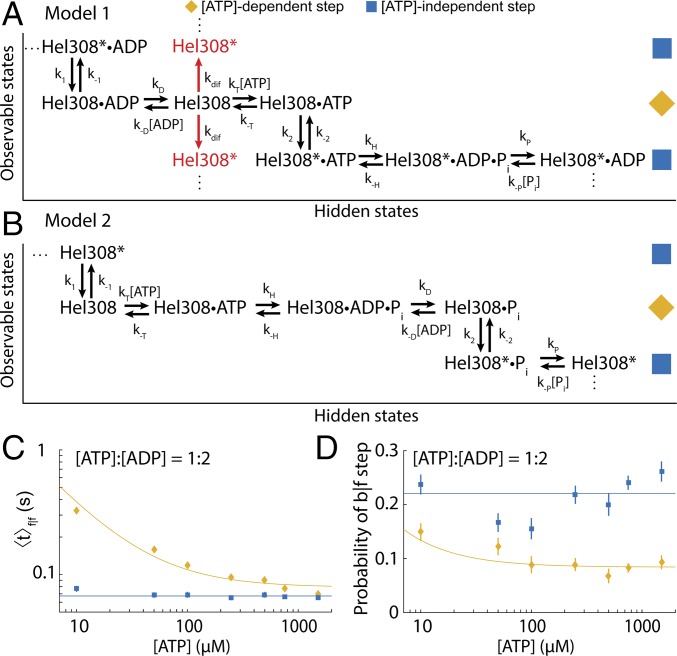
Because ATP and ADP binding/unbinding occurred during the [ATP]-dependent step, we were restricted to two general classes of model: those in which the ADP unbinding precedes the ATP binding, and vice versa. In model 1 (Fig. 6A), ADP unbinds from Hel308 at the end of the previous hydrolysis cycle during the [ATP]-dependent step and is followed by ATP binding. Then the enzyme undergoes a conformational change to the [ATP]-independent step. Hel308 then proceeds through the remainder of the hydrolysis cycle in the [ATP]-independent step before transitioning back to the [ATP]-dependent step with ADP still bound. A similar model in which ATP directly induces the transition from the [ATP]-dependent step to the [ATP]-independent step is explored in SI Appendix; we found it to be inconsistent with the data. In model 2 (Fig. 6B), the [ATP]-independent step concludes with a thermally driven conformational change that is rectified upon ATP binding during the [ATP]-dependent step. ATP is then hydrolyzed to ADP, whereupon ADP is released before Hel308 undergoes a conformational change back to the [ATP]-independent step.

Fig. 6.

Models of Hel308 translocation on ssDNA. (A) Kinetic model 1. The placement of the phosphate unbinding step is done so as not to lead to any contradictions to the data. The asterisk (*) indicates Hel308 is in the [ATP]-independent step. The red arrows indicate an alternative model, in which free Hel308 can diffuse between translocation states. (B) Kinetic model 2. The placement of the phosphate unbinding step is done somewhat arbitrarily, to maintain multiple rate constants for the [ATP]-independent step. (C) Average dwell time taken over DNA position of f|f [ATP]-dependent steps (yellow) and f|f [ATP]-independent steps (blue) at varied [ATP] while maintaining a constant ratio of [ATP]:[ADP] = 1:2. The best fit to Eq. 2 for the [ATP]-dependent step is plotted on top (yellow). The weighted average of [ATP]-independent step data are plotted on top (blue). (D) The probability of a b|f [ATP]-dependent step (yellow) and [ATP]-independent step (blue) at varied [ATP] while maintaining a constant ratio [ATP]:[ADP] = 1:2. The weighted average of the [ATP]-independent step data are plotted on top. The yellow line is fit based on model 1 + diffusion (SI Appendix, Eq. S42). The weighted average of the [ATP]-independent step data is plotted on the data (blue line). The experiments of C and D were done at elevated temperature T = 37 °C to increase the entry rate of DNA–Hel308 complexes into the pore. All error bars are SEM.

The data are more consistent with model 1 for two reasons.

First, model 1 and model 2 predict different dependences of the average dwell time of f|f [ATP]-dependent steps on [ATP] and [ADP] (SI Appendix, Fig. S8):

$${\langle t\rangle }_{f|f,\text{model}\hspace{0.17em}1}=\frac{K+\left[\mathrm{ATP}\right]+d\cdot \left[\mathrm{ADP}\right]}{V\cdot \left[\mathrm{ATP}\right]}\hspace{0.17em},$$ [1]

$${\langle t\rangle }_{f|f,\text{model}\hspace{0.17em}2}=\frac{K\prime +\left[\mathrm{ATP}\right]+d\prime \cdot \left[\mathrm{ADP}\right]+e\cdot \left[\mathrm{ATP}\right]\cdot \left[\mathrm{ADP}\right]}{V\prime \cdot \left[\mathrm{ATP}\right]}\hspace{0.17em}.$$ [2]

V and K are the standard Michaelis–Menten parameters. The $\prime$ in Eq. 2 indicates that the model parameters are related to the underlying rate constants differently in the two models (SI Appendix). In model 2, the term e couples the average dwell time of f|f [ATP]-dependent steps to the product [ATP]⋅[ADP]. Fig. 6C shows the dwell time averaged over all DNA positions versus [ATP] at fixed [ATP]:[ADP] = 1:2 ([ATP]:[ADP] = 1:4, SI Appendix, Fig. S9). Fitting to Eq. 2 for both experiments yields e ∼ 0, so that Eq. 2 takes the form of Eq. 1. It is unphysical for the parameter e to be 0 in model 2 (SI Appendix), implying that model 1 better describes the data.

Second, in model 1, ATP and ADP compete for the ATP binding site, implying that the probability of a b|f [ATP]-dependent step depends only on the ratio [ATP]:[ADP]. In model 2, [ATP] and [ADP] contribute separately to the probability of a b|f [ATP]-dependent step (SI Appendix, Fig. S8 and Eqs. S43 and S44). Fig. 6D shows the probability of a b|f step for [ATP]-dependent and [ATP]-independent steps as a function of [ATP], while maintaining a fixed ratio [ATP]:[ADP] = 1:2 ([ATP]:[ADP] = 1:4, SI Appendix, Fig. S9). We found that, in each experiment, the probability of a b|f step increases when [ATP] decreases, seemingly at odds with model 1, and in support of model 2, although neither model fits the data particularly well. With a slight modification to model 1, allowing for free diffusion of Hel308 with neither ATP nor ADP bound, we were able to simultaneously fit the probability of a b|f [ATP]-independent against both [ATP] and [ADP] much better, suggesting that model 1 + diffusion best describes the data [Fig. 6A, red, and SI Appendix, Fig. S9; one-dimensional diffusion has been observed in RNA polymerase at low [NTP] (33)]. These results are consistent with the distribution of f|b [ATP]-independent steps being the sum of exponentials; because there are two different modes through which Hel308 can move backward, the distribution of f|b [ATP]-independent dwell times will then be a mix of those dwell times which follow the on-pathway [ATP]-dependent backward step and those which follow the diffusive step.

Assuming model 1 (Fig. 6A) and analyzing the distribution of dwell times for each [ATP]-dependent f|f step, we calculated the parameters k_±T, k₂, k_±D for the [ATP]-dependent step at each DNA position (Fig. 6A and SI Appendix, Fig. S10 and Tables S6 and S7). We found that on average k_−T ∼ 30 s⁻¹, k_T ∼ 0.3 μM⁻¹⋅s⁻¹, k₂ ∼ 17 s⁻¹, k_D ∼ 170 s⁻¹ and k_−D ∼ 4 μM⁻¹⋅s⁻¹. We can also use that the probability of a b|f [ATP]-dependent step is ∼0.01 at [ADP] = 0 and saturating [ATP] to estimate that on average k₋₁ ∼ 2 s⁻¹. At saturating [ATP], the rate-limiting step of the f|f [ATP]-dependent step is k₂, implying that the conformational change of Hel308 is the rate-limiting step.

Discussion

We used SPRNT’s high spatiotemporal resolution to determine the mechanism of Hel308 translocation on ssDNA by analyzing previously unobservable transitions between two substates of its ATP hydrolysis cycle, while using SPRNT’s ability to provide the sequence-specific position of Hel308 along the DNA to find evidence for sequence-dependent translocation of Hel308 on ssDNA. We analyzed forward and backward steps of both observable substeps by varying [ATP], [ADP], force, and temperature to provide insights into the translocation mechanism of the [ATP]-dependent step. We found that bound ATP reduces the activation energy for Hel308 to change conformation at the end of the [ATP]-dependent step. This conformational change results in the DNA being moved forward by a half-nucleotide through the pore. ADP binding works nearly identically: ADP binds to Hel308, lowering the activation energy for Hel308 to change conformation, but this conformational change results in the DNA being moved backward a half-nucleotide instead. Our data show that, instead of directly causing the conformational change, bound ATP and ADP lower the activation energy for the change, while the nucleotide’s identity (ATP or ADP) determines the direction of motion. This suggests that Hel308 walks along ssDNA by taking advantage of energy differences between ATP and ADP bound states, which results in directed motion of Hel308 along ssDNA. Because the Walker and ATP binding domains are broadly conserved across SF1 and SF2 helicases, we suggest that the choreography revealed here in Hel308 applies generally to other SF1 and SF2 helicases as well. Performing SPRNT on other SF1 and SF2 helicases will settle this question.

Because subnucleotide steps are well resolved and the DNA bases near the enzyme are being simultaneously sequenced by nanopore sequencing, SPRNT is uniquely suited among single-molecule techniques to examine DNA position-dependent kinetics. Sequence-dependent unwinding kinetics have been observed in SF1/SF2 helicase systems, due to the relative energies required to unwind GC versus AT base pairs (18, 34, 35). However, this work presents an observation of sequence-dependent translocation of a helicase on ssDNA. Alternative hypotheses such as sequence-dependent force on the DNA in the nanopore (36), interactions between the DNA and the MspA nanopore, or the formation of DNA secondary structures on the trans side of MspA, each of which would result in sequence-dependent forces on the DNA can be ruled out because the translocation rate of Hel308 is independent of the applied force. As a control, we changed the DNA nucleotides in and around the MspA constriction while keeping the same nucleotides in Hel308 (SI Appendix, Fig. S11). We found that both the state dwell times and the probability of a b|f [ATP]-independent step did not change when we changed the DNA sequence in MspA, suggesting that the nucleotides in Hel308 determine the translocation kinetics. Further experiments comparing SPRNT with other techniques will help to determine what effect, if any, the pore has on enzyme kinetics. We were unable to find a significant correlation between single bases and either the dwell times or probability of b|f steps, suggesting that multiple bases affect kinetic parameters. The crystal structure of a Hel308 helicase conjugated with DNA shows ∼10 amino acid–DNA base interactions between the helicase and template DNA strand, suggesting that the role DNA sequence plays in determining translocation kinetic parameters may be complex (21). Most of the contacts made between the Walker and Winged-Helix domains and DNA are hydrogen-bonding interactions between the amino acids and the DNA backbone and therefore likely do not lead to sequence specificity. We suggest that the ratchet domain 4, which forms several base-specific contacts with the template DNA, is the most likely candidate to confer sequence specificity to the motion of Hel308 along ssDNA. Further SPRNT studies of Hel308 on a variety of sequences will be required to fully understand DNA sequence-dependent phenomena. Other nucleic acid-processing enzymes that have been measured with other single-molecule techniques that are blind to the underlying DNA sequence may have sequence-specific behavior that could not have been recognized and are thus worth revisiting with SPRNT.

While SPRNT stems from nanopore DNA sequencing, the ability to perform in-depth kinetic analysis of enzymes using SPRNT can be used to improve nanopore sequencing. Nanopore sequencing is hindered, in part, by enzyme stepping behaviors such as backward steps and missed ion current steps due to fast progression through the kinetic pathway. Mutations to promising enzymes can be investigated kinetically and selected for properties such as low probability of backstep, high throughput, and multiple rate constants per step (as opposed to a single rate-limiting step; Fig. 2B, Inset) to regularize the motion of the motor. An enzyme such as Hel308 with many kinetic substates that occur on similar timescales will have a more regular average dwell time per nucleotide compared with an enzyme with a single limiting rate constant, which can help to determine the lengths of homopolymer sequences. Optimization of the controlling motor enzyme will be an important step in maximizing nanopore sequencing accuracy.

Materials and Methods

A single M2-NNN MspA nanopore was established in a 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC) or a 1,2-di-O-phytanyl-sn-glycero-3-phosphocholine (DOPC) lipid bilayer using methods that have been well established (26). All experiments were run at 400 mM KCl, with 10 mM Hepes at pH 8.0 and 10 mM MgCl₂. ATP and ADP were perfused to the cis well to maintain constant concentration in the reaction volume (SI Appendix, Table S1). Reagents were reperfused every 45 min to prevent bulk accumulation of ADP. DNA, DTT, and Hel308 were added to final concentrations of 5 nM, 1 mM, and 50 nM, respectively. Full methods are described in SI Appendix (37–44).