Algorithm for cellular reprogramming

Significance

Reprogramming the human genome toward any desirable state is within reach; application of select transcription factors drives cell types toward different lineages in many settings. We introduce the concept of data-guided control in building a universal algorithm for directly reprogramming any human cell type into any other type. Our algorithm is based on time series genome transcription and architecture data and known regulatory activities of transcription factors, with natural dimension reduction using genome architectural features. Our algorithm predicts known reprogramming factors, top candidates for new settings, and ideal timing for application of transcription factors. This framework can be used to develop strategies for tissue regeneration, cancer cell reprogramming, and control of dynamical systems beyond cell biology.

Abstract

The day we understand the time evolution of subcellular events at a level of detail comparable to physical systems governed by Newton’s laws of motion seems far away. Even so, quantitative approaches to cellular dynamics add to our understanding of cell biology. With data-guided frameworks we can develop better predictions about, and methods for, control over specific biological processes and system-wide cell behavior. Here we describe an approach for optimizing the use of transcription factors (TFs) in cellular reprogramming, based on a device commonly used in optimal control. We construct an approximate model for the natural evolution of a cell-cycle–synchronized population of human fibroblasts, based on data obtained by sampling the expression of 22,083 genes at several time points during the cell cycle. To arrive at a model of moderate complexity, we cluster gene expression based on division of the genome into topologically associating domains (TADs) and then model the dynamics of TAD expression levels. Based on this dynamical model and additional data, such as known TF binding sites and activity, we develop a methodology for identifying the top TF candidates for a specific cellular reprogramming task. Our data-guided methodology identifies a number of TFs previously validated for reprogramming and/or natural differentiation and predicts some potentially useful combinations of TFs. Our findings highlight the immense potential of dynamical models, mathematics, and data-guided methodologies for improving strategies for control over biological processes.

In 1989, pioneering work by Weintraub et al. (1) successfully reprogrammed human fibroblasts into muscle cells via overexpression of transcription factor (TF) MYOD1, becoming the first study to demonstrate that the natural course of cell development could be altered. In 2007, Yamanaka and coworkers (2) changed the paradigm further by successfully reprogramming human fibroblasts into an embryonic stem-cell–like state [induced pluripotent stem cells (iPSCs)], using four TFs: POU5F1, SOX2, KLF4, and MYC. This work showed that a differentiated cell state could be reverted to a more pluripotent state. These discoveries have changed the trajectory of regenerative medicine, opening the possibility of generating needed cell types on demand for repairing damaged or diseased tissues. Ultimately, patient-derived fibroblasts could be used in autologous transplantations to minimize immune incompatibility.

These remarkable findings also demonstrate that the genome is a system capable of being controlled via an external input of TFs. In this context, determining how to push the cell from one state to another is, at least conceptually, a classical problem of control theory (3). The difficulty arises in the fact that the dynamics—and even proper representations of the cell state and inputs—are not well defined in the context of cellular reprogramming. Nevertheless, it seems natural to treat reprogramming as a problem in control theory, with the final state being the desired reprogrammed cell. In this paper, we provide such a framework based on empirical data and demonstrate the potential of this framework to provide insights into cellular reprogramming (4).

Our goal is to mathematically identify TFs that can directly reprogram human fibroblasts into a desired target cell type. As part of our methodology, we create a model for the natural dynamics of proliferating human fibroblasts, using time series data collected throughout the cell cycle. We couple data from bioinformatics with methods of mathematical control theory—a framework that we dub data-guided control (DGC). We use this model to determine a principled way to identify the best TFs for efficient reprogramming.

Previously, selection of TFs for reprogramming has been based largely on trial and error, typically relying on TF differential expression between cell types for initial predictions. Recent work has sought to predict TFs for reprogramming the cell state (5–8). Rackham et al. (7) devised a predictive method based on differential expression, as well as gene and protein network data. Our approach is fundamentally different in that we take a dynamical systems point of view, opening avenues for investigating efficiency (probability of conversion), timing (when to introduce TFs), and optimality (minimizing the number of TFs and amount of input).

Our method identifies TFs previously found to reprogram human fibroblasts into embryonic stem-cell–like cells, muscle cells, and many additional target cell types. Furthermore, our analysis predicts the points in the cell cycle at which the introduction of TFs might most efficiently affect a desired change of cell state. In addition, we demonstrate the efficacy of using topologically associating domains (TADs) for genome dimension reduction. Implicit in this approach is the notion of distance between cell types, which is measured in terms of the amount of transcriptional change required to transform one cell type into another. In this way, we are able to provide a comprehensive quantitative view of human cell types based on the respective distances between them.

Our framework separates into three parts:

• i)Define the state. Use structure and function observations of the initial and target cell types’ genomes to define a comprehensive state representation.
• ii)Model the dynamics. Apply model identification methods to approximate the natural dynamics of the genome from time series data.
• iii)Define and evaluate the inputs. Infer from bioinformatics (TF binding location and function) where TFs can influence the genome and then quantify controllability properties with respect to the target cell type.

The actual dynamics of the genome are undoubtedly very complicated, but as is often done in mathematical modeling studies, we use measurements to identify a linear approximation. This will take the form of a difference equation that is widely studied in the control systems literature, (9):

$$x_{k+1}=A_k{x}_k+B{u}_k.$$ [1]

In this case, the three items listed above correspond respectively to the value of the state $x_k$ at time $k$, the time-dependent state transition matrix $A_k$, and the input matrix $B$ (along with the input function $u_k$).

Methods

Genome-State Representation and Dimension Reduction: ${𝐱}_{\text{𝒌}}$.

The state representation $x$ in Eq. 1 is the foundation for any control system and is critical for controllability analysis. To fully represent the state of a cell, a high number of measurements would need to be taken, including gene expression, protein level, chromatin conformation, and epigenetic measurements. As a simplification, we assume that the gene expression profile is a sufficient representation of the cell state.

Gene expression for a given cell is dependent on a number of factors, including (but not limited to) cell type, cell-cycle stage, circadian-rhythm stage, and growth conditions. To best capture the natural fibroblast dynamics from population-level data, time series RNA-seq was performed on cells that were cell-cycle and circadian-rhythm synchronized in normal growth medium conditions (SI Appendix). Before data collection, all cells were temporarily held in the first stage of the cell cycle, G₀/G₁, via serum starvation. Upon release into the cell cycle, the population was observed every $\mathrm{\Delta }t=8$ h for 56 h, yielding eight time points (at 0 h, 8 h, 16 h, $\dots$, 56 h). Let $g_{i,k}$ be the measured activity of gene $i=1,\dots ,N$ at measurement time $k=1,\dots ,8$, where $N$ is the total number of human genes observed (22,083). Analysis of cell-cycle marker genes indicated that the synchronized fibroblasts took between 32 h and 40 h to complete one cell cycle after growth medium introduction (SI Appendix, Fig. S1). Because of this, we define $K=5$ to be the total number of time points used for this model.

An obstacle to using $g$ to represent $x$ in a dynamical systems approach is the computational feasibility of studying a system with over 20,000 variables, necessitating a dimension reduction. A comprehensive genome-state representation should include aspects of both structure and function and simultaneously have low enough dimension to be computationally reasonable. Along these lines, we propose a biologically inspired dimension reduction based on TADs.

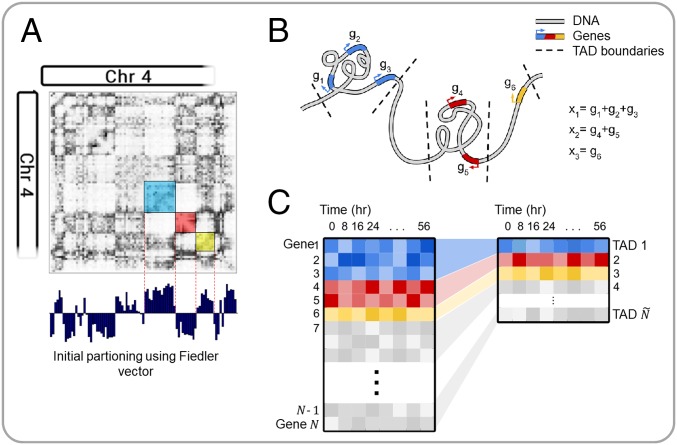
The advent of genome-wide chromosome conformation capture (Hi-C) allowed for the studying of higher-order chromatin structure and the subsequent discovery of TADs (10). TADs are inherent structural units of chromosomes: contiguous segments of the 1D genome for which empirical physical interactions can be observed (11). Moreover, genes within a TAD tend to exhibit similar activity, and TAD boundaries have been found to be largely cell-type invariant (11, 12). TADs group structurally and functionally similar genes, serving as a natural dimension reduction that preserves important genomic properties. Fig. 1 depicts an overview of this concept. We computed TAD boundaries from Hi-C data via an algorithm that uses Fielder vector partitioning, described in Chen et al. (13) (SI Appendix).

Fig. 1.

Overview of TAD dimension reduction. (A) Partitioning the Hi-C matrix based on the Fiedler vector. (B) Cartoon depiction of TAD genomic structure. (C) TAD dimension reduction summary.

Let $tad(i):=j$ if gene $i$ is contained within TAD $j$. We define each state variable $x_{j,k}$ to be the expression level of TAD $j=1,\dots ,\stackrel{\sim }{N}$ at time $k$, where $\stackrel{\sim }{N}=2,245$ is the total number of TADs that contain genes. Specifically, $x_{j,k}$ is defined as the sum of the expression levels of all genes within the TAD, measured in reads per kilobase of transcript per million (RPKM); i.e.,

$$x_{j,k}≔\sum _{\begin{array}{c}i\hspace{0.17em}\text{s.t.}\\ tad(i)=j\end{array}}{g}_{i,k}.$$ [2]

The vector of all TAD activities at measurement $k$ is denoted with a single subscript $x_k\in {ℝ}^{\stackrel{\sim }{N}\times 1},k=1,\dots ,K$.

State Transition Matrix: ${𝐀}_{\text{𝒌}}$.

Given the data we have, perhaps the most direct way to model the evolution of TAD activity level would be to assume a model of the form $x_{k+1}=x_k+u_k$, where $x_k$ and $x_{k+1}$ come from data, and $u_k$ is the exogenous input. However, in a time-varying situation, it will typically not be the best way to use the data to create a model because it fails to capture the idea that an input applied at one point in the cell cycle can be expected to have a different effect if applied at a different point in the cell cycle. Taken over a full cycle, the average value of the expression level of the 2,245 TADs is known within experimental error. Assuming that there is a function $f$ which maps $x_k$ to $x_{k+1}$, we can subtract the steady-state average, $\overline{x}$, and focus on measuring the deviation from average as the cycle evolves. With this in mind, we consider the first-order approximation $f(x)=\overline{x}+A(x-\overline{x})$, where $A$ is allowed to depend on where one is in the cell cycle. This is a time-varying linear model for the variation from $\overline{x}$. If the model is to match data and capture variability over the cell cycle, we will need to have a different $A$ for each time step. Using the principle that $A$ should differ as little from the identity as possible, we let $A_k$ be the identity plus a rank one matrix chosen to match the data for each time step $k$; we impose the condition that without inputs we have $x_{k+1}-\overline{x}=A_k(x_k-\overline{x})$.

Define a time-dependent state transition matrix $A_k$ as

$$A_k:=I_{\stackrel{\sim }{N}}+\frac{(x_{k+1}-x_k)x_k^T}{x_k^T{x}_k}\in {ℝ}^{\stackrel{\sim }{N}\times \stackrel{\sim }{N}},k=\mathrm{1,2,3,4,5},$$ [3]

where $I_{\stackrel{\sim }{N}}$ is the $\stackrel{\sim }{N}\times \stackrel{\sim }{N}$ identity matrix. Let the measured values of the state of the unforced evolution be $x_1,x_2,\mathrm{\cdots },x_5$; let the controls be labeled $u_1,u_2,\mathrm{\cdots },u_5$; let the values of the state with the controls acting be $z_2,z_3,\mathrm{\cdots },z_6$. Letting $z$ denote the deviation from the cell-cycle average, we have

$$z_{k+1}=(I+\frac{1}{x_k^T{x}_k}(x_{k+1}-x_k)x_k^T))z_k+B_{uk},$$

where $A_k$ is as above. Solving this difference equation, we have

$$z_k=\prod _{i=1}^{k-1}{A}_i{x}_1+\sum _{i=1}^{k-1}\prod _{j=i}^{k-1}{A}_{j-1}B{u}_i$$

with the understanding that $A_0=I$. This explicit expression shows that the effect of the $u(i)$ cannot be inferred from the sum of the $u_i$ because different $u_i$ are weighted in different ways, dependent on the stage in the cell cycle at which it is applied. This is a significant point relating to the model and plays a significant role in determining the optimal times for inserting TFs.

Input Matrix and Input Signal: $𝐁,{𝐮}_{\text{𝒌}}$.

With the natural TAD-level dynamics established in the context of our control Eq. 1, we turn our attention to quantifying methods for control.

A TF can regulate a gene positively or negatively by binding to a specific DNA sequence near a gene and encouraging or discouraging transcription. The degree to which a TF activates or represses gene expression depends on the specific TF–gene interaction, which is influenced by a variety of factors that are difficult to quantify. Let $w_{i,m}$ be the theoretical regulation weight of TF $m$ on gene $i$, where $w_{i,m}>0$ ($w_{i,m}<0$) if TF $m$ activates (represses) gene $i$, and $m=1,\dots ,M$, where $M$ is the total number of well-characterized TFs. Weights that are bigger in absolute value, $|w_{i,m}|\gg 0$, indicate stronger transcriptional influence, and weights equal to zero, $w_{i,m}=0$, indicate no influence.

Extensive TF perturbation experiments would be needed to determine $w_{i,m}$ for each TF $m$ on each gene $i$. Instead, we propose a simplified method to approximate $w_{i,m}$ from existing, publicly available data for TF binding sites (TFBSs), gene accessibility, and average activator/repressor activity. To determine the number of possible binding sites a TF $m$ recognizes near gene $i$, the reference genome was scanned for the locations of potential TFBSs following methods outlined by Neph et al. (14) (SI Appendix). Position frequency matrices (PFMs), which give information on TF–DNA binding probability, were obtained for 547 TFs from a number of publicly available sources ($\therefore M=547$). Let $c_{i,m}$ be the number of TF $m$ TFBSs found within $\pm 5$ kb of the transcriptional start site (TSS) of gene $i$ (SI Appendix, Fig. S2).

Although many TFs can do both in the right circumstances, most TFs have a tendency toward either activator or repressor activity (15). That is, if TF $m$ is known to activate (repress) most genes, we can say with some confidence that TF $m$ is an activator (repressor), so $w_{i,m}\ge 0$ ($w_{i,m}\le 0$) for all $i$. To determine a TF’s function, we performed a literature search for all 547 TFs and labeled 299 as activators and 124 as repressors (SI Appendix). The remaining TFs were labeled unknown for lack of conclusive evidence and were evaluated as both an activator and a repressor in separate calculations. Here, we define $a_m$ as the activity of TF $m$, with 1 and −1 denoting activator and repressor, respectively.

TFBSs are cell-type invariant since they are based strictly on the linear genome. However, it is known that for a given cell type, certain areas of the genome may be opened or closed, depending on epigenetic aspects. To capture cell-type–specific regulatory information, we obtained publicly available gene accessibility data (DNase-seq) on human fibroblasts (GSM1014531). DNase-seq extracts cell-type–specific chromatin accessibility information genome-wide by testing the genome’s sensitivity to the endonuclease DNase I and sequencing the nondigested genome fragments. These data are used for our initial cell type to determine which genes are available to be controlled by TFs (16). Here, we define $s_i$ to be the DNase I sensitivity information (accessibility; open/close) of gene $i$ in the initial state, with 1 and 0 denoting accessible and inaccessible, respectively (SI Appendix).

We approximate $w_{i,m}$ as

$$w_{i,m}:=a_m{s}_i{c}_{i,m},$$ [4]

so that the magnitude of influence is equal to the number of observed consensus motifs $c_{i,m}$, except when the gene is inaccessible ($s_i$ = 0) in which case $w_{i,m}=0$.

Since we are working off a TAD-dimensional model, our input matrix $B$ must match this dimension. Let $b_m$ be a 2,245-dimensional vector, where the $j$th component is

$$b_{j,m}≔\sum _{\begin{array}{c}i\hspace{0.17em}\text{s.t.}\\ tad(i)=j\end{array}}{w}_{i,m},$$ [5]

and define a matrix $B=\left[\begin{array}{c}\hfill b_1{b}_2\mathrm{\cdots }{b}_M\hfill \end{array}\right]$.

The amount of control input is captured in $u_k$, which is an ${ℝ}^{M\times 1}$ vector representing the quantity of the external TFs we are inputting to the system (cell) at time $k$. This can be controlled by the researcher experimentally through manipulation of the TF concentration (17). In this light, we restrict our analysis to $u_k\ge 0$ for all $k$, as TFs cannot be subtracted from the cell. $u_{m,k}$ is defined as the amount of TF $m$ to be added at time point $k$.

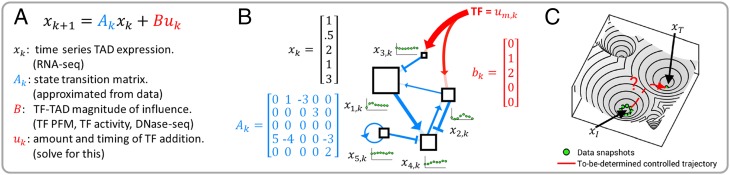
With all variables of our control Eq. 1 defined, we can now attempt to predict which TFs will most efficiently achieve cellular reprogramming from some $x_I$ (initial state; fibroblast in our setting) to $x_T$ (target state; any human cell type for which compatible RNA-seq data are available) through manipulation of $u_k$. An overview of our DGC framework is given in Fig. 2.

Fig. 2.

DGC overview. (A) Summary of control equation variables. (B) Each TAD is a node in a dynamic network. The blue connections represent the edges of the network and are determined from time series fibroblast RNA-seq data. The green plots represent the expression of each TAD changing over time. The red arrows indicate additional regulation imposed by exogenous TFs. (C) A conceptual illustration of the problem: Can we determine TFs to push the cell state from one basin to another?

Selection of TFs.

Our general procedure for scoring TFs is explained as follows. Eq. 1 has an explicit solution that is given below. The first few terms are

$$\begin{array}{c}{z}_2=A_1{x}_1+B{u}_1\hfill \\ z_3=A_2{A}_1{x}_1+A_{2}B{u}_1+B{u}_2\hfill \\ z_4=A_3{A}_2{A}_1{x}_1+A_3{A}_{2}B{u}_1+A_{3}B{u}_2+B{u}_3\hfill \\ \hfill ⋮\hfill \end{array}$$

This shows how $z_4$ depends on $u_1,u_2,$ and $u_3$.

If $x_T$ is a target condition, then the Euclidean distance $\parallel \cdot \parallel$ can be used to measure how close a state is to the target state. We define

$$d=\parallel x_T-z_6(u)\parallel ,$$ [6]

where the notation $z_6(u)$ is used to emphasize the dependence of $z_6$ on $u$. Considering all possible input signals, one can compute the optimal control that finds the minimum distance for a given initial and target cell type. Let $u_{\ast }$ denote the optimal $u$ used to minimize $d$ and $d_{\ast }$ denote this minimum distance value.

When appropriate, we write $z_6(u)$ to emphasize the fact that the final state depends on the input. The Euclidean distance $\parallel \cdot \parallel$ can be used to measure how close a given state is to the target. If there were no restrictions on the $u$ terms, the control that minimizes the distance between $z_6$ and the target could be computed without difficulty. However, there are reasons for restricting the number of different TFs used in any one trial. Transfection of cells with too many TFs can lower the efficiency of transfection and even lead to cell death. Moreover, many confirmed direct reprogramming experiments use $\le$4 TFs to achieve reprogramming. For these reasons, we modify the optimization problem by adding the constraint that there are no more than a fixed number of TFs (components of $u$) used in a given trial.

Let $\widehat{p}$ be a set of integers that identifies the subset of the components of $u$ (read: TFs) that are allowed to be nonzero. For example, $\widehat{p}=\{\mathrm{1,4,7}\}$ refers to TFs 1, 4, and 7. Let $p$ be the number of elements in $\widehat{p}$. Given a set of TFs, $\widehat{p}$, we determine the quantity and timing of TF input, $u_{\ast k}$, that minimizes the difference between $x_6$ and the target cell state, $x_T$. Mathematically, this can be written as

$$\begin{array}{cc}\underset{u}{\text{minimize}}\hfill & \parallel x_T-z_6(u)\parallel \hfill \\ \text{subject to}\hfill & \{\begin{array}{cc}{u}_{m,k}\ge 0,\hfill & k=1,\mathrm{\dots },5\hfill \\ u_{m,k}=0,\hfill & \text{if}\hspace{0.17em}m\notin \widehat{p}\hfill \\ u_{m,k+1}\ge u_{m,k}\hspace{1em}\hfill & \end{array}\hfill \end{array}.$$ [7]

We use MATLAB’s lsqnonneg function to solve Eq. 7, which gives $u_{\ast k}$ and $d_{\ast }$.

Let $d_0:=\parallel x_T-x_0\parallel$ be the distance between the final state and target state with no control input. Define a score $\mu :=d_0-d_{\ast }$, which can be interpreted as the improvement provided by a particular choice of $u$. This can be calculated for each $\widehat{p}$ and sorted (high to low) to determine which TF or TF combination is the best candidate for direct reprogramming between $x_0$ and $x_T$.

We consider different scenarios for the type of input regime in the results. The first one assumes the input signal is constant $u_1=u_k=\overline{u}$, intended to mimic empirical regimes where TFs are given at a single time point. Later, we also consider inputting TFs at different times $\widehat{k}$, which can be viewed mathematically as requiring $u_{m,k}=0$ for all $k<\widehat{k}$, and $u_{m,k}$ is a constant value for all $k\ge \widehat{k}$. This is intended to mimic inputting a TF at time $\widehat{k}$, which will continue to express at a constant level until time point $k=6$.

Remark.

Subsets of TFs were chosen for each calculation based on the following criteria: $\ge$10-fold expression increase in target state compared with initial state and $\ge$10 RPKM in target state. These criteria are used to select differentially expressed TFs and TFs that are sufficiently active in the target state.

Results

Quantitative Measure Between Cell Types.

To best use our algorithm to predict TFs for reprogramming, compatible data on target cell types must be collected. For this, we explore a number of publicly available databases where RNA-seq has been collected, along with RNA-seq data collected in our laboratory. The ENCODE Consortium has provided data on myotubes and embryonic stem cells (ESCs) (SI Appendix) (18). The GTEx portal provides RNA-seq data on a large variety of different human tissue types (19). Although each GTEx experiment is performed on tissue samples, thus containing multiple different cell types, we use these data as more general cell-state targets.

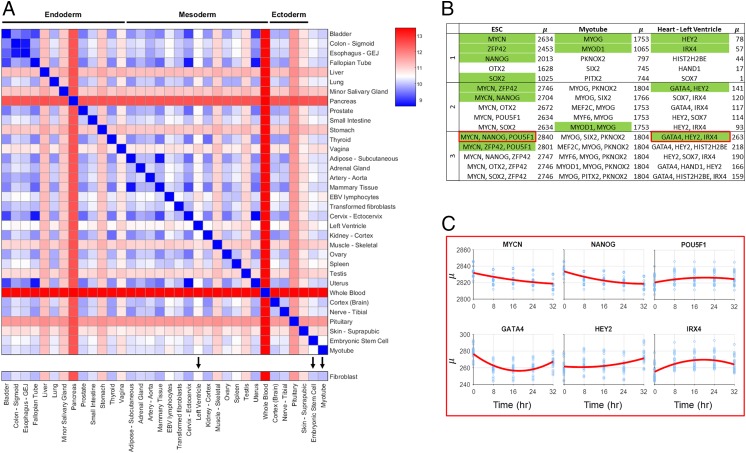
To give a numerical structure to cell-type differences, conceptually similar to Waddington’s epigenetic landscape, we calculate $d_0$ between all cell types collected. Fig. 3A shows $d_0$ values for 32 tissue samples collected from the GTEx portal, along with ESC, myotube, and our fibroblast data (additional cell-type $d_0$ values shown in SI Appendix). GTEx RNA-seq data are scaled to keep total RPKM difference between time series fibroblast and GTEx fibroblast RNA-seq minimal (SI Appendix).

Fig. 3.

Quantitative measure between cell types and TF scores. (A) $d_0$ values between GTEx tissue types and ESC, myotube, and fibroblast. Tissue types and cell types with black arrows have predicted TFs for reprogramming from fibroblasts shown in B. (B) Table of predicted TFs for a subset of cell and tissue types. Top five TFs for combinations of one to three are shown. Green labeled TFs are highly associated with the differentiation process of the target cell type and/or validated for reprogramming. These TFs are discussed in the main text. (C) Time-dependent scores for selected combinations of three TFs for fibroblast to ESC and fibroblast to “heart - left ventricle.” x axis refers to time of TF addition, and y axis refers to $\mu$.

TF Scores.

To assess our method’s predictive power, a subset of target cell types is presented here that has validated either TF reprogramming methods or TFs highly associated with the target cell type. Additional predicted TFs for reprogramming are included in SI Appendix. We note that although experimentally validated TFs provide the best current standard for comparison, we believe experimental validation with our predicted TFs may provide more efficient and comprehensive reprogramming results. For all reprogramming regimes presented in this section, fibroblast is used as the initial cell type due to the availability of synchronized time series data, and all TFs are introduced at $k=1$ (11).

For conversion of fibroblast to myotubes, the top predicted single-input TFs are MYOG and MYOD1, both of which are known to be crucial for myogenesis. While MYOD1 is the classic master regulator reprogramming TF for myotube conversion, activation of downstream factor MYOG is necessary for full conversion (20). For fibroblast to ESC conversion, a number of TFs known to be necessary for pluripotency are predicted, including MYCN, ZFP42, NANOG, and SOX2 (2). With the knowledge that no single TF has been shown to fully reprogram a fibroblast to an embryonic state, combinations of TFs are more informative for this analysis. The top-scoring combination of three TFs is MYCN, NANOG, and POU5F1—three well-known markers for pluripotency (2). Interestingly, POU5F1 scores poorly when input individually, but is within the top set of three TFs when used in combination with MYCN and NANOG. Left ventricle reprogramming includes TFs that are known to be necessary for natural differentiation in the top score for all one to three combinations. These include GATA4 (a known TF in fibroblast to cardiomyocyte reprogramming), HEY2, and IRX4 (21–23).

Time-Dependent TF Addition.

Fibroblast to ESC conversion was of particular interest in our analysis as this is a well-studied regime with a number of validated TFs (with a variety of reported efficiencies), and this conversion is promising for its regenerative medicine application. High-scoring TFs yield many that are known markers for pluripotency, but the top combination of three, MYCN, NANOG, and POU5F1, has not been used specifically together, to our knowledge. Here, we analyzed how the TF combination would score if input at different points throughout the cell cycle.

Time-dependent analysis of the top-scoring ESC TFs reveals that scores vary widely, depending on the time of input. MYCN and NANOG show a strong preference for input at the beginning of the cell cycle, while POU5F1 shows a slight preference for input toward the end of the cell cycle, with the highest score achieved when MYCN and NANOG are input at 0 h and POU5F1 is input at 32 h. Analysis on how the time of input control affects $\mu$ is shown in Fig. 3C. Time-dependent analysis was also conducted for the top combination of three TFs for fibroblast to left ventricle. This analysis predicted that the best reprogramming results would occur if GATA4 is given immediately (0 h), with IRX4 and HEY2 given later (24 and 32 h, respectively).

Discussion

The results from this algorithm show promise in their prediction of known reprogramming TFs and demonstrate the importance of including time series data for gene network dynamics. Time of input control has shown to have an impact on the end cell state, in line with what has been shown in natural differentiation (24).

While we believe that this is the best model currently available for predicting TFs for reprogramming, we are aware of its limitations and assumptions. TAD-based dimension reduction is based on the observation that genes within them correlate in expression over time, although we lack definitive proof of regulation by shared transcriptional machinery (11). This assumption was deemed necessary for dimension reduction in the context of deriving transition matrix $A_k$. With finer time steps in RNA-seq data, the assumption may not be necessary for TF prediction, at the cost of increased computation time. Additionally, a 5-kb window flanking the TSS of each gene was used to ensure that all potential regulators are found, at the cost of potential inclusion of false positive motifs.

Although this program can score TFs relative to other TFs in a given reprogramming regime, it is difficult to predict a $\mu$ threshold that would guarantee conversion. Additionally, rigorous experimental testing will be required to validate these findings and determine how our $u$ vector translates to TF concentration. This is a product of the large number of assumptions that we have made to develop the initial framework for a reprogramming algorithm. With finer resolution in the time series gene expression, more subtle aspects of the genomic network may be observed, allowing for better prediction.

Our proposed DGC framework successfully identified known TFs for fibroblast to ESC and fibroblast to muscle cell reprogramming regimes. We use a biologically inspired dimension reduction via TADs, a natural partitioning of the genome. This comprehensive state representation was the foundation of our framework, and the success of our methods motivates further investigation of the importance of TADs as functional units to control the genome.

A dynamical systems view of the genome allows for analysis of timing, efficiency, and optimality in the context of reprogramming. Our framework is the first step toward this view. The successful implementation of time-varying reprogramming regimes would open unique avenues for direct reprogramming. This template can be used to develop regimes for changing any cell into any other cell, for applications that include reprogramming cancer cells and controlling the immune system. Our DGC framework is well equipped for designing personalized cellular reprogramming regimes. Finally, this framework can serve as a general technique for investigating the controllability of networks strictly from data.

Materials and Methods

Hi-C and RNA-seq data were collected from cell-cycle– and circadian-rhythm–synchronized proliferating human fibroblasts of normal karyotype. Data were collected every 8 h, spanning 56 h. Publicly available data were used for target cell types. Detailed materials and methods are provided in Chen et al. (11), Dataset S1, and in SI Appendix.