Strong attractions and repulsions mediated by monovalent salts

Significance

The physical properties of proteins and polyions in electrolyte solutions are of crucial importance for understanding biological processes and for controlling biotechnological processes. The concentration of salt controls the range and strength of the interactions in these complex electrolytes. Here, multiscale coarse-grained molecular dynamics simulations reveal long-range interactions between nanoparticles in aqueous solutions at high monovalent salt concentrations. The simulations explain the crystallization of nanoparticles even when they are strongly charged and explain the reentrant attractive to repulsive to attractive interactions as the nanoparticle charge density increases in high monovalent salt-concentration conditions.

Abstract

Controlling interactions between proteins and nanoparticles in electrolyte solutions is crucial for advancing biological sciences and biotechnology. The assembly of charged nanoparticles (NPs) and proteins in aqueous solutions can be directed by modifying the salt concentration. High concentrations of monovalent salt can induce the solubilization or crystallization of NPs and proteins. By using a multiscale coarse-grained molecular dynamics approach, we show that, due to ionic correlations in the electrolyte, NPs pairs at high monovalent salt concentrations interact via remarkably strong long-range attractions or repulsions, which can be split into three regimes depending on the surface charge densities of the NPs. NPs with zero-to-low surface charge densities interact via a long-range attraction that is stronger and has a similar range to the depletion attraction induced by polymers with radius of gyrations comparable to the NP diameter. On the other hand, moderately charged NPs with smooth surfaces as well as DNA-functionalized NPs with no possibility of hybridization between them interact via a strong repulsion of range and strength larger than the repulsion predicted by models that neglect ionic correlations, including the Derjaguin–Landau–Vervey–Overbeek (DLVO) model. Interactions between strongly charged NPs (>2 e/nm²), both types smooth and DNA-functionalized NPs, show an attractive potential well at intermediate-to-high salt concentrations, which demonstrates that electrolytes can induce aggregation of strongly charged NPs. Our work provides an improved understanding of the role of ionic correlations in NP assembly and design rules to utilize the salting-out process to crystallize NPs.

The physical properties of nanoparticles (NPs), including proteins, in electrolyte solutions are of central importance to life and physical sciences as well as to bio- and nanotechnology. Interactions between NPs determine their stability and phase behavior (1, 2). These interactions are modified by the concentration of salt in the electrolyte. Specifically, high concentrations of salt induce the crystallization or flocculation of proteins and NPs, a phenomenon commonly referred to as “salting out” (3–5). Moreover, functionalization of NPs with charged groups is a technique extensively used to assemble or disperse NPs (6, 7). The widespread use of both dispersion and flocculation of NPs by adding high concentrations of monovalent salt suggests the possibility of an underlying robust principle responsible of these phenomena. Here, we investigate interactions between neutral and charged NPs in aqueous solutions at high monovalent salt concentrations, where steric interactions among ions (8) as well as hydration effects cannot be ignored (9, 10), to elucidate the origin, range, and strength of the attraction and/or repulsions between identical NPs as the NP surface charge density increases.

Many charged NPs, regardless of their structure and surface chemistry, undergo a precipitation transition at concentrations of monovalent salts of around 0.5–1 M (3, 11, 12). Recent experimental work, for example, showed that strongly charged DNA-functionalized gold NPs with no possibility of hybridization among NPs crystallize at high ionic strengths of monovalent salts (around 750 mM of NaCl) or divalent salt (around 50 mM of CaCl₂) solutions (2). These experiments and preliminary simulations for idealized divalent salts demonstrated an attraction with much longer range than the diameter of the ions (2), which shows that the precipitation cannot be attributed to the formation of ion bridges (13, 14) and/or to correlated condensed multivalent ions (15–17). Models of like-charge attraction by multivalent ions generate only short-range attractions for dsDNA as well as charged smooth NPs (18), and the resulting aggregates redissolve when the concentration of monovalent or multivalent salts is increased (13, 14, 19). Furthermore, the observed precipitation of charged NPs (2) and of proteins (3, 11, 12) at very high concentrations of monovalent ions cannot be explained by models that linearize the electrostatic interactions such as the Derjaguin–Landau–Vervey–Overbeek (DLVO) theory (20, 21) even when fluctuations (22) or excluded volume effects (4) are included in the analysis.

It has been known for decades that mean-field Poisson–Boltzmann approaches for ionic systems (including the DLVO theory) break down even at moderate monovalent salt concentrations because of multiple oversimplifications including the failure to consider correlations, hydration forces, and steric effects (23–26). A signature of the DLVO theory breakdown as the salt concentration increases is the formation of clusters (27) of positive and negative ions, which lead to an oscillatory ion–ion correlation in bulk concentrated electrolytes (25, 27). The association energy of ions is strongly dependent on the distance of closest approach between ions in the electrolyte solution and thus on hydration effects, as well as on the relative static permittivity (or dielectric permittivity) of the medium ε_r, via the Bjerrum length l_B, which determines the length scale at which the interaction between two ions is equal to the thermal energy (k_BT). Interestingly, studies using the so-called primitive model (PM), where ions are modeled as repulsive hard spheres, show at high monovalent salt concentrations: (i) a strong repulsion between charged nanoions (8), observed experimentally (28), and (ii) attractions between neutral surfaces (26) and weakly charged NPs (29). Therefore, at high monovalent salts where DLVO and related mean-field approaches predict only negligible electrostatic repulsions between charged particles, the Debye length is clearly not sufficient to determine the interactions between NPs given the propensity of the ions to clusters via ionic correlations, which are strongly dependent on the value of ε_r and hydration effects. While the PM captures the discrete nature of ions and some steric effects, the interaction mediated by the solvent (water) molecules is complicated (30) and cannot be properly modeled by the PM or other implicit solvent models that are not properly coarse-grained to account for hydration effects and changes in ε_r as the salt concentration increases (31).

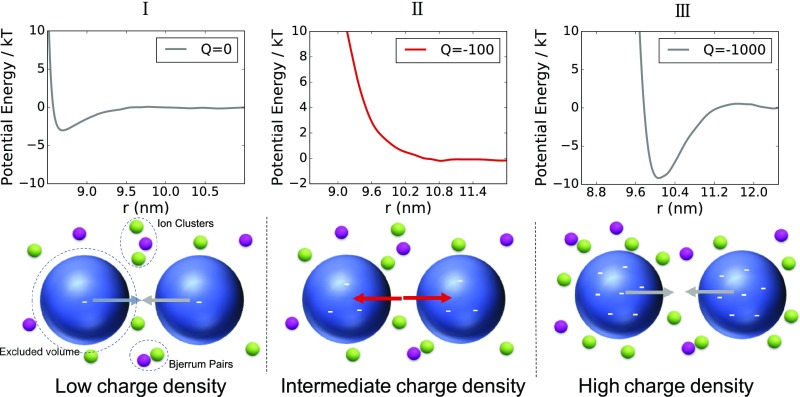
Here, we develop a model to compute the effect of ionic correlations on NP interactions in aqueous salt solutions including hydration effects and changes in the dielectric permittivity. We carry out multiscale molecular dynamics (MD) simulations to compute effective interactions between smooth spherical NPs with different surface charge densities as well as of DNA-functionalized gold NPs with different DNA-grafting densities in aqueous solutions at various NaCl concentrations. We first perform full-atom MD simulations with explicit solvent and ions at the targeted salt concentrations to capture ionic correlations considering solvent effects. From the ionic radial distribution function (RDF) calculated from the atomistic simulations, we build ion–ion interaction potentials using the iterative Boltzmann inversion method (32) for coarse-grained MD simulations with implicit solvent. A dielectric constant that depends on NaCl concentration is calculated from full-atom simulations and used in the Coulomb potential in coarse-grained simulations (31). We then use these ion–ion interaction potentials and corrected Coulomb potentials, which reproduce the full-atom ion-correlation functions, in implicit solvent and explicit ions coarse-grained simulations of NPs and calculate the mean force between NPs. With this approach, we find that NP interactions in NaCl solutions have three distinct regimes as the NP charge density increases (shown in Fig. 1), hereafter referred to as regimes I, II, and III, where the interactions are attractive in I at low NP charge densities, repulsive in II at intermediate to high NP charge densities, and attractive in III at exceedingly high NP charge densities. We compare the attractive interactions induced by monovalent salts in regime I to the widely used depletion attractions induced by polymers in neutral colloids (33–35), which is a technique also extensively used to crystallize proteins (36). Moreover, we related the range of the interactions in regimes I to III to the formation of ionic clusters beyond Bjerrum pairs, which naturally introduce another length scale besides the Debye length and the Bjerrum length in the problem.

Fig. 1.

Three regimes of NP–NP interactions are found in the simulations. In regime I, where the NPs have zero or low charge densities, the interaction is attractive due to depletion interactions mediated by the clustering of ions. In regime II, where the charge is sufficiently large, we find a repulsion that is stronger and longer range than the double-layer force predicted by the DLVO theory. In regime III, where the NPs have very high charge densities resulting in strong counterion condensation on the NP surfaces, the potential shows a strong short-range repulsion and a deep long-range attractive well. van der Waals interactions between NPs are not included in our model.

Results and Discussion

The mean force between two NPs with smooth surfaces shown in Fig. 2 is simulated using the coarse-grained potential mentioned above that we computed for NaCl aqueous solutions. van der Waals attractions between NPs are not included in the calculation to specifically analyze the contribution from charge and ion correlations. A purely repulsive short-range Weeks–Chandler–Andersen (WCA) potential is added to the potential after integration to represent steric effects between NPs. Average forces are integrated to get the effective potential between NPs. More details of the simulations are described in Methods and SI Appendix.

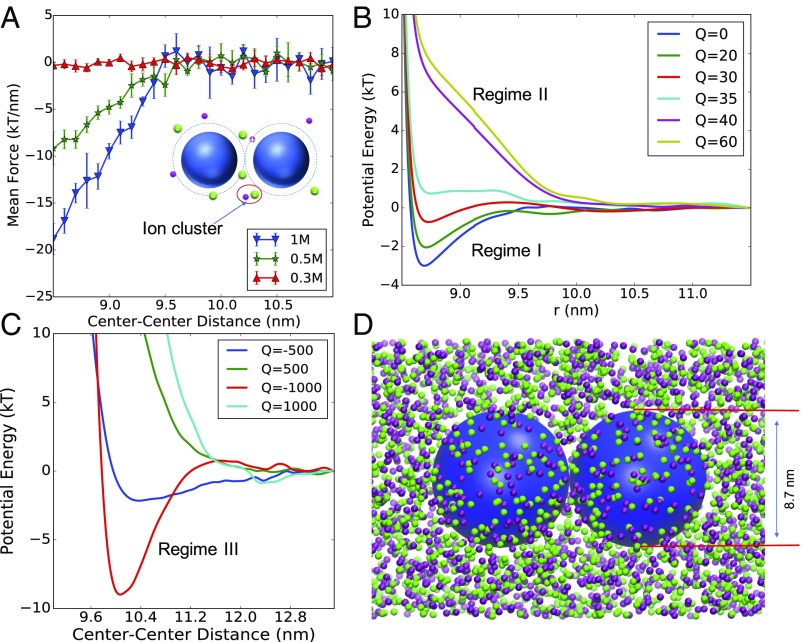
Fig. 2.

Interactions between NPs in NaCl solutions. (A) Simulated average force between two electroneutral NPs in solutions with different NaCl concentrations. (B and C) NP–NP Interaction potentials in 0.5 M NaCl, calculated from integration of simulated force for NPs with different charges. NPs have an effective diameter of 8.7 nm. The charge Q is in elementary charges (for example, Q = 20 corresponds to a surface charge density of 0.084 e/nm²). As the NP surface charge density increases in B, the interaction changes from regime I to regime II as discussed in Fig. 1. In C, the potential is strongly repulsive at small surface–surface distance, and has a potential well for negatively charged NPs, the corresponding NP charge density is referred to as regime III. (D) Snapshot of MD simulation probing the interaction between two NPs immersed in 0.5 M NaCl salt. Small purple and green beads represent sodium and chloride ions, respectively. Large blue spheres represent the NPs. Sizes of the ions are not to scale.

We first compute the average forces on neutral NPs at different salt concentrations, as shown in Fig. 2A. At 0.3 M, the force from surrounding ions is very weakly attractive, and demonstrates an oscillatory behavior at small surface–surface distances (<2 nm). In general, ion entropic forces are weak in the low salt-concentration regime. As the salt concentration increases, an attractive mean force is observed that increases dramatically with salt concentration. The attraction has a range of about 1 nm, and resembles Asakura–Oosawa-type depletion interaction (37) of correlated chains of molecules, such as polymers which are often used to crystallize proteins (3, 36, 38). With a simple cluster analysis, we show that this attraction comes from the depletion effect of correlated ions. Above 0.5 M, Na ions and Cl ions become increasingly correlated, forming ionic clusters, evident in the pair-correlation function (SI Appendix, Fig. S3). The size distribution of clusters at different concentrations is shown in Fig. 3. The correlated ions have large effective volumes that lead to a strong and long-ranged depletion-type attraction.

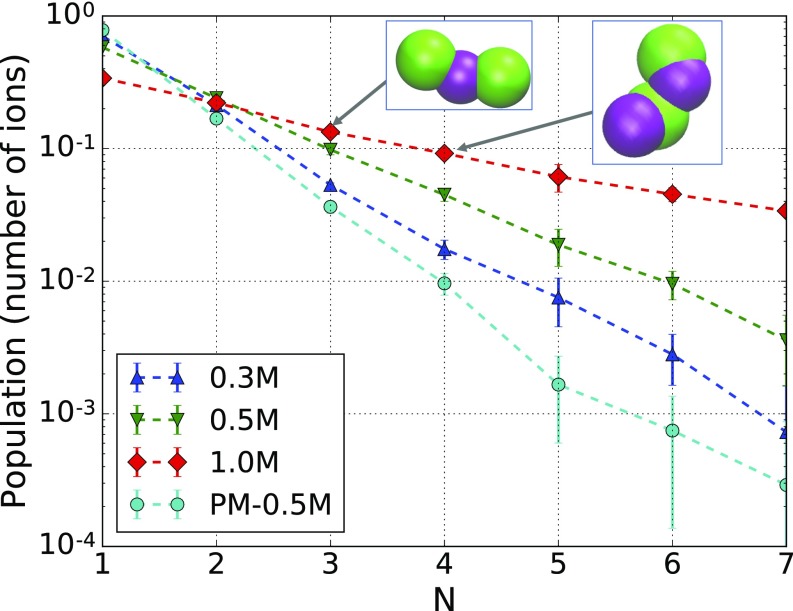
Fig. 3.

Cluster-size distribution in NaCl solutions without NPs. N denotes the number of ions in a cluster, regardless of ion type, as a measure of cluster size. Dashed lines are guide to the eyes. The linearity indicates that the number of clusters of size N decays exponentially as a function of N. Simulation results for the PM show a much lower number of clusters of ions. (Insets) Examples of ion trimers (n = 3) and tetramers (n = 4) found in simulation snapshots.

To verify that the attraction comes from the depletion of ion clusters, the spatial distributions of ion clusters around NPs are recorded and averaged over time (shown in SI Appendix, Fig. S15). A depleted region is found around the NP surfaces that extends beyond the hard-core radius of the NP, and the gap between two NPs has low cluster concentration, confirming that the attractive interaction is depletion in nature. The attraction range is larger than the diameter of a bare ion or the ion hydration shell, which is different from the ordinary depletion from isolated particles which have an interaction range of the depletant size. By analyzing the pair-correlation function between ions (SI Appendix, Fig. S3), we find that the attraction range is comparable to the correlation length of the electrolyte solution. The correlation length is defined here as the distance at which the pair-correlation functions decays to bulk value, which in Na–Cl is 1.1 nm at 1 M. This means that the strong, long-range attraction between NPs is associated with the depletion of correlated ionic structures around NP surfaces. This attraction adds to the van der Waals interaction, and changes the DLVO picture explaining why NPs flocculate or crystalize in concentrated monovalent salt solutions.

Similar depletion effects are also present in polymer–colloid mixtures (33–35). To test such an analogy, we also perform MD simulations of electroneutral NPs immersed in short-chain polymers in the regime where the NP diameter is comparable to the polymer’s radius of gyration ($R_g$), assuming the chains obey self-avoiding walk (SAW) statistics (39). A simple harmonic bead-spring model with repulsive Lennard-Jones potential is used, and mean forces on two NPs are calculated in the same way as NaCl simulations described above. The NP–NP interaction potentials in polymers are plotted in SI Appendix, Fig. S11. The potentials demonstrate an attractive well near NP surfaces. The interaction range is smaller than twice the radius of gyration expected by SAW. In the polymer case, the depletion force is weaker than in concentrated salt solutions due to the lower osmotic pressure in the polymer simulation system because there is a smaller number density of molecules. The similarity in the potential curves corroborates our hypothesis of correlation-induced depletions.

The effect of the surface charge density on the interaction between NPs with 0–60 elementary charges in 0.5 M NaCl is shown in Fig. 2B (other concentrations and negatively charged NPs are analyzed in SI Appendix). For NPs with low charge density (<30 ${\text{e}}^{-}$ per NP, or 0.13 ${\text{e}}^{-}/{\text{nm}}^2$), the interaction near contact remains attractive as in the case of neutral NPs. A weak, long-range repulsion is observed about 0.8 nm away from the NP surface, which resembles the double-layer repulsion predicted by DLVO theory. Neutral and low charge-density NPs can be described in regime I (Fig. 1) since the NP–NP interactions are dominated by the depletion attraction created by correlated ions.

By increasing the charge on each NP, the interaction can change from partially attractive to completely repulsive (regime II in Fig. 1). In this regime, both the range and strength of the repulsion exceed the values predicted by the DLVO theory (SI Appendix, Fig. S9), even when correcting it for a decrease of the water dielectric constant as the concentration of salt increases (31). Corrections to the classical Debye length have been discussed by various methods (25, 27, 40–42). When the approximations in refs. 25, 27, 40, 41 are extrapolated to high salt concentrations, a minimum in the screening length as a function of salt concentration is predicted; an increase in the ion–ion correlation associated screening length is observed in the coarse-grained simulations (SI Appendix, section 4). Interestingly, recent experiments on interactions between surfaces (28, 43) and capacitance predictions (44–46), when fitting an exponential decay, also reveal an increase in screening length at high salt concentrations. As shown below, this increase in screening length is observed when fitting the effective interaction between DNA-functionalized NPs to an exponential decay (Yukawa potential), which cannot be fitted for the case of the much smaller smooth NPs. This suggests that the increase in screening length is probably enhanced by confinement.

For smooth NPs, the increase in repulsion can be explained by the formation of salt microclusters, which results in fewer free ions being available to screen the electrostatic interactions (42). In addition, it has been reported that charged surfaces at high ionic strength experience a short-range repulsion often referred to as hydration force (24, 47), which can be either oscillatory or purely repulsive according to the property of the surface. Interestingly, polarization effects due to the dielectric contrast between dielectric surfaces and the water, which are neglected here for simplicity, produce oscillatory ionic profiles in slabs when excluded volume effects are included even in the PM (48, 49). Within our approach, since there is a nonuniform distribution of ions with a range of ∼0.8 nm from the NP surfaces (SI Appendix, Fig. S13), a steric repulsion from the condensed ions around the NPs can indeed arise, which when the NPs are charged is expected to be only slightly modified by polarization effects (26). In summary, at high ionic strength, NPs with intermediate charge densities (in regime II) experience a strong repulsion at short surface-to-surface distances due to steric effects and ion correlations, and a screened electrostatic repulsion with a larger associated screening length than that predicted by the DLVO theory due to the formations of ionic clusters which effectively decrease the screening of the electrostatic interactions.

Densely grafted DNA-Au NPs carry a very high density of negative charge, which is one order of magnitude larger than the regime discussed above for smooth NPs. Surprisingly, smooth NPs with extremely high charge density (>2 e/nm²) can also have a long-range attraction that extends up to 3.5 nm from the NP surface, as shown in Fig. 2C. The simulation snapshot (SI Appendix, Fig. S14) and ion RDF show a counterion condensation qualitatively different from NPs with low charge density. In this regime III of NP charge (Fig. 1), the enhanced repulsion due to ion clustering is still present, leading to an extremely high potential for $r<9.5$ nm. Since the adsorbed counterions are restricted to a thin layer (of ∼0.5 nm thickness), the two NPs can be viewed as two renormalized NPs with larger diameter and smaller charge density, and correlated ions and counterions outside of the shell lead to a depletion attraction. Hence, the attractive potential well is shifted away from the NP surface. However, the NP interactions in this regime are strongly dependent on the sign of NP charge. For salt concentration of 0.5 M, a long-range attraction is found for negatively charged NPs. Instead, a weak long-range attraction is found for positively charged NPs only at 1 M NaCl concentrations (SI Appendix, Fig. S8). A diminished long-ranged attraction/repulsion was found in an earlier study of smaller NPs in monovalent salt using the PM (8). The complicated charge-asymmetric behavior shows the importance of developing models that capture accurately the hydration structure of different types of ions.

To compare the smooth NP results with a more realistic model, we computed the potential interaction between noncomplementary DNA-grafted NPs (2, 50) with a multiscale MD model that includes the DNA chains explicitly (51, 52). The interaction potential fitted from simulation data are shown in Fig. 4 (see also SI Appendix, section 3.2). Two grafting densities of DNA chains (indicated in the figure legend) are studied. An exact comparison of charge density to the smooth-sphere model is not possible because the charge is spread along the DNA strands. Therefore, the ion distribution is mediated by the conformation of the DNA chains as well as electrostatic potentials originating from the chains, which extends for a few nanometers. Both the geometry and charge density on the NP surfaces can have a nontrivial impact on the potential of mean force. Nevertheless, a potential minimum is discovered in DNA-grafted NPs at intermediate distance (∼34 nm from NP center) which is also reproduced in 8.7-nm smooth NP simulations at similar charge density ($2.2\hspace{0.17em}{\text{e}}^{-}/{\text{nm}}^2$) (Fig. 2C). In the case of higher DNA-grafting density, the increased charge density leads to a stronger repulsion, overcoming the potential minimum. Interestingly, the screening lengths fitted from explicit chain simulations demonstrate a decrease followed by an increase as the salt concentration increases, as reported recently (43). We estimate the minimum of the screening length to be found at around 500 mM for NaCl. By analyzing the results in the smooth-sphere and DNA-functionalized NPs models, we find that in concentrated monovalent salts, ion correlations can lead to attractions not only between neutral or weakly charged NPs but also between strongly charged NPs at proper charge densities and salt concentrations.

Fig. 4.

Potential of mean force between two DNA-coated NPs with (A) DNA surface density of 0.2 strands/nm² (total bare charge Q = −6,480 e) and (B) DNA surface density of 0.325 strands/nm² (Q = −110,580 e) for salt concentrations between 300 and 700 mM. The DNA strands consist of 20 base pairs (bp) of dsDNA and 6 bp of ssDNA. All curves are obtained from fits (SI Appendix). In both cases the effective Debye length is nearly equal for 300 and 700 mM, going through a minimum at 500 mM. Onset of DNA overlap regime is around 35.0 nm. (C) Simulation snapshot for DNA-grafted gold NP interactions in NaCl solution. Ten percent of the actual ions are shown for visual clarity; water is treated as a continuous medium with a dielectric constant calculated from all atomistic simulations. The simulation box is larger than shown in the figure due to cropping.

In both the smooth and DNA-functionalized NP models we simulate two NPs. These simulations describe NP–NP interactions in the highly dilute regime. In practice, however, multibody effects cannot be disregarded. To test the effectiveness of the calculated potential of mean force between two NPs, we introduce a third NP in our simulation. For three NPs located at the vertices of an equilateral triangle, the total force and potential along one edge is shown in SI Appendix, Fig. S4. The qualitative behavior of the effective force is maintained in the presence of three-body effects, and is in close quantitative agreement with two-NP simulations when the charge of the NPs is low. As the concentration of NPs increases, glasses can be obtained, given that the attractions are sufficiently strong to generate nonequilibrium morphologies (53) as found in the experiments of DNA-functionalized NPs without hybridization (2).

Conclusions

By analyzing interactions between two NPs models, (i) between smooth-sphere NPs and (ii) between DNA-functionalized NPs, in aqueous solutions at high monovalent salts using empirical salt potentials derived from full atom simulations, we find a nonmonotonic in range and strength dependence on NP charge density and salt concentration. The multiscale, explicit ions approach reveals a depletion-type interaction for neutral and slightly charged smooth NPs, providing an explanation of the salting-out phenomena in weakly charged NPs. This attractive interaction, contrary to like-charge attraction by condensed counterions or by Coulomb depletion (13, 17, 54), is present even in electrically neutral NPs and in monovalent salt solutions. When the surface charge density increases, both smooth NPs and DNA-functionalized NPs interact via a long-range electrostatic repulsion that extends beyond the range expected by DLVO models. With further increase in charge density, both strongly charged smooth NPs and functionalized NPs show a minimum in the interaction potential as a function of NP separation at intermediate to large salt concentrations, which explains the observed crystallization of strongly charged NPs and proteins induced by adding a large concentration of monovalent salts (1, 2). In the case of DNA-functionalized NPs, we find that the repulsion range as a function of salt concentration has a minimum at intermediate salt concentrations (∼500 mM), in reasonable agreement with the minimum found in recent experiments (28, 43) and with the coarse-grained ion correlation computed for the bulk NaCl electrolyte (i.e., without NPs) as predicted by liquid theory using the PM (25, 27), and by recent phenomenological arguments (28).

The proposed interaction mechanism can help to direct NP assembly and aggregation, and reveals that electrostatics at high ionic strengths strongly deviate from the description of the widely used DLVO theory. Our coarse-grained model and the NP interaction mechanism can be applied to other monovalent or divalent salts to study ion-specific effect in NP suspensions, such as the Hofmeister series (55). Moreover, the iterative Boltzmann inversion method can be easily extended to derive a more accurate coarse-grained potential to study interactions between proteins with specific surface groups and between polyelectrolytes (PE) in salt solutions (56, 57). Interestingly, strongly charged colloids and PE that aggregate at low concentrations of multivalent ions often redissolve in the solution when the concentration of multivalent and/or monovalent salts is increased further (13, 14, 18). This redissolution is in part due to a decrease in chemical potential of the multivalent ions in the solution via their clustering with coions (58–60). However, the redissolution is often followed by salting out at very high monovalent salt concentrations. This suggests that the nonmonotonic dependence on the range and strength of the interactions found here is observed in a broad range of charged systems.

Methods

Atomistic Calculations and Iterative Boltzmann Inversion.

All-atom MD simulations provide RDFs (SI Appendix, Fig. S3) and dielectric permittivity for parameterizing the tabulated pairwise ion–ion interactions in implicit solvent simulations using Boltzmann inversion methods. At high ionic strengths, the dielectric permittivity of water decreases because of the many-body effects in ion–water interaction. This effect is included in our multiscale method via the full-atom calculated dielectric permittivity of water, which is a function of ion concentration (see SI Appendix for details).

We derive a coarse-grained model that reproduces the atomistic salt ion pair-correlation functions. The ion–ion interactions are broken down into long-ranged Coulomb potentials, which are handled by particle–particle–particle–mesh Ewald sum (61) with concentration-dependent dielectric constant (31, 62), and short-ranged solvent mediated interactions, calculated using a tabulated potential in MD simulation with a cutoff distance of 1.3 nm. Initially, a guessed short-ranged potential is used as an input. We use the Boltzmann inversion method [U(r)/k_BT = −ln g(r)]. The atomistic pair-correlation function is used as the initial coarse-grained ion potentials, and an iterative correction to the short-range potential is then performed, in a manner similar to the description of refs. 32 and 63. The converged short-range tabulated potential together with the corrected Coulombic potential yield atomistic pair correlation functions within a small error. Some examples of calculated short-range salt potentials are shown in SI Appendix, Fig. S3. The potentials between coarse-grained ions models have multiple minima due to the hydration effects of water molecules, which lead to a very different ion behavior compared with the PM. MD simulations of NaCl solution are performed at constant number of particles, volume, and temperature using Langevin dynamics to maintain constant temperature (of T = 1, corresponding to room temperature 298 K). For ions at different concentrations, corrected dielectric permittivities described in the previous section are used for the Coulomb potentials. RDFs of salt ions are calculated from coarse-grained simulation trajectories using VMD and compared with atomistic RDFs.

Coarse-Grained Simulations.

Two spherical NPs are placed in the tetragonal simulation box dispersed with Na and Cl ions (Fig. 2D). Ions interact with each other via the aforementioned coarse-grained potential derived using the iterative Boltzmann inversion method, so that correlated ion structures at high ionic strength are reproduced. We assume no specific binding of ions to NPs and apply shifted “hard-sphere” potential between smooth-sphere NPs and salt ions using the WCA equation (64), V_WCA (r) = $4\epsilon \left\{{\left[\sigma /\left(r-\mathrm{\Delta }\right)\right]}^{12}-{\sigma /\left(r-\mathrm{\Delta }\right)]}^6\right\}$. Actual length units (nanometers) are used in the simulations. Several values of $\epsilon$ and $\sigma$ are used to model different NPs softness giving qualitatively similar results; $\mathrm{\Delta }$ is given in a similar manner as Lorenz combining rules (65) of radii, which are found in SI Appendix, Tables S1 and S2.

A schematic demonstration of the explicit DNA chain NP model (described in SI Appendix) is shown in Fig. 4C. The total force on the gold NP core and on each DNA bead connected to the NP is recorded and averaged using 300 points over the range 28–40 nm. The mean force is numerically integrated and then fitted to a superposition of Yukawa-type potential and generalized sigmoid function to obtain potentials in Fig. 4.

Salt Ion Cluster Analysis.

In the cluster analysis, ions are considered to be part of a cluster if their distance to any one of the cluster members is shorter than $r_{\text{cut}}$, which is taken to include the second peak in Na–Cl RDF (SI Appendix, Fig. S3). The cluster-size distribution in relative percentage is plotted in Fig. 3. Concentrated NaCl solutions form a significantly higher fraction of larger clusters, which contribute to the strong attractive/repulsive interaction at high concentrations. The clustering is facilitated by the iterative Boltzmann-derived short-range interaction because there are multiple minima in the potential. Cluster formation is found to be much less likely in simulations of the PM for the same concentrations. Both the depletion-type attraction and the extraordinary repulsion at high NP charge depend on the formation of ion clusters; therefore, the interaction is highly nonlinear and nonmonotonic with increasing ionic strength.