MWPCR: Multiscale Weighted Principal Component Regression for High-dimensional Prediction

Abstract

We propose a multiscale weighted principal component regression (MWPCR) framework for the use of high dimensional features with strong spatial features (e.g., smoothness and correlation) to predict an outcome variable, such as disease status. This development is motivated by identifying imaging biomarkers that could potentially aid detection, diagnosis, assessment of prognosis, prediction of response to treatment, and monitoring of disease status, among many others. The MWPCR can be regarded as a novel integration of principal components analysis (PCA), kernel methods, and regression models. In MWPCR, we introduce various weight matrices to prewhitten high dimensional feature vectors, perform matrix decomposition for both dimension reduction and feature extraction, and build a prediction model by using the extracted features. Examples of such weight matrices include an importance score weight matrix for the selection of individual features at each location and a spatial weight matrix for the incorporation of the spatial pattern of feature vectors. We integrate the importance score weights with the spatial weights in order to recover the low dimensional structure of high dimensional features. We demonstrate the utility of our methods through extensive simulations and real data analyses of the Alzheimer’s disease neuroimaging initiative (ADNI) data set.

1 Introduction

The Alzheimer’s Disease Neuroimaging Initiative (ADNI) study began in 2004 and is the first “Big Data” project for Alzheimer’s disease (AD), which has been a groundbreaking project. It has collected imaging, genetic, clinical, and cognitive data from thousands of subjects in order to delineate the complex relationships among the clinical, cognitive, imaging, genetic and biochemical biomarker characteristics of the entire spectrum of AD as the pathology evolves from normal aging (NC), to mild cognitive impairment (MCI), to dementia or AD. This paper is motivated by the joint analysis of fluorodeoxyglucose positron emission tomography (FDG-PET) data and clinical and behavioral variables from n = 196 subjects in the ADNI study. After applying a standard preprocessing pipeline, the dimension of the processed FDG-PET images is 79 × 95 × 69. We are particularly interested in addressing two questions:

• (Q1) the first one is to identify FDG-PET imaging biomarkers for classifying subjects to either AD or NC group;

• (Q2) the second one is to identify FDG-PET imaging biomarkers observed at baseline to accurately predict the change in the Alzheimer’s Disease Assessment Scale-Cognitive (ADAS-Cog) test score at least two years later after initial assessment.

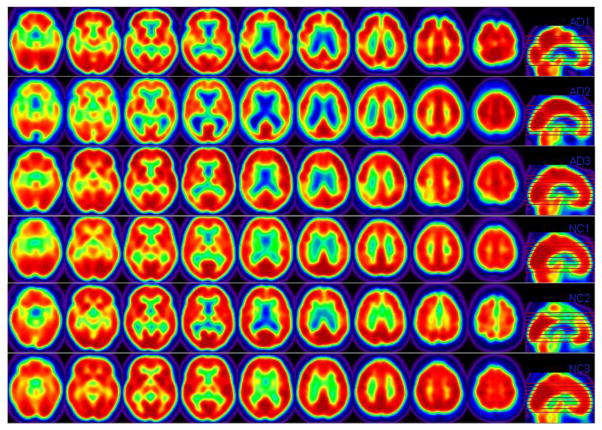
Statistically, these questions of interest can be formulated as the use of a high-dimensional vector of features (or FDG-PET), denoted as x = (x_g: g ∈ 𝒢), to predict an outcome variable, denoted as y, where 𝒢 = {g₁, …, g_p} is a set of locations, in which p is the total number of locations in 𝒢: In this case, x is a vector of FDG-PET imaging measures on a 3-dimensional (3D) lattice and y is either disease status in (i) or the change in the ADAS-cog score in (ii). Figure 1 shows some selected slices of the processed PET images from 3 randomly selected Alzheimer’s Disease (AD) subjects and 3 randomly selected normal control (NC) subjects.

Figure 1.

ADNI PET Data. Each row consists of pre-selected 2-dimensional (2D) slides obtained from a randomly selected subject. The first three rows come from 3 randomly selected AD subjects and the last three rows come from 3 randomly selected NC subjects.

To answer questions (Q1) and (Q2), we develop a multiscale weighted principal component regression (MWPCR) framework to deal with three challenges arising from the use of high-dimensional x with strong spatial features (e.g., FDG-PET) to predict y. Such challenges include (i) noisy functional data, (ii) complex spatial information, and (iii) the remarkable variability of brain structure and function across subjects. For instance, in most neuroimaging studies, the dimension of neuroimaging data (or x) can be much larger than the number of subjects, which varies from several dozens to a few thousands. Moreover, different components of x may be highly correlated with each other and share some specific spatial structures (Friston, 2009; Vincent et al., 2011; Hinrichs et al., 2009; Cuingnet et al., 2012).

Many existing supervised learning and variable selection methods (Hastie et al., 2009; Clarke et al., 2009; Fan and Fan, 2008; Bickel and Levina, 2004; Buhlmann et al., 2012; Tibshirani, 1996), however, can be sub-optimal for high-dimensional prediction problem considered here, since the effect of high dimensional data x (e.g., image biomarker) on y is often non-sparse (Li et al., 2015; Zhou et al., 2013; Friston, 2009; Hinrichs et al., 2009). First, the existing unstructured regularization methods can suffer from diverging spectra and noise accumulation in high dimensional feature space (Reiss and Ogden, 2010; Bickel and Levina, 2004; Buhlmann et al., 2012; Fan and Fan, 2008), whereas the structured ones (e.g., fused Lasso or Ising prior) can be computationally challenging for high-dimensional imaging predictor (Vincent et al., 2011; Cuingnet et al., 2012; Fan et al., 2012; Goldsmith et al., 2014). Alternatively, it is imperative to use some dimension reduction methods, such as principal component analysis and/or screening methods, to extract and select important ‘low-dimensional’ features, while eliminating redundant features (Skocaj et al., 2007; Bair et al., 2006; Fan and Fan, 2008; Krishnan et al., 2011; Zhao et al., 2012). Moreover, most supervised learning methods coupled with dimension reduction methods do not account for the strong spatial features of high-dimensional imaging data as discussed above (Allen et al., 2014; Guo et al., 2015).

A general framework of MWPCR is developed to address some of the challenges discussed above. The MWPCR provides a simple solution to the problem of interest by hierarchically and spatially extracting low-dimensional ‘transformed’ variables from x in order to dramatically improve prediction accuracy. Compared with the existing literature (Allen et al., 2014; Guo et al., 2015; Shen and Zhu, 2015), we make several major contributions as follows:

• (i) MWPCR provides a comprehensive and powerful dimension reduction framework for integrating feature selection, smoothing, and feature extraction for continuous and discrete response variables (e.g., binary response for classification).

• (ii) We evaluate the finite sample properties of MWPCR by using both simulation studies and the analysis of ADNI data. Our numerical results reveal that MWPCR significantly outperforms many competing methods under some scenarios.

• (iii) We systematically investigate the theoretical properties of MWPCR under the high-dimensional binary classification setting. Specifically, we are able to reveal the importance of incorporating different types of weights for improving classification accuracy.

• (iv) The code for MWPCR was written in Matlab, which along with its documentation will be freely accessible from the public website http://www.nitrc.org and our lab website http://odin.mdacc.tmc.edu/bigs2/.

The paper is organized as follows. In Section 2, we introduce the model setup of MWPCR. We discuss various strategies of determining global and local weights that account for an association between y and each individual feature x_g across g ∈ 𝒢 and the spatial patterns of x. In Section 3, simulation studies are conducted to examine the finite sample performance of MWPCR. We conduct real data analysis in Section 4 based on ADNI data to address the two questions (Q1) and (Q2) discussed above. We give some concluding remarks in Section 5. We also investigate some theoretical properties of MWPCR under the high-dimensional binary classification setting and put them in the supplementary document.

2 Multiscale Weighted Principal Component Regression

In this section, we describe data structure and then introduce the model setup and estimation method of MWPCR.

2.1 Data Structure

Consider data from n independent subjects. For each subject, we observe a q_y × 1 vector of discrete or continuous responses, denoted by y_i = (y_i,1, …, y_i,qy)^T, a q_z × 1 vector of discrete and/or continuous clinical covariates, denoted by z_i = (z_i,1, …, z_i,qz)^T, and a p × 1 vector of data x_i = {x_i,g: g ∈ 𝒢} measured on 𝒢 for i = 1, …, n. Let X^T = (x₁| …|x_n) be a p × n matrix. In many cases, both q_y and q_z are relatively small compared with n, whereas p is much larger than n. For instance, in many imaging studies, it is common to use high dimensional imaging data to classify a class variable, such as disease status. In this case, q_y is as small as one, whereas p can be several millions. Moreover, 𝒢 = {g₁, …, g_p} is a set of prefixed locations, such as voxels in 3D lattices, so it is possible to define an edge set 𝒮 = {(g_k, g_j): g_k, g_j ∈ 𝒢} associated with 𝒢. For instance, in spatial statistics and imaging analysis, one often uses pixels and their first-order (or high-order) neighboring pixels to construct edges in 𝒮.

2.2 Model Setup

The proposed MWPCR consists of two components: a low-rank model for multi-scale weighted PCA (MWPCA) and a prediction model. Let Q^(ℓ) be a p × p weight matrix at the ℓ–th scale for ℓ = 1, …, L. The low-rank model for MWPCA can be written as

$${\stackrel{\sim }{\mathbf{X}}}^{(\ell )}=(\mathbf{X}-{\mathbf{1}}_n{\mathit{\mu }}^T)Q^{(\ell )}=U^{(\ell )}{D}^{(\ell )}{V}^{(\ell )T}+{\mathcal{E}}^{(\ell )}=\sum _{k=1}^K{d}_k^{(\ell )}{\mathbf{u}}_k^{(\ell )}{\mathbf{v}}_k^{(\ell )T}+{\mathcal{E}}^{(\ell )}$$ (1)

for ℓ = 1, …, L, where E(x_i) = μ, K ≤ min(n, p), and ${\mathcal{E}}^{(\ell )}={({\mathit{\epsilon }}_1^{(\ell )},\dots ,{\mathit{\epsilon }}_n^{(\ell )})}^T$ is an n × p matrix of measurement errors that follows a matrix-variate distribution with mean 0_n,p and an arbitrary covariance matrix. Moreover, $U^{(\ell )}=({\mathbf{u}}_1^{(\ell )},\dots ,{\mathbf{u}}_K^{(\ell )}),D^{(\ell )}=\text{diag}(d_1^{(\ell )},\dots ,d_K^{(\ell )})$, and $V^{(\ell )}=({\mathbf{v}}_1^{(\ell )},\dots ,{\mathbf{v}}_K^{(\ell )})$ are, respectively, n × K, K × K, and p × K matrices such that diag(D^(ℓ)) ≥ 0 and U^(ℓ)TU^(ℓ) = V^(ℓ)TV^(ℓ) = I_K, where I_K is a K × K identity matrix.

We combine all {U^(ℓ)}_ℓ≥1 from different scales into an n × (KL) matrix given by U_C = (u_C,1 ··· u_C,n)^T = (U⁽¹⁾, …, U^(L)). We then build a prediction model R(y_i; u_C,i, z_i, θ) with y_i as response and u_C,i and z_i as covariates, where θ is a vector of unknown (finite-dimensional or non-parametric) parameters. For instance, when q_y = 1, a popular prediction model is the generalized linear model given by

$$f({\mathbf{y}}_i;{\mathbf{u}}_{C,i},{\mathbf{z}}_i,\mathit{\theta })=exp(\varphi \{{\eta }_i{\mathbf{y}}_i-b({\eta }_i)\}+s(y_i,\varphi )),$$ (2)

where ϕ is a dispersion parameter and b(·) and s(·, ·) are known functions. Moreover, it is assumed that ḃ(η_i) = db(η_i)/dη_i = E(y_i|u_C,i, z_i) satisfies $h(\stackrel{.}{b}({\eta }_i))={\mathbf{z}}_i^T{\mathit{\beta }}_z+{\mathbf{u}}_{C,i}^T{\mathit{\beta }}_u$, where β_z and β_u are coefficient vectors associated with z_i and u_C,i, respectively, and h(·) is a link function. In this case, we have θ = (ϕ, β_z, β_u). Our prediction model can be various parametric and nonparametric regression models for continuous and discrete responses and multivariate and univariate responses, such as survival data and classification problems (Hastie et al., 2009; Clarke et al., 2009).

The key novelty of MWPCR is the use of MWPCA to extract important low-dimensional features of x that are predictive of y. Our MWPCA can be regarded as a novel extension of various supervised and unsupervised dimension reduction models for matrix decomposition (Allen et al., 2014; Skocaj et al., 2007; Huang et al., 2009). Specifically, the three key features of MWPCA include the integration of importance score weights and spatial weights, a multiscale strategy for feature extraction, and its computational efficiency. In contrast, although a general duality diagram method (Dray and Jombart, 2011; Skocaj et al., 2007) explicitly incorporates two weight matrices, it only accounts for structural dependencies (e.g., smoothness) in x.

2.3 Estimation Procedure

We introduce a three-stage algorithm for MWPCR as follows.

• Stage 1. Build an importance score vector (or function) W_I = (w_I,g): 𝒢 → R⁺ and a spatial weight matrix W_E = (w_E,gg′): 𝒢 × 𝒢 → R.

• Stage 2. At the ℓ–th scale, use W_E and W_I to build a spatial weight matrix Q^(ℓ) and then compute the first K principal components in U^(ℓ) according to model (1). Repeat it for ℓ = 1, …, L.

• Stage 3. Build the prediction model R(y; u_C, z, θ).

We slightly elaborate on these stages. In Stage 1, the importance scores w_I,g play an important feature screening role in MWPCR and they can be learnt directly either from {x, y} or other sources. Examples of w_I,g in the literature are primarily based on some statistics (e.g., Pearson correlation or distance correlation) between x_g and y at each location g used in the sure independence screening (Bair et al., 2006; Li et al., 2012). However, most importance scores w_I,g are independently calculated at each location, so they largely ignore complex spatial structures at different locations.

In Stage 1, W_E = (w_E,gkgj) ∈ R^p×p can be either symmetric or asymmetric. The elements w_E,gkgj are usually calculated by using various similarity criteria, such as Gaussian similarity from Euclidean distance, local neighborhood relationship, correlation, and prior information obtained from other data (Yan et al., 2007). Then, we can threshold W_E to create an adjacency matrix with elements of either 1 or 0, which leads to 𝒮, depending on whether the corresponding correlation value exceeds a prefixed threshold or not. By choosing different thresholds, we can obtain different edge sets 𝒮. In Section 2.4, we will discuss how to determine W_E and W_I, while explicitly accounting for the complex spatial structure among different locations.

In Stage 2, we construct the weight matrix Q^(ℓ) at the ℓ–th scale as follows. To extract important features from x, we construct a matrix $Q_1^{(\ell )}=\text{diag}(1\{w_{I,{\mathbf{g}}_1}\ge s_{I,\ell }\},\dots ,1\{w_{I,{\mathbf{g}}_p}\ge s_{I,\ell }\})$, where 1{·} is an indicator function and s_I,1 ≤ … ≤ s_I,L are pre-specified thresholds. The use of $Q_1^{(\ell )}$ is similar to various marginal screening methods (Fan and Lv, 2008; Fan and Fan, 2008; Bair et al., 2006). By tuning the value of s_I,ℓ, we can screen out ‘uninformative’ features at different scales.

To capture the spatial features of x, we may construct a spatial similarity matrix $Q_2^{(\ell )}=(\mid w_{E,{\mathbf{g}}_k{\mathbf{g}}_j}\mid 1\{\mid w_{E,{\mathbf{g}}_k{\mathbf{g}}_j}\mid \ge s_{E,\ell ;1},D({\mathbf{g}}_k,{\mathbf{g}}_j)\le s_{E,\ell ;2}\})$, where s_E,ℓ = (s_E,ℓ;1, s_E,ℓ;2)^T and D(g_k, g_j) is a specific distance (e.g., Euclidean) between g_k and g_j. The value of s_E,ℓ;2 controls the number of locations in {g_j ∈ 𝒢: D(g_k, g_j) ≤ s_E,ℓ;2}, which is a patch set at g_k (Taylor and Meyer, 2012), whereas s_E,ℓ;1 is used to shrink small |w_E,gkgj | to zero.

Given $Q_1^{(\ell )}$ and $Q_2^{(\ell )}$, we may set Q^(ℓ) as either $Q_1^{(\ell )}{Q}_2^{(\ell )}$ or $Q_2^{(\ell )}{Q}_1^{(\ell )}$. Specifically, $Q^{(\ell )}=Q_1^{(\ell )}{Q}_2^{(\ell )}$ corresponds to selecting important features from x first and then smoothing those selected features. In contrast, $Q^{(\ell )}=Q_2^{(\ell )}{Q}_1^{(\ell )}$ corresponds to smoothing x first and then extracting important features from the smoothed x. According to our experiences, $Q_2^{(\ell )}{Q}_1^{(\ell )}$ outperforms $Q_1^{(\ell )}{Q}_2^{(\ell )}$ in terms of prediction accuracy in many scenarios, even though the use of $Q_2^{(\ell )}{Q}_1^{(\ell )}$ can be computationally demanding when p is extremely large.

Given Q^(ℓ), we can ‘prewhiten’ (X − 1_nμ^T) and calculate X̃^(ℓ) and its singular value decomposition (SVD) (U^(ℓ), D^(ℓ), V^(ℓ)) in (1). In practice, a simple criterion for determining K is to include all components up to a prefixed proportion of the total variance, say 85%. For high dimensional data, we consider a regularized PCA by iteratively solving a single-factor two-way regularized matrix factorization. Specifically, for a given K, we minimize with respect to (U^(ℓ), D^(ℓ), V^(ℓ)) the following objective function given by

$${\Vert {\stackrel{\sim }{\mathbf{X}}}^{(\ell )}-\sum _{k=1}^K{d}_k^{(\ell )}{\mathit{u}}_k^{(\ell )}{\mathit{v}}_k^{(\ell )T}\Vert }^2+{\lambda }_{\mathbf{u}}\sum _{k=1}^K{P}_1(d_k^{(\ell )}{\mathit{u}}_k^{(\ell )})+{\lambda }_{\mathit{v}}\sum _{k=1}^K{P}_2(d_k^{(\ell )}{\mathit{v}}_k^{(\ell )})$$ (3)

subject to ${\mathit{u}}_k^{(\ell )T}{\mathit{u}}_k^{(\ell )}\le 1$ and ${\mathit{v}}_k^{(\ell )T}{\mathit{v}}_k^{(\ell )}\le 1$ for all k, where λ_v and λ_u are two tuning parameters and P₁(·) and P₂(·) are two penalty functions. We use adaptive Lasso penalties for P₁(·) and P₂(·) and then iteratively solve (3) (Aharon et al., 2006). For each k₀, we use the sparse method in Lee et al. (2010) to estimate ( $d_{k_0}^{(\ell )},{\mathit{u}}_{k_0}^{(\ell )},{\mathit{v}}_{k_0}^{(\ell )}$). In this way, we can sequentially compute ( $d_k^{(\ell )},{\mathit{u}}_k^{(\ell )},{\mathit{v}}_k^{(\ell )}$) for k = 1, …, K.

In Stage 3, based on {(y_i, u_C,i, z_i)}_i≥1, we use an estimation method to estimate θ as follows:

$$\widehat{\mathit{\theta }}={\text{argmin}}_{\mathit{\theta }}\{\rho (R,\mathit{\theta },{\{({\mathbf{y}}_i,{\mathit{u}}_{C,i},{\mathbf{z}}_i)\}}_{i\ge 1})+\lambda P_3(\mathit{\theta })\},$$ (4)

where ρ(…) is a loss function, λ is a tuning parameter and P₃(·) is a penalty function. Given test vectors x^* and z^*, we can do prediction as follows:

• Calculate ${\mathbf{u}}_C^{\ast }={(u^{(1)\ast },\dots ,u^{(L)\ast })}^T$ by setting u^(ℓ)* = (x^* − μ)^TQ^(ℓ)V^(ℓ){D^(ℓ)}⁻¹, in which μ, Q^(ℓ), V^(ℓ), and D^(ℓ) are learnt from the training data.

• Optimize an objective function based on $R(\mathbf{y};{\mathbf{u}}_C^{\ast },{\mathbf{z}}^{\ast },\widehat{\mathit{\theta }})$ to calculate an estimate of y.

2.4 Importance Score Weights and Spatial Weights

There are two sets of weights in MWPCR, including (i) importance score weights enabling a selective treatment for individual features and (ii) spatial weights accommodating the underlying spatial dependence among features across neighboring locations. As shown in simulation studies, the use of the two sets of weights can dramatically improve prediction accuracy. Below, we propose several specific strategies to determine them.

2.4.1 Importance Score Weights

As discussed in Section 2.3, at each location g, w_I,g is calculated based on a statistical model between (x_g, z) and y in order to perform feature selection according to each feature’s discriminative importance. Statistically, most existing methods (Bair et al., 2006; Li et al., 2012) use a marginal model by assuming

$$f({\mathbf{x}}_i,{\mathbf{y}}_i,{\mathbf{z}}_i)=\prod _{\mathbf{g}\in \mathcal{G}}f({\mathbf{x}}_{i,\mathbf{g}},{\mathbf{y}}_i,{\mathbf{z}}_i;\mathit{\beta }(\mathbf{g})),$$ (5)

where β = (β(g): g ∈ 𝒢) and β(g) is introduced to quantify the association between y_i and x_i,g at each location g ∈ 𝒢. At the g–th location, w_I,g is a statistic based on the marginal model ${\prod }_{i=1}^{n}f({\mathbf{x}}_{i,\mathbf{g}},{\mathbf{y}}_i,{\mathbf{z}}_i;\mathit{\beta }(\mathbf{g}))$. A simple example is to use the Pearson correlation between each feature and class label as the importance score weight. Noninformative features (e.g., correlation less than a given threshold) can be simply discarded by setting w_I,g = 0. However, those w_I,g’s largely ignore complex spatial structure, such as homogenous patches defined below, across all locations (Bair et al., 2006; Li et al., 2012).

It is common to assume that β(g) across all locations are naturally clustered into G homogeneous patches, denoted by {𝒢_j: j = 1, …, G}, such that

$$G\ll p,\mathcal{G}={\cup }_{j=1}^G{\mathcal{G}}_j,\text{and}\mathit{\beta }(\mathbf{g})\text{varies}\text{smoothly}\text{in}\text{each}{\mathcal{G}}_j.$$ (6)

Note that a patch 𝒢_j consists of a set of locations that are spatially connected through edges in 𝒮. It has been shown that algorithms based on patch information have led to state-of-the art techniques for classification and denoising (Taylor and Meyer, 2012; Li et al., 2011; Polzehl and Spokoiny, 2006; Arias-Castro et al., 2012).

We propose two strategies to learn the homogenous patches 𝒢_j in (6) by jointly modelling (x_i, z_i) and y_i. The first strategy is to model the conditional distribution of x_i given y_i and z_i, denoted by f(x_i|y_i, z_i, β). The second strategy is to model the conditional distribution of y_i given x_i and z_i, denoted by f (y_i|x_i, z_i, β). Finally, we can learn patches 𝒢_j from the estimated β and then construct importance score weights.

The first strategy is to model f(x_i|y_i, z_i, β). Let 𝒮_g(h) be an edge set at scale h at each location g. We consider a sequence of nested edge sets across multiscales h_s such that h₀ = 0 ≤ h₁ ≤ … ≤ h_S and 𝒮_g(h₀) = {g} ⊂ … ⊂ 𝒮_g(h_S). To learn the homogeneous patches, a general framework of Multiscale Adaptive Regression Model (MARM) developed in Li et al. (2011) is to maximize a sequence of weighted functions as follows:

$$\widehat{\mathit{\beta }}(\mathbf{g};h_s)={\text{argmax}}_{\mathit{\beta }(\mathbf{g})}\sum _{i=1}^n\sum _{{\mathbf{g}}^{\prime }\in {\mathcal{S}}_g(h_s)}\omega (\mathbf{g},{\mathbf{g}}^{\prime };h_s)logf\left({\mathbf{x}}_{i,{\mathbf{g}}^{\prime }}\mid {\mathbf{y}}_i,{\mathbf{z}}_i,\mathit{\beta }(\mathbf{g})\right)\text{for}s=1,\dots ,S,$$ (7)

where ω(g, g′; h) characterizes the similarity between the observations at g′ and those at g with ω(g, g; h) = 1. If ω(g, g′; h) ≈ 0, then the observations at g′ do not provide information on β(g). Therefore, ω(g, g′; h) can prevent incorporation of locations, whose observations do not contain information on β(g) and preserve the edges of homogeneous regions.

Let D₁(g, g′) and D₂(β̂(g; h_s−1), β̂(g′; h_s−1)) be, respectively, the spatial distance between locations g and g′ and a similarity measure between β̂ (g; h_s−1) and β̂(g′; h_s−1). The ω(g, g′; h_s) can be defined as

$$\omega (\mathbf{g},{\mathbf{g}}^{\prime };h_s)=K_1(D_1(\mathbf{g},{\mathbf{g}}^{\prime })/h_s)·K_2(D_2(\widehat{\mathit{\beta }}(\mathbf{g};h_{s-1}),\widehat{\mathit{\beta }}({\mathbf{g}}^{\prime };h_{s-1}))/{\gamma }_n),$$ (8)

where K₁(·) and K₂(·) are two nonnegative kernel functions and γ_n is a bandwidth parameter that may depend on n. The weights K₁ (D₁(g, g′)/h_S) give less weight to location g′ ∈ 𝒮_g(h_S), which is far from the location g. The weights K₂(u) downweight location g′ with large D₂(β̂(g; h_S), β̂ (g′; h_S)), which indicates a large difference between β̂(g′; h_S) and β̂(g; h_S). Moreover, by following Li et al. (2011) and Polzehl and Spokoiny (2006), we set K₁(x) = (1−x)₊ and K₂(x) = exp(−x). See the detailed algorithm of MARM in Li et al. (2011).

The second strategy is to model f(y_i|x_i, z_i, β) and the prior distribution of β, given by f (β). Since x_i is often high dimensional, it is much difficult to carry out statistical inference based on f(y_i|x_i, z_i, β) compared with f (x_i|y_i, z_i, β). Moreover, our primary goal is to perform feature selection in order to eventually use a small subset of x_i to predict y_i, while correcting for z_i. Similar to the first strategy, we also take the marginal method and then incorporate a specific structure to estimate β as follows:

$$\prod _{\mathbf{g}\in \mathcal{G}}\prod _{i=1}^{n}f({\mathbf{y}}_i\mid {\mathbf{x}}_{i,g},{\mathbf{z}}_i;\mathit{\beta }(\mathbf{g}))\{\prod _{\mathbf{g}\in \mathcal{G}}f(\mathit{\beta }(\mathbf{g})\mid \mathit{\beta }({\mathbf{g}}^{\prime }):{\mathbf{g}}^{\prime }\in {\mathcal{N}}_g)\},$$ (9)

where 𝒩_g is a set of the neighboring locations of location g.

Similar to the first strategy, we propose an adaptive smoothing algorithm to estimate β as follows. Consider a sequence of nested edge sets 𝒮_g(h₀) = {g} ⊂ … ⊂ 𝒮_g(h_S) for h₀ = 0 ≤ h₁ ≤ … ≤ h_S.

• [Step (i)] Calculate β̂(g; h₀) and Cov(β̂(g; h₀)) according to ${\prod }_{i=1}^{n}f({\mathbf{y}}_i\mid {\mathbf{x}}_{i,g},{\mathbf{z}}_i;\mathit{\beta }(\mathbf{g}))$ across all locations g.

• [Step (ii)] Smooth {β̂(g; h₀): g ∈ 𝒢} to sequentially estimate β̂(g; h_s) for s = 1, …, S across all g ∈ 𝒢. Candidate methods include local polynomial, nonlocal mean, and propagation-separation, among others (Polzehl and Spokoiny, 2006; Arias-Castro et al., 2012).

For both strategies, after the iteration h_S, we can obtain β̂(g; h_S) and its covariance matrix, denoted by Cov(β̂(g; h_S)), across all g ∈ 𝒢. Finally, we calculate w_I,g as a function of β̂(g; h_S) and Cov(β̂(g; h_S)), such as the Wald test and its p-value. Then, we use a clustering algorithm, such as the K-mean algorithm, to group {β̂(g; h_S): g ∈ 𝒢} into several homogeneous clusters (Hastie et al., 2009), in which β̂(g; h_S) varies very smoothly in each cluster.

2.4.2 Spatial Weights

As discussed in Section 2.3, w_E,gg′ often characterizes the degree of certain ‘similarity’ between locations g and g′. We consider three spatial weight matrices, including (i) the precision matrix, (ii) a locally spatial weight matrix, and (iii) a cluster-based spatial weight matrix as follows.

For the precision matrix, let Σ be the covariance matrix of x_i, we can set $Q_2^{(\ell )}={\mathrm{\sum }}^{-1/2}$ ; thus, $Q_2^{(\ell )}{Q}_2^{(\ell )T}={\mathrm{\sum }}^{-1}$ is the precision matrix of x_i. When Σ⁻¹ has certain sparsity structures (e.g., factor model), various estimation methods have been developed even for extremely large p.

The locally spatial weight matrix consists of non-negative weights assigned to the spatial neighboring locations of each location. Specifically, we set w_E,gg′ as

$$w_{E,\mathbf{g}{\mathbf{g}}^{\prime }}=\frac{\omega (\mathbf{g},{\mathbf{g}}^{\prime };h_S)\mathbf{1}\{{\mathbf{g}}^{\prime }\in {\mathcal{S}}_g(h_S)\}}{{\sum }_{{\mathbf{g}}^{″}\in {\mathcal{S}}_g(h_S)}\omega (\mathbf{g},{\mathbf{g}}^{″};h_S)1\{{\mathbf{g}}^{″}\in {\mathcal{S}}_g(h_S)\}},$$ (10)

in which ω(g, g′; h_S) is defined in (8). Thus, we have w_E,gg′ = 0 for all g′ ∉ 𝒮_g(h_S) and Σ_g′∈𝒢 w_E,gg′ = 1.

The cluster-based spatial weight matrix consists of non-negative weights assigned to locations in the same homogeneous cluster. Specifically, we use the Laplace-Beltrami operator to construct W_E (Luxburg, 2007). It is assumed that each edge between two locations g and g′ carries a non-negative weight w_gg′. Thus, matrix W = (w_gg′) is a weighted adjacency matrix of 𝒢. The degree of a location g ∈ 𝒢 is defined as d_g = Σ_g′∈𝒢 w_gg′ and the degree matrix WD is given by W_D = diag(d_g1, …, d_gp).The unnormalized Laplacian matrix L of the graph 𝒢 is defined as W_L = W_D − W, which can be regarded as a discrete representation of the Laplace-Beltrami operator. Finally, we set W_E = exp(−0.5W_L/γ), where exp(·) denotes the matrix exponential. In practice, when p is extremely large, it is computationally infeasible to directly use the huge p × p matrix W_E. In this case, based on the clustering results in (6), we only consider locations in each cluster and each cluster forms a connected subgraph, which leads to dramatically computational savings (Cuingnet et al., 2012).

2.4.3 Weights Selection

A critical question is how to select spatial weights and/or importance score weights for constructing Q^(ℓ) in different applications. Ideally, we may either use one of them or combine some of them together to construct Q^(ℓ). Theoretically, we have investigated the effects of applying importance score weights and different spatial weights in MWPCR on classification accuracy for high dimensional binary classification and put them in the supplementary document. We have three key theoretical results as follows.

• The use of feature selection can substantially improve classification accuracy for high dimensional binary classification.

• The use of spatial kernel weights and importance score weights in MWPCR can substantially improve classification accuracy even when signals are weak.

• The use of the true Σ^−1/2 can improve classification accuracy, where Σ is the covariance matrix of x.

Based on these results, we suggest to first apply the locally spatial weight matrix (or the cluster-based spatial weight matrix) and then use the importance score weights based on β̂(g; h_S). Although the use of Σ^−1/2 can improve classification accuracy, estimating Σ^−1/2 can be very challenging when p is even moderate. Thus, we avoid estimating Σ^−1/2 in all simulations and real data analysis.

3 Simulation Studies: Binary Outcome

We use two sets of simulation studies, including binary and continuous outcomes, to examine the finite sample performance of MWPCR under different scenarios. We demonstrate that MWPCR outperforms or at least is compatible with many state-of-the-art methods. For the sake of space, we include all simulation results for continuous outcome in the supplementary document.

We applied MWPCR to a high-dimensional binary classification problem as follows. We simulated 20 × 20 × 10 3D-images from a linear model given by

$${\mathbf{x}}_{i,\mathbf{g}}={\beta }_0(\mathbf{g})+{\beta }_1(\mathbf{g})l_i+{\epsilon }_i(\mathbf{g})\text{for}i=1,\dots ,n,$$ (11)

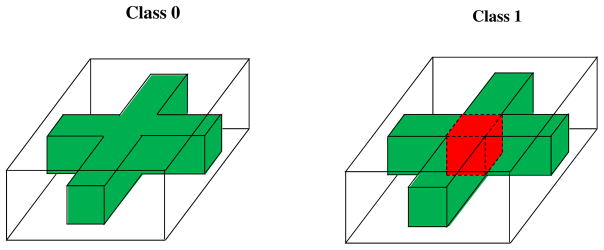
where l_i is the class label coded as either 0 or 1 and ε_i(g) are random variables with zero mean. Figure 2 presents the true mean images of class l_i = 0 and class l_i = 1, in which a red cuboid 3 × 3 × 4 region characterizes the maximum difference 1 between classes 0 and 1. In this case, we have p = 4, 000. Then, we set n = 100 with 60 images from Class 0 and the rest from Class 1.

Figure 2.

True mean images for the first set of simulations: Class 0 in the left panel and Class 1 in the right panel. The white, green, and red colors, respectively, correspond to 0, 1, and 2.

We consider three types of noise ε_i(g) in (11). First, ${\epsilon }_i^{(1)}(\mathbf{g})$ were independently generated from a N(0, 2²) generator across all voxels. Second, ${\epsilon }_i^{(2)}(\mathbf{g})={\sum }_{{\Vert {\mathbf{g}}^{\prime }-\mathbf{g}\Vert }_1\le 1}{\epsilon }_i^{(1)}({\mathbf{g}}^{\prime })/m_{\mathbf{g}}$ were generated from ${\epsilon }_i^{(1)}(\mathbf{g})$ by introducing the short range spatial correlation, where || · ||₁ is the L₁ norm of a vector and m_g is the number of locations in the set {|| g′−g ||₁≤ 1}. Third, to introduce the long range spatial correlation, ${\epsilon }_i^{(3)}(\mathbf{g})$ were generated according to ${\epsilon }_i^{(3)}(\mathbf{g})=2sin(\pi g_1/10){\xi }_{i,1}+2cos(\pi g_2/10){\xi }_{i,2}+2sin(\pi g_3/5){\xi }_{i,3}+{\epsilon }_i^1(\mathbf{g})$, where g = (g₁, g₂, g₃)^T and ξ_i,k for k = 1, 2, 3 were independently generated from a N(0, 1) generator. Moreover, the noise variances in all voxels of the red cuboid region equal 4, 4/6, and 4{sin(πg₁/10)² + cos(πg₂/10)² + sin(πg₃/5)²} + 4 for Type I, II, and III noises, respectively. Therefore, among the three types of noise, Type III noise has the smallest signal-to-noise ratio and Type II noise has the largest one.

We ran the three stages of MWPCR as follows. In Stage 1, let {h_s = 1.2^s, s = 0, 1, …, S = 5}, and for each g ∈ 𝒢, we set w_I,g = −p log(p(g))/{−Σ_g∈𝒢 log(p(g))}, where p(g) is the p-value of Wald test β₁(g) = 0 in (11) at voxel g. The spatial weight W_E is given by (10). We set the spatial weight W_E according to (10) and (8). Specifically, we considered three types of spatial weights W_E, including MWPCR1: only the location kernel function K₁(.) in (8); MWPCR2: only the similarity kernel function K₂(.) in (8); and MWPCR3: the combination of kernel functions K₁(.) and K₂(.) in (8). Then, we selected the bandwidth {h_s = 1.2^s, s = 0, …, S = 5} in these kernel functions in order to determine W_I and W_E. In Stage 2, we used different numbers of principal components in MWPCA to reconstruct the low dimensional representation of simulated images. In Stage 3, we tried different classification methods, including linear regression, k-nearest neighbor (k-NN) and support vector machine (SVM), on these low dimensional representations. Since their performances are similar to each other, we only report the results based on the linear regression throughout the paper. The linear regression uses class label l_i as dependent variable and principal components as explanatory variables. An image is classified as Class 0, if its predictive value is less than 0, and as Class 1, otherwise.

We first used the leave-one-out cross validation to calculate the misclassification rates for MWPCR1, MWPCR2, MWPCR3, and a standard principal component analysis (PCA). Table 1 presents the classification results based on 5, 7 and 10 principal components. The misclassification errors for all MWPCR methods are quite stable for different numbers of principal components under different types of noise. All MWPCR methods perform relatively well for Type II noise compared with Type I and III noises, since Type II noise has the largest signal-to-noise ratio. Moreover, MWPCR3 is slightly better than MWPCR1 and MWPCR2, which may be due to the fact that MWPCR3 combines both the local smooth and similarity kernels. Moreover, it seems that MWPCR3 is very robust to the long-range correlation structure of Type III noise. Compared with all MWPCR methods, PCA performs very poor, since it does not incorporate the class label information.

Table 1.

Classification results for the first set of simulations: misclassification rates for MWPCR1, MWPCR2, MWPCR3, and PCA based on three numbers of principal components under three types of noise.

Noise	Number of PCs	PCA	MWPCR1	MWPCR2	MWPCR3
Type I	5	0.47	0.11	0.09	0.10
	7	0.48	0.13	0.11	0.10
	10	0.49	0.13	0.11	0.10
Type II	5	0.41	0.04	0.08	0.03
	7	0.39	0.03	0.09	0.04
	10	0.42	0.03	0.07	0.04
Type III	5	0.27	0.13	0.10	0.09
	7	0.26	0.13	0.10	0.10
	10	0.28	0.13	0.10	0.10

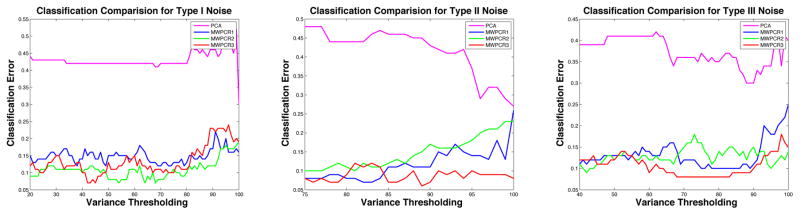
Second, we used the same variance thresholding to compare the three MWPCR methods with PCA. Figure 3 shows that the classification error (magenta curve) for PCA is much larger than that for all other methods. For each fixed variance threshold, the number of extracted principal components from PCA is less than that of MWPCR1, MWPCR2 and MWPCR3. Overall, MWPCR3 outperforms all other methods for all three types of noises. The variance threshold in the middle panel of Figure 3 starts from 70%, since the first principal component of PCA almost accounts for 70% of the total variance for Type II noise.

Figure 3.

Classification results for the first set of simulations: classification rate curves for MW- PCR1, MWPCR2, MWPCR3, and PCA based on the variance thresholding method for the three types of noise. Overall classification errors for MWPCR3 (red curve) are smaller than those of others, confirming the good performance of MWPCR3. Also MWPCR3 is quite robust to different variance thresholds. The performance of PCA is very poor and its classification error (magenta curve) is much larger than all MWPCR methods for the three types of noises.

Third, we compared MWPCR3, in which 5 principal components were used, with eight other state-of-the-art classification methods. These eight classification methods include sparse discriminant analysis (sLDA) (Clemmensen et al., 2011), sparse partial least squares (SPLS) analysis (Chun and Keles, 2010), sparse logistic regression (SLR) (Yamashita, 2011), support vector machine (SVM) (Chang and Lin, 2011), regularized optimal affine discriminant (ROAD) (Fan et al., 2012), wavelet-based multicscale PCA (WMSPCA)(Bakshi, 1998), the combination of sure independence screening (SIS) (Fan et al., 2010) and principal component analysis (PCA) (SIS+PCA), and graph-constrained elastic-net (GraphNet) (Grosenick et al., 2013). We chose these classification methods due to their excellent performance in various simulated and real data sets.

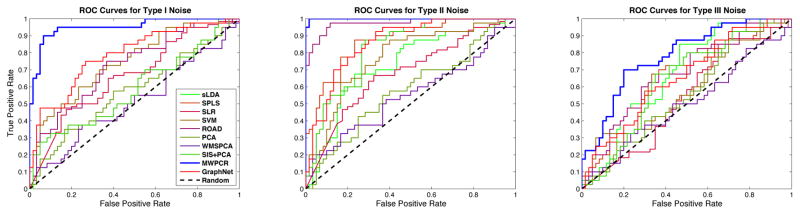
Fourth, for all classification methods, we first calculated their misclassification rates by using the leave-one-out cross validation and then generated the receiver operating characteristics (ROC) curves of all nine methods. For ROC, we used model (11) to independently generate a testing set with the same sample size and the same proportion of Class 0 to Class 1 as the training set. For each method, we applied 10-fold cross validation to the training set in order to select the tuning parameter(s) and build the model based on the training set. Then, we applied the fitted model to the testing set in order to generate the ROC curves of all nine classification methods in Figure 4. Based on these ROC curves, we calculated their area under curve (AUC) values (Fawcett, 2006).

Figure 4.

ROC curves of different classification methods for the three types of noise in the first set of simulations. The blue curves correspond to MWPCR and have the highest AUC value.

Table 2 presents the classification results, including both misclassification rates and AUC values. Table 2 reveals that MWPCR outperforms all other classification methods, especially when the signal-to-noise ratio is low for Type I and II noises. Except WMSPCA, SIS+PCA, and MWPCR, all other classification methods are also sensitive to the presence of the long-range correlation structure in Type III noise. However, if high dimensional features do not have strong spatial structures, then it is expected that MWPCR may perform worse than other competing classification methods.

Table 2.

Misclassification Rates (MRs) and AUC values for the first set of simulations: comparison between MWPCR and eight other state-of-the-art classification Methods. sLDA denotes sparse discriminant analysis; SPLS denotes sparse partial least squares; SLR denotes sparse logistic regression; SVM denotes support vector machine; ROAD denotes regularized optimal affine discriminant; WMSPCA denotes wavelet based multiscale principal component analysis; SIS+PCA combines sure independence screening (SIS) and principal component analysis; and GraphNet denotes graph-constrained elastic-net.

Type/Measure	sLDA	SPLS	SLR	SVM	ROAD	WMSPCA	SIS+PCA	GraphNet	MWPCR
I/MR	0.28	0.43	0.45	0.38	0.36	0.20	0.33	0.32	0.10
II/MR	0.27	0.08	0.18	0.26	0.08	0.13	0.46	0.22	0.03
III/MR	0.52	0.30	0.61	0.60	0.50	0.21	0.10	0.35	0.09
I/AUC	0.59	0.59	0.66	0.75	0.72	0.52	0.59	0.79	0.95
II/AUC	0.73	0.87	0.68	0.77	0.97	0.55	0.83	0.86	0.99
III/AUC	0.68	0.65	0.54	0.59	0.68	0.50	0.64	0.66	0.78

4 Real Data Analysis

4.1 ADNI PET Data

Alzheimer’s disease (AD) is the most common form of dementia and results in the loss of memory, thinking and language skills. AD is an escalating national epidemic and a genetically complex, progressive, and fatal neurodegenetive disease. The incidence of AD doubles every five years after the age of 65 and the number of AD patients has dramatically increased recently, which has caused a heavy socioeconomic burden. AD is the sixth-leading cause of death in the United States, while there is no means to prevent, cure or even slow its progression.

The development of MWPCR is motivated by using the baseline FDG-PET data set to address questions (Q1) and (Q2). The ADNI PET data set downloaded from the ADNI web site (www.loni.usc.edu/ADNI) consists of 196 subjects with 102 NCs and 94 AD subjects. There are three subjects, missing the gender and age information. Among all the rest of the subjects, there are 117 males whose mean age is 76.20 years with standard deviation 6.06 years and 76 females whose mean age is 75.29 years with standard deviation 6.29 years. FDG-PET images acquired 30–60 minutes post-injection were processed by using a standard image processing pipeline. A detailed description of PET protocols and acquisition can be found at www.adni-info.org. Such pipeline consists of average, spatially alignment, interpolation to a standard voxel size, intensity normalization, and smoothing to a common resolution of 8-mm full width at half maximum.

4.2 Binary Classification

The first goal is to use MWPCR to classify subjects from ADNI to either AD or NC group based on their FDG-PET images. It is associated with the second primary objective of ADNI aiming at developing new diagnostic methods for AD intervention, prevention, and treatment. We first applied MWPCR3 to ADNI and used the same setting as simulations in Section 3 except that we considered a linear model for f(x_i,g|y_i, z_i, β(g)), in which z_i includes both age and gender and y_i is diagnosis status (AD versus NC). We also compare MWPCR3 with nine other classification methods, including PCA and the eight state-of-the-art classification methods discussed in Section 3. For the PCA method, we applied PCA with five principal components, which account for around 90% of the total variance, and then used the same linear regression as MWPCR3 to perform classification analysis. Figure 5 presents three selected slices of the weight matrix W_I. The red regions, such as supramarginal gyrus right, correspond to the voxels with large importance score weights and contain the most important information for classification.

Figure 5.

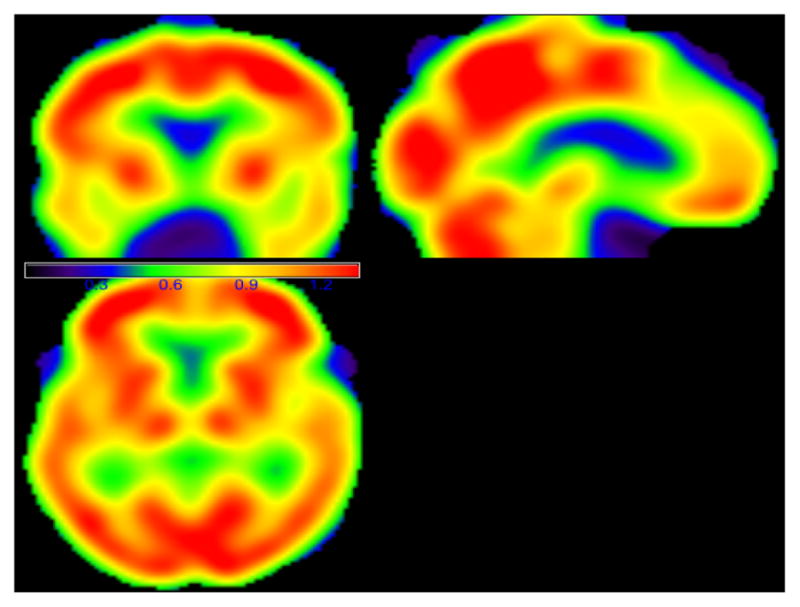
The images of the importance score weight matrix for the ADNI binary classification analysis. The red regions have large weight score values and contain the important classification information.

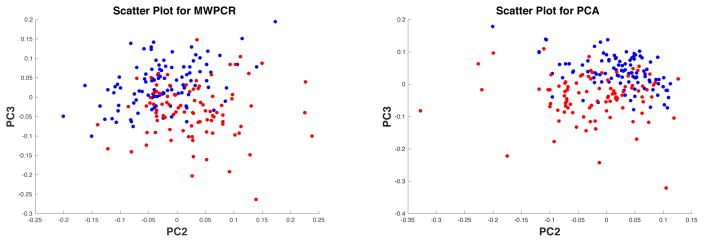
Second, for both PCA and MWPCA, we extracted their corresponding first five principal component scores and directions. Figure 6 shows the scatter plot of PC2 and PC3 scores for PCA and that for MWPCA, in which blue and red points correspond to NC and AD subjects, respectively, where PC2 and PC3 represent the second and third principal components, respectively. It seems that compared with PCA, the blue and red points are more separable for MWPCA. Furthermore, Figure 7 presents some selected slides of the principal directions corresponding to PC2 and PC3 for MWPCA. We are able to identify several key regions of interest, such as “ supramarginal gyrus”, “ superior temporal gyrus”, and “inferior frontal gyrus”. For instance, the superior temporal gyrus is in the temporal lobe of the human brain and contains several important structures of the brain, including Brodmann areas 41, 42, and 22p. It is probably involved with language perception and processing (Marcus et al., 2014). Moreover, within the brain, the anatomical regions that show the greatest decrease in FDG uptake with aging are the bilateral superior medial frontal, motor, anterior, and middle cingulate and bilateral parietal cortices. Among them, the superior temporal pole was found to be particularly affected.

Figure 6.

ADNI binary classification results: scatter plots of PC2 and PC3 scores for MWPCR (left panel) and PCA (right panel). Blue and red points in both panels correspond to NC and AD subjects, respectively.

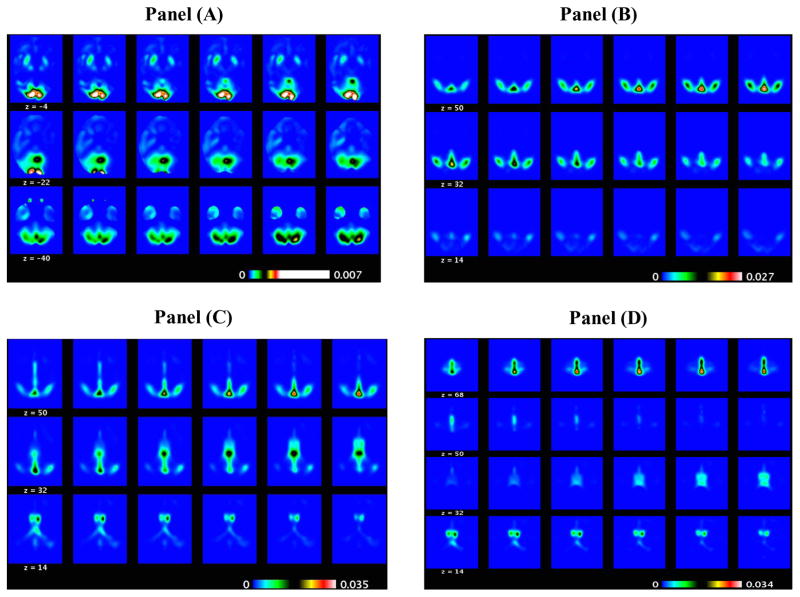
Figure 7.

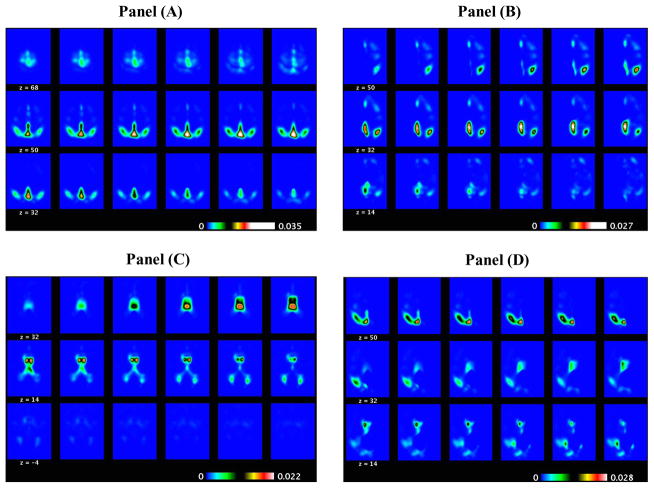
ADNI PET binary classification results: the selected slides of the PC2 direction image (positive elements in Panel (A) and negative elements in Panel (B)) and those of the PC3 direction image (positive elements in Panel (C) and negative elements in Panel (D)) obtained from MWPCR.

Third, similar to Section 3, we calculated the misclassification rates of all classification methods by using the leave-one-out cross validation and then generated their receiver operating characteristics (ROC) curves. For the ROC analysis, we randomly and proportionally split the data set into 2 parts, a training set and a testing set. For each part, the sample sizes are same (98/98). Within each part, the proportion of AD to NC remains the same. For each classification method, we used 10-fold cross validation on the training set to select the tuning parameter(s) and build the model, and then we applied the fitted model to the testing set in order to calculate the relative scores. Subsequently, we generated all ROC curves and their AUC values.

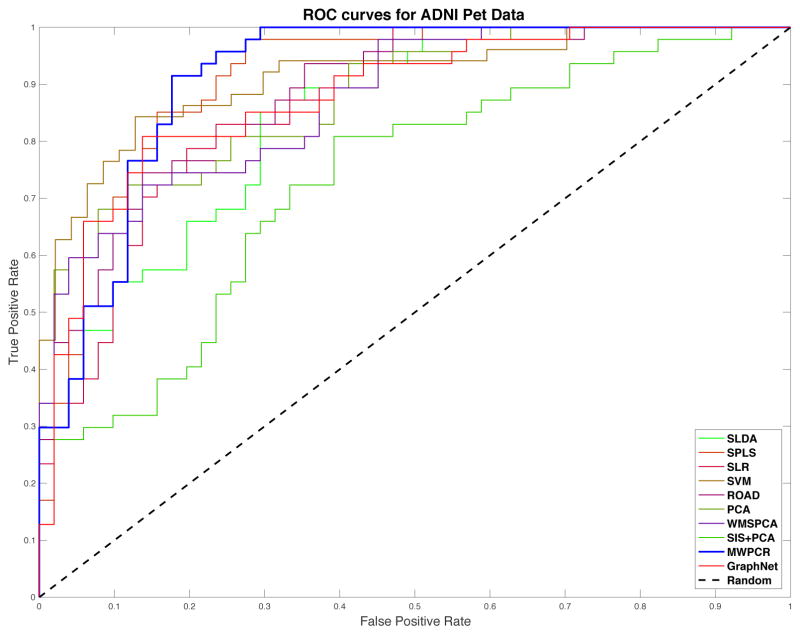
Table 3 presents the classification results based on classification error and AUC, while Figure 8 presents the ROC curves of all ten classification methods. sLDA and SIS+PCA perform much worse than all other methods. In general, SPLS, SVM and WMSPCA are comparable with each other, but they outperform SLR and ROAD. In terms of misclassification rate, MWPCR outperforms all nine other classification methods. In contrast, in terms of AUC, MWPCR, SPLS, and SVM are compatible with each other. It may indicate that the classification accuracy can be significantly improved by incorporating spatial smoothness and correlation.

Table 3.

Misclassification Rates (MRs) and AUC values of different classification methods for ADNI PET data

	sLDA	SPLS	SLR	SVM	ROAD	PCA	WMSPCA	SIS+PCA	GraphNet	MWPCR
MR	0.255	0.163	0.179	0.168	0.189	0.194	0.168	0.255	0.128	0.117
AUC	0.845	0.912	0.863	0.912	0.878	0.877	0.873	0.730	0.879	0.913

Figure 8.

ADNI PET binary classification results: ROC curves of the ten different classification methods. The blue line corresponds to MWPCR.

4.3 ADAS-Cog Score Prediction

The second goal is to use MWPCR to identify FDG-PET imaging biomarkers observed at baseline to accurately predict the change in the ADAS-Cog test score (or TOTAL₁₁) at least two years later after initial assessment. The TOTAL₁₁, which measures the cognitive performance of each subject, was calculated from the 11-item ADAS-Cog, such as Word Recall, whose details can be found in http://adni.loni.usc.edu/data-samples/data-faq/. Since three subjects are missing gender and age information and ten other subjects only have the baseline TOTAL₁₁, we only use 183 subjects in this analysis.

We ran MWPCR as follows. We first fitted a linear model with the TOTAL₁₁ score at the latest time point as response and the baseline TOTAL₁₁ score, age, gender, time since baseline, and years of education, and then we used the residual obtained from the linear model as the response y and the FDG-PET image as x. In Stage 1, we fitted a linear model for f(x_i,g|y_i, β(g)), in which we dropped off z_i. Then, W_I is calculated based on the p-value of Wald test associated with the correlation between x_i,g and y_i at each voxel g. In Stage 2, following the simulations in Section 3, we chose MWPCR3 with different numbers of principal components for MWPCA in order to construct the low-dimensional latent variables {u_k,i}. In Stage 3, we fitted a linear latent variable regression given by ${\mathbf{y}}_i={\alpha }_0+{\sum }_{k=1}^K{\alpha }_k{\mathbf{u}}_{k,i}+{\epsilon }_i$ to do prediction.

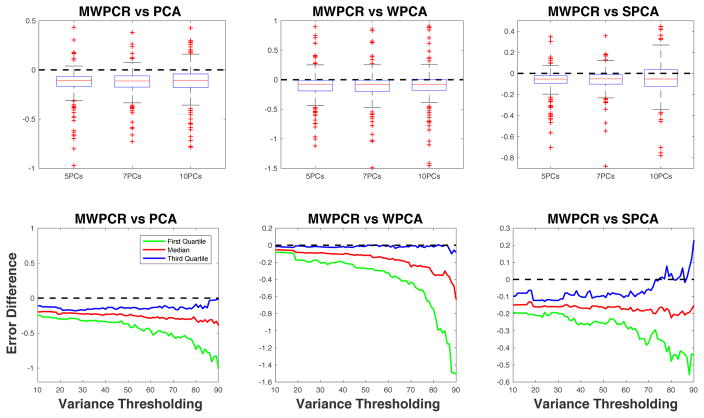
Second, we compared MWPCR and three other dimensional reduction methods including PCA, weighted PCA (WPCA) (Skocaj et al., 2007), and supervised PCA (SPCA) (Bair et al., 2006). We used the leave-one-out cross validation method to compute the prediction errors of all methods. Let ŷ_i be the fitted response value based on the linear latent variable regression, we define the prediction error as |ŷ_i − y_i|/|y_i|. Subsequently, we calculated the prediction error differences between MWPCR and all other three methods and their quantile curves across different numbers of principal components and variance thresholds. Figure 9 presents the comparison results based on the prediction error differences and their quantile curves. Both the error differences and the quantile curves are less than 0 (below the dashed line), confirming the better performance of MWPCR in predicting changes in ADAS-Cog score.

Figure 9.

ADAS-Cog Score Prediction for ADNI PET Data: comparison between MWPCR with PCA, WPCA, and SPCA. The panels in the first row show the boxplots of error differences between MWPCR and PCA (WPCA and SPCA) for different numbers of principal components. The panels in the second row show the first, second and third quantile curves of error differences between MWPCR and PCA (WPCA and SPCA) for different variance thresholds.

Third, for MWPCA, we extracted their corresponding first five principal component scores and directions. Figure 10 presents some selected slides of the principal directions corresponding to PC1 and PC5 for MWPCA, where PC1 and PC5 represent the first and fifth principal components, respectively. We are able to identify several key regions of interest, such as “right lateral ventricle”, “right middle temporal gyrus”, “right fornix”, and “ right middle frontal gyrus”. For instance, the fornix is on the medial aspects of the cerebral hemispheres connecting the medial temporal lobes to the hypothalamus. Since the fornix serves a vital role in memory functions, it has become the subject of recent research emphasis in Alzheimer’s disease (AD) and mild cognitive impairment (MCI) (Nowrangi and Rosenberg, 2015).

Figure 10.

ADAS-Cog Score Prediction for ADNI PET Data: the selected slides of the PC1 direction image (positive elements in Panel (A) and negative elements in Panel (B)) and those of the PC5 direction image (positive elements in Panel (C) and negative elements in Panel (D)) obtained from MWPCR.

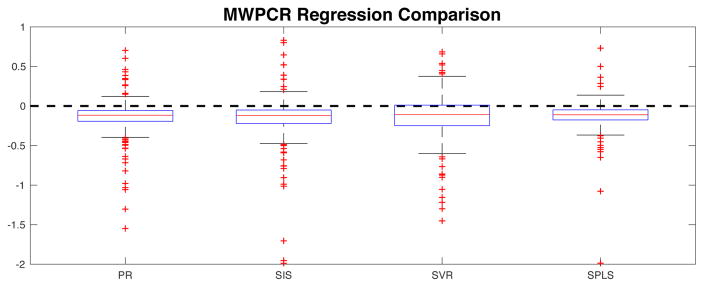
Finally, we compare MWPCR with four other high-dimensional regression methods including penalized regression (PR) (Tibshirani, 1996), sure independence screening (SIS) regression (Fan and Lv, 2008), support vector regression (SVR) (Basak et al., 2007), and SPLS (Chun and Keles, 2010). Figure 11 shows the boxplots of the prediction error differences between MWPCR and all the other regression methods, indicating that MWPCR outperforms all other regression methods.

Figure 11.

ADAS-Cog score prediction for ADNI PET Data: comparison of MWPCR with the four other regression methods, including PR, SIS, SVR and SPLS.

5 Discussion

We have developed a general MWPCR framework for the use of high-dimensional data on graph to predict a low-dimensional response. MWPCR enables an efficient and selective treatment of individual features, accommodates the complex dependence among features, and has the ability of utilizing the underlying spatial pattern possessed by image data. MWPCR integrates feature selection, smoothing, and feature extraction in a single framework. In the simulation studies and real data analyses, MWPCR shows substantial improvement over many state-of-the-art methods for high-dimensional problems. Moreover, both theoretically and numerically, we have demonstrated the importance of using both importance score weights and spatial weights in prediction problems.